Concept Lattice Simplification in Formal Concept Analysis Using Attribute Clustering

Abstract

In Formal Concept Analysis (FCA), a concept lattice graphically portrays the underlying relationships between the objects and attributes of an information system. One of the key complexity problems of concept lattices lies in extracting the useful information. The unorganized nature of attributes in huge contexts often does not yield an informative lattice in FCA. Moreover, understanding the collective relationships between attributes and objects in a larger many valued context is more complicated. In this paper, we introduce a novel approach for deducing a smaller and meaningful concept lattice from which excerpts of concepts can be inferred. In existing attribute-based concept lattice reduction methods for FCA, mostly either the attribute size or the context size is reduced. Our approach involves in organizing the attributes into clusters using their structural similarities and dissimilarities, which is commonly known as attribute clustering, to produce a derived context. We have observed that the deduced concept lattice inherits the structural relationship of the original one. Furthermore, we have mathematically proved that a unique surjective inclusion mapping from the original lattice to the deduced one exists.

1 Introduction

Formal Concept Analysis (FCA) has emerged as a key tool in data analysis and knowledge processing (Ganter and Wille 1999; Carpineto and Romano 2004; Priss 2006). It creates a hierarchical order of concepts in which each concept is comprised of two items—the extent and the intent. This hierarchical order of sets forms a poset (partially ordered set), which can be represented by means of a lattice diagram. FCA focuses on obtaining two forms of outputs from any information system. The first one is a concept lattice, which is a poset of certain clusters of objects and attributes. The second one is a set of formulas known as attribute implications, which describe attribute dependencies that exist in the information system. FCA has been established to have wide range of applications in any knowledge discovery system. Some of the areas of its applications include artificial intelligence, decision-making systems, gene expression data analysis, information retrieval, ontology design, fault diagnosis, software code analysis, expert systems, and so on (Carpineto and Romano 1996; Sumangali and Kumar 2014, 2013; Kumar and Sumangali 2012; Kumar et al. 2015). In Li et al. (2015), the authors analyzed the cognitive mechanism of framing concepts from the principles of philosophy and psychology. Recently, Poelmans et al. presented a detailed survey on the applications of FCA in Poelmans et al. (2013). The generalization of the formalism of FCA determines the best patterns in pattern mining (Buzmakov et al. 2015).

FCA also has few short falls. FCA often produces a large number of formal concepts in the case of huge contexts, and this was pointed out as an open problem at ICFCA 2006 for the first time. Furthermore, the independent treatment of attributes yields much bigger and more complicated concept lattices (Carpineto and Romano 1996; Kumar 2011; Kumar and Srinivas 2010; Wu et al. 2009; Elloumi et al. 2004), and it is very difficult for the users to explore the truly relevant aspects from such lattices. So, after the formation of concept lattices, a prime task is to determine a minimal concept lattice that can avoid redundancy and at the same time maintain structural consistency. To this end, we aim at grouping the attributes by their structural similarities and then modify the context into a simplified form. Since the attributes are interrelated by nature, it is clear that the grouping (clustering) of attributes can play a useful role in the process of knowledge extraction.

Clustering is a common approach by which a dataset is partitioned into groups of similar items. Cluster analysis has been used as an effective tool in extracting the data in various domains of knowledge mining (Han and Kamber 2006). It is an unsupervised grouping of patterns obtained from observations, data collections, and attributes into sets (groups). In general, this type of clustering is performed on the group of objects. However, in order to achieve our aim we process the clustering on the attributes of the context. Standard clustering methods restrain the clusters to be mutually exclusive and exhaustive, implying that each item of the set is subsumed in exactly one of the clusters.

Researchers have handled the clustering techniques effectively in FCA environments too (Kumar and Srinivas 2010). Tversky (1977) used conceptual clustering based on numerical data in his human psychology analysis. The clustering method was used by Wen et al. (Wen et al. 2010) to reduce the size of the interval concept lattices based on the similarity threshold of the distance measure of concepts. Elloumi et al. (2004) used the clustering technique in FCA under a fuzzy environment to reduce the context size using association rules such that the resulting context retains the association rules. Kumar and Srinivas (2010) used the fuzzy k-means clustering technique in order to reduce the size of the concept lattice. Martin et al. (2013) proposed the clustering approach to measure the changes in fuzzy concept lattices under different fuzzy environments of same context.

2 Motivation

Next, we will explain the necessity for the need of a new methodology on the extraction procedure of knowledge discovery in bigger concept lattices. We list some of the drawbacks of the existing methods of knowledge extraction process from the literature.

Liu et al. (2007) carried out a rough set-based concept lattice reduction method in using discernibility functions. In this method, some features and objects of the original context are entirely neglected. In Kumar (2011), a random projection-based reduction technique for FCA was experimented with using a healthcare dataset in which the dimensionality of the context was reduced using expert rules. However, the analysis was for the discovery of rules and did not extract the concept lattices.

Another clustering method presented in Stumme et al. (2002) only focused on the abstraction of the concepts located at the peak of the concept lattice of a large database system, neglecting the concepts at the bottom and middle of the concept lattice. Thus, the information retrieved was not with full entity. Large concept lattice was browsed into simplified trees in Melo et al. (2013) and were then reduced with fault tolerance and conceptual clustering methods. It extracts and visualizes large concept lattices into simplified trees and thereby, the hierarchical structure of the lattice is dismantled.

Thus, the existing methods for concept lattice reduction lack the information in view of the factors listed below.

• 1. Very few methods deal with MV contexts and several methods are only applicable for rough/fuzzy contexts.

• 2. Some of the methods are aimed at the reduction of rules by which lattice reduction is not possible (Dias and Vieira 2010).

• 3. In some other methods, few sub contexts and concepts are neglected using some criterion and thereby the entity of the contexts/concept lattices lags (Stumme et al. 2002).

• 4. In several methods, the preservation of the original lattice in the reduced lattice is not discussed/validated mathematically (Kumar and Srinivas 2010).

Our proposed method for extracting knowledge from concept lattices by means of attribute clustering aims to address these issues.

In the process of simplification techniques it is very important to validate the structure preservation of concept lattices due to the modified closure operators (Dias and Vieira 2015). To this end, concept stability and support measures, concept independence and concept probability measures are used to prune the concept lattices. The notion of inclusion related measures, namely the zeta function and degrees of inclusion, already exist in Xu et al. (2002); Mi et al. (2008); Knuth (2007). But such measures are dealt with in the concepts of a single lattice, and there are no such appropriate measures available for studying the inclusion of concepts of between two different lattices. Since there is a need for such comparisons, in our proposed work we define and use the concept inclusion map zeta ($\zeta$) to validate the experimental results. We compare the original concept lattice with the deduced one mathematically to ascertain the inclusion relationship between them using the concept inclusion map zeta. It has been established that the zeta ($\zeta$) map is a surjective homomorphism from the original lattice to the deduced one.

We organize our work as follows: in Sect. 3, we focus few basic terminologies related to FCA, and introduce some terms and notions related to our proposed work. We also discuss a few properties of the notions introduced. The background of the proposed work is outlined. Further, we outline some preliminaries about attribute clustering and our approach to using them in our proposed work. Next, we present the proposed work in a detailed manner and mathematically simplify the original lattice. In Sect. 4, we illustrate the proposed work via real life context. Finally, we conclude this article by presenting the possible extensions and scope of our proposed method.

3 Preliminaries

FCA is a mathematical model that was introduced by R. Wille (Ganter and Wille 1999) to formalize the notion of a concept. It is comprised of certain units of elements called concepts, wherein each concept subsumes two parts—extension and intension. The study of FCA begins with the organization of a context into a formal context.

3.1 Basic notions of concepts and concept hierarchies

The collection of data in the form of a table is the first step towards the study of FCA and the data table is called a (formal) context. Crosses and blank spaces denote the presence or absence of a relationship between objects and attributes. Let G be the set of objects and M be the set of attributes and $I \subseteq G \times M$ be the incidence relation between G and M. Then, the triple ($G,M,I$) is referred to as a context, which is denoted by K. An object $g \in G$, possessing an attribute $m \in M$ is given by $(g,m) \in I$ or gIm, and we say that the object g has the attribute m.

For $A \subseteq G$ and $B \subseteq M$, we define:

$A^{\prime}=\left\{ {m \in M\,\left| {g\,I\,m,\,\forall g \in A} \right.} \right\}$ (i.e., the set of attributes common to the objects in A)

$B^{\prime}=\left\{ {g \in G\,\left| {g\,I\,m,\,\forall m \in B} \right.} \right\}$ (i.e., the set of objects that have all attributes in B)

If $A \subseteq G$ and $B \subseteq M$, such that $A^{\prime}=B$ and $B^{\prime}=A$ for the context (G, M, I), then the pair (A, B) is called a concept and A, B are said to be the extent and intent of the concept (A, B), respectively. Thus, the intent and the extent are the identities of a concept. The set of all objects belonging to the concept constitutes the extent; whereas the intent constitutes the set of all attributes that are shared by the objects.

3.2 Many-valued contexts and conceptual scaling

Features or attributes whose values are numerous in nature, such as weight, size, score, gender, etc., distinguishes several objects in real life. Such attributes are known as many-valued attributes. Contexts with general attributes are efficiently handled by the many-valued (MV) context representation scheme in FCA. Unlike one-valued contexts, concept lattices cannot be directly derived for MV contexts. For this reason, a MV context is converted into a one-valued context using the conversion process known as conceptual scaling which is user specified one (Ganter and Wille 1999).

In literature we can find several research articles focusing on MV contexts. It was first studied by Messai et al. (2008). They found that concept lattices derived from MV contexts have higher precision levels forming a multi-level concept lattice. In order to retrieve efficient information from complex queries, the use of MV context techniques will be more fruitful.

The remainder of this section focuses some basic terminologies and notions so that the article may be fully self-contained. A brief foundation on FCA can be found in (Sumangali and Kumar 2017). Definitions 1–6 exist in Ganter and Wille (1999), while Definitions 7–9 are introduced in this paper in order to mathematically substantiate the proposed work.

Definition 1a

(Join and Meet) Let $(L, \leq )$ be a partially ordered set and let S be its subset $(S \subseteq L)$. An upper bound of S is an element $x \in S$ such that $s \leq x$ for all $s \in S$. Dually, a lower bound of S is an element $y \in S$ such that $y \leq s$ for all $s \in S$. A smallest element amongst the set of all upper bounds of S is called the supremum or least upper bound of S and is denoted by $\vee S$. Dually, the greatest element amongst the lower bounds of S is called the infimum or greatest lower bound of S and is denoted by $\wedge S$. If $S=\{ x,y\}$, we write simply $x \vee y$ instead of $\vee S$ and $x \wedge y$ instead of $\wedge S$. The terms supremum and infimum are also referred to as join and meet respectively.

Definition 1b

(Lattice) A poset $(L, \leq )$ is called a lattice, if $\forall a,b \in L,\,\,a \vee b$ and $a \wedge b$ exist in L. In other words, join and meet operations exist for any two elements of the poset L. If every subset of L has both infimum and supremum, then L is called a complete lattice.

Definition 2

(Context) A triple K = (G, M, I) is called a formal context, if G and M are non-empty sets of objects and attributes, respectively, and $I \subseteq G \times M$ is the incidence (binary) relation between G and M.

Definition 3

(Many-valued context) A many-valued (MV) context $(G,M,W,I)$ is comprised of sets of objects G, attributes M, attribute values W together with a ternary relation/between G and M, W.

In other words, $I \subseteq G \times M \times W$, wherein $(G,M,W)\, \in I$ and $(g,m,v)\, \in I$ imply w = v. By$(g,m,w)\, \in I$, we mean ‘for the object g, the attribute m possesses the value w’. If $W$contains n elements, then the quadruple $(G,M,W)\, \in I$ is called an n-valued context. Every MV attribute is a partial map $m:G \to W$ such that $m(g)=w$.

Definition 4

(Concept) Let (G, M, I) be a formal context, then for any $A \subseteq G$ and $B \subseteq M$, the pair (A, B) is called a formal concept, if $A^{\prime}=B$ and $B^{\prime}=A$. The sets A and B are respectively known as the extent and the intent. $A^{\prime}$ and $B^{\prime}$ are the concept-forming operators (Carpineto and Romano 2004). The set of all concepts (A, B) of a context (G, M, I) forms a complete lattice and is denoted by B(G, M, I) or B(K).

Definition 5

(Conceptual hierarchy) Let (G, M, I) be the set of all concepts.

For any two concepts $({A_1},{B_1}),({A_2},{B_2}) \in {\text{B}}$, the sub-super concept relation ‘$\leq$’ is defined as follows: $\left( {{A_1},{B_1}} \right) \leq \left( {{A_2},{B_2}} \right) \Leftrightarrow {A_1} \subseteq {A_2}\,or\,{B_1} \supseteq B{}_{2}$. The lower concept is called the subconcept while the upper one is called the super concept.

Definition 6

(Lattice homomorphism) Let L₁, L₂ be two lattices. A map $f:{L_1} \to {L_2}$ is said to be a lattice homomorphism if ‘f’ preserves join and meet operations i.e. $\forall a,b \in L\;f(a \wedge b)=f(a) \wedge f(b)$ and $f(a \vee b)=f(a) \vee f(b)$ .

Definition 7

(Concept inclusion) For any two concepts ${l_1},\,{l_2}$ from different concept lattices we say that ${l_1}$ is contained in ${l_2}$ if both the extent and the intent of ${l_1}$ are contained respectively in those of ${l_2}$ and we denote ${l_1} \subseteq {l_2}$. In other words, for ${l_1}=(A,B) \in {L_1}$ and ${l_2}=(A^{\prime},B^{\prime}) \in {L_2}$, ${l_1} \subseteq {l_2}$if and only if $A \subseteq A^{\prime}$ and$B \subseteq B^{\prime}$.

Definition 8

(Cluster context) Let M be the set of all attributes and let $\Pi (M)$ denote the set of all partitions of the set M. For any partition $N \in \Pi (M)$, let B (G, N, J) denote the concept lattice corresponding to the context (G, N, J) in which $J \subseteq G \times N$ such that for any object $g \in G$, and, $N^{\prime} \in N,\,\,(g,N^{\prime}) \in J$if and only if there exists an attribute $m \in M$such that $(g,m) \in I$and $m \in N^{\prime}$. It can also be denoted as $gJN^{\prime}$. We call the context (G, N, J) thus formed a cluster context.

Definition 9

(Zeta ($\zeta$) map) Let L₁ = B (G, M, I) and L₂ = B (G, N, J). We define the concept inclusion map $\zeta$ from L₁ to L₂ as follows:

$\zeta :{L_1} \to {L_2}$ is a mapping from the lattice L₁ to the lattice L₂ such that for any two concepts${l_1}=(A,B) \in {L_1}$ and ${l_2}=(A^{\prime},B^{\prime}) \in {L_2}$, $\zeta ({l_1})={l_2}$ if and only if ${l_1} \subseteq {l_2}$ and there exists no other concept ${l_k} \in {L_2}$ such that ${l_k} \leq {l_2}$and ${l_1} \subseteq {l_k}$ where the relations $\leq$ and $\subseteq$ are the usual partial ordering and concept inclusion respectively.

In Sect. 3.7, we prove that the map $\zeta$ is well defined, which enabled us to prove the mathematical foundations of our proposed work.

3.3 Background on simplification techniques in FCA

The huge context available in nature often yields a complicated concept lattice, which is difficult to understand in terms of magnitude and underlying relationships without losing relevant information. Since the crucial problem of the concept lattice is often deemed to be its complexity in terms of size, structural hierarchy, underlying information, etc., several methods with various characteristics have been suggested in literature for concept lattice reduction. Dias and Vieira have classified and analyzed the types of concept lattice reduction techniques (Dias and Vieira 2015).

In some of these methods, the redundant information is removed from the concept lattice. Generally, the reduction methods focus on finding the relevant set of objects or attributes that can maintain the structure of the original lattice and keep it unaltered (Medina 2012). Ganter and Wille (1999) obtained the clarified context by removing reducible objects and attributes, and the resulting concept lattice preserves the isomorphism with the original one. Extending FCA onto decision-based contexts, rough set oriented approaches unravel redundant knowledge from any information system. Attribute reduction in the three frameworks of formal, object-oriented, and property-oriented concept lattices were studied by Medina (2012). Irrespective of the frameworks, it has been found that attributes can be classified into three levels of necessity and in any level the attribute reducts are identical.

The next class of reduction methods attempts to construct a summary of the concept lattices. In these methods, the researchers sought to attain a high level of simplification that unravels really important aspects (Belohlavek and Vychodil 2009; Aswani Kumar and Srinivas 2010). Since our proposed work in this paper is a simplification related technique on lattice reduction, we will elaborate on this discussion a little. By shrinking the number of concepts from a bigger concept lattice, simplification techniques have more utility than the previous ones. These methods are an abstraction of the concept lattice. In other words, they seek a broad overview of the lattice that only preserves important facets.

In some other simplification techniques, various levels of granularity (scales) are set on the attributes (Belohlávek and Sklenář 2005a, b). The granularity of an attribute increases with multi-valued attributes. Increasing or decreasing an attribute’s level of granularity can adjust its importance. The three-way decisions (acceptance, rejection, non-commitment) theory has been introduced recently in FCA. Li et al. (2017) have proposed an axiomatic approach to generalize three-way concept learning via granular computing. The reduction of incidence relations from the formal context also controls the complexity of the concept lattice. The use of background knowledge in the simplification process of reduction techniques of FCA is another familiar approach in literature. Such techniques can be found from (Belohlavek and Vychodil 2009; Belohlavek and Macko 2011; Cheung and Vogel 2005; Dias and Vieira 2010). Dias and Vieira (2010) introduced junction-based on object similarity (JBOS) method that utilizes the background knowledge in order to replace similar objects with representative elements using attribute similarity.

Next we will discuss matrix related simplification techniques. A dimensionally bigger matrix can be projected to a smaller dimensional matrix by the Singular Value Decomposition (SVD) method in linear algebra. Cheung and Vogel (2005) reduced the dimensionality of the concept lattice using the equivalence classes of objects in the process of information retrieval in which the SVD matrix reduction technique was adopted. Ch et al. (2015) addressed the issue of knowledge reduction in FCA, based on the non-negative matrix factorization (NMF) of the original context matrix. Kumar and Srinivas (2010) developed the fuzzy k-means algorithm, which is an extension of the existing k-means algorithm. In the fuzzy k-means algorithm, objects are clustered. The members of a cluster are bonded with the cluster by their membership values and any object may belong to more than one cluster. Fuzzy conceptual clustering method has been adopted in (Quan et al. 2004) to generate automatic concept hierarchy on uncertain data. Some more interesting investigations/methods under fuzzy FCA and crisp FCA environment for concept/lattice reduction can be found in (Sumangali et al. 2017, Kauer and Krupka 2014, Kumar 2012).

Another class of reduction methods works by the selection of formal concepts, objects, or attributes through applicable principles or standards (Stumme et al. 2002; Sumangali and Kumar 2014). Belohlávek and Sklenář (2005a, b) proposed a method that reduces the number of concepts using certain constraints, which are derived from attribute dependency formulas (ADFs) that are additionally inputted along with the formal context. The set of concepts, which are compatible with the given set of ADFs, are reduced as important concepts. Another concept selection method using weights on attributes is proposed in (Belohlavek and Macko 2011). An attribute priority-based background knowledge method was carried out in (Belohlavek and Vychodil 2009) for concept reduction.

3.4 Attribute clustering

Attribute clustering is a method of grouping attributes that are correlated or interrelated with each other (Au et al. 2005). The attributes within a cluster are more correlated themselves, whereas attributes from different clusters are less correlated. Use of attribute clustering can minimize the search dimension of the data-mining algorithm. Each cluster consists of a unique centroid, which possesses more common properties of the attributes within the cluster. Researchers mostly predefine the number of required clusters (Pham et al. 2005; Han and Kamber 2006).

The use of clustering related techniques in the process of simplification are available in literature. Jain, Murty, and Flynn (1999) have presented an overview of clustering techniques using statistical pattern recognition techniques. According to them, basic steps in the process of clustering are: (1) data representation, (2) similarity measures, (3) grouping, and (4) cluster representation. Furthermore, they have identified a few areas, such as information retrieval, object and character recognition, image segmentation, and data mining, as applicable areas of clustering techniques. Clustering techniques can be adopted with sets of objects or attributes or formal concepts. The clustering technique was already adopted in the FCA environment with incomplete contexts. Li et al. (2016) to compress a concept lattice by choosing median concepts that are centrally located.

Very few papers deal with attribute clustering-based reduction techniques in literature. Attribute clustering techniques has been utilized in the rough set background for the computation of reducts (Janusz and Slezak 2012). Belohlavek et al. (2005) presented a method for the reduction of concepts in FCA using clustering techniques. However, the partition is only carried out on objects.

There are several clustering techniques available in the literature. Among them k-means, hierarchical, DB Scan, OPTICS, and STING are a few of the popular clustering techniques (Han and Kamber 2006). The proximity measures are explicitly or implicitly used in almost all clustering techniques (Xu and Wunsch 2005). Since the comparison of the quality of the clusters produced by the above techniques is a difficult task in the study of FCA, sometimes these clustering techniques may not be appropriate. Furthermore, developing a suitable measure of comparison for determining the quality of the clusters remains a daunted task, as the clusters do not exhibit the entire set of relationships among the objects/attributes. To obviate this shortcoming we have proposed attribute clustering based on the well-known notions of similarity measures. Additionally, such clustering techniques do not require any validation, since the validation measures are similarity measures themselves. The proximity of data in the process of data mining is often measured using similarity/distance related measures. In keeping with this, Jaccard coefficients of similarity and distance measures are widely used (Han and Kamber 2006).

Euclidean or related distance measures cannot be applied to measure the distances between the attributes in the case of binary, categorical, ordinal, or mixed attributes. So, the distance measure is revised by the notion of dissimilarity between attributes/objects (Han and Kamber 2006). Usually the distance measures are performed on the set of objects and the the clustering techniques are only performed on the set of objects. But, in order to achieve our aim, we use these measures on the set of attributes.

The distance between any two attributes can be easily calculated by the use of a contingency table (Han and Kamber 2006) in the case of binary natured attributes. A binary attribute is symmetric if both of its states are equally important; otherwise it is an asymmetric binary attribute. In the case of binary attributes, the distance measure varies depending on their symmetricity. The binary states 1 and 0 respectively denote the presence or absence of the corresponding attribute. Further, the cardinalities given in the cells of the contingency table denote the number of objects with stated properties. The measure that is used the most often on the similarity between the objects or attributes is the Jaccard index or the Jaccard similarity coefficient.

A sample contingency table for binary data is shown in Table 1.

Table 1 Contingency table for binary data

Using the contingency table shown in Table 1, the Jaccard index between two attributes/objects can be stated briefly as:

$$J(i,j)=\frac{q}{{q+r+s}}$$

(1)

In a similar manner, the distance between two attributes/objects is measured using the formula:

$$d(i,j)=\frac{{r+s}}{{q+r+s+t}}$$

(2)

Clearly, the distance measure is metric by nature and the range of these two measures lies between 0 and 1. (i.e., $0 \leq J(i,j),\,d(i,j) \leq 1)$.

3.5 Proposed method

We organize our proposed method as follows: During initialization first we obtain the original information system. In the case of numerical data, it can be transformed into a categorical (many-valued) context. We then determine its formal concepts and thereby its concept lattice. We use the clustering measures viz., Jaccard index and distance measure in the process of attribute clustering, which were used, respectively, to determine the centroids of clusters and to group the attributes. After framing the attribute clusters we form the cluster context (G, N, J), where $N \in \Pi (M)$ and $\Pi (M)$ denote the set of all partitions of the set M, respectively, derived from the original one. In this cluster context, the objects remain the same while the attributes are the newly formed clusters. In the formation of the cluster context, we adopt the union principle to determine the presence or absence of features of a cluster for an object. In other words, any object is considered to be present in a particular cluster if it possesses at least any one of the attributes of the cluster. We infer that this derived cluster context was also a clarified context (Ganter and Wille 1999). The context that was derived was analyzed to yield a concept lattice. Furthermore, we mathematically prove that the extracted concept lattice preserves the original lattice of the given context using the concept inclusion map zeta. We analyze few properties of the concept inclusion $(\zeta )$map to substantiate the conclusion that the extracted concept lattice is the core information system. The entire procedure for our proposed method can be systematically carried out according to the following steps:

Step 1: Initialization: (a) Input many-valued context, (b) transform formal context, (c) obtain formal concepts, (d) obtain concept lattice

Step 2: Attribute clustering

• a. Centroids selection

  • i. Compute the Jaccard similarity coefficient matrix for the given attributes.

  • ii. Predefine the number of clusters and accordingly select an equal number of centroids from the attributes that have a higher average Jaccard coefficient.

• b. Clustering of attributes

  • i. Compute the distance matrix for the given attributes.

  • ii. Choose each non-centroid attribute row-wise and group it with the centroid that has the lowest value than other centroids in the distance matrix.

Step 3: Cluster context: Form the cluster context (G, N, J), where$N \in \Pi (M)$ and $\Pi (M)$ denotes the set of all partitions of the set M. (refer to Definition 8 in Sect. 3.)

Step 4: Concept lattice: Obtain the lattice B(G, N, J).

Step 5: Mapping: Map the concepts of the original lattice to the simplified lattice using the concept inclusion map zeta $\zeta$ (refer to Sect. 4).

Step 6: Output assessment: Analyze the extraction of concepts from the resulting lattice with those of the original lattice using concept comparison measures (refer to Sect. 4).

Now we will look at the computational aspects of our proposed method. Kumar and Srinivas pointed out that the computational cost of reduction techniques using algebraic methods remains high (Kumar and Srinivas 2010). The generation of all concepts and their hierarchical classification exhibits exponential behavior in the worst case (Kuznetsov 2001). In our proposed method, we compute the two symmetric matrices on the proximity measure whose complexity is $\frac{1}{2}O({m^2})$, where each totals $O({m^2})$ and where m is the number of attributes. The computation of the average Jaccard measure yields the complexity measure as $O(m)$. The selection of centroids gives the complexity measure as $O(m\log m)$, and when in the process of grouping the attributes into clusters it is $O({m^2})$. On the whole, the total complexity is obtained as $O({m^2})$.

3.6 Experimental analysis

In this section we demonstrate the proposed method using two examples. To be exhaustive in the demonstration, we consider a numerical context. This is often useful to analyze the interrelationship between various attributes or between groups of attributes. For instance, in the post-examination result analysis of students from a class, we may be interested to know the interrelationship between the mark ranges of different subjects in an examination. In such cases, the clustering of categorical attributes can portray this situation. As such, we cluster the attributes before scrutinizing under FCA. Usually FCA-based analysis concentrates on the hierarchical relationship between individual attributes, whereas the FCA produced after the clustering of attributes depicts the hierarchical relationship between more similar sets of attributes.

Example 1

In the first example we consider the following information system (Agarwal 2009) of the examination scores obtained by ten students in three different subjects as shown in Table 2. In order to analyze this MV context using FCA, one may be aware that this context must be transformed into a formal context. As such, we transform it into a formal context by covering the numerical values of each attribute over several ranges.

Table 2 Many-valued context for student marks data

Though the result analyzer may prefer his/her own split up of ranges for each attribute, we split the range of numerical values into three ranges, in order to be simple and uniform, and it resulted in a formal context, as shown in Table 3.

Table 3 Formal context transformed from student data Table 2

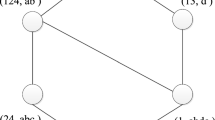
The set of all concepts of the context presented in Table 3 were determined to be as shown in Table 4 using the next closure algorithm (Carpineto and Romano 2004). With the help of the ConExp tool (http://sourceforgenet/projects/conexp), the above set of all of the concepts form a complete lattice under the partial order relation ≤, as shown in Fig. 1. Even though there are only 24 concepts, the information they provide may not be interesting or useful for the result analyzer. For instance, the analyzer may want to know the interrelationship in various ranges of marks between different subjects.

Table 4 Set of all concepts derived from a formal context of Table 3

Fig. 1

Concept lattice for the formal context of Table 3

This can help the teacher or analyzer to identify the potentials and flaws of a group of students falling in a cluster. The result analysis on individual students performed subject-wise may not yield good reasons about the individual’s status, whereas cluster-based analysis can bring effective results in identifying the students’ problems. He/she may also want to identify the overall levels of students and may want to train the weaker students in many subjects by using the overall brighter students. In such cases it is necessary to identify the interrelated score ranges between different subjects. For this purpose, we cluster the attributes of the MV context.

In the clustering process, we first identify the centroids of the clusters. In each cluster, an attribute more similar to the remaining attributes can better serve as a centroid. Hence, we select the attributes that have, on average, high similarity measure as the centroids of the clusters. Thus, the Jaccard index is more optimal for the selection of the centroids. The Jaccard index of attributes for the given context is computed as shown in Table 5 using Eq. (1).

Table 5 Similarity Jaccard coefficient

For the selection of k, the number of clusters is usually defined by the user (Han and Kamber 2006). Though the selection of k can be exclusively discussed as done in (Pham et al. 2005), we limit our scope by excluding such discussions and assumed k to be the user’s choice. We deem it reasonable to consider the number of clusters as three. We then proceed to select the centroids of the clusters. Attributes with a high Jaccard coefficient average become centroids. Note that for each attribute the average measure is computed over the number of non-zero measures. The computations are presented in Table 6. Whenever there is a tie in the average Jaccard coefficient of attributes, centroids can be selected randomly from all of them or sometimes some of them if the constraint on the number of clusters is reached. In our example, the centroids were E1, P3, and M1. Though the categorical attributes E3 and P3 had the same average Jaccard index, we prefer P3, since the previously selected centroid E1 and E3 both fall within the attribute of “English.” Yet, it is left to the user to choose.

Table 6 Computation of average Jaccard coefficient

After having selected the centroids of the clusters, the next process is to cluster the remaining attributes with the centroids. In order to do this, we determine the binary distance matrix of the attributes, which was symmetric, as shown in Table 7 using Eq. (2). We start with the centroids of the clusters. Each of the remaining attributes was added to the cluster whose centroid was closer than other centroids. In case of a tie, (i.e., if two or more centroids are equidistant from the attribute) the attribute can be grouped into any one of the clusters whose centroids are equidistant from it. Thus, the attributes of the given context are clustered as shown below. The first member in cluster denotes its centroid.

Table 7 Distance matrix derived from Table 3 using Table 1

Cluster1: E1, P2; Cluster2: P3, E2, E3, M2, M3; Cluster3: M1, P1.

Once the clusters were framed, we modify the given context wherein each clusters served as an attribute. For any object, the possession of any attribute (cluster) is determined using the union principle of individual attributes within any particular cluster. We found that the context that was derived was also a clarified context, as shown in Table 8.

Table 8 Example 1- Cluster context (G, N, J) where $N \in \Pi (M)$

The context deduced for the clusters, as presented above, yielded the concept lattice that is shown in Fig. 2. The concept lattice of the derived context for clusters, which is shown below, contains 8 concepts with a height of 3, which are comparatively less than the respective measures of the original lattice that contained 24 concepts with a height of 4. It can be inferred that the lattice structure of the extracted one, as shown in Fig. 2, subsumes the original lattice structure, which is shown in Fig. 1. Furthermore, the extracted lattice in this case is a complemented, distributive lattice, which makes it Boolean algebra. In Sect. 3.7, we mathematically prove these inheritance properties using the concept inclusion map zeta (defined in Sect. 3), from the original lattice to the extracted lattice.

Fig. 2

Simplified concept lattice derived from context Table 8

Example 2

We next consider a many-valued information system on drive concepts for motorcars dealt in (Ganter and Wille 1999) to implement our method on lattice simplification and analyze the results.

Table 9 A many-valued context: Drive concepts for motorcars (Ganter and Wille 1999)

The above context Table 9 can be transformed into a one-valued context in FCA using conceptual scaling as shown in Table 10. The attributes are abbreviated according to the list presented below the table. The derived context contains 5 objects and 25 attributes, which is comparatively bigger than the context dealt in previous example. The concept lattice of the context Table 10 contains 26 concepts and the same is presented in the Fig. 3.

Table 10 A derived one-valued context for motorcars

Fig. 3

Concept lattice derived from context Table 10

The transformed context produced 24 concepts. In the lattice structure, they are numbered from bottom to top and left to right. For brevity, the labels of the extreme concepts only are shown in the Fig. 3. In view of the conciseness of the work we omit the interpretations on the inherited concepts and their units viz, intents and extents. In the process of concept lattice simplification we next compute the two proximity measures discussed earlier. The matrix representation of these measures require a square matrix of order 25. Since they can be found as in the previous example, we do not present them for brevity reasons. We fix the number of clusters to be six. We select six attributes as centroids from the high valued Jaccard coefficients.

The remaining attributes are clustered to the nearest centroid using distance measure. The following Table 11, lists the six attribute clusters row-wise with each cluster starting with its centroid.

Table 11 Attribute clusters of the given context example 2

After framing the clusters we determine the cluster context using the union principle discussed earlier and the same is presented in Table 12.

Table 12 Example 2- Cluster context (G, N, J) where $N \in \Pi (M)$

Finally, the simplified concept lattice is determined and the same is presented in Fig. 4. The simplified concept lattice contains 12 concepts and it preserves the structure of the original concept lattice.

Fig. 4

Simplified concept lattice derived from context Table 12

3.7 Mathematical results: concept inclusion map zeta for validation

In this section we demonstrate some of the algebraic properties of the concept inclusion map, zeta$\zeta$. To this end, throughout this section we let L = B (G, M, I) and $L^{\prime}$ = B (G, N, J). (For further clarification on these notions, readers may refer to Sect. 3.)

Theorem 1

The map $\zeta :L \to L^{\prime}$ defined in Sect. 3is well defined.

Proof

Let $l=\left( {A,B} \right) \in L$ be arbitrary.

For any $l^{\prime}=\left( {A^{\prime},B^{\prime}} \right) \in L^{\prime}$, we know that $A^{\prime}$ and $B^{\prime}$are the set of extents and intents in the cluster (partition) context, respectively. In particular, $B^{\prime}$ is the union of attributes from one or more set of clusters. This implies that for any intent $B \subseteq M$ of the original concept lattice $L$, there exists some intent $B^{\prime} \subseteq M$ in the cluster concept lattice $L^{\prime}$ such that $B \subseteq B^{\prime}$. Since$B \subseteq B^{\prime}$, and the union principle is adopted in the formation of cluster context (G, N, J), (see Definition 7 in Sect. 3) we must have $A \subseteq A^{\prime}$. Therefore, $\left( {A,B} \right) \subseteq \left( {A^{\prime},B^{\prime}} \right)$ (i.e., $l \subseteq {l_{}}^{\prime }$).

Furthermore, without the loss of generality, we can choose$l^{\prime} \in L^{\prime}$, such that $l^{\prime}$is the smallest concept containing $l$, which in turn results as $\zeta \left( l \right)={l_{}}^{\prime }$. The uniqueness of $l^{\prime} \in L^{\prime}$ is clear.

Since $l \in L$ is arbitrary, the map $\zeta$is well defined.

Theorem 2

The map $\zeta :L \to L^{\prime}$ is surjective.

Proof

Let $l^{\prime}=\left( {A^{\prime},B^{\prime}} \right) \in L^{\prime}$ be any concept in $L^{\prime}$. Then, $A^{\prime}$ and $B^{\prime}$ are the extents and intents of some concept in the cluster context (G, N, J). Since attributes are clustered in the context (G, N, J), $B^{\prime}$ contains more attributes than those in the intents of concepts at the same level in the original lattice $L$. Clearly, there must exist some concept $l=\left( {A,B} \right) \in L$ whose intent $B$ is such that $B \subseteq B^{\prime}$. If $B \subseteq B^{\prime}$, obviously, $A \subseteq A^{\prime}$, implying that $l \subseteq {l_{}}^{\prime }$.

Furthermore, suppose that there exists a concept ${l_1}^{\prime }=\left( {{A_1}^{\prime },{B_1}^{\prime }} \right) \in L^{\prime}$ such that $l \subseteq {l_1}^{\prime }$. This implies $A \subseteq {A^{\prime}_1}$ and $B \subseteq {B_1}^{\prime }$.

Suppose that ${l_1}^{\prime }<{l_{}}^{\prime }$. Then $\left( {{A_1}^{\prime },{B_1}^{\prime }} \right) \leq \left( {{A_{}}^{\prime },{B_{}}^{\prime }} \right)$. According to the properties of concept lattices this means that ${A^{\prime}_1} \subseteq A^{\prime}$and ${B_1}^{\prime } \supseteq B^{\prime}$. Since $l \subseteq {l_{}}^{\prime }$, we deduce that $A \subseteq A^{\prime}$ but $B \subseteq {B_1}^{\prime } \supseteq B^{\prime}$. This implies that $B \not\subset B^{\prime}$. This deduction leads to a contradiction of the fact that $l \subseteq {l_{}}^{\prime }$. Thus, the assumption that ${l_1}^{\prime }<{l_{}}^{\prime }$ is wrong. Summarizing our arguments, we state that for any ${l_{}}^{\prime } \in L^{\prime}$, there exists some $l \in L$ such that $l \subseteq {l_{}}^{\prime }$, and there exists no other concept ${l_1}^{\prime } \in L^{\prime}$, such that $l \subseteq {l_1}^{\prime }$ and${l_1}^{\prime }<{l_{}}^{\prime }$. From the definition of the $\zeta$ map we conclude that $\zeta \left( l \right)=l^{\prime}$. Therefore, the map $\zeta :L \to L^{\prime}$ is surjective (onto).

Theorem 3

The zeta map $\zeta :L \to L^{\prime}$ is unique.

Proof

Suppose that there exist two distinct surjective zeta maps ${\zeta _1}$ and ${\zeta _2}$.

Since ${\zeta _1} \ne {\zeta _2}$, there exists some $l \in L$, such that ${\zeta _1}\left( l \right) \ne {\zeta _2}\left( l \right)$.

Let ${\zeta _1}\left( {{l_1}} \right)={l_1}^{\prime }$and ${\zeta _2}\left( l \right)={l_2}^{\prime }$ for some ${l_1}^{\prime },{l_2}^{\prime } \in L^{\prime}$. Clearly, ${l_1}^{\prime } \ne {l_2}^{\prime }$. Since ${l_1}^{\prime },{l_2}^{\prime }$ are the nodes of a lattice, two possibilities arise, either ${l_1}^{\prime }<{l_2}^{\prime }$ or ${l_2}^{\prime }<{l_1}^{\prime }$.

Obviously, $l \subseteq {l_1}^{\prime }$ and ${l_{}} \subseteq {l_2}^{\prime }$.

• i. If ${l_1}^{\prime }<{l_2}^{\prime }$, then since $l \subseteq {l_1}^{\prime }$ and ${l_1}^{\prime }<{l_2}^{\prime }$, the map ${\zeta _2}\left( l \right)={l_2}^{\prime }$ is wrong.

• ii. If ${l_2}^{\prime }<{l_1}^{\prime }$, then since ${l_1} \subseteq {l_2}^{\prime }$ and ${l_2}^{\prime }<{l_1}^{\prime }$, the map ${\zeta _1}\left( {{l_1}} \right)={l_1}^{\prime }$ is wrong.

From (i) and (ii) we can infer that the zeta mapping is unique.

Note: However, the zeta map $\zeta :L \to L^{\prime}$ seems to preserve the homomorphism under the join and meet operations of the lattices $L$ and $L^{\prime}$, it is not so.

As an example, consider the lattice $L$ and $L^{\prime}$, which are given in Figs. 3 and 4 respectively.

Consider the concepts ${l_{14}}$ and ${l_{15}}$ in Fig. 3.

$$\zeta \left( {{l_{14}} \vee {l_{15}}} \right)=\zeta \left( {{l_{20}}} \right)={l_6}^{\prime },\;\zeta \left( {{l_{14}}} \right) \vee \zeta \left( {{l_{15}}} \right)={l_4}^{\prime } \vee {l_6}^{\prime }={l_6}^{\prime }$$

Similarly,

$$\zeta \left( {{l_{14}} \wedge {l_{15}}} \right)=\zeta \left( {{l_5}} \right)={l_4}^{\prime },\;\zeta \left( {{l_{14}}} \right) \wedge \zeta \left( {{l_{15}}} \right)={l_4}^{\prime } \wedge {l_6}^{\prime }={l_4}^{\prime }$$

Whereas, for concepts ${l_{16}}$ and ${l_{17}}$, the homomorphism of the map $\zeta$ is not preserved, as seen below.

$$\zeta \left( {{l_{16}} \vee {l_{17}}} \right)=\zeta \left( {{l_{24}}} \right)={l_8}^{\prime },\;\zeta \left( {{l_{16}}} \right) \vee \zeta \left( {{l_{17}}} \right)={l_2}^{\prime } \vee {l_2}^{\prime }={l_2}^{\prime }$$

$$\zeta \left( {{l_{16}} \wedge {l_{17}}} \right)=\zeta \left( {{l_8}} \right)={l_2}^{\prime },\;\zeta \left( {{l_{16}}} \right) \wedge \zeta \left( {{l_{17}}} \right)={l_2}^{\prime } \wedge {l_2}^{\prime }={l_2}^{\prime }$$

The mathematical Theorem 1 on well definedness of the zeta map strongly establishes the inclusion of the derived concepts from those of original one. The second theorem about the surjective nature of the zeta map concludes that every extracted concept forms a basis for several original concepts. And finally, the uniqueness theorem substantiates that the extraction thus derived is the best and that the procedure cannot be improved anymore. As such, we can conclude that our proposed work is the best method for extraction.

3.8 Quality of structures between original and simplified lattices

In this section, we clarify the extraction of the concepts of the resulting lattice with those of the original lattice.

Under the topic of “morphisms and bonds”, Ganter and Wille (1999) discussed the concept comparison measures between two concept lattices B(K₁) and B(K₂) corresponding to the contexts ${K_1}$ and ${K_2}$.

We used their idea to compare the two concept lattices B (G, M, I) and B (G, N, J) .

In our discussion we have two contexts viz., ${K_1}:=(G,M,I)$ and ${K_2}:=(G,N,J),N \in \Pi (M),$ where the first one is the original context and the next one is the modified cluster context.

For comparison purpose two maps $\alpha :G \to H$ and $\beta :M \to N$ are defined. These maps actually map from the original context to the cluster context. In our proposed method “$\left( {\alpha ,\beta } \right)$” is an identical map $\alpha :G \to G$. The map $\left( {\alpha ,\beta } \right)$maps the extents of ${K_1}$ to those of ${K_2}$. The map $\beta$maps intents in a similar manner.

Consider the map $\alpha :{K_1} \to {K_2}$. The map $\left( {\alpha ,\beta } \right)$ is called “extensionally continuous,” if for every extent “$U$” of ${K_2}$, the pre-image ${\alpha ^{ - 1}}\left( U \right)$ is an extent of ${K_1}$. Furthermore, $\left( {\alpha ,\beta } \right)$ is said to be “extensionally closed,” if the image $\alpha \left( U \right)$ of an extent “$U$” of ${K_1}$ is always an extent of ${K_2}$. The analogous terms of intensionally continuous and intensionally closed can be defined for $\beta$ with respect to the intents of ${K_1}$ and ${K_2}$.

The pair of maps $\left( {\alpha ,\beta } \right):{K_1} \to {K_2}$ will be known as “incidence preserving” if $g\,I\,m \Rightarrow \alpha \left( g \right)J\beta (m)$. (i.e., $g\,I\,m \Rightarrow gJ\beta (m)$).

The pair of maps $\left( {\alpha ,\beta } \right):{K_1} \to {K_2}$ is said to be “continuous” if $\left( {\alpha ,\beta } \right)$ is extensionally continuous and $\beta$ is intensionally continuous. The map pair $\left( {\alpha ,\beta } \right)$ is said to be “concept preserving” if, for every concept $\left( {A,B} \right) \in {\text{B}}({K_1})$, the pair $\left( {\beta \left( {B^{\prime}} \right),\alpha (A)^{\prime}} \right)$ is a concept of ${K_2}$. In our discussion, the pair of maps given by $\left( {\alpha ,\beta } \right)$ is replaced by the concept inclusion map $\zeta :L \to L^{\prime}$ In fact, ${K_1}$ and ${K_2}$ can play the role of $L$ and $L^{\prime}$ without loss of generality.

The concept inclusion zeta map, maps the intents and extents of ${K_1}$ with those of ${K_2}$, respectively. Hence, we find that the map $\zeta :L \to L^{\prime}$ is: (i) extensionally continuous, (ii) extensionally closed, (iii) intensionally continuous, (iv) intensionally closed, and, hence, (v) continuous, (vi) incidence preserving, and (vii) concept preserving, since the $\zeta$ maps every concept in $L$ to a concept in $L^{\prime}$.

Krotzsch et al. (2005) used these terms mentioned above to study the structural properties of available knowledge in a formal context. The extent and intent of a concept not only plays an important role in the process of reduction in FCA, but sometimes they are also used to measure the quality of reduction. In Codocedo et al. (2011), extensional and intensional stability measures are carried out to measure the good quality of the reduced context in the absence of some of the objects and attributes in a large original context.

4 Discussion

This paper has mainly focused on the analysis of the FCA involving the MV context. We classify the attributes categorically and grouped the attributes that had more similar outputs. Then we analyze the interrelationship between these attribute groups.

Generally, the analysis of a MV context in an FCA background is a critical task for arriving at valid decisions. For example, in the analysis of the student mark data above the class teacher may wish to determine the various mark layers of each subject in which many students lie, and he/she may wish to find out the set of common score layers from different subjects. The teacher is now able to identify the group of students who are poor in many subjects, in a few, or on average in the learning platform. Accordingly, the teacher can split the students into a few teams, which may include excellent students who can serve as peer-tutors to train the weaker students in the team. Moreover, one can easily determine whether a student who struggles in one subject struggles in other subjects, and, hence, the teacher can monitor the progress of the students individually and more closely.

In the first example presented, the original lattice of the given MV context contains 24 concepts, which is vague and complex from the decision-making point of view; whereas, the simplified concept lattice contains only 8 concepts, which is easy and clear for any reader to understand and analyze. The set of original concepts that are mapped to a common concept in the extracted lattice is encircled by closed curves, as shown in Fig. 5, and this set of concepts is termed “conceptual clusters”.

Fig. 5

Conceptual clusters obtained from zeta map in example 1

Let us analyze the extraction of concepts by using our proposed method. The concepts of the original lattice are mapped to the simplified lattice using a concept inclusion $\zeta$ map. Obviously, this mapping does not need to be one-to-one mapping. Let there be “n” concepts in the extracted lattice; label them as 1, 2,…, n. We group the concepts in the original lattice, which are mapped to the same i^th concept in the extracted lattice, by the zeta map to form an i^th conceptual cluster. We infer that the extent and intent of each concept in any i^th conceptual cluster is subsumed in the corresponding i^th concept of the extracted lattice. As a result, we realize that there is no loss in the extraction of the concept lattice shown in Fig. 6.

Fig. 6

Simplified lattice obtained out of clusters in example 1

For example, the concepts 6, 7, 8, 16, and 17 from the 2nd conceptual cluster of the original lattice have the following extents and intents in pairs, respectively, ({S7}, {E2, M3, P1}), ({S4},{M2, E3, P1}), ({S8}, {E2, M2, P1}), ({S7, S8}, {E2, P1}), ({S4, S8}, {M2, P1}) and are mapped to the 2nd concept of the extracted lattice with the extent and intent pair ({S4, S7, S8}, {E2, E3, P1, P3, M1, M2, M3}) according to the zeta map. We can easily infer that the extent and the intent of each of these original concepts are subsumed in those of the 2nd concept of the extracted lattice. The same can be verified for any conceptual cluster of the original lattice. The consolidated concept clusters are presented in the Table 13. Thus, the concept inclusion zeta map, maps the concepts from the original lattice to the extracted lattice without a loss of any information in regards to the extents and intents of concepts and, thereby, the zeta map maintains the structure of the original lattice with regard to the hierarchical order of the concept lattice.

Table 13 Concepts and their Clusters

In terms of practical understanding from the original context, we see that the students S4, S7, and S8 possess one or more characteristics either individually or as a group. This generates more concepts in which it is very difficult to perceive any information. By adopting our proposed method, one can more generally arrive at the conclusion that as a group, all of the students S4, S7, and S8, possess most of the characteristics of the item-set E2, E3, P1, P3, M1, M2, and M3. Thus, our proposed method reduces the number of subsets on the intents and extents, and the information is extracted within the minimum number of concepts. As such, the user can arrive at a conclusion more precisely and concisely.

Similarly in the second example presented, the inclusion of concepts from the original lattice can be observed in clusters as in the first example. We leave the same as an exercise to the readers. As a hint we have shown conceptual clusters 6 and 9 from the original concept lattice (Fig. 7) which are mapped using the zeta map to the concept nodes 6 and 9 in the reduced concept lattice (Fig. 8) respectively. The reduced number of concepts can be increased or decreased by enlarging or diminishing the size of the clusters.

Fig. 7

Conceptual clusters obtained from zeta map in example 2

Fig. 8

Simplified lattice obtained out of clusters in example 2

5 Conclusions

We have devised a method to simplify a larger concept lattice derived out from many-valued (MV) contexts using an attribute clustering technique. We found that the resulting lattice maintains the structural consistency and information of the original lattice. In order to validate the simplified concepts, we defined and used the concept inclusion map zeta ($\zeta$). Consequent to the mathematical establishment of its well definition and some of its properties, the logical validity of the method becomes evident. Furthermore, the proposed method is easy to understand and compute. The similarity of the structural morphisms between the original and the simplified concept lattices were established by using measures on morphisms and bonds.