1 Introduction

Granular computing (GrC for short) has become a fast growing field of computational intelligence and human-centric systems (see e.g., [1, 41, 43, 51]). Its purpose is to seek for an approximation scheme which can effectively solve a complex problem at a certain level of granulation. Among others, formal concept analysis [6] represents one concrete model which popularizes GrC. It is a method to derive concept hierarchies from data tables and has proved to be useful in data analysis and knowledge discovery with growing popularity across various domains [7, 11, 12, 22, 30, 40].

In the basic setting of formal concept analysis [6], it is assumed that the input data is in the form of a table containing 0s and 1s describing which attributes apply to which objects. Such an input data is called a formal context, from which one can construct (objects, properties) pairs known as the formal concepts. The collection of all formal concepts forms a complete lattice and is useful for capturing relevant patterns and structure in the input data. However, in the traditional setting of formal concept analysis, the attributes are considered fixed, or in other words, the attributes are always used at a fixed level of granularity. Contrarily, for data sets in the real world, it is a common phenomenon that attributes are measured at different levels of granularity. For instance, when describing when a car accident happened, “before noon” and “after noon” are attributes with high level of granularity while “early morning”,“late evening” are attributes with low level of granularity. If one uses attributes with a higher level of granularity, then the derived concept lattice may not contain interesting formal concepts because the selected attributes are too coarse. If one uses attributes with lower level of granularity, then the derived formal concepts may reveal more detailed information of the input data because the chosen attributes are relatively fine. Therefore, the capability to change the level of granularity of an attribute in formal concept analysis to capture relevant patterns in the input data has become a necessity.

Following the idea of granularity of attributes in formal concept analysis, Bělohlávek et al. [2] proposed a method to control the structure of the derived concepts lattice by specifying granularity levels of attributes. More precisely, if the resulting formal concepts are too specific and there is a large number of them, the user can choose to use a coarser level of granularity. Similarly, if the resulting formal concepts are too coarse and there is a small number of them, the user can choose to use a finer level of granularity. And thus, the proposed method is capable of capturing relevant patterns in data. Recent years have witnessed a growing interests towards this topic [10, 13,14,15,16, 19, 20, 24, 31, 48, 49, 52,53,54]. In [13], a unified model for concept lattice building and rule extraction on a fuzzy granularity base for different granulations was introduced. In [14], information granularity in formal concept analysis based on concept-base was studied in detail. In [16], the relationship between multigranulation rough sets and concept lattices via rule acquisition was investigated. In [24], multi-level granularity in formal concept analysis was studied. In [52], an efficient algorithm was designed to increase the granularity levels of attributes in formal concept analysis. Similar topics have also been investigated in the research filed of data mining and rough set theory [9, 17, 18, 25,26,27, 29, 32,33,34, 40, 42, 50]. In [3], the authors proposed a global AOI (GAOI) method, which employs the multiple-level mining technique with multiple minimum supports to generate all interesting generalized knowledge at one time. The generalization abilities of classifiers were extensively investigated in [37, 38], where the proposed approaches provide some important guidelines as to the improvement of generalization aspects of classifiers. In [39], the authors further proposed a new DL approach to train multi-layer feed-forward neural networks, and the proposed approach has many advantages such as quick training, better generalization, and high understandability, etc. In [35], two interesting diversity criteria, i.e., clustering-based diversity and fuzzy rough set based diversity, were proposed for MIAL by utilizing a support vector machine (SVM) based MIL classifier. In [32], the concept of multi-scale information tables was introduced, and then information granules at different levels of scales in multi-scale information tables were described. To date, different types of approaches to optimal scale selection have been presented [17, 18, 29, 32,33,34, 40]. However, it should be noted that both rough set theory and formal concept analysis have been studied separately regarding the issue of attribute granularity. Since they provide two related methods for data analysis and model the notion of concepts from different perspectives, an integrated study of rough set theory and formal concept analysis has become a necessity. Such an issue has been studied extensively in the context of single-scale formal contexts [4, 5, 8, 21, 23, 28, 36, 44,45,46,47], on the contrary, an integrated study in the context of multi-scale formal contexts has not been conducted yet.

Thus, the main objective of the present paper is to undertake a theoretical study in the context of multi-scale formal contexts, where attributes with different level of granularity possess different attribute values. The rest of the paper proceeds as follows: in order to make the paper as self-contained as possible, we recapitulate in Sect. 2 the definition of formal context, concepts, and the existing approach to granularity of attributes. In Sect. 3, we consider object-oriented concept lattices in multi-scale formal contexts and investigate the relationship between the structure of concept lattices derived at different granularity levels. In Sect. 4, we consider property-oriented concept lattices in multi-scale formal contexts and exhibit a corresponding bidirectional approach to concept construction(i.e., from coarser to finer and from finer to coarser, respectively). And in Sect. 5, we complete this paper with some concluding remarks.

2 Preliminaries

2.1 Context and concept

The basic notions of formal concept analysis are those of a formal context and a formal concept.

Definition 2.1

[6] A formal context \(K=(G,M,I)\) consists of two sets G and M and a relation I between G and M. The elements of G are called objects and the elements of M are called attributes of the context. In order to express that an object g is in a relation I with an attribute m, we write gIm or \((g,m)\in I\) and read it as “the object g has the attribute m”.

Since in a formal context \(K=(G,M,I)\), an object has an attribute or not, that is, the relation between objects and attributes is binary, and so we also call the formal context \(K=(G,M,I)\) a one-valued context.

Definition 2.2

[6] For a set \(A\subseteq G\) of objects we define

$$\begin{aligned} A^{\uparrow }={\{m\in M\mid gIm\,\text {for}\,\text {all}\,g\in A\}} \end{aligned}$$
(1)

(the set of attributes common to the objects in A). Correspondingly, for a set B of attributes we define

$$\begin{aligned} B^{\downarrow }={\{g\in G\mid gIm\,\text {for}\,\text {all}\,m\in B\}} \end{aligned}$$
(2)

(the set of objects which have all attributes in B).

Definition 2.3

[6] A formal concept of the context (G, M, I) is a pair (A, B) with \(A\subseteq G, B\subseteq M, A^{\uparrow }=B, B^{\downarrow }=A.\) We call A the extent and B the intent of the concept (A, B).

2.2 Granularity of attributes in formal concept analysis

As we have seen in Sect. 2.2, in traditional formal concept analysis, the attributes in the formal context are considered fixed. However, for data sets in the real world, attributes always have different levels of granularity, we call such types of formal contexts multi-scale formal contexts in the following discussion.

To facilitate our discussion, some fundamental notions such as granularity tree and cut in [2] are recalled as follows.

Definition 2.4

[2] Let \(K=(G,M,I)\) be a formal context. A granularity tree \(T_{y}\) for attribute y is a rooted tree with the following properties:

\(\bullet \) each node of the tree is labeled by a unique attribute name; the root is labeled by y;

\(\bullet \) to each label z of a node, a set \({\{z\}}^{\downarrow }\subseteq G\) is associated; elements in \({\{z\}}^{\downarrow }\) are the objects to which attribute z applies;

\(\bullet \) if the nodes labeled by \(z_{1},\ldots ,z_{n}\) are the successors of the node labeled by z, then \(\{\{z_{1}\}^{\downarrow },\ldots ,\{z_{n}\}^{\downarrow }\}\) is a partition of \(\{z\}^{\downarrow }\).

In what follows, we use \(z^{\downarrow }\) instead of \({\{z\}}^{\downarrow }\) for simplicity.

Definition 2.5

[2] A cut in a granularity tree for y is a set C of nodes of the granularity tree for y such that for each leaf node u, there exists exactly one node v on the path from the root y to u such that the label of v belongs to C.

The refinement relation induces a partial order on the set of all cuts of a given granularity tree by putting for two cuts \(C_{1}={\{y_{1},\ldots ,y_{r}\}}\) and \(C_{2}={\{z_{1},\ldots ,z_{s}\}}\), \(C_{1}\le C_{2}\) if and only if \(C^{\downarrow }_{1}={\{y_{1}^{\downarrow },\ldots ,y_{r}^{\downarrow }}\}\) is a subpartition of \(C^{\downarrow }_{2}={\{z_{1}^{\downarrow },\ldots ,z_{s}^{\downarrow }\}}\).

Let (G, M, I) be an input data table. Suppose that for each attribute \(m\in M\) we have a granularity tree \(T_{m}\) and for each \(m\in M\), \(C_{m}\) be a cut in \(T_{m}\), the collection of all cuts induces a data table \((G,M_{C},I_{C})\) such that

\(M_{C}=\bigcup _{m\in M}C_{m}\)

and we put for each \(z\in M_{C}\)

\((g,m)\in I_{C}\) if and only if \(g\in m^{\downarrow }\).

Each collection C of cuts represents a particular selection of granularity levels of attributes. Given two granularity levels, represented by \(C_{1}\) and \(C_{2}\), We use \(C_{1}\le C_{2}\) to mean that for each \(m\in M\), \(C_{1m}\le C_{2m}\). In other words, \(C_{1}\) is a refinement of \(C_{2}\).

Example 2.1

Table 1 depicts a multi-scale formal context, where the attribute G has two levels of granularity, \({\{G\}}\) and \({\{IG,dG\}}\) are all cuts in the granularity tree \(T_{G}\). Note that \({\{G,dG\}}\) is not a cut of the granularity tree \(T_{G}\), since there are two nodes on the path from the root G to dG, similar conclusion also holds for \({\{G,IG\}}\).

Table 1 Multi-scale formal contexts describing objects \(a,\ldots ,g\) and their attributes L (large), R (red), G (green), IG (light green), dG (dark green)
Full size table

The following theorem states that if we refine our attributes, then each formal concept in the concept lattice corresponding to the coarser attributes can be split into a partition of concepts in the concept lattice of the finer attributes.

Theorem 2.1

[2] If\(C_{1}\le C_{2}\), then for each formal concept\(<A,B>\in \mathbf{B }(G,M_{C_{2}},I_{C_{2}})\)there exist uniqueformal concepts\(<A_{k},B_{k}>\in {\mathbf{B }}(G,M_{C_{1}},I_{C_{1}}),k\in K\)such that\(\bigcup _{k\in K}A_{k}=A\). Moreover, the\(A_{k}s\)are mutuallydisjoint.

3 Multi-scale concept analysis using modal-style operators

Modal-style operators provide useful tools for data analysis. Different operators lead to different styles of rules summarizing the knowledge embedded in a formal context. Object-oriented and property-oriented formal concept analysis are two representative data analysis models. Although they have been investigated extensively in the literature, both studies are restricted to single-scale formal contexts [4, 5, 8, 21, 23, 28, 45,46,47]. In this section, we focus on rough set approximations in multi-scale formal concept analysis. Precisely, by using rough set approximations, object-oriented multi-scale concept analysis is presented, and the relationship between concept lattices derived at different granularity levels is investigated.

Let (G, M, I) be a formal context, we define a pair of dual approximation operators, \(\diamond ,\Box : 2^{G}\rightarrow 2^{M}:\)

$$\begin{aligned}&X^{\Box }=\{m\in M\mid \forall g\in G(gIm\Rightarrow g\in X)\} \nonumber \\&\quad =\{m\in M\mid Im\subseteq X\}, \end{aligned}$$
(3)
$$\begin{aligned}&X^{\diamond }=\{m\in M\mid \exists g\in G(gIm\wedge g\in X)\} \nonumber \\&\quad =\{m\in M\mid Im\cap X\ne \emptyset \}. \end{aligned}$$
(4)

They are related by \(X^{c\Box c} = X^{\diamond }\) and \(X^{c\diamond c} = X^{\Box }\), where c denotes the complement of a set. According to (3) and (4), an object having a property in \(X^{\Box }\) is necessarily in X, and an object having a property in \(X^{\diamond }\) is only possibly in X. Thus, the operators \(\Box \) and \(\diamond \) are also referred to as the necessity and the possibility operators [45, 46].

Conversely, we define a pair of dual approximation operators, \(\Box ,\diamond : 2^{M}\rightarrow 2^{G}:\)

$$\begin{aligned}&Y^{\Box }=\{g\in U\mid \forall m\in M(gIm\Rightarrow m\in Y)\} \nonumber \\&\quad =\{g\in G\mid gI\subseteq Y\}, \end{aligned}$$
(5)
$$\begin{aligned}&Y^{\diamond }=\{g\in U\mid \exists m\in M(gIm\wedge m\in Y)\} \nonumber \\&\quad =\{g\in G\mid gI\cap Y\ne \emptyset \}. \end{aligned}$$
(6)

Proposition 3.1

[45, 46] Let\(K=(G,M,I)\)be a formal context and\(X\subseteq G, Y\subseteq M\), then

  1. (i)

    for each\(m\in M\), \(m^{\downarrow }\)is an extent of some object-oriented concept,

  2. (ii)

    if there exists\(Y\subseteq M\)such that\(X=\cup _{y\in Y}y^{\downarrow }\), then\(X\in \)EXT\((\mathbf{B }(G,M,I))\),

  3. (iii)

    for any\(X\in \)EXT\((\mathbf{B }(G,M,I))\), there exists\(Y\subseteq M\)such that\(X=\cup _{m\in Y}m^{\downarrow }\),

  4. (iv)

    \(X\subseteq X^{\Box \diamond }, Y\subseteq Y^{\diamond \Box }.\)

The object-oriented concept lattice was introduced by Yao [45]. A pair (X, Y), \(X\subseteq G, Y\subseteq M \), is called an object-oriented formal concept if \(X=Y^{\diamond }\) and \(Y=X^{\Box }.\) If an object has a property in Y then the object belongs to X. Furthermore, only objects in X have properties in Y . The set of objects X is called the extension of the concept (X, Y), and the set of the properties Y is called the intension. The family of all object-oriented concepts forms a lattice with meet \(\wedge \) and join \(\vee \) defined by:

$$\begin{aligned}&(X_{1},Y_{1})\wedge (X_{2},Y_{2})=((Y_{1}\cap Y_{2})^{\diamond },Y_{1}\cap Y_{2} ) \nonumber \\&\quad =((X_{1}\cap X_{2})^{\Box \diamond },Y_{1}\cap Y_{2}),\\&(X_{1},Y_{1})\vee (X_{2},Y_{2})=(X_{1}\cup X_{2} , (X_{1}\cup X_{2})^{\Box }) \nonumber \\&\quad =(X_{1}\cup X_{2},(Y_{1}\cup Y_{2})^{\diamond \Box }). \end{aligned}$$

Suppose that (G, M, I) is an input data table. For each attribute \(m\in M\), we have a granularity tree \(T_{m}\) and for each \(m\in M\), \(C_{m}\) be a cut in \(T_{m}\), the collection of all cuts induces a data table \((G,M_{C},I_{c})\) such that

\(M_{C}=\bigcup _{m\in M}C_{m}\)

and we put for each \(y\in M_{C}\)

\((g,y)\in I_{C}\) if and only if \(g\in y^{\downarrow }\).

We use \(\mathbf{B }^{o}(G,M_{C},I_{c})\), \(\hbox {EXT}(\mathbf{B }^{o}(G,M_{C},I_{c}))\) to denote the collection of object-oriented concepts induced from \((G,M_{C},I_{c})\) and the collection of extents in \(\mathbf{B }^{o}(X,Y_{C},I_{c})\), respectively.

The following theorem establishes the close relationship between object-oriented concepts produced at different levels of granularity.

Theorem 3.1

[54] If\(C_{1}\le C_{2}\), then\(\hbox {EXT}(\mathbf{B }^{o}(G,M_{C_{2}},I_{C_{2}}))\subset \,\hbox {EXT}(\mathbf{B }^{o}(G,M_{C_{1}},I_{C_{1}})).\)

To facilitate our discussion, we will use the following notations. Let \((G,M_{C_{1}},I_{C_{1}})\) and \((G,M_{C_{2}},I_{C_{2}})\) be two formal contexts satisfying \(C_{1}\le C_{2}\). For \(y\in M_{C_{1}}\), we denote by \(F_{C_{2}}(y)\) the father node of y in \(M_{C_{2}}\), in other words, y is the refining attribute of \(F_{C_{2}}(y)\). For \(Y\subseteq M_{C_{1}}, F_{C_{2}}(Y)={\{F_{C_{2}}(y)\mid y\in Y\}}\). Similarly, for \(m\in M_{C_{2}}\), we denote by \(S_{C_{1}}(m)\) the set of son nodes (or successors) of m in \(M_{C_{1}}\). For \(M\subseteq M_{C_{2}}\), \(S_{C_{1}}(M)={\{S_{C_{1}}(m)\mid m\in M\}}\). According to the definition of granularity tree and cut, we conclude that the \(F_{C_{2}}(y)\) is a singleton while \(S_{C_{1}}(m)\) is not necessarily a singleton.

The following proposition provides the changing law of rough approximation when the level of granularity becomes coarser.

Proposition 3.2

If\(C_{1}\le C_{2}\), then for any\(X\subseteq G, S(X^{\Box _{C_{2}}})\subseteq X^{\Box _{C_{1}}}, F(X^{\diamond _{C_{1}}})\subseteq X^{\diamond _{C_{2}}}.\)

Proof

Choose arbitrarily \(y_{1}\in S(X^{\Box _{C_{2}}}),\) then there exists \(y_{2}\in X^{\Box _{C_{2}}}\) such that \(y_{1}\) is the refining attribute of \(y_{2}\). According to the definition of \(\Box _{C_{2}},\)\(y_{2}\in X^{\Box _{C_{2}}}\) means that \(Iy_{2}\subseteq X\), which, together with \(Iy_{1}\subseteq Iy_{2}\) implies that \(Iy_{1}\subseteq X\), and therefore, \(y_{1}\in X^{\Box _{C_{1}}}.\)

Similarly, we choose arbitrarily \(y_{2}\in F(X^{\diamond _{C_{1}}}),\) then there exists \(y_{1}\in X^{\diamond _{C_{1}}}\) such that \(y_{2}\) is the father node of \(y_{1}\). We have from \(y_{1}\in X^{\diamond _{C_{1}}}\) and the definition of \(\diamond _{C_{1}}\) that there exists \(x\in X\) such that \(xI_{C_{1}}y_{1}\), which means that \(xI_{C_{2}}y_{2}\), and hence \(y_{2}\in X^{\diamond _{C_{2}}},\) as desired.

Under the preliminary condition \(C_{1}\le C_{2}\), it is important to note that for each \(Y\in \hbox {INT}(\mathbf{B }^{o}(G,M_{C_{2}},I_{C_{2}}))\), by replacing each attribute y in Y with \(S_{C_{1}}(y)\), the obtained set \(Y^{'}\) is not necessarily contained in \(\hbox {INT}(\mathbf{B }^{o}(G,M_{C_{1}},I_{C_{1}}))\). Please see the following example. \(\square \)

Example 3.1

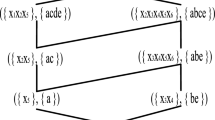
We observe from Table 2 that \(({\{a,b,c,d,e\}},{\{L,R,G\}})\) is an object-oriented concept derived from the formal context in the left side. By replacing G with IG and dG, we obtain \({\{L,R,IG,dG\}}\), which, however, is not an intent of any concept derived from the right side of Table 2.

Table 2 Multi-scale formal contexts describing objects \(a,\ldots ,g\) and their attributes L (large), R (red), H (high),G (green), IG (light green), dG (dark green), vH (very high), mH (moderately high)
Full size table

The following theorem provides an approach to constructing \((\mathbf{B }^{o}(G,M_{C_{2}},I_{C_{2}}))\) from \((\mathbf{B }^{o}(G,M_{C_{1}},I_{C_{1}}))\).

Theorem 3.2

If\(C_{1}\le C_{2}\), then\(\mathbf{B }^{o}(G,M_{C_{2}},I_{C_{2}})=\{(U,V)\mid \exists (X,Y)\in \mathbf{B }^{o}(G,M_{C_{1}},I_{C_{1}}),U=\bigcup {\{Z^{\diamond _{C_{1}}}\mid Z={\{y\in Y\mid S_{C_{1}}(F_{C_{2}}(y))\subseteq Y\}}\}},V=F_{C_{2}}(Y)\setminus {\{F_{C_{2}}(y)\mid \exists y^{'}\in S_{C_{1}}(F_{C_{2}}(y)),y^{'\diamond _{C_{1}}}\not \subseteq X\}}\}.\)

Proof

For the convenience of proof, we denote \(H=\{(U,V)\mid \exists (X,Y)\in \mathbf{B }^{o}(G,M_{C_{1}},I_{C_{1}}),U=\bigcup {\{Z^{\diamond _{C_{1}}}\mid Z={\{y\in Y\mid S_{C_{1}}(F_{C_{2}}(y))\subseteq Y\}}\}},V=F_{C_{2}}(Y)\setminus {\{F_{C_{2}}(y)\mid \exists y^{'}\in S_{C_{1}}(F_{C_{2}}(y)),y^{'\diamond _{C_{1}}}\not \subseteq X\}}\}.\)

It suffices to prove \(\mathbf{B }^{o}(G,M_{C_{2}},I_{C_{2}})\subseteq H\) and \(H\subseteq \mathbf{B }^{o}(G,M_{C_{2}},I_{C_{2}})\).

Take arbitrarily \((U,V)\in H,\) we will show \((U,V)\in \mathbf{B }^{o}(G,M_{C_{2}},I_{C_{2}})\) below. Indeed, we have from \(U=\bigcup {\{Z^{\diamond _{C_{1}}}\mid Z={\{y\in Y\mid S_{C_{1}}(F_{C_{2}}(y))\subseteq Y\}}\}}\) that \(U=({\{F_{C_{2}}(y)\mid S_{C_{1}}(F_{C_{2}}(y))\subseteq Y\}})^{\diamond _{C_{2}}}.\) Moreover, according to the definition, V can also be equivalently written as \(V={\{F_{C_{2}}(y)\mid S_{C_{1}}(F_{C_{2}}(y))\subseteq Y\}},\) and therefore, \(U=V^{\diamond _{C_{2}}}.\) Similarly, we can show that \(V=U^{\Box _{C_{2}}}\). Hence, \((U,V)\in \mathbf{B }^{o}(G,M_{C_{2}},I_{C_{2}}).\)

Conversely, choose arbitrarily \((U,V)\in \mathbf{B }^{o}(G,M_{C_{2}},I_{C_{2}}),\) we then have from Theorem 3.1 that \((U,U^{\Box _{C_{1}}})\in \mathbf{B }^{o}(G,M_{C_{1}},I_{C_{1}}).\) Define \(X=U, Y=S_{C_{1}}(V)\cup {\{y\in M_{C_{1}}\mid y^{\diamond _{C_{1}}}\subseteq U\}}.\) A trivial proof shows that \(U=\bigcup {\{Z^{\diamond _{C_{1}}}\mid Z={\{y\in Y\mid S_{C_{1}}(F_{C_{2}}(y))\subseteq Y\}}\}}\) and \(V=F_{C_{2}}(Y)\setminus {\{F_{C_{2}}(y)\mid \exists y^{'}\in S_{C_{1}}(F_{C_{2}}(y)),y^{'\diamond _{C_{1}}}\not \subseteq X\}},\) and hence, \((U,V)\in H\), as desired. \(\square \)

Remark

In most cases, \(\hbox {EXT}(\mathbf{B }^{o}(G,M_{C_{2}},I_{C_{2}}))\) is just a proper subset of \(\hbox {EXT}(\mathbf{B }^{o}(G,M_{C_{1}},I_{C_{1}})).\) Please refer to the following example.

Table 3 Left: object-oriented concepts of the left table from Table 1. Right: object-oriented concepts of the right table from Table 1
Full size table

Observe from Table 3 that the collection of extents of object-oriented concepts of the left table from Table 1 is contained in that of object-oriented concepts of the right table from Table 1. However, the converse conclusion is not true. For example, \({\{c,e,f,g\}}\) is an extent of an object-oriented concept from the right side of Table 1, but is not an extent of any object-oriented concept from the left side of Table 1.

It is important to note that in some particular cases of \(C_{1}\le C_{2}\), \(\hbox {EXT}(\mathbf{B } (G,M_{C_{1}},I_{C_{1}}))=\hbox {EXT}(\mathbf{B }\,(G,M_{C_{2}},I_{C_{2}}))\), as shown in Tables 4 and 5.

Table 4 Multi-scale formal contexts describing objects \(a,\ldots ,g\) and their attributes L (large), R (red), H (high),G (green), IG (light green), dG (dark green)
Full size table
Table 5 Left: object-oriented concepts of the left table from Table 4. Right: object-oriented concepts of the right table from Table 4
Full size table

For more general cases, one can obtain the following characterization theorem. We denote by \(M_{C_{2}}^{0}\) the collection of attributes in \(M_{C_{2}}\) whose refinement set of attributes in \(M_{C_{1}}\) remains unchanged. We use \(M_{C_{2}}^{1}\) to denote the collection of attributes in \(M_{C_{2}}\) whose refinement set of attributes in \(M_{C_{1}}\) has been changed. For instance, in Table 4, \(M_{C_{2}}^{0}={\{L,R,H\}},M_{C_{2}}^{1}={\{G\}}.\)

Theorem 3.3

[54] If\(C_{1}\le C_{2}\), then\(\hbox {EXT}(\mathbf{B }^{o}(G,M_{C_{1}},I_{C_{1}}))=\hbox {EXT}(\mathbf{B }^{o} (G,M_{C_{2}},I_{C_{2}}))\)if and only if\(M_{C_{2}}^{0}\ne \emptyset \)and for each\(y\in M_{C_{2}}^{1}\)and , there exists\(Z\subseteq M_{C_{2}}\)such that\(y_{i}^{\downarrow }=\cup _{z\in Z}z^{\downarrow }(i=1,\ldots ,p),\)where\({\{y_{1},\ldots ,y_{p}\}}\)is the refinement set ofyin\(M_{C_{1}}\).

4 Property-oriented multi-scale concept analysis

The property-oriented concept lattice was introduced by \(\hbox {D}\ddot{\text {u}}\hbox {ntsch}\) and Gediga [4]. A pair \((X,Y), X\subseteq G, Y\subseteq M,\) is called a property-oriented formal concept if \(X=Y^{\Box }\) and \(Y=X^{\diamond }\). If a property is possessed by an object in X then the property must be in Y. Furthermore, only properties Y are possessed by objects in X.

The family of all property-oriented formal concepts forms a lattice with meet \(\wedge \) and join \(\vee \) defined by:

$$\begin{aligned}&(X_{1},Y_{1})\wedge (X_{2},Y_{2})=(X_{1}\cap X_{2},(X_{1}\cap X_{2}) ^{\diamond }) \\&\quad =(X_{1}\cap X_{2},(Y_{1}\cap Y_{2}) ^{\Box \diamond }),\\&(X_{1},Y_{1})\vee (X_{2},Y_{2})=((Y_{1}\cup Y_{2}) ^{\Box }, Y_{1}\cup Y_{2}) \\&\quad =((X_{1}\cup X_{2}) ^{\diamond \Box },Y_{1}\cup Y_{2}). \end{aligned}$$

In this section, we consider property-oriented concepts in a multi-scale formal context. Suppose that (G, M, I) is an input data table. For each attribute \(m\in M\), we have a granularity tree \(T_{m}\) and for each \(m\in M\), \(C_{m}\) be a cut in \(T_{m}\), the collection of all cuts induces a data table \((G,M_{C},I_{c})\) such that (Table 6)

\(M_{C}=\bigcup _{m\in M}C_{m}\)

and we put for each \(y\in M_{C}\)

\((x,y)\in I_{C}\) if and only if \(x\in y^{\downarrow }\).

We use \(\mathbf{B }^{p}(G,M_{C},I_{c})\) and \(\hbox {EXT}(\mathbf{B }^{p}(X,Y_{C},I_{c}))\) to denote the collection of property-oriented concepts induced from \((G,M_{C},I_{c})\) and the collection of extents in \(\mathbf{B }^{p}(X,Y_{C},I_{c})\), respectively. Moreover, to underline the formal context where the necessity and possibility operators are conducted, we sometimes use \(\Box _{C},\diamond _{C}\) instead.

The following theorem establishes the close relationship between property-oriented concepts produced at different levels of granularity.

Theorem 4.1

If\(C_{1}\le C_{2}\), then\(\hbox {EXT}(\mathbf{B }^{p}(G,M_{C_{2}},I_{C_{2}}))\subseteq \hbox {EXT}(\mathbf{B }^{p}(G,M_{C_{1}},I_{C_{1}})).\)

Proof

Take arbitrarily \(X\in \hbox {EXT}(\mathbf{B }^{p}(G,M_{C_{2}},I_{C_{2}}))\), i.e., there exists \(Y\subseteq M_{C_{2}}\) such that \((X,Y)\in \mathbf{B }^{p}(G,M_{C_{2}},I_{C_{2}})\). Take \(Y^{'}=X^{\diamond _{C_{1}}}\), then it can be checked that \(Y^{'}\subseteq S_{C_{1}}(Y)\). Indeed, for any \(z\in Y^{'}\), we have from \(Y^{'}=X^{\diamond _{C_{1}}}\) that there exists \(x\in X\) such that \(xI_{C_{1}}z\). Since z is a refinement attribute of an attribute(say as y) in \(C_{2}\), we obtain \(xI_{C_{2}}y\), which together with \(X^{\diamond _{C_{2}}}=Y\) implies \(y\in Y\), as desired. We will then be able to prove \((X,Y^{'})\in \mathbf{B }^{p}(G,M_{C_{1}},I_{C_{1}}))\), which is equivalent to show that \(Y^{'\Box _{C_{1}}}=X.\) Take arbitrarily \(x\in Y^{'\Box _{C_{1}}},\) to prove \(x\in X\), it is equivalent to show that \(x\in Y^{\Box _{C_{2}}}\) owing to the fact \(Y^{\Box _{C_{2}}}=X\), that is, for any \(y\in M_{C_{2}}\) satisfying \(xI_{C_{2}}y,\) we have \(y\in Y.\) Indeed, \(xI_{C_{2}}y\) means that there exists \(y_{i}\in S_{C_{1}}(y)\) such that \(xI_{C_{1}}y_{i}\), which together with \(x\in Y^{'\Box _{C_{1}}}\) implies that \(y_{i}\in Y^{'}.\) Since \(Y^{'}=X^{\diamond _{C_{1}}}\), there exists \(x^{'}\in X\) such that \(x^{'}I_{C_{1}}y_{i}\), and thus, \(x^{'}I_{C_{2}}y\), then by applying \(X^{\diamond _{C_{2}}}=Y\), we can obtain \(y\in Y.\) That is, we have proved \(Y^{'\Box _{C_{1}}}\subseteq X.\)\(\square \)

The converse inclusion, i.e., \(X\subseteq Y^{'\Box _{C_{1}}}\), follows immediately from \(Y^{'}=X^{\diamond _{C_{1}}}\) and \(X\subseteq X^{\diamond _{C_{1}}\Box _{C_{1}}}.\)

Table 6 Left: property-oriented concepts of the left table from Table 1. Right: property-oriented concepts of the right table from Table 1
Full size table

Theorem 4.1 yields the following corollary.

Corollary 4.1

If\(C_{1}\le C_{2}\), then\((X,Y)\in \mathbf{B }^{p}(G,M_{C_{2}},I_{C_{2}})\)implies that\((X,X^{\diamond _{C_{1}}})\in \mathbf{B }^{p}(G,M_{C_{1}},I_{C_{1}}).\)

Theorem 4.1 provides us with an approach to constructing \(\mathbf{B }^{p}(G,M_{C_{1}},I_{C_{1}})\), \(\hbox {EXT}(\mathbf{B }^{p}(X,Y_{C_{1}},I_{C_{1}}))\) and \(\hbox {INT}(\mathbf{B }^{p}(X,Y_{C_{1}},I_{C_{1}}))\) from the counterparts derived from \((G,M_{C_{2}},I_{C_{2}})\). Concretely, if X is an extent in \((G,M_{C_{2}},I_{C_{2}})\), then it is also an extent in \((G,M_{C_{1}},I_{C_{1}});\) if Y is an intent in \((G,M_{C_{2}},I_{C_{2}})\), then \(Y^{\Box _{C_{2}}\diamond _{C_{1}}}\) an intent in \((G,M_{C_{1}},I_{C_{1}});\) if (X, Y) is a property-oriented concept in \((G,M_{C_{2}},I_{C_{2}})\), then \((X,Y^{\Box _{C_{2}}\diamond _{C_{1}}})\) is a property-oriented concept in \((G,M_{C_{1}},I_{C_{1}}).\)

The following theorem can be treated as the converse direction of Theorem 4.1, that is, it provides an approach to constructing \(\mathbf{B }^{p}(G,M_{C_{2}},I_{C_{2}})\) from \(\mathbf{B }^{p}(G,M_{C_{1}},I_{C_{1}})\).

Theorem 4.2

Let\((G,M_{C_{1}},I_{C_{1}})\)and\((G,M_{C_{2}},I_{C_{2}})\)be two formal contexts satisfying\(C_{1}\le C_{2}\), then

$$\begin{aligned}&\mathbf{B }^{p}(G,M_{C_{2}},I_{C_{2}})=\left\{ \left( \bigcup _{y\in Y}S_{C_{1}}(F_{C_{2}}(y))\right) ^{\Box _{C_{1}}},Z)\mid \exists (X,Y)\right. \\&\left. \quad \in \mathbf{B }^{p}(G,M_{C_{1}},I_{C_{1}}),Z=\left\{ F_{C_{2}}(y)\mid y\in Y\right\} \right\} . \end{aligned}$$

To prove Theorem 4.2, we need the following lemma.

Lemma 4.1

Let \((G,M_{C_{1}},I_{C_{1}})\) and \((G,M_{C_{2}},I_{C_{2}})\) be two formal contexts with \(C_{1}\le C_{2}\) and \(X\subseteq G,\) then we have \((\bigcup S_{C_{1}}(X^{\diamond _{C_{2}}}))^{\Box _{C_{1}}}=X^{\diamond _{C_{2}}\Box _{C_{2}}}.\)

Proof

It suffices to show that for any \(x\in G,\)\(x\in (\bigcup S_{C_{1}}(X^{\diamond _{C_{2}}}))^{\Box _{C_{1}}}\) if and only if \(x\in X^{\diamond _{C_{2}}\Box _{C_{2}}}.\)

“\(\Rightarrow \)” Choose arbitrarily \(x\in (\bigcup S_{C_{1}}X^{\diamond _{C_{2}}})^{\Box _{C_{1}}}\) and \(m\in M_{C_{2}}\) satisfying \(xI_{C_{2}}m\). We have from \(xI_{C_{2}}m\) that there exists \(y\in S_{C_{1}}(m)\) such that \(xI_{C_{1}}y\) holds, which, together with \(x\in (\bigcup S_{C_{1}}(X^{\diamond _{C_{2}}}))^{\Box _{C_{1}}}\), jointly implies \(y\in \bigcup S_{C_{1}}(X^{\diamond _{C_{2}}}),\) and therefore, there exists \(m^{'}\in X^{\diamond _{C_{2}}}\) such that \(y\in S_{C_{1}}(m^{'}).\) Since \(F_{C_{2}}(y)\) is a singleton, we have \(m=m^{'}\) and \(m\in X^{\diamond _{C_{2}}}\). The above proof shows that for any \(m\in M_{C_{2}}\) satisfying \(xI_{C_{2}}m\), we have \(m\in X^{\diamond _{C_{2}}}\), then according to (5), we obtain \(x\in X^{\diamond _{C_{2}}\Box _{C_{2}}}\).

“\(\Leftarrow \)” Choose arbitrarily \(x\in X^{\diamond _{C_{2}}\Box _{C_{2}}}\) and \(y\in M_{C_{1}}\) satisfying \(xI_{C_{1}}y\). We have from \(xI_{C_{1}}y\) that \(xI_{C_{2}}F_{C_{2}}(y)\), which, together with \(x\in X^{\diamond _{C_{2}}\Box _{C_{2}}}\), implies that \(F_{C_{2}}(y)\in X^{\diamond _{C_{2}}}\), and hence, there exists \(x^{'}\in X\) such that \(x^{'}I_{C_{2}}F_{C_{2}}(y),\) which in turn shows that \(F_{C_{2}}(y)\in X^{\diamond _{C_{2}}}\), and therefore, \(y\in \bigcup S_{C_{1}}(X^{\diamond _{C_{2}}}).\) The above proof shows that for any \(y\in M_{C_{1}}\) satisfying \(xI_{C_{1}}y\), we have \(y\in \bigcup S_{C_{1}}(X^{\diamond _{C_{2}}}).\) And hence, \(x\in (\bigcup S_{C_{1}}X^{\diamond _{C_{2}}})^{\Box _{C_{1}}}.\)\(\square \)

Now, we are ready to give the proof of Theorem 4.2.

Proof

The detailed proof consists of two parts, i.e.,

(i) \({\{(\bigcup _{y\in Y}S_{C_{1}}(F_{C_{2}}(y)))^{\Box _{C_{1}}},Z)\mid \exists (X,Y)\in \mathbf{B }^{p}(G,M_{C_{1}},I_{C_{1}}),Z={\{F_{C_{2}}(y)\mid y\in Y\}}\}}\subseteq \mathbf{B }^{p}(G,M_{C_{2}},I_{C_{2}}),\)

and

(ii) \(\mathbf{B }^{p}(G,M_{C_{2}},I_{C_{2}})\subseteq {\{(\bigcup _{y\in Y}S_{C_{1}}(F_{C_{2}}(y)))^{\Box _{C_{1}}},Z)\mid \exists (X,Y)\in \mathbf{B }^{p}(G,M_{C_{1}},I_{C_{1}}),Z={\{F_{C_{2}}(y)\mid y\in Y\}}\}}.\)

We will firstly show two preliminary results as follows: for \((X,Y)\in \mathbf{B }^{p}(G,M_{C_{1}},I_{C_{1}}),Z={\{F_{C_{2}}(y)\mid y\in Y\}},\)

$$\begin{aligned}&\bigcup _{y\in Y}S_{C_{1}}(F_{C_{2}}(y))=\bigcup S_{C_{1}}(X^{\diamond _{C_{2}}}). \end{aligned}$$
(7)
$$\begin{aligned}&X^{\diamond _{C_{2}}}=Z. \end{aligned}$$
(8)

To prove (7), choose arbitrarily \(y^{'}\in \bigcup _{y\in Y}S_{C_{1}}(F_{C_{2}}(y))\), then there exists \(y\in Y\) such that \(y^{'}\in S_{C_{1}}(F_{C_{2}}(y))\). We have from \(X^{\diamond _{C_{1}}}=Y\) and \(y\in Y\) that there exists \(x\in X\) such that \(xI_{C_{1}}y\), and hence \(xI_{C_{2}}F_{C_{2}}(y)\) and \(F_{C_{2}}(y)\in X^{\diamond _{C_{2}}}.\) Consequently, \(y\in \bigcup S_{C_{1}}(X^{\diamond _{C_{2}}}).\) Conversely, choose arbitrarily \(y\in \bigcup S_{C_{1}}(X^{\diamond _{C_{2}}}),\) then there exists \(m\in X^{\diamond _{C_{2}}}\) such that \(y\in S_{C_{1}}(m).\)\(m\in X^{\diamond _{C_{2}}}\) means that there exists \(x\in X\) such that \(xI_{C_{2}}m\), which in turn implies that there exists \(y^{'}\in M_{C_{1}}\) such that \(xI_{C_{1}}y^{'}\). Since \(X^{\diamond _{C_{1}}}=Y\), we further have \(y^{'}\in Y.\) Then \(y^{'}\in Y\), \(y\in S_{C_{1}}(m)\) and \(y^{'}\in S_{C_{1}}(m)\) jointly imply \(y\in \bigcup _{y\in Y}S_{C_{1}}(F_{C_{2}}(y))\), as desired.

To prove (8), choose arbitrarily \(z\in Z\), according to the definition of Z, there exists \(y\in Y\) such that \(z=F_{C_{2}}(y)\). Moreover, we have from \(X^{\diamond _{C_{1}}}=Y\) that there exists \(x\in X\) such that \(xI_{C_{1}}y\), which, together with \(z=F_{C_{2}}(y)\), implies that \(xI_{C_{2}}z\), and hence, \(z\in X^{\diamond _{C_{2}}}\). The converse direction can be shown in a similar manner.

For (i), we need to show that \(((\bigcup _{y\in Y}S_{C_{1}}(F_{C_{2}}(y)))^{\Box _{C_{1}}},Z)\in \mathbf{B }^{p}(G,M_{C_{2}},I_{C_{2}})\), or equivalently, \((\bigcup _{y\in Y}S_{C_{1}}(F_{C_{2}}(y)))^{\Box _{C_{1}}\diamond _{C_{2}}}=Z, Z^{\Box _{C_{2}}}=(\bigcup _{y\in Y}S_{C_{1}}(F_{C_{2}}(y)))^{\Box _{C_{1}}}.\) Indeed, we have from Lemma 4.1, (7) and (8) that \((\bigcup _{y\in Y}S_{C_{1}}(F_{C_{2}}(y)))^{\Box _{C_{1}}\diamond _{C_{2}}}=X^{\diamond _{C_{2}}\Box _{C_{2}}\diamond _{C_{2}}} =X^{\diamond _{C_{2}}}=Z,\) and \(Z^{\Box _{C_{2}}}=X^{\diamond _{C_{2}}\Box _{C_{2}}}=(\bigcup _{y\in Y}S_{C_{1}}(F_{C_{2}}(y)))^{\Box _{C_{1}}}.\)

For (ii), let (X, Z) be arbitrarily chosen in \(\mathbf{B }^{p}(G,M_{C_{2}},I_{C_{2}}),\) i.e., \(X^{\diamond _{C_{2}}}=Z\) and \(Z^{\Box _{C_{2}}}=X.\) We have from Corollary 4.1 that \((X,X^{\diamond _{C_{1}}})\in \mathbf{B }^{p}(G,M_{C_{1}},I_{C_{1}}).\) Define \(W=F(X^{\diamond _{C_{1}}}),\) then we have that \(W=X^{\diamond _{C_{2}}}=Z\)(an easy proof shows that \(F(X^{\diamond _{C_{1}}})=X^{\diamond _{C_{2}}}\), the details are omitted here), moreover, we have from Lemma 4.1 and (7) that \((\bigcup _{y\in X^{\diamond _{C_{1}}}}S_{C_{1}}(F_{C_{2}}(y)))^{\Box _{C_{1}}}=(\bigcup S_{C_{1}}(X^{\diamond _{C_{2}}}))^{\Box _{C_{1}}}=X^{\diamond C_{2}\Box _{C_{2}}}=X,\) as desired. \(\square \)

5 Concluding remarks

In this paper, we present an integrated study of rough set theory and formal concept analysis in multi-scale formal contexts. We mainly consider multi-scale formal concept analysis by using modal-style operators. The collection of object-oriented concept lattices and property-oriented concept lattices can be obtained at different granularity levels of attributes. It has been shown that the set of extents in the derived concept lattices increases when we choose to use a finer level of scale. Moreover, a bidirectional construction approach to concepts (i.e., from coarser to finer and from finer to coarser, respectively) is exhibited.

The present study is conducted at a theoretical level. The topics for future research include:

  1. 1.

    In case \(C_{1}\le C_{2}\), how to develop corresponding incremental algorithms that enable us to compute \((\mathbf{B }(G,M_{C_{2}},I_{C_{2}}))\) from \((\mathbf{B }(G,M_{C_{1}},I_{C_{1}}))\), or compute \((\mathbf{B }(G,M_{C_{1}},I_{C_{1}}))\) from \((\mathbf{B }(G,M_{C_{2}},I_{C_{2}}))\).

  2. 2.

    (2) The present study is confined to Boolean data, how to extend the present study to other types of formal contexts. For this topic, we will start with a many-valued context and use different scaling methods to achieve this goal, particularly the one related to that introduced in [47].