Keywords

1 Introduction

Formal Concept Analysis (FCA), as an effective methodology for knowledge discovery, has attracted much attention from the artificial intelligence community. At present, FCA has been widely used in machine learning [1], pattern recognition, expert systems [2], decision-making and data mining, and other related fields [3].

Knowledge reduction is an essential direction for knowledge discovery. In particular, attribute reduction in concept lattice provides powerful data reduction solution for knowledge discovery and data mining. Besides, attribute reduction as a key issue of FCA, its goal is to find minimal attribute set to maintain the invariant property. Generally, attribute reduction in FCA can be categorized as follows in terms of different reduction purpose: (1) concept lattice complexity based attribute reduction: this reduction aims to reduce the number of nodes in concept lattice and to delete the redundant concepts [4]; (2) rule-based attribute reduction: this reduction aims to maintain the rule sets unchanged [5]; (3) lattice structure based attribute reduction: this type of reduction is commonly studied in literature. It targets to keep the same structure of concept lattice and deletes the redundant attributes [6]. The attribute reduction in this work falls into the category (3).

This paper focuses on investigating the relation between concept stability in the original lattice and reduced lattice. For this, we introduce the definition of concept stability, which is used to measure the strength of dependency between intent and objects of extent. The main contributions of this paper are two-fold: (1) we present a theorem to prove that the concept stability is not changed during the attribute reduction of concept lattice (2).

The rest of this paper is organized as follows. Section 2 provides the preliminaries about Formal Concept Analysis methodology and elaborates the attributes reduction in concept lattice. By observing the concept stability of concepts in original concept lattice and reduced concept lattice, a theorem about the invariance of concept stability for attribute reduction in concept lattice is presented and proved mathematically in Sect. 3. Finally, Sect. 4 concludes this work.

2 Attribute Reduction in Concept Lattice

Before the presentation of attribute reduction in concept lattice, we briefly provide the preliminaries of FCA. FCA is a powerful methodology for describing the binary relationships between object and attribute and has been applied to many areas. Formally, a formal context is formulated as C = (O, A, I) where O indicates the object set and A denotes the attribute set respectively, and the relation \(I \subseteq O \times A\) refers to a binary relation between object and attribute. Generally, \(o \in O\) and \(a \in A\), \((o,a) \in I\) is interpreted as objective o has the attribute a.

For the sake clarity of formal concept lattice and its generated formal concepts, the following two operators are given [7].

(Operator for extracting the common attribute of objects subset X) For \(X \subseteq O\), we define a set of common attributes of X,

$$ X^{ \uparrow } = {\text{\{ a}} \in {\text{A|(x,a)}} \in {\text{I, }}\forall {\text{x}} \in {\text{X\} }} $$
(1)

(Operator for extracting the common objects of attributes subset X) For \(Y \subseteq A\), we also define a set of common objects of Y,

$$ Y^{ \downarrow } = {\text{\{ o}} \in {\text{O|(o,y)}} \in {\text{I, }}\forall {\text{y}} \in {\text{Y\} }} $$
(2)

In a formal context C = (O, A, I), for \(X \subseteq O\), \(Y \subseteq A\), if \(X^{ \uparrow \downarrow } = Y\), then this pair (X,Y) is called as a concept where X, Y are the extent and intent of the concept. Let Ext(C) be the set of extents w.r.t. the formal context C. With the above operators, a concept lattice L(C) can be defined as concepts organized according to a special hierarchical partial order, i.e., (X1, Y1) ≤ (X2, Y2)\(\Leftrightarrow\) X1 \(\subseteq\) X2 (\(\Leftrightarrow\) Y1 \(\supseteq\) Y2).

Suppose that C = (O, A, I) is a formal context, \(\mathrm{D}\subseteq \mathrm{A},{I}_{D}=I\cap (O\times D)\), then \({C}_{D}=(O,D,{I}_{D})\) is a formal context as well and regarded as a sub-formal context of C.

Theorem 1

Suppose C = (O, A, I) as a formal context, if \(\mathrm{D}\subseteq \mathrm{A}\), then Ext(C)\(\supseteq \) Ext(\({C}_{D}\)) holds.

Theorem 1 demonstrates that the set of extents of sub-formal context is contained with the set of extents of original formal context.

Definition 1

Let \({C}_{1}=(O,{A}_{1},{I}_{1})\) and \({C}_{2}=(O,{A}_{2},{I}_{2})\) be two formal contexts, \(\mathrm{L}({C}_{1})\) and \(\mathrm{L}({C}_{2})\) be the corresponding concept lattices. For any concept \(({X}_{2},{Y}_{2})\in \mathrm{L}({K}_{1})\), there exists \(({X}_{1},{Y}_{1})\in \mathrm{L}({K}_{2})\) that satisfies \({X}_{1}={X}_{2}\), then we say that \(\mathrm{L}({C}_{1})\) is a refined version of \(\mathrm{L}({C}_{2})\), denoted as \(\mathrm{L}\left({C}_{1}\right)\le \mathrm{ L}({C}_{2})\).

Particularly, if \(\mathrm{L}\left({C}_{1}\right)\le \mathrm{ L}({C}_{2})\) and \(\mathrm{L}\left({C}_{2}\right)\le \mathrm{ L}({C}_{1})\) hold simultaneously, then the concept lattices of \({C}_{1}=(O,{A}_{1},{I}_{1})\) and \({C}_{2}=(O,{A}_{2},{I}_{2})\) are isomorphism, i.e., \(\mathrm{L}\left({C}_{1}\right)\cong \mathrm{ L}({C}_{2})\).

Definition 2

Let \(\mathrm{C}=(\mathrm{O},\mathrm{A},\mathrm{I})\) be a formal context,\( \mathrm{D}\subseteq \mathrm{A}\). If \(\mathrm{L}\left(\mathrm{C}\right)\cong \mathrm{L}({C}_{D})\), then D is the consistent set of C. Additionally, for any \(\mathrm{d}\in \mathrm{D}\), \(\mathrm{L}({C}_{D})\ncong \mathrm{L}({C}_{D-\{d\}})\), then D is the reduction of C.

For the sake of better presentation, this paper takes the above consistent set/reduction as the consistent/reduction of the concept lattice. As matter of fact, a consistent set D of a formal context C is a type of attributes set that maintains the invariant of extent set, i.e., \(\mathrm{Ext}\left(\mathrm{C}\right)=\mathrm{Ext}({C}_{D})\).

Example 1

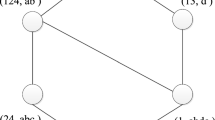
Table 1 shows a formal context \(\mathrm{C}=(\mathrm{O},\mathrm{A},\mathrm{I})\), \(\mathrm{O}=\{\mathrm{1,2},\mathrm{3,4}\}\), \(\mathrm{A}=\{\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d},\mathrm{e}\}\), the corresponding concept lattice and its reduction are presented as follows.

Table 1 A formal context \(\mathrm{C}=(\mathrm{O},\mathrm{A},\mathrm{I})\)
Full size table

By invoking the concept lattice generation algorithm, the corresponding concept lattice for \(\mathrm{C}=(\mathrm{O},\mathrm{A},\mathrm{I})\) is shown in Fig. 1(a). Particularly, there are 6 concepts: (1, abde), (24,abc), (13,d), (124,ab), (1234,\(\upphi \)), (\(\upphi ,\mathrm{abcde}\)), denoted as \({FC}_{i}(i=\mathrm{1,2}\dots 6)\).

Fig. 1
figure 1

Concept lattices \(\mathrm{L}(\mathrm{O},\mathrm{A},\mathrm{I})\) and \(\mathrm{L}(\mathrm{O},{R}_{1},{I}_{R1})\)

Full size image

There are two reductions of this formal context, i.e., \({R}_{1}=\left\{a,c,d\right\}, {R}_{2}=\{b,c,d\}\). In this example, the attributes c and d are core attributes, attributes a and b are relatively necessary attributes, while attribute e is the redundant one. Figure 1(b) is the concept lattice of the formal context \((\mathrm{O},{R}_{1},{I}_{R1})\). Obviously, \(\mathrm{L}(\mathrm{O},{R}_{1},{I}_{R1})\cong \mathrm{L}(\mathrm{O},\mathrm{A},\mathrm{I})\).

As can be seen from Fig. 1a, b, the extent of concepts are not changed, and the intent (i.e., attribute) are reduced from Fig. 1a. The structure of the lattices is an isomorphism.

3 On Invariance of Concept Stability for Attribute Reduction in Concept Lattice

In this section, we attempt to explore the relation between concept stability and attribute reduction in concept lattices. Firstly, we define concept stability. Further, the relation between concept stability and attribute reduction in concept lattices is figured out.

Definition 3

(Stability Index) [7] Let \(\mathrm{c}=(\mathrm{X},\mathrm{Y})\) be a concept of formal context \(\mathrm{C}=(\mathrm{O},\mathrm{A},\mathrm{I})\), then the intensional stability of \((\mathrm{X},\mathrm{Y})\) is defined as follows.

$$\upsigma (\mathrm{c})=\frac{|\{e\in \wp (X)|{e}^{^{\prime}}=Y\}|}{{2}^{|X|}}$$
(3)

In Eq. (3), intensional stability \(\upsigma (\mathrm{c})\) is used to measure the strength of dependency between the intent Y and the objects of the extent X. Specifically, it expresses the probability to maintain Y closed when a subset of noisy objects in X are deleted with equal probability. In other words, this index quantifies the amount of noise in the extent X and overfitting in the intent Y.

Inspired by this stability index, we think the redundant attributes will not affect the intensional stability \(\upsigma (\mathrm{c})\) when we delete some of them. Therefore, to answer our guess, it is necessary to investigate the relation between concept stability and attribute reduction in concept lattices.

Let us continue the Example 1, the stability for each concept in \(\mathrm{L}(\mathrm{O},\mathrm{A},\mathrm{I})\) can be obtained (as shown in Table 2) according to Definition 3.

Table 2 Concept stability of each concept in \(\mathrm{L}(\mathrm{O},\mathrm{A},\mathrm{I})\)
Full size table

Similarly, the stability for each concept in \(\mathrm{L}(\mathrm{O},{R}_{1},{I}_{R1})\) are also obtained as shown in Table 3.

Table 3 Concept stability of each concept in \(\mathrm{L}(\mathrm{O},{R}_{1},{I}_{R1})\)
Full size table

By observing the above concept stability, we found that there is no any change from the original concept lattice to the reduced concept lattice which is obtained after deleting the redundant attributes. Therefore, the following theorem can be derived.

Theorem 2

Given a formal context \(\mathrm{C}=(\mathrm{O},\mathrm{A},\mathrm{I})\), its corresponding concept lattice is represented as \(\mathrm{L}\left(\mathrm{O},\mathrm{A},\mathrm{I}\right).\) After deleting the redundant attributes, the reduced concept lattice is \(\mathrm{L}(\mathrm{O},{R}_{1},{I}_{R1})\). The stability of concepts is not changed during the reduction.

Proof

Since the extracted concepts \(\left(\mathrm{X},\mathrm{ R}\right),\mathrm{ R}\in {R}_{1}\) in reduced concept lattice \(\mathrm{L}(\mathrm{O},{R}_{1},{I}_{R1})\) have the same extent with original concept lattice \(\mathrm{L}\left(\mathrm{O},\mathrm{A},\mathrm{I}\right).\) In addition, the redundant attributes are deleted from original attributes, that is to say, the \(|\{e\in \wp (X)|{e}^{^{\prime}}=Y\}|\) equals to \(\left|\left\{e\in \wp \left(X\right)|{e}^{^{\prime}}=R\right\}\right|\). Due to these, redundant attributes cannot affect the discernibility for a given extent X. Hence, we have the following equation:

$$\upsigma \left(\mathrm{c}\right)=\frac{\left|\left\{e\in \wp \left(X\right)|{e}^{^{\prime}}=R\right\}\right|}{{2}^{\left|X\right|}}=\frac{|\{e\in \wp (X)|{e}^{^{\prime}}=Y\}|}{{2}^{|X|}}$$

The above Theorem 1 holds.

4 Conclusions

This paper is the first work to explore the internal relation between concept stability and attribute reduction. First, this paper introduced the definition of stability index, then the concept stability of concepts in original concept lattice and reduced concept lattice are observed respectively; further, a theorem about the invariance of concept stability for attribute reduction in concept lattice is presented and proved mathematically. In the future, we will fully adopt the proposed theorem and devise a quick attribute reduction algorithm that can be used in other social system applications.