Abstract
In this paper, we propose and study the pseudo almost periodic high-order cellular neural networks with oscillating leakage coefficients and complex deviating arguments, which has not been studied in the existing literature. Applying the contraction mapping fixed point theorem and inequality analysis techniques, we establish a set of criteria for the existence and uniqueness of pseudo almost periodic solutions for this model, which can be easily tested in practice by simple algebra computations. The obtained results play an important role in designing high-order cellular neural networks with state-dependent delays. Moreover, some illustrative examples are given to demonstrate our theoretical results.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Over the past 30 years, compared with the ordinary neural networks, the high-order neural networks (HNNs) have stronger approximation property, faster convergence rate, great stronger capacity and higher fault tolerance, and high-order cellular neural networks (HCNNs) has become an active research topic in different application areas, such as associtative memory, pattern recognition and signal processing (see [1,2,3,4,5,6,7] and the references cited therein). Recently, as pointed out in [8], it is significantly important in theory and application to study cellular neural networks (CNNs) with complex deviating arguments, which has a wider meaning than CNNs with time-varying delays or distributed delays since the models describing the complexity of real problems should reflect the effects of fluctuation factors (see [9,10,11,12]). Furthermore, a typical time delay called Leakage (or “forgetting”) delay may exist in the negative feedback terms of the neural network system, and these terms are variously known as forgetting or leakage terms (see [1, 13, 14]). Usually, HCNNs with complex deviating arguments and involving time-varying delays, and continuously distributed delays in the leakage terms can be described as follows:
and
respectively. Here n corresponds to the number of units in a neural network, \(x_{i}(t)\) corresponds to the state vector of the ith unit at the time t, \(c_{i}(t)\) represents the rate with which the ith unit will reset its potential to the resting state in isolation when disconnected from the network and external inputs at the time t, \(a_{ij}(t)\), \(b_{ij}(t)\) and \(e_{ijl}(t)\) are the connection weights at the time t, \(\eta _{i}(t)\ge 0\) denotes the leakage delay, \(\delta _{i}(s)\ge 0\) denotes the leakage delay kernel, and \(I_{i}(t)\) denotes the external inputs at time t, \(f_{j}\), \(g_{j}\) and \(\bar{g}_{j}\) are activation functions of signal transmission, \(i,j\in J=\{1, 2, \ldots , n\}\). From the basic theory on state-dependent delay-differential equations in [15], HCNNs (1.1) and (1.2) are special types of state-dependent delay-differential equations.
It should be mentioned that, compared with almost periodic phenomenon, pseudo almost periodic phenomenon which can be represented as an almost periodic process plus a ergodic component is more common [10, 16]. Therefore, it is more realistic to study the pseudo almost periodic phenomenon in neural networks models [17,18,19,20,21,22]. However, to the best of our knowledge, there is no result on the existence of pseudo almost periodic solutions for HCNNs with oscillating leakage coefficients and complex deviating arguments. This motivates us to derive some sufficient criteria on the existence of pseudo almost periodic solutions for Eqs. (1.1) and (1.2).
The remaining of this paper is organized as follows. In Sect. 2, we recall some basic definitions and lemmas, which play an important role in Sect. 3 to establish the existence and uniqueness of pseudo almost periodic solutions of Eqs. (1.1) and (1.2). The paper concludes with two examples to illustrate the effectiveness of the obtained results.
2 Preliminaries
In this section, we shall first recall some basic definitions, lemmas which are used in what follows. We designate by \(AP(\mathbb {R},\mathbb {R}^{n})\) the set of the almost periodic functions from \(\mathbb {R}\) to \(\mathbb {R}^{n}\). Hereafter, we denote by \(\mathbb {R}^{n}\)\((\mathbb {R}=\mathbb {R}^{1})\) the set of all \(n-\)dimensional real vectors (real numbers). For any \(\{x_{i} \}=(x_{1} , \ x_{2} , \ldots , x_{ n} ) \in \mathbb {R}^{ n}\), we let |x| denote the absolute-value vector given by \(|x|=\{|x_{i }|\}\), and define \(\Vert x \Vert =\max \nolimits _{ i\in J} |x_{i } | .\) A matrix or vector \(A\ge 0\) means that all entries of A are greater than or equal to zero. \(A>0\) can be defined similarly. For matrices or vectors \(A_{1}\) and \(A_{2}\), \(A_{1}\ge A_{2}\) (resp. \(A_{1}> A_{2}\)) means that \(A_{1}- A_{2}\ge 0\) (resp. \(A_{1}- A_{2}>0)\). \(BC(\mathbb {R},\mathbb {R}^{n})\) denotes the set of bounded and continuous functions from \(\mathbb {R}\) to \(\mathbb {R}^{n}\), and \(BUC(\mathbb {R},\mathbb {R}^{n})\) denotes the set of bounded and uniformly continuous functions from \(\mathbb {R}\) to \(\mathbb {R}^{n}.\) Note that \((BC(\mathbb {R},\mathbb {R}^{n}), \Vert \cdot \Vert _{\infty })\) is a Banach space, where \(\Vert \cdot \Vert _{\infty }\) denotes the supremum norm \(\Vert f\Vert _{\infty } := \sup \nolimits _{ t\in \mathbb {R}} \Vert f (t)\Vert\). For \(h\in BC(\mathbb {R},\mathbb {R} )\), let \(h^+\) and \(h^-\) be defined as
Besides, we define the class of functions \(PAP_{0}(\mathbb {R},\mathbb {R}^{n})\) as follows:
A function \(f\in {BC(\mathbb {R},\mathbb {R}^{n})}\) is called pseudo almost periodic if it can be expressed as
where \(h\in {AP(\mathbb {R},\mathbb {R}^{n})}\) and \(\varphi \in {PAP_{0}(\mathbb {R},\mathbb {R}^{n})}.\) The collection of such functions will be denoted by \(PAP(\mathbb {R},\mathbb {R}^{n}).\) Then, \((PAP(\mathbb {R},\mathbb {R}^{n}),\Vert .\Vert _{\infty })\) is a Banach space and \(AP(\mathbb {R},\mathbb {R}^{n})\) is a proper subspace of \(PAP(\mathbb {R},\mathbb {R}^{n})\) [23].
For \(i, \ j\in J,\) it will be assumed that \(c_{i}:\mathbb {R}\rightarrow \mathbb {R}\) is an almost periodic function, \(\eta _{i }: \mathbb {R}\rightarrow [0, \ +\infty )\), \(I_{i}, \ a_{ij}, \ b_{ij}, e_{ijl}\ :\mathbb {R}\rightarrow \mathbb {R}\) are pseudo almost periodic on \(\mathbb {R}\).
Let \(L>0, \ l>0\) and \(0<\theta <1\) be three constants such that
and
where
We also make the following assumptions which will be used later.
\((S_0)\) For each \(i \in J\),
and there exist a bounded and continuous function \(\tilde{c}_{i} :\mathbb {R}\rightarrow (0, \ +\infty )\) and a positive constant \(K_{i}\) such that
\((S_1)\) For each \(j\in J\), there exist nonnegative constants \(L ^{f}_{j},\)\(L^{g}_{j},\)\(L^{\bar{g}}_{j}\) and \(M^{\bar{g}}_{j}\) such that
Lemma 2.1
(see [19, Lemma 4 and Remark 5]). Let\(\mathbf {Z}=\{f|f,f'\in PAP(\mathbb {R},\mathbb {R}^{n }) \}\) be equipped with the induced norm defined by
Then, \(\mathbf {Z}\)is a Banach space.
Lemma 2.2
(see [5, Lemma 2.2]) \(B^{L}\)is a closed subset of\(PAP(\mathbb {R},\mathbb {R}^{n})\).
3 Main results
In this section, we establish some sufficient conditions on the existence and uniqueness of pseudo almost periodic solutions of Eqs. (1.1) and (1.2).
Theorem 3.1
Let\((S_0)\) and\((S_1)\) hold. Suppose that there exist constants\(\theta>0, \ \alpha _{i}>0\) and\(L>0,\) such that
and
Then (1.1) has a unique pseudo almost periodic solution in the region \(\mathbf {B}= B^{L}\bigcap B^{*} .\)
Proof
By Lemmas 2.1 and 2.2, one can show that \(\mathbf {B }\) is a closed subset of \(\mathbf {Z}\). For any \(\varphi \in \mathbf {B}\), notice that \(M[c_{i}]>0, \ i=1, \ 2,\ldots , n\), using a similar argument as that in the proof of Theorem 3.1 in [11], we obtain that the nonlinear pseudo almost periodic differential equations,
has exactly one pseudo almost periodic solution:
and
Now, we define a mapping \(T:\mathbf {B } \rightarrow PAP(\mathbb {R},\mathbb {R}^{n})\) by setting
First we show that for any \(\varphi \in \mathbf {B} , \ T \varphi =x^{\varphi } \in \mathbf {B}\).
Note that
We get
It follows from Eqs. (3.1), (3.2) and (3.3) that
and
Consequently,
and
where \(\text{ for } \text{ all } \ t_{1}, t_{2}\in \mathbb {R}, \ \Delta \in (0, \ 1)\), and \(t_{1}+\Delta (t_{2}-t_{1})\) is the mean point in Lagrange’s mean value theorem. Thus, Eqs. (3.8) and (3.9) yield \(T\varphi \in \mathbf {B}\). So, the mapping T is a self-mapping from \(\mathbf {B}\) to \(\mathbf {B}\).
Furthermore, for \(\varphi , \psi \in \mathbf {B}\), according to \((S_{0})\), \((S_{1})\), Eqs. (3.1), (3.2), (3.5) and (3.6), we get
and
In view of Eq. (3.3), we have
which, together with Eqs. (3.10) and (3.11), give us that \(\Vert T \varphi -T \psi \Vert _{\mathbf {Z}} \le \rho \Vert \varphi -\psi \Vert _{\mathbf {Z}},\) and the mapping \(T :\mathbf {B} \longrightarrow \mathbf {B}\) is a contraction mapping. Therefore, the mapping T possesses a unique fixed point
By Eq. (3.6), \(x^{* }\) satisfies Eq. (1.1). So Eq. (1.1) has a unique continuously differentiable pseudo almost periodic solution \(x^{* }\) . The proof of Theorem 3.1 is now completed.
Remark 3.1
Obviously, Theorem 3.1 of [11] is only a special case of Theorem 3.1 without high-order term \(\sum \nolimits _{j=1}^{n}\sum \nolimits _{l=1}^{n}e_{ijl}(t)\bar{g}_{j}(x_{j}( x_{j}( t ) ))\bar{g}_{l}(x_{l}( x_{l}( t ) )).\)
Remark 3.2
From (3.1), (3.2) and (3.3), one can check that the conditions in Theorem 3.1 can be easily satisfied under the sufficiently small leakage delays \(\eta _{i}(t)\), and (3.3) is not satisfied when the leakage delays in (1.1) are sufficiently large. This implies that the delays (oscillating leakage coefficients) effect the stability of (1.1).
Next, we will show the existence of pseudo almost periodic solutions of (1.2). We assume that the following conditions are satisfied.
\((\hat{S}_0)\) For each \(i \in J\),
and there exist a bounded continuous function \(\bar{c}_{i} :\mathbb {R}\rightarrow (0, \ +\infty )\) and a positive constant \(K_{i}\) such that
\((\hat{S}_{2})\) for \(i \in J\), the delay kernel \(\delta _{i} :\mathbb {R}\rightarrow [0, \ +\infty )\) is a continuous function with \(0<\int _0^\infty {\delta _i }(v) dv <+\infty\) and \(\int _0^\infty v{\delta _i }(v)e^{\kappa v} dv <+\infty\) for a certain positive constant \(\kappa\).
Let \(L>0, \ l>0\) and \(0<\theta <1\) be three constants such that
and
where
Then, we get
Theorem 3.2
Let\((\hat{S}_0)\), \((S_1)\) and\((\hat{S}_2)\) hold. Moreover, assume that there exist constants\(\theta>0, \ \alpha _{i}>0\) and\(L>0,\) such that
and
Then Eq. (1.2) has a unique pseudo almost periodic solution in the region \(\mathbf {\bar{B}}= B^{L}\bigcap \bar{B}^{*} .\)
Proof
For any \(\varphi \in \mathbf {\bar{B}}\), in view of \((\hat{S}_{2})\), an argument similar to the one used in Lemma 3.1 of [17] shows that
for all \(i\in J.\) Thus, the nonlinear pseudo almost periodic differential equations,
has exactly one pseudo almost periodic solution:
and
Then we complete the proof similarly to that of Theorem 3.1.
4 Examples and remarks
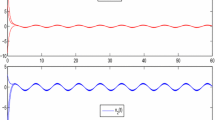
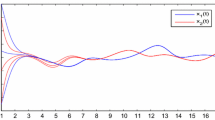
Consider the following HCNNs with oscillating leakage coefficients and complex deviating arguments:
and
Obviously, it is straightforward to show directly that system (4.1) and system (4.2) satisfy the conditions in Theorem 3.1 and Theorem 3.2, respectively. Therefore, either system (4.1) or system (4.2) has exactly one pseudo almost periodic solution in the region \(\mathbf {B}= B^{\frac{1}{5}}\bigcap B^{*} .\)
Remark 4.1
Systems (4.1) and (4.2) are a very simple HCNNs with oscillating leakage coefficients and complex deviating arguments in [1,2,3,4,5, 7], only HCNNs with nonoscillating leakage coefficients are studied. One can observe that all results there and the references cited therein can not be applicable for system (4.1) or (4.2). Moreover, the existence of pseudo almost periodic solutions on HCNNs with complex deviating arguments has not been touched in [1, 6, 8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33] and hence the results there cannot be applied to system (4.1) or (4.2).
5 Conclusions
In this paper, the existences and uniqueness of pseudo almost periodic solutions for high-order cellular neural networks models with complex deviating arguments and involving time-varying delays, and continuously distributed delays in the leakage terms have been discussed. By employing differential inequality techniques, several sufficient conditions have been obtained to ensure the existence and uniqueness of pseudo almost periodic for the considered neural networks. The proposed results extend and improve some known results. In order to demonstrate the usefulness of the presented results, some numerical examples are given. The established results are compared with those of recent methods existing in the literature. We expect to extend this work to the anti-periodic solution and weighted pseudo almost periodic solution problems on high-order cellular neural networks models with oscillating leakage coefficients and complex deviating arguments.
References
Zhang A (2013) Existence and exponential stability of anti-periodic solutions for HCNNs with time-varying leakage delays. Adv Differ Equ 2013(162):1–14
Cao J, Ho DWC (2005) A deneral framework for global asymptotic stability analysis of delayed neural networks based on LMI approach. Chaos Solitons Fractals 24:1317–1329
Vidyasagar M (1993) Nonliear systems analysis. Englewood Cliffs, New Jersey
Ou CX (2008) Anti-periodic solutions for high-order Hopfield neural networks. Comput Math Appl 56(7):1838–1844
Tunc C (2015) Pseudo almost periodic solutions for HCNNs with time-varying leakage delays. Moroc J Pure Appl Anal 1:51–69
Yu Y (2016) Global exponential convergence for a class of HCNNs with neutral time-proportional delays. Appl Math Comput 285:1–7
Xu C, Li P (2017) Pseudo almost periodic solutions for high-order Hopfield neural networks with time-varying leakage delays. Neural Process Lett 46:41–58
Liu B, Huang L (2007) Existence of periodic solutions for cellular neural networks with complex deviating arguments. Appl Math Lett 20:103–109
Yang X, Li F, Long Y, Cui X (2010) Existence of periodic solution for discrete-time cellular neural networks with complex deviating arguments and impulses. J Frankl Inst 347:559–566
Liu B, Tunc C (2015) Pseudo almost periodic solutions for CNNs with leakage delays and complex deviating arguments. Neural Comput Appl 26:429–435
Zhang A (2017) Pseudo almost periodic solutions for CNNs with oscillating leakage coefficients and complex deviating arguments. J Exp Theor Artif Intell. doi:10.1080/0952813X.2017.1354084
Zhou Q (2016) Pseudo almost periodic solutions for SICNNs with leakage delays and complex deviating arguments. Neural Process Lett 44:375–386
Gopalsamy K (2007) Leakage delays in BAM. J Math Anal Appl 325:1117–1132
Liu B (2013) Global exponential stability for BAM neural networks with time-varying delays in the leakage terms. Nonlinear Anal Real World Appl 14:559–566
Hartung F, Krisztin T, Walther HO, Wu J (2006) Functional differential equations with state-dependent delays: theory and applications. In: Handbook of differential equations, vol. 3. Elsevier, Amsterdam
Liu B (2015) Pseudo almost periodic solutions for neutral type CNNs with continuously distributed leakage delays. Neurocomputing 148:445–454
Liu B (2015) Pseudo almost periodic solutions for CNNs with continuously distributed leakage delays. Neural Process Lett 42:233–256
Wang W, Liu B (2014) Global exponential stability of pseudo almost periodic solutions for SICNNs with time-varying leakage delays. Abstr Appl Anal 2014(967328):1–18
Diagana T (2006) Weighted pseudo almost periodic functions and applications. C R Acad Sci Paris Ser I 343(10):643–646
Diagana T (2008) Weighted pseudo-almost periodic solutions to some differential equations. Nonlinear Anal 68:2250–2260
Zhou Q, Shao J (2016) Weighted pseudo anti-periodic SICNNs with mixed delays. Neural Comput Appl. doi:10.1007/s00521-016-2582-3
Yu Y (2017) Exponential stability of pseudo almost periodic solutions for cellular neural networks with multi-proportional delays. Neural Process Lett 45:141–151
Zhang C (2003) Almost periodic type functions and ergodicity. Kluwer Academic/Science Press, Beijing
Liu X (2016) Improved convergence criteria for HCNNs with delays and oscillating coefficients in leakage terms. Neural Comput Appl 27:917–925
Liu X (2015) Exponential convergence of SICNNs with delays and oscillating coefficients in leakage terms. Neurocomputing 168:500–504
Long Z (2016) New results on anti-periodic solutions for SICNNs with oscillating coefficients in leakage terms. Neurocomputing 171(1):503–509
Wang C, Agarwal RP (2016) Almost periodic dynamics for impulsive delay neural networks of a general type on almost periodic time scales. Commun Nonlinear Sci Numer Simul 36:238–251
Wang C (2016) Piecewise pseudo almost periodic solution for impulsive non-autonomous high-order Hopfield neural networks with variable delays. Neurocomputing 171(1):1291–1301
Wang C (2015) Uniformly rd-piecewise almost periodic functions with applications to the analysis of impulsive-dynamic system on time scales. Appl Math Comput 259(15):271–292
Wang C (2014) Almost periodic solutions of impulsive BAM neural networks with variable delays on time scales. Commun Nonlinear Sci Numer Simul 19(8):2828–2842
Wang C, Agarwal RP (2015) Relatively dense sets, corrected uniformly almost periodic functions on time scales, and generalizations. Adv Differ Equ 2015:312
Wang C, Agarwal RP, ORegan D (2016) Periodicity, almost periodicity for time scales and related functions. Nonauton Dyn Syst 3(1):24–41
Wu J (2001) Introduction to neural dynamics and signal trasmission delay. Walter de Gruyter, Berlin
Acknowledgements
The author would like to express the sincere appreciation to the editor and reviewers for their helpful comments in improving the presentation and quality of the paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zhang, A. Pseudo almost periodic high-order cellular neural networks with complex deviating arguments. Int. J. Mach. Learn. & Cyber. 10, 301–309 (2019). https://doi.org/10.1007/s13042-017-0715-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13042-017-0715-3
Keywords
- High-order cellular neural networks
- Pseudo almost periodic solution
- Existence
- Oscillating leakage coefficient
- Complex deviating argument