Introduction

Knowing about the rock mechanical parameters, including Young’s modulus and Poisson’s ratio, is one of the most essential tasks in the oil and gas industry. These parameters are important in geomechanics applications, such as the determination of mud weight windows, casing design, hydraulic fracturing, and sand production. Rock elastic parameters can be calculated by two methods of laboratory tests and downhole measurements. In laboratory tests, the elastic parameters are measured using core samples and the downhole measurements are done using well-logging data, such as compressional and shear velocities. The result of laboratory tests and downhole measurements is called the static and dynamic elastic parameters, respectively (Mavko et al. 2020; Tiab and Donaldson 2015).

The problems of laboratory methods are the unavailability of sample tests, lack of access to appropriate facilities, and the high cost of tests. Therefore, in recent years, attention to downhole measurements has increased. The advantages of using dynamic measurement methods includes: non-destructive testing, cost-effective in terms of cost and time, as well as covering the whole reservoir intervals, which has made this method efficient (Zhang and Bentley 2005). Dynamic and static values are very different from each other and static values are more important; therefore, different empirical correlations will be used to convert dynamic values to static values (Du et al. 2001). The dynamic parameters require the data of shear velocity Vs; however, this information is not always determined in all intervals of wells. To predict the mechanical parameters, in recent years, many researchers have used machine learning methods. Ranjbar-Karami et al. (2014) predicted the rock elastic parameters such as Young’s modulus, Poisson’s ratio, shear modulus, and bulk modulus using an improved Fuzzy Inference System (FIS) based on the South Pars Gas Field data. Results of this study showed FIS is successful in the estimation of static mechanical properties. Armaghani et al. (2015) predicted the E and UCS using ANFIS and ANN methods. The results showed that the ANFIS method is a more appropriate one than the ANN in predicting these parameters. Yin et al. (2016) developed a new method for assessing Young’s modulus and Poisson’s ratio in reservoir rocks. Aboutaleb et al. (2018) predicted Estatic and UCS using the ANN and SVM models based on the data of the Asmari Formation. Elkatatny et al. (2019) used the ANFIS, ANN, SVM machine learning methods for estimation of static Young’s modulus based on Well-logging data including RHOB, DTc, and DTs as input. The results showed that the ANN was the model with high accuracy for estimating static Young’s modulus. Mahmoud et al. (2019) developed the ANN-based empirical correlation for calculating the static Young’s modulus based on the data from sandstone formation. Abdulraheem (2019) predicted static Poisson’s ratio applying compressional and shear wave velocity data using ANN and Fuzzy Logic Type-2 (FLT2). This study was done based on 75 data from carbonate rocks and the results showed that the ANN method has better results. Gowida et al. (2020) predicted the static Poisson’s ratio using the ANN and ANFIS models. The input data were RHOB, DTc, and DTs and the results indicated that the ANN model has more appropriate results. Ahmed et al. (2021b) applied functional network (FN) and random forest (RF) methods based on the drilling data to predict the static Poisson's ratio. This study was done based on the 1775 sample data of different rocks, including shale, sand, and carbonate. The results showed that the RF method has a high correlation coefficient and a low error value. In the other study, these researchers used drilling data as input and using the ANN, ANFIS, and SVM, the static Poisson’s ratio was predicted. The results showed that the SVM method has more suitable results for calculating the static Poisson’s ratio than the other two methods (Ahmed et al. 2021a). Siddig and Elkatatny (2021) constructed a model to predict the static Young’s modulus based on the drilling data using ANN and SVM methods. The results showed that the two methods have appropriate results to predict Young’s modulus. Lawal et al. (2021) predicted UCS, tensile strength (TS), shear strength (SS), and YM of coal using the MARS (multivariate adaptive regression spline), double input–single output ANN ((DISO–ANN) and genetic algorithm (GA). It was found that the proposed models are capable of predicting mechanical properties of coal to a high degree of accuracy, and the relationships between the best fitness and mean fitness in GA dictated its prediction capability. Fattahi and Shirinzade (2022) developed a new method to estimate the mechanical properties of carbonate rocks based on physical properties and petrographic characteristics using support vector regression (SVR) improved by metaheuristic algorithms (harmony search (HS), grey wolf optimizer (GWO), cuckoo search (CS), dolphin echolocation (DE) and genetic algorithm (GA)). As the literature review shows, there is no single model to be superior to others in all cases and the performances of different models may be different according to condition of each input parameters. Thus, ensemble techniques can be used as post-process approaches to improve prediction models by combining the outputs from different single models. The main idea of these models is to use the unique capabilities of each model to better estimate the data series pattern.In various studies, it has been shown that ensemble methods can improve performance and reduce modeling error (Bates and Granger 1969; Clemen 1989; Nourani et al. 2018). Shamseldin et al. (1997) used three different methods to estimate the runoff model and showed that the output combination of different models gives an appropriate estimate of runoff compared to the initial single models. Zhang (2003) used an ensemble model of neural networks model in combination with an autoregressive integrated moving average (ARIMA) to predict time series, which showed that the model combination increased prediction accuracy.

Many studies have been conducted using artificial intelligence to predict elastic parameters from well logs. Based on these studies, the main components of single AI methods were identified and modeled. However, ensemble models have not been much discussed despite their higher accuracy and efficiency in predicting the elastic parameters of well logs. Therefore, this study creates ensemble models using the results of single models and evaluates their efficiency. The following steps have been done to determine the static elastic parameters. First, the empirical correlations between dynamic and static modulus were developed using the results of 34 laboratory core samples. Then, the static values of parameters YM and PR in whole logged intervals were calculated using the proposed correlations. Due to the lack of access to shear wave velocity (Vs) data, well log data including compressional wave transit time (DT), density (RHOB), and porosity (NPHI) were used as inputs. Moreover, the static elastic parameters data obtained from the empirical correlations are used as the output of the models. To predict the elastic parameters, machine learning methods, including adaptive Neuro-fuzzy inference system (ANFIS), artificial neural network (ANN) and support vector machine (SVM) have been used. Finally, the best model for determining the static YM and static PR has been selected by determining the value of the coefficient of determination (R2) and the error value. Then, as a new innovation in the study is that ensemble models were developed from the outputs of the single models, thereby improving the modeling results. Different AI models have been used to predict elastic parameters, but this study is the first to utilize three ensemble methods, including simple averaging ensembles, weighted averaging ensembles, and neural network ensembles.

Geological setting

The sample data and petrophysical logs used in this study belong to one of the gas fields in southern Iran. The reservoir part of this field is mainly related to Kangan and Dalan formations. Figure 1 shows these formations that are divided into five layers K1 to K5, in which layers K1 and K2 are related to Kangan, layers K3 and K4 are related to the upper Dalan, and layer K5 belongs to the lower Dalan and Nar section. Geologically, reservoir layers in Dalan and Kangan Formations have Upper Permian to Lower Triassic age, and based on petrophysical studies, the rocks are carbonate including dolomite, anhydrite, and iron ores, such as siderite, hematite, and magnetite.

Fig. 1
figure 1

Stratigraphy of the studied formations in southern Iran

Full size image

Theory

Rock elastic parameters

Rock mechanics is defined as the science of studying the behavior and deformation of rock against external and internal factors. The importance of this deformation process has led petroleum engineers to pay attention to this science. Knowing the rock elastic parameters at the lifecycle of a well helps engineers to understand the conditions and possible changes. In addition, it is very essential to determine the rock elastic parameters for analyzing wellbore stability, predicting hydraulic fracture, and sand production. The main rock elastic parameters include Young’s modulus and Poisson’s ratio. Young’s modulus can be defined as the ratio between stress and strain and Poisson’s ratio can be expressed as the ratio between lateral strain to axial strain (Zhang 2019). Calculation of rock elastic parameters can be done by two general methods, including laboratory measurement methods on core samples (static) and determination of elastic parameters using the results of density logs and sonic wave velocity (dynamic). According to the previous studies, static parameters are less than dynamic values (Plona and Cook 1995). This difference is due mainly to strain amplitude. In the dynamic method, this value is much smaller than in the static method (Ranjbar-Karami et al. 2014).

This study imposes limitations on modeling due to the lack of correlation between the input and output data, since there are 2790 samples and 34 samples, respectively. Therefore, empirical correlations between dynamic and static modulus were obtained. Then, with the help of these relationships, the dynamic values were converted to static values and the data for all the well intervals (2790 samples) were calculated and these data were used as the output of the models. In addition, since the static parameters are dependent on the dynamic parameters, this limitation has caused the dynamic modulus to be calculated solely to develop empirical correlation. As a result of these limitations, 34 core samples at depths between 2650 and 2820 from one of the southern Iranian gas fields were tested using the UCS test. Static YM is defined as the tangential modulus (Et) at 50% of maximum strength. The static PR is derived from the ratio of radial to axial strain. As well, dynamic elastic parameters based on the shear wave velocity, compression wave velocity, and density are calculated as follows (Fjar et al. 2008):

$${E}_{d}=\rho {V}_{s}^{2}\frac{3 {V}_{p}^{2}-4 {V}_{s}^{2}}{ {V}_{p}^{2}- {V}_{s}^{2}}$$
(1)
$${\vartheta }_{d}= \frac{{V}_{p}^{2}- 2 {V}_{s}^{2}}{2\left( {V}_{p}^{2}- {V}_{s}^{2}\right)}$$
(2)

where Ed is dynamic Young’s modulus (GPa), \(\rho\) is bulk density (g/cm3), Vs is shear wave velocity (km/s), Vp is compressional wave velocity (km/s) and \({\vartheta }_{d}\) is dynamic Poisson’s ratio.

The empirical correlations between static and dynamic elastic parameters were developed using the dynamic and static results, as shown in Fig. 2. The results obtained for the Poisson’s ratio in the linear mode indicate a low correlation coefficient; however, to determine the empirical relationship with the high correlation, it is essential to remove the y-intercept from the model. Results without y-intercept showed a higher correlation coefficient and a higher accuracy. The empirical model considering the y-intercept is expressed in Eq. (3), which has a correlation coefficient of 0.96. In addition, the empirical relationships and its correlation coefficients for static YM is shown in Eq. (4):

Fig. 2
figure 2

Correlation between dynamic and static elastic parameters

Full size image
$${\vartheta }_{s}=0.72 {\vartheta }_{d} {R}^{2}=0.96$$
(3)
$${E}_{s}=0.5624 {E}_{d}-13.91 {R}^{2}=0.86$$
(4)

Lower correlation coefficient of Eq. (5) may be due to dependence of the equation to y-intercept. Furthermore, Poisson’s ratio in Eq. (3) (with no y-intercept) has higher correlation of coefficient. Therefore, it has been used for predicting Poisson’s ratio:

$${\vartheta }_{S}= 0.504 {\vartheta }_{d} + 0.0768 {R}^{2}=0.30$$
(5)

where E and \(\vartheta\) are Young’s modulus and Poisson’s ratio, respectively. The subscripts d and s represent the dynamic and static values. Then, the static YM and PR were calculated using the equations obtained from Fig. 2 for depth intervals 2650–2820, the results of them are illustrated in Fig. 3.

Fig. 3
figure 3

Comparing dynamic and static elastic parameter values versus depth

Full size image

Machine learning methods

Adaptive neuro-fuzzy inference system (ANFIS)

The ANFIS system was first introduced by Jang (1993). In the fuzzy part of the ANFIS system using the membership functions and rules (if and then), a relationship is established between the input and output variables, and the characteristics related to the fuzzy part membership functions are determined by the neural network (Grima et al. 2000; Sezer et al. 2014). A fuzzy system is defined as Eq. (6) (Kalkan et al. 2009):

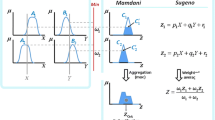
$$A=\left\{ \left(x . {\mu }_{A \left(x\right)}. x \in X\right)\right\}$$
(6)

where x is a member of X and \({\mu }_{A}\) is the degree of membership of x, the value of which is between zero and one variable. Membership functions are used to consider the degree of membership. These functions include a variety of functions, including triangular, trapezoidal, Gaussian, s-shape, z-shape, and sigmoidal. Fuzzy inference systems rely on two kinds of Mamdani (Mamdani and Assilian 1975) and Takagi–Sugeno-Kang (TSK–FIS) (Sugeno and Kang 1988). ANFIS model uses the Sugeno system as the main modeling system. Figure 4 shows a first-order fuzzy Sugeno model with two inputs (x, y), one output (f), and two membership functions for each input. In this model two rules (if and then) are defined as Eq. (7) (Takagi and Sugeno 1985):

$$\mathrm{If} x \mathrm{is} {A}_{1} \mathrm{and} y \mathrm{is} {B}_{1} \mathrm{then} {f}_{1}= {p}_{1 }x+ {q}_{1}y+{r}_{1} \left(\mathrm{rule} 1\right)$$
(7)
$$\mathrm{If }x\mathrm{ is }{A}_{2}\mathrm{ and }y\mathrm{ is }{B}_{2}\mathrm{ then }{f}_{2}= {p}_{2} x+ {q}_{2}y+ {r}_{2} \left(\mathrm{rule }2\right)$$

where A1, A2, B1, and B2 are the membership functions for x, y inputs, respectively, and p1, p2, q1, q2, r1, and r2 are the parameters of the output function.

Fig. 4
figure 4

Schematic of ANFIS architecture (Kalkan et al. 2009)

Full size image

The fuzzy system has steps, including, fuzzified inputs, applying the fuzzy operator and implication method, applying aggregation method, and defuzzification. In the first step, the input set will be fuzzy using the membership functions and these membership functions are defined through clustering. In the next step, a set of fuzzy rules was created to communicate the input and output parameters, and finally outputs are created that uses diffuse methods to convert the fuzzy output of the system into a non-fuzzy output.

Artificial neural network (ANN)

The artificial neural network system is inspired by the biological neural system to process information, and it processes information like the human brain. The main task of an artificial neural network is to pattern recognition, identification, classification information, and approximate a function during a learning process (Kalkan et al. 2009). Figure 5 shows the neural network system in which this system, including input layer, hidden layer, and output layer parts, each of layer has responsible for receiving data, processing, and producing output layers. Artificial neural networks are created from simple processing units called neurons. Neurons receive the information in the input layer and transfer it to the hidden layer for processing, and finally transfer the processed data to the output layer. The number of neurons in the input and output layers depends on the input and output parameters in the model, and usually, the number of neurons in the hidden layer will be determined based on the complexity of the problem. The signal is transmitted between neurons through weighted communication links that connect all layers of the network with connections of different weights.

Fig. 5
figure 5

Schematic of the ANN method

Full size image

The most common type of artificial neural network is the feed-forward Multilayer Perceptron (MLP). These types of networks consist of an input layer, one or more hidden layers, and one output layer, and weight is considered for each connection (Adhikary and Mutsuyoshi 2006). The back-propagation algorithm is one of the widest algorithms for training feed-forward MLP artificial neural networks. In this method, the gradient descent technique is used. The errors will be split from the input layer to the output layer and the weights will be corrected until the error was minimized. Therefore, the training process of this system is a gradual correction of weights to minimize the error function. This operation continues until the model responds positively to one of the applied stop criteria (Mukherjee and Biswas 1997).

Support vector machine (SVM)

SVM is based on statistical learning theory developed by Vapnik (1999). This model uses the inductive principle of structural error minimization. The two main categories of SVM are Support Vector Classification (SVC) and Support Vector Regression (SVR). SVC is used to solve data classification with different classes and SVR is used for predictive data. The aim of SVR is to create a linear regression hyperplane expressed in Eq. (8) that allows as many deviations from the true values as is possible (Fig. 6) while at the same time trying to find a solution that is as flat (Chapelle and Vapnik 1999; Cortes and Vapnik 1995; Gholami and Moradzadeh 2012):

$$y= {W}_{0}^{t} {\phi }_{\left(x\right)}+b$$
(8)

where b is the bias, \({W}_{0}^{t}\) is the optimum weight vector, and \({\phi }_{\left(x\right)}\) is input variable transformed to a higher dimensional feature space by means of a mapping function. Solving the above minimization problem leads to an optimum hyperplane that results in the smallest possible generalization error. The formula to calculate the SVR model prediction is as follows (Dutta et al. 2010):

$$\begin{aligned} f_{\left( x \right)} & = \mathop \sum \limits_{i = 1}^{n} \left( { \alpha_{i} - \alpha_{i}^{*} } \right) . \phi_{{\left( {x_{i} } \right)}} . \phi_{\left( x \right)} + b \\ & = { }\mathop \sum \limits_{{i = 1{ }}}^{n} \left( {{ }\alpha_{i} - { }\alpha_{i}^{*} } \right){ }.{ }K_{{\left( {x_{{i{ }}} ,{ }x} \right)}} + b \\ \end{aligned}$$
(9)

where \({\alpha }_{i}, {\alpha }_{i}^{*}\) are the weights corresponding to individual input parameters, and K(xi, x) is a user-defined kernel function. A common kernel function is the isotropic Gaussian RBF defined as follows (Dutta et al. 2010):

$${K}_{\left( {x}_{i} , x\right)}={e}^{\frac{- \left|{x}_{i}-{\left.x\right|}^{2}\right.}{2 {\sigma }^{2}}}$$
(10)

where \(\sigma\) is the kernel bandwidth.

Fig. 6
figure 6

Schematic of the SVM

Full size image

Ensemble learning techniques

Ensemble techniques predict the needed results with higher accuracy than single methods, so their use has become more widespread, and researchers are paying more attention to them. In this method, the capability of single model is used to enhance the performance of the ensemble technique. In this study, several ensemble techniques were used to improve the performance of the single models, including simple averaging ensemble (SAE), weighted average ensemble (WAE), and neural network ensemble (NNE).

The SAE method consists of training ANFIS, ANN, and SVM models separately, then comparing their output results with the measured values. The equation for SAE is as follows:

$${P}_{(d)}=\frac{1}{N}{\sum }_{i=1}^{N}{p}_{i}(d)$$
(11)

where N is number of learners (N = 3) and pi is output of single model (ANFIS, ANN, and SVM) at depth d.

Weighted averaging assigns different weights to single model outputs based on their relative significance. In general, WAE is expressed in the following formula:

$${P}_{(d)}={\sum }_{i=1}^{N}{{w}_{i }p}_{i}(d)$$
(12)

where wi is applied weight on output model. This parameter canbe determined using Eq. (13) as follows:

$${w}_{i}=\frac{{R}_{i}^{2}}{{\sum }_{I=1}^{N}{R}_{i}^{2}}$$
(13)

\({R}_{i}^{2}\) is the coefficient of determination for single models.

In the NNE method, new neural networks are trained. The neural ensemble model's input layer is derived from the outputs of the ANN, ANFIS, and SVM models. The training of a neural ensemble model such as single ANN can be achieved using the BP algorithm by considering tangent sigmoid as activation functions. Furthermore, the best epoch number and structure for the ensemble network can be determined through trial and error. There are many different non-linear kernels (e.g., ANFIS, SVM, etc.) that can be used in a non-linear assembly, but in this study, the ANN was used, since it is the most widely used AI method. Figure 7 illustrates the proposed neural ensemble method.

Fig. 7
figure 7

Schematic of neural ensemble model

Full size image

Evaluation criteria

The efficiency and accuracy of machine learning models are evaluated using several criteria. These criteria include the coefficient of determination (R2), Mean Absolute Percentage Error (MAPE), and Root Mean Square Error (RMSE), which examine the performance of the model as essential statistical criteria. Equations (14)–(16) will be used to calculate these parameters:

$${R}^{2}= \frac{\left(\sum_{i=1}^{n}\left({M}_{rm}-{\overline{M} }_{rm}\right){\left.\left({M}_{rp}-{\overline{M} }_{rp}\right)\right)}^{2} \right.}{\sum_{i=1}^{n}({\left.{M}_{rm}-{\overline{M} }_{rm}\right)}^{2} \sum_{i=1}^{n}({\left.{M}_{rp}-{\overline{M} }_{rp}\right)}^{2}}$$
(14)
$$\mathrm{MAPE}= \frac{1}{n} \sum_{i=1}^{n}\left(\left|\frac{{M}_{rm}- {M}_{rp}}{{M}_{rm}}\right|\right)$$
(15)
$$\mathrm{RMSE}= \sqrt{\frac{\sum_{i=1}^{n}{\left({M}_{rp}- {M}_{rm}\right)}^{2}}{n}}$$
(16)

where \({M}_{rm} \mathrm{and} {M}_{rp}\) are the measured and predicted values, respectively, \({\overline{M} }_{rm} , {\overline{M} }_{rp}\) is the average measured and predicted values, respectively, and n is the number of samples. According to previous studies, systems indicate high efficiency when it has a high coefficient of determination (close to 1) and low error value (close to zero) (Armaghani et al. 2015; Elkatatny et al. 2019; Ranjbar-Karami et al. 2014).

Methodology

Data analysis

Artificial intelligence (AI) models are data-driven, the use of different data as input of AI models cannot guarantee high accuracy results. Therefore, having a criterion for reviewing the data helps to select the appropriate data as input data. One of these criteria is the correlation coefficient (CC) between input and output data (Eq. 17) (Elkatatny et al. 2019):

$$\mathrm{CC}= \frac{n \sum xy - (\sum x) ( \sum y)}{\sqrt{n (\sum {x}^{2}) - {\left(\sum x\right)}^{2} }. \sqrt{n (\sum {y}^{2}) - {\left(\sum y\right)}^{2}}}$$
(17)

where n is the sample size, x and y are the input and output data. In this study, CC was calculated between conventional well logs as inputs (DT, NPHI, and RHOB) and the elastic parameters as output. As is seen from Fig. 8, static Young’s modulus parameter has an inverse relationship with DT, NPHI, and also a linear relationship with RHOB. The figure also shows the static Poisson’s ratio is an inverse relationship to all parameters. The DT shows the highest correlation and the NPHI shows the lowest correlation with the elastic parameters.

Fig. 8
figure 8

Relative importance of input parameters with a static value of YM and PR

Full size image

Data description

The performance of AI models depends on having high-quality data. In this study, data related to shear wave velocity (Vs) were not measured, and also according to the results of correlation coefficient (Fig. 8) from well logs data including DT, RHOB, and NPHI have been used as modeling inputs. 2790 data are used which are the result of well-logging data. DT range is between 45.11 and 71.78 (\(\mathrm{\mu s}/\mathrm{ft}\)), NPHI is between 0 and 0.29 (\(\mathrm{v}/\mathrm{v}\)) and RHOB range is between 1.37 to 3.95 (g/cm3). Data are divided into three parts: 70% (1953) are used for training, 20% (559) for testing, and 10% (278) for validation. Table 1 lists the statistical analysis of the data.

Table 1 Statistical description of the data
Full size table

ANFIS architecture

The structure of ANFIS entails determining the number of input and output membership functions. The subtractive clustering method has been used to determine the membership function. In this method, the clustering radius for 10 TSK–FIS was changed from 0.1 to 0.55 with 0.05 intervals to obtain the number of rules for ANFIS modeling. The evaluation criterion of the model is based on the error in testing data. Therefore, based on the results obtained for estimating the static value of YM and PR, the optimal clustering radius is 0.4 and 0.1, which correspond to error values of 0.76 and 0.0037, respectively. Accordingly, the number of membership functions generated for YM and PR are 2 and 10, respectively. Gaussian function as input and linear function as output were used and the hybrid algorithm was used to train the model. Table 2 shows the results of the clustering radius and the error obtained in each step. Figure 9 also shows the structure of two ANFIS models for estimating the static value of static elastic parameters.

Table 2 Error values and clustering radius for estimating YM and PR
Full size table
Fig. 9
figure 9

Schematic of ANFIS for determining the static value of YM and PR

Full size image

ANN architecture

The main challenge of the neural network method is to determine the number of hidden layers, many people have introduced different methods to determine the hidden layer. Ham and Kostanic (2001) explained trial and error method can be determined by hidden layers. In addition, many studies have stated that one or two hidden layers can estimate almost all complicated problems well (Basheer 2000; Gordan et al. 2016; Hecht-Nielsen 1987; Hornik et al. 1989). In this study, one hidden layer was used to construct the ANN model. To determine the number of neurons in this layer in each step, the number of neurons was changed between 1 and 20, and by measuring the error in each step, the appropriate number of neurons in the hidden layer was selected. Based on the results obtained for estimating the static value of YM and PR, the number of neurons used to create the ANN model for YM and PR are 10 and 8, which correspond to error values of 0.309 and 2.09796e–06, respectively. Input and hidden layers are transferred using linear-type activation function and hidden and output layers by TAN-sigmoidal-type activation function. As a training algorithm, Levenberg–Marquardt backpropagation is used. Figure 10 illustrates the various steps taken by the ANN model to estimate YM and PR.

Fig. 10
figure 10

Schematic of ANN for determining the static value of YM and PR

Full size image

SVM architecture

In the SVM method, the input and output data are entered and then the calculations related to the SVM regression will be performed according to the kernel selection. In this case, there are different kernels, including linear, quadratic, cubic, fine Gaussian, medium Gaussian, and coarse Gaussian. SVM model in each step determines the RMSE error for different kernels and finally, the appropriate result with low RMSE was selected. In this study, by modeling for different kernels, the RMSE errors obtained are shown in Table 3. By comparing the error values, in this case, it was concluded that cubic kernel functions have lower error values for estimating the YM and PR.

Table 3 RMSE error values of kernels
Full size table

Results and discussion

Single model predictions

In this study, the ability of ANFIS, ANN and SVM models to predict the static value of Young’s modulus and Poisson’s ratio has been investigated. ANFIS, ANN, and SVM models were created using three inputs DT, NPHI, RHOB, and two outputs YM and PR. According to the above, one of the criteria for evaluating the performance of models is the coefficient of determination (R2) between the measured and predicted values. Figures 11 and 12 show the results for predicting the static value of YM and PR using ANFIS for training, testing, and validation data. As shown in Fig. 11, the value of R2 between the measured and predicted static YM for training, testing, and validation data are 0.968, 0.926, and 0.907, respectively. In addition, these values for the static PR are 0.935, 0.851, and 0.896, respectively (Fig. 12).

Fig. 11
figure 11

Crossplot of R2 between measured and predicted static YM using ANFIS

Full size image
Fig. 12
figure 12

Crossplot of R2 between measured and predicted static PR using ANFIS

Full size image

Figures 13 and 14 show the static value of YM and PR predicted using the ANN model against the measured value for training, testing, and validation data, respectively. R2 obtained to predict static YM for training, testing, and validation data were 0.98, 0.958, and 0.948, respectively, as well as these values, are 0.958, 0.886, and 0.910 for static PR. In addition, using the SVM method, the values of R2 for the training, testing, and validation data are 0.946, 0.915, and 0.898 for the static YM, and the values of 0.927, 0.847, and 0.890 for the static PR, respectively, which in Figs. 15 and 16 were shown.

Fig. 13
figure 13

Crossplot of R2 between measured and predicted static YM using ANN

Full size image
Fig. 14
figure 14

Crossplot of R2 between measured and predicted static PR using ANN

Full size image
Fig. 15
figure 15

Crossplot of R2 between measured and predicted static YM using SVM

Full size image
Fig. 16
figure 16

Cross plot of R2 between measured and predicted static PR using SVM

Full size image

The efficiency of ANFIS, ANN, and SVM methods in predicting the static value of YM and PR, were compared using the parameters of coefficient of determination (R2), RMSE, and MAPE error value. As mentioned, the model has high accuracy results when the value of R2 is close to 1 and also the error values are close to zero. In this study, using the results obtained for the coefficient of determination (Figs. 11, 12, 13, 14, 15 and 16) and RMSE, MAPE values (Table 4), the efficiency of ANFIS, ANN, and SVM models are investigated, and finally the appropriate model for estimating the elastic parameters was selected. As shown in Table 4, performance indices have been derived by predictive models for training, testing, and validation data. According to this table, ANN predictive models perform better than other models at predicting elastic parameters. The results obtained from ANFIS and SVM methods show that these methods can also be used in predicting elastic parameters. However, these approaches should be used according to the situation and will be used when less accuracy is required.

Table 4 Performance indices of the predictive models
Full size table

Ensemble model predictions

The single model has appropriate performance in modeling in part of the reservoir depths and weak performance in prediction other parts; therefore, using ensemble methods, the results are improved compared to using single models. In this study, ANFIS, ANN, and SVM outputs based on NNE, SAE, and WAE are used to improve single model performance. According to this method, the data same as single model divided into 70% for training data, 20% for testing data and 10% for validation data, and the results from ensemble models for these data are shown in Table 5. The results of R2, MAPE, and RMSE show that ensemble techniques perform better than single models. Integrating outputs of different models reduces variance, bias, and improves overall modeling performance. Since each single model has its own strengths and weaknesses, so the effectiveness of ensemble techniques depends on the accuracy of the single models. The results of SAE and WAE are very similar, because they are both directly affected by single models. In addition, WAR is better than SAE, since weights are assigned based on relative importance parameters, whereas these factors are not considered in simple averages. Compared to two ensemble linear methods, the NNE performs better and predicts results more accurately due to its robustness in dealing with non-linear interactions and its ability to back propagate the generated error during the calibration phase to achieve the desired result. By contrast, two linear ensemble techniques are directly affected by single models, and weakness in one of them leads to weakness in the whole system, so applying the NNE method provides a higher level of accuracy. As shown in Figs. 17 and 18, the error values for the static value of YM and PR are calculated between the measured and predicted values. These values can be used to compare the performance between single and ensemble models. In addition, Fig. 19 shows the outputs obtained between the measured and predicted data for ANN and NNE models at depths between 2650 and 2820 for one of the gas wells in southern Iran.

Table 5 Results of ensemble techniques
Full size table
Fig. 17
figure 17

Comparison of the RMSE values of single and ensemble predictive models

Full size image
Fig. 18
figure 18

Comparison of the MAPE values of single and ensemble predictive models

Full size image
Fig. 19
figure 19

Comparison of elastic parameters measured and predicted based on depth for single and ensemble models

Full size image

Conclusion

ANFIS, ANN, SVM machine learning methods were used to predict the static elastic parameters based on the data of one of the gas fields in southern Iran. DT, NPHI, and RHOB well-logging data were used as input to create three models for prediction of static elastic. The created models were evaluated comparing the values of R2, the RMSE, and MAPE errors for the training, testing, and validation data of all the predictive models. Input data, including DT, RHOB, and NPHI logs could predict the results with high accuracy. The results for Young’s modulus and Poisson’s ratio showed that the coefficient of determination of the ANN method for training data was 0.979 and 0.958, respectively. The error values for this data were 0.0055 and 0.0019 for MAPE and 0.763 and 0.0051 for RMSE, respectively. According to these results and comparison with ANFIS and SVM methods, ANN had high accuracy in determining static elastic parameters. In addition, it can be concluded that these methods have high performance in predicting elastic parameters by considering the coefficient of determination of 0.968 and 0.935 for the ANFIS method and the values of 0.946 and 0.927 for the SVM method for static YM and static PR, respectively. The ANN method was more accurate than the other two methods and provided more accurate predictions. Finally, ensemble models, including simple averaging ensembles (SAE), weighted averaging ensembles (WAE), and neural network ensembles (NNE), have been developed to improve single models. The RMSE, MAPE, and R2 results indicate ensemble models produce better results than single models. The results of SAE and WAE are very similar, since they are both directly affected by single models; however, WAE slightly outperformed SAE. In addition, NNE results showed that this method was more reliable, robust, and accurate than both linear methods.