1 Introduction

Characterization of petroleum-bearing rocks needs a very high degree of accuracy. Minor error can lead to enormous loss of money and man-hours. On the contrary, a slight improvement in the prediction scenarios can have exponential improvement on production and exploration projects [1,2,3,4,5]. Current predictive models are fulfilling the basic needs of the petroleum industry, but there is an ever going quest for improved and better results [6]. AI tools once optimized for training can predict required feature more accurately than the nonlinear regression methods [7,8,9,10]. Some of the domains of the petroleum engineering in which AI techniques brought improvements include porosity–permeability predictions [11,12,13,14], hydraulic flow unit identification [15], geomechanics parameters estimation [16,17,18,19,20,21,22], geophysical well logs estimation [9, 23], well test parameters estimation [24, 25], asphaltene prediction [26, 27], water saturation prediction [28, 29], and many other oil and gas applications.

Elastic parameters are required to determine the in situ stresses of the rock which in turn are needed to construct the geo-mechanical earth models [30,31,32,33,34]. Determining elastic parameters of the rock is very substantial in minimizing the risk associated with the oil and gas well drilling. Their accurate estimation helps in well placement optimization, calculating safe mud weight window, handling wellbore stability, optimizing fracturing operations, etc. [35,36,37]. These factors contribute to maximize the hydrocarbon recovery. Inaccurate estimation of the elastic parameters can falsely steer to wrong economic decisions and unsuitable field development strategies [9, 16, 38, 39].

Retrieving core samples and conducting laboratory experiments on them under a simulated reservoir condition is the accurate way to measure the in situ rock mechanical parameters, but this approach is very expensive as well as time-consuming [9, 17, 19, 40]. Often majority of the wells completed have very limited rock mechanical data. Alternatively, well log data are always recorded and readily available. Then, the correlations are developed between the elastic parameters obtained from the rock mechanical tests on the retrieved core sample and the available petrophysical well logs such as bulk density, neutron porosity, and sonic logs [41].

The correlations derived from the petrophysical logs are used to produce continuous static Poisson’s ratio profile throughout the depth of interest [17, 30, 39]. However, core samples are taken from limited intervals, and the applicability of these correlations is mostly narrow [16, 38]. Often the calibration of dynamic Poisson’s ratio profiles is carried out by computing the difference between the static Poisson’s ratio and the dynamic Poisson’s ratio of the selected core samples. This difference is added to the dynamic Poisson’s ratio profiles to shift them near the points of static Poisson’s ratio values [19, 40, 42]. This technique is very expensive and only limited to the sections where the core samples were obtained. Most important aspect of this relationship is that most of the time the scatter is too large to come up with a reasonable relationship and this relationship does not work for the entire interval in the case of lithology heterogeneity especially in carbonate reservoirs.

In the absence of the core data and other direct downhole strength measurement, static Poisson’s ratio is estimated from the well log data using empirical correlations. D’Andrea et al. [43] investigated the effect of ultrasonic wave transit time on static Poisson’s ratio for different rock specimens and found that static Poisson’s ratio decreases with the increase in transit time. Kumar et al. [44] applied nonlinear regression technique to predict static Poisson’s ratio using P-wave and S-wave velocities. Phani [45] investigated the effect of shear wave velocity on static Poisson’s ratio for materials with different pore size distributions. He found that materials containing needle-like and spherical shaped pores show that Poisson’s ratio decreases with the decrease in S-wave velocity. Edimann et al. [46] and Kumar et al. [44] found that increase in porosity of the rock results in higher Poisson’s ratio. They developed a correlation to predict static Poisson’s ratio using porosity. Al-Shayea [47] investigated the impact of micro-cracks and lithological variations on static Poisson’s ratio values. He also correlated confining pressure with the static Poisson’s ratio. Singh and Singh [48] used neuro-fuzzy approach to predict Poisson’s ratio of sandstone and shale rocks. The input parameters of their model were uniaxial and triaxial strength parameters. Shalabi et al. [49] related static Poisson’s ratio with rock hardness and unconfined compressive strength (UCS) using linear regression technique. Their correlation is valid for shale rocks only. Al-Anazi and Gates [50] used SVR to estimate static Poisson’s ratio. The input variables of their SVR model were rock porosity, bulk density, pore pressure, minimum horizontal stress, overburden stress, P-wave velocity, and S-wave velocity.

With the reference of vast literature review and to the authors’ knowledge, till now, no significant work has been done to formulate empirical correlation to estimate the static Poisson’s ratio directly from petrophysical well logs for carbonate rocks. Most of the reported correlations in the literature were built using nonlinear regression technique which may not be generalized for unseen datasets [51]. On the down side, most of the AI models reported in the literature to predict static Poisson’s ratio are black boxes [16, 50]. Therefore, the objectives of this study are to: (1) develop a generalized model using AI tools to predict the static Poisson’s ratio from the commonly available conventional well logs such as bulk density, P-wave transit time, and S-wave transit time; (2) formulate tangible mathematical expression from the AI model to transform black box into white box to predict static Poisson’s ratio of carbonate rocks.

2 Materials and methods

2.1 Log data analysis

Petrophysical well log data were taken from ten wells. The well logs data include neutron porosity, bulk density, P-wave transit time, and S-wave transit time. The petrophysical log data were picked from the reservoir depth where the cores were available for static tests. Lithology cross-plot of neutron porosity and bulk density shows that most of the samples lie in limestone formation with a low percentage of sandstone and dolomite and with no gas effects as shown in Fig. 1. The range of bulk density was in between 2.00 and 3.05 g/cc, P-wave transit time between 44 and 97 µs/ft, and S-wave transit time between 73 and 170 µs/ft. A complete statistical description of the data used for training is given in Table 1.

Fig. 1
figure 1

Lithology cross-plot between neutron porosity and bulk density of the training data used for static Poisson’s ratio model

Full size image
Table 1 Training data statistics
Full size table

2.2 Laboratory experiments

Core data were generated from the experiments performed using triaxial compressional tests. A total of 120 samples were tested to measure static Poisson’s ratio. Extra care was taken to select homogeneous and sound samples free from any in situ cracks or weak stylolites. The dimensions of the prepared core samples were approximately 3″ length and 1.5″ diameter. The samples were prepared by cutting along the length of the reservoir core using a disk saw. The end faces of each core samples were carefully sliced and grounded parallelly to ensure fine smoothening. The fine smoothening is very essential; otherwise, it would have affected the experiment adversely by not allowing the pulse to transmit through the specimen because of air gap present in between crystal holder and specimen. To clean the core samples, toluene was used, and samples were then vacuum-dried in oven at 60 °C. Triaxial experiments were performed by placing the core sample axially while keeping a constant confining pressure corresponding to the effective in-situ horizontal stress. Each experiment was performed under dried and unsaturated condition. The samples were tested under room temperature, and confining pressures range from 1000 to 1500 psi. The samples were jacketed inside a heat-resistant rubber tubing. The rubber-jacketed core sample was then positioned between the steel end cap platens. Vacuum was used to remove any trapped air between steel end cap platens and jacketed sample. Using aluminum wires, the sample was then tightly secured with the end cap platens. After that, linear variable differential transducers (LVDTs) were mounted on the jacketed sample. The axial displacement was recorded using two LVDTs instrumented on the hardened steel platens opposite to each other with the help of an LVDT holder. The radial displacement was measured using radial LVDT fixed at the center along the length of the sample.

The confining pressure was increased to the required stage using desired rate in psi/sec by loading instrumented assembly in the confining chamber. The sample was loaded axially, after reaching the required value of confining pressure. The loading piston was lowered at a displacement rate of 0.025 mm/min. This displacement rate enabled the operator to complete the test according to the recommended practice of the American Society of Testing and Materials (ASTM D 2664-86, ASTM D 3148-93) and the International Society of Rock Mechanics (ISRM Suggested Methods, 13-127) [52]. During the loading phase, axial and radial displacements were recorded using LVDTs and the load on the sample was recorded using a load cell. Data acquisition was carried out using computer-controlled software. The stress–strain responses were generated for all samples, and elastic parameters (Poisson’s ratio and Young’s modulus) were calculated at 50% of the maximum peak stress. Figure 2 shows the stress–strain curve for one of the sample. A tangent line was drawn on axial stress–strain curve (right side) at 50% of peak stress which is 8000 psi. The slope of this line yields static Young’s modulus. On radial stress–strain curve (left side), another tangent line was drawn, and the slope of this line yields static Poisson’s ratio. This procedure was repeated for all 120 samples.

Fig. 2
figure 2

Laboratory determination of static Poisson’s ratio from the stress–strain curve

Full size image

2.3 Core and log data depth matching

Depth measured from well log values using wireline cables is usually not the same as the core depth, measured using drill strings. To remove any depth discrepancy, the first step taken was to match the log and the core depths. To achieve this, the petrophysical well log (neutron porosity) and laboratory measured values of core porosity were plotted together to visualize the difference between the log and the core depths. If there was any depth shift needed, then the correction was added or subtracted to the log depth, as given by Eq. (1)

$${\text{Depth}}_{\text{Log}} = {\text{Depth}}_{\text{Core}} \pm {\text{Depth}}_{\text{Shift}}$$
(1)

After that, depth column was removed to bring all the data on one set.

2.4 Correlation coefficient study

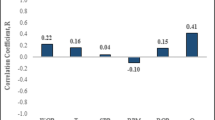
All AI models are data driven. The optimum way to select best input parameters is to find the relative importance by studying the correlation coefficient (CC) between inputs and the output parameter. The value of CC between the pair of two variables always lies in between − 1 and 1. A CC value close to ‘− 1’ shows the strong inverse relationship between a pair of two variables, while a value close to ‘1’ shows the strong direct relationship between the two variables. A CC value of zero shows that no relationship exists between the two variables. In this study, Pearson CC is used to find the relative importance between inputs and the static Poisson’s ratio. The definition of Pearson CC is given in “Appendix A”. Figure 3 shows the CC of P-wave transit time, S-wave transit time, bulk density, and neutron porosity with the static Poisson’s ratio. P-wave transit time, S-wave transit time, and neutron porosity show an inverse relation with static Poisson’s ratio, while bulk density shows a direct relation with static Poisson’s ratio. P-wave transit time has the highest CC of − 0.37, while static Poisson’s ratio, bulk density, and S-wave transit times have moderate CC of 0.35 and 0.29 with static Poisson’s ratio. Neutron porosity has the lowest CC of − 0.19 with the static Poisson’s ratio. Due to the low CC of neutron porosity with the static Poisson’s ratio, this input parameter was not used in the predictive modeling of static Poisson’s ratio.

Fig. 3
figure 3

Relative importance of the petrophysical well logs with the static Poisson’s ratio

Full size image

2.5 Data stratification

Dataset was divided randomly into two parts. 70% of the dataset was utilized for the training of the model, while the remaining 30% of the dataset was kept separate for the testing of the trained model. Data were stratified randomly by the MATLAB in a way that the testing data bounded within the limits of the training dataset. This splitting process ensured that the testing data fall within the range of training data. Figure 4 shows the location of the data points for both the training and testing.

Fig. 4
figure 4

Location of data points used for training and testing of the static Poisson’s ratio models

Full size image

2.6 Design and implementation of the artificial intelligence techniques

2.6.1 Artificial neural network (ANN)

An ANN is a supervised data learning AI technique which is based on natural learning features of biological neurons found in human brain [54, 55]. ANN stands on the elemental information processing units called as neurons. Each neuron in the system is linked to a system of nodes, and the resulting structure looks like a biological neurons network [56]. Every connection has an associated weight [57, 58]. Several studies [39, 59, 60] suggested that backpropagation feedforward neural network is more robust than the multilayer perceptron (MLP). A typical ANN model comprises of an input layer, one or more hidden layers and an output layer. Signals are received by the input layer, transferred to the hidden layer(s) where they are processed, and then sent to the output layer. The hidden layer processes each dataset based on a transfer function. This function is based on different mathematical forms such as tan-sigmoid form expressed as \(\sigma \left( x \right) = (2/1 + e^{ - 2x} ) - 1\), the log-sigmoid form expressed as \(\sigma \left( x \right) = 1/1 + e^{ - x}\), or the linear function which is commonly implemented in multilayer networks trained by the backpropagation algorithm. Optimization of the number of layers and neurons is recommended since having too many neurons in the system can result in over-fitting or memorization problem. Having a fewer number of neurons in the system can result in under-fitting [53, 61].

2.6.2 Adaptive network-based fuzzy interference systems (ANFIS)

ANFIS is a supervised data learning technique, based on fuzzy logic to translate input data to the output by a combination of interconnected neural networks, initiated by Jang in 1993 [62]. It is a learning technique which uses Sugeno fuzzy inference system [62–64]. It is based on the application of conventional Boolean logic, i.e., zeros and ones, which describes the principle of truthiness [62, 64, 65]. The steps needed to apply for a typical ANFIS model are as follows: define inputs and an output variable; declare fuzzy sets; define fuzzy rules; create and train the network [66, 67]. In ANFIS, the important parameter is cluster radius which plays a vital role in the predictive performance. Cluster radius defines the number of if–then rules. Smaller value of cluster radius generates higher number of rules, while larger value of cluster radius generates smaller number of rules. In principle, higher number of rules causes the problems like overprediction and memorization [63].

2.6.3 Support vector regression (SVR)

SVR is a supervised learning technique that can be used for regression problems. SVR has a special feature of transforming a dataset into n-dimensional feature space by increasing the space of training examples in an optimum hyperplane [12, 68]. SVR’s performance relies on several factors that must be tuned properly to obtain an optimum predictive model. The use of SVR as related to oil and gas is both interesting and challenging because of scarcity of data as in geomechanics. It therefore becomes difficult to find enough dataset for training and testing of the model. The SVR has been used frequently in the past for the prediction of petroleum-related parameters [1,2,3, 26, 39, 69–74].

A linear regression-based function for SVR modeling can be expressed as Eq. (2)

$$f\left( \varvec{x} \right) = \varvec{w}^{\varvec{T}} \varvec{x} + b$$
(2)

with input parameters \(\varvec{x}_{\varvec{k}} \in R^{{N{\text{x}}n}}\) and output value \(\varvec{y}_{\varvec{k}} \in R^{n}\) for N given training points. The empirical risk factor is given by

$$R_{\text{emp}} = \frac{1}{N}\mathop \sum \limits_{j = 1}^{N} \left| {y_{k} - \varvec{w}^{\varvec{T}} \varvec{x} - b} \right|_{\varepsilon }$$
(3)

with Vapnik’s \(\varepsilon\)-insensitive loss function defined as

$$\left| {y - f\left( \varvec{x} \right)} \right|_{\varepsilon } = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {\left| {y - f\left( \varvec{x} \right)} \right|_{\varepsilon } \le \varepsilon } \hfill \\ {y - \left. {f\left( \varvec{x} \right)} \right| - \varepsilon ,} \hfill & {otherwise} \hfill \\ \end{array} } \right.$$
(4)

This problem can be reformulated in dual space as

$${ \hbox{max} }J_{\text{D}} \left( {\alpha ,\alpha^{*} } \right) = - \frac{1}{2}\mathop \sum \limits_{j,l = 1}^{N} \left( {\alpha_{k} - \alpha_{k}^{*} } \right)\left( {\alpha_{1} - \alpha_{1}^{*} } \right)\varvec{x}_{\varvec{k}}^{\varvec{T}} \varvec{x}_{\varvec{l}} - \varepsilon \mathop \sum \limits_{j = 1}^{N} \left( {\alpha_{k} + \alpha_{k}^{*} } \right) + \mathop \sum \limits_{j = 1}^{N} y_{k} \left( {\alpha_{k} - \alpha_{k}^{*} } \right)$$
(5)

subject to \(\left\{ {\begin{array}{*{20}l} {\mathop \sum \limits_{k = 1}^{N} \left( {\alpha_{k} - \alpha_{k}^{*} } \right)} \hfill \\ {\alpha_{k} ,\alpha_{k}^{*} \in \left[ {0,c} \right]} \hfill \\ \end{array} } \right.\)

where \(\alpha_{k} ,\alpha_{k}^{*} \ge 0\) are Lagrange multipliers.

Once the Lagrange multipliers are computed, the linear hypersurface regression function is given by Eq. (6)

$$f\left( \varvec{x} \right) = \mathop \sum \limits_{j = 1}^{N} \left( {\alpha_{k} - \alpha_{k}^{*} } \right)\varvec{x}_{\varvec{k}}^{\varvec{T}} \varvec{x} + b$$
(6)

with

$$\varvec{w} = \mathop \sum \limits_{j = 1}^{N} \left( {\alpha_{k} - \alpha_{k}^{*} } \right)\varvec{x}_{\varvec{k}}$$
(7)

The training points with all nonzero values of \(\alpha_{k}\) are assigned to the free support vectors, which allows the computation of the bias term \(b\).

The nonlinear hyperplane regression equation can be given by Eq. 8

$$f\left( \varvec{x} \right) = \mathop \sum \limits_{j = 1}^{N} \left( {\alpha_{k} - \alpha_{k}^{*} } \right)K\left( {\varvec{x},\varvec{x}_{\varvec{K}} } \right) + b$$
(8)

where \(\alpha_{k}\), \(\alpha_{k}^{*}\) are the solution of the quadratic programming problem in Eq. (8) and \(b\) is computed as a mean value for the free support vectors. The solution obtained will be unique and global if the kernel functions are positive and definite.

2.6.4 Particle swarm optimization (PSO)

Particle swarm optimization (PSO) is a computational technique that optimizes a given objective function by iterative method, originally applied by Kennedy and Eberhart [75]. A PSO technique is developed on the basis of inspiration earned from the social movements of various living organisms such as fish flocking and birds schooling [76, 77]. It is a stochastic optimization algorithm, computationally efficient and very simple to implement. PSO sets the best function evaluation particle as the global best and initializes each particle location as its local best. After initialization, PSO moves to the next iteration where by each particle in the swarm updates its velocity iteratively [78], using Eq. (9)

$$v_{i} \left( {n + 1} \right) = wv_{i} \left( n \right) + \left\{ {c_{1} \times {\text{rand}}\left[ {0,1} \right] \times \left( {p_{i}^{\text{b}} - p_{i} \left( n \right)} \right)} \right\} + \left\{ {c_{2} \times {\text{rand}}\left[ {0,1} \right] \times \left( {p_{\text{gb}} - p_{i} \left( n \right)} \right)} \right\}$$
(9)

where \(w\) weight \(\left( {0 \le w \le 1.2} \right)\); \(v_{i}\) weight \(\left( {0 \le w \le 1.2} \right)\); \(c_{1}\) cognitive parameter \(\left( {0 \le c_{1} \le 1.2} \right)\); \(c_{2}\) cognitive parameter \(\left( {0 \le c_{2} \le 1.2} \right)\); \(n\) iteration number; \(p_{i}^{\text{b}}\) particle best solution; \(p_{\text{gb}}\) global best solution; \(p_{i}\) particle \(i\) position at any iteration.

The inertia term in the particle velocity equation \(\left( {wv_{i} \left( n \right)} \right)\) ensures that the particle moves toward its original direction, while its weight \(\left( w \right)\) ensures that the particle rate of acceleration moves toward its original direction. The cognitive component \(c_{1} \times {\text{rand}}\left[ {0,1} \right] \times \left( {p_{i}^{\text{b}} - p_{i} \left( n \right)} \right)\) memorizes the particles’ previous best solution. The social component \(c_{2} \times {\text{rand}}\left[ {0,1} \right] \times \left( {p_{\text{gb}} - p_{i} \left( n \right)} \right)\) moves the particle toward the global best fitness. New position for each candidate solutions in the solution search space is generated by sum of the current position and velocity:

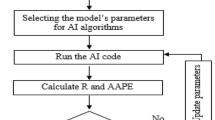
$$p_{i} \left( {n + 1} \right) = p_{i} \left( n \right) + v_{i} \left( n \right)$$
(10)

Objective function is evaluated to update the local best for each particle and then global best particle if the current best is better than the previous iteration. The whole process of velocity and particle position updating is repeated after objective function is evaluated to determine new improved quality solutions until a stopping criterion of maximum number of iteration is reached. Figure 5 summarizes the workflow adopted in this study to reach to the optimum model for the prediction of static Poisson’s ratio. Steps related to the model testing and development of ANN equation are given in the next sections.

Fig. 5
figure 5

Workflow of the proposed research study to model static Poisson’s ratio

Full size image

3 Prediction of static Poisson’s ratio using artificial intelligence methods

A total of 120 data points were divided randomly into two sets with the proportion of 0.7:0.3. The set with 70% of the data (84 data points) was utilized for training of models, and the second set with 30% of the data (36 data points) was used to test the prediction competencies of trained models.

Three AI techniques, namely, ANN, ANFIS, and SVR, were implemented to develop models to predict static Poisson’s ratio. A comparison was made between these three techniques based on the lowest AAPE and the highest R2 between actual and predicted values. In ANN, two types of models were investigated, namely, feedforward neural network (FFNN) and radial basis function of neural network (RBF). In ANFIS too, two types of ANFIS models were studied, namely, Genfis-1 (Grid Partitioning) and Genfis-2 (Subtractive clustering). In SVR, two types of kernel functions were studied, namely, polynomial and Gaussian. Based on highest R2 and lowest AAPE, FFNN, Genfis-2, and polynomial SVR were selected as best ANN, ANFIS, and SVR types to predict static Poisson’s ratio.

For ANN, several runs were executed with various values of the model parameters. At every run, the parameters changed were learning rate, number of hidden layers with corresponding number of neurons, and different transfer functions. The SVR components of the model were tuned by optimizing several parameters, viz. kernel function, lambda, regularization parameters, epsilon, and kernel options. For ANFIS, in Genfis-2 the sensitivity of cluster radii was performed to reach the optimum model. The proposed model(s) were tuned by optimizing their several parameters by using particle swarm optimization. The complete list of AI techniques with optimizing parameters with their ranges is given in Table 2.

Table 2 Summary of optimized parameters used for each technique in this study
Full size table

From PSO optimizer, optimized values of AI model parameters were obtained. The optimized FFNN model was based on three input layers, one hidden layer, and one output layer. In ANN, the optimum hidden layer number of neurons was found to be 20. Optimum transfer functions between input hidden layer were found to be tan-sigmoid, and between hidden output layer found to be pure linear. Optimum learning algorithm found was backpropagation Levenberg–Marquardt with an optimum learning rate of 0.12. Hagan and Menhaj [79] also proved that the performance of FFNN with Levenberg–Marquardt learning algorithm is better than other learning algorithms in ANN. Figure 6 shows the architecture of the optimized FFNN model to predict static Poisson’s ratio. The optimized Genfis-2 model was based on three input parameters and the one output parameter. Optimum cluster radius was found to have a value of 0.3. The optimized SVR model consists of three input parameters and one output parameter. Optimum kernel function was found to be the ‘Gaussian’ type with kernel options value of 3.0. Optimum value of regularization parameter was found to have a value of 4500. Optimum epsilon value found was 0.05 with an error tolerance of 1 × 10−3. Multiple realizations were performed during the use of each AI technique to avoid them to get stuck at local minima.

Fig. 6
figure 6

Architecture of the trained FFNN model to predict static Poisson’s ratio

Full size image

On comparing the performance of all three models (ANN, ANFIS, and SVR), it was observed that during training, PSO-optimized ANN model yielded lowest AAPE and highest R2 compared to PSO-optimized ANFIS and SVR, as shown in Fig. 7. During the testing on unseen data, PSO-optimized ANN also outperformed PSO-optimized ANFIS and SVR by show casing less AAPE and high R2 values, as shown in Fig. 8. Table 3 lists the comparison of results for both training and testing of all three methods. Figure 9 shows the performance cross-plot by three models on overall data.

Fig. 7
figure 7

Prediction of static Poisson’s ratio using three different AI techniques: ANN, ANFIS, and SVR (training comparison)

Full size image
Fig. 8
figure 8

Prediction of static Poisson’s ratio using three different AI techniques: ANN, ANFIS, and SVR (testing comparison)

Full size image
Table 3 Training and testing performances of AI methods
Full size table
Fig. 9
figure 9

Cross-plot comparison of the three different AI techniques on the overall data (training and testing)

Full size image

From the comparison analysis, it can be clearly observed that on the given set of the data, the developed ANN model was very generalized and can give good results on any unseen data within the range defined in Table 1. Therefore, ANN with three input parameters is suggested here as the best model for the prediction of static Poisson’s ratio.

4 Development and validation of an equation of ANN

A FFNN model is created by a series of layers. Hidden layer neuron uses its weight \(w_{1}\), and bias \(b_{1}\), and its parameters are described by Eq. (11)

$$\sigma_{L} \left( {\mathop \sum \limits_{j = 1}^{{N_{P} }} w_{{1_{j} }} x_{j} + b_{1} } \right)$$
(11)

where \(N_{P}\) is the total number of inputs, \(x\) are the input parameters, and \(\sigma_{L}\) is the transfer function between the input and the hidden layer. The output of the whole network can be expressed as in Eq. (12):

$$\mu_{P} \left( \varphi \right) = \sigma_{o} \left[ {\mathop \sum \limits_{i = 1}^{{N_{h} }} w_{{2_{i} }} \sigma_{L} \left( {\mathop \sum \limits_{j = 1}^{{N_{P} }} w_{{1_{i, j} }} x_{j} + b_{{1_{i} }} } \right) + b_{2} } \right]$$
(12)

where \(N_{\text{h}}\) are the optimized number of neurons in the hidden layer, \(\sigma_{\text{o}}\) is the transfer function between the hidden layer and the output layer, and \(\varphi\) is a vector denoting the network parameters \(w_{1}\), \(w_{2}\), \(b_{1}\), and \(b_{2}\). In this study, ANN model is trained with three input variables (\(\rho\), \(\Delta t_{\text{C}}\), and \(\Delta t_{\text{S}}\)), with one hidden layer having twenty number of neurons, tan-sigmoid as an activation function between input and hidden layer, and pure linear as an activation function between hidden and output layer. Figure 10 shows the architecture of the trained ANN for the prediction of static Poisson’s ratio. An empirical expression is developed based on weights and biases of the trained ANN model. These extracted weights and biases are given in Table 4. Weights between the input layer and the hidden layer are a matrix which are referred as \(w_{1}\), and weights between the hidden layer and the output layer are a vector referred as \(w_{2}\). Biases between the input layer and the hidden layer are a vector referred as \(b_{1}\), and bias between the hidden layer and the output layer is a scalar referred as \(b_{2}\). The proposed equation of ANN of the static Poisson’s ratio can be written more specifically as in Eq. (13)

$${\text{PR}}_{{{\text{static}}_{n} }} = \sigma_{o} \left[ {\mathop \sum \limits_{i = 1}^{{N_{h} }} w_{{2_{i} }} \sigma_{L} \left( {w_{{1_{i,1} }} \rho_{n} + w_{{1_{i,2} }} \Delta t_{{C_{n} }} + w_{{1_{i,3} }} \Delta t_{{S_{n} }} + b_{{1_{i} }} } \right) + b_{2} } \right]$$
(13)

where \(\sigma_{L} \left( x \right) = (2/1 + e^{ - 2x} ) - 1\), \(\sigma_{o} \left( x \right) = x\)

Fig. 10
figure 10

Bulk density and neutron porosity lithology cross-plot of the well no. 1

Full size image
Table 4 Weights and biases of the new proposed equation of ANN
Full size table

The black box nature of ANN has been transformed into a white box by mining the weights and biases. This will allow the users of this paper to apply ANN-based mathematical model to predict static Poisson’s ratio by simply plugging in the required input variables (\(\rho\), \(\Delta t_{\text{C}}\), and \(\Delta t_{\text{S}}\)) without the need of using AI software. Previously, artificial intelligence/machine learning-based models [80,81,82,83,84,85,86] were all black boxes in nature. In all these papers, authors mentioned only the approach they have used to train their models.

4.1 Procedure to use new equation of ANN for the prediction of static Poisson’s ratio

The following three steps are required for using the new equation to predict static Poisson’s ratio.

Step 1 Normalize input parameters (\(\rho\),\(\Delta t_{\text{C}}\), and \(\Delta t_{\text{S}}\)) between − 1 and 1. Input parameters are denoted here by ‘\(x\).’ Normalization is needed to match the results from MATLAB ANN and equation of ANN. The difference of prediction from MATLAB ANN function and coding ANN (weights from MATLAB) is due to the normalization of input and output data. To get the same results with equation of ANN as from MATLAB ANN, normalization of input and output is required. The normalization of input is done by Eq. (14).

$${\text{Input}}_{\text{norm}} = \frac{{\left( {{\text{Input}}_{ \hbox{max} } - {\text{Input}}_{ \hbox{min} } } \right)\left( {x - x_{\hbox{min} } } \right)}}{{x_{\hbox{max} } - x_{\hbox{min} } }} + {\text{Input}}_{\hbox{min} }$$
(14)

\({\text{Input}}_{ \hbox{min} } = - 1\); \({\text{Input}}_{ \hbox{max} } = 1\); \(x\) is the input parameter, \(x_{ \hbox{max} }\) is the maximum value of the trained input parameter, and \(x_{ \hbox{min} }\) is the minimum value of trained input parameter. \(x_{ \hbox{max} }\) and \(x_{ \hbox{min} }\) for each input parameters (\(\rho\), \(\Delta t_{\text{C}}\), and \(\Delta t_{\text{S}}\)) are given in Table 1. To perform the normalization for (\(\rho\),\(\Delta t_{\text{C}}\), and \(\Delta t_{\text{S}}\)), Eqs. (15)–(17) can be used.

$$\rho_{n} = 2 \times \left( {\frac{\rho - 2.01}{3.05 - 2.01}} \right) - 1$$
(15)
$$\Delta t_{{{\text{C}}_{n} }} = 2 \times \left( {\frac{{\Delta t_{\text{C}} - 44.375}}{96.887 - 44.375}} \right) - 1$$
(16)
$$\Delta t_{{S_{\text{n}} }} = 2 \times \left( {\frac{{\Delta t_{\text{S}} - 73.187}}{170.496 - 73.187}} \right) - 1$$
(17)

Step 2 To apply Eq. (13), weights and biases are needed which are given in Table 4. The sequence of parameters that goes into the model is given as: bulk density, P-wave and S-wave transit times

Step 3 Equation (13) gives static Poisson’s ratio in normalized form in the range of [− 1 1]. It should be reversed back to original values by using Eq. (20).

$${\text{Output}} = \frac{{\left( {y_{\hbox{max} } - y_{\hbox{min} } } \right)\left( {{\text{Output}}_{\text{norm}} - \left( { - 1} \right)} \right)}}{{1 - \left( { - 1} \right)}} + y_{\hbox{min} }$$
(18)

\(y_{ \hbox{max} }\) and \(y_{ \hbox{min} }\) values (minimum and maximum values of static Poisson’s ratio) are given in Table 1. Therefore, Eq. (18) becomes

$${\text{PR}}_{\text{Static}} = \frac{{\left( {0.475 - 0.167} \right)\left( {{\text{PR}}_{{{\text{static}}_{n} }} + 1} \right)}}{2} + 0.167$$
(19)
$${\text{PR}}_{\text{Static}} = 0.154*{\text{PR}}_{{{\text{static}}_{n} }} + 0.321$$
(20)

4.2 Validation

The newly proposed equation of ANN to predict static Poisson’s ratio is validated by three methods, namely, field validation, validation on published data, and validation by comparing the results with commonly used methods in the industry to predict static Poisson’s ratio.

4.2.1 Field validation

To validate the proposed model, the data from three separate wells were used. These data were not used in the training of the model.

Case 1

The input well log data consist of bulk density, P-wave transit time, and S-wave transit time. Laboratory data consist of measured static Poisson’s ratio using triaxial compressional tests. Lithology cross-plot of bulk density and neutron porosity is shown in Fig. 10 which depicts that most of the data in well no. 1 lie in limestone formation, with some percentage in dolomite and sandstone regions. Figure 11 shows the petrophysical well log data of well no. 1 for an interval of 1000 ft. The range of bulk density is in between 2.2 and 3.0 g/cc, the range of P-wave transit time is 40–70 µs/ft, and the range of S-wave transit time is 80–120 µs/ft. This well has thirteen core data points. The comparison of equation of ANN predicted and actual laboratory measured static Poisson’s ratio for well no. 1 is given in Fig. 12 which shows that equation of ANN predicted the static Poisson’s ratio for an interval of 1000 ft with R2 of 0.9.

Fig. 11
figure 11

A suite of petrophysical well log data for well no. 1. Track 1 represents bulk density log, track 2 represents P-wave transit time log, and track 3 represents S-wave transit time log

Full size image
Fig. 12
figure 12

Static Poisson’s ratio prediction using proposed equation of ANN on well no. 1

Full size image

Case 2

Well no. 2 lithology cross-plot between bulk density and neutron porosity is shown in Fig. 13 which indicates that most of the data lie in limestone formation, with some part in an anhydrite and dolomite regions. Anhydrites regions have zero porosity and density up to 3.0 g/cc. Input data of well no. 2 are given in Fig. 14. This well has five static Poisson’s ratio values measured in the laboratory. Figure 15 shows that equation of ANN predicted these five values with R2 of 0.8.

Fig. 13
figure 13

Bulk density and neutron porosity lithology cross-plot of the well no. 2

Full size image
Fig. 14
figure 14

A suite of petrophysical well log data for well no. 2. Track 1 represents bulk density log, track 2 represents P-wave transit time log, and track 3 represents S-wave transit time log

Full size image
Fig. 15
figure 15

Static Poisson’s ratio prediction using proposed equation of ANN on well no. 2

Full size image

Case 3

Well no. 3 lithology cross-plot between bulk density and neutron porosity is shown in Fig. 16 which indicates very scattered data, but majority of the data lie in the limestone formation, with some part in anhydrite and sandstone zones. Figure 17 shows the petrophysical well log input data for Well No. 3 for an interval of 400 ft. This well has four measured static Poisson’s ratio values. Figure 18 shows the continuous profile of static Poisson's ratio for Well no. 3, including the accurate prediction of four laboratory measured static Poisson’s ratio values with R2 of 0.91.

Fig. 16
figure 16

Bulk density and neutron porosity lithology cross-plot of well no. 3

Full size image
Fig. 17
figure 17

A suite of petrophysical well log data for well no. 3. Track 1 represents bulk density log, track 2 represents P-wave transit time log, and track 3 represents S-wave transit time log

Full size image
Fig. 18
figure 18

Static Poisson’s ratio prediction using proposed equation of ANN on Well No. 3

Full size image

4.2.2 Validation on published data

The new proposed equation of ANN is also tested on the published data by D’Andrea et al. [43]. In their work, 49 rock samples from different regions were tested for obtaining tensile strength, P-wave and S-wave velocities, Young’s modulus, and Poisson’s ratio. Figure 19 shows the input parameters, actual static Poisson’s ratio, and predicted static Poisson’s ratio values. From the analysis of Fig. 19, it is observed that new proposed equation of ANN can predict the static Poisson’s ratio with AAPE of 6.5% and RMSE of 0.0228.

Fig. 19
figure 19

Static Poisson’s ratio prediction using proposed equation of ANN on published data by D’Andrea et al. [43]

Full size image

4.2.3 Validation by comparison with common methods of estimating static Poisson’s ratio

It is customary in the petroleum industry to generate a continuous profile of the static Poisson’s ratio for the whole reservoir section by obtaining different correlations. These correlations are obtained by relating petrophysical well logs such as neutron porosity, bulk density, P-wave transit time, and S-wave transit times with the laboratory measured values of the static Poisson’s ratio of the core samples. The core samples are obtained from the offset wells of the same field.

In this study, this approach of determining static Poisson’s ratio is tested against the results of the new proposed equation of ANN. Figure 20 shows the linear cross-plots of the static Poisson’s ratio with the dynamic Poisson’s ratio, bulk density, P-wave transit time, and S-wave transit time. Figure 20a shows the relationship between static Poisson’s ratio and dynamic Poisson’s ratio having R2 of 0.026, Fig. 20b shows the linear relation between static Poisson’s ratio and bulk density with R2 of 0.1, Fig. 20c shows the linear relation between static Poisson’s ratio and P-wave transit time with R2 of 0.1, and Fig. 20d shows the relationship between static Poisson’s ratio and S-wave transit time with R2 of 0.08.

Fig. 20
figure 20

Linear relation of static Poisson’s ratio with petrophysical well logs. a Relationship between static Poisson’s ratio and dynamic Poisson’s ratio. b Relationship between static Poisson’s ratio and bulk density. c Relationship between static Poisson’s ratio and P-wave transit time. d Relationship between static Poisson’s ratio and S-wave transit time

Full size image

Equations (21)–(24) are developed by correlating with these petrophysical well logs. These linear correlations were developed on the same dataset that was used for the training of the AI models.

$${\text{PR}}_{\text{Static}} = 0.2416 {\text{PR}}_{\text{Dyn}} + 0.2314$$
(21)
$${\text{PR}}_{\text{Static}} = 0.1686 \rho + 0.1358$$
(22)
$${\text{PR}}_{\text{Static}} = 0.4526 - 0.0025 \Delta t_{\text{C}}$$
(23)
$${\text{PR}}_{\text{Static}} = 0.4523 - 0.0041 \Delta t_{\text{S}}$$
(24)

The dynamic Poisson’s ratio is calculated using Eq. 25.

$${\text{PR}}_{\text{dyn}} = \frac{{V_{\text{P}}^{2} - 2V_{\text{S}}^{2} }}{{2\left( {V_{\text{P}}^{2} - V_{\text{S}}^{2} } \right)}}$$
(25)

VP is the velocity of P-wave in km/s, and VS is the velocity of S-wave in km/s.

Figure 21 shows continuous profiles of static Poisson’s ratio obtained from Eqs. (21)–(24). The profiles generated from \({\text{PR}}_{\text{dyn}}\), P-wave transit time, and S-wave transit time show under-estimated values, while the profile generated from bulk density shows over-estimated values. From these correlations, the static Poisson’s ratio profiles generated did not match with any laboratory determined static Poisson’s ratio values, while the new proposed equation of ANN matched with almost every actual data point. Figure 21 shows the AAPE bar chart for each correlation, demonstrating the high accuracy of proposed equation of ANN.

Fig. 21
figure 21

Validation comparison of new equation of ANN against linear correlations (Eqs. 21–24) to predict static Poisson’s ratio

Full size image

5 Conclusions and recommendations

The predictive efficiency of AI techniques (ANN, ANFIS, and SVR) to model static Poisson’s ratio is investigated in this study. The results reveal that

  1. 1.

    ANN performed better than ANFIS and SVR by giving less AAPE and high R2.

  2. 2.

    By the development of equation of ANN, the black box nature of an ANN is converted into a white box by obtaining tangible weights and biases from the trained ANN model.

  3. 3.

    Equation of ANN can predict the static Poisson’s ratio using three commonly available petrophysical well logs namely, bulk density, P-wave, and S-wave transit times

  4. 4.

    Equation of ANN provides better static Poisson’s ratio estimations compared to available methods as shown by lower AAPE and higher R2.

  5. 5.

    Equation of ANN can be used in wells with no static Poisson’s ratio data or the wells with cased hole, where estimation of the static Poisson’s ratio is not possible.

  6. 6.

    The new equation of ANN can be used for the prediction in new wells without the need of any AI software.

  7. 7.

    The new equation can give the real-time values of static Poisson’s ratio of carbonate rocks wherever the real-time logs are available.

  8. 8.

    From overall results produced, it can be said that AI techniques can be used as a cost-effective alternative in terms of saving the number of experiments to calculate static Poisson’s ratio.

In this study, the core samples tested were in dry condition and the equation of ANN developed is valid for dry conditions. It is recommended to conduct the same testing under saturated condition and observe the difference of static Poisson’s ratio values in both dry and saturated conditions, and the model performance in saturated conditions. Also, more AI techniques can be explored such as decision trees, type 2 fuzzy logic, and functional networks.