Uncertain multi-objective multi-item fixed charge solid transportation problem with budget constraint

Abstract

Modeling of real-world problems requires data as input parameter which include information represented in the state of indeterminacy. To deal with such indeterminacy, use of uncertainty theory (Liu in Uncertainty theory, Springer, Berlin, 2007) has become an important tool for modeling real-life decision-making problems. This study presents a profit maximization and time minimization scheme which considers the existence of possible indeterminacy by designing an uncertain multi-objective multi-item fixed charge solid transportation problem with budget constraint (UMMFSTPwB) at each destination. Here, items are purchased at different source points with different prices and are accordingly transported to different destinations using different types of vehicles. The items are sold to the customers at different selling prices. In the proposed model, unit transportation costs, fixed charges, transportation times, supplies at origins, demands at destinations, conveyance capacities and budget at destinations are assumed to be uncertain variables. To model the proposed UMMFSTPwB, we have developed three different models: (1) expected value model, (2) chance-constrained model and (3) dependent chance-constrained model using uncertain programming techniques. These models are formulated under the framework of uncertainty theory. Subsequently, the equivalent deterministic transformations of these models are formulated and are solved using three different methods: (1) linear weighted method, (2) global criterion method and (3) fuzzy programming method. Finally, numerical examples are presented to illustrate the models.

1 Introduction

The notion of classical transportation problem (TP) is to determine an optimal solution (transportation plan) such that the transportation cost is minimized. The noteworthy work of Hitchcock (1941) introduced the term transportation problem, by modeling it as a conventional optimization problem with two dimensional properties, i.e., supply and demand. However, apart from supply and demand constraints, in real-world scenarios, often we need to consider the mode of transportation (e.g., goods train, cargo flights and trucks), types of goods, etc. Under such circumstances, a TP is extended to a solid transportation problem (STP), where apart from source and destination constraints, an additional constraint, related to the modes of transportation (convenience) or types of goods, is considered. Schell (1955) first extended the classical TP to solid transportation problem (STP). Later, Bhatia et al. (1976) minimized the shipping time of an STP. Afterward, Jiménez and Verdegay (1999), in their work, dealt with an STP and solved the problem by considering the supply quantities, demand quantities and conveyance capacities as interval values instead of point values.

Table 1 Some recent studies on variants of transportation problem under diverse uncertain frameworks

Hirsch and Dantzig (1968) presented another variant of TP, called fixed charge transportation problem (FTP). In FTP, the objective is to determine an optimal transportation plan that minimizes the overall cost between sources and destinations. The overall cost has two components: variable shipping cost and an independent fixed charge. The shipping cost depends directly on the quantity of the transported item(s) from sources to destinations, whereas the fixed charge, which commonly appears due to the expenditure related to permit fees, property tax or toll charges, etc., is associated with every feasible transportation plan. Several researchers (Kennington and Unger 1976; Sun et al. 1998; Adlakha and Kowalski 2003) have proposed different solution approaches for FTP.

Most of the real-life decision-making problems can be well expressed with multiple conflicting criteria and are usually formulated as multi-objective optimization problems. Moreover, the associated parameters for such problems may be imprecise because to insufficient or inexact information due to incompleteness or lack of evidence, statistical analysis, etc. Therefore, in order to process and represent imprecise or ill-defined data for decision-making problems, many researchers have presented a number of theories, e.g., fuzzy set (Zadeh 1965), type-2 fuzzy set (Zadeh 1975a, b), rough set (Pawlak 1982). The uncertainty theory proposed by Liu (2007) deals with the belief degrees of human being, which can appropriately evaluate personal belief degree of experts in terms of uncertain measure.

In the literature, there are many works done in the field of TP with uncertain input parameters. Kaur and Kumar (2012) described a new solution technique for TP by considering the transportation costs as generalized trapezoidal fuzzy numbers. In multi-objective domain, Bit et al. (1993) solved the multi-objective STP using Zimmermann’s fuzzy programming technique (1978). Later, Gen et al. (1995) proposed a bi-objective STP with fuzzy parameters. Recently, Kundu et al. (2017a) used interval type-2 fuzzy multi-criteria group decision-making (MCGDM) approach to solve a transportation mode selection problem. Considering the budget limitation of a TP, Kundu et al. (2013a) discussed a multi-objective STP by imposing budget constraints at destinations with fuzzy random hybrid parameters. Later, Baidya and Bera (2014) proposed a budget constraint STP by representing transportation cost, availability and demand, and conveyance capacity as interval numbers. In addition, Kundu et al. (2014a) also investigated a fuzzy multi-criteria decision-making (MCDM) approach to determine the most preferred transportation mode, in order to solve an STP. Recently, Das et al. (2017) solved the green STP under type-2 fuzzy environment. Considering fixed charge in imprecise domain, Liu et al. (2008) presented an FTP in fuzzy environment and solved it by genetic algorithm. Later, Pramanik et al. (2015) revisited the FTP by considering the shipping cost, fixed charge, availability and demand in a two-stage supply chain under type-2 Gaussian fuzzy transportation network.

Under the framework of uncertainty theory (Liu 2007), different variants of TP have been studied in the literature (Sheng and Yao 2012a, b; Cui and Sheng 2013; Mou et al. 2013; Guo et al. 2015; Chen et al. 2017). In Table 1, we have furnished some recent reviews of different variants of TP under diverse uncertain environments.

In spite of all the developments of TP, there are several gaps in the literature which are listed below.

• To the best of our knowledge, none has considered, a multi-objective multi-item profit maximization and time minimization fixed charge STP model with budget constraint.

• Use of Liu’s uncertainty theory to formulate the multi-objective solid transportation problem using dependent chance-constrained programming technique is yet to be studied.

• Implementation and analysis of results for EVM, CCM and DCCM for any fixed charge STP with budget constraint, using zigzag and normal uncertain variables, under the framework of uncertainty theory (Liu 2007), has not yet been done.

In order to address the above-mentioned lacunas, in the present study we have considered uncertain multi-objective multi-item fixed charge STP with budget constraint (UMMFSTPwB) at destinations, under the framework of uncertainty theory (Liu 2007). The problem is formulated in three different models: expected value model (EVM), chance-constrained model (CCM) and dependent chance-constrained model (DCCM). Consecutively, each model is solved by three different multi-objective compromise techniques: linear weighted method, global criterion method and fuzzy programming method.

The subsequent sections of this study are organized as follows. The preliminary concepts for our study are given in Sect. 2. The uncertain programming models, EVM, CCM and DCCM, of the proposed UMMFSTPwB are presented in Sect. 3. The crisp equivalent for each of the models of UMMFSTPwB is formulated in Sect. 4. Three different compromise multi-objective solution methodologies and some related theorems are explained in Sect. 5. In Sect. 6, we present the numerical examples to illustrate the model and the results are discussed with comparative analysis. Finally, the epilogue of our study is presented in Sect. 7.

2 Preliminaries

Uncertainty theory, founded by Liu (2007) and refined by Liu (2009, 2010, 2015), is a branch of axiomatic mathematics for modeling human uncertainty. Nowadays, uncertainty theory has been applied to many areas such as economics (Yang and Gao 2016, 2017), management (Gao and Yao 2015; Gao et al. 2017) and finance (Chen and Gao 2013; Guo and Gao 2017).

In this section, some fundamental concepts associated with uncertainty theory (Liu 2007) required to design UMMFSTPwB are discussed.

Definition 2.1

(Liu 2007) Let ${\Gamma }$ be a nonempty set, $\mathcal {L}$ be a $\sigma$ algebra over ${\Gamma }$ and $\mathcal {M}$ be the uncertain measure of any element and ${\Omega }$ is contained in $\mathcal {L}$. Then $\left( {\Gamma ,\mathcal {L},\mathcal {M}} \right)$ represents an uncertainty space.

Fig. 1

Uncertain distribution of a$\mathcal {Z}(6,8,14)$b$\mathcal {N}\mathrm {(10,2)}$

In an uncertainty space $\left( {\Gamma ,\mathcal {L},\mathcal {M}} \right)$, for each event ${\Omega }$ in $\mathcal {L,}\, \mathcal {M}$ is the uncertain measure which maps $\mathcal {L}$ to ${\mathfrak {R}}(0,1)$, i.e., $\mathcal {M}:~ \mathcal {L}\mapsto \mathfrak {R}(0,1)$. In order to define uncertain measure axiomatically, a number $\mathcal {M}\left\{ {\Omega } \right\}$ is assigned with each event ${\Omega }$ which determines the belief degree with which the event ${\Omega }$ has occurred. To establish the mathematical properties of the uncertain measure, Liu (2009) proposed the following axioms.

• Axiom 1. (Normality) $\mathcal {M}\left\{ {\Gamma } \right\} =1$ for the universal set ${\Gamma }.$

• Axiom 2. (Self-Duality) $\mathcal {M}\left\{ {\Omega } \right\} +\mathcal {M}\left\{ {\Omega }^{\mathrm {c}} \right\} =1$ for any event ${\Omega }.$

• Axiom 3. (Subadditivity) For every countable sequence of events ${\Omega }_{\mathrm {1}},{{\Omega }}_{\mathrm {2}},\ldots ,$ we have $\mathcal {M}\left\{ \bigcup \nolimits _{{i=1}}^{\infty } {\Omega }_{{i}} \right\} {\le }\sum \nolimits _{{i=1}}^{\infty } {\mathcal {M}\left\{ {\Omega }_{{i}} \right\} }$.

• Axiom 4. (Product) Let $\left( {\Gamma }_{{j}},\mathcal {L}_{{j}},\mathcal {M}_{{j}} \right)$ be the uncertainty spaces for ${j=1,2,\ldots }$ then the product uncertain measure $\mathcal {M}$ is an uncertain, measure satisfying, $\mathcal {M}\left\{ \prod \nolimits _{{j=1}}^{\infty } {\Omega }_{{j}} \right\} \mathrm {=}\bigwedge _{{j=1}}^{{\infty }} {\mathcal {M}_{{j}}\left\{ {\Omega }_{{j}} \right\} }$, where ${\Omega }_{{j}}$ is arbitrary chosen event from $\mathcal {L}_{{j}}$, for every ${j=1,2,\ldots }$, respectively.

Definition 2.2

(Liu 2007) An uncertain variable $\zeta$ is said to be zigzag uncertain variable if $\zeta$ follows a zigzag uncertainty distribution as given below in (1).

$$\begin{aligned} {\Phi }\left( x \right) \mathrm {=}\left\{ {\begin{array}{ll} 0, &{} \mathrm{if}~ x\le a~ \\ \frac{x-a}{2\left( b-a \right) }, &{}\mathrm{if}~ a<x\le b \\ \frac{(x+c-2b)}{2(c-b)},&{} \mathrm{if}~ b<~ x\le c~ \\ 1, &{} \mathrm{if}~ x>c,~ \\ \end{array}} \right. \end{aligned}$$

(1)

where $\zeta$ is denoted by $\mathcal {Z}(a,b,c)$ such that $a<b<c$ and $a,b,c\in \mathfrak {R}.$

Example 2.1

The uncertainty distribution of a zigzag uncertain variable $\mathcal {Z}{(6,8,14)}$ is displayed in Fig. 1a.

Definition 2.3

(Liu 2007) Let $\zeta$ be an uncertain variable such that $\zeta$ follows a normal uncertainty distribution as defined in (2). Then $\zeta$ becomes a normal uncertain variable

$$\begin{aligned} {\Phi }\left( x \right) {=}\left( \mathrm {1+}\exp \left( \frac{\pi (\rho -x)}{\sigma \sqrt{3} } \right) \right) ^{\mathrm {-1}},\,x \in {\mathfrak {R}}, \end{aligned}$$

(2)

where $\zeta$ is denoted by $\mathcal {N}(\rho ,\sigma )$ such that $\rho ,~ \sigma \in \mathfrak {R}$ and $\sigma >0.$

Example 2.2

The uncertainty distribution of a normal uncertain variable $\mathcal {N}\left( \mathrm {10,2} \right)$ is presented in Fig. 1b.

Definition 2.4

(Liu 2010) Let $\zeta$ be an uncertain variable with regular uncertainty distribution ${\Phi }\left( x \right)$, then the inverse function ${\Phi }^{{-1}}\left( {\alpha } \right)$ is said to be inverse uncertainty distribution of $\zeta$, where $\alpha \in \left[ 0,1 \right]$.

Example 2.3

(i) The inverse uncertainty distribution of zigzag uncertain variable $\mathcal {Z}(a,b,c)$ is

$$\begin{aligned} {\Phi }^{\mathrm {-1}}\left( \alpha \right) \mathrm {=}\left\{ \begin{array}{ll} \left( \mathrm {1-2}\alpha \right) a\mathrm {+2}\alpha b,&{}\quad \mathrm{if}~ \alpha <0.5 \\ \left( \mathrm {2-2}\alpha \right) b+\left( 2\alpha -1 \right) c, &{}\quad \mathrm{if}~ \alpha \ge 0.5. \\ \end{array} \right. \end{aligned}$$

(ii) The inverse uncertainty distribution of a normal uncertain variable $\mathcal {N}(\rho ,\sigma )$ is

$$\begin{aligned} {\Phi }^{\mathrm {-1}}\left( \alpha \right) \mathrm {=}\,\rho \mathrm {+}\frac{\sigma \sqrt{3} }{{\uppi }}\mathrm {ln}\frac{\alpha }{\mathrm {1-}\alpha }\cdot \end{aligned}$$

Theorem 2.1

(Liu 2010) Let $\zeta _{1},\zeta _{2},\ldots ,\zeta _{n}$ be the independent uncertain variables, respectively, of regular uncertainty distributions ${\Phi }_{\mathrm {1}},{\Phi }_{\mathrm {2}}\mathrm {,\ldots ,}{\Phi }_{n}$, respectively. If $f( \zeta _{1},\zeta _{2},\ldots ,\zeta _{n} )$ is strictly increasing function with respect to $\zeta _{1},\zeta _{2},\ldots , \zeta _{m}$, and strictly decreasing with respect to $\zeta _{m+1},\zeta _{m+2},\ldots ,\zeta _{n}$, then the inverse uncertainty distribution of

$$\begin{aligned} \zeta =f\left( \zeta _{1},\zeta _{2},\ldots ,\zeta _{n} \right) \end{aligned}$$

(3)

becomes

$$\begin{aligned} {{\Phi }~ }^{-1}\left( \alpha \right)= & {} f\left( {\Phi }_{1}^{-1}\left( \alpha \right) ,{\Phi }_{2}^{-1}\left( \alpha \right) ,\ldots ,{\Phi }_{m}^{-1}\left( \alpha \right) ,{\Phi }_{m+1}^{-1}\right. \nonumber \\&\left. (1-\alpha ),\ldots ,{\Phi }_{n}^{-1}\left( 1-\alpha \right) \right) \end{aligned}$$

(4)

Definition 2.5

(Liu 2007) Let $\zeta$ be an uncertain variable then the expected value of $\zeta$ is defined below in (5).

$$\begin{aligned} E\left[ \zeta \right] =\int _{0}^{+\infty } {\mathcal {M}\left\{ \zeta \ge t \right\} } -\int _{-\infty }^{0} {\mathcal {M}\left\{ \zeta \le t \right\} }, \end{aligned}$$

(5)

provided at least one of the two integrals is finite.

Theorem 2.2

(Liu 2010) If $\zeta$ be an uncertain variable with regular uncertainty distribution ${\Phi }$, then

$$\begin{aligned} {E}\left[ \zeta \right] {=}\int _{0}^\mathrm {1} {{{\Phi }~ }^{-1}\left( \alpha \right) \mathrm {d}\alpha }. \end{aligned}$$

(6)

Definition 2.6

(Liu 2007) Let $\zeta$ be an uncertain variable and ${\alpha }\in (0,1]$ be the confidence level, then $\zeta _{\mathrm{sup}}\left( {\alpha } \right)$ and $\zeta _{\mathrm{inf}}\left( {\alpha } \right)$ are the respective ${\alpha }$-optimistic and ${\alpha }$-pessimistic values of $\zeta$ such that

$$\begin{aligned} \zeta _{\mathrm{sup}}\left( {\alpha } \right) =\mathrm{sup} \left\{ t\vert \mathcal {M}\left\{ \zeta \ge t \right\} \ge {\alpha } \right\} \end{aligned}$$

(7.1)

and

$$\begin{aligned} \zeta _{\mathrm{inf}}\left( {\alpha } \right) ={\mathrm{inf}} \left\{ t\vert \mathcal {M}\left\{ \zeta \le t \right\} \ge {\alpha } \right\} . \end{aligned}$$

(7.2)

Example 2.4

• (i) Let $\zeta$ be a zigzag uncertain variable denoted as $\mathcal {Z}(a,b,c)$, then its ${\alpha }$-optimistic and ${\alpha }$-pessimistic values are, respectively,

  $$\begin{aligned} \zeta _{\mathrm{sup}}\left( {\alpha } \right) {=}\left\{ {\begin{array}{ll} \mathrm {2\alpha }b\mathrm {+}\left( \mathrm {1-2\alpha }\right) c,&{}\quad \mathrm{if}~{ \alpha }<0.5 \\ \left( \mathrm {2\alpha -1} \right) a\mathrm {+}\left( \mathrm {2-2\alpha } \right) b,&{}\quad \mathrm{if}~{\alpha \ge 0.5} \\ \end{array}} \right. \end{aligned}$$

  and

  $$\begin{aligned} \zeta _{\mathrm{inf}}\left( {\alpha } \right) \mathrm {=}\left\{ {\begin{array}{ll} \left( \mathrm {1-2\alpha } \right) a\mathrm {+2\alpha }b,&{}\quad \mathrm{if}~\mathrm {\alpha }<0.5 \\ \left( \mathrm {2-2\alpha } \right) b\mathrm {+}\left( \mathrm {2\alpha -1} \right) c,&{}\quad \mathrm{if}~\mathrm {\alpha \ge 0.5.} \\ \end{array}} \right. \end{aligned}$$

• (ii) Let $\zeta$ be a normal uncertain variable denoted as $\mathcal {N}(\rho ,\sigma )$ then the respective ${\alpha }$-optimistic and ${\alpha }$-pessimistic values of $\zeta$ are,

  $$\begin{aligned} \zeta _{\mathrm{sup}}\left( {\alpha } \right) \mathrm {=}\,\rho \mathrm {-}\frac{\sigma \sqrt{\mathrm {3}}}{{\uppi }}\mathrm {ln}\frac{\alpha }{\mathrm {1-}\alpha } \end{aligned}$$

  and

  $$\begin{aligned} \zeta _{\mathrm{inf}}\left( {\alpha } \right) \mathrm {=}\,\rho \mathrm {+}\frac{\sigma \sqrt{3} }{{\uppi }}\mathrm {ln}\frac{\alpha }{\mathrm {1-}\alpha }\cdot \end{aligned}$$

3 Problem description

A solid transportation problem is concerned with transportation of homogeneous products from source i to destination j via conveyance $k~ \left( \ge 2 \right)$ (trucks, cargo van, goods train, etc.) for which we need to find an optimal transportation plan so that the total transportation cost is minimized. A balanced condition in STP assumes that the total supply at source depots, total demand at destinations and total conveyance capacities are equal. But, in reality, we may encounter following situations in the context of TP. They are mentioned as follow.

• (i) Adequate quantities of the item at the sources to satisfy the demands at destinations.

• (ii) The conveyances have the ability to suffice the demand at destinations.

• (iii) There may be a requirement of multiple items or products at destinations for which we may need to consider shipment of heterogeneous items from source i to destination j via conveyance k.

• (iv) Limited budget at destinations.

• (v) Besides transportation cost, fixed charge cost can also exist when a transportation activity is initiated from source i to destination j.

• (vi) In some situations, often we require to optimize several objectives at the same time, which are conflicting in nature. In the context of transportation problem, these objectives may be minimization of total transportation cost, total delivery time, deterioration of breakable goods, maximization of profit, etc.

In order to consider some of the practical situations mentioned above, in our study, we have presented a profit maximization and time minimization of multi-item fixed charge solid transportation problem with budget constraint. The following notations are used to formulate a multi-objective multi-item fixed charge solid transportation problem with budget constraint (MMFSTPwB) model.

• m :  Number of origins/source depots.

• n :  Number of destinations/demand points.

• K :  Number of conveyances utilize for transportation of products.

• r :  Number of different types of items to be transported.

  For $i=1,2,\ldots ,m{,}~ j=1,2,\ldots ,n$, $k=1,2,\ldots ,K$, $p=1,2,\ldots ,r$

• $a_{i}^{p}:$ Amount of item p available at source i.

• $b_{j}^{p}:$ Demand of item p at destination j.

• $e_{k}:$ Transportation capacity of conveyance k.

• $c_{ijk}^{p}:$ Cost for transporting one unit of item p from source i to destination j by conveyance k.

• $f_{ijk}^{p}$: Fixed charge with respect to the transportation activity for transporting item p from source i to destination j by conveyance k.

• $x_{ijk}^{p}:$ Quantity of item p transported from source i to destination j by conveyance k.

• $t_{ijk}^{p}:$ Time required for transporting item p with respect to transportation activity from source i to destination j by conveyance k.

• $s_{j}^{p}:$ Selling price per unit of item p at the destination j.

• $v_{i}^{p}:$ Purchasing cost per unit of item p at the source i.

• $B_{j}:$ Budget at destination j.

To initiate a transportation activity from source i to destination j, we need to reserve conveyance k, leading to fixed charge. In other words, a fixed charge will be added to the direct transportation cost, if $x_{ijk}^{p}>0$. Therefore, in our problem, the fixed charge is incorporated using a binary decision variable $y_{ijk}^{p}$, where $y_{ijk}^{p}=\left\{ {\begin{array}{l} 1,{~ \mathrm{if}~x}_{ijk}^{p}>0 \\ 0,~ \mathrm{otherwise}~ \\ \end{array}} \right. \forall ~ p,i,j,k.$

The mathematical model of MMFSTPwB is presented in model (8).

$$\begin{aligned} \left\{ {\begin{array}{l} \mathrm{Max}~ { Z}_{1}=\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m\sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left\{ \left( s_{j}^{p}-v_{i}^{p}-c_{ijk}^{p}\right) x_{ijk}^{p}\right. ~\\ \quad \quad \quad \quad \quad \left. -f_{ijk}^{p}y_{ijk}^{p}\right\} ~ \\ \mathrm{Min}~ { Z}_{2}=\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m\sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left\{ t_{ijk}^{p}y_{ijk}^{p} \right\} ~ \\ \mathrm{subject~ to} \\ \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K x_{ijk}^{p} \le a_{i}^{p},~ i=1,2,\ldots ,m,~ p=1,2,\ldots ,r \\ \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K {x_{ijk}^{p}\ge b_{j}^{p}} ,~ j=1,2,\ldots ,n,~ p=1,2,\ldots ,r~ \\ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n x_{ijk}^{p} \le e_{k},~ k=1,2,\ldots ,K~ \\ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K \left\{ \left( v_{i}^{p}+c_{ijk}^{p} \right) x_{ijk}^{p}+f_{ijk}^{p}y_{ijk}^{p}\right\} \le B_{j}\mathrm {,~ }~\\ \quad \quad \quad \quad j=1,2,\ldots ,n~ \\ x_{ijk}^{p}\ge 0,~ y_{ijk}^{p}= \left\{ {\begin{array}{ll} 1;&{}\quad {x}_{ijk}^{p}>0 \\ 0;&{}\quad \mathrm{otherwise} \\ \end{array}} \right. ~ \forall ~ p,i,j,k.~ \\ \end{array}}~ \right. \end{aligned}$$

(8)

In model (8), the first objective is to maximize the overall profit earned after transporting all the required items from each source to every destination points through the available conveyances. The second objective minimizes the total transportation time for shipment of all the required items from all sources to all destinations. The significance of the constraints of model (8) is discussed below.

The first constraint determines that the total quantity of item p which is shipped from source i does not exceed the availability $a_{i}^{p}.$ The second constraint determines the shipment of total quantity of item p at destination j, satisfies at least the demand ${b}_{j}^{p}$. Third constraint implies that the quantity of item p shipped from source i to destination j by means of conveyance k does not exceed ${e}_{k}$. Finally, the fourth constraint indicates that the total expenditure at destination j including the purchase price of item p at source i, transportation cost and fixed charge for transporting item p from source i to destination j via conveyance k is not more than the allocated budget $B_{j}$.

Estimation of an effective transportation plan generally depends on previous records. But, often the data of these previous records may be ill-defined due to uncertainty in the judgment, lack of evidence, fluctuation in market price, etc. For example, the transportation cost and transportation time cannot be exact since these parameters depend on labor charges, toll tax, fluctuation in fuel price, traffic congestion, etc. Similarly, the supply at source may be inexact due to availability of manpower, raw materials, demand of products, etc. Under such circumstances, uncertain programming, proposed by Liu (2007), becomes one of the possible techniques to deal with uncertain information. Uncertain programming is a mathematical programming which models decision-making approaches in uncertain environments using belief degrees.

In order to propose the formulation of MMFSTPwB problem under the framework of uncertainty theory, we categorically termed the problem as uncertain MMFSTPwB, i.e., uncertain multi-objective multi-item fixed charge solid transportation problem with budget constraint (UMMFSTPwB). The UMMFSTPwB is essentially converted to uncertain programming models, i.e., expected value model (EVM), chance-constrained model (CCM) and dependent chance-constrained model (DCCM). Here, the associated uncertain parameters of UMMFSTPwB are considered as transportation cost, fixed charge, transportation time, availability of item at source, demand of item at destination, conveyance capacities and budget at destinations. These parameters are, respectively, represented as $\xi _{c_{ijk}^{p}}{,}~ \xi _{f_{ijk}^{p}}{,}~ \xi _{t_{ijk}^{p}}$, $\xi _{a_{i}^{p}}$, $\xi _{b_{j}^{p}}$, $\xi _{e_{k}}$ and $\xi _{B_{j}}$.

The corresponding formulations of expected value model (EVM), chance-constrained model (CCM) and dependent chance-constrained model (DCCM) are discussed below. These models of UMMFSTPwB along with the solution techniques are graphically represented in Fig. 2.

Fig. 2

Graphical representation of UMMFSTPwB: from model formulation to solution techniques

3.1 Expected value model (EVM)

Liu and Liu (2002) presented the expected value model of uncertain programming. The model optimizes the expected value of an objective function under the expected constraints. Here, we formulate EVM for UMMFSTPwB and present the model in (9).

$$\begin{aligned} \left\{ {\begin{array}{l} \mathrm{Max}~ {E}\left[ {Z}_{\mathrm {1}} \right] ={E}\left[ \sum \nolimits _{p=1}^r\sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left\{ \left( s_{j}^{p}-v_{i}^{p}\right. \right. \right. ~\\ \qquad \qquad \qquad \quad \left. \left. \left. -\xi _{c_{ijk}^{p}} \right) x_{ijk}^{p}-\xi _{f_{ijk}^{p}}y_{ijk}^{p} \right\} \right] ~ \\ \mathrm{Min}~ {E}\left[ { Z}_{2} \right] ={E}\left[ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n\sum \nolimits _{k=1}^K {\xi _{t_{ijk}^{p}}y_{ijk}^{p}} \right] ~ \\ \mathrm{subject~ to}~ \\ {E}\left[ \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K{x_{ijk}^{p}-\xi _{a_{i}^{p}}} \right] \le 0,~ i=1,2,\ldots ,m,~\\ \quad \quad \quad \quad p=1,2,\ldots ,r \\ {E}\left[ \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K {x_{ijk}^{p}-\xi _{b_{j}^{p}}} \right] \ge 0,~ j=1,2,\ldots ,n,~\\ \quad \quad \quad \quad p=1,2,\ldots ,r~ \\ {E}\left[ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m {\sum \nolimits _{j=1}^n x_{ijk}^{p} -\xi _{e_{k}}} \right] \le 0,~ k=1,2,\ldots ,K~ \\ {E}\left[ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K \left\{ {\left( v_{i}^{p}+\xi _{c_{ijk}^{p}} \right) }x_{ijk}^{p}+\xi _{f_{ijk}^{p}}y_{ijk}^{p} \right\} \right. ~\\ \quad \quad \quad \quad \left. -\xi _{B_{j}} \right] \le 0,~ j=1,2,\ldots ,n~ \\ x_{ijk}^{p}\ge 0,~ y_{ijk}^{p}=\left\{ {\begin{array}{ll} 1&{}{ ;\quad x}_{ijk}^{p}>0~ \\ 0&{} ;\quad \mathrm{otherwise}~ \\ \end{array}} \right. ~ \forall ~ p,i,j,k.~ \end{array}}~ \right. \end{aligned}$$

(9)

In model (9), the first objective is to maximize the overall expected profit. The second objective is to minimize the expected total transportation time. These objectives are subjected to some expected constraints.

3.2 Chance-constrained model (CCM)

Chance-constrained programming is an alternate method to deal with optimization of a problem under uncertain environment. The basic idea of CCM (Charnes and Cooper 1959; Liu 2002) is that it allows violation of constraints, but we need to ensure that the constraints should hold at some chance level (confidence level). Here, we develop the chance-constrained model for UMMFSTPwB and present it in model (10).

$$\begin{aligned} \left\{ {\begin{array}{l} \mathrm{Max}~ \bar{Z}_{1}~ \\ \mathrm{Min}~ \bar{Z}_{2}~ \\ \mathrm{subject~ to} \\ \quad \mathcal {M}\left\{ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left[ \left( s_{j}^{p}-v_{i}^{p}-\xi _{c_{ijk}^{p}} \right) x_{ijk}^{p}~\right. \right. \\ \quad \quad \quad \quad \left. \left. -\xi _{f_{ijk}^{p}}y_{ijk}^{p} \right] \ge \bar{Z}_{1} \right\} \ge {\alpha }_{\mathrm {1}} \\ \quad \mathcal {M}\left\{ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left[ \xi _{t_{ijk}^{p}}y_{ijk}^{p} \right] \le \bar{Z}_{2} \right\} \ge {\alpha }_{\mathrm {2}} \\ \quad \mathcal {M}\left\{ \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K {x_{ijk}^{p}-\xi _{a_{i}^{p}}} \le 0 \right\} \ge \beta _{i}^{p},~ i=1,2,\ldots ,m,~\\ \quad \quad \quad \quad p=1,2,\ldots ,r~ \\ \quad \mathcal {M}\left\{ \sum \nolimits _{i=1}^n \sum \nolimits _{k=1}^K {x_{ijk}^{p}-\xi _{b_{j}^{p}}} \ge 0 \right\} \ge \gamma _{j}^{p},~\\ \quad \quad \quad \quad j=1,2,\ldots ,n,~ p=1,2,\ldots ,r~ \\ \quad \mathcal {M}\left\{ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m {\sum \nolimits _{j=1}^n x_{ijk}^{p} -\xi _{e_{k}}} \le 0 \right\} \ge \delta _{k},~\\ \quad \quad \quad \quad k=1,2,\ldots ,K~ \\ \quad \mathcal {M}\left\{ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K \left\{ {\left( v_{i}^{p}+\xi _{c_{ijk}^{p}} \right) }x_{ijk}^{p}+\xi _{f_{ijk}^{p}}y_{ijk}^{p} \right\} \right. ~\\ \quad \quad \quad \quad \left. -\xi _{B_{j}}\le 0 \right\} \ge \rho _{j},~ j=1,2,\ldots ,n~ \\ \quad x_{ijk}^{p}\ge 0,~ y_{ijk}^{p}=\left\{ {\begin{array}{l} 1;\quad x_{ijk}^{p}>0~ \\ 0;\quad \mathrm{otherwise}~ \\ \end{array}} \right. ~ \forall ~ p,i,j,k.~ \\ \end{array}} \right. \end{aligned}$$

(10)

In CCM, ${\alpha }_{\mathrm {1}}{,}~ {\alpha }_{\mathrm {2}}{,}~ \beta _{i}^{p}~ {,}~ \gamma _{j}^{p}$, $\delta _{k}$ and $\rho _{j}$ are predetermined confidence levels. The objectives $\bar{Z}_{1}$ and $\bar{Z}_{2}$ determine the critical values corresponding to the first and second constraints. The first constraint determines the ${\alpha }_{\mathrm {1}}$-optimistic value of the overall profit corresponding to ${\alpha }_{\mathrm {1}}$transportation plan, and the second constraint determines the ${\alpha }_{\mathrm {2}}$-pessimistic value of the shipping/transportation time with respect to ${\alpha }_{\mathrm {2}}$-transportation plan. Moreover, the remaining constraints (third to sixth) of model (10) also hold at their corresponding chance levels, which are at least ${\beta }_{i}^{p},{~ \gamma }_{j}^{p}{,}~ \delta _{k}$ and $\rho _{j}$.

3.3 Dependent chance-constrained model (DCCM)

The main idea of dependent chance programming is to optimize the chance of an uncertain event. For the proposed problem, a DM has to satisfy predetermined minimum profit margin and predetermined maximum transportation time limit and then to maximize the uncertain measures (confidence level) that satisfy the following.

• Total profit is not less than a predetermined profit margin.

• Total transportation time is not more than the predetermined time.

We formulate the dependent chance programming model under chance constraints in model (11) to obtain the most suitable transportation plan.

$$\begin{aligned} \left\{ {\begin{array}{l} \mathrm{Max}~ \nu _{Z_{1}^{'}}=\mathcal {M}\left\{ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left[ \left( s_{j}^{p}-v_{i}^{p}\right. \right. \right. ~\\ \quad \quad \qquad \qquad \left. \left. \left. -\xi _{c_{ijk}^{p}} \right) x_{ijk}^{p}-\xi _{f_{ijk}^{p}}y_{ijk}^{p} \right] \ge {Z_{1}^{'}} \right\} ~ \\ \mathrm{Max}~ \nu _{Z_{2}^{'}}=\mathcal {M}\left\{ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left[ \xi _{t_{ijk}^{p}}y_{ijk}^{p} \right] \right. \\ \quad \quad \qquad \qquad \left. \le Z_{2}^{'} \right\} ~ \\ \mathrm{subject~ to~ third~ to~ seventh~ constraints~ of} (10), \\ \end{array}} \right. \end{aligned}$$

(11)

where $Z_{1}^{'}$ and $Z_{2}^{'}$ are, respectively, the predetermined values of minimum profit and maximum transportation time.

4 Crisp equivalents of the models

The crisp equivalent of EVM is provided below in Theorem 4.1.

Theorem 4.1

Let $\xi _{c_{ijk}^{p}}$, $\xi _{f_{ijk}^{p}}$, $\xi _{t_{ijk}^{p}}{,}~ \xi _{a_{i}^{p}}{,}~ \xi _{b_{j}^{p}}{,}~ \xi _{e_{k}}$ and $\xi _{B_{j}}$ are the independent uncertain variables, respectively, associated with uncertainty distributions ${\Phi }_{\xi _{c_{ijk}^{p}}}{,}~ {\Phi }_{\xi _{f_{ijk}^{p}}}{,}~ {\Phi }_{\xi _{t_{ijk}^{p}}}{,} {\Phi }_{\xi _{a_{i}^{p}}}{,}~ {\Phi }_{\xi _{b_{j}^{p}}}{,}~ {\Phi }_{\xi _{e_{k}}}$ and ${\Phi }_{\xi _{B_{j}}}$. Then the crisp equivalent of EVM is presented below in model (12.1).

$$\begin{aligned} \left\{ {\begin{array}{l} \mathrm{Max}~ {E}\left[ {Z}_{\mathrm {1}} \right] =\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left\{ \left( s_{j}^{p}-v_{i}^{p}\right. \right. ~\\ \quad \qquad \qquad \qquad \left. \left. -\int _0^1{{\Phi }_{\xi _{c_{ijk}^{p}}}^{\mathrm {-1}}\left( {\alpha }_{\mathrm {1}} \right) \mathrm{d}{\alpha }_{\mathrm {1}}} \right) x_{ijk}^{p}\right. \\ \quad \qquad \qquad \qquad \left. -\int _0^1 {{\Phi }_{\xi _{f_{ijk}^{p}}}^{\mathrm {-1}}\left( {\alpha }_{\mathrm {1}} \right) \mathrm{d}{\alpha }_{\mathrm {1}}} y_{ijk}^{p} \right\} \\ \mathrm{Min}~ {E}\left[ Z_{2} \right] =\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K {\int _0^1 {{\Phi }_{\xi _{t_{ijk}^{p}}}^{\mathrm {-1}}\left( {\alpha }_{\mathrm {2}} \right) \mathrm{d}{\alpha }_{\mathrm {2}}} y_{ijk}^{p}}~ \\ \mathrm{subject~ to}~ \\ ~\sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K {x_{ijk}^{p}-\int _0^1 {{\Phi }_{\xi _{a_{i}^{p}}}^{\mathrm {-1}}\left( {1-\beta }_{i}^{p} \right) } d\beta _{i}^{p}} \le 0,~\\ \quad \quad \quad \quad i=1,2,\ldots ,m,~ p=1,2,\ldots ,r~ \\ \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K {x_{ijk}^{p}-\int _0^1 {{\Phi }_{\xi _{b_{j}^{p}}}^{\mathrm {-1}}\left( \gamma _{j}^{p} \right) } d\gamma _{j}^{p}} \ge 0,~\\ \quad \quad \quad \quad j=1,2,\ldots ,n,~ p=1,2,\ldots ,r~ \\ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m {\sum \nolimits _{j=1}^n x_{ijk}^{p} -\int _0^1 {{\Phi }_{\xi _{e_{k}}}^{\mathrm {-1}}\left( \mathrm {1-}\delta _{k} \right) } d\delta _{k}} \le 0,~\\ \quad \quad \quad \quad k=1,2,\ldots ,K~ \\ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K \left\{ {~ \left( v_{i}^{p}+\int _0^1 {{\Phi }_{\xi _{c_{ijk}^{p}}}^{\mathrm {-1}}\left( \rho _{j} \right) } \mathrm{d}\rho _{j}\right) } x_{ijk}^{p}\right. \\ \quad \quad \quad \quad \left. +\int _0^1 {{\Phi }_{\xi _{f_{ijk}^{p}}}^{\mathrm {-1}}\left( \rho _{j} \right) }\mathrm{d}\rho _{j}y_{ijk}^{p} \right\} \\ \quad \quad \quad \quad -\int _0^1 {{\Phi }_{\xi _{B_{j}}}^{\mathrm {-1}}\left( \mathrm {1-}\rho _{j} \right) } \mathrm{d}\rho _{j}\le 0,~ j=1,2,\ldots , n \\ x_{ijk}^{p}\ge 0,~ y_{ijk}^{p}=\left\{ {\begin{array}{l} 1;~~ {x}_{ijk}^{p}>0~ \\ 0;~~ \mathrm{otherwise}~ \\ \end{array}} \right. ~ \forall ~ p,i,j,k.~ \\ \end{array}} \right. \end{aligned}$$

(12.1)

Proof

From the linearity property of expected value operator, crisp equivalent of EVM in model (12.1) can be formulated as follows.

$$\begin{aligned} \left\{ {\begin{array}{l} \mathrm{Max}~ {E}\left[ {Z}_{\mathrm {1}}\right] =\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n\sum \nolimits _{k=1}^K \left\{ \left( s_{j}^{p}-v_{i}^{p}\right. \right. \\ \quad \quad \quad \qquad \left. \left. -{E}\left[ \xi _{c_{ijk}^{p}}\right] \right) x_{ijk}^{p}-{E}\left[ \xi _{f_{ijk}^{p}} \right] y_{ijk}^{p} \right\} \\ \mathrm{Min}~ {E}\left[ Z_{2} \right] =\sum \nolimits _{p=1}^r\sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K{{E}\left[ \xi _{t_{ijk}^{p}} \right] y_{ijk}^{p}} ~ \\ \mathrm{subject~ to}~ \\ \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K {x_{ijk}^{p}-{E}\left[ \xi _{a_{i}^{p}} \right] } \le 0,~ i=1,2,\ldots ,m,~ p=1,2,\ldots ,r~ \\ \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K {x_{ijk}^{p}-{E}\left[ \xi _{b_{j}^{p}} \right] } \ge 0,~ j=1,2,\ldots ,n,~ p=1,2,\ldots ,r~ \\ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m {\sum \nolimits _{j=1}^n x_{ijk}^{p}-{E}\left[ \xi _{e_{k}} \right] } \le 0,~k=1,2,\ldots ,K~ \\ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K \left\{ {~ \left( v_{i}^{p}+{E}\left[ \xi _{c_{ijk}^{p}}\right] \right) } x_{ijk}^{p}+{E}\left[ \xi _{f_{ijk}^{p}}\right] y_{ijk}^{p} \right\} \\ \quad \quad \quad \qquad -{E}\left[ \xi _{B_{j}} \right] \le 0,~ j=1,2,\ldots ,n~ \\ x_{ijk}^{p}\ge 0,~ y_{ijk}^{p}=\left\{ {\begin{array}{l} 1;~ ~{x}_{ijk}^{p}>0~ \\ 0;~ ~\mathrm{otherwise}~ \\ \end{array}} \right. ~ \forall ~ p,i,j,k.~ \\ \end{array}} \right. \end{aligned}$$

(12.2)

Following Theorem 2.2, model (12.2) can be written as model (12.1).

Corollary 1

If ${\xi }_{c_{ijk}^{p}}$, $\xi _{f_{ijk}^{p}}$, $\xi _{t_{ijk}^{p}}{,}~ \xi _{a_{i}^{p}}{,}~ \xi _{b_{j}^{p}}{,}~ \xi _{e_{k}}$ and $\xi _{B_{j}}$ are the independent zigzag uncertain variables of the form $\mathcal {Z}\left( g,h,l \right)$ with $g,h,l\in \mathcal {R}$ and $g<h<l$, then the crisp equivalent of the model (12.1) can be written as shown in the model (12.3).

$$\begin{aligned} \left\{ {\begin{array}{l} \mathrm{Max}~ E\left[ Z_{1} \right] =\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left\{ \left( s_{j}^{p}-v_{i}^{p}\right. \right. \\ \quad \quad \quad \qquad \left. \left. -\frac{\left( g_{c_{ijk}^{p}}+2h_{c_{ijk}^{p}}+l_{c_{ijk}^{p}} \right) }{4} \right) x_{ijk}^{p}-\frac{\left( g_{f_{ijk}^{p}}+2h_{f_{ijk}^{p}}+l_{f_{ijk}^{p}} \right) }{4}y_{ijk}^{p} \right\} \\ \mathrm{Min}~ E\left[ Z_{2} \right] =\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K {\frac{\left( g_{t_{ijk}^{p}}+2h_{t_{ijk}^{p}}+l_{t_{ijk}^{p}} \right) }{4}y_{ijk}^{p}} \\ \quad \mathrm{subject~ to} \\ \quad \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K {x_{ijk}^{p}-\frac{\left( g_{a_{i}^{p}}+2h_{a_{i}^{p}}+l_{a_{i}^{p}} \right) }{4}} \le 0,~ i=1,2,\ldots ,m,\\ \quad \quad \quad \qquad p=1,2,\ldots ,r~ \\ \quad \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K {x_{ijk}^{p}-\frac{\left( g_{b_{j}^{p}}+2h_{b_{j}^{p}}+l_{b_{j}^{p}} \right) }{4}{\ge 0}},~ j=1,2,\ldots ,n,\\ \quad \quad \quad \qquad p=1,2,\ldots ,r~ \\ \quad \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m {\sum \nolimits _{j=1}^n x_{ijk}^{p}-\frac{\left( g_{e_{k}}+2h_{e_{k}}+l_{e_{k}} \right) }{4}} \le 0,~ k=1,2,\ldots ,K~ \\ \quad \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K \left\{ {\left( v_{i}^{p}+\frac{\left( g_{c_{ijk}^{p}}+2h_{c_{ijk}^{p}}+l_{c_{ijk}^{p}} \right) }{4}\right) }x_{ijk}^{p}\right. \\ \quad \quad \qquad \qquad \left. +\frac{\left( g_{f_{ijk}^{p}}+2h_{f_{ijk}^{p}}+l_{f_{ijk}^{p}}\right) }{4}y_{ijk}^{p} \right\} -\frac{\left( g_{B_{j}}+2h_{B_{j}}+l_{B_{j}} \right) }{4}{\le 0,~ } \\ \quad j=1,2,\ldots ,n \\ \quad x_{ijk}^{p}\ge 0,~ y_{ijk}^{p}=\left\{ {\begin{array}{l} 1{~ ;x}_{ijk}^{p}>0~ \\ 0~ ;\mathrm{otherwise}~ \\ \end{array}} \right. ~ \forall ~ p,i,j,k. \\ \end{array}} \right. \end{aligned}$$

(12.3)

Corollary 2

If ${\xi }_{c_{ijk}^{p}}$, $\xi _{f_{ijk}^{p}}$, $\xi _{t_{ijk}^{p}}{,}~ \xi _{a_{i}^{p}}{,}~ \xi _{b_{j}^{p}}{,}~ \xi _{e_{k}^{p}}$ and $\xi _{B_{j}^{p}}$ are the independent normal uncertain variables of the form $\mathcal {N}(\mu ,\sigma )$, where $\mu ,~ \sigma \in \mathfrak {R}$ and $\sigma >0$, then model (12.1) can be written as follows.

$$\begin{aligned} \left\{ {\begin{array}{l} \mathrm{Max}~ E\left[ Z_{1} \right] =\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left\{ \left( s_{j}^{p}-v_{i}^{p}\right. \right. \\ \quad \qquad \qquad \qquad \left. \left. -\mu _{c_{ijk}^{p}} \right) x_{ijk}^{p}-\mu _{f_{ijk}^{p}}y_{ijk}^{p} \right\} \\ \mathrm{Min}~ E\left[ Z_{2} \right] =\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K {\mu _{t_{ijk}^{p}}y_{ijk}^{p}} \\ \quad \mathrm{subject~ to} \\ \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K {x_{ijk}^{p}-\mu _{a_{i}^{p}}} \le 0,~ i=1,2,\ldots ,m,\\ \quad \qquad \qquad \qquad p=1,2,\ldots ,r \\ \quad \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K {x_{ijk}^{p}-\mu _{b_{j}^{p}}{\ge 0}} ,~ j=1,2, \ldots ,n,\\ \quad \qquad \qquad \qquad p=1,2,\ldots ,r \\ \quad \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m {\sum \nolimits _{j=1}^n x_{ijk}^{p} -\mu _{e_{k}}} \le 0,~ k=1,2,\ldots ,K~ \\ \quad \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K \left\{ {\left( v_{i}^{p}+\mu _{c_{ijk}^{p}} \right) }x_{ijk}^{p}+\mu _{f_{ijk}^{p}}y_{ijk}^{p} \right\} \\ \quad \qquad \qquad \qquad -\mu _{B_{j}}{\le 0,~ j=1,2,\ldots ,n}~ \\ \quad x_{ijk}^{p}\ge 0,~ y_{ijk}^{p}=\left\{ {\begin{array}{l} 1;\quad x_{ijk}^{p}>0~ \\ 0;\quad \mathrm{otherwise}~ \\ \end{array}} \right. ~ \forall ~ p,i,j,k.~ \\ \end{array}} \right. \end{aligned}$$

(12.4)

Some related theorems for the crisp equivalents of CCM, and DCCM and their corresponding proofs and corollaries are presented in “Appendix B.”

5 Methodologies for crisp equivalence

In this section, we discuss three different multi-objective programming techniques: (i) linear weighted method, (ii) global criterion method and (iii) fuzzy programming method. These methods are used to generate the compromise solutions of EVM, CCM and DCCM.

5.1 Linear weighted method

The linear weighted method converts a multi-objective optimization problem to its equivalent SOOP by weighted sum of the objective functions, where the weights are the relative importance of the objectives as determined by the DM.

The crisp equivalent multi-objective models, models (12.1) and (B1) (cf. “Appendix B”), are converted to their equivalent compromise SOOPs by weighted sum of the objective functions and are represented in models (13.1) and (13.2), respectively. For DCCM, model (B5) (cf. “Appendix B”), presented in model (13.3), can be converted to equivalent compromise SOOP.

$$\begin{aligned}&\left\{ {\begin{array}{l} \mathrm{Min}~ \left\{ {-\lambda }_{1}{E}\left[ Z_{1} \right] +\lambda _{2}{E}\left[ Z_{2} \right] \right\} ~ \\ \quad \mathrm{subject~ to~ the~ constraints~of}~ \left( 12.1 \right) ~ \\ \quad ~ \lambda _{1}+\lambda _{2}=1,~ \lambda _{1},\lambda _{2}\in \left[ 0,1 \right] .~ \\ \end{array}} \right. \end{aligned}$$

(13.1)

$$\begin{aligned}&\left\{ {\begin{array}{l} \mathrm{Min}~ \left\{ {-\lambda }_{1}\bar{Z}_{1}+\lambda _{2}\bar{Z}_{2} \right\} ~ \\ \quad \mathrm{subject~ to~ the~ constraints~of}~ \left( {B}1 \right) ~ \mathrm{in}~ \mathrm {``Appendix~ B''}~ \\ \quad \lambda _{1}+\lambda _{2}=1,{~ \lambda }_{1},\lambda _{2}\in \left[ 0,1 \right] .~ \\ \end{array}} \right. \end{aligned}$$

(13.2)

$$\begin{aligned}&\left\{ {\begin{array}{l} \mathrm{Max}~ \left\{ \lambda _{1}\upsilon _{Z_{1}^{'}}+\lambda _{2}\upsilon _{Z_{2}^{'}} \right\} ~ \\ \quad \mathrm{subject~ to~ the~constraints~of}~ \left( {B}1 \right) ~\mathrm{in}~ \mathrm {``Appendix~B''} \\ \quad \lambda _{1}+\lambda _{2}=1,~ \lambda _{1},\lambda _{2}\in \left[ 0,1 \right] .~ \\ \end{array}} \right. \end{aligned}$$

(13.3)

Theorem 5.1

A feasible solution of the crisp equivalent of EVM in (12.1) is

• (i) an optimal solution of the compromise model (13.1), if it is Pareto optimal to the multi-objective model (12.1),

• (ii) a Pareto optimal solution of multi-objective model (12.1), if it is an optimal solution of the compromise model (13.1).

Proof

• (i) Let $t^{*}$ is the optimal solution of the compromise model (13.1), which is not Pareto optimal to multi-objective model (12.1). Then, there exists a Pareto optimal solution t, which dominates $t^{*}$ or $t\prec t^{*}$. It follows, $\left( {-\lambda }_{1}{E}\left[ Z_{1}^{t} \right] +\lambda _{2}{E}\left[ Z_{2}^{t} \right] \right) <\big ( {-\lambda }_{1}{E}\left[ Z_{1}^{t^{*}} \right] +\lambda _{2}{E}\left[ Z_{2}^{t^{*}} \right] \big )$, where $\lambda _{1}+\lambda _{2}=1,~ \lambda _{1},\lambda _{2}\in \left[ 0,1 \right]$. This eventually implies that $t^{*}$ is not an optimal solution of model (13.1) which contradicts our previous hypothesis that $t^{*}$ is the optimal solution of model (13.1).

• (ii) Let $t^{*}$ be the Pareto optimal solution of model (12.1), which is not an optimal solution of the model (13.1). Then there exist an optimal solution $t{'}$ of model (13.1) such that $\left( {-\lambda }_{1}{E}\left[ Z_{1}^{t{'}} \right] +\lambda _{2}{E}\left[ Z_{2}^{t{'}} \right] \right) <\big ( {-\lambda }_{1}{E}\left[ Z_{1}^{t^{*}} \right] +\lambda _{2}{E}\left[ Z_{2}^{t^{*}} \right] \big )$, where $\lambda _{1},\lambda _{2}\in \left[ 0,1 \right]$ and $\lambda _{1}+\lambda _{2}=1$. This implies $t{'}$ is Pareto optimal to model (12.1). It contradicts our initial hypothesis that $t^{*}$ is the Pareto optimal solution of model (12.1).

Similar proofs can be done for multi-objective model (B1) and compromise model (13.2) of CCM, and for multi-objective model (B5) and compromise model (13.3) of DCCM. $\square$

5.2 Global criterion method

The global criterion method (Rao 2006; Kundu et al. 2013a, b) transforms a multi-objective optimization problem to its equivalent SOOP and minimizes the sum of deviation of the ideal solutions from the corresponding objective functions. Here, we use the global criterion method in ${L}_{\mathrm {2}}$ norm to convert the crisp equivalent multi-objective models to their equivalent compromise SOOPs as presented below in (14.1), (14.2) and (14.3).

$$\begin{aligned} \left\{ {\begin{array}{l} \mathrm{Min}\left\{ \sqrt{\left( \frac{{E\left[ {Z}_{\mathrm {1}} \right] }^{\mathrm{max}}-E\left[ Z_{1} \right] }{{E\left[ {Z}_{\mathrm {1}} \right] }^{\mathrm{max}}} \right) ^{2}+\left( \frac{E\left[ Z_{2} \right] -{E\left[ {Z}_{\mathrm {2}} \right] }^{\mathrm{min}}}{{E\left[ {Z}_{\mathrm {2}} \right] }^{\mathrm{min}}} \right) ^{2}} \right\} \\ \mathrm{subject~ to~ the~ constraints~ of}~ \left( 12.1 \right) , \\ \end{array}} \right. \end{aligned}$$

(14.1)

where ${E\left[ {Z}_{\mathrm {1}} \right] }^{\mathrm{max}}$ and ${E\left[ {Z}_{\mathrm {2}} \right] }^{\mathrm{min}}$ are the ideal objective values of the crisp equivalent of EVM in (12.1).

$$\begin{aligned} \left\{ {\begin{array}{l} \mathrm{Min}\left\{ \sqrt{\left( \frac{\overline{Z}_{1}^{\mathrm{max}}-\overline{Z}_{1}}{\bar{Z}_{1}^{\mathrm{max}}} \right) ^{2}+\left( \frac{\overline{Z}_{\mathrm {2}}-\bar{Z}_{2}^{\mathrm{min}}}{\overline{Z}_{2}^{\mathrm{min}}} \right) ^{2}}\right\} ~ \\ ~ \mathrm{subject~ to~ the~ constraints~ of} (B1)~ \mathrm{in}~ {``\mathrm Appendix~B}'',~ \\ \end{array}} \right. \end{aligned}$$

(14.2)

where $\overline{Z}_{1}^{\mathrm{max}}$ and $\overline{Z}_{2}^{\mathrm{min}}$ are the ideal objective values of the crisp equivalent of CCM in (B1).

$$\begin{aligned} \left\{ {\begin{array}{l} \mathrm{Min}\left\{ \sqrt{\left( \frac{\upsilon _{Z_{1}^{'}}^{\mathrm{max}}-\upsilon _{Z_{1}^{'}}}{\upsilon _{Z_{1}^{'}}^{\mathrm{max}}} \right) ^{2}+\left( \frac{\upsilon _{Z_{2}^{'}}^{\mathrm{max}}-\upsilon _{Z_{2}^{'}}}{\upsilon _{Z_{2}^{'}}^{\mathrm{max}}} \right) ^{2}} \right\} ~ \\ ~ \mathrm{subject~ to~ the~constraints~ of}~ (B1)~ \mathrm{in}~ \mathrm {``Appendix~B''},~ \\ \end{array}} \right. \end{aligned}$$

(14.3)

where $\upsilon _{Z_{1}^{'}}^{\mathrm{max}}$ and $\upsilon _{Z_{2}^{'}}^{\mathrm{max}}$ are the ideal objective values of the crisp equivalent of DCCM in (B5).

Theorem 5.2

A feasible solution of the crisp equivalent of EVM in (12.1) is

• (i) an optimal solution of the compromise model (14.1), if it is Pareto optimal to multi-objective model (12.1),

• (ii) a Pareto optimal solution of multi-objective model (12.1), if it is optimal solution of compromise model (14.1).

Proof

• (i) Let $t^{*}$ is the optimal solution of compromise model (14.1) which is not Pareto optimal to multi-objective model (12.1). Then, there exists a Pareto optimal solution t, such that t dominates $\left( \prec \right) ~ t^{*}$. This implies

  $$\begin{aligned}&\sqrt{\left( \frac{{E\left[ Z_{1} \right] }^{\mathrm{max}}-E\left[ Z_{1}^{t} \right] }{{E\left[ Z_{1} \right] }^{\mathrm{max}}} \right) ^{2}+\left( \frac{E\left[ Z_{2}^{t} \right] -{E\left[ Z_{2} \right] }^{\mathrm{min}}}{{E\left[ Z_{2} \right] }^{\mathrm{min}}} \right) ^{2}} \\&\quad <\sqrt{\left( \frac{{E\left[ Z_{1} \right] }^{\mathrm{max}}-E\left[ Z_{1}^{t^{*}} \right] }{{E\left[ Z_{1} \right] }^{\mathrm{max}}} \right) ^{2}+\left( \frac{E\left[ Z_{2}^{t^{*}} \right] -{E\left[ Z_{2} \right] }^{\mathrm{min}}}{{E\left[ Z_{2} \right] }^{\mathrm{min}}} \right) ^{2}}. \end{aligned}$$

  It implies that $t^{*}$ is not the optimal solution of (14.1), which directly contradicts our previous assumption that $t^{*}$ is the optimal solution of (14.1).

• (ii) Let $t^{*}$ be the Pareto optimal solution of (12.1) which is not an optimal solution of (14.1). Then there exists an optimal solution $t{'}$ of (14.1) such that

  $$\begin{aligned}&\sqrt{\left( \frac{{E\left[ {Z}_{1} \right] }^{\mathrm{max}}-E\left[ Z_{1}^{t{'}} \right] }{{E\left[ {Z}_{\mathrm {1}} \right] }^{\mathrm{max}}} \right) ^{2}+\left( \frac{E\left[ Z_{2}^{t{'}} \right] -{E\left[ {Z}_{2} \right] }^{\mathrm{min}}}{{E\left[ {Z}_{2} \right] }^{\mathrm{min}}} \right) ^{2}} \\&\quad <\sqrt{\left( \frac{{E\left[ {Z}_{\mathrm {1}} \right] }^{\mathrm{max}}-E\left[ Z_{1}^{t^{*}} \right] }{{E\left[ {Z}_{\mathrm {1}} \right] }^{\mathrm{max}}} \right) ^{2}+\left( \frac{E\left[ Z_{2}^{t^{*}} \right] -{E\left[ {Z}_{\mathrm {2}} \right] }^{\mathrm{min}}}{{E\left[ {Z}_{\mathrm {2}} \right] }^{\mathrm{min}}} \right) ^{2}} . \end{aligned}$$

  Therefore, it follows that $t{'}$ is Pareto optimal to (12.1), which contradicts with our previous assumption that $t^{{*}}$ is the Pareto optimal solution of the model (12.1).

Similar proofs can be done for multi-objective model (B1) and compromise model (14.2) of CCM, and for multi-objective model (B5) and compromise model (14.3) of DCCM.

5.3 Fuzzy programming method

Zimmermann (1978) presented the Fuzzy programming technique (FPT) for solving multi-objective linear programming (MOLP) problem. In this paper, the FPT is applied on crisp equivalent multi-objective models, (12.1) for EVM presented above, (B1) for CCM and (B5) for DCCM and convert those to their equivalent compromise SOOPs by introducing an auxiliary variable $\lambda$. These compromise models are represented, respectively, in (15.1), (15.2) and (15.3).

$$\begin{aligned} \left\{ {\begin{array}{l} \mathrm{Max}~ \lambda ~ \\ \mathrm{subject~ to}~ \\ \left( \frac{{{E}\left[ Z_{1} \right] -{E}\left[ {Z}_{\mathrm {1}} \right] }^{{\mathrm {LB}}_{1}}}{{{E}\left[ {Z}_{\mathrm {1}} \right] }^{{\mathrm {UB}}_{1}}-{{E}\left[ {Z}_{\mathrm {1}} \right] }^{{\mathrm {LB}}_{1}}} \right) \ge \lambda ~ \\ \left( \frac{{{E}\left[ {Z}_{\mathrm {2}} \right] }^{{\mathrm {UB}}_{2}}-{E}\left[ Z_{2} \right] }{{{E}\left[ {Z}_{\mathrm {2}} \right] }^{{\mathrm {UB}}_{2}}-{{E}\left[ {Z}_{\mathrm {2}} \right] }^{{\mathrm {LB}}_{2}}} \right) \ge \lambda ~ \\ \mathrm{constraints~of}~ \left( 12.1 \right) , \\ \end{array}} \right. \end{aligned}$$

(15.1)

where ${{E}\left[ {Z}_{\mathrm {1}} \right] }^{{\mathrm {UB}}_{1}}$ and ${{E}\left[ {Z}_{\mathrm {2}} \right] }^{{\mathrm {LB}}_{\mathrm {2}}}$ are, respectively, the expected optimal solutions of ${E}\left[ {Z}_{\mathrm {1}} \right]$ and ${E}\left[ {Z}_{\mathrm {2}} \right]$, ${{E}\left[ {Z}_{\mathrm {1}} \right] }^{{\mathrm {LB}}_{1}}$ is the expected lower bound of ${{E[Z}}_{\mathrm {1}}\mathrm {]~ }$corresponding to ${{E}\left[ {Z}_{\mathrm {2}} \right] }^{{\mathrm {LB}}_{\mathrm {2}}}$, and ${{E}\left[ {Z}_{\mathrm {2}} \right] }^{{\mathrm {UB}}_{\mathrm {2}}}$ is the expected upper bound of ${{E[Z}}_{\mathrm {2}}]~$ corresponding to ${{E}\left[ {Z}_{\mathrm {1}} \right] }^{{\mathrm {UB}}_{1}}$.

$$\begin{aligned} \left\{ {\begin{array}{l} \mathrm{Max}~ \lambda ~ \\ \mathrm{subject~ to}~ \\ \left( \frac{{\overline{Z}_{1}-\overline{Z}_{1}}^{{\mathrm {LB}}_{1}}}{\overline{Z}_{1}^{{\mathrm {UB}}_{1}}-\overline{Z}_{1}^{{\mathrm {LB}}_{1}}} \right) \ge \lambda ~ \\ \left( \frac{\overline{Z}_{2}^{{\mathrm {UB}}_{2}}-\overline{Z}_{2}}{\overline{Z}_{2}^{{\mathrm {UB}}_{2}}-\overline{Z}_{2}^{{\mathrm {LB}}_{2}}} \right) \ge \lambda ~ \\ ~ \mathrm{constraints~ of}~ \left( {B}1 \right) ~ \mathrm{in}~ \mathrm {``Appendix~B''}, \\ \end{array}} \right. \end{aligned}$$

(15.2)

where $\overline{{Z}}_{\mathrm {1}}^{{\mathrm {UB}}_{1}}$ and $\overline{ {Z}}_{\mathrm {2}}^{{\mathrm {LB}}_{\mathrm {2}}}$ are, respectively, the optimal solutions of $\overline{Z}_{\mathrm {1}}$ and $\overline{Z}_{\mathrm {2}}$, $\overline{Z}_{1}^{{\mathrm {LB}}_{1}}$ is the lower bound of $\overline{Z}_{1}$ corresponding to $\overline{{Z}} _{\mathrm {2}}^{{\mathrm {LB}}_{\mathrm {2}}}$, and $\overline{{Z}} _{\mathrm {2}}^{{\mathrm {UB}}_{2}}$ is the upper bound of $\overline{Z}_{\mathrm {2}}$ corresponding to $\overline{{Z}} _{\mathrm {1}}^{{\mathrm {UB}}_{1}}$.

$$\begin{aligned} \left\{ {\begin{array}{l} \mathrm{Max}~ \lambda ~ \\ \mathrm{subject~ to}~ \\ \left( \frac{\upsilon _{Z_{1}^{'}}-\upsilon _{Z_{1}^{'}}^{{\mathrm {LB}}_{\mathrm {1}}}}{\upsilon _{Z_{1}^{'}}^{{\mathrm {UB}}_{\mathrm {1}}}-\upsilon _{Z_{1}^{'}}^{{\mathrm {LB}}_{\mathrm {1}}}} \right) \ge \lambda ~ \\ \left( \frac{\upsilon _{Z_{2}^{'}}-\upsilon _{Z_{2}^{'}}^{{\mathrm {LB}}_{\mathrm {2}}}}{\upsilon _{Z_{2}^{'}}^{{\mathrm {UB}}_{\mathrm {2}}}-\upsilon _{Z_{2}^{'}}^{{\mathrm {LB}}_{\mathrm {2}}}} \right) \ge \lambda ~ \\ \mathrm{constraints~of}~ \left( {B}1 \right) ~ \mathrm{in}~ \mathrm {``Appendix~B''} \\ \end{array}} \right. \end{aligned}$$

(15.3)

where $\upsilon _{Z_{1}^{'}}^{{\mathrm {UB}}_{\mathrm {1}}}$ and $\upsilon _{Z_{2}^{'}}^{{\mathrm {UB}}_{\mathrm {2}}}$ are, respectively, the optimal solutions of $\upsilon _{Z_{1}^{'}}$ and $\upsilon _{Z_{2}^{'}}$, $\upsilon _{Z_{1}^{'}}^{{\mathrm {LB}}_{\mathrm {1}}}$ is the lower bound of $\upsilon _{Z_{1}^{'}}~$corresponding to $\upsilon _{Z_{2}^{'}}^{{\mathrm {UB}}_{\mathrm {2}}}$, and $\upsilon _{Z_{2}^{'}}^{{\mathrm {LB}}_{\mathrm {2}}}$ is the lower bound of $\upsilon _{Z_{2}^{'}}$ corresponding to $\upsilon _{Z_{1}^{'}}^{{\mathrm {UB}}_{\mathrm {1}}}$.

Theorem 5.3

A feasible solution of the crisp equivalent of EVM in (12.1) is

• (i) an optimal solution of compromise model (15.1), if it is Pareto optimal to multi-objective model (12.1),

• (ii) a Pareto optimal solution of multi-objective model (12.1), if it is optimal to compromise model (15.1).

Proof

• (i) Let $t^{*}$ is the optimal solution of compromise model (15.1) which is not the Pareto optimal to multi-objective model (12.1). Then, there exists a Pareto optimal solution t, such that t dominates $\left( \prec \right) ~ t^{*}$. It implies

  $$\begin{aligned}&\frac{{{E}\left[ Z_{1}^{t} \right] -{E}\left[ {Z}_{\mathrm {1}} \right] }^{{\mathrm {LB}}_{1}}}{{{E}\left[ {Z}_{\mathrm {1}} \right] }^{{\mathrm {UB}}_{1}}-{{E}\left[ {Z}_{\mathrm {1}} \right] }^{{\mathrm {LB}}_{1}}}\\&\quad>\frac{{{E}\left[ Z_{1}^{t^{*}~} \right] -{E}\left[ {Z}_{\mathrm {1}} \right] }^{{\mathrm {LB}}_{1}}}{{{E}\left[ {Z}_{\mathrm {1}} \right] }^{{\mathrm {UB}}_{1}}-{{E}\left[ {Z}_{\mathrm {1}} \right] }^{{\mathrm {LB}}_{1}}} \hbox { and } \frac{{{E}\left[ {Z}_{\mathrm {2}} \right] }^{{\mathrm {UB}}_{2}}{-E}\left[ Z_{2}^{t} \right] }{{{E}\left[ {Z}_{2} \right] }^{{\mathrm {UB}}_{2}}\mathrm {-}{{E}\left[ {Z}_{2} \right] }^{{\mathrm {LB}}_{2}}}\\&\quad<\frac{{{E}\left[ {Z}_{2} \right] }^{{\mathrm {UB}}_{2}}{-E}\left[ Z_{2}^{t^{*}~} \right] }{{{E}\left[ {Z}_{2} \right] }^{{\mathrm {UB}}_{2}}\mathrm {-}{{E}\left[ {Z}_{2} \right] }^{{\mathrm {LB}}_{2}}} \\&\quad \Leftrightarrow \eta _{1}\left( {E}\left[ Z_{1}^{t} \right] \right) >\eta _{1}\left( {E}\left[ Z_{1}^{t^{*}} \right] \right) \hbox { and } \eta _{2}\left( {E}\left[ Z_{2}^{t} \right] \right) \\&\quad <\eta _{2}\left( {E}\left[ Z_{2}^{t^{*}} \right] \right) , \end{aligned}$$

where $\eta _{1}\left( {E}\left[ Z_{1}^{T} \right] \right)$$=\left\{ ~ {\begin{array}{ll} 1,&{}\quad \mathrm{if}~ {{E}\left[ Z_{\mathrm {1}} \right] }^{{\mathrm {UB}}_{1}}\le {E}\left[ Z_{1}^{T} \right] \\ \frac{{E}\left[ Z_{1}^{T} \right] \mathrm {-}{{E}\left[ Z_{\mathrm {1}} \right] }^{{\mathrm {LB}}_{1}}}{{{E}\left[ {Z}_{\mathrm {1}} \right] }^{{\mathrm {UB}}_{1}}-{{E}\left[ Z_{\mathrm {1}} \right] }^{{\mathrm {LB}}_{1}}},&{}\quad \mathrm{if}~ {{E}\left[ Z_{\mathrm {1}} \right] }^{{\mathrm {LB}}_{1}}<{E}\left[ Z_{1}^{T} \right] <{{E}\left[ Z_{\mathrm {1}} \right] }^{{\mathrm {UB}}_{1}} \\ 0,&{}\quad \mathrm{if}~ {E}\left[ Z_{1}^{T} \right] \le {{E}\left[ {Z}_{\mathrm {1}} \right] }^{{\mathrm {LB}}_{1}} \\ \end{array}} \right.$

and

$$\begin{aligned}&\eta _{2}\left( {E}\left[ Z_{2}^{T} \right] \right) \\&\quad =\left\{ ~ {\begin{array}{ll} 1,&{} \mathrm{if}~ {E}\left[ Z_{2}^{T} \right] \le {{E}\left[ Z_{\mathrm {2}} \right] }^{{\mathrm {LB}}_{\mathrm {2}}} \\ \frac{{{E}\left[ Z_{\mathrm {2}} \right] }^{{\mathrm {UB}}_{2}}{-E}\left[ Z_{2}^{T} \right] }{{{E}\left[ Z_{\mathrm {2}} \right] }^{{\mathrm {UB}}_{2}}-{{E}\left[ Z_{\mathrm {2}} \right] }^{{\mathrm {LB}}_{2}}},&{} \mathrm{if}~ {{E}\left[ {Z}_{\mathrm {2}} \right] }^{{\mathrm {LB}}_{2}}<{E}\left[ Z_{2}^{T} \right] <{{E}\left[ Z_{\mathrm {2}} \right] }^{{\mathrm {UB}}_{\mathrm {2}}} \\ 0,&{} \mathrm{if}~ {{E}\left[ Z_{\mathrm {2}} \right] }^{{\mathrm {UB}}_{2}}\le {E}\left[ Z_{2}^{T} \right] \\ \end{array}} \right. \end{aligned}$$

for $T\in \left\{ t,~t^{*} \right\}$.

Table 2 Optimum results of EVM and CCM for zigzag and normal uncertain variables using linear weighted method

This means there exists a $\lambda$, such that $\lambda >\lambda ^{*}$. Therefore, it follows $t^{*}$ is not the optimal solution of model (15.1) which contradicts our initial assumption that $t^{*}$ is the optimal solution of model (15.1).

(ii) Let $t^{*}$ be the Pareto optimal solution of model (12.1), which is not an optimal solution of model (15.1). Then there exists an optimal solution $t{'}$ of (15.1) such that $\eta _{1}\left( {E}\left[ Z_{1}^{t{'}} \right] \right) >\eta _{1}\left( {E}\left[ Z_{1}^{t^{*}} \right] \right)$ and $\eta _{2}\left( {E}\left[ Z_{2}^{t{'}} \right] \right) <\eta _{2}\left( {E}\left[ Z_{2}^{t^{*}} \right] \right)$. Therefore, $\frac{{{E}\left[ Z_{1}^{t{'}} \right] -{E}\left[ {Z}_{\mathrm {1}} \right] }^{{\mathrm {LB}}_{1}}}{{{E}\left[ {Z}_{\mathrm {1}} \right] }^{{\mathrm {UB}}_{1}}-{{E}\left[ {Z}_{\mathrm {1}} \right] }^{{\mathrm {LB}}_{1}}}$$>\frac{{{E}\left[ Z_{1}^{t^{*}~} \right] -{E}\left[ {Z}_{\mathrm {1}} \right] }^{{\mathrm {LB}}_{1}}}{{{E}\left[ {Z}_{\mathrm {1}} \right] }^{{\mathrm {UB}}_{1}}-{{E}\left[ {Z}_{\mathrm {1}} \right] }^{{\mathrm {LB}}_{1}}}$ and $\frac{{{E}\left[ {Z}_{\mathrm {2}} \right] }^{{\mathrm {UB}}_{2}}{-E}\left[ Z_{2}^{t{'}} \right] }{{{E}\left[ {Z}_{2} \right] }^{{\mathrm {UB}}_{2}}\mathrm {-}{{E}\left[ {Z}_{2} \right] }^{{\mathrm {LB}}_{2}}}$$<\frac{{{E}\left[ {Z}_{2} \right] }^{{\mathrm {UB}}_{2}}{-E}\left[ Z_{2}^{t^{*}~} \right] }{{{E}\left[ {Z}_{2} \right] }^{{\mathrm {UB}}_{2}}\mathrm {-}{{E}\left[ {Z}_{2} \right] }^{{\mathrm {LB}}_{2}}}.$ Hence, $t^{*}$ is not the Pareto optimal solution of model (12.1) which contradicts our initial hypothesis that $t^{*}$ is the Pareto optimal solution of (12.1).

Similar proofs can be done for multi-objective model (B1) and compromise model (15.2) of CCM, and for multi-objective model (B5) and compromise model (15.3) of DCCM.

6 Results and discussion

This section, presents the results of three models: (i) EVM, (ii) CCM and (iii) DCCM of the proposed UMMFSTPwB problem using three compromise programming methods: (i) linear weighted method, (ii) global criterion method and (iii) fuzzy programming method. For numerical illustration of the proposed UMMFSTPwB, we have considered shipment of two items from two sources to three destinations using two types of conveyance, i.e., $r=2$, $m=2$, $n=3$ and $K=2$. The values of all the input parameters are provided in 9 tables, which are, tables 10, 11, 12, 13, 14, 15, 16, 17 and 18 as reported in the “Appendix C.” We have used the standard optimization software LINGO 11.0, to determine the results of three models for which a personal computer with Intel $\left( R \right)$ Core $\left( TM \right)$ i3 @ 2.93GHz and 2 GB memory is used.

We have presented the results for crisp equivalent of EVM and CCM followed by the results of DCCM along with their transportation plans. For CCM, ${cl}_{1}$ and ${cl}_{2}$ represent all the chance levels having the values within the interval $\left[ 0,0.5 \right)$ and $\left[ 0.5,~ 1.0 \right]$, respectively. For ${cl}_{1}$, the values of chance levels are set as $\alpha _{1}=0.4{,}~ \alpha _{2}=0.4{,}~ \beta _{i}^{p}=0.45{,}~ \gamma _{j}^{p}=0.35{,}~ \delta _{k}=0.45$ and $\rho _{j}=0.4 \quad \forall ~ i,j,k,p$. For ${cl}_{2}$, the chance level values are set as ${\alpha }_{1}=0.9{,}~ \alpha _{2}=0.9{,}~ \beta _{i}^{p}=0.8{,}~ \gamma _{j}^{p}=0.75$, $\delta _{k}=0.85$ and $\rho _{j}=0.8 \quad \forall ~ i,j,k,p$. EVM and CCM optimize the objective values, and DCCM maximizes the satisfaction levels. Hence, we have combined the results of EVM and CCM, but the results of DCCM are presented separately.

Table 3 Comparative results of three different solution methodologies

For EVM, the models, (12.3) and (12.4), are solved to generate the results, respectively, for zigzag and normal uncertain variables. In case of CCM, the models, (B2) and (B3), are solved for zigzag uncertain variables at chance levels ${cl}_{1}$ and ${cl}_{2}$, respectively, and model (B4) is solved for normal uncertain variables at chance level ${cl}_{2}$ . The results of DCCM are obtained by solving models (B6) and (B7), respectively, for zigzag and normal uncertain variables.

Table 2 shows the results of EVM and CCM for zigzag and normal uncertain variables. Here, the linear weighted method is used to generate the results of the corresponding models with different values of the weights, $\lambda _{1}$ and ${\lambda }_{2}$. From Table 2, it is observed that, as $\lambda _{1}$ decreases, both the maximization functions, ${E}\left[ Z_{1} \right] ~$ and $\bar{Z}_{1}$, proportionately decrease their values. Similarly, the minimization functions, ${E}\left[ Z_{2} \right]$ and $\bar{Z}_{2}$, decrease their values when $\lambda _{2}$ increases. Moreover, from Table 2 it is observed, for both the zigzag and normal uncertain variables, the results of EVM and CCM are nondominated to each other at different values of $\lambda _{1}$ and ${\lambda }_{2}$.

The results generated by three solution methodologies to solve the crisp equivalent models of EVM and CCM are reported in Table 3. Here, the values of the weights for linear weighted method, i.e., $\lambda _{1}$ and ${\lambda }_{2}$, are considered the same. From Table 3, it is observed that, in the case of EVM, for both uncertain variables (zigzag and normal uncertain variables), the solutions generated by global criterion method and fuzzy programming method, which are the same, and the solution generated by linear weighted method are nondominated to each other. However, for CCM and for zigzag uncertain variables, the solutions generated by linear weighted method and global criterion method are nondominated to each other, and the solutions generated by linear weighted method and fuzzy programming method are nondominated to each other but the solution generated by global criterion method dominates the solution of fuzzy programming method. While, for CCM with normal uncertain variables, the solutions generated by linear weighted method, global criterion method and fuzzy programming method are nondominated to each other.

Table 4 shows the transportation plans corresponding to the results provided in Table 3, for EVM and CCM. Subsequently, Table 5 reports the corresponding execution time (in seconds), require by LINGO, to solve the EVM and CCM for both the uncertain variables using three different solution methodologies.

Table 4 Optimal transportation plan of EVM and CCM for normal uncertain variables using three different solution methodologies

Table 5 Execution time of three different solution methodologies of EVM and CCM for zigzag and normal uncertain variables using LINGO

From Table 5, we observe that linear weighted method is computationally efficient, compared to global criterion method and fuzzy programming method, for both EVM and CCM.

For DCCM, the results for three solution methodologies are shown in Table 6. Similar to Table 3, the associated weights of linear weighted method in Table 6 are considered as equal. Moreover, to solve the crisp equivalents of DCCM the predetermined limits of $Z_{1}^{'}$ and $Z_{2}^{'}$, are set to, 325 and 94, respectively, for model (B6), and 419 and 83, respectively, for model (B7). It is observed from Table 6 that, for zigzag uncertain variables, the solution generated by global criterion method dominates each of the solutions generated by linear weighted method and fuzzy programming method. Moreover, the solution generated by fuzzy programming method dominates the solution generated by linear weighted method. However, for normal uncertain variables, the solutions generated by linear weighted method and global criterion method, which are the same, and the solution generated by fuzzy programming method are nondominated to each other.

Table 6 Results of DCCM for zigzag and normal uncertain variables

Table 7 Optimal transportation plan for DCCM for normal uncertain variables

Table 7 shows the transportation plans corresponding to the results presented in Table 6, of DCCM, for zigzag and normal uncertain variables. Subsequently, Table 8 reports the execution time (in seconds), to solve the DCCM for zigzag and normal uncertain variables using three different solution methodologies by LINGO.

Table 8 Execution time of three different solution methodologies required for DCCM for zigzag and normal uncertain variables using LINGO

From Table 8, it is observed that linear weighted method is efficient compared to global criterion method and fuzzy programming method, for both the uncertain variables, while generating the results of DCCM.

Sensitivity analysis

We have analyzed the sensitivity of CCM with input parameters of UMMFSTPwB, considering as zigzag and normal uncertain variables. The corresponding results of the CCM are reported in Table 9. Here, the models for both the uncertain variables (zigzag and normal uncertain variables) are solved, using global criterion method, by changing the values of the chance levels, $\alpha _{1}$ and $\alpha _{2}$. For zigzag uncertain variables, model (B2) is solved when the values of $\alpha _{1}$ and $\alpha _{2}$ change their respective values between 0.1 to 0.4. In this case, all other chance levels, except $\alpha _{1}$ and $\alpha _{2}$, are set to ${\beta }_{i}^{p}=0.45{,}~ \gamma _{j}^{p}=0.35$, $\delta _{k}=0.45$ and $\rho _{j}=0.4$. When the values of $\alpha _{1}$ and $\alpha _{2}$ are changed within the range from 0.5 to 1.0, model (B3) is solved with the remaining chance levels set to, $\beta _{i}^{p}=0.8$, $\gamma _{j}^{p}=0.75$, $\delta _{k}=0.85$ and $\rho _{j}=0.8$. However, for normal uncertain variables, model (B4) is solved at different values of $\alpha _{1}$ and $\alpha _{2}$ by considering the values of the remaining chance levels, the same, as set for model (B3).

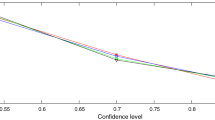
From Table 9, we observe that, for all the models, and for both the uncertain variables (zigzag and normal uncertain variables), as the values of $\alpha _{1}$ and $\alpha _{2}$ are increased, the corresponding values of maximizing objective $\bar{Z}_{1}$ and minimizing objective $\bar{Z}_{2}$ increase and decrease, respectively.

Subsequently, the values of $\bar{Z}_{1}$ and $\bar{Z}_{2}$ are also displayed graphically at different values of $\alpha _{1}$ and $\alpha _{2}$, for models (B2) and (B3), for zigzag uncertain variables in Fig. 3a, and for model (B4), for normal uncertain variables in Fig. 3b.

Table 9 Results for CCM for zigzag and normal uncertain variables at different chance levels of $\alpha _{1}$ and $\alpha _{2}$

Fig. 3

Uncertainty distribution of CCM at different chance levels of $\alpha _{1}$ and ${\alpha }_{2}$, for a zigzag uncertain variables; b normal uncertain variables

7 Conclusion

In this paper, we have designed an uncertain multi-objective multi-item fixed charge solid transportation problem with budget constraint (UMMFSTPwB). The uncertain model has been developed by considering different uncertain parameters as zigzag and normal uncertain variables. We have formulated the three models, EVM, CCM and DCCM, for UMMFSTPwB to transform it into deterministic ones. The equivalent multi-objective deterministic models are solved using linear weighted method, global criterion method and fuzzy programming method. Further, the features of these models are studied and some related theorems are also established. The models are numerically illustrated by analyzing there results.

In future, the models we have developed can be extended to include price discounts and breakable/deteriorating items. The models can also be extended for uncertain-random environment where the associated indeterminate parameters can be represented as uncertain and random variables.

Appendices

Appendix A

In this section, some theorems related to uncertain programming are revisited.

Theorem A.1

(Liu 2010) Let $\zeta _{1}$, $\zeta _{2}{,}~ .~ .~ .$ , $\zeta _{n}$ are independent uncertain variables with uncertainty distributions ${\Phi }_{\mathrm {1}}$, ${\Phi }_{\mathrm {2}}$,...,$~{\Phi }_{n}$, respectively, and $f_{1}\left( x \right)$, $f_{2}\left( x \right) {,}~ .~ .~ .{,}~ f_{n}\left( x \right)$, $\overline{f} (x)$ are real valued functions. Then,

$$\begin{aligned} \mathcal {M}\left\{ \sum \nolimits _{i=1}^n {{\zeta _{i}f}_{i}\left( x \right) } \le \overline{f} (x)~\right\} \ge {\alpha } \end{aligned}$$

holds if and only if,

$$\begin{aligned}&\sum \nolimits _{i=1}^n {{\Phi }_{i}^{-1}\left( {\alpha } \right) f_{i}^{+}\left( x \right) } -\sum \nolimits _{i=1}^n {{\Phi }_{i}^{-1}\left( 1-\alpha \right) f_{i}^{-}\left( x \right) } \le \overline{f} \left( x \right) , \end{aligned}$$

(A1)

where

$$\begin{aligned} f_{i}^{+}\left( x \right) =\left\{ {\begin{array}{rl} f_{i}\left( x \right) ~ ;&{}f_{i}\left( x \right) >0 \\ 0~ ;&{}f_{i}\left( x \right) \le 0 \\ \end{array}} \right. \end{aligned}$$

(A2)

and

$$\begin{aligned} f_{i}^{-}\left( x \right) =\left\{ {\begin{array}{rl} 0~ ;&{}f_{i}\left( x \right) \ge 0 \\ -f_{i}\left( x \right) ~ ;&{}f_{i}\left( x \right) <0 \\ \end{array}} \right. \hbox { for } i=1,2,\ldots ,n. \end{aligned}$$

(A3)

If $f_{1}\left( x \right) {,}~ f_{2}\left( x \right) {,}~ .~ .~ .{,}~ f_{n}\left( x \right)$ are all nonnegative, then $\mathrm {(A1)}$ becomes $\sum \nolimits _{i=1}^n {{\Phi }_{i}^{-1}\left( {\alpha } \right) f_{i}\left( x \right) } \le \overline{f} \left( x \right)$, and if $f_{1}\left( x \right)$, $f_{2}\left( x \right) {,}~ .~ .~ .{,}~ f_{n}\left( x \right)$ are all nonpositive, then $\mathrm {(A1)}$ becomes $\sum \nolimits _{i=1}^n {{\Phi }_{i}^{-1}\left( 1-\alpha \right) f_{i}\left( x \right) } \le \overline{f} \left( x \right) .$

Theorem A.2

(Liu 2010) Let $x_{1}{,}~ x_{2}{,}~\ldots , x_{n}$ are nonnegative decision variables and $\zeta _{1}$, $\zeta _{2}$, .  .  ., $\zeta _{n}$ are independent zigzag uncertain variables which are represented as $\mathcal {Z}\left( g_{1},h_{1},l_{1} \right)$, $\mathcal {Z}\left( g_{2},h_{2},l_{2} \right) {,}~ .~ .~ .{,}~ \mathcal {Z}\left( g_{n},h_{n},l_{n} \right)$, respectively. Then,

(A4)

Theorem A.3

(Liu 2010) Let $x_{1}{,}\, x_{2}{,}~\ldots , x_{n}$ are nonnegative decision variables and $\zeta _{1}$, $\zeta _{2}, \ldots , \zeta _{n}$ are independent normal uncertain variables which are denoted as $\mathcal {N}\left( \rho _{1},\sigma _{1} \right)$, $\mathcal {N}\left( \rho _{2},\sigma _{2} \right) {,}~\ldots , \mathcal {N}\left( \rho _{n},\sigma _{n} \right)$, respectively. Then,

$$\begin{aligned}&\mathcal {M}\left\{ \sum \nolimits _{i=1}^n {\zeta _{i}x_{i}} \le c~\right\} \nonumber \\&\quad =\left( 1+\exp \left( \frac{\pi \left( \sum \nolimits _{i=1}^n {\rho _{i}x_{i}-c} \right) }{\sqrt{3} \sum \nolimits _{i=1}^n {\sigma _{i}x_{i}}} \right) \right) ^{-1}. \end{aligned}$$

(A5)

Theorem A.4

(Liu 2010) Let $\zeta$ be an uncertain variable with continuous uncertainty distribution ${\Phi }$. Then, for any real number x, we have

$$\begin{aligned} \mathcal {M}\left\{ \zeta \le x \right\} ={\Phi }(x),\quad \mathcal {M}\left\{ \zeta \ge x \right\} =1-{\Phi }(x). \end{aligned}$$

(A6)

Appendix B

In this section, we state the relevant theorems to formulate the crisp equivalents of chance-constrained model (CCM) and dependent chance-constrained model (DCCM) of UMMFSTPwB.

Crisp equivalents of chance-constrained model (CCM)

Lemma B.1

If a and r are positive real numbers, $\xi$ is an independent uncertain variable with uncertainty distribution ${\Phi }$ and $\alpha$ is the chance level. Then, $\mathcal {M}\left\{ a-\xi \ge r \right\} \ge \alpha$ holds if and only if $a-{\Phi }^{-1}\left( \alpha \right) \ge r$.

Proof

$$\begin{aligned} \mathcal {M}\left\{ a-\xi \ge r \right\}\ge & {} \alpha \quad \Leftrightarrow \quad \mathcal {M}\left\{ \xi \le a-r \right\} \ge \alpha \quad \Leftrightarrow \\ a-r\ge & {} {\Phi }^{-1}\left( \alpha \right) \quad \Leftrightarrow \quad a-{\Phi }^{-1}\left( \alpha \right) \ge r. \end{aligned}$$

Theorem B.1

Let $\xi _{c_{ijk}^{p}}$, $\xi _{f_{ijk}^{p}}$, $\xi _{t_{ijk}^{p}}{,}~ \xi _{a_{i}^{p}}{,}~ \xi _{b_{j}^{p}}{,}~ \xi _{e_{k}}$ and $\xi _{B_{j}}$ are the independent uncertain variables, respectively, associated with uncertainty distributions ${\Phi }_{\xi _{c_{ijk}^{p}}}{,}~ {\Phi }_{\xi _{f_{ijk}^{p}}}{,}~ {\Phi }_{\xi _{t_{ijk}^{p}}}{,}~ {\Phi }_{\xi _{a_{i}^{p}}}{,} {\Phi }_{\xi _{b_{j}^{p}}}{,}~ {\Phi }_{\xi _{e_{k}}}$ and ${\Phi }_{\xi _{B_{j}}}$ then the crisp equivalent of chance-constrained model ($\mathrm {CCM})$ in model (10) can be equivalently formulated as model (B1).

$$\begin{aligned} \left\{ {\begin{array}{l} \mathrm{Max}~ \bar{Z}_{1}=\left[ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left\{ \left( s_{j}^{p}-v_{i}^{p}\right. \right. \right. \\ \quad \quad \quad \qquad \left. \left. \left. -{\Phi }_{\xi _{c_{ijk}^{p}}}^{\mathrm {-1}}\left( {\alpha }_{\mathrm {1}} \right) \right) x_{ijk}^{p}-{\Phi }_{\xi _{f_{ijk}^{p}}}^{\mathrm {-1}}\left( {\alpha }_{\mathrm {1}} \right) y_{ijk}^{p} \right\} \right] \\ \mathrm{Min}~ \bar{Z}_{2}=\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K {{\Phi }_{\xi _{t_{ijk}^{p}}}^{\mathrm {-1}}\left( {\alpha }_{\mathrm {2}} \right) y_{ijk}^{p}} ~ \\ \mathrm{subject~ to} \\ \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K {x_{ijk}^{p}-{\Phi }_{\xi _{a_{i}^{p}}}^{\mathrm {-1}}\left( {\mathrm {1-\upbeta }}_{{i}}^{p} \right) } \le 0,\\ \quad \quad \quad \qquad i=1,2,\ldots ,m,~ p=1,2,\ldots ,r~ \\ \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K {x_{ijk}^{p}-\Phi _{\xi _{b_{j}^{p}}}^{-1}\left( {\upgamma }_{{j}}^{p} \right) {\ge 0}} ,\\ \quad \quad \quad \qquad j=1,2,\ldots ,n,~ p=1,2,\ldots ,r\\ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m {\sum \nolimits _{j=1}^n x_{ijk}^{p} -{\Phi }_{\xi _{e_{k}}}^{\mathrm {-1}}\left( \mathrm {1-}\delta _{k} \right) } \le 0,\\ \quad \quad \quad \qquad k=1,2,\ldots ,K \\ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K \left\{ {\left( v_{i}^{p}+{\Phi }_{\xi _{c_{ijk}^{p}}}^{\mathrm {-1}}\left( \rho _{j} \right) \right) }x_{ijk}^{p}\right. \\ \quad \quad \quad \qquad \left. +\,{\Phi }_{\xi _{f_{ijk}^{p}}}^{\mathrm {-1}}\left( \rho _{j} \right) y_{ijk}^{p} \right\} ~- \Phi _{B_{j}}^{-1}\left( \mathrm {1-}\rho _{j} \right) \le 0, j=1,2,\ldots ,n \\ x_{ijk}^{p}\ge 0,~ y_{ijk}^{p}=\left\{ {\begin{array}{l} 1;~~{x}_{ijk}^{p}>0~ \\ 0;~~\mathrm{otherwise}~ \\ \end{array}} \right. ~ \forall ~ p,i,j,k.~ \\ \end{array}} \right. \end{aligned}$$

(B1)

Proof

Considering the CCM of UMMFSTPwB presented in model (10), the corresponding constraints can be written as follow.

• (i) The constraint $\mathcal {M}\left\{ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K\right. \left. \left[ \left( s_{j}^{p}-v_{i}^{p}-\xi _{c_{ijk}^{p}} \right) x_{ijk}^{p}-\left( \xi _{f_{ijk}^{p}} \right) y_{ijk}^{p} \right] \ge \bar{Z}_{1} \right\} \ge {\alpha }_{\mathrm {1}}$ can be rewritten as $\mathcal {M}\left\{ Z_{1}\ge \bar{Z}_{1} \right\} \ge {\alpha }_{\mathrm {1}}$, since $\xi _{c_{ijk}^{p}}$ and $\xi _{f_{ijk}^{p}}$ are the independent uncertain variables with regular uncertainty distributions ${\Phi }_{\xi _{c_{ijk}^{p}}}$ and ${\Phi }_{\xi _{f_{ijk}^{p}}}$, respectively. Then according to Theorem 2.1 provided in Section 2 and the Lemma B.1, $\mathcal {M}\left\{ Z_{1}\ge \bar{Z}_{1} \right\} \ge {\alpha }_{\mathrm {1}}$ can be reformulated as

  $$\begin{aligned}&\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left[ \left( s_{j}^{p}-v_{i}^{p}\right. \right. \\&\quad \left. \left. -{\Phi }_{c_{ijk}^{p}}^{\mathrm {-1}}\left( {\alpha }_{\mathrm {1}} \right) \right) x_{ijk}^{p}-{\Phi }_{f_{ijk}^{p}}^{\mathrm {-1}}\left( {\alpha }_{\mathrm {1}} \right) y_{ijk}^{p} \right] \ge \bar{Z}_{1}. \end{aligned}$$

  In similar way, constraint $\mathcal {M}\left\{ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m\right. \left. \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left[ \xi _{t_{ijk}^{p}}y_{ijk}^{p} \right] \le \bar{Z}_{2} \right\} \ge {\alpha }_{\mathrm {2}}$ can be restructured as

  $$\begin{aligned} \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K {{\Phi }_{t_{ijk}^{p}}^{\mathrm {-1}}\left( {\alpha }_{\mathrm {2}} \right) y_{ijk}^{p}} \le \bar{Z}_{2}. \end{aligned}$$

• (ii) Constraint $\mathcal {M}\left\{ \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K {x_{ijk}^{p}-\xi _{a_{i}^{p}}} \le 0 \right\} \ge \beta _{i}^{p}$$\Leftrightarrow ~ \mathcal {M}\left\{ \xi _{a_{i}^{p}}\ge \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K x_{ijk}^{p} \right\} \ge \beta _{i}^{p}$. Since, ${\Phi }_{\xi _{a_{i}^{p}}}$ is the uncertainty distribution of $\xi _{a_{i}^{p}}$ then from Theorem A.4 (cf. “Appendix A”),

  $$\begin{aligned}&\mathcal {M}\left\{ \xi _{a_{i}^{p}}\ge \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K x_{ijk}^{p} \right\} \\&\quad \ge \beta _{i}^{p}\Leftrightarrow \mathrm {1-}{\Phi }_{\xi _{a_{i}^{p}}}\left( \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K x_{ijk}^{p} \right) \ge \beta _{i}^{p}\\&\quad \Leftrightarrow \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K x_{ijk}^{p} -{\Phi }_{a_{i}^{p}}^{\mathrm {-1}}\left( {{1-\upbeta }}_{{i}}^{\mathrm {p}} \right) \le 0 . \end{aligned}$$

• (iii) Constraint $\mathcal {M}\left\{ \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K {x_{ijk}^{p}-\xi _{b_{j}^{p}}} \ge 0 \right\} \ge \gamma _{j}^{p}$$\Leftrightarrow ~ \mathcal {M}\left\{ \xi _{b_{j}^{p}}\le \sum \nolimits _{i=1}^n \sum \nolimits _{k=1}^K x_{ijk}^{p} \right\} \ge \gamma _{j}^{p}$.

  Since, ${\Phi }_{\xi _{b_{j}^{p}}}$ is the uncertainty distribution of $\xi _{b_{j}^{p}}$ then from Theorem A.4,

  $$\begin{aligned}&\mathcal {M}\left\{ \xi _{b_{j}^{p}}\le \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K x_{ijk}^{p} \right\} \nonumber \\&\quad \ge \gamma _{j}^{p}\Leftrightarrow {\Phi }_{\xi _{b_{j}^{p}}}\left( \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K x_{ijk}^{p} \right) \\&\quad \ge \gamma _{j}^{p}\Leftrightarrow \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K x_{ijk}^{p} -{\Phi }_{\xi _{b_{j}^{p}}}^{\mathrm {-1}}\left( \gamma _{j}^{p} \right) \ge 0. \end{aligned}$$

  Similarly, constraint $\mathcal {M}\left\{ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n x_{ijk}^{p} \right. \left. -\xi _{e_{k}} \le 0 \right\} \ge \delta _{k}$ can be equivalently transformed into $\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m {\sum \nolimits _{j=1}^n x_{ijk}^{p} -{\Phi }_{e_{k}}^{\mathrm {-1}}\left( \mathrm {1-}\delta _{k} \right) } \le 0$.

• (iv) From Theorem A.1 and Theorem A.4, the crisp transformation of constraint

  $$\begin{aligned}&\mathcal {M}\left\{ \left\{ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K {\left( v_{i}^{p}+\xi _{c_{ijk}^{p}} \right) x}_{ijk}^{p}\right. \right. \\&\quad \left. \left. +\,\xi _{f_{ijk}^{p}} y_{ijk}^{p} \right\} -\xi _{B_{j}^{p}}\le 0 \right\} \ge \rho _{j} \qquad \hbox { is equivalently becomes}, \\&\quad \left\{ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K \left( v_{i}^{p} +{\Phi }_{c_{ijk}^{p}}^{\mathrm {-1}}\left( \rho _{j} \right) \right) x_{ijk}^{p} +{\Phi }_{f_{ijk}^{p}}^{\mathrm {-1}}\left( \rho _{j} \right) y_{ijk}^{p} \right\} \\&\quad -\,\Phi _{B_{j}}^{-1}\left( {1-\rho }_{j} \right) {\le 0}. \end{aligned}$$

Therefore, considering (i), (ii), (iii) and (iv) shown above, the crisp equivalent of model (10) follows directly, the model (B1).

Corollary B.1

If $\xi _{c_{ijk}^{p}}$, $\xi _{f_{ijk}^{p}}$, $\xi _{t_{ijk}^{p}}{,}~ \xi _{a_{i}^{p}}{,}~ \xi _{b_{j}^{p}}{,}~ \xi _{e_{k}^{p}}$ and $\xi _{B_{j}^{p}}$ are the independent zigzag uncertain variables of the form $\mathcal {Z}\left( g,h,l \right)$ with $g<h<l.$ Then, according to Theorem B.1 and the inverse uncertainty distribution of zigzag uncertain variables, we can conclude the following.

(i) For all chance levels $<0.5$, model (B1) becomes

$$\begin{aligned} \left\{ {\begin{array}{l} \mathrm{Max}~ \bar{Z}_{1}=~ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left[ \left( s_{j}^{p}-v_{i}^{p}-\left( \left( 1-2{\alpha }_{\mathrm {1}} \right) g_{c_{ijk}^{p}}\right. \right. \right. \\ \quad \quad \quad \qquad \left. \left. \left. +2{\alpha }_{\mathrm {1}}h_{c_{ijk}^{p}} \right) \right) x_{ijk}^{p}-~ \left( \left( 1-2{\alpha }_{\mathrm {1}} \right) g_{f_{ijk}^{p}}+2{\alpha }_{\mathrm {1}}h_{f_{ijk}^{p}} \right) y_{ijk}^{p} \right] \\ \mathrm{Min}~ \bar{Z}_{2}=\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left[ \left( \left( 1-2{\alpha }_{\mathrm {2}} \right) g_{t_{ijk}^{p}}+2{\alpha }_{\mathrm {2}}h_{t_{ijk}^{p}} \right) y_{ijk}^{p} \right] ~ \\ \mathrm{subject~ to} \\ \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K {x_{ijk}^{p}-\left( 2\beta _{i}^{p}h_{a_{i}^{p}}+\left( 1-2\beta _{i}^{p} \right) l_{a_{i}^{p}} \right) } \le 0,~\\ \quad \quad \quad \qquad i=1,2,\ldots ,m,~ p=1,2,\ldots ,r~ \\ \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K {x_{ijk}^{p}-\left( {\left( 1-2\gamma _{j}^{p} \right) }g_{b_{j}^{p}}+2\gamma _{j}^{p}h_{b_{j}^{p}} \right) \ge 0} ,\\ \quad \quad \quad \qquad j=1,2,\ldots ,n,~ p=1,2,\ldots ,r~ \\ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m {\sum \nolimits _{j=1}^n x_{ijk}^{p} -\left( 2\delta _{k}h_{e_{k}}+\left( 1-2\delta _{k} \right) l_{e_{k}} \right) } \le 0,\\ \quad \quad \quad \qquad k=1,2,\ldots ,K~ \\ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K {\left[ v_{i}^{p}+\left( \left( 1-2\rho _{j} \right) g_{c_{ijk}^{p}}+2\rho _{j}^{p}h_{c_{ijk}^{p}} \right) \right] }x_{ijk}^{p}\\ \quad \quad \quad \qquad +\left[ \left( \left( 1-2\rho _{j} \right) g_{f_{ijk}^{p}}+2\rho _{j}h_{f_{ijk}^{p}} \right) \right] y_{ijk}^{p}\\ \quad \quad \quad \qquad -\left( {2\rho _{j}h}_{B_{j}}+\left( 1-2\rho _{j} \right) l_{B_{j}} \right) {\le 0,~ j=1,2,\ldots ,n} \\ x_{ijk}^{p}\ge 0,~ y_{ijk}^{p}=\left\{ {\begin{array}{l} 1;~~x_{ijk}^{p}>0~ \\ 0;~~\mathrm{otherwise}~ \\ \end{array}} \right. ~ \forall ~ p,i,j,k.~ \\ \end{array}} \right. \end{aligned}$$

(B2)

(ii) For all chance levels $\ge ~ 0.5$, model (B1) can be described as given in (B3).

$$\begin{aligned} \left\{ {\begin{array}{l} \mathrm{Max}~ \bar{Z}_{1}=\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left[ \left( s_{j}^{p}-v_{i}^{p}-\left( \left( 2-2{\alpha }_{\mathrm {1}} \right) h_{c_{ijk}^{p}}\right. \right. \right. \\ \quad \quad \quad \qquad \left. \left. \left. +\left( 2{\alpha }_{\mathrm {1}}-1 \right) l_{c_{ijk}^{p}} \right) \right) x_{ijk}^{p}-\left( \left( 2-2{\alpha }_{\mathrm {1}} \right) h_{f_{ijk}^{p}}\right. \right. \\ \quad \quad \quad \qquad \left. \left. +{\left( 2{\alpha }_{\mathrm {1}}-1 \right) l}_{f_{ijk}^{p}} \right) y_{ijk}^{p} \right] \\ \mathrm{Min}~ \bar{Z}_{2}=~ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left[ \left( \left( 2-2{\alpha }_{\mathrm {2}} \right) h_{t_{ijk}^{p}}\right. \right. \\ \quad \quad \quad \qquad \left. \left. +\left( 2{\alpha }_{\mathrm {2}}-1 \right) l_{t_{ijk}^{p}} \right) y_{ijk}^{p} \right] ~ \\ \mathrm{subject~ to} \\ \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K {x_{ijk}^{p}-\left( \left( 2\beta _{i}^{p}-1 \right) g_{a_{i}^{p}}+\left( 2-2\beta _{i}^{p} \right) h_{a_{i}^{p}} \right) } \le 0,\\ \quad \quad \quad \qquad i=1,2,\ldots ,m,~ p=1,2,\ldots ,r~ \\ \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K {x_{ijk}^{p}-\left( \left( 2-2\gamma _{j}^{p} \right) h_{b_{j}^{p}}+\left( 2\gamma _{j}^{p}-1 \right) l_{b_{j}^{p}} \right) \ge 0} ,\\ \quad \quad \quad \qquad j=1,2,\ldots ,n,~ p=1,2,\ldots ,r~ \\ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m {\sum \nolimits _{j=1}^n x_{ijk}^{p} -\left( \left( 2\delta _{k}-1 \right) g_{e_{k}}+\left( 2-2\delta _{k} \right) h_{e_{k}} \right) } \le 0,\\ \quad \quad \quad \qquad k=1,2,\ldots ,K \\ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K {\left[ v_{i}^{p}+\left( \left( 2-2\rho _{j} \right) h_{c_{ijk}^{p}}+\left( 2\rho _{j}-1 \right) l_{c_{ijk}^{p}} \right) \right] }x_{ijk}^{p}\\ \quad \quad \quad \qquad +\left[ \left( 2-2\rho _{j} \right) h_{f_{ijk}^{p}}+\left( 2\rho _{j}-1 \right) l_{f_{ijk}^{p}} \right] y_{ijk}^{p} ~ \\ \quad \quad \quad \qquad -\left( \left( 2\rho _{j}-1 \right) g_{B_{j}}+\left( 2-2\rho _{j} \right) h_{B_{j}} \right) {\le 0,~ j=1,2,\ldots ,n} \\ x_{ijk}^{p}\ge 0,~ y_{ijk}^{p}=\left\{ {\begin{array}{l} 1{~ ;}x_{ijk}^{p}>0~ \\ 0~ ;\mathrm{otherwise}~ \\ \end{array}} \right. ~ \forall ~ p,i,j,k.~ \\ \end{array}} \right. \end{aligned}$$

(B3)

Corollary B.2

If $\xi _{c_{ijk}^{p}}$, $\xi _{f_{ijk}^{p}}$, $\xi _{t_{ijk}^{p}}{,}~ \xi _{a_{i}^{p}}{,}~ \xi _{b_{j}^{p}}{,}~ \xi _{e_{k}}$ and $\xi _{B_{j}}$ are independent normal uncertain variables of the form $\mathcal {N}(\mu ,\sigma )$, such that $\mu ,~ \sigma \in \mathcal {R}$ and $\sigma >0.$ Then, according to Theorem B.1 and the inverse uncertainty distribution of normal uncertain variables, model (B1) can be written as follows.

$$\begin{aligned} \left\{ {\begin{array}{l} \mathrm{Max}~ \bar{Z}_{1}=\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left[ \left( s_{j}^{p}-v_{i}^{p}-\left( \mu _{c_{ijk}^{p}}\right. \right. \right. ~\\ \quad \quad \quad \qquad \left. \left. \left. +\frac{\sqrt{3} \sigma _{c_{ijk}^{p}}}{\pi }ln\frac{{\alpha }_{\mathrm {1}}}{1-{\alpha }_{\mathrm {1}}} \right) \right) x_{ijk}^{p}\right. ~\\ \quad \quad \qquad \qquad \left. -\left( \mu _{f_{ijk}^{p}}+\frac{\sqrt{3} \sigma _{f_{ijk}^{p}}}{\pi }ln\frac{{\alpha }_{\mathrm {1}}}{1-{\alpha }_{\mathrm {1}}} \right) y_{ijk}^{p} \right] ~ \\ ~ \mathrm{Min}~ \bar{Z}_{2}=\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left[ \left( \mu _{t_{ijk}^{p}}\right. \right. ~\\ \quad \quad \qquad \qquad \left. \left. +\frac{\sqrt{3} \sigma _{t_{ijk}^{p}}}{\pi }ln\frac{{\alpha }_{\mathrm {2}}}{1-{\alpha }_{\mathrm {2}}} \right) y_{ijk}^{p} \right] ~ \\ \mathrm{subject~ to} \\ ~\sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K {x_{ijk}^{p}-\left( \mu _{a_{i}^{p}}-\frac{\sqrt{3} \sigma _{a_{i}^{p}}}{\pi }ln\frac{\beta _{i}^{p}}{1-\beta _{i}^{p}} \right) } \le 0,~\\ \quad \quad \quad \quad i=1,2,\ldots ,m,~ p=1,2,\ldots ,r~ \\ \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K {x_{ijk}^{p}-\left( \mu _{b_{j}^{p}}+\frac{\sqrt{3} \sigma _{b_{j}^{p}}}{\pi }ln\frac{\gamma _{j}^{p}}{{1-\gamma }_{j}^{p}} \right) {\ge 0}} ,~\\ \quad \quad \quad \quad j=1,2,\ldots ,n,~ p=1,2,\ldots ,r~ \\ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m {\sum \nolimits _{j=1}^n x_{ijk}^{p} -\left( \mu _{e_{k}}-\frac{\sqrt{3} \sigma _{e_{k}}}{\pi }ln\frac{\delta _{k}}{1-\delta _{k}} \right) } \le 0,~\\ \quad \quad \quad \quad k=1,2,\ldots ,K~ \\ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{k=1}^K {\left[ v_{i}^{p}+\mu _{c_{ijk}^{p}}+\frac{\sqrt{3} \sigma _{c_{ijk}^{p}}}{\pi }ln\frac{\rho _{j}}{1-\rho _{j}} \right] }x_{ijk}^{p} \\ \quad \quad \quad \quad +\left[ \mu _{f_{ijk}^{p}}+\frac{\sqrt{3} \sigma _{f_{ijk}^{p}}}{\pi }ln\frac{\rho _{j}}{1-\rho _{j}} \right] y_{ijk}^{p}\\ \quad \quad \quad \quad -\left( \mu _{B_{j}}-\frac{\sqrt{3} \sigma _{B_{j}}}{\pi }ln\frac{\rho _{j}}{1-\rho _{j}} \right) \le 0,~ ~ j=1,2,\ldots ,n \\ x_{ijk}^{p}\ge 0,~ y_{ijk}^{p}=\left\{ {\begin{array}{l} 1;\quad x_{ijk}^{p}>0~ \\ 0;\quad \mathrm{otherwise}~ \\ \end{array}} \right. ~ \forall ~ p,i,j,k.~ \\ \end{array}} \right. \end{aligned}$$

(B4)

Crisp equivalents of dependent chance-constrained model (DCCM)

For DCCM, the following model in (B5) is considered as a general case of crisp equivalent for DCCM corresponding to models (B6) and (B7), respectively, for zigzag and normal uncertain variables.

$$\begin{aligned} \left\{ {\begin{array}{l} \mathrm{Max}~ \upsilon _{Z_{1}^{'}}~ \\ \mathrm{Max}~ \upsilon _{Z_{2}^{'}}~ \\ \mathrm{subject~ to~ the~ constraints~of}~ \left( \mathrm {B}1 \right) . \\ \end{array}} \right. \end{aligned}$$

(B5)

Theorem B.2

Let $\xi _{c_{ijk}^{p}}{,}~ \xi _{f_{ijk}^{p}}{,}~ \xi _{t_{ijk}^{p}}{,}~ \xi _{a_{i}^{p}}{,}~ \xi _{b_{j}^{p}}{,}~ \xi _{e_{k}}$ and $\xi _{B_{j}}$ are the independent zigzag uncertain variables denoted as $\mathcal {Z}\left( g_{c},h_{c},l_{c} \right)$ with $c\in \left\{ \xi _{c_{ijk}^{p}}\mathrm {,~ }\xi _{f_{ijk}^{p}}\mathrm {,~ }\xi _{t_{ijk}^{p}}{,}~ \xi _{a_{i}^{p}}{,}~ \xi _{b_{j}^{p}}{,}~ \xi _{e_{k}}\mathrm {,~ }\xi _{B_{j}} \right\}$ and $0.5\le \eta \le 1,$ where

$\eta \in \left\{ {~ \beta }_{i}^{p},{~ \gamma }_{j}^{p},\delta _{k},\rho _{j} \right\} .$ Then, the crisp equivalent of DCCM, presented in model (11), is equivalent to model (B6).

$$\begin{aligned} \left\{ {\begin{array}{l} \mathrm{Max}~ \nu _{Z_{1}^{'}}~ \\ \mathrm{Max}~ \nu _{Z_{2}^{'}}~ \\ \mathrm{subject~ to~ the~ constraints~of}~ \left( \mathrm {B3} \right) , \\ \end{array}} \right. \end{aligned}$$

(B6)

where

$$\begin{aligned} \nu _{Z_{1}^{'}}= & {} \left\{ {\begin{array}{l@{\quad }l} 1,&{} \mathrm{if}~ Z_{1}^{'}\le \bar{g}~ \\ \frac{2\bar{h}-\bar{g}-Z_{1}^{'}}{2\left( \bar{h}-\bar{g} \right) },&{} \mathrm{if}~ \bar{g}<Z_{1}^{'}\le \bar{h} \\ \frac{\bar{l}-Z_{1}^{'}}{2\left( \bar{l}-\bar{h} \right) },&{} \mathrm{if}~ \bar{h}<Z_{1}^{'}\le \bar{l}~ \\ 0,&{} \mathrm{if}~ Z_{1}^{'}>\bar{l}~ \\ \end{array}} \right. {\mathrm{and} } \\ \nu _{Z_{2}^{'}}= & {} \left\{ {\begin{array}{l@{\quad }l} 0,&{} \mathrm{if}~ Z_{2}^{'}\le \overline{\overline{g}} \\ \frac{Z_{2}^{'}-\bar{\bar{g}}}{2\left( \bar{\bar{h}}-\bar{\bar{g}} \right) },&{} \mathrm{if}~ \overline{\overline{g}}<Z_{2}^{'}\le \overline{\overline{h}} \\ \frac{Z_{2}^{'}+\overline{\overline{l}}-2\overline{\overline{h}}}{2\left( \overline{\overline{l}}-\overline{\overline{h}} \right) },&{} \mathrm{if}~ \overline{\overline{h}}<Z_{2}^{'}\le \overline{\overline{l}} \\ 1,&{} \mathrm{if}~ Z_{2}^{'}>\overline{\overline{l}}, \\ \end{array}} \right. \end{aligned}$$

such that

$$\begin{aligned} \bar{g}= & {} \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left[ \left( s_{j}^{p}-v_{i}^{p}-l_{\xi _{c_{ijk}^{p}}} \right) x_{ijk}^{p}\right. \\&\quad \left. -\left( l_{\xi _{f_{ijk}^{p}}} \right) y_{ijk}^{p} \right] ,\\ \bar{h}= & {} \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left[ \left( s_{j}^{p}-v_{i}^{p}-h_{\xi _{c_{ijk}^{p}}} \right) x_{ijk}^{p}\right. \\&\quad \left. -\left( h_{\xi _{f_{ijk}^{p}}} \right) y_{ijk}^{p} \right] ,\\ \bar{l}= & {} \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left[ \left( s_{j}^{p}-v_{i}^{p}-g_{\xi _{c_{ijk}^{p}}} \right) x_{ijk}^{p}\right. \\&\quad \left. -\left( g_{\xi _{f_{ijk}^{p}}} \right) y_{ijk}^{p} \right] \\ \overline{\overline{g}}= & {} \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left[ \left( g_{\xi _{t_{ijk}^{p}}} \right) y_{ijk}^{p} \right] ,\\&\quad \overline{\overline{h}}=\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left[ \left( h_{\xi _{t_{ijk}^{p}}} \right) y_{ijk}^{p} \right] \hbox { and} \\ \overline{\overline{l}}= & {} \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left[ \left( l_{\xi _{t_{ijk}^{p}}} \right) y_{ijk}^{p} \right] . \end{aligned}$$

Proof

Considering the objective $\mathcal {M}\left\{ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n\right. \left. \sum \nolimits _{k=1}^K \left[ \left( s_{j}^{p}-v_{i}^{p}-\xi _{c_{ijk}^{p}} \right) x_{ijk}^{p}-\left( \xi _{f_{ijk}^{p}} \right) y_{ijk}^{p} \right] \ge Z_{1}^{'} \right\}$, $\xi _{c_{ijk}^{p}}$ and $\xi _{f_{ijk}^{p}}$ are independent zigzag uncertain variables. $x_{ijk}^{p},~ s_{j}^{p}$ and $v_{i}^{p}$ are greater or equal to zero, and $y_{ijk}^{p}$ are binary variables. Consequently, $\mathcal {M}\left\{ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K\right. \left. \left[ \left( s_{j}^{p}-v_{i}^{p}-\xi _{c_{ijk}^{p}} \right) x_{ijk}^{p}-\left( \xi _{f_{ijk}^{p}} \right) y_{ijk}^{p} \right] \ge Z_{1}^{'} \right\}$ follows zigzag uncertainty distribution and therefore is a zigzag uncertain variable say $\mathcal {Z}\left( \bar{g},\bar{h},\bar{l} \right)$, where $\bar{g},\bar{h}$ and $\bar{l}$ are defined above in (B6). Then, from Definition 2.2, and theorems A.2 and A.4, we write

$$\begin{aligned}&\mathcal {M}\left\{ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left[ \left( s_{j}^{p}-v_{i}^{p}-\xi _{c_{ijk}^{p}} \right) x_{ijk}^{p}\right. \right. \\&\left. \left. -\left( \xi _{f_{ijk}^{p}} \right) y_{ijk}^{p} \right] \ge Z_{1}^{'} \right\} \\&\quad \Leftrightarrow 1-\mathcal {M}\left\{ \mathcal {Z}\left( \bar{g},\bar{h},\bar{l} \right) \le Z_{1}^{'} \right\} =\nu _{Z_{1}^{'}}\\&\quad = \left\{ \begin{array}{l@{\quad }l} 1, &{} \mathrm{if}~ Z_{1}^{'}\le \bar{g}~ \\ \frac{2\bar{h}-\bar{g}-Z_{1}^{'}}{2\left( \bar{h}-\bar{g} \right) },&{} \mathrm{if}~ \bar{g}<Z_{1}^{'}\le \bar{h} \\ \frac{\bar{l}-Z_{1}^{'}}{2\left( \bar{l}-\bar{h} \right) },&{} \mathrm{if}~ \bar{h}<Z_{1}^{'}\le \bar{l} \\ 0,&{} \mathrm{if}~ Z_{1}^{'}>\bar{l}. \\ \end{array} \right. \end{aligned}$$

Similarly, for the second objective of model (11), $\xi _{t_{ijk}^{p}}$are independent zigzag uncertain variables. Hence, $\mathcal {M}\left\{ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left[ \left( \xi _{t_{ijk}^{p}} \right) y_{ijk}^{p} \right] \le Z_{2}^{'} \right\}$ follows zigzag uncertainty distribution for a zigzag uncertain variable say $\mathcal {Z}\left( \bar{\bar{g}},\bar{\bar{h}},\bar{\bar{l}} \right)$, where $\bar{\bar{g}},\bar{\bar{h}}$ and $\bar{\bar{l}}$ are defined above in model (B6). So, from Definition 2.2 and Theorem A.2 we have

$$\begin{aligned}&\mathcal {M}\left\{ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \left[ \left( \xi _{t_{ijk}^{p}} \right) y_{ijk}^{p} \right] \le Z_{2}^{'} \right\} =\nu _{Z_{2}^{'}}\\&\quad =\left\{ {\begin{array}{l@{\quad }l} 0,&{} \mathrm{if}~ Z_{2}^{'}\le \overline{\overline{g}} \\ \frac{Z_{2}^{'}-\bar{\bar{g}}}{2\left( \bar{\bar{h}}-\bar{\bar{g}} \right) },&{} if\, \overline{\overline{g}}<Z_{2}^{'}\le \overline{\overline{h}} \\ \frac{Z_{2}^{'}+\overline{\overline{l}}-2\overline{\overline{h}}}{2\left( \overline{\overline{l}}-\overline{\overline{h}} \right) },&{} \mathrm{if}~ \overline{\overline{h}}<Z_{2}^{'}\le \overline{\overline{l}} \\ 1,&{} \mathrm{if}~ Z_{2}^{'}>\overline{\overline{l}}. \\ \end{array}} \right. \end{aligned}$$

Moreover, from Corollary B.1 (ii) the crisp transformations of the constraint set of model (11) become same to that of the constraint set of model (B3). Hence, it directly follows model (B6).

Theorem B.3

Le $\xi _{c_{ijk}^{p}}$, $\xi _{f_{ijk}^{p}}$, $\xi _{t_{ijk}^{p}}{,}~ \xi _{a_{i}^{p}}{,}~ \xi _{b_{j}^{p}}{,}~ \xi _{e_{k}^{p}}$ and $\xi _{B_{j}^{p}}$ are the independent normal uncertain variables of the form $\mathcal {N}\left( \mu _{q},\sigma _{q} \right)$ with $q\in \left\{ \xi _{c_{ijk}^{p}}\mathrm {,~ }\xi _{f_{ijk}^{p}}\mathrm {,~ }\xi _{t_{ijk}^{p}}{,}~ \xi _{a_{i}^{p}}{,}~ \xi _{b_{j}^{p}}{,}~ \xi _{e_{k}^{p}}\mathrm {,~ }\xi _{B_{j}^{p}} \right\}$. Then the crisp equivalent of model (11) is given in model (B7).

$$\begin{aligned} \left\{ {\begin{array}{l} \mathrm{Max}~ \nu _{Z_{1}^{'}}={1-\left( 1+\mathrm {exp}\left( \frac{\pi \left( \mu _{1}-Z_{1}^{'} \right) }{\sqrt{3} ~ \sigma _{1}} \right) \right) }^{-1}~ \\ Max{~ \nu }_{Z_{2}^{'}}=~ \left( 1+\mathrm {exp}\left( \frac{\pi \left( \mu _{2}-Z_{2}^{'} \right) }{\sqrt{3} ~ \sigma _{2}} \right) \right) ^{-1}~ \\ \mathrm{subject~ to~ the~ constraints}~\mathrm{of}~\mathrm{(B4)}.\\ \end{array}} \right. \end{aligned}$$

(B7)

Proof

Considering the first objective of model (11), i.e., $\mathcal {M}\Big \{ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \Big [ \Big ( s_{j}^{p}-v_{i}^{p}-\xi _{c_{ijk}^{p}} \Big )x_{ijk}^{p}-\Big ( \xi _{f_{ijk}^{p}} \Big )y_{ijk}^{p} \Big ] \ge Z_{1}^{'} \Big \}{,}~ \xi _{c_{ijk}^{p}}$ and $\xi _{f_{ijk}^{p}}$ are independent normal uncertain variables. $x_{ijk}^{p},~ s_{j}^{p}$ and $v_{i}^{p}$ are greater or equal to zero, and $y_{ijk}^{p}$ are binary variables. Then $\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \Big [ \Big ( s_{j}^{p}-v_{i}^{p}-\xi _{c_{ijk}^{p}} \Big )x_{ijk}^{p}-\Big ( \xi _{f_{ijk}^{p}} \Big )y_{ijk}^{p} \Big ]$ can be considered as a normal uncertain variable $\mathcal {N}\Big ( \mu _{1},\sigma _{1} \Big )$, such that $\mu _{1}$ and $\sigma _{1}$ are, respectively, $\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \Big [ \Big ( s_{j}^{p}-v_{i}^{p}{-\mu }_{\xi _{c_{ijk}^{p}}} \Big )x_{ijk}^{p}+\Big ( \mu _{\xi _{f_{ijk}^{p}}} \Big )y_{ijk}^{p} \Big ]$ and $\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \Big [ {\sigma _{\xi _{c_{ijk}^{p}}}}x_{ijk}^{p}+\sigma _{\xi _{f_{ijk}^{p}}}y_{ijk}^{p} \Big ] .$ Therefore, from Definition 2.3, and theorems A.3 and  A.4, $\mathcal {M}\Big \{ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \Big [ \Big ( s_{j}^{p}-v_{i}^{p}-\xi _{c_{ijk}^{p}} \Big )x_{ijk}^{p}-\Big ( \xi _{f_{ijk}^{p}} \Big )y_{ijk}^{p} \Big ] \ge Z_{1}^{'} \Big \}={1-\Big (1}{+\exp \Big ( \frac{\pi \Big ( \mu _{1}-Z_{1}^{'} \Big )}{\sqrt{3} ~ \sigma _{1}} \Big ) \Big )}^{-1}$.

Table 10 Unit purchase costs of items 1 and 2 at two different sources

Table 11 Unit selling prices of items 1 and 2 at three different destinations

Table 12 Transportation costs for item 1 and item 2 represented as zigzag and normal uncertain variables

Table 13 Fixed charge costs for item 1 and item 2 represented as zigzag and normal uncertain variables

Table 14 Transportation time for item 1 and item 2 represented as zigzag and normal uncertain variables

Similarly, for the second objective of model (11), $\xi _{t_{ijk}^{p}}$ are the independent normal uncertain variables. Therefore, $\mathcal {M}\Big \{ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \Big [ \xi _{t_{ijk}^{p}}y_{ijk}^{p} \Big ] \le Z_{2}^{'} \Big \}$ is a normal uncertain variable, $\mathcal {N}\Big ( \mu _{2},\sigma _{2} \Big )$ such that $\mu _{2}$ and $\sigma _{2}$ are, respectively, $\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \Big [ \mu _{\xi _{t_{ijk}^{p}}}y_{ijk}^{p} \Big ]$ and $\sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \Big [ \sigma _{\xi _{t_{ijk}^{p}}}y_{ijk}^{p} \Big ]$.

Accordingly, from Definition 2.3, and theorems A.3 and A.4, $\mathcal {M}\Big \{ \sum \nolimits _{p=1}^r \sum \nolimits _{i=1}^m \sum \nolimits _{j=1}^n \sum \nolimits _{k=1}^K \Big [ \xi _{t_{ijk}^{p}}y_{ijk}^{p} \Big ] \le Z_{2}^{'} \Big \}=\Big ( 1+\mathrm {exp}\Big ( \frac{\pi \Big ( \mu _{2}-Z_{2}^{'} \Big )}{\sqrt{3} ~ \sigma _{2}} \Big ) \Big )^{-1}.$ Further, from Corollary B.2 the crisp transformations of the constraints of model (11) becomes same to that of the constraint set of model (B4). Hence, the model (B7) follows directly.

Appendix C

Data tables for input parameters

The input parameters related to UMMFSTPwB are reported in tables 10, 11, 12, 13, 14, 15, 16, 17 and 18. The parameters shown in tables 10 and 11 are crisp. The parameters, presented in tables 12, 13, 14, 15, 16, 17 and 18 are uncertain. These uncertain parameters are represented as: (i) zigzag uncertain variables and (ii) normal uncertain variables.

Table 15 Available amounts of item 1 and item 2 represented as zigzag and normal uncertain variables

Table 16 Demands for item 1 and item 2 represented as zigzag and normal uncertain variables

Table 17 Transportation capacities of two conveyances expressed as zigzag and normal uncertain variables

Table 18 Budget availability at destinations represented as zigzag and normal uncertain variables