Multi-objective fixed-charge solid transportation problem with product blending under intuitionistic fuzzy environment

Abstract

This paper analyzes multi-objective fixed-charge solid transportation problem with product blending in intuitionistic fuzzy environment. The parameters of multi-objective fixed-charge solid transportation problem may not be defined precisely because of globalization of the market and other unmanageable factors. So, we often hesitate in prediction of market demand and other parameters connected with transporting systems in a period. Based on these facts, the parameters of the formulated model are chosen as triangular intuitionistic fuzzy number. New ranking method is used to convert intuitionistic fuzzy multi-objective fixed-charge solid transportation problem with product blending to a deterministic form. New intuitionistic fuzzy technique for order preference by similarity to ideal solution (TOPSIS) is initiated to derive Pareto-optimal solution from the proposed model. Furthermore, we solve the formulated model using intuitionistic fuzzy programming; and a comparison is drawn between the obtained solutions extracted from the approaches. Finally, a practical (industrial) problem is incorporated to illustrate the applicability and feasibility of the proposed study. Conclusions with future research based on the paper are described at last.

1 Introduction

Product blending is an ordinary event in many industries such as petroleum, chemical and process industries which involve blending raw materials with various attributes and concentration levels into required homogeneous intervening or final products. One of the important goals in blending for raw materials is to minimize the transportation shipping cost for a particular product that meets the demand at the destination of the final product and satisfying pre-determined requirements for such type of product.

Researchers have studied the product blending in some industries such as oil refining, chemical and others. A very few number of papers has been published on fixed-charge transportation problem with product blending. Papageorgiou et al. [31] first presented the fixed-charge transportation problem with product blending. Of late, Kundu et al. [18] solved a solid transportation model with product blending under rough environment.

Transportation problem (TP) is one of the important network problems in decision making problems. In classical TP, the product is shipped from various source points (i.e., factories) to different demand points (i.e., warehouses) in such a way that total transportation cost is minimized. Fixed-charge transportation problem (FCTP) is the generalized version of the classical TP. Generally, in TP, it is considered that the shipping cost is directly proportional to unit quantity of transported product. Many real-life situations happen where an additional cost namely, fixed-charge is taken into account to the transportation cost in each route for shipping the product from sources to destinations. For those cases, TP turns into FCTP, it was first initiated by Hirsch and Dantzig [13]. The fixed-charge may be due to costs of renting a vehicle, toll tax, permit fees etc.

The solid transportation problem (STP) is an expanded version of the TP, was first proposed by Haley [11]. It deals with three types of constraints namely, supply constraints, demand constraints, and conveyance constraints whereas TP considers two types of constraints such as supply and demand constraints. In STP, a homogeneous product is shipped from a source to a destination by several transportation modes, called conveyances, such as cargo fights, ships, goods trains, trucks, etc. The fixed-charge solid transportation problem (FCSTP) is a modified structure of STP in which a fixed-charge is added for an open route from a source to a destination by a specified transportation mode. A FCSTP reduces into a FCTP when the number of conveyances is exactly one.

In FCSTP, several objective functions are normally considered due to various aspects of decision maker as well as real-life situations for an industrial problem. Furthermore, FCSTP with multi-objective optimization is another influential trend worthy of study. In comparison with single objective FCSTP, it is more reasonable and practical in terms of actual applications. As for example, the objective functions which are minimized may be the total (variable and fixed) cost, the delivery time of transportation, the deterioration rate of goods during transportation, etc. Again, in real-life situations, the multi-objective functions of FCSTP generally conflicting and non-commensurable in nature. Due to this argument, FCSTP can be further modified by adopting the multi-objective functions into FCSTP. This modified version is called multi-objective fixed-charge solid transportation problem (MFCSTP).

In real-life transporting system, the liquid products (i.e., petroleum, gasoline, chemical product, etc.) are shipped from several sources with different quality levels by various transportation modes, and the products are received at several demand points with different quality levels. Moreover, each demand point has required the minimum quality level of the particular product. For this case, the different quality of the product is transported from different sources to several destinations by various transportation modes in such a way that the product taken at each destination can be blended together to satisfy the required quality of the product to the destination. To tackle this type of industrial problem, we incorporate a blending constraint in our proposed MFCSTP; and hence this type of industrial problem is called multi-objective fixed-charge solid transportation problem with product blending (MFSTPB).

Many researchers have chosen multi-objective TP/FCTP/ STP/FCSTP in various uncertain environments. A few of them is summarized as: Midya and Roy [27] analyzed fixed-charge multi-objective (multi-index) stochastic transportation problem using fuzzy programming approach. Sengupta et al. [38] solved solid transportation problem considering carbon emission in gamma type-2 defuzzification environment. Maity et al. [24] discussed multi-objective transportation problem with cost reliability in uncertain environments. Das et al. [8] analyzed breakable multi-item multi-stage solid transportation problem under budget with Gaussian type-2 fuzzy parameters. Maity and Roy [23] solved multi-objective transportation problem with nonlinear cost and multi-choice demand. Mahapatra et al. [22] formulated multi-objective stochastic transportation problem involving log-normal. Roy et al. [36] tackled conic scalarization for solving multi-objective transportation problem under multi-choice environment with interval goal. Rani et al. [32] solved multi-objective non-linear programming problem in intuitionistic fuzzy environment.

Literature survey revealed that few papers have appeared on FCTP/STP with product blending as a constraint but, they acquired FCTP/STP with product blending by considering single objective function with crisp or rough data. Till now, none of them are not treated MFSTPB whose parameters are intuitionistic fuzzy number.

Generally, in a MFSTPB problem (planning), the available data such as transportation cost, fixed-charge, transporting time, deterioration rate of goods, availabilities, demands, the capacity of conveyances to transport the products from sources to destinations are not defined precisely. Due to various aspects, like lack of input information, fluctuating of financial market, bad statistical analysis, weather and road conditions, etc. the parameters of MFSTPB are uncertainty in nature. To tackle the uncertain parameters in FCTP/STP, researchers have studied fuzzy, random, rough, etc. environments. A few of them are described as follows. Zhang et al. [47] included an algorithm to solve a fixed-charge solid transportation problem under uncertain environments. Jimenez and Verdegay [16] studied STP under two types of uncertain environments which are interval-number and fuzzy-number, and they solved it. Zavardehi et al. [46] presented a fuzzy fixed-charge solid transportation problem and solved it by meta-heuristics. Roy and Maity [36] formulated minimizing cost and time through single objective function in multi-choice interval valued transportation problem. Roy et al. [34] solved multi-objective two-stage grey transportation problem using utility function with goals. Midya and Roy [28] studied fixed-charge transportation problem using interval programming. Recently, Roy et al. [37] formulated multi-objective fixed-charge transportation problem under rough and random rough environments.

Furthermore, to tackle hesitancy in decision making problem, researchers have used the concept of hesitant fuzzy set such as Zhou et al. [48] designed a prospect theory-based group decision approach considering consensus for portfolio selection with hesitant fuzzy information. Tian et al. [40] examined sequential funding the venture projector with a prospect consensus process in probabilistic hesitant fuzzy preference information. Liao et al. [20] introduced hesitant fuzzy linguistic preference utility set and its application in selection of fire rescue plans. Moreover, Capuano et al. [6] studied fuzzy group decision making with incomplete information guided by social influence. Hao et al. [12] presented a dynamic weight determination approach based on the intuitionistic fuzzy bayesian network and its application to emergency decision making.

The intuitionistic fuzzy set was initiated by Atanassov [4] which is the generalization of fuzzy set [45]. The main advantage of intuitionistic fuzzy set is that it is characterized by membership function as well as non-membership function in such a way that the sum of both values fall between zero and one. Whereas, fuzzy set is characterized by membership function. So, the intuitionsitic fuzzy set is highly useful to deal with ill-known quantities. For this reason, an intuitionistic fuzzy number is used to express an ill-known quantity. In daily life transporting systems, available information about the parameters are frequently vague or uncertain in nature due to several factors. In this situation, the decision maker (DM) of a company takes an opinion from experts for the parameters. Usually, possible values of the parameters are given by the experts in almost interval value, linguistic term and others. For example, transporting time of a route is “around 11 hour”, the supply of a factory is “in 26-28 barrel/day”, etc. In this situation, DM cannot predict the value about the parameters exactly and thus hesitancy character arises in decision making process. Such type of cases where data set is not only uncertainty in nature but also hesitancy character which can be represented by intuitionistic fuzzy number. Therefore, the membership values cannot be evaluated exactly according to DM satisfaction. Due to the reasons, the parameters in the proposed model are treated as intuitionistic fuzzy number instead of fuzzy number. If we consider the parameters of MFSTPB in an intuitionistic fuzzy number then the information about the degree of acceptance and degree of non-acceptance of the parameters are to be specified which is more realistic in practical applications. To realize the fact, we describe an example as follows:

Example 1.1

Assume $\mathcal {D}$ “demand of ethanol blended petrol” of a specific province in India approximately changes in nearly 25 barrel/day. The approximate value of $\mathcal {D}$ is expressed using any value between 24 to 26 barrel/day by taking different degrees of membership and any value between 23 to 27 barrel/day by choosing different degrees non-membership functions. In a nutshell, the optimistic value of $\mathcal {D}$ is 24 to 26 barrel/day with membership degree 1 and the pessimistic value of $\mathcal {D}$ is 23 to 27 barrel/day with non-membership degree 1. This implies that the demand of ethanol blended petrol per day can be treated by a triangular intuitionistic fuzzy number $\widetilde {\mathcal {D}}=\langle (24,25,26),(23,25,27)\rangle$.

In this regard, the parameters of MFSTPB are taken as intuitionistic fuzzy numbers. Generally, two kinds of intuitionistic fuzzy number such as triangular intuitionistic fuzzy number and trapezoidal intuitionistic fuzzy number are used to deal with uncertainty. But for defuzzification, computational complexity of triangular intuitionistic fuzzy number is less than trapezoidal intuitionistic fuzzy number. Because of that, triangular intuitionistic fuzzy number is considered in the study. To the best of the knowledge, proposed study (i.e., MFSTPB in intuitionistic fuzzy environment) is the first contribution to formulate and to solve the MFSTPB model. The main achievements of our designed work are summarized as follows:

• Intuitionistic fuzzy MFSTPB is designed.

• The parameters of MFSTPB are assumed as triangular intuitionistic fuzzy number.

• New ranking index is introduced for defuzzification of an intuitionistic triangular fuzzy number; and to convert intuitionistic fuzzy MFSTPB into a deterministic form.

• Intuitionistic fuzzy TOPSIS approach is proposed to obtain Pareto-optimal solution from deterministic MFSTPB.

• Deterministic MFSTPB is also solved by intuitionistic fuzzy programming.

• A comparative study is shown between the Pareto-optimal solutions extracted from the approaches.

• Investigate the solution procedures between the proposed approach and the existing methods.

• An industrial problem is included to illustrate the MFSTPB in intuitionistic fuzzy environment.

The outline of the paper is set out as follows. In Section 2, basic knowledge of intuitionistic fuzzy number with arithmetic are presented; and new procedure to defuzzification of an intuitionistic triangular fuzzy number are also discussed. Notations and assumptions are put in Section 3. Mathematical model of intuitionistic fuzzy MFSTPB and its deterministic form are depicted in Section 4. In Section 5, defects of the existing methods are pointed. In Section 6, the solution procedures of the formulated model are described. In Section 7, an application example with real-life data on MFSTPB is included; and results and discussion are reflected in Section 8. Finally, conclusions and future research directions are provided in Section 9.

2 Preliminaries

Here, we include some basic definitions of intuitionistic fuzzy set and intuitionistic fuzzy number.

Definition 2.1

[4] Let X be a nonempty set. An intuitionistic fuzzy set $\widetilde {C}$ in X is chosen as $\widetilde {C}=\{\langle x,\mu _{\widetilde {C}}(x),\nu _{\widetilde {C}}(x):x\in X\rangle \},$ where $\mu _{\widetilde {C}}(x):X\rightarrow [0,1]$ and $\nu _{\widetilde {C}}(x):X\rightarrow [0,1]$ such that $0\leq \mu _{\widetilde {C}}(x)+\nu _{\widetilde {C}}(x)\leq 1$. The numbers $\mu _{\widetilde {C}}(x), \nu _{\widetilde {C}}(x)\in [0,1]$ consider the membership degree and non-membership degree of x to $\widetilde {C}$ respectively. Each intuitionistic fuzzy subset $\widetilde {C}$ in X, the condition $0\leq \pi _{\widetilde {C}}(x)\leq 1$ satisfies, where $\pi _{\widetilde {C}}(x)=1-\mu _{\widetilde {C}}(x)-\nu _{\widetilde {C}}(x)$, is called hesitancy degree of x to $\widetilde {C}$.

Definition 2.2

[10] An intuitionistic fuzzy number $\widetilde {D}=\{\langle x,\mu _{\widetilde {D}}(x),\nu _{\widetilde {D}}(x)\rangle \}$ in the set of real numbers $\mathbb {R}$, its membership and non-membership functions are described mathematically as:

$$ \begin{array}{@{}rcl@{}} \mu_{\widetilde{D}}(x)&=&\left\{ \begin{array}{lll} 0, & \text{for} \hspace{0.20cm}x<a_{1}, \\ f_{\widetilde{D}}(x), & \text{for} \hspace{0.20cm}a_{1}\leq x\leq a_{2}, \\ 1, & \text{for} \hspace{0.20cm}x=a_{2},\\ g_{\widetilde{D}}(x), & \text{for} \hspace{0.20cm}a_{2}\leq x\leq a_{3}, \\ 0, & \text{for} \hspace{0.20cm}x>a_{3}, \end{array} \right. \mathrm\&,\\ \nu_{\widetilde{D}}(x)&=&\left\{ \begin{array}{lll} 1, & \text{for} \hspace{0.20cm}x<a^{\prime}_{1}, \\ \phi_{\widetilde{D}}(x), & \text{for} \hspace{0.20cm}a^{\prime}_{1}\leq x\leq a_{2}, \\ 0, & \text{for} \hspace{0.20cm} x=a_{2},\\ \psi_{\widetilde{D}}(x), &\text{for} \hspace{0.20cm} a_{2}\leq x\leq a^{\prime}_{3}, \\ 1, & \text{for} \hspace{0.20cm} x>a^{\prime}_{3}, \end{array} \right. \end{array} $$

where $0\leq \mu _{\widetilde {D}}(x)+\nu _{\widetilde {D}}(x)\leq 1;$ and $a_{1},a_{2},a_{3},a^{\prime }_{1},a^{\prime }_{3}$ are real numbers such that $a^{\prime }_{1}\leq a_{1} \leq a_{2}\leq a_{3}\leq a^{\prime }_{3},$and four functions $f_{\widetilde {D}}(x), g_{\widetilde {D}}(x), \phi _{\widetilde {D}}(x), \psi _{\widetilde {D}}(x):\mathbb {R}\rightarrow [0,1]$ are treated the legs of membership functions $\mu _{\widetilde {D}}(x)$ and non-membership functions $\nu _{\widetilde {D}}(x)$ respectively. The functions $f_{\widetilde {D}}(x)$ and $\psi _{\widetilde {D}}(x)$ are non-decreasing continuous; and the functions $g_{\widetilde {D}}(x)$ and $\phi _{\widetilde {D}}(x)$ are non-increasing continuous functions.

Definition 2.3

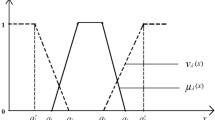
[30] A triangular intuitionistic fuzzy number $\widetilde {A}$ is noted as $\widetilde {A}= \langle (a_{1},a_{2},a_{3}),(a^{\prime }_{1}, a_{2}, a^{\prime }_{3})\rangle$, $a^{\prime }_{1}\leq a_{1}\leq a_{2}\leq a_{3}\leq a^{\prime }_{3}$ in the set of real numbers $\mathbb {R}$, whose pictorial representation is shown in Fig. 1. Its membership and non-membership functions are denoted as $\mu _{\widetilde {A}}(x)$ and $\nu _{\widetilde {A}}(x)$ respectively, and they are defined as below:

$$ \begin{array}{@{}rcl@{}} \mu_{\widetilde{A}}(x)&=&\left\{ \begin{array}{lll} 0, & \text{for} \hspace{0.25cm}x<a_{1}, \\ \frac{x-a_{1}}{a_{2}-a_{1}}, & \text{for} \hspace{0.25cm}a_{1}\leq x\leq a_{2}, \\ 1, & \text{for} \hspace{0.25cm} x=a_{2},\\ \frac{a_{3}-x}{a_{3}-a_{2}}, & \text{for} \hspace{0.25cm}a_{2}\leq x\leq a_{3}, \\ 0, & \text{for} \hspace{0.25cm} x>a_{3}. \end{array} \right. \mathrm\&,\\ \nu_{\widetilde{A}}(x)&=&\left\{ \begin{array}{lll} 1, & \text{for} \hspace{0.25cm} x<a^{\prime}_{1}, \\ \frac{a_{2}-x}{a_{2}-a^{\prime}_{1}}, & \text{for} \hspace{0.25cm}a^{\prime}_{1}\leq x\leq a_{2}, \\ 0, & \text{for} \hspace{0.25cm} x = a_{2},\\ \frac{x-a_{2}}{a^{\prime}_{3}-a_{2}}, & \text{for} \hspace{0.25cm}a_{2}\leq x\leq a^{\prime}_{3}, \\ 1, & \text{for} \hspace{0.25cm} x>a^{\prime}_{3}. \end{array} \right. \end{array} $$

Fig. 1

The graph of a triangular intuitionistic fuzzy number

Algebraic Operations on intuitionistic fuzzy numbers

Let $\widetilde {A}=\langle (a_{1},a_{2},a_{3}),(a^{\prime }_{1}, a_{2}, a^{\prime }_{3})\rangle$ and $\widetilde {B}=\langle (b_{1},b_{2},b_{3}),$$(b^{\prime }_{1}, b_{2}, b^{\prime }_{3})\rangle$ be two triangular intuitionistic fuzzy numbers and ρ be a positive scalar. Then

• $\widetilde {A}+\widetilde {B}=\langle (a_{1}+b_{1}, a_{2}+b_{2}, a_{3}+b_{3}),(a^{\prime }_{1}+b^{\prime }_{1}, a_{2}+b_{2}, a^{\prime }_{3}+b^{\prime }_{3})\rangle$;

• $\rho \widetilde {A}=\langle (\rho a_{1}, \rho a_{2}, \rho a_{3},),(\rho a^{\prime }_{1}, \rho a_{2}, \rho a^{\prime }_{3})\rangle$ if ρ ≥ 0;

• $\rho \widetilde {A}=\langle (\rho a_{3}, \rho a_{2}, \rho a_{1}),(\rho a^{\prime }_{3}, \rho a_{2}, \rho a^{\prime }_{1})\rangle$ if ρ < 0;

• $\widetilde {A}-\widetilde {B}=\langle (a_{1}-b_{3}, a_{2}-b_{2}, a_{3}-b_{1}),(a^{\prime }_{1}-b^{\prime }_{3}, a_{2}-b_{2}, a^{\prime }_{3}-b^{\prime }_{1})\rangle$;

• $\widetilde {A}\cdot \widetilde {B}=\langle (a_{1}b_{1}, a_{2}b_{2}, a_{3}b_{3}),(a^{\prime }_{1}b^{\prime }_{1}, a_{2}b_{2}, a^{\prime }_{3}b^{\prime }_{3})\rangle$.

2.1 Defuzzified value of an intuitionistic fuzzy number

In this subsection, we incorporate a definition to extract the defuzzified value or the ranking index (i.e., deterministic value) of a triangular intuitionistic fuzzy number. Literature survey elicits that several methods exist for defuzzification of an intuitionistic fuzzy number, but the centroid method is widely practiced among them. The centroid method of a fuzzy number $\tilde {c}$ in its geometric center is provided by the formula [29]:

$$ \begin{array}{@{}rcl@{}} M(\tilde{c})=\frac{{\int}_{x}x\zeta(x)dx}{{\int}_{x}\zeta(x)dx} (A^{*}), \end{array} $$

where ζ(x) is the membership function of a fuzzy number $\tilde {c}$. Based on the formula (A^∗), we write the definition as follows:

Definition 2.4

Let $\widetilde {A}=\langle (a_{1},a_{2},a_{3}),(a^{\prime }_{1},a_{2},a^{\prime }_{3})\rangle$ be a triangular intuitionistic fuzzy number in the set of real numbers, $\mathbb {R}$. Then its ranking index is denoted by $\mathcal {R}(\widetilde {A})$ and is prescribed as follows:

$$ \begin{array}{@{}rcl@{}} \mathcal{R}(\widetilde{A})=[\lambda\mathcal{R}^{*}(\mu_{\widetilde{A}}(x))+(1-\lambda)\mathcal{R}_{*}(\nu_{\widetilde{A}}(x))], \end{array} $$

where λ ∈ (0,1) is a parameter, $\mathcal {R}^{*}(\mu _{\widetilde {A}}(x))$ and $\mathcal {R}_{*}(\nu _{\widetilde {A}}(x))$ can be defined as follows:

$$ \begin{array}{@{}rcl@{}} \mathcal{R}^{*}(\mu_{\widetilde{A}}(x))\!&=&\!\left[{\int}_{a_{1}}^{a_{3}}x\mu_{\widetilde{A}}(x)dx\right]\left/\left[{\int}_{a_{1}}^{a_{3}}\mu_{\widetilde{A}}(x)\right]dx\right.\\ \!&=&\!\left[{\int}_{a_{1}}^{a_{2}}\frac{x(x-a_{1})}{a_{2}-a_{1}}dx + {\int}_{a_{2}}^{a_{3}}\frac{x(a_{3}-x)}{a_{3}-a_{2}}dx\right]\left/\vphantom{\left[{\int}_{a_{1}}^{a_{3}}x\mu_{\widetilde{A}}(x)dx\right]}\right.\\ &&\left[{\int}_{a_{1}}^{a_{2}}\frac{x-a_{1}}{a_{2}-a_{1}}dx+{\int}_{a_{2}}^{a_{3}}\frac{a_{3}-x}{a_{3}-a_{2}}dx\right]\\ \!&=&\!\left[\frac{(a_{3}-a_{1})(a_{3}+a_{2}+a_{1})}{6}\right]\left/\left[\frac{a_{3}-a_{1}}{2}\right]\right.\\ \!&=&\!\frac{a_{1}+a_{2}+a_{3}}{3}, \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} \mathcal{R}_{*}(\nu_{\widetilde{A}}(x))\!&=&\!\left[{\int}_{a^{\prime}_{1}}^{a^{\prime}_{3}}x\nu_{\widetilde{A}}(x)dx\right]\left/\left[{\int}_{a^{\prime}_{1}}^{a^{\prime}_{3}}\nu_{\widetilde{A}}(x)\right]dx\right.\\ \!&=&\!\left[{\int}_{a^{\prime}_{1}}^{a_{2}}\frac{x(a_{2}-x)}{a_{2}-a^{\prime}_{1}}dx + {\int}_{a_{2}}^{a^{\prime}_{3}}\frac{x(x-a_{2})}{a^{\prime}_{3}-a_{2}}dx\right]\left/\vphantom{\left[{\int}_{a_{1}}^{a_{3}}x\mu_{\widetilde{A}}(x)dx\right]}\right.\\ &&\left[{\int}_{a^{\prime}_{1}}^{a_{2}}\frac{a_{2}-x}{a_{2}-a^{\prime}_{1}}dx+{\int}_{a_{2}}^{a^{\prime}_{3}}\frac{x-a_{2}}{a^{\prime}_{3}-a_{2}}dx\right]\\ \!&=&\!\left[\frac{(a^{\prime}_{3}-a^{\prime}_{1})(2a^{\prime}_{3}-a_{2}+2a^{\prime}_{1})}{6}\right]\left/\left[\frac{a^{\prime}_{3}-a^{\prime}_{1}}{2}\right]\right.\\ \!&=&\!\frac{2a^{\prime}_{1}-a_{2}+2a^{\prime}_{3}}{3}. \end{array} $$

Hence the ranking index of a triangular intuitionistic fuzzy number $\widetilde {A}=\langle (a_{1},a_{2},a_{3}), (a^{\prime }_{1},a_{2},a^{\prime }_{3})\rangle$ is

$$ \begin{array}{@{}rcl@{}} \mathcal{R}(\widetilde{A})=\left[\lambda\frac{a_{1}+a_{2}+a_{3}}{3}+(1-\lambda)\frac{2a^{\prime}_{1}-a_{2}+2a^{\prime}_{3}}{3}\right]. \end{array} $$

Remark 2.1

If $\lambda =\frac {1}{2}$, then the ranking index of a triangular intuitionistic fuzzy number $\widetilde {A}=\langle (a_{1},a_{2},a_{3}),(a^{\prime }_{1},a_{2},a^{\prime }_{3})\rangle$ is calculated as:

$$ \begin{array}{@{}rcl@{}} \mathcal{R}(\widetilde{A})=\frac{2a^{\prime}_{1}+a_{1}+a_{3}+2a^{\prime}_{3}}{6}. \end{array} $$

Theorem 2.1

Let$\widetilde {A}$and$\widetilde {B}$beany two triangular intuitionistic fuzzy numbers and c and d be any real numbers. Then

$$ \begin{array}{@{}rcl@{}} \mathcal{R}[c\widetilde{A}+d\widetilde{B}]=c\mathcal{R}[\widetilde{A}]+d\mathcal{R}[\widetilde{B}]. \end{array} $$

Proof

Let $\widetilde {A}=\langle (a_{1}, a_{2}, a_{3}),(a^{\prime }_{1}, a_{2}, a^{\prime }_{3})\rangle$ and $\widetilde {B}=\langle (b_{1}, b_{2}, b_{3}),(b^{\prime }_{1}, b_{2}, b^{\prime }_{3})\rangle$ be two triangular intuitionistic fuzzy numbers. Assuming that c and d are positive real numbers. Using the algebraic operation of two triangular intuitionistic fuzzy numbers, we have

$$ \begin{array}{@{}rcl@{}} c\widetilde{A}+d\widetilde{B}&=&\langle(ca_{1}+db_{1}, ca_{2}+db_{2}, ca_{3}+db_{3}),\\ &&(ca^{\prime}_{1}+db^{\prime}_{1}, ca_{2}+db_{2}, ca^{\prime}_{3}+db^{\prime}_{3})\rangle, \end{array} $$

is a triangular intuitionistic fuzzy number. From Definition 2.4, the ranking index of $c\widetilde {A}+d\widetilde {B}$ is given by

$$ \begin{array}{@{}rcl@{}} &&\mathcal{R}(c\widetilde{A}+d\widetilde{B})\\ &=&\left[\lambda\frac{ca_{1}+db_{1}+ca_{2}+db_{2}+ca_{3}+db_{3}}{3}\right.\\ &&\left.+(1-\lambda)\frac{2ca^{\prime}_{1}+2db^{\prime}_{1}-ca_{2}-db_{2}+2ca^{\prime}_{3}+2db^{\prime}_{3}}{3}\right]\\ &=&c\left[\lambda\frac{a_{1}+a_{2}+a_{3}}{3}+(1-\lambda)\frac{2a^{\prime}_{1}-a_{2}+2a^{\prime}_{3}}{3}\right]\\ &&+d\left[\lambda\frac{b_{1}+b_{2}+b_{3}}{3}+(1-\lambda)\frac{2b^{\prime}_{1}-b_{2}+2b^{\prime}_{3}}{3}\right]\\ &=&c\mathcal{R}[\widetilde{A}]+d\mathcal{R}[\widetilde{B}]. \end{array} $$

This evinces the proof of the theorem. □

3 Notations and assumptions

The following notations and assumptions are put for designing the paper.

Notations:

• m : number of sources,

• n : number of destinations,

• p : number of conveyances (i.e., various transportation modes),

• x_ijk : unit amount of the product to be transported from i^th source to j^th destination by k^th conveyance,

• η(x_ijk ) : binary variable takes the value “1” if the source i is used, and “0” otherwise,

• $\widetilde {c}_{ijk}:$ intuitionistic fuzzy transportation (variable) cost for unit quantity of the product from i^th source to j^th destination by k^th conveyance,

• $\widetilde {f}_{ijk}:$ intuitionistic fuzzy fixed cost associated with i^th source to j^th destination by k^th conveyance,

• $\widetilde {t}_{ijk}:$ intuitionistic fuzzy time of transportation of the product from i^th source to j^th destination by k^th conveyance,

• $\widetilde {d}_{ijk}:$ intuitionistic fuzzy deterioration rate of goods of the product from i^th source to j^th destination by k^th conveyance,

• $\widetilde {a}_{i}:$ intuitionistic fuzzy availability of the product at i^th source,

• $\widetilde {b}_{j}:$ intuitionistic fuzzy demand of the product at j^th destination,

• $\widetilde {e}_{k}:$ total intuitionistic fuzzy capacity of the product which can be carried by k^th conveyance,

• $\widetilde {Z}_{K}:$ objective function in intuitionistic fuzzy nature (K = 1,2,3),

• Z_K : objective function in deterministic form, where $Z_{K}=\mathcal {R}[\widetilde {Z}_{K}]$ (K = 1,2,3),

• q_i : nominal quality (i.e., clarity) of the product which is available from source i,

• $q_{j}^{min}:$ least quality of the product needs at destination j.

Assumptions:

• 1. $\widetilde {a}_{i}>0, \widetilde {b}_{j}>0, \forall i, j$.

• 2. Each chosen triangular intuitionistic fuzzy variable is positive in all of its components.

4 Mathematical model

In this intended study, we take three objective functions in which the first objective function assumes the total transportation cost (the variable cost and the fixed cost), the second objective function considers the transporting time and the last one refers to the deterioration rate of goods; all of the three goals are to be minimized. The second objective function is taken to maximize the customers’ satisfaction level; in fact, to measure it, we treat the total transportation time. So, with respect to maximizing the customers’ satisfaction level, the value of the objective function should be minimized. There are m factories (supply points), n customers (demand points) and p conveyances (different transportation modes such as trucks, air freight, goods trains, ships, etc.). Each of the m factories can transport to any of the n customers by the p conveyances at a transporting cost of c_ijk per unit commodity and a fixed cost of f_ijk. The problem is to calculate the amount x_ijk, for any i,j,k of the product conveyed from i^th source to j^th destination by k^th transportation mode, in such a way that the overall value of three objective functions are to be minimized. In several practical situations such as gasoline, petroleum and others industries, blending of raw materials with different attributes and purities into analogous intermediate or final products is a common topic. Blending raw materials give an organization/company for the chance to perceive more cost savings, while meeting demand for an array to the end of the products and fulfilling pre-decided quality requirements for such kind of product. The intrinsic flexibility of the blending activity can be utilized to optimize the allotment and transportation of raw materials to production facilities. So, in MFSTPB an additional proportionality requirement on the quality of the product is adopted. The additional constraints (4.4) in Model 1 is indicated as linear blending constraints. The average quality of all products received at destination j is as follows:

$$ \begin{array}{@{}rcl@{}} \frac{\sum\limits_{i=1}^{m}\sum\limits_{k=1}^{p}q_{i}x_{ijk}}{\sum\limits_{i=1}^{m}\sum\limits_{k=1}^{p}x_{ijk}}, j=1,2,\ldots,n. \end{array} $$

We assume the least quality (i.e., clarity) of the product at destination j is $q_{j}^{min}$. So, the constraints on the quality requirement of the product can be defined as:

$$ \begin{array}{@{}rcl@{}} &&\frac{\sum\limits_{i=1}^{m}\sum\limits_{k=1}^{p}q_{i}x_{ijk}}{\sum\limits_{i=1}^{m}\sum\limits_{k=1}^{p}x_{ijk}}\geq q_{j}^{min}, j=1,2,\ldots,n,\\ \text{i.e.},&&\sum\limits_{i=1}^{m}\sum\limits_{k=1}^{p}\left( q_{i}-q_{j}^{min}\right)x_{ijk}\geq0, j=1,2,\ldots,n. \end{array} $$

Thus, the proposed problem including blending constraints can be formulated as follows:

Model 1

$$ \begin{array}{@{}rcl@{}} \text{minimize}&& \widetilde{Z}_{1}=\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{n}\sum\limits_{k=1}^{p}\left[\widetilde{c}_{ijk}x_{ijk}+ \widetilde{f}_{ijk}\eta(x_{ijk})\right], \end{array} $$

(4.1)

$$ \begin{array}{@{}rcl@{}} \text{minimize}&&\widetilde{Z}_{2}=\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{n} \sum\limits_{k=1}^{p}\left[\widetilde{t}_{ijk}\eta(x_{ijk})\right], \end{array} $$

(4.2)

$$ \begin{array}{@{}rcl@{}} \text{minimize}&&\widetilde{Z}_{3}=\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{n}\sum\limits_{k=1}^{p}\widetilde{d}_{ijk}x_{ijk} \end{array} $$

(4.3)

$$ \begin{array}{@{}rcl@{}} \text{subject to}&&\sum\limits_{i=1}^{m}\sum\limits_{k=1}^{p}\left( q_{i}-q_{j}^{min}\right)x_{ijk}\\ &&\geq0 (j=1,2,\ldots,n), \end{array} $$

(4.4)

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{j=1}^{n}\sum\limits_{k=1}^{p}x_{ijk}\leq\widetilde{a}_{i} (i=1,2,\ldots,m), \end{array} $$

(4.5)

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{i=1}^{m}\sum\limits_{k=1}^{p}x_{ijk}\geq\widetilde{b}_{j} (j=1,2,\ldots,n), \end{array} $$

(4.6)

$$ \begin{array}{@{}rcl@{}} &&\sum\limits\limits_{i=1}^{m}\sum\limits_{j=1}^{n}x_{ijk}\leq\widetilde{e}_{k} (k=1,2,\ldots,p), \end{array} $$

(4.7)

$$ \begin{array}{@{}rcl@{}} &&\eta(x_{ijk})=\left\{ \begin{array}{lll}0\ \text{if\ } x_{ijk}=0,\\ 1 \text{\ if\ } x_{ijk}>0, \end{array} \right. \end{array} $$

(4.8)

$$ \begin{array}{@{}rcl@{}} &&x_{ijk}\geq0, (i=1,2,\ldots,m; j=1,2,\ldots,\\ &&\qquad\qquad\quad n; k=1,2,\ldots,p). \end{array} $$

(4.9)

The feasibility condition of Model 1 is chosen as follows:

$$ \begin{array}{@{}rcl@{}} \sum\limits_{i=1}^{m}\widetilde{a}_{i}\geq\sum\limits_{j=1}^{n}\widetilde{b}_{j}, \text{and} \sum\limits_{k=1}^{p}\widetilde{e}_{k}\geq\sum\limits_{j=1}^{n}\widetilde{b}_{j}. \end{array} $$

4.1 Deterministic model

Intuitionistic fuzzy MFSTPB model cannot be tackled directly due to the presence of intuitionistic fuzzy number. So, we include the ranking index to transform Model 1 into a deterministic MFSTPB model (i.e., Model 2) by using Theorem 2.1 (which is stated in Section 2.1).

Model 2

$$ \begin{array}{@{}rcl@{}} \text{minimize}&& \mathcal{R}(\widetilde{Z}_{1})=\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{n}\sum\limits_{k=1}^{p}\\ &&\left[\mathcal{R}(\widetilde{c}_{ijk})x_{ijk}+ \mathcal{R}(\widetilde{f}_{ijk})\eta(x_{ijk})\right], \end{array} $$

(4.10)

$$ \begin{array}{@{}rcl@{}} \text{minimize}&&\mathcal{R}(\widetilde{Z}_{2})=\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{n} \sum\limits_{k=1}^{p}\left[\mathcal{R}(\widetilde{t}_{ijk})\eta(x_{ijk})\right], \end{array} $$

(4.11)

$$ \begin{array}{@{}rcl@{}} \text{minimize}&&\mathcal{R}(\widetilde{Z}_{3})=\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{n}\sum\limits_{k=1}^{p}\mathcal{R}(\widetilde{d}_{ijk})x_{ijk} \end{array} $$

(4.12)

$$ \begin{array}{@{}rcl@{}} \text{subject to}&&\sum\limits_{i=1}^{m}\sum\limits_{k=1}^{p}\left( q_{i}-q_{j}^{min}\right)x_{ijk}\\ &&\geq0 (j=1,2,\ldots,n), \end{array} $$

(4.13)

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{j=1}^{n}\sum\limits_{k=1}^{p}x_{ijk}\leq\mathcal{R}(\widetilde{a}_{i}) (i=1,2,\ldots,m), \end{array} $$

(4.14)

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{i=1}^{m}\sum\limits_{k=1}^{p}x_{ijk}\geq\mathcal{R}(\widetilde{b}_{j}) (j=1,2,\ldots,n), \end{array} $$

(4.15)

$$ \begin{array}{@{}rcl@{}} &&\sum\limits_{i=1}^{m}\sum\limits_{j=1}^{n}x_{ijk}\leq\mathcal{R}(\widetilde{e}_{k}) (k=1,2,\ldots,p), \end{array} $$

(4.16)

$$ \begin{array}{@{}rcl@{}} &&\text{constraints (4.8) \text{and} (4.9)}. \end{array} $$

Definition 4.1

A feasible solution $x^{*}=(x_{ijk}^{*}:i=1,2,$ …,m;j = 1,2,…,n;k = 1,2,…,p) is called to be a Pareto-optimal solution (compromise solution) of Model 2 if there does not contain any feasible solution x = (x_ijk : i = 1,2,…,m;j = 1,2,…,n;k = 1,2,…,p) such that

$$ \begin{array}{@{}rcl@{}} Z_{K}(x)&\leq&Z_{K}(x^{*}) \text{\ for} \ K=1,2,3,\ \text{and}\\ Z_{K}(x)&<&Z_{K}(x^{*}) \text{\ for at least one }K. \end{array} $$

5 Drawbacks of the existing methods

From literature survey, it can be observed that several researchers have developed to solve multi-objective TP/STP/FCSTP either in certain or in uncertain environments. In this section, we mainly extract the defects of the existing methods which are mentioned below:

• A very few research papers had been published on TP/STP under intuitionistic fuzzy environment such as Aggarwal and Gupta [2], Singh and Yadav [39] where they considered single objective function in their models. But, our formulated model is designed under multi-objective environment with an additional cost as fixed-charge, which is more realistic for real-life transportation problem.

• Several existing methods are available in literature like Das and Guha [9], Varghese and Kuriakose [42] to find the centroid of an intuitionistic fuzzy number. But these are very complicated than our proposed approach to deduce the defuzzified value of a triangular intuitionistic fuzzy number. One can choose the desired centroid value of a triangular intuitionistic fuzzy number by using our approach for different values of λ ∈ (0,1).

• In existing methods such as Li and Lai [21], Kundu et al. [17] solved multi-objective TP/STP using fuzzy programming. But, in fuzzy programming, only the degree of acceptance is considered for the objective functions and constraints, and the priorities (i.e., preferences) of the objective functions are not taken into consideration. In this proposed (intuitionistic fuzzy TOPSIS) approach, we assume the degree of acceptance and the degree of rejection for the objective functions and constraints as well as the priorities of the objective functions.

• Abo-Sinna et al. [1] solved multi-objective non-linear programming problem by TOPSIS based on fuzzy programming. But, in TOPSIS based on fuzzy programming, the degree of rejection is not included to the objective functions and constraints. In this proposed approach, we accomodate both features i.e., the degree of acceptance and the degree of rejection.

• Roy et al. [33] solved multi-objective TP by intuitionistic fuzzy programming. But, in intuitionistic fuzzy programming, the priorities of the objective functions are not incorporated. Also, the tolerances of lower and upper bounds to the objective functions in the case of non-membership function are not chosen. In our proposed approach, we overcome the mentioned defects.

• Wahed and Lee [43] solved multi-objective TP using interactive fuzzy goal programming. Also, other researchers (like Maity and Roy [25] and others) have used goal programming to solve TP/STP. But in goal programming, it is difficult to choose the proper goals corresponding to the objective functions. If we do not properly select the target values to the objective functions, then for that case, goal programming will provide the worst optimal solution. Such cases are not arisen to obtain the Pareto-optimal solution in intuitionistic fuzzy TOPSIS approach.

• Zhang et al. [47] considered the parameters of FCSTP as uncertain variables to deal with indeterminacy phenomenon in transporting systems. They incorporated uncertain distribution when historical data is not valid because of unwanted events that has happened. For example, when natural disaster occurs, it may be better to consider uncertain variable as the parameters in transporting systems. But, it is a special case and would not happen in daily life industrial transporting systems. From this viewpoint, we treat intuitionistic fuzzy number as the parameters in our proposed study which efficiently deals with hesitancy character as well uncertainty in practical problems. Thus, intuitionistic fuzzy number is more reliable to represent uncertainty as well as hesitancy nature of the parameters in MFSTPB than uncertain variables.

• Majumder et al. [26] solved multi-objective multi-item fixed-charge solid transportation problem by using fuzzy programming, global criterion method and linear weighted method. In Table 8, we see that the proposed intuitionistic fuzzy TOPSIS is more preferable than fuzzy programming and global criterion method. Also, if we want to solve multi-objective mixed optimization problem by linear weighted method, it is necessary to transfer the objective function into same type. But for the intuitionistic fuzzy TOPSIS, no such difficulty arises. In this point of view, it says that intuitionistic fuzzy TOPSIS is more suitable to obtain Pareto-optimal solution from multi-objective optimization problem.

• To solve decision making problems, researchers such as Chen and Tsao [7], Boran et al. [5], Wang et al. [44] have been used TOPSIS approach and extended it. But in their study, they first ranked the alternatives from the best to the worst and then selected the best alternative for the considered decision making problems. Here, the main aim is to obtain Pareto-optimal solution from our proposed problem and then we desire to find the satisfaction and dissatisfaction levels of the objective functions. In this stand point, intuitionistic fuzzy TOPSIS approach is proposed to extract a better Pareto-optimal solution of this study.

6 Solution methodology

In order to solve MFSTPB (i.e., Model 2), we consider the following:

• Intuitionistic Fuzzy Programming (IFP) and

• Intuitionistic fuzzy TOPSIS.

6.1 Intuitionistic fuzzy programming

Angelov [3] first initiated IFP to solve optimization problems. He found that intuitionistic fuzzy linear programming always provides an optimal compromise solution. The solution of MFSTPB (i.e., Model 2) using IFP can be obtained by the following steps:

Step 1.1::

Solve the MFSTPB as a single objective FCSTPB, using at a time only one objective function Z_K(K = 1,2,3) and ignoring the others. The optimal solution for K^th(K = 1,2,3) objective function is denoted by X^K∗.

Step 1.2::

Based on the results of Step 1.1, calculate the corresponding value of each objective function at each solution derived.

Step 1.3::

From Step 1.2, we choose a lower bound $(L^{\mu }_{K})$ and an upper bound $(U^{\mu }_{K})$ for membership function corresponding to each objective function. As the objective functions are conflicting in nature, so, $U^{\mu }_{K}=L^{\mu }_{K}$ is not possible for any X^K∗(K = 1,2,3). We construct the payoff table which is given in Table 1, from which $U^{\mu }_{K}$ and $L^{\mu }_{K}$ are determined in the following way:

$$ \begin{array}{@{}rcl@{}} U^{\mu}_{K}:=&&\underset{1\leq r\leq 3}{\max}\left\{ Z_{K}(X^{r*})\right\},\\ \text{and} \ L^{\mu}_{K}:=&&Z_{K}(X^{K*}); K=1,2,3. \end{array} $$

In a similar way, we calculate a lower bound $(L^{\nu }_{K})$ and an upper bound $(U^{\nu }_{K})$ for non-membership function corresponding to each objective function. We calculate $U^{\nu }_{K}$ and $L^{\nu }_{K}$ in the following way:

$$ \begin{array}{@{}rcl@{}} U^{\nu}_{K}:=&&U^{\mu}_{K}+\alpha_{K},\\ \text{and} \ L^{\nu}_{K}:=&&L^{\mu}_{K}, K=1,2,3. \end{array} $$

Where α_K is the respective tolerance of lower bound $(L^{\mu }_{K})$ and upper bound $(U^{\mu }_{K})$ of each objective function.

Table 1 Payoff table

Step 1.4: :

A membership function μ_K(x) and a non-membership function ν_K(x) corresponding to K^th(K = 1,2,3) objective function of MFSTPB are defined as:

$$ \begin{array}{@{}rcl@{}} \mu_{K}(x)&=&\left\{ \begin{array}{ll} 1, & \text{if} \hspace{0.1cm}Z_{K}\leq L^{\mu}_{K},\\ \frac{U^{\mu}_{K}-Z_{K}}{U^{\mu}_{K}-L^{\mu}_{K}}, & \text{if} \hspace{0.1cm} L^{\mu}_{K}\leq Z_{K}\leq U^{\mu}_{K},\\ 0, & \text{if} \hspace{0.1cm}Z_{K}\geq U^{\mu}_{K}. \end{array} \right. \text\&,\\ \nu_{K}(x)&=&\left\{ \begin{array}{ll} 0, & \text{if} \hspace{0.1cm}Z_{K}\leq L^{\nu}_{K}, \\ \frac{Z_{K}-L^{\nu}_{K}}{U^{\nu}_{K}-L^{\nu}_{K}}, & \text{if} \hspace{0.1cm} L^{\nu}_{K}\leq Z_{K}\leq U^{\nu}_{K},\\ 1, & \text{if} \hspace{0.1cm}Z_{K}\geq U^{\nu}_{K}. \end{array} \right. \end{array} $$

Step 1.5: :

Using max-min operator [49], the intuitionistic fuzzy linear programming problem can be designed in the following way:

$$ \begin{array}{@{}rcl@{}} \text{maximize} &&\lambda_{1} \\ \text{minimize} &&\eta_{1} \\ \text{subject to} && \lambda_{1}\leq \frac{U^{\mu}_{K}-Z_{K}}{U^{\mu}_{K}-L^{\mu}_{K}} (K=1,2,3), \\ && \eta_{1}\geq \frac{Z_{K}-L^{\nu}_{K}}{U^{\nu}_{K}-L^{\nu}_{K}} (K=1,2,3),\\ &&\text{constraints\ } (4.8)\ \text{and} \ (4.9),\\ &&\text{constraints} \ (4.13)-(4.16),\\ &&\lambda_{1}+\eta_{1}\leq1, \\ &&\lambda_{1}, \eta_{1}\geq0. \end{array} $$

Here, λ₁ = min{μ_K(x) : K = 1,2,3} and η₁ = max{ν_K(x) : K = 1,2,3} are the satisfaction level and dissatisfaction level of the objective function. This bi-objective problem can further be simplified to a single objective programming problem as:

Model 3

$$ \begin{array}{@{}rcl@{}} \text{maximize} &&(\lambda_{1}-\eta_{1}) \\ \text{subject to} && Z_{K}+\lambda_{1}(U^{\mu}_{K}-L^{\mu}_{K})\leq U^{\mu}_{K} (K=1,2,3), \\ &&Z_{K}-\eta_{1}(U^{\nu}_{K}-L^{\nu}_{K})\leq L^{\nu}_{K} (K=1,2,3), \\ &&\text{constraints } (4.8) \ \text{and } (4.9),\\ &&\text{constraints } (4.13)-(4.16),\\ &&\lambda_{1}+\eta_{1}\leq1, \\ &&\lambda_{1}, \eta_{1}\geq0. \end{array} $$

Step 1.6: :

From Model 3, finally we derive the Pareto-optimal solution of our proposed MFSTPB.

Theorem 6.1

If $x^{*}=(x_{ijk}^{*}: i=1,2,\ldots ,m; j=1,2,\ldots ,n; k=1,2,\ldots ,p)$ is an optimal solution of Model 3, then it is also a Pareto-optimal (non-dominated) solution of Model 2.

Proof

Let x^∗ is not a Pareto-optimal (non-dominated) solution of Model 2. Therefore, from Definition 4.1, it can be considered that there exists at least one x such

$$ \begin{array}{@{}rcl@{}} Z_{K}(x)&\leq&Z_{K}(x^{*})\ \text{for} \ K=1,2,3, \text{and}\\ Z_{K}(x)&<&Z_{K}(x^{*}) \text{\ for at least one} \ K. \end{array} $$

Since the membership function μ_K(x) strictly decreases with respect to the corresponding objective function Z_K in [0,1] and the non-membership function ν_K(x) strictly increases with respect to the corresponding objective function Z_K in [0,1], so we have μ_K(x) ≥ μ_K(x^∗)∀K,and μ_K(x) > μ_K(x^∗) for at least one K. Also, ν_K(x) ≤ ν_K(x^∗)∀K, and ν_K(x) < ν_K(x^∗) for at least one K.

Hence, (λ₁ − η₁) = min {μ_K(x),ν_K(x)}≥ min{μ_K(x^∗),ν_K(x^∗)}= $(\lambda _{1}^{*}-\eta _{1}^{*})$ which contradicts the fact that x^∗ an optimal solution of Model 3, where $\lambda _{1}^{*} \ \text {and} \ \eta _{1}^{*}$ are the values of λ₁ and η₁ at x^∗ respectively. This completes the proof of the theorem. □

6.2 Intuitionistic fuzzy TOPSIS

Hwang and Yoon [14] initiated TOPSIS for deriving Pareto-optimal solutions to multi-attribute decision making problems. It is based on the idea that the chosen alternatives should have the shortest distance from the Positive Ideal Solution (PIS) and the farthest distance from the Negative Ideal Solution (NIS). Classical TOPSIS has been competently used for solving many selection/ranking problems. It basically focuses on three kinds of decisions: (i) find the rank of all alternatives, (ii) the alternatives are ranked from the best to the worst, (iii) select the best alternative. Generally, TOPSIS is used to reduce a given multi-objective optimization problem into a bi-objective optimization problem. Abo-Sinna et al. [1] applied TOPSIS method to solve a multi-objective large-scale nonlinear programming problem with a block-angular structure. Later on, Li [19] developed a TOPSIS-based nonlinear-programming methodology for multi-attribute decision making problems. Many researchers acquainted with TOPSIS approach for decision making problem such as Izadikhah [15], Vahdani et al. [41] and others. They investigated the ranking order of the criteria. But we propose intuitionistic fuzzy TOPSIS approach to obtain the Pareto-optimal solution for Model 2 and we also calculate the optimal values of the objective functions. The main advantages of proposed approach are that it generates a better Pareto-optimal solution and it also gives the satisfaction and dissatisfaction levels of the objective functions. Moreover, it is easy to apply (i.e., less computational burden) for solving MFSTPB and similar type of decision making problems.

Definition 6.1

If a multi-objective optimization problem is reduced to a bi-objective problem by TOPSIS approach, then the reduced problem is called a TOPSIS-based bi-objective optimization problem.

We extend the concept of TOPSIS approach by incorporating intuitionistic fuzzy programming with TOPSIS in our proposed study. It is a hybridization to obtain the Pareto-optimal solution of MFSTPB (i.e., Model 2). In our proposed approach, first, we formulate TOPSIS-based bi-objective problem of MFSTPB. Thereafter, the bi-objective problem is solved by introducing membership function and non-membership function of intuitionistic fuzzy programming to represent the satisfaction level (i.e., maximizing the degree of membership) and dissatisfaction level (i.e., minimizing the degree of non-membership) of the objective functions. The developed TOPSIS approach is described by the following steps:

Step 2.1: :

Determine the individual minimum and maximum values of all the objective functions for MFSTPB (i.e., Model 2).

Step 2.2: :

Identify PIS (Z⁺) and NIS (Z⁻) for Model 2, which are defined as follows:

$$ \begin{array}{@{}rcl@{}} Z^{+} &=(Z_{1}^{+}, Z_{2}^{+}, Z_{3}^{+}),\\ Z^{-} &=(Z_{1}^{-}, Z_{2}^{-}, Z_{3}^{-}), \end{array} $$

where for every K (i.e., K = 1,2,3), we express $Z_{K}^{+}$ and $Z_{K}^{-}$ which are as:

$$ \begin{array}{@{}rcl@{}} \left\{\begin{array}{lll} Z_{K}^{+}&=\min Z_{K}, \text{subject to constraints} \ (4.8) \text{\ and} \ (4.9), (4.13)-(4.16),\\ Z_{K}^{-}&=\max Z_{K}, \text{subject to constraints\ } (4.8) \text{\ and\ } (4.9), (4.13)-(4.16). \end {array} \right. \end{array} $$

We note that the range of the objective functions in MFSTPB with $Z_{K}^{+} <Z_{K}^{-}$ can be estimated by $Z_{K}^{-} -Z_{K}^{+} (K=1,2,3)$. The concepts of PIS and NIS are depicted in Fig. 2.

Fig. 2

The graphical representation of PIS (Z⁺) and NIS (Z⁻)

Step 2.3: :

Using PIS and NIS, we calculate the distance function from PIS$\left (\text {i.e.}, d^{PIS}_{u}(x)\right )$ and the distance function from NIS $\left (\text {i.e.}, d^{NIS}_{u}(x)\right )$ as follows:

$$ \begin{array}{@{}rcl@{}} d^{PIS}_{u}(x)&=&\left[\sum\limits_{K=1}^{3}\left[W_{K}\frac{Z_{K}(x)-Z_{K}^{+}}{Z_{K}^{-}-Z_{K}^{+}}\right]^{u}\right]^{\frac{1}{u}}, \end{array} $$

(6.17)

$$ \begin{array}{@{}rcl@{}} d^{NIS}_{u}(x)&=&\left[\sum\limits_{K=1}^{3}\left[W_{K}\frac{Z_{K}^{-}-Z_{K}(x)}{Z_{K}^{-}-Z_{K}^{+}}\right]^{u}\right]^{\frac{1}{u}}, \end{array} $$

(6.18)

$$ \begin{array}{@{}rcl@{}} \sum\limits_{K=1}^{3}W_{K}&=&1, W_{K}\geq0, K=1,2,3. \end{array} $$

The parameters W_K(K = 1,2,3) in (6.17) and (6.18) denote the weights of the objective functions. Here, we consider the priorities by weights, and they are W₁ = 0.3,W₂ = 0.4,W₃ = 0.3 for three objective functions, respectively, of Model 2. The indices u(= 1,2,…,∞) is employed to control the Pareto-optimal solution in TOPSIS. In general, u = 1,u = 2,andu = ∞ are widely used to deal with multi-objective optimization problem. Different values of u refer to different distances, e.g., u = 1 indicates to the Manhattan distance (the farthest distance in the geometrical sense), u = 2 represents to the Euclidean distance (the least distance in the geometrical sense), and u = ∞ refers to the Tchebycheff distance (the shortest distance in the numerical sense). Other distances are used less because they have no concrete meaning in practice.

Step 2.4: :

Set u = 2 into the (6.17) and (6.18). To obtain Pareto-optimal solution, Model 2 transforms into the following bi-objective problem.

$$ \begin{array}{@{}rcl@{}} \text{minimize}&&d^{PIS}_{2}(x), \\ \text{maximize}&&d^{NIS}_{2}(x) \\ \text{subject to}&&\text{constraints}\ (4.8) \ \text{and\ } (4.9),\\ &&\text{constraints\ } (4.13)-(4.16). \end{array} $$

Step 2.5: :

Calculate the individual values to minimize $d^{PIS}_{2}(x)$ and to $\text {maximize}~d^{NIS}_{2}(x)$ subject to the constraints (4.8) and (4.9), and (4.13)-(4.16). Now, we construct the payoff table of ideal solutions (shown in Table 2) as:

Table 2 Payoff table of ideal solutions

For convenience, we introduce notation as: $(d^{PIS}_{2})^{*}= d^{PIS}_{2}(x^{PIS})$, $(d^{NIS}_{2})^{*}=d^{NIS}_{2}(x^{NIS})$, $(d^{PIS}_{2})^{\prime }=d^{PIS}_{2}$ (x^NIS), $(d^{NIS}_{2})^{\prime }=d^{NIS}_{2}(x^{PIS})$.

Step 2.6: :

Based on the preference concept, we formulate the membership functions μ₁(x) and μ₂(x), and non-membership functions ν₁(x) and ν₂(x) for two objective functions respectively from Step 2.5. They are defined respectively as follows:

$$ \begin{array}{@{}rcl@{}} \mu_{1}(x)=\left\{ \begin{array}{ll} 1, & \text{if} \hspace{0.25cm} d^{PIS}_{2}(x)\leq(d^{PIS}_{2})^{*} , \\ \frac{(d^{PIS}_{2})^{\prime}-d^{PIS}_{2}(x)}{(d^{PIS}_{2})^{\prime}-(d^{PIS}_{2})^{*}}, & \text{if} \hspace{0.25cm} (d^{PIS}_{2})^{*}\leq d^{PIS}_{2}(x)\leq (d^{PIS}_{2})^{\prime}, \\ 0, & \text{if} \hspace{0.25cm} (d^{PIS}_{2})^{\prime}\leq d^{PIS}_{2}(x), \end{array} \right. \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} \mu_{2}(x)=\left\{ \begin{array}{ll} 1, & \text{if} \hspace{0.25cm} (d^{NIS}_{2})^{*}\leq d^{NIS}_{2}(x) , \\ \frac{d^{NIS}_{2}(x)-(d^{NIS}_{2})^{\prime}}{(d^{NIS}_{2})^{*}-(d^{NIS}_{2})^{\prime}}, & \text{if} \hspace{0.25cm} (d^{NIS}_{2})^{\prime}\leq d^{NIS}_{2}(x)\leq (d^{NIS}_{2})^{*}, \\ 0, & \text{if} \hspace{0.25cm} d^{NIS}_{2}(x)\leq(d^{NIS}_{2})^{\prime} , \end{array} \right. \end{array} $$

$$ \begin{array}{@{}rcl@{}} \nu_{1}(x) = \left\{ \begin{array}{ll} 0, & \text{if} \hspace{0.25cm} d^{PIS}_{2}(x)\!\leq\!(d^{PIS}_{2})^{*} , \\ \frac{d^{PIS}_{2}(x)-(d^{PIS}_{2})^{*}}{(d^{PIS}_{2})^{\prime}+\beta_{1}-(d^{PIS}_{2})^{*}}, & \text{if} \hspace{0.25cm} (d^{PIS}_{2})^{*}\!\leq\! d^{PIS}_{2}(x)\!\leq\! (d^{PIS}_{2})^{\prime} + \beta_{1}, \\ 1, & \text{if} \hspace{0.25cm} (d^{PIS}_{2})^{\prime} + \beta_{1}\!\leq\! d^{PIS}_{2}(x), \end{array} \right. \end{array} $$

and

$$ \begin{array}{@{}rcl@{}} \nu_{2}(x) = \left\{ \begin{array}{ll} 0, & \text{if} \hspace{0.25cm} (d^{NIS}_{2})^{*}\!\leq\! d^{NIS}_{2}(x) , \\ \frac{(d^{NIS}_{2})^{*}-d^{NIS}_{2}(x)}{(d^{NIS}_{2})^{*}-\left( (d^{NIS}_{2})^{\prime}-\beta_{2}\right)}, & \text{if} \hspace{0.25cm} (d^{NIS}_{2})^{\prime} - \beta_{2}\!\leq\! d^{NIS}_{2}(x)\!\leq\! (d^{PIS}_{2})^{*}, \\ 1, & \text{if} \hspace{0.25cm} d^{NIS}_{2}(x)\!\leq\!(d^{NIS}_{2})^{\prime} - \beta_{2}, \end{array} \right. \end{array} $$

where β₁ and β₂ are the respective tolerances of lower bound and upper bound corresponding to the objective functions.

Step 2.7: :

Using the max-min operator, the intuitionistic fuzzy linear programming of the bi-objective problem in Step 2.4 can be written in the following way:

Model 4

$$ \begin{array}{@{}rcl@{}} \text{maximize} &&(\lambda_{2}-\eta_{2}) \\ \text{subject to} && \mu_{1}(x)\geq\lambda_{2}, \mu_{2}(x)\geq\lambda_{2},\\ &&\nu_{1}(x)\leq\eta_{2}, \nu_{2}(x)\leq\eta_{2},\\ &&\text{constraints\ } (4.8)\ \text{and} \ (4.9),\\ &&\text{constraints\ } (4.13)-(4.16),\\ &&\lambda_{2}+\eta_{2}\leq1, \\ &&\lambda_{2}, \eta_{2}\geq0. \end{array} $$

Here, λ₂ = min{μ₁(x), μ₂(x)} and η₂ = max{ν₁(x),ν₂(x)} are the satisfaction level and dissatisfaction level for the criteria of the minimum distance from the PIS and the maximum distance from the NIS of Model 2.

Step 2.8: :

From Step 2.7, we finally obtain the Pareto-optimal solution of our proposed MFSTPB (i.e., Model 2).

Theorem 6.2

If an optimal solution of Model 4 exists, then it is a Pareto-optimal solution of Model 2.

The proof is similar to Theorem 6.1.

A reputed oil production company in India (namely, IOC Ltd.) produces ethanol blended petrol (EBP) product. The company has three plants (m = 3) at Barauni (in Bihar), Haldia (in West Bengal), Paradip (in Odisha) and three distribution centers (n = 3) situated at Kolkata, Jamshedpur, Patna in the country. The company transports EBP from plants to demand points through tankers by two types of conveyances (p = 2) namely, highways and railways. Decision maker (DM) desires that the total transporting cost (variable cost per unit and fixed cost), total transporting time to transport EBP from plants to distribution centers and deterioration rate of EBP are to be minimized. In this real-life problem fixed-charge is considered in two ways. For highway transportation the oil company would pay a certain amount of toll charge to National Highway Authority of India for different types of tankers to move EBP and maintenance cost of tankers is also included. For railways transportation the oil company would pay a certain amount to Indian Rail Authority for booking train tankers. Furthermore, DM decides to find a Pareto-optimal solution to the problem in which the values of the objective functions are to be minimized. The relative importance of three objective functions are considered as the weight factors which are specified by DM. The transportation cost in rupees per barrel, fixed-charge in rupees for an open route, time in hour and deterioration rate in litre are considered. Data for transportation cost and fixed-charge are shown in Table 3 and for transporting time and deterioration rate of EBP are listed in Table 4. Table 6 presents the supply and demand parameters; and Table 7 shows the capacity of conveyance. Also, each plant consists the formal quality (i.e., purity) of the produced EBP which are q₁ = 0.85 (i.e., 85% clarity of the product), q₂ = 0.90, q₃ = 0.80 and the least quality of the produced EPB needs at each distribution center which are $q_{1}^{min}=0.90$, $q_{2}^{min}=0.80$, $q_{3}^{min}=0.85$.

Table 3 Transportation cost and fixed-charge $(\widetilde {c}_{ijk},\widetilde {f}_{ijk})$

Table 4 Transporting time and deterioration rate $(\widetilde {t}_{ijk},\widetilde {d}_{ijk})$

7 Application example based on real-life data

Using Definition 2.4 and Remark 2.1 which are stated in Section 2.1 for ranking index of the triangular intuitionistic fuzzy number, Tables 3 and 4 reduce in Table 5. Also, intuitionistic fuzzy supply, demand and capacity of conveyance parameters are converted to their deterministic form by using the proposed ranking index.

Table 5 Crisp form of $\widetilde {c}_{ijk},\widetilde {f}_{ijk},\widetilde {t}_{ijk},\widetilde {d}_{ijk}$

8 Results and discussion

Here, we derive the Pareto-optimal solutions of the equivalent deterministic Model 2 using two approaches which are as follows:

Intuitionistic fuzzy programming

Utilizing the crisp data of each intuitionistic triangular fuzzy numbers from Tables 5, 6 and 7 in Model 2, applying the solution procedure described in Section 6.1 and using LINGO iterative scheme, we obtain the Pareto-optimal solution by intuitionistic fuzzy programming which is shown in Table 8.

Table 6 Supply $(\widetilde {a}_{i})$ and demand $(\widetilde {b}_{j})$ and their deterministic value $\left (\mathcal {R}(\widetilde {a}_{i}), \mathcal {R}(\widetilde {b}_{j})\right )$

Table 7 Capacity of $k^{th}$ conveyance $(\widetilde {e}_{k})$ and its deterministic value $(\mathcal {R}[\widetilde {e}_{k}])$

Table 8 The Pareto-optimal solutions of proposed MFSTPB

Intuitionistic fuzzy TOPSIS

Considering the crisp data of each intuitionistic triangular fuzzy number from Tables 5, 6 and 8 in Model 2, utilizing the solution procedure delineated in Section 6.2 and using LINGO iterative scheme, we derive the subsequent Pareto-optimal solution by intuitionistic fuzzy TOPSIS which is displayed in Table 8.

In Table 8, we put the results of our proposed model (i.e., Model 2) which are derived from existing methods such as fuzzy programming (Li and Lai [21]), global criterion method (Majumder et al. [26]), Intuitionistic fuzzy programming and our proposed approach respectively. From Table 8, we conclude that the Pareto-optimal solution for MFSTPB, extracted from proposed intuitionistic fuzzy TOPSIS is more preferable than intuitionistic fuzzy programming, fuzzy programming and global criterion method. The optimal values of the objective functions (Z₁,Z₂andZ₃) are calculated from intuitionistic fuzzy TOPSIS are better than intuitionistic fuzzy programming and fuzzy programming proposed by Li & Lai [21]. Furthermore, as the optimal values of the objective functions (Z₁andZ₂) are obtained from proposed approach are minimum than global criterion method [26], so we conclude that suggested intuitionistic fuzzy TOPSIS is better than global criterion method. It is observed from obtaining Pareto-optimal solution of suggested MFSTPB that the factories satisfied with a minimum quality level of the product at distribution centers. From the above discussion, the advantage of the proposed intuitionistic fuzzy TOPSIS approach can be described as: (i) It provides a better Pareto-optimal solution than the mentioned existing methods. (ii) It transfers multiple objective functions into two conflicting objective functions. (iii) It represents the satisfaction and dissatisfaction levels of the objective functions. (iv) It generates different Pareto-optimal solutions for different weights setting. Also using different distance functions for 1 ≤ u < ∞, in intuitionistic fuzzy TOPSIS, DM can obtain different Pareto-optimal solutions. Thereafter, DM may find the different Pareto-optimal solutions by setting the different weights corresponding to the priority of the objective functions in intuitionistic fuzzy TOPSIS method. In this regard, we conclude that the proposed approach can be easily applicable to get better Pareto-optimal solution from different types of TP/STP than the mentioned existing methods. However, one of the limitations of the intuitionistic fuzzy TOPSIS is that the weights should be setting properly; otherwise, the optimal solutions may not be satisfied to all the objective functions.

9 Conclusions and future research scopes

For the first time in research, we have designed a multi-objective fixed-charge solid transportation problem with product blending under intuitionistic fuzzy environment. New ranking index based on the centroid value of a triangular intuitionistic fuzzy number has been defined and applied to reduce intuitionistic fuzzy MFSTPB to deterministic form. We have introduced triangular intuitionistic fuzzy number as parameter in our proposed model to tackle the imprecise data in real-life transporting system. The distinguish feature of the suggested model is that it has been considered the multi-objective functions in FCSTP with product blending as an additional constraint.

To solve deterministic MFSTPB, we have proposed intuitionistic fuzzy TOPSIS approach which is the hybridization of TOPSIS with intuitionistic fuzzy programming. One of the important features of the proposed approach is the satisfaction and dissatisfaction levels of the objective functions. The different Pareto-optimal solutions have been achieved from the proposed approach when we vary the weight coefficients to the objective functions. Intuitionistic fuzzy programming has been applied to resolve the suggested deterministic model. A comparative study has been made among the Pareto-optimal solutions extracted from the approaches including existing methods. Finally, from the applied viewpoint, we can conclude that our proposed model and approach both are highly significant in real-life situations.

In future scope of researches, the contents of this study can be extended a new direction to investigate fixed-charge solid transportation problem with product blending in two fold uncertain (intuitionistic-rough) environment. The present problem can be applied to multi-item MFSTPB. One may solve the different types of multi-objective transportation problems and decision making problems by using proposed intuitionistic fuzzy TOPSIS approach to obtain better results.