1 Introduction

    In many nonlinear physical systems, the diffusion of local pulses or solitons are controlled by different types of complex Ginzburg–Landau equations (CGLEs) including the dispersion and nonlinear effects of the conservative and dissipative forms[1, 2]. As universal models of mode formation in nonlinear dissipative media [3], complex Ginzburg–Landau equations (CGLEs) describe a variety of phenomena at the qualitative and even quantitative levels, from nonlinear wave to second–order transitions, from superconducting supercurrent, Bose-Einstein condensates (BEC) to strings and plasmas in liquid crystal field theory [4,5,6,7,8]. Therefore, it is very important to solve the exact solutions of partial differential equations, especially CGLEs [9,10,11]. So far, different types of solutions to one–dimensional complex Ginzburg–Landau equations have been analyzed such as impulse, quasi–impact, source, sink, periodic and quasi–periodic solutions [1].

As a kind of general amplitude equations in physics [12], complex cubic Ginzburg–Landau equations (CCGLEs) are also used to research many practical problems. For example, chemical turbulence, Rayleigh–Beynard convection [13], Taylor–Coutte flow, Poiseuille flow, reaction–diffusion systems, nonlinear optical and hydromechanical stability problems [14]. Specially, Its dark solitary waves were also discovered by Nazaki and Bekki, although they are unstable [16].

In this paper, we investigate the (1+1) dimensional complex cubic Ginzburg–Landau equation (CCGLE) which is used to describe dissipative systems above the bifurcation point [17], examples of applications include pulse generation by passive mode–locked soliton lasers [18], signal transmission in optical communications lines, traveling waves in binary fluid mixtures [19] and pattern formation [20] in many other physical systems [12]. The (1+1) dimensional complex cubic Ginzburg–Landau equation has the following form [14, 21]

$$\begin{aligned} \chi _t = r \chi - (1+i b) |\chi |^{2} \chi + (1+i a) \chi _{xx}, \end{aligned}$$
(1)

where \(\chi (x,t)\) is a complex function from \(\mathrm {R^{2}}\) to \(\textrm{C}\) representing the modulation of the oscillating field, b and r are two real control parameters [14]. \(r \chi \) and \((1+i b) |\chi |^{2} \chi \) describe the local dynamics of the oscillators, \(r \chi \) leads to the linear instability mechanism of the oscillation and \((1+i b) |\chi |^{2} \chi \) produces nonlinear amplitude saturation and frequency renormalization. \((1+i a) \chi _{xx}\) is the spatial coupling which explains diffusion and dispersion of oscillating motion [21].

As far as we know, many different types of solutions of the (1+1) dimensional CCGLE have been given. Such as, the traveling wave solutions were obtained by the first integral and the \(\mathrm {(G'/G)}\)–expansion methods [12], the implicit and explicit solutions were obtained by using the methods of variable separation and plane wave solutions [14], the singular bright solitons, the hybrid periodic solitons, the dark solitons and the periodic M-shaped solitons solutions were acquired via the Sardar sub-equation method [15], the periodic solitons solutions were also gotten through the energy balance method [15], the existence of time quasi–periodic solutions under periodic boundary conditions has been discussed [22]. In addition, by constructing the KAM theorem for dissipative systems with unbounded pertubations and multi–normal frequencies, a Contorian branches of the two dimensional invariant torus for CCGLE also have been obtained [22]. Finally, the kink solitons and periodic solitons solutions were attained based on the foundation of the notions of the planar dynamical theory for CCGLE [23].

However, there are still some solutions that are not used by the (1+1) dimensional CCGLE, such as the Hirota bilinear method has remarkable characteristics, which make it suitable for determining different kinds of solutions [24,25,26,27,28,29,30,31,32]. In this paper, we will attain the multiple solitons, lump and rogue wave solutions of Eq. (1) by using the Hirota bilinear method and setting different forms of auxiliary equations.

In order to gain the exact solutions of Eq. (1), we choose following equations to convert it

$$\begin{aligned} \chi =u +i v, ~~~~~~~~|\chi |= \sqrt{u^{2} + v^{2}}, \end{aligned}$$
(2)

where u, v are undetermined functions of independent variables x and t.

Inserting Eq. (2) into Eq. (1) and seperating its real and imaginary parts, we can gain

$$\begin{aligned} \text{ Re }: u_t -u_{xx}+ a v_{xx}- r u+ u^{3}+ v^{2} u- b u^{2} v-b v^{3}= 0. \end{aligned}$$
(3)
$$\begin{aligned} \text{ Im }: v_t -v_{xx}- a u_{xx}- r v+ v^{3}+ u^{2} v+ b v^{2} u+ b u^{3}= 0. \end{aligned}$$
(4)

The structure of this article is shown below. In Sect. 2, we can obtain the multiple solitons solutions of the (1+1) dimensional CCGLE through the Hirota bilinear method. The lump solutions can be given in Sect. 3 and the lump–one stripe soliton interaction solutions also can be obtained in Sect. 4. In Sect. 5, the rogue wave solutions can be acquired. In Sect. 6, we discuss the physical meanings of images that we have obtained. Finally, the conclusion is stated in Sect. 7.

2 Multiple solitons solutions

    In this section, we will apply the Hirota bilinear method to attain the multiple solitons solutions of the (1+1) dimensional CCGLE.

Firstly, substituting

$$\begin{aligned} u= e^{\theta _i},~~~~ \theta _i= k_i x+ m_i t+ c_i,~~ i= 1,2, \dots , N, \end{aligned}$$
(5)

where \(k_i, m_i\) and \(c_i\) are undetermined constants, into the linear terms of Eq. (3) and Eq. (4) and solving the corresponding equations, we can gain the dispersion relations as follows

$$\begin{aligned} m_i= k_i^{2}+ r,~~~~ \theta _i= k_i x+ (k_i^{2}+ r) t+ c_i,~~ i= 1,2, \dots , N, \end{aligned}$$
(6)

where \(k_i\) and \(c_i\) are undetermined constants.

From Eq. (6), we can notice that the dispersion relations \(m_i\) only depend on the coefficients \(k_i\) of x.

In order to get the multiple solitons solutions of the (1+1) dimensional CCGLE, we substitute

$$\begin{aligned} \begin{aligned}&u= R_1 (\text{ In }f)_x,\\&v= R_2 (\text{ In }f)_x, \end{aligned} \end{aligned}$$
(7)

where \(R_1\) and \(R_2\) are undetermined constants. f as the auxiliary functions will be determined later.

2.1 Single soliton solutions

    To gain the single soliton solutions of the (1+1) dimensional CCGLE, we take account the form of f like following

$$\begin{aligned} f= 1+ e^{\theta _1}, \end{aligned}$$
(8)

where \(\theta _1= k_1 x+ (k_1^{2}+ r) t+ c_1\) and \(k_1, c_1\) are undetermined constants.

Inserting Eq. (8) with Eq. (7) into Eq. (3) and Eq. (4), collecting all power coefficients of \(e^{\theta _1}\) and making their results to zero, we can get

$$\begin{aligned} \begin{aligned}&a= 0,~~~ b= 0,~~~R_1= \sqrt{2-R_2^{2}},\\&k_1=\sqrt{\frac{r}{2}},~~~~ r= r,~~~~ R_2= R_2. \end{aligned} \end{aligned}$$
(9)

Substituting Eq. (9) with Eq. (8) into Eq. (7), we know

$$\begin{aligned} \begin{aligned} f&= 1+ e^{\sqrt{\frac{r}{2}}x+ \frac{3}{2} r t+ c_1},\\ u&= \frac{\sqrt{\frac{r (2- R_2^{2})}{2}}~~e^{\sqrt{\frac{r}{2}}x+ \frac{3}{2} r t+ c_1}}{1+ e^{\sqrt{\frac{r}{2}}+ \frac{3}{2} r t+ c_1}}, v= \frac{R_2 \sqrt{\frac{r}{2}} e^{\sqrt{\frac{r}{2}}x+ \frac{3}{2} r t+ c_1}}{1+ e^{\sqrt{\frac{r}{2}}+ \frac{3}{2} r t+ c_1}},\\ \chi&= \frac{(\sqrt{2- R_2^{2}}+ R_2 i)\sqrt{\frac{r}{2}} e^{\sqrt{\frac{r}{2}}x+ \frac{3}{2} r t+ c_1}}{1+ e^{\sqrt{\frac{r}{2}}x+ \frac{3}{2} r t+ c_1}}, \end{aligned} \end{aligned}$$
(10)

where \(c_1, r\) and \(R_2\) are arbitrary constants.

Fig. 1
figure 1

Single soliton solution \(\chi (x,t)\) with \(r=-\frac{1}{3},\ c_1=\frac{1}{2},\ R_2=-2.\ ({\textbf {a}}) \ 3 \text{ D-plot }.\ ({\textbf {b}}) \ 2 \text{ D-plot }. ({\textbf {c}}) \ 2 \text{ D-plot }.\ ({\textbf {d}}) \ \text{ density } \text{ plot }\)

Full size image

2.2 Double solitons solutions

    The auxiliary function f for the double solitons solutions is given by

$$\begin{aligned} f= 1+ e^{\theta _1}+ e^{\theta _2}+ a_{12} e^{\theta _1+ \theta _2}, \end{aligned}$$
(11)

where \(\theta _1= k_1 x+ (k_1^{2}+ r) t+ c_1, \theta _2= k_2 x+ (k_2^{2}+ r) t+ c_2\) and \(k_1, k_2, c_1, c_2\) are undetermined constants.

Interposing Eq. (11) with Eq. (7) into Eq. (3) and Eq. (4), collecting all coefficients of the same power and making them to zero, we can gain

  1. Set-1:
    $$\begin{aligned} \begin{aligned}&~~a= 0,~~~ b= 0,~~ k_1= -\sqrt{\frac{r}{2}},~~k_2=\sqrt{\frac{r}{2}},\\&R_1= \sqrt{2-R_2^{2}},~~ a_{12}=0,~~ r= r,~~ R_2= R_2. \end{aligned} \end{aligned}$$
    (12)
  2. Set-2:
    $$\begin{aligned} \begin{aligned}&~~a= 0,~~~ b= 0,~~ k_1= \sqrt{\frac{r}{2}},~~k_2= -\sqrt{\frac{r}{2}},\\&R_1= \sqrt{\frac{1- 2 R_2^{2}}{2}},~~ a_{12}=1,~~ r= r,~~ R_2= R_2. \end{aligned} \end{aligned}$$
    (13)

    Plugging above equations with Eq. (11) into Eq. (7), different double solitons solutions can be given.

  • Case 1: \(a_{12}= 0\).

    $$\begin{aligned} \begin{aligned} ~f&= 1+ e^{- \sqrt{\frac{r}{2}} x+\frac{3}{2} r t+ c_1}+ e^{\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_2},\\ v&=\frac{R_2 \sqrt{\frac{r}{2}} (e^{\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_2}- e^{-\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_1})}{1+ e^{- \sqrt{\frac{r}{2}} x+\frac{3}{2} r t+ c_1}+ e^{\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_2}},\\&u=\frac{\sqrt{\frac{r (2- R_2^{2})}{2}} (e^{\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_2}- e^{-\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_1})}{1+ e^{- \sqrt{\frac{r}{2}} x+\frac{3}{2} r t+ c_1}+ e^{\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_2}},\\ \chi&= \frac{(\sqrt{2- R_2^{2}} +R_2 i) \sqrt{\frac{r}{2}} (e^{\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_2}- e^{-\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_1})}{1+ e^{- \sqrt{\frac{r}{2}} x+\frac{3}{2} r t+ c_1}+ e^{\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_2}}, \end{aligned} \end{aligned}$$
    (14)

    where \(R_2, r, c_1\) and \(c_2\) are arbitrary constants.

  • Case 2: \(a_{12} \ne 0\).

    $$\begin{aligned} \begin{aligned} f&= 1+ e^{\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_1}+ e^{-\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_2}+ e^{3 r t+ c_1+ c_2},\\&v=\frac{R_2 \sqrt{\frac{r}{2}} (e^{\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_1}- e^{-\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_2})}{1+ e^{\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_1}+ e^{-\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_2}+ e^{3 r t+ c_1+ c_2}},\\ u&=\frac{\frac{\sqrt{r (1- 2 R_2^{2})}}{2} (e^{\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_1}- e^{-\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_2})}{1+ e^{\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_1}+ e^{-\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_2}+ e^{3 r t+ c_1+ c_2}},\\ \chi&= \frac{(\sqrt{\frac{1- 2 R_2^{2}}{2}}+ R_2 i) \sqrt{\frac{r}{2}} (e^{\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_1}- e^{-\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_2})}{1+ e^{\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_1}+ e^{-\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_2}+ e^{3 r t+ c_1+ c_2}}. \end{aligned} \end{aligned}$$
    (15)

    where \(R_2, r, c_1\) and \(c_2\) are arbitrary constants.

    Fig. 2
    figure 2

    Double solitons solution \(\chi (x,t)\) with \(r=-\frac{1}{3},\ c_1=\frac{1}{2},\ c_2=\dfrac{1}{4}+i,\ R_2=2.\ ({\textbf {a}}) \ 3 \text{ D-plot }. ({\textbf {b}}) \ 2 \text{ D-plot }.\ ( {\textbf {c}}) \ 2 \text{ D-plot }.\ ({\textbf {d}}) \ \text{ density } \text{ plot }\)

    Full size image

2.3 Three solitons solutions

    The auxiliary function f for the three solitons solutions is given in the following form

$$\begin{aligned} f&= 1+ e^{\theta _1}+ e^{\theta _2}+ e^{\theta _3}+ a_{12} e^{\theta _1+ \theta _2}\nonumber \\&+ a_{13} e^{\theta _1+ \theta _3}+ a_{23} e^{\theta _2+ \theta _3}&+ b_{123} e^{\theta _1+ \theta _2+ \theta _3}, \end{aligned}$$
(16)

where \(\theta _1= k_1 x+ (k_1^{2}+ r) t+ c_1, \theta _2= k_2 x+ (k_2^{2}+ r) t+ c_2, \theta _3= k_3 x+ (k_3^{2}+ r) t+ c_3\) and \(k_1, k_2, k_3, c_1, c_2, c_3\) are undetermined constants.

Inserting Eq. (16) with Eq. (7) into Eq. (3) and Eq. (4), combining similar terms and making their coefficients to zero, we can know

$$\begin{aligned} \begin{aligned} a&= 0, b= 0, k_1= -\sqrt{\frac{r}{2}}, k_2= \sqrt{\frac{r}{2}}, k_3= \sqrt{\frac{r}{2}},\\&a_{12}= 1, a_{23}= 1, a_{13}= 1, b_{123}= 1,~r= r, R_1= \frac{\sqrt{2- 9 R_2^{2}}}{3}. \end{aligned} \end{aligned}$$
(17)

Substituting Eq. (17) with Eq. (16) into Eq. (7), three solitons solutions can be obtained as follows

$$\begin{aligned} \begin{aligned}&f= 1+ e^{-\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_1}+ e^{\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t} W_1+ e^{3 r t} W_2\\&\quad + e^{2 \sqrt{\frac{r}{2}} x+ 3 r t+ A_{23}}+ e^{\sqrt{\frac{r}{2}} x+ \frac{9}{2} r t+ B_{123}},\\&v= \frac{R_2 \sqrt{\frac{r}{2}} (-e^{-\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_1}+ e^{\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t} W_1+ 2 e^{2 \sqrt{\frac{r}{2}} x+ 3 r t+ A_{23}}+ e^{\sqrt{\frac{r}{2}} x+ \frac{9}{2} r t+ B_{123}})}{1+ e^{-\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_1}+ e^{\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t} W_1+ e^{3 r t} W_2+ e^{2 \sqrt{\frac{r}{2}} x+ 3 r t+ A_{23}}+ e^{\sqrt{\frac{r}{2}} x+ \frac{9}{2} r t+ B_{123}}},\\&u= \frac{\frac{\sqrt{r (2- 9 R_2^{2})}}{3 \sqrt{2}} (-e^{-\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_1}+ e^{\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t} W_1+ 2 e^{2 \sqrt{\frac{r}{2}} x+ 3 r t+ A_{23}}+ e^{\sqrt{\frac{r}{2}} x+ \frac{9}{2} r t+ B_{123}})}{1+ e^{-\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_1}+ e^{\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t} W_1+ e^{3 r t} W_2+ e^{2 \sqrt{\frac{r}{2}} x+ 3 r t+ A_{23}}+ e^{\sqrt{\frac{r}{2}} x+ \frac{9}{2} r t+ B_{123}}},\\&\chi = \frac{(\frac{\sqrt{r (2- 9 R_2^{2})}}{3 \sqrt{2}}+ R_2 i) (-e^{-\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_1}+ e^{\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t} W_1+ 2 e^{2 \sqrt{\frac{r}{2}} x+ 3 r t+ A_{23}}+ e^{\sqrt{\frac{r}{2}} x+ \frac{9}{2} r t+ B_{123}})}{1+ e^{-\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t+ c_1}+ e^{\sqrt{\frac{r}{2}} x+ \frac{3}{2} r t} W_1+ e^{3 r t} W_2+ e^{2 \sqrt{\frac{r}{2}} x+ 3 r t+ A_{23}}+ e^{\sqrt{\frac{r}{2}} x+ \frac{9}{2} r t+ B_{123}}}, \end{aligned} \end{aligned}$$
(18)

where \(W_1= e^{c_2}+ e^{c_3}, W_2= e^{A_{12}}+ e^{A_{13}}, A_{12}= c_1+c_2, A_{13}= c_1+ c_3, A_{23}= c_2+ c_3, B_{123}= c_1+ c_2+ c_3\) and \( R_2, r, c_1, c_2, c_3\) are arbitrary constants.

Fig. 3
figure 3

Three solitons solution \(\chi (x,t)\) with \(r=-\frac{1}{3},\ c_1=\frac{1}{4}+i,\ c_2=2, \ c_3=\frac{1}{2}, R_2=\frac{1}{4}.\ ({\textbf {a}}) 3 \text{ D-plot }.\ ({\textbf {b}}) \ 2 \text{ D-plot }.\ ({\textbf {c}}) \ 2 \text{ D-plot }.\ ({\textbf {d}}) \ \text{ density } \text{ plot }\)

Full size image

3 Lump solutions

    To gain the lump solutions of the (1+1) dimensional CCGLE, we use the following transformations

$$ u = (In{\text{ }}f)_{x} ,v = (In{\text{ }}g)_{x} , $$
(19)

where f, g as the auxiliary functions will be decided later.

Equation(19) transforms Eq. (3) and Eq. (4) into the following bilinear forms

$$\begin{aligned} \begin{aligned}&f^{2} g^{3} (f_{xt}- f_{xxx})+ f g^{3} (- f_x f_t+ 3 f_x f_{xx}\\&\quad - 2 g^{3} f_x^{3}+ a f^{3} g^{2} g_{xxx}- 3 a f^{3} g g_x g_{xx}+ 2 a f^{3} g_x^{3}\\&- r f^{2} g^{3} f_x+g^{3} f_x^{3}+ f^{2} g g_x^{2} f_x- b f g^{2} f_x^{2} g_x- b f^{3} g_x^{3}=0. \end{aligned} \end{aligned}$$
(20)
$$\begin{aligned} \begin{aligned}&g^{2} f^{3} (g_{xt}- g_{xxx})+ g f^{3} (- g_x g_t+ 3 g_x g_{xx}\\&\quad - 2 f^{3} g_x^{3}- a g^{3} f^{2} f_{xxx}+ 3 a g^{3} f f_x f_{xx}+ 2 a g^{3} f_x^{3}\\&- r g^{2} f^{3} g_x+ f^{3} g_x^{3}+ g^{2} f f_x^{2} g_x+ b g f^{2} g_x^{2} f_x+ b g^{3} f_x^{3}. \end{aligned} \end{aligned}$$
(21)

For lump solutions, we assume f and g have the following bilinear forms

$$\begin{aligned} f= \xi _1^{2}+ \xi _2^{2}+ \alpha , \, g= \xi _1^{2}+ \xi _2^{2}+ \beta , \end{aligned}$$
(22)

where \(\xi = p_1 x+ l_1 t, \xi _2= p_2 x+ l_2 t\) and \(p_1, p_2, l_1, l_2, \alpha , \beta \) are undecided constants.

Inserting Eq. (22) into Eq. (20) and Eq. (21) and solving corresponding equations, we can attain

$$\begin{aligned} p_1= p_1,~~ l_1= l_1,~~ \alpha = \alpha ,~~ \beta =\beta ,~~ p_2= -p_1 i,~~l_2= l_1 i. \end{aligned}$$
(23)

Interposing Eq. (23) into Eq. (22) and Eq. (19), the form of lump solution can be given

$$\begin{aligned} \begin{aligned} f&= 4 p_1 l_1 x t+ \alpha ,\,g= 4 p_1 l_1 x t+ \beta ,\\ u&= \frac{4 p_1 l_1 t}{4 p_1 l_1 x t+ \alpha },\,v= \frac{4 p_1 l_1 t}{4 p_1 l_1 x t+ \beta },\\ \chi&=\frac{4 p_1 l_1 t}{4 p_1 l_1 x t+ \alpha }+ i \frac{4 p_1 l_1 t}{4 p_1 l_1 x t+ \beta }, \end{aligned} \end{aligned}$$
(24)

where \(p_1, l_1, \alpha , \beta \) are arbitrary constants.

Fig. 4
figure 4

Lump solution \(\chi (x,t)\) with \(\alpha =1-0.4 i,\ l_1=0.2+0.1 i,\ p_1=1-0.5 i,\ \beta =-1.5+ 0.3 i.\ ({\textbf {a}}) \ 3 \text{ D-plot }.\ ({\textbf {b}}) \ 2 \text{ D-plot }.\ ({\textbf {c}}) \ 2 \text{ D-plot }.\ ({\textbf {d}}) \ \text{ density } \text{ plot }\)

Full size image

4 Lump-one stripe soliton interaction solutions

    The auxiliary functions f and g for the lump-one stripe soliton interaction solutions can be given as

$$\begin{aligned} f= \xi _3^{2}+ \xi _4^{2}+ e^{\xi _5} +\delta , \,g= \xi _3^{2}+ \xi _4^{2}+ e^{\xi _5} +\epsilon , \end{aligned}$$
(25)

where \(\xi _3= p_3 x+ l_3 t, \xi _4= p_4 x+ l_4 t, \xi _5= p_5 x+ l_5 t\) and \(p_3, p_4, p_5, l_3, l_4, l_5, \delta , \epsilon \) are undecided constants.

Plugging Eq. (25) into Eq. (20) and Eq. (21), the values of undetermined constants can be gotten.

  1. Set-1:
    $$\begin{aligned} \begin{aligned} a&= 1, b= \frac{1}{2}, l_3=i, l_4= 1, r=r,\\&\delta = 0, \epsilon = 0, p_3= p_3, p_5= \sqrt{r}, l_5= r,p_4= p_3 i. \end{aligned} \end{aligned}$$
    (26)
  2. Set-2:
    $$\begin{aligned} \begin{aligned} ~a&= 1, b= 1, r=0, p_5= 0,\delta = 0, \epsilon = 0,\\&l_3= l_3, p_3= p_3,p_4= p_3 i,l_4=- l_3 i,l_5= l_5. \end{aligned} \end{aligned}$$
    (27)

    Inserting these results into Eq. (25) and Eq. (19), we can get following different lump-one stripe soliton interaction solutions of the (1+1) dimensional CCGLE.

  • Case 1: \(r \ne 0, p_5 \ne 0.\)

    $$\begin{aligned} \begin{aligned} f&= 4 p_3 i x t+ e^{\sqrt{r} x+ r t},g= 4 p_3 i x t+ e^{\sqrt{r} x+ r t},\\ u&= \frac{4 p_3 i t+ \sqrt{r} e^{\sqrt{r} x+r t}}{4 p_3 i x t+ e^{\sqrt{r} x+ r t}},v= \frac{4 p_3 i t+ \sqrt{r} e^{\sqrt{r} x+r t}}{4 p_3 i x t+ e^{\sqrt{r} x+ r t}},\\ \chi&= \frac{(1+ i) (4 p_3 i t+ \sqrt{r} e^{\sqrt{r} x+r t})}{4 p_3 i x t+ e^{\sqrt{r} x+ r t}}, \end{aligned} \end{aligned}$$
    (28)

    where \(p_3, r\) are arbitrary constants.

  • Case 2: \(r= 0, p_5= 0.\)

    $$\begin{aligned} \begin{aligned} f&= 4 p_3 l_3 x t+ e^{l_5 t},g= 4 p_3 l_3 x t+ e^{l_5 t},\\ u&= \frac{4 p_3 l_3 t}{4 p_3 l_3 x t+ e^{l_5 t}},v= \frac{4 p_3 l_3 t}{4 p_3 l_3 x t+ e^{l_5 t}},\\ \chi{} & {} = \frac{(1+ i) 4 p_3 l_3 t}{4 p_3 l_3 x t+ e^{l_5 t}}, \end{aligned} \end{aligned}$$
    (29)

    where \(p_3, l_3, l_5\) are arbitrary constants.

    Fig. 5
    figure 5

    Lump-one stripe soliton interaction solution \(\chi (x,t)\) with \(p_3=1,\ r=-4.\ ({\textbf {a}}) \ 3 \text{ D-plot }. ({\textbf {b}}) \ 2 \text{ D-plot }.\ ({\textbf {c}}) \ 2 \text{ D-plot }.\ ({\textbf {d}}) \ \text{ density } \text{ plot }\)

    Full size image

5 Rogue wave solutions

    To gain rogue wave solutions, the bilinear forms of auxiliary functions f and g can be assumed as follows

$$\begin{aligned} f= \xi _6^{2}+ \xi _7^{2}+ \mathrm {cosh(\xi _8)}+ \sigma , g= \xi _6^{2}+ \xi _7^{2}+ \mathrm {cosh(\xi _8)}+ \zeta , \end{aligned}$$
(30)

where \(\xi _6= p_6 x+ l_6 t, \xi _7= p_7 x+ l_7 t, \xi _8= p_8 x+ l_8 t\) and \(p_6, p_7, p_8, l_6, l_7, l_8, \sigma , \zeta \) are undecided constants.

Inserting Eq. (30) into Eq. (20) and Eq. (21), we can understand

  1. Set-1:
    $$\begin{aligned} \begin{aligned} b&= a,p_7= p_6 i, l_7= -l_6 i, p_6= p_6, l_6= l_6,\\&\sigma = 0,~~\zeta = 0, r=r,l_8= 0, p_8= \frac{\sqrt{r}}{\sqrt{2 (1-a)}}. \end{aligned} \end{aligned}$$
    (31)
  2. Set-2:
    $$\begin{aligned} \begin{aligned} b&= 0,a= 0,l_8= 0, p_8= \sqrt{\frac{r}{2}}, r=r,\\&\sigma = 0,\zeta = 0,~~p_7= p_6 i, l_7= l_6 i, p_6= p_6,l_6= l_6, \end{aligned} \end{aligned}$$
    (32)

    where \(p_6, l_6, r\) are arbitrary constants.

    Plugging above results into Eq. (30) and Eq. (19), we can acquire different forms of rogue wave solutions of the (1+1) dimensional CCGLE.

  • Case 1: \(a \ne 0\).

    $$\begin{aligned} \begin{aligned} f&= 4 p_6 l_6 x t+ \text{ cosh } (\sqrt{\frac{r}{2 (1-a)} \textit{x})},~ g\\&\quad = 4 p_6 l_6 x t+ \text{ cosh }(\sqrt{\frac{r}{2 (1-a)} \textit{x})},\\ u&= \frac{4 p_6 l_6 t+ \sqrt{\frac{r}{2 (1-a)}} \text{ cosh } (\sqrt{\frac{r}{2 (1-a)}} \textit{x})}{4 p_6 l_6 x t+ \text{ cosh } (\sqrt{\frac{r}{2 (1-a)}} \textit{x})},~ v\\&\quad = \frac{4 p_6 l_6 t+ \sqrt{\frac{r}{2 (1-a)}} \text{ cosh } (\sqrt{\frac{r}{2 (1-a)}} \textit{x})}{4 p_6 l_6 x t+ \text{ cosh } (\sqrt{\frac{r}{2 (1-a)} \textit{x})}},\\ \chi&=\frac{(1+ i) (4 p_6 l_6 t+ \sqrt{\frac{r}{2 (1-a)}} \text{ cosh } (\sqrt{\frac{r}{2 (1-a)}} \textit{x}))}{4 p_6 l_6 x t+ \text{ cosh }(\sqrt{\frac{r}{2 (1-a)} \textit{x})}}, \end{aligned} \end{aligned}$$
    (33)

    where \(r, p_6, l_6\) are arbitrary constants.

  • Case 2: \(a= 0\).

    $$\begin{aligned} \begin{aligned} f&= 4 p_6 l_6 x t+ \text{ cosh }(\sqrt{\frac{r}{2}} \textit{x}), g= 4 p_6 l_6 x t+ \text{ cosh }(\sqrt{\frac{r}{2}} \textit{x}),\\ u&= \frac{4 p_6 l_6 t+ \sqrt{\frac{r}{2)}} \text{ cosh }(\sqrt{\frac{r}{2}} \textit{x})}{4 p_6 l_6 x t+ \text{ cosh }(\sqrt{\frac{r}{2}} \textit{x})},~ v= \frac{4 p_6 l_6 t+ \sqrt{\frac{r}{2}} \text{ cosh }(\sqrt{\frac{r}{2}} \textit{x})}{4 p_6 l_6 x t+ \text{ cosh }(\sqrt{\frac{r}{2}} \textit{x})},\\ \chi&=\frac{(1+ i) (4 p_6 l_6 t+ \sqrt{\frac{r}{2}} \text{ cosh }(\sqrt{\frac{r}{2}} \textit{x}))}{4 p_6 l_6 x t+ \text{ cosh }(\sqrt{\frac{r}{2}} \textit{x})}, \end{aligned} \end{aligned}$$
    (34)

    where \(r, p_6, l_6\) are arbitrary constants.

    Fig. 6
    figure 6

    Rogue solution \(\chi (x,t)\) with \(a=\frac{1}{4},\ l_6=\frac{1}{2},\ p_6=1+i,\ r=-2.\ ({\textbf {a}}) \ 3 \text{ D-plot }.\ ({\textbf {b}}) \ 2 \text{ D-plot }. ({\textbf {c}}) \ 2 \text{ D-plot }.\ ({\textbf {d}}) \ \text{ density } \text{ plot }\)

    Full size image

6 Images analyses

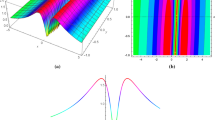
    By taking special values to r, \(R_2\) and \(c_1\), we can gain the single soliton of Eq. (1) as shown in Fig. 1. We can know that a list of single solitons that are symmetric about the plane \(x=0\) appear in the \(x-t\) plane and the solitons only have one peak, which can be seen in Fig. 1b. When the values of t are fixed, it is clear that the solitons with the same shapes and amplitudes appear periodically and the same situation doesn’t occur when the values of x are fixed, which indicates that the single solitons propagate along the x-axis. Besides, we can see that the single solitons here are optical solitons from the density plot.

Similarly, as Figs. 2 and 3 showing, the double and three solitons of Eq. (1) can be given by assigning special values to r, \(R_2\) and \(c_j\). We can observe that the double and three solitons also propagate periodically along the x-axis and the shapes and amplitudes keep unchange when the values of t are fixed. However, unlike the single solitons, the double solitons have two peaks and the three solitons have three peaks in the propagation process, which can be seen in Figs. 2a and 3a. In general, each line in Fig. 2b should contain two peaks and in Fig. 3b should contain three peaks. However, we can see that the lines only have two peaks in Fig. 3b and this is due to the arrangement of the three solitons in Fig. 3a. To prove this point, we find that each line in Fig. 3c also contains two peaks.

We can acquire the image of the lump solution as shown in Fig. 4 by giving \(\alpha \), \(\beta \), \(l_1\) and \(p_1\) special values. It seems that the image of the lump solution is simliar to the single soliton solution from Fig. 4b, but we also can notice that the image appears in chunk at the base of the soliton. When the values of x are fixed, it is obvious that the two lump solitons appear symmetrically on either side of the line \(t=0\) and the function values gradually approache 0 as t approache 0. Finally, we can know that there exists a lump region between the two lump solitons.

The image of the lump-one stripe soliton interaction solution can be given as shown in Fig. 5 by taking special values to \(p_3\) and r. As t gradually approache \(t=0\) from the negative half-axis of t, solitons that propagate periodically along the x-axis appear. While \(x=0\), soliton is periodic along the t-axis only if \(t>0\). This result also can be drawn from the density plot.

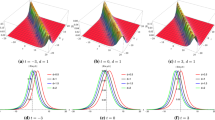
As Fig. 6 showing, the diagram of the rogue wave solution can be obtained by giving a, \(l_6\), \(p_6\) and r. It is obvious that there is a list of waves with the same amplitudes in the middle of the plane and the amplitudes of the waves increase for a short period of time, which is exactly the characteristic of the rogue wave. In addition, we also can find that at the amplitudes of the waves \(t=-0.2\) and 0.2 are significantly lower than those at \(t=-10\) and 10 from Fig. 6b, which also show that the amplitudes of the waves increase sharply as they approache the line \(t=0\).

7 Conclusion

    In this article, we gain solitons solutions of the (1+1) dimensional CCGLE via the transformations of \(u=(\text{ In }f)_x\) and \(v=(\text{ In }f)_x\). On this basis, by taking different forms of f, the single, double and three solitons solutions can be obtained. Besides, we also attain the lump and rogue wave solutions of the (1+1) dimensional CCGLE by applying the transformations \(u=(\text{ In }f)_x\) and \(v=(\text{ In }g)_x\) and taking different functions forms of f and g. Finally, through \(\text{3D }\), 2D, density images and proper interpretation, we can know the features and the contours differences of different solutions. This article is different from previous literatures that need to transform partial differential equations into ordinary differential equations. At the same time, this article also provides ideas and ways for those equations that can’t be completely reduced to bilinear forms but whose solitons solutions are desired.