1 Introduction

The \((1+1)\) dimensional complex Ginzburg–Landau equation (CGLE) describes the evolution of a complex-valued field \(u=u(x,t)\) by

$$\begin{aligned} u_{t}+\alpha _{0}u_{x}=\gamma u+(\alpha _{1}+\iota \alpha _{2})u_{xx}-(\beta _{1}+\iota \beta _{2})|u|^{2}u. \end{aligned}$$

It has a long history in physics as a generic amplitude equation near the onset of instabilities that lead to chaotic dynamics in fluid mechanical systems as well as in the theory of phase transitions and superconductivity. In this role these types of equations had remarkable success in describing evolution phenomena in a broad range of physical systems, from fluids to optics. More recently, CGLE has been proposed and studied as a model for turbulent, dynamics in nonlinear partial differential equations. It is a particularly interesting model in this respect because it is a dissipative version of the nonlinear Schrodinger equation, a Hamiltonian equation which can possess solutions that form localized singularities in finite time. The fact that the CGLE reduces to a relaxational equation in one limit and to a Hamiltonian equation in another limit makes the equation very interesting from a theoretical point of view.

The CGLE is one of the universal models used in describing dissipative systems. Examples of its application include pulse generation by passively mode-locked soliton lasers (Ippen 1994), signal transmission in all-optical communication lines (Bakonyi et al. 2002), traveling waves in binary fluid mixtures (Kolodner 1991), as well as pattern formation in many other physical systems (Cross and Hohenberg 1993). Depending on the system parameters, the CGLE has different types of solutions, including solitons, fronts (Akhmediev and Ankiewicz 1997), and pulsating solitons (Sakaguchi and Malomed 2001).

Over the last few years, the soliton solutions of picosecond of the CGLE and their potential applications in optical communication have been the subject of intense investigation. With the rapid development of nonlinear sciences based on computer algebraic system, many effective methods have been presented to solve nonlinear partial differential equations (NPDEs) such as, first integral method (Darvishi et al. 2016), the Exp-function method (Gurefe and Misirli 2011), Bernouli’s approach (Mirzazadeh et al. 2015), sech–tanh method (Triki and Wazwaz 2009), tanh method (Wazwaz 2006), sine–cosine method (Akram and Batool 2017; Wazwaz 2004), the \((\frac{G'}{G})\)-expansion method (Akram and Batool 2017; Zhang 2009), and so on. Feng (2002) first proposed the first integral method in solving Burgers–KdV equation which is based on the ring theory of commutative algebra. The basic idea of this method is to construct a first integral with polynomial coefficients of an explicit form to an equivalent autonomous planar system using the division theorem. The \((\frac{G'}{G})\)-expansion method is developed by Wang et al. (2008) and successfully used by many authors for finding exact solutions of partial differential equations in mathematical physics.

The current paper suggests the first integral method and \((\frac{G'}{G})\)-expansion method to find the exact solutions of nonlinear complex Ginzburg Landau equation. The format of this paper is as follows. In the next section description of algorithms for solving nonlinear partial differential equations by utilizing the first integral method and \((\frac{G'}{G})\)-expansion method have been given. In Sect. 3, the solutions of complex Ginzburg Landau equation has been obtained using these method. The last section concludes the main findings.

2 Algorithms for the methods

Consider nonlinear partial differential equation of the form, as

$$\begin{aligned} P(u, u_{x}, u_{t}, u_{xx}, u_{xt},\ldots )=0, \end{aligned}$$
(1)

where \(u=u(x,t)\) is the solution of nonlinear partial differential equation (1).

Seek the wave variable, to convert partial differential equation Eq. (1) into ordinary differential equation, as

$$\begin{aligned} u(x,t)=u(\xi ), \quad \xi =kx+ct, \end{aligned}$$
(2)

where k and c are arbitrary constants such that the nonlinear partial differential Eq. (1) can be turned into an ordinary differential equation, as

$$\begin{aligned} Q(u,-cu{'}, ku{'}, c^{2}u{''}, k^{2}u{''}, -kcu{''},\ldots )=0, \end{aligned}$$
(3)

where prime denotes the derivatives with respect to \(\xi\).

2.1 The first integral method

Step 1 Suppose the solution of Eq. (3) can be written, as

$$\begin{aligned} u(x,t) = f(\xi ). \end{aligned}$$
(4)

Introducing a new independent variable, as

$$\begin{aligned} X(\xi )= & {} f(\xi ), \nonumber \\ Y(\xi )= & {} \frac{\partial f(\xi )}{\partial \xi }. \end{aligned}$$
(5)

Step 2 Under the conditions of Step 1, Eq. (3) can be converted to a system of nonlinear ordinary differential equations, as

$$\begin{aligned}&X{'}(\xi )= Y(\xi ),\nonumber \\&Y{'}=F(X(\xi ),Y(\xi )). \end{aligned}$$
(6)

By the qualitative theory of ordinary differential equations (Ding and Li 1996), if the integrals to Eq. (6) can be found under the same conditions, then the general solutions to Eq. (6) can be constructed directly. By applying the Division theorem for two variables in the complex domain \({\mathbb {C}}\) which is based on the Hilbert-Nullstellensatz theorem (Bourbaki 1972), one first integral to Eq. (6) can be obtained which reduces Eq. (3) to a first order integrable ordinary differential equation. An exact solution to Eq. (1) is then obtained by solving this equation directly.

Theorem 1

(Division Theorem) Suppose that P(w, z) and Q(w, z) are polynomials in \({\mathbb {C}}[w,z]\), and P(w, z) is irreducible in \({\mathbb {C}}[w,z]\). If Q(w, z) vanishes at all zero points of P(w, z), then there exists a polynomial G(w,z) in \({\mathbb {C}}[w,z]\) such that \(Q(w,z)=P(w,z)G(w,z)\).

Theorem 2

(Hilbert-Nullstellensatz Theorem (Bourbaki 1972)) Let K be a field and L be an algebraic closure of K. Then:

  1. (i)

    Every ideal \(\gamma\) of \(K[X_{1},X_{2},\ldots ,X_{n}]\) not containing 1 admits at least one zero in \(L^{n}\).

  2. (ii)

    Let \(x=x(x_{1},x_{2},\ldots ,x_{n})\) and \(y=y(y_{1},y_{2},\ldots ,y_{n})\) be two elements of \(L^{n}\). For the set of polynomials of \(K[X_{1},X_{2},\ldots ,X_{n}]\) zero at x to be identical with the set of polynomials of \(K[X_{1},X_{2},\ldots ,X_{n}]\) zero at y, it is necessary and sufficient that there exists a K-automorphism S of L such that \(y_{i}=S(x_{i})\) for \(1\le i\le n\).

  3. (iii)

    For an ideal \(\alpha\) of \(K[X_{1},X_{2},\ldots ,X_{n}]\) be maximal, it is necessary and sufficient that there exists an x in \(L^{n}\) such that \(\alpha\) is the set of polynomials of \(K[X_{1},X_{2},\ldots ,X_{n}]\) zero at x .

  4. (iv)

    For a polynomial Q of \(K[X_{1},X_{2},\ldots ,X_{n}]\) to be zero on the set of zeros in \(L^{n}\) of an ideal \(\gamma\) of \(K[X_{1},X_{2},\ldots ,X_{n}]\) it is necessary and sufficient that there exists an integer \(m>0\) such that \(Q^{m}\in \gamma\).

2.2 The \({(\frac{G'}{G})}\)-expansion method

Step 1 According to the \((\frac{G'}{G})\)-expansion method (Wang et al. 2008), the solution of Eq. (3) can be expressed by a polynomial in \((\frac{G'}{G})\), as

$$\begin{aligned} u(\xi )=\sum ^{i=m}_{i=1}\alpha _{i} \left( \frac{G'}{G}\right) ^{i}+ \alpha _{0}, \quad \alpha _{m}\ne 0, \end{aligned}$$
(7)

where \(\alpha _{0}\) and \(\alpha _{i}\) for \(i=1,2,\ldots ,m\) are constants to be determined later, \(G=G(\xi )\) satisfies a second order linear ordinary differential equation,

$$\begin{aligned} \frac{d^2 G(\xi )}{d\xi ^2}+\lambda \frac{d G(\xi )}{d\xi }+\mu G(\xi )=0, \end{aligned}$$
(8)

where \(\lambda\) and \(\mu\) are real constants.

Step 2 The positive integer m can be determined by balancing the highest derivative term with the nonlinear term in Eq. (3). Substituting Eq. (7) together with Eq. (8) in Eq. (3) yields an algebraic equation involving powers of \((\frac{G'}{G})\). Equating the coefficients of each power of \((\frac{G'}{G})\) to zero gives a system of algebraic equations for \(k, c, \lambda , \mu ,\) and \(\alpha _{i}\).

Step 3 Substituting \(\alpha _{i}, \lambda , \mu , k, c\) and general solution of Eq. (8) into Eq. (7). Depending on the sign of the discriminant \((\lambda ^{2}-4\mu )\), the solution of Eq. (1) can be obtained.

3 Exact solution by first integral method

In this section, the new exact solutions of (1+1)D complex Ginzburg–Landau equation

$$\begin{aligned} u_{t}+\alpha _{0}u_{x}=\gamma u+(\alpha _{1}+\iota \alpha _{2})u_{xx}-(\beta _{1}+\iota \beta _{2})|u|^{2}u, \end{aligned}$$
(9)

has been obtained.

The following transformation is introduced, as

$$\begin{aligned} u=v(\xi )e^{\iota \eta } ,\quad \eta =px+st, \quad \xi =kx+ct. \end{aligned}$$
(10)

where p, s and c are constants to be determined (Fig. 1).

Substituting the transformation (10) into Eq. (9), the real part and the imaginary part, respectively, can be separated, as

$$\begin{aligned} \left\{ \begin{array}{l} k^{2}\alpha _{1}v{''}-(c+k\alpha _{0}+2\alpha _{2}pk)v{'}+(\gamma -\alpha _{1}p^{2})v-\beta _{1}v^{3}=0, \\ k^2\alpha _{2}v{''}+2p\alpha _{1}kv{'}-(s+p\alpha _{0}+p^2\alpha _{2})v-\beta _{2}v^{3}=0. \end{array}\right. \end{aligned}$$
(11)

Under the constraint conditions:

$$\begin{aligned} r= & {} \frac{c+k\alpha _{0}+2pk\alpha _{2}}{\alpha _{1}k^{2}}=-\frac{2pk\alpha _{1}}{\alpha _{2}k^{2}},\nonumber \\ l= & {} \frac{\gamma -p^{2}\alpha _{1}}{\alpha _{1}k^{2}}=-\frac{s+p\alpha _{0}+p^{2}\alpha _{2}}{\alpha _{2}k^{2}},\nonumber \\ m= & {} \frac{\beta _{1}}{\alpha _{1}k^{2}}=\frac{\beta _{2}}{\alpha _{2}k^{2}}, \end{aligned}$$

Equation (11) can be transformed to the following nonlinear ordinary differential equation, as

$$\begin{aligned} v{''}-rv{'}+lv-mv^{3}=0. \end{aligned}$$
(12)

Let \(X(\xi )=v(\xi ), Y(\xi )=v{'}(\xi ),\) then Eq. (12) can be reformulated as a planar dynamic system

$$\begin{aligned} \left\{ \begin{array}{l} \frac{d X}{d \xi }=Y(\xi ),\\ \frac{d Y}{d \xi }=rY(\xi )-lX(\xi )+mX^{3}(\xi ). \end{array}\right. \end{aligned}$$
(13)

According to the first integral method, suppose that \(X(\xi )\) and \(Y(\xi )\) are nontrivial solutions of Eq. (13), and

$$\begin{aligned} Q(Y,X)=\sum _{i=0}^{m}a_{i}(X)Y^{i}, \end{aligned}$$

is irreducible polynomial in \({\mathbb {C}}[X,Y]\), such that

$$\begin{aligned} Q[Y(\xi ),X(\xi )]=\sum _{i=0}^{m}a_{i}(X(\xi ))Y^{i}(\xi )=0, \end{aligned}$$
(14)

where \(a_{i}(X)(i=0,1,2,\ldots ,m)\), are polynomials of X and \(a_{m}(X)\ne 0\). Equation (14) is called the first integral to Eq. (13). Applying the division theorem, there exists a polynomial \(g(X)+h(X)Y\) in the complex domain \({\mathbb {C}}[X,Y]\), such that

$$\begin{aligned} \frac{dQ}{d\xi }=\frac{\partial Q}{\partial X}\frac{d X}{d \xi }+\frac{\partial Q}{\partial Y}\frac{d Y}{d \xi }=(g(X)+h(X)Y)\sum _{i=0}^{m}a_{i}(X)Y^{i}. \end{aligned}$$
(15)

Suppose that \(m=1\) in Eq. (14), and then by equating the coefficients of \(Y^{i}\), \((i = 0, 1, 2)\) on both sides of Eq. (15), following equations can be obtained, as

$$\begin{aligned}&Y^{0}: a_{1}(X)(lX+mX^{3}) = a_{0}(X)g(X), \end{aligned}$$
(16)
$$\begin{aligned}&Y^{1}:{\dot{a}}_{0}(X)+ra_{1}(X) = a_{0}(X)h(X)+a_{1}(X)g(X) , \end{aligned}$$
(17)
$$\begin{aligned}&Y^{2}: {\dot{a}}_{1}(X) = a_{1}(X)h(X). \end{aligned}$$
(18)

Since \(a_{i}(X), (i=0, 1)\) are polynomials in X, so from Eq. (18) it is conclude that \(a_{1}(X)\) is a constant and \(h(X)=0\). For simplicity, take \(a_{1}(X)=1\). Then balancing the degrees of g(X) and \(a_{0}(X)\) in Eq. (17), it is concluded that deg(g(X)) = 1 only. Assume that

$$\begin{aligned} g(X)= & {} A_{1}X+B_{0} ,\\ a_{0}(X)= & {} A_{1}\frac{X^2}{2}+(B_{0}-r)X+A_{0}, \quad (A_{1}\ne 0) \end{aligned}$$

where \(A_{1}, B_{0}\) and \(A_{0}\) are all constants to be determined.

Substituting \(a_{0}(X)\) and g(X) in Eq. (16) and equating the coefficients of \(X^{i}, (i = 0, 1, 2, 3)\) to zero, the following system of nonlinear algebraic equations are obtained, as

$$\begin{aligned}&X^{0}:m-\frac{A_{1}^2}{2} =0 \end{aligned}$$
(19)
$$\begin{aligned}&X^{1}:\frac{3}{2}A_{1}B_{0}-rA_{1}=0 \end{aligned}$$
(20)
$$\begin{aligned}&X^{2}:B_{0}^{2}-l-rB_{0}+A_{0}A_{1}=0 \end{aligned}$$
(21)
$$\begin{aligned}&X^{3}:A_{0}B_{0}= 0 \end{aligned}$$
(22)

Using Eq. (12) and solving the system of Eqs. (19–22), simultaneously the following nontrivial solutions can be obtained, as

$$\begin{aligned} A_{1}=\pm \sqrt{2m}, \quad A_{0}=0, \quad B_{0}=\frac{2r}{m}. \end{aligned}$$
(23)

Taking the solution (23) into account, Eq. (14) can be written, as

$$\begin{aligned} Y(\xi )=\mp \frac{\sqrt{2m}}{2}X^{2}+\frac{r}{3}X. \end{aligned}$$
(24)

Combining Eq. (24) with the system given by Eq. (14), following expression can be obtained, as

$$\begin{aligned} X(\xi )=\frac{2r}{2C_{1}re^{\frac{-r\xi }{3}}\pm 3\sqrt{2m}}, \end{aligned}$$
(25)

where \(C_{1}\) is arbitrary constant. Combining Eq. (25) with Eq. (13), the exact solution to Eq. (9) can be written, as

$$\begin{aligned} u_{1}(x,t)=\frac{2re^{\iota \eta }}{2C_{1}re^{\frac{-r\xi }{3}}+3\sqrt{2m}} \end{aligned}$$
(26)

and

$$\begin{aligned} u_{2}(x,t)=\frac{2re^{\iota \eta }}{2C_{1}re^{\frac{-r\xi }{3}}-3\sqrt{2m}} \end{aligned}$$
(27)

where \(\eta =px+st\) and \(\xi =kx+ct\) (Fig. 2).

Fig. 1
figure 1

3D graphics of real part of \(u_{1}\) with \(t>0\)

Full size image
Fig. 2
figure 2

3D graphics of real part of \(u_{2}\) with \(t>0\)

Full size image

3.1 Exact solution by \({(\frac{G'}{G})}\)-expansion method

Balancing the order of \(v''\) and \(v^{3}\) in Eq. (12), one can found the value of \(m=1\), therefore the solution takes the form, as

$$\begin{aligned} v(\xi )=a_{0}+a_{1}\left( \frac{G'}{G}\right) , \quad \, a_{1}\ne 0. \end{aligned}$$
(28)

The following algebraic equations are obtained from Eqs. (8), (12) and (28), as

$$\begin{aligned}&\left( \frac{G'}{G}\right) ^{3}:2a_{1}-ma^{3}_{1}=0,\\&\left( \frac{G'}{G}\right) ^{2}: 3\lambda a_{1}+ra_{1}-3ma_{0}a_{1}^{2}=0,\\&\left( \frac{G'}{G}\right) ^{1}: 2a_{1}\mu +a_{1}\lambda ^{2}+ra_{1}\lambda +la_{1}-3ma_{0}^{2}a_{1}=0,\\&\left( \frac{G'}{G}\right) ^{0}: a_{1}\lambda \mu +ra_{1}\mu +la_{0}-ma_{0}^{3}=0. \end{aligned}$$

Solving these algebraic equations with the aid of Maple the following solution can be obtained, as

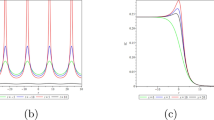
$$\begin{aligned} a_{0}=\frac{\lambda a_{1}}{2}+\frac{ra_{1}}{6}, \quad a_{1}=a_{1}, \quad \mu =\frac{\lambda ^{2}}{4}-\frac{r^{2}}{36}. \end{aligned}$$

Using Eq. (28) and the solution of Eq. (8), three types of traveling wave solutions of Eq. (1) can be calculated (Fig. 3).

If \(\lambda ^2-4\mu >0\), hyperbolic function solution is obtained, as

$$\begin{aligned} \begin{aligned} u_{3}(\xi )= & {} \frac{e^{\iota \eta }ra_{1}}{6}\left[ 1+\left\{ \frac{A_{1} \sinh \left( \frac{r\xi }{6}\right) +A_{2}\cosh \left( \frac{r\xi }{6}\right) }{A_{1}\cosh \left( \frac{r\xi }{6}\right) +A_{2}\sinh \left( \frac{r\xi }{6}\right) } \right\} \right] . \end{aligned} \end{aligned}$$
(29)

If \(\lambda ^2-4\mu <0\), the trigonometric function solution is obtained, as

$$\begin{aligned} \begin{aligned} u_{4}(\xi )=\frac{e^{\iota \eta }ra_{1}}{6}\left[ 1+\iota \left\{ \frac{-A_{1}\sin \left( \frac{r\iota \xi }{6}\right) +A_{2}\cos \left( \frac{r\iota \xi }{6}\right) }{A_{1} \cos \left( \frac{r\iota \xi }{6}\right) +A_{2} \sin \left( \frac{r\iota \xi }{6}\right) } \right\} \right] . \end{aligned} \end{aligned}$$
(30)

If \(\lambda ^2-4\mu =0\), rational function solution is obtained, as

$$\begin{aligned} u_{5}(\xi )=\frac{a_{1}e^{\iota \eta }C_{2}}{C_{1}+C_{2}\xi }. \end{aligned}$$
(31)
Fig. 3
figure 3

3D graphics of real part of \(u_{3}\) with \(t>0\)

Full size image

4 Conclusion

The present analysis indicates that the first integral method and \((\frac{G'}{G})\)-expansion method are effective and efficient for solving nonlinear complex Ginzburg Landau equations. The obtained solutions may be worthwhile for explanation of some physical phenomena accurately. Different from other methods, the first integral method and \((\frac{G'}{G})\)-expansion method have many advantages, which is the avoidance of a great deal of complicated and tedious calculations resulting in more exact and explicit traveling wave solutions with high accuracy. Apart from the elemental application, the exact solutions of nonlinear partial differential equations aid the numerical solvers to assess the correctness of their results and assist them in stability analysis. The solutions presented here are found for the first time and they might serve as seeding solutions for a wider class of localized structures which, no doubt exist in these systems.