1 Introduction

Stochastic resonance (SR) is a nonlinear phenomenon occurred in a noisy system, which means that, owning to the cooperation between the system and the noise, the system output performance (signal amplitude, signal variance, signal-to-noise ratio, etc.) can be improved with the presence of certain amount of noise [1,2,3,4,5,6,7,8,9,10,11]. The SR in a broad sense indicates the non-monotonous dependence of the system output on the parameters of the noise and on those of the system. Many previous works of SR are concentrated on nonlinear noisy system driven by Gaussian white noise and some non-Gaussian colored noise. However, in sensory system, particularly one kind of crayfish as well as results for rat skin, the noise source in neural system could be non-Gaussian stochastic processes: bounded noise [12,13,14,15,16]. In general, the bounded noise can be expressed as a harmonic function with a constant average frequency and a random phase varying as a unit Wiener process. Owning to possessing finite power, the bounded noise can simulate environmental noise more realistic and has wide application [17,18,19]. For example, in practical engineering application, telegraph noise, i.e., dichotomous Markov noise is such a kind of bounded noises [16]. Thus, the investigation of SR phenomenon with bounded noise is of great significance.

Thanks to the advantages of time memory and long-range spatial correlation, fractional calculus can describe physical processes and biochemical reaction processes with memory and path dependence. It has been shown that many physical and biochemical processes, as well as materials and media have memory. Fractional calculus is widely used in the study of anomalous diffusion, chaos and viscoelastic materials [20,21,22,23,24,25]. The containment control of linear discrete-time fractional-order multi-agent systems with time-delays [20], the dynamical behavior of a fractional-order mutualism parasitism food web module [21], as well as fractional Brownian motions ruled by nonlinear equations [22] has been investigated. The dynamic behavior for a fractional-order delay tumor-immune system [23], the nonlinear dynamic [24] and stability analysis [25] for a fractional-order rotor-bearing-seal system has also been studied.

In addition, the SR for fractional linear oscillators has been paid much attention. SR for a fractional linear oscillator with trichotomous noise [26], and stochastic multiresonance for a fractional linear oscillator with random damping subject to signal-modulated noise [27] and with fluctuate damping and time-delayed kernel subject to quadratic noise [28] has been researched. The SR for an underdamped fractional oscillator with fluctuating frequency subject to trichotomous noise [27] and signal-modulated noise [29], as well as the SR for a linear oscillator with random frequency and two kinds of fractional derivatives driven by dichotomous noise [30] has also been investigated. The SR for a fractional oscillator with random mass driven by trichotomous noise [31] and signal-modulated noise [32], as well as the SR for a two coupled fractional harmonic oscillator with fluctuating mass [33] has also been studied. Several quantifiers have been used to characterize SR in noisy dynamic systems, such as signal-to-noise ratio (SNR), the average output amplitude gain, or the spectral amplification (SPA), etc. SNR is often used in various nonlinear and linear noisy systems [1,2,3,4,5,6,7], while the average output gain is usually used in linear systems [26,27,28,29,30,31,32,33]. In this paper, we use the average output gain to describe the non-monotonous behavior for the system output signal.

As described above, many works have been done on the investigation of the SR phenomenon for a fractional oscillator with memory-damping [26,27,28,29,30,31,32,33], little attention has been paid on the non-monotonous resonance behavior for a fractional oscillator with two kinds of memory kernels. In the following section, we will introduce this kind of oscillator and analyze the SR phenomenon occurred in the oscillator.

2 The fractional linear oscillator with memory-inertia and memory-damping

There are large number of electric and magnetic phenomena where the fractional calculus can be used [34,35,36,37,38,39,40,41]. A fractional capacitor model has been proposed based on Curie's empirical law [35]. A fractional-order Chua’s system based on the concept of Chua’s oscillator with fractional derivatives has been considered [36]. A second-order filter [37] and an asymmetric-slope band-pass filter [38] with a fractional-order capacitor has been studied. Fractional inductor and fractional capacitor have been used in an LC tank circuit [39], used in a fractional-order multiple RLC circuit [40], as well as used in a fractional-order low-pass filter circuit [41]. The Caputo definition of a fractional derivative is usually used in electric circuit and communication system because the initial conditions for this definition take the same form as the more familiar integer-order differential equations [34,35,36,37,38,39,40,41]. The relationship between the voltage \(v_{c} (t)\) and the current \(i_{c} (t)\) for a fractional-order capacitor C can be given by [34, 35]

$$ v_{c} (t) = \frac{1}{C\Gamma (\alpha )}\int_{0}^{t} {\frac{i(\tau )}{{(t - \tau )^{1 - \alpha } }}} d\tau , $$
(1)

where \(\Gamma (.)\) is the Euler’s Gamma function, \(\alpha\) is the fractional exponent, \(0 \le \alpha \le 1\). Now we consider a serial RLC circuit consisting of a resistor R, a fractional capacitor C and an inductor L. Based on electric circuit theory, the voltage for the fractional capacitor satisfies the following equation

$$ LC\int_{0}^{t} {\frac{{\ddot{v}_{c} (u)du}}{{\Gamma (1 - \alpha )(t - u)^{\alpha } }}} + RC\int_{0}^{t} {\frac{{\dot{v}_{c} (u)du}}{{\Gamma (1 - \alpha )(t - u)^{\alpha } }}} + v_{c} (t) = v_{i} (t), $$
(2)

where \(v_{i} (t)\) is the input voltage supply of the RLC circuit, \(\ddot{v}_{c} (t) = d^{2} v_{c} (t)/dt^{2}\), \(\dot{v}_{c} (t) = dv_{c} (t)/dt\). One can see that system (2) denotes a fractional linear oscillator. From the point of view of the force on an object, the first part of the left side of Eq. (2) indicates an inertia force, and the second part a damping force. Thus, Eq. (2) denotes an oscillator with two kinds of memory kernel, i.e., one memory-inertia kernel and one memory-damping kernel. Let \(\beta = R/L\), \(\omega_{0}^{2} { = }1/\sqrt {LC}\), \(v_{i} (t) = f(t) = A\cos (\Omega_{A} t)\), \(x(t) = v_{c} (t)\), and considering the resistor fluctuation \(\xi (t)\) and the external environment noise, one can obtain the following equation

$$ \int_{0}^{t} {\frac{{\ddot{x}(u)du}}{{\Gamma (1 - \alpha )(t - u)^{\alpha } }}} + [\beta + \xi (t)]\int_{0}^{t} {\frac{{\dot{x}(u)du}}{{\Gamma (1 - \alpha )(t - u)^{\alpha } }}} + \omega_{0}^{2} x(t) = \omega_{0}^{2} A\cos (\Omega_{A} t) + \eta (t), $$
(3)

here \(\beta\) and \(\omega_{0}^{{}}\) are the damping coefficient and natural frequency of the oscillator, respectively. \(A\) and \(\Omega_{A}\) denote the amplitude and frequency of the input signal, respectively. \(\eta (t)\) is an external environment noise from the environment temperature, with zero mean and noise strength \({\text{Q}}\). \(\xi (t)\) is a dichotomous noise [16], i.e., a kind of bounded stochastic process [12,13,14,15], \(\xi (t) = \pm a\), with zero mean and correlation function

$$ \left\langle {\xi (t_{1} )\xi (t_{2} )} \right\rangle = a^{2} \exp ( - \lambda \left| {t_{1} - t_{2} } \right|) = D\exp ( - \lambda \left| {t_{1} - t_{2} } \right|), $$
(4)

where \(D\) and \(\lambda\) are the intensity and correlate rate of the dichotomous noise, respectively. The correlation noise intensity between multiplicative and additive noises is always assumed as a constant, yet in an actual physical system, noise and time varying signal may appear multiplicatively, so that the former is modulated by the later, i.e., the noise strength varies periodically with time. For example, at the output of an amplifier in optics or radio astronomy, periodically modulated noise should be used [42]. The SR in a double-well potential with periodically modulated noise has been investigated [42]. SR driven by time-modulated correlated white noise sources [43], and SR in bistable systems driven by correlated periodically modulated additive and multiplicative noises [44] has been analyzed. Moreover, Stochastic multiresonance in a single-mode laser with periodically modulated noise [45] has been studied. In this work, we assume that the correlation strength between \(\eta (t)\) and \(\xi (t)\) is a time-modulated one, which can be given by [43,44,45]

$$ \left\langle {\xi (t_{1} )\eta (t_{2} )} \right\rangle = {2}\sqrt {{\text{DQ}}} \rho (t)\delta (t_{1} - t_{2} ),\;\rho (t){ = }\rho_{B} \cos (\Omega_{B} t), $$
(5)

where \(\rho (t)\) denotes the strength of the time-modulated correlated noise, with amplitude \(\rho_{B}\) and frequency \(\Omega_{B}\), respectively. It is worth to mention that, to maintain the positivity of the perturbed damping coefficient, it must be \(\beta + \xi (t) > 0\). Since \(\xi (t)\) is a bounded noise [16], consequently it must be \(\beta - a > 0\). Since \(D = a^{2}\), this result in the constraint \(\beta > \sqrt D\). In the following contents of this paper, the parameters are appropriately selected to satisfy this condition. To find the system output amplitude, one can apply statistical average on both sides of Eq. (3), then one obtains

$$ \int_{0}^{t} {\frac{{\left\langle {\ddot{x}(u)} \right\rangle du}}{{\Gamma (1 - \alpha )(t - u)^{\alpha } }}} + \beta \int_{0}^{t} {\frac{{\left\langle {\dot{x}(u)} \right\rangle du}}{{\Gamma (1 - \alpha )(t - u)^{\alpha } }}} + e^{ - \lambda t} \int_{0}^{t} {\frac{{e^{\lambda u} \left\langle {\xi (u)\dot{x}(u)} \right\rangle du}}{{\Gamma (1 - \alpha )(t - u)^{\alpha } }}} + \omega_{0}^{2} \left\langle x \right\rangle = \omega_{0}^{2} A\cos (\Omega_{A} t) $$
(6)

Multiplying \(\xi (t)\) on both sides of Eq. (3), one get

$$ e^{ - \lambda t} \int_{0}^{t} {\frac{{e^{\lambda u} \left\langle {\xi (u)\ddot{x}(u)} \right\rangle du}}{{\Gamma (1 - \alpha )(t - u)^{\alpha } }}} + \beta e^{ - \lambda t} \int_{0}^{t} {\frac{{e^{\lambda u} \left\langle {\xi (u)\dot{x}(u)} \right\rangle du}}{{\Gamma (1 - \alpha )(t - u)^{\alpha } }}} + D\int_{0}^{t} {\frac{{\left\langle {\dot{x}(u)} \right\rangle du}}{{\Gamma (1 - \alpha )(t - u)^{\alpha } }}} + \omega_{0}^{2} \left\langle {\xi x} \right\rangle = 2\sqrt {DQ} \rho_{B} \cos (\Omega_{B} t) $$
(7)

Using the Shapiro–Loginov procedure [46], one can obtain the following equations

$$ \frac{d}{dt}\left\langle {\xi x} \right\rangle = \left\langle {\xi \dot{x}} \right\rangle { - }\lambda \left\langle {\xi x} \right\rangle , $$
(8)
$$ \left\langle {\xi \ddot{x}} \right\rangle = \left( {\frac{d}{dt} + \lambda } \right)^{2} \left\langle {\xi x} \right\rangle $$
(9)

Let \(\left\langle x \right\rangle = x_{1} ,\;\left\langle {\dot{x}} \right\rangle = x_{2} ,\;\left\langle {\ddot{x}} \right\rangle = x_{3} ,\;\left\langle {\xi x} \right\rangle = x_{4} ,\;\left\langle {\xi \dot{x}} \right\rangle = x_{5} ,\;\left\langle {\xi \ddot{x}} \right\rangle = x_{6}\), one can easily find that

$$ x_{2} = \dot{x}_{1} ,\;x_{3} = \dot{x}_{2} $$
(10)

Applying Laplace transformation (LT) on both sides of Eqs. (6)-(10), i.e., \(x_{i} \underrightarrow {LT}X_{i} ,i = 1,2,...,6\), one can obtain the following six equations

$$ X_{2} = sX_{1} ,\;X_{3} = sX_{2} $$
(11)
$$ X_{5} = (s + \lambda )X_{4} ,\;X_{6} = (s + \lambda )^{2} X_{4} , $$
(12)
$$ s^{\alpha - 1} X_{3} + \beta s^{\alpha - 1} X_{2} + (s + \lambda )^{\alpha - 1} X_{5} + \omega_{0}^{2} X_{1} = LT[\omega_{0}^{2} A\cos (\Omega_{A} t)], $$
(13)
$$ (s + \lambda )^{\alpha - 1} X_{6} + \beta (s + \lambda )^{\alpha - 1} X_{5} + Ds^{\alpha - 1} X_{2} + \omega_{0}^{2} X_{4} = LT[2\sqrt {DQ} \rho_{B} \cos (\Omega_{B} t)] $$
(14)

By solving Eqs. (11)-(14), one can get the expression for \(X_{1}\). Assuming the system average output has the form \(\left\langle x \right\rangle = h_{A} \cos (\Omega_{A} t) + h_{B} \cos (\Omega_{B} t)\), applying inverse Laplace transform, one can get, in the long-time limit \(t \to \infty\), the system output amplitude gain for input signal \(f(t)\) and that for time-modulated correlated signal \(\rho (t)\), respectively, i.e.,

$$ G_{A} = \frac{{h_{A} }}{A} = \omega_{0}^{2} \sqrt {\frac{{f_{2A}^{2} + f_{4A}^{2} }}{{[f_{1A} f_{2A} + f_{3A} f_{4A} - D(f_{5A} f_{6A} + f_{7A} f_{8A} )]^{2} + [f_{1A} f_{4A} + f_{2A} f_{3A} - D(f_{5A} f_{7A} + f_{6A} f_{8A} )]^{2} }}} $$
(14)
$$ G_{B} = \frac{{h_{B} }}{{\rho_{B} }} = 2\sqrt {DQ} \sqrt {\frac{{f_{6B}^{2} + f_{8B}^{2} }}{{[f_{1B} f_{2B} + f_{3B} f_{4B} - D(f_{5B} f_{6B} + f_{7B} f_{8B} )]^{2} + [f_{1B} f_{4B} + f_{2B} f_{3B} - D(f_{5B} f_{7B} + f_{6B} f_{8B} )]^{2} }}}, $$
(15)

where

$$ f_{1i} = \Omega_{i}^{\alpha + 1} \cos \left( {(\alpha + 1)\pi /2} \right) + \beta \Omega_{i}^{\alpha } \cos \left( {\alpha \pi /2} \right) + \omega_{0}^{2} ,\begin{array}{*{20}c} {} \\ \end{array} i = A,B, $$
(16)
$$ f_{2i} = (\Omega_{i}^{2} + \lambda^{2} )^{(\alpha + 1)/2} \cos \left( {(\alpha + 1)\arctan (\Omega_{i} /\lambda )} \right) + \beta (\Omega_{i}^{2} + \lambda^{2} )^{\alpha /2} \cos \left( {\alpha \arctan (\Omega_{i} /\lambda )} \right) + \omega_{0}^{2} ,\begin{array}{*{20}c} {} \\ \end{array} i = A,B $$
(17)
$$ f_{3i} = \Omega_{i}^{\alpha + 1} \sin \left( {(\alpha + 1)\pi /2} \right) + \beta \Omega_{i}^{\alpha } \sin \left( {\alpha \pi /2} \right),\begin{array}{*{20}c} {} \\ \end{array} i = A,B, $$
(18)
$$ f_{4i} = (\Omega_{i}^{2} + \lambda^{2} )^{(\alpha + 1)/2} \sin \left( {(\alpha + 1)\arctan (\Omega_{i} /\lambda )} \right) + \beta (\Omega_{i}^{2} + \lambda^{2} )^{\alpha /2} \sin \left( {\alpha \arctan (\Omega_{i} /\lambda )} \right),\begin{array}{*{20}c} {} \\ \end{array} i = A,B, $$
(19)
$$ f_{5i} = \Omega_{i}^{\alpha } \cos \left( {\alpha \pi /2} \right),\begin{array}{*{20}c} {} \\ \end{array} i = A,B, $$
(20)
$$ f_{6i} = (\Omega_{i}^{2} + \lambda^{2} )^{\alpha /2} \cos \left( {\alpha \arctan (\Omega_{i} /\lambda )} \right),\begin{array}{*{20}c} {} \\ \end{array} i = A,B, $$
(21)
$$ f_{7i} = \Omega_{i}^{\alpha } \sin \left( {\alpha \pi /2} \right),\begin{array}{*{20}c} {} \\ \end{array} i = A,B, $$
(22)
$$ f_{8i} = (\Omega_{i}^{2} + \lambda^{2} )^{\alpha /2} \sin \left( {\alpha \arctan (\Omega_{i} /\lambda )} \right),\begin{array}{*{20}c} {} \\ \end{array} i = A,B $$
(23)

3 Results and discussion

In the previous sections, by introducing a fractional capacitor to a serial RLC circuit, we have obtained a fractional linear oscillator with memory-inertia and memory-damping kernels. Considering the damping fluctuation and time-modulated correlation noise between the multiplicative and additive noises, we have derived the expressions for the output amplitude gains \(G_{A}\) for the input driving signal and \(G_{B}\) for the time-modulated correlation signal. From Eqs. (14)-(23), one can find that the two amplitude gains are nonlinear functions of the parameters of the noises and those of the oscillator. Now we discuss the non-monotonous dependence of \(G_{A}\) and \(G_{B}\) on these parameters from Figs. 1–9.

Fig. 1
figure 1

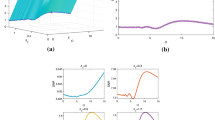
Amplitude gains versus the fractional exponent \(\alpha\) for \(\Omega_{A} = 0.5\), \(\Omega_{B} = 0.5\), \(\lambda = 0.01\), \(\omega_{0} = 0.5\), \(D = 0.15\), \(Q = 0.1\) for different values of the damping coefficient \(\beta\). It is shown that the amplitude gains obtain one resonant peak with the increase of the fractional exponent \(\alpha\) and they vary nonmonotonically with the increase of the damping coefficient \(\beta\)

Full size image

From Figs. 1 and 2 one can find that, with the increase of the fractional exponent \(\alpha\), the two amplitude gains can obtain one peak value, respectively. This phenomenon means that the system output can be maximized by tuning the memory exponent to an appropriate value, a similar effect to those occurred in memory-damping oscillators with fluctuating frequency [47] or with random damping coefficient [26]. The resonant behavior for the amplitude gains versus the fractional exponent \(\alpha\) can be explained based on the cage effect [48]. For small values of fractional exponent \(\alpha\), the force induced by the medium is the main force, which not just slowing down the particle but also causing the particle to develop a rattling motion. The particle is binded by the medium and moves slowly; therefore, the system output signal is suppressed. As \(\alpha\) increasing, this cage effect is weakened and the output amplitude increases, at some values of \(\alpha\) it reaches a maximum value. At the same time, as the particle moves more rapidly, the damping force induced by the rapid velocity becomes the main force, which effectively restricts the particle’s movement and results in the decrease of the system output. Furthermore, from Fig. 1 and Fig. 2 one can easily conclude that the two amplitude gains also vary nonmonotonically with the increase of the damping coefficient \(\beta\) and the noise correlate rate \(\lambda\).

Fig. 2
figure 2

Amplitude gains versus the fractional exponent \(\alpha\) for \(\Omega_{A} = 0.8\), \(\Omega_{B} = 0.8\), \(\beta = 0.4\), \(\omega_{0} = 0.1\), \(D = 0.15\), \(Q = 0.8\) for different values of noise correlate rate \(\lambda\). The lines with no markers are the theoretical results, and the lines with markers are numerical simulation results. It is shown that the amplitude gains obtain one resonant peak with the increase of the fractional exponent \(\alpha\) and they vary nonmonotonically with the increase of the noise correlate rate \(\lambda\)

Full size image

We analyze the effect of the multiplicative noise on the system output amplitude gains from Figs. 3, 4, 5. By virtue of the cooperation between the noise and the system, for some intermediate noise intensity, the system output can be optimized, as shown from the three figures. Thus, the traditional SR phenomenon takes place, a similar effect to that found in a memory-damping oscillator with random damping coefficient [26]. Figure 3 shows that with the increase of the fractional exponent \(\alpha\), the resonance peak of the system amplitude gains moves to lower multiplicative noise strength. In addition, the maximum value shifts to small noise strength with the increase of fractional exponent \(\alpha\) or with the decrease of the damping coefficient \(\beta\) and the noise correlate rate \(\lambda\). This suggests that, for small values of noise intensity \(D\), relatively small values of \(\beta\) and \(\lambda\) or relatively large values of \(\alpha\) should be selected to enhance the system output, as seen from these three figures.

Fig. 3
figure 3

Amplitude gains versus the multiplicative noise strength \(D\) for \(\Omega_{A} = 0.2\), \(\Omega_{B} = 0.2\), \(\beta = 1.2\), \(\lambda = 0.001\), \(\omega_{0} = 0.1\), \(Q = 0.1\) for different values of fractional exponent \(\alpha\). It is shown that the amplitude gains obtain one resonant peak with the multiplicative noise strength \(D\) and they vary nonmonotonically with the increase of the fractional exponent \(\alpha\)

Full size image

Figure 6 shows that one peak exists on the curves of the amplitude gains versus the signal frequencies, i.e., bona fide SR takes place. Moreover, the resonance peaks of the two amplitude gains become more sharper and higher with the increase of fractional exponent \(\alpha\), which indicates that relatively weak memory (large values of \(\alpha\)) narrows the system frequency band and makes it harder to tune the system to its resonate state.

In order to examine the validity of theoretical results, numerical simulations are performed by directly integrated Eq. (3) using the method in Refs. [49, 50]. Some simulation results are shown in Figs. 2, 4 and 6. From these figures, one can conclude that the theoretical results are consistent with the numerical simulations. We point out that the frequencies of the periodic modulations are equivalent, i.e., \(\Omega_{A} = \Omega_{B}\) in Figs. 1–6, for the case \(\Omega_{A} \ne \Omega_{B}\), the resonant peak of the SNR versus the fractional exponent and versus the multiplicative noise strength, as well as the nonmonotonically variety of the SNR with the damping coefficient and with noise correlate rate can be also observed, as seen from Figs. 7, 8, 9.

Fig. 4
figure 4

Amplitude gains versus the multiplicative noise strength \(D\) for \(\Omega_{A} = 0.2\), \(\Omega_{B} = 0.2\), \(\alpha = 0.99\), \(\lambda = 0.001\), \(\omega_{0} = 0.1\), \(Q = 0.01\) for different values of the damping coefficient \(\beta\). The lines with no markers are the theoretical results, and the lines with markers are numerical simulation results. It is shown that the amplitude gains obtain one resonant peak with the variety of multiplicative noise strength \(D\) and they vary nonmonotonically with the increase of the damping coefficient \(\beta\)

Full size image
Fig. 5
figure 5

Amplitude gains versus the multiplicative noise strength \(D\) for \(\Omega_{A} = 0.2\), \(\Omega_{B} = 0.2\), \(\alpha = 0.99\), \(\beta = 1.2\), \(\omega_{0} = 0.1\), \(Q = 0.01\) for different values of noise correlate rate \(\lambda\). It is shown that the amplitude gains obtain one resonant peak with the increase of the multiplicative noise strength \(D\) and they vary nonmonotonically with the increase of the noise correlate rate \(\lambda\)

Full size image
Fig. 6
figure 6

Amplitude gains versus the signal frequencies for \(\beta = 0.7\), \(\lambda = 1\), \(\omega_{0} = 0.5\), \(D = 0.4\), \(Q = 0.2\) for different values of fractional exponent \(\alpha\). The lines with no markers are the theoretical results, and the lines with markers are numerical simulation results. It is shown that the amplitude gains obtain one resonant peak with the variety of the signal frequencies and they vary nonmonotonically with the increase of the fractional exponent \(\alpha\)

Full size image
Fig. 7
figure 7

Amplitude gains versus the fractional exponent \(\alpha\) for \(\Omega_{A} = 0.4\), \(\Omega_{B} = 0.5\), \(\lambda = 0.01\), \(\omega_{0} = 0.5\), \(D = 0.15\), \(Q = 0.1\) for different values of the damping coefficient \(\beta\). It is shown that the amplitude gains obtain one resonant peak with the increase of the fractional exponent \(\alpha\) and they vary nonmonotonically with the increase of the damping coefficient \(\beta\)

Full size image
Fig. 8
figure 8

Amplitude gains versus the fractional exponent \(\alpha\) for \(\Omega_{A} = 0.7\), \(\Omega_{B} = 0.8\), \(\beta = 0.4\), \(\omega_{0} = 0.1\), \(D = 0.15\), \(Q = 0.8\) for different values of noise correlate rate \(\lambda\).The lines with no markers are the theoretical results, and the lines with markers are numerical simulation results. It is shown that the amplitude gains obtain one resonant peak with the increase of the fractional exponent \(\alpha\) and they vary nonmonotonically with the increase of the noise correlate rate \(\lambda\)

Full size image
Fig. 9
figure 9

Amplitude gains versus the multiplicative noise strength \(D\) for \(\Omega_{A} = 0.15\),\(\Omega_{B} = 0.2\),\(\alpha = 0.99\),\(\lambda = 0.001\),\(\omega_{0} = 0.1\), \(Q = 0.01\) for different values of the damping coefficient \(\beta\). The lines with no markers are the theoretical results, and the lines with markers are numerical simulation results. It is shown that the amplitude gains obtain one resonant peak with the variety of multiplicative noise strength \(D\) and they vary nonmonotonically with the increase of the damping coefficient \(\beta\)

Full size image

4 Conclusions

In conclusion, in this work, by introducing a fractional capacitor to an RLC serial circuit, a fractional linear oscillator with memory-inertia and memory-damping is obtained. The correlation intensity between the multiplicative and additive noise is assumed as a time-variant one. By virtue of the characteristics of the dichotomous noise and that of fractional calculus, using Laplace transform, the long-time system output amplitude gains for the input signal and that for the time-modulated correlation signal have been derived. One-peak resonant phenomenon has been observed on the curves for the two amplitude gains versus the fractional exponent and versus the multiplicative noise intensity. A resonance behavior of the amplitude gains as a function of the input signal frequency has also been observed.