1 Introduction

The concept of stochastic resonance (SR) was first introduced in 1981 by Benzi et al. to explain the periodic recurrence of ice ages on Earth [1]. Since then, the phenomenon of SR has been studied extensively in theory and experiment [2–27, 30–35], and has been found in many fields such as biological system, laser system, optical system, and so on. In the early researches, the SR phenomenon is typically found in non-linear dynamical systems driven by periodic signal and noise [2–4]. Nevertheless, the recent researches show that SR can also take place in linear systems subjected to periodic signal and multiplicative noise or linear systems driven just by multiplicative noises [5, 6]. In addition, the original understanding of SR is extended. The conventional SR refers to the phenomenon that the SNR is non-monotonic with the changes of characteristic parameters of noise (such as the noise intensity and the correlation rate). However, the SR in the wide sense was introduced by Gitterman, which means that the non-monotonic behaviors of some functions of system response (such as the moments, the autocorrelation function, the power spectrum and the SNR) depend on the changes of characteristic parameters (such as the amplitude and the frequency of input signal, the noise intensity and the correlation rate, etc.) [7].

As the simplest model to describe the different phenomena in nature, the harmonic oscillators driven by multiplicative noise have attracted great attention [9–21]. A great number of literatures have investigated the problems where particle dynamic behaviors can be modeled as a harmonic oscillator with random frequency [9–12], and random damping [13, 14]. For example, these include problems of spin precession in a random external field [15], open flows of liquids [14], to name a few. In contrast, the harmonic oscillator with random mass [16–20] has received less attention from researchers. In fact, there are many situations in chemical and biological solutions in which the viscous medium contains molecules which are capable of both colliding with the Brownian particle and adhering to it randomly. Therefore, the mass of Brownian particle in viscous medium is fluctuant. One application of such a model is a nano-mechanical resonator which randomly absorbs and desorbs molecules [21]. Recently, Gitterman and Shapiro [16] have examined the stability conditions for the averaged moment of a harmonic oscillator having a quadratic random mass, and investigated the SR phenomenon in this kind of linear system. Gitterman [17, 18] considered an oscillator with random mass, which describes a new type of Brownian motion—Brownian motion with adhesion, and analyzed the stability of the averaged moment as well as the SR phenomenon in this linear system. Zhong et al. [20] obtained the expressions of the first moment and the amplitude of the output signal, and investigated the SR phenomenon in an underdamped linear harmonic oscillator with fluctuating mass and fluctuating frequency under an external periodic force.

In most of the aforementioned studies, the models which are used to demonstrate SR are usually restricted to normal diffusion [9, 10, 13–21]. However, anomalous diffusion processes can be found in a wide range of areas [22–27], which can be described by the fractional Langevin equation. Examples of such systems include nuclear fusion reactions [22], amorphous semiconductors [23], molecular motor in viscoelastic cytosol [27], and so on. As mathematical descriptions of anomalous diffusion processes, the fractional oscillators (FO) [28, 29] play a significant role and the characteristic of fractional operators makes it suitable for describing those systems with long-range dependence and long-memory. Therefore, close attention has been paid to exploring SR mechanics in fractional oscillators in recent years [30–35]. For example, Shen et al. [30] obtained the first-order approximate solutions and studied the subharmonic resonance of van der Pol (VDP) oscillator with fractional-order derivative by the averaging method. Mankin et al. [32] investigated the long-time limit behavior of the positional distribution for an underdamped Brownian particle in a fluctuating harmonic potential well by using the generalized Langevin equation with a power-law-type memory kernel. Laas [33] investigated the resonant behavior of a fractional oscillator with random damping. Yu et al. [35] used the fractional Shapiro–Loginov formula with Laplace transformation technique to study the resonant behavior of a fractional harmonic oscillator with fluctuating mass. However, the synergy of the random mass and random frequency was still missing in literature. Due to the synergy of random mass and random frequency, the dynamics of a system can be influenced. Motivated by the aforementioned discussion, a fractional linear oscillator with random mass and random frequency is proposed in this paper to investigate the characteristics of Brownian motion in viscous medium.

The paper is organized as follows. Section 2 presents the model of the fractional linear oscillator with random mass and random frequency, and gives analytical expression of the first-order moment of the system’s steady response. Section 3 presents the simulation results. Section 4 concludes.

2 System Model

We consider an under-damped fractional linear oscillator subjected to two multiplicative dichotomous noises \(\xi ( t)\) and \(\eta ( t)\), an additive internal noise \(\zeta ( t)\), and an external periodic force, which is described by the generalized Langevin equation (GLE) with \(m=1\):

$$\begin{aligned} \left[ {1+\xi ( t)} \right] \frac{\text{ d }^2x( t)}{\text{ d }t^2}+\gamma \int _0^t {\beta ( {t-{t}'})} \dot{x}( {{t}'})\text{ d }{t}'+\omega ^2\left[ {1+\eta ( t)} \right] x( t)=R\cos ( {\Omega t})+\zeta ( t), \end{aligned}$$
(1)

where \(x( t)\) is the displacement of a particle, \(\ddot{x}( t)\) is the Newton’s acceleration term, \(\gamma \) is the friction coefficient, \(\omega \) is the intrinsic frequency of the system, and \(R\) and \(\Omega \) are the amplitude and frequency of the periodic signal, respectively.

In many physical and biological environments, viscous medium usually has a power-law memory that represents the dependence of the viscous force on the velocity history of particle [36, 37]. Therefore, the damping kernel function \(\beta (t)\) is expressed as \(\beta (t)=\frac{1}{\Gamma (1-\alpha )}\vert t\vert ^{-\alpha }\). According to Caputo’s definition of fractional derivative, Eq. (1) can be written as:

$$\begin{aligned} \left[ {1+\xi ( t)} \right] \frac{\text{ d }^2x( t)}{\text{ d }t^2}+\gamma { }_0^C D_t^\alpha x( t)+\omega ^2\left[ {1+\eta ( t)} \right] x( t)=R\cos ( {\Omega t})+\zeta ( t), \end{aligned}$$
(2)

and Eq. (2) was named as a fractional Langevin equation.

We investigate this fractional linear oscillator mentioned above, which is described by Eq. (2). The “external noises”\(\xi ( t)\) and \(\eta ( t)\) are modeled as symmetric dichotomous noises. \(\xi ( t)\) is the fluctuation of the mass and takes two values \(\sigma _\xi \) and \(-\sigma _\xi \). For the sake of \(1+\xi ( t)>0\), \(\sigma _\xi <1\) must be hold. \(\eta ( t)\) is the fluctuation of the intrinsic frequency \(\omega \) and takes two values \(\sigma _\eta \) and \(-\sigma _\eta \). The statistical properties of \(\xi (t)\) and \(\eta ( t)\) are

$$\begin{aligned}&\left\langle {\xi \left( t \right) } \right\rangle = 0,\left\langle {\xi \left( t \right) \xi \left( {t'} \right) } \right\rangle = \sigma _\xi ^2\exp \left( { - {\lambda _\xi }\left| {t - t'} \right| } \right) , \nonumber \\&\left\langle {\eta \left( t \right) } \right\rangle = 0,\left\langle {\eta \left( t \right) \eta \left( {t'} \right) } \right\rangle = \sigma _\eta ^2\exp \left( { - {\lambda _\eta }\left| {t - t'} \right| } \right) , \end{aligned}$$
(3)

where \(\sigma _\xi ^2 \) and \(\lambda _\xi \) are the noise intensity and the correlation rate of \(\xi (t)\), \(\sigma _\eta ^2 \) and \(\lambda _\eta \) are the noise intensity and the correlation rate of \(\eta (t)\), respectively. In addition, \(\zeta ( t)\) represents the “internal noise” which drives the GLE and share the same origin as the damping force of system [38]. Therefore, the relationship between the damping kernel function \(\beta (t)\)and the additive noise \(\zeta ( t)\) can be established via the fluctuation-dissipation theorem [39]:

$$\begin{aligned} \left\langle {\zeta (t)\zeta ({t}')} \right\rangle =\kappa _B T\gamma \beta ( {t-{t}'})=\kappa _B T\gamma \frac{\left| {t-{t}'} \right| ^{-\alpha }}{\Gamma ( {1-\alpha })}, \end{aligned}$$
(4)

where \(\kappa _B \) is the Boltzmann constant and \(T\) is the absolute temperature.

In this paper, \(\zeta ( t)\) is modeled as the fractional Gaussian noise (fGn) [40, 41], and satisfies

$$\begin{aligned} \left\langle {\zeta ( t)} \right\rangle =0,\;\left\langle {\zeta (t)\zeta ({t}')} \right\rangle =2DH( {2H-1})\left| {t-{t}'} \right| ^{2H-2}, \end{aligned}$$
(5)

where \(D\) is the noise intensity of \(\zeta ( t)\) and \(H\) is the Hurst parameter. By comparing Eq. (4) with Eq. (5), we obtain:

$$\begin{aligned} H = \left( {2 - \alpha } \right) /2,\;\;\;D = {\kappa _B}T\gamma /\Gamma \left( {3 - \alpha } \right) . \end{aligned}$$
(6)

We assume that the “external noises” \(\xi (t)\), \(\eta (t)\) and the “internal noise”\(\zeta ( t)\) are uncorrelated for they have different origins, that is, the three noises satisfy:

$$\begin{aligned} \left\langle {\xi ( t)\zeta ( {{t}'})} \right\rangle =\left\langle {\eta ( t)\zeta ( {{t}'})} \right\rangle =0. \end{aligned}$$
(7)

In addition, we assumed that “external noises” \(\xi (t)\) and \(\eta (t)\) are statistically independent, i.e.,

$$\begin{aligned} \left\langle {\xi ( t)\eta ( {{t}'})} \right\rangle =0. \end{aligned}$$
(8)

In the next part, we will obtain the exact expression of the first-order moment of the system’s steady response.

2.1 First-Order Moment of the System Stationary State Response

Average Eq. (2), then we will obtain

$$\begin{aligned} \frac{\text{ d }^2\left\langle {x( t)} \right\rangle }{\text{ d }t^2}+\left\langle {\xi ( t)\ddot{x}( t)} \right\rangle +\gamma { }_0^C D_t^\alpha \left\langle {x( t)} \right\rangle +\omega ^2\left[ {\left\langle {x( t)} \right\rangle +\left\langle {\eta ( t)x( t)} \right\rangle } \right] =R\cos ( {\Omega t}). \end{aligned}$$
(9)

To obtain the first-order moment of the system stationary state response, we use the well-known formula for splitting the correlations [17] as bellows:

$$\begin{aligned} \left\langle {\xi ( t)\eta ( t)x( t)} \right\rangle =\left\langle {\xi ( t)\eta ( t)} \right\rangle \left\langle {x( t)} \right\rangle . \end{aligned}$$
(10)

Multiplying both sides of Eq. (2) by \(\xi (t)\) and averaging all terms by using Eqs. (3), (8) and (10), we have

$$\begin{aligned} \sigma _\xi ^2 \frac{\text{ d }^2\left\langle {x( t)} \right\rangle }{\text{ d }t^2}+\left\langle {\xi ( t)\ddot{x}( t)} \right\rangle +\gamma \left\langle {\xi ( t){ }_0^C D_t^\alpha x( t)} \right\rangle +\omega ^2\left\langle {\xi ( t)x( t)} \right\rangle =0. \end{aligned}$$
(11)

Multiplying both sides of Eq. (2) by \(\eta (t)\) and averaging all terms by using Eqs. (3), (8) and (10), we have

$$\begin{aligned} \left\langle {\eta ( t)\ddot{x}( t)} \right\rangle +\gamma \left\langle {\eta ( t){ }_0^C D_t^\alpha x( t)} \right\rangle +\omega ^2\sigma _\eta ^2 \left\langle {x( t)} \right\rangle +\omega ^2\left\langle {\eta ( t)x( t)} \right\rangle =0, \end{aligned}$$
(12)

To perform the splitting of correlators, we use the well-known Shapiro–Loginov formula [42], which reads as

$$\begin{aligned} \left\langle {\xi \frac{{{{\text {d}}^n}g}}{{{\text {d}}{t^n}}}} \right\rangle = {\left( {\frac{{\text {d}}}{{{\text {d}}t}} + {\lambda _\xi }} \right) ^n}\left\langle {\xi g} \right\rangle ,\left\langle {\eta \frac{{{{\text {d}}^n}g}}{{{\text {d}}{t^n}}}} \right\rangle = {\left( {\frac{{\text {d}}}{{{\text {d}}t}} + {\lambda _\eta }} \right) ^n}\left\langle {\eta g} \right\rangle . \end{aligned}$$
(13)

At the same time, applying the fractional Shapiro–Loginov formula [35] to \(\left\langle {\xi ( t){ }_0^C D_t^\alpha x( t)} \right\rangle \) and \(\left\langle {\eta ( t){ }_0^C D_t^\alpha x( t)} \right\rangle \), we have

$$\begin{aligned} \left\langle {\xi ( t){ }_0^C D_t^\alpha x( t)} \right\rangle= & {} e^{-\lambda _\xi t}{ }_0^C D_t^\alpha ( {\left\langle {\xi ( t)x( t)} \right\rangle e^{\lambda _\xi t}}), \nonumber \\ \left\langle {\eta ( t){ }_0^C D_t^\alpha x( t)} \right\rangle= & {} e^{-\lambda _\eta t}{ }_0^C D_t^\alpha ( {\left\langle {\eta ( t)x( t)} \right\rangle e^{\lambda _\eta t}}). \end{aligned}$$
(14)

Inserting Eqs. (13) and (14) into Eqs. (9), (11) and (12), we obtain the fractional differential equations:

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {\left( {\frac{\text{ d }^2}{\text{ d }t^2}+\gamma { }_0^C D_t^\alpha +\omega ^2}\right) \left\langle {x( t)} \right\rangle +\left( {\frac{\text{ d }}{\text{ d }t}+\lambda _\xi }\right) ^2\left\langle {\xi ( t)x( t)} \right\rangle +\omega ^2\left\langle {\eta ( t)x( t)} \right\rangle =R\cos \Omega t,} \\ {\left( {\sigma _\xi ^2 \frac{\text{ d }^2}{\text{ d }t^2}}\right) \left\langle {x( t)} \right\rangle +\left[ {\left( {\frac{\text{ d }}{\text{ d }t}+\lambda _\xi }\right) ^2+\omega ^2} \right] \left\langle {\xi ( t)x( t)} \right\rangle +\gamma e^{-\lambda _\xi t}{ }_0^C D_t^\alpha \left( {\left\langle {\xi ( t)x( t)} \right\rangle e^{\lambda _\xi t}}\right) =0,} \\ {\left( {\omega ^2\sigma _\eta ^2 }\right) \left\langle {x( t)} \right\rangle +\left[ {\left( {\frac{\text{ d }}{\text{ d }t}+\lambda _\eta }\right) ^2+\omega ^2} \right] \left\langle {\eta ( t)x( t)} \right\rangle +\gamma e^{-\lambda _\eta t}{ }_0^C D_t^\alpha \left( {\left\langle {\eta ( t)x( t)} \right\rangle e^{\lambda _\eta t}}\right) =0.} \\ \end{array} } \right. \end{aligned}$$
(15)

To solve the Eqs. (15) with three variables \(x_1 =\left\langle {x( t)} \right\rangle \), \(x_2 =\left\langle {\xi ( t)x( t)} \right\rangle \) and \(x_3 =\left\langle {\eta ( t)x( t)} \right\rangle \), we use the Laplace transformation technique and obtain [43]:

$$\begin{aligned} \left\{ {\begin{array}{ll} {{d_{11}}{X_1}\left( s \right) + {d_{12}}{X_2}\left( s \right) + {d_{13}}{X_3}\left( s \right) = \frac{{Rs}}{{{s^2} + {\Omega ^2}}} + {d_{14}},} \\ {{d_{21}}{X_1}\left( s \right) + {d_{22}}{X_2}\left( s \right) + {d_{23}}{X_3}\left( s \right) = {d_{24}},} \\ {{d_{31}}{X_1}\left( s \right) + {d_{32}}{X_2}\left( s \right) + {d_{33}}{X_3}\left( s \right) = {d_{34}},} \\ \end{array}} \right. \end{aligned}$$
(16)

where \(X_i ( s)=L\left\{ {x_i ( t)} \right\} \buildrel \Delta \over = \int _0^{+\infty } {x_i ( t)e^{-st}dt} \), \(i=1,2,3\),

$$\begin{aligned} \begin{array}{l} d_{11} =s^2+\gamma s^\alpha +\omega ^2,d_{12} =( {s+\lambda _\xi })^2,d_{13} =\omega ^2, \\ d_{14} =( {s+\gamma s^{\alpha -1}})x_1 ( 0)+\dot{x}_1 ( 0)+( {s+2\lambda _\xi })x_2 ( 0)+\dot{x}_2 ( 0), \\ d_{21} =\sigma _\xi ^2 s^2,d_{22} =( {s+\lambda _\xi })^2+\gamma ( {s+\lambda _\xi })^\alpha +\omega ^2,d_{23} =0, \\ d_{24} =\sigma _\xi ^2 sx_1 ( 0)+\sigma _\xi ^2 \dot{x}_1 ( 0)+\left[ {s+2\lambda _\xi +\gamma ( {s+\lambda _\xi })^{\alpha -1}} \right] x_2 ( 0)+\dot{x}_2 ( 0), \\ d_{31} =\omega ^2\sigma _\eta ^2 ,d_{32} =0,d_{33} =( {s+\lambda _\eta })^2+\gamma ( {s+\lambda _\eta })^\alpha +\omega ^2, \\ d_{34} =\left[ {s+2\lambda _\eta +\gamma ( {s+\lambda _\eta })^{\alpha -1}} \right] x_3 ( 0)+\dot{x}_3 ( 0), \\ \end{array} \end{aligned}$$

and \(x_1 ( 0)\), \(x_2 ( 0)\) and \(x_3 ( 0)\) are the initial conditions.

The solutions of Eqs. (16) can be represented as

$$\begin{aligned} \left\{ {\begin{array}{ll} {{X_1}\left( s \right) = \frac{{{d_{22}}{d_{33}}}}{{{d_{11}}{d_{22}}{d_{33}} - {d_{12}}{d_{21}}{d_{33}} - {d_{13}}{d_{22}}{d_{31}}}}\frac{{Rs}}{{{s^2} + {\Omega ^2}}} + \frac{{{d_{14}}{d_{22}}{d_{33}} - {d_{12}}{d_{24}}{d_{33}} - {d_{13}}{d_{22}}{d_{34}}}}{{{d_{11}}{d_{22}}{d_{33}} - {d_{12}}{d_{21}}{d_{33}} - {d_{13}}{d_{22}}{d_{31}}}},} \\ {{X_2}\left( s \right) = - \frac{{{d_{21}}{d_{33}}}}{{{d_{11}}{d_{22}}{d_{33}} - {d_{12}}{d_{21}}{d_{33}} - {d_{13}}{d_{22}}{d_{31}}}}\frac{{Rs}}{{{s^2} + {\Omega ^2}}} + \frac{{{d_{13}}\left( {{d_{21}}{d_{34}} - {d_{24}}{d_{31}}} \right) + {d_{33}}\left( {{d_{11}}{d_{24}} - {d_{14}}{d_{21}}} \right) }}{{{d_{11}}{d_{22}}{d_{33}} - {d_{12}}{d_{21}}{d_{33}} - {d_{13}}{d_{22}}{d_{31}}}},} \\ {{X_3}\left( s \right) = - \frac{{{d_{22}}{d_{31}}}}{{{d_{11}}{d_{22}}{d_{33}} - {d_{12}}{d_{21}}{d_{33}} - {d_{13}}{d_{22}}{d_{31}}}}\frac{{Rs}}{{{s^2} + {\Omega ^2}}} + \frac{{{d_{31}}\left( {{d_{12}}{d_{24}} - {d_{22}}{d_{14}}} \right) + {d_{34}}\left( {{d_{11}}{d_{22}} - {d_{12}}{d_{21}}} \right) }}{{{d_{11}}{d_{22}}{d_{33}} - {d_{12}}{d_{21}}{d_{33}} - {d_{13}}{d_{22}}{d_{31}}}}.} \\ \end{array}} \right. \nonumber \\ \end{aligned}$$
(17)

Applying the inverse Laplace transformation technique, we obtain

$$\begin{aligned} {x_i}\left( t \right) = R\int _0^t {{h_{i0}}\left( {t - t'} \right) } \cos \left( {\Omega t'} \right) {\text {d}}t' + \sum \limits _{k = 1}^3 {{h_{ik}}\left( t \right) } {x_k}\left( 0 \right) ,i = 1,2,3, \end{aligned}$$
(18)

where \(H_{ik} ( s)\) are the Laplace transforms of \(h_{ik} ( t),k=0,1,2,3\), and can be determined by Eq. (17). Specifically, \(H_{10} ( s)\) is the transfer function of system, which is written as:

$$\begin{aligned} H_{10} ( s)=\frac{d_{22} d_{33} }{d_{11} d_{22} d_{33} -d_{13} d_{22} d_{31} -d_{12} d_{21} d_{33} }. \end{aligned}$$
(19)

In the long-time regime \(t\rightarrow \infty \), the functions \(h_{ik} ( t),k=1,2,3\) tend to zero only if

$$\begin{aligned} \sigma _\eta ^2 < {\left( {\sigma _\eta ^2} \right) _{cr}} = 1 + \frac{{\lambda _\eta ^2 + \gamma \lambda _\eta ^\alpha }}{{{\omega ^2}}},{\lambda _\eta } > 0. \end{aligned}$$
(20)

In this paper, we assume that the condition is satisfied. Thus, in the case of the long-time limit \(t\rightarrow \infty \), the influence of initial conditions will vanish, and the asymptotic expression of \(\left\langle {x(t)} \right\rangle \) is written in the following forms:

$$\begin{aligned} \left\langle {x( t)} \right\rangle _{as} =\left\langle {x( t)} \right\rangle \left| {_{t\rightarrow \infty } } \right. =R\int _0^t {h_{10} ( {t-{t}'})} \cos ( {\Omega {t}'})\text{ d }{t}'. \end{aligned}$$
(21)

Using the linear response theory, Eq. (21) can be further expressed as [43]:

$$\begin{aligned} \left\langle {x( t)} \right\rangle _{as} =\left\langle {x( t)} \right\rangle \left| {_{t\rightarrow \infty } } \right. =A\cos ( {\Omega t+\varphi }), \end{aligned}$$
(22)

where \(A\) and \(\varphi \) are the amplitude and the phase shift of the system stationary state response \(\left\langle {x( t)} \right\rangle _{as} \), respectively, and they satisfy:

$$\begin{aligned} A=R\left| {H_{10} ( {j\Omega })} \right| , \quad \varphi =\arg ( {H_{10} ( {j\Omega })}). \end{aligned}$$
(23)

Using Eqs. (16) and (19), one can obtain that

$$\begin{aligned} A=R\sqrt{\frac{f_7^2 +f_8^2 }{f_9^2 +f_{10}^2 }} , \end{aligned}$$
(24)
$$\begin{aligned} \varphi =\arctan \left( {\frac{f_8 f_9 -f_7 f_{10} }{f_7 f_9 +f_8 f_{10} }}\right) , \end{aligned}$$
(25)

where

$$\begin{aligned}&{f_1} = {\omega ^2} - {\Omega ^2} + \gamma {\Omega ^\alpha }\cos \left( {\frac{\pi }{2}\alpha } \right) , \qquad \qquad {f_2} = \gamma {\Omega ^\alpha }\sin \left( {\frac{\pi }{2}\alpha } \right) , \\&{f_3} = {\omega ^2} - {\Omega ^2} + \lambda _\xi ^2 + \gamma b_1^\alpha \cos \left( {\alpha {\theta _1}} \right) , \qquad \qquad {f_4} = 2\Omega {\lambda _\xi } + \gamma b_1^\alpha \sin \left( {\alpha {\theta _1}} \right) , \\&{f_5} = {\omega ^2} - {\Omega ^2} + \lambda _\eta ^2 + \gamma b_2^\alpha \cos \left( {\alpha {\theta _2}} \right) , \qquad \qquad {f_6} = 2\Omega {\lambda _\eta } + \gamma b_2^\alpha \sin \left( {\alpha {\theta _2}} \right) , \\&{f_7} = {f_3}{f_5} - {f_4}{f_6}, \qquad \qquad {f_8} = {f_4}{f_5} + {f_3}{f_6}, \\&{f_9} = \left[ {{f_5}\left( {{f_1}{f_3} - {f_2}{f_4}} \right) - {f_6}\left( {{f_2}{f_3} + {f_1}{f_4}} \right) } \right] - {\omega ^4}\sigma _\eta ^2{f_3} + {\Omega ^2}\sigma _\xi ^2\left[ {{f_5}\left( {\lambda _\xi ^2 - {\Omega ^2}} \right) - 2{f_6}\Omega {\lambda _\xi }} \right] , \\&{f_{10}} = \left[ {{f_5}\left( {{f_2}{f_3} + {f_1}{f_4}} \right) + {f_6}\left( {{f_1}{f_3} - {f_2}{f_4}} \right) } \right] - {\omega ^4}\sigma _\eta ^2{f_4} + {\Omega ^2}\sigma _\xi ^2\left[ {{f_6}\left( {\lambda _\xi ^2 - {\Omega ^2}} \right) + 2{f_5}\Omega {\lambda _\xi }} \right] , \\&{b_1} = \sqrt{{\Omega ^2} + \lambda _\xi ^2} , \qquad {\theta _1} = \arctan \left( {\frac{\Omega }{{{\lambda _\xi }}}} \right) , \\&{b_2} = \sqrt{{\Omega ^2} + \lambda _\eta ^2} ,\qquad {\theta _2} = \arctan \left( {\frac{\Omega }{{{\lambda _\eta }}}} \right) . \\ \end{aligned}$$

3 Numerical Discussion

Now we do the numerical work on the above analytical expression in Eq. (24), which show the behaviors of the output amplitude A for any combination of the parameters \(\alpha \), \(\Omega \), \(\gamma \), \(\sigma _\xi ^2 \), \(\lambda _\xi \), \(\sigma _\eta ^2 \), \(\lambda _\eta \).

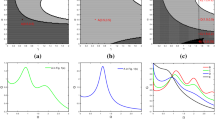
In Fig. 1, we plot the curves of the output amplitude A each as a function of the noise intensity \(\sigma _\xi ^2 \) with different values of parameters (including \(\alpha \), \(\Omega \), \(\gamma \), \(\lambda _\xi \), \(\sigma _\eta ^2 \) and \(\lambda _\eta )\). Moreover, from the equation

$$\begin{aligned} \frac{\text{ d }( A)}{\text{ d }( {\sigma _\xi ^2 })}=0, \end{aligned}$$
(26)

the position of the peak of the curve \(A( {\sigma _\xi ^2 })\) is determined by

$$\begin{aligned} \sigma _\xi ^2 =-\frac{\left[ {f_1 f_7 \!-\! f_2 f_8 \!-\! \omega ^4\sigma _\eta ^2 f_3 } \right] \left[ {f_5 ( {\lambda _\xi ^2 \!-\! \Omega ^2})\!-\! 2f_6 \Omega \lambda _\xi } \right] \!+\!\left[ {f_2 f_7 \!+\! f_1 f_8 \!-\! \omega ^4\sigma _\eta ^2 f_4 } \right] \left[ {f_6 ( {\lambda _\xi ^2 -\Omega ^2})+2f_5 \Omega \lambda _\xi } \right] }{\Omega ^2\left[ {f_5 ( {\lambda _\xi ^2 -\Omega ^2})-2f_6 \Omega \lambda _\xi } \right] ^2+\Omega ^2\left[ {f_6 ( {\lambda _\xi ^2 -\Omega ^2})+2f_5 \Omega \lambda _\xi } \right] ^2}.\nonumber \\ \end{aligned}$$
(27)

As shown in Fig. 1, each curve shows that A attains a maximum value with increasing \(\sigma _\xi ^2 \), indicating that the SR in the wide sense takes place. Under the synergy between external noises, internal noise and periodic signal, the power of multiplicative noise transforms into the power of periodic signal, therefore, it enhances the output amplitude. Figure 1a shows that with the increase of the fractional order \(\alpha \), the maximum of A decreases, and the resonance peak gets flat. Figure 1a also shows that the position of the peak shifts toward the left with the increase of \(\alpha \) for \(\alpha <0.6\), however, the position of the peak shifts toward the right slightly with the increase of \(\alpha \) in the range \(\alpha >0.6\). From Eq. (27), the positions of resonance peaks can be determined. The position of the peaks of Fig. 1a are \(\sigma _\xi ^2 =\) 0.224, 0.2078, 0.193, 0.1699, 0.1697, 0.1884 for \(\alpha =\) 0.1, 0.2, 0.3, 0.5, 0.7, 0.8, respectively. In Fig. 1b, with the increase of the frequency of periodic signal \(\Omega \), the maximum of A increases and the position of the peak shifts toward the right. From Eq. (27), we can obtain the position of the peaks of Fig. 1b, which are \(\sigma _\xi ^2 =\) 0.0705, 0.1739, 0.2717, 0.4351 for \(\Omega =\) 1.7, 1.9, 2.1, 2.5, respectively. In Fig. 1c, with the increase of the noise intensity \(\sigma _\eta ^2 \), the maximum of A decreases and the position of the peak shifts toward the left slightly. From Eq. (27), we can obtain the position of the peaks of Fig. 1c, which are \(\sigma _\xi ^2 =\) 0.2343, 0.2308, 0.2274, 0.224 for \(\sigma _\eta ^2 =\) 0.1, 0.4, 0.7, 1, respectively. In Fig. 1d, with the increase of friction coefficient \(\gamma \), the maximum of A decreases and the position of the peak shifts toward the left obviously. From Eq. (27), we can obtain the position of the peaks of Fig. 1d, which are \(\sigma _\xi ^2 =\) 0.368, 0.224, 0.1113, 0.0298 for \(\gamma =\) 0.5, 1, 1.5, 2, respectively. In Fig. 1e, with the increase of \(\lambda _\xi \) in the range \(\lambda _\xi <0.75\), the maximum of A decreases and the position of the peak shifts toward the right slightly, however, with the increase of \(\lambda _\xi \) in the range \(\lambda _\xi >0.75\), the maximum of A increases and the position of the peak shifts toward the right obviously. From Eq. (27), we can obtain the position of the peaks of Fig. 1e, which are \(\sigma _\xi ^2 =\) 0.224, 0.2404, 0.28, 0.3612, 0.4028, 0.4348 for \(\lambda _\xi =\) 0.1, 0.4, 0.7, 1.2, 1.5, 1.8, respectively. In Fig. 1f, with the increase of \(\lambda _\eta \) in the range \(\lambda _\eta <0.6\), the maximum of A decreases and the position of the resonance peak shifts toward the right, however, with the increase of \(\lambda _\eta \) in the range \(\lambda _\eta >0.6\), the maximum of A increases and the position of the resonance peak shifts toward the right. From Eq. (27), we can obtain the position of the peaks of Fig. 1f, which are \(\sigma _\xi ^2 =\)  0.1734, 0.194, 0.2128, 0.224, 0.2328, 0.2365 for \(\lambda _\eta =\) 0.1, 0.4, 0.7, 1, 1.5, 2, respectively.

Fig. 1
figure 1

SR in the wide sense for the response function \(A\) versus the parameter \(\sigma _\xi ^2 \). Other parameter values: a \(R=1,\,\omega =1,\,\Omega =2,\,\gamma =1,\,\lambda _\xi =0.1,\,\sigma _\eta ^2 =1,\,\lambda _\eta =1\); b \(R=1,\,\omega =1, \quad \gamma =1,\,\lambda _\xi =0.1,\,\sigma _\eta ^2 =1,\lambda _\eta =1,\,\alpha =0.1\); c \(R=1,\,\omega =1,\,\Omega =2,\,\gamma =1,\,\lambda _\xi =0.1,\,\lambda _\eta =1\), \(\alpha = 0.1\); d \(R=1,\,\omega =1,\,\Omega =2,\lambda _\xi =0.1,\,\sigma _\eta ^2 =1,\,\lambda _\eta =1,\,\alpha =0.1\); e \(R=1,\,\omega =1,\,\Omega =2, \, \gamma =1,\,\sigma _\eta ^2 =1,\,\lambda _\eta =1,\,\alpha =0.1\); f \(R=1,\omega =1,\,\Omega =2,\,\gamma =1,\,\lambda _\xi =0.1,\,\sigma _\eta ^2 =1,\,\alpha =0.1\)

Full size image

In Fig. 2, we present the curves of the output amplitude A versus noise intensity \(\sigma _\eta ^2 \) with different values of parameters (including \(\alpha \), \(\Omega \), \(\gamma \), \(\sigma _\xi ^2 \), \(\lambda _\xi \) and \(\lambda _\eta )\).

Fig. 2
figure 2

SR in the wide sense for the response function \(A\) versus the parameter \(\sigma _\eta ^2 \). Other parameter values: a \(R=1,\omega =1,\Omega =1,\gamma =1,\sigma _\xi ^2 =0.1,\lambda _\xi =0.1,\lambda _\eta =0.5\); b \(R=1, \omega = 1, \gamma =1,\sigma _\xi ^2 =0.1,\lambda _\xi =0.1,\lambda _\eta =0.4,\alpha =0.1\); c \(R=1,\omega =2,\Omega =1,\sigma _\xi ^2 =0.1, \, \lambda _\xi =0.1,\lambda _\eta =2,\alpha =0.5\); d \(R=1,\omega =2,\Omega =1,\gamma =0.1,\lambda _\xi =1,\lambda _\eta =2,\alpha =0.2\); e \(R=1,\omega =1,\Omega =1,\gamma =1,\sigma _\xi ^2 =0.1,\lambda _\eta =0.5,\alpha =0.1\); f \(R=1,\omega =1,\Omega =1, \, \gamma =1, \, \sigma _\xi ^2 =0.1,\lambda _\xi =0.1,\alpha =0.2\)

Full size image

As shown in Fig. 2, each curve shows that A attains a maximum value with increasing \(\sigma _\eta ^2 \), indicating that the SR in the wide sense occurs. In Fig. 2a, with the increase of \(\alpha \) for \(\alpha <0.35\), the maximum of A decreases, the resonance peak gets flat and the position of the peak shifts toward the left. In addition, the resonance peak vanishes for \(\alpha >0.35\). In Fig. 2b, with the increase of \(\Omega \) in the range \(0.7<\Omega <2\), the maximum of A increases, the resonance peak gets sharp slightly and the position of the peak shifts toward the left, and there is no resonance peak for about \(\Omega <0.7\) and \(2<\Omega \). In Fig. 2c, with the increase of \(\gamma \), the maximum of A decreases, the resonance peak gets flat and the position of the peak shifts toward the right. In Fig. 2d, with the increase of \(\sigma _\xi ^2 \), the maximum of A decreases and the position of the peak shifts toward the left slightly. In Fig. 2e, with the increase of \(\lambda _\xi \), the maximum of A increases and the position of the peak shifts toward the right slightly. Moreover, there exists a critical noise intensity \(( {\sigma _\eta ^2 })_c \). When \(\sigma _\eta ^2 <( {\sigma _\eta ^2 })_c \), A gradually lowers with the increase of \(\lambda _\xi \); when \(\sigma _\eta ^2 >( {\sigma _\eta ^2 })_c \), A gradually increases with the increase of \(\lambda _\xi \) . In Fig. 2f, with the increase of \(\lambda _\eta \), the maximum of A increases and the position of the peak shifts toward the right obviously. Moreover, there exists a critical noise intensity \(( {\sigma _\eta ^2 })_c \). When \(\sigma _\eta ^2 <( {\sigma _\eta ^2 })_c \), A gradually lowers with the increase of \(\lambda _\eta \); when \(\sigma _\eta ^2 >( {\sigma _\eta ^2 })_c \), A gradually increases with the increase of \(\lambda _\eta \). From the equation

$$\begin{aligned} \frac{\text{ d }( A)}{\text{ d }( {\sigma _\eta ^2 })}=0, \end{aligned}$$
(28)

we can determine the position of the resonance peaks in Fig. 2.

Figure 3 shows the curves of the output amplitude A versus the frequency of periodic signal \(\Omega \) for different values of parameters (including \(\alpha \), \(\gamma \), \(\sigma _\xi ^2 \), \(\sigma _\eta ^2 \), \(\lambda _\xi \) and \(\lambda _\eta )\).

Fig. 3
figure 3

SR in the wide sense for the response function \(A\) versus the parameter \(\Omega \). Other parameter values: a \(R=1,\omega =1,\gamma =1,\sigma _\xi ^2 =0.1,\lambda _\xi =0.1,\sigma _\eta ^2 =1,\lambda _\eta =1\); b \(R=1,\omega =1, \sigma _\xi ^2 =0.1, \lambda _\xi =0.5,\sigma _\eta ^2 =0.5,\lambda _\eta =1,\alpha =0.2\); c \(R=1,\omega =1,\gamma =1,\lambda _\xi =0.1,\sigma _\eta ^2 =1,\lambda _\eta =1, \alpha =0.2\); d \(R=1,\omega =1,\gamma =1,\sigma _\xi ^2 =0.1,\lambda _\xi =0.1,\lambda _\eta =1,\alpha =0.2\); e \(R=1,\omega =1,\gamma =1, \sigma _\xi ^2 =0.1, \sigma _\eta ^2 =1,\lambda _\eta =1,\alpha =0.2\); f \(R=1,\omega =1,\gamma =1,\sigma _\xi ^2 =0.1,\lambda _\xi =1,\sigma _\eta ^2 =0.5,\alpha =0.2\)

Full size image

As shown in Fig. 3, all the curves show that A attains a maximum value with increasing \(\Omega \), indicating that SR in the wide sense occurs. Figure 3a shows that there are two peaks in the response \(A( \Omega )\) for \(\alpha <0.4\), where the resonance and the inhibition both exist at the same time. Figure 3a also shows that there exists one peak in the curve \(A( \Omega )\) for \(0.4<\alpha <0.6\), and there is no resonance peak for about \(0.7<\alpha \). In Fig. 3b, with the increase of \(\gamma \), the maximum of A decreases, the resonance peak gets flat and the position of the peak shifts toward the right. In Fig. 3c, there are two peaks in the response \(A( \Omega )\), the left peak decreases and the position of the left peak shifts toward the left slightly with the increase of \(\sigma _\xi ^2 \). Moreover, the right peak does not change obviously, and the position of the right peak shifts toward the right with the increase of \(\sigma _\xi ^2 \). Figure 3d shows that there are two peaks in the response \(A( \Omega )\), and the two peaks decreases slightly with the increase of \(\sigma _\eta ^2 \). Figure 3d also shows that the position of the left peak shifts toward the left slightly, however, the right peak shifts toward the right with the increase of \(\sigma _\eta ^2 \). Moreover, there exists a critical frequency \(\Omega _c \). When \(\Omega <\Omega _c \), A gradually increases with the increase of \(\sigma _\eta ^2 \); when \(\Omega >\Omega _c \), A gradually lowers with the increase of \(\sigma _\eta ^2 \). Figure 3e shows that there are two peaks in the response \(A( \Omega )\) for \(\lambda _\xi <0.25\), and there exists one peak in the curve \(A( \Omega )\) for \(0.25<\lambda _\xi \). Figure 3f shows that there are two peaks in the response \(A( \Omega )\) for \(\lambda _\eta <0.4\), and there exists one peak in the curve \(A( \Omega )\) for \(0.4<\lambda _\eta \). It is worth emphasizing that the peak in the one-peak resonance and the valley in the two-peak resonance appear at the same position.

Specially, as shown in Fig. 3, there is more than one peak in each curve of A versus \(\Omega \), i.e., stochastic multi-resonance (SMR) [44, 45] phenomenon occurs, which is not observed in conventional linear system.

From the equation

$$\begin{aligned} \frac{\text{ d }A}{\text{ d }\Omega }=0, \end{aligned}$$
(29)

we can determine the position of the resonance peaks in Fig. 3.

Figure 4 shows the curves of the output amplitude A versus the fractional order \(\alpha \) for different values of parameters (including \(\sigma _\xi ^2 ,\sigma _\eta ^2 ,\lambda _\xi ,\lambda _\eta \) and \(\gamma )\).

Fig. 4
figure 4

SR in the wide sense for the response function \(A\) versus the parameter \(\alpha \). Other parameter values: a \(R=1,\omega =1,\Omega =2,\gamma =0.9,\lambda _\xi =0.1,\sigma _\eta ^2 =0.1,\lambda _\eta =0.1\); b \(R=1,\omega =1,\Omega =2,\gamma =0.9,\sigma _\xi ^2 =0.15,\lambda _\xi =0.1,\lambda _\eta =0.1\); c \(R=1,\omega =1,\Omega =2,\gamma =0.9, \sigma _\xi ^2 =0.15,\sigma _\eta ^2 =0.2,\lambda _\eta =0.1\); d \(R=1,\omega =1,\Omega =2,\gamma =0.9,\sigma _\xi ^2 =0.15,\sigma _\eta ^2 =0.2, \lambda _\xi =0.1\); e \(R=1,\omega =1,\Omega =2,\sigma _\xi ^2 =0.15,\lambda _\xi =0.1,\sigma _\eta ^2 =0.2,\lambda _\eta =0.1\)

Full size image

As shown in Fig. 4, each curve shows that A attains a maximum value with increasing \(\alpha \), indicating that SR in the wide sense appears. In Fig. 4a, with the increase of \(\sigma _\xi ^2 \) for \(\sigma _\xi ^2 <0.2\), the maximum of A increases, the resonance peak gets sharp and the position of the peak shifts toward the left slightly. The resonance peak vanishes for \(\sigma _\xi ^2 >0.2\). In Fig. 4b, with the increase of \(\sigma _\eta ^2 \) for \(\sigma _\eta ^2 <0.7\), the maximum of A increases, and the position of the peak shifts toward the left slightly. The resonance peak vanishes for \(\sigma _\eta ^2 >0.7\). In Fig. 4c, with the increase of \(\lambda _\xi \) for \(\lambda _\xi <0.2\), the maximum of A decreases, and the position of the peak shifts toward the left slightly. The resonance peak vanishes for \(\lambda _\xi >0.2\). In Fig. 4d, with the increase of \(\lambda _\eta \), the maximum of A decreases and the position of the peak shifts toward the right slightly. In Fig. 4e, with the increase of \(\gamma \) for \(\gamma <1.1\), the maximum of A increases, the resonance peak gets sharp slightly and the position of the peak shifts toward the left slightly. The resonance peak vanishes for \(\gamma >1.1\). From the equation

$$\begin{aligned} \frac{\text{ d }A}{\text{ d }\alpha }=0, \end{aligned}$$
(30)

we can determine the position of the resonance peaks in Fig. 4.

Figure 5 shows the curves of the output amplitude A versus the friction coefficient \(\gamma \) for different values of parameters (including \(\alpha ,\,\Omega ,\,\sigma _\xi ^2 ,\,\sigma _\eta ^2 \) and \(\lambda _\xi )\).

Fig. 5
figure 5

SR in the wide sense for the response function \(A\) versus the parameter \(\gamma \). Other parameter values: a \(R=1,\omega =1,\Omega =2,\sigma _\xi ^2 =0.1,\lambda _\xi =0.1,\sigma _\eta ^2 =0.1,\lambda _\eta =0.1\); b \(R=1, \omega =1,\alpha =0.1,\sigma _\xi ^2 =0.1,\lambda _\xi =0.1,\sigma _\eta ^2 =0.1,\lambda _\eta =0.1\); c \(R=1,\omega =1,\Omega =2,\alpha =0.1, \lambda _\xi =0.1,\sigma _\eta ^2 =0.1,\lambda _\eta =0.1\); d \(R=1,\omega =1,\Omega =2,\alpha =0.1,\sigma _\xi ^2 =0.1,\lambda _\xi \!=\!0.1,\lambda _\eta \!=\!0.1\); e \(R=1,\omega =1,\Omega =2,\alpha \!=\!0.1,\sigma _\xi ^2 =0.15,\sigma _\eta ^2 =0.2,\lambda _\eta =0.1\)

Full size image

As shown in Fig. 5, each curve shows that A attains a maximum value with increasing \(\gamma \), indicating that SR in the wide sense appears. In Fig.5a, there are two peaks in the response \(A( \gamma )\) for \(\alpha <0.25\), and there is one peak for \(0.25<\alpha \). Figure 5a also shows that the maximum of A decreases, the resonance peak gets flat and the position of the peak shifts toward the left with the increase of \(\alpha \). Figure 5b shows that there are two peaks in the response \(A( \gamma )\), and the two resonance peaks decrease and get flat, and their positions shift toward the right obviously with the increase of \(\Omega \). Figure 5c shows that there are two peaks in the response \(A( \gamma )\), the left peak increases sharply and the position of the left peak shifts toward the left slightly with the increase of \(\sigma _\xi ^2 \). However, the right peak decreases and the right peak shifts toward the right with the increase of \(\sigma _\xi ^2 \). Figure 5d shows that there are two peaks in the response \(A( \gamma )\), the left peak increases and the position of the left peak shifts toward the left slightly with the increase of \(\sigma _\eta ^2 \). However, the right peak decreases and the right peak shifts toward the right with the increase of \(\sigma _\eta ^2 \). Figure 5e shows that there are two peaks in the response \(A( \gamma )\) for \(\lambda _\xi <0.45\), and the two peaks decreases with the increase of \(\lambda _\xi \). Moreover, the position of the left peak shifts toward the right slightly and the position of the right peak shifts toward the left slightly with the increase of \(\lambda _\xi \) for \(\lambda _\xi <0.45\). Figure 5e also shows that there is one peak in the response \(A( \gamma )\) for \(\lambda _\xi >0.45\), the maximum of A increases, the resonance peak gets sharp slightly, and the position of the peak shifts toward the right slightly with the increase of \(\lambda _\xi \). From the equation

$$\begin{aligned} \frac{\text{ d }A}{\text{ d }\gamma }=0, \end{aligned}$$
(31)

we can calculate the position of the resonance peak in Fig. 5.

4 Conclusions

In this paper, we investigate the phenomenon of stochastic resonance in a fractional linear system subjected to two multiplicative dichotomous noises and a fractional Gaussian noise and driven by a periodic signal, since random mass and random frequency affect the dynamics of the particles at the same time. We detect SR in the wide sense existing in this linear system. Specially, the evolution of the output amplitude A with \(\Omega \) presents one-peak oscillation and two-peak oscillation. Moreover, the friction coefficient \(\gamma \) can induce stochastic multi-resonance (SMR).

In conclusion, with the proper adjustments of the parameters mentioned above, we can effectively control the stochastic resonance of this fractional linear system within a certain range. In addition, we expect that the model of a fractional oscillator with a random mass and random frequency will find many application in modern science.