Stochastic resonance in a fractional oscillator subjected to multiplicative trichotomous noise

Abstract

In this paper, stochastic resonance in a fractional oscillator with a power-law friction kernel subject to random damping is investigated both theoretically and numerically. The influence of a fluctuating damping is modeled as multiplicative trichotomous noise. The exact expression of the first moment of the system$'$s steady response has been calculated. It is shown that the interplay between multiplicative trichotomous noise and memory effect leads to stochastic resonance in the proposed system. The output amplitude gain (OAG) shows non-monotonic dependence on the driving frequency of the input signal and the characteristics of the noise. Furthermore, a multiresonance-like behavior of the OAG as function of the driving frequency and the inverse-stochastic resonance behavior of the OAG as function of the noise switching rate are observed, which is previously reported and believed to be absent in the case of the non-memory oscillator. Finally, some numerical simulations are performed to support the theoretical analyses.

1 Introduction

Recent decades, the effect of noise on dynamic system has been highly valued, stochastic resonance(SR) [1] phenomenon is exactly one of the most interesting examples among them. Although the term “SR” was originally used in a specific field, it is now widely applied to various fields including physics [2, 3], chemistry [4], biology [5], signal detection and recovery [6], circuit [7], molecular motor [8], and stock market [9, 10] due to its potential applicability. It is worth mentioning that the original understanding of SR has been extended [11], meaning the non-monotonic behavior of the certain functions of the output signal (such as moments, amplitude, signal power amplification, signal-to-noise ratio) in response to noise or system parameters.

Most of the previous researches about SR are based on the classic Langevin equation [12,13,14,15,16], i.e., the friction term is only dependent on the current speed and the correlation function of the fluctuating is a Dirac $\delta$ function. As a matter of fact, this case is suitable to describe the physical phenomena in ideal fluctuating environments such as water; however, it is not suitable to describe the environments with memory [17], such as supercooled liquids [18], dense polymer solutions [19], and semiconductors [20]. For systems with viscoelastic environment, the friction term is not only dependent on the current speed but also associated with the historical speed, so an important generalization is proposed where the friction term is replaced by a generalized friction term with a power-law type memory friction term (fractional Langevin equation: FLE) [21,22,23]. Such fractional-order models are of importance when describing the memory and hereditary properties of various viscoelastic materials and processes.

In recent years, due to the development of fractional calculus theory [24, 25] and the applications of FLE in the modeling of many phenomena in various fields, the research of the SR phenomenon in FLE has drawn great attention. Zhong et al investigated the SR phenomenon in a harmonic oscillator with fractional-order external and intrinsic damping under the external periodic force [26], Romi Mankin et al considered the long-time limit behavior of the memory-enhanced energetic stability for a fractional oscillator with fluctuating frequency [27], Litak considered a bistable dynamical system with Duffing potential, fractional damping and random excitation and found that the SR appeared for sufficiently high noise intensity [28]. So far, the plentiful achievements mainly focus on Gaussian noise or simply non-Gaussian noise such as dichotomous noise; however, since physical, chemical, biological systems can take several unusual stationary states when their parameters are affected by a noise-like influence from the surrounding environment, a more general case of random three-level telegraph processes called trichotomous noise should also be considered more often.

Indeed, trichotomous noise [29,30,31,32]has been successfully applied to investigate the reversals of the noise-induced flow, and it is more flexible in modeling natural colored fluctuations, including all cases of dichotomous noise. Lang et al investigated the SR in an underdamped system subjected to multiplicative trichotomous noise [33]. Furthermore, for trichotomous noise the flatness parameter $\delta$ can be anything from 1 to $\infty$, unlike the flatness for Gaussian colored noise $\delta =3$, and symmetric dichotomous noise $\delta$ = 1. As can be expected, this can induce a more abundant dynamic behavior, in particular a nontrivial dependence on the flatness parameter [34].What’s more, theoretical investigations motivated by recent advances in experimental study of motor proteins have indicated that noise-induced non-equilibrium effects are sensitive to noise flatness [35, 36].

In all of the above-mentioned papers, the trichotomous noise is considered only as the fluctuations of frequency or mass of harmonic oscillator [37, 38]. As presented in Ref [39], the fluctuations of damping in the model need also to be taken into account. Jiang et al. [40] considered that the disturbance of the digital signal to the analog circuit (RLC circuit) is equivalent to the action of an asymmetric dichotomous noise randomizing the damping coefficient of the harmonic oscillator; Gitterman et al. [41] found that the non-monotonic effect of the output signal exists for no matter the damping fluctuating noise is a dichotomous noise or a white noise. In fact, in many situations, which, for example, the water waves influenced by a turbulent wind field [42] and the motion of vortices [43], the velocity enters the convective term with fluctuations.

Therefore, it is of interest, both from theoretical and experimental viewpoints, to analyze the potential consequences of interplay between damping coefficient fluctuations and memory effects. The structure of the paper is arranged as follows. In Section two, the model of fractional oscillator with multiplicative trichotomous damping noise and its exact solutions will be presented. In section three, the dependence of the output amplitude gain (OAG) on the noise and system parameters are investigated by the theoretical simulations based on the exact solutions. Finally, some numerical simulations are proposed to verify the effectiveness of the analytical results.

2 Model and exact solution

As an archetypical toy model for a fractional oscillatory system strongly coupled with a noisy environment, we consider the FLE model in the fluctuating damping parameter with a memory kernel, an additive periodic force $A_0\cos (\varOmega t)$, and an internal fractional Gaussian white noise $\eta _\alpha (t)$ of zero-mean:

$$\begin{aligned} {\frac{\mathrm{d}^2 x}{\mathrm{d}t^2}}+2\gamma (1+\xi (t)) {\frac{\mathrm{d}^{\alpha }{x}}{\mathrm{d}t^{\alpha }}}+\omega ^2 x =A_0\cos (\varOmega t)+\eta _\alpha (t), \end{aligned}$$

(1)

where $2 \gamma$ is the dimensionless damping rate, the fluctuation of damping $\xi (t)$ is modeled as the symmetric trichotomous noise. The term ${\frac{\mathrm{d}^{\alpha }{x}}{\mathrm{d}t^{\alpha }}}={\frac{1}{\varGamma (1-\alpha )}}\int _{0}^{t}{\frac{\dot{x}(u)}{(t-u)^\alpha }}\mathrm{d}u$ is the Caputo fractional derivative operator, and $\alpha$ is the fractional order which satisfies $0<{\alpha }\le 1$. In particular, in the case of$\alpha =1$, Eq. (1) reduces to the classic Langevin equation with random damping which has been studied by Lang in [33].

Multiplicative noise $\xi (t)$ here we consider it to be a symmetric three-level random telegraph process which is also called the trichotomous process. As the term suggests, trichotomous noise consists of jumps between three values $\{a,0,-a\}$. The jumps follow in time according to a Poisson process, while the values occur with the stationary probabilities:

$$\begin{aligned} P_s(a)= P_s(a) =q, P_s(0)=1-2q. \end{aligned}$$

(2)

The mean value and the correlation function of $\xi (t)$ are

$$\begin{aligned} \langle \xi (t) \rangle =0,\langle \xi (t) \xi (s)\rangle = 2qa^2e^{-\nu |t-s|}. \end{aligned}$$

(3)

here, $\nu$ is the switching rate of the noise, and it is the reciprocal of the noise correlation time $\tau$: $\nu ={\frac{1}{\tau }}$. The flatness parameter $\delta$ proves to be an expression of the probability q:

$$\begin{aligned} \delta ={\frac{\langle \xi ^4(t)\rangle }{{\langle \xi ^2(t)\rangle }^2}}=\frac{1}{2q}. \end{aligned}$$

(4)

Next, to get the exact expression of output signal amplitude, we take average of Eq. (1), then we get

$$\begin{aligned}&{\frac{\mathrm{d}^2 \langle x(t) \rangle }{\mathrm{d}t^2}}+2\gamma {\frac{\mathrm{d}^{\alpha }{ \langle x(t) \rangle }}{\mathrm{d}t^{\alpha }}}+2 \gamma \langle \xi (t){\frac{\mathrm{d}^{\alpha }{x(t)}}{\mathrm{d}t^{\alpha }}} \rangle +\omega ^2 \langle x(t) \rangle \nonumber \\&\quad = A_0\sin (\varOmega t). \end{aligned}$$

(5)

To the new correlator $\xi (t){\frac{\mathrm{d}^{\alpha }{x}}{\mathrm{d}t^{\alpha }}}$, using the well-known Shapiro-Loginov procedure [45] yields

$$\begin{aligned} \langle \xi (t){\frac{\mathrm{d}^{\alpha }{x(t)}}{\mathrm{d}t^{\alpha }}} \rangle =e^{-\nu t}{\frac{\mathrm{d}^{\alpha }}{\mathrm{d}t^{\alpha }}}(\langle \xi (t) x(t) \rangle e^{\nu t}). \end{aligned}$$

(6)

Substituting Eq. (6) into Eq. (5) results in

$$\begin{aligned}&\left( {\frac{\mathrm{d}^2 }{\mathrm{d}t^2}}+2\gamma {\frac{\mathrm{d}^{\alpha }}{\mathrm{d}t^{\alpha }}}+\omega ^2\right) \langle x(t) \rangle \nonumber \\&\qquad +\,2 \gamma e^{-\nu t}{\frac{\mathrm{d}^{\alpha }}{\mathrm{d}t^{\alpha }}}{ (\langle \xi (t) x(t) \rangle e^{\nu t})}\nonumber \\&\quad =A_0\sin (\varOmega t). \end{aligned}$$

(7)

Multiplying (1) by $\xi (t)$ and averaging yields

$$\begin{aligned}&\left\langle \xi (t){\frac{\mathrm{d}^2 x(t)}{\mathrm{d}t^2}} \right\rangle +2 \gamma \left\langle \xi (t){\frac{\mathrm{d}^\alpha x(t)}{\mathrm{d}t^\alpha }}\right\rangle +2\gamma \left\langle \xi ^2(t){\frac{\mathrm{d}^\alpha x(t)}{d t^\alpha }}\right\rangle \nonumber \\&\quad +\,\omega ^2\langle \xi (t) x(t)\rangle =0. \end{aligned}$$

(8)

Analogously, to split the correlator$\langle \xi ^2(t){\frac{\mathrm{d}^\alpha x(t)}{\mathrm{d}t^\alpha }}\rangle$ we use Shapiro-Loginov procedure again which yields

$$\begin{aligned}&\left\langle \xi ^2(t){\frac{\mathrm{d}^\alpha x(t)}{\mathrm{d}t^\alpha }}\right\rangle =\langle \xi ^2(t) \rangle {\frac{\mathrm{d}^\alpha x(t)}{\mathrm{d}t^\alpha }}\nonumber \\&\quad +\,e^{-\nu t}{\frac{\mathrm{d}^\alpha x(t)}{\mathrm{d}t^\alpha }}[\langle \xi ^2(t) x(t) \rangle -\langle \xi ^2(t) \rangle x(t)e^{\nu t}]. \end{aligned}$$

(9)

Then, substituting Eqs. (6) and (9) into Eq. (8) results in

$$\begin{aligned} \begin{aligned}&4qa^2\gamma \left( {\frac{\mathrm{d}^{\alpha }}{\mathrm{d}t^{\alpha }}}\langle {x(t)}\rangle +e^{-\nu t}{\frac{\mathrm{d}^{\alpha }}{\mathrm{d}t^{\alpha }}}\left( -2qa^2\langle {x(t)}\rangle e^{\nu t}\right) \right) \\&\quad +\left( \left( {\frac{\mathrm{d}}{\mathrm{d}t}}+\nu \right) ^2+\omega ^2\right) \langle \xi (t)x(t)\rangle \\&\quad +2\gamma {e^{-\nu t}}{\frac{\mathrm{d}^{\alpha }}{\mathrm{d}t^{\alpha }}}\left( \langle \xi (t)x(t)\rangle e^{\nu t}\right) \\&\quad +2\gamma {e^{-\nu t}}{\frac{\mathrm{d}^{\alpha }}{\mathrm{d}t^{\alpha }}}\left( \langle \xi ^2(t)x(t)\rangle e^{\nu t}\right) =0. \end{aligned} \end{aligned}$$

(10)

A new correlator $\langle \xi ^2(t) x(t)\rangle$ occurs; then, we need to establish a new equation to solve these variables simultaneously. So, multiplying Eq. (1) by $\xi ^2(t)$ and averaging yields

$$\begin{aligned}&2qa^2\left( 2{\gamma }\frac{\mathrm{d}^{\alpha }}{\mathrm{d}t^{\alpha }}-2{\nu }\frac{\mathrm{d}}{\mathrm{d}t}-{\nu }^2\right) \langle {x(t)\rangle }\nonumber \\&+2{\gamma }e^{-{\nu }t}\frac{\mathrm{d}^{\alpha }}{\mathrm{d}t^{\alpha }}\left( -2qa^2\langle {x(t)\rangle }e^{{\nu }t}\right) \nonumber \\&+\left( \left( \frac{\mathrm{d}}{\mathrm{d}t}+{\nu }\right) ^2+{\omega }^2\right) \langle {{\xi }^2(t)x(t)\rangle }\nonumber \\&+2{\gamma }e^{-{\nu }t}\frac{\mathrm{d}^{\alpha }}{\mathrm{d}t^{\alpha }}\left( \langle {{\xi }^2(t)x(t)\rangle }e^{{\nu }t}\right) \nonumber \\&+2{\gamma }a^2e^{-{\nu }t}\frac{\mathrm{d}^{\alpha }}{\mathrm{d}t^{\alpha }}\left( \langle {{\xi }(t)x(t)\rangle }e^{{\nu }t}\right) =2qa^2A_0\sin ({\varOmega }t). \end{aligned}$$

(11)

we used the properties of trichotomous noise $\xi (t)$ in Eq. (11), that is,$\xi ^3(t)=a^2 \xi (t),\langle \xi ^2(t)\rangle =2qa^2$. For convenience of calculation, multiplying Eq. (7) by $2qa^2$, minusing Eq. (11) yields

$$\begin{aligned}&-2qa^2\left( \left( \frac{\mathrm{d}^{\alpha }}{\mathrm{d}t^{\alpha }}+({\omega }^2+{\nu }^2)+2{\nu }\frac{\mathrm{d}}{\mathrm{d}t}\right) \right) \langle {x(t)\rangle }\nonumber \\&\quad +2{\gamma }e^{-{\nu }t}\frac{\mathrm{d}^{\alpha }}{\mathrm{d}t^{\alpha }}\left( \langle {x(t)\rangle }e^{{\nu }t}\right) \nonumber \\&\quad +2{\gamma }(1-2q)a^2e^{-{\nu }t}\frac{\mathrm{d}^{\alpha }}{\mathrm{d}t^{\alpha }}\left( \langle {{\xi }(t)x(t)\rangle }e^{{\nu }t}\right) \nonumber \\&\quad +\left( \left( \frac{\mathrm{d}}{\mathrm{d}t}+{\nu }\right) ^2+{\omega }^2\right) \langle {{\xi }^2(t)x(t)\rangle } \nonumber \\&\quad +2{\gamma }e^{-{\nu }t}\frac{\mathrm{d}^{\alpha }}{\mathrm{d}t^{\alpha }}\left( \langle {{\xi }^2(t)x(t)\rangle }e^{{\nu }t}\right) =0. \end{aligned}$$

(12)

Therefore, we get a close system of three equations: Eqs(7),(10) and (12), for three variables, $x_1=\langle x(t)\rangle$,$x_2=\langle \xi (t) x(t)\rangle$ and $x_3=\langle \xi ^2(t) x(t)\rangle$. From these equations, one can easily find the solutions of these variables by using the Laplace transformation technique:

$$\begin{aligned} \left\{ \begin{aligned}&d_{11}X_{1}(s)+d_{12}X_{2}(s)+d_{13}X_{3}(s)=A_{0}{\frac{{\varOmega }}{{\varOmega }^2+s^2}}+d_{14}, \\&d_{21}X_{1}(s)+d_{22}X_{2}(s)+d_{23}X_{3}(s)=d_{24}, \\&d_{31}X_{1}(s)+d_{32}X_{2}(s)+d_{33}X_{3}(s)=d_{34}. \end{aligned} \right. \end{aligned}$$

(13)

where $X_i(s)=L{x_i(t)}\doteq \int _{0}^{\infty }x_i(t)e^{-st}\mathrm{d}t,i=1,2,3$. Here, we consider the solutions in the long-time limit which means the influence of the initial conditions will vanish and the expression of $X_1(s)$ can be obtained by solving the linear system of equations (13)

$$\begin{aligned} X_{1}(s)={\frac{d_{22}d_{33}-d_{23}d_{32}}{d_{12}d_{23}d_{31}-d_{11}d_{23}d_{32}-d_{12}d_{21}d_{33}+d_{11}d_{22}d_{33}}} \cdot {\frac{A_(0){\varOmega }}{{\varOmega }^2+s^2}}. \end{aligned}$$

(14)

where,

$$\begin{aligned} \begin{aligned} d_{11}&= s^2+2{\gamma }s^{\alpha }+{\omega }^2, \\ d_{12}&= 2{\gamma }(s+{\nu })^{\alpha }, \\ d_{13}&= 0,\\ d_{21}&= 4qa^2{\gamma }(s^{\alpha }-(s+{\nu })^{\alpha }), \\ d_{22}&= (s+{\nu })^2+{\omega }^2+2{\gamma }(s+{\nu })^{\alpha }, \\ d_{23}&= 2{\gamma }(s+{\nu })^{\alpha }, \\ d_{31}&= 2qa^2(s^2+{\omega }^2+{\nu }^2+2{\nu }s)+2{\gamma }(s+{\nu })^{\alpha }, \\ d_{32}&= 2qa^2(1-2q)(s+{\nu })^2, \\ d_{33}&= (s+{\nu })^2+{\omega }^2+2{\gamma }(s+{\nu })^{\alpha }. \end{aligned} \end{aligned}$$

(15)

Next, applying the inverse Laplace transform technique to Eq. (14), one gets

$$\begin{aligned} \langle {x(t)\rangle }_{as} =\lim _{t \rightarrow +\infty } \langle {x(t)\rangle }= A_{0}\int _{0}^{t}h_{10}(t-{\tau })\sin (\varOmega \tau ) \mathrm{d}{\tau }. \end{aligned}$$

(16)

The Laplace transform of $h_{10}(t)$ is $H_{10}(s)$,$H_{10}(s)$ is determined by Eq. (13):

$$\begin{aligned} H_{10}(s)=\frac{d_{22}d_{33}-d_{23}d_{32}}{d_{12}d_{23}d_{31}-d_{11}d_{23}d_{32}-d_{12}d_{21}d_{33}+d_{11}d_{22}d_{33}}. \end{aligned}$$

(17)

On the other hand, using the linear response theory, $\langle x(t) \rangle$ can be given by means of the complex susceptibility as:

$$\begin{aligned} \langle {x(t)\rangle }_{as} = A\sin ({\varOmega }t+{\phi }), \end{aligned}$$

(18)

where $A,\phi$ are the amplitude and the phase shift of the system stationary state response, respectively, which satisfy

$$\begin{aligned} A=|H_{10}(j\varOmega )|,\phi =\arctan (H_{10}(j\varOmega )). \end{aligned}$$

(19)

Finally, according to its definition, we obtain the output amplitude gain (OAG:G):

$$\begin{aligned} G=\sqrt{\frac{A}{A_0}} =\sqrt{\frac{\left| {H_{10}(j{\varOmega }}\right| }{A_0}} =\sqrt{\frac{f_1^2+f_2^2}{f_3^2+f_4^2}}. \end{aligned}$$

(20)

where

$$\begin{aligned} f_1=&\, \varOmega ^{4}-6\varOmega ^{2}\nu ^{2}+\nu ^{4}-2\varOmega ^{2}\omega ^{2}+2\nu ^{2}\omega ^{2}\\&+\omega ^{4} -4\gamma r^{2\alpha } b\cos {\alpha \theta } \\&+ 4{\gamma ^2}{r^{2\alpha }}{\cos }\left( {2 \alpha \theta } \right) - 8\gamma \varOmega \nu {r^{\alpha }}{\cos }\left( {\alpha \theta } \right) ,\\ f_2=&- 4\left( {{\varOmega ^2} - {\nu ^2} - {\omega ^2} - 2\gamma {r^{2\alpha }}\cos \left( {\alpha \theta } \right) } \right) \left( \varOmega \nu \right. \\&\left. + \gamma r^{2\alpha } \sin \left( {\alpha \theta } \right) \right) ,\\ f_3=&- {\varOmega ^6} + 6{\varOmega ^4}{v^2} - {\varOmega ^2}{v^4} + 3{\varOmega ^4}{w^2} - 8{\varOmega ^2}{v^2}{\omega ^2} \\&+ {v^4}{\omega ^2} - 3{\varOmega ^2}{\omega ^4} + 2{v^2}{\omega ^4} \\&+ {\omega ^6} +2\gamma {\varOmega ^\alpha }\left( {\varOmega ^4} + {{\left( {{v^2} + {\omega ^2}} \right) }^2} \right. \\&\left. - 2{\varOmega ^2}\left( {3{v^2} + {\omega ^2}} \right) \right) \cos \left( {\frac{{\alpha \pi }}{2}} \right) \\&+ 4\gamma {r^\alpha }\left( {{\varOmega ^2} - {\omega ^2}} \right) \left( {{\varOmega ^2} - {v^2} - {\omega ^2}} \right) \cos \left( {\alpha \theta } \right) \\&- 4\gamma {\varOmega ^2}{r^{2\alpha }}\cos \left( {2\alpha \theta } \right) \left( {1 - {\omega ^2}} \right) \left( \gamma \right. \\&+\left. 2{q^2}{a^2} - q{a^2} \right) \\&+8{\gamma ^3}{r^{3\alpha }}\cos \left( {3\alpha \theta } \right) \left( {1 + 2q{a^2}} \right) \end{aligned}$$

$$\begin{aligned}&- 8{\gamma ^2}{\varOmega ^\alpha }{r^\alpha }\cos \left( {\frac{{\alpha \pi }}{2} + \theta } \right) \left( {\varOmega ^2} - {v^2}\right. \\&-\left. {\omega ^2} \right) \left( {1 - q{a^2}} \right) \\&+ 8{\gamma ^2}{\varOmega ^\alpha }{r^{2\alpha }}\left( \gamma - q{a^2} - 2q{a^2}\gamma \right. \\&+\left. 2{q^2}{a^2} \right) \cos \left( {\frac{{\alpha \pi }}{2} + 2\theta } \right) \\&+ \gamma {\varOmega ^{1 + \alpha }}\nu \sin \left( {\frac{{\alpha \pi }}{2}} \right) \left( {{\varOmega ^2} - {\nu ^2} - {\omega ^2}} \right) \\&+ 8\gamma \varOmega {r^\alpha }\sin \left( {\alpha \theta } \right) \left( {{\varOmega ^2} - {\omega ^2}} \right) \\&- 16{\gamma ^2}{\varOmega ^{1 + \alpha }}\nu {r^\alpha }\sin \left( {\frac{{\alpha \pi }}{2} + \theta } \right) \left( {1 - q{a^2}} \right) ,\\ f_4=&\, 2 \left( {\varOmega ^5}\nu - 2{\varOmega ^3}{\nu ^3} - 4{\varOmega ^3}\nu {\omega ^2} + 2\varOmega {\nu ^3}{\omega ^2} \right. \\&+\left. 2\varOmega \nu {\omega ^4} \right) - \mathrm{{8}}\gamma {\varOmega ^{1 + \alpha }}v b\cos \left( {\frac{{\alpha \pi }}{2}} \right) \\&- \mathrm{{8}}\gamma \varOmega v{r^\alpha }\cos \left( {\alpha \theta } \right) \\&+ \mathrm{{16}}{\gamma ^2}{\varOmega ^{1 + \alpha }}v{r^\alpha }\cos \left( {\frac{{\alpha \pi }}{2} + \theta } \right) \left( {1 - q{a^2}} \right) \\&+ \mathrm{{2}}\gamma {\varOmega ^\alpha }\sin \left( {\frac{{\alpha \pi }}{2}} \right) \left( {\varOmega ^4} - 6{\varOmega ^2}{v^2} + {v^4} \right. \\&-\left. 2{\varOmega ^2}{\omega ^2} + 2{v^2}{\omega ^2} + {\omega ^4} \right) \\&+\, \mathrm{{4}}\gamma {r^\alpha }\sin \left( {\alpha \theta } \right) \left( {\varOmega ^4} - {\varOmega ^2}{v^2} - 2{\varOmega ^2}{\omega ^2} \right. \\&\left. + \,{v^2}{\omega ^2} + {\omega ^4} \right) \\&- \mathrm{{4}}\gamma {r^\alpha }\sin \left( {2\alpha \theta } \right) \left( {\gamma - q{a^2} + 2{q^2}{a^2}} \right) \left( {{\varOmega ^2} - {\omega ^2}} \right) \\&+ \mathrm{{8}}{\gamma ^3}{r^{3\alpha }}\sin \left( {3\alpha \theta } \right) \left( {1 + 2q{a^2}} \right) \\&- 8{\gamma ^2}{\varOmega ^\alpha }{r^\alpha }b\sin \left( {\frac{{\alpha \pi }}{2} + \theta } \right) \left( {1 - q{a^2}} \right) \\&+ 8{\gamma ^2}{\varOmega ^\alpha }{r^\alpha }\left( \gamma - q{a^2} - 2q{a^2}\gamma \right. \\&\left. +\, 2{q^2}{a^2} \right) \sin \left( {\frac{{\alpha \pi }}{2} + 2\theta } \right) ,\\ r=&\, \sqrt{{{\left( {{{\left( {{\varOmega ^2} + {\nu ^2}}\right) }}}\right) }}} , \theta = \arctan \left( {\frac{\varOmega }{\nu }} \right) ,\ b\\&\quad = {\varOmega ^2} - {v^2} - {\omega ^2}. \end{aligned}$$

3 Trichotomous noise-induced stochastic resonance

According to the formula (20), we can obtain the analytical expression of the output amplitude gain G. It would be very interesting to explore the dynamic behaviors of G, so in the next section, we will discuss the effects of the system parameters (including the driving frequency$\varOmega$, the damping coefficient $\gamma$, the memory exponent$\alpha$.) and the noise parameters (including noise switching rate$\nu$ and noise amplitude a.) on the output amplitude gain G.

3.1 Bona fide stochastic resonance

3.1.1 Response to the driving frequency $\varOmega$

In Fig. 1, several graphs depict the dependence between G and the driven frequency $\varOmega$ for various values of parameters (including the switching rate $\nu$ and the amplitude of the multiplicative noise a, the friction coefficient $\gamma$ and the fractional order $\alpha$). These graphs show a typical resonance-like behavior of $G(\varOmega )$ for the other fixed parameters, which indicates the bona fide SR takes place. Moreover, for some values of the system parameters a double-peak SR appears.

Fig. 1

The OAG G versus the driving frequency $\varOmega$ at $\omega =1, q=0.2$, Other parameter values: $\mathbf a \, \alpha =0.8, \gamma =0.2, a=0.5; \mathbf b \, \alpha =0.8, \gamma =0.2, \nu =0.1; \mathbf c \, \alpha =0.8, \nu =0.01, a=0.8; \mathbf d \, \gamma =0.2, \nu =0.01, a=0.8$

In Fig. 1a, it can be seen that when the appropriate noise is applied, G increases non-monotonously as a function of $\varOmega$ which indicate the occurrence of the bona fide SR phenomenon. Obviously, there are two different types of the bona fide SR which are represented as depending on $\nu$: (i) when $\nu =0.01,0.1$, both of their graphs display two maximum values of $G(\varOmega )$, i.e., the stochastic mulit-resonance (SMR) phenomenon occurs, which is not observed in the conventional linear system [33]. (ii) when $\nu >0.1$, no SMR phenomenon is met and with increasing $\nu$ the graph increases at first and then decreases (one-peak form SR phenomenon).

In Fig. 1b, we depict the behaviors of the OAG G versus the input signal frequency $\varOmega$ for different values of the noise amplitude a. These graphs show a typical resonance-like behavior of $G(\varOmega )$ which indicates that the bona fide SR occurs. As a rule, the maximal value of G changes non-monotonically as the value of a increases, while the positions of the maxima are monotonically shifted to a lower $\varOmega$ when $a<2$ and almost keep still when $a>2$ as $\nu$ rises. These graphs show that the increasing noise amplitude enhances the SR phenomenon first and then weaken it.

In Fig. 1c, we depict the behaviors of $G(\varOmega )$ for different representative values of the frictional coefficient $\gamma$. These graphs show a typical resonance-like behavior of $G(\varOmega )$. As a rule, three characteristic regions can be discerned for the frictional coefficient $\gamma$. (i) In the case of $\gamma <=0.6$, a multiresonance of $G(\varOmega )$ with two peaks occurs. (ii) If $\gamma >0.6$, there exists one resonance peak of $G(\gamma )$. (iii) when $\gamma$ continue to increase, the SR phenomenon disappears. G depends on $\varOmega$ monotonically. It is seen from Eq. (19) that the formation of the multiresonance versus $\varOmega$ can be explained as an interplay of two different effects: one caused by the energetic instability of the oscillator and another, which is due to the friction induced resonance of the memory effect.

Figure 1d shows output amplitude gain G as a function of the driving frequency $\varOmega$ for different values of $\alpha$, respectively. One can observe the nonmontonic relationship between G and $\varOmega$ clearly which indicates that the bona fide stochastic resonance occurs in the figure. What’s more, there is more than one peak in these curves, i.e., stochastic multiresonance (SMR) phenomenon occurs, which is not observed in the conventional system in [33]. With the increase in the memory exponent $\alpha$, the first peak value increases and the position of the peak shifts to the left slightly, while the second peak value changes non-monotonically and the position of the peak almost keep still around $\varOmega \approx 1$.

3.2 Stochastic resonance in a broad sense

3.2.1 Response to the noise amplitude a

Fig. 2

The OAG G versus the multiplicative noise amplitude a at $\omega =1$, Other parameter values: $\mathbf a \, \alpha =1, \gamma =0.2, q=0.2, \varOmega =1; \mathbf b \, \alpha =0.6, \nu =0.6, q=0.2, \varOmega =1; \mathbf c \, \alpha =0.6, \nu =0.6, q=0.2, \varOmega =1; \mathbf d \, \alpha =0.6, \gamma =0.2, \nu =0.3, \varOmega =1; \mathbf e \, \alpha =0.6, \gamma =0.2, q=0.2, \nu =0.3; \mathbf f \, \gamma =0.6, \nu =0.6, q=0.3, \varOmega =1$

In Fig. 2, we depict the behavior of G versus the noise amplitude a for different representative values of the parameters. These graphs show a typical resonance-like behavior, which means that SR appears in a broad sense. As a rule, the maximal values of G(a) increases as the value of a increases for some fixed parameters. In particular, for some fixed parameters, by increasing the memory effect, the SR of the fractional oscillator is significantly enhanced as compared to an ordinary oscillator (without memory, $\alpha = 1$).

In Fig. 2a, we show the G as a function of the noise amplitude a for different values of $\nu$. The non-monotonic behavior is shown in these graphs, which means the SR phenomenon in a broad sense existed. What’s more, the peak value of the maximum depends on $\nu$ non-monotonically while the position the peak shift to a higher a with the increasing $\nu$.

In Fig. 2b, c we depict, on two panels, the behavior of G for small and large values of the friction coefficient $\gamma$ versus the noise amplitude a. The variation trend of the peak of the presented curves in Fig. 2b is very different with those curves in Fig. 2c. With the increase in $\gamma$, the peak is increased in the case of small value of $\gamma$ in Fig. 2c but decreased in large value of $\gamma$ in Fig. 2b. These indicate that the friction coefficient $\gamma$ has complex effect on the output gain G, and for an optimal friction coefficient $\gamma$, G possesses a maximum.

In Fig. 2d, the graph shows typical SR non-monotonic behavior. With a rise in q the positions of the maxima shift to a smaller a, while the heights are monotonically increasing with the value of q. When $q=0.5$, the trichotomous noise degenerates into the dichotomous noise, and then the curve in Fig. 3d represents the SR induced by dichotomous noise. The peak value of the curve can be increased by adjusting the stationary probability.

In Fig. 2e, we show the dependence of the output amplitude gain G on the multiplicative noise amplitude a for different frequencies $\varOmega$ of the external field. These graphs show typical SR non-monotonic behavior for $\varOmega ~<\omega$. With a rise in $\varOmega$, the positions of the maxima are shifted to lower a, while the heights are non-monotonic functions of $\varOmega$. On the other hand, when $\varOmega>1.2>\omega$, the SR phenomenon disappears.

Figure 2f shows the relationship between the system output amplitude gain G and the noise amplitude a for different values of the memory exponent $\alpha$ which shows the following facts clearly. (i) With the increasing noise amplitude a, the maximum value occurs, namely the SR occurs in a broad sense in the system. (ii) With the increase in the memory exponent $\alpha$, the peak value of the curve is monotonic and the position of the peak almost keeps still. In conclusion, the phenomenon of SR can be enhanced by decreasing the order of the memory order.

3.2.2 Response to the noise switching rate $\nu$

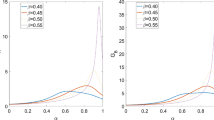
In Fig. 3, we aim to examine the dependence of G on the noise switching rate $\nu$ under various values of other parameters. All these figures show a typical non-monotonic behavior of $G(\nu )$, which means the SR takes place in a broad sense. Moreover, G reaches the minimum by increasing the value of $\nu$; this new phenomenon is called reverse-resonance [33] which has not been found in the non-memory system.

Firstly, in Fig. 3a, we plot the curves of the output amplitude gain G as a function of the noise switching rate $\nu$ with various values of the driving frequency $\varOmega$. It can be seen that when $\varOmega =0.8$, with the increasing $\nu$, G firstly decreases, then increases and finally decreases, which means that the one-peak and one-valley SR phenomenon takes place. In addition, with the increase in $\nu$, the position of the peak shifted to a lower $\nu$ as $\varOmega$ rises.

Fig. 3

The OAG G versus the multiplicative noise switching rate $\nu$, Other parameter values: $\mathbf a \, \alpha =0.8, \omega =1, \gamma =0.5, q=0.2, a=1.6; \mathbf b \, \alpha =0.5,\omega =1, q=0.2, q=0.2, a=1.6, \varOmega =1; \mathbf c \, \alpha =0.8, \omega =1, \gamma =2.1, q=0.5, \varOmega =0.3; \mathbf d \, \alpha =0.6, \omega =1, \gamma =0.5, a=1, \varOmega =0.3$

In Fig. 3b, we present the curves of the output amplitude gain G as a function of the noise switching rate $\nu$ with increase in the friction coefficient $\gamma$. It is obviously that G reaches a maximum as $\nu$ increases, which means that the one-peak SR phenomenon takes place. Moreover, with the increases in $\gamma$, the maximum of G decreases and the position of the peak moves to the right side slightly.

Figure 3c shows a non-monotonic behavior that is different from other figures. The curves of output amplitude gain G as a function of the noise switching rate $\nu$ for different noise amplitude a have a minimum. The new phenomenon is called reverse-resonance [33], which has not been found in corresponding linear system.

In Fig. 3d, we depict the curves of G versus the switching rate $\nu$ for different values of q. It is obvious that the SR phenomenon occurs for proper values of $\gamma$. For an optimal friction coefficient $\gamma$, the output amplitude gain G possesses a maximum. What’s more, the increasing q enhances the SR phenomenon.

4 Numerical simulation

In this section, in order to verify the effectiveness of the analytic result, the numerical simulations of the fractional Eq. (1) are presented by using the predictor–corrector approach [46]. In Fig. 4, we plot the frequency spectrum of the output signal of Eq. (1) with different noise amplitudes. The execution time and the step of the algorithm are: $T=1000\pi (s), T_s=0.001(s)$, respectively.

Fig. 4

The frequency spectrum of the output signal with four different multiplicative noise intensities. $\mathbf a \, a=0; \mathbf b \, a=1; \mathbf c \, a=0.3; \mathbf d \, a=1.2$. Other parameter values: $\alpha =0.8, \gamma =0.1, \omega =1, q=0.2, \nu =1$

In the absence of noise, i.e., the noise amplitude $a=0$, Fig. 4a shows that the frequency spectrum of the output signal $A_1(\varOmega _1)$ attains the maximum value at $\varOmega _1=\varOmega =1$, and the maximum value is $A_1(\varOmega _1=1)=4.9801$; Meanwhile, we have the analytic result $A(\varOmega =1)=4.9932$ in Eq. (19). Comparing these two values, we can see that both of them are statistically uniformity.

In the case of the noisy background, we depict the frequency spectrum $A_1(\varOmega _1)$ when the noise amplitude $a=1$, Fig b shows that there is a peak at $\varOmega _1=\varOmega =1$, and the maximum value is $A_1(\varOmega _1=1)=5.2493$. In the range of allowable error, we see that the numerical simulation result agrees statistically with the analytical result $A(\varOmega =1)=5.2408$ calculated by Eq. (20).

Finally, to identify the SR behavior in the fractional system, we plot the power spectral as a function of frequency when the noise amplitude $a=0.3,1.2$, respectively. In all of the subplots, the power spectrum of the fractional system has a sharp peak at the driving frequency of the periodic signal $\omega =1$. Furthermore, it can be observed that as the noise amplitude a is increased, the height of the peak value increases at first and then decreases which shows the possibility of an occurrence of SR.

5 Conclusion

To summarize, we investigated, in the long-time regime, the stochastic resonance in a stochastic fractional oscillator with a power-law kernel subject to multiplicative trichotomous Markovian noise. A closed system of equations for the first-order moments $\langle x\rangle$ are given by using the property of the trichotomous noise and the Shapiro-Loginov formula. According to the definition of the output amplitude gain (OAG), the exact expression has been obtained, and then the non-monotonic behaviors of G as a function of noise parameters have been shown in figures.

A major virtue of the investigated model is that an interplay of the colored trichotomous noise, the external periodic forcing, and memory effects in a noisy, fractional oscillator can generate rich variety of non-equilibrium cooperation phenomena, i.e., three different forms of SR which contains the single-peak SR, the multi-peak SR (SMR) and the inverse SR. Besides, we have the following conclusion:

• (i) The OAG reaches a maximum value with the increases in the driving frequency $\varOmega$, in Sect. 3.1, which means the bona fide SR takes place. Moreover, the influence of noise switching rate $\nu$, the frictional coefficient $\gamma$ and the memory exponent $\alpha$ can induce stochastic multiresonance, which have not been observed in the case of the non-memory oscillator system [29].

• (ii) The dependence of OAG on the noise amplitude a and the noise switching rate $\gamma$ are given in Sect. 3.2, the results indicated that the SR exists in a broad sense when other parameters are fixed. We found that the phenomenon of SR can be enhanced by decreasing the value of the memory order (see Fig. 2f). What’s more, at intermediate values of the memory exponent and the noise switching rate, the SR of the fractional oscillator is significantly enhanced as compared to an ordinary oscillator with $\alpha =0$.

Furthermore, some numerical simulations are proposed to verify the effectiveness of the analytical results, showing the reliability of the results of this study and its guiding value for practical applications.