1 Introduction

A novel category of working liquids, consisting of a mixture or composite of two or more types of nanoparticles (or carbon nanotubes) suspended in the base fluid, termed as hybrid nanofluids, has been studied recently by various researchers. Due to their enhanced thermal conductivity in comparison with the nanofluids with one type of nanoparticles, these hybrid nanoliquids are finding applications in different kind of heat exchangers (e.g., tube in tube, parallel plate, coiled or helical coil heat exchanger), mini- or micro-channel heat sinks, heat pipes, etc. Firstly, Jana et al. [1] prepared Au–CNTs/water and Cu–CNTs/water hybrid nanofluids and measured their thermal conductivities. Suresh et al. [2] designed Cu–Al2O3/water hybrid nanofluid and calculated the hike in thermal conductivity and the viscosity of the hybrid nanofluid by suspending different volume fractions of Cu–Al2O3 hybrid nanocomposites in water. Their experimental results reported a 12.11% hike in thermal conductivity with a 2% volume fraction of hybrid nanoparticles in water. Esfahani et al. [3] investigated the impact of temperature and volume fraction on thermal conductivity of ZnO–Ag (50:50%)/water hybrid nanofluid. They observed an enhancement in thermal conductivity with an increment in volume fraction at higher temperatures due to the Brownian motion and particle clustering. Sarkar et al. [4] and Huminic et al. [5] presented a comprehensive review of the recent research work done in heat transfer enhancement using hybrid nanoliquids.

Nanofluids comprising carbon nanotubes (CNTs) have applications in heat transfer enhancement processes in various industries due to their ultra-high thermal conductive nature, chemical inertness, and lightweight. Sundar et al. [6] examined the heat and flow characteristics of Fe3O4–MWCNTs/water hybrid nanofluid experimentally at two different Reynolds numbers. Their experimental results reveal that with a 0.3% volume fraction of hybrid nanocomposite in water, 29% enhancement in thermal conductivity, and nearly 31% increment in Nusselt number of the hybrid nanofluid compared to water. Tong et al. [7] experimentally analyzed photo-thermal energy conversion and optical characteristics of Fe3O4–MWCNTs/water–EG hybrid nanofluid. Their results disclosed that Fe3O4–MWCNTs/water–EG hybrid nanofluid’s photo-thermal energy conversion efficiency doubled than the nanofluid with Fe3O4 only, as a result of which the hybrid nanofluid offers a significant enhancement in heat transfer rate when compared to Fe3O4 nanofluid. Afshari et al. [8] experimentally investigated the rheological behavior of hybrid nanofluid of aluminum oxide and multi-walled CNTs in a mixture of water (80%) and ethylene glycol (20%). Their results revealed that the nanofluid and base fluid samples with solid volume fractions of less than 0.5% had Newtonian behavior while high solid volume fractions (0.75 and 1%) exhibit a pseudoplastic rheological behavior with a power-law index of less than unity. Zadkhast et al. [9] experimentally investigated enhancement in thermal conductivity of water with the addition of CuO and MWCNTs. Their experimental investigations reported an enhancement in thermal conductivity of CuO–MWCNTs/water hybrid nanofluid with temperature and higher solid concentration of nanoparticles and CNTs. Experimental studies by Shahsavar et al. [10] reported that the hybrid nanofluid exhibits Newtonian behavior at high shear rates while it behaves as a shear-thinning fluid at low shear rates. Their results also showed that thermal conductivity experiences a peak on the application of the external magnetic field. Shahsavani et al. [11] and Mirbagheri et al. [12] studied the water–ethylene glycol mixture at different solid volume fractions of functionalized multi-walled carbon nanotubes experimentally. Esfe et al. [13,14,15] experimentally investigated SiO2–MWCNTs/EG, MgO–MWCNTs/EG–water, and ZnO–DWCNTs/EG hybrid nanofluids for different nanoparticle volume fractions at a temperature range of 30–40 °C. They found that hybrid nanofluids are not only beneficial in terms of enhanced rate of heat transfer (or thermal conductivity), but are economically sound too when compared to monoparticle nanofluids (i.e., nanofluids with one type of nanoparticles or CNTs). They developed Sork (ANN) models based on their experimental thermal conductivity ratio (TCR) data. They suggested that the use of artificial and mathematical methods can increase economic efficiency to a significant level.

Some recent numerical investigations on the heat and flow characteristics of a hybrid nanofluid with mathematical modeling are mentioned in [16,17,18,19,20,21,22,23,24,25]. Hayat et al. [16, 17] numerically investigated Ag–CuO hybrid nanofluid flow past a stretching surface using a Newtonian fluid flow model. They found that the extent of heat transfer using a hybrid nanofluid is more than Ag–water or CuO–water nanofluid. Numerical investigation on entropy production in MHD flow of Al2O3–Cu/water hybrid nanofluid through a square porous cavity, a porous channel, and a square enclosure was carried out by Mansour et al. [18], Das et al. [19], and Abdel-Nour et al. [20] respectively. Slimani et al. [21] examined the impact of porosity ratio, Hartmann number on Nusselt number for MHD convective flow of Cu–Al2O3/water hybrid nanofluid through a porous conical enclosure. MHD-driven boundary layer flows have various applications in medical sciences for targeted drug delivery or to control blood flow during surgery and space weather forecasting or in high-speed electromagnetic propulsion systems, power generation, etc. Hong et al. [26] have experimented and reported that under the application of a magnetic field, \({\text{Fe}}_{2} {\text{O}}_{3}\) nanoparticles help in connecting carbon nanotubes by forming aligned chains in composite nanofluids. It implies that the impact of the external magnetic field results in the enrichment of heat transfer in nanofluids. Sheikholeslami et al. [27] investigated the effect of volume fraction of \({\text{Fe}}_{3} {\text{O}}_{4}\) nanoparticles on MHD forced convective heat exchange in \({\text{Fe}}_{3} {\text{O}}_{4}\)–water nanofluid flow in a lid-driven enclosure. Sandeep et al. [28] explored the impact of incorporating magnetite \({\text{Fe}}_{3} {\text{O}}_{4}\) nanoparticles in the Oldroyd-B and Jeffery fluids flowing over a stretching sheet. Acharya and Mabood [29] examined hydrothermal features of ferrous graphene/water hybrid nanofluid flow over a bended structure in the presence of magnetic field and thermal radiation. Mabood et al. [30] investigated unsteady MHD boundary layer flow of Cu–\({\text{Fe}}_{3} {\text{O}}_{4}\)/water hybrid nanofluid over a flat/slandering stretching surface. Some more recent works on MHD nanofluids are mentioned in [31,32,33,34]. Recently, Saba et al. [35] have studied the heat and the flow characteristics of Fe3O4–CNTs/water hybrid nanofluid flow through a channel and observed that the addition of CNTs to Fe3O4–water nanofluid affect the heat transfer characteristics significantly. However, minimal numerical studies are available to analyze the heat transport characteristics of a metal oxide–CNTs hybrid nanofluid flow past different geometries using mathematical modeling.

The concept of activation energy was furnished by Svante Arrhenius in 1889. It has significant applications in geothermal processes, oil emulsions, chemical engineering, and hydrodynamics. Activation energy is the minimum amount of energy required to convert the reactants into products. The energy stored in the molecules in the form of potential energy or kinetic energy is used in the form of activation energy to perform a chemical reaction. The impact of Arrhenius activation energy on Newtonian or non-Newtonian boundary layer flow of a nanoliquid is analyzed numerically by various researchers [36,37,38,39,40,41,42,43,44,45] by employing Buongiorno’s nanofluid. However, Lu et al. [46] and Khan et al. [47] have studied the impact of the binary chemical reaction and Arrhenius activation energy on boundary layer flow by employing Tiwari and Das model [48]. While using Tiwari and Das’s model [48], the thermophysical properties like thermal conductivity, viscosity, etc., are calculated by considering the nanofluid to be a two-phase or two-component mixture, and the nanoparticles are assumed to be of uniform shape and size. Prabavathi et al. [49] examined the MWCNTs–water and SWCNTs–water nanofluid flow over a cone. In contrast, Kandasamy et al. [50] examined SWCNTs–water, Cu–water, and alumina–water nanofluid flow over a plate in the presence of chemical reaction by employing Tiwari and Das model.

Hybrid nanofluids are finding applications in the various types of heat exchangers or micro-heat sinks due to their enhanced thermal conductivity and better rheological behavior than monotype nanofluids. Hybrid nanofluids with carbon nanotubes are investigated experimentally by a wide variety of researchers [6,7,8,9,10,11,12,13,14,15], as discussed in the above paragraphs due to the extremely high thermal conductivity of carbon nanotubes. However, limited numerical studies are conducted to investigate the heat and mass transport characteristics of a metal oxide–CNTs hybrid nanofluid using mathematical modeling. To the best of the author’s knowledge, a numerical study on the impact of activation energy on heat and mass transfer characteristics of unsteady viscoelastic boundary layer flow of a hybrid nanofluid, comprising metallic oxide nanoparticles and carbon nanotubes, has not been reported yet. Motivated by this, the authors analyzed the heat and mass transport characteristics of hybrid nanofluids comprising metal oxide nanoparticles and MWCNTs in ethylene glycol using the Tiwari and Das model. The unsteady MHD non-Newtonian flow is modeled with the help of a viscoelastic second-grade fluid model, energy equation, and concentration equation, taking into account the effect of Arrhenius activation energy on the flow. The flow governing equations are coupled PDEs of a highly nonlinear nature, which are solved by shooting strategy after transforming them to ODEs with suitable similarity transformations. The impact of different thermofluidic parameters such as unsteadiness parameter, activation energy parameter, chemical reaction parameter, magnetic number, temperature difference parameter and Eckert number on the hybrid nanofluid flow is visualized through graphical profiles of the Sherwood number, Nusselt number, and skin friction coefficient.

2 Physical and mathematical description of the problem

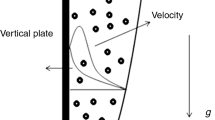
Consider an incompressible, two-dimensional laminar flow of a hybrid nanoliquid over a permeable stretching sheet in an unsteady MHD environment. The hybrid nanoliquid comprises metal oxide nanoparticles, and multi-walled carbon nanotubes (MWCNTs) immersed in a viscoelastic fluid. The flow is induced by the permeable sheet stretching with velocity \(u_{{\text{w}}} (x,t) = {{ax} \mathord{\left/ {\vphantom {{ax} {\left( {1 - ct} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1 - ct} \right)}}\) in the quiescent surrounding nanofluid. Here \(a,\,c > 0\) are constants, and the term \({a \mathord{\left/ {\vphantom {a {(1 - ct)}}} \right. \kern-\nulldelimiterspace} {(1 - ct)}}\) represents the effective stretching rate where \(ct < 1\). The dimensions of \(a\) and \(c\) are of (time)−1. The flow region is exposed to the time-varying magnetic field \(B(t) = {{B_{0} } \mathord{\left/ {\vphantom {{B_{0} } {\sqrt {1 - ct} }}} \right. \kern-\nulldelimiterspace} {\sqrt {1 - ct} }}\) oriented in the positive direction of the Y-axis, as depicted in Fig. 1. The temperature at the sheet’s surface is taken as \(T_{{\text{w}}} (x,t) = T_{\infty } + {{ax^{2} T_{0} } \mathord{\left/ {\vphantom {{ax^{2} T_{0} } {2v(1 - ct)^{3/2} }}} \right. \kern-\nulldelimiterspace} {2v(1 - ct)^{3/2} }}\). Here \(T_{\infty }\) and \(T_{0}\) are the ambient fluid temperature and constant reference temperature, respectively, as specified in Andersson et al. [51]. Similarly, the volume fraction of nanoparticles \(C_{{\text{w}}}\) at the sheet surface is given by \(C_{{\text{w}}} (x,t) = C_{\infty } + {{ax^{2} C_{0} } \mathord{\left/ {\vphantom {{ax^{2} C_{0} } {2\nu (1 - ct)^{3/2} }}} \right. \kern-\nulldelimiterspace} {2\nu (1 - ct)^{3/2} }}\) where \(C_{\infty }\) represents nanoparticles volume fraction in the ambient fluid. The conservation of mass, momentum and heat equations in the Cartesian coordinates for unsteady MHD viscoelastic second-grade fluid flow [52,53,54,55] are expressed in Eqs. (1)–(4).

$$\nabla .\overline{V} = 0$$
(1)
$$\rho_{{{\text{hnf}}}} \left[ {\frac{{\partial \overline{V} }}{\partial t} + (\overline{V} .\nabla )\overline{V} } \right] = - \nabla p + \nabla .\tau - \overline{J} \times \overline{B}$$
(2)
$$\left( {\rho C_{{\text{p}}} } \right)_{{{\text{hnf}}}} \left[ {\frac{\partial T}{{\partial t}} + (\overline{V} .\nabla )T} \right] = \kappa_{{{\text{hnf}}}} \nabla^{2} T + tr(\tau .L) + \frac{{\overline{J}^{2} }}{{\sigma_{{{\text{hnf}}}} }}$$
(3)
$$\frac{\partial C}{{\partial t}} + (\overline{V} .\nabla )C = D_{0} \nabla^{2} C - K_{{\text{r}}} (C - C_{\infty } )$$
(4)
Fig. 1
figure 1

Geometrical representation of the flow

Full size image

The constitutive stress relation for viscoelastic second-grade fluid is stated in Eq. (5).

$$\tau = - pI + A_{1} \left( {\mu \, + \alpha_{2} \,A_{1} } \right) + \alpha_{1} \,A_{2}$$
(5)

where

$$\begin{array}{*{20}l} {A_{1} = \nabla \bar{V} + \left( {\nabla \bar{V}} \right)^{T} ,} \hfill \\ {A_{2} = \frac{{{\text{d}}A_{1} }}{{{\text{d}}t}} + A_{1} \nabla \bar{V} + \left( {\nabla \bar{V}} \right)^{T} A_{1} ,} \hfill \\ {\mu \ge 0,\quad \alpha _{1} \ge 0,\quad \alpha _{1} + \alpha _{2} = 0.} \hfill \\ \end{array}$$

where \(p\) denotes the hydrostatic pressure, \(\alpha_{1}\) and \(\alpha_{2}\) are the material moduli, \(\mu\) represents the coefficient of dynamic viscosity, \(pI\) is the spherical stress, \(\overline{V}\) represents velocity, and \(I\) is the identity tensor, as mentioned in Garg and Rajagopal [56, 57]. Further, \(\sigma_{{{\text{hnf}}}}\) denotes the electrical conductivity, \(\overline{J}\) indicates the electrical current, and \(\kappa _{{{\text{hnf}}}}\) represents the effective thermal conductivity of the hybrid nanofluid.

After applying Prandtl’s boundary layer theory as in [58], the time-dependent two-dimensional viscoelastic nanofluid flow for the problem is governed by the continuity Eq. (6) and momentum Eq. (7). Here, the terms \({{\partial^{2} u} \mathord{\left/ {\vphantom {{\partial^{2} u} {\partial x^{2} }}} \right. \kern-\nulldelimiterspace} {\partial x^{2} }},\,\,{{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}},\,\,u\) are presumed to be of \(O\left( 1 \right)\) and y to be \(O\left( \delta \right)\) where \(\delta\) denotes the width of the boundary layer as discussed in [52, 53]. The energy Eq. (8) and concentration Eq. (9) are employed to study the heat and mass transport characteristics of ZnO–MWCNTs/ethylene glycol hybrid nanofluid as in [46,47,48,49,50].

$$\frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0$$
(6)
$$\begin{aligned} \rho_{\text{hnf}} \left( {\frac{\partial u}{{\partial u}} + u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}}} \right) & = \mu_{{{\text{hnf}}}} \frac{{\partial^{2} u}}{{\partial y^{2} }} + k_{1}\left( {\frac{{\partial^{3} u}}{\partial y^{2}\partial t}} + u\frac{{\partial^{3} u}}{\partial x\partial y^{2}} + v\frac{{\partial^{3} u}}{\partial y^{3}} + \frac{{\partial {u}}}{\partial x}\frac{\partial^{2} u}{{\partial y^{2}}} + \, {\frac{{\partial u}}{{\partial y}}\frac{\partial^{2} v}{{\partial y^{2}}}} \right) \\ & \quad - \sigma_{{{\text{hnf}}}} B^{2} u \\ \end{aligned}$$
(7)
$$\begin{aligned} \left( {\rho c_{{\text{p}}} } \right)_{{{\text{hnf}}}} \left( {\frac{\partial T}{{\partial t}} + u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}}} \right) & = \kappa_{{{\text{hnf}}}} \frac{{\partial^{2} T}}{{\partial y^{2} }} + k_{1} \left( {\frac{\partial u}{{\partial y}}\frac{{\partial^{2} u}}{\partial y\partial t}} \right. + u\frac{{\partial^{2} u}}{\partial x\partial y}\frac{\partial u}{{\partial y}} + \,\left. {v\frac{{\partial^{2} u}}{{\partial y^{2} }}\frac{\partial u}{{\partial y}}} \right) \\ & \quad + \mu_{{{\text{hnf}}}} \left( {\frac{\partial u}{{\partial y}}} \right)^{2} + \sigma_{{{\text{hnf}}}} B^{2} u^{2} \\ \end{aligned}$$
(8)
$$\frac{\partial C}{{\partial t}} + u\frac{\partial C}{{\partial x}} + v\frac{\partial C}{{\partial y}} = D_{0} \frac{{\partial^{2} C}}{{\partial y^{2} }} - k_{{\text{r}}}^{2} \left( {\frac{T}{{T_{\infty } }}} \right)^{m} e^{{\left( {\frac{{ - E_{{\text{a}}} }}{KT}} \right)}} (C - C_{\infty } ).$$
(9)

The last term in Eq. (9) on the right-hand side represents the modified Arrhenius equation with \(K_{{\text{r}}} \, = \,k_{{\text{r}}}^{2} \left( {\frac{T}{{T_{\infty } }}} \right)^{m} e^{{\left( {\frac{{ - E_{{\text{a}}} }}{KT}} \right)}}\), where \(k_{{\text{r}}}\) represents the rate of chemical reaction, \(K\) is Boltzmann constant, \(E_{{\text{a}}}\) is the Activation energy, and \(m\) is the fitted rate constant as described in [36, 59].

2.1 Hybrid nanofluid composition:

The ZnO–MWCNTs/ethylene glycol hybrid nanofluid comprises metal oxide nanoparticles (ZnO) with volume fraction \(\phi_{1}\) and multi-walled carbon nanotubes (MWCNTs) with volume fraction \(\phi_{2}\) incorporated in the viscoelastic base fluid (ethylene glycol). To calculate the effective viscosity \(\mu_{{{\text{hnf}}}}\), density \(\rho_{{{\text{hnf}}}}\), heat capacity \((\rho C_{{\text{p}}} )_{{{\text{hnf}}}}\), and thermal conductivity \(\kappa_{{{\text{hnf}}}}\) of the zinc oxide–MWCNT/EG hybrid nanofluid, firstly, the effective viscosity \(\mu_{{{\text{nf}}}}\), density \(\rho_{{{\text{nf}}}}\), heat capacity \((\rho C_{{\text{p}}} )_{{{\text{nf}}}}\), and thermal conductivity \(\kappa _{{{\text{nf}}}}\) of the metal oxide–ethylene glycol nanofluid is calculated. The effective viscosity of the nanofluid with metal oxide nanoparticles is calculated by applying the Brinkman model [60], whereas the effective heat capacity is calculated using the linear relationship as given in Xuan and Roetzel [61] as follows

$$\mu_{{{\text{nf}}}} = \frac{{\mu_{{\text{f}}} }}{{\left( {1 - \phi_{1} } \right)^{2.5} }}$$
(10)
$$\rho_{{{\text{nf}}}} = \left( {1 - \phi_{1} } \right)\rho_{{\text{f}}} + \phi_{1} \rho_{{\text{s}}}$$
(11)
$$\left( {\rho C_{{\text{p}}} } \right)_{{{\text{nf}}}} = \left( {1 - \phi_{1} } \right)\left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}} + \phi_{1} \left( {\rho C_{{\text{p}}} } \right)_{{\text{s}}}$$
(12)

Here \(\rho_{{\text{s}}}\) and \((\rho C_{{\text{p}}} )_{{\text{s}}}\) denote the density and heat capacity of the metal oxide nanoparticles, respectively, while \(\rho_{{\text{f}}}\) and \((\rho C_{{\text{p}}} )_{{\text{f}}}\) represent the density and heat capacity of the base fluid, respectively. On similar lines, the hybrid nanofluid’s effective viscosity \(\mu_{{{\text{hnf}}}}\), density \(\rho_{{{\text{hnf}}}}\), and heat capacity \((\rho C_{{\text{p}}} )_{{{\text{hnf}}}}\) are calculated using Eqs. (13)–(15).

$$\mu_{{{\text{hnf}}}} = \frac{1}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }}\mu_{{\text{f}}}$$
(13)
$$\rho_{{{\text{hnf}}}} = \left\{ {\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \phi_{1} \frac{{\rho_{{\text{s}}} }}{{\rho_{{\text{f}}} }}} \right) + \phi_{2} \frac{{\rho_{{{\text{CNT}}}} }}{{\rho_{{\text{f}}} }}} \right\}\rho_{{\text{f}}}$$
(14)
$$\left( {\rho C_{{\text{p}}} } \right)_{{{\text{hnf}}}} \, = \left\{ {\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \phi_{1} \frac{{\left( {\rho C_{{\text{p}}} } \right)_{{\text{s}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}} }}} \right) + \phi_{2} \frac{{\left( {\rho C_{{\text{p}}} } \right)_{{{\text{CNT}}}} }}{{\left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}} }}} \right\}\left( {\rho C_{{\text{p}}} } \right)_{{\text{f}}}$$
(15)

The effective thermal conductivity of the metal oxide–EG nanofluid is determined through Hamilton and Crosser model [62] as given in Eq. (16).

$$\kappa_{{{\text{nf}}}} = \frac{{\kappa_{{\text{s}}} + (n - 1)\kappa_{{\text{f}}} - (n - 1)\phi_{1} \left( {\kappa_{{\text{f}}} - \kappa_{{\text{s}}} } \right)}}{{\kappa_{{\text{s}}} + (n - 1)\kappa_{{\text{f}}} + \phi_{1} \left( {\kappa_{{\text{f}}} - \kappa_{{\text{s}}} } \right)}}\kappa_{f}$$
(16)

Here \(\kappa_{s}\) denote the thermal conductivity of the metal oxide nanoparticles and \(n\) is termed as the shape factor [63] defined as \(n = {3 \mathord{\left/ {\vphantom {3 \psi }} \right. \kern-\nulldelimiterspace} \psi }\) where \(\psi\) represents the sphericity (\(\psi = 1\) for spherical nanoparticles).

CNTs are rolled-up sheets of graphene (single-layered sp2-hybridized carbon atoms) to form a cylindrical structure having a diameter of the order of 1–100 nm. By taking the large axial ratio and spatial distribution of the carbon nanotubes into account, Xue [64] suggested a new model for calculating the effective thermal conductivity of CNT-based composites. This model by Xue is used here to determine the effective thermal conductivity of the metal oxide–CNTs/EG hybrid nanofluid as governed by Eq. (17).

$$\kappa_{{{\text{hnf}}}} = \left( {\frac{{1 - \phi_{2} + 2\phi_{2} \left( {\frac{{\kappa_{{{\text{CNT}}}} }}{{\kappa_{{{\text{CNT}}}} - \kappa_{{{\text{nf}}}} }}} \right)\ln \left( {\frac{{\kappa_{{{\text{CNT}}}} + \kappa_{{{\text{nf}}}} }}{{2\kappa_{{{\text{nf}}}} }}} \right)}}{{1 - \phi_{2} + 2\phi_{2} \left( {\frac{{\kappa_{{{\text{nf}}}} }}{{\kappa_{{{\text{CNT}}}} - \kappa_{{{\text{nf}}}} }}} \right)\ln \left( {\frac{{\kappa_{{{\text{CNT}}}} + \kappa_{{{\text{nf}}}} }}{{2\kappa_{{{\text{nf}}}} }}} \right)}}} \right)\kappa_{{{\text{nf}}}}$$
(17)

where \(\kappa_{{{\text{CNT}}}}\) is the thermal conductivity of CNTs and \(\kappa_{{{\text{nf}}}}\) is the thermal conductivity of the zinc oxide–EG nanofluid.

The effective electrical conductivity of the nanofluid, as well as hybrid nanofluid, is calculated using Maxwell’s model [65, 66] as given in Eqs. (18) and (19).

$$\sigma_{{{\text{nf}}}} = \left( {1 + \frac{{3(\sigma_{{\text{s}}} - \sigma_{{\text{f}}} )\phi_{1} }}{{(\sigma_{{\text{s}}} + 2\sigma_{{\text{f}}} ) - (\sigma_{{\text{s}}} - \sigma_{{\text{f}}} )\phi_{1} }}} \right)\sigma_{{\text{f}}}$$
(18)
$$\sigma_{hnf} = \left( {1 + \frac{{3(\sigma_{CNT} - \sigma_{nf} )\phi_{2} }}{{(\sigma_{CNT} + 2\sigma_{nf} ) - (\sigma_{CNT} - \sigma_{nf} )\phi_{2} }}} \right)\sigma_{nf}$$
(19)

The experimentally determined values of the thermal conductivity, electrical conductivity, and other thermophysical properties of metal oxide nanoparticles (ZnO, TiO2, Al2O3, and Fe3O4) and MWCNTs, are mentioned in Table 2. Assuming that for \(t \le 0\) no fluid flow occurs, the governing boundary layer Eqs. (6)–(9) will be solved for \(t > 0\) by subjecting them to the boundary conditions given by Eqs. (20) and (21).

$$u = u_{{\text{w}}} ,v = v_{{\text{w}}} ,\,T = T_{{\text{w}}} + m_{1} \frac{\partial T}{{\partial y}},\;C = C_{{\text{w}}} + m_{2} \frac{\partial C}{{\partial y}},\;{\text{at}}\;y = 0$$
(20)
$$u \to 0,\,T \to T_{\infty } ,\,C \to C_{\infty } ,\,\frac{\partial u}{{\partial y}} \to 0\;{\text{as}}\;y \to \infty$$
(21)

As the governing equations for the prescribed second-grade fluid flow are one order higher than that of the Navier Stokes equation, an additional boundary condition is required for solving the present problem. Here \({{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}} \to 0\) when \(y \to \infty\) represents the augmented boundary condition at infinity as the flow is in an unbounded domain (Garg and Rajagopal [57]). Further, \(v_{{\text{w}}} = - {{v_{0} } \mathord{\left/ {\vphantom {{v_{0} } {\sqrt {1 - ct} }}} \right. \kern-\nulldelimiterspace} {\sqrt {1 - ct} }}\) denotes suction or injection velocity depending upon whether \(v_{w} < 0\) or \(v_{w} > 0\). In heat transfer studies, the Nusselt number and the skin friction coefficient, both parameters are of engineering importance as they indicate heat transfer rate and the drag at the surface, respectively. The Nusselt number \(\left( {{\text{Nu}}_{x} } \right)\), Sherwood number \(\left( {{\text{Sh}}_{x} } \right)\), and skin friction coefficient \(\left( {C_{{\text{f}}} } \right)\) are calculated using Eqs. (22)–(24).

$${\text{Nu}}_{x} = \frac{ - x}{{(T_{{\text{w}}} - T_{\infty } )}}\frac{{\kappa_{{{\text{hnf}}}} }}{{\kappa_{{\text{f}}} }}\left( {\frac{\partial T}{{\partial y}}} \right)_{y = 0}$$
(22)
$${\text{Sh}}_{x} = \frac{{xj_{{\text{w}}} }}{{D_{{\text{B}}} (C_{{\text{w}}} - C_{\infty } )}}\;{\text{where}}\;j_{w} = - D_{{\text{B}}} \left( {\frac{\partial C}{{\partial y}}} \right)_{y = 0}$$
(23)
$$\,C_{{\text{f}}} = \frac{{\tau_{{\text{w}}} }}{{\rho_{{\text{f}}} u_{{\text{w}}}^{2} }}\;{\text{where}}\;\tau_{{\text{w}}} = \left( {\mu_{{{\text{hnf}}}} \frac{\partial u}{{\partial y}} + k_{1} \left( {\frac{{\partial^{2} u}}{\partial y\partial t} + u\frac{{\partial^{2} u}}{\partial x\partial y} + 2\frac{\partial u}{{\partial x}}\frac{\partial u}{{\partial y}} + v\frac{{\partial^{2} u}}{{\partial y^{2} }}} \right)} \right)_{y = 0}$$
(24)

3 Solution process

The solution process of the governing partial differential Eqs. (6)–(9) subject to the boundary conditions (20)–(21) consists of two parts. In the first part, we convert PDEs (partial differential equations) governing the flow to ODEs (ordinary differential equations) with the help of similarity transformations. In the second part, we solve the resulting ODEs numerically using the fourth-order Runge–Kutta method and the Shooting strategy.

3.1 Non-dimensionalization

The coupled PDEs (6)–(9), which are of highly nonlinear nature along with the boundary conditions (20)–(21), are transformed to the set of non-dimensional coupled ODEs by making use of similarity transformations and stream function \(\psi\). In accordance with the continuity equation, the stream function must satisfy: \(u = \frac{\partial \psi }{{\partial y}},\,\,\,v = - \frac{\partial \psi }{{\partial x}}\). The appropriate form of the stream function \(\psi\) and the other similarity transformations are given by Eq. (25).

$$\psi = \sqrt {\frac{{a\nu_{{\text{f}}} }}{1 - ct}} xf(\eta ),\,\,\eta = \sqrt {\frac{a}{{\nu_{{\text{f}}} (1 - ct)}}} y,\,\,\theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{{\text{w}}} - T_{\infty } }},\,\,\phi (\eta ) = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }}$$
(25)
$$\Rightarrow u = \frac{ax}{{1 - ct}}f^{\prime } (\eta )\;{\text{and}}\;v = - \sqrt {\frac{{a\nu_{{\text{f}}} }}{1 - ct}} f(\eta )$$
(26)

By use of the above similarity transformations, the non-dimensionalized form of governing equations is obtained as given by Eqs. (27)–(29).

$$\begin{aligned} & \frac{1}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }}f^{\prime \prime \prime } + b^{*} \left( {2f^{\prime } \,f^{{^{\prime \prime \prime } }} - \left( {f^{\prime \prime } } \right)^{2} - ff^{\prime \prime \prime \prime } + A\left( {2f^{\prime \prime \prime } + \frac{\eta }{2}f^{\prime \prime \prime \prime } } \right)} \right) \\ & \quad - A_{4} M^{2} f^{\prime } \; - A_{1} \left( {\left( {f^{\prime } } \right)^{2} - f^{\prime \prime } f + A\left( {f^{\prime } + \frac{\eta }{2}f^{\prime \prime } } \right)} \right) = 0 \\ \end{aligned}$$
(27)
$$\begin{aligned} & A_{3} \theta^{\prime \prime } + b^{*} \Pr {\text{Ec}}\left( {\frac{A}{2}\left( {\eta f^{\prime \prime } \,f^{\prime \prime \prime } + 3\left( {f^{\prime \prime } } \right)^{2} } \right) + f^{\prime } \left( {f^{\prime \prime } } \right)^{2} - ff^{\prime \prime } \,f^{\prime \prime \prime } } \right) \\ & \quad - A_{2} \Pr \left( {2f^{\prime } \theta - f\theta^{\prime } + \frac{A}{2}\left( {3\theta + \eta \theta^{\prime } } \right)} \right)\, + A_{4} M^{2} {\text{Ec}}\Pr \left( {f^{\prime } } \right)^{2} \\ & \quad + \frac{1}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }}\Pr {\text{Ec}}\left( {f^{} } \right)^{2} \, = 0 \\ \end{aligned}$$
(28)
$$\phi^{\prime\prime} - \frac{{A{\text{Sc}}}}{2}\left( {3\phi + \eta \phi^{\prime } } \right) - Sc(2f^{\prime } \phi - f\phi^{\prime } ) + k^{*} Sc(1 + \delta \theta )^{m} \phi e^{{\left( {\frac{ - E*}{{1 + \delta \theta }}} \right)}} = 0$$
(29)

After the process of non-dimensionalization, boundary conditions (20)–(21) are converted to (30) and (31).

$$f(0) = S,\,f^{\prime } (0) = 1,\,\theta (0) = 1 + d_{1} *\theta^{\prime } (0),\,\phi (0) = 1 + d_{2} *\phi^{\prime } (0)$$
(30)
$$f^{\prime } (\infty ) \to 0,\,\theta (\infty ) \to 0,\,\phi (\infty ) \to 0,\,f^{\prime \prime } (\infty ) \to 0$$
(31)

Here \(\eta ,\,f,\,f^{\prime } ,\,f^{\prime \prime } ,\,f^{\prime \prime \prime } ,\,f^{\prime \prime \prime \prime },\) and \(\theta\) all are non-dimensional quantities where prime symbolizes the differentiation with respect to \(\eta\) and the constants \(A_{1} ,\,A_{2} ,A_{3},\) and \(A_{4}\) are defined as in Eq. (32).

$$A_{1} = \frac{{\rho_{{{\text{hnf}}}} }}{{\rho_{{\text{f}}} }}\quad A_{2} = \frac{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{hnf}}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }},\quad A_{3} = \frac{{\kappa_{{{\text{hnf}}}} }}{{\kappa_{{\text{f}}} }},\quad A_{4} = \frac{{\sigma_{{{\text{hnf}}}} }}{{\sigma_{{\text{f}}} }}$$
(32)

After non-dimensionalization, the Nusselt number and the skin friction coefficient are expressed as

$${\text{Nu}}_{{\text{r}}} = {\text{Nu}}_{x} {\text{Re}}_{x}^{ - 1/2} = - \frac{{\kappa_{{{\text{hnf}}}} }}{{\kappa_{{\text{f}}} }}\theta^{\prime } (0)\, = \, - A_{3} \theta^{\prime } (0)$$
(33)
$${\text{Sh}}_{{\text{r}}} = {\text{Sh}}_{x} {\text{Re}}_{x}^{ - 1/2} = - \phi^{\prime } (0)$$
(34)
$$C_{{\text{f}}} r = C_{{\text{f}}} {\text{Re}}_{x}^{1/2} = \left( {\frac{{\mu_{{{\text{hnf}}}} }}{{\mu_{{\text{f}}} }}f^{\prime \prime } (\eta ) + b^{*} \left( {3f^{\prime } (\eta )f^{\prime \prime } (\eta ) + \frac{A}{2}\left( {\eta f^{\prime \prime \prime } (\eta ) + 3f^{\prime \prime } (\eta )} \right) - f(\eta )f^{\prime \prime \prime } (\eta )} \right)} \right)_{\eta = 0}$$
(35)

Here \({\text{Nu}}_{{\text{r}}}\) represents the reduced local Nusselt number, \({\text{Sh}}_{{\text{r}}}\) represents the Sherwood number, \(C_{{\text{f}}} r\) represents the reduced skin friction coefficient, and \({\text{Re}}_{x} = {{U_{{\text{w}}} x} \mathord{\left/ {\vphantom {{U_{{\text{w}}} x} {\nu_{{\text{f}}} }}} \right. \kern-\nulldelimiterspace} {\nu_{{\text{f}}} }} = {{ax^{2} } \mathord{\left/ {\vphantom {{ax^{2} } {\nu_{{\text{f}}} (1 - ct)}}} \right. \kern-\nulldelimiterspace} {\nu_{{\text{f}}} (1 - ct)}}\) is the local Reynolds number. Apart from the temperature \(\theta\) and nanoparticle volume fraction \(\phi\) for studying the heat and mass transport, the other substantial non-dimensional physical quantities for the ongoing investigation are the reduced Nusselt number \({\text{Nu}}_{{\text{r}}}\), Sherwood number \({\text{Sh}}_{{\text{r}}}\), and the reduced skin friction coefficient \(C_{{\text{f}}} r\).

3.2 Numerical Solution

For finding the solution of highly nonlinear ODEs numerically, the immediate step after non-dimensionalization is to transform them into a system of first-order ODEs. The nonlinear ODEs obtained in the last section is transformed into the first-order ODEs using the substitution provided by Eq. (36).

$$(f,f^{\prime } ,f^{\prime \prime } ,f^{\prime \prime \prime } ,\theta ,\theta^{\prime } ,\phi ,\phi^{\prime } ) = (y_{1} ,y_{2} ,y_{3} ,y_{4} ,y_{5} ,y_{6} ,y_{7} ,y_{8} )$$
(36)
$$\left. \begin{gathered} \frac{{{\text{d}}y_{1} }}{{{\text{d}}\eta }} = y_{2} ,\,\,\frac{{{\text{d}}y_{2} }}{{{\text{d}}\eta }} = y_{3} ,\,\,\frac{{{\text{d}}y_{3} }}{{{\text{d}}\eta }} = y_{4} , \hfill \\ \frac{{{\text{d}}y_{4} }}{{{\text{d}}\eta }} = \frac{1}{{\left[ {\left( {y_{1} - \frac{A\,\eta }{2}} \right)b^{*} } \right]}}\left\{ \begin{gathered} \frac{1}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }}y_{4} - A_{1} \left( {y_{2}^{2} - y_{1} y_{3} + A(y_{2} + \frac{\eta }{2}y_{3} )} \right) \hfill \\ + b^{*} (2y_{2} y_{4} - y_{3}^{2} + 2A\,y_{4} ) - A_{4} M^{2} y_{2} \hfill \\ \end{gathered} \right\}, \hfill \\ \frac{{{\text{d}}y_{5} }}{{{\text{d}}\eta }} = y_{6} , \hfill \\ \frac{{{\text{d}}y_{6} }}{{{\text{d}}\eta }} = \frac{{\Pr A_{2} }}{{A_{3} }}\left\{ {2y_{5} y_{2} - y_{1} y_{6} + \frac{A}{2}(3y_{5} + \eta y_{6} )} \right\} - \frac{{M^{2} E\Pr A_{4} }}{{A_{3} }}y_{2}^{2} \hfill \\ \quad - \frac{{b^{*} \Pr Ec}}{{A_{3} }}\left\{ {\frac{A}{2}(\eta y_{3} y_{4} + 3y_{3}^{2} ) + y_{2} y_{3}^{2} - y_{1} y_{3} y_{4} } \right\} - \frac{1}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }}\frac{{\Pr {\text{Ec}}}}{{A_{3} }}y_{3}^{2} , \hfill \\ \frac{{{\text{d}}y_{7} }}{{{\text{d}}\eta }} = y_{8} , \hfill \\ \frac{{{\text{d}}y_{8} }}{{{\text{d}}\eta }} = \frac{{A{\text{Sc}}}}{2}(3y_{7} + \eta y_{8} ) + {\text{Sc}}\left( {2y_{2} y_{7} - y_{1} y_{8} } \right) - {\text{Sc}}\,k^{*} \,(1 + \delta \theta )^{m} \exp \left( {\frac{ - E*}{{1 + \delta \theta }}} \right)y_{7} \hfill \\ \end{gathered} \right\}$$
(37)

The transformed form of the boundary conditions in terms of \((y_{1} ,y_{2} ,y_{3} ,y_{4} ,y_{5} ,y_{6} ,y_{7} ,y_{8} )\) is

$$y_{1} (0) = S,y_{2} (0) = 1,y_{5} (0) = 1 + d_{1} *y_{6} (0),y_{7} (0) = 1 + d_{2} *y_{8} (0)$$
(38)
$$y_{2} (\infty ) = 0,\,\,\,y_{3} (\infty ) = 0,\,\,\,\,y_{5} (\infty ) = 0,\,\,\,\,y_{7} (\infty ) = 0$$
(39)

The above-transformed equations are solved using the fourth-order Runge–Kutta scheme along with the well-known shooting method. While obtaining the solution of the above system of ODEs, one has to choose the required initial guesses very carefully.

3.3 Code validation

A MATLAB code is developed to obtain the numerical solution using the numerical scheme mentioned in Sect. 3.2. The accuracy of the code generated for the present numerical method is verified by comparing local Nusselt number values and skin friction coefficient as shown in Table 1 against Devi and Devi [67] for hydromagnetic Cu–Al2O3/water hybrid nanofluid flow over a permeable sheet. The code validation is performed for the Newtonian case for different values of magnetic number M, suction parameter S, and volume fraction of Cu nanoparticles (\(\phi_{2}\)) while keeping \(\Pr = 6.135\) and volume fraction of Al2O3 nanoparticles equal to 0.1 (i.e., \(\phi_{1} = 0.1\)). The calculated values are in perfect harmony with the existing literature. It was observed during code verification that a fair initial guess and an appropriate value of \(\eta\) at infinity would lead to the faster convergence of the solution, and a bad guess can lead to a singularity in the Jacobian iterations. So, while obtaining results, one should be very careful in choosing an initial guess.

Table 1 Resemblance of local Nusselt number and skin friction values for Cu–Al2O3/water hybrid nanofluid calculated using present code with already published results
Full size table

4 Results and discussion

The heat and mass exchange in the ZnO–MWCNTs/ethylene glycol hybrid nanofluid’s boundary layer flow is analyzed by plotting the numerical results. The graphical profiles depicting the variation in the hybrid nanofluid temperature, Nusselt number, nanoparticle volume fraction, Sherwood number, and skin friction for various thermofluidic parameters are presented in this section. All numerical results are discussed comprehensively to understand the heat or mass exchange and flow mechanics of ZnO–MWCNTs/ethylene glycol hybrid nanofluid. All the computations are performed by assigning the values \({\text{Ec }} = \, 0.8,\,\, b^{*} = { 0}{\text{.5}},\;{\text{Pr }} = { 51},\;A = 0.1,\,{\text{Sc}}\, = \,1,\) \(k^{*} = 0.5,\;E^{*} = 1,\;M = 1,\;\delta = 0.5,\;S = 2,\) \(d_{1} = d_{2} = 1\,\) to the parameters unless otherwise specified in the graphs. The volume fraction of nanoparticles is kept equal to 0.08, i.e., \(\phi_{1} + \phi_{2} = \, 0.08\) (for base fluid: \(\phi_{1} = \phi_{2} = \, 0\); for ZnO/EG nanofluid: \(\phi_{1} = \, 0.08,\,\,\phi_{2} = 0\) and for \({\text{ZnO}} - {\text{MWCNTs}}/\)ethylene glycol hybrid nanofluid:\(\phi_{1} = \, 0.04,\,\,\phi_{2} = 0.04\)) (Table 2).

Table 2 Experimental values of thermophysical properties for metallic oxide nanoparticles, MWCNTs and ethylene glycol [49, 68,69,70,71,72,73,74,75,76,77,78,79,80,81,82]
Full size table

4.1 Analysis of heat transfer: temperature and Nusselt number profiles

The heat transfer rate from the sheet surface to the ambient fluid is visualized with the help of Nusselt number \({\text{Nu}}_{x} {\text{Re}}_{x}^{ - 1/2}\) profiles. The Nusselt number profiles are plotted for four different hybrid nanofluids comprising metal oxide nanoparticles (ZnO, TiO2, Al2O3, or Fe3O4) and MWCNTs in ethylene glycol as base fluid. Figures 2, 3, 4 and 5 represents the Nusselt number profiles of ZnO–MWCNTs/ethylene glycol, TiO2–MWCNTs/ethylene glycol, Al2O3–MWCNTs/ethylene glycol, and Fe3O4–MWCNTs/ethylene glycol hybrid nanofluids with variation in parameters \(A,\,M,\,S\) and \(k^{*}\). A comparative analysis among the Nusselt number profiles reveals that the magnitude of the Nusselt number is maximum for ZnO–MWCNTs/EG hybrid nanofluid. Zinc oxide nanoparticles have a larger surface area, making ZnO–MWCNTs/EG hybrid nanofluid a better heat transporter than the other hybrid nanofluids. In particular, the following order in the magnitude of Nusselt number is observed among the four hybrid nanofluids:

Fig. 2
figure 2

Nusselt number profiles with variation in A

Full size image
Fig. 3
figure 3

Nusselt number profiles with variation in S

Full size image
Fig. 4
figure 4

Nusselt number profiles with variation in M

Full size image
Fig. 5
figure 5

Nusselt number profiles with variation in k*

Full size image

ZnO–MWCNTs/EG > TiO2–MWCNTs/EG > Al2O3–MWCNTs/EG > Fe3O4–MWCNTs/EG.

Furthermore, the magnitude of the Nusselt number decreases with an increment in unsteadiness parameter or suction (Figs. 2, 3) at the sheet surface for all four hybrid nanofluids. Figure 4 indicates that the magnetic field enriches the heat transport by lifting the magnitude of the Nusselt number. Figures 6, 7, 8, 9 and 10 represent the variation in the hybrid nanofluid temperature inside the boundary layer with parameters \(A,\,S,\,M,\,{\text{Ec}}\) and \(b^{*}\) respectively. The temperature profile of ZnO–MWCNTs/ethylene glycol hybrid nanofluid asymptotically goes to zero toward the edge of the boundary layer. In other words, \(\theta\) vanish asymptotically as \(\eta\) approaches infinity. Figures 6 and 7 illustrate that the hybrid nanofluid temperature reduces with an increment in unsteadiness parameter \(A\) or suction parameter \(S\). The hybrid nanofluid temperature at the sheet surface (i.e., at \(\eta = 0\)) increases with an increment in magnetic parameter \(M\) (Fig. 8). The application of the transverse magnetic field augments the resistive Lorentz force. This Lorentz force resists the motion of the hybrid nanofluid particles leading to an enhanced hybrid nanofluid temperature. An increment in Eckert number \(Ec\) is followed by an increase in internal energy of the fluid system, which in turn boosts up the hybrid nanofluid temperature (Fig. 9).

Fig. 6
figure 6

Influence of A on hybrid nanofluid temperature profile

Full size image
Fig. 7
figure 7

Influence of S on hybrid nanofluid temperature profile

Full size image
Fig. 8
figure 8

Influence of M on hybrid nanofluid temperature profile

Full size image
Fig. 9
figure 9

Influence of Ec on hybrid nanofluid temperature profile

Full size image
Fig. 10
figure 10

Influence of b* on hybrid nanofluid temperature profile

Full size image

4.2 Analysis of mass transfer: nanoparticle volume fraction and Sherwood number profiles

Figures 11, 12, 13, 14, 15 and 16 represent the influence of thermofluidic parameters such as unsteadiness parameter \(A\), chemical reaction rate parameter \(k^{*}\), activation energy parameter \(E*\), Suction parameter \(S\), Schmidt number \({\text{Sc}}\), and concentration slip parameter \(d_{2}\) on nanoparticle volume fraction profile of ZnO–MWCNTs/ethylene glycol hybrid nanofluid. The nanoparticle volume fraction decreases with rising values of parameter \(A,\,\, k^{*} ,\,\,S,\,\,{\text{Sc}}\) or \(d_{2}\). The chemical reaction parameter \(k^{*}\), unsteadiness parameter \(A\), Schmidt number \(Sc\), Suction parameter \(S\), or concentration slip \(d_{2}\) contributes to enhancing the mass exchange rate at the lower boundary \(\eta = 0\) by reducing the width of the boundary layer. Physically, the thickness of the concentration boundary layer is reduced with an increment in Schmidt number due to a decrease in mass diffusivity. Figure 16 depicts that nanoparticle volume fraction increases with an increase in activation energy. Physically, an increment in \(E*\) is accompanied by the generative chemical reaction and a decrease in modified Arrhenius function \(K_{{\text{r}}} \, = \,k_{{\text{r}}}^{2} \left( {\frac{T}{{T_{\infty } }}} \right)^{m} e^{{\left( {\frac{{ - E_{{\text{a}}} }}{KT}} \right)}}\)as a result of which \(\phi\) increases. The reaction process is improved significantly by using activation energy, and subsequently, an enhancement in nanoparticle volume fraction is observed. Figure 17, 18 and 19 shows the impact of parameters \(A,\,\, k^{*} ,\,\delta ,\,\,Sc\) and \(\, b^{*}\) on Sherwood number \({\text{Sh}}_{x} {\text{Re}}_{x}^{ - 1/2}\) profiles. These figures illustrate that the unsteadiness parameter, chemical reaction parameter, viscoelastic fluid parameter Schmidt number, and an increment in temperature difference parameter enhance the rate of mass exchange at the sheet surface.

Fig. 11
figure 11

Influence of A on nanoparticle volume fraction profile

Full size image
Fig. 12
figure 12

Influence of S on nanoparticle volume fraction profile

Full size image
Fig. 13
figure 13

Influence of concentration slip on nanoparticle volume fraction profile

Full size image
Fig. 14
figure 14

Influence of k* on nanoparticle volume fraction profile

Full size image
Fig. 15
figure 15

Influence of Sc on nanoparticle volume fraction profile

Full size image
Fig. 16
figure 16

Influence of E* on nanoparticle volume fraction profile

Full size image
Fig. 17
figure 17

Sherwood number profile with variation in A and k*

Full size image
Fig. 18
figure 18

Sherwood number profile with variation in A and b*

Full size image
Fig. 19
figure 19

Sherwood number profile with variation in \(\delta\) and Sc

Full size image

4.3 Skin friction coefficient profiles

The impact of parameters unsteadiness parameter \(A\), fluid parameter \(b^{*}\), and magnetic number \(M\) on skin friction coefficient \(C_{{\text{f}}} {\text{Re}}_{x}^{1/2}\) profiles of ZnO–MWCNTs/ethylene glycol hybrid nanofluid is presented in Figs. 20 and 21. The sign of the skin friction coefficient is negative. Figure 20 indicates that a significant enhancement in the magnitude of skin friction coefficient is observed with a rise in magnetic number. It happens due to the opposition offered to the flow by the Lorentz force. The skin friction coefficient rises by an augmentation in unsteadiness parameter as indicated in Figs. 20 and 21. So, the skin friction at the sheet surface can be reduced by lowering the magnetic number or unsteadiness parameter values. A similar kind of behavior in skin friction is noticed for the viscoelastic fluid parameter (Fig. 21).

Fig. 20
figure 20

Influence of A and M on skin friction coefficient

Full size image
Fig. 21
figure 21

Influence of A and b* on skin friction coefficient

Full size image

5 Conclusions

The impact of Arrhenius energy on the unsteady MHD boundary layer flow of ZnO–MWCNTs/EG hybrid nanofluid is analyzed by employing a non-Newtonian flow model. The effect of influential thermofluidic parameters on heat and mass exchange processes is examined and discussed for ZnO–MWCNTs/EG hybrid nanofluid. Apart from this, the Nusselt number profiles of various metal oxide–MWCNTs/EG hybrid nanofluids are compared. A few of the significant findings of this investigation are summarized as.

  • ZnO–MWCNTs/EG hybrid nanofluid is a better transporter of heat than TiO2–MWCNTs/EG, Al2O3–MWCNTs/EG, or Fe3O4–MWCNTs/EG hybrid nanofluids.

  • At the sheet surface, the rate of heat transfer in ZnO–MWCNTs/EG hybrid nanofluid is enhanced by an increment in the unsteadiness or Suction parameter.

  • The temperature of the hybrid nanofluid contained in the boundary layer increases with an increment in \(M,\;{\text{Ec}}\) or \(b^{*}\).

  • The presence of chemical reaction and the suction and concentration slip at the boundary enhance the mass transport rate in ZnO–MWCNTs/ethylene glycol hybrid nanofluid by reducing the width of the boundary layer.

  • The nanoparticle volume fraction decreases with rising values of unsteadiness parameter or Schmidt number.

  • Smaller values of the viscoelastic fluid parameter, unsteadiness parameter, and magnetic number are recommended to reduce the magnitude of skin friction.