Introduction

Nanofluids refer to the dilute suspensions of ultrafine particles in base fluids. Such liquids have preferable thermophysical properties rather than the pure working fluids. The inclusion of carbon, copper and other high thermal conductivity material nanoparticles to water, ethylene glycol and oils has been established as an effective route to increase heat transfer capabilities of these liquids. The exceptional thermal performance of nanofluids needs to be fully exploited in order to overcome the ever-increasing challenges of heat removal in cooling applications. In 1995, the nanofluid’s word was coined by Choi [1]. The nanofluids are engineered to increase thermal properties and/or diminish drag coefficients for application ranging from electronics cooling to microfluidics. The suspended nanoparticles can significantly improve the transport properties of base fluids, and the resulting nanofluids display attractive properties such as high thermal conductivity and high boiling heat transfer coefficient [2]. Nakhchi and Esfahani [3] gave a numerical analysis for Cu–water nanofluid flow through a circular duct inserted with crosscut twisted tape with alternate axis. Three-dimensional k − ϵ turbulence model was applied to simulate this problem. It was shown that the thermal performance increases by increasing the volume fraction of nanoparticles inside the duct. Laein et al. [4] applied the particle image velocimetry (PIV) to measure the laminar boundary layer thickness of TiO2–water nanofluid free convection over the vertical and horizontal flat plates with constant heat flux. The effects of nanoparticles and heat flux strength on the boundary layer thickness and velocity profiles were investigated in detail. Finally, a comparison was made between the experimental, theoretical and numerical results for different conditions. Further, Bahiraei [5] summarized the studies conducted on nanofluids, considering particle migration, including those conducted via methods such as Eulerian–Lagrangian, Buongiorno model, molecular dynamics simulation and different theoretical approaches. It was shown that there are still several hot debates about flow and thermal mechanisms in nanofluids, particularly regarding the behavior of nanoparticles. He [6] also summarized the numerical investigations implemented on nanofluids including conventional and novel computational fluid dynamics methods like Lattice–Boltzmann method. In spite of some inconsistencies in the earlier published results and insufficient understanding of the mechanism of the heat transfer in nanofluids, it has been emerged as a promising heat transfer fluid. In the continuation of nanofluids investigations, the researchers have also tried to employ hybrid nanofluids recently, which are developed by suspending two or more dissimilar nanoparticles either in mixture or in composite form. The idea of using hybrid nanofluids is to further modification of heat transfer and pressure drop characteristics by a trade-off between advantages and disadvantages of mono-nanofluids, attributed to good aspect ratio, higher thermal network and the synergistic effect of nanoparticles. However, the satisfactory stability, production process, choosing of relevant nanoparticles combination to get synergistic effect and the cost of nanofluids may be major challenges behind the practical applications [7]. The hybrid nanofluids are a new class of nanofluids, and their performance evaluation is still in the development phase. It is expected to use hybrid nanofluids for similar applications with nanofluid, and a better thermal efficiency is expected due to the high performance of hybrid nanofluids. A lot of researches related to various applications of nanofluids have been conducted after the discovery of nanofluids. Some of the applicative areas include: electronic cooling [8], heat pipes, car radiators, coolant in welding and machining, nuclear plant, heat exchanger [9], solar heating [10], etc. [11]. Moreover, there are many experimental researches about hybrid nanofluids [12,13,14]. Esfe et al. [15] investigated experimentally the thermal conductivity of SiO2–MWCNT/EG hybrid nanofluid at solid volume fraction ranging from 0.025 to 0.86% and temperatures ranging from 30 to \(50\) °C. A new correlation was proposed to predict experimental thermal conductivity ratio based on the solid volume fraction and the temperature. Karami [16] focused on energy and entropy analysis of a residential-type direct absorption solar collector using Fe3O4–SiO2/DI water hybrid nanofluid, experimentally. Results of energy analysis displayed that the collector efficiency is increased by mass flow rate and volume fraction of nanofluid asymptotically. Besides, Dinarvand et al. [17] modeled the steady laminar MHD mixed convection boundary layer flow of a SiO2–Al2O3/water hybrid nanofluid near the stagnation point on a vertical permeable flat plate. The similarity solution [18] was applied, and the final ODEs solved numerically by a collocation technique from MATLAB. It was demonstrated that the local Nusselt number enhances with increasing volume fraction of silica and alumina nanoparticles.

The classical von Kármán [19] problem is the flow close to a flat disk rotating in a fluid, which is otherwise at rest with constant angular velocity about an axis normal to its plane. According to the no-slip condition and the viscosity effects, the layer of fluid directly at the disk is carried along with it and driven outward by the centrifugal force. New fluid bulks are then continuously pulled onto the disk in the axial direction and then ejected centrifugally again. This is, therefore, a fully three-dimensional flow which acts as a pump [20]. Kármán used this flow to introduce his well-known momentum–integral relation derived in the same paper in 1921 [21]. The importance of heat transfer from a rotating body can be ascertained in aeronautical science as well as in other engineering fields like thermal-power generating systems, rotating machinery, medical equipments, computer storage devices, gas turbine rotors, air cleaning machines, electronic devices and crystal growth processes [22]. Further, the flow over a stretching surface is an important problem in many engineering applications in industries such as extrusion, melt-spinning, the hot rolling, wire drawing, glass-fiber production, manufacture of plastic and rubber sheet, and cooling of a large metallic plate in a bath, which may be an electrolyte [23]. An extension of the von Kármán viscous pump problem to the configuration with a stretchable disk with or without rotation was first studied by Fang [24]. In 2009, Rashidi and Dinarvand [25] found the totally analytic solutions of the system of nonlinear ordinary differential equations derived from similarity transform for the steady three-dimensional problem of fluid deposition on an inclined rotating disk by using homotopy analysis method (HAM). The velocity and temperature profiles were shown, and the influence of the Prandtl number on the heat transfer and the Nusselt number was discussed in detail. In 2010, Dinarvand [26] also worked on analytically examining the off-centered stagnation flow toward a rotating disk with the help of HAM. An important point to note was that the nonalignment complicates the flow field and surface shear, but does not affect the torque. Recently, Yin et al. [27] in an interesting research article investigated flow and heat transfer of nanofluids over a rotating disk with uniform stretching rate along with three types of nanoparticles of Cu, Al2O3 and CuO with water as the base fluid. Results indicated that with increasing stretching strength parameter the velocity in radial direction increases, whereas the velocities in tangential and axial directions decrease. In addition, researchers also tried to study rotational and swirl flows in other different geometries like annular flows between two concentric cylinders with smooth and slotted surface [28], convective heat transfer in the entrance region of an annulus with an external grooved surface [29], annular flow with outer grooved cylinder and rotating inner cylinder [30], Taylor–Couette–Poiseuille flows between an inner rotating cylinder and an outer grooved stationary cylinder [31] and turbulent flow around a rotating cylinder [32].

Considering the above studies, we have understood that there is no work on the von Kármán problem with the use of hybrid nanofluids as working fluid. So, the main goal in the present study is to extend the work of Yin et al. [27] with the help of an innovative mass-based hybrid nanofluid’s model. This new model proposes the new definition of an equivalent solid volume fraction, equivalent solid density and equivalent solid specific heat computed from thermophysical properties of both base fluid and nanoparticles, simultaneously. The nanoparticles and the base fluid have been chosen: ZnO (29 or 77 nm), Au (3–40 nm) and pure water, respectively. Foregoing parameters along with other governing parameters including stretching strength parameter, shape factors of first and second nanoparticles and Prandtl number are putting into the governing dimensionless similarity ODEs which are then numerically solved by bvp4c routine from MATLAB software. Finally, after validity of our numerical procedure, the effect of foregoing parameters on the flow and heat transfer characteristics of the problem is discussed in detail.

Mathematical formulation

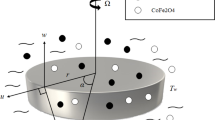
Let us consider an incompressible laminar steady and axially symmetric aqueous hybrid nanofluid flow past a rotating disk that is placed at \(z = 0\) and rotates with a constant angular velocity \(\omega\) and radially stretches at a uniform rate \(s\) as shown in Fig. 1.

Fig. 1
figure 1

Schematic diagram of problem, the coordinate system and streamlines

Full size image

We have selected zinc oxide (ZnO) and gold (Au) as nanoparticles with pure water as base fluid. These nanoparticles may be applicable in direct absorption solar collectors [33] or microcollectors, although technically their production is expensive. It is assumed that the base fluid and nanoparticles are in thermal equilibrium and that no slip occurs between them. It is worth noticing that, to analytically modeling ZnO–Au/water hybrid nanofluid, zinc oxide is firstly scattered into base fluid and subsequently gold is dispersed in ZnO/water mono-nanofluid that is known as the new base fluid, now. Thus, the subscripts (1), (2) and (f) correspond to first nanoparticle (ZnO), second nanoparticle (Au) as well as pure water, respectively. Table 1 demonstrates thermophysical properties of the base fluid and the nanoparticles at \(25\) °C [34,35,36,37,38,39]. It is expected that the heat transfer rate of hybrid nanofluid would be much higher than ZnO–water due to the dispersing of gold nanoparticle that has the high thermal conductivity with respect to zinc oxide.

Table 1 Thermophysical properties of the base fluid and the nanoparticles at 25 °C [34,35,36,37,38,39]
Full size table

The schematic diagram of problem, the cylindrical coordinate system \((r,\theta ,z),\) as well as the velocity components \((V_{\text{r}} ,V_{\uptheta} ,V_{\text{z}} )\) is shown in Fig. 1. The constant temperature of the rotating disk is \(T_{\text{w}} ,\) while the temperature and pressure of the free stream are \(T_{\infty }\) and \(P_{\infty } ,\) respectively. After using the above approximations, the boundary layer theory as well as Tiwari–Das [40] mathematical model, the governing nonlinear PDEs including conservation of mass, momentum and energy can be expressed as follows [21, 27]:

$$\frac{{\partial V_{\text{r}} }}{\partial r} + \frac{{V_{\text{r}} }}{r} + \frac{{\partial V_{\text{z}} }}{\partial z} = 0,$$
(1)
$$V_{\text{r}} \frac{{\partial V_{\text{r}} }}{\partial r} + V_{\text{z}} \frac{{\partial V_{\text{r}} }}{\partial z} - \frac{{V_{\uptheta}^{2} }}{r} + \frac{1}{{\rho_{\text{hnf}} }}\frac{\partial P}{\partial r} = \frac{{\mu_{\text{hnf}} }}{{\rho_{\text{hnf}} }}\left( {\frac{{\partial^{2} V_{\text{r}} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial V_{\text{r}} }}{\partial r} - \frac{{V_{\text{r}} }}{{r^{2} }} + \frac{{\partial^{2} V_{\text{r}} }}{{\partial z^{2} }}} \right),$$
(2)
$$V_{\text{r}} \frac{{\partial V_{\uptheta} }}{\partial r} + V_{\text{z}} \frac{{\partial V_{\uptheta} }}{\partial z} + \frac{{V_{\text{r}} V_{\uptheta} }}{r} = \frac{{\mu_{\text{hnf}} }}{{\rho_{\text{hnf}} }}\left( {\frac{{\partial^{2} V_{\uptheta} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial V_{\uptheta} }}{\partial r} - \frac{{V_{\uptheta} }}{{r^{2} }} + \frac{{\partial^{2} V_{\uptheta} }}{{\partial z^{2} }}} \right),$$
(3)
$$V_{\text{r}} \frac{{\partial V_{\text{z}} }}{\partial r} + V_{\text{z}} \frac{{\partial V_{\text{z}} }}{\partial z} + \frac{1}{{\rho_{\text{hnf}} }}\frac{\partial P}{\partial z} = \frac{{\mu_{\text{hnf}} }}{{\rho_{\text{hnf}} }}\left( {\frac{{\partial^{2} V_{\text{z}} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial V_{\text{z}} }}{\partial r} + \frac{{\partial^{2} V_{\text{z}} }}{{\partial z^{2} }}} \right),$$
(4)
$$V_{\text{r}} \frac{\partial T}{\partial r} + V_{\text{z}} \frac{\partial T}{\partial z} = \alpha_{\text{hnf}} \left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{\partial r} + \frac{{\partial^{2} T}}{{\partial z^{2} }}} \right),$$
(5)

under these dimensional boundary conditions [27]

$$\begin{aligned} V_{\text{r}} = sr,\quad V_{\uptheta} = \omega .r,\quad V_{\text{z}} = 0,\quad \quad T = T_{\text{w}} \,\,\quad \,at\,\,\;\,\,z = 0, \hfill \\ V_{\text{r}} \to 0,\quad V_{\uptheta} \to 0,\quad T \to T\infty ,\quad \,\,\,P \to P\infty \,\,\,\,\;as\;\,\,\,\,z \to \infty . \hfill \\ \end{aligned}$$
(6)

where \(T\) and \(P\) are the temperature and the pressure of the hybrid nanofluid within the boundary layer, respectively; \(\rho_{\text{hnf}} ,\)\(\mu_{\text{hnf}}\) and \(\alpha_{\text{hnf}}\) are the effective density, the effective viscosity and the effective thermal diffusivity of the hybrid nanofluid, respectively, that are illustrated in Table 2.in which \(k_{\text{nf}}\) is the effective thermal conductivity of the mono-nanofluid that is calculated from Hamilton–Crosser model [43]

$$\frac{{k_{\text{nf}} }}{{k_{\text{f}} }} = \frac{{k_{1} + (n_{1} - 1)k_{\text{f}} - (n_{1} - 1)\phi_{1} (k_{\text{f}} - k_{1} )}}{{k_{1} + (n_{1} - 1)k_{\text{f}} + \phi_{1} (k_{\text{f}} - k_{1} )}}$$
(7)

and \(n\) is the empirical shape factor for the nanoparticle and is displayed in Table 3.

Table 2 Applied models for thermophysical properties of the hybrid nanofluid [17, 41, 42]
Full size table
Table 3 Values of shape factor of different shapes of nanoparticles [44, 45]
Full size table

Here \(\phi ,\)\(\rho_{\text{s}}\) and \((C_{\text{P}} )_{\text{s}}\) imply the equivalent volume fraction of nanoparticles, the equivalent density of nanoparticles and the equivalent specific heat at constant pressure of nanoparticles, respectively, as well as \(\phi_{1}\) and \(\phi_{2}\) are the volume fractions of first and second nanoparticles, respectively, that are approximated from the following relations [42, 46, 47]:

$$\rho_{\text{s}} = \frac{{(\rho_{1} \times w_{1} ) + (\rho_{2} \times w_{2} )}}{{w_{1} + w_{2} }},$$
(8)
$$(C_{\text{P}} )_{\text{s}} = \frac{{\{ (C_{\text{P}} )_{1} \times w_{1} \} + \{ (C_{\text{P}} )_{2} \times w_{2} \} }}{{w_{1} + w_{2} }},$$
(9)
$$\phi_{1} = \frac{{\frac{{w_{1} }}{{\rho_{1} }}}}{{\frac{{w_{1} }}{{\rho_{1} }} + \frac{{w_{2} }}{{\rho_{2} }} + \frac{{w_{\text{f}} }}{{\rho_{\text{f}} }}}},$$
(10)
$$\phi_{2} = \frac{{\frac{{w_{2} }}{{\rho_{2} }}}}{{\frac{{w_{1} }}{{\rho_{1} }} + \frac{{w_{2} }}{{\rho_{2} }} + \frac{{w_{\text{f}} }}{{\rho_{\text{f}} }}}},$$
(11)
$$\phi = \phi_{1} + \phi_{2} .$$
(12)

It is worth mentioning that in Eqs. (8)–(12), \(w_{1} ,\)\(w_{2}\) and \(w_{\text{f}}\) are masses of the first nanoparticle, the second nanoparticle and the base fluid, respectively. It should be noted that in all previous analytic single-phase nanofluid models, the volume fraction of first and second nanoparticles was initial inputs (for example, see Dinarvand et al. [17] and Yousefi et al. [42]), but according to the above formulas, we are offering base fluid mass as well as first and second nanoparticle masses as initial inputs.

Now, following von Kármán [19] we can introduce the following similarity variables [27]:

$$\begin{aligned} \eta & = \left( {\frac{\omega }{{\nu_{\text{f}} }}} \right)^{1/2} z,\quad V_{\text{r}} = \omega_{{}} rF(\eta ),\quad V_{\uptheta} = \omega_{{}} rG(\eta ), \\ V_{\text{z}} & = \left( {\omega \nu_{\text{f}} } \right)^{1/2} H(\eta ),\quad P - P\infty = 2\mu_{\text{f}} \omega P(\eta ),\quad \varTheta (\eta ) = \frac{T - T\infty }{{T_{\text{w}} - T\infty }}, \\ \end{aligned}$$
(13)

Consequently, after substituting Eq. (13) into nonlinear PDEs (1)–(5) along with taking Eqs. (10)–(12) into account, we will find the following set of dimensionless nonlinear ODEs:

$$2F + H^{{\prime }} = 0,$$
(14)
$$A_{1} \,F^{{{\prime \prime }}} - HF^{{\prime }} - F^{2} + G^{2} = 0,$$
(15)
$$A_{1} G^{{{\prime \prime }}} - HG^{{\prime }} - 2FG = 0,$$
(16)
$$\frac{1}{Pr}\frac{{k_{\text{hnf}} }}{{k_{\text{f}} }}A_{2} \varTheta^{{{\prime \prime }}} - H\varTheta^{{\prime }} = 0,$$
(17)
$$A_{1} = \left( {1 - \frac{{\frac{{w_{1} }}{{\rho_{1} }} + \frac{{w_{2} }}{{\rho_{2} }}}}{{\frac{{w_{1} }}{{\rho_{1} }} + \frac{{w_{2} }}{{\rho_{2} }} + \frac{{w_{\text{f}} }}{{\rho_{\text{f}} }}}}} \right)^{ - 2.5} \left( {1 - \frac{{\frac{{w_{1} }}{{\rho_{1} }} + \frac{{w_{2} }}{{\rho_{2} }}}}{{\frac{{w_{1} }}{{\rho_{1} }} + \frac{{w_{2} }}{{\rho_{2} }} + \frac{{w_{\text{f}} }}{{\rho_{\text{f}} }}}} + \frac{{\frac{{w_{1} }}{{\rho_{1} }} + \frac{{w_{2} }}{{\rho_{2} }}}}{{\frac{{w_{1} }}{{\rho_{1} }} + \frac{{w_{2} }}{{\rho_{2} }} + \frac{{w_{\text{f}} }}{{\rho_{\text{f}} }}}}\frac{{\rho_{\text{s}} }}{{\rho_{\text{f}} }}} \right)^{ - 1}$$
$$A_{2} = \frac{{(\rho C_{\text{P}} )_{\text{f}} }}{{\left[ {\left( {1 - \frac{{\frac{{w_{1} }}{{\rho_{1} }} + \frac{{w_{2} }}{{\rho_{2} }}}}{{\frac{{w_{1} }}{{\rho_{1} }} + \frac{{w_{2} }}{{\rho_{2} }} + \frac{{w_{\text{f}} }}{{\rho_{\text{f}} }}}}} \right)(\rho_{\text{f}} ) + \frac{{\frac{{w_{1} }}{{\rho_{1} }} + \frac{{w_{2} }}{{\rho_{2} }}}}{{\frac{{w_{1} }}{{\rho_{1} }} + \frac{{w_{2} }}{{\rho_{2} }} + \frac{{w_{\text{f}} }}{{\rho_{\text{f}} }}}}(\rho_{\text{s}} )} \right] \times \left[ {\left( {1 - \frac{{\frac{{w_{1} }}{{\rho_{1} }} + \frac{{w_{2} }}{{\rho_{2} }}}}{{\frac{{w_{1} }}{{\rho_{1} }} + \frac{{w_{2} }}{{\rho_{2} }} + \frac{{w_{\text{f}} }}{{\rho_{\text{f}} }}}}} \right)(C_{\text{P}} )_{\text{f}} + \frac{{\frac{{w_{1} }}{{\rho_{1} }} + \frac{{w_{2} }}{{\rho_{2} }}}}{{\frac{{w_{1} }}{{\rho_{1} }} + \frac{{w_{2} }}{{\rho_{2} }} + \frac{{w_{\text{f}} }}{{\rho_{\text{f}} }}}}(C_{\text{P}} )_{\text{s}} } \right]}}$$

subject to these dimensionless boundary conditions

$$F(0) = C,\quad \quad G(0) = 1,\quad \quad H(0) = 0,\quad \quad \varTheta (0) = 1,$$
(18)
$$F(\infty ) \to 0,\quad \quad G(\infty ) \to 0,\quad \quad \varTheta (\infty ) \to 0.$$
(19)

The Prandtl number \((Pr\,)\) as well as the stretching strength parameter \((C)\) possesses these definitions:

$$Pr = \frac{{\upsilon_{\text{f}} }}{{\alpha_{\text{f}} }},\quad C = \frac{s}{\omega },$$
(20)

It should be highlighted that the range of \(\phi ,\)\(\phi_{1} ,\)\(\phi_{2}\) and \(C\) can be changed between 0 and 1 [27].

Our parameters of engineering interest, i.e., the total skin friction coefficient \(C_{\text{f}}\) and the local Nusselt number \(Nu\), are expressed as follows [27, 48]:

$$C_{\text{f}} = \frac{{\sqrt {(\tau_{\text{wr}} )^{2} + (\tau_{{{\text{w}}\uptheta}} )^{2} } }}{{^{{\rho_{\text{f}} (\omega_{{}} r)^{2} }} }},\,\,\,\,\,\,\,\,\,\,\,\,Nu = \frac{{rq_{\text{w}} }}{{k_{\text{f}} (T_{\text{w}} - T_{\infty } )}}.$$
(21)

where \(\tau_{\text{wr}}\) and \(\tau_{{{\text{w}}\uptheta}}\) are in turn the radial and transversal shear stress at the surface of the rotating disk as well as \(q_{\text{w}}\) is the surface heat flux from it, which are defined by [27, 48]

$$\tau_{\text{wr}} = \mu_{\text{hnf}} \left( {\frac{{\partial V_{\text{r}} }}{\partial z} + \frac{1}{r}\frac{{\partial V_{\text{z}} }}{\partial \theta }} \right)_{z = 0} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tau_{{{\text{w}}\uptheta}} = \mu_{\text{hnf}} \left( {\frac{{\partial V_{\uptheta} }}{\partial z} + \frac{1}{r}\frac{{\partial V_{\text{z}} }}{\partial \theta }} \right)_{z = 0} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,q_{w} = - k_{\text{hnf}} \left( {\frac{\partial T}{\partial z}} \right)_{z = 0} .$$
(22)

At last, after using Eqs. (21), (22) and (13), we can prove

$$\left[ {Re} \right]^{{\frac{1}{2}}} C_{\text{f}} = \left( {1 - \frac{{\frac{{w_{1} }}{{\rho_{1} }} + \frac{{w_{2} }}{{\rho_{2} }}}}{{\frac{{w_{1} }}{{\rho_{1} }} + \frac{{w_{2} }}{{\rho_{2} }} + \frac{{w_{\text{f}} }}{{\rho_{\text{f}} }}}}} \right)^{ - 2.5} \sqrt {\{ F^{{\prime }} (0)\}^{2} + \{ G^{{\prime }} (0)\}^{2} } ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left[ {Re} \right]^{{\frac{ - 1}{2}}} Nu = - \frac{{k_{\text{hnf}} }}{{k_{\text{f}} }}\varTheta^{{\prime }} (0).$$
(23)

in which \(Re = \omega r^{2} /\upsilon_{\text{f}}\) is the local Reynolds number.

Results and discussion

We have to solve numerically the similarity governing Eqs. (14)–(17) subject to the boundary conditions (18) and (19) for some values of the governing parameters \(w_{1} ,\)\(w_{2} ,\)\(w_{\text{f}} ,\)\(\phi ,\)\(\phi_{1} ,\)\(\phi_{2} ,\)\(\rho_{\text{s}} ,\)\((C_{\text{P}} )_{\text{s}} ,\)\(C,\)\(n_{1} ,\)\(n_{2}\) and Pr using an efficient finite difference code (bvp4c) from MATLAB that is recognized as a collocation method and implements the 3-stage Lobatto IIIa formula (see Shampine et al. [49] as well as Kierzenka and Shampine [50]). In this approach, we have considered \(8 \le \eta_{\infty } \le 13,\) an initial uniform step size of \(\Delta \eta = \eta_{\infty } /100,\) and \(0.001\) as default value of the tolerance.

To achieve the validity of our numerical procedure, Table 4 presents the values of the similarity radial skin friction coefficient \((F'(0)),\) the similarity tangential skin friction coefficient \(( - G'(0)),\) the similarity axial velocity at the edge of the boundary layer \(( - H(\infty ))\) and the similarity local Nusselt number \(( - \varTheta '(0))\) for pure water \((w_{1} = w_{2} = \phi = \phi_{1} = \phi_{2} = 0),\) rotating disk without radial stretching rate \((C = 0)\) and \(Pr = 6.2,\) respectively. From Table 4, we understand that the present results are in excellent agreement with the previous reports obtained by White [21], Schlichting and Gersten [20], Bachok et al. [51], Rashidi et al. [48], Turkyilmazoglu [22] and Yin et al. [27].

Table 4 Comparison of the numerical solutions for \(F'(0),\)\(- G'(0),\)\(- H(\infty ),\)\(- \varTheta '(0),\) when \(\phi = \phi_{1} = \phi_{2} = \,w_{1} = w_{2} = C = 0 ,\,\)\(w_{\text{f}} = 100\,{\text{g}}\) and \(Pr = 6.2\)
Full size table

Boundary layer behavior: dimensionless velocity and temperature profiles

Figure 2 illustrates the effect of the stretching strength parameter (C) on the dimensionless fluid velocity components in radial, tangential and axial directions as well as the dimensionless temperature distribution, when \(w_{\text{f}} = 100\,{\text{g}},\)\(w_{1} = w_{2} = 10\,{\text{g}},\)\(n_{1} = n_{2} = 3\) and Pr = 6.2. From Fig. 2, we can see that with increasing \(C\) both tangential and axial components of dimensionless velocity profiles decrease, while the radial component of dimensionless velocity profile enhances and then decreases after a point near the disk that all dimensionless velocity profiles attain the same value on it. Moreover, with enhancing \(C\) we observe that the dimensionless temperature distributions as well as the thermal boundary layer thicknesses reduce. Consequently, the temperature gradients enhance and the local Nusselt numbers increase (see Eqs. (21) and (22)). Figure 3 portrays the foregoing dimensionless velocity components and temperature profiles based on different values of \(w_{2}\), when \(w_{\text{f}} = 100\,{\text{g}},\)\(w_{1} = 10\,{\text{g}},\)\(n_{1} = n_{2} = 3,\)\(C = 0.2\) and Pr = 6.2. As a result, when the second nanoparticle’s mass \((w_{2} )\) is elevated, simultaneously radial and tangential components of dimensionless velocity profiles as well as dimensionless temperature distribution along with thermal boundary layer thickness decrease, while axial component of dimensionless velocity profiles increases. Therefore, from Figs. 2 and 3, we can deduce that increasing the stretching strength parameter (C) and second nanoparticle’s mass \((w_{2} )\) has a desirable effect on heat transfer rate of our hybrid nanofluid. It is worth mentioning that by suspending the second nanoparticle (Au) into the zinc oxide/water mono-nanofluid, the effective thermal conductivity of our advanced working fluid elevates that it can amplify the local Nusselt number.

Fig. 2
figure 2

Dimensionless velocity profiles \((F(\eta ),\)\(G(\eta ),\)\(- H(\eta ))\) and temperature distribution \((\varTheta (\eta ))\) for different values of \(C,\) when \(w_{\text{f}} = 100\,{\text{g}},\)\(w_{1} = w_{2} = 10\,{\text{g}},\)\(n_{1} = n_{2} = 3\) and Pr = 6.2

Full size image
Fig. 3
figure 3

Dimensionless velocity profiles \((F(\eta ),\)\(G(\eta ),\)\(- H(\eta ))\) and temperature distribution \((\varTheta (\eta ))\) for different values of \(w_{2} ,\) when \(w_{\text{f}} = 100\,{\text{g}},\)\(w_{1} = 10\,{\text{g}},\)\(C = 0.2,\)\(n_{1} = n_{2} = 3\) and Pr = 6.2

Full size image

Effects of first and second nanoparticles mass on skin friction and heat transfer rate

Here, in Figs. 4 and 5, the main goal is comparison of the total skin friction coefficient \(([Re]^{1/2} C_{\text{f}} )\) and the local heat transfer rate \(([Re]^{ - 1/2} Nu)\) for various cases such as the regular fluid (pure water), mono-nanofluids (ZnO–water and Au–water) and hybrid nanofluids (ZnO–Au–water) with different values of first and second nanoparticle masses, when \(n_{1} = n_{2} = 3,\)\(C = 0.2,\)\(w_{\text{f}} = 100\,{\text{g}}\) and \(Pr = 6.2.\)

Fig. 4
figure 4

The total skin friction coefficient \([Re]^{1/2} C_{\text{f}}\) for various values of \(w_{1}\) and \(w_{2} ,\) when \(w_{\text{f}} = 100\,{\text{g}},\)\(n_{1} = n_{2} = 3,\)\(C = 0.2\) and \(Pr = 6.2\)

Full size image
Fig. 5
figure 5

The local heat transfer rate \([Re]^{ - 1/2} Nu\) for various values of \(w_{1}\) and \(w_{2}\), when \(w_{\text{f}} = 100\,{\text{g}},\)\(n_{1} = n_{2} = 3,\)\(C = 0.2\) and \(Pr = 6.2\)

Full size image

It is obvious that both the total skin friction coefficient and the local heat transfer rate boost with enhancing first and second nanoparticle masses for all cases. As we know, when the mass of the nanoparticles enhances, the effective thermal conductivity increases and affects the heat transfer rate of the working fluid. However, in Fig. 5, according to NF1 and NF3 (or NF2 and NF4) mono-nanofluid cases, the local heat transfer rate will be decreased when we add the gold particles into the pure water relative to dispersing the zinc oxide particles into it, while the thermal conductivity of Au is much higher than ZnO (see Table 1). This is because, according to Eq. (23), the local heat transfer rate enhancement depends on the following two important factors: (1) the thermal conductivity ratio \((k_{\text{hnf}} /k_{\text{f}} )\) and (2) the absolute value of dimensionless temperature profile’s slope at \(\eta = 0\)\(( - \varTheta^{{\prime }} (0)).\) In the NF3 (or NF4) case, the foregoing second factor diminishes relative to NF1 (or NF2) case.

From the present computations, the highest Nusselt number \(([Re]^{ - 1/2} Nu = 1.8928)\) and also the skin friction coefficient \(([Re]^{1/2} C_{\text{f}} = 1.2552)\) have been obtained for HNF4, which indicates an interesting heat transfer enhancement relative to mono-nanofluid and pure water. But, the high skin friction and the relevant pressure drop always should be controlled. Therefore, we can conclude that hybrid nanofluids efficiently can be used in all practical fields where ever mono-nanofluids are employed.

Effect of nanoparticles shape factor on heat transfer rate

Figure 6 presents dimensionless temperature distribution for some values of nanoparticles shape factor \((n_{1} = n_{2} )\) that are determined in Table 3, when \(w_{\text{f}} = 100\,{\text{g}},\)\(w_{1} = w_{2} = 10\,{\text{g}},\)\(C = 0.2\) and \(Pr = 6.2.\) Needless to mention that, the nanoparticles shape factors \((n_{1}\) and \(n_{2} )\) only affect the thermal characteristics of the problem that is because they are appeared clearly in the similarity energy Eq. (17) (see Eq. (17) and the effective thermal conductivity approximated in Table 2). It is seen that there is no major difference between these profiles under nanoparticles’ shape factor effects. Anyway, respective values of local heat transfer rate for nanoparticles shape factors from Fig. 6 are depicted in Fig. 7. It is worthwhile to notice that Fig. 7 illustrates when the nanoparticles shape is platelet \((n_{1} = n_{2} = 5.7),\) we have maximum heat transfer rate \(([Re]^{ - 1/2} Nu = 1.5842)\), while the opposite trend is true for spherical shape of nanoparticles \((n_{1} = n_{2} = 3)\) that are compatible with experimental observations.

Fig. 6
figure 6

Dimensionless temperature distribution \((\varTheta (\eta ))\) for some values of \(n_{1} = n_{2}\) when \(w_{\text{f}} = 100\,{\text{g}},\)\(w_{1} = w_{2} = 10\,{\text{g}},\)\(C = 0.2\) and Pr = 6.2

Full size image
Fig. 7
figure 7

The local heat transfer rate \([Re]^{ - 1/2} Nu\) for some values of \(n_{1} = n_{2}\), when \(w_{\text{f}} = 100\,{\text{g}},\)\(w_{1} = w_{2} = 10\,{\text{g}},\)\(C = 0.2\) and \(Pr = 6.2\)

Full size image

Finally, in Table 5 we have compared the local heat transfer rate for different shapes of first (ZnO) and second (Au) nanoparticles \((n_{1}\) and \(n_{2} )\) based on various cases of hybrid nanofluid masses that are indexed in Figs. 4 and 5 (entitled HNF1–HNF4), when \(w_{\text{f}} = 100\,{\text{g}},\)\(C = 0.2\) and \(Pr = 6.2.\) It is observed that the local heat transfer rate elevates along with increasing shape factor of first or second nanoparticles in all cases. Furthermore, it can be concluded that generally when the shape of second nanoparticles is spherical \((n_{2} = 3)\) and the shape of first nanoparticles is not \((n_{1} \ne 3),\) the heat transfer rate of hybrid nanofluid cases is more than opposite ones.

Table 5 The local heat transfer rate \([Re]^{ - 1/2} Nu\) for some values of \(n_{1}\) and \(n_{2}\) based on various cases of hybrid nanofluids mass, when \(C = 0.2,\) and \(Pr = 6.2\)
Full size table

Conclusions

The steady laminar 3D forced convective Von Kármán problem considering incompressible ZnO–Au–water hybrid nanofluid as the new working fluid with uniform stretching rate of the disk in the radial direction was investigated semi-analytically. Our specific goal of this article was to introduce a novel hybrid nanofluid model according to nanoparticles and base fluid masses instead of volume fractions. The Prandtl number of the base fluid (water) was fixed at 6.2. After using Tiwari–Das mathematical model, the nonlinear dimensional governing PDEs were first altered into nonlinear dimensionless ODEs using similarity transformations, before being solved numerically by a ready finite difference scheme from MATLAB software. The major conclusions of this study can be summarized as follows: (1) the increase in stretching strength parameter (C) and second nanoparticle’s mass \((w_{2} )\) causes an enhancement in the local heat transfer rate of the hybrid nanofluid, (2) mass increases of first and second nanoparticles demand enhancement on total skin friction coefficient \(([Re]^{1/2} C_{\text{f}} )\) and local heat transfer rate \(([Re]^{ - 1/2} Nu)\) of our working fluid, simultaneously, (3) when the nanoparticles shape is assumed spherical, the local heat transfer rate enhancement will be smaller than other shapes of nanoparticles, (4) the largest heat transfer rate between all studied cases of nanofluids and hybrid nanofluids is related to HNF4, because it has higher heat transfer rate relative to mono-nanofluid as well as pure water, respectively.

As the future works, it is suggested that the present research would be accomplished with other nanoparticles (metallic or nonmetallic) as well as with various base fluids (like SAE oil or diathermic oil). This is vital for the selection of optimum hybrid nanofluid to achieve the maximum heat transfer rate and the minimum skin friction for heat transfer applications.