Numerical investigation of boundary layer flow past a thin heated needle immersed in hybrid nanofluid

Abstract

The heat transfer in flow past thin needle has applications in instruments like hot wire anemometers. The objective of this article is to study the influence of hybrid nanoparticles on heat transfer distribution of the boundary layer flow over a parabolically shaped thin hot needle. The Sakiadis and Blasius 2-D flow scenarios have been analyzed by implementing a mathematical model with the Navier–Stokes and the energy equations. The resulting equations are solved numerically by using a similarity solution technique. This technique results in a differential equation in terms of a single variable, representing the curves parallel to the needle surface. The results show that using distinct nanoparticles allows us to control the heat transfer rate apart from the physical parameters, such as, needle size or velocity ratio parameter. A comparative analysis of Nusselt number, frictional drag, temperature, and velocity profiles for Ag–water nanofluid, Ag–CuO/water hybrid nanofluid, and CuO–water nanofluid has been carried out for different flow conditions, including Sakiadis and Blasius flow. The addition of nanoparticles hikes the heat transfer rate by 27–28% in Blasius flow and 6–8% in Sakiadis flow.

1 Introduction

The benefit of studying heat exchange and fluid flow around a thin heated needle immersed in the fluid stream is quite evident in applications, like anemometers, shielded thermocouple, and microscale cooling devices, etc. for heat evacuation. A hot wire anemometer is used to measure the direction and velocity of the fluid. At first, Mark [1] investigated laminar boundary layer characteristics of slender bodies of revolution in axial compressible and incompressible flows using Mangler transformations and the von-Karman Integral method. Mark [1] used modified boundary layer equations to analyze the fluid flow past paraboloids of revolution for the axial incompressible case. Lee [2] investigated the boundary layer flow over a thin needle submerged in an incompressible fluid and shaped like a paraboloid of revolution. Lee [2] introduced a similarity variable, which represents the curves parallel to the needle surface. Chen and Smith [3] examined the influence of the needle size on the nonuniform incompressible flow over the nonisothermal thin needle. Narain and Uberoi [4] and Grosan and Pop [5] examined forced convection while Narain and Uberoi [6, 7] investigated forced as well as free convective heat transport in the axisymmetric boundary layer flow past needle immersed vertically in a uniform stream of fluid.

The heat transport in the boundary layer can be enhanced significantly by the incorporation of nanoparticles in traditional fluids. Choi and Eastman [8] addressed the low thermal conductivity of conventional fluids by proposing nanofluids. They suspended nanometer-sized metallic particles (Eastman [9]; Eastman et al. [10]) or carbon nanotubes (Choi et al. [11]) in conventional heat transfer fluid, and noted that the thermal conductivity of the resulting liquid is exceptionally high. The exceptional heat augmentation behavior of nanofluids has attracted the worldwide attention of researchers as it offers a fine control over heat transfer in various industries. Godson et al. [12] reported a 9.2–13.2% increment in the heat transfer coefficient with 0.01–0.04% of the volume fraction of silver nanoparticles in water. Hasan [13] reported that for diamond-water nanofluid, there is a 9.12%, 9.78%, and 9.9% increment in the heat exchange rate, respectively, for circular, triangular, and square fins when compared with pure water. A detailed review of the work done by various researchers for heat augmentation in fluid flow through different geometries using different nanofluid models can be found in Sheikholeslami and Ganji [14] and Das et al. [15]. Ahmad et al. [16] investigated nanofluid flow past thin needle by taking into account Brownian motion and thermophoresis via the Buongiorno nanofluid model. Soid et al. [17] studied the flow and heat transport characteristics for a thin needle, moving axially in the Cu–water nanofluid. Khan et al. [18] calculated the entropy generation minimization and the heat transfer characteristics for three nanofluid models (copper, aluminum oxide, titanium oxide in water) in the radiative flow around a thin needle. Hamid et al. [19] studied the heat exchange in the boundary layer flow of graphene oxide–water nanofluid past a thin needle and observed that higher nanoparticle volume fraction leads to high skin friction values. Some more investigations on Newtonian nanofluids with various nanoparticles have been discussed in [20,21,22,23,24,25]. Non-Newtonian fluids like Casson fluid also come under the purview of this research. For example, Souayeh et al. [26] and Raza et al. [27, 28] investigated the radiative heat transport in magnetohydrodynamic flow by using Casson model. This work can be extended to other non-Newtonian shear-thinning models like Cross and Carreau–Yasuda models [29,30,31,32].

Some types of nanoparticles may have high thermal conductivity, while some other types might result in a nanofluid with remarkable rheological properties. Then the concept of hybrid nanofluids comes into the picture. Hybrid nanofluids can be synthesized either by suspending two or more distinct kinds of nanoparticles in the base fluid or by dispersing synthetic hybrid nanoparticles in the base fluid. Hybrid nanoparticles show outstanding physicochemical characteristics in comparison with mono-type nanoparticles. Experimental investigations of Suresh et al. [33] indicated a 12.11% increment in thermal conductivity of Al₂O₃–Cu/water hybrid nanofluid for a 2% volume fraction of hybrid nanocomposites in water. The experiment revealed that not only thermal conductivity, a significant increment in viscosity, is also observed. However, experimental investigations of Jana et al. [34] demonstrated that Cu nanoparticles, Au nanoparticles, or CNTs show more enhancement in thermal conductivity than that of their hybrid suspensions (Cu–CNTs or Au–CNTs) in water. They reported a 74% increment in thermal conductivity with 0.3% inclusion of copper nanoparticles in water, whereas a 37% increment in the same with 1.4% volume fraction of Au nanoparticles. They observed a drastic decrease in the thermal conductivity for mono-type nanoparticle suspensions (only Cu or only Au in water) with time due to aggregation and sedimentation. A detailed review of hybrid nanofluids is enlisted in Sarkar [35]. Recently, Hayat and Nadeem [36] investigated the effect of dispersing hybrid nanoparticles on three-dimensional rotating fluid flow over a linearly stretching surface with mathematical modeling. Researchers such as Nadeem et al. [37], Maskeen et al. [38], Devi et al. [39, 40], Mansour et al. [41], Khan et al. [42], Abdel-Nour et al. [43] investigated hybrid nanofluid flow over various geometries like cylinders, sheet or through a porous cavity, etc. Izadi et al. [44] studied the free convective flow of MWCNTs–Fe₃O₄/water nanofluid filled in a T-shaped enclosure. Tayebi [45] reported that hybrid nanofluid (consisting of Cu and Al₂O₃) leads to a greater heat exchange than Al₂O₃ –water in fluid flow through annular space between eccentric cylinders. The heat transfer characteristics of micropolar hybrid nanofluid (Cu and TiO₂ nanoparticles) were investigated by Subhani [46]. Ghadikolaei and Gholinia [47] studied the Nusselt number and skin friction profiles for heat transfer in natural convective MHD flow of GO–MoS₂/water–ethylene glycol (50–50%).

In the present article, a comparative analysis of Nusselt number, frictional drag, temperature, and velocity profiles among Ag–water nanofluid, Ag–CuO/water hybrid nanofluid, and CuO–water nanofluid is performed for different flow conditions, including Sakiadis and Blaisus flows past a thin heated needle. The influence of various flow conditions and needle size on heat and flow characteristics is investigated. To visualize the impact of the addition of nanoparticles, the percentage increments in Nusselt number and skin friction coefficient are calculated and analyzed in detail for Sakiadis flow, Blasius flow, and other cases to have a deeper understanding.

2 Mathematical model and physical description of the flow

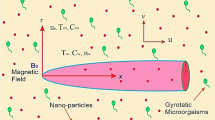
Consider the boundary layer flow around a thin heated needle immersed in a viscous fluid comprising of Ag and CuO nanoparticles. The needle is paraboloid shaped such that the axis of the paraboloid lies in the direction of mainstream flow. The nanofluid flow past the needle is assumed to be steady and incompressible. The needle itself moves with the uniform velocity $u_{w}$ horizontally either in the same or opposite direction to the mainstream of fluid flowing over it with velocity $u_{\infty }$. The thickness of the needle is assumed to be smaller than that of the boundary layer formed over it. As the needle is assumed to be thin, its transverse curvature has significant influence, but the pressure gradient along the needle surface is negligible. Without loss in generosity, it is assumed that the temperature $T_{w}$ at the needle surface is higher than the temperature $T_{\infty }$ of the ambient fluid (i.e., $T_{w}$ > $T_{\infty }$). The needle is placed over X-axis such that it is symmetric about the axis as depicted in Fig. 1, in which $x$ and $r$ denote the axial and radial directions, respectively, in the cylindrical coordinates $(x,\,\,r)$. The surface shape of the needle is defined by $R(x)$ as follows

$$ R(x) = \left( {\frac{{\nu_{\text{f}} cx}}{U}} \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} . $$

(1)

Fig. 1

Schematic flow representation around thin needle

Here $U = u_{w} + u{}_{\infty }$ represents the composite velocity, $c$ depicts the needle size, and $\nu_{f}$ denotes the kinematic viscosity of the surrounding fluid.

In order to study the flow and heat transfer of the system, the boundary layer assumptions (Schlichting and Gersten [48]) are applied to the Navier–Stokes equations. The terms ${{\partial^{2} u} \mathord{\left/ {\vphantom {{\partial^{2} u} {\partial x^{2} }}} \right. \kern-0pt} {\partial x^{2} }},\,\,{{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial x}}} \right. \kern-0pt} {\partial x}},\,\,u$ in the axial direction are assumed to be of $O\left( 1 \right)$, whereas $r$ and $v$ in the radial direction are assumed to be of $O\left( \delta \right)$ where $\delta$ denotes the width of the boundary layer, as discussed in Mark [1]. The order of $\mu_{hnf}$ is assumed to be $O\left( {\delta^{2} } \right)$, so that the inertial and viscous terms in the equations of motion should be of the same order [49, 50]. The continuity equation and conservation of momentum are presented by Eqs. (2) and (3) after applying Prandtl’s order of magnitude assumptions.

$$ \frac{{\partial \left( {ru} \right)}}{\partial x} + \frac{{\partial \left( {rv} \right)}}{\partial r} = 0, $$

(2)

$$ u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial r} = \frac{{\mu_{\text{hnf}} }}{{\rho_{\text{hnf}} }}\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial u}{\partial r}} \right), $$

(3)

$$ \left( {\rho C_{p} } \right)_{\text{hnf}} \left( {u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial r}} \right) = \kappa_{\text{hnf}} \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial T}{\partial r}} \right). $$

(4)

where $u$ and $v$ are the velocity components in axial and radial direction, respectively. The energy equation given in Eq. (4) is employed to study the heat transport in the boundary layer around the thin needle. It is a mathematical formulation of the first law of thermodynamics, which says that the energy of a closed system cannot be changed in the absence of external influence. It is assumed that both viscosity and velocity gradients are small enough to neglect the viscous dissipation in the energy Eq. (4). Here $\kappa_{\text{hnf}}$, $\rho_{\text{hnf}}$ and $\mu_{\text{hnf}}$ in Eqs. (3) and (4) represent the thermal conductivity, density, and dynamic viscosity of the hybrid nanofluid. Equations (2)–(4) governing the boundary layer fluid transport are subjected to the following conditions

$$ ({\text{i}})\quad {\text{At}}\;r = R(x),\;T = T_{w} ,\;u = u_{w} ,v = 0, $$

(5)

$$ \left( {\text{ii}} \right)\quad {\text{As}}\;r \to \infty ,\;T \to T_{\infty } ,\;u \to u_{\infty } . $$

(6)

The hybrid nanofluid consists of CuO (copper oxide) and Ag (silver) nanoparticles dispersed in water. Firstly, CuO-nanoparticles with volume fraction $\phi_{1}$ are dispersed in water to synthesize CuO–water nanofluid. In order to obtain Ag–CuO/water hybrid nanofluid, Ag nanoparticles with volume fraction $\phi_{2}$ are suspended in CuO–water nanofluid.

The effective viscosity $\mu_{\text{nf}}$, density $\rho_{\text{nf}}$, and heat capacity $(\rho C_{p} )_{\text{nf}}$ of the CuO–water nanofluid are calculated using the following equations

$$ \mu_{\text{nf}} = \frac{{\mu_{f} }}{{\left( {1 - \phi_{1} } \right)^{2.5} }}, $$

(7)

$$ \rho_{\text{nf}} = \left( {1 - \phi_{1} } \right)\rho_{\text{f}} + \phi_{1} \,\rho_{s1} , $$

(8)

$$ \left( {\rho C_{p} } \right)_{\text{nf}} = \left( {1 - \phi_{1} } \right)\left( {\rho C_{p} } \right)_{\text{f}} + \phi_{1} \left( {\rho C_{p} } \right)_{s1} . $$

(9)

Here $\rho_{s1}$ and $(\rho C_{p} )_{s1}$ denote the density and heat capacity of the CuO nanoparticles, respectively, while $\rho_{\text{f}}$ and $(\rho C_{p} )_{\text{f}}$ denote the density and heat capacity of the base fluid water, respectively. The effective viscosity is calculated by using Brinkman model [51].

The effective thermal conductivity of the nanofluid $\kappa_{\text{nf}}$ is calculated by using Hamilton Crosser model [52]. If $\kappa_{s1}$ denote the thermal conductivity of the CuO nanoparticles and $\kappa_{\text{f}}$ denote the thermal conductivity of the base fluid water, then the effective thermal conductivity of the nanofluid is defined as

$$ \kappa_{\text{nf}} = \frac{{\kappa_{p} + (n - 1)\kappa_{\text{f}} - (n - 1)\phi \left( {\kappa_{\text{f}} - \kappa_{p} } \right)}}{{\kappa_{p} + (n - 1)\kappa_{\text{f}} + \phi \left( {\kappa_{\text{f}} - \kappa_{p} } \right)}}\kappa_{\text{f}} . $$

(10)

Here $n$ is termed as the shape factor and $n = {3 \mathord{\left/ {\vphantom {3 \psi }} \right. \kern-0pt} \psi }$ where $\psi$ represents the sphericity. For spherical nanoparticles $n = 3$. After putting this value of $n$, the effective thermal conductivity is defined as

$$ \kappa_{\text{nf}} = \frac{{\kappa_{s1} + 2\kappa_{\text{f}} - 2\phi_{1} \left( {\kappa_{\text{f}} - \kappa_{s1} } \right)}}{{\kappa_{s1} + 2\kappa_{\text{f}} + \phi_{1} \left( {\kappa_{\text{f}} - \kappa_{s1} } \right)}}\kappa_{\text{f}} . $$

(11)

The effective heat capacity is calculated using the linear relationship as stated by Xuan and Roetzel [53]. Similarly, the effective viscosity $\mu_{\text{hnf}}$, density $\rho_{\text{hnf}}$, heat capacity $(\rho C_{p} )_{\text{hnf}}$, and thermal conductivity $\kappa_{\text{hnf}}$ of the Ag–CuO/water hybrid nanofluid are calculated by using Eqs. (12)–(15).

$$ \mu_{\text{hnf}} = \frac{1}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }}\mu_{\text{f}} , $$

(12)

$$ \rho_{\text{hnf}} = \left\{ {\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \phi_{1} \frac{{\rho_{s1} }}{{\rho_{\text{f}} }}} \right) + \phi_{2} \frac{{\rho_{s2} }}{{\rho_{\text{f}} }}} \right\}\rho_{\text{f}} , $$

(13)

$$ \left( {\rho C_{p} } \right)_{\text{hnf}} = \left\{ {\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \phi_{1} \frac{{\left( {\rho C_{p} } \right)_{s1} }}{{\left( {\rho C_{p} } \right)_{\text{f}} }}} \right) + \phi_{2} \frac{{\left( {\rho C_{p} } \right)_{s2} }}{{\left( {\rho C_{p} } \right)_{\text{f}} }}} \right\}\left( {\rho C_{p} } \right)_{\text{f}} , $$

(14)

$$ \kappa_{\text{hnf}} = \frac{{\kappa_{s2} + 2\kappa_{\text{nf}} - 2\phi_{2} \left( {\kappa_{\text{nf}} - \kappa_{s2} } \right)}}{{\kappa_{s2} + 2\kappa_{\text{nf}} + \phi_{2} \left( {\kappa_{\text{nf}} - \kappa_{s2} } \right)}}\kappa_{\text{nf}} . $$

(15)

Here $\rho_{s2}$, $(\rho C_{p} )_{s2} ,$ and $\kappa_{s2}$ denote the density, heat capacity, and thermal conductivity of the Ag nanoparticles, respectively. We put $\phi_{1} = 0$ in the Eqs. (12)–(15) to calculate the effective viscosity $\mu_{\text{nf}}$, density $\rho_{\text{nf}}$, heat capacity $(\rho C_{p} )_{\text{nf}} ,$ and thermal conductivity $\kappa_{\text{nf}}$ of the Ag–water nanofluid. The local Nusselt number ${\text{Nu}}_{x}$ and skin friction coefficient $C_{\text{f}}$ are defined by Eq. (16) as stated in [16, 17].

$$ {\text{Nu}}_{x} = {{xq_{w} } \mathord{\left/ {\vphantom {{xq_{w} } {\kappa_{\text{f}} \left( {T_{w} - T_{\infty } } \right)}}} \right. \kern-0pt} {\kappa_{\text{f}} \left( {T_{w} - T_{\infty } } \right)}}\quad {\text{and}}\quad C_{\text{f}} = {{\tau_{w} } \mathord{\left/ {\vphantom {{\tau_{w} } {\rho_{\text{f}} U^{2} }}} \right. \kern-0pt} {\rho_{\text{f}} U^{2} }}. $$

(16)

The expression for the heat flux and the shear stress at the needle surface is as stated in Eq. (17).

$$ q_{w} = - \kappa_{\text{hnf}} \left( {\frac{\partial T}{\partial r}} \right)_{r = R} \quad {\text{and}}\quad \tau_{w} = \mu_{\text{hnf}} \left( {\frac{\partial u}{\partial r}} \right)_{r = R} . $$

(17)

3 Numerical solution

The heat exchange in the channel commences as soon as the hot needle is inserted. So, it is sensible to study the heat transfer and flow characteristics along the surfaces parallel to the needle. The parabolic shape of the needle allows the similarity solution to exist. As discussed by Lee [2], a non-dimensional variable ($\eta$) proportional to the ratio of $r^{2}$ and $x$ is used.

$$ \,\eta = \frac{{Ur^{2} }}{{\nu_{\text{f}} x}}. $$

(18)

As the study is a streamlined flow, it is reasonable to assume that a stream function exists in form $\psi = g(x) \cdot f(\eta )$. The g(x) is supposed to be of the linear form so that the partial differential equations can be converted to ordinary differential equations. After plugging the g(x), the stream function reduces to (19),

$$ \psi = \nu_{\text{f}} x \cdot f(\eta ), $$

(19)

such that the velocity components are given by the relations (20).

$$ u = \frac{1}{r}\frac{\partial \psi }{\partial r},\quad v = - \frac{1}{r}\frac{\partial \psi }{\partial x}. $$

(20)

The temperature is non-dimensionalized with the temperature difference of the needle and the ambient fluid is

$$ \theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }}. $$

(21)

After using Eqs. (12)–(15) and applying similarity transformations (20–21), the non-dimensional momentum and energy equations are

$$ \frac{2}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }}\left( {f^{\prime \prime } + \eta f^{\prime \prime \prime } } \right) + \left\{ {\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \phi_{1} \frac{{\rho_{s1} }}{{\rho_{\text{f}} }}} \right) + \phi_{2} \frac{{\rho_{s2} }}{{\rho_{\text{f}} }}} \right\}\;ff^{\prime \prime } = 0, $$

(22)

$$ \frac{2}{\Pr } \cdot \frac{{\kappa_{\text{hnf}} }}{{\kappa_{\text{f}} }}\left( {\theta^{\prime } + \eta \theta^{\prime \prime } } \right) + {\mkern 1mu} \left\{ {\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \phi_{1} \frac{{\left( {\rho C_{p} } \right)_{s1} }}{{\left( {\rho C_{p} } \right)_{\text{f}} }}} \right) + \phi_{2} \frac{{\left( {\rho C_{p} } \right)_{s2} }}{{\left( {\rho C_{p} } \right)_{\text{f}} }}} \right\}f\theta^{\prime } = 0. $$

(23)

The non-dimensional form of the boundary conditions is

$$ f^{\prime}(c) = \frac{\lambda }{2},\;f(c) = \frac{\lambda c}{2},\;\theta (c) = 1, $$

(24)

$$ f^{\prime}(\infty ) \to \frac{1 - \lambda }{2},\;\theta (\infty ) \to 0. $$

(25)

Here, $\Pr = \frac{{\nu_{\text{f}} }}{{\alpha_{\text{f}} }}$ represent the Prandtl number. The velocity ratio parameter $\lambda = \frac{{u_{w} }}{U}$ is an important attribute as it governs different flow conditions as mentioned below

• (a) $\lambda = 0$ represents the Blasius flow when the needle is at rest in a moving fluid.

• (b) $\lambda = 1$ represents the Sakiadis flow when the needle is moving, but the fluid is at rest.

• (c) $0 < \lambda < 1$ represents the case when the velocities of the needle and the fluid are oriented in the same direction.

• (d) $\lambda < 0$ and $\lambda > 1$ represent the case when the direction in which the needle is moving opposite to that of the free stream of fluid. Here, $\lambda < 0$ describes the case when the needle is moving in the negative x-direction, but the surrounding fluid is moving toward the positive x-direction. On the contrary, $\lambda > 1$ represents the case when the needle is moving in the positive x-direction, but the surrounding fluid is moving toward the negative x-direction.

After non-dimensionalization, the local Nusselt number and the skin friction coefficient in terms of local Reynold’s number $\text{Re}_{x} = {{Ux} \mathord{\left/ {\vphantom {{Ux} {\nu_{\text{f}} }}} \right. \kern-0pt} {\nu_{\text{f}} }}$ are given by

$$ {\text{Nu}}_{x} {\text{Re}}_{x}^{ - 1/2} = - 2\frac{{\kappa_{\text{hnf}} }}{{\kappa_{\text{f}} }}c^{1/2} \theta^{\prime } (c), $$

(26)

$$ C_{\text{f}} {{\rm Re}}_{x}^{1/2} = 4c^{1/2} \frac{{\mu_{\text{hnf}} }}{{\mu_{\text{f}} }}f^{\prime \prime } (c) = \frac{1}{{\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} }}4c^{1/2} f^{\prime \prime } (c). $$

(27)

The system of higher-order ODE’s (22)–(23) subject to boundary conditions (24)–(25) is converted to the system of first-order equations using the following substitution:

$$ \left( {f,f^{\prime } ,f^{\prime \prime } ,\theta ,\theta^{\prime } } \right) = \left( {y_{1} ,y_{2} ,y_{3} ,y_{4} ,y_{5} } \right), $$

(28)

$$ \begin{aligned} \frac{{{\text{d}}y_{1} }}{{{\text{d}}\eta }} & = y_{2} , \\ \frac{{{\text{d}}y_{2} }}{{{\text{d}}\eta }} & = y_{3} , \\ \frac{{{\text{d}}y_{3} }}{{{\text{d}}\eta }} & = \frac{1}{\eta }\left\{ { - y_{3} - \frac{1}{2}\left\{ {\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \phi_{1} \frac{{\rho_{s1} }}{{\rho_{\text{f}} }}} \right) + \phi_{2} \frac{{\rho_{s2} }}{{\rho_{\text{f}} }}} \right\}\left( {1 - \phi_{1} } \right)^{2.5} \left( {1 - \phi_{2} } \right)^{2.5} y_{1} y_{3} } \right\}, \\ \frac{{{\text{d}}y_{4} }}{{{\text{d}}\eta }} & = y_{5} , \\ \frac{{{\text{d}}y_{5} }}{{{\text{d}}\eta }} & = \frac{1}{\eta }\left\{ { - y_{5} - \frac{\Pr }{2} \cdot \frac{{\kappa_{\text{f}} }}{{\kappa_{\text{hnf}} }}\left\{ {\left( {1 - \phi_{2} } \right)\left( {\left( {1 - \phi_{1} } \right) + \phi_{1} \frac{{\left( {\rho C_{p} } \right)_{s1} }}{{\left( {\rho C_{p} } \right)_{\text{f}} }}} \right) + \phi_{2} \frac{{\left( {\rho C_{p} } \right)_{s2} }}{{\left( {\rho C_{p} } \right)_{\text{f}} }}} \right\}y_{1} y_{5} } \right\}. \\ \end{aligned} $$

(29)

The boundary conditions in terms of $(y_{1} ,y_{2} ,y_{3} ,y_{4} ,y_{5} )$ are given by

$$ y_{1} (c) = \frac{\lambda c}{2},\;y_{2} (c) = \frac{\lambda }{2},\;y_{4} (c) = 1,\;y_{2} (\infty ) = \frac{1 - \lambda }{2},\;y_{4} (\infty ) = 0. $$

(30)

The above system of Eqs. (29) and (30) is solved by the fourth-order Runge–Kutta method along with the well-known shooting strategy. To integrate the system of the first-order ODE’s given in (29), the initial guess values $s_{1}$ and $s_{2}$ are chosen to have the set of initial conditions at $\eta = c$ given by Eq. (31).

$$ y_{1} (c) = \frac{\lambda c}{2},\;y_{2} (c) = \frac{\lambda }{2},\;y_{3} (c) = s_{1} ,\;y_{4} (c) = 1,\;y_{5} (c) = s_{2} . $$

(31)

After choosing the initial guess values $s_{1}$ and $s_{2}$, the initial value problem given by Eqs. (29) and (30) is integrated using the Runge–Kutta method till $\eta_{\infty }$. A system of algebraic equations is formulated by equating the results obtained using numerical integration to the conditions given in (30), which are further solved using the Newton–Raphson method (Jaan Kiusalaas [54]), with an error tolerance of order of magnitude 10⁻⁹. A reasonably good guess is required to ensure the desired error tolerance while obtaining a solution as a bad guess will lead to singular Jacobian matrix. A MATLAB code is developed to achieve the numerical solution by using the above numerical scheme. The accuracy of the code was checked by verifying the results obtained using the current algorithm against already published results by treating it as a limiting case shown in Table 1. The validation is performed for the viscous base fluid case. The values of $f^{\prime \prime } (c)$ obtained using the present code are compared against the values obtained by bvp4c solver method as calculated by Soid et al. [17] using bvp 4c solver and Ishak et al. [55] using the finite difference method by putting $\lambda = 0,\;\phi_{1} = 0,\;\phi_{2} = 0$ in the non-dimensionalized governing Eqs. (21)–(22). The computed results when compared with the already published literature are in good agreement (Table 1). It was observed during the code verification that a fair initial guess and an appropriate value of $\eta$ at infinity would lead to the faster convergence of the solution, and an unsuitable guess can lead to a singularity in the Jacobian iterations. While obtaining the results, one should be very careful in choosing an initial guess. Also, the smaller step size ensures an accurate solution.

Table 1 Resemblance of $f^{\prime\prime}(c)$ values with already published results for code verification

4 Results and discussion

Inducing a heated needle in the fluid initiates a heat transfer at the solid–fluid boundary. This heat propagates into the fluid around the needle. To study the enhancement of heat transfer in the system, the results are computed for the rate of heat transfer at the solid–fluid boundary and fluid temperature. The percentage increment in the Nusselt number after dispersing the nanoparticles $\left( {{{({\text{Nu}}_{\text{nanofluid}} - {\text{Nu}}_{\text{water}} )} \mathord{\left/ {\vphantom {{({\text{Nu}}_{\text{nanofluid}} - {\text{Nu}}_{\text{water}} )} {{\text{Nu}}_{\text{water}} }}} \right. \kern-0pt} {{\text{Nu}}_{\text{water}} }}} \right)*100$ is calculated and the influence of each parameter can be studied on a non-dimensional scale to see that the study can be extended to any length within the limitations of the boundary layer approximations. The velocity and skin friction are also computed to understand the flow characteristics. The impact of needle size ($c$) and velocity ratio parameter ($\lambda$) on heat transfer and fluid flow is enquired in detail. The study has been performed for different flow conditions governed by flow parameter ($\lambda$ < 0, = 0, = 0.5, = 1, > 1) to visualize the influence for each of the flow condition. The physical data for the thermophysical quantities are given in Table 2. All the numerical simulations have been performed with the volume fraction of the nanoparticles as 0.1 (i.e., $\phi_{1} + \phi_{2} = 0.1$).

Table 2 Details of the nanoparticles and the base fluid

4.1 The effect of needle size on heat exchange in Sakiadis flow

Sakiadis flow refers to the situation when the thin heated needle is moving in static fluid and is governed by the case when $\lambda = 1$. The size of the needle is directly proportional to the factor $c ,$ i.e., the thickness of the needle. Hence, the study has been performed by taking $c$ as a parameter, meaning that the flow and heat transport characteristics are studied by varying needle size $c$. Such flow situations are of considerable importance as these “needles” could be identified with very small diameter cylinders such as “wires” or “sensors” of hot wire anemometers. The effect of needle size on heat exchange at the boundary as well as in the ambient nanofluid is visualized with the help of Nusselt number profiles and temperature distribution curves for pure water, (Ag–water)_nf (Ag–water nanofluid), (CuO–water)_nf (CuO–water nanofluid) and (Ag–CuO/water)_hnf (Ag–CuO/water hybrid nanofluid). The graphical results of skin friction and velocity are also presented to visualize the flow characteristics.

4.1.1 Heat transfer at the boundary

As the heat transfer in the fluid is initiated by the hot needle, studying the heat transfer rate at the boundary is one of the primary objectives of the problem. The rate of heat exchange is studied through the Nusselt number profiles by varying $c$. The profiles of the Nusselt number against $c$ are shown in Fig. 2 for the Sakiadis flow (i.e., $\lambda = 1$). As there would be a larger surface area for the bigger size of the needle, the needle dissipates more heat into the fluid. This can be easily inferred from Fig. 2 that the heat transfer rate gradually increases with the size of the needle. As the Nusselt number profiles increase in a nearly linear manner with $c$, it implies that the rate of heat exchange at the boundary can be increased by increasing the needle size. Table 3 gives the Nusselt number values for pure water, (CuO–water)_nf, (Ag–water)_nf and (Ag–CuO/water)_hnf as well as the percentage increments in the Nusselt number, i.e., $\left( {\left( {{{({\text{Nu}}_{\text{nanofluid}} - {\text{Nu}}_{\text{water}} )} \mathord{\left/ {\vphantom {{({\text{Nu}}_{\text{nanofluid}} - {\text{Nu}}_{\text{water}} )} {{\text{Nu}}_{\text{water}} }}} \right. \kern-0pt} {{\text{Nu}}_{\text{water}} }}} \right)*100\% } \right)$ due to the inclusion of nanoparticles in pure water. It is calculated from Table 3 that at the needle surface (i.e., at $\eta = c = 0.2$), there has been 8.894%, 6.4476%, and nearly 8% increment in Nusselt number for (CuO–water)_nf, (Ag–water)_nf, and (Ag–CuO/water)_hnf, respectively. This implies that for Sakiadis flow, (CuO–water)_nf has more heat transfer enhancement than (Ag–water)_nf. This can also be seen in Fig. 2, where the Nusselt number profiles for various nanofluid models follow the trend for a fixed value of $c$ in Sakiadis flow:

$$ \left( {{\text{CuO}} - {\text{water}}} \right)_{\text{nf}} > \left( {{\text{Ag}} - {\text{CuO/water}}} \right)_{\text{hnf}} > ({\text{Ag}} - {\text{water}})_{\text{nf}} > {\text{ Pure}}\;{\text{water}} $$

Fig. 2

Nusselt number profile for Sakiadis flow

Table 3 Nusselt number table

4.1.2 Heat transfer around the needle

The temperature profiles for pure water, (CuO–water)_nf, (Ag–water)_nf, and (Ag–CuO/water)_hnf have been plotted against $\eta$ from $\eta = c$ to $\eta_{\infty }$. For computational purposes, the infinite boundary values $\eta_{\infty }$ have been considered till 9 or 10, depending on the asymptotic convergence of velocity and thermal boundary layers. Since it is a coupled differential equation, the maximum of the two has to be opted for obtaining accurate results. The (Ag–water)_nf has more temperature values than the (Ag–CuO/water)_hnf, which in turn has more temperature values than (CuO–water)_nf. In the earlier section, we have seen that the (CuO–water)_nf has more rate of heat transfer when compared to the other three fluids. In support of this argument, Fig. 3 shows that the thickness of the thermal boundary layer is the least for (CuO–water)_nf among the three nanofluids. This is because of the fact that the thinner the boundary layer, the more will be the rate of heat transfer. So there is more rapid heat exchange for (CuO–water)_nf than (Ag–water)_nf in Sakiadis flow. The impact of the needle size on the temperature is visualized by plotting the temperature curves for two different values of needle size $c$ (a magnified version of this is shown in Fig. 4 for better understanding). Figure 4 shows that an increment in needle size rises the fluid temperature. In other words, the thickness of thermal boundary layer increases with increasing needle size, meaning that the effect of needle transverse curvature is important and a more slender needle enhances heat transfer.

Fig. 3

Temperature profile for Sakiadis flow

Fig. 4

Influence of $c$ on temperature profile for Sakiadis flow

4.1.3 Velocities around the needle

Similar to the temperature profiles, an asymptotic behavior of axial velocities can be seen in Fig. 5. It is observed that the inclusion of nanoparticles results in a thin velocity boundary layer for Sakiadis flow. Among the three nanofluids, the fluid velocity is lowest for (Ag–water)_nf and highest for (CuO–water)_nf, i.e., the velocity boundary layer is thinner for (Ag–water)_nf and thicker for (CuO–water)_nf at a given needle size. It is also noticed that with the increase in needle size (Fig. 6), fluid velocity increases for all the three nanofluids.

Fig. 5

Velocity profile for Sakiadis flow

Fig. 6

Influence of $c$ on velocity profile for Sakiadis flow

4.1.4 Skin friction at the boundary

The magnitude of skin friction at the boundary follows the trend:

$$ ({\text{Ag}} - {\text{water}})_{\text{nf}} > \left( {{\text{Ag}} - {\text{CuO/water}}} \right)_{\text{hnf}} > \left( {{\text{CuO}} - {\text{water}}} \right)_{\text{nf}} $$

This trend is in synchronicity with the axial velocity profiles, since the skin friction depends upon the velocity gradient. Table 4 reveals that there has been a 72% rise in the magnitude of skin friction coefficient for (Ag–water)_nf, 63% for (Ag–CuO/water)_hnf, and nearly 58% for (CuO–water)_nf, when calculated in reference to pure water. In Sakiadis flow, a heated needle moves through a quiescent fluid, so there is a drag force on the needle, leading to a negative skin friction coefficient (Fig. 7).

Table 4 Skin friction coefficient table

Fig. 7

Skin friction profile for Sakiadis flow

4.2 Effect of different flow conditions on heat transfer (Blasius flow and other cases)

The previous section explores the heat exchange in the system, when the needle is moving through quiscent fluid, particularly the case where $\lambda = 1$ (termed as Sakiadis flow). The present section will shed light on the heat exchange taking place for different flow conditions categorized as: (a) $\lambda = 0$ (termed as Blasius flow in which needle is at rest), (b) $0 < \lambda < 1$ (when the needle and the surrounding nanofluid are moving in the same direction) (c) $\lambda < 0$ or $\lambda > 1$ (when the needle moves in an opposite direction to that of the surrounding nanofluid). To visualize the influence of the different flow conditions, Nusselt number profiles, temperature distribution curves, skin friction profiles, and velocity curves for different values of flow parameter $\lambda$ have been presented.

4.2.1 Heat transfer at the boundary

The rate of heat transfer is studied through the Nusselt number profiles for different $c$. The profiles of Nusselt numbers against $c$ for the different flow conditions governed by $\lambda$ are shown in Fig. 8(a) to Fig. 8(c). As there would be a larger surface area for the bigger size of the needle, it dissipates more heat into the fluid. It can be inferred from the figures that the Nusselt number profiles increase gradually with $c$ for all the fluids (water, (CuO–water)_nf, (Ag–water)_nf, and (Ag–CuO/water)_hnf). It implies that the rate of heat exchange at the boundary can be enhanced by increasing the needle size. The value of the Nusselt number increases due to the addition of nanoparticles, whether it is CuO-nanoparticles, Ag nanoparticles, or both CuO and Ag nanoparticles.

Fig. 8

(a) Nusselt number profile for $\lambda = - \,0.2$. (b) Nusselt number profile for Blasius flow. (c) Nusselt number profile for $\lambda = 0.8$

For different flow conditions (i.e., $\lambda = - 0.2,\,0,\,0.3,\,0.8,\,1.2\,$), Table 3 gives the Nusselt number values for pure water, (CuO–water)_nf, (Ag–water)_nf, and (Ag–CuO/water)_hnf along with the increment percentage in the Nusselt number. It is calculated that for $\lambda = - 0.2$, there has been nearly 33% increment in Nusselt number value for (CuO–water)_nf, approximately 35% increment for (Ag–water)_nf, and 34% increment for (Ag–CuO/water)_hnf by considering the value of pure water as reference at the needle surface (i.e., at $\eta = c = 0.2$) (Fig. 8(a)). Whereas, for Blasius flow (i.e.,$\lambda = 0$), (Fig. 8(b)), there has been almost a 27% increment in Nusselt number for (CuO–water)_nf, nearly 28.7% increment for (Ag–water)_nf and nearly 28.5% increment for (Ag–CuO/water)_hnf. So, for $\lambda = - \,0.2,\,0$ the following trend in Nusselt number values is observed:

$$ ({\text{Ag}} - {\text{water}})_{\text{nf}} > \left( {{\text{Ag}} - {\text{CuO/water}}} \right)_{\text{hnf}} > \left( {{\text{CuO}} - {\text{water}}} \right)_{\text{nf}} $$

Nusselt number behavior for Blasius flow (i.e., fixed needle in a moving fluid) has a reverse outcome for all the three nanofluids, when compared with that of Sakiadis flow (i.e., moving needle in quiescent fluid). The rate of heat exchange is maximum for (Ag–water)_nf in case of Blasius flow, whereas it is maximum for (CuO–water)_nf in case of Sakiadis flow.

Each of the flow conditions has a remarkable influence on the flow and heat transfer of the system. Table 3 illustrates that the Nusselt number increases with increment in flow parameter $\lambda$. Now, $\lambda$ being the ratio of the needle velocity to the composite velocity, the rate of heat transfer can be enhanced by increasing the needle velocity or by decreasing the velocity of nanofluid stream.

The percentage increments in Nusselt number for the (CuO–water)_nf, (Ag–water)_nf, and (Ag–CuO/water)_hnf when calculated in reference to that of pure water decreases with increase in $\lambda$. This means that for smaller values of $\lambda$, the inclusion of nanoparticles on heat exchange is much more effective than for a higher value of $\lambda$. For Blasius flow($\lambda = 0$), there has been approximately 27–28% increment in Nusselt number upon the addition of nanoparticles in pure water. However, for Sakiadis flow ($\lambda = 1$), it’s only 6–8%.

Table 3 illustrates that for $\lambda = 0.3$ there has been nearly 20–21% increment in Nusselt number, for $\lambda = 0.5$, there has been approximately 16%, whereas for $\lambda = 0.8$ there has been nearly 11% increment in Nusselt number for the (CuO–water)_nf, (Ag–water)_nf, and (Ag–CuO/water)_hnf in comparison with pure water. On the other hand, when $\lambda = 1.2$, there is only 6% of increment in the Nusselt number for (CuO–water)_nf, approximately 5% increment for (Ag–CuO/water)_hnf and nearly 3% increase for (Ag–water)_nf in comparison with that of pure water.

4.2.2 Heat transfer around the needle

The values for the temperature have been plotted against $\eta$ from $\eta = c$ to $\eta_{\infty }$. For computational purposes, the infinite boundary values of $\eta$ have been simulated till 9 or 10, depending on the convergence of velocity and thermal boundary layers. For Blasius flow, the temperature distribution around the needle (Fig. 9(a)) follows the trend:

$$ {\text{water}} < ({\text{Ag}} - {\text{water}})_{\text{nf}} < \left( {{\text{Ag}} - {\text{CuO/water}}} \right)_{\text{hnf}} < \left( {{\text{CuO}} - {\text{water}}} \right)_{\text{nf}} $$

Fig. 9

(a) Temperature profile for Blasius flow. (b) Temperature profile for $\lambda = 0.3$. (c) Temperature profile for $\lambda = 0.5$. (d) Temperature profile for $\lambda = 1.2$

When $0 < \lambda < 0.5$, the maximum rise in temperature is seen (Fig. 9(b)) in the case of (Ag–CuO/water)_hnf. After $\lambda = 0.5$, the following trend in temperature profiles (Fig. 9(c) to Fig. 9(d)) is noticed:

$$ {\text{water}} < \left( {{\text{CuO}} - {\text{water}}} \right)_{\text{nf}} < \left( {{\text{Ag}} - {\text{CuO/water}}} \right)_{\text{hnf}} < ({\text{Ag}} - {\text{water}})_{\text{nf}} $$

Section 4.2.1 shows that as $\lambda$ increases, the percentage increments in Nusselt number decrease for the (CuO–water)_nf, (Ag–water)_nf, and (Ag–CuO/water)_hnf. Figure 10 shows that as $\lambda$ increases, the thickness of the thermal boundary layer increases. The thicker the boundary layer is, the lesser will be the heat exchange. It accounts for the reason behind the decrement in the heat transfer rate with an increment in $\lambda$.

Fig. 10

Effect of $\lambda$ on temperature profile of hybrid nanofluid

4.2.3 Velocities around the needle

The influence of the flow parameter $\lambda$ on hybrid nanofluid velocity is shown in Fig. 11. It is depicted in the figure that $\lambda = 0.5$ acts as a critical value of flow parameter, after which the direction of velocity profiles got reversed. $\lambda < 0.5$ represents the case when the velocity of the ambient fluid $u_{\infty }$ is more than that of the needle $u_{w}$, $\lambda = 0.5$ represents the case when the needle velocity is equal to that of the surrounding nanofluid stream (i.e., $u_{w} = u_{\infty }$) and $\lambda > 0.5$ represents the case when the velocity of the needle $u_{w}$ is more than that of the ambient fluid $u_{\infty }$. This implies as the needle velocity becomes more than that of the surrounding fluid (i.e., $\lambda > 0.5$), the trend and direction of velocity profiles get reversed. At a particular value of flow parameter such that $\lambda < 0.5$, the axial velocity ($f^{\prime}$) profiles of the base fluid, nanofluids and hybrid nanofluid (e.g. as in Fig. 12(a)) follow the trend:

$$ {\text{water}} < \left( {{\text{CuO}} - {\text{water}}} \right)_{\text{nf}} < \left( {{\text{Ag}} - {\text{CuO/water}}} \right)_{\text{hnf}} < ({\text{Ag}} - {\text{water}})_{\text{nf}} $$

Fig. 11

Effect of $\lambda$ on velocity profile of hybrid nanofluid

Fig. 12

(a) Velocity profile for Blasius flow. (b) Velocity profile for $\lambda = 0.8$

But for $\lambda > 0.5$, the above trend in axial velocity profiles is reversed (Fig. 12(b)):

$$ ({\text{Ag}} - {\text{water}})_{\text{nf}} < \left( {{\text{Ag}} - {\text{CuO/water}}} \right)_{\text{hnf}} < \left( {{\text{CuO}} - {\text{water}}} \right)_{\text{nf}} < {\text{water}} $$

4.2.4 Skin friction at the boundary

In order to visualize the influence of different flow conditions, skin friction profiles are plotted (Fig. 13(a)–13(b)) and the skin friction coefficient is calculated at the needle boundary (Table 4) for distinct values of flow parameter $\lambda$. Table 4 depicts that for $\lambda = - \,0.2,0$ and $0 < \lambda < 0.5$, the sign of the skin friction coefficient is positive and among various nanofluids, the skin friction profiles (Fig. 13(a)) follow the trend:

$$ {\text{water}} < \left( {{\text{CuO}} - {\text{water}}} \right)_{\text{nf}} < \left( {{\text{Ag}} - {\text{CuO/water}}} \right)_{\text{hnf}} < ({\text{Ag}} - {\text{water}})_{\text{nf}} $$

Fig. 13

(a) Skin friction profile for Blasius flow. (b) Skin friction profile for $\lambda = 0.8$

When $\lambda < 0.5$, the velocity of the nanofluid stream is greater than that of the needle due to which it exerts a drag force on the needle, leading to the positive skin friction coefficient. $\lambda = 0.5$ acts as a critical value at which the magnitude of skin friction is zero (Table 4) and after which the sign of the skin friction coefficient along with the direction of skin friction profiles got reversed (see Table 4 and Fig. 13(b)). This is because at $\lambda = 0.5$, the needle velocity and the velocity with which nanofluid move are equal, $u_{w} = u_{\infty }$. This results in a negligible skin friction at the needle–fluid interface. Furthermore, when $\lambda > 0.5$, the velocity of the nanofluid stream is less than that of the needle due to which the needle exerts drag force on the nanofluid stream. It leads to the negative sign of the skin friction coefficient. However, the magnitude of the skin friction coefficient follows the same trend after $\lambda = 0.5$ as discussed above. From Table 4, it can be observed that for all the flow conditions, the magnitude of the skin friction follows the trend:

$$ {\text{water}} < \left( {{\text{CuO}} - {\text{water}}} \right)_{\text{nf}} < \left( {{\text{Ag}} - {\text{CuO/water}}} \right)_{\text{hnf}} < ({\text{Ag}} - {\text{water}})_{\text{nf}} $$

As $\lambda$ increases, percentage increments in skin friction also increase for all the nanofluids implying that the effect of adding nanoparticles on skin friction is magnified with an increment in $\lambda$. Furthermore, with the increase in the magnitude of the relative velocity ($\left| {u_{w} - u_{\infty } } \right|$), the magnitude of the skin friction coefficient (ratio of wall shear stress to local dynamic energy) increases (Table 3). Through this experiment, we see that the wall shear stress has more effect on skin friction coefficient than the local dynamic energy for each of the nanofluids.

5 Conclusions

In this paper, a comparative analysis is performed for Ag–CuO/water hybrid, CuO–water, and Ag–water nanofluids to study their impact on heat transfer in the boundary layer flow past a thin needle. The influence of needle size and the different flow conditions involving Sakiadis and Blasius flows are examined numerically. The significant outcomes of the analysis are summarized as

• 1. By increasing the needle size $c$, the rate of heat transfer at the boundary can be enhanced. Also, increment in the needle size $c$ rises the fluid temperature.

• 2. As $\lambda$ increases, the Nusselt number increases for all the fluids, whether it is a base fluid (water) or nanofluids (CuO–water or Ag–water) or hybrid nanofluid (Ag–CuO/water)_hnf.

• 3. For Blasius flow ($\lambda = 0$), there has been approximately 27–28% increment in Nusselt number upon the addition of nanoparticles in pure water. However, for Sakiadis flow ($\lambda = 1$) it is only 6–8%. It implies that the effect of the addition of nanoparticles on the heat exchange is much more effective for a smaller value of $\lambda$ than for a higher value.

• 4. Hybrid nanoparticles have tremendous control over a heat exchange at the solid–fluid boundary in Sakiadis and Blasius flows. The heat transfer can be controlled by using a particular volume fraction of nanoparticles so that it would meet the required criteria.

• 5. Ag–CuO/water hybrid nanofluid experiences the maximum temperature compared to the other fluids when the needle velocity is less than that of the ambient fluid velocity (i.e., $0 < \lambda < 0.5$)

• 6. $\lambda = 0.5$ acts as a critical value of flow parameter, after which the whole trend and direction of velocity profiles get reversed. The velocity profiles of Blasius flow and Sakiadis flows are opposite in nature.

The results reveal that the use of hybrid nanoparticles leads to a great control over heat transfer at the boundaries. Apart from the heat transfer at the boundaries, the velocities and skin friction can be controlled to a certain extent.