1 Introduction

Since the nonlinear evolution equations often describe the underlying dynamics of real systems, they have attractive applications in such fields as optics, plasma physics, condensed matter physics, fluids and arterial mechanics [1, 2]. Recently, much interest has arisen in the investigation of equations with inhomogeneities. This is because there exist many realistic physics problems in the inhomogeneous systems. The solutions, in the inhomogeneous media, have their potential applications in describing, e.g., the ultrashort optical pulses in long-distance communication and spin dynamics in an inhomogeneous classical continuum biquadratic Heisenberg ferromagnetic spin chain [3–10].

The inhomogeneous nonlinear Schr\({\mathrm{\ddot{o}}}\)dinger equation (NLSE) which describes the transmission of solitons through the varying dispersion-managed optical fiber have been explored in various branches of physics [11, 12]. There have also been interesting studies of inhomogeneous NLSEs, including the dc-ac system, the Painlev\({\mathrm{\acute{e}}}\) test of inhomogeneous NLSEs and constructions of modified NLSEs [13–20]. Another development of inhomogeneous integrable equation is the problem of the Heisenberg spin chain with a site-dependent interaction term. They can be treated by the inverse scattering problem with variable spectral parameters [21–23].

It is well known that the Darboux transformation (DT) is a powerful means in the construction of solutions for nonlinear evolution equations [24–26]. It is noticed that by using the Darboux matrix, a unified explicit form of auto-B\({\mathrm{\ddot{a}}}\)cklund transformations can be obtained for some hierarchies of isospectral nonlinear evolution equations, such as isospectral KdV, MKdV, sine-Gordon and AKNS hierarchy. This approach is to construct the Darboux matrix first, and then to prove the gauge equivalence of the related Lax pairs. However, it is hard to employ this method to obtain the B\({\mathrm{\ddot{a}}}\)cklund transformations for hierarchies of nonisopspectral nonlinear evolution equations since the demonstration of the t part of Lax pair is quite difficult.

The inhomogeneous system generally is a problem in which the spectral parameter depends on the time or space variables. A lot of excellent applications of the Darboux matrix method to nonisospectral problems has been given in Refs. [27–35]. However, the Darboux transformation for the nonisospectral AKNS hierarchy has an essential difference from the standard case, that its integral constants may not be conserved by the transformation. So one may not get the nontrivial soliton solution of the relevant nonlinear equation by acting the Darboux transformation on the seed solution of the same equation. Recently, Zhou has proved that the relation of the integral constants between the relevant nonisospectral AKNS hierarchies can be calculated through the asymptotic property of the elementary solution [36]. Then the soliton solution of a certain differential equation can be found by acting the Darboux transformation on the seed solution of another equation. And for some special cases, it becomes auto-B\({\mathrm{\ddot{a}}}\)cklund transformation [37]. All the developments show that a systematic analysis based on DT for inhomogeneous integrable equations with variable spectral parameters is strongly feasible.

In this paper, we consider a generalized inhomogeneous Hirota equation as follows

$$\begin{aligned}&iq_{t} +i{\mu _{1}}\,q +i \left( {\nu _{1}}+{\mu _{1}}\,x \right) q_{x} +\left( {\nu _{2}}+\mu _2 x\right) \, \left( q_{xx} +2\, |q|^{2}q\right) \nonumber \\&\quad +2\mu _2 \left( q_x+q\int _{-\infty }^{x}|q|^2dx^{'}\right) +i\nu \, \left( q_{xxx} +6\,|q|^{2}q_{x} \right) =0, \end{aligned}$$
(1)

where q(x, t) is a complex function with respect to the spatial coordinates x and normalized time \(t\), the subscripts denote the temporal and spatial partial derivatives. The terms \(q_{xx}\), \({|q|^{2}q}\), \({q_{xxx}}\) and \({|q|^{2}q_{x}}\) represent the group velocity dispersion, self-phase modulation, third-order dispersion and self-steepening, respectively. Here \({\nu ,\nu _{1},\nu _{2},\mu _{1},\mu _{2}}\) are all real numbers and \({{\nu _{1}}+{\mu _{1}}\,x,{\nu _{2}}+{\mu _{2}}\,x}\) are the linear inhomogeneous coefficients. If \({\nu _{1}=\mu _{1}=\mu _{2}=0}\), Eq. (1) reduces to the standard Hirota equation, which describes the propagation of the femtosecond soliton pulse in the single-mode fibers. Furthermore, the dynamics of dispersive optical solitons modeled by Hirota equation are studied by Biswas et al. [38–42]. If \({\nu _{1}=\mu _{1}=\mu _{2}=\nu =0,\nu _{2}=1}\), Eq. (1) degenerates to the standard Schr\({\mathrm{\ddot{o}}}\)dinger equation, which describes the dynamics of nonlinear spin excitation in the Heisenberg ferromagnetism.

Consequently, Eq. (1) is one of the completely integrable equations, the Lax pair of which can be given by the AKNS method as follows

$$\begin{aligned} \left\{ \begin{aligned} \Psi _{x}&=U\Psi = \left( -iJ\lambda +U_1\right) \Psi ,\\ \Psi _{t}&=V\Psi =\left( V_{1}\lambda ^{3}+V_{2}\lambda ^{2}+V_{3} \lambda +V_{4}\right) \Psi , \end{aligned} \right. \end{aligned}$$
(2)

where

$$\begin{aligned} J= & {} \left( \begin{array}{cc} 1 &{} 0\\ 0 &{} -1 \\ \end{array} \right) ,~U_1=\left( \begin{array}{cc} 0 &{} q \\ -q^{*} &{} 0 \\ \end{array} \right) , \end{aligned}$$
(3)
$$\begin{aligned} V_{1}= & {} \left( \begin{array}{cc} -4i\nu &{} 0 \\ 0 &{} 4i\nu \\ \end{array} \right) , V_{2}=\left( \begin{array}{cc} -2i(\nu _{2}+\mu _2x) &{} 4\nu q \\ -4\nu q^{*} &{} 2i(\nu _{2}+\mu _2x) \\ \end{array} \right) , \end{aligned}$$
(4)
$$\begin{aligned} V_{3}= & {} \left( \begin{array}{cc} i(\nu _{1}+\mu _{1}x)+2i\nu |q|^{2} &{} 2i\nu q_{x}+2(\nu _{2}+\mu _2x)q\\ 2i\nu q_{x}^{*}-2(\nu _{2}+\mu _2x)q^{*}&{} -i(\nu _{1}+\mu _{1}x)-2i\nu |q|^{2} \\ \end{array} \right) , \end{aligned}$$
(5)
$$\begin{aligned} V_{4}= & {} \left( \begin{array}{cc} A &{} B \\ -B^{*} &{} -A \\ \end{array} \right) , \end{aligned}$$
(6)

with

$$\begin{aligned} A&= i\mu _2\int _{-\infty }^{x}|q|^2dx^{'}+i \left( \nu _{2}+\mu _2x\right) |q|^{2} + \nu \left( q q_{x}^{*}-q^{*}q_{x}\right) , \end{aligned}$$
(7)
$$\begin{aligned} B&= i\left( \nu _{2}+\mu _2x\right) q_{x}-\nu q_{xx}-\left( \nu _{1}+\mu _{1}x\right) q-2\nu |q|^{2}q+i\mu _2q. \end{aligned}$$
(8)

In the above eigenvalue problem the spectral parameter \(\lambda\) is nonisospectral obeying the equation

$$\begin{aligned} \lambda _t=-\mu _1\lambda +2\mu _2\lambda ^2. \end{aligned}$$
(9)

It is obvious that the compatibility condition \(U_{t}-V_{x}+[U,V]=0\) generates Eq. (1), where the square brackets denote the usual matrix commutator.

In Ref. [43], Porsezian et al. have investigated the singularity structure and the integrability properties of the generalized \(x-\)dependent Hirota equation. Also, they have constructed the associated Lax pairs and B\({\mathrm{\ddot{a}}}\)cklund transformation for the inhomogeneous equation. Eq. (1) has also been earlier studied by constructing the equivalent spin system and carrying out the inverse scattering analysis [44, 45]. In Ref. [46], the authors have obtained the \(N-\)soliton solution for Eq. (1) through the Hirota bilinear method and symbolic computation. But, a little detail is worth mentioning in the process of bilinearization. To be specific, through the transformation

$$\begin{aligned} q=\frac{g}{f} \end{aligned}$$
(10)

where \(g=g(x,t)\) is a complex function and \(f=f(x,t)\) is a real function, the bilinear form of Eq. (1) is found to be

$$\begin{aligned}&{D_{{x}}}^{2}f\cdot f=2\,gg^{*}, \end{aligned}$$
(11)
$$\begin{aligned}&\left[ { i}D_{{t}}+{ i} \left( { \nu _1}+{ \mu _1}\,x \right) D_{{x}}+ \left( { \nu _2}+{ \mu _2}\,x \right) {D_{{x}}}^{2} \right. \nonumber \\&\qquad \left. +2\,{ \mu _2}\,D_{{x}}+{ i}\nu \,{D _{{x}}}^{3}+{ i}{ \mu _1}\right] g\cdot f=-2\,{ \mu _2}\,gf_{{{x}}}. \end{aligned}$$
(12)

Here the well-known bilinear operator D is defined as

$$\begin{aligned} D^m_{t}D^n_{x}G\cdot F= \left( \frac{\partial }{\partial t}-\frac{\partial }{\partial t^{'}}\right) ^m \left( \frac{\partial }{\partial x}-\frac{\partial }{\partial x^{'}}\right) ^n G(x,t) F\left( x^{'},t^{'}\right) \Big |_{x^{'}=x,t^{'}=t} \end{aligned}$$
(13)

and the relation

$$\begin{aligned} \int _{-\infty }^{x}|q|^2dx^{'}=\int _{-\infty }^{x}\frac{{D_{{x^{'}}}}^{2}f\cdot f}{2f^2}dx^{'}=\frac{f_x}{f} \end{aligned}$$
(14)

is used. Therefore, the asymptotic condition should satisfy

$$\begin{aligned} \lim _{x\rightarrow -\infty }\frac{f_x}{f}=\lim _{x\rightarrow -\infty } \int _{-\infty }^{x}|q|^2dx^{'}=0 \end{aligned}$$
(15)

which asks for special parameters in the expression of f and this point is often ignored in the reference.

In the following, we first derive the representation of DT for Eq. (1) to construct the nonautonomous soliton solutions from zero seed solution. Furthermore, the one- and two-soliton solutions are explicitly constructed by using the transformation. These solutions are both suitably controlled by the physical parameters associated with the system and their dynamics are investigated graphically.

2 Darboux transformation

Actually, a unified approach to construct DT for a class of isospectral integrable systems is founded by C.H. Gu [24]. Meanwhile, various results are presented on nonisospectral problems in which the spectral parameter depends on the time or space variables [27–35]. In Ref. [36], Zhou has generalized Gu’s formula for DT to the nonisospectral AKNS hierarchy. He has showed that the DT for the nonisospectral AKNS hierarchy is not an auto-Bäcklund transformation except for some special cases. In order to get more details about his method, the reader can see Ref. [37]. Therefore, the Darboux transformation for the nonisospectral AKNS problem (Eq. (2)) can be constructed in the following way.

If q satisfies the asymptotic condition

$$\begin{aligned} \lim _{x\rightarrow \infty } |x|^k\partial _{x}^{m}q=0 \end{aligned}$$
(16)

for t and nonnegative integer k, m, let \(\Psi _1=(f_1,g_1)^{T}\) be the known complex vector-valued eigenfunction of Eq. (2) corresponding to the parameter \(\lambda _1=\alpha _1(t)+i\beta _1(t)\), one can easily prove that \(\Psi _2=(-g_1^{*},f_1^{*})^{T}\) is the vector-valued eigenfunction of Eq. (2) which relates to the parameter \(\lambda _1^{*}=\alpha _1(t)-i\beta _1(t)\). Here the symbol \(*\) denotes complex conjugation. Set

$$\begin{aligned} D(\lambda )=p(\lambda )G(t)T(\lambda ) \end{aligned}$$
(17)

where

$$\begin{aligned} G(t)&=diag \left( e^{-2i\mu _2\int _{-\infty }^{t}\beta _1 dt^{'}},e^{2i\mu _2\int _{-\infty }^{t}\beta _1 dt^{'}}\right) , \end{aligned}$$
(18)
$$\begin{aligned} p(\lambda )&= \left[ det \left( \lambda I-H\Lambda H^{-1}\right) \right] ^{-1/2}= \left[ \left( \lambda -\lambda _1\right) \left( \lambda -\lambda _1^{*}\right) \right] ^{-1/2}, \end{aligned}$$
(19)
$$\begin{aligned} T(\lambda )&= \lambda I-S,~S=H\Lambda H^{-1},~H= \left( \Psi _1, \Psi _2\right) , \Lambda =diag \left( \lambda _1,\lambda _1^{*}\right) , \end{aligned}$$
(20)

here I is the identity matrix. Then the gauge transformation

$$\begin{aligned} \hat{\Psi }=D(\lambda )\Psi \end{aligned}$$
(21)

is the Darboux transformation for Eq. (2) and \(\hat{\Psi }\) is the vector eigenfunction satisfying the eigenvalue equations

$$\begin{aligned} \left\{ \begin{aligned} \hat{\Psi }_{x}&=\hat{U }\hat{\Psi },\\ \hat{\Psi }_{t}&=\hat{V }\hat{\Psi }, \end{aligned} \right. \end{aligned}$$
(22)

with \(\hat{U}\) and \(\hat{V}\) have the same forms as those of U and V except for replacing \(q^{[0]}\) with a new potential function \(q^{[1]}\).

The appearance of factors \(p(\lambda )\) and G(t) is the most distinguishing feature of the present formalism. For the standard isospectral AKNS hierarchy, all the factors degenerate to vanish. Here, for equations with variable spectral parameters the scalar factor \(p(\lambda )\) is introduced to make \(\hat{V}\in sl(2)\). The gauge factor G(t) keeps the integral constants invariant of V and \(\hat{V}\). Also, the imaginary part of spectral parameter should be taken to satisfy the condition \(\beta _1(t)<0\) to assure the asymptotic property of the elementary solution of Lax pair.

Under the DT, it is easy to find out that

$$\begin{aligned} \hat{U}=G \left( U_1+i[S,J]\right) G^{-1}. \end{aligned}$$
(23)

Hence, we obtain the representation of one-fold DT as

$$\begin{aligned} q^{[1]}=e^{-4i\mu _2\int _{-\infty }^{t}\beta _1 dt^{'}} \left[ q^{[0]}-2i \frac{\left( \lambda _1 -\lambda _1^{*}\right) f_1g_1^{*}}{|f_{1}|^{2}+|g_{1}|^{2}}\right] . \end{aligned}$$
(24)

Iterating the transformation N times with N as a positive integer, we can give the N-th iterated potential transformation

$$\begin{aligned} q^{[N]}=e^{-4i\mu _2\sum \limits _{j=1}^{N}\int _{-\infty }^{t}\beta _j dt^{'}}\left[ q^{[0]}-2i\sum _{k=1}^{N}e^{4i\mu _2\sum \limits _{m=1}^{k-1} \int _{-\infty }^{t}\beta _m dt^{'}} \frac{\left( \lambda _k -\lambda _k^{*}\right) f_kg_k^{*}}{|f_{k}|^{2} +|g_{k}|^{2}}\right] , \end{aligned}$$
(25)

where \(\lambda _k=\alpha _k(t)+i\beta _k(t) (k=1,2,\ldots ,N)\) are the different nonisospectral parameters with negative imaginary parts and \(\Psi _k=(f_k,g_k)^{T}\) is the vector eigenfunction of Eq. (2) corresponding to the parameter \(\lambda _k\) and \(q=q^{[k-1]}\). This formula is used to construct multi-soliton solutions later.

3 Nonautonomous soliton solutions

It is now generally accepted that solitary waves in nonautonomous nonlinear and dispersive systems can propagate in the form of so-called nonautonomous solitons or solitonlike similaritons. Nonautonomous solitons interact elastically and generally move with varying amplitudes and speeds. Dynamics of nonautonomous soliton in different aspects such as soliton dispersion management, soliton energy control, soliton intensity management and soliton pulse width management are explained in Refs. [47–49]. Especially, in these papers, investigations have been made to understand the properties of nonautonomous solitons under the variation of nonlinearity parameter, dispersion parameters and gain or loss terms. Propagation of nonautonomous soliton in external potential is also discussed [50, 51]. Meanwhile, it is found that the weak dissipations also lead to change in the soliton parameters, the amplitude and the velocity, the creation of small solitons and the formation of a tail behind the initial soliton [52–54]. However, dissipative solitons in systems with high-order nonlinear dissipation cannot survive in the presence of trapping potentials of the rigid wall or asymptotically increasing type. Solitons in such systems can survive in the presence of a weak potential but only with energies out of the interval of existence of linear quantum mechanical stationary states [55]. In this section, we take \(q^{[0]}=0\) to construct the nonautonomous soliton solutions of the generalized inhomogeneous Hirota equation in explicit forms.

3.1 One-soliton solution

To obtain the one-soliton solution for Eq. (1), we take spectral parameter \(\lambda _1=\alpha _1+i\beta _1\) with

$$\begin{aligned} \alpha _{1t} = -\mu _{1}\alpha _1+2\mu _2 \left( \alpha _1^2 -\beta _1^2\right) , \quad \beta _{1t} = -\mu _{1}\beta _1 +4\mu _2\alpha _1\beta _1, \end{aligned}$$
(26)

then obtain the following eigenfunctions by directly solving the corresponding Lax pair

$$\begin{aligned} f_{1} = e^{-i\rho _1},\quad g_{1} = e^{i\rho _1}, \end{aligned}$$
(27)

with

$$\begin{aligned} \rho _1=\lambda _1\,x -\int \left( {\nu _{1}}\lambda _1-2\,\, {\nu _{2}}\lambda _1^2-4\nu \,{\lambda _1}^{3} \right) \,dt+\rho _{10}. \end{aligned}$$
(28)

After the DT, we can get the one-soliton solution for Eq. (1) as follows

$$\begin{aligned} q^{[1]}=2\beta _1 sech \left( 2\theta _1\right) e^{-2i \left( \zeta _1+2\mu _2\int _{-\infty }^{t}\beta _1 dt^{'}\right) } \end{aligned}$$
(29)

with

$$\begin{aligned} \theta _1= & {} \,\beta _1 x- \int \left[ \,{\nu _{1}}\, \beta _1-4\,{\nu _{2}}\,\alpha _1\,\beta _1+4\,\nu \, \left( {\beta _1}^{3}-3{\alpha _1 }^{2}\beta _1\right) \right] dt+\theta _{10}, \end{aligned}$$
(30)
$$\begin{aligned} \zeta _1&= \alpha _1 x-\int \left[ {\nu _{1}}\,\alpha _1-2\,{\nu _{2}}\left( \,{\alpha _1}^{2}-\,{\beta _1}^{2} \right) -4\nu \left( \alpha _1^{3}-3\alpha _1\beta _1^{2}\right) \right] dt+\zeta _{10}, \end{aligned}$$
(31)

where \(\theta _{10},\zeta _{10}\) are real constants.

From the single soliton, we can find that amplitude for the envelope is determined by

$$\begin{aligned} 2|\beta _1|= \left\{ \begin{array}{llll} {c_1e^{-\mu _1t}}&{}~\text {if}~&{} \mu _2=0;&{}\\ {\frac{4c_1}{c_1^2 \left( t+c_2\right) ^2+64\mu _2^2}}&{}~\text {if}~&{} \mu _1=0,\mu _2\ne 0;&{}\\ {\frac{4c_1\mu _1^2e^{-\mu _1t}}{c_1^2\left( e^{-\mu _1t}+c_2\mu _1\right) ^2+64\mu _1^2\mu _2^2}}&{}~\text {if}~&{} \mu _1\ne 0,\mu _2\ne 0;&{} \end{array} \right. \end{aligned}$$
(32)

with a positive arbitrary real constant \(c_1\) and an arbitrary real constant \(c_2\). It relies on time and has relationship with \(\mu _{1}\) and \(\mu _2\), but it is independent from \(\nu ,\nu _1\) and \(\nu _2\). The trajectory of its wave center is described by

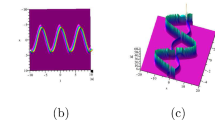
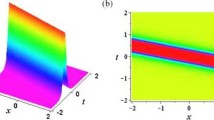
$$\begin{aligned} \,\beta _1 x- \int \left[ \,{\nu _{1}}\, \beta _1-4\,{\nu _{2}}\, \alpha _1\,\beta _1+4\,\nu \,\left( {\beta _1}^{3}-3{\alpha _1 }^{2}\beta _1\right) \right] dt+\theta _{10}=0. \end{aligned}$$
(33)

This analytical solution shows a feature of the nonautonomous soliton: it evolves along a curve contrast with a straight line of the usual soliton [56, 57]. The special case of \(\mu _2=0\) has been discussed by us before [58]. Here we focus on other cases and depict \(|q^{[1]}|^2\) in Figs. 1 and 2.

Fig. 1
figure 1

One soliton via solution (29). (a) Intensity \(|q|^2\), (b) contour plot of Fig. 1(a), (c) one-dimensional profiles of single soliton at different times, \(t=-4(\textit{red}),0(\textit{green}),4(\textit{blue})\) (d) trajectory of the single soliton in Fig. 1(a). Paremeters are \({\displaystyle \nu =\nu _{1}=\nu _{2}= \mu _2=1,\mu _{1}=0, \alpha _{1}= -\frac{t}{2(t^2+64)}, \beta _{1}= -\frac{4}{t^2+64}}\)

Full size image
Fig. 2
figure 2

One soliton via solution (29). (a) Intensity \(|q|^2\), (b) contour plot of Fig. 2(a), (c) one-dimensional profiles of single soliton at different times, \(t=-3(\textit{red}),-3\ln 2(\textit{green}),-1(\textit{blue})\) (d) trajectory of the single soliton in Fig. 2(a). Paremeters are \({\nu =\nu _{1}= \mu _{1}=\mu _2=1, \nu _{2}=-1,}\) \({\displaystyle \alpha _{1}= \frac{e^{-2t}}{2(e^{-2t}+64)}}\), \({\displaystyle \beta _{1}=-\frac{4e^{-t}}{e^{-2t}+64}}\)

Full size image

There is an important difference in the evolution dynamics of the solution of the homogeneous case and the inhomogeneous one. In the homogeneous case, the peak of the pulse is located at the constant arbitrary position. In contrast, the presence of inhomogeneity results in a movable pulse. However, the results presented before are qualitatively different since the characteristic scales of inhomogeneity of the plasma density and the external magnetic field are taken into account [59].

In Fig. 1, the soliton is central symmetric around the peak point \((-1,0)\) with parameter \(\mu _{1}=0,\mu _{2}=1\). The width experiences the process of decreasing-increasing with time while the amplitude experiences increasing-decreasing. This means that at large times, the pulse has a small amplitude and large width. The symmetric S-type trajectory is clear in the contour plot. The one-dimensional profiles of single soliton at different times and the monotonically increasing trajectory are also given. In Fig. 2, the amplitude of the bright soliton also grows and decays with time. But the velocities before and after the peak time are different which can be observed clearly from the non-symmetric contour plot. The slope of trajectory shows that the collapsing process after the soliton amplitude reaches the largest value is quicker and it vanishes rapidly. Such explode-decay solitons have been reported in many inhomogeneous systems [60–63].

3.2 Two-soliton solution

Soliton management can be realized by adjusting the control parameters related with soliton dynamics and it is meaningful to investigate the multi-soliton transmission. In this section, we mainly focus on the propagation and interaction between two solitons.

To calculate the two-soliton solution, we need a solution of Eq. (2) with \(q=q^{[1]}\) and \(\lambda = \lambda _2 = \alpha _2+i\beta _2\) to obtain \(\Psi _2=(f_2,g_2)^{T}\). The DT in Eq. (9) gives the required solution such that

$$\begin{aligned} f_2= & {} \frac{\left( \lambda _2-\lambda _1\right) e^{-i\rho _2} + \left( \lambda _1^{*} -\lambda _1\right) e^{i\rho _2-2i\rho _1^{*}} +\left( \lambda _2-\lambda _1^{*}\right) e^{2i\left( \rho _1-\rho _1^{*} \right) -i\rho _2}}{\left[ \left( \lambda _2-\lambda _1\right) \left( \lambda _2 -\lambda _1^{*}\right) \right] ^{1/2}\left( 1+e^{2i\left( \rho _1-\rho _1^{*}\right) }\right) } e^{-2i\mu _2\int _{-\infty }^{t}\beta _1 dt^{'}} \end{aligned}$$
(34)
$$\begin{aligned} g_2= & {} \frac{\left( \lambda _2-\lambda _1\right) e^{2i \left( \rho _1-\rho _1^{*}\right) +i\rho _2} +\left( \lambda _1^{*} -\lambda _1\right) e^{2i\rho _1-i\rho _2}+ \left( \lambda _2-\lambda _1^{*} \right) e^{i\rho _2}}{\left[ \left( \lambda _2- \lambda _1\right) \left( \lambda _2-\lambda _1^{*}\right) \right] ^{1/2}\left( 1+e^{2i \left( \rho _1-\rho _1^{*}\right) }\right) } e^{2i\mu _2\int _{-\infty }^{t} \beta _1 dt^{'}} \end{aligned}$$
(35)

where

$$\begin{aligned} \rho _i=\lambda _i\,x -\int \left( {\nu _{1}}\lambda _i-2\,\,{\nu _{2}}\lambda _i^2-4\nu \,{\lambda _i}^{3} \right) \,dt+\rho _{i0}. \end{aligned}$$
(36)

Until now, one can easily obtain the explicit two-soliton solution given by

$$\begin{aligned} q^{[2]}=2ie^{-4i\mu _2\int _{-\infty }^{t}\left( \beta _1+\beta _2\right) dt^{'}}\frac{A_1+A_2+A_3+A_4}{B_1+B_2+B_3+B_4} \end{aligned}$$
(37)

where the components assume the following form

$$\begin{aligned} A_1= & {} \left( \lambda _1-\lambda _1^{*}\right) \left( \lambda _2^{*}-\lambda _1^{*}\right) \left( \lambda _2^{*} -\lambda _1\right) e^{2i\rho _1}, \end{aligned}$$
(38)
$$\begin{aligned} A_2= & {} \left( \lambda _2^{*}-\lambda _1^{*}\right) \left( \lambda _2-\lambda _2^{*}\right) \left( \lambda _2- \lambda _1^{*}\right) e^{2i\rho _2}, \end{aligned}$$
(39)
$$\begin{aligned} A_3= & {} \left( \lambda _1-\lambda _1^{*}\right) \left( \lambda _1^{*}- \lambda _2\right) \left( \lambda _1-\lambda _2\right) e^{2i\left( \rho _1+\rho _2-\rho _2^{*}\right) }, \end{aligned}$$
(40)
$$\begin{aligned} A_4= & {} \left( \lambda _2^{*}-\lambda _1\right) \left( \lambda _2^{*}- \lambda _2\right) \left( \lambda _1-\lambda _2\right) e^{2i\left( \rho _1+\rho _2-\rho _1^{*}\right) }, \end{aligned}$$
(41)
$$\begin{aligned} B_1= & {} \left( \lambda _1-\lambda _2\right) \left( \lambda _2^{*}- \lambda _1^{*}\right) , \end{aligned}$$
(42)
$$\begin{aligned} B_2= & {} \left( \lambda _1^{*}-\lambda _2\right) \left( \lambda _2^{*}- \lambda _1\right) \left[ e^{2i\left( \rho _1 -\rho _1^{*}\right) }+e^{2i\left( \rho _2-\rho _2^{*}\right) }\right] , \end{aligned}$$
(43)
$$\begin{aligned} B_3= & {} \left( \lambda _1^{*}-\lambda _1\right) \left( \lambda _2- \lambda _2^{*}\right) \left[ e^{2i\left( \rho _1-\rho _2^{*}\right) } +e^{2i \left( \rho _2-\rho _1^{*}\right) }\right] , \end{aligned}$$
(44)
$$\begin{aligned} B_4= & {} \left( \lambda _1-\lambda _2\right) \left( \lambda _2^{*}-\lambda _1^{*}\right) e^{2i\left( \rho _1+\rho _2-\rho _1^{*}-\rho _2^{*}\right) }. \end{aligned}$$
(45)

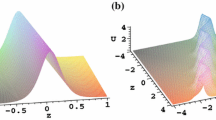
We discuss the properties of the soliton interactions under different cases which are portrayed in Figs. 3, 4, 5, 6. In Fig. 3, two solitons propagate along same directions with different velocities and trajectories. The collision occur at the interaction area and both amplitudes increase initially and gradually decrease with a phase change. The smaller pulse with faster velocity overtakes the greater pulse with lower velocity. Furthermore, the propagation of the greater pulse owns a S-type trajectory which implies temporary change of propagation direction. Whereas, Fig. 4 describes two parallel solitons whose amplitudes also undergo an increasing-decreasing process. The two solitons travel along paralleled curve trajectories due to the influence of inhomogeneous parameters. A special two-soliton solution which are localized both in space and time is presented in Fig. 5. It exhibits the similar feature of the so-called rogue waves, but it is based on a zero background rather than a plane wave background. Although the significant difference in amplitude at tiny different times leads to the observation of only one peak, in fact, the profiles before and after the interaction are demonstrated in Fig. 6 to exhibit the essence of two solitons. This figure indicates a sharp compression and strong amplification of the nonautonomous soliton under the action of inhomogeneity. More on the similar soliton interactions can be seen, e.g., in Refs. [64–67].

Fig. 3
figure 3

Two soliton via solution (37). (a) Head-on interactions, (b) contour plot of Fig. 3(a), (c) soliton profiles of Fig. 3(a) at \(t=-5(\textit{red}), 3(\textit{green})\), (d) soliton profiles of Fig. 3(a) at \(t=3(\textit{red}), 10(\textit{green})\). Parameters are \(\nu =\nu _{1}=\nu _{2}=\mu _2=1,\mu _{1}=0, {\displaystyle \alpha _{1}=-\frac{t}{2(t^2+64)}}, {\displaystyle \beta _{1}=-\frac{4}{t^2+64},\alpha _{2}=-\frac{t+1}{2[(t+1)^2+64]}, \beta _{2}=-\frac{4}{(t+1)^2+64}}\)

Full size image
Fig. 4
figure 4

Two soliton via solution (37). (a) Paralleled solitons, (b) contour plot of Fig. 5(a). Parameters are \({\nu =5,\nu _{1}=\nu _{2}=\mu _2=1,\mu _{1}=0,}\) \({\displaystyle \alpha _{1}=-\frac{t-1}{2[(t-1)^2+1]}}\), \({\displaystyle \beta _{1}=-\frac{1}{2[(t-1)^2+1]}}\),\({\displaystyle \alpha _{2}=-\frac{t+1}{2[(t+1)^2+1]}}\), \({\displaystyle \beta _{2}=-\frac{1}{2[(t+1)^2+1]}}\)

Full size image
Fig. 5
figure 5

Two soliton via solution (37). (a) Intensity \(|q|^2\), (b) soliton profiles of Fig. 5(a) at \(t=0.2(\textit{red})\), \(t=0.6(\textit{green})\). Parematers are \({\displaystyle \nu =\nu _{1}=\nu _{2}=\mu _{1}=1}\), \({\displaystyle \mu _2=2}\), \({\displaystyle \alpha _{1}=\frac{e^{-2t}+e^{-t}}{2[(e^{-t}+1)^2+4]}}\), \({\displaystyle \beta _{1}= -\frac{e^{-t}}{2[(e^{-t}+1)^2+4]}}\), \({\displaystyle \alpha _{2}=\frac{e^{-2t}-3e^{-t}}{4[(e^{-t}-3)^2+4]}}\), \({\displaystyle \beta _{2}=-\frac{e^{-t}}{2[(e^{-t}-3)^2+4]}}\)

Full size image
Fig. 6
figure 6

Two soliton profiles via solution (37) in Fig. 5 at various times: \({\mathbf {(a)}}\,t=-6, {\mathbf {(b)}}\, t=-3, {\mathbf {(c)}}\, t=-0.8, {\mathbf {(d)}}\, t=0.2\)

Full size image

4 Conclusions

In this paper, an inhomogeneous nonlinear Hirota equation is investigated following the Darboux transformation method. The representation of the DT is given by a detailed deduction. Based on the DT, the analytic one- and two-soliton solutions are given. All of these solutions have parameters denoting the contribution of inhomogeneity, which can be used to control the dynamics of solitons. We expect that our results can find applications in some real physical cases. We hope that our results will be verified in some physics experiments in the future, which will be helpful to understand the generation mechanism and find possible applications of the nonautonomous wave in realistic systems.