Darboux Transformation, Soliton Solutions of a Generalized Variable Coefficients Hirota Equation

Abstract

It is known that the variable coefficients Hirota equations have been widely studied in the amplification or absorption of propagating pulses, as well as in the generation of supercontinuum in inhomogeneous optical fibers. In this paper, a generalized variable coefficients Hirota equation is considered. Firstly, we constructed the classical and generalized Darboux transformations of the equation. Next, we obtained multisoliton solutions based on the classical Darboux transformation and rogue wave solutions using the generalized Darboux transformation. Finally, we discussed the evolutions of solitons.

Introduction

In recent years, people pay more and more attention to the study of nonlinear evolution equations, such as Schrödinger equation, Korteweg–de Vries equation, sine-Gorden equation, see e.g. [1,2,3,4]. Seeking exact solutions of the equations is helpful to understand the essential properties, algebraic structure and physical phenomena [5,6,7]. There are many methods to obtain the exact solutions, for instance, Painlevé analysis [8, 9], inverse scattering transformation [10, 11], Hirota bilinear method [12, 13], Bäcklund transform [14], Darboux transformation (DT) [15,16,17], Lie symmetry analysis [18, 19], Riemann–Hilbert formulation [20], elliptic wave function method [21,22,23], Lie group analysis [24,25,26], etc.

DT is an effective method to obtain a new solution from the initial solution, and it can be repeated any number of times. The main idea of DT approach is to prove the canonical equivalence of the Lax pairs and to obtain soliton solutions through continuous iteration. To construct the explicit solutions, Gu and his collaborators constructed a classical DT in matrix form and provided purely algebraic algorithms for a group of isospectral integrable systems [15, 27]. To obtain the rogue waves of nonlinear Schrödinger equation, Guo et al. [28] derived a generalized DT through a limit procedure. These methods have also been extended to study the variable coefficients and nonlocal equations.

For the problem at hand, we focus on studying a generalized variable coefficients Hirota equation

$$\begin{aligned} i{u_t} + \alpha {u_{xx}} + i\beta {u_{xxx}} + 3i\beta \gamma {\left| u \right| ^2}{u_x} + \alpha \gamma {\left| u \right| ^2}u + \delta u = 0, \end{aligned}$$

(1)

where $i = \sqrt{ - 1}$ and u is a complex function with the variables (t, x), $\alpha = \alpha (t),\beta = \beta (t),\delta = \delta (t)$ are real functions with variable t and the parameter $\gamma$ is a nonzero constant. The significance of the study for this equation is that it is often associated with the amplification or absorption of propagating pulses and the generation of supercontinuum in inhomogeneous optical fibers [29,30,31]. In optical fibers, $\alpha , \beta , \gamma ,\delta$ represent the group dispersion velocity, third order dispersion, self-steepening and the amplification or absorption coefficient respectively [32]. For different value of $\alpha ,\beta ,\gamma ,\delta$, the amplitude, intensity, width and period of the oscillation show different results. We constructed the classical and generalized DTs of Eq. (1) and obtained the multisolutions and rogue wave solutions. The evolutions of solutions are discussed. The propagation of solitons can be controlled by adjusting the values of relevant parameters. The results might be of potential applications in the design of optical communication systems. Some related works associated with (1) have been researched. The auto-Bäcklund transformation and a family of the analytic solutions has also been given, see [33]. When $\alpha , \beta , \delta$ are all constants, multisolitons, breathers and rogue waves have been derived, see [34,35,36,37]. When $\alpha = \delta = 0,\beta = \beta (t),\gamma = \gamma (t)$, the multisoliton solutions have been obtained, see [38,39,40,41]. When $\beta = 0,\alpha = \alpha (t),\delta = \delta (t),\gamma = \gamma (t)$, multisoliton solutions, rogue wave solutions, semi-rational solutions, breathers are obtained, please see [42,43,44,45,46] for details.

The paper is organized as follows. In section “Lax Pair and Darboux Transformation”, we derive the Lax pair, classical DT and generalized DT of Eq. (1). In section “Multisoliton Solutions”, we use the classical DT to obtain multisoliton solutions from the zero seed solution. In section “Rogue Wave Solutions”, we use the generalized DT to obtain the rogue wave solutions from the non-zero seed solution. Finally, the main results are summeried.

Lax Pair and Darboux Transformation

In this section, we will derive the Lax pair and DTs of Eq. (1) which include classical DT and generalized DT. The Lax pair of soliton equation means that the equation can be written as a pair of linear problems. The DTs build the relationships between the seed solution u[0] and the new solution u[N].

Lax Pair

Theorem 1

The Lax pair for the generalized variable coefficients Hirota equation (1) can be expressed as follows

$$\begin{aligned} {\varphi _x}&= U\varphi ,\nonumber \\ {\varphi _t}&= V\varphi , \end{aligned}$$

(2)

where U, V are the matrices determined by u and ${u^*}$ with isospectral parameter $\lambda$ (* denotes the complex conjugate),

$$\begin{aligned} U=\left( {\begin{array}{*{20}{c}} { - i\lambda }&{}{\sqrt{\frac{\gamma }{2}} u}\\ { - \sqrt{\frac{\gamma }{2}} {u^*}}&{}{i\lambda } \end{array}} \right) , V = \left( {\begin{array}{*{20}{c}} A&{}B\\ C&{}{ - A} \end{array}} \right) , \end{aligned}$$

(3)

with

$$\begin{aligned} A&= - 4i\beta {\lambda ^3} - 2i\alpha {\lambda ^2} + i\beta \gamma {\left| u \right| ^2}\lambda + \frac{i}{2}\alpha \gamma {\left| u \right| ^2} + \frac{1}{2}\beta \gamma (uu_x^* - {u^*}{u_x}) + \frac{i}{2}\delta ,\nonumber \\ B&= 4\beta \sqrt{\frac{\gamma }{2}} u{\lambda ^2} + \left( 2\alpha \sqrt{\frac{\gamma }{2}} u + 2i\beta \sqrt{\frac{\gamma }{2}} {u_x}\right) \lambda + i\alpha \sqrt{\frac{\gamma }{2}} {u_x} - \beta \sqrt{\frac{\gamma }{2}} {u_{xx}} - \beta \gamma \sqrt{\frac{\gamma }{2}} {\left| u \right| ^2}u,\nonumber \\ C&= - 4\beta \sqrt{\frac{\gamma }{2}} {u^*}{\lambda ^2} + \left( - 2\alpha \sqrt{\frac{\gamma }{2}} {u^*} + 2i\beta \sqrt{\frac{\gamma }{2}} u_x^*\right) \lambda + i\alpha \sqrt{\frac{\gamma }{2}} u_x^* + \beta \sqrt{\frac{\gamma }{2}} u_{xx}^*\nonumber \\&\quad + \beta \gamma \sqrt{\frac{\gamma }{2}} {\left| u \right| ^2}{u^*}. \end{aligned}$$

(4)

Proof

According to the compatibility condition, i.e. ${\varphi _{xt}} = {\varphi _{tx}}$, of Eq. (2), we can obtain zero-curvature equation ${U_t} - {V_x} + \left[ {U,V} \right] = 0$ (here $\left[ {U,V} \right] = UV - VU$), namely

$$\begin{aligned}&\left( {\begin{array}{*{20}{c}} 0&{}{\sqrt{\frac{\gamma }{2}} {u_t}}\\ {\sqrt{\frac{\gamma }{2}} u_t^*}&{}0 \end{array}} \right) - \left( {\begin{array}{*{20}{c}} {{A_x}}&{}{{B_x}}\\ {{C_x}}&{}{ - {A_x}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} { - i\lambda }&{}{\sqrt{\frac{\gamma }{2}} u}\\ { - \sqrt{\frac{\gamma }{2}} {u^*}}&{}{i\lambda } \end{array}} \right) \left( {\begin{array}{*{20}{c}} A&{}B\\ C&{}{ - A} \end{array}} \right) \nonumber \\&\quad - \left( {\begin{array}{*{20}{c}} A&{}B\\ C&{}{ - A} \end{array}} \right) \left( {\begin{array}{*{20}{c}} { - i\lambda }&{}{\sqrt{\frac{\gamma }{2}} u}\\ { - \sqrt{\frac{\gamma }{2}} {u^*}}&{}{i\lambda } \end{array}} \right) = 0. \end{aligned}$$

(5)

Substituting Eqs. (4) and (1) into Eq. (5), we can verify the validity of ${U_t} - {V_x} + \left[ {U,V} \right] = 0$. Therefore, we can give the Lax pair for Eq. (1). $\square$

Darboux Transformation

Taking $j= 1,2,3 \ldots$, we assume u[j] is j soliton solution of Eq. (1), $\varphi [j]$ be j solution of the Lax pair (2) at u[j] and T[j] is a gauge transformation between $\varphi [j - 1]$ and $\varphi [j]$ which represents the transformation relationship between two sets of solutions of Lax pair. The iteration process of the DT is described using a flowchart

$$\begin{aligned} \begin{array}{l} \varphi {[0]}\xrightarrow {T[1]}\varphi [1]\xrightarrow {T[2]}\varphi [2]\xrightarrow {T[3]}\cdots \xrightarrow {T[N-1]}\varphi [N-1]\xrightarrow {T[N]}\varphi [N]\\ \;\;\uparrow \qquad \quad \;\;\;\uparrow \qquad \quad \;\;\;\uparrow \qquad \qquad \qquad \qquad \quad \;\;\;\;\uparrow \qquad \quad \quad \;\;\;\uparrow \\ u[0]\;\longrightarrow {}\;u[1]\;\longrightarrow {}\;u[2]\;\longrightarrow {} \; \;\cdots \;\;\longrightarrow {}\;\;u[N-1]\;\;\longrightarrow {}\;u[N] \end{array}. \end{aligned}$$

(6)

Theorem 2

The N-fold classical DT of the generalized variable coefficient Hirota equation (1) is

$$\begin{aligned} \varphi [N] = T[N] \cdots T[2]T[1]\varphi {[0]}, u[N] = u[0] - 2\sqrt{\frac{2}{\gamma }} i\sum \limits _{j = 1}^N {\frac{{({\lambda _j} - \lambda _j^*){f_j}[j - 1]g_j^*[j - 1]}}{{{{\left| {{f_j}[j - 1]} \right| }^2} + {{\left| {{g_j}[j - 1]} \right| }^2}}}}. \end{aligned}$$

(7)

Here the gauge transformation $T[j] = \lambda I - S[j - 1]$, $S[j - 1] = \frac{1}{{{{\left| {{f_j}[j - 1]} \right| }^2} + {{\left| {{g_j}[j - 1]} \right| }^2}}}\left( {\begin{array}{*{20}{c}} {{\lambda _j}{{\left| {{f_j}[j - 1]} \right| }^2} + \lambda _j^*{{\left| {{g_j}[j - 1]} \right| }^2}}&{}{({\lambda _j} - \lambda _j^*){f_j}[j - 1]{g_j}{{[j - 1]}^*}}\\ {({\lambda _j} - \lambda _j^*){f_j}{{[j -1 ]}^*}{g_j}[j - 1]}&{}{\lambda _j^*{{\left| {{f_j}[j - 1]} \right| }^2} + {\lambda _j}{{\left| {{g_j}[j - 1]} \right| }^2}} \end{array}} \right)$. ${\varphi _j}[j - 1]={({f_j}[j-1],{g_j}[j-1])^T}$ is a solution of Lax pair (2) at $\lambda =\lambda _j$ and $u={u[j-1]}$ which satisfies $\left( {\begin{array}{*{20}{l}} {{f_j}[j - 1]}\\ {{g_j}[j - 1]} \end{array}} \right) = ({\lambda _j}I - S[j - 2])({\lambda _j}I - S[j - 3]) \cdots ({\lambda _j}I - S[0])\left( {\begin{array}{*{20}{l}} {{f_j}[0]}\\ {{g_j}[0]} \end{array}} \right) .$

Proof

• (1) Gauge transformation

Assuming $\varphi$ satisfies the Lax pair Eq. (2) and $\varphi '$ satisfies the Lax pair

$$\begin{aligned} {\varphi '}_x&= {U'}{\varphi '},\nonumber \\ {\varphi '}_t&= {V'}{\varphi '}, \end{aligned}$$

(8)

here ${U'},{V'}$ have the same forms with U, V except that $u,{u^*}$ in the matrices U, V are replaced with ${u'},{u'}^*$ in the matrices ${U'},{V'}$. If we set

$$\begin{aligned} {\varphi '} = T\varphi , \end{aligned}$$

(9)

and call T a gauge transformation. We can obtain the gauge transformation T satisfies

$$\begin{aligned}{} & {} {T_x} + TU - {U'}T = 0, \end{aligned}$$

(10)

$$\begin{aligned}{} & {} {T_t} + TV - {V'}T = 0. \end{aligned}$$

(11)

Substituting $T = \lambda I - S$ into Eqs. (10) and (11), we have

$$\begin{aligned}{} & {} - {S_x} + (\lambda I - S)U - {U'}(\lambda I - S) = 0, \end{aligned}$$

(12)

$$\begin{aligned}{} & {} - {S_t} + (\lambda I - S)V - {V'}(\lambda I - S) = 0. \end{aligned}$$

(13)

Setting ${(f,g)^T}$ is a solution of the Lax pair (2) at $\lambda = {\lambda _0}$, we see that ${( - g^*,f^*)^T}$ is a solution of Lax pair (2) when $\lambda = {{\lambda _0} ^*}$. Denoting $\Lambda = \left( {\begin{array}{*{20}{c}} {{\lambda _0}}&{}0\\ 0&{}{\lambda _0^*} \end{array}} \right) ,H[0] = \left( {\begin{array}{*{20}{c}} {{f}}&{}{ - g^*}\\ {{g}}&{}{f^*} \end{array}} \right)$, it can be verified that

$$\begin{aligned} S = H\Lambda {H^{ - 1}} = \frac{1}{{{{\left| f \right| }^2} + {{\left| g \right| }^2}}}\left( {\begin{array}{*{20}{c}} {{\lambda _0}{{\left| {f} \right| }^2} + \lambda _0^*{{\left| g \right| }^2}}&{}{({\lambda _0} - \lambda _0^*)f{g^*}}\\ {({\lambda _0} - \lambda _0^*){f^*}g}&{}{\lambda _0^*{{\left| f \right| }^2} + {\lambda _0}{{\left| g \right| }^2}} \end{array}} \right) , \end{aligned}$$

(14)

satisfies Eqs. (12) and (13). Then we find the gauge transformation of the Lax pair (2),

$$\begin{aligned} \varphi ' = T\varphi ,T = \lambda I - S. \end{aligned}$$

(15)

Denoting $S = \left( {\begin{array}{*{20}{c}} {{s_{11}}}&{}\quad {{s_{12}}}\\ {{s_{21}}}&{}\quad {{s_{22}}} \end{array}} \right)$, and comparing the coefficients of $\lambda$ in (12), the following relationship between two sets of solutions in Eq. (1) will be derived,

$$\begin{aligned} u' = u - 2\sqrt{\frac{2}{\gamma }} i{s_{12}}. \end{aligned}$$

(16)

Based on Eq. (14), we can see

$$\begin{aligned} {s_{12}} = \frac{{({\lambda _0} - \lambda _0^*)f{g^*}}}{{{{\left| f \right| }^2} + {{\left| g \right| }^2}}}. \end{aligned}$$

(17)

Substituting Eq. (17) into Eq. (16), we obtain

$$\begin{aligned} u' = u - 2\sqrt{\frac{2}{\gamma }} i\frac{{({\lambda _0} - \lambda _0^*)f{g^*}}}{{{{\left| f \right| }^2} + {{\left| g \right| }^2}}}. \end{aligned}$$

(18)

• (2) One-fold classical DT

Assuming ${({f_1[0]},{g_1[0]})^T}$ is a solution of Lax pair (2) when $\lambda = {\lambda _1}$ and $u=u[0]$. We can use Eqs. (14) and (15) to obtain the gauge transformation

$$\begin{aligned} T[1]&= \lambda I - S[0],\nonumber \\ S[0]&= \frac{1}{{{{\left| {{f_1}[0]} \right| }^2} + {{\left| {{g_1}[0]} \right| }^2}}}\left( {\begin{array}{*{20}{c}} {{\lambda _1}{{\left| {{f_1}[0]} \right| }^2} + \lambda _1^*{{\left| {{g_1}[0]} \right| }^2}}&{}{({\lambda _1} - \lambda _1^*){f_1}[0]{g_1}{{[0]}^*}}\\ {({\lambda _1} - \lambda _1^*){f_1}{{[0]}^*}{g_1}[0]}&{}{\lambda _1^*{{\left| {{f_1}[0]} \right| }^2} + {\lambda _1}{{\left| {{g_1}[0]} \right| }^2}} \end{array}} \right) . \end{aligned}$$

(19)

According to Eqs. (15) and (18), we can obtain the one-fold classical DT

$$\begin{aligned} \varphi [1] = T[1]\varphi [0],u[1] = u[0] - 2\sqrt{\frac{2}{\gamma }} i\frac{{({\lambda _1} - \lambda _1^*){f_1}[0]{g_1}{{[0]}^*}}}{{{{\left| {{f_1}[0]} \right| }^2} + {{\left| {{g_1}[0]} \right| }^2}}}. \end{aligned}$$

(20)

• (3) Two-fold classical DT

Assuming ${({f_2[k]},{g_2[k]})^T}$ is a solution of Lax pair (2) when $\lambda = {\lambda _2}$ and $u=u[k]$, where $k=0,1$. By means of Eqs. (14) and (15), the gauge transformation

$$\begin{aligned} T[2]&= \lambda I - S[ 1],\nonumber \\ S[ 1]&= \frac{1}{{{{\left| {{f_2}[1]} \right| }^2} + {{\left| {{g_2}[1]} \right| }^2}}}\left( {\begin{array}{*{20}{c}} {{\lambda _2}{{\left| {{f_2}[1]} \right| }^2} + \lambda _2^*{{\left| {{g_2}[ 1]} \right| }^2}}&{}{({\lambda _2} - \lambda _2^*){f_2}[ 1]{g_2}{{[ 1]}^*}}\\ {({\lambda _2} - \lambda _2^*){f_2}{{[1]}^*}{g_2}[ 1]}&{}{\lambda _2^*{{\left| {{f_2}[1]} \right| }^2} + {\lambda _2}{{\left| {{g_2}[1]} \right| }^2}} \end{array}} \right) . \end{aligned}$$

(21)

Applying Eq. (20), we get

$$\begin{aligned} \left( {\begin{array}{*{20}{l}} {{f_2}[1]}\\ {{g_2}[1]} \end{array}} \right) = ({\lambda _2}I - S[0])\left( {\begin{array}{*{20}{l}} {{f_2}[0]}\\ {{g_2}[0]} \end{array}} \right) , \end{aligned}$$

(22)

and

$$\begin{aligned} \varphi [2] = T[2]\varphi [1] = T[2]T[1]\varphi [0]. \end{aligned}$$

(23)

By Eq. (18), we derive

$$\begin{aligned} u[2] = u[1] - 2\sqrt{\frac{2}{\gamma }} i\frac{{({\lambda _2} - \lambda _2^*){f_2[1]}g_2[1]^*}}{{{{\left| {{f_2[1]}} \right| }^2} + {{\left| {{g_2[1]}} \right| }^2}}}. \end{aligned}$$

(24)

Substituting Eq. (20) into Eq. (24), we obtain the two-fold classical DT

$$\begin{aligned} \varphi [2] = T[2]T[1]\varphi [0],u[2] = u[0] - 2\sqrt{\frac{2}{\gamma }} i\sum \limits _{j = 1}^2 {\frac{{({\lambda _j} - \lambda _j^*){f_j}[j - 1]g_j^*[j - 1]}}{{{{\left| {{f_j}[j - 1]} \right| }^2} + {{\left| {{g_j}[j - 1]} \right| }^2}}}}. \end{aligned}$$

(25)

• (4) Three-fold classical DT

Assuming ${({f_3[k]},{g_3[k]})^T}$ is a solution of Lax pair (2) when $\lambda = {\lambda _3}$ and $u=u[k]$, where $k=0,1,2$. From Eqs. (14) and (15), the gauge transformation

$$\begin{aligned} T[3]&= \lambda I - S[2],\nonumber \\ S[2]&= \frac{1}{{{{\left| {{f_3}[2]} \right| }^2} + {{\left| {{g_3}[2]} \right| }^2}}}\left( {\begin{array}{*{20}{c}} {{\lambda _3}{{\left| {{f_3}[2]} \right| }^2} + \lambda _3^*{{\left| {{g_3}[2]} \right| }^2}}&{}{({\lambda _3} - \lambda _3^*){f_3}[2]{g_3}{{[2]}^*}}\\ {({\lambda _3} - \lambda _3^*){f_3}{{[2]}^*}{g_3}[2]}&{}{\lambda _3^*{{\left| {{f_3}[2]} \right| }^2} + {\lambda _3}{{\left| {{g_3}[2]} \right| }^2}} \end{array}} \right) . \end{aligned}$$

(26)

Utilizing Eq. (25), we get

$$\begin{aligned} \left( {\begin{array}{*{20}{l}} {{f_3}[2]}\\ {{g_3}[2]} \end{array}} \right) = ({\lambda _3}I - S[1])({\lambda _3}I - S[0])\left( {\begin{array}{*{20}{l}} {{f_3}[0]}\\ {{g_3}[0]} \end{array}} \right) , \end{aligned}$$

(27)

and

$$\begin{aligned} \varphi [3] = T[3]\varphi [2] = T[3]T[2]T[1]\varphi [0]. \end{aligned}$$

(28)

By using Eq. (18), we observe

$$\begin{aligned} u[3] = u[2] - 2\sqrt{\frac{2}{\gamma }} i\frac{{({\lambda _3} - \lambda _3^*){f_3}[2]{g_3}{{[2]}^*}}}{{{{\left| {{f_3}[2]} \right| }^2} + {{\left| {{g_3}[2]} \right| }^2}}}. \end{aligned}$$

(29)

Substituting Eq. (25) into Eq. (29), we obtain the three-fold classical DT

$$\begin{aligned} \varphi [3] =T[3]T[2]T[1]\varphi [0],u[3] = u[0] - 2\sqrt{\frac{2}{\gamma }} i\sum \limits _{j = 1}^3 {\frac{{({\lambda _j} - \lambda _j^*){f_j}[j - 1]g_j^*[j - 1]}}{{{{\left| {{f_j}[j - 1]} \right| }^2} + {{\left| {{g_j}[j - 1]} \right| }^2}}}}.\nonumber \\ \end{aligned}$$

(30)

• (5) N-fold classical DT

Assuming ${({f_N[k]},{g_N[k]})^T}$ is a solution of Lax pair (2) when $\lambda = {\lambda _N}$ and $u=u[k]$, where $k = 0,1, \ldots ,N-1$. Continuing the above iteration process, we obtain

$$\begin{aligned} T[N]&= \lambda I - S[N- 1], \nonumber \\ S[N - 1]&= \frac{1}{{{{\left| {{f_N}[N - 1]} \right| }^2} + {{\left| {{g_N}[N- 1]} \right| }^2}}}\nonumber \\&\quad \times \left( {\begin{array}{*{20}{c}} {{\lambda _N}{{\left| {{f_N}[N - 1]} \right| }^2} + \lambda _N^*{{\left| {{g_N}[N - 1]} \right| }^2}}&{}{({\lambda _N} - \lambda _N^*){f_N}[N - 1]{g_N}{{[N - 1]}^*}}\\ {({\lambda _N} - \lambda _N^*){f_N}{{[N -1 ]}^*}{g_N}[N - 1]}&{}{\lambda _N^*{{\left| {{f_N}[N - 1]} \right| }^2} + {\lambda _N}{{\left| {{g_N}[N - 1]} \right| }^2}} \end{array}} \right) . \end{aligned}$$

(31)

The relationship between ${({f_N[0]},{g_N[0]})^T}$ and ${({f_N}[N-1],{g_N}[N-1])^T}$ is

$$\begin{aligned} \left( {\begin{array}{*{20}{l}} {{f_N}[N - 1]}\\ {{g_N}[ N- 1]} \end{array}} \right) = ({\lambda _N}I - S[N - 2])({\lambda _N}I - S[N - 3]) \cdots ({\lambda _N}I - S[0])\left( {\begin{array}{*{20}{l}} {{f_N}[0]}\\ {{g_N}[0]} \end{array}} \right) . \end{aligned}$$

(32)

We obtain the N-fold classical DT

$$\begin{aligned} \varphi [N] = T[N] \cdots T[2]T[1]\varphi [0],u[N] = u[0] - 2\sqrt{\frac{2}{\gamma }} i\sum \limits _{j = 1}^N {\frac{{({\lambda _j} - \lambda _j^*){f_j}[j - 1]g_j^*[j - 1]}}{{{{\left| {{f_j}[j - 1]} \right| }^2} + {{\left| {{g_j}[j - 1]} \right| }^2}}}}. \end{aligned}$$

(33)

$\square$

Theorem 3

The N-fold generalized DT of the generalized variable coefficients Hirota equation (1) is

$$\begin{aligned} \varphi [N] = {T_1}[N] \cdots {T_1}[2]{T_1}[1]\varphi {[0]},u[N] = u[0] - 2\sqrt{\frac{2}{\gamma }} i\sum \limits _{j = 1}^N {\frac{{({\lambda _1} - \lambda _1^*){f_1}[j - 1]g_1^*[j - 1]}}{{{{\left| {{f_1}[j - 1]} \right| }^2} + {{\left| {{g_1}[j - 1]} \right| }^2}}}}. \end{aligned}$$

(34)

Here the gauge transformation ${T_1}[j]=\lambda I - {S_1}[j - 1]$, ${S_1}[j - 1] = \frac{1}{{{{\left| {{f_1}[j - 1]} \right| }^2} + {{\left| {{g_1}[j - 1]} \right| }^2}}}\left( {\begin{array}{*{20}{c}} {{\lambda _1}{{\left| {{f_1}[j - 1]} \right| }^2} + \lambda _1^*{{\left| {{g_1}[j - 1]} \right| }^2}}&{}{({\lambda _1} - \lambda _1^*){f_1}[j - 1]{g_1}{{[j - 1]}^*}}\\ {({\lambda _1} - \lambda _1^*){f_1}{{[j - 1]}^*}{g_1}[j - 1]}&{}{\lambda _1^*{{\left| {{f_1}[j - 1]} \right| }^2} + {\lambda _1}{{\left| {{g_1}[j - 1]} \right| }^2}} \end{array}} \right)$. ${\varphi _1}[j - 1]={({f_1}[j-1],{g_1}[j-1])^T}$ is a solution of Lax pair (2) at $\lambda ={\lambda _1}$ and $u={u[j-1]}$ which satisfies

$$\begin{aligned} {\varphi _1}[j - 1]&= \mathop {\lim }\limits _{\varepsilon \rightarrow 0} \frac{{{{\left. {({T_1}[j - 1] \cdots {T_1}[2]{T_1}[1])} \right| }_{\lambda = {\lambda _1} + \varepsilon }}{\varphi _1}({\lambda _1} + \varepsilon )}}{{{\varepsilon ^{j - 1}}}}\nonumber \\&= {\varphi _1}[0]+ {\left. {\left( \sum \limits _{k = 1}^{j - 1} {{T_1}[k]} \right) } \right| _{\lambda = {\lambda _1}}}\varphi _1^{[1]} + {\left. {\left( \sum \limits _{1 \le k< l \le j - 1} {{T_1}[l]{T_1}[k]} \right) } \right| _{\lambda = {\lambda _1}}}\varphi _1^{[2]}\nonumber \\&\quad + {\left. {\left( \sum \limits _{1 \le k< l < m \le j - 1} {{T_1}[m]{T_1}[l]{T_1}[k]} \right) } \right| _{\lambda = {\lambda _1}}}\varphi _1^{[3]} + \cdots \nonumber \\&\quad + {\left. {({T_1}[j - 1]{T_1}[j - 2] \cdots {T_1}[1])} \right| _{\lambda = {\lambda _1}}}\varphi _1^{[j - 1]}, \end{aligned}$$

(35)

where ${\varphi _1}({\lambda _1} + \varepsilon )$ is a solution of Lax pair (2) at $\lambda = {\lambda _1} + \varepsilon , u = u[0]$ and $\varphi _1^{[k]} = {({f_1}^{[k]},{g_1}^{[k]})^T} = {\left. {\frac{1}{{k!}}\frac{{{\partial ^k}{\varphi _1}(\lambda )}}{{\partial {\lambda ^k}}}} \right| _{\lambda = {\lambda _1}}}$.

Proof

From Eqs. (14) and (15), we see that if $\lambda =\lambda _0$, the gauge transformation

$$\begin{aligned} \varphi ' = {T_0}\varphi = ({\lambda _0}I - S)\varphi = 0. \end{aligned}$$

(36)

It means that the same solution can not be reused in the iteration of DT. In the generalized DT, we consider the case of $\lambda = {\lambda _1} + \varepsilon$, where $\varepsilon$ is a small complex parameter. Assuming ${\varphi _1}({\lambda _1} + \varepsilon )$ is a solution of Lax pair (2) at $\lambda = {\lambda _1} + \varepsilon$ and $u = u[0]$, and it can be expanded at $\varepsilon = 0$ as the following Taylor series

$$\begin{aligned} {\varphi _1}({\lambda _1} + \varepsilon ) = \varphi _1^{[0]} + \varphi _1^{[1]}\varepsilon + \varphi _1^{[2]}{\varepsilon ^2} + \cdots + \varphi _1^{[n]}{\varepsilon ^n} + \cdots , \end{aligned}$$

(37)

where $\varphi _1^{[k]} = {({f_1}^{[k]},{g_1}^{[k]})^T} = {\left. {\frac{1}{{k!}}\frac{{{\partial ^k}{\varphi _1}(\lambda )}}{{\partial {\lambda ^k}}}} \right| _{\lambda = {\lambda _1}}}(k = 0,1,2, \ldots )$, and $\varphi _1^{[0]} = {\varphi _1}({\lambda _1}) = {\varphi _1}[0]$.

• (1) One-fold generalized DT

The one-fold generalized DT of Eq. (1) is the same as the one-fold classical DT. The gauge transformation

$$\begin{aligned} {T_1}[1]&= \lambda I - {S_1}[0],\nonumber \\ {S_1}[0]&= \frac{1}{{{{\left| {{f_1}[0]} \right| }^2} + {{\left| {{g_1}[0]} \right| }^2}}}\left( {\begin{array}{*{20}{c}} {{\lambda _1}{{\left| {{f_1}[0]} \right| }^2} + \lambda _1^*{{\left| {{g_1}[0]} \right| }^2}}&{}{({\lambda _1} - \lambda _1^*){f_1}[0]{g_1}{{[0]}^*}}\\ {({\lambda _1} - \lambda _1^*){f_1}{{[0]}^*}{g_1}[0]}&{}{\lambda _1^*{{\left| {{f_1}[0]} \right| }^2} + {\lambda _1}{{\left| {{g_1}[0]} \right| }^2}} \end{array}} \right) , \end{aligned}$$

(38)

and the one-fold generalized DT

$$\begin{aligned} {\varphi [1]} = {T_1}[1]{\varphi [0]}, u[1] = u[0] - 2{\sqrt{\frac{2}{\gamma }}} \frac{{({\lambda _1} - \lambda _1^*){f_1[0]}g_1[0]^*}}{{{{\left| {{f_1[0]}} \right| }^2} + {{\left| {{g_1[0]}} \right| }^2}}}. \end{aligned}$$

(39)

• (2) Two-fold generalized DT

From the classical DT (7), we see that ${\left. {{T_1}[1]} \right| _{\lambda = {\lambda _1} + \varepsilon }}{\varphi _1}({\lambda _1} + \varepsilon )$ is a solution of Lax pair (2) at $\lambda = {\lambda _1} + \varepsilon$ and $u = u[1]$, and so is $\frac{{{{\left. {{T_1}[1]} \right| }_{\lambda = {\lambda _1} + \varepsilon }}{\varphi _1}({\lambda _1} + \varepsilon )}}{\varepsilon }$. Then $\mathop {\lim }\limits _{\varepsilon \rightarrow 0} \frac{{{{\left. {{T_1}[1]} \right| }_{\lambda = {\lambda _1} + \varepsilon }}{\varphi _1}({\lambda _1} + \varepsilon )}}{\varepsilon }$ is a solution of Lax pair (2) at $\lambda = {\lambda _1}$ and $u = u[1]$. We write ${\varphi _1}[1] = {({f_1}[1],{g_1}[1])^T} = \mathop {\lim }\limits _{\varepsilon \rightarrow 0} \frac{{{{\left. {{T_1}[1]} \right| }_{\lambda = {\lambda _1} + \varepsilon }}{\varphi _1}({\lambda _1} + \varepsilon )}}{\varepsilon }$, and can calculate that

$$\begin{aligned} \mathop {\lim }\limits _{\varepsilon \rightarrow 0} \frac{{{{\left. {{T_1}[1]} \right| }_{\lambda = {\lambda _1} + \varepsilon }}{\varphi _1({\lambda _1} + \varepsilon )}}}{\varepsilon }&= \mathop {\lim }\limits _{\varepsilon \rightarrow 0} \frac{{{{\left. {{T_1}[1]} \right| }_{\lambda = {\lambda _1} + \varepsilon }}({\varphi _1}[0] + \varphi _1^{[1]}\varepsilon + \cdots )}}{\varepsilon }\nonumber \\&= \mathop {\lim }\limits _{\varepsilon \rightarrow 0} \frac{{({{\left. {{T_1}[1]} \right| }_{\lambda = {\lambda _1}}} + \varepsilon I)({\varphi _1}[0] + \varphi _1^{[1]}\varepsilon + \cdots )}}{\varepsilon }\nonumber \\&= \mathop {\lim }\limits _{\varepsilon \rightarrow 0} \frac{{{{\left. {{T_1}[1]} \right| }_{\lambda = {\lambda _1}}}{\varphi _1}[0] + ({\varphi _1}[0] + {{\left. {{T_1}[1]} \right| }_{\lambda = {\lambda _1}}}\varphi _1^{[1]} )\varepsilon + \cdots }}{\varepsilon }\nonumber \\&= {\varphi _1}[0] + {\left. {{T_1}[1]} \right| _{\lambda = {\lambda _1}}}\varphi _1^{[1]}, \end{aligned}$$

(40)

where ${\left. {{T_1}[1]} \right| _{\lambda = {\lambda _1}}}{\varphi _1}[0]= 0$. By means of Eqs. (14) and (15), we get the gauge transformation

$$\begin{aligned} {T_1}[2]&= \lambda I - {S_1}[1],\nonumber \\ {S_1}[1]&= \frac{1}{{{{\left| {{f_1}[1]} \right| }^2} + {{\left| {{g_1}[1]} \right| }^2}}}\left( {\begin{array}{*{20}{c}} {{\lambda _1}{{\left| {{f_1}[1]} \right| }^2} + \lambda _1^*{{\left| {{g_1}[1]} \right| }^2}}&{}{({\lambda _1} - \lambda _1^*){f_1}[1]{g_1}{{[1]}^*}}\\ {({\lambda _1} - \lambda _1^*){f_1}{{[1]}^*}{g_1}[1]}&{}{\lambda _1^*{{\left| {{f_1}[1]} \right| }^2} + {\lambda _1}{{\left| {{g_1}[1]} \right| }^2}} \end{array}} \right) . \end{aligned}$$

(41)

Combining with Eqs. (16) and (39), we find the two-fold generalized DT

$$\begin{aligned} \varphi [2]&= {T_1}[2]\varphi [1] = {T_1}[2]{T_1}[1]\varphi [0],\nonumber \\ u[2]&= u[1] - 2\sqrt{\frac{2}{\gamma }} i\frac{{({\lambda _1} - \lambda _1^*){f_1}[1]{g_1}{{[1]}^*}}}{{{{\left| {{f_1}[1]} \right| }^2} + {{\left| {{g_1}[1]} \right| }^2}}}\nonumber \\&= u[0] - 2\sqrt{\frac{2}{\gamma }} i\sum \limits _{j = 1}^2 {\frac{{({\lambda _1} - \lambda _1^*){f_1}[j - 1]g_1^*[j - 1]}}{{{{\left| {{f_1}[j - 1]} \right| }^2} + {{\left| {{g_1}[j - 1]} \right| }^2}}}}. \end{aligned}$$

(42)

• (3) Three-fold generalized DT

Similarly, we see that ${\left. {({T_1}[2]{T_1}[1])} \right| _{\lambda = {\lambda _1} + \varepsilon }}{\varphi _1}({\lambda _1} + \varepsilon )$ is a solution of Lax pair (2) at $\lambda = {\lambda _1} + \varepsilon$ and $u = u[2]$, and so is $\frac{{{{\left. {({T_1}[2]{T_1}[1])} \right| }_{\lambda = {\lambda _1} + \varepsilon }}{\varphi _1}({\lambda _1} + \varepsilon )}}{{{\varepsilon ^2}}}$. Then $\mathop {\lim }\limits _{\varepsilon \rightarrow 0} \frac{{{{\left. {({T_1}[2]{T_1}[1])} \right| }_{\lambda = {\lambda _1} + \varepsilon }}{\varphi _1}({\lambda _1} + \varepsilon )}}{{{\varepsilon ^2}}}$ is a solution of Lax pair (2) at $\lambda = {\lambda _1}$ and $u = u[2]$. We write ${\varphi _1}[2] = {({f_1}[2],{g_1}[2])^T} = \mathop {\lim }\limits _{\varepsilon \rightarrow 0} \frac{{{{\left. {({T_1}[2]{T_1}[1])} \right| }_{\lambda = {\lambda _1} + \varepsilon }}{\varphi _1}({\lambda _1} + \varepsilon )}}{{{\varepsilon ^2}}}$, and can calculate that

$$\begin{aligned}&\mathop {\lim }\limits _{\varepsilon \rightarrow 0} \frac{{{{\left. {({T_1}[2]{T_1}[1])} \right| }_{\lambda = {\lambda _1} + \varepsilon }}{\varphi _1({\lambda _1} + \varepsilon )}}}{{{\varepsilon ^2}}} \nonumber \\&\quad = \mathop {\lim }\limits _{\varepsilon \rightarrow 0} \frac{{{{\left. {({T_1}[2]{T_1}[1])} \right| }_{\lambda = {\lambda _1} + \varepsilon }}({\varphi _1}[0] + \varphi _1^{[1]} \varepsilon + \varphi _1^{[2]}{\varepsilon ^2} \cdots )}}{{{\varepsilon ^2}}}\nonumber \\&\quad = \mathop {\lim }\limits _{\varepsilon \rightarrow 0} \frac{{({{\left. {{T_1}[2]} \right| }_{\lambda = {\lambda _1}}} + \varepsilon I)({{\left. {{T_1}[1]} \right| }_{\lambda = {\lambda _1}}} + \varepsilon I)({\varphi _1}[0] + \varphi _1^{[1]}\varepsilon + \varphi _1^{[2]}{\varepsilon ^2} \cdots )}}{{{\varepsilon ^2}}}\nonumber \\&\quad = {\varphi _1}[0] + {\left. {({T_1}[2] + {T_1}[1])} \right| _{\lambda = {\lambda _1}}}\varphi _1^{[1]} + {\left. {({T_1}[2]{T_1}[1])} \right| _{\lambda = {\lambda _1}}}\varphi _1^{[1]}, \end{aligned}$$

(43)

where ${\left. {{T_1}[1]} \right| _{\lambda = {\lambda _1}}}{\varphi _1}[0] = 0$ and ${\left. {{T_1}[2]} \right| _{\lambda = {\lambda _1}}}({\varphi _1}[0] + {\left. {{T_1}[1]} \right| _{\lambda = {\lambda _1}}}\varphi _1^{[1]}) = {\left. {{T_1}[2]} \right| _{\lambda = {\lambda _1}}}{\varphi _1}[1] = 0$. Then we have the gauge transformation

$$\begin{aligned} {T_1}[3]&= \lambda I - {S_1}[2],\nonumber \\ {S_1}[2]&= \frac{1}{{{{\left| {{f_1}[2]} \right| }^2} + {{\left| {{g_1}[2]} \right| }^2}}}\left( {\begin{array}{*{20}{c}} {{\lambda _1}{{\left| {{f_1}[2]} \right| }^2} + \lambda _1^*{{\left| {{g_1}[2]} \right| }^2}}&{}{({\lambda _1} - \lambda _1^*){f_1}[2]{g_1}{{[2]}^*}}\\ {({\lambda _1} - \lambda _1^*){f_1}{{[2]}^*}{g_1}[2]}&{}{\lambda _1^*{{\left| {{f_1}[2]} \right| }^2} + {\lambda _1}{{\left| {{g_1}[2]} \right| }^2}} \end{array}} \right) , \end{aligned}$$

(44)

and the three-fold generalized DT

$$\begin{aligned} \varphi [3]&= {T_1}[3]\varphi [2] = {T_1}[3]{T_1}[2]{T_1}[1]\varphi [0],\nonumber \\ u[3]&= u[2] - 2\sqrt{\frac{2}{\gamma }} i\frac{{({\lambda _1} - \lambda _1^*){f_1}[2]{g_1}{{[2]}^*}}}{{{{\left| {{f_1}[2]} \right| }^2} + {{\left| {{g_1}[2]} \right| }^2}}}\nonumber \\&= u[0] - 2\sqrt{\frac{2}{\gamma }} i\sum \limits _{j = 1}^3 {\frac{{({\lambda _1} - \lambda _1^*){f_1}[j - 1]g_1^*[j - 1]}}{{{{\left| {{f_1}[j - 1]} \right| }^2} + {{\left| {{g_1}[j - 1]} \right| }^2}}}}. \end{aligned}$$

(45)

• (4) N-fold generalized DT

Continuing the above process, we see that $\mathop {\lim }\limits _{\varepsilon \rightarrow 0} \frac{{{{\left. {({T_1}[N - 1] \cdots {T_1}[2]{T_1}[1])} \right| }_{\lambda = {\lambda _1} + \varepsilon }}{\varphi _1}({\lambda _1} + \varepsilon )}}{{{\varepsilon ^{N - 1}}}}$ is a solution of Lax pair (2) at $\lambda = {\lambda _1} + \varepsilon$ and $u = u[N-1]$. We write ${\varphi _1}[N - 1] = {({f_1}[N - 1],{g_1}[N - 1])^T} = \mathop {\lim }\limits _{\varepsilon \rightarrow 0} \frac{{{{\left. {({T_1}[N - 1] \cdots {T_1}[2]{T_1}[1])} \right| }_{\lambda = {\lambda _1} + \varepsilon }}{\varphi _1}({\lambda _1} + \varepsilon )}}{{{\varepsilon ^{N - 1}}}}$ and can calculate that

$$\begin{aligned}&\mathop {\lim }\limits _{\varepsilon \rightarrow 0} \frac{{{{\left. {({T_1}[N - 1] \cdots {T_1}[2]{T_1}[1])} \right| }_{\lambda = {\lambda _1} + \varepsilon }}{\varphi _1}({\lambda _1} + \varepsilon )}}{{{\varepsilon ^{N - 1}}}}\nonumber \\&\quad = {\varphi _1}[0] + {\left. {\left( \sum \limits _{k = 1}^{N - 1} {{T_1}[k]} \right) } \right| _{\lambda = {\lambda _1}}}\varphi _1^{[1]} + {\left. {\left( \sum \limits _{1 \le k< l \le N - 1} {{T_1}[l]{T_1}[k]} \right) } \right| _{\lambda = {\lambda _1}}}\varphi _1^{[2]}\nonumber \\&\quad + {\left. {\left( \sum \limits _{1 \le k< l < m \le N - 1} {{T_1}[m]{T_1}[l]{T_1}[k]} \right) } \right| _{\lambda = {\lambda _1}}}\varphi _1^{[3]} + \cdots \nonumber \\&\quad + {\left. {({T_1}[N - 1]{T_1}[N - 2] \cdots {T_1}[1])} \right| _{\lambda = {\lambda _1}}}\varphi _1^{[N - 1]}. \end{aligned}$$

(46)

Then the gauge transformation

$$\begin{aligned} {T_1}[N]&= \lambda I - {S_1}[N - 1],\nonumber \\ {S_1}[N - 1]&= \frac{1}{{{{\left| {{f_1}[N - 1]} \right| }^2} + {{\left| {{g_1}[N - 1]} \right| }^2}}}\nonumber \\&\quad \times \left( {\begin{array}{*{20}{c}} {{\lambda _1}{{\left| {{f_1}[N - 1]} \right| }^2} + \lambda _1^*{{\left| {{g_1}[N - 1]} \right| }^2}}&{}{({\lambda _1} - \lambda _1^*){f_1}[N - 1]{g_1}{{[N - 1]}^*}}\\ {({\lambda _1} - \lambda _1^*){f_1}{{[N - 1]}^*}{g_1}[N - 1]}&{}{\lambda _1^*{{\left| {{f_1}[N - 1]} \right| }^2} + {\lambda _1}{{\left| {{g_1}[N - 1]} \right| }^2}} \end{array}} \right) , \end{aligned}$$

(47)

and the N-fold generalized DT

$$\begin{aligned} \varphi [N]&= {T_1}[N]\varphi [N - 1] = {T_1}[N]{T_1}[N - 1] \cdots {T_1}[1]\varphi [0],\nonumber \\ u[N]&= u[N - 1] - 2\sqrt{\frac{2}{\gamma }} i\frac{{({\lambda _1} - \lambda _1^*){f_1}[N - 1]{g_1}{{[N - 1]}^*}}}{{{{\left| {{f_1}[N - 1]} \right| }^2} + {{\left| {{g_1}[N - 1]} \right| }^2}}}\nonumber \\&= u[0] - 2\sqrt{\frac{2}{\gamma }} i\sum \limits _{j = 1}^N {\frac{{({\lambda _1} - \lambda _1^*){f_1}[j - 1]g_1^*[j - 1]}}{{{{\left| {{f_1}[j - 1]} \right| }^2} + {{\left| {{g_1}[j - 1]} \right| }^2}}}}, \end{aligned}$$

(48)

have been established. $\square$

Multisoliton Solutions

In order to obtain the multisoliton solutions for Eq. (1), we start from the seed solution $u[0] = 0$. Substituting $u[0] = 0$ into Lax pair (2), we get

$$\begin{aligned} {\varphi [0] _x}&= \left( {\begin{array}{*{20}{c}} { - i\lambda }&{}0\\ 0&{}{i\lambda } \end{array}} \right) \varphi [0],\nonumber \\ {\varphi [0] _t}&= \left( {\begin{array}{*{20}{c}} { - 4i\beta {\lambda ^3} - 2i\alpha {\lambda ^2} + \frac{i}{2}\delta }&{}0\\ 0&{}{4i\beta {\lambda ^3} + 2i\alpha {\lambda ^2} - \frac{i}{2}\delta } \end{array}} \right) \varphi [0]. \end{aligned}$$

(49)

Through direct calculation, the solution ${\varphi _1}[0] = {({f_1[0]},{g_1[0]})^T}$ of Lax pair (49) at $\lambda ={\lambda _1}$ is

$$\begin{aligned} {f_1}[0]&= {e^{ - i{\lambda _1}x - 4i\lambda _1^3\int {\beta dt} - 2i\lambda _1^2\int {\alpha dt} + \frac{i}{2}\int {\delta dt} }},\nonumber \\ {g_1}[0]&= {e^{i{\lambda _1}x + 4i\lambda _1^3\int {\beta dt} + 2i\lambda _1^2\int {\alpha dt} - \frac{i}{2}\int {\delta dt} }}. \end{aligned}$$

(50)

From Eq. (20), if we take ${\lambda _1} = 1 + 2i$, we find the one-soliton solution

$$\begin{aligned} u[1] = 8\sqrt{\frac{2}{\gamma }} \frac{{{f_1}[0]{g_1}{{[0]}^*}}}{{{{\left| {{f_1}[0]} \right| }^2} + {{\left| {{g_1}[0]} \right| }^2}}}. \end{aligned}$$

(51)

The solution ${\varphi _2}[0] = {({f_2[0]},{g_2[0]})^T}$ of Lax pair (49) at $\lambda ={\lambda _2}$ is

$$\begin{aligned} {f_2}[0]&= {e^{ - i{\lambda _2}x - 4i\lambda _2^3\int {\beta dt} - 2i\lambda _2^2\int {\alpha dt} + \frac{i}{2}\int {\delta dt} }},\nonumber \\ {g_2}[0]&= {e^{i{\lambda _2}x + 4i\lambda _2^3\int {\beta dt} + 2i\lambda _2^2\int {\alpha dt} - \frac{i}{2}\int {\delta dt} }}. \end{aligned}$$

(52)

Substituting Eqs. (22) and (52) into (25) and taking ${\lambda _2} = 2 + 3i$, we get the two-soliton solution

$$\begin{aligned} u[2] = 8\sqrt{\frac{2}{\gamma }} \frac{{{f_1}[0]g_1^*[0]}}{{{{\left| {{f_1}[0]} \right| }^2} + {{\left| {{g_1}[0]} \right| }^2}}} + 12\sqrt{\frac{2}{\gamma }} \frac{{{f_2}[1]g_2^*[1]}}{{{{\left| {{f_2}[1]} \right| }^2} + {{\left| {{g_2}[1]} \right| }^2}}}. \end{aligned}$$

(53)

Next, we will discuss the evolutions of the soliton solutions and show the relationship between solitons and the group dispersion velocity $\alpha$, third order dispersion $\beta$ and the amplification or absorption coefficient $\delta$.

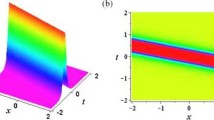
In Figs. 1, 2, 3, 4, 5, 6 and 7, (a) and (b) represent three- and two- dimensional plots of one-soliton solution depicted by Eq. (51), respectively. (c) and (d) represent three- and two- dimensional plots of two-soliton solution depicted by Eq. (53), respectively.

Fig. 1

Parameters are $\alpha = 0,\beta = \sin t,\gamma = 2,\delta = 0$ in Eqs. (51) and (53)

Fig. 2

Parameters are $\alpha = 0,\beta = {e^t},\gamma = 2,\delta = 0$ in Eqs. (51) and (53)

Fig. 3

Parameters are $\alpha = 0,\beta = {t^2},\gamma = 2,\delta = 0$ in Eqs. (51) and (53)

Fig. 4

Parameters are $\alpha = \sin t,\beta = 0,\gamma = 2,\delta = t$ in Eqs. (51) and (53)

Fig. 5

Parameters are $\alpha = {e^t},\beta = 0,\gamma = 2,\delta = t$ in Eqs. (51) and (53)

Fig. 6

Parameters are $\alpha = {t^2},\beta = 0,\gamma = 2,\delta = t$ in Eqs. (51) and (53)

Fig. 7

Parameters are $\alpha = sin t,\beta = t, \gamma = 2,\delta ={e^t}$ in Eqs. (51) and (53)

In Fig. 1, the soliton structure oscillates periodically because third order dispersion coefficient $\beta$ is a trigonometric function. In Fig. 2, the image of the soliton solution has an upper convex shape and converges at $x = 0$ because third order dispersion coefficient $\beta$ is an exponential function. In Fig. 3, the soliton with variable propagation velocities illustrates the non-travelling-wave characteristics because third order dispersion coefficient $\beta$ is of parabolic-type. In Figs. 1c, 2c and 3c, the head-on interactions form a peak at each interaction region between the two solitons, respectively. In Figs. 4, 5 and 6, we can see that the image of the soliton solutions are related to the characteristics of the group dispersion velocity coefficient $\alpha$. In Fig. 7, the soliton image is affected by several nonzero parameters including the group dispersion velocity coefficient $\alpha$, third order dispersion coefficient$\beta$, self-steepening coefficient$\gamma$, and amplification or absorption coefficient $\delta$.

Rogue Wave Solutions

In this section, we will derive the rogue wave solutions for Eq. (1). we start with the seed solution $u[0] = {e^{i\int {(\alpha (t)\gamma + \delta (t))dt} }}$. By combining it with Eqs. (39) and (42), we can describe one-rogue wave solution and two-rogue wave solution as follows

$$\begin{aligned} u[1]= & {} {e^{i\int {(\alpha \gamma + \delta )dt} }}- 4\sqrt{\frac{2}{\gamma }}\frac{{{f_1[0]}g_1[0]^*}}{{{{\left| {{f_1[0]}} \right| }^2} + {{\left| {{g_1[0]}} \right| }^2}}}, \end{aligned}$$

(54)

$$\begin{aligned} u[2]= & {} {e^{i\int {(\alpha \gamma + \delta )dt} }} - 4\sqrt{\frac{2}{\gamma }} \frac{{{f_1}[0]{g_1}{{[0]}^*}}}{{{{\left| {{f_1}[0]} \right| }^2} + {{\left| {{g_1}[0]} \right| }^2}}} - 4\sqrt{\frac{2}{\gamma }} \frac{{{f_1}[1]{g_1}{{[1]}^*}}}{{{{\left| {{f_1}[1]} \right| }^2} + {{\left| {{g_1}[1]} \right| }^2}}}, \end{aligned}$$

(55)

here we take ${\lambda _1} = - i$.

Next, we will use an example to demonstrate the process. When we take $\alpha =t, \beta = 0.5, \gamma = 2,\delta =3$, we can obtain $u[0] = {e^{i({t^2} + 3t)}}$. Assuming ${\varphi _1}(-i + \varepsilon )$ is a solution of Lax pair (2) at $\lambda = -i + \varepsilon$ and $u = u[0]$, with the aid of Eq. (37), we can find ${\varphi _1}[0] = {({f_1}[0],{g_1}[0])^T}$ with

$$\begin{aligned} {f_1}[0]&= ( - 2 + 2i){e^{\frac{1}{2}it(t + 3)}}(i{t^2} + 3t - x),\nonumber \\ {g_1}[0]&= ( - 2 + 2i){e^{ - \frac{1}{2}it(t + 3)}}(i{t^2} + 3t - x- 1). \end{aligned}$$

(56)

From Eq. (40), we find ${\varphi _1}[1] = {({f_1}[1],{g_1}[1])^T}$ with

$$\begin{aligned} {f_1}[1]&= - \frac{2}{3}\frac{1}{{2{t^4} + 18{t^2} - 12tx + 2{x^2} - 6t + 2x + 1}}{e^{\frac{1}{2}it(t + 3)}}( - 4{t^8} + 24{t^7} - 8{t^6}x\nonumber \\&\quad + 4{t^6}+ 252{t^5}- 228{t^4}x+ 72{t^3}{x^2}- 8{t^2}{x^3}+ 204{t^4}- 360{t^3}x + 204{t^2}{x^2} \nonumber \\&\quad - 48t{x^3}+ 4{x^4}- 84{t^3}+108{t^2}x- 36t{x^2}+ 4{x^3} - 63{t^2} + 24tx + 33t \nonumber \\&\quad - 3x + 4i{t^8} + 24i{t^7}- 8i{t^6}x+ 4i{t^6}+ 180i{t^5}- 204i{t^4}x+ 72i{t^3}{x^2}\nonumber \\&\quad - 8i{t^2}{x^3} - 420i{t^4} + 504i{t^3}x- 228i{t^2}{x^2}+ 48it{x^3} - 4i{x^4} + 132i{t^3}\nonumber \\&\quad - 108i{t^2}x + 36it{x^2}- 4i{x^3} + 81i{t^2} - 24itx- 33it + 3ix ),\nonumber \\ {g_1}[1]&= \frac{2}{3}\frac{1}{{2{t^4} + 18{t^2} - 12tx + 2{x^2} - 6t + 2x + 1}}{e^{ - \frac{1}{2}it(t + 3)}}(- 4{t^8}+ 24{t^7}- 8{t^6}x \nonumber \\&\quad - 12{t^6} + 180{t^5} - 204{t^4}x+ 72{t^3}{x^2}- 8{t^2}{x^3} + 216{t^4}- 360{t^3}x + 204{t^2}{x^2}\nonumber \\&\quad - 48t{x^3}+ 4{x^4}- 300{t^3} + 324{t^2}x - 108t{x^2}+ 12{x^3}+ 33{t^2} - 48tx + 12{x^2}\nonumber \\&\quad - 27t + 9x + 3+ 4i{t^8} + 24i{t^7}- 8i{t^6}x - 12i{t^6}+ 252i{t^5} - 228i{t^4}x \nonumber \\&\quad + 72i{t^3}{x^2}- 8i{t^2}{x^3}- 432i{t^4} + 504i{t^3}x - 228i{t^2}{x^2}+ 48it{x^3} - 4i{x^4}\nonumber \\&\quad + 348i{t^3}- 324i{t^2}x + 108it{x^2} - 12i{x^3} - 39i{t^2}+ 48itx- 12i{x^2} + 27it \nonumber \\&\quad - 9ix - 3i ). \end{aligned}$$

(57)

From Eqs. (54) and (55), the one-rouge wave solution and two-rogue wave solution of $\alpha =t, \beta = 0.5, \gamma = 2,\delta =3$ are obtained.

Then we will discuss the evolutions of the rogue wave solutions and show the relationship between rogue waves and the group dispersion velocity $\alpha$, third order dispersion $\beta$ and the amplification or absorption coefficient $\delta$. In Figs. 8, 9 and 10, (a) and (b) represent three- and two- dimensional plots of one-rogue wave solution depicted by Eq. (54) respectively. (c) and (d) represent three- and two- dimensional plots of two-rogue wave solution depicted by Eq. (55) respectively. Figure 11 show the evolutions of one-rogue wave solution with different values of $\alpha ,\beta$.

Fig. 8

Parameters are $\alpha =t, \beta = 0.5, \gamma = 2,\delta =3$ in Eqs. (54) and (55)

Fig. 9

Parameters are $\alpha = 1, \beta = t, \gamma = 2,\delta = 3$ in Eqs. (54) and (55)

Fig. 10

Parameters are $\alpha = 1, \beta = 0.5, \gamma = 2,\delta = t$ in Eqs. (54) and (55)

Fig. 11

Evolutions of the one-rogue wave solution represented by Eq. (54) with $\gamma = 2,\delta =3$

In Figs. 8, 9 and 10, we take the group dispersion velocity coefficient $\alpha$, third order dispersion coefficient$\beta$, amplification or absorption coefficient $\delta$ as t respectively, and observe the evolutions of the rogue wave solutions. In Fig. 11a, b, the one-rogue wave increases in amplitude and rotates counterclockwise as the third-order dispersion coefficient $\beta$ increases. In Fig. 11a, c, the shape and width of the one-rogue wave change as the group dispersion velocity coefficient $\alpha$ take different functions.

Conclusion

In summary, we have studied the generalized variable coefficients Hirota equation Eq. (1) and derived its Lax pair and DTs. Specifically, we have constructed a classical DT and got multisoliton solutions. Furthermore, rogue wave solutions also have been proposed explicitly by generalized DT. Finally, we have analyzed the dynamical features of these exact solutions. We believe that the results could be valuable in solving the inhomogeneity problems in optical fibers and plasma.