1 Introduction

An optimization problem refers to a problem with multiple possible solutions, and the process of selecting the optimal solution among these options is known as optimization [1]. An optimization problem consists of decision variables, constraints, and an objective function [2, 3]. Advances in science and technology have led to more complicated and emerging optimization difficulties that require the use of relevant tools. There are two types of strategies for addressing optimization problems: deterministic and stochastic [4, 5]. Deterministic approaches, categorized as gradient-based and non-gradient-based, excel in solving linear, convex, and basic optimization problems. However, these approaches are ineffective for complicated, non-differentiable, nonlinear, non-convex, and NP-hard problems. These are the primary characteristics of optimization problems in real-life applications. Due to the limitations of deterministic methods, researchers have developed stochastic approaches like meta-heuristic algorithms [6]. Meta-heuristic algorithms are widely regarded as the most effective optimization algorithms due to their robustness, performance reliability, simplicity, and ease of implementation. Meta-heuristic algorithms are categorized into literary categories, like: (1) Evolutionary-based algorithms are based on evolutionary theory. (2) Swarm-based algorithms mimic the social behavior and decision-making of different groups. These algorithms rely on bio-community information and collaborative action to achieve certain goals. (3) Physics-based algorithms are influenced by natural physical principles. (4) Human behavior-based algorithms are inspired by human social behavior. (5) Hybrid and advanced algorithms use features from multiple optimization strategies to improve outcomes. Tables 1 and 2 show the classification of meta-heuristic algorithms in the literature.

Table 1 Classification of meta-heuristic algorithms
Full size table
Table 2 Classification of meta-heuristic algorithms
Full size table

The GWO algorithm is a meta-heuristic based on the hunting behavior and leadership hierarchy of grey wolves. It has been used to optimize key values in cryptography algorithms [70], time forecasting [71], feature subset selection [72], economic dispatch problems [73], optimal power flow problems [74], optimal design of double later grids [75], and flow shop scheduling problems [76]. Several algorithms have been developed to improve the convergence performance of the GWO algorithm, including binary GWO algorithm [77], parallelized GWO algorithm [78, 79], hybrid DE algorithm with GWO algorithm [80], hybrid GA algorithm with GWO algorithm [81], hybrid GWO algorithm using Elite Opposition Based Learning strategy and simplex method [82], Mean Grey Wolf Optimizer Algorithm (MGWOA) [83], integration of DE algorithm with GWO algorithm [84], and hybrid PSO algorithm with GWO algorithm [85]. The optimization problems have been simplified and solved using linear or integer programming techniques. Existing fuzzy and intuitionistic fuzzy optimization methods, such as FMODI, IFMODI, IFMZMCM, FHM, IFHM, and IFRM, can be complicated due to their numerous steps. Usually, fuzzy and intuitionistic fuzzy optimization problems are 1st translated to equivalent crisp optimization problems. Then second, to solve TORA software, crisp optimization problems are transformed into equivalent linear programming problems. It uses branch and bound methods to solve problems. The use of fuzzy and intuitionistic fuzzy sets to solve optimization problems has been in the literature [86,87,88,89,90,91]. The methodology of estimating theory, statistical learning, and data mining is known as multivariate adaptive regression splines (MARS) [92]. Nowadays it is used in many different domains including science, technology, management, and economics [93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118]. Non-parametric regression analysis such as MARS does not require certain preconditions on the functional relationships between the explanatory and involved response variables. Since it automatically models interactions and non-linearities, it can be considered an extension of linear models [119]. MARS is unable to completely handle variable uncertainty despite all of its accomplishments.

Some of the issues/challenges in the existing literature. A fundamental challenge is that achieving global optimum value requires sluggish convergence and considerable computing overhead. A lot of algorithms lack a proper balance between exploration and exploitation abilities. A few algorithms converge prematurely to the local optimum, making them unsuitable for real-life engineering problems. Another drawback is that the algorithm has a large number of algorithm-specific parameters, and picking optimum values requires a high computing load.

The main research question in the study of meta-heuristic algorithms is whether there is still a need to propose new approaches despite the abundance of optimization algorithms created. In answer to this difficulty, the No Free Lunch (NFL) theorem [120] says that an algorithm’s strong performance in dealing with a set of optimization problems does not ensure the same performance in other optimization problems. Therefore, claiming that an algorithm is optimal for all optimization applications is inaccurate. The NFL theorem encourages authors to propose innovative algorithms to solve optimization problems.

In this paper, a Modified Grey Wolf Optimization Algorithm (MGWO) is proposed by modifying the position update equation of the original GWO algorithm. The leadership hierarchy is simulated using four different types of grey wolves: lambda (\(\lambda\)), mu (\(\mu\)), nu (\(\nu\)), and xi (\(\xi\)). The MGWO algorithm addresses the shortcomings of leading wolves in GWO by enhancing their performance. The performance of the proposed algorithm has been evaluated on 23 benchmark functions, and the results were compared to popular meta-heuristic algorithms. MGWO is applied to three real-life engineering problems, and the results were compared to popular meta-heuristic algorithms.

The paper is organized as follows: Sect. 2 provides a brief introduction to the GWO algorithm. In Sect. 3 modified version of GWO named MGWO has been proposed. Results and discussion on CEC 2005 benchmark functions have been presented in Sect. 4. In Sect. 5 MGWO for solving real-life engineering problems are presented. Finally, in Sect. 6 we conclude the paper and suggest future works.

2 Grey wolf optimization algorithm (GWO)

The GWO algorithm is inspired by the hierarchy and hunting behavior of grey wolf groups. The method optimizes grey wolf populations by mathematically replicating the tracking, surrounding, hunting, and attacking processes. The grey wolf hunting procedure consists of three steps: social hierarchy stratification, encircling the prey, and attacking the prey.

2.1 Social hierarchy

Grey wolves are gregarious canids that live at the top of the food chain and have a tight social dominance structure. The best solution is indicated as the lambda (\(\lambda\)); the second-best solutions are marked as the mu (\(\mu\)); the third-best solutions are marked as the nu (\(\nu\)); and the other solutions are marked as xi (\(\xi\)). Figure 1 illustrates its dominating social hierarchy.

Fig. 1
figure 1

Hierarchy of wolves

Full size image

2.2 Encircling the prey of GWO

The wolves encircling approach around the prey is mathematically represented by the following equations:

$$\begin{aligned} Z (t+1)= & {} Z _{p}(t)- L \times D , \end{aligned}$$
(1)
$$\begin{aligned} D= & {} \ \mid N \times Z _{p}(t) - Z (t) \mid , \end{aligned}$$
(2)

where \(Z\) is the grey wolf’s position vector, \(Z _{p}\) represents the position vectors of the prey, t represents the current iteration, and \(L\) and \(N\) are coefficient vectors.

The vectors \(L\) and \(N\) are calculated as follows:

$$\begin{aligned} L= & {} 2 *r_{1} \times b - b , \end{aligned}$$
(3)
$$\begin{aligned} N= & {} 2 \times r_{2}, \end{aligned}$$
(4)

where \(b\) components are linearly decreasing from 2 to 0 over iterations and \(r_{1}\), \(r_{2}\) are random vectors in [0, 1].

2.3 Attacking the prey of GWO

Grey wolves can recognize possible prey locations, and the search is primarily carried out with the assistance of \(\lambda\), \(\mu\), and \(\nu\) wolves. The best three wolves (\(\lambda\), \(\mu\), and \(\nu\)) in the current population are preserved in each iteration, while the positions of other search agents are updated based on their position information. The following formulas are provided in this regard:

$$\begin{aligned} Z _{1}= & {} Z _{\lambda }- L _{1} \times D _{\lambda },\ Z _{2}= Z _{\mu }- L _{2} \times D _{\mu },\ Z _{3}= Z _{\nu }- L _{3} \times D _{\nu }, \end{aligned}$$
(5)
$$\begin{aligned} D _{\lambda }= & {} \ \mid N _{1} \times Z _{\lambda }- Z \mid ,\ D _{\mu }= \ \mid N _{2} \times Z _{\mu }- Z \mid ,\ D _{\nu }= \ \mid N _{3} \times Z _{\nu }- Z \mid , \end{aligned}$$
(6)
$$\begin{aligned} Z (t+1)= & {} \frac{ Z _{1}+ Z _{2}+ Z _{3}}{3}, \end{aligned}$$
(7)
Fig. 2
figure 2

Position updating in the gray wolf optimization (GWO)

Full size image

In the above equation, \(Z _{\lambda }\), \(Z _{\mu }\), and \(Z _{\nu }\) are the position vectors of \(\lambda\), \(\mu\), and \(\nu\) wolves, respectively; the calculations of \(L _{1}\), \(L _{2}\), and \(L _{3}\) are similar to \(L\), while the calculations of \(N _{1}\), \(N _{2}\), and \(N _{3}\) are similar to \(N\). The distance between the current candidate wolves and the best three wolves is represented by \(D _{\lambda }\), \(D _{\mu }\), and \(D _{\nu }\).

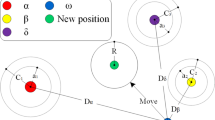
Figure 2 shows that the candidate solution eventually falls within the random circle formed by \(\lambda\), \(\mu\), and \(\nu\). The other contenders then update their locations near the prey at random, guided by the current best three wolves. They begin searching for prey position information in a disorganized way before focusing on assaulting the prey.

3 A modified grey wolf optimization algorithm (MGWO)

A Modified Grey Wolf Optimization Algorithm (MGWO) was inspired by the GWO algorithm, which is already discussed in Sect. 2. Then the mathematical form of the MGWO algorithm is provided as follows:

3.1 Encircling the prey of MGWO

The wolves’ encircling approach around the prey is mathematically described by providing the following equations as

$$\begin{aligned} Z ^{\prime }(t+1)= & {} Z ^{\prime }_{p}(t)- L ^{\prime } \times D ^{\prime }, \end{aligned}$$
(8)
$$\begin{aligned} L ^{\prime }= & {} 2 \times r_{1} \times b ^{\prime } - b ^{\prime }, \end{aligned}$$
(9)

where \(Z ^{\prime }\) is the grey wolf’s position vector, \(Z ^{\prime }_{p}\) represents the position vectors of the prey, t represents the current iteration, \(L ^{\prime }\) is coefficient vector, \(b ^{\prime }\) components are linearly decreasing from 2 to 0 over iterations and \(r_{1}\) is random vectors in [0, 1].

$$\begin{aligned} D ^{\prime }= & {} \ \mid N ^{\prime } \times Z ^{\prime }_{p}(t) - Z ^{\prime }(t) \mid , \end{aligned}$$
(10)
$$\begin{aligned} N ^{\prime }= & {} 2 \times r_{2}, \end{aligned}$$
(11)

where \(N ^{\prime }\) is coefficient vector, \(b ^{\prime }\) components are linearly decreasing from 2 to 0 over iterations and \(r_{2}\) is random vectors in [0, 1].

3.2 Attacking the prey of MGWO

Grey wolf attacking technique can be mathematically described by approximating the prey position using \(\lambda\), \(\mu\), and \(\nu\) solutions (wolves). As a result, by using this estimate, each wolf can update their positions by

$$\begin{aligned} Z ^{\prime }(t+1)= \frac{2}{3} Z ^{\prime }_{1}+\frac{1}{4} Z ^{\prime }_{2}+\frac{1}{12} Z ^{\prime }_{3}, \end{aligned}$$
(12)

where \(Z ^{\prime }_{1}\), \(Z ^{\prime }_{2}\), and \(Z ^{\prime }_{3}\) are calculated by using Eq. 13.

$$\begin{aligned} Z ^{\prime }_{1}= Z ^{\prime }_{\lambda }- L ^{\prime }_{1} \times D ^{\prime }_{\lambda },\ Z ^{\prime }_{2}= Z ^{\prime }_{\mu }- L ^{\prime }_{2} \times D ^{\prime }_{\mu },\ Z ^{\prime }_{3}= Z ^{\prime }_{\nu }- L ^{\prime }_{3} \times D ^{\prime }_{\nu }, \end{aligned}$$
(13)

where \(L ^{\prime }_{1}\), \(L ^{\prime }_{2}\), \(L ^{\prime }_{3}\), \(D ^{\prime }_{\lambda }\), \(D ^{\prime }_{\mu }\), and \(D ^{\prime }_{\nu }\) are calculated by using Eq. 14 and 15.

$$\begin{aligned} L ^{\prime }_{1}= & {} 2 \times r^{\prime }_{1} \times b ^{\prime } - b ^{\prime },\ L ^{\prime }_{2}=2 \times r^{\prime }_{2} \times b ^{\prime } - b ^{\prime },\ L ^{\prime }_{3}=2 \times r^{\prime }_{3} \times b ^{\prime } - b ^{\prime }, \end{aligned}$$
(14)
$$\begin{aligned} D ^{\prime }_{\lambda }= & {} \ \mid N ^{\prime }_{1} \times Z ^{\prime }_{\lambda }- Z ^{\prime } \mid ,\ D ^{\prime }_{\mu }= \ \mid N ^{\prime }_{2} \times Z ^{\prime }_{\mu }- Z ^{\prime } \mid ,\ D ^{\prime }_{\nu }= \ \mid N ^{\prime }_{3} \times Z ^{\prime }_{\nu }- Z ^{\prime } \mid , \end{aligned}$$
(15)

where \(N ^{\prime }_{1}\), \(N ^{\prime }_{2}\), and \(N ^{\prime }_{3}\) are calculated by using Eq. 16.

$$\begin{aligned} N ^{\prime }_{1}=2 \times r^{\prime \prime }_{1},\ N ^{\prime }_{2}=2 \times r^{\prime \prime }_{2},\ N ^{\prime }_{3}=2 \times r^{\prime \prime }_{3}, \end{aligned}$$
(16)

The candidate solution eventually falls within the random circle formed by \(\lambda\), \(\mu\), and \(\nu\). The other contenders then update their locations near the prey at random, guided by the current best three wolves. They begin searching for prey position information in a disorganized way before focusing on assaulting the prey. The pseudo code of the MGWO algorithm is presented in Algorithm 1. The flowchart of the MGWO is given in Fig. 3.

Fig. 3
figure 3

Flowchart of MGWO

Full size image
Algorithm 1
figure a

Pseudo-code of the MGWO algorithm.

Full size image

3.3 Computational complexity

The computational complexity of the proposed MGWO algorithm depends on three main processes: initialization, evaluation of the fitness function, and updating each particle. The computational complexity of the basic process with a n particle is O(n), and updating the MGWO mechanism is equal to \(O(M \times n)+O (M \times n \times D)\), where M signifies the maximum number of iterations and D signifies the dimension of the problems. Therefore, the total computational complexity of the proposed MGWO is equals \(O(n\times (M+M \times D+1))\).

4 Results and discussion

In this section, to analyze the performance of the MGWO algorithm, seven uni-modal test functions, six multi-modal optimization functions, and 10 fixed-dimensional multi-modal optimization functions are selected. Table 4 lists these functions’ precise expressions, dimensions, search space, and optimal values. The uni-modal test functions are represented by F1–F7, the multi-modal test functions by F8–F13, and the fixed dimensional multi-modal test functions by F14–F23. The uni-modal test function is primarily used to calculate the MGWO’s convergence speed and accuracy of the solution. The primary purpose of the multi-modal test function is to gauge the MGWO’s global surveying capability. To increase the experiment’s accuracy, the six chosen algorithms use identical experimental parameters: swarm size (n = 30), dimension (D = 30), maximum number of iterations (M = 1000), each algorithm is run 30 times independently and the results are recorded. The values set for the control parameters of the competitor algorithms are given in Table 3. The experiments are performed on Windows 11, Intel Core i3, 2.10GHz, 8.00 GB RAM, MATLAB R2022b (Table 4).

Table 3 The values set for the control parameters of the competitor algorithms
Full size table
Table 4 Twenty-three test functions
Full size table

4.1 Sensitivity analysis

The proposed MGWO algorithm employs two parameters, i.e., the number of grey wolves and the maximum number of iterations.

4.2 Number of grey wolves

The MGWO algorithm was simulated for different values of grey wolf (i.e., 10, 15, 20, 25, 30). Figure 4 shows the variations of different numbers of search agents on benchmark test functions. Figure 4 shows that the value of the fitness function reduces as the number of search agents rises.

Fig. 4
figure 4

Sensitivity analysis of the proposed MGWO algorithm for the number of grey wolves

Full size image

4.3 Maximum number of iterations

The MGWO algorithm was run for different numbers of iterations. The values of Maximum iteration used in experimentation are 200, 400, 600, 800, and 1000. Figure 5 demonstrates the impact of the number of iterations on benchmark test functions. As the number of iterations increases, the MGWO algorithm converges to the optimum.

Fig. 5
figure 5

Sensitivity analysis of the proposed MGWO algorithm for the number of iterations

Full size image

4.4 In comparison to other algorithms

To further evaluate the performance of the MGWO, the MGWO algorithm was tested on 23 benchmark functions, and the results were compared with the PSO [15], TSA [20], SSA [121], MVO [39], GWO [16], and IGWO [122] algorithms. Each algorithm is evaluated using the average values and standard deviation after 30 runs, the solution with the highest accuracy is bolded in the table. Tables 5 and 6 displays the results of the 23 test functions. The MGWO’s convergence accuracy and optimization capacity can be seen in the average values and standard deviation shown in Tables 5 and 6. When solving the F1–F5 and F7 functions for the seven uni-modal functions, the MGWO performs better in terms of accuracy and standard deviation, even though the optimization accuracy falls short of the theoretically ideal value of 0. When solving the F9 and F11 functions, the optimization accuracy for the six multi-modal functions reaches the theoretical optimal value of 0, and the algorithm’s great robustness and precision of the solution are clearly demonstrated. Meanwhile, when solving the F8 and F10 functions, the MGWO also yields a better result when compared to other optimization techniques. When it comes to the ten fixed dimensional multi-modal functions, F14, F15, and F20–F23 outperforms other algorithms in terms of value, while the remaining functions’ outcomes mostly agree with the contrast algorithm’s.

Table 5 The results of the 23 test functions are mentioned in bold; these results are the global best solutions
Full size table
Table 6 The results of the 23 test functions are mentioned in bold; these results are the global best solutions
Full size table
Table 7 Results of Wilcoxon rank-sum test and t-test on 23 benchmark functions
Full size table
Table 8 Validation of Wilcoxon rank-sum test and t-test on 23 benchmark functions
Full size table

4.5 Statistical analysis

This subsection presents a statistical analysis of the performance of competitor algorithms and MGWO to establish whether or not MGWO has a statistically significant advantage. The Wilcoxon rank sum test [123] is utilized to ascertain the statistically significant difference between the average of two data samples. Using an index defined as a p-value, the Wilcoxon rank sum test is used to establish whether or not the statistical advantage of MGWO over any of the competing algorithms is significant. Two-tailed t-tests [124] have been used to compare different statistical outcomes at a consequence of 0.05. The t values are determined with the help of average and std values. A -t value indicates that the statistical outcomes of the MGWO optimization mistakes are significantly less, and vice versa. The corresponding t value is highlighted if the difference is a statistically significant error. The symbols \(+/=/-\) represent that MGWO wins functions, ties functions, and loses functions. The statistical outcomes of the optimization mistakes demonstrate that MGWO has much superior total achievement when compared with the other algorithms. Tables 7 and 8 present results of the Wilcoxon rank-sum test and t-test on 23 benchmark functions and validation of the Wilcoxon rank-sum test and t-test on 23 benchmark functions comparing the performance of competing algorithms with MGWO. MGWO outperforms the corresponding algorithm statistically in situations where the p-value and t-value are less than 0.05, according to these data.

4.6 Convergence analysis

Figures 6, 7, and 8 displays the convergence graph of MGWO and other algorithms. As illustrated in Figs. 6, 7, and 8 the suggested method in uni-modal functions adheres to a certain pattern that prioritizes the exploitation stage (functions F1 and F3). The proposed method exhibits a distinct pattern in multi-modal functions with numerous local optimal values. It gives more consideration to the early algorithmic stages of the exploration process. Nevertheless, exploration is carried out in broken form (functions F12 and F13) during the algorithm’s final stages, which are often the exploitation phase. The suggested algorithm offers a superior pattern of convergence for almost all functions.

Fig. 6
figure 6

Convergence graph of MGWO and other algorithms

Full size image
Fig. 7
figure 7

Convergence graph of MGWO and other algorithms

Full size image
Fig. 8
figure 8

Convergence graph of MGWO and other algorithms

Full size image

5 MGWO for solving real-life engineering problems

This section evaluates the proposed algorithm performance in three real-life engineering problems using constrained engineering benchmarks. The tension/compression spring, the gear train, and the three-bar truss are all part of the engineering design problems. The MGWO runs independently for each engineering problem 30 times, with a selected grey wolf population size of 30, with 1000 iterations, and a number of function evaluations (NFEs) of 15,000.

5.1 Tension/compression spring design problem

This problem aims to optimize the weight of a tension/compression spring [125], as shown in Fig. 9. The problem has constraints on minimum deflection, shear stress, surge frequency, outside diameter limits, and design variables. The design variables are the mean coil diameter D, the wire diameter d, and the number of active coils N. Table 9 presents the outcomes of this experiment. The MGWO algorithm outperformed other algorithms in this problem.

Fig. 9
figure 9

The design of the tension/compression spring problem

Full size image
Table 9 The comparison outcomes of the tension/compression spring problem
Full size table

5.2 Gear train design problem

Sandgren presented the gear train design problem [126, 127], an unconstrained discrete problem in mechanical engineering. This benchmark task aims to minimize the gear ratio, which is the ratio of the angular velocity of the output shaft to the input shaft. The number of teeth of gears \({\mathcal {C}}_{1}\), \({\mathcal {C}}_{2}\), \({\mathcal {C}}_{3}\), and \({\mathcal {C}}_{4}\) are considered as the design variables, as shown in Fig. 10. Table 10 presents the outcomes of this experiment. The MGWO algorithm outperformed other algorithms in this problem.

Fig. 10
figure 10

The design of the gear train problem

Full size image
Table 10 The comparison outcomes of the gear train problem
Full size table

5.3 Three-bar truss design problem

This optimization problem from civil engineering has a confined and troublesome space [128]. The primary goal of this challenge is to reduce the weight of bar constructions. The restrictions for this problem are determined by the stress constraints of each bar. The resulting problem contains a non-linear objective function and three non-linear constraints, as shown in Fig. 11. The results are presented in Table 11 The proposed method successfully identified the optimal value for the problem.

Fig. 11
figure 11

The design of the three-bar truss problem

Full size image
Table 11 The comparison outcomes of the three-bar truss problem
Full size table

6 Conclusion

The original GWO algorithm has premature convergence and poor accuracy while solving global optimization problems. In this study, a modified GWO is proposed to overcome the shortcomings. The MGWO algorithm is proposed by modifying the position update equation of the original GWO algorithm. We investigated 23 functions with various features, including uni-modal, multi-modal, and fixed-dimensional multi-modal, and compared the outcomes to six algorithms. The experimental results indicate that the MGWO algorithm outperforms compare with six different algorithms in terms of optimization performance and stability. Then three real-life engineering optimization design problems (tension/compression spring, gear train, and three-bar truss) are solved using various objective functions, constraint conditions, and features. Meanwhile, the Wilcoxon rank-sum test and t-test were used to evaluate the results of the MGWO algorithm. The experimental results demonstrate that the MGWO algorithm outperforms other comparison algorithms and is capable of dealing with engineering design problems. However, the proposed MGWO algorithm has shown insignificant and mediocre results for one uni-modal (F6) and two multi-modal (F12 and F13) functions. In future work, the MGWO suggests several improvements, such as the inclusion of adaptive inertia factors, image segmentation, feature selection, levy flight distribution, binary, and multi-objective problems.