1 Introduction

Meta-heuristic algorithms play an important role in solving complex problems in different applications due to their simple structure and easy implementation (Manna et al. 2021; Kumar et al. 2021), such as chip design (Venkataraman et al. 2020), diseases diagnosis (Arjenaki et al. 2015), production inventory problem (Das et al. 2021; Manna and Bhunia 2022), feature selection (Hu et al. 2021), and path planning (Qu et al. 2020). Many nature-inspired algorithms have been proposed by simulating the swarm intelligence behavior of various biological systems in nature, such as particle swarm optimization (PSO) (Eberhart and Kennedy 1995), fruit fly optimization algorithm (FOA) (Wang et al. 2013), whale optimization algorithm (WOA) (Mirjalili and Lewis 2016), butterfly optimization algorithm (BOA) (Arora and Singh 2019), conscious neighborhood-based crow search algorithm (CCSA) (Zamani et al. 2019), sparrow search algorithm (SSA) (Xue and Shen 2020), slime mold algorithm (SMA) (Li et al. 2020), etc.

Grey wolf optimizer (GWO) (Mirjalili et al. 2014) is a relatively novel meta-heuristic inspired by the hunting behavior of grey wolf pack and is the only swarm intelligence algorithm based on leadership hierarchy (Luo and Zhao 2019). Due to its excellent optimization performance, GWO has been increasingly focused and successfully applied to many practical engineering problems. Zhang et al. (2016) used GWO to solve the unmanned combat aerial vehicle two-dimension path planning problem. Hadavandi et al. (2018) hybridized GWO and neural network to achieve the prediction of yarns tensile strength. Samuel et al. (2020) combined empirical method and GWO to optimize the extraction process of biodiesel from waste oil. Sundaramurthy and Jayavel (2020) hybridized GWO and PSO with C4.5 approach to realize the prediction of rheumatoid arthritis. Kalemci et al. (2020) designed a reinforced concrete cantilever retaining wall using GWO algorithm. Karasu and Saraç (2020) classified the power quality disturbances by combining GWO and k-Nearest Neighbor (KNN). Saxena et al. (2020) utilized GWO to solve the problem of harmonic estimation in power networks. Zareie et al. (2020) developed a GWO-based method to identify the influential users in viral marketing and achieved the best results so far. Naserbegi and Aghaie (2021) applied GWO to optimize the exergy of nuclear-solar dual proposed power plant.

However, the “no free lunch” theorem (Wolpert and Macready 1997) has logically demonstrated that no meta-heuristic can perfectly handle all optimization problems. For example, GWO is prone to get stuck at local optimum when dealing with complex multimodal problems (Long et al. 2018a). Therefore, several variants of GWO have been developed. Rodríguez et al. (2017) introduced a fuzzy operator in GWO algorithm to optimize the leadership hierarchy of grey wolves. Long et al. (2017) added a modulation index into GWO algorithm to balance the exploration and exploitation. Tawhid and Ali (2017) embedded genetic mutation operator in GWO to avoid premature convergence. Gupta and Deep (2020) optimized the search mechanism of GWO algorithm by applying crossover and greedy selection. Adhikary and Acharyya (2022) introduced random walk with student’s t distribution into GWO to balance the exploration and exploitation. Mohakud and Dash (2022) proposed a neighborhood based searching strategy that integrates individual haunting strategies and global haunting strategies to balance the exploration and exploitation of GWO.

The above researches indicate that increasing population diversity and balancing exploration and exploitation are an effective approach to improve the performance of GWO. For this purpose, this paper proposed a modified GWO called information entropy-based GWO (IEGWO). In the IEGWO, an initial population generation method based on information entropy is proposed to optimize the distribution of initial grey wolf pack, a dynamic position update mechanism based on information entropy is introduced to maintain the population diversity in the process of iteration, and a nonlinear convergence factor strategy is proposed to balance the exploration and exploitation. The proposed IEGWO algorithm is tested on 10 well-known benchmark functions to analyze the influence of information entropy and nonlinear strategy. The performance of IEGWO is tested and compared with other GWO variants on CEC2014 (Liang et al. 2013) and CEC2017 (Awad et al. 2016) problems. In this paper, the IEGWO is also applied to solve two engineering design problems and to optimize the model parameters in the field of hyperspectral imaging.

The rest of this paper is structured as follows. The next section introduces the original GWO. In Sect. 3 we present the proposed IEGWO in detail. In Sect. 4, the IEGWO is tested by 10 well-known benchmark functions, CEC2014 and CEC2017. In Sect. 5, results on two engineering optimization problems and one practical problem are presented. The last section concludes this paper and provides some ideas for future study.

2 Grey wolf optimizer

The GWO algorithm (Mirjalili et al. 2014) mimics the social leadership and hunting behavior of the grey wolf pack. In this algorithm, the wolves are divided into two parts, one is dominant wolf pack, and the other wolves are named as ω. The dominant wolf pack includes α, β and δ wolves, representing the optimal solution, suboptimal solution, and the third optimal solution, respectively.

To mimic the hunting behavior, the following motion equations are used:

$$ \vec{D} = |\vec{C} \cdot \vec{X}_{P} (t) - \vec{X}(t)| $$
(1)
$$ \vec{X}(t + 1) = \vec{X}_{P} (t) - \vec{A} \cdot \vec{D} $$
(2)

where t represents the current iteration; \(\vec{X}_{P}\) and \(\vec{X}\) are the position vectors of the prey and a grey wolf, respectively; \(\vec{A}\) and \(\vec{C}\) denote the coefficient vectors, which can be calculated as follows:

$$ \vec{A} = 2\vec{a} \cdot \vec{r}_{1} - \vec{a} $$
(3)
$$ \vec{C} = 2 \cdot \vec{r}_{2} $$
(4)

where \(\vec{r}_{1}\) and \(\vec{r}_{2}\) denote random vectors between 0 and 1; \(\vec{a}\) is the convergence factor linearly decreased from 2 to 0 as follows:

$$ \vec{a}(t) = 2 - \frac{2t}{m} $$
(5)

where m indicates the maximum number of iterations.

Figure 1 shows the movement mechanism of GWO, where the red, yellow, purple and blue circles represent α, β, δ and ω wolves, respectively. In this process, the ω wolves move to the center of α, β and δ wolves by applying the following formulas:

$$ \vec{D}_{\alpha } = |\vec{C}_{1} \cdot \vec{X}_{\alpha } - \vec{X}|,_{{}} \vec{D}_{\beta } = |\vec{C}_{2} \cdot \vec{X}_{\beta } - \vec{X}|,_{{}} \vec{D}_{\delta } = |\vec{C}_{3} \cdot \vec{X}_{\delta } - \vec{X}| $$
(6)
$$ \vec{X}_{1} = \vec{X}_{\alpha } - \vec{A}_{1} \cdot \vec{D}_{\alpha } ,_{{}} \vec{X}_{2} = \vec{X}_{\beta } - \vec{A}_{2} \cdot \vec{D}_{\beta } ,_{{}} \vec{X}_{3} = \vec{X}_{\delta } - \vec{A}_{3} \cdot \vec{D}_{\delta } $$
(7)
$$ \vec{X}(t + 1) = \frac{{\vec{X}_{1} + \vec{X}_{2} + \vec{X}_{3} }}{3} $$
(8)

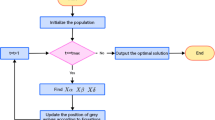
where \(\vec{A}_{1}\), \(\vec{A}_{2}\) and \(\vec{A}_{3}\) are the same as \(\vec{A}\), \(\vec{C}_{1}\), \(\vec{C}_{2}\) and \(\vec{C}_{3}\) are the same as \(\vec{C}\). Figure 2 presents the pseudocode of GWO algorithm.

Fig. 1
figure 1

Evolution of position in GWO

Full size image
Fig. 2
figure 2

Pseudocode of GWO algorithm

Full size image

3 Information entropy-based grey wolf optimizer

The theorem of entropy was originally proposed by Shannon (1948) to describe the complexity of spatial energy distribution, which plays a fundamental and important role in the field of modern information theory. The formula of information entropy is as follows (Feng et al. 2022):

$$ H(p_{1} ,p_{2} , \ldots p_{n} ) = - \sum\limits_{i = 1}^{n} {p_{i} (x)\log_{2} p_{i} (x)} $$
(9)

where n is the number of information records in a system and pi(x) is the probability of the ith record. For meta-heuristic algorithms, the information entropy can also be used to reflect the diversity of population. Inspired by this idea, the information entropy is introduced into GWO to increase the population diversity in the process of generating initial population and updating position. Besides, a nonlinear convergence factor \(\vec{a}\) is proposed to balance the exploration and exploitation.

3.1 Initial population generation based on information entropy

In the original GWO, the initial population is generated by random sampling. However, in practical application, it is inevitable that some grey wolves may be overly concentrated in a local area, resulting in a restricted search range. To optimize the distribution of initial population in the solution space, an information entropy-based sampling method was proposed. Suppose that there is a population with group size of N and dimension of D, the entropy Hj of the jth dimension can be defined by:

$$ \begin{aligned} H_{j} & = \sum\limits_{i = 1}^{N - 1} {\frac{1}{N - 1}\sum\limits_{k = i + 1}^{N} {\frac{{ - P_{ik} \log_{2} P_{ik} - (1 - P_{ik} )\log_{2} (1 - P_{ik} )}}{N - i}} } \\ P_{ik} & = 1 - \frac{{|x_{{_{j} }}^{i} - x_{j}^{k} |}}{{2(ub_{j} - lb_{j} )}} \\ \end{aligned} $$
(10)

where ubj and lbj denote the upper and lower limits of the jth dimension, respectively. The value of Pik describes the similarity probability of the jth dimension between the ith and the kth individuals. The entropy value of the whole population H is defined by:

$$ H = \frac{1}{D}\sum\limits_{j = 1}^{D} {H_{j} } $$
(11)

The process of generating initial population is as follows:

  • Step1: Set a critical value H0 for entropy (for example, H0 = 0.25).

  • Step2: Generate the first individual by random sampling method in the solution space.

  • Step3: Generate a new individual by random sampling. If the entropy value of the population H > H0, the new individual will be retained; otherwise, a new individual will be regenerated until H > H0.

  • Step4: Repeat Step 3 until enough individuals are generated.

3.2 Dynamic position update equation

In the original GWO algorithm, all the ω wolves constantly move to the center of α, β and δ wolves in the process of iteration. As a consequence, GWO is prone to fall into local optimum due to the over learning from the dominant wolf pack and the rapid reduction in population diversity. To maintain the population diversity during the process of updating position and weaken the influence of dominant wolf pack, we modified the position-updating equation as follows:

$$ \begin{aligned} \vec{X}(t + 1) & = w_{1} \vec{X}_{1} + w_{2} \vec{X}_{2} + w_{3} \vec{X}_{3} \\ w_{1} & = \frac{{P_{\omega \alpha } }}{{P_{\omega \alpha } + P_{\omega \beta } + P_{\omega \delta } }},w_{2} = \frac{{P_{\omega \beta } }}{{P_{\omega \alpha } + P_{\omega \beta } + P_{\omega \delta } }},w_{1} = \frac{{P_{\omega \delta } }}{{P_{\omega \alpha } + P_{\omega \beta } + P_{\omega \delta } }} \\ \end{aligned} $$
(12)

where Pωα, Pωβ and Pωδ are the same of Pik in Eq. (10). It can be seen from Eq. (12) that each w wolf updates its position according to its similarity to the dominant wolf pack to avoid over-concentration of wolves. It should be noted that the weights of w1, w2 and w3 are constantly changing in the process of iteration. Thus, it can bring more information and maintain the diversity of population.

3.3 Nonlinear convergence factor \(\vec{a}\)

From the original paper of GWO, the grey wolves attack toward prey when the value |A|< 1 and diverge from prey when the value |A|> 1. Therefore, the exploration and exploitation are balanced by the linear convergence factor \(\vec{a}\) using Eq. (5), and the ratio is 1:1. However, the real search process is highly complex, and the linear strategy is difficult to adapt to it. Based on the above consideration, we proposed a nonlinear convergence factor \(\vec{a}\) as follows:

$$ \vec{a} = \left\{ \begin{gathered} \begin{array}{*{20}l} {2 - 2k + 2k\left[ { - P_{1} \log_{2} P_{1} - (1 - P_{1} )\log_{2} (1 - P_{1} )} \right],P_{1} = \frac{1}{2}\left( {1 + \frac{t}{km}} \right),} \hfill & {0 < t < km} \hfill \\ {2 - 2k,} \hfill & {t = km} \hfill \\ \end{array} \hfill \\ (2 - 2k)\left[ {1 - ( - P_{2} \log_{2} P_{2} - (1 - P_{2} )\log_{2} (1 - P_{2} ))} \right]_{{}} ,P_{2} = \frac{1}{2}\left( {\frac{t - km}{{m - km}}} \right),\;km < t < m \hfill \\ \end{gathered} \right. $$
(13)

where t denotes the current iteration, m indicates the maximum number of iterations and k is the nonlinear modulation parameter in [0, 1]. The iterative curves of convergence factor \(\vec{a}\) with different values of k are shown in Fig. 3.

Fig. 3
figure 3

Iterative curves of nonlinear convergence factor \(\vec{a}\) with different values of k

Full size image

Compared with the original GWO algorithm, the value of \(\vec{a}\) is increased in the early stage to explore more unknown regions and then reduced to narrow the search range in the later stage. In other words, the modification is to enhance the global exploration in the early stage and the local exploitation in the later stage, and the parameter k is used to control the proportion of exploration and exploitation. The ratio of iterations used for exploration and exploitation with different values of k is shown in Table 1.

Table 1 Ratio of exploration and exploitation with different values of k
Full size table

The pseudocode of the proposed IEGWO is presented in Fig. 4. The influence of parameter k to the performance of IEGWO will be discussed in the parameter setting experiment.

Fig. 4
figure 4

Pseudocode of IEGWO algorithm

Full size image

4 Results and discussion

4.1 Comparison with GWO

4.1.1 Benchmark functions and parameter settings

In this section, the impact of information entropy and nonlinear convergence factor on the performance of IEGWO is analyzed by 10 well-known benchmark functions, including 5 unimodal benchmark functions and 5 multimodal benchmark functions. These functions are listed in Table 2, where fmin denotes the theoretical optimal value in search range. The 2-D versions of these functions are shown in Fig. 5.

Table 2 Test functions
Full size table
Fig. 5
figure 5

2-D version of test functions

Full size image

In all experiments, the maximum number of iterations, the population size, and the dimension of test functions were fixed as 500, 30, and 30, respectively. Each algorithm was executed 30 times independently. All programs were coded in MATLAB 2016b and ran on a computer with CPU of AMD Ryzen7 5800U (4.4 GHz) under Windows 10 system.

4.1.2 The impact of information entropy and nonlinear convergence factor

To investigate the impact of information entropy and nonlinear convergence factor, the GWO, IEGWO with original linear convergence factor (IEGWO-L), and IEGWO with different k values were executed on the 10 benchmark functions, and the results are shown in Table 3. The unimodal functions (F1–F5) can be used to evaluate the exploitation performance of algorithms, while the multimodal functions (F6–F10) are utilized to examine the exploration strength and the ability of avoiding local optimum of algorithms. As seen from Table 3, the optimization performance of IEGWO-L outperforms that of GWO on all benchmark functions. Although the improvement in solution accuracy is small on the unimodal functions, it is significant on the multimodal functions, which is because the increase in population diversity improves the ability of the algorithm to jump out of the local optimum. The reduction in standard deviation (Std Dev) indicates that the introduction of information entropy can effectively improve the robustness of GWO. With the increase in k, the performance of IEGWO is evidently improved, and when the value of k is greater than 0.75, the IEGWO outperforms GWO and IEGWO-L obviously. Therefore, for unimodal functions, more exploration helps to improve the optimization accuracy and robustness, while for multimodal functions, the optimization performance of IEGWO increases and then decreases as the proportion of exploration increases, and when the value of k is 0.875, the error of the objective function values reaches the lowest, indicating that the exploration and exploitation are well balanced.

Table 3 Experimental results of GWO and IEGWO
Full size table

4.1.3 Wilcoxon test

In order to statistically assess the performance of GWO and IEGWO, Wilcoxon test at a 5% significance is utilized. The results are recorded in Table 4, where the following rating criteria are applied.

  1. 1.

    A—IEGWO has better performance and p-value ≤ 0.05.

  2. 2.

    B—The performance of the two algorithms is comparable and p-value > 0.05.

  3. 3.

    C—IEGWO has poor performance and p-value ≤ 0.05.

Table 4 Results of Wilcoxon test
Full size table

From Tables 1 and 4, it can be seen that when the exploration ratio is greater than 65.8%, the performance of IEGWO is significantly better than that of GWO. When the exploration ratio reaches 72.2%, all the ratings of IEGWO are A, indicating that more proportion of exploration can effectively improve the optimization performance of IEGWO. However, with the increasing proportion of exploration, the performance of IEGWO on multimodal functions decreases due to the scarcity of exploitation. Therefore, 0.875 is an appropriate value for the parameter k, which provides a good balance between exploitation and exploration.

4.1.4 Computational complexity and running time

The computational complexity is an important index to evaluate the running time of an optimization algorithm, which can be defined based on the structure of the algorithm (Gupta and Deep 2019). The major computational cost of GWO and IEGWO is in the while loop, both equal to O (N × D × T), where N is the population size, D is the dimension of the problem, and T is the maximum number of iterations. Figure 6 shows the total time consumed by GWO and IEGWO to run 30 times on each function. As shown in Fig. 6, the running time of IEGWO is approximately 6% longer than that of GWO, which is mainly due to the fact that some grey wolf individuals need to be regenerated to meet the critical value of information entropy in the process of generating initial population.

Fig. 6
figure 6

Running time of GWO and IEGWO

Full size image

4.1.5 Convergence analysis

The convergence curves of GWO and IEGWO (k = 0.875) are shown in Fig. 7. Due to the expansion of the search range in the early stage, the error in objective function values of IEGWO is larger than that of GWO in some functions (F1–F4, F7). However, the expansion also increases the possibility of finding better solutions by exploring more unknown regions, so the error reduction rate of IEGWO is accelerated in the middle stage. In the late stage of optimization, IEGWO has higher solution accuracy due to the enhancement of local exploitation. From Fig. 7, it can be concluded that the proposed strategies effectively improve the performance of GWO.

Fig. 7
figure 7

Convergence curves of GWO and IEGWO

Full size image

4.1.6 Comparison with other modified GWO algorithms

The previous section shows that IEGWO has better performance than GWO in terms of exploitation and exploration. In this section, the IEGWO is compared with E-GWO (Duarte et al. 2020), IGWO (Long et al. 2018a), EEGWO (Long et al. 2018b), and FH-GWO (Rodríguez et al. 2017) on 30 dimensional CEC2014 and CEC2017 problems based on the average error in objective function value. The parameter setting of the three algorithms is the same as reported in their original papers. The comparison is presented in Tables 5 and 6. For clarity, the best solutions are marked in boldface. Tables 5 and 6 show that the proposed IEGWO has the smallest error in 21 of the 30 functions on CEC 2014 and 18 of the 29 functions on CEC 2017. The outcomes obtained by applying the Wilcoxon test are also recorded in the same tables. Whether for the unimodal, multimodal, and hybrid benchmark problems, the IEGWO provides better results compared to other GWO variants in most of the tested functions. Therefore, it can be concluded that the performance of IEGWO is significantly better than that of the other modified GWO algorithms.

Table 5 Comparison of average error in objective function values on CEC 2014
Full size table
Table 6 Comparison of average error in objective function values on CEC 2017
Full size table

5 Real applications of IEGWO

The proposed IEGWO algorithm is applied to two classical engineering applications: tension/compression spring design and pressure vessel design, which are often used as constrained optimization benchmark problems (Mirjalili et al. 2014). Besides, the IEGWO is also employed to optimize the model parameters in the field of hyperspectral imaging.

5.1 Tension/compression spring design

The aim of the problem is to minimize the weight of a spring with constraints such as minimum deflection, shear stress, and surge frequency. The design variables include wire diameter d(x1), the mean coil diameter D(x2), and the number of active coils N(x3). The mathematical formulation of this problem is stated as follows:

$$ {\text{Minimize}}\quad \quad f(x) = x_{1}^{2} x_{2} (x_{3} + 2) $$
$$ {\text{s.t}}{.}\quad \quad \begin{array}{*{20}l} {g_{1} (x) = \frac{{x_{2}^{3} x_{3} }}{{71785x_{1}^{4} }} + 1 \le 0} \hfill \\ {g_{2} (x) = \frac{{4x_{2}^{2} \;x_{1} x_{2} }}{{12566(x_{1}^{3} x_{2} \;x_{1}^{4} )}} + \frac{1}{{5108x_{1}^{2} }} - 1 \le 0} \hfill \\ {g_{3} (x) = \frac{{140.45x_{1} }}{{x_{2}^{2} x_{3} }} + 1 \le 0} \hfill \\ {g_{4} (x) = \frac{{x_{1} + x_{2} }}{1.5} - 1 \le 0} \hfill \\ \end{array} $$
$$ {\text{Variable range}}\quad \quad 0.05 \le x_{1} \le 2,\;0.25 \le x_{2} \le 1.3,\;2 \le x_{3} \le 15 $$

The GA (Coello and Montes 2002), CPSO (He and Ling 2007), SMA (Li et al. 2020), FH-GWO (Rodríguez et al. 2017), IGWO (Long et al. 2018a), EEGWO (Long et al. 2018b), E-GWO (Duarte et al. 2020), and the proposed IEGWO are applied to solve this problem. The population size and maximum iterations of all algorithms are set to 20 and 1500. The results obtained by conducting 30 runs are shown in Table 7. In the same table, the outcomes of the statistical results obtained by using Wilcoxon test are also recorded. The table verified the better performance of IEGWO compared to other meta-heuristic algorithms.

Table 7 Comparison results of IEGWO and other algorithms for spring design problem
Full size table

5.2 Pressure vessel design

The goal of this problem is to minimize the cost including material, forming and welding of a vessel as shown in Fig. 8. The design variables include shell thickness Ts(x1), head thickness Th(x2), inner radius R(x3), and shell length L(x4). The mathematical formulation of this problem is as follows:

$$ {\text{Minimize}}\quad \quad f(x) = 0.6224x_{1} x_{3} x_{4} + 1.7781x_{2} x_{3}^{2} + 3.1661x_{1}^{2} x_{4} + 19.84x_{1}^{2} x_{3} $$
$$ {\text{s.t}}{.}\quad \quad \begin{array}{*{20}l} {g_{1} (x) = - x_{1} + 0.0193x_{3} \le 0} \hfill \\ {g_{2} (x) = - x_{2} + 0.00954x_{3} \le 0} \hfill \\ {g_{3} (x) = - \pi x_{3}^{2} x_{4} - \tfrac{4}{3}\pi x_{3}^{3} + 1296000 \le 0} \hfill \\ {g_{4} (x) = x_{4} - 240 \le 0} \hfill \\ \end{array} $$
$$ {\text{Variable range}}\quad \quad \begin{array}{*{20}l} {0 \le x_{1} ,\;x_{2} \le 99} \hfill \\ {10 \le x_{3} ,\;x_{4} \le 200} \hfill \\ \end{array} $$
Fig. 8
figure 8

Pressure vessel design problem

Full size image

The proposed IEGWO, GA (Coello and Montes 2002), CPSO (He and Ling 2007), SMA (Li et al. 2020), FH-GWO (Rodríguez et al. 2017), IGWO (Long et al. 2018a), EEGWO (Long et al. 2018b), and E-GWO (Duarte et al. 2020) are applied to solve this problem. The population size and maximum iterations of all algorithms are set to 20 and 2000. The results obtained by conducting 30 runs are shown in Table 8. In the same table, the outcomes of the statistical results obtained by using Wilcoxon test are also recorded. Except for SMA, the performance of IEGWO is significantly better than that of the other algorithms. However, the optimal solution found by IEGWO is better than the best known solution so far.

Table 8 Comparison results of IEGWO and other algorithms for pressure vessel design problem
Full size table

5.3 Optimization of model parameters in the field of hyperspectral imaging

In recent years, many researchers have applied hyperspectral imaging (HSI) technique in the nondestructive testing of food and agricultural products and developed various methods to improve the performance of models (Yao et al. 2022; Suktanarak and Teerachaichayut 2017). Among them, parameter optimization is a commonly used and effective way to improve the accuracy and robustness of the models.

Support vector regression (SVR) is a classical machine learning algorithm, which has been widely used to solve regression prediction problems (Xu et al. 2016). The performance of SVR is mainly influenced by three parameters, namely penalty factor (c), kernel parameter (g), and insensitive loss function parameter (ε). In this section, the SVR model is used to establish a prediction model for Haugh unit (HU) values of eggs based on HSI technique, and the proposed IEGWO is used to optimize the three parameters.

Figure 9 shows the reflectance spectral curves of 330 egg samples with different HU values in the wavelength range of 479–986 nm. The spectral reflectance is taken as the input of SVR and the HU value is taken as the output. As an example, the 330 egg samples are randomly divided into training set and test set according to the ratio of 3:1 to evaluate the performance of GA, PSO, GWO, and IEGWO.

Fig. 9
figure 9

Spectral curves of egg samples

Full size image

In the process of parameter optimization, the fivefold cross-validation root mean square error (RMSECV) of training set is taken as the fitness function. The optimization range of parameters c, g, and ε are set to [10−4, 103], [10−4, 103] and [10−4, 100]. The population size and the maximum iteration are set to 20 and 50.

Figure 10 shows the optimal fitness curves of IEGWO-SVR, GWO-SVR, PSO-SVR and GA-SVR models for 30 runs. As shown in Fig. 9, the IEGWO-SVR model has higher accuracy and faster convergence speed than the other three models.

Fig. 10
figure 10

Optimal fitness curves of GA-SVR, PSO-SVR, GWO-SVR, and IEGWO-SVR models

Full size image

6 Conclusion

This study proposes a modified version of GWO called information entropy-based GWO (IEGWO). In the IEGWO, an initial population generation method and a dynamic position update equation based on information entropy are proposed to maintain the population diversity. In addition, a nonlinear convergence strategy is applied to balance the exploration and exploitation. The IEGWO is tested on 10 well-known benchmark functions, CEC2014 and CEC2017, and compared with the other meta-heuristic algorithms. Two engineering design problems and one real-world parameter optimization problem in the field of hyperspectral imaging are also solved using IEGWO. The experimental results show that the IEGWO has better robustness and solution accuracy than the other compared algorithms.

Although the IEGWO is efficient, it also has some drawbacks that should be addressed. One is that the number of parameters is larger than the original GWO algorithm, and another is that the current study does not have automatic adjustment for the parameter k. In the future wok, we tend to study an adaptive parameter k to achieve the optimal optimization effect. In addition, we are going to investigate how to extend the IGWO algorithm to handle multi-objective optimization and combinatorial optimization problems.