1 Introduction

In the literature, there are some unconventional beams, and cosh-Gaussian beam is one of them. Bearing this in mind, we present that cosh-Gaussian beam with small Gaussian source size provides the highest signal-to-noise ratio at close propagation distance in atmosphere [1]. Point like scintillation of cosh-Gaussian beam is derived in [2]. In case of aperture averaged scintillation, cosh-Gaussian beam is advantageous as compared to Gaussian beam [3]. Since its scintillation index is low, cosh-Gaussian beam brings us mitigation in bit error rate [4]. One of the recent studies shows that Airy-related beams can be obtained when cosh-Gaussian beam is used as an input of spatial light modulator [5]. Second harmonic of cosh-Gaussian beam is generated and controlled by adjusting the plasma density [6]. Cosh-Gaussian beam with power-exponent-phase vortex expands directly proportional with topological charge [7]. Moreover, stimulated Brillouin scattering of cosh-Gaussian beam increases directly proportional with decentered parameter [8]. Self-focusing property becomes more effective if cosh-Gaussian beam propagates in relativistic cold quantum deeply [9]. In addition to this, self-focusing of cosh-Gaussian beam can be controlled by adjusting the plasma frequency [10]. Beam size of Hermite-cosh-Gaussian beam propagating in semiconductor quantum plasma decreases when decentered parameter enhances [11]. Besides, mode index and beam width have a direct relationship while Hermite-cosh-Gaussian beam propagating in plasma [12]. Hermite-cosh-Gaussian beam evolves into Airy like distribution after the beam propagates in Airy transform optical system [13]. Lastly, partially coherent Generalized Flattened Hermite-Cosh-Gaussian beam turns into doughnut like shape by increasing the waist width [14].

From the other perspective, propagation characteristics of untraditional beams in uniaxial crystal orthogonal to optical axis attract the attention of scientists. Regarding with this, we show that Ariyprime beam has a flat-topped shape after propagation in uniaxial crystal [15]. Furhermore, hyperbolic sinusoidal beam evolves into elliptic shape after propagation [16]. It is investigated in [17] that larger initial angle causes off-axis intensity distribution if Airy Gaussian beam is used. Spin and orbital currents are controlled by adjusting the distribution factor of Airy Gaussian vortex beam [18]. Longitudinal gradient force decreases if fictional crystal is used instead of quartz when rotating elliptical chirped Gaussian beam is selected as initial profile [19]. In addition, more concentrated beams can be obtained if chirped factor of chirped Airy vortex beam [20]. Using radially polarized chirped Airy Gaussian beam, another study is concluded as focused beam that can be obtained at the observation plane by selecting appropriate refractive index ratios of the crystal [21]. Four-petal Lorentz-Gauss beam turns into elliptical Gauss beam after propagation [22]. Partially coherent Lorentz-Gauss beam loses its hollow in the center after short propagation distance [23]. Ordinary and extraordinary beams are generated if elliptical Gaussian beam is selected [24].

In this article, we analyse the propagation of cosh-Gaussian beam propagating in uniaxial crystal orthogonal to optical axis. Received field is derived applying Huygens-Fresnel integration. Results are plotted considering the variations in source beam parameters, crystal settings and propagation distance. We believe that our results will be beneficial to generate new beams and optical tracking application.

2 Derivation of received field in uniaxial crystal

Applying Euler expansion, cosh-Gaussian beam is written as

$$ u_{s} \left( {s_{x} ,s_{y} } \right) = \frac{1}{4}\left( {\begin{array}{*{20}c} {\exp \left( {as_{x} + bs_{y} } \right) + \exp \left( {as_{x} - bs_{y} } \right)} \\ { + \exp \left( { - as_{x} + bs_{y} } \right) + exp\left( { - as_{x} - bs_{y} } \right)} \\ \end{array} } \right)exp\left( { - \frac{{s_{x}^{2} + s_{y}^{2} }}{{w^{2} }}} \right) $$
(1)

where \(a\) and \(b\) are arguments of cosh function, \(\left( {s_{x} ,s_{y} } \right)\) refer to transverse source plane coordinates, and \(w\) is the Gaussian source size. Di-electric tensor of crystal is taken from [25] as

$$ \in = \left( {\begin{array}{*{20}c} {n_{e}^{2} } & 0 & 0 \\ 0 & {n_{0}^{2} } & 0 \\ 0 & 0 & {n_{0}^{2} } \\ \end{array} } \right) $$
(2)

where \(n_{0}\) and \(n_{e}\) denote ordinary and extraordinary refractive indices of crystal. In this study, \(n_{0}\) is taken as 2.62, and ratio of refractive indices is defined as \(e = n_{e} /n_{0}\). Based on Huygens-Fresnel integral [26], received field is written as

$$ u_{r} \left( {r_{x} ,r_{y} } \right) = \frac{{kn_{0} }}{2\pi jz}exp\left( { - jkn_{e} z} \right) $$
$$ x\mathop \smallint \limits_{ - \infty }^{\infty } \mathop \smallint \limits_{ - \infty }^{\infty } u_{s} \left( {s_{x} ,s_{y} } \right)exp\left( {\frac{jk}{{2zn_{e} }}\left[ {n_{0}^{2} \left( {r_{x} - s_{x} } \right)^{2} + n_{e}^{2} \left( {r_{y} - s_{y} } \right)^{2} } \right]} \right)ds_{x} ds_{y} $$
(3)

where \(z\) being the propagation distance which is selected based upon Rayleigh distance \(z_{R} = kw^{2}\). \(k = 2\pi /\lambda\) Indicates the wave number, and \(\lambda =0.53\mu m\) refers to operating wavelength. Additionally, \(\left( {r_{x} ,r_{y} } \right)\) are the transverse receiver plane coordinates. After doing some rigorous derivation relying on the expression given in [27], received field is obtained as

$$ u_{r} \left( {r_{x} ,r_{y} } \right) = - \frac{{kn_{0} }}{2\pi jz}exp\left( {jkn_{e} z} \right)\frac{\pi }{{\sqrt {p_{x} p_{y} } }}exp\left( {\frac{{jkn_{0}^{2} }}{{2zn_{e} }}r_{x}^{2} + \frac{{jkn_{e} }}{2z}r_{y}^{2} } \right) $$
$$ x\left\{ \begin{gathered} \exp \left( {\frac{{\left( { - \frac{{jkn_{0}^{2} r_{x} }}{{zn_{e} }} + a} \right)^{2} }}{{4\left( {\frac{{jkw^{2} n_{0}^{2} - 2zn_{e} }}{{2zn_{e} w^{2} }}} \right)}} + \frac{{\left( { - \frac{{jkn_{e} r_{y} }}{z} + b} \right)^{2} }}{{4\left( {\frac{{jkw^{2} n_{e} - 2z}}{{2zw^{2} }}} \right)}}} \right) + \exp \left( {\frac{{\left( { - \frac{{jkn_{0}^{2} r_{x} }}{{zn_{e} }} + a} \right)^{2} }}{{4\left( {\frac{{jkw^{2} n_{0}^{2} - 2zn_{e} }}{{2zn_{e} w^{2} }}} \right)}} + \frac{{\left( { - \frac{{jkn_{e} r_{y} }}{z} - b} \right)^{2} }}{{4\left( {\frac{{jkw^{2} n_{e} - 2z}}{{2zw^{2} }}} \right)}}} \right) \hfill \\ + \exp \left( {\frac{{\left( { - \frac{{jkn_{0}^{2} r_{x} }}{{zn_{e} }} - a} \right)^{2} }}{{4\left( {\frac{{jkw^{2} n_{0}^{2} - 2zn_{e} }}{{2zn_{e} w^{2} }}} \right)}} + \frac{{\left( { - \frac{{jkn_{e} r_{y} }}{z} + b} \right)^{2} }}{{4\left( {\frac{{jkw^{2} n_{e} - 2z}}{{2zw^{2} }}} \right)}}} \right) + \exp \left( {\frac{{\left( { - \frac{{jkn_{0}^{2} r_{x} }}{{zn_{e} }} - a} \right)^{2} }}{{4\left( {\frac{{jkw^{2} n_{0}^{2} - 2zn_{e} }}{{2zn_{e} w^{2} }}} \right)}} + \frac{{\left( { - \frac{{jkn_{e} r_{y} }}{z} - b} \right)^{2} }}{{4\left( {\frac{{jkw^{2} n_{e} - 2z}}{{2zw^{2} }}} \right)}}} \right) \hfill \\ \end{gathered} \right\} $$
(4)

3 Results and discussion

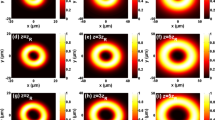
In this part of the research, numeric evaluations are made based on the derivations of Sect. 2. Geometry of the research is given in Fig. 1. Here, cosh-Gaussian beam is applied to the input of uniaxial crystal, and received field is obtained at the receiver plane. Intensity distribution of cosh-Gaussian beam propagating in uniaxial crystals with \(e = 0.7, 1.1,{\text{ and}} 2\) are plotted in Figs. 2, 3 and 4, respectively. We observe that cosh-Gaussian beam evolves into elliptic Gaussian beam at near field. Intensity of the beam decreases and beam enlarges when propagation distance increases. More concentrated beam can be obtained if larger \(e\) value is selected for the crystal. In Figs. 5, 6 and 7, we plot intensity distribution of cosh-Gaussian beam with \(a = 1, b = 10\). We see that intensity lies along y-axis, and it has cosine like distribution vanishing toward to the edge of the observation plane. This cosine shape is seen at \(z = z_{R}\) in Figs. 5 and 6. However, cosine like shape occurs at \( z = 2z_{R}\) when \(e = 2\). Since beam size increases along the propagation, intensity regions get far away from each other. Peak intensity of the beam decreases by \(10^{ - 1}\). Moreover, we can see the effect of \(a\) by comparing Figs. 2, 3, 4 and 8, 9, 10, respectively. We investigate from these figures that change in \(a\) brings off-axis intensity distribution at close distance. Additionally, a weak intensity is observed which is placed symmetrically to the origin. When propagation distance increases beam loses its peak intensity by amount of \(10^{22}\). Figures 11, 12 and 13 present intensity distribution of cosh-Gaussian beam having \(a = 20, b = 20\). It is seen from these figures that there are two weak intensities which are located in positive y-axis and symmetric to the y-axis and one brighter intensity which takes place in positive part of x-axis and negative part of y-axis. When the propagation distance increases, weak couple come together and two strong intensities are generated as in Fig. 13. Then, cosine like shapes are observed again at longer distances. This evolution occurs slower when ratio of refractive indices is high. Peak intensity reduces by amount of \(10^{87}\) times due to the structure of the crystal. Moreover, in order to see beam evolution clearly 3D plot is given in Fig. 14. This figure involves intensity evolution of cosh-Gaussian beam with \(a = 1, b = 10\) and \(a = 20, b = 20\) in a uniaxial crystal having ratio of refractive index 2. Due to the machine accuracy of MATLAB large values as peak intensity are presented in Figs. 11, 12, 13 and 14. These values can be assumed as infinity. In reverse manner, reduction by amount of \(10^{87}\) indicates that decrease is in level of zero.

Fig. 1
figure 1

View for the propagation in uniaxial crystal

Full size image
Fig. 2
figure 2

Intensity distribution of cosh-Gaussian beam having \(a = b = 1\) in crystal with \(e = 0.7\)

Full size image
Fig. 3
figure 3

Intensity distribution of cosh-Gaussian beam having \(a = b = 1\) in crystal with \(e = 1.1\)

Full size image
Fig. 4
figure 4

Intensity distribution of cosh-Gaussian beam having \(a = b = 1\) in crystal with \(e = 2\)

Full size image
Fig. 5
figure 5

Intensity distribution of cosh-Gaussian beam having \(a = 1, b = 10\) in crystal with \(e = 0.7\)

Full size image
Fig. 6
figure 6

Intensity distribution of cosh-Gaussian beam having \(a = 1, b = 10\) in crystal with \(e = 1.1\)

Full size image
Fig. 7
figure 7

Intensity distribution of cosh-Gaussian beam having \(a = 1, b = 10\) in crystal with \(e = 2\)

Full size image
Fig. 8
figure 8

Intensity distribution of cosh-Gaussian beam having \(a = 10, b = 1\) in crystal with \(e = 0.7\)

Full size image
Fig. 9
figure 9

Intensity distribution of cosh-Gaussian beam having \(a = 10, b = 1\) in crystal with \(e = 1.1\)

Full size image
Fig. 10
figure 10

Intensity distribution of cosh-Gaussian beam having \(a = 10, b = 1\) in crystal with \(e = 2\)

Full size image
Fig. 11
figure 11

Intensity distribution of cosh-Gaussian beam having \(a = 20, b = 20\) in crystal with \(e = 0.7\)

Full size image
Fig. 12
figure 12

Intensity distribution of cosh-Gaussian beam having \(a = 20, b = 20\) in crystal with \(e = 1.1\)

Full size image
Fig. 13
figure 13

Intensity distribution of cosh-Gaussian beam having \(a = 20, b = 20\) in crystal with \(e = 2\)

Full size image
Fig. 14
figure 14

3D intensity distribution of cosh-Gaussian beam having \(a = 1, b = 10\) and \(a = 20, b = 20\) in crystal with \(e = 2\)

Full size image

4 Conclusions

Propagation properties of cosh-Gaussian beam in uniaxial crystal orthogonal to optical axis are studied in this article. We investigate that focused beam can be obtained for larger values of refractive index ratio. Furthermore, \(a\) causes off-axis distribution while \(b\) brings rapid vanishing cosine like distribution. For larger values of both cosh arguments, higher peak intensity values can be measured but this peak intensity rapidly decreases along propagation. Beam enlarges while propagation distance raises. We anticipate that our results will be helpful to generate new beams. These generated beams can be used in optical wireless communication systems since untraditional beams have less scintillation than fundamental Gaussian beam. Additionally, outputs of this study have potential application in optical tracking applications.