Introduction

Scholars and enterprises are increasingly focusing on the utilisation of various electromagnetic waves including terahertz waves in various domains such as molecular identification, crystal structure refinement, non-destructive testing, spectral analysis, and medical imaging [1,2,3,4,5]. Casperson and Tovar [6] introduced the paraxial wave solution of the Hermite-cosh-Gaussian function. Belafhal et al. [7] conducted a theoretical investigation on the wave propagation characteristics of the Hermite-cosh-Gaussian function in the ABCD system using a paraxial wave solution. Patil et al. [8] conducted a study on the Hermite-cosh-Gaussian laser beam in magneto-active plasma. The researchers conducted an investigation into the impact of the decentred parameter and the mode index on self-focusing. Nanda et al. [9] conducted a study on the self-focusing of a Hermite-cosh-Gaussian laser beam in plasma profiles with ramp density and under density. Kaur et al. [10] conducted a numerical study on the Hermite-cosh-Gaussian laser beam in ripple density plasma. Wadhwa et al. [11] investigated the formation of second harmonics in the Hermite–Gaussian beam in collisional plasma. The examination of the impact of mode indices on the production of harmonics and the occurrence of self-focusing was carried out by the researchers. Hamster et al. [12, 13] examine the interaction between a brief and intense laser pulse and plasma to produce Terahertz waves. The inquiry was undertaken by the researchers to examine the impact of nonlinear ponderomotive force on the generation of Terahertz waves. Safari et al. [14] conducted a study to examine the characteristics of collisional plasma using laser beams characterised by Hermite and Laguerre Gaussian profiles. The researchers reached the determination that the amplitude of the Terahertz field is significantly influenced by plasma and laser characteristics [15,16,17,18]. Chaudhary et al. [19] conducted a study on the creation of Terahertz waves using a radially polarised Hermite-cosh-Gaussian laser beam in a hot collisional plasma. The study conducted by Hashemzadeh [20] investigated the generation of Terahertz waves in magnetised plasma through the utilisation of laser beams exhibiting Hermite-cosh-Gaussian and hollow Gaussian characteristics. According to the researchers, the presence of external magnetic fields leads to a radial amplification in the intensity of the Terahertz field. Wu et al. [21] investigated the generation of phase-sensitive Terahertz pulses from gas targets. Gurjar et al. [22] conducted a study to investigate the nonlinear interaction between chirped laser pulse interaction and slanting plasma modulation for the purpose of generating Terahertz waves at beat frequency. The authors provide evidence that the amplitude of the generated Terahertz wave is significantly influenced by the slanting plasma profile. In a theoretical study, Frolov et al. [23] investigated the impact of p-polarized radiation on semi-bounded plasma. Significant THz amplification is found when a laser pulse of extremely short duration is directed at or close to the critical angle. Xie et al. [24] did a study that aims to examine the generation of THz waves through the application of laser-induced air plasma. The results indicate that the generation of high-frequency THz radiation is effective when the incident laser exhibits identical polarisation condition. Hashemzadeh [25] conducted a study on the interaction between a chirped laser pulse and a hot inhomogeneous ripple density plasma. The researcher investigates the effects of frequency chirp, laser intensity, electron temperature, and electron density disparity on the generation of THz waves. Huang et al. [26] conducted a study that examined the simultaneous emission of THz and X-rays arising from the interaction between a high-intensity, short-duration laser pulse and a thin, unconfined water flow in the atmosphere. They exemplify the evolution of material modification. Liao et al. [27] conducted a thorough examination of the various methodologies utilised in the production of THz radiation. These methods involve using plasma waves, electron transport, and emission to generate time-domain hyperspectral THz radiation. Amouamouha et al. [28] did a study that centres on the generation of THz radiation by means of the interaction between a super Gaussian laser beam and a plasma that exhibits ripple density. The investigators utilised the paraxial approximation methodology in their study. The researchers adjusted different laser plasma parameters to attain a total harmonic distortion THz efficiency of 6.5%. Jahangiri et al. [29] did a study that centres on the advancement of high-frequency (THz) radiation, namely within the range of 10–70 mJ, derived from plasma generated by argon clusters. Sharma et al. [30] conducted a study to examine the properties of the cosh-Gaussian laser beam in a wiggler magnetised plasma setting, with a particular emphasis on its capacity to produce second harmonics. Bakhtiari et al. [31] did a study that centres on the generation of THz radiation through the application of two Gaussian laser array beams. The researchers are conducting an investigation into the factors related to laser and array structure with the aim of optimising the generation of THz radiation to achieve improved efficiency.

Mou et al. [32] did a study to examine the influence of laser chirp on the polarisation of THz radiation. The results indicate that the effects of positive and negative chirp on the polarisation state and phase difference of THz waves are distinct. Nguyen et al. [33] did a numerical analysis to assess the influence of chirp and time delay on the effectiveness of THz generation. In order to attain a conversion efficiency of 10(−4) for THz radiation, the researchers utilise three-dimensional simulation approaches. A range of laser and plasma properties are utilised by scientists and academics to explore different mechanisms, such as nonlinear optics, harmonic generation, self-focusing, filamentation, electron acceleration, and terahertz wave generation, Wakefield acceleration [34,35,36,37,38,39,40,41].

The present investigation involves the propagation of two linearly polarised Hermite–Gaussian beams in the z direction. The laser beams exhibit positive chirp characteristic. In the presence of a dense collision-less plasma and a transverse static magnetic field, the laser beams exhibited propagation. The phenomenon of laser-plasma interaction leads to the production of highly energetic THz waves. By manipulating the laser and plasma characteristics, it is possible to attain a THz radiation source that is both tuneable and efficient. The analytical derivation of the ponderomotive force, equation of motion, nonlinear plasma current density, and the subsequent production of THz fields are covered in “Analytical study of THz generation” section of this paper. In this study, “Results and discussion” investigates the correlation between the normalised THz electric field and various parameters, such as the incident laser electric field, normalised THz frequency, normalised transverse distance, and chirp parameter. In the fourth section, the Conclusions are derived. The paper closes by incorporating citations.

Analytical study of THz generation

Two linearly polarized Hermite Gaussian laser beams are propagating in z direction.

Electric field of two linearly polarized Hermite Gaussian laser beams

$$\overrightarrow {{{\text{E}}_{1} }} \left( {{\text{x}},{\text{z}}} \right) = ~{\hat{\text{x}E}}_{0} {\text{H}}_{{\text{s}}} \left( {\frac{{\sqrt {\text{2}} x}}{{{\text{w}}_{0} }}} \right)e^{{ - \left( {{\text{x}}^{2} /{\text{w}}_{0}^{2} } \right)}} {\text{e}}^{{{\text{i}}\left( {{\text{k}}_{1} {\text{z}} - {\omega }_{1} {\text{t}}} \right)}}$$
(1)
$$\overrightarrow {{{\text{E}}_{2} }} \left( {{\text{x}},{\text{z}}} \right) = {{\hat{\text{x}}E}}_{0} {\text{H}}_{{\text{s}}} \left( {\frac{{\sqrt 2 {\text{x}}}}{{{\text{w}}_{0} }}} \right){\text{e}}^{{ - \left( {{\text{x}}^{2} /{\text{w}}_{0} ^{2} } \right)}} {\text{e}}^{{{\text{i}}({\text{k}}_{2} {\text{z}} - \omega _{2} {\text{t}})}}$$
(2)

Here, E0 is amplitude of laser pulse, w0 is beam waist, s is the mode index of Hermite polynomial Hs .

Corresponding magnetic field of laser beam are

$$\overrightarrow {{{\text{B}}_{{\text{J}}} }} \left( {r,z} \right) = \frac{{\left\{ {\overrightarrow {{{\text{k}}_{{\text{j}}} }} \times \overrightarrow {{{\text{E}}_{J} }} \left( {r,z} \right)} \right\}}}{{\upomega _{{\text{J}}} }}\quad {\text{where}}\;\;J = 1,2$$
(3)

The positive frequency chirp is

$$\omega_{1} = \omega_{0} + b\omega_{0}^{2} \left( {t - \frac{z}{c}} \right),$$
(4)
$${\omega }_{2}={\omega }_{1}-\omega =\left\{{\omega }_{0}+b{\omega }_{0}^{2}\left(t-\frac{z}{c}\right)\right\}-\omega$$
(5)

An external static magnetic field is applied along the y-axis i.e. \({\text{B}}_{\text{s}}={\text{B}}_{0}\widehat{\text{y}}\).

In the initial stage, electrons can be considered at rest so electrons will not experience any magnetic force. So, from equation of motion \(m\frac{d\overrightarrow{{V}_{1}} }{dt}= -e \overrightarrow{{E}_{1}}\) \(-m\overrightarrow{{V}_{1}}\) ν oscillatory velocity of plasma electron is

$$\Rightarrow \overrightarrow{{V}_{1}}= \frac{e \overrightarrow{{E}_{1}}}{im{\omega }_{0}\left\{1+b{\omega }_{0}\left(2t-\frac{z}{c}\right)\right\}-m\upnu }=\frac{e \overrightarrow{{E}_{1}}}{im{\omega }_{1}-m\upnu }=\frac{e \overrightarrow{{E}_{1}}}{m\left(i{\omega }_{1}-\upnu \right) }$$
(6)
$$\Rightarrow \overrightarrow{{V}_{2}}= \frac{e \overrightarrow{{E}_{2}}}{im{\omega }_{0}\left\{1+b{\omega }_{0}\left(2t-\frac{z}{c}\right)-\frac{\omega }{{\omega }_{0}}\right\}-m\upnu }=\frac{e \overrightarrow{{E}_{2}}}{im{\omega }_{2}-m\upnu }=\frac{e \overrightarrow{{E}_{2}}}{m\left(i{\omega }_{2}-\upnu \right)}$$
(7)

Here, \({\omega }_{1}={\omega }_{0}\left\{1+b{\omega }_{0}\left(2t-\frac{z}{c}\right)\right\}\), \({\omega }_{2}={\omega }_{0}\left\{1+b{\omega }_{0}\left(2t-\frac{z}{c}\right)-\frac{\omega }{{\omega }_{0}}\right\}\), and e, m, \(\upnu\) is charge, rest mass and collisional frequency of the plasma electron respectively.

This oscillatory velocity of plasma electron give rise to nonlinear ponderomotive force.

Nonlinear ponderomotive force is

$${\overrightarrow{{F}_{P}}}^{NL}=-\frac{m}{2}\overrightarrow{\nabla }\left(\overrightarrow{{V}_{1}} {\overrightarrow{{V}_{2}}}^{*}\right)$$
(8)

Here, * represents the complex conjugate.

Solving this equation by putting values of \(\overrightarrow{{V}_{1}},{\overrightarrow{{V}_{2}}}^{*}\), we get

$$\begin{aligned} \overrightarrow {{F_{P} }}^{NL} &= - \hat{z} \frac{{e^{2} E_{1} E_{2}^{*} }}{{2im\omega_{0} c}} \left( {\frac{{2\frac{{\upnu }}{{\omega_{0} }}{ } - \frac{\omega }{{\omega_{0} }}}}{{\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{{\upnu }}{{i\omega_{0} }}{ }} \right\}\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{\omega }{{\omega_{0} }} + \frac{{\upnu }}{{i\omega_{0} }}} \right\}}}{ }} \right) \hfill \\ & \quad - \hat{z} \frac{{be^{2} E_{1} E_{2}^{*} }}{{m\omega_{0} c}}\left( {\frac{{\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{\omega }{{2\omega_{0} }}} \right\}}}{{\left\{ {\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right)} \right\} - \frac{{\upnu }}{{i\omega_{0} }}} \right\}^{2} \left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{\omega }{{\omega_{0} }} + \frac{{\upnu }}{{i\omega_{0} }}} \right\}^{2} { }}} } \right) \hfill \\ \end{aligned}$$
(9)

The movement of plasma electrons on a circular trajectory is initiated by the Lorentz force exerted by an external static magnetic field. The interaction between the circular motion of a plasma electron and the electric field of a laser beam leads to the generation of angular motion in the plasma electron, which is associated with the cyclotron frequency \({\omega }_{c}.\)

By solving the equation of motion \(\frac{\partial {\overrightarrow{V}}_{\omega }^{NL}}{\partial t}=\frac{{\overrightarrow{F}}_{P}^{NL}}{m}-\nu {\overrightarrow{V}}_{\omega }^{NL}-\frac{e}{mc}\left\{{\overrightarrow{V}}_{\omega }^{NL}\times \overrightarrow{B}\right\}\)

Here \({\overrightarrow{V}}_{\omega }^{NL}\) is the nonlinear velocity of electrons, \({\overrightarrow{F}}_{P}^{NL}\) is the non-linear ponderomotive force, \(\nu\) is collisional frequency of electron. \(\overrightarrow{B}\) is external magnetic field.

We get the oscillatory velocity of plasma electron such as

$$\overrightarrow{{V}_{\omega }^{NL}}=\frac{{\omega }_{c}\widehat{x}-i\omega \widehat{z}}{m \left({{\omega }_{c}}^{2}-{\omega }^{2}\right)}{F}_{Pz}^{NL}$$

Here, we consider \({\omega }_{1,}{\omega }_{2}{>>\omega }_{c},{\omega }_{P}\).

Where \({\omega }_{P}\) is plasma frequency is such as \({{\omega }_{P}}^{2}=\frac{4\pi n{e}^{2}}{m}\) and \(\omega _{c} = eB_{0} /mc\) is cyclotron frequency. Nonlinear oscillatory current density can be calculated by solving this equation \({\overrightarrow{J}}^{NL}=-\frac{1}{2}ne{\overrightarrow{V}}^{NL}\),

$$\Rightarrow \vec{J}^{NL} = - \frac{{\omega_{P}^{2} }}{8\pi e}\frac{{\omega_{c} \hat{x} - i\omega \hat{z}}}{{\left( {\omega_{c}^{2} - \omega^{2} } \right)}}F_{Pz}^{NL}$$
(10)

This nonlinear current density is responsible for THz generation. By using III and IV Maxwell’s equation, we can calculate the THz wave generation equation.

From Maxwell’s equations \(\overrightarrow{\nabla }\times \overrightarrow{E}=-\frac{1}{c}\frac{\partial \overrightarrow{B}}{\partial t}\)

$$\text{As} \overrightarrow{\nabla }\times \overrightarrow{B}=\frac{\varepsilon }{c}\frac{\partial \overrightarrow{E}}{\partial t}+\frac{4\pi }{c}{\overrightarrow{J}}^{NL}$$

Equation for THz generation is

$$\Rightarrow \overrightarrow{\nabla }\left(\overrightarrow{\nabla }\overrightarrow{{.E}_{THz}}\right)-{\nabla }^{2}\overrightarrow{{E}_{THz}}= \frac{{\omega }^{2}}{{c}^{2}}\varepsilon \overrightarrow{{E}_{THz}}+\frac{4\pi i\omega }{{c}^{2}}{\overrightarrow{J}}^{NL}$$
(11)

In order to neglect higher order derivatives due to fast variation of THz field So

$$\begin{aligned} E_{THz} & = \frac{{\omega_{P}^{2} }}{{2e\varepsilon \omega \sqrt {\omega_{c}^{2} - \omega^{2} } }}\left\{ { - \frac{{e^{2} E_{1} E_{2}^{*} }}{{2im\omega_{0} c}} \left( {\frac{{2\frac{{\upnu }}{{\omega_{0} }}{ } - \frac{\omega }{{\omega_{0} }}}}{{\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{{\upnu }}{{i\omega_{0} }}{ }} \right\}\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{\omega }{{\omega_{0} }} + \frac{{\upnu }}{{i\omega_{0} }}} \right\}}}{ }} \right){ }} \right. \\ & \quad \left. { - \frac{{be^{2} E_{1} E_{2}^{*} }}{{m\omega_{0} c}}\left( {\frac{{\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{\omega }{{2\omega_{0} }}} \right\}}}{{\left\{ {\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right)} \right\} - \frac{{\upnu }}{{i\omega_{0} }}} \right\}^{2} \left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{\omega }{{\omega_{0} }} + \frac{{\upnu }}{{i\omega_{0} }}} \right\}^{2} { }}} } \right)} \right\} \\ \end{aligned}$$
(12)
$$\begin{aligned} \frac{{E_{THz} }}{{E_{0} }} & = \frac{{e\omega_{P}^{2} }}{{2\varepsilon \omega \sqrt {\omega_{c}^{2} - \omega^{2} } }}\frac{{\left\{ {H_{s} \left( {\frac{\sqrt 2 x}{{w_{0} }}} \right)} \right\}^{2} e^{{ - \left( {2{\raise0.7ex\hbox{${x^{2} }$} \!\mathord{\left/ {\vphantom {{x^{2} } {w_{0}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${w_{0}^{2} }$}}} \right)}} E_{0} { }}}{{m\omega_{0} c\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right){ }} \right\}\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{\omega }{{\omega_{0} }}} \right\}}} \\ & \sqrt {b^{2} \left( {\frac{{\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{\omega }{{2\omega_{0} }}} \right\}}}{{\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right){ }} \right\}\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{\omega }{{\omega_{0} }}} \right\}{ }}}} \right)^{2} - \frac{1}{4}\left[ {\frac{\omega }{{\omega_{0} }}} \right]^{2} } \\ \end{aligned}$$
(13)

Equation 13 represents the normalised THz amplitude.

Results and discussion

This study focuses on the creation of THz by examining the behaviour of two Hermite–Gaussian polarised laser beams under the influence of cold collision-less under dense plasma. In this investigation, we have selected an appropriate laser parameter, specifically the femtosecond Ti:Sapphire laser has a wavelength of 800 nm and an angular frequency of \(2.35{\times 10}^{15}\) rad/s. It has a chirp parameter of 0.0099, a beam waist of \({5\times 10}^{-5}\) m, and an electric field amplitude of 2.\(5 \times {10}^{12}\) V/m. The optimisation of plasma parameters is achieved by maintaining a plasma density of \(9.74\times {10}^{22}{ \text{m}}^{-3}\) and a corresponding plasma frequency of \(1.76\times {10}^{13} \text{Hz}\) [19, 42]. In this investigation, we selected a value of \({\upomega =1.07\upomega }_{P},\) where \({\upomega }_{1},{\upomega }_{2}>{\upomega }_{P}\), and an external static magnetic field of 10 Tesla is applied.

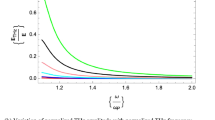
Variation of on normalised THz amplitude with normalised frequency for different Hermite polynomial mode index

This work aims to theoretically investigate the relationship between the normalised amplitude of terahertz (THz) radiation and the normalised frequency of THz waves. The current investigation focuses on various values of the Hermite polynomial mode index, specifically s = 0, 1, 2.

The study involves adjusting the chirp parameter b to 0.0099 and applying a static magnetic field of 10 T. The amplitude of the terahertz signal increases as the Hermite polynomial mode with index for values s = 0, 1, 2 increases. When the frequency of the THz exceeds 1.2 times the frequency of the plasma (\(\upomega\) > 1.2 \({\upomega }_{P}\)), it becomes apparent that the amplitude of the normalised THz experiences a substantial reduction and ultimately approaches zero.

Hermite–Gaussian modes index depict the spatial arrangement of the beam’s intensity in the transverse plane. Higher-order modes, characterised by higher indices, exhibit intricate intensity patterns that include many lobes and nodes. The mode shape has a direct impact on mechanism used for generating THz waves which can be seen in Fig. 1.

Fig. 1
figure 1

Variation of normalized THz amplitude with normalized THz frequency with mode index a s = 0, b s = 1, c s = 2 are shown. For decentered parameter a = 0 (black), b = 1 (green) and b = 2 (blue) for chirp parameter b = .0099. Other parameters are same as mentioned above

Full size image

Variation of on normalised THz amplitude with normalised THz frequency for different chirp parameter

The primary objective of this study is to investigate the correlation between the normalised amplitude of the terahertz (THz) signal and its corresponding normalised frequency. The study investigates several chirp levels, specifically b = 0.0011, 0.0044, 0.0066, and 0.0099 (Fig. 2).

Fig. 2
figure 2

Variation of normalized THz amplitude with normalized THz frequency For b = 0.0011 (red), b = .0044 (blue), b = .0066 (green), b = 0.0099 (black). Other parameters are same as mentioned above

Full size image

A significant increase in the normalised amplitude of the THz frequency is evident, with values ranging from around 0.014 to 0.6. This pattern is visible as the chirp parameter (b) is adjusted throughout a variety of values, specifically 0.0011, 0.0044, 0.0066, and 0.0099. The amplitude of the normalised THz frequency exhibits a substantial reduction above the threshold of 1.2 and approaches to zero.

Positive frequency chirping enhances THz efficiency by optimizing nonlinear interactions, and assuring superior temporal and spatial alignment of frequency components. These elements together enhance the efficiency of generating THz waves.

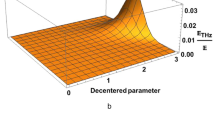
Variation of on normalised THz amplitude with normalised transverse distance for different Hermite polynomial index value

This study aims to examine the impact of normalised THz distance on normalised THz amplitude, specifically focusing on a chirp parameter value of 0.0099. This study focuses on conducting theoretical analysis for various Hermite index mode values, specifically s = 0, 1, and 2.

The research entails the modification of the Hermite mode index s at values of 0, 1, and 2, while subjecting the system to a static magnetic field of 10 Tesla. As the Hermite polynomial mode with index increases from 0 to 2, the amplitude of the terahertz signal also increases. As we increase the Hermite polynomial mode index from 0 to 2, the peak of the normalised THz amplitude shifts towards higher values, corresponding to an increase in the normalised transverse distance.

With the change in Hermite mode index, the transverse intensity distribution of laser electric field varies. As a result, the transverse distance for optimized THz efficiency varies with Hermite mode index. This variation can be seen in Fig. 3.

Fig. 3
figure 3

Variation of normalized THz amplitude with normalized THz frequency with Hermite mode index s = 0 (black), s = 1 (green), s = 2 (blue) are shown. For chirp parameter b = .0099. Other parameters are same as mentioned above

Full size image

Variation of on normalised THz amplitude with normalised transverse distance for different chirp parameter

This work conducted a theoretical analysis to examine the impact of normalised transverse distance on normalised THz amplitude, specifically focusing on the Hermite polynomial mode index value of s = 1. The analysis is applicable to many values of the chirp parameter, specifically 0.0011, 0.0044, 0.0066, and 0.0099.

The study involves altering the chirp parameter at certain values of 0.0011, 0.0044, 0.0066, and 0.0099, while simultaneously subjecting the device to a static magnetic field of 10 Tesla. In the investigation of the relationship between normalised THz amplitude and normalised transverse distance, it was shown that an increase in the chirp parameter from 0.0011 to 0.0099 corresponded to a similar rise in the amplitude of the terahertz signal from 0.4 to 0.6.

With the increase in chirp parameter, the transverse intensity distribution of laser electric field does not vary. As a result, the transverse distance for optimized THz efficiency remains same with chirp parameter. The variation in THz amplitude varies due to variation in transverse intensity variation due to change in Hermite mode index as can be seen in Fig. 4.

Fig. 4
figure 4

Variation of normalized THz amplitude with normalized transverse distance with mode index a s = 1 are shown For b = 0.0011 (red), b = .0044 (blue), b = .0066 (green), b = 0.0099 (black). Other parameters are same as mentioned above

Full size image

The findings of this study align with the outcomes documented by Choudhary et al. [19]. Based on their findings, the researchers have determined that the utilisation of the Hermite-cosh-Gaussian beam is a feasible method for producing terahertz (THz) radiation. Throughout our inquiry, we employed a Hermite-cosh-Gaussian beam as a method to generate terahertz (THz) waves in a plasma profile with slanting density.

Conclusion

The objective of this study is to examine the propagation of two Hermite–Gaussian chirped laser beams within a plasma medium characterised by low density and low collision rates. An analytical method is used to calculate the efficiency of THz generation. This solution considers various elements, including the normalised THz frequency, normalised transverse distance, Hermite polynomial mode index, and frequency chirp. In order to achieve a THz source that is both tuneable and energy-efficient, the produced solution is subjected to further examination to optimise the aforementioned properties. The normalised THz amplitude exhibits significant values up to 0.6 for normalised transverse lengths corresponding to s = 1. The findings indicate a significant rise in the normalised amplitude of the THz signal as the index value of the Hermite polynomial mode transitions from 0 to 2. Additionally, it is evident that the peak demonstrates a significant shift towards higher values of normalised transverse distance.