Introduction

THz waves are electromagnetic signals in the frequency range of 0.1 to 10 THz that are non-invasive and non-ionizing. THz waves are used for various diagnostic applications such as early cancer detection, oral tissue detection, concealed objects detection, food safety and quality inspection, bacteria detection and burn diagnosis [1,2,3,4,5]. The interaction between laser and plasma is a significant phenomenon used in generating terahertz (THz) waves, Wakefield acceleration [6, 7], self-focusing and defocusing, harmonics generation, and fusion research [8,9,10,11,12,13,14,15,16,17,18,19]. Scholars and scientists have analyzed the generation of THz waves through theoretical and experimental methods [20,21,22,23,24,25,26,27,28]. Sharma et al. [29] researched the Hermite-Gaussian laser pulse in a uniform plasma within the context of laser wakefield acceleration in low-density collisionless plasma. The theoretical research revealed a higher energy gain for mode indices s = 0 and s = 2 compared to s = 1. They analyze the electron energy increase based on pulse duration, plasma density, and beam width for a certain mode index. Pramanik et al. [30] researched the use of a radially polarized Hermite-cosh-Gaussian laser beam for accelerating electrons in an ion channel. They analyzed the relationship between electron energy gain and intensity parameter, laser spot size, decentered parameter, and ion density.

Verma et al. [31] researched the interaction of an electron Bernstein wave with a Hermite-cosh-Gaussian laser beam in a collisional plasma under the influence of a static magnetic field. The researchers visually confirmed that the nonlinear absorption coefficient is influenced by the Hermite mode index, laser beam width, and decentered parameter.

Tian et al. [32] researched the Hermite-cosh-Gaussian laser beam in inhomogeneous plasma by employing high-order paraxial theory and WKB approximation to analyze self-focusing filamentation instability. The researchers noted that the higher order mode index has a considerable impact on filamentation instability. Ghotra et al. [33] researched the Hermite-cosh-Gaussian laser pulse in low-order axisymmetric modes in a vacuum for electron acceleration. Pandari et al. [34] conducted simulation research on THz generation via femtosecond laser wakefield acceleration in a helium gas jet. Frolov [35] researched the production of THz waves using ultra-short tightly concentrated p-polarized laser pulses on a near-critical plasma slab. The THz wave signal and conversion rate occur at almost normal incidence, as demonstrated by him. Varaki et al. [36] analyze the theoretical aspects of THz wave generation from Wakefield-driven collisional plasma using a skew-cosh-Gaussian laser beam in the presence of an undulator magnetic field. He demonstrates that a low collisional frequency significantly affects Wakefield amplitudes. When the collisional frequency matches the plasma frequency, the amplitude of the Wakefield is reduced. Ashish et al. [37] researched the creation of THz radiation from the interaction of a modulated laser field with plasma in the presence of an axially magnetic field. greater THz field strength is achieved with greater values of mode index.

Zare et al. [38] theoretically analyze the localization of Gaussian beams in hot quantum plasma with a density ramp. An experiment was conducted to study how varying laser intensity affects the critical normalized beam radius at different Fermi temperatures. Punia et al. [39] researched the skew-cosh Gaussian beam in spherical and cylindrical nanoparticles to create a tunable THz radiation source. They demonstrate a shift in the resonance peak towards higher frequencies. Khandale et al. [40] investigated the skew-cosh-Gaussian laser beam in collisional plasma using the Akhmanov parabolic wave equation and paraxial approximation. The study demonstrated that the skewness parameter has a considerable impact on the self-focusing and defocusing of a laser beam.

Two Hermite Gaussian (HG) lasers with radial polarization are moving in the z direction and interacting with a homogenous plasma in this study. The laser beams are characterized by frequencies \({\omega }_{1}\) and \({\omega }_{2}\), and wave numbers\({\overrightarrow{k}}_{1} , {\overrightarrow{k}}_{2}\). By solving the equations of motion, continuity, and Poisson, we derive a non-linear current density. THz fields are generated due to the presence of a non-linear current density. This investigation considers the impact of electron collision. Section II presents the mathematical derivation of the ponderomotive force, the nonlinear plasma current density, and the creation of THz fields. This is achieved through the examination of the interaction between high-energy laser pulses and an inclined plasma profile. Section III examines the relationship between the normalized THz electric field and the beat frequency, as well as the collisional frequency normalized with the plasma frequency. Section IV presents the ultimate conclusions and results. Citations are provided at the conclusion of the document.

Investigation of THz generation via analytical study

Two Hermite-Gaussian laser beams with radial polarization are propagating in the z-direction and interacting with a homogenous plasma of density \({n}_{0}\). The equations given represent the electric and magnetic fields of laser pulses.

$$\overrightarrow{{\mathrm{E}}_{\mathrm{j}}}\left(\mathrm{r},\mathrm{z}\right)= \widehat{\mathrm{r}}{\mathrm{E}}_{0}{\mathrm{H}}_{\mathrm{s}}\left(\frac{\sqrt{2}\mathrm{r}}{{\mathrm{r}}_{0}}\right){\mathrm{e}}^{-\left(\frac{{\mathrm{r}}^{2}}{{{\mathrm{r}}_{0}}^{2}}\right)}{\mathrm{e}}^{\mathrm{i}({\mathrm{k}}_{\mathrm{J}}\mathrm{z}-{\upomega }_{\mathrm{J}}\mathrm{t})}$$
(1)
$$\begin{array}{cc}\overrightarrow{{\mathrm{B}}_{\mathrm{j}}}\left(\mathrm{r},\mathrm{z}\right)= \frac{\left\{{\overrightarrow{\mathrm{k}}}_{\mathrm{J}}\times \overrightarrow{{\mathrm{E}}_{J}}\left(\mathrm{r},\mathrm{z}\right)\right\}}{{\upomega }_{\mathrm{J}}}& \mathrm{where }J=\mathrm{1,2}\end{array}$$
(2)

here, \(\overrightarrow{{\mathrm{B}}_{\mathrm{j}}}\left(\mathrm{r},\mathrm{z}\right)\) represents the magnetic field of laser pulse, \(r=r\left(x,y\right)=\sqrt{{x}^{2}+{y}^{2}}\) is radius of Gaussian pulse, \({r}_{0}\) is pulse waist which is a transverse distance where electric field remains 1/e times its value at axis, \({E}_{0}\) is amplitude of laser pulse and \(s\) is the mode index of Hermite polynomial \({H}_{s}\).

Hermite functions are defined as follows: \({H}_{0}\left(x\right)=1, {H}_{1}\left(x\right)=2x, {H}_{2}\left(x\right)=4{x}^{2}-2.\) The outcome is dependent on the value of x.

Electrons at rest do not experience any magnetic force in the initial stage. Laser pulses induce oscillatory velocity in plasma electrons as they pass through the plasma.

By employing the equation of motion \({~}^{md\overrightarrow{{V}_{j}}}\!\left/ \!{~}_{dt}\right.= -e \overrightarrow{{E}_{j}}-m{\gamma }_{en}\overrightarrow{{V}_{j}}\) where \({\gamma }_{en}\), \(e\) and \(m\) represent collision frequency, charge of plasma electron and rest mass, respectively. We determine the velocity of plasma electrons as

$$\overrightarrow{{V}_{j}}= \frac{e \overrightarrow{{E}_{j}}}{m(i{\omega }_{J}-{\gamma }_{en})}$$
(3)

The oscillating velocity results in a nonlinear ponderomotive force. This force can be defined as

$${\overrightarrow{{F}_{P}}}^{NL}= - \frac{m}{2} \overrightarrow{\nabla }\left(\overrightarrow{{V}_{1}}. {\overrightarrow{{V}_{2}}}^{*}\right)$$

so, we get

$$\Rightarrow {\overrightarrow{{F}_{P}}}^{NL} = {\overrightarrow{{F}_{or}}}^{NL}{e}^{i(({k}_{1}-{k}_{2})z-({\omega }_{1}-{\omega }_{2})t)}={\overrightarrow{{F}_{or}}}^{NL}{e}^{i({k}{\prime}z-{\omega }{\prime}t)}$$
(4)
$$\mathrm{where }\Delta = {~}^{{{E}_{0}}^{2}{e}^{2}{H}_{s}\left({~}^{\sqrt{2}r}\!\left/ \!{~}_{{r}_{0}}\right.\right){e}^{-\left({~}^{2{r}^{2}}\!\left/ \!{~}_{{{r}_{0}}^{2}}\right.\right)}{e}^{i{k}{\prime}z-{\omega }{\prime}t)}}\!\left/ \!{~}_{\left[2m (i{\omega }_{1}-{\gamma }_{en})(i{\omega }_{2}+{\gamma }_{en})\right]}\right.$$
(4a)
$${k}{\prime}=\left({k}_{1}-{k}_{2}\right) , {\omega }{\prime}={(\omega }_{1}-{\omega }_{2}),$$
(4b)

and

$${\overrightarrow{{F}_{or}}}^{NL}=\Delta \left[\widehat{r}\left\{s\left({~}^{4\sqrt{2}r}\!\left/ \!{~}_{{r}_{0}}\right.\right){H}_{s-1}\left({~}^{\sqrt{2}r}\!\left/ \!{~}_{{r}_{0}}\right.\right)+{\left({~}^{2b}\!\left/ \!{~}_{{r}_{0}}\right.\right)H}_{s}\left({~}^{\sqrt{2}r}\!\left/ \!{~}_{{r}_{0}}\right.\right)-\left({~}^{4r}\!\left/ \!{~}_{{{r}_{0}}^{2}}\right.\right){H}_{s}\left({~}^{\sqrt{2}r}\!\left/ \!{~}_{{r}_{0}}\right.\right)\right\}+ \left\{\widehat{z}i{k}{\prime}{H}_{s}\left({~}^{\sqrt{2}r}\!\left/ \!{~}_{{r}_{0}}\right.\right)\right\}\right]$$
(4c)

By solving the equation of motion, \({~}^{\partial {\overrightarrow{V}}_{{\omega }{\prime}}^{NL}}\!\left/ \!{~}_{\partial t}\right.=\left({~}^{{\overrightarrow{F}}_{P}^{NL}}\!\left/ \!{~}_{m}\right.\right)-{\nu }_{en}{\overrightarrow{V}}_{{\omega }{\prime}}^{NL}\) and the equation of continuity \({~}^{\partial {n}_{{\omega }{\prime}}^{NL}}\!\left/ \!{~}_{\partial t}\right.+\overrightarrow{\nabla }. {n\overrightarrow{V}}_{{\omega }{\prime}}^{NL}=0\), the value of \({\overrightarrow{V}}_{{\omega }{\prime}}^{NL}\) can be determined.

The plasma density profile is homogeneous with \(n={n}_{0}\) where, \({n}_{0}\) represents the initial unperturbed plasma density.

The equation given produces both nonlinear oscillatory velocity and nonlinear density perturbation of plasma electrons.

$$\Rightarrow {\overrightarrow{V}}_{{\omega }{\prime}}^{NL}=\frac{i{\omega }{\prime}{\overrightarrow{F}}_{P}^{NL}}{m\left({{\omega }{\prime}}^{2}+i{\omega }{\prime}{\gamma }_{en}\right)}$$
(5)
$$\Rightarrow {n}_{{\omega }{\prime}}^{NL}= \frac{{n}_{0}\overrightarrow{\nabla }.{\overrightarrow{F}}_{P}^{NL}}{m\left({{\omega }{\prime}}^{2}+i{\omega }{\prime}{\gamma }_{en}\right)}$$
(6)

In this derivation, we assume the value of n remains constant throughout time and is solely dependent on z.

$${~}^{\partial (\mathrm{n})}\!\left/ \!{~}_{\partial \mathrm{t}}\right.=0.$$

Nonlinear density perturbations \({n}_{{\omega }{\prime}}^{NL}\) lead to the creation of a self-consistent space charge potential and field by causing electrons to separate from ions.

This gives rise to linear density perturbation as \({n}_{{\omega }{\prime}}^{L}=-{~}^{{\chi }_{P}\overrightarrow{\nabla }.(\overrightarrow{\nabla }\phi )}\!\left/ \!{~}_{4\pi e}\right.\) where, \({\chi }_{P}\) represents the electric susceptibility of collisional plasma and is calculated as \(-{~}^{{\omega }_{P}^{2}}\!\left/ \!{~}_{\left({{\omega }{\prime}}^{2}+i{\omega }{\prime}{\gamma }_{en}-{{k}{\prime}}^{2}{V}_{th}^{2}\right)}\right.\).

The Poisson’s equation\({\nabla }^{2}\phi =4\pi \left({n}_{{\omega }{\prime}}^{L}+{n}_{{\omega }{\prime}}^{NL}\right)e\), is used to calculate the space charge field’s linear force, represented as \({\overrightarrow{F}}_{P}^{L}\), acting on the electrons such as

$${\overrightarrow{F}}_{P}^{L}=\mathrm{e}\overrightarrow{\nabla }\phi =\frac{{\omega }_{P}^{2} {\overrightarrow{F}}_{P}^{NL}}{\left(1+{\chi }_{P}\right)\left({{\omega }{\prime}}^{2}+i{\omega }{\prime}{\gamma }_{en}\right)}$$
(7)

as, \({\omega }_{P}=\sqrt{\left({~}^{4\pi {n}_{0}{e}^{2}}\!\left/ \!{~}_{m}\right.\right)}\) is \(\mathrm{plasma\;frequency}\).

To get the nonlinear oscillatory velocity of electrons, one can calculate the equation of motion \({~}^{\partial {\overrightarrow{V}}^{NL}}\!\left/ \!{~}_{\partial t}\right.={~}^{\left({\overrightarrow{F}}_{P}^{NL}+{\overrightarrow{F}}_{P}^{L}\right)}\!\left/ \!{~}_{m}\right.-{\gamma }_{en}{\overrightarrow{V}}^{NL}\), which consider the influence of both linear and nonlinear ponderomotive forces.

$$\Rightarrow {\overrightarrow{V}}^{NL}=\frac{1}{m}\left\{\frac{{{\omega }{\prime}}^{2}+i{\omega }{\prime}{\gamma }_{en}-{\omega }_{P}^{2}+{\omega }_{P}^{2} }{\left(-i{\omega }{\prime}+{\gamma }_{en}\right)\left({{\omega }{\prime}}^{2}+i{\omega }{\prime}{\gamma }_{en}-{\omega }_{P}^{2}\right)}\right\}{\overrightarrow{F}}_{P}^{NL}$$
(8)

Nonlinear oscillatory current density is shows as

$${\overrightarrow{J}}^{NL}=-\frac{1}{2}{n}_{0}e{\overrightarrow{V}}^{NL}=-\frac{{n}_{0}e}{2m}\left\{\frac{{\omega }^{2}+i\omega {\gamma }_{en}-{\omega }_{P}^{2}+{\omega }_{P}^{2}}{\left(-i\omega +{\gamma }_{en}\right)\left({{\omega }{\prime}}^{2}+i\omega {\gamma }_{en}-{\omega }_{P}^{2}\right)}\right\}{\overrightarrow{{F}_{or}}}^{NL}{e}^{i(kz-\omega t)}$$
(9)

where, \(\left({k}_{1}-{k}_{2}\right)=k\approx {k}{\prime}, \left({\omega }_{1}-{\omega }_{2}\right)=\omega \approx {\omega }{\prime}\).

\(k\) and \(\omega\) denote the propagation constant and frequency of the terahertz (THz) field, respectively. The vector \({\overrightarrow{J}}^{NL}\) results in the production of THz fields.

By solving Maxwell’s equations \(\overrightarrow{\nabla }\times \overrightarrow{E}=-\frac{1}{c}\left({~}^{\partial \overrightarrow{B}}\!\left/ \!{~}_{\partial t}\right.\right)\) and \(\overrightarrow{\nabla }\times \overrightarrow{B}=\frac{\varepsilon }{c}\left({~}^{\partial \overrightarrow{E}}\!\left/ \!{~}_{\partial t}\right.\right)+\frac{4\pi }{c}{\overrightarrow{J}}^{NL}\)

The equation for generating terahertz waves is as follows.

$$\Rightarrow \overrightarrow{\nabla }.\left(\overrightarrow{\nabla }. {\overrightarrow{E}}_{THz}\right)-{\nabla }^{2}{\overrightarrow{E}}_{THz}= \frac{{\omega }^{2}}{{c}^{2}}\varepsilon {\overrightarrow{E}}_{THz}+\frac{4\pi i\omega }{{c}^{2}}{\overrightarrow{J}}^{NL}$$
(10)

The symbol \({\overrightarrow{E}}_{THz}\) denotes the electric field of the produced THz pulse.

Here, we ignore the higher order derivatives due to the frequent variations in the THz field.

here, the expression expresses the electrical permittivity of collisional plasma as

$$\varepsilon =1-\left[{~}^{{\omega }_{P}^{2}}\!\left/ \!{~}_{\left\{{\omega }^{2}+i\omega {\gamma }_{en}\right\}}\right.\right].$$

For the Solution of Eq. (10), we utilize the nonlinear oscillatory current density value from Eq. (9) along with the ε value to determine the normalized amplitude of the THz field. We are examining the electric field component along the radial direction.

$$\begin{array}{c}\frac{{E}_{THz}}{E}=\frac{i{\omega }_{P}^{2}}{\varepsilon \omega }\frac{e}{2{r}_{0}}\left\{\frac{{\omega }^{2}+i\omega {\gamma }_{en}-{\omega }_{P}^{2}+{\omega }_{P}^{2}}{\left(-i\omega +{\gamma }_{en}\right)\left({\omega }^{2}+i\omega {\gamma }_{en}-{\omega }_{P}^{2}\right)}\right\}\frac{{E}_{0}{H}_{s}\left(\frac{\sqrt{2}r}{{r}_{0}}\right){e}^{-\left({~}^{{r}^{2}}\!\left/ \!{~}_{{{r}_{0}}^{2}}\right.\right)}}{2m \left(i{\omega }_{1}-{\gamma }_{en}\right)\left(i{\omega }_{2}+{\gamma }_{en}\right)}\\ \left[\widehat{r}\left\{s\left(4\sqrt{2}\right){H}_{s-1}\left(\frac{\sqrt{2}r}{{r}_{0}}\right)+{\left(2b\right)H}_{s}\left(\frac{\sqrt{2}r}{{r}_{0}}\right)-\left(\frac{4r}{{r}_{0}}\right){H}_{s}\left(\frac{\sqrt{2}r}{{r}_{0}}\right)\right\}\right]\end{array}$$
(11)

The ratio, \(\frac{{E}_{THz}}{E}\) represents the relationship between the generated THz electric field and the applied laser electric field. This ratio is known as THz conversion efficiency.

Result and discussion

The study examines the generation of terahertz (THz) radiation by HG laser pulses interacting in a collisional plasma. The plasma density is \(9.74\times {10}^{22} {m}^{-3}\), and the related plasma frequency is \(1.76\times {10}^{13}\mathrm{ Hz}\). The frequencies of the CO2 laser are \({\omega }_{1}=1.973\times {10}^{14}\mathrm{rad}/\mathrm{s and }{\omega }_{2}=1.783\times {10}^{14}\mathrm{ rad}/\mathrm{s}\), both exceeding \({\omega }_{P}\). The laser pulses have wavelengths of \({\lambda }_{1}=9.57 \mu m\;\mathrm{ and }\;{\lambda }_{2}=10. 57 \mu m\). The Gaussian laser beam waist is \({r}_{0}=5\times {10}^{-5}\mathrm{ m}\), and the amplitude of the laser field is \({E}_{0}=2\times {10}^{11} V/\mathrm{m}\).

Effect of laser frequency

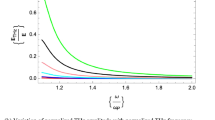
This section examines the change in normalized THz amplitude at various normalized THz frequencies. Curves are graphed for various values of s = 0, 1 and 2 with a collisional frequency \({\gamma }_{en}\) of \(0.1 {\upomega }_{\mathrm{P}}\). The graphs are displayed in Fig. 1a, b, and c. Figure 1d displays the comparative graph.

Fig. 1
figure 1

a Variation of normalized THz amplitude with normalized THz frequency. For r = 0.3r0 s = 0. b Variation of normalized THz amplitude with normalized THz frequency. For r = 0.3r0 s = 1. c Variation of normalized THz amplitude with normalized THz frequency. For r = 0.3r0 s = 2. d Variation of normalized THz amplitude with normalized THz frequency. For r = 0.3r0, s = 0 (blue), 1 (red), 2 (black)

Full size image

The normalized amplitude of THz waves grows as the Hermite polynomial mode index value (s = 0,1,2) increases. At resonance (\(\upomega ={\upomega }_{\mathrm{P}}\)), the normalized THz amplitude reaches its peak. When the ratio of \(\upomega / {\upomega }_{\mathrm{P}}\) exceeds one, the amplitude of THz diminishes and tends towards zero for values of \(\upomega / {\upomega }_{\mathrm{P}}\) greater than 1.8. The normalized amplitude of THz waves is approximately 0.08 and 0.25 for Hermite polynomial mode indices s = 0 and 1, and it approaches to 0.9 for s = 2.

The Hermite mode index quantifies the spatial distribution of the laser beam’s intensity profile. Various Hermite modes have distinct spatial distributions. The selection of the mode has an impact on the spatial distribution of laser energy, which subsequently impacts the dynamics of the plasma and the formation of THz waves. Same can be seen in the theoretical study of this study.

Effect of collision frequency (\({\gamma }_{en}\))

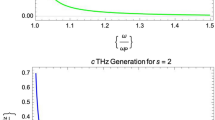
This section examines the change in normalized THz amplitude at various normalized collisional frequencies. We have plotted curves for s values of 0, 1, and 2 at a THz frequency of \(\omega =1.9\times {10}^{13}\mathrm{ Hz}\), depicted in Fig. 2a, b, and c. Figure 2d displays the comparative graph.

Fig. 2
figure 2

a Variation of normalized THz amplitude with normalized collisional frequency. For r = 0.3r0, s = 0. b Variation of normalized THz amplitude with normalized collisional frequency. For r = 0.3r0, s = 1. c Variation of normalized THz amplitude with normalized collisional frequency. For r = 0.3r0, s = 2. d Variation of normalized THz amplitude with normalized collisional frequency. For r = 0.3r0, s = 0 (blue), 1 (red), 2 (black)

Full size image

Normalized terahertz amplitude rises with the increase in Hermite polynomial mode index value (s = 0,1,2). At resonance (\(\upomega ={\upomega }_{\mathrm{P}}\)), the normalized THz amplitude reaches its peak. When the value of \({\gamma }_{en}/ {\upomega }_{\mathrm{P}}\) exceeds one, the THz amplitude declines and tends towards zero for \({\gamma }_{en}/ {\upomega }_{\mathrm{P}}\) values greater than four. The normalized amplitude of the THz signal is around 0.012 and 0.04 for Hermite polynomial modes with index s = 0 and 1 and increases to 0.15 for s = 2. The Hermite polynomial undergoes large changes in its values with variations in the s values. A new type of laser electric field is produced, leading to a major impact on THz generation. Similar findings are seen in our analytical data.

Effect of normalized collisional frequency (\({~}^{{\gamma }_{en}}\!\left/ \!{~}_{{w}_{P}}\right.\)) and normalised frequency

The normalized amplitude of THz waves is calculated for various normalized collisional frequency and varied levels of normalised frequency from 0 to 1.30. A 3D curve is presented for Hermite polynomial mode index value s = 1 at \({E}_{0}=\) \(2\times {10}^{11}\) V/m (Fig. 3).

Fig. 3
figure 3

Variation of normalized THz amplitude with normalized collisional frequency and normalised frequency for s=1. Other parameters are same as mentioned above

Full size image

With the Hermite polynomial mode index value s = 1, the normalized collisional frequency and normalized THz amplitude both increase from 0 to more than 0.6 for different values of normalised frequency ranging from zero to 1.30. This study’s results show a notable increase in normalized Terahertz (THz) amplitude at resonance conditions, and it reduces significantly and tends to zero in off-resonant conditions.

At high collisional frequencies, the plasma does not result in an increase in THz generation. The reason for this is because collisional processes have a greater influence than the nonlinear interactions that are responsible for generating THz waves.

This investigation’s results are consistent with the findings reported by Choudhary et al. [41]. Researchers have found that using the Hermite-cosh-Gaussian beam is a viable approach for generating terahertz (THz) radiation. We utilized a Hermite-Gaussian beam to generate terahertz (THz) waves in a collisional plasma profile with a homogeneous plasma.

Conclusion

This work examines the propagation of two Hermite-Gaussian laser beams in a collisional homogeneous plasma. The plasma density is constant in the pulse direction. This study generates efficient THz waves through the technique of nonlinear laser plasma interaction. The results analyze the correlation between normalized THz amplitude and normalized THz frequency, as well as collisional frequency, across various Hermite polynomial mode index values (s = 0,1,2). As we deviate from resonance, the efficiency of generated THz declines quickly and eventually approaches zero for various values of normalized THz frequency and normalized collisional frequency. The THz conversion efficiency is low, with values of for s = 0 and 1, respectively. It increases significantly for s = 2, reaching 0.9 and 0.15 for normalized THz frequency and normalized collisional frequency, respectively. The THz conversion efficiency increases with higher values of the Hermite polynomial mode index (s = 0,1,2). This approach is particularly advantageous for producing an effective, adjustable THz source.