1 Introduction

Terahertz wave applications in the fields of chemical analysis, non-destructive testing, medical imaging and research is gaining attention of scholars and industries [1,2,3,4]. A wide variety of fields such as nonlinear optics, harmonic generation, self-focusing, filamentation, electron acceleration, wake field generation, terahertz wave generation, etc. uses the laser plasma interaction process [5,6,7,8,9,10]. Hermite-cosh-Gaussian beam is the member of Hermite sinusoidal Gaussian family. The Hermite-cosh-Gaussian function is utilized to represent a laser beam profile that encompasses Hermite polynomials, Gaussian and hyperbolic cosine components, and Gaussian-like spatial variation. The Hermite-cosh-Gaussian function's paraxial wave solution is introduced by Casperson and Tovar [11]. Through the use of a paraxial wave solution, Belafhal et al. [12] theoretically examined the wave propagation characteristics of the Hermite-cosh-Gaussian function in the ABCD system.

Researchers investigate the Hermite-cosh-Gaussian laser beam in diverse laser plasma interaction process. The Hermite-cosh-Gaussian laser beam in magneto-active plasma was studied by Patil et al. [13]. They investigated the role of decentred parameter and the mode index on self-focusing. The self-focusing of a Hermite-cosh-Gaussian laser beam in ramp density and under density plasma profiles was investigated by Nanda et al. [14, 15]. The Hermite-cosh-Gaussian laser beam in ripple density plasma was studied numerically by Kaur et al. [16]. In semiconductor plasma, Wani et al. [17] looked at the self-focusing of a Hermite-cosh-Gaussian beam. The third harmonics generation by Hermite-cosh-Gaussian beam in the presence of wiggler magnetic field was theoretically investigated by Sharma et al. [18]. The beat wave of Hermite-cosh-Gaussian laser beam absorption in collisional nano cluster plasma profile was studied by Verma et al. [19]. In this research, they looked at the Bernstein wave parameters. In collisional plasma, the second harmonics generation of the Hermite Gaussian beam was explored by Wadhwa et al. [20]. The researchers conducted an investigation on the influence of mode indices on the generation of harmonics and the phenomenon of self-focusing. In order to generate terahertz waves, Hamster et al. [21] investigate the interaction between a short, powerful laser pulse and plasma. The researchers conducted an investigation on the nonlinear ponderomotive force effect in the production of terahertz waves. In their study, Safari et al. [22] investigated the properties of collisional plasma by employing laser beams with Gaussian and Hermite-cosh-Gaussian profiles. They came to the conclusion that plasma and laser parameters are crucial for terahertz field amplitude. The terahertz wave generation with radially polarized Hermite-cosh-Gaussian laser beam in hot collisional plasma was studied by Chaudhary et al. [23]. In their theoretical inquiry, Malik et al. [24] looked at the creation of terahertz waves using two Hermite-cosh-Gaussian laser beams in a periodically varying plasma density profile with an applied magnetic field. They investigated how terahertz wave production was affected by the decentred parameter, Hermite function order, and applied magnetic field. Hashemzadeh [25] looked into the production of terahertz waves in magnetized plasma using laser beams that were Hermite-cosh-Gaussian and hollow Gaussian. In their study, Sharma et al. [26] examined the phenomenon of second harmonic generation in a wiggler magnetized plasma by employing a cosh-Gaussian laser beam. In collisional inhomogeneous plasma, Safari et al. [27] looked at the nonlinear processes of Hermite-cosh-Gaussian and Laguerre-Gaussian beam interaction. For the greatest electric field amplitude at terahertz frequencies, they examined various laser parameters and density ripple. The Hermite-cosh-Gaussian laser pulse is investigated by Rajput et al. [28] in their work on electron acceleration in a vacuum. The researchers utilized laser pulses with both circular and linear polarization. The terahertz production was investigated by Mehta et al. [29, 30] by the utilization of a transverse external magnetic field in conjunction with underdense plasma and chirped laser pulses. The authors of the study illustrate the enhancement of the terahertz electric field in the presence of a magnetic field, as well as the optimization of the chirp value. They also investigate the impact of chirped laser pulses on the ripple in density.

Wu et al. [31] studied the chirped laser pulse-induced terahertz pulse production in a lithium niobate crystal at ambient temperature. They produce a 0.2 mJ terahertz pulse for their research. Jiang et al. [32] generated 0.3 mW terahertz pulses while studying the GaP crystal using a negatively chirped femtosecond laser pulse. In order to generate terahertz waves at beat frequency, Gurjar et al. [33] looked at the nonlinear interaction of chirped laser pulse interaction with slanting plasma modulation. They demonstrate that the generated terahertz wave amplitude is strongly affected by the slanting plasma profile. Mehta et al. [29] investigated how frequency chirp affected the generation of THz waves in magneto-active plasma. Scientists and researchers investigate several phenomena related to the interaction between lasers and plasma [34,35,36,37,38,39,40,41,42,43].

In the current study, two linearly polarized chirped Hermite-cosh-Gaussian beams are propagating in z direction. These laser beams propagated in underdense plasma with externally applied transverse static magnetic field. The interaction between laser and plasma results in the generation of intense terahertz (THz) waves. Tuneable efficient THz radiation source can be achieved by adjusting the laser and plasma parameters. Section 2 of this study encompasses the analytical derivation of the ponderomotive force, equation of motion, nonlinear plasma current density, and subsequently, the creation of THz fields. Section 3 of this paper examines the relationship between the normalized THz electric field and several factors, including the normalized THz frequency, normalized transverse distance, and chirp parameter. In Sect. 4, we draw the Conclusions. The document concludes with the inclusion of references.

2 Analytical study of THz generation

Two waves, which are linearly polarized and have the Hermite-cosh-Gaussian profile, are propagating in the z direction. The direction of polarization of the electric field is aligned with the x-axis, and can be mathematically expressed by the following equation.

$$\vec{E}_{J} = \hat{x}E_{0} H_{s} \left( {\frac{\sqrt 2 x}{{w_{0} }}} \right)\cosh \left( {\frac{ax}{{w_{0} }}} \right)e^{{ - \left( {\frac{{x^{2} }}{{w_{0}^{2} }}} \right)}} e^{{i\left( {k_{J} z - \omega_{J} t} \right)}} \quad {\text{where}},\quad J = 1,2$$
(1)

In this context, \({E}_{0}\) represents the amplitude of the laser beam, \({\text{w}}_{0}\) denotes the beam waist, \(a\) signifies the decentred parameter of the cosh profile, and \(s\) represents the mode index of the Hermite polynomial \({H}_{s}\).

Corresponding magnetic field of laser beam are

$$\vec{B}_{j} = \frac{{\overrightarrow {{k_{J} }} \times \vec{E}_{j} }}{{\omega_{J} }}\quad {\text{where}},\quad J = 1,2$$
(2)

Incident laser beam is positively chirped and chirp is represented as \(\omega_{1} =\) \(\omega_{0} + b\omega_{0}^{2} \left( {t - \frac{z}{c}} \right),\) where, \(\omega_{0}\) is the frequency of incident laser beam in the absence of chirp, b is chirp parameter, c is velocity of light. We choose \({\upomega }_{2}\) such as \(\omega_{1} - \omega_{2} = \omega\) lies in THz range.

So

$$\omega_{2} = \omega_{1} - \omega = \left\{ {\omega_{0} + b\omega_{0}^{2} \left( {t - \frac{z}{c}} \right)} \right\} - \omega$$
(3)

An external static magnetic field is applied along the y-axis i.e. \(B_{s} = B_{0} \hat{y}\).

Here, \({\text{B}}_{0}\) is the amplitude of static magnetic field.

During the initial stage, it can be assumed that electrons are in a state of rest, resulting in the absence of any magnetic force acting upon them. The oscillatory velocity of a plasma electron can be determined by using the equation of motion \(m\left( {d\overrightarrow {{V_{J} }} /dt} \right) = - e \overrightarrow {{E_{J} }}\) \(- m\overrightarrow {{V_{J} }}\)ν.

By solving this equation, we get.

$$\overrightarrow {{V_{1} }} = \frac{{e \overrightarrow {{E_{1} }} }}{{im\omega_{0} \left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right)} \right\} - m\nu }}$$
(4)
$$\overrightarrow {{V_{2} }} = \frac{{e \overrightarrow {{E_{2} }} }}{{im\omega_{0} \left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{\omega }{{\omega_{0} }}} \right\} - m\nu }}$$
(5)

here, e, m, \(\upnu\) is charge, rest mass and collisional frequency of the plasma electron respectively.

This oscillatory velocity of plasma electron give rise to nonlinear ponderomotive force.

Nonlinear ponderomotive force is

$$\overrightarrow {{F_{P} }}^{NL} = - \frac{e}{2c} \left( {\overrightarrow {{V_{1} }} \times \overrightarrow {{B_{2} }}^{*} + \overrightarrow {{V_{2} }}^{*} \times \overrightarrow {{B_{1} }} } \right) - \frac{m}{2}\vec{\nabla }\left( {\overrightarrow {{V_{1} }} \overrightarrow {{V_{2} }}^{*} } \right)$$
(6)

here, * represents the complex conjugate.

Solving this equation by putting values of \(\overrightarrow {{V_{1} }} ,\overrightarrow {{V_{2} }}^{*} , \overrightarrow {{B_{1} }} ,\;{\text{and}}\;\overrightarrow {{B_{2} }}^{*}\), we get

$$\begin{aligned} \overrightarrow {{F_{P} }}^{NL} & = - \hat{z} \frac{{e^{2} E_{1} E_{2}^{*} }}{{2im\omega_{0} c}} \left( {\frac{{2\frac{\nu }{{\omega_{0} }} - \frac{\omega }{{\omega_{0} }}}}{{\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{\nu }{{i\omega_{0} }} } \right\}\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{\omega }{{\omega_{0} }} + \frac{\nu }{{i\omega_{0} }}} \right\}}} } \right) \\ & - \hat{z} \frac{{be^{2} E_{1} E_{2}^{*} }}{{m\omega_{0} c}}\left( {\frac{{\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{\omega }{{2\omega_{0} }}} \right\}}}{{\left\{ {\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right)} \right\} - \frac{\nu }{{i\omega_{0} }}} \right\}^{2} \left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{\omega }{{\omega_{0} }} + \frac{\nu }{{i\omega_{0} }}} \right\}^{2} }} } \right) \\ \end{aligned}$$
(7)

Plasma electrons starts moving in circular path due to Lorentz force by external static magnetic field. Circular motion of plasma electron interacts with electric field of laser beam result into angular motion of plasma electron with cyclotron frequency \({\omega }_{c}\).

By solving the equation of motion \(\partial \vec{V}_{\omega }^{NL} /\partial t = \vec{F}_{P}^{NL} /m - \nu_{en} \vec{V}_{\omega }^{NL} - e\left\{ {\vec{V}_{\omega }^{NL} \times \vec{B}} \right\}/\left( {mc} \right)\), we get the oscillatory velocity of plasma electron such as

$$\overrightarrow {{V_{\omega }^{NL} }} = \frac{{\omega_{c} \hat{x} - i\omega \hat{z}}}{{m \left( {\omega_{c}^{2} - \omega^{2} } \right)}}F_{P}^{NL}$$
(8)

here, we consider \(\omega_{1,} \omega_{2} > > \omega_{c} ,\omega_{P}\).

Where, \(\omega_{P} {\text{is plasma frequency is such as}}\;\omega_{P}^{2} = 4\pi ne^{2} /m\) and \(\omega_{c} = eB_{0} /mc\) is cyclotron frequency. Nonlinear oscillatory current density can be calculated by solving this equation

$$\vec{J}^{NL} = - \frac{1}{2}ne\vec{V}^{NL} , \Rightarrow \vec{J}^{NL} = - \frac{{\omega_{P}^{2} }}{8\pi e}\frac{{\omega_{c} \hat{x} - i\omega \hat{z}}}{{\left( {\omega_{c}^{2} - \omega^{2} } \right)}}F_{Pz}^{NL}$$
(9)

This nonlinear current density is responsible for THz generation. By using III and IV Maxwell’s equation, \(\vec{\nabla } \times \vec{E} = - \frac{1}{c}\left( {\partial \vec{B}/\partial t} \right)\) and \(\vec{\nabla } \times \vec{B} = \left( {\varepsilon /c} \right) \left( {\partial \vec{E}/\partial t} \right) + \left( {4\pi /c} \right)\vec{J}^{NL}\), we can calculate the THz wave generation equation.

Equation for THz generation is

$$\vec{\nabla }.\left( {\vec{\nabla }\overrightarrow {{E_{THz} }} } \right) - \nabla^{2} \overrightarrow {{E_{THz} }} = \frac{{\omega^{2} }}{{c^{2} }}\varepsilon \overrightarrow {{E_{THz} }} + \frac{4\pi i\omega }{{c^{2} }}\vec{J}^{NL}$$
(10)

In order to neglect higher order derivatives due to fast variation of THz field. So

$$E_{THz} = \frac{{\omega_{P}^{2} }}{{2e\varepsilon \omega \sqrt {\omega_{c}^{2} - \omega^{2} } }}\left\{ { - \frac{{e^{2} E_{1} E_{2}^{*} }}{{2im\omega_{0} c}} \left( {\frac{{2\frac{\nu }{{\omega_{0} }} - \frac{\omega }{{\omega_{0} }}}}{{\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{\nu }{{i\omega_{0} }} } \right\}\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{\omega }{{\omega_{0} }} + \frac{\nu }{{i\omega_{0} }}} \right\}}} } \right) - \frac{{be^{2} E_{1} E_{2}^{*} }}{{m\omega_{0} c}}\left( {\frac{{\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{\omega }{{2\omega_{0} }}} \right\}}}{{\left\{ {\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right)} \right\} - \frac{\nu }{{i\omega_{0} }}} \right\}^{2} \left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{\omega }{{\omega_{0} }} + \frac{\nu }{{i\omega_{0} }}} \right\}^{2} }}} \right)} \right\}$$
(11)

For collisionless plasma, the Eq. (11) becomes

$$\frac{{E_{THz} }}{{E_{0} }} = \frac{{e\omega_{P}^{2} }}{{2\varepsilon { }\omega \sqrt {\omega_{c}^{2} - \omega^{2} } }}\frac{{\left\{ {H_{s} \left( {\frac{\sqrt 2 x}{{w_{0} }}} \right)\cosh \left( {\frac{ax}{{w_{0} }}} \right)} \right\}^{2} { }e^{{ - \left( {2x^{2} /w_{0}^{2} } \right)}} E_{0} { }}}{{m\omega_{0} c\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right){ }} \right\}\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{\omega }{{\omega_{0} }}} \right\}}}\sqrt {b^{2} \left( {\frac{{\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{\omega }{{2\omega_{0} }}} \right\}}}{{\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right){ }} \right\}\left\{ {1 + b\omega_{0} \left( {2t - \frac{z}{c}} \right) - \frac{\omega }{{\omega_{0} }}} \right\}{ }}}} \right)^{2} - \frac{1}{4}\left[ {\frac{\omega }{{\omega_{0} }}} \right]^{2} }$$
(12)

3 Result and discussion

In this investigation of THz generation, two Hermite-cosh Gaussian polarised laser beams are positively chirped and propagating in cold collisionless underdense plasma. For this study we choose suitable laser parameter such as femtosecond Ti–Sapphire laser with wave length of 800 nm having angular frequency \(2.35 \times 10^{15}\) rad/sec, chirp parameter of \(0.0099\), beam waist of \(5 \times 10^{ - 3}\) cm and electric field amplitude of \(5{ } \times 10^{7}\) V/cm.. Plasma parameters are optimised as plasma density is \(9.74 \times 10^{16} {\text{cm}}^{ - 3}\), whose corresponding plasma frequency \({\upomega }_{P}\) is\(1.76 \times 10^{13} {\text{Hz}}\). Here in present study we choose \(\omega = 1.07 \omega_{P}\) where, \(\omega_{1} ,\omega_{2} > \omega_{P}\) and applied external static magnetic field \(B_{0} {\text{is}}\) 10 \(\times 10^{4}\) gauss.

3.1 Effect of normalised transverse distance (\(\user2{x/}{\mathbf{w}}_{0}\)) and decentred parameter (b)

Variation of normalized THz wave amplitude is calculated at different normalized transverse distance and different decentred values \(a = 0,1,2,3\). A three dimensional curve is plotted for different values of Hermite polynomial mode index values \(s = 0,1,2\) at \(E_{0} =\) \(5{ } \times 10^{7}\) V/cm and external static magnetic field is 10 \(\times 10^{4}\) gauss (Fig. 1).

Fig. 1
figure 1

Variation of normalized THz amplitude with normalized transverse distance and decentered parameter. (\(s = 0,\quad r = 0.5r_{0} ,\) \({\mathbf{a}})\quad s = 0\), b s \(=\) 1, c s \(=\) 2. Other parameters are same as mentioned above

Full size image

When the Hermite polynomial mode index value is varied for \(s = 0,1\;{\text{and}}\;2\), the normalized transverse distance and normalised THz amplitude exhibit a shift towards higher values, specifically from 1.4 to 1.9 and from 0.0015 to 0.8, respectively. The findings of this study indicate a significant rise in normalised terahertz (THz) amplitude when the decentred parameter exceeds a value of 2.

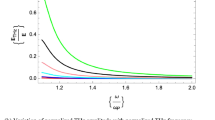
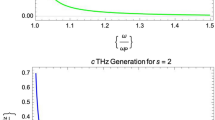
3.2 Effect of normalised THz frequency (\(\omega /\omega_{{\varvec{P}}}\))

This study aims to conduct a theoretical analysis of the relationship between the normalised amplitude of THz radiation and the normalised frequency of THz waves (Fig. 2). The analysis focuses on various values of the Hermite polynomial mode index, specifically \(s = 0,1,2{\text{ and different decentered parameter values }}a = 0,1,2.\)

Fig. 2
figure 2

Variation of normalized THz amplitude with normalized THz frequency with mode index a \(s = 0,\quad r = 0.5\;r_{0} ,\) s \(= 0,\quad {\mathbf{b}}{ }s = 1,{ }{\mathbf{c}}{ }s = 2\;{\text{are shown}}.{\text{ For decentered parameter }}a = 0{ }\left( {{\text{red}}} \right),\;{\text{a}} = 1{ }\left( {{\text{blue}}} \right){\text{and}}\;{\text{a}} = 2\left( {{\text{magenta}}} \right){\text{for}}\) \({\text{chirp parameter b}} = { }0.0099.\) Other parameters are same as mentioned above

Full size image

The normalized terahertz amplitude with the Hermite polynomial mode with index \(s = 0,1, 2\) rises when the chirp parameter b is set to 0.0099 and a static magnetic field of 10 \(\times 10^{4}\) gauss is applied. In the case of larger values of normalised THz frequency, it can be observed that the normalised THz amplitude experiences a rapid decline and eventually approaches zero when the frequency exceeds 1.2 times the normalised plasma frequency (\(\omega\)> 1.2 \(\omega_{P}\)). There is a lack of substantial impact observed when considering the decentred parameter and chirp parameter beyond the specified threshold.

3.3 Effect of chirp parameter (b)

This study focuses on examining the relationship between the normalised THz amplitude and the normalised THz frequency. The examination explores various values of the Hermite polynomial mode index (\(s = 0,1, 2\)) and the decentred parameter value (a = 2) under varied chirp levels b = 0.0011, 0.0044, 0.0066 and 0.0099 (Fig. 3).

Fig. 3
figure 3

Variation of normalized THz amplitude with normalized transverse distance with mode index a \(s = 0,\quad r = 0.5\;r_{0} ,\) s \(= 0,{ }{\mathbf{b}}{\text{ s}} = 1,\quad {\mathbf{c}}{\text{ s}} = 2{\text{ are shown}}.{\text{ For}}\;{\text{b}} = 0.0011\left( {{\text{red}}} \right),\quad {\text{b}} = 0.0044{ }\left( {{\text{blue}}} \right),\quad {\text{b}} = 0.0066{ }\left( {{\text{magenta}}} \right),\quad {\text{b}} = 0.0099{ }\left( {{\text{green}}} \right){\text{ for decentered parameter a}} = 2.\) Other parameters are same as mentioned above

Full size image

As the Hermite polynomial mode index value is incremented from 0 to 2, there is an observed increase in the normalised THz amplitude, ranging from around 0.0016 to 0.26 and there is a noticeable shift in the peak towards larger normalized transverse distance values from 0.92 to 1.63. The THz normalized amplitude exhibits an increasing trend as the chirp parameter (b) varies across multiple values, specifically \(0.0011{ },\;0.0044{ },\;0.0066\quad {\text{and}}\quad 0.0099\).

The results of this investigation align with the findings reported by Choudhary et al. [23]. The researchers reached the conclusion that the utilization of the Hermite-cosh-Gaussian beam is an effective method for generating terahertz (THz) radiation. In the course of our inquiry, we employed a chirped Hermite-cosh-Gaussian beam as a means to generate terahertz (THz) waves.

4 Conclusion

This study examines the propagation of two Hermite-cosh-Gaussian chirped laser beams in a collisionless underdense plasma medium. An analytical solution is derived to determine the efficiency of terahertz (THz) generation, considering various characteristics such as the normalized THz frequency, normalized transverse distance, and frequency chirp. The resulting solution is then analysed to optimize these parameters, aiming to achieve a tuneable and energy-efficient THz source. The normalized THz amplitude exhibits significant values up to 0.8 for normalized transverse distances corresponding to s values of 0, 1, and 2. The findings indicate that as the index value of the Hermite polynomial mode increases from 0 to 2, there is a discernible rise in the normalized amplitude of the THz signal. Additionally, there is an observable displacement of the peak towards higher values of normalized transverse distance.