Prey–Predator Dynamics with Two Predator Types and Michaelis–Menten Predator Harvesting

Abstract

We consider the population dynamics of prey under the effect of the two types of predators. One of the predator types is harvested, modelled with a term with a Michaelis–Menten type functional form. Besides local stability analysis, we are interested that how harvesting could directly affect the dynamics of the ecosystem, such as existence and dynamics of coexistence equilibria and periodic solutions. Theoretical and numerical methods are used to study the role played by several bifurcations in the mathematical models.

Introduction

The dynamic relationship between prey and predators remains an important issue in mathematical ecology [1, 4, 17, 23, 24, 37, 48, 57]. Common models of ecological prey–predator interactions consist of two-dimensional ordinary differential equations with terms representing the growth of the prey and predator populations and the consumption of prey by the predator. In these models, the species normally follow different growth functions [20, 26, 56]. Among these functions, the logistic growth function is an important one, first used by Verhulst [49] to model growth of human populations. Although there exist some other growth functions [22, 40], Feller [16] argued that for almost every population that increases to asymptotically approach a finite size, it is adequate to model its growth with the logistic growth function. The most crucial element in these models is the “functional response”, that describes the rate at which the prey are consumed by the predator. The first prey–predator models (Lotka–Volterra) [36, 39, 49, 50] used a simple functional response proportional to the population of predators. Several other types of response functions were formulated later, such as the Holling types [25, 26], the ratio-dependence type [2, 33], and the Beddington–DeAngelis type [3, 15]. Two-species predator–prey models have been studied extensively, for example [6, 11, 13, 29, 30].

The long-term dynamics of ecological systems and the persistence of species within them are substantial concerns in ecology. Mathematical models have been used to investigate these issues in a variety of ecological systems. For example, Bian et al. [5] considered a stochastic prey–predator system in a polluted environment with a Beddington–DeAngelis functional response, and obtained a sufficient condition to ensure the existence of boundary and positive periodic solutions.

Furthermore, from the point of view of the management of renewable resources, the effects of harvesting of populations are vitally important to predict [9, 54]. Many authors have studied prey–predator models with harvesting functions that are constant, linear or rational [14, 31, 35, 43, 46, 55, 58,59,60]. Two- and three-dimensional models with linear harvesting and/or refuge, as well as harvesting with the habitat divided into two patches, have been studied in [12, 32, 44]. A detailed study of the impact of harvesting of one or two species and its relationship to maximum sustainable yield is given in [21, 41]. In 1979, May et al. [41] proposed the following model to describe the interaction of a prey species and a predator species, subjected to various harvesting terms:

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{P}}=rP\left( 1-\frac{P}{k}\right) -aPU-H_1, \\ \\ {\dot{U}}=sU\left( 1-\frac{U}{bP}\right) -H_2, \end{array}\right. \end{aligned}$$

(1)

where P(t) and U(t) represent the population densities of prey and predators at time t, respectively; r and k describe the intrinsic growth rate and the carrying capacity of the prey in the absence of predators, respectively; a is the maximum value at which per capita reduction rate of the prey P can attain; s is the intrinsic growth rate of predators; bP takes on the role of a prey-dependent carrying capacity for predators and b is a measure of the quality of the food for predators. The terms $H_1$ and $H_2$ describe the effects of harvesting on the prey and predators, respectively. In [7], Chakraborty et al. proposed a two-dimensional prey–predator model where predator’s functional response is ratio-dependent and predator population is harvested at catch-per-unit effort hypothesis. Ratio-dependent prey–predator models with harvesting have been studied more recently [38, 55] mainly from a mathematical point of view. In [27], Hu and Cao give a detailed analysis for a system (1) with a Michaelis–Menten type functional form of harvesting rate for predators $H_2=\frac{qEU}{cE+lU}$, and with $H_1 = 0$. The existence and stability of equilibria, and the existence of codimension one bifurcations, such as saddle-node, transcritical and Hopf, and as well as a codimension two Bogdanov–Takens bifurcation, are shown. Song et al. [47] proposed a prey–predator model with Michaelis–Menten type predator harvesting and a diffusion term. They derived sufficient conditions to ensure that the coexistence equilibrium is asymptotically stable by analyzing the distribution of characteristic roots, and investigated a Hopf bifurcation.

In recent decades, it has been demonstrated that complex dynamics, including chaos, can appear in continuous-time models with three or more species [18, 45, 51]. For instance, to study the impact of predation by different types of predators on prey population dynamics, Mukhopadhyay and Bhattacharyya [42] formulate a model describing the population dynamics of one prey species (P) and two species of predators (U, V)

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{P}}=rP\left( 1-\frac{P}{k}\right) -g(P,U,V)-h(P,U,V), \\ \\ {\dot{U}}=sU\left( 1-\frac{\gamma U}{P}\right) ,\\ \\ {\dot{V}}=eh(P,U,V)-mV, \end{array}\right. \end{aligned}$$

(2)

where it is assumed that g(P, U, V), h(P, U, V) are Holling type II and type III functional responses, respectively. They analyze the model from a thermodynamic perspective and study the thermodynamic stability of the different equilibria.

Motivated by these two papers [27, 42], in this work we consider a three-species model which is similar to (2), but with harvesting of one predator species with a Michaelis–Menten type functional form. Also, instead of Holling types II and III functional responses, we assume Holling types I and II functional responses, respectively. Generally, the effects of harvesting in prey–predator systems is a relatively new issue and most previous studies of prey–predator systems with harvesting consist of two-species models. Here, we study a three-species continuous-time prey–predator model with two predator types where one species of predator is harvested, using a Michaelis–Menten type function to model the harvesting. To the best of our knowledge, a three-species system such as (2) with a nonlinear harvesting function in prey or predator species has not yet been studied as mathematical model, hence this study can be considered complementary to the studies of systems (1) and (2). Our study includes local stability analysis, existence of periodic solutions and codimension one and two bifurcations, as well as conditions for the nonexistence of periodic orbits in the model. We give more details in the last paragraph of “Conclusion”.

The layout of this paper is as follows: the basic assumptions and the model formation are given in “Mathematical Model”. In “Equilibria and Invariant Region”, the existence of equilibria and the dissipative properties of the system are studied. The stability properties of equilibria are discussed in “Linearized Stability”. “Local Bifurcations” studies the existence of bifurcations. We show that, in addition to codimension one bifurcations, such as saddle-node, transcritical and Hopf, there is also a codimension two Hopf-steady state bifurcation. Numerical calculations are used to illustrate and extend the theoretical results. Finally, a conclusion is given in “Conclusion”.

Mathematical Model

In this section, we present the system of differential equations describing the prey–predator model with Michaelis–Menten type predator harvesting. The model takes in to account one prey population P and two different types of predators: U and V are the population sizes of the two predator species at any time t and we suppose that there is no direct competition between them. We considered our system with a Michaelis–Menten type functional form of harvesting rate in one of the predators. In this paper, we consider the model

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{P}}=rP\left( 1-\frac{P}{k}\right) -c_{1}PU-\frac{c_{2}PV}{P+d_{2}}, \\ \\ {\dot{U}}=sU\left( 1-\frac{\gamma U}{P}\right) -\frac{qEU}{cE+lU},\\ \\ {\dot{V}}=\frac{ec_{2}PV}{P+d_2}-mV, \end{array}\right. \end{aligned}$$

(3)

where, we assume that the prey population experiences logistic growth in the absence of both predators with carrying capacity k and maximum intrinsic growth rate r. The parameter $c_1$ is the search rates of the first type of predator on the prey species, and $c_{2}$ is the search rate by the second type of predator. The parameter $d_{2}$ is the half-saturation constant for a Holling type 2 predator. Also, the growth for the first type of predator is supposed to follow a logistic law with $s(>0)$ as the predator’s intrinsic growth rate of population and the carrying capacity is taken to be dynamic and is proportional to the prey density ($\frac{P}{\gamma }$). We assumed that the first type of predator is harvested at a rate harvesting, $H(E,U)=\frac{qEU}{cE+lU}$, proposed by Clark [10], the so-called Michaelis–Menten type functional form, where q is the catchability coefficient, E is the external effort devoted to harvesting, c and l are constants. The second type of predator is supposed to follow a Holling type 2 functional response; e is the conversion efficiency, denoting the number of newly born of the second type of predator for each captured prey species; m is the natural death rate of the second type of the predator.

In order to simplify system (3), we take the following scalings as in [28],

$$\begin{aligned} \overline{t}=rt, \quad \overline{P}=\frac{ec_2}{r}P, \quad \overline{U}=\frac{c_1}{r}U, \quad \overline{V}=\frac{c_2}{r}V, \end{aligned}$$

drop the bars, then rewrite the system (3) as:

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{P}}=P \left[ ( 1-\alpha P)-U-\frac{V}{\beta P+d_{2}}\right] , \\ \\ {\dot{U}}=U\left[ \left( \delta -\eta \frac{ U}{P}\right) -\frac{\xi }{\mu +U}\right] ,\\ \\ {\dot{V}}=V\left[ \frac{P}{\beta P+d_2}-\frac{m}{r}\right] , \end{array}\right. \end{aligned}$$

(4)

where $\beta =\frac{r}{ec_2}$, $\alpha =\frac{r}{ec_2k}=\frac{\beta }{k}$, $\delta =\frac{s}{r}$, $\eta =\frac{s\gamma ec_2}{rc_1}=\frac{s\gamma }{c_1\beta }$, $\xi =\frac{c_1qE}{lr^2}$ and $\mu =\frac{c_1cE}{lr}$ are positive constants.

If we change the parameters $c_2$ (or r, or e) and q while keeping all other parameters in (3) fixed, we equivalently change parameters $\beta$ and $\xi$ in (4), but with

$$\begin{aligned} \alpha =\frac{\beta }{k}, \quad \eta =\frac{s\gamma }{c_1\beta }, \end{aligned}$$

(5)

and k, s, $\gamma$, $c_1$ fixed. In our numerical exploration of the dynamics of (4), we vary $\beta$ and $\xi$ and use (5).

Equilibria and Invariant Region

Equilibria

In order to obtain the equilibria of system (4), we consider the nullclines, which are given by:

$$\begin{aligned} \left\{ \begin{array}{l} P\left[ 1-\alpha P-U-\frac{V}{\beta P+d_{2}}\right] =0, \\ \\ U\left[ \delta -\eta \frac{ U}{P}-\frac{\xi }{\mu +U}\right] =0,\\ \\ V\left[ \frac{P}{\beta P+d_2}-\frac{m}{r} \right] =0. \end{array}\right. \end{aligned}$$

(6)

Equilibria are in the intersections of these nullclines. We easily see that system (4) possesses a unique axial equilibrium $E_1$ and a ($U=0$) boundary equilibrium $E_2$, respectively, given by

$$\begin{aligned} E_1=\left( \frac{1}{\alpha },0,0\right) ,\qquad E_2=(P_2,0,V_2), \end{aligned}$$

where $P_2=\frac{md_2}{r-m\beta }$, $V_2=\frac{rP_2}{m}(1-\alpha P_2)$, with $r-m\beta >0$ and parameters such that $V_2>0$, i.e, $\beta <\min \left\{ \frac{r}{m},\frac{rk}{m(k+d_2)}\right\} =\frac{rk}{m(k+d_2)}$. For other possible ($V=0$) boundary equilibria, we need to consider the positive solutions $P>0$, $U>0$ of the following system:

$$\begin{aligned} \left\{ \begin{array}{l} 1-\alpha P-U=0, \\ \\ \delta -\eta \frac{U}{P}-\frac{\xi }{\mu +U}=0. \end{array}\right. \end{aligned}$$

(7)

About the number of $V=0$ boundary equilibria $E_j=(P_j,U_j,0)$ of system (4), we have the following theorem [27].

Theorem 1

The $V=0$ boundary equilibria of system (4) are the axial state $E_1$ and:

• (a) If $\xi >\xi _1=\delta \mu +\delta +\eta \mu \alpha +2\eta \alpha -2 \sqrt{\eta \alpha (1+\mu )(\eta \alpha + \delta )}$, then system (4) has no positive $V=0$ boundary equilibria.

• (b) If $\xi =\xi _1$ and $\mu <\frac{\delta }{\eta \alpha }$, then system (4) has a unique positive $V=0$ boundary equilibrium

  $$\begin{aligned} E_3=(P_3,U_3,0), \end{aligned}$$

  where $P_3=\frac{\sqrt{\eta \alpha (1+\mu )(\eta \alpha + \delta )}}{\alpha (\delta +\eta \alpha )}>0$ and $U_3=\frac{\delta +\eta \alpha -\sqrt{\eta \alpha (1+\mu )(\eta \alpha + \delta )}}{\delta + \eta \alpha }>0$.

• (c) If $\delta \mu<\xi <\xi _1$ and $\mu <\frac{\delta }{\eta \alpha }$ then system (4) has two distinct positive $V=0$ boundary equilibria

  $$\begin{aligned} E_4=(P_4,U_4,0),\qquad E_5=(P_5,U_5,0) \end{aligned}$$

  such that $P_{4,5}=\frac{\delta \mu +\delta +\eta \mu \alpha +2\eta \alpha -\xi \mp \sqrt{\varDelta (\xi )}}{2\alpha (\delta + \eta \alpha )}>0$, $U_{4,5}=1-\alpha P_{4,5}>0$, where

  $$\begin{aligned} \varDelta (\xi )=\xi ^2 -2 \xi (\delta \mu +\delta +\eta \mu \alpha +2\eta \alpha )+(\delta \mu +\delta + \eta \mu \alpha )^2. \end{aligned}$$

• (d) If $\xi =\delta \mu$, $\mu <\frac{\delta }{\eta \alpha }$, then the $V=0$ boundary equilibrium $E_5$ coincides with the axial equilibrium $E_1$ and system (4) has a remaining positive $V=0$ boundary equilibrium

  $$\begin{aligned} E_4=(P_4, U_4,0), \end{aligned}$$

  where $P_4$ and $U_4$ from case (c) now simplify to $P_4=\frac{\eta (1+\mu )}{\delta +\eta \alpha }>0$, $U_4=\frac{\delta -\eta \alpha \mu }{\delta +\eta \alpha }>0$.

• (e) If $0<\xi <\delta \mu$, then system (4) has a unique positive $V=0$ boundary equilibrium $E_4=(P_4,U_4,0)$, where $P_4$ and $U_4$ are the same as in case (c).

Proof

See [27]. $\square$

Now we analyze the existence of internal equilibria, which are positive solutions of the following algebraic equations

$$\begin{aligned} \left\{ \begin{array}{l} 1-\alpha P-U-\frac{V}{\beta P+d_{2}}=0, \\ \\ \delta -\eta \frac{ U}{P}-\frac{\xi }{\mu +U}=0,\\ \\ \frac{P}{\beta P+d_2}-\frac{m}{r}=0. \end{array}\right. \end{aligned}$$

(8)

The last equation gives the solution

$$\begin{aligned} P^*=\frac{md_2}{r-m\beta }, \end{aligned}$$

which is positive if

$$\begin{aligned} \beta <\frac{r}{m}. \end{aligned}$$

Eliminating the variable V, we obtain an equation for the variable U,

$$\begin{aligned} \eta U^2+(\eta \mu -\delta P^*)U+P^*(\xi -\delta \mu )=0. \end{aligned}$$

Let

$$\begin{aligned} g(U)=\eta U^2+(\eta \mu -\delta P^*)U+P^*(\xi -\delta \mu ). \end{aligned}$$

Lemma 1

• (i) If $0<\xi <\delta \mu$ and $\beta <\frac{r}{m}$, then g(U) has a unique positive root

  $$\begin{aligned} U^{*}_{0}=\frac{-(\eta \mu -\delta P^*)+\sqrt{(\eta \mu -\delta P^*)^2-4\eta P^*(\xi -\delta \mu )}}{2 \eta }. \end{aligned}$$

• (ii) If $\xi =\delta \mu$, $\delta P^*-\eta \mu >0$ and $\beta <\frac{r}{m}$, then g(U) has a unique positive root

  $$\begin{aligned} U^{*}_{1}=\frac{ \delta P^*-\eta \mu }{\eta }. \end{aligned}$$

• (iii) If $\delta \mu<\xi <\delta \mu +\frac{(\eta \mu -\delta P^*)^2}{4\eta P^*}$, $\delta P^*-\eta \mu >0$ and $\beta <\frac{r}{m}$ then g(U) has two distinct positive roots

  $$\begin{aligned} U^*_{2,3}=\frac{-(\eta \mu -\delta P^*) \mp \sqrt{(\eta \mu -\delta P^*)^2-4\eta P^*(\xi -\delta \mu )}}{2 \eta }. \end{aligned}$$

  .

• (iv) If $\xi =\delta \mu +\frac{(\eta \mu -\delta P^*)^2}{4\eta P^*}:=\xi _2$, $\delta P^*-\eta \mu >0$ and $\beta <\frac{r}{m}$ then g(U) has a unique positive root

  $$\begin{aligned} U^{*}_{4}=\frac{ \delta P^*-\eta \mu }{2\eta }. \end{aligned}$$

  .

For positive internal equilibria, we need solutions $E_j^*=(P^*_j,U^*_j,V^*_j)$ of (8) with $P^*_j=P^*>0$, $U^*_j>0$ and $V^*_j>0$ for $j=0,\ldots ,4$. We have

$$\begin{aligned} V^*_j=\frac{rP^*}{m}\left( 1-\alpha P^*-U^*_j\right) , \end{aligned}$$

(9)

but we are unable to find simple criteria for $V^*_j>0$ in terms of parameters, other than substituting the parameter expressions for $P^*$, $U^*_j$ into (9). For specific parameter values we can find curves where $V^*_j=0$ numerically using the path continuation software Auto and obtain parameter regions where positive internal equilibria exist, such as in Fig. 1.

Fig. 1

Regions in $(\xi ,\beta )$ parameter space where (4) has positive internal equilibria, for fixed parameter values $r=2$, $k=100$, $d_2=10$, $s=0.4$, $\gamma =0.44$, $c_1=0.1$, $m=0.4$, $\delta =0.2$, $\mu =0.29050$

Invariant Region

Definition 1

If there exists a compact set $K\subseteq Int{\mathbb {R}}_{+}^{3}=\varOmega$, such that all solutions of (4) with initial condition in $\varOmega$ eventually enter and remain in K, then the system (4) is called uniformly persistent.

Theorem 2

Let

• (i) $\frac{k}{\beta (k+d_2)}-\frac{m}{r}>0$

• (ii) $\xi <\delta \mu$

• (iii) $P_4>P_2$

where $P_2=\frac{md_2}{r-m\beta }$ and $P_4=\frac{\delta \mu +\delta +\eta \mu \alpha +2\eta \alpha -\xi - \sqrt{\xi ^2 -2 \xi (\delta \mu +\delta +\eta \mu \alpha +2\eta \alpha )+(\delta \mu +\delta + \eta \mu \alpha )^2}}{2\alpha (\delta + \eta \alpha )}$ are given in Theorem 1. Then the system (4) is uniformly persistent.

Proof

We use the method of average Lyapunov function [19]. Consider a function of the form $\nu (P,U,V)=PUV$. We define

$$\begin{aligned} \zeta (P,U,V)&=\frac{{\dot{\nu }}}{\nu }=\frac{{\dot{P}}}{P}+\frac{{\dot{U}}}{U}+\frac{{\dot{V}}}{V}\\&=\left[ (1-\alpha P)-U-\frac{V}{\beta P+d_2}\right] +\left[ \delta -\eta \frac{U}{P}-\frac{\xi }{\mu +U}\right] \\&\quad +\,\left[ \frac{P}{\beta P+d_2}-\frac{m}{r}\right] . \end{aligned}$$

Now, we prove that this function is positive at each of the boundary equilibria. Then

$$\begin{aligned} \zeta (E_1)&=\zeta \left( \frac{1}{\alpha },0,0\right) =\delta -\frac{\xi }{\mu }+\frac{k}{\beta (k+d_2)}-\frac{m}{r}>0,\\ \zeta (E_2)&=\zeta (P_2,0,V_2) =\delta -\frac{\xi }{\mu }>0. \end{aligned}$$

The first relation holds by condition (i), and $\zeta (E_2)>0$ by (ii). Since we assume $\xi <\delta \mu$, from Theorem 1, the system (4) has a unique positive boundary equilibrium $E_4$. Therefore, we have:

$$\begin{aligned} \zeta (E_4)&=\zeta (P_4,U_4,0)=1-\alpha P_4-U_4+\delta -\eta \frac{U_4}{P_4}-\frac{\xi }{\mu +U_4}+\frac{P_4}{\beta P_4+d_2}-\frac{m}{r}\\&=\frac{P_4}{\beta P_4+d_2}-\frac{m}{r}>0, \end{aligned}$$

which is positive from the condition (iii). The proof is completed by applying Theorem 5 in [19]. $\square$

We note that the conditions (i)–(iii) in Theorem 2 are quite restrictive. Below we consider a variety of interesting dynamics where the conditions may not necessarily hold.

In the following we are interested in the existence of solutions to Eq. (4) which are bounded by positive functions.

Theorem 3

Let $\varepsilon _1$, $\varepsilon _2$ be any positive constants and define $M_{P}=\frac{1}{\alpha }+\epsilon _1$, $M_{U}=\frac{\delta M_{P}}{\eta }+\epsilon _2$. Let

$$\begin{aligned} \varOmega =\left\{ (P,U,V) \in {\mathbb {R}}_{+}^{3}:0<P+U+V\le \frac{r}{m}W\right\} , \end{aligned}$$

where

$$\begin{aligned} W=\frac{\left( 1+\frac{m}{r}\right) ^{2}}{4\alpha }+\frac{M_{P}\left( \delta +\frac{m}{r}-\frac{\xi }{\mu +M_U}\right) ^{2}}{4\eta }. \end{aligned}$$

Then $\varOmega$ is positively invariant.

Proof

First of all, it is clear that the planes $U=0$ and $V=0$ are invariant. Assume that (P(t), U(t), V(t)) is an arbitrary positive solution of system (4), then the first equation of system (4) yields

$$\begin{aligned} \frac{dP}{dt}=P(1-\alpha P)-PU-\frac{PV}{\beta P+d_2}\le P(1-\alpha P). \end{aligned}$$

From Lemma 2.4 in [52], there exists a constant $T_{1}>0$ such that $P(t)\le \frac{1}{\alpha }+\epsilon _1=M_{P}$, for any small constant $\epsilon _1>0$ and for $t\ge T_{1}$.

Similarly, from the second equation of system (4) and Lemma 2.4 in [52], there exist two positive constants $M_{U}$ and $T_{2}>0$ such that

$$\begin{aligned} U(t)\le \frac{\delta M_{P}}{\eta }+\epsilon _2=M_{U} \end{aligned}$$

for $t\ge T_{2}$ and $\epsilon _2>0$.

Defining that $\chi (t)=P(t)+U(t)+V(t)$, then we get:

$$\begin{aligned} {\dot{\chi }}+\frac{m}{r}\chi&\le (-\alpha ) P^2+\left( 1+\frac{m}{r}\right) P-\frac{\eta }{M_P}U^2+\left( \delta +\frac{m}{r}-\frac{\xi }{\mu +M_U}\right) U \\&\le \frac{\left( 1+\frac{m}{r}\right) ^{2}}{4\alpha }+\frac{M_{P}\left( \delta +\frac{m}{r}-\frac{\xi }{\mu +M_U}\right) ^{2}}{4\eta }=W \end{aligned}$$

Thus ${\dot{\chi }}+\frac{m}{r}\chi$ is bounded. According to Lemma 2.1 in [8], we have:

$$\begin{aligned} \chi \le \frac{r}{m}W+\left( \chi (0)-\frac{rW}{m}\right) e^{-\frac{m}{r} t}. \end{aligned}$$

Therefore $\chi (t)$ is ultimately bounded, and if follows that each positive solutions of system (4) is uniformly ultimately bounded. Hence, there are two positive constants $M_{V}$ and $T_{3}$ such that $V(t)\le M_{V}$, for $t\ge T_{3}$. Let $T=max\big \{T_{1},T_{2},T_{3} \big \}$, then we have $0<P(t)\le M_{P}$, $0\le U(t)\le M_{U}$ and $0\le V(t)\le M_{V}$ for $t\ge T$. This ensures the existence of compact set $\varOmega$ which is a proper subset of ${\mathbb {R}}_{+}^{3}$ such that as $t\longrightarrow \infty$, the solutions of (3) will be always within the set $\varOmega$. Thus, the system (3) is dissipative. The proof of the theorem is completed.

Linearized Stability

In this section we study the linearized stability of the different steady states. Invariance of solutions $U(t)=V(t)=0$ under the flow of system (4), implies that the U(t) and V(t) components of all solutions with positive initial conditions, remain positive for all time. Hence, in the following, first we consider the system (4) in the absence of “type one” and “type two” predators and analyze the stability of the system in these cases. Next we study the stability of equilibria for (4) in 3 dimensions.

Stability and Bifurcations in the Absence of “Type One” Predators

The $U=0$ plane is clearly invariant for (4). In the absence of predators of “type one” (U), the model (4) reduces to the well known Rosenzweig–MacArthur model with Holling type II functional response

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{P}}=P( 1-\alpha P)-\frac{PV}{\beta P+d_2}, \\ \\ {\dot{V}}=\frac{PV}{\beta P+d_2}-\frac{m}{r}V, \end{array}\right. \end{aligned}$$

(10)

which has three equilibria, the origin $G_0=(0,0)$, the axial equilibrium $G_1=(\frac{1}{\alpha },0)$, and $G_2=(P_2,V_2)$, where $P_2=\frac{md_2}{r-m\beta }$ and $V_2=\frac{r}{m}P_2(1-\alpha P_2)$ are both positive provided that $\frac{rk}{m(k+d_2)}<\beta <\frac{r}{m}$.

Linear stability analysis shows that the trivial state $G_0$ is an unstable saddle. At the boundary equilibrium point $G_1=(\frac{1}{\alpha },0)$, the eigenvalues are $\lambda _1=-1<0$ and $\lambda _2=\frac{k}{\beta (k+d_2)}-\frac{m}{r}=\frac{m}{r\beta }(\beta _0-\beta )$, where, $\beta _0=\frac{rk}{m(k+d_2)}$. If $0<\beta <\beta _0$, then the axial state $G_1$ is an unstable saddle; if $\beta >\beta _0$, then $G_1$ is a stable node. Also, the system (10) undergoes a transcritical bifurcation about the point $G_1$ as $\beta$ passes through $\beta _{0}$.

Fig. 2

Phase portraits of the two-dimensional system (10) with P on the horizontal axis and V on the vertical axis, for $r=2$, $k=100$, $m=0.4$, $d_2=10$, $c_2=1.5$, $e= 0.6$: a When $\beta =3.9<\beta _1$, then $G_2$ is a source and $G_0$ and $G_1$ are saddles and there is a stable periodic orbit around $G_2$; b for $\beta =4.199\in (\beta _1,\beta _0)$, $G_2$ is a sink, $G_0$ and $G_1$ are saddles, and there is no periodic orbit; c $G_1$ is a stable node and there are no equilibria in the interior of the first quadrant for $\beta =4.8>\beta _0$

For $\frac{r(k-d_2)}{m(k+d_2)}=\beta _1<\beta <\beta _0$, the interior equilibrium $G_2$ is asymptotically stable and for $0<\beta <\beta _1$, $G_2$ is unstable. There is a supercritical Hopf bifurcation as $\beta$ decreases through $\beta _1$ and a stable periodic orbit exists for $\beta <\beta _1$ (e.g. [34, Example 3.1]). For $r=2$, $k=100$, $m=0.4$, $d_2=10$, $c_2=1.5$, $e= 0.6$, we get $\beta _0=4.5455$ and $\beta _1=4.0909$. In Fig. 2 we show typical phase portrates for the planar system (10). For $\beta =3.9<\beta _1$, there is a stable periodic orbit around $G_2$, while $G_0$ and $G_1$ are saddle points. Also, for this value of $\beta$ the interior equilibrium $G_2$ is a spiral source and unstable. The corresponding phase portrait is shown in Fig. 2a. For $\beta _1<\beta =4.199<\beta _0$, there is a spiral sink for system (10) at $G_2$ and for this value of $\beta$, the boundary equilibrium $G_1$ is a saddle. The phase portrait is shown in Fig. 2b. For $\beta =4.8>\beta _0$ the axial equilibrium $G_1$ is a stable node and there are no equilibria in the interior of the first quadrant. The corresponding phase portrait is shown in Fig. 2c.

Stability and Bifurcations in the Absence of “Type Two” Predators

Likewise, it is clear that the $V=0$ plane is invariant for (4). Hence, in the absence of predators of “type two” (V), the model (4) becomes:

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{P}}=P\left[ ( 1-\alpha P)-U\right] , \\ \\ {\dot{U}}=U\left[ \left( \delta -\eta \frac{ U}{P}\right) -\frac{\xi }{\mu +U}\right] . \end{array}\right. \end{aligned}$$

(11)

The equilibria of system (11) correspond to the $V=0$ boundary equilibria of system (4), which we discussed in Theorem 1. Hu and Cao [27] give the existence and linearized stability of the equilibria of the planar system (11). They also study bifurcations in (11), and show there is a transcritical bifurcation at $\xi =\delta \mu$, and generically a saddle node bifurcation at $\xi =\xi _1$, if $\mu <\frac{\delta }{\eta \alpha }$, where $\xi _1$ is given in Theorem 1. They show parameter values exist, where there is a Hopf bifurcation of unstable periodic orbits, and where there is a codimension 2 Bogdanov–Takens bifurcation. For these latter two bifurcations, analytical expressions are derived for normal form coefficients which are then evaluated numerically to show these bifurcations exist and are nondegenerate for specific parameter values. Numerical simulations are carried out to demonstrate the validity of the theoretical results. For more detail the reader is referred to [27].

Linearized Stability in Three Dimensions

In this section, we assume the conditions of Theorem 2 are satisfied. Now, we study the local stability around the axial state $E_1$, the boundary state $E_2$ (the type one predator-free), and $E_4$ (the type two predator-free) equilibrium points.

First, we denote the Jacobian matrix ($J=[J_{ij}]$) as follows:

$$\begin{aligned} J_{(P,U,V)}=\begin{pmatrix} 1-2\alpha P-U-\frac{d_2V}{\left( \beta P+d_2\right) ^{2}}&{}\quad -P &{}\quad -\frac{P}{\beta P+d_2} \\ \\ \frac{\eta U^{2}}{P^{2}} &{}\quad \delta -2\eta \frac{U}{P}-\frac{\xi \mu }{(\mu +U)^2} &{}\quad 0 \\ \\ \frac{d_{2}V}{\left( \beta P+d_{2}\right) ^{2}} &{}\quad 0 &{}\quad \frac{P}{\left( \beta P+d_{2}\right) }-\frac{m}{r} \end{pmatrix}. \end{aligned}$$

(12)

It can be easily seen that one of the eigenvalues of Jacobian matrix about $E_1$ and $E_2$ is $\lambda =\delta -\frac{\xi }{\mu }$ and therefore, by condition (ii) of Theorem 2, these equilibria are unstable. Next we study the stability of equilibrium point $E_4$. At this point, the Jacobian matrix takes the form:

$$\begin{aligned} J_{E_4}=\begin{pmatrix} -\alpha P_4 &{}\quad -P_4 &{}\quad -\frac{P_4}{\beta P_4+d_2} \\ \\ \frac{\eta U^{2}_{4}}{P^{2}_{4}} &{}\quad \delta -2\eta \frac{U_4}{P_4}-\frac{\xi \mu }{(\mu +U_4)^2} &{}\quad 0 \\ \\ 0&{}\quad 0 &{}\quad \frac{P_4}{\left( \beta P_4+d_{2}\right) }-\frac{m}{r} \end{pmatrix}. \end{aligned}$$

Thus one of the eigenvalues of $J_{E_4}$ is

$$\begin{aligned} \lambda =\frac{P_4}{\beta P_4+d_2}-\frac{m}{r}, \end{aligned}$$

which is positive (according to condition (iii) of Theorem 2). Therefore, the boundary equilibrium point $E_4$ is unstable.

Next we study the interior equilibrium points $E_j^{*}$, $j=0,\ldots ,4$. For convenience, we denote $E_j^{*}:=E^*=(P^*,U^*,V^*)$. The Jacobian matrix about this equilibrium is:

$$\begin{aligned} J_{E^*}=[j_{i,k}]_{3\times 3}= \begin{pmatrix} 1-2\alpha P^*-U^*-\frac{d_2V^*}{\left( \beta P^*+d_2\right) ^{2}}&{}\quad -P^*&{} \quad -\frac{P^*}{\beta P^*+d_2} \\ \\ \frac{\eta U^{*2}}{P^{*2}}&{}\quad \delta -2\eta \frac{U^*}{P^*}-\frac{\xi \mu }{(\mu +U^*)^2}&{}\quad 0 \\ \\ \frac{d_{2}V^*}{\left( \beta P^*+d_{2}\right) ^{2}}&{}\quad 0&{}\quad 0 \end{pmatrix}. \end{aligned}$$

(13)

Then, the characteristic polynomial is

$$\begin{aligned} h(\lambda )= \lambda ^3+{\mathcal {A}}^*\lambda ^2 +{\mathcal {B}}^* \lambda +{\mathcal {C}}^*, \end{aligned}$$

(14)

where

$$\begin{aligned} {\mathcal {A}}^*&= -(j_{11}+j_{22}),\nonumber \\ {\mathcal {B}}^*&=(j_{11}j_{22}-j_{12}j_{21} -j_{13}j_{31}),\nonumber \\ {\mathcal {C}}^*&=j_{13}j_{31}j_{22}. \end{aligned}$$

(15)

If we assume $j_{22}<0$, then it is clear that ${\mathcal {C}}^*>0$. Now, we consider the two following cases:

• (1) $j_{11}<0$. Then it can be easily verified that ${\mathcal {A}}^*>0$, ${\mathcal {B}}^*>0$ and ${\mathcal {D}}^*={\mathcal {A}}^*{\mathcal {B}}^*-{\mathcal {C}}^*>0$. Therefore, by the Routh–Hurwitz criteria all of roots of $h(\lambda )$ have negative real parts and the interior equilibrium point $E^*$ is stable.

• (2) $j_{11}>0$. In this case, if the conditions:

  • (i) $\left| j_{22}\right| >j_{11}$,

  • (ii) $j_{12}j_{21}<j_{11}j_{22}$,

  are satisfied, then it can be easily checked that ${\mathcal {A}}^*>0$, ${\mathcal {B}}^*>0$. Furthermore

  $$\begin{aligned} {\mathcal {D}}^*={\mathcal {A}}^*\mathcal {B}^*-{\mathcal {C}}^*=(-j_{11}-j_{22})(j_{11}j_{22}-j_{12}j_{21}-j_{13}j_{31})-j_{13}j_{31}j_{22}>0, \end{aligned}$$

  since

  $$\begin{aligned} j_{22}(j_{12}j_{21}-j_{11}^2)&>j_{11}j_{22}^2-j_{11}j_{12}j_{21}-j_{11}j_{13}j_{31}\\&=j_{11}j_{22}^2+j_{11}(-j_{12}j_{21}-j_{13}j_{31})\\&>j_{11}j_{22}^2+j_{11}(-j_{11}j_{22}). \end{aligned}$$

  The second inequality holds by condition (ii) and the fact that $-j_{13}j_{31}>0$. But $j_{22}<0$, therefore we have

  $$\begin{aligned} j_{22}j_{12}j_{21}-j_{22}j_{11}^2-j_{11}j_{22}^2+j_{11}^2j_{22}=j_{22}(j_{12}j_{21}-j_{11}j_{22})>0, \end{aligned}$$

  which is positive from the condition (ii). Hence by the Routh–Hurwitz criteria all of roots of $h(\lambda )$ have negative real parts and the interior equilibrium $E^*$ is stable.

Summarizing the above discussions, we arrive at the following theorem:

Theorem 4

Suppose that the conditions of Theorem 2 are satisfied. Then the boundary equilibria $E_1$, $E_2$ and $E_4$ are unstable. Also, if $j_{22}=\delta -2\eta \frac{U^*}{P^*}-\frac{\xi \mu }{(\mu +U^*)^2}$ is negative in (13), the interior equilibrium $E^*_0$ is locally asymptotically stable.

If $\xi <\delta \mu$ and $\beta$ is sufficiently small, there is a unique interior equilibrium $E^*_0$ (see Lemma 1). For $r=2$, $k=100$, $m=0.4$, $d_2=10$, $\beta =2.2222$, $\delta =0.2$, $\eta =0.79201$, $\mu =0.29050$, $\xi =0.03$, $\delta \mu =0.058100$, we have $j_{11}=-0.018644$ and $j_{22}=-0.15164$, which both are negative, and therefore the interior equilibrium point $E^*_0$ is asymptotically stable. A sample trajectory is shown in Fig. 3.

Fig. 3

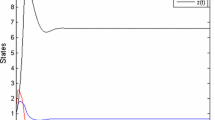
Numerical simulation of the three dimensional model (4) with parameter values $r=2$, $k=100$, $m=0.4$, $d_2=10$, $\beta =2.2222$, $\delta =0.2$, $\eta =0.79201$, $\mu =0.29050$, $\xi =0.03$. The interior state $E^*_0$ is (3.6, 0.78195, 2.4849) and initial conditions are (3.16, 0.54, 6.22). a The trajectory in 3 dimensions, b populations as functions of time t. The simulation illustrates the stability of $E^*_0$

Local Bifurcations

In this section, we will discuss various possible bifurcations of system (4). Conditions for transcritical bifurcations, saddle-node bifurcations, Hopf bifurcations and Hopf-steady state bifurcations are studied. We also use numerical methods to explore some global dynamics.

Transcritical Bifurcations

System (4) has many transcritical bifurcations of equilibria, within both the two-dimensional $U=0$ and $V=0$ boundary planes both involving the axial equilibrium $E_1$, and in ${\mathbb {R}}_{+}^{3}$ involving boundary equilibria.

At $E_1=(\frac{1}{\alpha },0,0)$, the eigenvalues of the Jacobian matrix of the linearization at $E_1$ are $\lambda _1=-1<0$, $\lambda _2=\frac{m}{r\beta }(\frac{rk}{m(k+d_2)}-\beta )$ and $\lambda _3=\delta -\frac{\xi }{\mu }$. Thus we can expect bifurcation involving $E_1$ at parameters values where $\lambda _2=0$, or $\lambda _3=0$. At $\beta =\beta _0=\frac{rk}{m(k+d_2)}$, there is a transcritical bifurcation within the $U=0$ boundary plane where $E_1$ coincides with $E_2$ (e.g. Fig. 4). Similarly, at $\xi =\xi _0=\delta \mu$ there is a transcritical bifurcation within the $V=0$ boundary plane, where $E_1$ coincides with $E_5$ [27]. The existence of these bifurcations can be analyzed with center manifold calculations, which are minor modifications of the corresponding calculations for the two-dimensional systems (10) and (11). There are several transcritical bifurcations where a boundary equilibrium coincides with an interior equilibrium. At the $U=0$ boundary equilibrium $E_2$, the characteristic equation of the Jacobian matrix of the linearization at $E_2$ is

$$\begin{aligned} \left[ \delta -\frac{\xi }{\mu }-\lambda \right] \left[ \lambda (\lambda +2\alpha P_2+\frac{d_2V_2}{(\beta P_2+d_2)^2}-1)+\frac{md_2 V_2}{r(\beta P_2+d_2)^2}\right] =0. \end{aligned}$$

(16)

Fig. 4

One-parameter bifurcation diagrams for the two-dimensional system (10), produced by Auto, showing a transcritical bifurcation at $\beta _0=4.5455$ and a Hopf bifurcation at $\beta _1=4.0909$. The left panel shows $\beta$ on the horizontal axis and P on the vertical axis, while the right panel shows $\beta$ on the horizontal axis and V on the vertical axis. Solid red lines correspond to branches of stable equilibria, solid black lines to unstable equilibria. Closed green circles correspond to maximum and minimum P or V values on stable periodic orbits. Portions of solution branches corresponding to $V<0$ have no significance in the model, but are shown to clarify the transcritical bifurcation and change of stability (color figure online)

Therefore at $\xi =\xi _0=\delta \mu$, we can expect transcritical bifurcations involving $E_2$. Depending on the value of $\beta$, the interior equilibrium involved can be $E_0^*$ or $E_2^*$; see Lemma 1 and also Fig. 1.

If $\xi =\xi _0$, the Jacobian matrix $J_{E_2}$ has a zero eigenvalue. By using the translation $(X_2,Y_2,Z_2,\varphi )=(P-P_2,U,V-V_2,\xi -\xi _0)$, we transform the equilibrium $E_2$ to the origin:

$$\begin{aligned} \left\{ \begin{array}{l} \dot{X_2}=(1-2\alpha P_2-\frac{d_2V_2}{(\beta P_2+d_2)^2})X_2-P_2Y_2-\frac{P_2}{\beta P_2+d_2}Z_2+(-\alpha +\frac{\beta d_2V_2}{(\beta P_2+d_2)^3}) X_2^2-X_2Y_2\\ -\frac{d_2}{(\beta P_2+d_2)^2}X_2Z_2 +\frac{\beta d_2}{(\beta P_2+d_2)^3}X_2^2 Z_2-\frac{d_2\beta ^2 V_2}{(\beta P_2+d_2)^4}X_2^3+O\left| (X_2,Y_2,Z_2,\varphi )\right| ^{4}, \\ \\ \dot{Y_2}=-\frac{\varphi }{\mu }Y_2+(\frac{\varphi +\delta \mu }{\mu ^2}-\frac{\eta }{P_2})Y_2^2-\frac{\varphi +\delta \mu }{\mu ^3}Y_2^3+\frac{\eta }{P_2^2}X_2Y_2^2+O\left| (X_2,Y_2,Z_2,\varphi )\right| ^{4}, \\ \\ \dot{Z_2}=\frac{d_2V_2}{(\beta P_2+d_2)^2}X_2+(\frac{P_2}{\beta P_2+d_2}-\frac{m}{r})Z_2-\frac{\beta d_2 V_2}{(\beta P_2+d_2)^3}X_2^2+(\frac{d_2}{(\beta P_2+d_2)^2})X_2Z_2\\ -\frac{\beta d_2}{(\beta P_2+d_2)^3}X_2^2Z_2+\frac{\beta ^2d_2V_2}{(\beta P_2+d_2)^4}X_2^3+O\left| (X_2,Y_2,Z_2,\varphi )\right| ^{4}. \end{array}\right. \end{aligned}$$

(17)

For convenience, we denote $tr:=1-2\alpha P_2-\frac{d_2V_2}{(\beta P_2+d_2)^2}$ and $Det:=\frac{md_2V_2}{r(\beta P_2+d_2)^2}$.

Then under the transformation

$$\begin{aligned} \begin{pmatrix} X_2\\ Y_2\\ Z_2 \end{pmatrix}= \begin{pmatrix}0&{}\quad A&{}\quad B\\ 1&{}\quad 0&{}\quad 0\\ -\frac{P_2r}{m}&{}\quad 0&{}\quad 1 \end{pmatrix} \begin{pmatrix} x_2\\ y_2\\ z_2 \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} A:=\frac{-m\sqrt{Det-\left( \frac{tr}{2}\right) ^2}}{rDet},\quad B:=\frac{m.tr}{2rDet}, \end{aligned}$$

(18)

system (17) becomes:

$$\begin{aligned} \dot{x_2}&=\frac{-\varphi }{\mu } x_2+(\frac{\varphi +\delta \mu }{\mu ^2}-\frac{\eta }{P_2})x_2^2-\frac{\varphi +\delta \mu }{\mu ^3}x_2^3+\frac{\eta (Ay_2+Bz_2)}{P_2^2}x_2^2+O\left( \left| x_2,y_2,z_2,\varphi \right| ^{4} \right) \\ \dot{y_2}&=\frac{tr}{2}y_2+\sqrt{Det-\left( \frac{tr}{2}\right) ^2}z_2+O\left( \left| x_2,y_2,z_2,\varphi \right| ^{2} \right) \\ \dot{z_2}&=-\sqrt{Det-\left( \frac{tr}{2}\right) ^2}y_2+\frac{tr}{2}z_2+O\left( \left| x_2,y_2,z_2,\varphi \right| ^{2} \right) . \end{aligned}$$

Then, we obtain the vector field reduced to the center manifold

$$\begin{aligned} \dot{x_2}=\frac{-\varphi }{\mu } x_2+\left( \frac{\delta }{\mu }-\frac{\eta }{P_2}\right) x_2^2+ O\left( \left| \varphi \right| \left| x_2 \right| ^{2} +\left| x_2 \right| ^{3} \right) . \end{aligned}$$

Thus, we have a transcritical bifurcation provided $\delta P_2-\eta \mu \ne 0$. Note that at the bifurcation point we have $P_2=P^*$.

Summarizing what can be obtained analytically, we have the following theorem.

Theorem 5

The system (4) has a transcritical bifurcation at the axial equilibrium $E_1$ when $\xi =\delta \mu$. If $\delta P^*-\eta \mu \ne 0$, then (4) has a transcritical bifurcation at the boundary equilibrium $E_2$ when $\xi =\delta \mu$.

There can be further transcritical bifurcations at $V=0$ boundary equilibria $E_3$, $E_4$, $E_5$. Due to the algebraic complexity of the relevant characteristic equations, we have used numerical calculations to explore these, by numerically evaluating the quantities ${\mathcal {A}}^*$, ${\mathcal {B}}^*$, ${\mathcal {C}}^*$ in (15) and with the path continuation software Auto. See Figs. 1, 5, 9.

Saddle-Node Bifurcations

In “Equilibria and Invariant Region”, we have given conditions for the existence of two boundary ($E_4$ and $E_5$) and two interior ($E_2^*$ and $E_3^*$) equilibria. The boundary equilibria are distinct if $\delta \mu<\xi <\xi _1$, and they coincide at $E_3$ if $\xi =\xi _1$, where $\xi _1$ is given in Theorem 1. Likewise, the interior equilibria are distinct if $\delta \mu<\xi <\delta \mu +\frac{(\eta \mu -\delta P^*)^2}{4\eta P^*}:=\xi _2$ and they coincide at $E^*_4$ if $\xi =\xi _2$. The coincidence of equilibria is due to the occurrence of saddle-node bifurcations for boundary and interior equilibria.

The characteristic equation for the equilibrium $E_3$ is given by:

$$\begin{aligned} \left( \frac{P_3}{\beta P_3+d_2}-\frac{m}{r}-\lambda \right) \left( \lambda ^2 +A\lambda +B\right) =0, \end{aligned}$$

where

$$\begin{aligned} A&=-1+2\alpha P_3+U_3-\delta +2\eta \frac{U_3}{P_3}+\frac{\xi \mu }{(\mu +U_3)^2},\\ B&=\left( 1-2\alpha P_3-U_3\right) \left( \delta -2\eta \frac{U_3}{P_3}-\frac{\xi \mu }{(\mu +U_3)^2}\right) +\frac{\eta U_3^2}{P_3}, \end{aligned}$$

are the same as for the characteristic equation $\lambda ^2+A\lambda +B=0$ for the two-dimensional system (11). The analysis of the saddle-node bifurcation of $V=0$ boundary equilibria in (4) at $\xi =\xi _1$ is a minor modification of the analysis of the same bifurcation in (11) given by [27].

Next, let $\xi =\xi _2$ and consider the interior equilibrium $E^*_4$. The Jacobian matrix about this equilibrium $J_{E^*_4}=[j_{ik}]_{3\times 3}$ is:

$$\begin{aligned} J_{(P^*,U^*_4,V^*_4)}=\begin{pmatrix} 1-2\alpha P^*-U^*_4-\frac{d_2V^*_4}{\left( \beta P^*+d_2\right) ^{2}}&{}&{}&{}&{} -P^* &{}&{}&{}&{} -\frac{P^*}{\beta P^*+d_2} \\ \\ \frac{\eta U^{*2}_4}{P^{*2}} &{}&{}&{}&{} 0 &{}&{}&{}&{} 0 \\ \\ \frac{d_{2}V^*_4}{\left( \beta P^*+d_{2}\right) ^{2}} &{}&{}&{}&{} 0 &{}&{}&{}&{} 0 \end{pmatrix}, \end{aligned}$$

(19)

and the characteristic equation is:

$$\begin{aligned} \left[ \lambda ^2 -j_{11}\lambda -(j_{12}j_{21}+j_{13}j_{31})\right] \lambda =0. \end{aligned}$$

(20)

One of eigenvalues is $\lambda _3=0$, and the two other eigenvalues $\lambda _1$ and $\lambda _2$ satisfy

$$\begin{aligned} \lambda _1.\lambda _2=-(j_{12}j_{21}+j_{13}j_{31})>0, \quad \lambda _1+\lambda _2=j_{11}=1-2\alpha P^*-U^*_4-\frac{d_2V^*_4}{\left( \beta P^*+d_2\right) ^{2}}. \end{aligned}$$

If $j_{11}$ is negative, then $\lambda _1$ and $\lambda _2$ have negative real parts. By calculations similar to those above, we obtain the vector field reduced to the one-dimensional center manifold

$$\begin{aligned} \dot{x_3}=-\frac{U_4^*}{\mu +U_4^*}\psi -\left( \frac{\eta }{P^*}-\frac{\xi _2}{(\mu +U_4^*)^2}\right) x_3^2+O\left| (x_3,\psi )\right| ^{3}, \end{aligned}$$

where $\psi := \xi -\xi _2$. Then, we have a saddle-node bifurcation provided

$$\begin{aligned} \frac{\eta }{P^*}-\frac{\xi _2}{(\mu +U_4^*)^2}\ne 0. \end{aligned}$$

We summarize the above discussion in the following theorem.

Theorem 6

The system (4) has a saddle-node bifurcation at the boundary equilibrium $E_3$ when $\xi =\xi _1$. If $j_{11}=1-2\alpha P^*-U^*_4-\frac{d_2V^*_4}{\left( \beta P^*+d_2\right) ^{2}}$ is negative in (19) and $\frac{\eta }{P^*}-\frac{\xi _2}{(\mu +U_4^*)^2}\ne 0$ then (4) has a saddle-node bifurcation at the interior equilibrium $E^*_4$ when $\xi =\xi _2$.

For $r=2$, $k=100$, $m=0.4$, $d_2=10$, $\beta =2.2222$, $\delta =0.2$, $\eta =0.7920000001$, $\mu =0.29050$, we obtain $\xi =\xi _2=0.07914600920$, and all conditions of the saddle-node bifurcation are satisfied. Furthermore, if we consider ${\mathcal {C}}^*$ in Eq. (14) as a function of $\xi$, then ${\mathcal {C}}^*(\xi )=0$ when $\xi =\xi _2$.

Hopf Bifurcations

In “Linearized Stability” we have studied conditions required for local asymptotic stability of an interior equilibrium $E^*$. It is possible for an internal equilibrium $E^*(=E^*_0 \ \text {or} \ E^*_2 \ \text {or} \ E^*_3)$ to lose its stability through a Hopf bifurcation.

Considering $\beta$ as the bifurcation parameter, we investigate conditions under which the characteristic equation (14) at the equilibrium $E^*$ has a pair of purely imaginary roots for a critical value $\beta =\beta _{crit}$. Then we check if the stability of $E^*$ changes when $\beta$ passes through $\beta _{crit}$.

For the characteristic equation (14), purely imaginary roots $\lambda =\pm i\omega$ exist if and only if ${\mathcal {D}}^*= {\mathcal {A}}^* {\mathcal {B}}^*- {\mathcal {C}}^*=0$ with ${\mathcal {B}}^*>0$. If we consider $\beta$ as the bifurcation parameter and ${\mathcal {D}}^*(\beta )=0$ at a critical value $\beta =\beta _{crit}$, then $\frac{d}{d\beta }{\text {Re}}\lambda (\beta )|_{\beta =\beta _{crit}}\ne 0$ is equivalent to $\frac{d}{d\beta }\mathcal {D^*}(\beta )|_{\beta =\beta _{crit}}\ne 0$. To verify the existence of a Hopf bifurcation at $\beta =\beta _{crit}$, the first Lyapunov number $l_1$ in the normal form must be shown to be nonzero. This has been done for the two-dimensional system (10) at the equilibrium $G_2$ [34] which corresponds to the $U=0$ boundary equilibrium $E_2$ for system (4). For system (11) when $V=0$, see [27]. For positive interior equilibria for system (4) we have not found a useful expression for $l_1$. Instead, for particular parameter values we have numerically solved ${\mathcal {D}}^*(\beta )=0$ to find $\beta _{crit}$ where we expect a Hopf bifurcation, and checked with the path continuation Auto to numerically find the direction of the Hopf bifurcation and the stability of the bifurcating periodic orbits.

For example, when $r=2$, $k=100$, $m=0.4$, $d_2=10$, $\delta =0.2$, $\eta =0.95017$, $\mu =0.29050$, $\xi =0.03$, we obtain $\beta _{crit}=1.852291$. This suggests that a periodic orbit is created near $E^*_0=(3.1769, 0.5493, 6.2249)$. Auto agrees with this and also finds the periodic orbit, which is unstable, see Fig. 5.

Fig. 5

One-parameter bifurcation diagrams for system (4) produced by Auto, with $\xi =0.03$ and $\beta$ as the bifurcation parameter, showing a transcritical bifurcation of $E_4$ and $E^*_0$ at $\beta =2.387532005$ and a Hopf bifurcation of $E^*_0$ at $\beta =1.852291$. Other parameter values are $r=2$, $k=100$, $m=0.4$, $d_2=10$, $\delta =0.2$, $\eta =0.95017$, $\mu =0.29050$. All panels show $\beta$ on the horizontal axis while the vertical axes are P, U, V in the left, middle and right panels, respectively. Solid red lines correspond to branches of stable equilibria, solid black lines to unstable equilibria, and open blue circles to maximum and minimum values on unstable periodic orbits. The portions of branches corresponding to $V<0$ have no significance in the model, but are shown to clarify the transcritical bifurcation and change of stability (color figure online)

Hopf-Steady State Bifurcation

In “Equilibria and Invariant Region”, we showed when $\xi =\xi _2$, then the three-dimensional system (4) has an interior equilibrium $E_4^*$, provided that $V^*_4>0$. In “Linearized Stability”, it is shown that if $\xi =\xi _2$, then there exists a zero eigenvalue at $E^*_4$ and generically a saddle-node bifurcation of steady states occurs. In addition, if $\beta =\beta _{crit}$, which is general depends on $\xi$, then we have a Hopf bifurcation. In this section we study the codimension two Hopf-steady state bifurcation that can occur if we vary the parameter pair $(\xi , \beta )$. Let $\xi =\xi _2$, so the characteristic equation for $J_{E^*_4}$ is given by (20). Then considering $j_{11}$ as a function of $\beta$, solve $j_{11}(\beta )=0$ to obtain $\beta =\beta _{crit}$. Then for $(\xi ,\beta )=(\xi _2,\beta _{crit})$ the linearization of (4) at the equilibrium $E^*_4$ has a pair of purely imaginary eigenvalues $\lambda _{1,2}=\pm i\omega$ and one zero eigenvalue $\lambda _3=0$.

We translate the equilibrium $E^*_4$ of system (4) to the origin by using the transformation $X=P-P^*$, $Y=U-U^*_4$ and $Z=V-V^*_4$. Then under the transformation

$$\begin{aligned} \left\{ \begin{array}{l} X=\frac{\omega }{j_{31}}x \\ Y=\frac{j_{21}}{j_{31}}y+z \\ Z=y-\frac{j_{12}}{j_{13}}z, \end{array}\right. \end{aligned}$$

we obtain:

$$\begin{aligned} \begin{pmatrix} {\dot{x}}\\ {\dot{y}}\\ {\dot{z}} \end{pmatrix}= \begin{pmatrix} 0&{}\quad -\omega &{}\quad 0\\ \omega &{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0 \end{pmatrix} \begin{pmatrix} x\\ y\\ z \end{pmatrix}+ \begin{pmatrix} \frac{j_{31}}{\omega }K_{11}\\ -\frac{j_{12}j_{31}}{\omega ^2}K_{21}-\frac{j_{13}j_{31}}{\omega ^2} K_{31}\\ -\frac{j_{13}j_{31}}{\omega ^2} K_{21}+\frac{j_{21}j_{13}}{\omega ^2}K_{31} \end{pmatrix}, \end{aligned}$$

(21)

where

$$\begin{aligned} K_{11}&:=\left( \frac{\omega }{j_{31}}x\right) ^2\left( -\alpha +\frac{\beta _{crit} d_2V^*_4}{(\beta _{crit} P^*+d_2)^3}\right) -\frac{\omega }{j_{31}}x\left( \frac{j_{21}}{j_{31}}y+z\right) \\&\quad -\,\frac{d_2}{(\beta _{crit} P^*+d_2)^2}\left( \frac{\omega }{j_{31}}x\right) \left( y-\frac{j_{12}}{j_{13}}z\right) \\&\quad -\,\frac{\beta ^2_{crit}d_2V^*_4}{(\beta _{crit} P^*+d_2)^4}\left( \frac{\omega }{j_{31}}x\right) ^3+\left( \frac{\omega }{j_{31}}x\right) ^2\left( y-\frac{j_{12}}{j_{13}}z\right) \frac{\beta _{crit} d_2}{(\beta _{crit} P^*+d_2)^3}\\&\quad -\,\left( \frac{\omega }{j_{31}}x\right) ^3\left( y-\frac{j_{12}}{j_{13}}z\right) \left( \frac{\beta ^2_{crit} d_2}{(\beta _{crit} P^*+d_2)^4}\right) +\ldots ,\\ K_{21}&:=-\frac{\eta U^{*2}_4}{P^{*3}} \left( \frac{\omega }{j_{31}}x\right) ^2+\frac{2\eta U^*_4}{P^{*2}}\left( \frac{\omega }{j_{31}}x\right) \left( \frac{j_{21}}{j_{31}}y+z\right) \\&\quad +\,\left( \frac{\xi _2 \mu }{(\mu +U^*_4)^3}-\frac{\eta }{P^*}\right) \left( \frac{j_{21}}{j_{31}}y+z\right) ^2\\&\quad +\,\frac{\eta }{P^{*2}}\left( \frac{j_{21}}{j_{31}}y+z\right) ^2\left( \frac{\omega }{j_{31}}x\right) -\frac{2\eta U^*_4}{P^{*3}}\left( \frac{j_{21}}{j_{31}}y+z\right) \left( \frac{\omega }{j_{31}}x\right) ^2\\&\quad -\,\frac{\xi _2 \mu }{(\mu +U^*_4)^4}\left( \frac{j_{21}}{j_{31}}y+z\right) ^3\\&\quad +\,\frac{\eta U^{*2}_4}{P^{*4}}\left( \frac{\omega }{j_{31}}x\right) ^3+\ldots ,\\ K_{31}&:=\left( \frac{-\beta _{crit} V^*_4d_2}{(\beta _{crit} P^*+d_2)^3}\right) \left( \frac{\omega }{j_{31}}x\right) ^2+\left( \frac{\omega }{j_{31}}x\right) \left( y-\frac{j_{12}}{j_{13}}z\right) \frac{d_2}{(\beta _{crit} P^*+d_2)^2}\\&\quad -\,\frac{\beta _{crit} d_2}{(\beta _{crit} P^*+d_2)^3}\left( \frac{\omega }{j_{31}}x\right) ^2\left( y-\frac{j_{12}}{j_{13}}z\right) +\frac{\beta ^2 _{crit} d_2V^*_4}{(\beta _{crit} P^*+d_2)^4}\left( \frac{\omega }{j_{31}}x\right) ^3\\&\quad +\,\frac{\beta ^2 _{crit} d_2}{(\beta _{crit} P^*+d_2)^4}\left( \frac{\omega }{j_{31}}x\right) ^3\left( y-\frac{j_{12}}{j_{13}}z\right) +\ldots . \end{aligned}$$

For convenience, we denote $f^1:=\frac{j_{31}}{\omega }K_{11}$, $f^2:=-\frac{j_{12}j_{31}}{\omega ^2}K_{21}-\frac{j_{13}j_{31}}{\omega ^2} K_{31}$ and $f^3:=-\frac{j_{13}j_{31}}{\omega ^2} K_{21}+\frac{j_{21}j_{13}}{\omega ^2}K_{31}$.

Now we consider $W=x+iy$, ${\bar{W}}=x-iy$ and $Z=z$. Then, under this transformation:

$$\begin{aligned} x=\frac{W+{\bar{W}}}{2}, \qquad y=\frac{i({\bar{W}}-W)}{2}, \qquad z=Z, \end{aligned}$$

the system (21) becomes:

$$\begin{aligned} \begin{pmatrix} {\dot{W}}\\ \dot{{\bar{W}}}\\ {\dot{Z}} \end{pmatrix}= \begin{pmatrix} i\omega &{}\quad 0&{}\quad 0\\ 0&{}\quad -i\omega &{}\quad 0\\ 0&{}\quad 0&{}\quad 0 \end{pmatrix} \begin{pmatrix} W\\ {\bar{W}}\\ Z \end{pmatrix}+ \begin{pmatrix} F^1(W,{\bar{W}},Z)\\ F^2(W,{\bar{W}},Z)\\ F^3(W,{\bar{W}},Z) \end{pmatrix}, \end{aligned}$$

(22)

such that $F^{1,2}=f^{1}(x(W,{\bar{W}}),y(W,{\bar{W}}),z)\pm if^{2}(x(W,{\bar{W}}),y(W,{\bar{W}}),z)$ and $F^{3}=f^{3}(x(W,{\bar{W}}),y(W,{\bar{W}}),z)$. We check that:

$$\begin{aligned} F^{1,2}&=\frac{j_{31}}{\omega }K_{11}\pm i\left[ -\frac{j_{12}j_{31}}{\omega ^2}K_{21}-\frac{j_{13}j_{31}}{\omega ^2} K_{31}\right] ,\\ F^3&=-\frac{j_{13}j_{31}}{\omega ^2}K_{21}+\frac{j_{21}j_{13}}{\omega ^2}K_{31}. \end{aligned}$$

Therefore, all we really need to study is

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{W}}=i\omega W+F^1(W,{\bar{W}},Z), \\ \\ {\dot{Z}}=F^3(W,{\bar{W}},Z), \end{array}\right. \end{aligned}$$

(23)

since the second component of (22) is simply the complex conjugate of the first component. We put (23) in normal form. In the following we simplify second and third order terms. The normal form is obtained as:

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{W}}=i\omega W+\tilde{A_1}WZ+\tilde{A_2}WZ^2+\tilde{A_3}W^2{\bar{W}}+\ldots , \\ \\ \dot{{\bar{W}}}=-i\omega {\bar{W}}+\bar{\tilde{A_1}} {\bar{W}}Z+\bar{\tilde{A_2}} {\bar{W}} Z^2+\bar{\tilde{A_3}}W\bar{W^2}+\ldots ,\\ \\ {\dot{Z}}=\tilde{B_1}W{\bar{W}}+\tilde{B_2}Z^2+\tilde{B_3}W{\bar{W}}Z+\tilde{B_4}Z^3+\ldots , \end{array}\right. \end{aligned}$$

(24)

where,

$$\begin{aligned} \omega&:=\sqrt{{\mathcal {B}}^*},\\ \tilde{A_1}&:=-\frac{1}{2}+\frac{d_2j_{12}}{2(\beta _{crit} P^*+d_2)^2j_{13}}-\frac{j_{12}j_{21}}{\omega ^2}\left( -\frac{\eta }{P^*}+\frac{\xi _2 \mu }{(\mu +U^*_4)^3}\right) \\&\quad +\,i\left( \frac{d_2j_{12}}{2\omega (\beta _{crit} P^*+d_2)^2}-\frac{j_{12}\eta U^*_4}{\omega P^{*2}}\right) ,\\ \tilde{A_2}&:=\frac{3\xi _2 \mu j_{12}j_{21}}{2\omega ^2(\mu +U^*_4)^4}-i\frac{j_{12}\eta }{2\omega P^{*2}},\\ \tilde{A_3}&:=\frac{\eta U^*_4j_{12}j_{21}}{4P^{*3}j_{31}^2}+\frac{3\xi _2 \mu j_{21}^3j_{12}}{8\omega ^2(\mu +U^*_4)^4j_{31}^2}-\frac{3\omega ^2\beta ^2_{crit}d_2V^*_4}{8(\beta _{crit} P^*+d_2)^4j_{31}^2}-\frac{\beta _{crit} d_2j_{13}}{16(\beta _{crit} P^*+d_2)^3}\\&\quad -\,i\left[ \frac{\beta _{crit} d_2\omega }{8(\beta _{crit} P^*+d_2)^3j_{31}}+\frac{\eta j_{12}j_{21}^2}{8P^{*2}\omega j_{31}^2}+\frac{3\eta \omega U^{*2}_4j_{12}}{8P^{*4}j_{31}^2}+\frac{3\beta ^2 _{crit}V^*_4d_2\omega j_{13}}{8(\beta _{crit} P^*+d_2)^4j_{31}^2}\right] \\ \tilde{B_1}&:=\frac{\eta U^{*2}_4 j_{13}}{2j_{31}P^{*3}}-\frac{j_{13}j_{21}^2}{2\omega ^2j_{31}}\left( \frac{-\eta }{P^*}+\frac{\xi _2 \mu }{(\mu +U^*_4)^3}\right) -\frac{j_{21}j_{13}\beta _{crit} d_2V^*_4}{2j_{31}^2(\beta _{crit} P^*+d_2)^3},\\ \tilde{B_2}&:=-\frac{j_{13}j_{31}}{\omega ^2}\left( \frac{-\eta }{P^*}+\frac{\xi _2 \mu }{(\mu +U^*_4)^3}\right) ,\\ \tilde{B_3}&:=\frac{\eta U^*_4j_{13}}{P^{*3}j_{31}}-\frac{\beta _{crit} d_2j_{21}j_{12}}{2j_{31}^2(\beta _{crit} P^*+d_2)^3},\\ \tilde{B_4}&:=\frac{\xi _2 \mu j_{13}j_{31}}{\omega ^2(\mu +U^*_4)^4}. \end{aligned}$$

Likewise, by considering the $\tilde{A_j}=\tilde{a_j}+i\tilde{c_j}$ and $\tilde{B_j}=\tilde{b_j}$ for $j=1,2,3,\ldots$, in cylindrical coordinates a normal form can be expressed as:

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{r}}=\tilde{a_1}rZ+\tilde{a_2}rZ^2+\tilde{a_3}r^3+O(\left| r\right| ^{4}, \left| Z\right| ^{4}), \\ \\ {\dot{Z}}=\tilde{b_1}r^2+\tilde{b_2}Z^2+\tilde{b_3}r^2Z+\tilde{b_4}Z^3+O(\left| r\right| ^{4}, \left| Z\right| ^{4}),\\ \\ {\dot{\theta }}=\omega +\tilde{c_1}Z+O(\left| r\right| ^{2}, \left| Z\right| ^{2}). \end{array}\right. \end{aligned}$$

(25)

For now we will neglect terms of O(3) and higher and the ${\dot{\theta }}$ component of (25). Thus, the vector field we will study is

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{r}}=\tilde{a_1}rZ, \\ \\ {\dot{Z}}=\tilde{b_1}r^2+\tilde{b_2}Z^2.\\ \end{array}\right. \end{aligned}$$

(26)

Rescaling by letting ${\bar{r}}=\varrho r$ and ${\bar{Z}}=\varsigma Z$, we get

$$\begin{aligned} \dot{{\bar{r}}}=\varrho \left[ \tilde{a_1}\frac{{\bar{r}}{\bar{Z}}}{\varrho \varsigma }\right] , \;\; \dot{{\bar{Z}}}= \varsigma \left[ \frac{\tilde{b_1}}{\varrho ^2}{\bar{r}}^2+\frac{\tilde{b_2}}{\varsigma ^2}{\bar{Z}}^2\right] . \end{aligned}$$

Now, letting $\varrho =-\sqrt{\vert \tilde{b_1}\tilde{b_2}\vert }$, $\varsigma =-\tilde{b_2}$, and dropping the bars on ${\bar{r}}$, ${\bar{Z}}$, we obtain

$$\begin{aligned} {\dot{r}}=arZ, \;\; {\dot{Z}}=br^2-Z^2, \end{aligned}$$

(27)

where $a=\frac{-\tilde{a_1}}{\tilde{b_2}}$ and $b=\frac{-\tilde{b_1}\tilde{b_2}}{\vert \tilde{b_1}\tilde{b_2}\vert }=\pm 1$. From [53] Sections 20.4 and 20.5, a candidate for a versal deformation is given by

$$\begin{aligned} {\dot{r}}&=\mu _1 r+arZ, \nonumber \\ {\dot{Z}}&=\mu _2 +br^2-Z^2, \quad b=\pm 1. \end{aligned}$$

(28)

The study of the local dynamics of (28) is similar to [53] Section 20.7. To summarize, the details will be omitted. For more details the reader is referred to [53].

Now we illustrate dynamics of the system at Hopf-steady state bifurcation point with specific choices for parameters.

We choose parameter values $r=2$, $k=100$, $m=0.4$, $d_2=10$, $\mu =0.29050$ and $\delta =0.2$. Then by using the bifurcation diagram (Fig. 9) we can see that for a set of value of bifurcation parameter ($\beta$ and $\xi$), the Hopf-Zero bifurcation can appear. We consider the threshold values $\beta =2.866$, $\xi =0.1081$, and $\eta =0.6140963015$. For these parameter values we obtain $P=4.687$, $U=0.6289$, $V=5.549$, $j_{11}=j_{22}=0$, $j_{12}=-4.686035614$, $j_{21}=0.01106084996$, $j_{13}=-0.2$, $j_{31}=0.1010796074$, $\omega =0.2684175851$, ${\tilde{a}}_{1}=-0.3518073871$, $\tilde{b_1}=-0.001148923185$, $\tilde{b_2}=-0.02543292168$. Then using these values we obtain $b=\frac{-\tilde{b_1}\tilde{b_2}}{\vert \tilde{b_1}\tilde{b_2}\vert }=-1$ and $a=\frac{-\tilde{a_1}}{\tilde{b_2}}=-13.83275549$ which is negative. The phase portraits of this case (in the different regions in the $\mu _1\mu _2$-plane), are shown in [53] Section 20.7.

To support this calculation we used Auto to obtain a two-parameter plot of bifurcation curves in a vicinity of $(\xi _2,\beta _{crit})$, see Fig. 6. Then we used Auto again to obtain bifurcation diagrams for one-parameter line segments in the vicinity of the codimension two point $(\xi _2,\beta _{crit})$. For example, see Figs. 7 and 9. These results agree with the results of the normal form computation above (Fig. 8).

Fig. 6

Two-parameter bifurcation diagram of system (4) showing curves of codimension one local bifurcations in the $(\xi ,\beta )$ parameter plane, in the vicinity of the codimension two point $(\xi _2,\beta _{crit})=(0.1081,2.866)$. Other parameter values are $r=2$, $k=100$, $m=0.4$, $d_2=10$, $\mu =0.29050$

Fig. 7

One-parameter bifurcation diagrams for system (4) produced by Auto, with $\beta =2.8$ and with $\xi \in [0.09,0.11]$ as the bifurcation parameter on the horizontal axis, showing transcritical, saddle-node, and Hopf bifurcations in the vicinity of the codimension two point $(\xi _2,\beta _{crit})$. The vertical axes are P, U, and V in the left, middle and right panels respectively. Other parameter values are as in Fig. 6. Line types are as in Fig. 5

Fig. 8

One-parameter bifurcation diagrams for system (4) produced by Auto, with $\beta =3$ and with $\xi \in [0.11,0.12]$ as the bifurcation parameter on the horizontal axis, showing transcritical, saddle-node, and Hopf bifurcations in the vicinity of the codimension two point $(\xi _2,\beta _{crit})$. The vertical axes are P, U, and V in the left, middle and right panels respectively. Other parameter values are as in Fig. 6. Line types are as in Fig. 5

Fig. 9

Two-parameter bifurcation diagram of system (4) showing curves of codimension one local bifurcations in the $(\xi ,\beta )$ parameter plane. Other parameter values are $r=2$, $k=100$, $m=0.4$, $d_2=10$, $\mu =0.29050$

Fig. 10

One-parameter bifurcation diagram for system (4) produced by Auto, with $\xi =0.04$ and with $\beta$ as the bifurcation parameter, showing a transcritical bifurcation at $\beta =2.443622$, a Hopf bifurcation at $\beta =1.977234$ and a saddle-node bifurcation of periodic orbit at $\beta =3.369468$. Other parameter values are $r=2$, $k=100$, $m=0.4$, $d_2=10$, $\mu =0.29050$. The horizontal axis is $\beta$ and the vertical axis is V (other variables P and U are not shown). Solid red lines correspond to branches of stable equilibria, solid black lines to unstable equilibria, open blue circles to maximum and minimum values on unstable periodic orbits, and closed green circles to maximum and minimum values on stable periodic orbits. The portions of branches corresponding to $V<0$ have no significance in the model, but are shown to clarify the transcritical bifurcation and change of stability (color figure online)

Some Global Dynamics

For global dynamics we have Theorems 2 and 3. In particular, if there are no compact attracting sets in the positive octant for system (4), then almost all trajectories are attracted to a stable equilibrium or periodic orbit in one of the two boundary planes $U=0$ or $V=0$.

For other global results we have used simulation and the path continuation software Auto. For $r=2$, $k=100$, $m=0.4$, $d_2=10$, $\mu =0.29050$ we used Auto to produce the two-parameter bifurcation diagram in Fig. 9, showing curves, in the $(\xi ,\beta )$ parameter plane, of codimension one local bifurcations that occur at internal equilibria. Then we can use Auto again to produce one-parameter bifurcation diagrams corresponding to parameter paths in the $(\xi ,\beta )$ plane. For example, we set $\xi =0.04$ and increase $\beta$ from 1. The unique interior equilibrium $E_0^*$ (see Fig. 1) has a Hopf bifurcation at $\beta _{crit}=1.977234$ and then it leaves the interior of the positive octant at a transcritical bifurcation with the $V=0$ boundary equilibrium $E_4$ at $\beta _{tr}=2.443622$. Following the branch of periodic orbits from the Hopf bifurcation point, Auto finds they exist for $\beta >\beta _{crit}$ and are unstable, until at $\beta _{snp}=3.369468$ there is a saddle-node bifurcation of periodic orbits, and a branch of stable periodic orbits exists for $\beta <\beta _{snp}$, see Fig. 10. Decreasing $\beta$ from $\beta _{snp}$ and following the branch of stable periodic orbits, we encountered numerical difficulties with Auto as the periodic orbits become more singular. However, using simulation it appears that the stable three-dimensional periodic orbits approach, as $\beta$ decreases from $\beta _{snp}$, the stable two-dimensional periodic orbits that exist in the $U=0$ plane for system (10), see Fig. 11.

Fig. 11

Comparison of two- and three-dimensional periodic orbits for $\xi =0.04$ and decreasing values of $\beta$. The blue trajectories are in the phase plane of the two-dimensional system (10) in the absence of predator type one, and the red trajectories are from the three-dimensional system (4) projected on to the PV-plane (horizontal axis P, vertical axis V). The values of $\beta$ are $3.369, \ 3.3, \ \text {and} \ 3$ in the left, middle and right panels respectively, and the other parameter values are $r=2$, $k=100$, $m=0.4$, $d_2=10$, $\mu =0.29050$

Conclusion

In this paper, a prey–predator model with two types of predator and Michaelis–Menten functional harvesting of one type of predator has been studied analytically and numerically. First, we have found an attracting region for this model which is ecologically meaningful. Then, the dynamics of the model are investigated. Sufficient conditions are given for a positive interior equilibrium to exist and be locally asymptotically stable. Theorem 4 provides more information about asymptotic stability of some equilibria. Next, we have considered bifurcations in the three-dimensional system (4) depending on one or two parameters. Using analytical and numerical methods, we studied codimension one transcritical, saddle-node and Hopf bifurcations, and a codimension two Hopf-steady state bifurcation.

Using numerical methods, we observed that there exist stable large-amplitude periodic orbits which for some parameter values approach the stable two-dimensional periodic orbits that exist in the U = 0 plane for system (10). For the periodic orbits mentioned in “Some Global Dynamics” (see also Figs. 10, 11), the maximum values of U on the periodic orbits are less than $10^{-4}$ when $\beta <3$. The relationship between these three-dimensional periodic orbits and the two-dimensional orbits in the $U=0$ plane is worth further study.

In our study, we consider the system (2) with an additional harvesting term of Michaelis–Menten functional form. The impacts of constant-effort harvesting on system (2) have been extensively studied. How more realistic nonlinear harvesting affects the dynamics of system (2) is not yet clear, but we have made a start with this work. We consider $\beta$, which is proportional to the maximum intrinsic growth rate of the prey species, and $\xi$, which is proportional to the catchability coefficient of the harvested (“type one”) prey species as bifurcation parameters. We have shown that for sufficiently small $\xi$ there is a stable interior equilibrium, which corresponds to coexistence of all three species. However, there are also stable large-amplitude oscillations involving all three species. For larger values of $\xi$ there is a variety of dynamical behaviour such as saddle-node, transcritical, Hopf and Hopf-steady state bifurcations involving all three species, but for sufficiently large values of $\xi$ the model not surprisingly predicts extinction of the harvested predator species.