1 Introduction

The mathematical study of predator–prey interactions is an important research component in mathematical ecology. Various types of interactions and population models with two or more trophic levels have been formulated and received significant attention from several researchers in the past and the more recent literature. The basic building block for a wide range of study are the two populations predator–prey models, in which mathematical models describe the interactions of a hunter species that feeds on a prey, thereby being beneficial for the former and detrimental for the latter. In real life situations this may occur when possibly also other resources are available for the predator. The latter can be subdivided into two broad sets, the specialist predators, that feed only on one species, see for instance the case of the weasel Mustela nivalis exploiting the field vole Microtus agrestis, [3], and the generalist predators with several options for their diet, e.g. the spiders, that hunt every possible insects, [13, 17]. In this latter situation, mainly with more than two resources available, predators focus generally on the most abundant one, changing to exploiting the substitute prey, the second most abundant population, when the primary becomes scarce, [4].

It is a matter of fact that the literature on predator–prey models with generalist predator appears to be smaller compared to that with specialist predator. Primarily, this is due to the fact that the models with a generalist predator are a little bit tougher to handle mathematically. Indeed in most of the cases the components of the coexisting equilibrium point cannot be obtained explicity when the functional responses are represented by highly nonlinear functions of both populations involved, prey and predators.

In case of a two species predator–prey model with a specialist predator, the latter cannot survive in the absence of prey as its reproduction and growth rates are functions of the prey density and in its absence these functions vanish. On the other hand, the growth rate of the generalist predator is different from zero even if the explicit prey disappears, because they can feed on other resources. The mathematical models of two-species generalist predator–prey models can be divided into two types: (i) those in which the predators growth rate follows a logistic law, to which the prey density contributes enhancing it with an additional growth; (ii) those whose predators growth rate follows logistic growth, where the carrying capacity is a function of prey population density. The second type of systems is known as Leslie–Gower [9] or Holling–Tanner [1, 6] model, depending upon the type of the functional response [7, 8, 19] term involved to describe the grazing pattern of the prey by their predator.

Predator–prey models with two-prey and one predator are investigated in particular because this leads to the question of prey switching, [10, 11]. This occurs when the primary resource by overexploitation becomes more difficult to find. The alternative, less palatable prey at that moment is seen as a new potential diet for their survival by the hungry predators. They thus switch their attention to it, instead of wasting time in a difficult search for the primary hard-to-find resource. As a result, in these cases the absence of either primary or substitute prey does not necessarily drive the predator towards extinction. The main objective of the present work is to elucidate the existing relationship between two predator–prey models with a generalist predator, distinguishing the model with implicit secondary prey and the one in which the latter population is explicitly modeled as an additional ecosystem’s variable.

The paper is organized as follows. In the next section the two types of models are formulated and their basic properties are analyzed. Global stability of the coexistence equilibria in both models is assessed in Sect. 3 and next the possible bifurcations are analytically, Sect. 4, and numerically, Sect. 5, investigated. Section 6 performs the system’s comparative study, the subsequent section contains further numerical simulations on bifurcations. A final discussion concludes the paper.

2 The predator–prey models

The predator population is denoted by Z, thriving in the presence respectively of one and two of its only resources, the prey are represented by X and Y. Considering the two possible demographic situations, the following two different predator–prey models can be formulated. The first one with two-populations, i.e. the primary food source for the predators, whose equilibria are denoted by [p_hp], the first “p” referring to predators, the second one to prey, “h” standing for the “hidden” substitute resource not explicitly modeled in the equations, is classical, see Chapter 3 of [15]:

$$\begin{aligned} \frac{dX}{dt}= & {} r X \left( 1- \frac{X}{K} \right) - a XZ, \nonumber \\ \frac{dZ}{dt}= & {} u Z \left( 1- \frac{Z}{L} \right) + ae XZ, \end{aligned}$$
(1)

The first equation models the logistic prey growth and its additional mortality due to encounters between prey individuals with the predators. The last term in the second one in the last term accounts for the benefits the latter gain from this successful hunting, while the first term indicates that the predators have alternative food sources. Its three dimensional counterpart, with the additional resource explicitly modeled, has equilibria denoted by [p_ep], “e” standing for “explicit”. As a one-predator-two prey system, it is also present in the literature, but here a correction on the mortality rate discussed below is made:

$$\begin{aligned} \frac{dX}{dt}= & {} r X \left( 1- \frac{X}{K} \right) - a ZX, \nonumber \\ \frac{dY}{dt}= & {} s Y \left( 1- \frac{Y}{H} \right) - b ZY,\nonumber \\ \frac{dZ}{dt}= & {} -m Z^2 + e (aZX + bZY). \end{aligned}$$
(2)

The first and second equations are replicae of the first equation in (1) for the prey, in this case there being explicitly two food resources in the ecosystem. Note that here the alternative prey Y is the unnamed resource in model (1). The predators’ equation is the same of the former model, with the exception that now they feed only on these two types of prey, and therefore are no more generalist as in (1), but two-population specialists on X and Y. This entails that they will not survive in the absence of both prey.

The parameters are nonnegative in both models. In (2) we take mortality in the quadratic form \(-mZ^2\) since this term is related to the intraspecific competition term \(-uL^{-1}Z^2\) of the system (1). Indeed, comparing the second equation of (1) with the third one of (2), the last term in the former is identical with the second one of the latter. The first (reproductive) term in the generalist model (1) is now replaced by the hunting on the Y prey, last term of (2). To make the comparison fair, then the mortality due to intraspecific competition in (1) must correspond to the first term in (2). This entails that in the specialist system the predators essentially die by intraspecific competition for the needed resources. Mathematically, the connection between (1) and (2) is given by

$$\begin{aligned} u= ebY, \quad L=eb\frac{Y}{m}, \quad {\text { i.e.}} \quad u=Lm. \end{aligned}$$
(3)

Here we should understand the value of the population Y at steady state, namely \(Y=Y^*\), otherwise (3) would be “unbalanced”, i.e. it would have only one time-dependent side.

The Jacobians for models (1) and (2) are respectively

$$\begin{aligned} J^{[p\_hp]} = \left( \begin{array}{cc} r- 2 \frac{r}{K} X - aZ &{} -aX\\ aeZ &{} u- 2 \frac{u}{L} Z + aeX\\ \end{array} \right) \end{aligned}$$
(4)

and

$$\begin{aligned} J^{[p\_ep]} = \left( \begin{array}{ccc} r- 2 \frac{r}{K} X - aZ &{} 0 &{} -aX\\ 0 &{} s- 2 \frac{s}{H} Y - bZ &{} - bY\\ aeZ &{} ebZ &{} - 2mZ + e(aX+bY)\\ \end{array} \right) . \end{aligned}$$
(5)

2.1 Boundedness of models (1) and (2)

In order to obtain a well-posed model, we need to show that the systems trajectories remain confined within a compact set. Consider the total environment population \(\varphi (t)=X(t)+Z(t)\). Let \(\varphi (t)\) be a differentiable function, then taking an arbitrary \(0<\mu \), summing the equations in model (1), and observing that \(e\le 1\) we find the estimate:

$$\begin{aligned} \frac{d\varphi (t)}{dt}+\mu \varphi (t) \le rX \left( 1-\frac{X}{K}+\frac{\mu }{r}\right) +uZ \left( 1-\frac{Z}{L}+\frac{\mu }{u}\right) = p_1(X) + p_2(Z). \qquad \end{aligned}$$
(6)

The functions \(p_1(X)\) and \(p_2 (Z)\) are concave parabolae, with maxima located at \(X^\star \), \(Z^\star \), and corresponding maximum values

$$\begin{aligned} M_1=p_1(X^\star )=\frac{rK}{4}\left( 1+\frac{\mu }{r} \right) ^2, \quad M_2=p_2(Z^\star )=\frac{uL}{4}\left( 1+\frac{\mu }{u} \right) ^2, \end{aligned}$$

Thus,

$$\begin{aligned} \frac{d\varphi (t)}{dt}+\mu \varphi (t) \le M_1+M_2=M. \end{aligned}$$

Integrating the differential inequality, we find

$$\begin{aligned} \varphi (t) \le \left( \varphi (0) - \frac{M}{\mu } \right) e^{-\mu t} + \frac{M}{\mu } \le \max \left\{ \varphi (0), \frac{M}{\mu } \right\} . \end{aligned}$$

From this the boundedness of the original ecosystem populations is immediate.

The proof for system (2) follows a similar patter, after remarking that setting \(\psi (t)=X(t)+Y(t)+Z(t)\) and summing the equations in model (2), we find again for an arbitrary \(0<\mu \),

$$\begin{aligned} \frac{d\psi (t)}{dt}+\mu \psi (t)\le & {} rX \left( 1-\frac{X}{K}+\frac{\mu }{r}\right) +sY \left( 1-\frac{Y}{H}+\frac{\mu }{s}\right) + Z(\mu -mZ). \end{aligned}$$

The above right hand side contains now three concave parabolae; the proofs follows then similarly from the previous steps and is therefore omitted.

Thus for both models, the solutions are always non-negative and remain bounded.

2.2 Equilibria of model (1)

The model (1) is standard in mathematical biology, see for instance Chapter 3 of [15] where also more complex models of such type are described. For this reason here we just summarize the equilibrium analysis, for the convenience of the reader and for later comparison purposes. The following equilibria are found: the origin \(P_1^{[p\_hp]}=(0,0)\), always unstable, (eigenvalues r, u) and the points \(P_2^{[p\_hp]}=(K,0)\), also unstable, (eigenvalues \(-r\), \(u+aeK\)), \(P_3^{[p\_hp]}=(0,L)\), (eigenvalues \(-u\), \(r-aL\)) which is stable for

$$\begin{aligned} r<aL; \end{aligned}$$
(7)

finally steady-state coexistence, \(P_4^{[p\_hp]}=(X_4^{[p\_hp]},Z_4^{[p\_hp]})\). For the latter, explicitly,

$$\begin{aligned} X_4^{[p\_hp]}=uK\frac{r-aL}{ur+a^2eKL}, \quad Z_4^{[p\_hp]}=\frac{r}{a} \left( 1- u\frac{r-aL}{ur+a^2eKL} \right) . \end{aligned}$$

The coexistence equilibrium \(P_4^{[p\_hp]}\) is feasible for \(K\ge X_4^{[p\_hp]} \ge 0\), which explicitly give just the condition

$$\begin{aligned} r\ge aL, \end{aligned}$$
(8)

as the first inequality is easily seen to be always satisfied, namely being equivalent to \(aeK +u \ge 0\). Note also the transcritical bifurcation at \(r=aL\) between \(P_3^{[p\_hp]}\) and \(P_4^{[p\_hp]}\). \(P_4^{[p\_hp]}\), whenever feasible, is unconditionally stable, because the Routh–Hurwitz conditions are satisfied:

$$\begin{aligned}&-{\text {tr}}\left( J_{P_4}^{[p\_hp]}\right) =rK^{-1}X_4^{[p\_hp]} + uL^{-1} Z_4^{[p\_hp]}>0, \\&\det \left( J_{P_4}^{[p\_hp]}\right) =\left( rK^{-1} uL^{-1} + a^2 e\right) X_4^{[p\_hp]} Z_4^{[p\_hp]}>0. \end{aligned}$$

Remark 1

In particular, note that the condition on the trace being strictly positive prevents the occurrence of Hopf bifurcations at this equilibrium. They cannot also occur at \(P_3^{[p\_hp]}\) since the corresponding eigenvalues are both real.

2.3 Equilibria of model (2)

In this subsection we outline the results for (2) and in the Appendix some mathematical details are provided. There are 7 possible equilibria. Four points are always unstable: the origin \(P_1^{[p\_ep]}=(0,0,0)\), (eigenvalues r, s, 0), \(P_2^{[p\_ep]}=(0,H,0)\), (eigenvalues r, \(-s\), ebH), \(P_3^{[p\_ep]}=(K,0,0)\), (eigenvalues \(-r\), s, eaK), \(P_4^{[p\_ep]}=(K,H,0)\), (eigenvalues \(-r\), \(-s\), \(aeK+beH\)). The conditionally stable points are instead the primary-prey-free equilibrium \(P_5^{[p\_ep]}=(0,Y_5^{[p\_ep]},Z_5^{[p\_ep]})\) and the substitute-prey-free point \(P_6^{[p\_ep]}=(X_6^{[p\_ep]},0,Z_6^{[p\_ep]})\), with population levels that are explicitly evaluable:

$$\begin{aligned}&Y_5^{[p\_ep]}=\frac{msH}{b^2eH+ms}, \quad Z_5^{[p\_ep]}=\frac{ebsH}{b^2eH+ms}, \\&X_6^{[p\_ep]}=\frac{mrK}{a^2eK+mr}, \quad Z_6^{[p\_ep]}=\frac{aerK}{a^2eK+mr}. \end{aligned}$$

Feasibility conditions are always satisfied for both equilibria. Stability of these equilibria hinges on the following inequalities: for \(P_5^{[p\_ep]}\)

$$\begin{aligned} a Z_5^{[p\_ep]}= \frac{abesH}{b^2eH+ms} > r, \end{aligned}$$
(9)

and for \(P_6^{[p\_ep]}\)

$$\begin{aligned} b Z_6^{[p\_ep]}= \frac{aberK}{a^2eK+mr} > s, \end{aligned}$$
(10)

as the characteristic equations factorize in both cases to give one explicit eigenvalue producing the above conditions, while the Routh–Hurwitz conditions for the remaining minors are always satisfied, namely

$$\begin{aligned}&\frac{s}{H} Y_5^{[p\_ep]}+m Z_5^{[p\_ep]}> 0,\quad \left( \frac{ms}{H} + b^2e \right) Y_5^{[p\_ep]} Z_5^{[p\_ep]}> 0,\\&\frac{r}{K} X_6^{[p\_ep]}+m Z_6^{[p\_ep]}> 0,\quad \left( \frac{mr}{K} + a^2e \right) X_6^{[p\_ep]} Z_6^{[p\_ep]} > 0. \end{aligned}$$

For the steady-state coexistence \(P_7^{[p\_ep]}=(K-aK r^{-1} Z_7^{[p\_ep]},H- bH s^{-1}Z_7^{[p\_ep]}, Z_7^{[p\_ep]})\), we find

$$\begin{aligned} Z_7^{[p\_ep]}= \frac{ers(bH+aK)}{s(a^2eK+mr)+b^2erH}>0. \end{aligned}$$

Feasibility requirements for \(X_7^{[p\_ep]} \ge 0\) and for \(Y_7^{[p\_ep]} \ge 0\) are given, respectively, by

$$\begin{aligned} r \ge a Z_7^{[p\_ep]}=\frac{abesH}{b^2eH+ms}, \quad s \ge b Z_7^{[p\_ep]}=\frac{aber K}{a^2eK+mr}. \end{aligned}$$
(11)

For stability of the latter, the diagonal entries in the generic Jacobian simplify to \(- rK^{-1} X_7^{[p\_ep]}, - sH^{-1} Y_7^{[p\_ep]}, -mZ_7^{[p\_ep]}\) and it then follows that

$$\begin{aligned}&- {\text {tr}}\left( J_{P_7}^{[p\_ep]}\right) =\frac{r}{K} X_7^{[p\_ep]}+\frac{s}{H} Y_7^{[p\_ep]}+mZ_7^{[p\_ep]}>0, \\&-\det \left( J_{P_7}^{[p\_ep]}\right) = \frac{X_7^{[p\_ep]} Y_7^{[p\_ep]} Z_7^{[p\_ep]}}{HK} \left( a^2esK+b^2erH+mrs\right) >0 \end{aligned}$$

and the remaining Routh–Hurwitz condition given by

$$\begin{aligned}&\frac{r^2s}{K^2H} \left( X_7^{[p\_ep]}\right) ^2 Y_7^{[p\_ep]} + \left( \frac{ra^2e}{K} + r^2m\right) \left( X_7^{[p\_ep]}\right) ^2 Z_7^{[p\_ep]}\\&\quad + \left( \frac{3rms}{KH} + \frac{rb^2e}{K} + \frac{sa^2e}{H} \right) X_7^{[p\_ep]} Y_7^{[p\_ep]} Z_7^{[p\_ep]}\\&\quad +\left( \frac{sm^2}{H}+ mb^2e \right) \left( Y_7^{[p\_ep]}\right) ^2 Z_7^{[p\_ep]}\\&\quad + \left( \frac{s^2m}{H^2} + \frac{sb^2e}{H} \right) \left( Y_7^{[p\_ep]}\right) ^2 Z_7^{[p\_ep]} + \left( \frac{m^2r}{K} + ea^2m \right) X_7^{[p\_ep]} \left( Z_7^{[p\_ep]}\right) ^2\\&\quad + \frac{s^2r}{KH^2} X_7^{[p\_ep]} \left( Y_7^{[p\_ep]}\right) ^2 \\&\quad + \left( \frac{b^2erH+a^2esK+rms}{KH}\right) \qquad X_7^{[p\_ep]} Y_7^{[p\_ep]} Z_7^{[p\_ep]} > 0 \end{aligned}$$

is clearly satisfied as well. Thus the coexistence equilibrium \(P_7^{[p\_ep]}\) of (2) is unconditionally stable, when feasible.

From (9) and the first condition of (11), there is a transcritical bifurcation linking \(P_7^{[p\_ep]}\) with \(P_5^{[p\_ep]}\) and, from (10) and the second condition of (11) there is a transcritical bifurcation linking \(P_7^{[p\_ep]}\) with \(P_6^{[p\_ep]}\).

All the details of the local stability analysis of Sects. 2.2 and 2.3 are presented in “Appendix A”.

3 Global stability for the equilibria of models (1) and (2)

The coexisting equilibrium point \(P_4^{[p\_hp]}\) of the model (1) cannot undergo any Hopf-bifurcation, recall Remark 1 in Sect. 2.2. Here we prove that the feasibility of \(P_4^{[p\_hp]}\) implies that it is globally asymptotically stable. For this purpose we consider the following Lyapunov function,

$$\begin{aligned} V_4^{[p\_hp]}(X(t),\,Z(t))= & {} \left( X-X_4^{[p\_hp]}-X_4^{[p\_hp]}\ln \frac{X}{X_4^{[p\_hp]}}\right) \\&+\,\alpha _1\left( Z-Z_4^{[p\_hp]}-Z_4^{[p\_hp]}\ln \frac{Z}{Z_4^{[p\_hp]}}\right) , \end{aligned}$$

where \(\alpha _1\) is a positive constant, yet to be determined. Differentiating the above function with respect to t along the solution trajectories of system (1), we find

$$\begin{aligned} \frac{dV_4^{[p\_hp]}}{dt}= & {} -\frac{r}{K}\left( X-X_4^{[p\_hp]}\right) ^2 -\alpha _1\frac{u}{L}\left( Z-Z_4^{[p\_hp]}\right) ^2 \\&+\,a(\alpha _1 e-1) \left( X-X_4^{[p\_hp]}\right) \left( Z-Z_4^{[p\_hp]}\right) . \end{aligned}$$

If we choose \(\alpha _1\,=\,\frac{1}{e}\,>\,0\), then the above derivative is negative definite except at the equilibrium point \(P_4^{[p\_hp]}\). Hence \(P_4^{[p\_hp]}\) is a globally stable equilibrium point whenever it is feasible.

For the equilibrium \(P_3^{[p\_hp]}\) we instead choose

$$\begin{aligned} V_3^{[p\_hp]}(X(t),\,Z(t))= \alpha _2 X +\alpha _1\left( Z-Z_3^{[p\_hp]}-Z_3^{[p\_hp]}\ln \frac{Z}{Z_3^{[p\_hp]}}\right) , \end{aligned}$$

and differentiation along the system trajectories leads to

$$\begin{aligned} \frac{dV_3^{[p\_hp]}}{dt}= -\alpha _2 \frac{r}{K} X^2 -\alpha _1\frac{u}{L}\left( Z-Z_3^{[p\_hp]}\right) ^2 + [aZ(\alpha _2 e-\alpha _1 ) + \alpha _1 r - \alpha _2 e aL] X \end{aligned}$$

so that choosing \(\alpha _2 e =\alpha _1\) and using the feasibility condition (7), the derivative of \(V_3^{[p\_hp]}\) becomes negative definite. Hence, when feasible, also \(P_3^{[p\_hp]}\) is globally asymptotically stable.

Similarly, by choosing the following Lyapunov function,

$$\begin{aligned} W_7^{[p\_ep]}(X(t),\,Y(t),\,Z(t))= & {} \left( X-X_7^{[p\_ep]}-X_7^{[p\_ep]}\ln \frac{X}{X_7^{[p\_ep]}}\right) \\&+\, \left( Y-Y_7^{[p\_ep]}-Y_7^{[p\_ep]}\ln \frac{Y}{Y_7^{[p\_ep]}}\right) \\&+\,\beta _1\left( Z-Z_7^{[p\_ep]}-Z_7^{[p\_ep]}\ln \frac{Z}{Z_7^{[p\_ep]}}\right) , \end{aligned}$$

\(\beta _1\) is a positive constant required to be determined. Differentiang the function \(W_7^{[p\_ep]}\) and along the solution trajectories of the system (2) we find, after some algebraic manipulation,

$$\begin{aligned} \frac{dW_7^{[p\_ep]}}{dt}= & {} -\,\frac{r}{K}\left( X-X_7^{[p\_ep]}\right) ^2-\frac{s}{H}\left( Y-Y_7^{[p\_ep]}\right) ^2 - m\beta _1\left( Z-Z_7^{[p\_ep]}\right) ^2\\&+\, \left[ a(1-e\beta _1)\left( X-X_7^{[p\_ep]}\right) +b(1-e\beta _1) \left( Y-Y_7^{[p\_ep]}\right) \right] \left( Z-Z_7^{[p\_ep]}\right) . \end{aligned}$$

Choosing \(\beta _1=\frac{1}{e}\) we find that the derivative of \(W_7^{[p\_ep]}\) is negative definite except at \(P_7^{[p\_ep]}\). Hence \(P_7^{[p\_ep]}\) is a global attractor whenever it is feasible.

For the other equilibria, again when locally asymptotically stable, they are also globally asymptotically stable. Indeed we consider instead, e.g. for \(P_5^{[p\_ep]}\), the function

$$\begin{aligned} W_5^{[p\_ep]}(X(t),\,Y(t),\,Z(t))= & {} \alpha _2 X + \alpha _3 \left( Y-Y_5^{[p\_ep]}-Y_5^{[p\_ep]}\ln \frac{Y}{Y_5^{[p\_ep]}}\right) \\&+ \,\alpha _1 \left( Z-Z_5^{[p\_ep]}-Z_5^{[p\_ep]}\ln \frac{Z}{Z_5 ^{[p\_ep]}}\right) . \end{aligned}$$

Once more, differentiation along the trajectories gives

$$\begin{aligned} \frac{dW_5^{[p\_ep]}}{dt}= & {} -\,\alpha _2 \frac{r}{K}\left( X-X_5^{[p\_ep]}\right) ^2 -\alpha _3 \frac{s}{H}\left( Y-Y_5^{[p\_ep]}\right) ^2 - \alpha _1 m \left( Z-Z_5^{[p\_ep]}\right) ^2\\&+ \,[a(1-e\alpha _1)\left( X-X_5^{[p\_ep]}\right) + X \left[ \alpha _2 r - \alpha _3 a Z_5^{[p\_ep]} - a Z (\alpha _3 -\alpha _2 )\right] \end{aligned}$$

and choosing \(\alpha _2 = \alpha _3 = e \alpha _1\) and using the local stability condition (9) the above derivative of \(W_5^{[p\_ep]}\) is negative definite. Hence the global stability for \(P_5^{[p\_ep]}\). For \(P_6^{[p\_ep]}\) the result is obtained in the same way, using (10).

4 Transcritical bifurcation of model (1)

Here we verify the analytical transversality conditions required for the transcritical bifurcation between the equilibrium points \(P_3^{[p\_hp]}\) and \(P_4^{[p\_hp]}\). For convenience we consider r as the bifurcation parameter. The axial equilibrium point \(P_3^{[p\_hp]}\) coincides with the coexistence equilibrium \(P_4^{[p\_hp]}\) at the parametric threshold \(r_{TC}=aL\).

The Jacobian matrix of the system (1) evaluated at \(P_3^{[p\_hp]}\) and at the parametric threshold \(r=aL\), we find

$$\begin{aligned} J_{P_{3}}^{[p\_hp]}(r_{TC}) =\left( \begin{array}{cc} 0 &{} 0 \\ eaL &{} -u \\ \end{array} \right) , \end{aligned}$$

and its right and left eigenvectors, corresponding to the zero eigenvalue, are given by \(V_1=\varphi _1(1, \frac{er}{u})^T\) and \(Q_1=\omega _1(1,0)^T\), where \(\varphi _1\) and \(\omega _1\) are arbitrary nonzero real numbers. Differentiating partially the right hand sides of the Eq. (1) with respect to r and calculating its Jacobian matrix, we respectively find

$$\begin{aligned} f_r=\left( \begin{array}{c} X_3^{[p\_hp]} (1-\frac{X_3^{[p\_hp]}}{K}) \\ 0 \\ \end{array} \right) , \quad Df_r = \left( \begin{array}{cc} 1-\frac{2X_3^{[p\_hp]}}{K} &{} 0 \\ 0 &{} 0 \\ \end{array} \right) . \end{aligned}$$

Here we use the same notations of [16] to verify the Sotomayor’s conditions for the existence of a transcritical bifurcation. Let \(D^2f((X,Z);r)(V_1,V_1)\) be defined by

$$\begin{aligned}\left( \begin{array}{c} \frac{\partial ^2f_1}{\partial X^2}\xi _1^2+2\frac{\partial ^2f_1}{\partial X\partial Z}\xi _1\xi _2 +\frac{\partial ^2f_1}{\partial Z^2}\xi _2^2 \\ \frac{\partial ^2f_2}{\partial X^2}\xi _1^2+2\frac{\partial ^2f_2}{\partial X\partial Z}\xi _1\xi _2 +\frac{\partial ^2f_2}{\partial Z^2}\xi _2^2\\ \end{array} \right) , \end{aligned}$$

where \(f_1=r X \left( 1- XK^{-1} \right) - a ZX\), \(f_2=u Z \left( 1- ZL^{-1} \right) + ae ZX\) are the right hand sides of (1) and \(\xi _1\), \(\xi _2\) are the components of the eigenvector \(V_1\).

After calculating \(D^2f\) we can easily verify the following three conditions

$$\begin{aligned}&Q_1^Tf_r((0,L);r_{TC})=0, \quad Q_1^TDf_r((0,L);r_{TC})V_1 = 1\,\ne \,0, \\&Q_1^TD^2f((0,L);r_{TC})(V_1,V_1) = -2aL\left( \frac{1}{K}+\frac{ae}{u}\right) \,\ne \,0. \end{aligned}$$

Hence all the conditions for transcritical bifurcation are satisfied. In the above expression, \(Df_r((0,L);r_{TC})\) denotes the Jacobian of the matrix \(f_r\) evaluated at (0, L) for \(r=r_{TC}\).

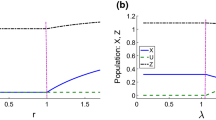
Figure 1 illustrates the simulation explicitly showing the transcritical bifurcation between \(P_3^{[p\_hp]}\) and \(P_4^{[p\_hp]}\) for the chosen parameters values (see the caption of Fig. 1) when the parameter r crosses the critical value \(r_{TC}\)

$$\begin{aligned} r_{TC}=aL = 1 \end{aligned}$$
(12)
Fig. 1
figure 1

Transcritical bifurcation between \(P_3^{[p\_hp]}\) and \(P_4^{[p\_hp]}\) for the parameter values: \( K = a = u= L=e=1\). Initial conditions \(X_0 = Z_0 = 0.01\). The equilibrium \(P_3^{[p\_hp]}\) is stable from 0.1 to 1 and \(P_4^{[p\_hp]}\) is stable past 1; the vertical line corresponds at the transcritical bifurcation threshold between the equilibria

Full size image

5 Numerical simulation results of model (2)

Similar to what was done in Sect. 4 we also verify the transversality conditions required for the transcritical bifurcations between the coexistence equilibrium \(P_7^{[p\_ep]}\) and first the equilibrium point \(P_5^{[p\_ep]}\), and secondly with the equilibrium point \(P_6^{[p\_ep]}\). Considering a and b for convenience as the bifurcation parameters in the two cases, these bifurcations occur respectively at the parametric thresholds

$$\begin{aligned} a_{TC}=\frac{mrs+b^2erH}{besH}, \quad b_{TC}=\frac{mrs+a^2esK}{aerK}. \end{aligned}$$

The Jacobian matrix of the system (2) evaluated at \(P_7^{[p\_ep]}\) and at the parametric threshold \(a_{TC}\) becomes

$$\begin{aligned} J_{P_{7}}^{[p\_ep]}(a_{TC})= & {} \left( \begin{array}{c@{\quad }c@{\quad }c} 0 &{} 0&{} 0 \\ 0&{} -\frac{ms^2}{b^2eH+ms} &{} -\frac{bmsH}{b^2eH+ms} \\ er &{} \frac{b^2e^2sH}{b^2eH+ms} &{} -\frac{bemsH}{b^2eH+ms} \\ \end{array} \right) , \end{aligned}$$

and its right and left eigenvectors, corresponding to the zero eigenvalue, are given by

$$\begin{aligned} V_2=\varphi _2\left( 1, -\frac{r}{s}, \frac{r}{bH}\right) ^T, \quad Q_2=\omega _2(1,0,0)^T, \end{aligned}$$

where \(\varphi _2\) and \(\omega _2\) represent arbitrary nonzero real numbers. Differentiating partially the right hand sides of (2) with respect to a, we find

$$\begin{aligned} f_a=\left( \begin{array}{c} -X_7^{[p\_ep]} Z_7^{[p\_ep]} \\ 0 \\ e X_7^{[p\_ep]} Z_7^{[p\_ep]} \\ \end{array} \right) , \end{aligned}$$

and calculating its Jacobian matrix, we get

$$\begin{aligned} Df_a=\left( \begin{array}{c@{\quad }c@{\quad }c} -Z_7^{[p\_ep]} &{} 0 &{} -X_7^{[p\_ep]} \\ 0 &{} 0 &{} 0 \\ e Z_7^{[p\_ep]} &{} 0 &{} e X_7^{[p\_ep]}\\ \end{array} \right) . \end{aligned}$$

After calculating \(D^2f\) we can then verify the following three conditions

$$\begin{aligned}&Q_2^Tf_a\left( P_7^{[p\_ep]};a_{TC}\right) =0, \end{aligned}$$
(13)
$$\begin{aligned}&Q_2^TDf_a\left( P_7^{[p\_ep]};a_{TC}\right) V_2= -\varphi _2 \omega _2 \frac{besH}{b^2eH+ms} \ne 0 \end{aligned}$$
(14)

and

$$\begin{aligned} Q_2^TD^2f\left( P_7^{[p\_ep]};a_{TC}\right) (V_2,V_2)=-{\varphi _2}^2 \omega _2 \left( \frac{2r}{K}+\frac{2r^2}{sH}+\frac{2mr^2}{b^2eH^2}\right) \ne 0. \end{aligned}$$
(15)

Now, considering the parametric threshold, \(b_{TC}\), the Jacobian matrix of the system (2) evaluated at \(P_7^{[p\_ep]}\) and at \(b_{TC}\) is

$$\begin{aligned} J_{P_{7}}^{[p\_ep]}(b_{TC})= & {} \left( \begin{array}{c@{\quad }c@{\quad }c} -\frac{mr^2}{a^2eK+mr} &{} 0&{} -\frac{amrK}{a^2eK+mr} \\ 0&{} 0 &{}0 \\ \frac{a^2e^2rK}{a^2eK+mr} &{} es &{} -\frac{aemrK}{a^2eK+mr} \\ \end{array} \right) , \end{aligned}$$

and its right and left eigenvectors, corresponding to the zero eigenvalue, are given by

$$\begin{aligned} V_3=\varphi _3\left( 1, -\frac{r}{s}, \frac{r}{aK}\right) ^T, \quad Q_3=\omega _3(0,1,0)^T, \end{aligned}$$

where \(\varphi _3\) and \(\omega _3\) are any nonzero real numbers. Differentiating partially the right hand sides of the Eq. (2) with respect to b, we find

$$\begin{aligned} f_b= & {} \left( \begin{array}{c} 0\\ -Y_7^{[p\_ep]} Z_7^{[p\_ep]} \\ e Y_7^{[p\_ep]} Z_7^{[p\_ep]} \\ \end{array} \right) , \end{aligned}$$

and calculating its Jacobian matrix, we get

$$\begin{aligned} Df_b= & {} \left( \begin{array}{ccc} 0 &{} 0 &{} 0 \\ 0 &{} -Z_7^{[p\_ep]} &{} -Y_7^{[p\_ep]} \\ 0 &{} e Z_7^{[p\_ep]} &{} Y_7^{[p\_ep]}\\ \end{array} \right) . \end{aligned}$$

After calculating \(D^2f\) we can once more easily verify the following three conditions

$$\begin{aligned} Q_3^Tf_b\left( P_7^{[p\_ep]};b_{TC}\right)= & {} 0, \end{aligned}$$
(16)
$$\begin{aligned} Q_3^TDf_b\left( P_7^{[p\_ep]};b_{TC}\right) V_3= & {} -\varphi _3 \omega _3 \frac{a^2er^2K^2+a^2ersHK+mr^2sH}{a^3esK^2+ab^2erHK+amrsK}\nonumber \\\ne & {} 0 \end{aligned}$$
(17)

and

$$\begin{aligned} Q_3^TD^2f\left( P_7^{[p\_ep]};b_{TC}\right) (V_3,V_3)=-{\varphi _3}^2 \omega _3 \left( \frac{2r}{K}+\frac{2r^2}{sH}+\frac{2mr^2}{b^2eH^2}\right) \ne 0. \end{aligned}$$
(18)

Hence all the conditions for transcritical bifurcation are satisfied. Note that \(Df_a(P_7^{[p\_ep]};a_{TC})\) and \(Df_b(P_7^{[p\_ep]};b_{TC})\) in the above expressions (14) and (17) denote the Jacobian of the matrix \(f_a\) and \(f_b\) evaluated at \(P_7^{[p\_ep]}\) for \(a=a_{TC}\) and \(b=b_{TC}\), respectively. Finally, (15) and (18) are obtained from

$$\begin{aligned}&{{D^2f((X,Y,Z);\psi )(V,V)}} \nonumber \\&\quad =\left( \begin{array}{c} \frac{\partial ^2 f_1}{\partial X^2} \xi _1^2+2\frac{\partial ^2 f_1}{\partial X \partial U} {\xi _1}{\xi _2}+2\frac{\partial ^2 f_1}{\partial X \partial Z} {\xi _1}{\xi _3} +2\frac{\partial ^2 f_1}{\partial U \partial Z} {\xi _2}{\xi _3} +\frac{\partial ^2 f_1}{\partial U^2} \xi _2^2+\frac{\partial ^2 f_1}{\partial Z^2} \xi _3^2 \\ \frac{\partial ^2 f_2}{\partial X^2} \xi _1^2+2\frac{\partial ^2 f_2}{\partial X \partial U} {\xi _1}{\xi _2}+2\frac{\partial ^2 f_2}{\partial X \partial Z} {\xi _1}{\xi _3} +2\frac{\partial ^2 f_2}{\partial U \partial Z} {\xi _2}{\xi _3} +\frac{\partial ^2 f_2}{\partial U^2} \xi _3^2+\frac{\partial ^2 f_2}{\partial Z^2} \xi _3^2 \\ \frac{\partial ^2 f_3}{\partial X^2} \xi _1^2+2\frac{\partial ^2 f_3}{\partial X \partial U} {\xi _1}{\xi _2}+2\frac{\partial ^2 f_3}{\partial X \partial Z} {\xi _1}{\xi _3} +2\frac{\partial ^2 f_3}{\partial U \partial Z} {\xi _2}{\xi _3} +\frac{\partial ^2 f_3}{\partial U^2} \xi _3^2+\frac{\partial ^2 f_3}{\partial Z^2} \xi _3^2 \end{array} \right) ,\nonumber \\ \end{aligned}$$
(19)

where

$$\begin{aligned}&f_1=r X \left( 1- \frac{X}{K} \right) - a ZX, \quad f_2=s Y \left( 1- \frac{Y}{H} \right) - b ZY, \\&f_3=-m Z^2 + e (aZX + bZY) \end{aligned}$$

are the right hand sides of (2), \(\psi \) is the bifurcation parameter and \(\xi _1\), \(\xi _2\), \(\xi _3\) are the components of the eigenvector V.

We now consider a numerical example to understand the dynamics of the model (2). We fix the parameter values \(r=3\), \(K=100\), \(s=4\), \(H=120\), \(m=0.2\) and \(e=0.5\). The other two parameters, a and b are considered as bifurcation parameters. We verify that the trivial equilibrium \(P_1^{[p\_ep]}\), two axial equilibria \(P_2^{[p\_ep]}\) and \(P_3^{[p\_ep]}\) and boundary equilibrium \(P_4^{[p\_ep]}\) are always unstable irrespective of the parameter values for a and b. \(P_5^{[p\_ep]}\) is stable for \(300b\,>\,3 (250b^2+1)\) and is unstable otherwise. Similary \(P_6^{[p\_ep]}\) is stable for \(250a\,>\,4 (250a^2+1)\). The coexistence equilibrium point \(P_7^{[p\_ep]}\) is feasible when the parametric restrictions \(300b\,<\,3 (250b^2+1)\) and \(250a\,<\,4 (250a^2+1)\) are satisfied simultaneously. The coexisting equilibrium point is stable whenever it is feasible.

Analytically we have discovered that the coexisting equilibrium point for the model (1) is stable whenever it is feasible. Now we can demonstrate how the stability of this coexisting equilibrium point is altered by explicitly considering the alternative prey population in the system. We fix the parameter values \(r=3\), \(K=100\) and \(e=0.5\). The existence and hence the stability of the coexistence equilibrium is determined by the grazing rate a and the carrying capacity L of the generalist predator. For \(a=0.1\), \(P_4^{[p\_hp]}\) is feasible and stable for \(L<30\) but for \(a=0.3\) we find \(P_4^{[p\_hp]}\) is feasible and stable only for \(L<10\). Here, the intrinsic growth rate of the generalist predator has no role in determining the stability of \(P_4^{[p\_hp]}\); rather, stable coexistence depends just on L. Now we consider the model (2) with two fixed parameter values of a, that is \(a=0.1\) and \(a=0.3\), respectively.

The components of \(P_1^{[p\_ep]}\), \(P_2^{[p\_ep]}=(0,H,0)\), \(P_3^{[p\_ep]}=(K,0,0)\), \(P_4^{[p\_ep]}=(K,H,0)\) and \(P_6^{[p\_ep]}=(54.54545455,0,13.63636364)\) are independent of b however

$$\begin{aligned}&P_5^{[p\_ep]}=\left( 0,\frac{12}{1+75b^2},\frac{300b}{1+75b^2}\right) , \\&P_7^{[p\_ep]}=\left( \frac{45{,}000b^2-6000b+600}{11+450b^2},\frac{1320-4500b}{11+450b^2},\frac{1800b+150}{11+450b^2}\right) . \end{aligned}$$

depend on b. The coexistence equilibrium is feasible and stable for \(b<0.29333333\). For \(b>0.29333333\), instead the coexistence point does not exists, the substitute prey species goes to extinction and \(P_6^{[p\_ep]}\) is stable.

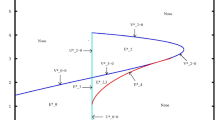
Next, we consider \(a=0.3\). In this case we discover an interesting situation: coexistence is feasible and stable for \(b<0.03670068382\) and \(0.3632993162< b < 0.4533333333\), while the primary prey resource becomes extinct and \(P_5^{[p\_ep]}\) is stable for \(0.03670068382<b<0.3632993162\) and finally, the substitute prey population vanishes and \(P_6^{[p\_ep]}\) is stable for \(b>0.4533333333\). Increasing grazing pressure on substitute prey leads to its extinction when the predation on the primary resource does not vary. On the other hand, extinction of the main prey is observed if the hunting on it increases while the grazing pressure on the second population remains fixed. These numerical results, obtained by our own MATLAB code, are in agreement with the bifurcation diagram shown in Fig. 2.

Fig. 2
figure 2

Bifurcation diagram in the \(a{-}b\) parameter space. The two transcritical bifurcation curves divide the parameter space into the three regions. In \(R_1\) the coexistence equilibrium \(P_7^{[p\_ep]}\) is stable; in \(R_2\) instead the primary-prey-free (\(X_5^{[p\_ep]}=0\)) equilibrium \(P_5^{[p\_ep]}\) is stable; in \(R_3\) we find the substitute-prey-free (\(Y_6^{[p\_ep]}=0\)) equilibrium \(P_6^{[p\_ep]}\) to be stable

Full size image

6 Comparing analytical findings for the models (1) and (2)

Both models are capable to represent the extinction of prey X(t) and the survival of the predators Z(t). In model (1) this situation corresponds to the equilibrium point \(P_3^{[p\_hp]}=(0,L)\) while the analogue situation in model (2) is represented by point \(P_5^{[p\_ep]}=(0,Y_5^{[p\_ep]},Z_5^{[p\_ep]})\). Note that in model (1) predator survival is due to the existence of a hidden resource, i.e., there is one population able to sustain the predator. This situation is represented by the equilibrium point \(P_5^{[p\_ep]}\) in (2), where here the resource is explicitly exhibited at the non-vanishing level \(Z_5^{[p\_ep]}\). If we now use these correspondences between the points and compare the coordinates X and Z of models (1) and (2) we obtain

$$\begin{aligned} L=Z_5^{[p\_ep]}=\frac{eb}{m} Y_5^{[p\_ep]}, \end{aligned}$$
(20)

which is consistent with the result obtained earlier, compare indeed the second condition in (3). In view of the first above equality, (20), stability of the two equilibria is completely analogous, compare indeed (7) and (9), while both are unconditionally feasible. Note also that the results on global stability of these corresponding equilibria is again analogous, whenever viable, they are also globally asymptotically stable. In summary, \(P_3^{[p\_hp]}\) and \(P_5^{[p\_ep]}\) are completely equivalent.

Using a similar reasoning for the coexistence situation in both models we obtain the correspondence between the equilibrium points \(P_4^{[p\_hp]}\) and \(P_7^{[p\_ep]}\). Indeed in both these equilibria, the main prey and the predators coexist. In this case, both are unconditionally locally and globally asymptotically stable. Note that substituting \(X_4^{[p\_hp]}\) into \(Z_4^{[p\_hp]}\) we find \(X_4^{[p\_hp]}=K (1-ar^{-1}Z_4^{[p\_hp]})\), which corresponds to the formula for \(X_7^{[p\_ep]}\). For feasibility we find a correspondence between the conditions (8) and the first one of (11), but in the latter case another additional condition is needed. Therefore acting on this second feasibility condition, essentially on the parameter s, \(P_7^{[p\_ep]}\) could be made unfeasible while \(P_4^{[p\_hp]}\) in principle retains its feasibility.

Note also that equilibrium \(P_6^{[p\_ep]}=(X_6^{[p\_ep]},0,Z_6^{[p\_ep]})\) does not have any correspondent point in the model (1), since this system assumes that the alternative prey is always available, because we cannot set \(L=0\) in it.

7 An application

In this section we provide a numerical example based on a realistic ecosystem. We consider as predator the pine marten Z, Martes martes L., that feeds possibly on the grey squirrel X, Sciurus carolinensis, taken here as the primary prey, and on the European hare Y, Lepus Europaeus, considered as the alternative resource. This example has practical relevance since both the European hare and the grey squirrel are nowadays established invasive species in Piemonte, NW Italy [5, 12]. Some indications on the parameter values are given in the available literature, first line of (21); for the parameters for which an estimate does not exist instead, we choose hypothetical values, second line of (21), and numerically explore the possible ecosystem behavior as they are varied. From [18], the pine marten net reproductive rate ranges in the interval 0.9–1.2; also, for the Swiss and Italian Alps, its density is about 0.1–0.8 individual per km\(^{2}\) [14]. For the hare, the net reproductive rate is about 1.96, while the density in the Alps ranges between 2 and 5 individuals to a maximum value of 10 individuals per km\(^{2}\) [12]. The grey squirrel has a net reproductive rate of 1.28 and density of 20 individuals per km\(^{2}\) [2]. The time unit is taken as the year.

Based on the above information, the parameter reference values that we use for the simulations are:

$$\begin{aligned}&r = 1.28, \quad K = 20, \quad s = 1.96, \quad H = 5, \quad u = 1.2, \quad L = 0.1; \nonumber \\&e = 0.8, \quad a = 1, \quad m = 12, \quad b = 1. \end{aligned}$$
(21)

We have assumed that in the absence of food a pine marten dies in about a month, thereby setting the value for m. Note that with this choice the last condition in (3) is satisfied.

In Fig. 3 we plot the equilibrium values of the three population densities as functions of the hunting parameters a and b. In agreement with the findings of the previous section, the squirrels, the main prey X, vanishes in the left portion of the parameter space, while the alternative prey thrives there and vanishes in the opposite portion of the space. The predator Z thrives instead in the whole parameter space by feeding on each surviving prey in the two different portions of the space. Both prey densities are depressed for larger values of both hunting rates. Somewhat counterintuitively, the predator density in such conditions drops also. This can be explained by the fact that in such case both prey are removed faster and therefore there are less resources for the pine marten, so that a large predator population cannot be sustained.

Fig. 3
figure 3

The coexistence equilibrium value in the \(a{-}b\) parameter space for the model (2). Left to right the squirrels X, hares Y and pine marten Z population densities. The remaining fixed parameters values are given in (21)

Full size image

We investigate then the behavior of the model (2) in the \(a{-}m\) parameter space for the subsequent comparison with the system with the generalist predator, i.e. with model (1), Fig. 4. Note that in the left part of the parameter space, the main prey X vanishes, while in the remaining part of the plane the ecosystem attains coexistence. Here again the predator population density drops as both its mortality and the hunting rate increase independently of each other. The prey experience a gain from higher predator mortalities. The main prey is also depressed by a higher hunting rate, while the alternative prey has a relief: indeed in this case the predation rate a concerns only the primary resource, so that if it is exploited more, the secondary prey suffers less.

Finally in Fig. 5 we consider model (1). In the \(a{-}u\) parameter space, we let u vary in a domain that is comparable with the range used for m in Fig. 4. Clearly, here the squirrels density behavior mimicks the one found in Fig. 2. Instead, the predators behave in the same way as for the mortality rate m in Fig. 4, when the reproduction rate u is concerned, but their density drops with increasing hunting rate, at least for low values of u, while in Fig. 4 it remains essentially constant.

Fig. 4
figure 4

The coexistence equilibrium value in the \(a{-}m\) parameter space for the model (2). Left to right the squirrels X, hares Y and pine marten Z population densities. The remaining fixed parameters values are given in (21)

Full size image
Fig. 5
figure 5

The coexistence equilibrium value in the \(a{-}u\) parameter space for the model (1). Left to right the squirrels X, hares Y and pine marten Z population densities. The remaining fixed parameters values are given in (21)

Full size image

8 Discussion

This paper is devoted to investigate the differences in the dynamics between two predator–prey models with a generalist predator. The alternative food source for the predator is implicit in the first model, but in the second model we have considered it explicitly. The most significant difference between the two models lies in the fact that the grazing pressure on the preferred prey and carrying capacity of the predator determine the stable coexistence of prey and predator when the alternative resource is implicit. It is interesting to note that for predator–prey models with specialist predator and logistic growth for the prey population, we cannot find any prey species extinction scenario due to overexploitation. However, if the predators have an alternative resource other than their favorite prey, higher rate of consumption of one prey species can drive them towards extinction. Due to the presence of the alternative food source for the generalist predator, no predators’ extinction scenario can be observed as the prey-only equilibrium point (K, 0) is always unstable. Although the predators have an alternative food source, they still survive on their most favorite food. As a result the ecosystem extinction and the predator-free equilibrium point (K, 0) are always non-achievable by the system trajectories, as they are unstable. The generalist predator grazing rate on the primary prey a determines which one of the equilibria is stable, the favorite prey-free point \(P_3^{[p\_hp]}\) or the coexistence \(P_4^{[p\_hp]}\).

To ensure the coexistence of both the prey populations and the generalist predator some balance between the respective grazing pressures exerted on them needs to be maintained. Higher grazing pressure only on one species always leads to its extinction, but we never find total system collapse, where extinction of both the prey populations is responsible for the extinction of the predator as well. For both types of models, the feasibility and local asymptotic stability of the equilibria imply also their global asymptotic stability.

Note finally that when we consider the ecosystem with both prey populations explicitly modeled, there is no equilibrium point of the form (0, 0, Z). In such case thus the survival of the predator population alone is not possible. This result is quite reasonable, because then the predator is left with no food available and thus starves to death. The model with implicit prey however cannot show the same behaviour, as the alternative food source is constant and thus remains unaltered and therefore predicts something different.

The numerical simulations performed on a concrete ecosystem show that there could be a difference in the model behavior whether or not the alternative resource is explicitly built into the system. The predator density drops with decreasing hunting rate for low values of the reproduction rate when the secondary prey is hidden and the predators are treated as generalist, while if they are specialist on both species their steady state level remains about constant. So at least in this case, apparently the hiding of the secondary prey as a generic alternative resource plays a significant role, in that it changes a bit the behavior of the predators steady state outcomes.