On Exponential Stability of Neural Networks with Proportional Delays and Periodic Distribution Impulsive Effects

Abstract

This paper is concerned with the problem of generalized exponential stability of impulsive neural networks with a proportional delay. More specifically, the considered network models are subject to both time-varying impulses, whose strengths are in a type of periodic distributions, and a special kind of unbounded time-varying delays called proportional delays. Based on the comparison principle, a unified delay-independent stability criterion is first derived. As an application of the derived stability conditions, the problem of designing a local state feedback control law with bounded controller gains is addressed. Finally, three examples with numerical simulations are given to demonstrate the effectiveness and advantages of the results.

Introduction

Neural networks (NNs) and, in particular, artificial neural networks (ANNs) have found applications in variety of disciplines. For instance, by their pattern-matching and learning capabilities, ANNs can be used to solve many problems in image realization, speech recognition, ecosystem evaluation or natural language processing which are difficult to solve by standard computational and statistical methods. Other applications of NNs can also be found in signal processing, control and monitoring, associative memory and computer security [1,2,3]. To the design of NNs subject to practical applications, stability and performance analysis is an essential and fundamental problem. On the other hand, in practical implementation of NNs, time-delay is frequently encountered as an inherent issue. The presence of time-delay typically makes the system behaviors more complicated and unpredictable [4, 5]. Thus, the problems of analysis and design of NNs both with and without delays have attracted considerable research attention in the past few decades. To mention a few results concerning stability of various types of neural network models, we refer the reader to recent works [6,7,8,9,10,11,12] and the references therein.

Typically, a model of neural networks is composed of layers with a large number of cells and connections. This fact reveals that NNs usually have a spatial nature due to the number of parallel pathways, axon sizes and lengths. Thus, time delays encountered in the practical implementation of NNs are usually time-varying [8, 9]. Proportional delays form a particular type of unbounded time-varying delays, which are widely used in modeling various models in the field of networking [13,14,15]. It is realized that proportional delay provides most well-known quality of service (QoS) models because of its controllable and predictable characteristics. Specifically, when a network with proportional delays is utilized to represent an applied model, dynamics of the system at time t is determined by its states x(t) and x(qt), where $0<q<1$ is a constant representing the ratio of time between current states and historical states. Thus, the network’s running time can be controlled by the proportional factor q. Recently, the problem of stability of various neural network models with proportional delays has attracted considerably increasing research attention and, consequently, a large number of interesting results have been reported in the literature. For example, the problem of finite-time stability was first studied for a class of time-varying neural networks with heterogeneous proportional delays in [16]. The results of [16] were later extended to the case of oscillating leakage coefficients in [17]. Exponential convergence and stability [18,19,20,21], passivity and dissipativity [22, 23] or synchronization [24, 25] problems were considered for Hopfield-type neural networks with proportional delays. Some problems involving periodic solutions or adaptive synchronization were also investigated for shunting inhibitory cellular neural networks or Cohen–Grossberg model with proportional delays in [26,27,28]. Besides practical meanings as mentioned before, the study of neural network models with proportional delays is typically more challenging in comparison to similar problems of neural networks with other types of delays. For example, due to the occurrence of a transformation coefficient in the time scale, the Lyapunov-Krasovskii function method, which is widely utilized for neural networks with time-varying delays [6, 7], is very hard to appy for similar network models with proportional delays. In the later situation, a suitable modification from the comparison principle, which has been successfully applied to many delay-differential equations [29,30,31], proves to be an effective approach.

On the other hand, impulsive dynamical systems (IDSs), in general, and impulsive neural networks with delays (IDNNs) have received considerable research attention in recent years [32,33,34,35,36,37]. It is because that, in many real-world systems and natural processes such as BNNs, bursting rhythm models in pathology, optimal control in economic or electronic and telecommunication networks, the system states are often subject to instantaneous perturbations and abrupt changes at certain instants. These may arise from switching phenomena or frequency changes which usually exhibit impulsive effects [35]. The presence of impulsive effects usually makes the system performance and behavior complex and unpredictable. For instance, even when the normal system (without impulses) is stable the corresponding impulsive system may be unstable. Vice versa, impulsive effects can stabilize the system. Besides that dealing with the problem of analysis and synthesis of IDSs require specific tools and techniques since the processes that represent the state and impulsive jumping trajectories are simultaneously coupled in the system. Thus, together with the effect of delays, impulsive effect has also significantly impact on the performance of IDSs. According to their strength, impulsive effects can be classified into two types named as stabilizing impulses (SI) and destabilizing impulses (DI). An impulsive sequence is said to be destabilizing if its effect can suppress the stability of dynamical systems while SI can enhance the stability of dynamical systems. In most of the existing works concerning stability of impulsive systems, SI and DI are considered separately. For example, the derived conditions for stability/synchronization of IDNNs in [33,34,35] are restricted to SI. Based on some comparison techniques and M-matrix theory, exponential stability conditions were derived in [38] for non-autonomous NNs with heterogeneous delays and destabilizing time-varying impulses. There are only a few results concerning unified criteria for stability or synchronization of IDSs where both SI and DI are taken into account simultaneously. In [39], by using the concept of average impulsive interval, a similar concept of average dwell-time which is widely used in the category of switched systems, a unified exponential synchronization criterion was derived for linear complex dynamical networks with a constant impulse. The problem of exponential stability was studied in [40] for a class of NNs with a bounded delay and time-varying impulses. Based on the Lyapunov function method, a unified algebraic stability condition was derived by utilizing some impulsive differential inequalities. Unfortulately, the results of [40] cannot be extended directly to impulsive neural networks (INNs) with proportional delays. Nevertheless, despite of potential applications in various areas, the problem of stability of INNs with proportional delays has received considerably less attention. Very recently, in [41], the problem of global asymptotic stability was studied for Hopfield-type INNs with multiple proportional delays. Based on an exponential transformation in time scale [18], the considered model is transformed to IDNNs with a constant delay. Then, by using a concept of nonlinear function measure combining with Halanay inequality, sufficient conditions were derived for the existence, uniqueness, and global asymptotic stability of an equilibrium point. The problem of exponential stability of impulsive recurrent neural networks (IRNNs) with proportional delays was considered in [42]. By using an explicit form of solutions resulted from the constant variation formula and by utilizing the fixed point theorem for contraction mappings, algebraic conditions ensuring exponential stability of the system were derived. It should be pointed out that the results of [41, 42] are only applicable to the case of SI. In addition, due to the diversity, and even randomness, of impulsive effects, it is interesting and relevant to study the problem of asymptotic behavior of INNs without the restriction that all impulsive effects are subject to SI. Up to date there has been no result in the literature dealing with this problem for INNs with proportional delays in the presence of SI and DI are simultaneously. This motivates the present study.

In this paper, the problem of generalized exponential stability of INNs with a proportional delay is considered. Both stabilizing and destabilizing impulsive effects are introduced in the model simultaneously. Based on the comparison principle, a unified stability criterion is first derived. Then, on the basis of the derived stability conditions, the problem of designing a local state feedback control law with bounded controller gains is addressed. The effectiveness and advantages of the obtained results is demonstrated by numerical examples.

Preliminaries

Notation. $\mathbb {N}$ is the set of natural numbers, $\mathbb {N}_0=\mathbb {N}\cup \{0\}$ and $[n]\triangleq \{1,2,\ldots ,n\}$ for an $n\in \mathbb {N}$. $\mathbb {R}^{n}$ and $\mathbb {R}^{n\times m}$ denote the n-dimensional vector space and the set of $n\times m$-matrices, respectively. For a matrix $M\in \mathbb {R}^{n\times n}$, $\lambda _{\max }(M)$ and $\lambda _{\min }(M)$ denote the maximum and minimum real part of eigenvalues of M. $\texttt {sym}(M)=M+M^{\top }$. The notation $M<0$ means that M is symmetric ($M=M^{\top }$) and negative definite ($x^{\top }Mx<0$ for all $x\in \mathbb {R}^n$, $x\ne 0$) whereas semi-negative definite matrix ($x^{\top }Mx\le 0$, $\forall x\in \mathbb {R}^n$) will be denoted as $M\le 0$. The upper right Dini derivative of a continuous function v(t) is denoted as $D^+v(t)$.

Consider a neural network model with a proportional delay described as

$$\begin{aligned} {\left\{ \begin{array}{ll} x'_i(t)=-d_ix_i(t) + \sum \limits ^{n}_{j=1}a_{ij}f_j(x_j(t))+\sum \limits ^{n}_{j=1}b_{ij}g_j(x_j(qt))+u_i(t), \; t_0\le t\ne t_k,\\ \Delta x_i(t_k)=x_i(t_k^+)-x_i(t_k^{-})= -\sigma _{ik}x_i(t_k^{-}),\\ x_i(t)=x_i^0, \; t \in [qt_0, t_0] , \; i\in [n], \end{array}\right. } \end{aligned}$$

(1)

where n is the number of neurons, $x_i(t)$ and $u_i(t)$ are the state variable and control input of ith neuron at time t, respectively; $x_i(t_k^{-})=\lim _{\epsilon \downarrow 0}x_i(t_k-\epsilon )$ and $x_i(t_k^{+})=\lim _{\epsilon \downarrow 0}x_i(t_k+\epsilon )$ denote the left- and right-hand limits of $x_i(t)$ at time $t=t_k$; $d_i>0$ is the self-inhibition coefficient (i.e. the rate at which the ith neuron will reset its potential to the resting state in isolation when disconnected from the network and external input); $a_{ij}$ and $b_{ij}$, $i,j\in [n]$, are the connection weights between neurons; $x^0=(x^0_1, x_2^0,\ldots ,x_n^0)^{\top }\in \mathbb {R}^n$ is the initial vector specifying initial states of neurons and $f_j(.)$, $g_j(.)$, $j\in [n]$, are neuron activation functions. The factor $q\in (0,1)$ is a constant involving history time. More specifically, in the interpretation of model (1), dynamics of ith neuron at time t is determined by the current states $x_j(t)$, $j\in [n]$, and the states $x_j(qt)$ at history time qt which is proportional to current time t with a constant rate q. In this meaning, the constant q is referred to as proportional delay. Since $qt=t-\tau (t)$, where $\tau (t)=(1-q)t\rightarrow \infty$ as $t\rightarrow \infty$, proportional delays form a class of unbounded time-varying delays. In model (1), $(t_k)_{k\in \mathbb {N}}$ is a strictly increasing sequence of impulsive moments, $\lim _{k\rightarrow \infty }t_k=\infty$ and, for each $k\in \mathbb {N}$, $\sigma _{ik}$, $i\in [n]$, are real scalars related to strength of abrupt changes of the state vector at impulsive time $t_k$.

Assumption (A1): The neuron activation functions $f_j(.)$, $g_j(.)$, $j\in [n]$, are continuous on $\mathbb {R}$, $f_j(0)=g_j(0)=0$ and there exist constants $l^{-}_{jf}$, $l^{+}_{jf}$, $l^{-}_{jg}$ and $l^{+}_{jg}$, $j\in [n]$, such that the following conditions hold for all $a, b\in {\mathbb {R}}$, $a\ne b$,

$$\begin{aligned} l^{-}_{jf}\le \frac{f_j(a)-f_j(b)}{a-b}\le l^{+}_{jf},\quad l^-_{jg}\le \frac{g_j(a)-g_j(b)}{a-b}\le l^+_{jg}. \end{aligned}$$

(2)

Assumption (A2): There exists a sequence of positive numbers $(\gamma _k)_{k\in \mathbb {N}}$ such that

$$\begin{aligned} 1-\gamma _k\le \sigma _{ik}\le 1+\gamma _k,\;\; \forall i\in [n], \;k\in \mathbb {N}. \end{aligned}$$

(3)

Proposition 1

Under Assumptions (A1)–(A2), for any initial condition $x^0\in \mathbb {R}^n$, there exists a unique solution $x(t)=x(t;x^0)$ of (1) which is piecewise continuous on $[1,\infty )$ with possible discontinuities at $t=t_k$.

Proof

The proof is similar to that of Theorem 1.17 in [43]. Thus, we omit it here. $\square$

Remark 1

It follows from (2) that

$$\begin{aligned} |f_j(a)-f_j(b)|\le F_j|a-b|,\quad |g_j(a)-g_j(b)|\le G_j|a-b|, \end{aligned}$$

where $F_j=\max \{l^+_{jf}, -l^{-}_{jf}\}$ and $G_j=\max \{l^+_{jg}, -l^{-}_{jg}\}$. In the following, we denote $F=\mathrm {diag}(F_i)$ and $G=\mathrm {diag}(G_i)$.

Remark 2

According to (1) and (3), $|x_i(t_k^+)|=|1-\sigma _{ik}||x(t_k^{-})|\le \gamma _k|x(t_k^{-})|$. Thus, $\gamma _k$ determines the impulsive strength at $t_k$. When $\gamma _k>1$, the absolute value of the state vector can be enlarged by impulsive perturbations and the impulses potentially destroy stability of system (1) [38]. This type of impulses are called destabilizing impulses since they can suppress stability of the system. When $\gamma _k < 1$, the impulses are stabilizing impulses since impulsive effects can enhance stability of the system.

In this paper, stabilizing impulses and destabilizing impulses are taken into account simultaneously. More specifically, the strengths of SI and DI are assumed to take values in finite sets $\mathbb {I}^s=\{\rho _1, \rho _2,\ldots ,\rho _M\}$ and $\mathbb {I}^u=\{\mu _1,\mu _2,\ldots ,\mu _N\}$, where $0<\rho _i<1$ for $i\in [M]$ and $\mu _j>1$ for $j\in [N]$. In addition, we denote as $t^s_{ik}$ and $t^u_{jk}$ the impulsive instances of stabilizing impulses with strength $\rho _i$ and the impulsive instances of destabilizing impulses with strength $\mu _j$, respectively. That means, for any $i\in [M]$ and $j\in [N]$, $t^s_{ik}=t_k$ if $\gamma _k=\rho _i$ and $t^u_{jk}=t_k$ if $\gamma _k=\mu _j$.

Remark 3

For general IDSs and, in particular, neural networks model (1), not only the strength of impulses but also the frequency of impulses are essential factors affecting stability of the system [38, 39]. To deal with stability problem of IDSs, where both SI and DI are introduced simultaneously as in model (1), we use a type of average impulsive interval conditions as the following assumption.

Assumption (A3): There exist positive numbers $\tau ^s_i$, $\tau ^u_j$, and integers $q_i\in \mathbb {N}_0$, $r_j\in \mathbb {N}_0$, $i\in [M]$, $j\in [N]$, satisfying the following conditions for any $t>s\ge t_0$

$$\begin{aligned}&\frac{t-s}{\tau ^s_i}-q_i\le N_{\rho _i}(t,s)\le \frac{t-s}{\tau ^s_i}+q_i,\nonumber \\&\frac{t-s}{\tau ^u_j}-r_j\le N_{\mu _j}(t,s)\le \frac{t-s}{\tau ^u_j}+r_j, \end{aligned}$$

(4)

where $N_{\rho _i}(t,s)$ and $N_{\mu _j}(t,s)$ present the frequencies of impulsive strengths $\rho _i$ and $\mu _j$ on interval (s, t), respectively.

In this paper, we also design a local state feedback control law (LSFCL) of the form

$$\begin{aligned} u_i(t)=-k_ix_i(t),\; i\in [n], \end{aligned}$$

(5)

to stabilize system (1), where $k_i$, $i\in [n]$, are controller gains. Due to practical configurations of the inputs, we assume the controller gains $k_i$, $i\in [n]$, are confined in intervals $[k_i^l,k_i^u]$, where $k_i^l$, $k_i^u$, $i\in [n]$, are known constants. Under the LSFCL (5), the closed-loop system of (1) can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} x'(t)=-D_cx(t)+Af(x(t))+Bg(x(qt)), \; t\ne t_k,\\ x(t_k^+)=J_kx(t_k^{-}), \; k \in {\mathbb {N}}, \end{array}\right. } \end{aligned}$$

(6)

where $D_c=\mathrm {diag}(d_i+k_i)$, $A=(a_{ij})$, $B=(b_{ij})$, $f(x(t))=(f_j(x_j(t)))$, $g(x(qt))=(g_j(x_j(qt)))$ and $J_k=\mathrm {diag}(1-\sigma _{ik})$.

Similar to [30], we give the following definition.

Definition 1

System (6) is said to be generalized globally exponentially stable (GGES) if there exist a positive scalar $\kappa$ and an increasing function $\sigma (t)>0$, $\sigma (t)\rightarrow \infty$ as $t\rightarrow \infty$, such that any solution $x(t)=x(t,x^0)$ of (6) satisfies the following estimation

$$\begin{aligned} \Vert x(t)\Vert \le \kappa \Vert x^0\Vert e^{-\sigma (t)},\; t\ge t_0. \end{aligned}$$

The main objective of this paper is to derive conditions for the existence of a controller gain matrix $K_c=\mathrm {diag}(k_i)$ in (5) that makes the closed-loop system (6) GGES. In the remaining of this section, we introduce the following auxiliary result which can be formulated by a similar proof presented in [30, 32].

Lemma 1

Let u(t), v(t), $t\in [q,\infty )$, be piecewise continuous functions satisfying

$$\begin{aligned} {\left\{ \begin{array}{ll} D^+u(t)\le F(t, u(t), u(qt)),\; t\ne t_k,\\ u(t^+_k)\le I_k(u(t^{-}_k)), \end{array}\right. } \end{aligned}$$

(7)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} D^+v(t)>F(t,v(t), v(qt)),\; t\ne t_k,\\ v(t^+_k)\ge I_k(v(t^{-}_k)), \end{array}\right. } \end{aligned}$$

(8)

where $F:\mathbb {R}^+\times \mathbb {R}^2\rightarrow \mathbb {R}$ and $I_k: \mathbb {R}\rightarrow \mathbb {R}$ are given functions. Assume that, for any (t, u), F(t, u, v) and $I_k(v)$ are nondecreasing with respect to v. Then $u(t)\le v(t)$ for all $t \ge t_0$ provided that $u(t)\le v(t)$ for $t\in [qt_0,t_0]$.

Main Results

In this section, we first derive conditions to ensure the closed-loop system (6) is GGES. To facilitate in presenting stability conditions of system (6), we denote the matrices $|A|= (|a_{ij}|)$, $|B|=(|b_{ij}|)$ and

$$\begin{aligned} {\mathscr {M}}=-2D_c+\texttt {sym}(|A|F)+\theta ^{-1}|B|GG^{\top }|B|^{\top },\; \theta >0, \end{aligned}$$

where $F=\mathrm {diag}(F_i)$ and $G=\mathrm {diag}(G_i)$.

Theorem 1

Let Assumptions (A1)–(A3) hold. Assume that there exist positive scalars $\alpha$ and $\theta$ satisfying the following conditions

$$\begin{aligned}&{\mathscr {M}}+\alpha I\le 0, \end{aligned}$$

(9a)

$$\begin{aligned}&\alpha >p\theta , \end{aligned}$$

(9b)

$$\begin{aligned}&\sum _{i=1}^M\frac{\ln (\rho _i)}{\tau ^s_i}+\sum _{j=1}^N\frac{\ln (\mu _j)}{\tau ^u_j}=0, \end{aligned}$$

(9c)

where $p=\prod _{i=1}^M\prod _{j=1}^N\mu ^{2r_j}_j\rho ^{-2q_i}_i$. Then, system (6) is GGES. More precisely, there exists a constant $\sigma >0$ such that any solution $x(t)=x(t,x^0)$ of (6) satisfies

$$\begin{aligned} \Vert x(t)\Vert \le \frac{\sqrt{p}}{\sqrt{(1+qt_0)^{\sigma }}}\Vert x^0\Vert e^{-1/2\sigma \ln (1+t)},\; t\ge t_0. \end{aligned}$$

(10)

Proof

We devide the proof into three parts.

• (a) Let $x(t)=(x_i(t))$, $t\ge t_0$, be a solution of (6) with initial condition $x(t)=x^0 \in \mathbb {R}^n$, $t\in [qt_0,t_0]$. Then, we have

  $$\begin{aligned} D^+|x_i(t)|\le \;&-(d_i+k_i)|x_i(t)|+ \sum ^{n}_{j=1}F_j|a_{ij}||x_j(t)|\nonumber \\&+\sum ^{n}_{j=1}G_j|b_{ij}||x_j(qt)|,\; t\in [t_{k-1}, t_k),\; k\in \mathbb {N}. \end{aligned}$$

  (11)

  At impulsive moment $t=t_k$, from (6) and (A2), we have

  $$\begin{aligned} |x_i(t^+_k)|= |1-\sigma _{ik}||x_i(t^{-}_k)|\le \gamma _k|x_i(t^{-}_k)|. \end{aligned}$$

  (12)

  As revealed by (11) and (12), we consider the following impulsive scaled system

  $$\begin{aligned} {\left\{ \begin{array}{ll} {\hat{x}}'(t)= \left( -D_c+|A|F\right) {\hat{x}}(t)+|B|G{\hat{x}}(qt),\;t\ne t_k,\\ {\hat{x}}(t_k)=\gamma _k {\hat{x}}(t^{-}_k),\\ {\hat{x}}(t)=|x^0|,\; t \in [qt_0, t_0]. \end{array}\right. } \end{aligned}$$

  (13)

  By Proposition 1, system (13) has a unique solution ${\hat{x}}(t)$ on $[1, \infty )$. On the other hand, since $-D_c+|A|F$ is a Metzler matrix and |B|G is nonnegative, system (13) is a positive system. Thus, ${\hat{x}}_i(t)\ge 0$ for all $t\ge q$, $i\in [n]$. Furthermore, by similar arguments used in the proof of Lemma 2.1 in [30], it is found that $|x_i(t)|\le {\hat{x}}_i(t)$, $\forall t\ge qt_0$, $i\in [n]$. Consider the function $V(t)= {\hat{x}}^{\top }(t){\hat{x}}(t)$, $t\ge t_0$. The derivative of V(t) on each interval $[t_{k-1}, t_k)$, $k\in \mathbb {N}$, with respect to system (13) is given by

  $$\begin{aligned} D^+V(t)&= 2{\hat{x}}^{\top }(t){\hat{x}}'(t)\nonumber \\&=2{\hat{x}}^{\top }(t)\left[ (-D_c+|A|F){\hat{x}}(t)+|B|G{\hat{x}}(qt)\right] . \end{aligned}$$

  (14)

  By the Cauchy-Schwarz inequality,

  $$\begin{aligned} 2u^{\top }v\le \theta ^{-1}u^{\top }u+\theta v^{\top }v \end{aligned}$$

  holds for any $u,v\in \mathbb {R}^n$. Therefore,

  $$\begin{aligned} 2{\hat{x}}^{\top }(t)|B|G{\hat{x}}(qt) \le \theta ^{-1}{\hat{x}}^{\top }(t)|B|GG^{\top }|B|^{\top }{\hat{x}}(t)+\theta {\hat{x}}^{\top }(qt){\hat{x}}(qt). \end{aligned}$$

  (15)

  Combining (14) and (15) gives

  $$\begin{aligned} D^+V(t)&\le {\hat{x}}^{\top }(t)\Big (-2D_c+\texttt {sym}(|A|F)+\theta ^{-1}|B|GG^{\top }|B|^{\top }\Big ){\hat{x}}(t) + \theta {\hat{x}}^{\top }(qt){\hat{x}}(qt)\nonumber \\&\le -\alpha V(t)+\theta V(qt), \; t\in [t_{k-1},t_k). \end{aligned}$$

  (16)

  At $t=t_k$, from (13), we have

  $$\begin{aligned} V(t^+_k)=\gamma ^2_kV(t^-_k), \; k\in \mathbb {N}. \end{aligned}$$

  (17)

  Now, for any $0<\epsilon <\frac{1}{2}\big (\frac{\alpha }{p\theta }-1\big )$, consider the following auxiliary system

  $$\begin{aligned} {\left\{ \begin{array}{ll} \varphi '(t)= -\alpha \varphi (t)+\beta \varphi (qt),\; t_0\le t\ne t_k,\\ \varphi (t_k^+)=\gamma _k^2\varphi (t^{-}_k),\\ \varphi (t)=\Vert x^0\Vert ^2,\; t\in [qt_0,t_0], \end{array}\right. } \end{aligned}$$

  (18)

  where $\beta =\theta (1+\epsilon )$. By Lemma 1, from (16)–(18), we have

  $$\begin{aligned} 0\le V(t)\le \varphi (t),\; t \in [qt_0,\infty ). \end{aligned}$$

  (19)

• (b) Next, we will show that there exists a $\sigma >0$ such that

  $$\begin{aligned} \varphi (t)\le \frac{p}{T_0}\Vert x^0\Vert ^2e^{-\sigma \ln (1+t)},\; \forall t\ge qt_0, \end{aligned}$$

  (20)

  where $p=\prod _{i=1}^M\prod _{j=1}^N\mu ^{2r_j}_j\rho ^{-2q_i}_i$ and $T_0=\frac{1}{(1+qt_0)^{\sigma }}$. For this, by condition (9b), there exists a scalar $\sigma >0$ such that

  $$\begin{aligned} \alpha >\frac{\alpha +p\theta }{2q^{\sigma }}. \end{aligned}$$

  (21)

  It is clear from (21) that the inequality $\alpha >\frac{p\beta }{q^{\sigma }}$ holds for all $0<\epsilon <\frac{1}{2}\big (\frac{\alpha }{p\theta }-1\big )$. Now, for any fixed $\delta >0$, from (20), we have

  $$\begin{aligned} \varphi (t)<\frac{1+\delta }{T_0}\Vert x^0\Vert ^2e^{-\sigma \ln (1+t)}, \; \forall t\in [qt_0,t_0]. \end{aligned}$$

  (22)

  If (22) does not hold for $t\in (t_0,t_1)$ then, by the continuity of $\varphi (t)$ on $[t_0,t_1)$, there exists a $t_f\in (t_0,t_1)$ such that $\varphi (t_f)=\frac{1+\delta }{T_0}\Vert x^0\Vert ^2e^{-\sigma \ln (1+t_f)}$ and (22) holds for $t\in [qt_0,t_f)$. By using the fact that $\hbar (t)=\frac{1+t}{1+qt}$ is an increasing function on $[t_0,\infty )$, $\hbar (t)\uparrow \frac{1}{q}$ as $t\rightarrow \infty$, it is found that

  $$\begin{aligned} \varphi (qt_f)&\le \frac{1+\delta }{T_0}\Vert x^0\Vert ^2e^{-\sigma \ln (1+qt_f)}\\&\le \left( \frac{1+t_f}{1+qt_f}\right) ^{\sigma }\varphi (t_f)\\&\le \frac{1}{q^{\sigma }}\varphi (t_f). \end{aligned}$$

  Combining with (18) we have

  $$\begin{aligned} \varphi '(t_f)&\le \Big (-\alpha +\frac{\beta }{q^{\sigma }}\Big )\varphi (t_f)\\&<\Big (-\alpha +\frac{p\beta }{q^{\sigma }}\Big )\varphi (t_f)< 0, \end{aligned}$$

  which clearly raises a contradiction since $\varphi '(t_f)\ge 0$. Therefore, inequality (22) holds for $t\in [qt_0,t_1)$. Let $\delta \downarrow 0$ in (22) we obtain

  $$\begin{aligned} \varphi (t)\le \frac{1}{T_0}\Vert x^0\Vert ^2e^{-\sigma \ln (1+t)}, \; \forall t\in [qt_0,t_1), \end{aligned}$$

  and hence,

  $$\begin{aligned} \varphi (t_1^+)\le \frac{\gamma _1^2}{T_0}\Vert x^0\Vert ^2e^{-\sigma \ln (1+t_1)}. \end{aligned}$$

  (23)

• (c) Motivated by the proof in part (b), we will prove by utilizing the mathematical induction method that

  $$\begin{aligned} \varphi (t)\le \frac{1}{T_0}\Vert x^0\Vert ^2\varGamma (t,t_0)e^{-\sigma \ln (1+t)},\; t\ge t_0, \end{aligned}$$

  (24)

  where the function $\varGamma (t,s)$, $t>s\ge qt_0$, is defined as

  $$\begin{aligned} \varGamma (t,s)={\left\{ \begin{array}{ll}\prod \limits _{k\in {\mathscr {I}}(t,s)}\gamma _k^2 &{}\text { if\;} {\mathscr {I}}(t,s)\ne \emptyset ,\\ 1 &{}\text { if\; } {\mathscr {I}}(t,s)=\emptyset ,\end{array}\right. } \end{aligned}$$

  (25)

  where ${\mathscr {I}}(t,s)=\{k:\; s<t_k<t\}$. By virtue of the induction method, it suffices to prove that (24) holds for all $t\in [t_{k-1},t_k)$, $k\ge 1$. To this end, it is noted that estimate (24) holds for $k=1$. Assume (24) holds for $t\in [t_{k-1},t_k)$, $k\ge 1$. Then, we have

  $$\begin{aligned} \varphi (t_k^+)&\le \frac{1}{T_0}\Vert x^0\Vert ^2\gamma _k^2\varGamma (t_k,t_0)e^{-\sigma \ln (1+t_k)}\nonumber \\&<\frac{1+\delta }{T_0}\Vert x^0\Vert ^2\gamma _k^2\varGamma (t_k,t_0)e^{-\sigma \ln (1+t_k)} \end{aligned}$$

  (26)

  for any fixed $\delta >0$. Assume that there exists a $t_f\in (t_k,t_{k+1})$ such that $\varphi (t_f)=\frac{1+\delta }{T_0}\Vert x^0\Vert ^2\varGamma (t_f,t_0)e^{-\sigma \ln (1+t_f)}$ and

  $$\begin{aligned} \varphi (t)<\frac{1+\delta }{T_0}\Vert x^0\Vert ^2\varGamma (t_f,t_0)e^{-\sigma \ln (1+t)},\;\forall t\in [t_k,t_f). \end{aligned}$$

  (27)

  Then, by (27) and the induction hypothesis in (24), we have

  $$\begin{aligned} \varphi (qt_f)&<\Big (\frac{1+t_f}{1+qt_f}\Big )^{\sigma }\frac{\varphi (t_f)}{\varGamma (t_f,qt_f)}\nonumber \\&\le \frac{\varphi (t_f)}{q^{\sigma }\varGamma (t_f,qt_f)}. \end{aligned}$$

  (28)

  For any $t>s\ge qt_0$, as defined in (25), we have

  $$\begin{aligned} \varGamma (t,s)=\prod _{k\in {\mathscr {I}}(t,s)}\gamma _k^2 =\prod _{i=1}^M\rho _i^{2n(\rho _i)}\prod _{j=1}^N\mu _j^{2n(\mu _j)}, \end{aligned}$$

  (29)

  where $n(\rho _i)=N_{\rho _i}(t,s)$ and $n(\mu _j)=N_{\mu _j}(t,s)$. By Assumption (A3), we have

  $$\begin{aligned} c(t,s)&\triangleq \sum _{i=1}^Mn(\rho _i)\ln (\rho _i)+\sum _{j=1}^Nn(\mu _j)\ln (\mu _j)\nonumber \\&\le \sum _{i=1}^M\Big (\frac{t-s}{\tau _i^s}-q_i\Big )\ln (\rho _i) +\sum _{j=1}^N\Big (\frac{t-s}{\tau ^u_j}+r_j\Big )\ln (\mu _j)\nonumber \\&\le \sum _{j=1}^Nr_j\ln (\mu _j)-\sum _{i=1}^Mq_i\ln (\rho _i). \end{aligned}$$

  (30)

  Similarly, we also have

  $$\begin{aligned} c(t,s)\ge \sum _{i=1}^Mq_i\ln (\rho _i)-\sum _{j=1}^Nr_j\ln (\mu _j). \end{aligned}$$

  (31)

  Taking (29) and (30) into account, we obtain

  $$\begin{aligned} \begin{aligned} \varGamma (t,s)&=e^{c(t,s)}\\&\le e^{\sum _{j=1}^Nr_j\ln (\mu _j)-\sum _{i=1}^Mq_i\ln (\rho _i)}=p. \end{aligned} \end{aligned}$$

  (32)

  Similar to (32), we also have

  $$\begin{aligned} \varGamma (t,s)\ge e^{-\sum _{j=1}^Nr_j\ln (\mu _j)+\sum _{i=1}^Mq_i\ln (\rho _i)}=\frac{1}{p}. \end{aligned}$$

  (33)

  It follows from (28) and (33) that

  $$\begin{aligned} \varphi (qt_f)\le \frac{p}{q^{\sigma }}\varphi (t_f), \end{aligned}$$

  and therefore,

  $$\begin{aligned} \varphi '(t_f)\le \Bigg (-\alpha +\frac{p\beta }{q^{\sigma }}\Bigg )\varphi (t_f)<0 \end{aligned}$$

  which contradicts with the fact that $\varphi '(t_f)\ge 0$ by the definition of $t_f$. This shows that the estimate

  $$\begin{aligned} \varphi (t)<\frac{1+\delta }{T_0}\Vert x^0\Vert ^2\varGamma (t,t_0)e^{-\sigma \ln (1+t)} \end{aligned}$$

  (34)

  holds for all $t\in (t_k,t_{k+1})$. Let $\delta \downarrow 0$, it can be deduced from (34) that (24) holds for $t\in [t_k,t_{k+1})$. Finally, from (19), (24), and (32), we readily obtain

  $$\begin{aligned} V(t)\le \varphi (t)\le \frac{p}{T_0}\Vert x^0\Vert ^2e^{-\sigma \ln (1+t)},\; t\ge t_0, \end{aligned}$$

  which yields the estimation (10) ensuring GGES of the closed-loop system (6). The proof is completed.

$\square$

Remark 4

It is necessary to mention here that existing methods proposed in the literature for IDNNs with bounded time-varying delays, where both SI and DI are encountered simultaneously, e.g. [40] cannot be adaptive or extended to INNs as described in (1). The key point obscured behind existing stability conditions is the structure of decaying solutions of the associated differential inequalities.

Remark 5

In regard to Remark 4, let us consider the following inequality

$$\begin{aligned} \varphi '(t)\le -a\varphi (t)+b\varphi (t-\tau (t)),\; t\ge t_0, \end{aligned}$$

(35)

where $0\le \tau (t)\le \tau ^*<\infty$ is a bounded time-varying delay. If $a>b>0$ then there exists a $\lambda >0$ such that any solution of (35) satisfies $\varphi (t)\le \Vert \varphi _0\Vert e^{-\lambda (t-t_0)}$, where $\Vert \varphi _0\Vert =\sup _{t_0-\tau ^*\le t\le t_0}|\varphi (t)|$ [30, 44]. Unfortunately, the estimating methods developed for differential inequalities in the form of (35) are not applicable to the case of proportional delay since the equation

$$\begin{aligned} \varphi '(t)=-a\varphi (t)+b\varphi (qt),\; t\ge t_0,\; 0<q<1, \end{aligned}$$

(36)

does not admit any exponential decaying solution. Thus, in comparison to the case of bounded time-varying delay, it is much more difficult and challenging to derive exponential stability conditions for IDNNs as model (1).

Remark 6

By the Schur complement lemma, conditions (9a) and (9b) can be recast into the following linear matrix inequalities (LMIs)

$$\begin{aligned}&\begin{pmatrix} -2D_c+\texttt {sym}(|A|F)+\alpha I_n &{} |B|G\\ G|B|^{\top }&{} -\theta I_n\end{pmatrix}<0, \end{aligned}$$

(37a)

$$\begin{aligned}&p\theta - \alpha <0. \end{aligned}$$

(37b)

Remark 7

By similar arguments used in the proof of Theorem 1, exponential stability conditions for IRNNs described in the form

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}(t)=-Dx(t)+Af(x(t))+Bg(x(t-\tau (t))), \; t\ne t_k,\\ x(t_k^+)=J_kx(t_k^{-}), \end{array}\right. } \end{aligned}$$

(38)

can be obtained, where $\tau (t)$ is unbounded time-varying delay.

As a special case of model (1), let us consider the following neural network model with alternatively impulsive effects

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{x}(t)=-Dx(t)+Af(x(t))+Bg(x(qt)), \; t\ne kT_s,\\ x(t_k^+)=\gamma _kx(t_k^{-}), \end{array}\right. } \end{aligned}$$

(39)

where $T_s>0$ is a sampling time. Assume that there exists a scalar $\gamma _*$, $0<|\gamma _*|\ne 1$, such that $\gamma _{2k+1}=\gamma _*$ and $\gamma _{2k+2}=\gamma _*^{-1}$ for any $k\in \mathbb {N}_0$. It is clear that

$$\begin{aligned}&\frac{t-s}{2T_s}-1\le N_{\gamma _*}(t,s)\le \frac{t-s}{2T_s}+1,\\&\frac{t-s}{2T_s}-1\le N_{\gamma _*^{-1}}(t,s)\le \frac{t-s}{2T_s}+1. \end{aligned}$$

By Theorem 1, we have the following result.

Corollary 1

Under Assumptions (A1)–(A3), system (39) is GGES if there exists a scalar $\theta >0$ satisfying the following condition

$$\begin{aligned} \theta \max \Big \{\gamma _*^2,\frac{1}{\gamma _*^2}\Big \}+m<0, \end{aligned}$$

(40)

where $m=\lambda _{\max }\left( -2D+\texttt {sym}(|A|F)+\theta ^{-1}|B|GG^{\top }|B|^{\top }\right)$.

Proof

The proof is straightforward to that of Theorem 1 with $\tau ^s_i=\tau ^u_j=2T_s$ and $p=\max \{\gamma _*^2,\frac{1}{\gamma _*^2}\}$. $\square$

Based on condition (37), the problem of designing a LSFCL (5) that makes the closed-loop system (6) GGES is presented in the following theorem.

Theorem 2

Under Assumptions (A1)–(A3), assume that condition (9c) is satisfied. Then, system (1) is exponentially stabilizable under LSFCL (5) if the following LMIs are feasible for scalar $\alpha >0$, $\theta >0$, and a diagonal matrix $Z=\mathrm {diag}(z_i)\in \mathbb {R}^{n\times n}$

$$\begin{aligned}&\begin{pmatrix} -2D+\texttt {sym}(|A|F)+\alpha I_n+Z &{} |B|G\\ G|B|^{\top } &{} -\theta I_n\end{pmatrix}<0, \end{aligned}$$

(41a)

$$\begin{aligned}&Z+2\mathrm {diag}(k_i^u)\ge 0,\quad Z+2\mathrm {diag}(k_i^l)\le 0, \end{aligned}$$

(41b)

$$\begin{aligned}&\alpha >p\theta . \end{aligned}$$

(41c)

Moreover, the controller gain matrix is given by

$$\begin{aligned} K_c=-\frac{1}{2}Z. \end{aligned}$$

(42)

Proof

The proof of Theorem 2 is straightforward from that of Theorem 1 and Remark 7. Thus, we omit it here. $\square$

Illustrative Examples

In this section, three numerical examples are given to illustrate the effectiveness of the obtained results.

Example 1

Consider system (6) without control input (i.e. $k_i=0$). The system parameters are given by

$$\begin{aligned} A&=\begin{pmatrix} 1.15 &{} 0.86 &{} 0.75 \\ 0.36 &{} 1.2 &{} 1.35 \\ 0.57 &{} 1.0 &{}1.25\end{pmatrix},\; B=\begin{pmatrix} 0.48 &{} 0.64 &{} 0.25 \\ 0.36 &{} 0.57 &{} 0.22 \\ 0.36 &{} 0.16 &{} 0.42\end{pmatrix},\\ D&=\mathrm {diag}(3.5,4.0,4.0),\quad q= 0.5,\\ f_j(s)&=g_j(s)=\frac{1}{4}\left( |s+1|-|s-1|\right) ,\; j=1,2,3. \end{aligned}$$

The impulsive effect is specified as follows

$$\begin{aligned} {\left\{ \begin{array}{ll} \gamma _1=\frac{1}{2},\; \gamma _2=\sqrt{2},\; \gamma _3=2,\\ \gamma _{k+3}=\gamma _k,\; k\ge 1. \end{array}\right. } \end{aligned}$$

Clearly, $\gamma _k\in \mathbb {I}^s\cup \mathbb {I}^u$, $\forall k\ge 1$, where $\mathbb {I}^s=\{0.5\}$ and $\mathbb {I}^u=\{\sqrt{2},2\}$. According to a proportional delay and the presence of stabilizing and destabilizing impulses simultaneously, the results of [38, 40, 42] cannot be applied to access stability of the system. We now apply Theorem 1 in this paper with $\rho =\gamma _1$, $\mu _1=\gamma _2$, $\mu _2=\gamma _3$, $p=(\mu _1\mu _2)^2\rho ^{-2}=16$, and $F_j=G_j=1/2$, $j=1,2,3$. We assume that the distributions of $\rho$, $\mu _1$ and $\mu _2$ are defined by (4) with $q_i=r_j=1$, $i,j=1,2$. Let $\tau ^s=0.25$, $\tau ^u_1=0.25$ and $\tau ^u_2=0.5$, then we have

$$\begin{aligned} \frac{\ln (\rho )}{\tau ^s}+\frac{\ln (\mu _1)}{\tau ^u_1}+\frac{\ln (\mu _2)}{\tau ^u_2}=0. \end{aligned}$$

Thus, condition (9c) is satisfied. By using the LMI Toolbox of Matlab to solve LMIs in (37), a feasible solution $(\alpha ,\theta )$ is obtained as

$$\begin{aligned} \alpha = 2.3977,\; \theta =0.1482. \end{aligned}$$

By Theorem 1, system (6) with the above parameters and impulsive effects is GGES. Moreover, by (21), we have

$$\begin{aligned} 0<\sigma <\frac{\alpha +p\theta }{2\alpha \ln 2}\simeq 1.4345. \end{aligned}$$

For $\sigma =1$, any solution x(t) of (6) satisfies

$$\begin{aligned} \Vert x(t)\Vert \le \frac{4}{\sqrt{1+0.5t_0}}\Vert x^0\Vert e^{-0.5\ln (1+t)},\; t\ge t_0. \end{aligned}$$

Example 2

Consider system (39) with the following parameters taken from [42]

$$\begin{aligned} D= & {} \begin{pmatrix} 6&{}&{}0\\ 0&{}&{}6\end{pmatrix},\; A=\begin{pmatrix} 1&{}-1\\ -1 &{} 1\end{pmatrix},\; B=\begin{pmatrix} 1&{}-2\\ 0&{}-1\end{pmatrix},\\ f_j(s)= & {} g_j(s)=\frac{1}{4}(|s+1|-|s-1|),\; q=0.5,\; T_s=0.5. \end{aligned}$$

By Theorem 3.1 in [42], system (39) is globally exponentially stable if the following condition is satisfied

$$\begin{aligned} \sum _{i=1}^2\frac{1}{d_i}\max _{j=1,2}\left( |a_{ij}|F_j+|b_{ij}|G_j\right) +\frac{1}{T_s}\max \left\{ |\gamma _*|\Big (\frac{1}{d_i}+T_s\Big ), \frac{1}{|\gamma _*|}\Big (\frac{1}{d_i}+T_s\Big )\right\} <1.\nonumber \\ \end{aligned}$$

(43)

Since $F_j=G_j=1/2$, $j=1,2$, condition (43) is satisfied if and only if $\frac{5}{12}+\frac{4}{3}\max \{|\gamma _*|,\frac{1}{|\gamma _*|}\}<1$, which is equivalent to the condition that

$$\begin{aligned} \max \Big \{|\gamma _*|,\frac{1}{|\gamma _*|}\Big \}<\frac{7}{16}. \end{aligned}$$

(44)

Clearly, condition (44) does not give any feasible solution since $\max \Big \{|\gamma _*|,\frac{1}{|\gamma _*|}\Big \}>1$ for any $0<|\gamma _*|\ne 1$. Thus, we cannot access stability of the system utilizing Theorem 3.1 in [42].

We now apply Corollary 1. Let $\alpha =\theta \max \{\gamma _*^2,\frac{1}{\gamma _*^2}\}$ then condition (40) is transformed to the following LMIs

$$\begin{aligned}&\begin{pmatrix} -2D+\alpha I_n+\texttt {sym}(|A|F) &{} |B|G\\ G|B|^{\top } &{} -\theta I_n\end{pmatrix}<0, \end{aligned}$$

(45a)

$$\begin{aligned}&\alpha -\lambda \theta >0, \end{aligned}$$

(45b)

$$\begin{aligned}&\max \Big \{\gamma _*^2,\frac{1}{\gamma _*^2}\Big \}<\lambda . \end{aligned}$$

(45c)

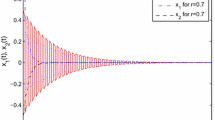
By iteratively solving LMIs (45) using Matlab LMI Toolbox, we obtain $\lambda =17.9046$, which gives $0.2363<|\gamma _*|<4.2314$, $|\lambda _*|\ne 1$. Thus, by Corollary 1, system (39) is GGES. To simulate the result, we fix $\gamma _*=4$. In Fig. 1, the solid line represents state trajectories of $x_1(t)$ and the dot-dashed line represents state trajectories of $x_2(t)$. It can be seen that all sample state trajectories converge to zero as revealed by the theoretical result. This shows the effectiveness of the obtained results.

Fig. 1

State trajectories of system (39) with $\gamma _*=4$

Example 3

This example is to illustrate the effectiveness of our control design given in Theorem 2. Consider system (1) with impulsive effects determined by strengths $\gamma _{2k-1}=\gamma _*$, $\gamma _{2k}=\gamma _*^{-1}$, where $0<|\gamma _*|\ne 1$, and impulsive time sequence $t_k=kT_s$. The system parameters are given as

$$\begin{aligned} D= & {} \begin{pmatrix} 0.8 &{}&{}0\\ 0&{}&{}0.9\end{pmatrix},\; A=\begin{pmatrix} 1.25&{}1.42\\ 0.98 &{} 1.55\end{pmatrix},\; B=\begin{pmatrix} 0.52 &{} 0.68\\ 0 &{} 0.84\end{pmatrix},\\ f_j(s)= & {} g_j(s)=\frac{1}{4}(|s+1|-|s-1|),\; j=1,2,\; q=0.5. \end{aligned}$$

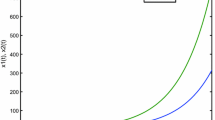
For illustrative purpose, let $T_s=0.5$ and $\gamma _*=0.8$. The simulation result given in Fig. 2 shows that the impulsive open-loop system is unstable.

Fig. 2

Unstable open-loop system with $T_s=0.5$ and $\gamma _*=0.8$

Fig. 3

Stable closed-loop system with $T_s=0.5$ and $\gamma _*=0.8$

We employ the result of Theorem 2 in this paper to design a stabilizing LSFCL (5). Let $K_l=\mathrm {diag}(k_i^l)=\mathrm {diag}(0.2,0.3)$ and $K_u=\mathrm {diag}(k_i^u)=\mathrm {diag}(2.5,1.5)$. Note also that $F=G=1/2I_2$ and $p=\gamma _*^{-4}\simeq 2.4414$. By using the Matlab LMI Toolbox to solve (41a)–(41c), we obtain

$$\begin{aligned} \alpha =1.5692, \theta =0.5191, Z=\mathrm {diag}( -4.3907, -2.6566), \end{aligned}$$

and the controller gain $K_c=\mathrm {diag}(2.1954,1.3283)$ according to (42). With the above controller gain, we have

$$\begin{aligned} {\mathscr {M}}=\begin{pmatrix} -4.3878 &{} 1.4751\\ 1.4751 &{} -2.5668\end{pmatrix}, \end{aligned}$$

and thus, $m=\lambda _{\max }({\mathscr {M}})=-1.7438<-\alpha$. By Theorem 2, the closed-loop system (6) is GGES. A simulation result with $T_s=0.5$ and $\gamma _*=0.8$ is presented in Fig. 3, where the solid line presents state trajectories of $x_1(t)$ and the dot-dashed line presents state trajectories of $x_2(t)$. Clearly, all state trajectories of the closed-loop system converge to zero, which demonstrates the effectiveness of the design scheme.

Conclusion

This paper has dealt with the problem of generalized exponential stability of neural networks with a proportional delay and time-varying impulsive effects. A unified delay-independent stability criterion has been derived based on an assumption of periodic-type distribution of impulsive strengths. On the basis of the derived stability conditions, LMI-based conditions have also been formulated to address the problem of designing a LSFCL with bounded controller gains to make the closed-loop system stable. Three numerical examples have been given to demonstrate the effecacy of the obtained results.