Global Power Stability of Neural Networks with Impulses and Proportional Delays

Abstract

By establishing two new impulsive delay differential inequalities from impulsive perturbation and impulsive control point of view, respectively, constructing some Lyapunov functionals, and employing the matrix measure approach, some novel and sufficient conditions are obtained to guarantee global power stability of neural networks with impulses and proportional delays. The obtained stability criteria are dependent on impulses and the proportional delay factor so that it is convenient to derive some feasible impulsive control laws according to the proportional delay factor allowed by such neural networks. It is shown that impulses can act as stabilizers to globally power stabilize an unstable neural network with proportional delay based on suitable impulsive control laws. Moreover, the power convergence rate can be estimated and obtained by simple computation. Three numerical examples are given to illustrate the effectiveness and advantages of the results obtained.

1 Introduction

The stability problem of delayed neural networks has been extensively studied over the past two decades for their potential applications in parallel computation, pattern recognition, associative memory complicated optimization, and so on, see [4, 6, 21, 25, 32, 35] and the references cited therein. Here, we would like to point out that proportional delay is one of the many delay types, and the corresponding systems with proportional delays have been used to model various problems in many fields including population biology, electrodynamics, control theory, and Web quality of service routing decision [1, 8, 9, 14, 22]. The proportional delay function $\tau (t)=(1-q)t\rightarrow +\infty$ as $t\rightarrow +\infty$, where the proportional delay factor q is a constant and satisfies $0<q<1$, and hence it is different from constant delay and bounded time-varying delay. Meanwhile, although proportional delay and unbounded distributed delay are all unbounded time delay, they are different each other. Unbounded distributed delay [3, 7, 12, 16, 28, 36, 43] often requires that the delay kernel functions $k_{ij}: {\mathbb {R}}_{+}\rightarrow {\mathbb {R}}_{+}$ satisfy $\int _{0}^{\infty }k_{ij}(s)\mathrm{d}s=1,~ \int _{0}^{\infty }sk_{ij}(s)\mathrm{d}s<\infty$, or there exist a positive number $\mu$ such that $\int _{0}^{\infty }e^{\mu s}k_{ij}(s)\mathrm{d}s<\infty$. The use of these inequalities can make distributed delay easier to handle. Compared with unbounded distributed delay, due to $\tau (t)=(1-q)t\rightarrow +\infty$ as $t\rightarrow +\infty$ and there being no any other conditions, it is relatively difficult to deal with proportional delay in the derivation of dynamic behaviors of systems. Therefore, it is necessary to investigate the dynamics of systems with proportional delays. To be noted that the presence of an amount of parallel pathways of a variety of axon sizes and lengths usually leads to the spatial structure of neural networks, it is reasonable to introduce proportional delays into the neural networks. In an amount of parallel pathways, affected by different materials and topology, there may be some unbounded delays that are proportional to the time; thus, we should choose suitable proportional delay factors in view of different cases and adopt proportional delays to characterize these unbounded delays [42]. In addition, the proportional delay function $\tau (t)=(1-q)t$ is monotonically increasing with respect to time $t>0$; then, one can control conveniently the system’s running time according to the time delays of networks [41]. However, because of its special structure and unboundedness nature, the study of the dynamics of neural networks with proportional delays has been recognized to be difficult. As a result, neural network models with proportional delays have received much consideration and some interesting results for stability of neural networks with proportional delays have been obtained in recent years, see [33, 37,38,39,40,41,42] and references therein.

On the other hand, besides delay effects, impulsive phenomena can be found in a wide variety of evolutionary process, particularly some biological systems such as biological neural networks and bursting rhythm models in pathology. Therefore, neural network models with delays and impulsive effects should be more accurate to describe the evolutionary process of the systems [34]. The stability analysis for delayed neural networks with impulses has attracted considerable attention, and a large number of results have been reported during the past two decades [2, 3, 5, 15,16,17,18,19, 23, 27,28,29, 36, 43]. For example, Rakkiyappan et al. [23] studied global exponential stability of impulsive neural networks with bounded time-varying delays or constant delays by using Lyapunov–Krasovskii method and LMI techniques. Stamova et al. [27, 29] addressed global exponential stability for a class of impulsive neural networks with bounded and unbounded distributed delays by applying piecewise continuous Lyapunov functions and Razumikhin technique. Zhou in [43] dealt with global exponential stability of BAM neural networks with unbounded distributed delays and impulses by constructing Lyapunov functional and employing some analysis techniques. Li and Rakkiyappan [16] studied the chaotic synchronization problem of neural networks with bounded time-varying and unbounded distributed delays by utilizing the stability theory for impulsive functional differential equations and LMI approach. As pointed out in [13], though for functional differential equations without impulses, stability results established for equations with bounded delays are not obviously true in general for unbounded delays. In addition, due to the restrictions imposed on the delay kernel functions, the stability results obtained for unbounded distributed delays are not valid for proportional delays. Thus, almost of all the existing stability results for impulsive systems with bounded delays and unbounded distributed delays cannot be applied to impulsive systems with proportional delays. As we know, proportional delay may occur in neural processing and signal transmission, which can cause instability and even chaos behaviors [41, 42]; a system in real life is often subjected to instantaneous perturbations and experiences abrupt changes at certain moments of time, and the presence of impulsive effect is often a key factor that affects the system performances [34]. Therefore, it is of great significance to investigate the stability and stabilization of neural networks with proportional delays and impulsive effects. To date, there is few papers dealing with the stability problem of impulsive systems with proportional delays [10, 19, 26], though many interesting results on stability and stabilization of systems with unbounded time-varying delays, especially proportional delays, have been reported in the literature [20, 24, 30, 33, 37,38,39,40,41,42]. Guan and Luo [10] obtained some Razumikhin-type theorems on asymptotic stability of impulsive differential systems with proportional delays by using the auxiliary function P, where $P(s)> Ms$, $M=\prod _{k=1}^{\infty }(1+\beta _{k})$. However, it is difficult to choose an appropriate function P since the presented Razumikhin condition is dependent on the concrete value of the impulsive constant M. Song et al. [26] obtained some results for global asymptotic stability of cellular neural networks (CNNs) with impulses and proportional delays by using the nonlinear transformation $y(t)=x(e^{t})$ to transform the CNNs with impulses and proportional delays into certain equivalent impulsive CNNs with time-varying coefficients and constant delays. It can be seen that, by means of the variable transformation, systems with proportional delays do become certain equivalent systems with constant delays and one may use the transformation on occasions, but it does not always simplify the analysis. Li and Cao [19] recently introduced a novel impulsive delay inequality to investigate the stability problem of impulsive systems with unbounded time-varying delays from impulsive perturbation point of view, but not impulsive control point of view. Moreover, it can be found that in these results [10, 19, 26], impulses act as perturbations rather than stabilizers, and the stability results obtained in [10, 26] are independent of time delays. It is well known that the delay-dependent criteria are less conservative than the delay-independent ones, and delay-dependent stability criteria are related to the size of delay so that they can be used to design some better networks according to the allowed time delays of networks. Therefore, it has both theoretical significance and practical value to employ some new methods to establish certain suitable delay-dependent stability criteria for NNs with proportional delays and impulses. It is noted that, by applying the matrix measure approach and constructing some Lyapunov functions, Bai [5] obtained some novel conditions ensuring global exponential stability for impulsive NNs with bounded time-varying delays. Since matrix measure can have positive as well as negative values, whereas a norm can assume only nonnegative values, the obtained results using matrix measure are more precise than the ones using norms.

Motivated by the above consideration and particularly inspired by the work of [5, 19], a natural and interesting idea is to study the stability problem of NNs with impulses and proportional delays by using the matrix measure method combined with new inequality techniques. To the best of our knowledge, the global power stability of impulsive neural networks with proportional delays by the matrix measure approach is seldom discussed. The remainder of this paper is organized as follows. In Sect. 2, model description and preliminaries are presented, and two novel impulsive delay differential inequalities involving proportional delay are established from impulsive perturbation and impulsive control point of view, respectively. In Sect. 3, based on the two inequalities obtained, some global power stability criteria are established by constructing some Lyapunov functionals and applying the matrix measure approach. In Sect. 4, three numerical examples are given to illustrate the effectiveness and advantages of our results. Some conclusions are given in Sect. 5.

2 Preliminaries and Model Description

Let ${\mathbb {R}}$ denote the set of real numbers, ${\mathbb {R}}_{+}$ the set of nonnegative real numbers, ${\mathbb {Z}}_{+}$ the set of positive integers, and ${\mathbb {R}}^{n}$ the n-dimensional real vector space, respectively. For any interval $J\subseteq {\mathbb {R}}$, set $C(J, {\mathbb {R}}^{n})=$$\{\psi : J\rightarrow {\mathbb {R}}^{n}$ is continuous$\}$ and $PC(J, {\mathbb {R}}^{n})=\{\psi : J\rightarrow {\mathbb {R}}^{n}| \psi (t^{+})=\psi (t)$ for $t\in J,~\psi (t^{-})$ exists for $t\in J$, $\psi (t^{-})=\psi (t)$ for all but points $t_{k}\in J\}$. For $x=(x_{1},\ldots ,x_{2})^{\mathrm{T}}\in {\mathbb {R}}^{n}$, the vector norm $\Vert x\Vert _{p}~(p=1,2,\infty )$ is defined as

$$\begin{aligned} \Vert x\Vert _{1}=\sum _{i=1}^{n}|x_{i}|, \quad \Vert x\Vert _{2}=\Big (\sum _{i=1}^{n}x_{i}^{2}\Big )^{\frac{1}{2}}, \quad \Vert x\Vert _{\infty }=\max _{1\le i\le n}|x_{i}|. \end{aligned}$$

And for a real square matrix $A=(a_{ij})_{n\times n}\in {\mathbb {R}}^{n\times n}$, the matrix measure of A is defined as follows [5, 31]:

$$\begin{aligned} \mu _{p}(A)=\lim _{h\rightarrow 0^{+}}\frac{\Vert E+h A\Vert _{p}-1}{h}, \end{aligned}$$

(2.1)

where $\Vert \cdot \Vert _{p}$ is an induced matrix norm on ${\mathbb {R}}^{n\times n}$, E is the identity matrix with appropriate dimensions, and $p=1, 2, \infty .$ The matrix measure $\mu _{p}(\cdot )$ defined in (2.1) has the following properties, and for the details of the $\Vert \cdot \Vert _{p}$ and $\mu _{p}(\cdot )$, we refer the reader to [5, 31].

Lemma 2.1

[5, 31] Let $A,B\in {\mathbb {R}}^{n\times n}$ and $\alpha \ge 0$. Then,

$$\begin{aligned}&(1)\,-\Vert A\Vert _{p}\le \mu _{p}(A)\le \Vert A\Vert _{p}; \quad (2) ~\mu _{p}(\alpha A)= \alpha \mu _{p}( A); \\&\quad (3) ~\mu _{p}(A+B)\le \mu _{p}(A)+\mu _{p}(B). \end{aligned}$$

Consider the following NNs with impulses and proportional delay

$$\begin{aligned} \left\{ \begin{array}{l}y'(t)=Ay(t)+BF(y(t))+CG(y(qt))\big )+I, \quad t\ne t_{k},\quad t \ge 1,\\ \Delta y(t_{k})= y(t_{k})-y(t^{-}_{k})=-\,D_{k}y(t^{-}_{k}),\quad k\in {\mathbb {Z}}_{+}, \end{array}\right. \end{aligned}$$

(2.2)

where $y\in {\mathbb {R}}^{n}$ is the state vector of (2.2) and $y'$ denotes the right-hand derivative of y; $F,G: {\mathbb {R}}^{n}\rightarrow {\mathbb {R}}^{n}$ are two activation functions; $y(qt)=(y_{1}(qt),\cdot \cdot \cdot ,y_{n}(qt) )^{\mathrm{T}}$; $q\in (0,1)$ is proportional delay factor and $qt=t-(1-q)t$, in which $(1-q)t$ is the transmission delay; $I=(I_{1}, I_{2}, \cdot \cdot \cdot , I_{n})^{\mathrm{T}}$ is the external input; $t_{k}$ denotes the moment when impulse occurs, $1= t_{0}<t_{1}<\ldots<t_{k}<t_{k+1}<\ldots$, with $\lim _{t\rightarrow \infty }t_{k}=\infty$; at time instant $t_{k}$, jumps in the state variable y are denoted by $\Delta y(t_{k})= y(t_{k})-y(t^{-}_{k})$, where $y(t_{k})=y(t_{k}^{+})$ and $y(t^{-}_{k})=\lim _{t\rightarrow t_{k}^{-}}y(t)$ exists; $A,B,C, D_{k}\in {\mathbb {R}}^{n\times n},$ where $D_{k}$ is usually called impulsive matrix.

Definition 2.1

A function $y(t)\!:[q,+\infty )\rightarrow {\mathbb {R}}^{n}$ is called a solution of system (2.2) with the initial condition given by

$$\begin{aligned} y(t)=\phi (t), \quad \phi \in C([q,1], {\mathbb {R}}^{n}), \end{aligned}$$

(2.3)

if y(t) is continuous at $t\ne t_{k}$ and $t \ge 1$, $y(t_{k})=y(t_{k}^{+})$ and $y(t_{k}^{-})=\lim _{t\rightarrow t_{k}^{-}}y(t)$ exists, y(t) satisfies (2.2) for $t\ge 1$ under the initial condition. Especially, a point $y^{*}=(y_{1}^{*},\cdot \cdot \cdot ,y_{n}^{*})^{\mathrm{T}}\in {\mathbb {R}}^{n}$ is said to be an equilibrium point of (2.2), if $y(t)=y^{*}$ is a solution of (2.2), i.e., $Ay^{*}+BF(y^{*})+CG(y^{*})+I={\mathbf {0}}$ (zero matrix) and $D_{k}y^{*}={\mathbf {0}}, k\in {\mathbb {Z}}_{+}.$

For any $\phi \in C([q,1], {\mathbb {R}}^{n})$, we assume that there exists on the interval $[q,\infty )$ a unique solution of the system (2.2) with the initial condition (2.3). Let $y^{*}$ be an equilibrium point of (2.2), y(t) be any solution of (2.2), and $x(t)=y(t)-y^{*}.$ Substituting them into (2.2), we get the following NNs with impulses and proportional delay

$$\begin{aligned} \left\{ \begin{array}{l}x'(t)=Ax(t)+Bf(x(t))+Cg\big (y(qt)\big ), \quad t\ne t_{k},\quad t \ge 1,\\ \Delta x(t_{k})= x(t_{k})-x(t^{-}_{k})=-D_{k}x(t^{-}_{k}),\quad k\in {\mathbb {Z}}_{+}, \end{array}\right. \end{aligned}$$

(2.4)

where $f(x(t))=F(x(t)+y^{*})-F(y^{*}), g(x(qt))=G(x(qt)+y^{*})-G(y^{*})$.

It is clear that the stability of the equilibrium point $y^{*}$ of (2.2) is equivalent to the stability of the zero solution of (2.4). In the present paper, we mainly investigate the stability of the zero solution of (2.4). We assume that the functions $f,g: {\mathbb {R}}^{n}\rightarrow {\mathbb {R}}^{n}$ satisfy $f(0)=g(0)=0$ and certain conditions such that system (2.4) has on the interval $[q, \infty )$ a unique zero solution with the initial condition $\phi (t)\equiv 0, ~t\in [q,1]$. For any $\phi \in C([q,1], {\mathbb {R}}^{n})$, let $x(t)=x(t,\phi )$ denote the solution of (2.4) with the initial condition $x(t)=\phi (t), t\in [q,1]$. We present the following definition.

Definition 2.2

The zero solution of system (2.4) is said to be power-rate globally stable with power convergence rate $\lambda$ (or simply globally power stable) if for any initial data $\phi \in C([q,1],{\mathbb {R}}^{n}),$ there exist constants $\lambda >0, M\ge 1$ such that

$$\begin{aligned} \Vert x(t)\Vert _{p}=\Vert x(t,\phi )\Vert _{p}\le M\Vert \phi \Vert _{p}t^{-\lambda },\quad t\ge 1, \end{aligned}$$

where $\Vert \phi \Vert _{p}=\sup _{q\le s\le 1}\Vert \phi (s)\Vert _{p}$.

Remark 2.1

One can easily find that global power stability implies global asymptotic stability.

In this paper, we always assume that

$(H_{1})$$f,~g: {\mathbb {R}}^{n}\rightarrow {\mathbb {R}}^{n}$ are Lipschtz continuous functions: There exist two positive constants $l_{1},l_{2}$ such that

$$\begin{aligned} \Vert f(x)-f(y)\Vert _{p}\le l_{1}\Vert x-y\Vert _{p},\quad \Vert g(x)-g(y)\Vert _{p}\le l_{2}\Vert x-y\Vert _{p}, \quad \forall ~x,y\in {\mathbb {R}}^{n}. \end{aligned}$$

In order to establish our main results, we first establish two impulsive differential inequalities involving proportional delay, which extend the famous Halanay differential inequality [11] and will play an important role in qualitative analysis of impulsive systems with proportional delays.

Lemma 2.2

Suppose that $a>b\ge 0$ and $u(t)\in PC([1,\infty ), {\mathbb {R}}_{+})$ satisfies the scalar impulsive differential inequality

$$\begin{aligned} \left\{ \begin{array}{l}D^{+}u(t)\le -au(t)+b \big (\sup _{qt\le s\le t}u(s)\big ),\quad t \ge t_{0}=1,\quad t\ne t_{k},\\ u(t_{k})\le \alpha _{k}u(t^{-}_{k}),\quad k\in {\mathbb {Z}}_{+},\\ u(t)=\phi (t),\quad t\in [q, 1], \end{array}\right. \end{aligned}$$

(2.5)

where $\alpha _{k}\in {\mathbb {R}}_{+}$, $\phi \in C([q, 1],{\mathbb {R}})$, and $D^{+}u(t)$ denotes the upper right-hand Dini derivative of u(t) at t. Then

$$\begin{aligned} u(t)\le \Big (\sup \nolimits _{q\le s\le 1}\Vert \phi (s)\Vert _{p}\Big )\Big (\prod \nolimits _{1<t_{k}\le t} \theta _{k}\Big ) t^{-\lambda },\quad t\ge 1, \end{aligned}$$

(2.6)

where $\theta _{k}=\max \{1, \alpha _{k}\}$ and $\lambda >0$ is a solution of the inequality $\lambda -a+bq^{-\lambda }\le 0.$

Proof

Define the function $h(\lambda )=\lambda -a+bq^{-\lambda },~\lambda \in [0,+\infty )$. Since $a>b\ge 0$ and $0<q<1$, simple computing fields that $h(0)=-a+b<0$ and $\lim _{\lambda \rightarrow +\infty }h(\lambda )=+\infty .$ One can see that there exists at least a solution $\lambda >0$ satisfying $\lambda -a+bq^{-\lambda }\le 0.$ Set ${\widehat{\phi }}=\sup _{q\le s\le 1}\Vert \phi (s)\Vert _{p},$ and it is easy to find that

$$\begin{aligned} u(t)\le {\widehat{\phi }}\le {\widehat{\phi }} t^{-\lambda },\quad t\in [q,1]. \end{aligned}$$

(2.7)

We shall prove that (2.7) implies that

$$\begin{aligned} u(t)\le {\widehat{\phi }} t^{-\lambda },\quad t\in [1,t_{1}). \end{aligned}$$

(2.8)

To this end, we consider the following two possible cases.

Case 1.  $b=0.$ From (2.5) and (2.7), u(t) satisfies

$$\begin{aligned} D^{+}u(t)\le -au(t), \quad u(1)\le {\widehat{\phi }},\quad t\in [1, t_{1}). \end{aligned}$$

Since $a\ge \lambda$ and the inequality $e^{x}\ge 1+x,~x>0$, we can get

$$\begin{aligned} u(t)\le {\widehat{\phi }} e^{-a(t-1)}\le {\widehat{\phi }} e^{-\lambda (t-1)}\le {\widehat{\phi }} t^{-\lambda }, \quad t\in [1, t_{1}). \end{aligned}$$

Case 2.  $b>0.$ We claim that for any $z>{\widehat{\phi }}\ge 0$,

$$\begin{aligned} u(t)\le zt^{-\lambda }=y(t), \quad t\in [1, t_{1}). \end{aligned}$$

(2.9)

If (2.9) is not true, from (2.7) and the continuity of u(t), y(t) as $t\in [1, t_{1})$, then there must exist a $t^{*}\in (1, t_{1})$ such that

$$\begin{aligned}&u(t^{*})=y(t^{*}), \quad D^{+}u(t^{*})\ge y'(t^{*}), \end{aligned}$$

(2.10)

$$\begin{aligned}&u(t)<y(t), \quad t\in [q,t^{*}). \end{aligned}$$

(2.11)

Using (2.5), (2.10), (2.11) and noting that $b>0$, we obtain

$$\begin{aligned} D^{+}u(t^{*})\le & {} -\,a u(t^{*})+ b \Big (\sup _{qt^{*}\le s\le t^{*}}u(s)\Big )\\< & {} -\,a y(t^{*})+b y(qt^{*})=z(-a+bq^{-\lambda }) (t^{*})^{-\lambda }\\\le & {} -\,\lambda z (t^{*})^{-\lambda } <-\lambda z (t^{*})^{-\lambda -1}=y'(t^{*}), \end{aligned}$$

which contradicts the inequality in (2.10). Thus, (2.9) holds for any $z>{\widehat{\phi }}$. Letting $z\rightarrow {\widehat{\phi }}$, we get (2.8).

Using (2.5), (2.7), and (2.8), we can get $u(t_{1})\le \alpha _{1}u(t^{-}_{1})\le \theta _{1}{\widehat{\phi }} t_{1}^{-\lambda },$ and so

$$\begin{aligned} u(t)\le \theta _{1}{\widehat{\phi }} t^{-\lambda }, \quad t\in [qt_{1}, t_{1}]. \end{aligned}$$

(2.12)

Next, we prove that (2.12) implies that

$$\begin{aligned} u(t)\le \theta _{1}{\widehat{\phi }} t^{-\lambda },\quad t\in [t_{1},t_{2}). \end{aligned}$$

(2.13)

If $b=0$, one can find that

$$\begin{aligned} D^{+}u(t)\le -au(t), \quad u(t_{1})\le \theta _{1}{\widehat{\phi }} t_{1}^{-\lambda }, \quad t\in [t_{1}, t_{2}). \end{aligned}$$

Thus, a calculation gives us

$$\begin{aligned} u(t)\le & {} u(t_{1}) e^{-a(t-t_{1})}\le \theta _{1}{\widehat{\phi }} t_{1}^{-\lambda } e^{-a(t-t_{1})}\\\le & {} \theta _{1}{\widehat{\phi }} t_{1}^{-\lambda } e^{-\lambda (t-t_{1})} =\theta _{1}{\widehat{\phi }} t_{1}^{-\lambda }\Big (e^{t_{1}\big (\frac{t}{t_1}-1\big )}\Big )^{-\lambda }\\\le & {} \theta _{1}{\widehat{\phi }} t_{1}^{-\lambda }\Big (e^{\big (\frac{t}{t_1}-1\big )}\Big )^{-\lambda } \le \theta _{1}{\widehat{\phi }} t^{-\lambda },\quad t\in [t_{1}, t_{2}). \end{aligned}$$

If $b>0$, one can also claim that for any $z>\theta _{1}{\widehat{\phi }}\ge 0$,

$$\begin{aligned} u(t)\le zt^{-\lambda }=y(t), \quad t\in [t_{1}, t_{2}). \end{aligned}$$

(2.14)

If (2.14) is not true, from (2.12) and the continuity of u(t), y(t) as $t\in [t_{1}, t_{2})$, then there must exist a $t^{*}\in (t_{1}, t_{2})$ such that

$$\begin{aligned}&u(t^{*})=y(t^{*}), \quad D^{+}u(t^{*})\ge y'(t^{*}), \end{aligned}$$

(2.15)

$$\begin{aligned}&u(t)<y(t), \quad t<t^{*}. \end{aligned}$$

(2.16)

By using (2.5), (2.7), (2.8), (2.15), (2.16) and $b>0$, we also obtain

$$\begin{aligned} D^{+}u(t^{*})\le & {} -\,a u(t^{*})+ b \Big (\sup \limits _{qt^{*}\le s\le t^{*}}u(s)\Big )\\< & {} -\,a y(t^{*})+b y(qt^{*})=z(-a+bq^{-\lambda }) (t^{*})^{-\lambda }\\\le & {} -\,\lambda z (t^{*})^{-\lambda } <-\lambda z (t^{*})^{-\lambda -1}=y'(t^{*}), \end{aligned}$$

which contradicts the inequality in (2.15). Thus, (2.14) holds for any $z>\theta _{1}{\widehat{\phi }}$. Letting $z\rightarrow \theta _{1}{\widehat{\phi }}$, we obtain (2.13). Similarly, we also have $u(t)\le \theta _{1}\theta _{2}{\widehat{\phi }} t^{-\lambda },~t\in [qt_{2}, t_{2}].$ By a simple induction, we can obtain

$$\begin{aligned} u(t)\le \theta _{1}\ldots \theta _{k-1}{\widehat{\phi }} t^{-\lambda },\quad t\in [t_{k-1}, t_{k}), \quad k\in {\mathbb {Z}}_{+}. \end{aligned}$$

This implies (2.6), and so the proof is completed. $\square$

Lemma 2.3

Suppose that $u(t)\in PC([1,\infty ), {\mathbb {R}}_{+})$ satisfies the scalar impulsive differential inequality

$$\begin{aligned} \left\{ \begin{array}{l}D^{+}u(t)\le au(t)+b \Big (\sup \limits _{qt\le s\le t}u(s)\Big ),\quad t \ge t_{0}=1,\quad t\ne t_{k},\\ u(t_{k})\le \alpha _{k}u(t^{-}_{k}), \quad k\in {\mathbb {Z}}_{+},\\ u(t)=\phi (t), \quad t\in [q, 1], \end{array}\right. \end{aligned}$$

(2.17)

where $a\in {\mathbb {R}}$, $b>0$, $0<\alpha _{k}<1$, and $1<\gamma =\sup _{k\in {\mathbb {Z}}_{+}}\big \{ \frac{1}{\alpha _{k} }\big \}<+\infty$. If there exists a small enough positive number $\lambda >0$ such that

$$\begin{aligned} a+2\lambda +b\gamma q^{-\lambda }< -\frac{\ln (\alpha _{k-1})}{t_{k}-t_{k-1}},\quad k\in {\mathbb {Z}}_{+}, \end{aligned}$$

(2.18)

then

$$\begin{aligned} u(t)\le \gamma \Big (\sup _{q\le s\le 1}\Vert \phi (s)\Vert _{p}\Big ) t^{-\lambda },\quad t\ge 1, \end{aligned}$$

(2.19)

where we define $\alpha _{0}=\gamma ^{-1}.$

Proof

From (2.18), we can choose a suitable positive constant $\sigma >0$ such that

$$\begin{aligned} a+\gamma bq^{-\lambda } <(\sigma -\lambda ), \end{aligned}$$

(2.20)

and

$$\begin{aligned} (\sigma +\lambda )(t_{k}-t_{k-1})<-\ln (\alpha _{k-1})\le \ln \gamma , \quad k\in {\mathbb {Z}}_{+}. \end{aligned}$$

(2.21)

To prove (2.19), it is sufficient to show that

$$\begin{aligned} u(t)\le \gamma {\widehat{\phi }}t^{-\lambda }, \quad t\in [t_{k-1},t_{k}),\quad k\in {\mathbb {Z}}_{+}, \end{aligned}$$

(2.22)

where ${\widehat{\phi }}=\sup _{q\le s\le 1}\Vert \phi (s)\Vert _{p}.$ From (2.21) and note that $0<q<1$, we have

$$\begin{aligned} 1<\exp \{(\sigma +\lambda )(t_{1}-1)\}< \gamma <\gamma q^{-\lambda }. \end{aligned}$$

(2.23)

From (2.23) and the inequality $\exp (x)>1+x,~x>0$, it then follows that

$$\begin{aligned} {\widehat{\phi }}<{\widehat{\phi }} \exp \{\sigma (t_{1}-1)\}< \gamma {\widehat{\phi }} \exp \{-\lambda (t_{1}-1)\}\le \gamma {\widehat{\phi }} t_{1}^{-\lambda }. \end{aligned}$$

(2.24)

We first prove that

$$\begin{aligned} u(t)\le \gamma {\widehat{\phi }}t^{-\lambda }, \quad t\in [1, t_{1}). \end{aligned}$$

(2.25)

For this purpose, we only need to show that

$$\begin{aligned} u(t)\le \gamma {\widehat{\phi }}t_{1}^{-\lambda }, \quad t\in [1, t_{1}). \end{aligned}$$

(2.26)

If (2.26) is not true, by (2.23), (2.24), and the inequality $\exp (x)>1+x,~x>0$, then there exists some ${\bar{t}}\in (1, t_{1})$ such that for any $s\in [q, 1]$,

$$\begin{aligned} u({\bar{t}})>\gamma {\widehat{\phi }}t_{1}^{-\lambda }\ge \gamma {\widehat{\phi }}\exp \big \{-\lambda (t_{1}-1)\big \}> {\widehat{\phi }}\exp \big \{\sigma (t_{1}-1)\big \}> {\widehat{\phi }}\ge u(s). \end{aligned}$$

This implies that there exists some ${\hat{t}}\in (1, {\bar{t}})$ such that

$$\begin{aligned} u({\hat{t}})=\gamma {\widehat{\phi }}t_{1}^{-\lambda },\quad u(t)\le u({\hat{t}}),\quad t\in [q, {\hat{t}}], \end{aligned}$$

(2.27)

and there exists $t^{*}\in [1, {\hat{t}}]$ such that

$$\begin{aligned} u(t^{*})= {\widehat{\phi }}, \quad u(t^{*})\le u(t)\le u({\hat{t}}),\quad t\in [t^{*}, {\hat{t}}]. \end{aligned}$$

(2.28)

Thus for any $t\in [t^{*}, {\hat{t}}]$, then $[qt,t] \subseteq [qt^{*}, {\hat{t}}]$. It follows from (2.23), (2.27), and (2.28) that for any $s\in [qt, t]$,

$$\begin{aligned} u(s)\le u({\hat{t}})=\gamma {\widehat{\phi }}t_{1}^{-\lambda }< \gamma q^{-\lambda } {\widehat{\phi }}=\gamma q^{-\lambda }u(t^{*})\le \gamma q^{-\lambda }u(t), \quad t\in [t^{*}, {\hat{t}}].\qquad \qquad \end{aligned}$$

(2.29)

It follows from (2.17), (2.20), and (2.29) that for $t\in [t^{*}, {\hat{t}}]$,

$$\begin{aligned} D^{+}u(t)\le au(t)+b \Big (\sup \limits _{qt\le s\le t}u(s)\Big ) \le (a+b\gamma q^{-\lambda })u(t) \le (\sigma -\lambda )u(t).\qquad \qquad \end{aligned}$$

(2.30)

Using (2.23), (2.27), (2.28), and (2.30), we can arrive at

$$\begin{aligned} u({\hat{t}})\le & {} u(t^{*})\exp \{(\sigma -\lambda )({\hat{t}}-t^{*})\} = {\widehat{\phi }}\exp \{(\sigma -\lambda )({\hat{t}}-t^{*})\}\\< & {} {\widehat{\phi }}\exp \{\sigma (t_{1}-1)\}< \gamma {\widehat{\phi }}\exp \{-\lambda (t_{1}-1)\}\le \gamma {\widehat{\phi }} t_{1}^{-\lambda }=u({\hat{t}}), \end{aligned}$$

which is a contradiction. So (2.26) holds and then (2.22) is true for $k=1$.

Now we assume that (2.22) holds for $k=1,2,\ldots , l~(l\ge 1,~l\in {\mathbb {Z}}_{+})$, i.e.,

$$\begin{aligned} u(t)\le \gamma {\widehat{\phi }}t^{-\lambda }, \quad t\in [t_{k-1},t_{k}),\quad k=1,2,\ldots ,l. \end{aligned}$$

(2.31)

Next, we shall prove that (2.22) holds for $k=l+1$, i.e.,

$$\begin{aligned} u(t)\le \gamma {\widehat{\phi }}t^{-\lambda }, \quad t\in [t_{l},t_{l+1}). \end{aligned}$$

(2.32)

For the sake of contradiction, suppose that (2.32) is not true, let ${\underline{t}}=\inf \{t\in [t_{l},t_{l+1})|u(t)>\gamma {\widehat{\phi }} t^{-\lambda } \}.$ Then by (2.17), (2.21), and (2.31), and applying again the inequality $\exp (x)>1+x,~x>0$, we obtain

$$\begin{aligned} u(t_{l})\le & {} \alpha _{l}u(t_{l}^{-})\le \alpha _{l}\gamma {\widehat{\phi }}t_{l}^{-\lambda }=\alpha _{l}\gamma {\widehat{\phi }}\Big ( \frac{t_{l}}{t_{l+1}}\Big )^{-\lambda } \Big ( \frac{t_{l+1}}{{\underline{t}}}\Big )^{-\lambda }{\underline{t}}^{-\lambda }\nonumber \\< & {} \alpha _{l}\gamma {\widehat{\phi }}\Big ( \frac{t_{l}}{t_{l+1}}\Big )^{-\lambda }{\underline{t}}^{-\lambda }< \gamma {\widehat{\phi }}\exp \Big \{-(\sigma +\lambda )(t_{l+1}-t_{l})\Big \}\Big ( \frac{t_{l}}{t_{l+1}}\Big )^{-\lambda } {\underline{t}}^{-\lambda }\nonumber \\= & {} \gamma {\widehat{\phi }}\exp \Big \{-(\sigma +\lambda )t_{l}\Big ( \frac{t_{l+1}}{t_{l}}-1\Big )\Big \}\Big ( \frac{t_{l}}{t_{l+1}}\Big )^{-\lambda } {\underline{t}}^{-\lambda }\nonumber \\< & {} \gamma {\widehat{\phi }}\exp \Big \{-(\sigma +\lambda )\Big ( \frac{t_{l+1}}{t_{l}}-1\Big )\Big \}\Big ( \frac{t_{l}}{t_{l+1}}\Big )^{-\lambda } {\underline{t}}^{-\lambda } \nonumber \\\le & {} \gamma {\widehat{\phi }}\Big ( \frac{t_{l+1}}{t_{l}}\Big )^{-\sigma } {\underline{t}}^{-\lambda } < \gamma {\widehat{\phi }}{\underline{t}}^{-\lambda }, \end{aligned}$$

(2.33)

and so ${\underline{t}}\ne t_{l}$. Since u(t) is continuous in the interval $[t_{l},t_{l+1})$, we have

$$\begin{aligned} u({\underline{t}})=\gamma {\widehat{\phi }}{\underline{t}}^{-\lambda }, \quad \mathrm{and} ~ u(t)\le u({\underline{t}}),\quad t\in [t_{l}, {\underline{t}}]. \end{aligned}$$

(2.34)

From (2.33), we can see that there exists some $t^{*}\in [t_{l}, {\underline{t}}]$ such that

$$\begin{aligned} u(t^{*})=\alpha _{l}\gamma {\widehat{\phi }}\Big ( \frac{t_{l}}{t_{l+1}}\Big )^{-\lambda }{\underline{t}}^{-\lambda }, \quad \mathrm{and } \quad u(t^{*})\le u(t)\le u({\underline{t}}),\quad t\in [t^{*}, {\underline{t}}].\qquad \end{aligned}$$

(2.35)

On the other hand, for $t\in [t^{*}, {\underline{t}}]$, either $qt\in [qt_0, t_{l})$ or $qt\in [t_{l}, {\underline{t}}]$. Consider the following two cases.

Case 1.$qt\in [qt_0, t_{l})$. Then, $[qt,t]=[qt,t_{l})\bigcup [t_{l},t]$. For any $s\in [qt, t]$, either $s\in [qt,t_{l})$ or $s\in [t_{l},t]$$\subseteq [t_{l}, {\underline{t}}]$. If $s\in [qt,t_{l})$, then by (2.31), we can deduce that

$$\begin{aligned} u(s)\le \gamma {\widehat{\phi }}s^{-\lambda }\le \gamma {\widehat{\phi }} q^{-\lambda } t^{-\lambda } \le q^{-\lambda }\gamma {\widehat{\phi }} \Big (\frac{t_{l}}{t_{l+1}}\Big )^{-\lambda } {\underline{t}}^{-\lambda }. \end{aligned}$$

(2.36)

While $s\in [t_{l},t]$, it follows from (2.34) that

$$\begin{aligned} u(s)\le u({\underline{t}})=\gamma {\widehat{\phi }}{\underline{t}}^{-\lambda }\le q^{-\lambda }\gamma {\widehat{\phi }} \Big (\frac{t_{l}}{t_{l+1}}\Big )^{-\lambda } {\underline{t}}^{-\lambda }. \end{aligned}$$

(2.37)

From (2.36) and (2.37), it follows that for any $s\in [qt,t]$,

$$\begin{aligned} u(s)\le q^{-\lambda }\gamma {\widehat{\phi }} \Big (\frac{t_{l}}{t_{l+1}}\Big )^{-\lambda } {\underline{t}}^{-\lambda }, \quad t\in [t^{*}, {\underline{t}}]. \end{aligned}$$

(2.38)

Case 2.$qt\in [t_{l}, {\underline{t}}]$. Then, $[qt, t] \subseteq [t_{l}, {\underline{t}}]$, and by (2.34), one can see that (2.37) holds for any $s\in [qt, t]$. This implies that (2.38) holds.

In any case, from (2.35) and (2.38), we all have for any $t\in [t^{*}, {\underline{t}}]$, $s\in [qt, t]$,

$$\begin{aligned} u(s)\le \frac{1}{\alpha _{l}}q^{-\lambda }u(t^{*})\le \frac{1}{\alpha _{l}}q^{-\lambda }u(t)\le \gamma q^{-\lambda }u(t), \end{aligned}$$

which implies that $\sup _{qt\le s\le t}u(s)\le \gamma q^{-\lambda }u(t).$ This together with (2.20) shows that for $t\in [t^{*}, {\underline{t}}]$,

$$\begin{aligned} D^{+}u(t)\le au(t)+b \Big (\sup _{qt\le s\le t}u(s)\Big ) \le (a+\gamma b q^{-\lambda })u(t) \le (\sigma -\lambda )u(t). \qquad \end{aligned}$$

(2.39)

Applying (2.21), (2.33)–(2.35), (2.39) and the inequality $\exp (x)>1+x,~x>0$, we can deduce that

$$\begin{aligned} u({\underline{t}})\le & {} u(t^{*})\exp \{(\sigma -\lambda )({\underline{t}}-t^{*})\} = \alpha _{l}\gamma {\widehat{\phi }}\Big ( \frac{t_{l}}{t_{l+1}}\Big )^{-\lambda }{\underline{t}}^{-\lambda } \exp \{(\sigma -\lambda )({\underline{t}}-t^{*})\}\\< & {} \gamma {\widehat{\phi }} \exp \big \{-( \sigma +\lambda )(t_{l+1}-t_{l})\big \} \exp \{(\sigma -\lambda )({\underline{t}}-t^{*})\}\Big ( \frac{t_{l}}{t_{l+1}}\Big )^{-\lambda }{\underline{t}}^{-\lambda }\\= & {} \gamma {\widehat{\phi }} \exp \big \{-( \sigma +\lambda )(t_{l+1}-t_{l})\big \} \exp \{\sigma ({\underline{t}}-t^{*})\} \exp \{-\lambda ({\underline{t}}-t^{*})\}\Big ( \frac{t_{l}}{t_{l+1}}\Big )^{-\lambda }{\underline{t}}^{-\lambda }\\< & {} \gamma {\widehat{\phi }} \exp \big \{-\lambda (t_{l+1}-t_{l})\big \} \Big ( \frac{t_{l}}{t_{l+1}}\Big )^{-\lambda }{\underline{t}}^{-\lambda }\\= & {} \gamma {\widehat{\phi }} \exp \Big \{-\lambda t_{l}\Big (\frac{t_{l+1}}{t_{l}}-1\Big )\Big \} \Big ( \frac{t_{l}}{t_{l+1}}\Big )^{-\lambda }{\underline{t}}^{-\lambda }\\\le & {} \gamma {\widehat{\phi }}\exp \Big \{-\lambda \Big (\frac{t_{l+1}}{t_{l}}-1\Big )\Big \} \Big ( \frac{t_{l}}{t_{l+1}}\Big )^{-\lambda }{\underline{t}}^{-\lambda }\\< & {} \gamma {\widehat{\phi }}{\underline{t}}^{-\lambda }=u({\underline{t}}), \end{aligned}$$

which is a contradiction. Hence, the assumption is not true, and then (2.22) holds for $k=l+1$. By the mathematical induction method, we can conclude that (2.22) holds for any $k\in {\mathbb {Z}}_{+}$. The proof is completed. $\square$

Remark 2.1

From the conditions of Lemmas 2.2 and 2.3, one can see that they are established from impulsive perturbation and impulsive control point of view, respectively. So they are complementary with each other. Moreover, Lemma 2.3 is different from Lemma 2 in [19] since it is given from the impulsive control point of view.

3 Main Results

In this section, we always assume that $\beta =\sup _{k\in {\mathbb {Z}}_{+}}\{\Vert E-D_{k}\Vert _{p}\}<+\infty$.

Theorem 3.1

Assume that $(H_{1})$ holds and $\delta =\inf _{k\in {\mathbb {Z}}^{+}}\big \{\frac{t_{k}}{t_{k-1}}\big \}>1$. If $\mu _{p}(A)<- l_{1}\Vert B\Vert _{p}-l_{2}\Vert C\Vert _{p}$, and there exists a positive constant $\lambda$ such that

$$\begin{aligned} \lambda >\frac{\ln (\max \{1,\beta \})}{\ln \delta }, \end{aligned}$$

(3.1)

and

$$\begin{aligned} \lambda +\mu _{p}(A)+l_{1}\Vert B\Vert _{p}+l_{2}\Vert C\Vert _{p} q^{-\lambda }\le 0, \end{aligned}$$

(3.2)

then the zero solution of (2.4) is globally power stable with power convergence rate $\lambda -\frac{\ln (\max \{1,\beta \})}{\ln \delta }$.

Proof

Define the Lyapunov function $V(t)=V(x(t))=\Vert x(t)\Vert _{p}.$ Then, the upper right-hand Dini derivative of V(x(t)) with respect to time t along the solution of system (2.4) is as follows:

$$\begin{aligned}&D^{+}V(x(t))\\&\quad = {\overline{\lim }}_{h\rightarrow 0^{+}}\frac{\Vert x(t+h)\Vert _{p}-\Vert x(t)\Vert _{p}}{h}\\&\quad = {\overline{\lim }}_{h\rightarrow 0^{+}}\frac{\Vert x(t)+hx'(t)+o(h)\Vert _{p}-\Vert x(t)\Vert _{p}}{h}\\&\quad = {\overline{\lim }}_{h\rightarrow 0^{+}}\frac{\Vert x(t)+h[Ax(t)+Bf(x(t))+Cg(x(qt))]+o(h)\Vert _{p}-\Vert x(t)\Vert _{p}}{h}\\&\quad \le {\overline{\lim }}_{h\rightarrow 0^{+}}\frac{\Vert x(t)+hAx(t)\Vert _{p}-\Vert x(t)\Vert _{p}}{h} +\Vert Bf(x(t))\Vert _{p}+\Vert Cg(x(qt))\Vert _{p}\\&\quad \le {\overline{\lim }}_{h\rightarrow 0^{+}} \frac{\Vert E+hA\Vert _{p}-1}{h}\Vert x(t)\Vert _{p} +\Vert Bf(x(t))\Vert _{p}+\Vert Cg(x(qt))\Vert _{p}. \end{aligned}$$

From Assumption $(H_{1})$, it follows that

$$\begin{aligned} \Vert f(x(t))\Vert _{p}\le l_{1}\Vert x\Vert _{p}, \quad \Vert g(x(qt))\Vert _{p}\le l_{2}\Vert x(qt)\Vert _{p}. \end{aligned}$$

(3.3)

Thus,

$$\begin{aligned} D^{+}V(x(t))\le & {} \mu _{p}(A)\Vert x(t)\Vert _{p} +l_{1}\Vert B\Vert _{p}\Vert x(t)\Vert _{p}+l_{2}\Vert C\Vert _{p}\Vert x(qt)\Vert _{p}\\\le & {} \mu _{p}(A)\Vert x(t)\Vert _{p} +l_{1}\Vert B\Vert _{p}\Vert x(t)\Vert _{p}+l_{2}\Vert C\Vert _{p}\Big (\sup _{qt\le s\le t}\Vert x(s)\Vert _{p}\Big )\\= & {} (\mu _{p}(A)+l_{1}\Vert B\Vert _{p})V(x(t))+l_{2}\Vert C\Vert _{p}\Big (\sup _{qt\le s\le t}V(x(s))\Big )\\= & {} -aV(x(t))+b\Big (\sup _{qt\le s\le t}V(x(s))\Big ),\quad t\ne t_{k}, t\ge 1, \end{aligned}$$

where $a=-(\mu _{p}(A)+l_{1}\Vert B\Vert _{p}),~ b= l_{2}\Vert C\Vert _{p}$. On the other hand, it follows from (2.4) that

$$\begin{aligned} V(t_{k})=\Vert x(t_{k})\Vert _{p}=\Vert (E-D_{k})x(t_{k}^{-})\Vert _{p}\le \Vert (E-D_{k})\Vert _{p}\Vert x(t_{k}^{-})\Vert _{p}\le \beta V(t_{k}^{-}). \end{aligned}$$

Note that $a=-(\mu _{p}(A)+l_{1}\Vert B\Vert _{p})> l_{2}\Vert C\Vert _{p}=b\ge 0$ and it follows from Lemma 2.2 that

$$\begin{aligned} V(x(t))\le & {} \Big (\prod \nolimits _{1< t_{k}\le t}\max \{1,\beta \}\Big )\Big (\sup _{q\le s\le 1}V(\phi (s))\Big )t^{-\lambda }\nonumber \\= & {} \Big (\prod \nolimits _{1< t_{k}\le t}\max \{1,\beta \}\Big )\Vert \phi \Vert _{p}t^{-\lambda },\quad t\ge 1, \end{aligned}$$

(3.4)

where $\lambda >0$ is a solution of the inequality $\lambda -a+bq^{-\lambda }=\lambda +\mu _{p}(A)+l_{1}\Vert B\Vert _{p}+l_{2}\Vert C\Vert _{p} q^{-\lambda }\le 0.$ Since the function $l(x)=\ln x$ is monotonically increasing on $[1,\infty )$, one can see that the number of points $t_{k}$ on [1, t] is equal to the number of points $\ln t_{k}$ on $[0,\ln t]$. Thus, it follows from (3.4) that

$$\begin{aligned} \Vert x(t)\Vert _{p}= & {} V(x(t))\le \big (\max \{1, \beta \}\big )^{\frac{\ln t}{\ln \delta }+1}\Vert \phi \Vert _{p}t^{-\lambda }\nonumber \\= & {} \big (\max \{1, \beta \}\big )\Vert \phi \Vert _{p} t^{-\big (\lambda -\frac{\ln \max \{1, \beta \}}{\ln \delta }\big )}. \end{aligned}$$

(3.5)

By (3.5) and Definition 2.2, the zero of system (2.4) is globally power stable. The proof is completed. $\square$

Remark 3.1

One can easily see that Theorem 3.1 only presents a result for the global power stability of the zero solution of (2.4) under the condition “$\mu _{p}(A)<0$,” which shows its limitation. In addition, it can be seen that Lemma 2.2 is established from the impulsive perturbation point of view, which implies that impulses may act as perturbations rather than stabilizers. From the impulsive control point of view, based on Lemma 2.3, the following desirable conditions can be derived to ensure the global power stability of system (2.4).

Theorem 3.2

Assume that $(H_{1})$ holds and $0<\beta <1,~C\ne {\mathbf {0}}$. If there exists a constant $\lambda >0$ such that

$$\begin{aligned} \mu _{p}(A)+l_{1}\Vert B\Vert _{p}+2\lambda +\frac{1}{\beta }l_{2}\Vert C\Vert _{p} q^{-\lambda }<-\frac{\ln \beta }{t_{k}-t_{k-1}},\quad k\in {\mathbb {Z}}_{+}, \end{aligned}$$

(3.6)

then the zero solution of (2.4) is globally power stable with power convergence rate $\lambda$.

Proof

Defining the Lyapunov function $V(t)=V(x(t))=\Vert x(t)\Vert _{p}$ as Theorem 3.1, we have

$$\begin{aligned} D^{+}V(t)\le & {} (\mu _{p}(A)+l_{1}\Vert B\Vert _{p})V(x(t))+l_{2}\Vert C\Vert _{p}\Big (\sup _{qt\le s\le t}V(x(s))\Big )\\= & {} aV(x(t))+b\Big (\sup _{qt\le s\le t}V(x(s))\Big ),\quad t\ne t_{k}, \quad t\ge 1, \end{aligned}$$

where $a=\mu _{p}(A)+l_{1}\Vert B\Vert _{p},$ and $b= l_{2}\Vert C\Vert _{p}>0$. On the other hand, it follows from (2.4) that

$$\begin{aligned} V(t_{k})= & {} \Vert x(t_{k})\Vert _{p}=\Vert (E-D_{k})x(t_{k}^{-})\Vert _{p}\\\le & {} \Vert (E-D_{k})\Vert _{p}\Vert x(t_{k}^{-})\Vert _{p}\le \beta V(t_{k}^{-}),\quad k\in {\mathbb {Z}}_{+}. \end{aligned}$$

This and (3.6) imply that the all conditions of Lemma 2.3 are satisfied, and thus

$$\begin{aligned} V(x(t))\le \beta ^{-1}\Big (\sup _{q\le s\le 1}V(\phi (s))\Big )t^{-\lambda }= \beta ^{-1}\Vert \phi \Vert _{p}t^{-\lambda },\quad t\ge 1. \end{aligned}$$

That is,

$$\begin{aligned} \Vert x(t)\Vert _{p}\le \beta ^{-1}\Vert \phi \Vert _{p}t^{-\lambda }, \quad t\ge 1. \end{aligned}$$

This shows that the zero of system (2.4) is globally power stable by Definition 2.2. The proof is completed. $\square$

Remark 3.2

From the conditions of Lemma 2.3 and Theorem 3.2, we can find that system (2.4) without impulses may be unstable; Theorem 3.2 shows that impulses can be used to globally power stabilize an unstable system with proportional delay. In addition, set $\psi (q,\lambda )=\mu _{p}(A)+l_{1}\Vert B\Vert _{p}+2\lambda +\frac{1}{\beta }l_{2}\Vert C\Vert _{p} q^{-\lambda }$, $(q,\lambda )\in (0,1)\times (0,\infty )$ and it can be verified that $\psi (q,\lambda )$ is decreasing with respect to q, and increasing in $\lambda$. Therefore, when impulses are used to globally power stabilize an unstable system, the impulses may act more frequently if the proportional delay factor q becomes smaller; and moreover, in order to gain higher power convergence rate, the impulses should act more frequently.

Below, we are in a position to establish a result for the global power stability of the following system with impulses and proportional delays:

$$\begin{aligned} \left\{ \begin{array}{l}x'(t)=Ax(t)+Bf(x(t))+\frac{1}{t}Cg(x(qt)), \quad t\ne t_{k},\quad t \ge 1,\\ \Delta x(t_{k})= x(t_{k})-x(t^{-}_{k})=-D_{k}x(t^{-}_{k}),\quad k\in {\mathbb {Z}}_{+}, \end{array}\right. \end{aligned}$$

(3.7)

where $q, A,B,C,D_{k}$ and f, g are defined as (2.4).

Remark 3.3

One may call system (3.7) Euler-type NNs since it is similar to first-order ordinary Euler equations. The following theorem 3.3 presents some conditions ensuring the global power stability of such NNs. It is shown that impulses can be used to globally power stabilize such NNs.

Theorem 3.3

Assume that $(H_{1})$ holds and $\rho =\sup _{k\in {\mathbb {Z}}^{+}}\{t_{k}-t_{k-1}\}<+\infty$. If $\beta -\frac{l_{2}\ln q}{q}\Vert C\Vert _{p}<1$ and

$$\begin{aligned}&- l_{1}\Vert B\Vert _{p}-\frac{l_{2}}{q}\Vert C\Vert _{p}<\mu _{p}(A)<- l_{1}\Vert B\Vert _{p}-\frac{l_{2}}{q}\Vert C\Vert _{p}\nonumber \\&\quad - \frac{1}{\rho }\ln \Big (\beta -\frac{l_{2}\ln q}{q}\Vert C\Vert _{p}\Big ), \end{aligned}$$

(3.8)

then the zero solution of (3.7) is globally power stable with power convergence rate $\lambda$, where $\lambda$ is the unique positive solution of the following equation

$$\begin{aligned} \lambda + \mu _{p}(A)+ l_{1}\Vert B\Vert _{p}+\frac{l_{2}}{q}\Vert C\Vert _{p}+\ln \Big (\beta -\frac{l_{2}\ln q}{q}\Vert C\Vert _{p}q^{-\lambda }\Big )=0. \end{aligned}$$

Proof

Let the Lyapunov functional be in the form of

$$\begin{aligned} V(t)=V(x_t)=\Vert x(t)\Vert _{p}+ \frac{l_{2}}{q}\Vert C\Vert _{p}\int _{qt}^{t}\frac{1}{s}\Vert x(s)\Vert _{p}\mathrm{d}s. \end{aligned}$$

Then, the upper right-hand Dini derivative of V(t) with respect to time t along the solution of system (3.7) is as follows:

$$\begin{aligned} D^{+}V(t)= & {} {\overline{\lim }}_{h\rightarrow 0^{+}}\frac{\Vert x(t+h)\Vert _{p}-\Vert x(t)\Vert _{p}}{h}+\frac{l_{2}}{qt}\Vert C\Vert _{p}\Vert x(t)\Vert _{p}- \frac{l_{2}}{t} \Vert C\Vert _{p}\Vert x(qt)\Vert _{p}\\= & {} {\overline{\lim }}_{h\rightarrow 0^{+}}\frac{\Vert x(t)+hx'(t)+o(h)\Vert _{p}-\Vert x(t)\Vert _{p}}{h}\\&+\,\frac{l_{2}}{qt}\Vert C\Vert _{p}\Vert x(t)\Vert _{p}- \frac{l_{2}}{t}\Vert C\Vert _{p}\Vert x(qt)\Vert _{p}\\= & {} {\overline{\lim }}_{h\rightarrow 0^{+}}\frac{\Vert x(t)+h[Ax(t)+Bf(x(t))+\frac{1}{t}Cg(x(qt))]+o(h)\Vert _{p}-\Vert x(t)\Vert _{p}}{h}\\&+\,\frac{l_{2}}{qt}\Vert C\Vert _{p}\Vert x(t)\Vert _{p}- \frac{l_{2}}{t}\Vert C\Vert _{p}\Vert x(qt)\Vert _{p}\\\le & {} {\overline{\lim }}_{h\rightarrow 0^{+}}\frac{\Vert x(t)+hAx(t)\Vert _{p}-\Vert x(t)\Vert _{p}}{h} +\Vert Bf(x(t))\Vert _{p}+\frac{1}{t}\Vert Cg(x(qt))\Vert _{p}\\&+\,\frac{l_{2}}{qt}\Vert C\Vert _{p}\Vert x(t)\Vert _{p}- \frac{l_{2}}{t}\Vert C\Vert _{p}\Vert x(qt)\Vert _{p}\\\le & {} {\overline{\lim }}_{h\rightarrow 0^{+}} \frac{\Vert E+hA\Vert _{p}-1}{h}\Vert x(t)\Vert _{p} +\Vert Bf(x(t))\Vert _{p}+\frac{1}{t}\Vert Cg(x(qt))\Vert _{p}\\&+\,\frac{l_{2}}{qt}\Vert C\Vert _{p}\Vert x(t)\Vert _{p}- \frac{l_{2}}{t}\Vert C\Vert _{p}\Vert x(qt)\Vert _{p}. \end{aligned}$$

From (3.3), it follows that

$$\begin{aligned} D^{+}V(t)\le & {} \Big (\mu _{p}(A)+l_{1}\Vert B\Vert _{p}+\frac{l_{2}}{q}\Vert C\Vert _{p}\Big ) \Vert x(t)\Vert _{p}\\= & {} \eta \Vert x(t)\Vert _{p}\le \eta V(t), \quad t\in [t_{k-1},t_{k}),\quad k\in {\mathbb {Z}}_{+}, \end{aligned}$$

where $\eta =\mu _{p}(A)+l_{1}\Vert B\Vert _{p}+\frac{l_{2}}{q}\Vert C\Vert _{p}>0$ (by (3.8)). Then, we have

$$\begin{aligned}&V(t)\le V(1)e^{\eta (t-1)}, \quad t\in [1,t_{1}), \end{aligned}$$

(3.9)

$$\begin{aligned}&V(t)\le V(t_{k-1})e^{\eta (t-t_{k-1})}, \quad t\in [t_{k-1},t_{k}),\quad k=2,3,\ldots . \end{aligned}$$

(3.10)

From (3.8), we have

$$\begin{aligned} 0<\eta \rho < -\ln \Big (\beta -\frac{l_{2}\ln q}{q}\Vert C\Vert _{p}\Big ). \end{aligned}$$

(3.11)

Define the function u given by

$$\begin{aligned} u(z)=(z+\eta )\rho +\ln \Big (\beta -\frac{l_{2}\ln q}{q}\Vert C\Vert _{p}q^{-z}\Big ), \quad z\in [0,+\infty ). \end{aligned}$$

From (3.11), we get $u(0)<0$. Since $u(z)\rightarrow +\infty$ as $z\rightarrow +\infty$, and

$$\begin{aligned} u'(z)=\rho +\frac{ql_{2}(\ln q)^{2}\Vert C\Vert _{p}q^{-z} }{q\beta -l_{2}\ln q\Vert C\Vert _{p}q^{-z}}>0, \quad z\in (0,+\infty ), \end{aligned}$$

there exists a unique positive constant $\lambda >0$ such that $u(\lambda )=0$, i.e.,

$$\begin{aligned} (\lambda +\eta )\rho =-\ln \Big (\beta -\frac{l_{2}\ln q}{q}\Vert C\Vert _{p}q^{-\lambda }\Big ). \end{aligned}$$

(3.12)

By (3.9), we have for $t\in [1,t_{1})$,

$$\begin{aligned} V(t)\le & {} \Big (\Vert (x(1)\Vert _{p}+\frac{l_{2}}{q}\Vert C\Vert _{p}\int _{q}^{1} \frac{1}{s}\Vert x(s)\Vert _{p}\mathrm{d}s\Big )e^{\eta (t-1)}\\\le & {} \Big (1-\frac{l_{2}\ln q}{q} \Vert C\Vert _{p}\Big )\Vert \phi \Vert _{p}e^{\eta (t-1)} \le \Big (1-\frac{l_{2}\ln q}{q}\Vert C\Vert _{p}\Big ) \Vert \phi \Vert _{p}e^{\eta (t_{1}-1)}. \end{aligned}$$

Thus, using again the inequality $e^{x}>1+x ~(x>0)$ yields

$$\begin{aligned} \Vert x(t)\Vert _{p}\le & {} V(t)\le \Big (1-\frac{l_{2}\ln q}{q} \Vert C\Vert _{p}\Big )\Vert \phi \Vert _{p}e^{\eta \rho }\nonumber \\= & {} \Big (1-\frac{l_{2}\ln q}{q} \Vert C\Vert _{p}\Big )e^{(\lambda +\eta )\rho }\Vert \phi \Vert _{p}e^{-\lambda \rho }\nonumber \\\le & {} \Big (1-\frac{l_{2}\ln q}{q} \Vert C\Vert _{p}\Big )e^{(\lambda +\eta )\rho }\Vert \phi \Vert _{p}e^{-\lambda (t-1)}\nonumber \\\le & {} \Big (1-\frac{l_{2}\ln q}{q} \Vert C\Vert _{p}\Big )e^{(\lambda +\eta )\rho }\Vert \phi \Vert _{p}t^{-\lambda }\nonumber \\= & {} M\Vert \phi \Vert _{p}t^{-\lambda },\quad t\in [1,t_{1}), \end{aligned}$$

(3.13)

where $\lambda >0$ as in (3.12), and $M=\Big (1-\frac{l_{2}\ln q}{q} \Vert C\Vert _{p}\Big )e^{(\lambda +\eta )\rho }>1.$ Obviously,

$$\begin{aligned} \Vert x(t)\Vert _{p}\le \Vert \phi \Vert _{p}\le M\Vert \phi \Vert _{p}\le M\Vert \phi \Vert _{p}t^{-\lambda },\quad t\in [q,1]. \end{aligned}$$

(3.14)

From (3.13) and (3.14), it follows that

$$\begin{aligned} \Vert x(t)\Vert _{p}\le M\Vert \phi \Vert _{p}t^{-\lambda },\quad t\in [q,t_{1}). \end{aligned}$$

(3.15)

On the other hand, from the second equation of (3.7), we have

$$\begin{aligned} \Vert x(t_{k})\Vert _{p}= & {} \Vert (E-D_{k})x(t_{k}^{-})\Vert _{p}\le \Vert E-D_{k})\Vert _{p}\Vert x(t_{k}^{-})\Vert _{p}\le \beta \Vert x(t_{k}^{-})\Vert _{p}\nonumber \\\le & {} \Vert x(t_{k}^{-})\Vert _{p},\quad k=1,2,\ldots . \end{aligned}$$

(3.16)

Thus, (3.15) and (3.16) imply that

$$\begin{aligned} \sup _{qt_{1}\le s\le t_{1}}\Vert x(s)\Vert _{p}\le M\Vert \phi \Vert _{p}(qt_{1})^{-\lambda }= Mq^{-\lambda }\Vert \phi \Vert _{p}t_{1}^{-\lambda }. \end{aligned}$$

(3.17)

It follows from (3.12), (3.15), and (3.17) that

$$\begin{aligned} V(t_{1})= & {} \Vert x(t_{1})\Vert _{p}+ \frac{l_{2}}{q}\Vert C\Vert _{p}\int _{qt_{1}}^{t_{1}}\frac{1}{s}\Vert x(s)\Vert _{p}\mathrm{d}s\nonumber \\\le & {} \beta \Vert x(t_{1}^{-})\Vert _{p}+ \frac{l_{2}}{q}\Vert C\Vert _{p}\int _{qt_{1}}^{t_{1}}\frac{1}{s}\Vert x(s)\Vert _{p}\mathrm{d}s\nonumber \\\le & {} M\Vert \phi \Vert _{p}t_{1}^{-\lambda }\left( \beta -\frac{l_{2}\ln q }{q} \Vert C\Vert _{p}q^{-\lambda }\right) \nonumber \\= & {} e^{-(\lambda +\eta )\rho }M\Vert \phi \Vert _{p}t_{1}^{-\lambda }. \end{aligned}$$

(3.18)

Next, we shall show that

$$\begin{aligned} V(t_{k})\le e^{-(\lambda +\eta )\rho }M\Vert \phi \Vert _{p}t_{k}^{-\lambda },\quad k=1,2,\ldots . \end{aligned}$$

(3.19)

Obviously, (3.19) holds for $k=1$ by (3.18). If we assume that it holds for $k=1,2,\ldots ,m(m\in Z_{+})$, i.e.,

$$\begin{aligned} V(t_{k})\le e^{-(\lambda +\eta )\rho }M\Vert \phi \Vert _{p}t_{k}^{-\lambda },\quad k=1,2,\ldots ,m. \end{aligned}$$

(3.20)

then we have for $t\in [t_{m}, t_{m+1})$,

$$\begin{aligned} \Vert x(t)\Vert _{p}\le & {} V(t)\le V(t_{m})e^{\eta (t-t_{m})}\nonumber \\\le & {} e^{-(\lambda +\eta )\rho }M\Vert \phi \Vert _{p}t_{m}^{-\lambda }e^{\eta (t-t_{m})}\le e^{-\lambda \rho }M\Vert \phi \Vert _{p}t_{m}^{-\lambda }\nonumber \\\le & {} e^{-\lambda (t-t_{m})}M\Vert \phi \Vert _{p}t_{m}^{-\lambda }= \Big (e^{t_{m}\big (\frac{t}{t_{m}}-1\big )}\Big )^{-\lambda }M\Vert \phi \Vert _{p}t_{m}^{-\lambda }\nonumber \\\le & {} \Big (e^{\big (\frac{t}{t_{m}}-1\big )}\Big )^{-\lambda } M\Vert \phi \Vert _{p}t_{m}^{-\lambda }\le M\Vert \phi \Vert _{p}t^{-\lambda }. \end{aligned}$$

(3.21)

Using (3.20) and (3.21), similar to (3.17), we can verify that

$$\begin{aligned} \sup _{qt_{m+1}\le s\le t_{m+1}}\Vert x(s)\Vert _{p}\le M\Vert \phi \Vert _{p}(q t_{m+1}) ^{-\lambda }= M\Vert \phi \Vert _{p}q^{-\lambda }t_{m+1}^{-\lambda }. \end{aligned}$$

(3.22)

From (3.12), (3.16), (3.21), and (3.22), we obtain

$$\begin{aligned} V(t_{m+1})= & {} \Vert x(t_{m+1})\Vert _{p}+ \frac{l_{2}}{q}\Vert C\Vert _{p}\int _{qt_{m+1}}^{t_{m+1}}\frac{1}{s}\Vert x(s)\Vert _{p}\mathrm{d}s\\\le & {} \beta \Vert x(t_{m+1}^{-})\Vert _{p}+ \frac{l_{2}}{q}\Vert C\Vert _{p}\int _{qt_{m+1}}^{t_{m+1}}\frac{1}{s}\Vert x(s)\Vert _{p}\mathrm{d}s\\\le & {} \beta \Vert x(t_{m+1}^{-})\Vert _{p}+\frac{l_{2}}{q}\Vert C\Vert _{p} \int _{qt_{m+1}}^{t_{m+1}}\frac{1}{s}\Vert x(s)\Vert _{p}\mathrm{d}s\\\le & {} M\Vert \phi \Vert _{p}t_{m+1}^{-\lambda }\left( \beta -\frac{l_{2}\ln q}{q} \Vert C\Vert _{p}q^{-\lambda }\right) \\= & {} e^{-(\lambda +\eta )\rho }M\Vert \phi \Vert _{p}t_{m+1}^{-\lambda }, \end{aligned}$$

which implies that (3.19) holds for $k=m+1$, and hence (3.19) holds for each $k=1,2,\ldots .$ Thus, for $t\in [t_{k}, t_{k+1}),~ k=1,2,\ldots$, we have by (3.19) that

$$\begin{aligned} \Vert x(t)\Vert _{p}\le & {} V(t)\le V(x(t_{k}))e^{\eta (t-t_{k})}\\\le & {} e^{-(\lambda +\eta )\rho }M\Vert \phi \Vert _{p}t_{k}^{-\lambda }e^{\eta (t-t_{k})}\le e^{-\lambda \rho }M\Vert \phi \Vert _{p}t_{k}^{-\lambda }\\\le & {} M\Vert \phi \Vert _{p}e^{-\lambda (t-t_{k})}t_{k}^{-\lambda }= M\Vert \phi \Vert _{p}\Big (e^{t_{k}\big (\frac{t}{t_{k}}-1\big )}\Big )^{-\lambda }t_{k}^{-\lambda }\\\le & {} M\Vert \phi \Vert _{p}\Big (e^{\big (\frac{t}{t_{k}}-1\big )}\Big )^{-\lambda } t_{k}^{-\lambda }\le M\Vert \phi \Vert _{p}t^{-\lambda }. \end{aligned}$$

This together with (3.13) shows that the zero solution of (3.7) is globally power stable in terms of Definition 2.2. The proof is completed. $\square$

Remark 3.4

The main contribution of this paper lies in the following aspects: (1) A new method is proposed based on establishing the novel impulsive delay differential inequalities from impulsive perturbation and impulsive control point of view, respectively, which is different from the past work on this topic. We also believe that the new inequalities will play an important role in qualitative analysis of impulsive systems with proportional delays. (2) The global power stability of neural networks with impulses and proportional delays by using the matrix measure approach is seldom discussed, which implies that the results obtained in the present paper are completely new and complement the previous studies to some extent. (3) Our sufficient conditions ensuring the stability and stabilization of neural networks with impulses and proportional delays are dependent on the proportional delay factors and impulses. It can be seen that our results are less conservative than those in [10, 26], and one can design some feasible impulsive controllers according to the proportional delay factor allowed by such neural networks. In particular, impulses can act as stabilizers to globally power stabilize an unstable neural network with proportional delay. (4) The sufficient conditions and the power convergence rates can be also easily checked by simple computing, and they are effective to implement in real problems. (5) The obtained results play an important role in establishing a QoS routing algorithm based on neural networks with proportional delays and impulses.

4 Examples

In this section, three numerical examples along with their simulations are given to illustrate the effectiveness and advantages of the results obtained.

Example 4.1

Consider the system with impulses and proportional delay

$$\begin{aligned} \left\{ \begin{array}{l}x'(t)=Ax(t)+Bf(x(t))+\frac{1}{t}Cg (x(qt)) ,\quad t \ge 1,\quad t\ne t_{k},\\ \triangle x(t_{k})=x(t_{k})-x(t_{k}^{-})=-D_{k}x(t_{k}^{-}),\quad t_{k}=k+1,\quad k\in {\mathbb {Z}}_{+},\\ x(t)=\phi (t), \quad t\in [q, 1], \end{array}\right. \end{aligned}$$

(4.1)

where $q=0.8,~f(t)=(f_{1}(t), f_{2}(t))^{\mathrm{T}}=g(t),~ f_{i}(t)=\sin t,~i=1,2$, $\phi =(\phi _{1}, \phi _{2})^{\mathrm{T}}\in C([0.8, 1],{\mathbb {R}}^{2})$, and

$$\begin{aligned} A= & {} \begin{pmatrix} a_{1} &{} 0 \\ 0&{} a_{2} \end{pmatrix} =\begin{pmatrix} 0.3 &{} 0 \\ 0&{} 0.3 \end{pmatrix} , \quad B=\begin{pmatrix} 0 &{} 0.4 \\ 0.3 &{} 0 \end{pmatrix} , \quad C=\begin{pmatrix} 0.05 &{} 0 \\ 0 &{} 0.1 \end{pmatrix},\\ \quad D_{k}= & {} \begin{pmatrix} 0.6 &{} 0 \\ 0&{} 0.6 \end{pmatrix}, \quad k\in {\mathbb {Z}}_{+}. \end{aligned}$$

It is clear that $l_{1}=l_{2}=1$ and $\rho =\sup _{k\in {\mathbb {Z}}_{+}}\{t_{k}-t_{k-1}\}=1$. A simple calculation fields that $\mu _{2}(A)=0.3,$$\Vert B\Vert _{2}=0.4,$$\Vert C\Vert _{2}=0.1,$ and $\beta =0.4$. Thus, we have

$$\begin{aligned} \beta -\frac{l_{2}\ln q}{q}\Vert C\Vert _{2}= & {} 0.4278<1,\quad - l_{1}\Vert B\Vert _{2}-\frac{l_{2}}{q}\Vert C\Vert _{2}- \frac{1}{\rho }\ln \Big (\beta -\frac{l_{2}\ln q}{q}\Vert C\Vert _{2}\Big ) \\= & {} 0.3239>\mu _{2}(A). \end{aligned}$$

By Theorem 3.3, it can be verified that the zero solution of (4.1) is globally power stable with the power convergence rate $\lambda = 0.024.$

Fig. 1

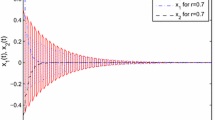
State trajectories of system (4.1) without impulses

Fig. 2

State trajectories of system (4.1)

Remark 4.1

(1) The zero solution of system (4.1) without impulsive effects is unstable (see Fig. 1). This shows that some appropriate conditions imposed on the jumps can make unstable equations globally power stable, and furthermore globally stable. Thus, impulses can be used to stabilize some unstable systems with proportional delays. The numerical simulations are shown in Figs. 1 and 2 when the initial condition $\phi (t)\equiv (1,2)^{\mathrm{T}},~t\in [0.8, 1]$. One can see that the results in [10] do not give any information on the global asymptotic stability of (4.1), and so our results in this paper complement those results in [10]. In addition, those results in [26] can also not be applied to (4.1) since the coefficients are variable and $a_{1}=a_{2}=0.3>0$.

(2) If we consider a differential system, in which f, g, A, B, C, and $D_{k}$ as same as (4.1) but the proportional delay factor q is variable. A calculation reveals the fact that the system with the above parameters is globally power stable as $q\in [0.2388,1)$, and that the proportional delay factor q is larger and the convergence is higher. Thus, one can stabilize the original system impulse free by choosing suitable impulsive control laws according to the proportional delay factor q. For example, let us consider the system

$$\begin{aligned} \left\{ \begin{array}{l}x'(t)=Ax(t)+Bf(x(t))+\frac{1}{t}Cg (x(0.5t)) ,\quad t \ge 1,\\ x(t)=\phi (t),\quad t\in [0.5, 1]. \end{array}\right. \end{aligned}$$

(4.2)

Applying Theorem 3.3, one can verify that system (4.2) can be stabilized via the impulsive controller $(t_{k}, H)_{k\in {\mathbb {Z}}_{+}}$:

$$\begin{aligned} \left\{ \begin{array}{l}H=dE,\quad d\in [0.7321, 1.2679],\\ \sup _{k\in {\mathbb {Z}}_{+}}\{t_{k}-t_{k-1}\}=1, \end{array}\right. \end{aligned}$$

where H is impulsive matrix. This shows the feasibility of our control schemes. In addition, the system (4.2) cannot be stabilized if one chooses the impulsive controller $(t_{k}, H)_{k\in {\mathbb {Z}}_{+}}$:

$$\begin{aligned} \left\{ \begin{array}{l}H=1.8E,\\ \sup _{k\in {\mathbb {Z}}_{+}}\{t_{k}-t_{k-1}\}=1. \end{array}\right. \end{aligned}$$

This partly shows the advantages of our results. The simulations are shown in Figs. 3 and 4 when the initial condition $\phi (t)\equiv (1,2)^{\mathrm{T}},~t\in [0.5, 1]$.

Fig. 3

State trajectories of system (4.2) with the impulsive controller $(1+k, 0.75E) k\in \mathbb {Z}_+$

Fig. 4

State trajectories of system (4.2) with the impulsive controller $(1+k, 1.8E)_{k\in \mathbb {Z}_+}$

(3) Here, we would like to point out that Theorem 3.3 can still be employed to investigate the global power stability of neural networks with negative feedback though the matrix $A=0.3E$ in Example 4.1 for some explanations. For instance, take $A=-0.3 E$ and the others $f,g,q, B,C,D_{k}$ are the same as (4.1); one can easily see that the all conditions of Theorem 3.3 are satisfied since $\beta -\frac{l_{2}\ln q}{q}\Vert C\Vert _{2}= 0.4278<1,$ and

$$\begin{aligned}&- l_{1}\Vert B\Vert _{2}-\frac{l_{2}}{q}\Vert C\Vert _{2}- \frac{1}{\rho }\ln \Big (\beta -\frac{l_{2}\ln q}{q}\Vert C\Vert _{2}\Big )= 0.3239>\mu _{2}(A)\\&\quad =-0.3>- l_{1}\Vert B\Vert _{2}-\frac{l_{2}}{q}\Vert C\Vert _{2}=-0.525. \end{aligned}$$

Therefore, the zero solution of (4.1) with the above parameters is globally power stable by Theorem 3.3. A simple calculation gives us the power convergence rate $\lambda = 0.6143.$

Example 4.2

Consider the following neural networks with impulses and proportional delay

$$\begin{aligned} \left\{ \begin{array}{l}x'(t)=Ax(t)+Bf(x(t))+Cg(x(0.5 t)), \quad t \ge 1, \quad t\ne t_{k},\\ \triangle x(t_{k})=-D_{k}x(t_{k}^{-}),\quad k\in {\mathbb {Z}}_{+},\\ x(t)=\phi (t),\quad 0.5\le t\le 1, \end{array}\right. \end{aligned}$$

(4.3)

where $f(t)=g(t)=(f_{1}(t), f_{2}(t))^{\mathrm{T}}, \quad f_{i}(t)=\frac{1}{2}\big (|t+1|-|t-1|\big ),~i=1,2$, $\phi =(\phi _{1}, \phi _{2})^{\mathrm{T}}\in C([0.5, 1],{\mathbb {R}}^{2})$, and

$$\begin{aligned} A= & {} \begin{pmatrix} -1.5 &{} 0 \\ 0&{} -1.5 \end{pmatrix} , \quad B=\begin{pmatrix} 0.5 &{} 0.5 \\ -0.5 &{} 0.5 \end{pmatrix} , \quad C=\begin{pmatrix} 0.3 &{} 0.3 \\ -0.2 &{} 0.2 \end{pmatrix},\\ \quad D_{k}= & {} \begin{pmatrix} -0.45 &{} 0 \\ 0&{} -0.45 \end{pmatrix}, \quad k\in {\mathbb {Z}}_{+}. \end{aligned}$$

It can be verified that $l_{1}=l_{2}=1$, $\beta =\sup _{k\in {\mathbb {Z}}_{+}}\{ \Vert E-D_{k}\Vert _{2}\}=1.45$, $\mu _{2}(A)=-1.5,$$\Vert B\Vert _{2}=0.7071,$ and $\Vert C\Vert _{2}=0.18.$ For simplicity, set $\delta =\frac{t_{k}}{t_{k-1}}=2.2,~k\in {\mathbb {Z}}_{+}$, and one can find that (3.1) and (3.2) hold for any positive number $\lambda \in (0.4713, 0.5325]$. In particular, choosing $\lambda =0.5$, we have

$$\begin{aligned} \lambda >\frac{\ln \big (\max \{1, \beta \}\big )}{\ln \delta }=\frac{\ln 1.45}{\ln 2.2}= 0.4713, \end{aligned}$$

and

$$\begin{aligned} \lambda + \mu _{2}(A)+l_{1}\Vert B\Vert _{2}+l_{2} \Vert C\Vert _{2}q^{-\lambda }=\lambda -0.7929+0.18 (0.5)^{-\lambda }= -0.0383<0. \end{aligned}$$

It can be concluded that the zero solution of (4.3) is globally power stable by Theorem 3.1.

Remark 4.2

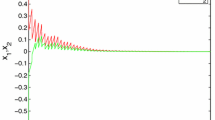
(1) It is well known that impulses potentially destroy system’s stability. Example 4.2 shows that one can still keep the stability of the original system under appropriate impulsive perturbations if one can work out an appropriate scheme according to the proportional delay factor allowed by such neural networks. The simulations are shown in Figs. 5 and 6, here the initial condition $\phi (t)\equiv ( -10, 20)^{\mathrm{T}},~t\in [0.5, 1]$.

Fig. 5

State trajectories of system (4.3) without impulses

Fig. 6

State trajectories of (4.3) as $\frac{t_k}{t_{k-1}}=2.2,\,k \in {\mathbb {Z}}_{+}$

(2) Theorem 5 in [26] cannot be applied to system (4.3) since one can see that for any positive numbers $a_{1}$, $a_{2}>0$,

$$\begin{aligned}&\max \Big \{ \frac{1}{d_{1}}\sum _{i=1}^{2}l_{i}\Big (\frac{a_{1}}{a_{i}} |a_{i1}|+\frac{a_{1}}{a_{i}}|b_{i1}|\Big ), \frac{1}{d_{2}}\sum _{i=1}^{2}l_{i}\Big (\frac{a_{2}}{a_{i}} |a_{i2}|+\frac{a_{2}}{a_{i}}|b_{i2}|\Big )\Big \}\\&\quad =\max \Big \{ \frac{1}{1.5} \Big (0.8+0.7 \times \frac{a_{1}}{a_{2}}\Big ), \frac{1}{1.5}\Big (0.7+0.8\times \frac{a_{2}}{a_{1}}\Big )\Big \}\ge 1. \end{aligned}$$

Therefore, our results complement the relative ones in [26].

Example 4.3

Consider the following neural networks with impulses and proportional delay

$$\begin{aligned} \left\{ \begin{array}{l}x'(t)=Ax(t)+Bf(x(t))+Cg(x(0.5 t)), \quad t \ge 1,\quad t\ne t_{k},\\ \triangle x(t_{k})=-D_{k}x(t_{k}^{-}),\quad k\in {\mathbb {Z}}_{+},\\ x(t)=\phi (t),\quad 0.5\le t\le 1, \end{array}\right. \end{aligned}$$

(4.4)

where f, g, B, C are defined as (4.3), and $A=\text {diag}(-0.1, 0.3),~D_{k}=\text {diag}(0.5, 0.5), k\in {\mathbb {Z}}_{+}.$

It can be verified that $\mu _{2}(A)=0.3$ and $\beta =\sup _{k\in {\mathbb {Z}}_{+}}\{ \Vert E-D_{k}\Vert _{2}\}=0.5$. For simplicity, we consider the equidistant impulsive interval $\Delta t=t_{k}-t_{k-1},$$k\in {\mathbb {Z}}_{+}$. Let $\lambda =0.5$, it is easy to verify that if the following inequality holds

$$\begin{aligned} \mu _{2}(A)+l_{1}\Vert B\Vert _{2}+2\lambda +\frac{1}{\beta }l_{2}\Vert C\Vert _{2} q^{-\lambda }= & {} 2.5162<-\frac{\ln \beta }{t_{k}-t_{k-1}}\nonumber \\= & {} \frac{0.6931}{\Delta t},\quad k\in {\mathbb {Z}}_{+}, \end{aligned}$$

(4.5)

then all the conditions of Theorem 3.2 hold, which means that the zero solution of system (4.4) is globally power stable with power convergence rate $\lambda =0.5$. It is clear that (4.5) holds if $\Delta t<0.2755$. Thus, we can construct the impulsive controller $(1+0.2k, 0.5E)_{k\in {\mathbb {Z}}_{+}}$ to ensure that system (4.4) is globally power stable. In Figs. 7 and 8 are shown the simulations when the initial condition $\phi (t)\equiv (-\,0.2,0.3)^{\mathrm{T}}, t\in [0.5, 1].$ Fig. 7 indicates the dynamics of system (4.4) without impulses on the time interval [1, 10], which shows that the system (4.4) without impulsive effects is unstable. And Fig. 8 depicts the state trajectories of system (4.4) with the impulsive controller $(1+0.2k, 0.5E)_{k\in {\mathbb {Z}}_{+}}$ on the time interval [1, 5]. This shows the validity of our scheme.

Remark 4.3

Example 4.3 shows that impulses can be used to globally stabilize an unstable system with proportional delays based on some suitable impulsive control laws. In addition, from the viewpoint of impulsive effects, Example 4.2 is given in terms of impulsive perturbation and Example 4.3 is presented in terms of impulsive control, which implies that Theorems 3.1 and 3.2 are complementary with each other.

Fig. 7

State trajectories of system (4.4) without impulses

Fig. 8

State trajectories of system (4.4) with the impulsive controller $(1+0.2k, 0.5E)_{k\in {\mathbb {Z}}_+}$

5 Conclusions

In this paper, we have investigated the global power stability and stabilization of neural networks with impulses and proportional delays. By establishing two new impulsive delay differential inequalities, constructing some Lyapunov functionals, and employing the matrix measure approach, some novel and sufficient conditions are obtained to guarantee the global power stability of neural networks with impulses and proportional delay from impulsive perturbation and impulsive control point of view, respectively. The obtained conditions can be easily checked in practice. Our results give some schemes of impulsive controller design based on the proportional delay factor. Three numerical examples are included to illustrate the effectiveness and advantages.