1 Introduction

For the sake of depicting the relationship between electric charge and magnetic flux, Chua [1] in 1971 originally envisaged the existence of the fourth basal circuit element which described as memristor (an abbreviation for memory and resistor). The other three essential circuit components are resistor, inductor and capacitor, respectively. Unfortunately, as the fourth fundamental passive circuit element, memristor was rarely valued by several researchers until the actual memristor device was triumphantly contrived by scientists at Hewlett-Packard Laboratories [2]. Thanks to memristor’s distinctive properties, such as nanometer scale dimensions, nonvolatile memory characteristics, lower power consumption, a alterable resistance known as memristance, and so on [3,4,5], a growing number of researchers have shown solicitude for memristor. Going one step further, scientists have explored memristor’s a number of prospective applications in neuromorphic systems [6], programmable analog circuits [7] and so on. It has been expounded at length that memristor is in a position to regard as synaptic connection weights in artificial neural networks [8], so a great deal of researchers took advantage of memristor to devise a novel model called memristor-based neural networks for the purpose of emulating the human brain. We are convinced that memristor-based neural networks can be widely used in many fields, when their dynamical characteristics are adequately exploited and utilized.

It is generally known that recurrent neural networks have blossomed into very significant nonlinear circuit systems in virtue of their extensive application value and prospect in solving Sylvester equation, computing the Drazin inverse, resolving real-time price problem, dealing with convex optimization problem and so on [9,10,11]. Taking fully into account the wide range of practical applications, numerous scholars were really quite interested in researching memristor-based recurrent neural networks (MRNNs) and have acquired many meaningful results. In reality, MRNNs with time delays have captured considerable attention of more and more scholars and a great deal of valuable achievements have been reported in [12,13,14,15]. The true cause lies in the fact that time delays are universal phenomena in nature as a result of the limited switching speed of amplifiers. In addition, time delays invariably have a marked impact on the dynamic behaviors of neural networks, and even cause various unstable phenomena, such as periodic oscillation, periodic instability, bifurcation and so on. In recent years, scholars have devoted a great deal of effort to investigating the delay-dependent exponential passivity and exponential stability of MRNNs with time-varying delays [12, 13]. Besides that, by constructing appropriate Lyapunov functionals and applying inequality techniques, a lot of sufficient conditions were obtained to ensure the passivity of the MRNNs with discrete and distributed delays in [14]. And Chandrasekar et al. [15] considered the \(\mu \)-stability of MRNNs with leakage time-varying delays by establishing proper Lyapunov-Krasovskii functionals, appropriate inequalities and linear matrix inequalities (LMIs).

As early as 1990, Pecora and Carroll [16] reported that chaotic systems can be synchronized by linking them with identical signals. After the ground-breaking research, a growing number of scholars from diverse scientific domains have extensively studied the synchronization owing to its several latent applications in security [17], image encryption [18], public traffic networks [19], private communications [20], inferring network topologies [21] and so on. Wang et al. [22] analyzed the synchronization conditions of coupled harmonic oscillators utilizing sampled data. And researchers have discussed the synchronization of many networks, containing complex networks, directed complex networks, duplex networks and so on. For example, see [23,24,25] and references therein. In [23], scholars expounded profoundly the synchronization phenomena when oscillating elements are confined to interact in the sophisticated network topology, and its applications from complex networks to diverse disciplines. The lower bounds for the coupling strengths of oscillators in the directed complex networks were given to guarantee the global synchronization in [24]. Li et al. [25] revealed several rules about synchronizability of the duplex networks comprised of two networks. In existent researching files, a lot of synchronization problems have been demonstrated, covering adaptive lag synchronization [26], impulsive synchronization [27], complex function projective synchronization [28], exponential synchronization [29] and so on. Numerous control techniques have been utilized to investigate the synchronization of discussed systems, which contain adaptive control, periodically intermittent control, delayed feedback control and so on. For example, see [30,31,32,33] and references therein. In recent years, the synchronization of MRNNs has aroused widespread concern due to its important significance in theory and practice. Taking into account the impact of time delays, researchers focused on the synchronization of MRNNs with time delays and have reported numerous significant achievements. Exponential synchronization and anti-synchronization, non-fragile \(H_{\infty }\) synchronization of MRNNs with time-varying delays were studied in [34, 35], respectively. In [36], Bao received some sufficient conditions to ensure the adaptive synchronization of fractional-order memristor-based neural networks with time delay, by utilizing the linear delay feedback control, adaptive control as well as a fractional-order inequality. By designing suitable controllers, several sufficient conditions were contained to ensure the finite-time synchronization and fixed-time synchronization of delayed MRNNs in [37, 38], respectively. The exponential synchronization of coupled stochastic memristor-based neural networks with probabilistic time-varying delay coupling and time-varying impulsive delay was investigated in [39]. In view of non-smooth analysis and a feedback controller, numerous sufficient conditions were achieved to guarantee the exponential synchronization of MRNNs with time-varying delays in [40].

In the late years, a new type of unbounded time-varying delay which differs from distributed delay, known as proportional delay, has stimulated scholars’ research interests owing to its important position of many areas, such as electrodynamics [41], dynamics [42], Web quality of service (QoS) routing decision [43] and so on. On the basis of the topological structures and inner parameters of considered neural networks, we lead into the proportional delays, which can make the process of performance analysis more complicated and interesting [44, 45]. It should be pointed out that the QoS routing algorithms in view of neural networks with proportional delays are regarded as the most appropriate algorithms. At the same time, the proportional delay function \(\tau (t)=(1-q)t \rightarrow +\,\infty \) as \(q\ne 1, t\rightarrow +\,\infty \), where q is a constant and meets \(0<q<1\), so it is remarkably facilitate to dominate the operation time in the light of the time delays of discussed neural networks. Therefore it’s of important theory and actual meanings to deal with the dynamic behaviors of neural networks with proportional delays. For example, see [46,47,48,49,50,51] and references therein. On the basis of matrix theories and proper Lyapunov functionals, global exponential stability and asymptotic stability of the equilibrium point of cellular neural networks with multi-proportional delays were studied in [46, 47], respectively. In addition to this, several sufficient conditions ensuring the global exponential periodicity and stability, exponential synchronization of recurrent neural networks with multi-proportional delays were reported in [48, 49], respectively. Nevertheless, it is a significant challenge to establish suitable Lyapunov functionals occasionally, researches try to deal with the problems by some other methods, for instance, by constructing novel delay differential inequalities. By means of constructing proper delay differential inequalities, Zhou [50, 51] investigated the exponential stability of hybrid BAM neural networks and competitive neural networks with proportional delays, respectively. Moreover, in the process of transferring the digital signals, security will be enhanced by means of utilizing synchronization to communication. Up to date, there has never been any results discussing the exponential synchronization of MRNNs with multi-proportional delays in the literature, and this question is challenging and meaningful.

Inspired by the above discussions, this paper researches the exponential synchronization of MRNNs with multi-proportional delays. In the sense of Filippov solutions, we manage to obtain a novel sufficient condition to ensure the exponential synchronization of considered systems via a feedback control, theories of set-valued maps and differential inclusions, proper Lyapunov functional method and inequality techniques. Moreover, two numerical examples and their simulations are given to clarify the improvement and advantages of the derived theoretical results in comparison with some existing results.

The rest of this paper is proposed as follows. Models and preliminaries are presented in Sect. 2. A sufficient condition is obtained in Sect. 3 for the exponential synchronization of MRNNs with multi-proportional delays. Section 4 presents two numerical examples and their simulations. Conclusions are exhibited in Sect. 5.

2 Model description and preliminaries

Consider the following class of MRNNs with multi-proportional delays:

$$\begin{aligned} \left\{ \begin{aligned} {\dot{x}}_{i}(t)&=-d_{i}\left( {x_{i}(t)}\right) x_{i}(t)+\sum \limits _{j=1}^{n}a_{ij}\left( {x_{j}(t)}\right) f_{j}\left( x_{j}(t)\right) \\&\quad +\sum \limits _{j=1}^{n}b_{ij}\left( {x_{j}\left( p_{j}t\right) }\right) g_{j}\left( x_{j}\left( p_{j}t\right) \right) +\sum \limits _{j=1}^{n}c_{ij}\left( {x_{j}\left( q_{j}t\right) }\right) h_{j}\left( x_{j}\left( q_{j}t\right) \right) \\&\quad +I_{i}, t\ge 1,\\ x_{i}(t)&=\varphi _{i}(t), \quad t\in [q,1], \end{aligned}\right. \end{aligned}$$
(1)

for \(i=1,2,\dots ,n\). where \(n\ge 2\) represents the number of neurons. \(x_{i}(t)\) is the voltage of the capacitor \(C_{i}\). \(d_{i}({x_{i}(t)})\) is the \(i{\text {th}}\) neuron self-inhibitions at time t. \(a_{ij}({x_{j}(t)}), b_{ij}({x_{j}(p_{j}t)})\) and \(c_{ij}({x_{j}(q_{j}t)})\) are memristor-based connection weights. \(f_{j},g_{j}\) and \(h_{j}: {\mathbb {R}}\rightarrow {\mathbb {R}}\) denote the nonlinear activation functions. \(I_{i}\) is an external constant input. \(p_{j}\) and \(q_{j}, j=1,2,\dots ,n\) are proportional delay factors and satisfy \(0<p_{j},q_{j}\le 1, q=\min \nolimits _{1\le j\le n}\{p_{j},q_{j}\}\), and \(p_{j}t=t-(1-p_{j})t, q_{j}t=t-(1-q_{j})t\), where \((1-p_{j})t\) and \((1-q_{j})t\) are the transmission delay functions, and \((1-p_{j})t\rightarrow +\,\infty , (1-q_{j})t\rightarrow +\,\infty \) as \(p_{j}, q_{j}\ne 1, t\rightarrow +\,\infty \). \(\varphi _{i}(t), t\in [q,1], i=1,2,\dots ,n\) are the initial values of system (1), \(\Phi =(\varphi _{1}(t),\varphi _{2}(t),\dots ,\varphi _{n}(t))^{\mathrm{T}}\in C([q,1],{\mathbb {R}}^{n})\), and

$$\begin{aligned} d_{i}\left( {x_{i}(t)}\right)= & {} \frac{1}{C_{i}}\left[ \sum \limits _{j=1}^{n}\left( M_{ij}+N_{ij}+W_{ij}\right) \times \delta _{ij}+\bar{\mathfrak {R}_{i}}\right] , a_{ij}\left( {x_{j}(t)}\right) =\frac{M_{ij}}{C_{i}}\times \delta _{ij},\\ b_{ij}\left( {x_{j}\left( p_{j}t\right) }\right)= & {} \frac{N_{ij}}{C_{i}}\times \delta _{ij}, c_{ij}\left( {x_{j}\left( q_{j}t\right) }\right) =\frac{W_{ij}}{C_{i}}\times \delta _{ij}, \end{aligned}$$

in which

$$\begin{aligned} \delta _{ij}=\left\{ \begin{array}{ll} 1,&{}\quad i\ne j,\\ -1,&{}\quad i=j, \end{array}\right. \end{aligned}$$

\(R_{i}\) and \(C_{i}\) are the resistor and capacitor, \(\bar{\mathfrak {R}_{i}}=\frac{1}{R_{i}}, i\in N, N=1,2,\dots , n\). \(M_{ij}, N_{ij}\) and \(W_{ij}\) denote the memductances of memristors \(R_{ij}^{*}, R_{ij}^{**}\) and \(R_{ij}^{***}\), respectively. Furthermore, \(R_{ij}^{*}\) denotes the memristor between the neuron activation function \(f_{j}(x_{j}(t))\) and \(x_{i}(t)\). \(R_{ij}^{**}\) stands for the memristor between the neuron activation function \(g_{j}(x_{j}(p_{j}t))\) and \(x_{i}(t)\). \(R_{ij}^{***}\) represents the memristor between the neuron activation function \(h_{j}(x_{j}(q_{j}t))\) and \(x_{i}(t)\). According to the properties of memristor and the previous works, here we take the threshold voltage is zero, then \(d_{i}({x_{i}(t)}), a_{ij}({x_{j}(t)}), b_{ij}({x_{j}(p_{j}t)})\) and \(c_{ij}({x_{j}(q_{j}t)})\) satisfy the following conditions:

$$\begin{aligned} d_{i}\left( {x_{i}(t)}\right)= & {} v\left\{ \begin{array}{ll} d_{i}^{*},&{}\quad x_{i}(t) \le 0,\\ d_{i}^{**},&{}\quad x_{i}(t)> 0, \end{array}\right. \qquad a_{ij}\left( {x_{j}(t)}\right) =\left\{ \begin{array}{ll} a_{ij}^{*}, &{}\quad x_{j}(t) \le 0,\\ a_{ij}^{**}, &{}\quad x_{j}(t)> 0, \end{array}\right. \\ b_{ij}\left( {x_{j}\left( p_{j}t\right) }\right)= & {} \left\{ \begin{array}{ll} b_{ij}^{*},&{}\quad x_{j}\left( p_{j}t\right) \le 0,\\ b_{ij}^{**},&{} \quad x_{j}\left( p_{j}t\right)> 0, \end{array}\right. \quad c_{ij}\left( {x_{j}\left( q_{j}t\right) }\right) =\left\{ \begin{array}{ll} c_{ij}^{*},&{} \quad x_{j}\left( q_{j}t\right) \le 0,\\ c_{ij}^{**},&{} \quad x_{j}\left( q_{j}t\right) > 0, \end{array}\right. \end{aligned}$$

where \(d_{i}^{*}>0, d_{i}^{**}>0, i\in N\). For \(i, j\in N, a_{ij}^{*}, a_{ij}^{**}, b_{ij}^{*}, b_{ij}^{**}, c_{ij}^{*}\) and \(c_{ij}^{**}\) are all constants. Before going any further, we bring forward the following condition for the neuron activation functions \(f_{j}(\cdot ), g_{j}(\cdot )\) and \(h_{j}(\cdot )\):

$$\begin{aligned} \left. \begin{array}{ll} \sigma _{j}^{-}\le \frac{f_{j}(s_{1})-f_{j}(s_{2})}{s_{1}-s_{2}}\le \sigma _{j}^{+},\quad \gamma _{j}^{-}\le \frac{g_{j}(s_{1})-g_{j}(s_{2})}{s_{1}-s_{2}}\le \gamma _{j}^{+},\\ \delta _{j}^{-}\le \frac{h_{j}(s_{1})-h_{j}(s_{2})}{s_{1}-s_{2}}\le \delta _{j}^{+}, \quad s_{1}\ne s_{2}, \quad f_{j}(0)=g_{j}(0)=h_{j}(0)=0, \end{array}\right\} \end{aligned}$$
(2)

in which \(j=1,2,\dots ,n, \sigma _{j}^{-}, \sigma _{j}^{+}, \gamma _{j}^{-}, \gamma _{j}^{+}, \delta _{j}^{-}\) and \(\delta _{j}^{+}\) are constants, \(f_{j}(\cdot ), g_{j}(\cdot )\) and \(h_{j}(\cdot )\) don’t be asked to be differential, monotonic and nondecreasing throughout this paper.

System (1) is deemed as the drive system, corresponding response system is defined as:

$$\begin{aligned} \left\{ \begin{aligned} {\dot{z}}_{i}(t)&=-d_{i}\left( {z_{i}(t)}\right) z_{i}(t)+\sum \limits _{j=1}^{n}a_{ij}\left( {z_{j}(t)}\right) f_{j}\left( z_{j}(t)\right) \\&\quad +\sum \limits _{j=1}^{n}b_{ij}\left( {z_{j}\left( p_{j}t\right) }\right) g_{j}\left( z_{j}\left( p_{j}t\right) \right) \\&\quad +\sum \limits _{j=1}^{n}c_{ij}\left( {z_{j}\left( q_{j}t\right) }\right) h_{j}\left( z_{j}\left( q_{j}t\right) \right) +I_{i}+u_{i}(t), \quad t\ge 1,\\ z_{i}(t)&=\psi _{i}(t), \quad t\in [q,1], \end{aligned}\right. \end{aligned}$$
(3)

where

$$\begin{aligned} d_{i}\left( {z_{i}(t)}\right)= & {} \left\{ \begin{array}{ll} d_{i}^{*}, &{}\quad z_{i}(t) \le 0,\\ d_{i}^{**},&{}\quad z_{i}(t)> 0, \end{array}\right. \qquad a_{ij}\left( {z_{j}(t)}\right) =\left\{ \begin{array}{ll} a_{ij}^{*}, &{}\quad z_{j}(t) \le 0,\\ a_{ij}^{**},&{} \quad z_{j}(t)> 0,\\ \end{array}\right. \\ b_{ij}\left( {z_{j}\left( p_{j}t\right) }\right)= & {} \left\{ \begin{array}{ll} b_{ij}^{*}, &{}\quad z_{j}\left( p_{j}t\right) \le 0,\\ b_{ij}^{**}, &{}\quad z_{j}\left( p_{j}t\right)> 0, \end{array}\right. \quad c_{ij}\left( {z_{j}\left( q_{j}t\right) }\right) =\left\{ \begin{array}{ll} c_{ij}^{*},&{}\quad z_{j}\left( q_{j}t\right) \le 0,\\ c_{ij}^{**}, &{}\quad z_{j}\left( q_{j}t\right) > 0, \end{array}\right. \end{aligned}$$

and \(u_{i}(t)\) is the state-feedback controller. \(\psi _{i}(t), t\in [q,1], i=1,2,\dots ,n\) are the initial values of response system (3), \(\Psi =(\psi _{1}(t),\psi _{2}(t),\dots ,\psi _{n}(t))^{\mathrm{T}} \in C([q,1],{\mathbb {R}}^{n})\).

Through appropriate transformations: \(y_{i}(t)=x_{i}({\text {e}}^{t}), v_{i}(t)=z_{i}({\text {e}}^{t})\) (see [46]), drive-response systems (1) and (3) are equivalently transformed into the following drive-response systems with multi-constant delays and time-varying coefficients:

$$\begin{aligned} \left\{ \begin{aligned} {\dot{y}}_{i}(t)&={\text {e}}^{t}\left\{ -d_{i}\left( {y_{i}(t)}\right) y_{i}(t)+\sum \limits _{j=1}^{n}a_{ij}\left( {y_{j}(t)}\right) f_{j}\left( y_{j}(t)\right) \right. \\&\quad +\sum \limits _{j=1}^{n}b_{ij}\left( {y_{j}\left( t-\tau _{j}\right) }\right) g_{j}\left( y_{j}\left( t-\tau _{j}\right) \right) \\&\quad \left. +\sum \limits _{j=1}^{n}c_{ij}\left( {y_{j}\left( t-\varsigma _{j}\right) }\right) h_{j}\left( y_{j}\left( t-\varsigma _{j}\right) \right) +I_{i}\right\} ,\quad t\ge 0,\\ y_{i}(t)&={\bar{\varphi }}_{i}(t), \quad t\in [-\eta ,0], \end{aligned}\right. \end{aligned}$$
(4)

and

$$\begin{aligned} \left\{ \begin{aligned} {\dot{v}}_{i}(t)&={\text {e}}^{t}\left\{ -d_{i}\left( {v_{i}(t)}\right) v_{i}(t)+\sum \limits _{j=1}^{n}a_{ij}\left( {v_{j}(t)}\right) f_{j}\left( v_{j}(t)\right) \right. \\&\quad +\sum \limits _{j=1}^{n}b_{ij}\left( {v_{j}\left( t-\tau _{j}\right) }\right) g_{j}\left( v_{j}\left( t-\tau _{j}\right) \right) \\&\quad \left. +\sum \limits _{j=1}^{n}c_{ij}\left( {v_{j}\left( t-\varsigma _{j}\right) }\right) h_{j}\left( v_{j}\left( t-\varsigma _{j}\right) \right) +I_{i}+U_{i}(t)\right\} ,\quad t\ge 0,\\ v_{i}(t)&={\bar{\psi }}_{i}(t),\quad t\in [-\eta ,0], \end{aligned}\right. \end{aligned}$$
(5)

for \(i=1,2,\dots ,n\). Where \(\tau _{j}=-\log p_{j}\ge 0, \varsigma _{j}=-\log q_{j}\ge 0\), we let \( \tau =\max \nolimits _{1\le j\le n}\{\tau _{j}\}, \varsigma =\max \nolimits _{1\le j\le n}\{\varsigma _{j}\}, \eta =\max \{\tau ,\varsigma \}\). \({\bar{\varphi }}_{i}(t)=\varphi _{i}({\text {e}}^{t}), {\bar{\psi }}_{i}(t)=\psi _{i}({\text {e}}^{t}), {\bar{\Phi }}=({\bar{\varphi }}_{1}(t),{\bar{\varphi }}_{2}(t),\dots ,{\bar{\varphi }}_{n}(t))^{\mathrm{T}} \in C([-\eta ,0],{\mathbb {R}}^{n}), {\bar{\Psi }}=({\bar{\psi }}_{1}(t),{\bar{\psi }}_{2}(t),\dots ,{\bar{\psi }}_{n}(t))^{\mathrm{T}}\in C([-\eta ,0],{\mathbb {R}}^{n}), U_{i}(t)=u_{i}({\text {e}}^{t})\), here \(U_{i}(t)\) is an feedback controller and defined as

$$\begin{aligned} U_{i}(t)=\rho _{i}\left( v_{i}(t)-y_{i}(t)\right) , \end{aligned}$$
(6)

where \(\rho _{i}\) is a constant for all \(i\in N\), which represents the control gain.

Remark 1

Drive-response systems (1) and (3) are equivalent to drive-response systems (4) and (5). Accordingly, for the sake of researching the exponential synchronization of drive-response systems (1) and (3), we can research the exponential synchronization of drive-response systems (4) and (5).

From the view of mathematics, memristor-based differential equations obey Bernoulli’s nonlinear differential equations (see [33]), and drive-response systems (4) and (5) are discontinuous systems. In this case, the solutions of (4) and (5) are considered in Filippov’s sense, we recommend several definitions and lemmas.

Definition 1

[14] Let E \(\subset {\mathbb {R}}^{n}\), then \(\chi \mapsto G(\chi )\) is called a set-valued map from \(E\hookrightarrow {\mathbb {R}}^{n}\), if there is a nonempty set \(G(\chi )\subset {\mathbb {R}}^{n}\) for each point \(\chi \) of a set \(E\subset {\mathbb {R}}^{n}\). A set-valued map G with nonempty values is described as upper-semi-continuous at \(\chi _{0}\in E\subset {\mathbb {R}}^{n}\), if for any open set N containing \(G(\chi _{0})\), there exists a neighborhood M of \(\chi _{0}\) such that \(G(M)\subset N\). \(G(\chi )\) is said to have a closed (convex, compact) image if to each \(\chi \in E, G(\chi )\) is closed (convex, compact).

Definition 2

[52] For the following differential system \({\dot{\chi }}(t)=g(t,\chi )\), in which \(g(t,\chi )\) is discontinuous at \(\chi \in {\mathbb {R}}^{n}\). The set-valued map is described as

$$\begin{aligned} G(t,\chi )=\bigcap \limits _{\varrho >0}\bigcap \limits _{\mu (N)=0}{\mathrm{co}}\left[ g\left( t,B\left( \chi ,\varrho \right) \backslash N\right) \right] , \end{aligned}$$

where \({\mathrm{co}}[\cdot ]\) denotes the closure of the convex hull. \(B(\chi ,\varrho )\) is the ball of center \(\chi \) and radius \(\varrho \). \(\mu (N)\) is Lebesgue measure of set N. A vector-value function \(\chi (t)\) which defined on a non-degenerate interval \(I \subseteq R\) is addressed as a Filippov solution of this system, if \(\chi (t)\) is an absolutely continuous function on any subinterval \([t_{1}, t_{2}]\) of I, and for almost all \(t\in I, \chi (t)\) fulfills the differential inclusion \({\dot{\chi }}(t)\in G(t,\chi )\).

According to Definitions 1 and 2, drive-response systems (4) and (5) can be written as:

$$\begin{aligned}&{\dot{y}}_{i}(t)\in {\text {e}}^{t}\left\{ -{\text {co}}\left[ d_{i}\left( y_{i}(t)\right) \right] y_{i}(t)+\sum \limits _{j=1}^{n}{\text {co}}\left[ a_{ij}\left( {y_{j}(t)}\right) \right] f_{j}\left( y_{j}(t)\right) \right. \nonumber \\&\quad +\sum \limits _{j=1}^{n}{\text {co}}\left[ b_{ij}\left( {y_{j}\left( t-\tau _{j}\right) }\right) \right] g_{j}\left( y_{j}\left( t-\tau _{j}\right) \right) \nonumber \\&\quad \left. +\sum \limits _{j=1}^{n}{\text {co}}\left[ c_{ij}\left( {y_{j}\left( t-\varsigma _{j}\right) }\right) \right] h_{j}\left( y_{j}\left( t-\varsigma _{j}\right) \right) +I_{i}\right\} , \quad t\ge 0, \end{aligned}$$
(7)

and

$$\begin{aligned}&{\dot{v}}_{i}(t)\in {\text {e}}^{t}\left\{ -{\text {co}}\left[ d_{i}\left( v_{i}(t)\right) \right] v_{i}(t)+\sum \limits _{j=1}^{n}{\text {co}}\left[ a_{ij}\left( {v_{j}(t)}\right) \right] f_{j}\left( v_{j}(t)\right) \right. \nonumber \\&\quad +\sum \limits _{j=1}^{n}{\text {co}}\left[ b_{ij}\left( {v_{j}\left( t-\tau _{j}\right) }\right) \right] g_{j}\left( v_{j}\left( t-\tau _{j}\right) \right) \nonumber \\&\quad \left. +\sum \limits _{j=1}^{n}{\text {co}}\left[ c_{ij}\left( {v_{j}\left( t-\varsigma _{j}\right) }\right) \right] h_{j}\left( v_{j}\left( t-\varsigma _{j}\right) \right) +I_{i}+U_{i}(t)\right\} ,\quad t\ge 0, \end{aligned}$$
(8)

where

$$\begin{aligned} {\text {co}}\left[ d_{i}\left( y_{i}(t)\right) \right]= & {} \left\{ \begin{aligned}&d_{i}^{*},&\quad y_{i}(t)<0,\\&{\text {co}}\left\{ d_{i}^{*},d_{i}^{**}\right\} ,&\quad y_{i}(t)=0,\\&d_{i}^{**},&\quad y_{i}(t)>0, \end{aligned}\right. \quad {\text {co}}\left[ d_{i}\left( v_{i}(t)\right) \right] =\left\{ \begin{aligned}&d_{i}^{*},&\quad v_{i}(t)<0,\\&{\text {co}}\left\{ d_{i}^{*},d_{i}^{**}\right\} ,&\quad v_{i}(t)=0,\\&d_{i}^{**},&\quad v_{i}(t)>0, \end{aligned}\right. \\ \\ {\text {co}}\left[ a_{ij}\left( y_{j}(t)\right) \right]= & {} \left\{ \begin{aligned}&a_{ij}^{*},&\quad y_{j}(t)<0,\\&{\text {co}}\left\{ a_{ij}^{*},a_{ij}^{**}\right\} ,&\quad y_{j}(t)=0,\\&a_{ij}^{**},&\quad y_{j}(t)>0, \end{aligned}\right. \quad {\text {co}}\left[ a_{ij}\left( v_{j}(t)\right) \right] =\left\{ \begin{aligned}&a_{ij}^{*},&\quad v_{j}(t)<0,\\&{\text {co}}\left\{ a_{ij}^{*},a_{ij}^{**}\right\} ,&\quad v_{j}(t)=0,\\&a_{ij}^{**},&\quad v_{j}(t)>0, \end{aligned}\right. \\ {\text {co}}\left[ b_{ij}\left( y_{j}\left( t-\tau _{j}\right) \right) \right]= & {} \left\{ \begin{aligned}&b_{ij}^{*},&\quad y_{j}(t-\tau _{j})<0,\\&{\text {co}}\left\{ b_{ij}^{*},b_{ij}^{**}\right\} ,&\quad y_{j}\left( t-\tau _{j}\right) =0,\\&b_{ij}^{**},&\quad y_{j}(t-\tau _{j})>0, \end{aligned}\right. \\ {\text {co}}\left[ b_{ij}\left( v_{j}\left( t-\tau _{j}\right) \right) \right]= & {} \left\{ \begin{aligned}&b_{ij}^{*},&\quad v_{j}\left( t-\tau _{j}\right)<0,\\&{\text {co}}\left\{ b_{ij}^{*},b_{ij}^{**}\right\} ,&\quad v_{j}\left( t-\tau _{j}\right) =0,\\&b_{ij}^{**},&\quad v_{j}\left( t-\tau _{j}\right)>0, \end{aligned}\right. \\ {\text {co}}\left[ c_{ij}\left( y_{j}\left( t-\varsigma _{j}\right) \right) \right]= & {} \left\{ \begin{aligned}&c_{ij}^{*},&\quad y_{j}\left( t-\varsigma _{j}\right)<0,\\&{\text {co}}\left\{ c_{ij}^{*},c_{ij}^{**}\right\} ,&\quad y_{j}\left( t-\varsigma _{j}\right) =0,\\&c_{ij}^{**},&\quad y_{j}\left( t-\varsigma _{j}\right)>0, \end{aligned}\right. \\ {\text {co}}\left[ c_{ij}\left( v_{j}\left( t-\varsigma _{j}\right) \right) \right]= & {} \left\{ \begin{aligned}&c_{ij}^{*},&\quad v_{j}\left( t-\varsigma _{j}\right) <0,\\&{\text {co}}\left\{ c_{ij}^{*},c_{ij}^{**}\right\} ,&\quad v_{j}\left( t-\varsigma _{j}\right) =0,\\&c_{ij}^{**},&\quad v_{j}\left( t-\varsigma _{j}\right) >0. \end{aligned}\right. \end{aligned}$$

Then, we give the definition of the synchronization error \(w(t):w(t)=(w_{1}(t),w_{2}(t),\dots ,w_{n}(t))^{\mathrm{T}}\), where \(w_{i}(t)=v_{i}(t)-y_{i}(t)\). By using Definitions 1 and 2, from drive-response systems (4) and (5), we can obtain the following synchronization error system:

$$\begin{aligned}&{\dot{w}}_{i}(t)\in {\text {e}}^{t}\left\{ -\left[ {\text {co}}\left[ d_{i}\left( v_{i}(t)\right) \right] v_{i}(t)-{\text {co}}\left[ d_{i}\left( y_{i}(t)\right) \right] y_{i}(t)\right] +\sum \limits _{j=1}^{n}\left[ {\text {co}}\left[ a_{ij}\left( {v_{j}(t)}\right) \right] f_{j}\left( v_{j}(t)\right) \right. \right. \nonumber \\&\quad \left.\left. -{\text {co}}\left[ a_{ij}\left( {y_{j}(t)}\right) \right] f_{j}\left( y_{j}(t)\right) \right] +\sum \limits _{j=1}^{n}\left[ {\text {co}}\left[ b_{ij}\left( {v_{j}\left( t-\tau _{j}\right) }\right) \right] g_{j}\left( v_{j}\left( t-\tau _{j}\right) \right) \right. \right. \nonumber \\&\quad \left. \left. -{\text {co}}\left[ b_{ij}\left( {y_{j}\left( t-\tau _{j}\right) }\right) \right] g_{j}\left( y_{j}\left( t-\tau _{j}\right) \right) \right] +\sum \limits _{j=1}^{n}\left[ {\text {co}}\left[ c_{ij}\left( {v_{j}\left( t-\varsigma _{j}\right) }\right) \right] h_{j}\left( v_{j}\left( t-\varsigma _{j}\right) \right) \right. \right. \nonumber \\&\quad \left. \left. -{\text {co}}\left[ c_{ij}\left( {y_{j}\left( t-\varsigma _{j}\right) }\right) \right] h_{j}\left( y_{j}\left( t-\varsigma _{j}\right) \right) \right] +U_{i}(t)\right\} ,\quad t\ge 0. \end{aligned}$$
(9)

Definition 3

[14] A vector-value function \(y(t)=(y_{1}(t), y_{2}(t),\dots , y_{n}(t))^{\mathrm{T}}\) is a solution of drive system (4) with the initial condition \({\bar{\Phi }}=({\bar{\varphi }}_{1}(t), {\bar{\varphi }}_{2}(t), \dots , {\bar{\varphi }}_{n}(t))^{\mathrm{T}}\in C([-\eta ,0],{\mathbb {R}}^{n})\), if y(t) is an absolutely continuous function and satisfies Definition 2.

Lemma 1

[14] If condition (2) holds, then the solutiony(t) of drive system (4) with initial condition\({\bar{\Phi }}=({\bar{\varphi }}_{1}(t), {\bar{\varphi }}_{2}(t),\dots , {\bar{\varphi }}_{n}(t))^{\mathrm{T}}\in C([-\eta ,0],{\mathbb {R}}^{n})\)exists and it can be extended to the interval\([0,+\infty )\).

Lemma 2

[40] If condition (2) holds, then the following inequalities

  1. (i)
    $$\left\{ {\text {co}}[d_{i}(v_{i}(t))]v_{i}(t)-{\text {co}}[d_{i}(y_{i}(t))]y_{i}(t)\right\} {\text {sgn}}\left( w_{i}(t)\right) \ge D_{i}|w_{i}(t)|,$$
  2. (ii)
    $$\left| {\text {co}}[a_{ij}({v_{j}(t)})]f_{j}(v_{j}(t))-{\text {co}}[a_{ij}({y_{j}(t)})]f_{j}(y_{j}(t))\right| \le A_{ij}\sigma _{j}|w_{j}(t)|,$$
  3. (iii)
    $$\left| {\text {co}}[b_{ij}({v_{j}(t-\tau _{j})})]g_{j}(v_{j}(t-\tau _{j}))-{\text {co}}[b_{ij}({y_{j}(t-\tau _{j})})]g_{j}(y_{j}(t-\tau _{j}))\right| \le B_{ij}\gamma _{j}|w_{j}(t-\tau _{j})|,$$
  4. (iv)
    $$\left| {\text {co}}[c_{ij}({v_{j}(t-\varsigma _{j})})]h_{j}(v_{j}(t-\varsigma _{j}))-{\text {co}}[c_{ij}({y_{j}(t-\varsigma _{j})})]h_{j}(y_{j}(t-\varsigma _{j}))\right| \le C_{ij}\delta _{j}|w_{j}(t-\varsigma _{j})|$$

hold. Where\(\sigma _{j}=\max \{|\sigma _{j}^{-}|,|\sigma _{j}^{+}|\}, \gamma _{j}=\max \{|\gamma _{j}^{-}|,|\gamma _{j}^{+}|\}, \delta _{j}=\max \{|\delta _{j}^{-}|,|\delta _{j}^{+}|\}, i,j\in N\).

Definition 4

[40] For \(\forall \,t\ge 0\), drive-response systems (4) and (5) are said to be exponentially synchronized if there exist constants \(M>1\) and \(\kappa >0\) such that

$$\begin{aligned} \left[ \sum \limits _{i=1}^{n}|v_{i}(t)-y_{i}(t)|^{p}\right] ^{\frac{1}{p}}\le M{\text {e}}^{-\kappa t}\left\| {\bar{\Psi }}-{\bar{\Phi }}\right\| \end{aligned}$$

holds, in which \(\kappa \) is described as degree of exponential synchronization.

Notations Solutions of all the considered systems are intended in Filippov’s sense in the whole paper. \({\mathbb {R}}^{n}\) and \({\mathbb {R}}^{n\times m}\) denote the n-dimensional Euclidean space and the space of \(n\times m\) real matrices, respectively. \(C([q,1],{\mathbb {R}}^{n})\) and \(C([-\eta ,0],{\mathbb {R}}^{n})\) denote the set of all functions \(\varphi :[q,1] \rightarrow {\mathbb {R}}^{n}\) and \(\psi :[-\eta ,0] \rightarrow {\mathbb {R}}^{n}\) such that \(\varphi \) and \(\psi \) are continuously differential and bounded, respectively. Let \(K=(k_{ij})_{n\times n} \in {\mathbb {R}}^{n\times n}\) stands for real square matrix. For any \(h=(h_{1},h_{2},\dots ,h_{n})\in {\mathbb {R}}^{n}\), the norm is defined by \(\Vert h\Vert =(\sum \nolimits _{i=1}^{n}|h_{i}|^{p})^{\frac{1}{p}}\), where \(p\ge 1\) is a positive integer. We define \(\Vert {\bar{\Phi }}\Vert =\sup _{-\eta \le t\le 0}[\sum \nolimits _{i=1}^{n}|{\bar{\varphi }}_{i}(t)|^{p}]^{\frac{1}{p}}\), for \(\forall \,{\bar{\Phi }}=({\bar{\varphi }}_{1}(t),{\bar{\varphi }}_{2}(t),\dots ,{\bar{\varphi }}_{n}(t))^{\mathrm{T}}\in C([-\eta ,0],{\mathbb {R}}^{n})\). \({\text {co}}\{{\underline{\xi }}_{i},{\bar{\xi }}_{i}\}\) represents the convex hull of \(\{{\underline{\xi }}_{i},{\bar{\xi }}_{i}\}\). For a continuous function \(p(t): {\mathbb {R}}\rightarrow {\mathbb {R}}, D^{+}p(t)\) is called to be the upper right dini derivative and defined as \(D^{+}p(t)=\lim _{h\rightarrow 0^{+}}\frac{1}{h}(p(t+h)-p(t))\). Let \(D_{i}={\mathrm {min}}\{d_{i}^{*},d_{i}^{**}\}, A_{ij}={\mathrm {max}}\{|a_{ij}^{*}|,|a_{ij}^{**}|\}, B_{ij}={\mathrm {max}}\{|b_{ij}^{*}|, |b_{ij}^{**}|\}, C_{ij}={\mathrm {max}}\{|c_{ij}^{*}|,|c_{ij}^{**}|\}\).

3 Main results

Theorem 1

Under condition (2), if there exist constants\(\alpha _{i}>0\)and\(p>1,\)such that

$$\begin{aligned}&-p\left( D_{i}-\rho _{i}\right) +\sum \limits _{j=1}^{n}\left[ (p-1)\left( A_{ij}+B_{ij}+C_{ij}\right) +\frac{\alpha _{j}}{\alpha _{i}}A_{ji}\sigma _{i}^{p}\right. \nonumber \\&\quad \left. +\frac{\alpha _{j}}{\alpha _{i}}B_{ji}\gamma _{i}^{p}+\frac{\alpha _{j}}{\alpha _{i}}C_{ji}\delta _{i}^{p}\right] <0 \end{aligned}$$
(10)

holds for\(i,j=1,2,\dots ,n,\)then drive-response systems (4) and (5) are exponentially synchronized with control input (6).

Proof

For \(i,j=1,2,\dots ,n\), we can choose a small \(\varepsilon >\frac{1}{p}\) such that

$$\begin{aligned}&p\left( \varepsilon -D_{i}+\rho _{i}\right) +\sum \limits _{j=1}^{n}\left[ (p-1)\left( A_{ij}+B_{ij}+C_{ij}\right) +\frac{\alpha _{j}}{\alpha _{i}}A_{ji}\sigma _{i}^{p}\right. \nonumber \\&\quad \left. +\frac{\alpha _{j}}{\alpha _{i}}{\text {e}}^{p\varepsilon \tau }B_{ji}\gamma _{i}^{p}+\frac{\alpha _{j}}{\alpha _{i}}{\text {e}}^{p\varepsilon \varsigma }C_{ji}\delta _{i}^{p}\right] <0. \end{aligned}$$
(11)

Consider the following Lyapunov functional

$$\begin{aligned} V(t)= & {} \sum \limits _{i=1}^{n}\alpha _{i}\left[ {\text {e}}^{-t}\left| w_{i}(t)\right| ^{p}{\text {e}}^{p\varepsilon t}+{\text {e}}^{p\varepsilon \tau }\gamma _{j}^{p}\sum \limits _{j=1}^{n}B_{ij} \int \limits _{t-\tau _{j}}^{t}\left| w_{j}(s)\right| ^{p}{\text {e}}^{p\varepsilon s}{\text {d}}s\right. \nonumber \\&\left. +{\text {e}}^{p\varepsilon \varsigma }\delta _{j}^{p}\sum \limits _{j=1}^{n}C_{ij}\int \limits _{t-\varsigma _{j}}^{t}\left| w_{j}(s)\right| ^{p}{\text {e}}^{p\varepsilon s}{\text {d}}s\right] . \end{aligned}$$
(12)

Under condition (2), by calculating the upper right derivation \(D^{+}V(t)\) of V(t) along system (9), we obtain

$$\begin{aligned}&D^{+}V(t)\nonumber \\&\quad =\sum \limits _{i=1}^{n}\alpha _{i}\left[ -{\text {e}}^{-t}\left| w_{i}(t)\right| ^{p}{\text {e}}^{p\varepsilon t} +p\varepsilon {\text {e}}^{-t}\left| w_{i}(t)\right| ^{p}{\text {e}}^{p\varepsilon t}+p{\text {e}}^{-t}\left| w_{i}(t)\right| ^{p-1}{\text {e}}^{p\varepsilon t}{\dot{w}}_{i}(t)\right. \nonumber \\&\qquad \cdot {\text {sgn}}\left( w_{i}(t)\right) +{\text {e}}^{p\varepsilon \tau }\gamma _{j}^{p} \sum \limits _{j=1}^{n}B_{ij}\left| w_{j}(t)\right| ^{p}{\text {e}}^{p\varepsilon t}-{\text {e}}^{p\varepsilon \tau }\gamma _{j}^{p}\sum \limits _{j=1}^{n}B_{ij}\left| w_{j}\left( t-\tau _{j}\right) \right| ^{p}{\text {e}}^{p\varepsilon \left( t-\tau _{j}\right) }\nonumber \\&\qquad \left. +{\text {e}}^{p\varepsilon \varsigma }\delta _{j}^{p}\sum \limits _{j=1}^{n}C_{ij}\left| w_{j}(t)\right| ^{p}{\text {e}}^{p\varepsilon t}-{\text {e}}^{p\varepsilon \varsigma }\delta _{j}^{p}\sum \limits _{j=1}^{n}C_{ij}\left| w_{j}\left( t-\varsigma _{j}\right) \right| ^{p}{\text {e}}^{p\varepsilon \left( t-\varsigma _{j}\right) }\right] \nonumber \\&\quad \le {\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}p\alpha _{i}\left[ \varepsilon \left| w_{i}(t)\right| ^{p}+\left| w_{i}(t)\right| ^{p-1}{\text {e}}^{-t} {\dot{w}}_{i}(t){\text {sgn}}\left( w_{i}(t)\right) \right] \nonumber \\&\qquad +{\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}{\text {e}}^{p\varepsilon \tau }\alpha _{i} \gamma _{j}^{p}B_{ij}\left[ \left| w_{j}(t)\right| ^{p}-{\text {e}}^{-p\varepsilon \tau _{j}}\left| w_{j}\left( t-\tau _{j}\right) \right| ^{p}\right] \nonumber \\&\qquad +{\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}{\text {e}}^{p\varepsilon \varsigma } \alpha _{i}\delta _{j}^{p}C_{ij}\left[ \left| w_{j}(t)\right| ^{p}-{\text {e}}^{-p\varepsilon \varsigma _{j}}\left| w_{j}\left( t-\varsigma _{j}\right) \right| ^{p}\right] \nonumber \\&\qquad \in {\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}p\alpha _{i}\left[ \varepsilon \left| w_{i}(t)\right| ^{p}+ \left| w_{i}(t)\right| ^{p-1}{\text {sgn}}\left( w_{i}(t)\right) \left\{ -\left[ {\mathrm {co}}\left[ d_{i}\left( v_{i}(t)\right) \right] v_{i}(t)\right. \right. \right. \nonumber \\&\qquad \left. -{\mathrm {co}}\left[ d_{i}\left( y_{i}(t)\right) \right] y_{i}(t)\right] +\sum \limits _{j=1}^{n}\left[ {\mathrm {co}}\left[ a_{ij}\left( v_{j}(t)\right) \right] f_{j}\left( v_{j}(t)\right) -{\mathrm {co}}\left[ a_{ij}\left( y_{j}(t)\right) \right] f_{j}\left( y_{j}(t)\right) \right] \nonumber \\&\qquad +\sum \limits _{j=1}^{n}\left[ {\mathrm {co}}\left[ b_{ij}\left( v_{j}\left( t-\tau _{j}\right) \right) \right] g_{j}\left( v_{j}\left( t-\tau _{j}\right) \right) -{\mathrm {co}}\left[ b_{ij}\left( y_{j}\left( t-\tau _{j}\right) \right) \right] g_{j}\left( y_{j}\left( t-\tau _{j}\right) \right) \right] \nonumber \\&\qquad + \sum \limits _{j=1}^{n}\left[ {\mathrm {co}}\left[ c_{ij}\left( v_{j}\left( t-\varsigma _{j}\right) \right) \right] h_{j}\left( v_{j}\left( t-\varsigma _{j}\right) \right) -{\mathrm {co}}\left[ c_{ij}\left( y_{j}\left( t-\varsigma _{j}\right) \right) \right] h_{j}\left( y_{j}\left( t-\varsigma _{j}\right) \right) \right] \nonumber \\&\qquad \left. \left. +U_{i}(t)\right\} \right] \nonumber \\&\qquad +{\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}{\text {e}}^{p\varepsilon \tau }\alpha _{i}\gamma _{j}^{p}B_{ij} \left[ \left| w_{j}(t)\right| ^{p}-{\text {e}}^{-p\varepsilon \tau _{j}}\left| w_{j}\left( t-\tau _{j}\right) \right| ^{p}\right] \nonumber \\&\qquad +{\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}{\text {e}}^{p\varepsilon \varsigma }\alpha _{i}\delta _{j}^{p}C_{ij}\left[ \left| w_{j}(t)\right| ^{p}-{\text {e}}^{-p\varepsilon \varsigma _{j}}\left| w_{j}\left( t-\varsigma _{j}\right) \right| ^{p}\right] . \end{aligned}$$
(13)

It follows from Lemma 2 and (13) that

$$\begin{aligned}&D^{+}V(t)\nonumber \\&\quad \le {\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}p\alpha _{i}\left| w_{i}(t)\right| ^{p-1}\left\{ \left( \varepsilon -D_{i}+\rho _{i}\right) \left| w_{i}(t)\right| +\sum \limits _{j=1}^{n}A_{ij}\sigma _{j}\left| w_{j}(t)\right| \right. \nonumber \\&\qquad \left. +\sum \limits _{j=1}^{n}B_{ij}\gamma _{j}\left| w_{j}\left( t-\tau _{j}\right) \right| +\sum \limits _{j=1}^{n}C_{ij}\delta _{j}\left| w_{j}\left( t-\varsigma _{j}\right) \right| \right\} \nonumber \\&\qquad +{\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}\alpha _{i}B_{ij} \left[ {\text {e}}^{p\varepsilon \tau }\gamma _{j}^{p}\left| w_{j}(t)\right| ^{p}-\gamma _{j}^{p}\left| w_{j}\left( t-\tau _{j}\right) \right| ^{p}\right] \nonumber \\&\qquad +{\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}\alpha _{i}C_{ij} \left[ {\text {e}}^{p\varepsilon \varsigma }\delta _{j}^{p}\left| w_{j}(t)\right| ^{p}-\delta _{j}^{p}\left| w_{j}\left( t-\varsigma _{j}\right) \right| ^{p}\right] \nonumber \\&\quad ={\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}\left\{ p\alpha _{i}\left( \varepsilon -D_{i}+\rho _{i}\right) \left| w_{i}(t)\right| ^{p} +\sum \limits _{j=1}^{n}A_{ij}p\alpha _{i}\sigma _{j}\left| w_{j}(t)\right| \left| w_{i}(t)\right| ^{p-1} \right. \nonumber \\&\qquad \left. +\sum \limits _{j=1}^{n}B_{ij}p\alpha _{i}\gamma _{j}\left| w_{j}\left( t-\tau _{j}\right) \right| \left| w_{i}(t)\right| ^{p-1} +\sum \limits _{j=1}^{n}C_{ij}p\alpha _{i}\delta _{j}\left| w_{j}\left( t-\varsigma _{j}\right) \right| \left| w_{i}(t)\right| ^{p-1}\right\} \nonumber \\&\qquad +{\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}\alpha _{i}B_{ij} \left[ {\text {e}}^{p\varepsilon \tau }\gamma _{j}^{p}\left| w_{j}(t)\right| ^{p}-\gamma _{j}^{p}\left| w_{j}\left( t-\tau _{j}\right) \right| ^{p}\right] \nonumber \\&\qquad +{\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}\alpha _{i}C_{ij} \left[ {\text {e}}^{p\varepsilon \varsigma }\delta _{j}^{p}\left| w_{j}(t)\right| ^{p}-\delta _{j}^{p}\left| w_{j}\left( t-\varsigma _{j}\right) \right| ^{p}\right] , \end{aligned}$$
(14)

by using Young inequality \(ab\le \frac{1}{\beta _{1}}a^{\beta _{1}}+\frac{1}{\beta _{2}}b^{\beta _{2}}\), where \(a, b>0, \beta _{1}>1, \frac{1}{\beta _{1}}+\frac{1}{\beta _{2}}=1\), we get

$$\begin{aligned} \sigma _{j}\left| w_{j}(t)\right| \left| w_{i}(t)\right| ^{p-1}\le & {} \frac{\sigma _{j}^{p}}{p}\left| w_{j}(t)\right| ^{p}+\frac{p-1}{p}\left| w_{i}(t)\right| ^{p},\\ \gamma _{j}\left| w_{j}\left( t-\tau _{j}\right) \right| \left| w_{i}(t)\right| ^{p-1}\le & {} \frac{\gamma _{j}^{p}}{p}\left| w_{j}\left( t-\tau _{j}\right) \right| ^{p}+\frac{p-1}{p}\left| w_{i}(t)\right| ^{p},\\ \delta _{j}\left| w_{j}\left( t-\varsigma _{j}\right) \right| \left| w_{i}(t)\right| ^{p-1}\le & {} \frac{\delta _{j}^{p}}{p}\left| w_{j}\left( t-\varsigma _{j}\right) \right| ^{p}+\frac{p-1}{p}\left| w_{i}(t)\right| ^{p}, \end{aligned}$$

which together with (11), we obtain

$$\begin{aligned}&D^{+}V(t)\nonumber \\&\quad \le {\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}p\alpha _{i}\left\{ \left( \varepsilon -D_{i}+\rho _{i}\right) \left| w_{i}(t)\right| ^{p} +\sum \limits _{j=1}^{n}A_{ij}\left[ \frac{\sigma _{j}^{p}}{p}\left| w_{j}(t)\right| ^{p}+\frac{p-1}{p}\left| w_{i}(t)\right| ^{p}\right] \right. \nonumber \\&\qquad +\sum \limits _{j=1}^{n}B_{ij}\left[ \frac{\gamma _{j}^{p}}{p}\left| w_{j}\left( t-\tau _{j}\right) \right| ^{p}+\frac{p-1}{p}\left| w_{i}(t)\right| ^{p}\right] \nonumber \\&\qquad \left. +\sum \limits _{j=1}^{n}C_{ij}\left[ \frac{\delta _{j}^{p}}{p}\left| w_{j}\left( t-\varsigma _{j}\right) \right| ^{p}+\frac{p-1}{p}\left| w_{i}(t)\right| ^{p}\right] \right\} \nonumber \\&\qquad +{\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}\alpha _{i}B_{ij}\left[ {\text {e}}^{p\varepsilon \tau } \gamma _{j}^{p}\left| w_{j}(t)\right| ^{p}-\gamma _{j}^{p}\left| w_{j}\left( t-\tau _{j}\right) \right| ^{p}\right] \nonumber \\&\qquad +{\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}\alpha _{i}C_{ij}\left[ {\text {e}}^{p\varepsilon \varsigma } \delta _{j}^{p}\left| w_{j}(t)\right| ^{p}-\delta _{j}^{p}\left| w_{j}\left( t-\varsigma _{j}\right) \right| ^{p}\right] \nonumber \\&\quad ={\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}\alpha _{i}\left\{ p\left( \varepsilon -D_{i}+\rho _{i}\right) \left| w_{i}(t)\right| ^{p} +\sum \limits _{j=1}^{n}A_{ij}\left[ \sigma _{j}^{p}\left| w_{j}(t)\right| ^{p}+(p-1)\left| w_{i}(t)\right| ^{p}\right] \right. \nonumber \\&\qquad +\sum \limits _{j=1}^{n}B_{ij}\left[ \gamma _{j}^{p}\left| w_{j}\left( t-\tau _{j}\right) \right| ^{p} +(p-1)\left| w_{i}(t)\right| ^{p}\right] \nonumber \\&\qquad \left. +\sum \limits _{j=1}^{n}C_{ij}\left[ \delta _{j}^{p}\left| w_{j}\left( t-\varsigma _{j}\right) \right| ^{p} +(p-1)\left| w_{i}(t)\right| ^{p}\right] \right\} \nonumber \\&\qquad +{\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}\alpha _{i}B_{ij}\left[ {\text {e}}^{p\varepsilon \tau } \gamma _{j}^{p}\left| w_{j}(t)\right| ^{p}-\gamma _{j}^{p}\left| w_{j}\left( t-\tau _{j}\right) \right| ^{p}\right] \nonumber \\&\qquad +{\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}\alpha _{i}C_{ij}\left[ {\text {e}}^{p\varepsilon \varsigma } \delta _{j}^{p}\left| w_{j}(t)\right| ^{p}-\delta _{j}^{p}\left| w_{j}\left( t-\varsigma _{j}\right) \right| ^{p}\right] \nonumber \\&\quad ={\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}\alpha _{i}\left\{ p\left( \varepsilon -D_{i}+\rho _{i}\right) \left| w_{i}(t)\right| ^{p} +\sum \limits _{j=1}^{n}A_{ij}\left[ \sigma _{j}^{p}\left| w_{j}(t)\right| ^{p}+(p-1)\left| w_{i}(t)\right| ^{p}\right] \right. \nonumber \\&\qquad \left. +\sum \limits _{j=1}^{n}B_{ij}(p-1)\left| w_{i}(t)\right| ^{p}+\sum \limits _{j=1}^{n}C_{ij}(p-1)\left| w_{i}(t)\right| ^{p}\right\} \nonumber \\&\qquad +{\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}\alpha _{i}B_{ij}{\text {e}}^{p\varepsilon \tau } \gamma _{j}^{p}\left| w_{j}(t)\right| ^{p}+{\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{n}\alpha _{i}C_{ij}{\text {e}}^{p\varepsilon \varsigma } \delta _{j}^{p}\left| w_{j}(t)\right| ^{p}\nonumber \\&\quad ={\text {e}}^{p\varepsilon t}\sum \limits _{i=1}^{n}\alpha _{i}\left| w_{i}(t)\right| ^{p}\left\{ p\left( \varepsilon -D_{i}+\rho _{i}\right) +\sum \limits _{j=1}^{n}\left[ (p-1)\left( A_{ij}+B_{ij}+C_{ij}\right) \right. \right. \nonumber \\&\qquad \left. \left. +\frac{\alpha _{j}}{\alpha _{i}}A_{ji}\sigma _{i}^{p}+\frac{\alpha _{j}}{\alpha _{i}}{\text {e}}^{p\varepsilon \tau }B_{ji}\gamma _{i}^{p} +\frac{\alpha _{j}}{\alpha _{i}}{\text {e}}^{p\varepsilon \varsigma }C_{ji}\delta _{i}^{p}\right] \right\} <0, \end{aligned}$$
(15)

thus, \(V(t)\le V(0)\). Since

$$\begin{aligned} V(0)= & {} \sum \limits _{i=1}^{n}\alpha _{i}\left[ \left| {\bar{\psi }}_{i}(0)-{\bar{\varphi }}_{i}(0)\right| ^{p}+{\text {e}}^{p\varepsilon \tau }\gamma _{j}^{p} \sum \limits _{j=1}^{n}B_{ij}\int \limits _{-\tau _{j}}^{0}\left| w_{j}(s)\right| ^{p}{\text {e}}^{p\varepsilon s}{\text {d}}s \right. \nonumber \\&\left. +{\text {e}}^{p\varepsilon \varsigma }\delta _{j}^{p}\sum \limits _{j=1}^{n}C_{ij} \int \limits _{-\varsigma _{j}}^{0}\left| w_{j}(s)\right| ^{p}{\text {e}}^{p\varepsilon s}{\text {d}}s\right] \nonumber \\\le & {} \left[ \max \limits _{1\le i\le n}\{\alpha _{i}\}+\gamma ^{p}\tau {\text {e}}^{p\varepsilon \tau }\sum \limits _{i=1}^{n} \alpha _{i}\max \limits _{1\le j\le n}\{B_{ij}\}\right. \nonumber \\&\left. +\delta ^{p}\varsigma {\text {e}}^{p\varepsilon \varsigma }\sum \limits _{i=1}^{n}\alpha _{i}\max \limits _{1\le j\le n}\{C_{ij}\}\right] \sup \limits _{-\eta \le t\le 0}\sum \limits _{i=1}^{n}\left| {\bar{\psi }}_{i}(t)-{\bar{\varphi }}_{i}(t)\right| ^{p}, \end{aligned}$$
(16)

where \(\gamma =\max \nolimits _{1\le i\le n}\{\gamma _{i}\}, \delta =\max \nolimits _{1\le i\le n}\{\delta _{i}\}\). And from (12), for \(t\ge 0\), we have

$$\begin{aligned}&V(t)\ge \sum \limits _{i=1}^{n}\alpha _{i}{\text {e}}^{-t}\left| w_{i}(t)\right| ^{p}{\text {e}}^{p\varepsilon t} \ge \min \limits _{1\le i\le n}\{\alpha _{i}\}{\text {e}}^{(p\varepsilon -1)t}\sum \limits _{i=1}^{n}\left| w_{i}(t)\right| ^{p}. \end{aligned}$$
(17)

It follows from (15)–(17) that

$$\begin{aligned} \left[ \sum \limits _{i=1}^{n}\left| v_{i}\left( t,{\bar{\psi }}\right) -y_{i}\left( t,{\bar{\varphi }}\right) \right| ^{p}\right] ^{\frac{1}{p}}\le M{\text {e}}^{-\kappa t}\sup \limits _{-\eta \le t\le 0} \left[ \sum \limits _{i=1}^{n}\left| {\bar{\psi }}_{i}(t)-{\bar{\varphi }}_{i}(t)\right| ^{p}\right] ^{\frac{1}{p}}, \end{aligned}$$

where \(\kappa =\frac{p\varepsilon -1}{p},\)

$$\begin{aligned}&M=\left[ \frac{\max \nolimits _{1\le i\le n}\{\alpha _{i}\}+\gamma ^{p}\tau {\text {e}}^{p\varepsilon \tau }\sum \nolimits _{i=1}^{n}\alpha _{i}\max \nolimits _{1\le j\le n}\{B_{ij}\}+\delta ^{p}\varsigma {\text {e}}^{p\varepsilon \varsigma }\sum \nolimits _{i=1}^{n}\alpha _{i}\max \nolimits _{1\le j\le n}\{C_{ij}\}}{\min \nolimits _{1\le i\le n}\{\alpha _{i}\}}\right] ^{\frac{1}{p}}\ge 1, \end{aligned}$$

this is to say,

$$\begin{aligned} \left[ \sum \limits _{i=1}^{n}\left| v_{i}(t)-y_{i}(t)\right| ^{p}\right] ^{\frac{1}{p}}\le M{\text {e}}^{-\kappa t}\left\| {\bar{\Psi }}-{\bar{\Phi }}\right\| . \end{aligned}$$

From Definition 4, we derive that drive-response systems (4) and (5) are exponentially synchronized with control input (6). The proof of Theorem 1 is completed. \(\square \)

Now, basing on 2-norm, we present the following Corollary.

Corollary 1

Under condition (2), if there exists constant\(\alpha _{i}>0\), such that

$$\begin{aligned} -2(D_{i}-\rho _{i})+\sum \limits _{j=1}^{n}\left[ A_{ij}+B_{ij}+C_{ij}+\frac{\alpha _{j}}{\alpha _{i}}A_{ji}\sigma _{i}^{2} +\frac{\alpha _{j}}{\alpha _{i}}B_{ji}\gamma _{i}^{2}+\frac{\alpha _{j}}{\alpha _{i}}C_{ji}\delta _{i}^{2}\right] <0 \end{aligned}$$
(18)

holds, then drive-response systems (4) and (5) are exponentially synchronized with control input (6), where\(i,j=1,2,\dots ,n.\)

Remark 2

Drive-response systems (4) and (5) are distinct from the drive-response systems in [40]. The coefficients in [40] are bounding time-varying, while the coefficients in this paper are unbound time-varying as a result of containing \({\text {e}}^{t}\), so the exponential synchronization results in [40] cannot be straightly applied to drive-response systems (4) and (5).

Remark 3

If \(p_{j}=q_{j}=1\), drive-response systems (1) and (3) become the following drive-response systems

$$\begin{aligned} {\dot{x}}_{i}(t)=-d_{i}\left( {x_{i}(t)}\right) x_{i}(t)+\sum \limits _{j=1}^{n}l_{ij}\left( {x_{j}(t)}\right) f_{j}\left( x_{j}(t)\right) +I_{i}, \end{aligned}$$

and

$$\begin{aligned} {\dot{z}}_{i}(t)=-d_{i}\left( {z_{i}(t)}\right) z_{i}(t)+\sum \limits _{j=1}^{n}l_{ij}\left( {z_{j}(t)}\right) f_{j}\left( z_{j}(t)\right) +I_{i}+u_{i}(t), \end{aligned}$$

where \(t\ge 1, l_{ij}({x_{j}(t)})=a_{ij}({x_{j}(t)})+b_{ij}({x_{j}(t)})+c_{ij}({x_{j}(t)}), l_{ij}({z_{j}(t)})=a_{ij}({z_{j}(t)})+b_{ij}({z_{j}(t)})+ c_{ij}({z_{j}(t)}), f_{j}(x_{j}(t))=g_{j}(x_{j}(t))=h_{j}(x_{j}(t)), i,j=1,2,\dots ,n\).

Above drive-response systems are MRNNs without delays, the result in this paper is equally true of above drive-response systems.

4 Numerical example

In this section, we will present two numerical examples and their simulations to clarify that the obtained conclusion is correct.

Example 1

Consider two-dimensional MRNNs with multi-proportional delays:

$$\begin{aligned} {\dot{x}}_{i}(t)= & {} -d_{i}\left( {x_{i}(t)}\right) x_{i}(t)+\sum \limits _{j=1}^{2}a_{ij}\left( {x_{j}(t)}\right) f_{j}\left( x_{j}(t)\right) +\sum \limits _{j=1}^{2}b_{ij}\left( {x_{j}\left( p_{j}t\right) }\right) g_{j}\left( x_{j}\left( p_{j}t\right) \right) \nonumber \\&+\sum \limits _{j=1}^{2}c_{ij}\left( {x_{j}\left( q_{j}t\right) }\right) h_{j}\left( x_{j}\left( q_{j}t\right) \right) +I_{i}, \quad i=1,2, \end{aligned}$$
(19)

where

$$\begin{aligned} d_{1}({x_{1}(t)})= & {} \left\{ \begin{array}{ll} 1,&{}\quad x_{1}(t) \le 0,\\ 1.5,&{}\quad x_{1}(t)> 0, \end{array}\right. \quad d_{2}\left( {x_{2}(t)}\right) =\left\{ \begin{array}{ll} 1.6,&{} \quad x_{2}(t) \le 0,\\ 1,&{}\quad x_{2}(t)> 0, \end{array}\right. \\ a_{11}\left( {x_{1}(t)}\right)= & {} \left\{ \begin{array}{ll} -\,1.5,&{}\quad x_{1}(t) \le 0,\\ -\,1,&{}\quad x_{1}(t)> 0, \end{array}\right. \quad a_{12}\left( {x_{2}(t)}\right) =\left\{ \begin{array}{ll} 20,&{} \quad x_{2}(t) \le 0,\\ 25,&{}\quad x_{2}(t)> 0, \end{array}\right. \\ b_{11}\left( {x_{1}\left( p_{1}t\right) }\right)= & {} \left\{ \begin{array}{ll} -\,1,&{}\quad x_{1}\left( p_{1}t\right) \le 0\\ -\,0.8,&{}\quad x_{1}\left( p_{1}t\right)> 0, \end{array}\right. \quad b_{12}\left( {x_{2}\left( p_{2}t\right) }\right) =\left\{ \begin{array}{ll} -0.03,&{} \quad x_{2}\left( p_{2}t\right) \le 0,\\ -0.05, &{}\quad x_{2}\left( p_{2}t\right)> 0, \end{array}\right. \\ c_{11}\left( {x_{1}\left( q_{1}t\right) }\right)= & {} \left\{ \begin{array}{ll} -\,1.36,&{} \quad x_{1}\left( q_{1}t\right) \le 0,\\ -\,1.5,&{}\quad x_{1}\left( q_{1}t\right)> 0, \end{array}\right. \quad c_{12}\left( {x_{2}\left( q_{2}t\right) }\right) =\left\{ \begin{array}{ll} -\,0.03,&{} \quad x_{2}\left( q_{2}t\right) \le 0,\\ -\,0.05,&{} \quad x_{2}\left( q_{2}t\right)> 0, \end{array}\right. \\ a_{21}({x_{1}(t)})= & {} \left\{ \begin{array}{ll} -\,2,&{}\quad x_{1}(t) \le 0,\\ -\,1.8,&{} \quad x_{1}(t)> 0, \end{array}\right. \quad a_{22}\left( {x_{2}(t)}\right) =\left\{ \begin{array}{ll} 2.7,&{} \quad x_{2}(t) \le 0,\\ 2.5, &{}\quad x_{2}(t)> 0, \end{array}\right. \\ b_{21}\left( {x_{1}\left( p_{1}t\right) }\right)= & {} \left\{ \begin{array}{ll} -\,0.5, &{}\quad x_{1}\left( p_{1}t\right) \le 0,\\ -\,0.1, &{}\quad x_{1}\left( p_{1}t\right)> 0, \end{array}\right. \quad b_{22}\left( {x_{2}\left( p_{2}t\right) }\right) =\left\{ \begin{array}{ll} -\,0.7,&{} \quad x_{2}\left( p_{2}t\right) \le 0,\\ -\,1,&{}\quad x_{2}\left( p_{2}t\right)> 0, \end{array}\right. \\ c_{21}\left( {x_{1}\left( q_{1}t\right) }\right)= & {} \left\{ \begin{array}{ll} -\,0.6,&{} \quad x_{1}\left( q_{1}t\right) \le 0,\\ -\,0.1, &{}\quad x_{1}\left( q_{1}t\right)> 0, \end{array}\right. \quad c_{22}\left( {x_{2}\left( q_{2}t\right) }\right) =\left\{ \begin{array}{ll} -\,1.1,&{} \quad x_{2}\left( q_{2}t\right) \le 0,\\ -\,0.6,&{}\quad x_{2}\left( q_{2}t\right) > 0, \end{array}\right. \end{aligned}$$

and \(I=(0,0)^{\mathrm{T}}, f_{i}(x_{i})=\tanh (x_{i}), g_{i}(x_{i})=\frac{1}{2}\tanh (x_{i}), h_{i}(x_{i})=\frac{1}{4}(|x_{i}+1|-|x_{i}-1|), i=1,2\). The drive system (19) satisfies condition (2) and \(\sigma _{i}=1, \gamma _{i}=\frac{1}{2}, \delta _{i}=\frac{1}{2}, i=1,2\). For the sake of achieving exponential synchronization, the responding response system is devised as

$$\begin{aligned} {\dot{z}}_{i}(t)= & {} -d_{i}\left( {z_{i}(t)}\right) z_{i}(t)+\sum \limits _{j=1}^{2}a_{ij}\left( {z_{j}(t)}\right) f_{j}\left( z_{j}(t)\right) +\sum \limits _{j=1}^{2}b_{ij}\left( {z_{j}\left( p_{j}t\right) }\right) g_{j}\left( z_{j}\left( p_{j}t\right) \right) \nonumber \\&+\sum \limits _{j=1}^{2}c_{ij}\left( {z_{j}\left( q_{j}t\right) }\right) h_{j}\left( z_{j}\left( q_{j}t\right) \right) +I_{i}+u_{i}(t), i=1,2. \end{aligned}$$
(20)

The control inputs are defined as \(u_{i}(t)=\rho _{i}e_{i}(t)\), in which \(e_{i}(t)=z_{i}(t)-x_{i}(t), i=1,2\), representing the synchronization error, here we take \(\rho _{1}=-16.9, \rho _{2}=-10.9\). Through calculating, we get

Fig. 1
figure 1

The phase plots of drive-response systems (19) and (20)

Full size image
$$\begin{aligned} D=\begin{pmatrix}1&{}\quad 0\\ 0&{}\quad 1 \end{pmatrix}, A=\begin{pmatrix}1.5&{}\quad 25\\ 2&{}\quad 2.7 \end{pmatrix}, B=\begin{pmatrix}1&{}\quad 0.05\\ 0.5&{}\quad 1 \end{pmatrix}, C=\begin{pmatrix}1.5&{}\quad 0.05\\ 0.6&{}\quad 1.1 \end{pmatrix}. \end{aligned}$$
Fig. 2
figure 2

The time response curve of synchronization error \(e_{i}(t)\)

Full size image

Furthermore, let \(\alpha _{1}=1, \alpha _{2}=2\), we obtain

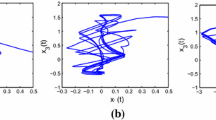
$$\begin{aligned}&-35.8+2A_{11}+A_{12}+2A_{21}+\frac{5B_{11}}{4}+B_{12}+\frac{B_{21}}{2}+\frac{5C_{11}}{4}\\&\quad +C_{12}+\frac{C_{21}}{2}=-0.0250<0, i=1\\&-23.8+\frac{A_{12}}{2}+A_{21}+2A_{22}+\frac{B_{12}}{8}+B_{21}+\frac{5B_{22}}{4}+\frac{C_{12}}{8}\\&\quad +C_{21}+\frac{5C_{22}}{4}=-0.1625<0, \quad i=2. \end{aligned}$$

The condition of Theorem 1 and Corollary 1 is satisfied. Thus, drive-response systems (19) and (20) are exponentially synchronized, their simulations are shown in Figs. 1 and 2. Figure 1a depicts the chaotic behavior of drive system (19) in phase space with initial value \(x(t)=[-\,20,0.5]^{\mathrm{T}}\). Without control input, Fig. 1b shows the chaotic behavior of response system (20) in phase space with initial value \(z(t)=[20,2.5]^{\mathrm{T}}\). Figure 1c displays the chaotic behavior of response system (20) in phase space with initial value \(z(t)=[20,2.5]^{\mathrm{T}}\). Figure 2 describes the time response curve of synchronization error \(e_{i}(t)\) between drive-response systems (19) and (20) with initial conditions \(x(t)=[-\,20,0.5]^{\mathrm{T}}\) and \(z(t)=[20,2.5]^{\mathrm{T}}\), respectively.

Example 2

Consider three-dimensional MRNNs with multi-proportional delays:

$$\begin{aligned} {\dot{x}}_{i}(t)= & {} -d_{i}\left( {x_{i}(t)}\right) x_{i}(t)+\sum \limits _{j=1}^{3}a_{ij}\left( {x_{j}(t)}\right) f_{j}\left( x_{j}(t)\right) +\sum \limits _{j=1}^{3}b_{ij}\left( {x_{j}\left( p_{j}t\right) }\right) g_{j}\left( x_{j}\left( p_{j}t\right) \right) \nonumber \\&+\sum \limits _{j=1}^{3}c_{ij}\left( {x_{j}\left( q_{j}t\right) }\right) h_{j}\left( x_{j}\left( q_{j}t\right) \right) +I_{i},\quad i=1,2,3, \end{aligned}$$
(21)

where

$$\begin{aligned} d_{1}\left( {x_{1}(t)}\right)= & {} \left\{ \begin{array}{ll} 1,&{}\quad x_{1}(t) \le 0,\\ 1.5,&{} \quad x_{1}(t)> 0, \end{array}\right. \quad d_{2}\left( {x_{2}(t)}\right) =\left\{ \begin{array}{ll} 3.5,&{}\quad x_{2}(t) \le 0,\\ 3,&{}\quad x_{2}(t)> 0, \end{array}\right. \\ d_{3}\left( {x_{3}(t)}\right)= & {} \left\{ \begin{array}{ll} 0.5, &{}\quad x_{3}(t) \le 0,\\ 0.7, &{}\quad x_{3}(t)> 0, \end{array}\right. \quad a_{12}\left( {x_{2}(t)}\right) =\left\{ \begin{array}{ll} -\,2.2,&{} \quad x_{2}(t) \le 0, \\ -\,2,&{}\quad x_{2}(t)> 0, \end{array}\right. \\ a_{13}\left( {x_{3}(t)}\right)= & {} \left\{ \begin{array}{ll} -\,24,&{}\quad x_{3}(t) \le 0\\ -\,21.5,&{}\quad x_{3}(t)> 0, \end{array}\right. \quad a_{22}\left( {x_{2}(t)}\right) =\left\{ \begin{array}{ll} -\,1.5,&{} \quad x_{2}(t) \le 0,\\ -\,0.5, &{}\quad x_{2}(t)> 0, \end{array}\right. \\ a_{32}\left( {x_{2}(t)}\right)= & {} \left\{ \begin{array}{ll} -\,7,&{}\quad x_{2}(t) \le 0,\\ -\,5.5,&{} \quad x_{2}(t)> 0, \end{array}\right. \quad a_{33}\left( {x_{3}(t)}\right) =\left\{ \begin{array}{ll} -\,0.8,&{} \quad x_{3}(t) \le 0, \\ -\,0.5,&{}\quad x_{3}(t)> 0, \end{array}\right. \\ a_{11}\left( x_{1}(t)\right)= & {} 1.4, \quad a_{21}\left( x_{1}(t)\right) =-3, \quad a_{23}\left( x_{3}(t)\right) =8,\quad a_{31}\left( x_{1}(t)\right) =4,\\ b_{13}\left( {x_{3}\left( p_{3}t\right) }\right)= & {} \left\{ \begin{array}{ll} 0.5, &{}\quad x_{3}\left( p_{3}t\right) \le 0,\\ 0.3, &{}\quad x_{3}\left( p_{3}t\right)> 0, \end{array}\right. \quad b_{21}\left( {x_{1}\left( p_{1}t\right) }\right) =\left\{ \begin{array}{ll} -\,0.5,&{} \quad x_{1}\left( p_{1}t\right) \le 0, \\ -\,0.3, &{}\quad x_{1}\left( p_{1}t\right)> 0, \end{array}\right. \\ b_{22}\left( {x_{2}\left( p_{2}t\right) }\right)= & {} \left\{ \begin{array}{ll} 0.4,&{} \quad x_{2}\left( p_{2}t\right) \le 0,\\ 0.1, &{}\quad x_{2}\left( p_{2}t\right)> 0, \end{array}\right. \quad b_{32}\left( {x_{2}\left( p_{2}t\right) }\right) =\left\{ \begin{array}{ll} 1.5,&{}\quad x_{2}\left( p_{2}t\right) \le 0, \\ 1,&{}\quad x_{2}\left( p_{2}t\right)> 0, \end{array}\right. \\ \\ b_{33}\left( {x_{3}\left( p_{3}t\right) }\right)= & {} \left\{ \begin{array}{ll} 0.2,&{}\quad x_{3}\left( p_{3}t\right) \le 0,\\ 0.4, &{}\quad x_{3}\left( p_{3}t\right)> 0, \end{array}\right. \quad c_{11}\left( {x_{1}\left( q_{1}t\right) }\right) =\left\{ \begin{array}{ll} 0.5,&{}\quad x_{1}\left( q_{1}t\right) \le 0, \\ 0.3,&{}\quad x_{1}\left( q_{1}t\right)> 0, \end{array}\right. \\ b_{11}\left( x_{1}\left( p_{1}t\right) \right)= & {} 1, \quad b_{12}\left( x_{2}\left( p_{2}t\right) \right) =0, \quad b_{23}\left( x_{3}\left( p_{3}t\right) \right) =-0.5, \quad b_{31}\left( x_{1}\left( p_{1}t\right) \right) =0.5,\\ c_{13}\left( {x_{3}\left( q_{3}t\right) }\right)= & {} \left\{ \begin{array}{ll} 0.4, &{}\quad x_{3}\left( q_{3}t\right) \le 0,\\ 0.5,&{} \quad x_{3}\left( q_{3}t\right)> 0, \end{array}\right. \quad c_{21}\left( {x_{1}\left( q_{1}t\right) }\right) =\left\{ \begin{array}{ll} -\,0.5,&{}\quad x_{1}\left( q_{1}t\right) \le 0,\\ -\,0.3,&{}\quad x_{1}\left( q_{1}t\right)> 0, \end{array}\right. \\ c_{23}\left( {x_{3}\left( q_{3}t\right) }\right)= & {} \left\{ \begin{array}{ll} -\,0.3,&{}\quad x_{3}\left( q_{3}t\right) \le 0,\\ -\,0.5,&{}\quad x_{3}\left( q_{3}t\right)> 0, \end{array}\right. \quad c_{32}\left( {x_{2}\left( q_{2}t\right) }\right) =\left\{ \begin{array}{ll} 0.5, &{} x_{2}\left( q_{2}t\right) \le 0,\\ 0.3,&{} x_{2}\left( q_{2}t\right) > 0, \end{array}\right. \\ c_{12}\left( x_{2}\left( q_{2}t\right) \right)= & {} 0, \quad c_{22}\left( x_{2}\left( q_{2}t\right) \right) =0.4,\quad c_{31}\left( x_{1}\left( q_{1}t\right) \right) =0.5, \quad c_{33}\left( x_{3}\left( q_{3}t\right) \right) =0.4,\\ \end{aligned}$$

and \(I=(0,0,0)^{\mathrm{T}},\, f_{i}(x_{i})=\sin (x_{i}), g_{i}(x_{i})=\frac{1}{\pi }\arctan (\frac{\pi }{2}x_{i}), h_{i}(x_{i})=\tanh (\frac{1}{4}x_{i}) +\frac{1}{4}x_{i}, i=1,2,3\). The drive system (21) satisfies condition (2) and \(\sigma _{i}=1, \gamma _{i}=\frac{1}{2}, \delta _{i}=\frac{1}{2}, i=1,2,3\), and the responding response system is

$$\begin{aligned} {\dot{z}}_{i}(t)= & {} -d_{i}\left( {z_{i}(t)}\right) z_{i}(t)+\sum \limits _{j=1}^{3}a_{ij}\left( {z_{j}(t)}\right) f_{j}\left( z_{j}(t)\right) +\sum \limits _{j=1}^{3}b_{ij}\left( {z_{j}\left( p_{j}t\right) }\right) g_{j}\left( z_{j}\left( p_{j}t\right) \right) \nonumber \\&\quad +\sum \limits _{j=1}^{3}c_{ij}\left( {z_{j}\left( q_{j}t\right) }\right) h_{j}\left( z_{j}\left( q_{j}t\right) \right) +I_{i}+u_{i}(t), \quad i=1,2,3. \end{aligned}$$
(22)

Taking the control inputs \(u_{i}(t)=\rho _{i}e_{i}(t), i=1,2,3\), in which \(\rho _{1}=-\,18.7, \rho _{2}=-\,10.5, \rho _{3}=-\,24.1\). Through calculating, we obtain

$$\begin{aligned} D=\begin{pmatrix}1&{}\quad 0&{}\quad 0\\ 0&{}\quad 3&{}\quad 0\\ 0&{}\quad 0&{}\quad 0.5 \end{pmatrix},\quad A=\begin{pmatrix}1.4&{}\quad 2.2&{}\quad 24\\ 3&{}\quad 1.5&{}\quad 8\\ 4&{}\quad 7&{}\quad 0.8 \end{pmatrix},\quad B=\begin{pmatrix}1&{}\quad 0&{}\quad 0.5\\ 0.5&{}\quad 0.4&{}\quad 0.5\\ 0.5&{}1.5&{}0.4 \end{pmatrix},\quad C=\begin{pmatrix}0.5&{}\quad 0&{}\quad 0.5\\ 0.5&{}\quad 0.4&{}\quad 0.5\\ 0.5&{}\quad 0.5&{}\quad 0.4 \end{pmatrix}. \end{aligned}$$
Fig. 3
figure 3

The phase plots of drive-response systems (21) and (22)

Full size image

In addition, let \(\alpha _{1}=\alpha _{2}=\alpha _{3}=2\), we get

$$\begin{aligned}&-\,39.4+2A_{11}+A_{12}+A_{13}+A_{21}+A_{31}+\frac{5B_{11}}{4}+B_{12}+B_{13}+\frac{B_{21}}{4}\\&\quad +\frac{B_{31}}{4}+\frac{5C_{11}}{4}+C_{12}+C_{13}+\frac{C_{21}}{4}+\frac{C_{31}}{4}=-\,0.0250<0, \quad i=1,\\&-\,27+A_{12}+A_{21}+2A_{22}+A_{23}+A_{32}+\frac{B_{12}}{4}+B_{21}+\frac{5B_{22}}{4}+B_{23}\\&\quad +\frac{B_{32}}{4}+\frac{C_{12}}{4}+C_{21}+\frac{5C_{22}}{4}+C_{23}+\frac{C_{32}}{4}=-\,0.3000<0, \quad i=2,\\&-\,49.2+A_{13}+A_{23}+A_{31}+A_{32}+2A_{33}+\frac{B_{13}}{4}+\frac{B_{23}}{4}+B_{31}+B_{32}\\&\quad +\frac{5B_{33}}{4}+\frac{C_{13}}{4}+\frac{C_{23}}{4}+C_{31}+C_{32}+\frac{5C_{33}}{4}=-\,0.1000<0, \quad i=3.\\ \end{aligned}$$
Fig. 4
figure 4

The time response curve of synchronization error \(e_{i}(t)\)

Full size image

The condition of Theorem 1 and Corollary 1 is satisfied. Obviously, drive-response systems (21) and (22) are exponentially synchronized, their simulations are shown in Figs. 3 and 4. Figure 3a depicts the chaotic behavior of drive system (21) in phase space with initial value \(x(t)=[5,1,1.5]^{\mathrm{T}}\). Figure 3b shows the chaotic behavior of response system (22) in phase space without control input with initial value \( z(t)=[10,0,1.5]^{\mathrm{T}}\). Figure 3c shows the chaotic behavior of response system (22) in phase space with initial value \(z(t)=[10,0,1.5]^{\mathrm{T}}\). Figure 4 describes the time response curve of synchronization error \(e_{i}(t)\) between drive-response systems (21) and (22) with initial conditions \(x(t)=[5,1,1.5]^{\mathrm{T}}\) and \(z(t)=[10,0,1.5]^{\mathrm{T}}\), respectively.

Remark 4

The change of memductances \(M_{ij}, N_{ij}, W_{ij}\) will lead to the change of \(d_{i}(x_{i}(t))\), yet the scholars only reflected on \(d_{i}(x_{i}(t))=d_{i}>0, i\in N\) in the literatures [37, 38]. So, the conclusions in this paper are more general than [37, 38].

5 Conclusions

The exponential synchronization of MRNNs with multi-proportional delays is investigated via a feedback control. The nonlinear transformations change the problem of unbounded time delays into bounded time delays, which can make the problem easier. However, the time-varying coefficients are asked to be bounded in the prior literatures, so how to research the unbounded coefficients becomes the key challenge. In this paper, by constructing a suitable Lyapunov functional and utilizing inequality analysis techniques, a fresh sufficient condition is received for the exponential synchronization of the drive-response systems. We can also apply the research methods here to deal with the stability, passivity and anti-synchronization of MRNNs with multi-proportional delays in the future.