Biological Conservation of Living Systems by Providing Additional Food Supplements in the Presence of Inhibitory Effect: A Theoretical Study Using Predator–Prey Models

Abstract

Ecological and biological conservation of living systems has been an active area of research over the years by agriculturalists, biologists and mathematicians. One of the studies involves additional food supplement feeding (also called as diversionary feeding) for the purpose of biological (wildlife in some cases) conservation. The idea in this approach is to distract (thereby supplement) the wildlife from predating upon the other species with the end goal of wildlife conservation. On the other hand in agricultural entomology, insect control and optimization, additional food is supplemented as a tool for effective pest control thereby achieving the biological control. The study of these ecosystems is usually done using the predator–prey systems. In nature, we find situations wherein the group defense (toxicity) of the prey reduces the predator’s predation rate. This type of behaviour of the prey is also known as inhibitory effect of the prey. Biological conservation of such predator prey systems in the presence of additional food supplements is quite challenging and interesting. In this paper, we consider an additional food provided predator–prey system which is a variation of the standard predator–prey model in the presence of the inhibitory effect of the prey. The predators functional response is assumed to be of Holling type IV (considering the inhibitory effect). This model is analyzed to understand the inherent dynamics of the system. The findings suggest that the quality and quantity of additional food provided to the predators, play a very significant role in determining the eventual state of the ecosystem. The outcomes of the analysis suggests eco friendly strategies to eco-managers for biological conservation of living systems.

Introduction

Ecological and biological conservation of living systems over the years has been a serious concern and has been intensely researched by agriculturalists, biologists and mathematicians. Some of the outcomes of these studies suggest that provision of additional food supplements can be used as a effective tool for achieving the said objective [1, 12, 17, 19, 20, 24, 32, 37, 38]. These studies can be broadly classified into two kinds.

The studies of the first kind involves additional food supplement feeding (also called as diversionary feeding) for the purpose of biological (wildlife in some cases) conservaration. The idea is to reduce the predation of one type of species (predators) on the other living species (target prey) by providing the predators with alternate food supplements in addition to the available target prey. Because of this the predator tends to get distracted and also get supplemented with additional food supplements thereby relieving the predating pressure on the target prey. This strategy is usually used in biological conservation and wildlife damage management. One must be cautious with the supplements provided as over nutrious additional food can increase the attack rate and reproductivity of the predators leading to heavy predation pressure on the target prey resulting in the opposite. From some of the field studies it can even be observed that diversionary feeding may need not always achieve the goal of conservation of the prey. The above discussions are substantiated with some examples in the following paragraph.

In an experiment conducted during the years of 1998 and 1999, in south Scotland, hen harriers on Langholm moor were provided with substitute food in order to reduce the rate at which they preyed on grouse. The outcomes from this work showed that harriers regularly fed on the substitute food and they reduced the intake of grouse chicks [12]. Voles of the genus Microtus and Clethrionomys feed on bark, tissues and roots of the coniferous and deciduous tree plantations in North America. Provision of diversionary food items such as alfalfa, canola oil, and bark mulch with wax has yielded good results suggesting that diversionary food may help reduce the tree damage [2]. On the other hand provision of supplement food to striped skunks for reducing the depredation of upland-duck nests has limited value [2]. Also studies on supplement feeding for northern bobwhite and its effects on wildlife species can be found in [1].

The studies of the second kind have motivation and application in the field of agricultural entomology, pest control and optimization of loss due to infestations by insects. One of the popular approaches for pest control include chemical control. In the method of chemical control, insecticides and pesticides are used to control the pests. Although, these chemicals serve as an effective solution for the problem of pest control, it has been proven that these chemicals cause major health hazards to human beings and environment. So, eco friendly bio control programmes seem to be the need of the hour.

In general, pest populations are regulated by their environment (e.g., resources, climate, and competition) and the influence of natural enemies [7]. “Natural enemy” is a collective term for parasites, parasitoids, pathogens, predators, and competitors that inflict mortality or injury on a population of a species. By feeding upon, infecting, or otherwise damaging individual plants, natural enemies help to mediate the host plants ability to compete in its environment. The method of control of the pests using their natural enemies is called as bio control. Off late mathematicians and field scientists working in the area of agricultural entomology have been conducting experiments on biological control of pests, by studying the interactions of the eco-system as predator–prey models. In these models, the pest is assumed to be as prey and natural enemy is viewed to be as predator. One of the approaches for achieving the biological conservation of ecosystems (in this case biological control), is to provide the predators with additional food supplements in order to enhance their longevity and fecundity, so as to effectively control the prey (pest) [17, 19, 20, 24, 37, 38].

These studies deal with consequences of providing continuous additional food supplements to the predator and the corresponding effects on the predator–prey dynamics of the system. Owing to this and evolving literature on differential equations, study on three species communities have become the focus of considerable attention both for the theoreticians and experimentalists. Thus, three-species systems (like plant–herbivore–parasitoid, plant-pest-predator) which can be modeled using two prey one predator, are being studied in different branches of ecology [8, 9, 11, 15, 21, 25, 33, 34, 36, 40].

Some of these studies have modeled one predator-two (non-interacting) prey systems [15, 34, 36]. These studies suggest, that providing additional food to the predator would decrease the target prey density. Also, by changing the additional food supply, the predators fecundity gets enhanced thereby reducing the equilibrium prey population level, thus, biologically controlling the ecosystem. This phenomenon of decrease in equilibrium prey densities in the presence of additional food supplements to the predator is termed as apparent competition [16]. Although, these theories have suggested ways of biological control of pests, it can be inferred from empirical data that, provision of additional food does not always decrease the target prey density [13, 15, 22, 39]. This apparent contradiction between the theoretical studies and empirical observations calls for a deeper understanding of the predator–prey dynamics under the provision of additional food.

Recent works [23, 27,28,29,30,31], have addressed some of the issues pertaining to this contradiction. In these studies the ‘Quality’ and ‘Quantity’ of the additional food were viewed to be as control parameters and by varying these parameters, it was observed that, if high quality additional food is provided to the predator, the predation pressure increases towards the target prey. Whereas low quality additional food would decrease the target prey. In these works, modified versions of Rosenzweig–MacArthur’s models have been developed to represent the predator–prey dynamics. The conclusions of these studies agreed with the experimental observations [4, 13, 14].

In [31], the predators functional response towards the target prey is of Holling type II, in which, the predators ability to detect available food is independent of prey density. The outcomes of this study caution the ecomanagers on the choice of quality and quantity of the additional food supplements used. In [3, 27, 35] modelling studies involving two prey one predator with Holling type III functional response for the predator is done. In these works the second prey type is, implicitly, assumed to be constant. In [27] it is concluded that the predators exhibit a different behaviour at low prey densities. It is observed that the system exhibits apparent competition only when the predators are provided with high quality additional food. Also, this study reveals that provision of additional food can drive the system to desired population state of the ecosystem. It is also possible to eliminate either of the species by suitable quality and quantity of additional food. This study suggest possible eco-friendly strategies to the ecomanagers.

In nature, we see that there are situations wherein Predators catchability towards the prey decreases at sufficiently high prey density, due to either prey interference or prey toxicity. This behaviour of the prey at high density is known as inhibitory effect of the prey and the predators functional response is coined as Holling type IV functional response [18]. Some examples include the following: Musk ox are more successful at fending off wolves when in herds than when alone [10]. Spider mites, at high densities, produce webbing interferes with its predators response [6].

From the above discussions, it is clear that, study of the predator–prey dynamics under the provision of additional food supplements to the predator is an important field of study. We also observe that, there are a wide range of species (prey) in nature, which exhibit inhibitory effect at high density. Hence, a study of additional food provided, predator–prey systems involving Holling type IV response is important in the current context. A preliminary study of a predator–prey model involving type IV functional response in the absence of additional food has been done in [18].

In this paper, we do a detailed study for additional food provided predator–prey model involving type IV functional response. We see that initially in the absence of additional food the system is prey dominated due to the inhibitory effect of the prey. We investigate the consequences of provision of additional food to predators in such systems. We observe and conclude that by provision of high quality additional food will help the predators to overcome the inhibitory effect of the target prey. Stable coexistence of the predator and the prey can also be obtained. Further increase of supply of additional food can even eliminate the prey from the ecosystem. On the other hand provision of low quality of additional food ensures the sustenance of the inhibitory effect of the prey and the system continues to be prey dominated. This qualitative and quantitative study reveals several other interesting insights and conclusions that can be applied for biological conservation of living systems and the eco managers can be cautioned appropriately.

The Initial System

Derivation of Holling Type IV Functional Response

Let N and P denote the density of the prey and predator respectively. We see that broadly, the total time taken by the predator to consume the prey is given by

$$\begin{aligned} \Delta T = \Delta T_S + \Delta T_N, \end{aligned}$$

where $\Delta T_S$ is the time taken by the predator to search the prey and $\Delta T_N$ is the time taken by the predator to handle the prey. Now, we see that the handling time for the prey caught equals the handling time for one prey item times the total number of prey caught and the prey caught is proportional to the search time and the total prey. Hence, number of prey caught is proportional to $\Delta T_S * N(= C* \Delta T_S * N),$ where C is the proportionality constant, which denotes the catchability of the prey and equals $\frac{ e_1}{bN^2 + 1},$ where, $e_1$ represents the search rate of the predator per unit prey availability and b represents the inhibitory effect or the group defense of the prey. For sufficiently large (small) b,  the catchability of the predator decreases (increases) because of the inhibitory effect of the prey. Now, let handling time for one prey item be $h_1$. Hence, we see that, the total handling time for the prey ($\Delta T_N$) equals $h_1$ times number of prey caught, which is given by,

$$\begin{aligned} \Delta T_N = h_1 \Delta T_S N \frac{e_1}{bN^2+1} \end{aligned}$$

(1)

The number of prey encountered per unit time is given by, $\frac{\text {Total no. of prey caught}}{\text {total time}}$, which equals,

$$\begin{aligned}= & {} \frac{ \Delta T_S N \frac{e_1}{bN^2+1} }{\Delta T_S + \Delta T_N} \\= & {} \frac{ \Delta T_S N \frac{e_1}{bN^2+1} }{\Delta T_S + \Delta T_S N h_1 \frac{e_1}{bN^2+1} }\\= & {} \frac{ N \frac{e_1}{bN^2+1} }{1 + N h_1 \frac{e_1}{bN^2+1} }\\= & {} \frac{ N e_1 }{(bN^2+1) + N e_1 h_1 }\\= & {} \frac{ N e_1 }{ bN^2 + N e_1 h_1 + 1 }\\= & {} \frac{\frac{N}{h_1}}{\frac{ 1}{e_1 h_1} bN^2 + N + \frac{ 1}{e_1 h_1} } \end{aligned}$$

So, the functional response of the predator (which is nothing but the number of prey encountered per unit time) in the presence of group defense of the prey, is given by, $F(N) = \frac{\frac{N}{h_1}}{\frac{ 1}{e_1 h_1} bN^2 + N + \frac{ 1}{e_1 h_1}}$. Now, let c = $\frac{1}{h_1}$ and $a =\frac{1}{e_1h_1}$. So, $F(N) = \frac{cN}{a(bN^2+1)+N}.$ Hence, the Holling Type IV functional response of the predator (considering the inhibitory effect) towards the prey is given by,

$$\begin{aligned} F(N) = \frac{cN}{a(bN^2+1)+N}. \end{aligned}$$

The Model

Let us now consider the following predator–prey model involving type IV functional response for the predators, given by,

$$\begin{aligned} \dot{N}= & {} rN\left( 1 - \frac{N}{K}\right) - F(N)P, \\ \dot{P}= & {} \epsilon _1 F(N)P - mP, \\ \end{aligned}$$

or equivalently,

$$\begin{aligned} \dot{N}= & {} rN\left( 1 - \frac{N}{K}\right) - \frac{c N}{a(bN^2 + 1) + N}P, \end{aligned}$$

(2)

$$\begin{aligned} \dot{P}= & {} \frac{eN}{a(bN^2 + 1) + N}P - mP. \end{aligned}$$

(3)

Here r, K represent the intrinsic growth rate and carrying capacity of the prey. m represents the death rate or starvation rate of the predators in the absence of the prey. Here b represents the inhibitory effect or the group defense of the prey. We have the parameters c and a, standing for the maximum rate of predation and half saturation value of the predators in the absence of inhibitory effect, to be $\frac{1}{h_1}$ and $\frac{1}{e_1h_1}.$ Also, if $\epsilon _1$ stands for the nutritive value of the prey item, then the maximum growth rate of predators due to consuming the prey is given by $e = \frac{\epsilon _1}{h_1}$ with $0< \epsilon _1 < 1$. $\epsilon _1$ is also referred to as conversion factor that represents the rate at which the prey biomass gets converted into predator biomass.

We now non-dimensionalize the system (2)–(3) so as to decrease the number of parameters, in order to reduce the complexity involved in the analysis.

Let N = ax; t = rT; P = y$\frac{ra}{c}$; which implies, $dN = adx ;$ $\frac{dt}{r}$ = dT; dP = dy $\frac{ra}{c}$ and also let

$$\begin{aligned} \gamma = \frac{K}{a}, \quad \omega = ba^2, \quad \beta = \frac{e}{r}, \quad \delta = \frac{m}{r}. \end{aligned}$$

(4)

Now, $\frac{dN}{dT} = rN\left( 1 - \frac{N}{K}\right) - \frac{c N}{a(bN^2 + 1) + N}P$, becomes,

$$\begin{aligned} \frac{dx}{dt}= & {} x\left( 1 - \frac{x}{\gamma }\right) - \left[ \frac{xy}{ \omega x^2 + x + 1} \right] \\ \end{aligned}$$

Also, $\frac{dP}{dT} = \frac{eN}{a(bN^2 + 1) + N}p - mP$, becomes,

$$\begin{aligned} \frac{dy }{dt}= & {} \beta \left[ {\frac{ xy}{ (\omega x^2 + 1) + x }} \right] - \delta y. \\ \end{aligned}$$

So, the system (2)–(3 ) reduces to

$$\begin{aligned} \dot{x}= & {} x\left( 1 - \frac{x}{\gamma }\right) - \left[ \frac{xy}{ \omega x^2 + x +1 }\right] , \\ \dot{y}= & {} \beta \left[ {\frac{ x y}{ \omega x^2 + x +1 }} \right] - \delta y. \\ \end{aligned}$$

Letting

$$\begin{aligned} \bar{f}(x)= & {} \frac{x}{\omega x^2 + x + 1}, \end{aligned}$$

(5)

$$\begin{aligned} \bar{g}(x)= & {} \left( \omega x^2 + x + 1\right) \left( 1 - \frac{x}{\gamma } \right) , \end{aligned}$$

(6)

system (2)–(3) takes the form

$$\begin{aligned} \dot{x}= & {} (\bar{g}(x) - y) \bar{f}(x), \ \end{aligned}$$

(7)

$$\begin{aligned} \dot{y}= & {} (\beta \bar{f}(x) - \delta )y. \end{aligned}$$

(8)

Here, the behavior of the system’s carrying capacity (K) can be understood by the behavior of the parameter $\gamma .$ Similarly, the inhibitory effect (b) of the prey can be understood by the change of the parameter $\omega$ (refer (4)).

Fig. 1

Prey isoclines of the initial system (7)–(8) with $\beta = 2.2$ and $\delta = 0.4$

We observe that the prey and predator isoclines of (7)–(8) are given by

$$\begin{aligned} y = (\omega x^2 + x + 1)\left( 1 - \frac{x}{\gamma }\right) , \quad x_{1,2} = \frac{(\beta - \delta ) \mp \sqrt{{(\beta - \delta )}^2 - 4 \omega {\delta }^2}}{2 \omega \delta }, \end{aligned}$$

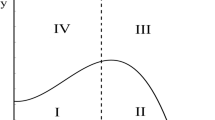
respectively. The prey isocline of (7)–(8) can exist in four different ways in the first quadrant. These different situations are illustrated in the Fig. 1. The conditions governing each of these cases can be obtained from the behavior of the derivative function $\bar{g}^{'}(x).$ We see that $\bar{g}^{'}(x) = 0$ implies that

$$\begin{aligned} 3\omega x^2 + 2(1-\omega \gamma )x + (1-\gamma ) = 0. \end{aligned}$$

(9)

The product and sum of the roots of the above equation equal $\frac{ 1-\gamma }{3\omega }$ and $\frac{2(\omega \gamma -1)}{3\omega }$ respectively and the discriminant of the above quadratic equation (9) is given by $4 ((1-\omega \gamma )^2 - 3\omega (1-\gamma )).$

Case 1 $(1-\gamma \omega )^2 - 3\omega (1-\gamma ) > 0,$ $\gamma < 1$ and $1-\omega \gamma < 0.$

The equation $\bar{g}^{'}(x) = 0$ has two positive real roots and the prey isocline $y = \bar{g}(x)$ has a crest and trough which can be seen from the frame A of Fig. 1.

Case 2 $(1-\gamma \omega )^2 - 3\omega (1-\gamma ) > 0$ and $\gamma > 1.$

The equation $\bar{g}^{'}(x) = 0$ has a positive and a negative real root. The prey isocline $y = \bar{g}(x)$ has a crest which can be seen from the frame B of Fig. 1.

Case 3 $(1-\gamma \omega )^2 - 3\omega (1-\gamma ) > 0$, $1-\omega \gamma > 0$ and $\gamma < 1.$

The equation $\bar{g}^{'}(x) = 0$ has 2 negative real roots and the prey isocline $y = \bar{g}(x)$ is monotonically decreasing, which can be seen from the frame C of Fig. 1.

Case 4 $(1-\gamma \omega )^2 - 3\omega (1-\gamma ) < 0.$

The equation $\bar{g}^{'}(x) = 0$ has only complex conjugate roots and the prey isocline $y = \bar{g}(x)$ is again monotonically decreasing as in case 3, which can be seen from the frame D of Fig. 1.

We see that the system (7)–(8) has $E_0 = (0,0)$ and $E_1 = (\gamma ,0)$ as its axial equilibrium points. Depending on the choice of the parameters of the system, we have the emergence of the interior equilibria

$$\begin{aligned} E_2= & {} (x_1,y_1) = \left( \frac{(\beta - \delta ) - \sqrt{{(\beta - \delta )}^2 - 4 \delta ^2 \omega } }{2 \delta \omega } , \bar{g}(x_1)\right) , \\ E_3= & {} (x_2,y_2) = \left( \frac{(\beta - \delta ) + \sqrt{{(\beta - \delta )}^2 - 4 \delta ^2 \omega } }{2 \delta \omega } ,\bar{g}(x_2)\right) , \end{aligned}$$

The equilibrium point $E_2$ exists for $\gamma > x_1$ and both equilibria $E_2 \ \& \ E_3$ exist for $\gamma > x_2$.

Local and Global Dynamics

In order to analyze the stability nature of the system (7)–(8) at its equilibrium points, we consider its community matrix denoted by J as follows:

$$\begin{aligned} J_{(x,y)} = \left( \begin{array}{c@{\quad }c} \bar{g}^{'}(x)\bar{f}(x) + \bar{f}^{'}(x)(\bar{g}(x) - y) &{} -\bar{f}(x) \\ \beta \bar{f}^{'}(x) y &{} \beta \bar{f}(x) - \delta \\ \end{array} \right) . \end{aligned}$$

Evaluating $J_{(x,y)}$ at each of the axial equilibrium points $E_0 = (0,0), \ E_1 = (\gamma ,0),$ we obtain,

$$\begin{aligned} J_{(0,0)}= & {} \left( \begin{array}{c@{\quad }c} 1 &{} 0 \\ 0 &{} - \delta \\ \end{array} \right) ,\end{aligned}$$

(10)

$$\begin{aligned} J_{(\gamma ,0)}= & {} \left( \begin{array}{c@{\quad }c} \bar{g}^{'}(\gamma )\bar{f}(\gamma ) &{} -\bar{f}(\gamma ) \\ 0 &{} \beta \left[ \frac{\gamma }{\omega \gamma ^2 + \gamma + 1} \right] - \delta \\ \end{array} \right) . \end{aligned}$$

(11)

From $J_{(0,0)}$, the determinant is $- \delta$, which shows that $E_0 = (0,0)$ is always a saddle. From $J_{(\gamma ,0)}$, the determinant is $\bar{g}^{'}(\gamma )\bar{f}(\gamma )\left( \beta \left[ \frac{\gamma }{(\omega \gamma ^2 + 1) + \gamma } \right] - \delta \right)$. This implies that the determinant is positive if $\left( \beta \left[ \frac{\gamma }{(\omega \gamma ^2 + \gamma + 1)} \right] - \delta \right) < 0$, since $\bar{g}^{'}(\gamma ) = \frac{-1}{\gamma }(\omega \gamma ^2 + \gamma + 1) <0$ and $\bar{f}(\gamma )= \frac{\gamma }{\omega \gamma ^2 + \gamma + 1} >0$. Evaluating the community matrix at the interior equilibria point $E_2 = (x_1,y_1)$ and $E_3 = (x_2,y_2)$, we obtain,

$$\begin{aligned} J_{(x_1,y_1)}= & {} \left( \begin{array}{c@{\quad }c} \bar{g}^{'}(x_1)\bar{f}(x_1) &{} -\bar{f}(x_1) \\ \beta \bar{f}^{'}(x_1) &{} 0 \\ \end{array} \right) , \end{aligned}$$

(12)

$$\begin{aligned} J_{(x_2,y_2)}= & {} \left( \begin{array}{c@{\quad }c} \bar{g}^{'}(x_2)\bar{f}(x_2) &{} -\bar{f}(x_2) \\ \beta \bar{f}^{'}(x_2) &{} 0 \\ \end{array} \right) . \end{aligned}$$

(13)

From the above equations, we see that, the determinant of $J_{(x_i,y_i)}, \ i = 1,2,$ is given by $\beta \bar{f}(x_i) \bar{f}^{'}(x_i).$

To understand the nature of these interior equilibria, we do the following analysis.

Now, let  $\bar{h}(x) = ( \beta \bar{f}(x) - \delta ),$ i.e., $\bar{h}(x) = \frac{-\delta \omega x^2+(\beta -\delta )x-\delta }{\omega x^2 + x + 1}$. We see that, if $\omega > \frac{(\beta -\delta )^2}{4\delta ^2}$ (i.e., roots of $\bar{h}(x)$ are complex conjugates), $\bar{h}(x) <0$ for all $x > 0.$ If $\omega < \frac{(\beta -\delta )^2}{4\delta ^2},$ then $\bar{h}(x)$ has two real roots $x_1 \ \& \ x_2$(predator isoclines). In this case sum of the roots of $\bar{h}(x)$ is given by $\frac{(\beta -\delta )}{\delta \omega }(\text {if} \ \beta > \delta )$ and product of the roots is given by $\frac{1}{\omega }(>0)$. So, it can be concluded that for $\omega < \frac{(\beta -\delta )^2}{4\delta ^2},$ $\bar{h}(x)$ has two positive roots $x_1 \ \& \ x_2.$ And so, $\bar{h}(x)$ is positive between its roots

$$\begin{aligned} \bar{h}(x) > 0,\quad x_1< x < x_2 \end{aligned}$$

(14)

and negative outside of this interval,

$$\begin{aligned} \bar{h}(x)< 0, \quad 0< x < x_1 \text { or } x > x_2. \end{aligned}$$

(15)

Inequalities (14) and (15) imply that

$$\begin{aligned} \bar{h}^{'}(x_1) > 0, \quad \bar{h}^{'}(x_2) < 0. \end{aligned}$$

(16)

From definition of $\bar{h}(x),$ we see that $\bar{h}^{'}(x) = \beta \bar{f}^{'}(x).$ Hence,

$$\begin{aligned} \bar{f}^{'}(x_1) > 0, \quad \bar{f}^{'}(x_2) < 0. \end{aligned}$$

(17)

The characteristic equation associated with the community matrix evaluated at the interior equilibrium $E_2 = (x_1,y_1)$ is given by

$$\begin{aligned} \lambda ^2 - Tr J|_{(x_1,y_1)} \lambda + Det J|_{(x_1,y_1)} = 0. \end{aligned}$$

(18)

We see that the existence of interior equilibrium $E_2$ implies that $\omega < \frac{(\beta -\delta )^2}{4\delta ^2}.$ Hence, it is clear that the $Det J|_{(x_1,y_1)}(= \beta \bar{f}(x_1)\bar{f}^{'}(x_1))$ is positive as $\bar{f}(x_1) = \frac{x_1}{\omega x_1^2 + x_1 + 1}> 0 \ \text {and} \ \bar{f}^{'}(x_1) > 0.$ From Routh–Hurwitz criterion [18], the necessary condition for $E_2 (= (x_1,y_1))$ to be locally asymptotically stable is $Tr J|_{(x_1,y_1)} < 0$ and it is unstable if $Tr J|_{(x_1,y_1)} > 0.$ We have the trace given by

$$\begin{aligned} Tr J|_{(x_1,y_1)} = \left( (3\omega {x_1}^2 + 2x_1(1 -\omega \gamma ) + (1 - \gamma ))\left( \frac{-1}{\gamma }\right) \right) \bar{f}(x_1). \end{aligned}$$

(19)

From the above equation, we see that the trace is negative whenever the slope of the prey isocline is negative (as the term in the brackets of R.H.S. of (19) represents the slope of the prey isocline $(= \bar{g}^{'}(x))$ at $(x_1,y_1)$). Now, let $H(x ) = \left( 3\omega {x}^2 + 2x(1 -\omega \gamma ) + (1 - \gamma )\right) .$ Hence the interior equilibrium $(x_1,y_1)$ is locally asymptotically stable if $H(x_1) > 0$ and unstable if $H(x_1) < 0.$

Conjecture 1

The interior equilibrium $E_2 = (x_1,y_1)$ loses its stability through Hopf bifurcation when $Tr J|_{(x_1,y_1)} = 0$ with respect to the bifurcation parameter $\omega$(while the other parameters are fixed). This can be seen from Table 2 which deals with the global dynamics of the initial system by varying the conditions on $\omega$. Also, a necessary condition for the occurrence of Hopf bifurcation can be obtained from the following equation.

$$\begin{aligned} H(x_1) = (3\omega {x_1}^2 + 2x_1(1 -\omega \gamma ) + (1 - \gamma )) = 0. \end{aligned}$$

(20)

Substituting for $x_1$ in the above equation, we obtain the following parametric relation

$$\begin{aligned}&3w\left[ \frac{(\beta - \delta ) - \sqrt{{(\beta - \delta )}^2 - 4 \delta ^2 w}}{2 \delta w} \right] ^2\\&\quad +\;(2-2w\gamma )\left[ \frac{(\beta - \delta ) - \sqrt{{(\beta - \delta )}^2 - 4 \delta ^2 w}}{2 \delta w} \right] + (1 - \gamma ) = 0 \end{aligned}$$

which is a necessary condition for the occurrence of Hopf bifurcation.

Also, from (17), we see that $\bar{f}^{'}(x_2) < 0,$ which implies that $Det J|_{(x_2,y_2)} < 0$ further implying that the product of eigen values is negative (as $\bar{f}^{'}(x_2) < 0$). Hence, interior equilibrium $E_3 = (x_2,y_2)$ continues to remain as saddle through out its existence.

As seen from previous discussion regarding the behavior of prey isocline, the nature of the interior equilibrium depends upon the shape of the prey isocline. This is discussed below in four different cases.

• If the equation $H(x) = 0$ has both positive roots ($H_1, H_2$ with $0< H_1 < H_2$), then $(x_1,y_1)$ is stable whenever $x_1$ does not belong to $(H_1,H_2)$(region wherein $\bar{g}^{'}(x_1) < 0$) and is unstable if $x_1$ belongs to $(H_1,H_2)$(region wherein $\bar{g}^{'}(x_1) > 0$).

• If the equation $H(x) = 0$ has a positive root and a negative root ($H_1, H_2$ with $H_1< 0 < H_2$), then $(x_1,y_1)$ is stable whenever $x_1$ does not belong to $(0,H_2)$(region wherein $\bar{g}^{'}(x_1) < 0$) and is unstable if $x_1$ belongs to $(0,H_2)$(region wherein $\bar{g}^{'}(x_1) > 0$) in the positive quadrant.

• If the equation $H(x) = 0$ has both negative roots ($H_1, H_2$ with $H_1< H_2 < 0),$ then, $(x_1,y_1)$ is always asymptotically stable (since, $\bar{g}^{'}(x_1) < 0$ always).

• If the equation $H(x) = 0$ does not admit any real root, then as in previous case, $(x_1,y_1)$ is always asymptotically stable.

The instability of the interior equilibrium $E_2$ in above cases induces a locally asymptotically stable limit cycle into the system (refer Conjecture).

The local and global dynamics of the system (7)–(8) can be summarised as follows.

• We observe that the system (7)–(8) admits only the axial equilibria $(0,0), (\gamma ,0)$ and does not even admit the predator isoclines $x_1$ and $x_2,$ whenever, $w > \frac{{(\beta - \delta )}^2}{4 \delta ^2}.$

• Whenever $w < \frac{{(\beta - \delta )}^2}{4 \delta ^2}$ and $\gamma < x_1,$ the system (7)–(8) admits axial equilibria and the predator isoclines but does not admit any interior equilibrium.

• If, $w< \frac{{(\beta - \delta )}^2}{4 \delta ^2}, \ x_1< \gamma < x_2,$ the system (7)–(8) admits axial equilibria as well as the interior equilibrium $E_2 = (x_1, y_1).$ If $\bar{g}^{'}(x_1) < 0,$ the interior equilibrium $E_2 = (x_1, y_1)$ is stable. If $\bar{g}^{'}(x_1) > 0,$ the interior equilibrium $E_2 = (x_1, y_1)$ is unstable. Thus the interior equilibrium $E_2 = (x_1, y_1)$ undergoes Hopf bifurcation when $\bar{g}^{'}(x_1) = 0,$ that is, whenever,

  $$\begin{aligned} 3 w x_1^2 + (2 - 2w\gamma )x_1 + (1 - \gamma ) = 0, \end{aligned}$$

  where $x_1 = \frac{(\beta - \delta ) - \sqrt{{(\beta - \delta )}^2 - 4 \delta ^2 w}}{2 \delta w}$(refer conjecture).

• If $w < \frac{{(\beta - \delta )}^2}{4 \delta ^2}, \ \gamma > x_2,$ the system (7)–(8) admits axial equilibria and the interior equilibrium $E_2 = (x_1, y_1)$ and the saddle interior equilibrium $E_3 = (x_2, y_2).$

Hence, we consider the following curves in the positive quadrant of the $(\omega ,\gamma )$ space:

$$\begin{aligned} \gamma -\frac{(\beta -\delta ) - \sqrt{(\beta -\delta )^2-4\delta ^2\omega }}{2\delta \omega } = 0 \end{aligned}$$

(21)

Transcritical bifurcation curve (TBC1) at $x_1 = \gamma$

$$\begin{aligned} \gamma -\frac{(\beta -\delta ) + \sqrt{(\beta -\delta )^2-4\delta ^2\omega }}{2\delta \omega } = 0 \end{aligned}$$

(22)

Transcritical bifurcation curve (TBC2) at $x_2 = \gamma$

$$\begin{aligned}&3\omega \left[ {\frac{(\beta - \delta )-\sqrt{(\beta - \delta )^2-4\delta ^2\omega }}{2\delta \omega }}\right] ^2 \nonumber \\&\quad +\, (2-2\omega \gamma )\left[ \frac{(\beta - \delta )-\sqrt{(\beta - \delta )^2-4\delta ^2\omega }}{2\delta \omega }\right] \nonumber \\&\quad +\, (1-\gamma ) = 0 \end{aligned}$$

(23)

Hopf bifurcation curve (HBC) at $(x_1,y_1)$

$$\begin{aligned} \omega - \left( \frac{(\beta -\delta )^2}{4\delta ^2}\right) = 0 \end{aligned}$$

(24)

Saddle node bifurcation/discriminant curve (DISC).

We see that each of the curves (21)–(24) divide the positive quadrant of $(\omega , \gamma )$ space into two regions which characterize the nature of the associated equilibrium point of (7)–(8).

From the discussions presented above, it can be seen that the global dynamics of the considered system can be understood under the following six natural conditions((Con-I)–(Con-VI)) pertaining to the existence, stability nature and occurrence of Hopf bifurcation associated with the interior equilibrium points of the system (7)–(8). These conditions can further be subdivided into sub conditions, depending on the behavior of the prey isocline and the location of the interior equilibrium in the positive quadrant. These 15 sub conditions along with the six main conditions are summarized in the Table 1.

Table 1 Stability conditions for the system (7)–(8)

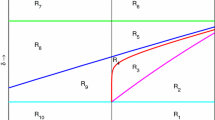
The bifurcation analysis of the system (7)–(8) can be seen in the Fig. 2. In this bifurcation diagram we consider the bifurcation curves (21)–(24) along with the 15 sub conditions mentioned in Table 1. The different regions in this diagram correspond to the different sub conditions discussed in Table 1.

The global dynamics of the initial system are summarized in Table 2 dealing with the nature of the equilibria in each of the regions in the $(\omega , \gamma )$ space. Also the space and time complexity analysis for the border cases are shown in Table 4 in Appendix.

Biological Insights

From the dynamics of the system (7)–(8), we see that, as long as the carrying capacity of the prey is less than one, higher growth rate of predators due to consumption of the prey item directly results in a stabilized interactive system with increased predator and decreased prey densities at the equilibrium. Also it can happen that the equilibrium predator density may suffer non monotonicity leading to oscillations in the interacting population. Presence of prey which promotes higher growth rate in the predators remove the oscillation from the system and later stabilize the system at low prey and high predator densities. For higher prey carrying capacity (greater than 1), although the equilibrium density of prey decreases with increase in predators growth rate, the equilibrium predator density may suffer non monotonicity leading to oscillations in the interacting population. It can happen that the predator population can collapse on further increase of carrying capacity beyond a critical value, which can be catastrophic for the predator. This behaviour can be attributed to the paradox of enrichment. Therefore for the system (2)–(3) with a given prey carrying capacity(less than the critical value), the growth rate of the predators dictates the ability of the predator to limit the prey in the environment.

The Additional Food Provided System

Derivation of Holling Type IV Functional Response for the Additional Food Provided System

Now, let additional food supplements of biomass A be provided to predators uniformly in the habitat as is the case with the prey and predators. We now see that the total time taken by the predator to consume the available food(both the target prey and the additional food) is given by $\Delta T = \Delta T_S + \Delta T_N + \Delta T_A$, where $\Delta T_S$ is the time taken by the predator to search the prey, $\Delta T_N$ is the time taken by the predator to handle the prey and $\Delta T_A$ is the time taken by the predator to handle the additional food provided. From (1), we have $\Delta T_N = h_1 \Delta T_S N \frac{e_1}{bN^2+1}.$ Now, the handling time for the additional food equals the handling time for one additional food item times the total density of additional food encountered. Also, the additional food encountered is proportional to the search time and the additional food density. Hence, additional food encountered is proportional to $\Delta T_S * A = C_2* \Delta T_S * A$, where $C_2$ is the proportionality constant, which denotes the catchability of the additional food and equals $e_2$. Here, $e_2$ represents the search rate of the predator per unit quantity of additional food. Now, let handling time for one additional food item be $h_2$. Hence, we see that, the total handling time for the additional food($\Delta T_A$) equals $h_2$ times additional food encountered, which is given by, $h_2 \Delta T_S$ A $e_2$.

The number of prey encountered per unit time is given by, $\frac{\text {Total No. of Prey caught}}{\text {Total Time}}$, which equals, $\frac{ \Delta T_S N \frac{e_1}{bN^2+1} }{\Delta T_S + \Delta T_N + \Delta T_A}$

$$\begin{aligned}= & {} \frac{ N \frac{e_1}{bN^2+1} }{1 + N h_1 \frac{e_1}{bN^2+1} + A e_2 h_2 }\\= & {} \frac{ N e_1 }{(bN^2+1) + N e_1h_1 + A e_2 h_2 (bN^2+1) }\\= & {} \frac{ N e_1 }{(A e_2 h_2 + 1) bN^2 + N e_1 h_1 + (A e_2 h_2 + 1) }\\= & {} \frac{\frac{N}{h_1}}{\left( A \frac{ e_2 h_2}{e_1 h_1} + \frac{ 1}{e_1 h_1}\right) bN^2 + N + \left( A \frac{ e_2 h_2}{e_1 h_1} + \frac{ 1}{e_1 h_1}\right) }. \end{aligned}$$

Fig. 2

Bifurcation diagram for the system (7)–(8) with $\beta = 2.2 \ \mathrm{and} \ \delta = 0.4$

Table 2 Global dynamics of the initial system (7)–(8)

The quantity of additional food encountered per unit time is given by, $\frac{\text {Total additional food encountered}}{\text {Total Time}}$, which equals, $\frac{ \Delta T_S A e_2 }{\Delta T_S + \Delta T_S N h_1 \frac{e_1}{bN^2+1} + \Delta T_S A e_2 h_2 }$

$$\begin{aligned}= & {} \frac{ A e_2 }{1 + N h_1 \frac{e_1}{bN^2+1} + A e_2 h_2 }\\= & {} \frac{ A e_2 ({bN^2+1})}{(bN^2+1) + N e_1h_1 + A e_2 h_2 (bN^2+1) }\\= & {} \frac{ A e_2 ({bN^2+1}) }{(A e_2 h_2 + 1) bN^2 + N e_1 h_1 + (A e_2 h_2 + 1) }\\= & {} \frac{A\frac{e_2}{e_1}\frac{1}{h_1} ({bN^2+1})}{\left( A \frac{ e_2 h_2}{e_1 h_1} + \frac{ 1}{e_1 h_1}\right) bN^2 + N + \left( A \frac{ e_2 h_2}{e_1 h_1} + \frac{ 1}{e_1 h_1}\right) }. \end{aligned}$$

So, the functional response of the predator towards the prey(the number of prey encountered per unit time) in the presence of inhibitory effect of the prey, is given by, $F(N) = \frac{\frac{N}{h_1}}{\left( A \frac{ e_2 h_2}{e_1 h_1} + \frac{ 1}{e_1 h_1}\right) bN^2 + N + \left( A \frac{ e_2 h_2}{e_1 h_1} + \frac{ 1}{e_1 h_1}\right) }.$ Now, let c = $\frac{1}{h_1}$ and $a =\frac{1}{e_1h_1}$. So, $F(N) = \frac{cN}{\left( A \frac{ e_2 h_2}{e_1 h_1} + a\right) bN^2 + N + \left( A \frac{ e_2 h_2}{e_1 h_1} + a\right) }.$ Hence, the Holling Type IV functional response of the predator towards the prey is given by,

$$\begin{aligned} F(N) = \frac{cN}{\left( A \frac{ e_2 h_2}{e_1 h_1} + a\right) bN^2 + N + \left( A \frac{ e_2 h_2}{e_1 h_1} + a\right) } \end{aligned}$$

(25)

The functional response of the predator towards the additional food (the quantity of additional food encountered per unit time), is given by, $G(A) = \frac{A\frac{e_2}{e_1} \frac{1}{h_1} ({bN^2+1})}{\left( A \frac{ e_2 h_2}{e_1 h_1} + \frac{ 1}{e_1 h_1}\right) bN^2 + N + \left( A \frac{ e_2 h_2}{e_1 h_1} + \frac{ 1}{e_1 h_1}\right) }.$ So, $G(A) = \frac{A\frac{e_2}{e_1}c(bN^2+1)}{\left( A \frac{ e_2 h_2}{e_1 h_1} + a\right) bN^2 + N + \left( A \frac{ e_2 h_2}{e_1 h_1} + a\right) }.$ Hence, the functional response of the predator towards the additional food is given by,

$$\begin{aligned} G(A) = \frac{A\frac{e_2}{e_1}c(bN^2+1)}{\left( A \frac{ e_2 h_2}{e_1 h_1} + a\right) bN^2 + N + \left( A \frac{ e_2 h_2}{e_1 h_1} + a\right) } \end{aligned}$$

(26)

The Model

From the above discussions and derivations, we see that the initial system(involving group defense of the prey) (2)–(3) under the provision of additional food gets modified to the following predator–prey model.

$$\begin{aligned} \dot{N}= & {} rN\left( 1 - \frac{N}{K}\right) - F(N)P, \\ \dot{P}= & {} (\epsilon _1 F(N) + \epsilon _2 G(A))P - mP, \\ \end{aligned}$$

or equivalently,

$$\begin{aligned} \dot{N}= & {} rN\left( 1 - \frac{N}{K}\right) - \frac{cN}{(A \frac{ e_2 h_2}{e_1 h_1} + a) bN^2 + N + (A \frac{ e_2 h_2}{e_1 h_1} + a) } P, \end{aligned}$$

(27)

$$\begin{aligned} \dot{P}= & {} \frac{\epsilon _1 cN + \epsilon _2 A\frac{e_2}{e_1}c(bN^2+1) }{\left( A \frac{ e_2 h_2}{e_1 h_1} + a\right) bN^2 + N + \left( A \frac{ e_2 h_2}{e_1 h_1} + a \right) }P - mP. \end{aligned}$$

(28)

Let $\epsilon _2$ stand for the nutritive value of the additional food. We let $\eta = \frac{e_2\epsilon _2}{e_1\epsilon _1}, \alpha = \frac{h_2\epsilon _1}{h_1\epsilon _2}$ and $e = \epsilon _1c$. Here the term $\eta \frac{A^2}{N} = A(\frac{e_2A}{e_1N})/(\frac{\epsilon _1}{\epsilon _2})$ denotes the quantity of additional food perceptible to the predator with respect to the prey relative to the nutritional value of prey to the additional food. Let $\alpha = \frac{\epsilon _1}{h_1}/\frac{\epsilon _2}{h_2}.$ The term $\alpha = \frac{\epsilon _1}{h_1}/\frac{\epsilon _2}{h_2},$ which is the ratio between the maximum growth rates of the predator when it consumes the prey and additional food respectively, indicates the relative efficiency of the predator to convert either of the available food into predator biomass. Thus, given the prey with specific conversion factor, $\alpha$ is inversely related to the conversion factor of the additional food into predator biomass and directly related to the handling time of the additional food. Observe that the above system reduces to the system (2)–(3) when $A = 0.$ Here also the parameters c and a, stand for the maximum rate of predation and half saturation value of the predators in the absence of inhibitory effect, which equals $\frac{1}{h_1}$ and $\frac{1}{e_1h_1}$ respectively.

With the above definitions of $\eta$ and $\alpha ,$ the system (27)–(28) becomes

$$\begin{aligned} \dot{N}= & {} rN\left( 1 - \frac{N}{K}\right) - \left( \frac{c N}{(A \eta \alpha + a)[b N^2 + 1] + N }\right) P, \end{aligned}$$

(29)

$$\begin{aligned} \dot{P}= & {} e\left( \frac{N + \eta A(bN^2 + 1)}{(A \eta \alpha + a)[b N^2 + 1] + N }\right) P -mP. \end{aligned}$$

(30)

We now study dynamics of the additional food provided predator–prey system (29)–(30). As earlier we non-dimensionalize the system (29)–(30) so as to reduce the complexity involved in the analysis.

Let $N = ax$; $t = rT$; $P= y \frac{ra}{c}$; which implies, $dN = adx ;$ $\frac{dt}{r}$ = dT; dP = dy $\frac{ra}{c}$ and let $\gamma = \frac{K}{a}$; $\xi = \eta \frac{A}{a}$ ; $\omega = ba^2$; $\beta = \frac{e}{r};$ $\delta = \frac{m}{r};$

So, $\frac{dN}{dT} = rN\left( 1 - \frac{N}{K}\right) - \left( \frac{c N}{(A \eta \alpha + a)[b N^2 + 1] + N }\right) P$, becomes

$$\begin{aligned} \frac{dx}{dt}= & {} x\left( 1 - \frac{x}{\gamma }\right) - \left[ \frac{xy}{(1 + \alpha \xi ) (\omega x^2 +1) + x} \right] \end{aligned}$$

and $\frac{dP}{dT} = e\left( \frac{N + \eta A(bN^2 + 1)}{(A \eta \alpha + a)[b N^2 + 1] + N }\right) P -mP$, becomes,

$$\begin{aligned} \frac{dy }{dt}= & {} \beta \left[ {\frac{ x + \xi ( {\omega x^2+1})}{ (1+ \alpha \xi ) (\omega x^2 + 1) + x }} \right] y - \delta y. \\ \end{aligned}$$

So, the system (29) - (30) reduces to

$$\begin{aligned} \dot{x}= & {} x\left( 1 - \frac{x}{\gamma }\right) - \left[ \frac{xy}{(1 + \alpha \xi ) (\omega x^2 +1) + x} \right] \\ \dot{y}= & {} \beta \left[ {\frac{ x + \xi ( {\omega x^2+1})y}{ (1+ \alpha \xi ) (\omega x^2 + 1) + x }} \right] - \delta y. \\ \end{aligned}$$

Letting

$$\begin{aligned} f(x)= & {} \frac{x}{(1+\alpha \xi )(\omega x^2 + 1)+x}, \end{aligned}$$

(31)

$$\begin{aligned} g(x)= & {} ( (1+\alpha \xi )(\omega x^2 + 1)+x ) \left( 1- \frac{x}{\gamma } \right) , \end{aligned}$$

(32)

system (29)–(30) takes the form

$$\begin{aligned} \dot{x}= & {} (g(x)-y) f(x) \end{aligned}$$

(33)

$$\begin{aligned} \dot{y}= & {} \left( \beta f(x) \left[ 1 + \frac{\xi }{x}(\omega x^2 + 1) \right] - \delta \right) y \end{aligned}$$

(34)

Here, the behavior of the system’s carrying capacity (K) can be understood by the behavior of the parameter $\gamma .$ Similarly, the inhibitory effect(b) of the prey can be understood by the change of the parameter $\omega .$ Also, from the construction of the model, we see that the parameters $\beta , \delta$ and $\gamma$ can be treated to be ecosystem characteristic parameters while $\xi$ (quantity of additional food) and $\alpha$ (quality of additional food) can be considered to be control parameters.

Stability Analysis

We observe that the prey and predator isoclines of (33)–(34) are given by

$$\begin{aligned} y= & {} ((1 + \alpha \xi )(\omega x^2 + 1) + x)\left( 1 - \frac{x}{\gamma }\right) , \\ x_{1,2}= & {} \frac{(\beta - \delta ) \mp \sqrt{{(\beta - \delta )}^2 - 4 \omega {[\delta (1 + \alpha \xi ) - \beta \xi ]}^2}}{2 \omega [\delta (1 + \alpha \xi ) - \beta \xi ]}, \end{aligned}$$

respectively. It is clear that the prey isocline of (33)–(34) is an increasing function of both $\alpha$ and $\xi$ in $[0,\gamma )$ which intersects the y-axis at $(0,1 + \alpha \xi )$ and x-axis at $(\gamma ,0).$ Basing on the equations of the prey isoclines of (7) and (33), we can conclude that provision of additional food causes an upward displacement to the prey isocline of (33) (relative to that of (7)) in the interval $[0,\gamma ).$ Further, as in the initial system (7)–(8) the prey isocline for the additional food provided system (33)–(34) also exhibits four different shapes.

Fig. 3

Prey isoclines of the additional food provided system (33)–(34) with $\beta = 2.2$ & $\delta = 0.4$

The conditions governing each of these cases can be obtained from the behavior of the derivative function ${g}^{'}(x).$ We see that $g^{'}(x) = 0$ implies that

$$\begin{aligned} (3\omega {x}^2(1 + \alpha \xi ) + 2x(1 -\omega \gamma (1 + \alpha \xi )) + (1 + \alpha \xi ) - \gamma ) = 0. \end{aligned}$$

(35)

The product and sum of the roots of the above equation equal $\frac{ (1+\alpha \xi )-\gamma }{3\omega (1+\alpha \xi )}$ and $\frac{2(\omega \gamma (1+\alpha \xi ) -1)}{3\omega (1+\alpha \xi )}$ respectively and the discriminant of the above quadratic equation (35) is given by $4((1-\gamma \omega (1+\alpha \xi ))^2 - 3\omega (1+\alpha \xi ) ((1+\alpha \xi )-\gamma )).$

Case 1 $(1- \gamma \omega (1+\alpha \xi ))^2 - 3\omega (1+\alpha \xi ) ((1+\alpha \xi )-\gamma ) > 0$ , $\gamma < 1+\alpha \xi$ and $1-\omega \gamma (1+\alpha \xi ) < 0.$

The equation $g^{'}(x) = 0$ has two positive real roots and the prey isocline $y = {g}(x)$ has a crest and trough which can be seen from the frame A of Fig. 3.

Case 2 $(1-\gamma \omega (1+\alpha \xi ))^2 - 3\omega (1+\alpha \xi ) ((1+\alpha \xi )-\gamma ) > 0$ and $\gamma > (1+\alpha \xi ).$

The equation $g^{'}(x) = 0$ has a positive and a negative real root. The prey isocline $y = {g}(x)$ has a crest which can be seen from the frame B of Fig. 3.

Case 3 $(1-\gamma \omega (1+\alpha \xi ))^2 - 3\omega (1+\alpha \xi ) ((1+\alpha \xi )-\gamma ) > 0$, $1-\omega \gamma (1+\alpha \xi ) > 0$ and $\gamma < (1+\alpha \xi ).$

The equation $g^{'}(x) = 0$ has 2 negative real roots and the prey isocline $y = {g}(x)$ is monotonically decreasing, which can be seen from the frame C of Fig. 3.

Case 4 $(1-\gamma \omega (1+\alpha \xi ))^2 - 3\omega (1+\alpha \xi ) ((1+\alpha \xi )-\gamma ) < 0.$

The equation $g^{'}(x) = 0$ has only complex conjugate roots and the prey isocline $y = {g}(x)$ is again monotonically decreasing as in case 3, which can be seen from the frame D of Fig. 3.

Coming to the predator isoclines of (33)–(34), we see that they are straight lines as that of (7)–(8) but now a function of $\alpha$ and $\xi .$ We observe that the isocline $x_2$ always moves towards right with provision of additional food.

We see that the systems (7)–(8) and (33)–(34) have $E_0 = E_{0}^* = (0,0)$ and $E_1 = E_1^* = (\gamma ,0)$ as their common equilibrium points. Depending on the choice of parameters of the system, we have the emergence of the interior equilibria

$$\begin{aligned} E_2^*= & {} (x_1^*,y_1^*) = \left( \frac{(\beta - \delta ) - \sqrt{{(\beta - \delta )}^2 - 4 \omega {[\delta (1 + \alpha \xi ) - \beta \xi ]}^2}}{2 \omega [\delta (1 + \alpha \xi ) - \beta \xi ]}, g(x_1^*)\right) , \\ E_3^*= & {} (x_2^*,y_2^*) = \left( \frac{(\beta - \delta ) + \sqrt{{(\beta - \delta )}^2 - 4 \omega {[\delta (1 + \alpha \xi ) - \beta \xi ]}^2}}{2 \omega [\delta (1 + \alpha \xi ) - \beta \xi ]}, g(x_2^*)\right) . \end{aligned}$$

The equilibria appear when $\gamma> x_1^*, \gamma > x_2^*$ respectively. From the expressions of the interior equilibria, we see that whenever $\alpha = \frac{\beta }{\delta },$ the equilibrium prey components of the systems (7)–(8) and (33)–(34) are one and same, whereas the equilibrium predator population increases for (33)–(34) with respect to (7)–(8). If (7)–(8) does not admit an interior equilibrium then (33)–(34) shall never admit interior equilibrium whenever $\alpha > \frac{\beta }{\delta }$. On the contrary, if $\alpha < \frac{\beta }{\delta }$ then system (33)–(34) admits interior equilibrium even if (7)–(8) does not, provided $\xi \in \left( {\frac{\beta - (1-2\sqrt{w})\delta }{2\sqrt{w}(\beta - \delta \alpha )}},{\frac{\delta }{(\beta - \delta \alpha )}}\right) .$ To get more insights on the the consequences of providing additional food to the predators, we perform the stability analysis of the system (33)–(34) and compare it with that of (7)–(8).

In order to analyze the stability nature of the system (33)–(34), we consider its community matrix J given by,

$$\begin{aligned} J_{(x^*,y^*)} = \left( \begin{array}{c@{\quad }c} g^{'}(x^*)f(x^*) + f^{'}(x^*)(g(x^*) - y) &{} -f(x^*) \\ \left( \beta f^{'}(x^*)\left( 1 + \frac{\xi }{x^*}(\omega {x^*}^2 + 1)) + \beta f(x^*) \frac{\xi }{{x^*}^2}(\omega {x^*}^2 - 1\right) \right) y &{} \beta f({x^*})\left( 1 + \frac{\xi }{{x^*}}(\omega {x^*}^2 + 1)\right) - \delta \\ \end{array} \right) . \end{aligned}$$

Evaluating $J_{(x^*,y^*)}$ at each of the axial equilibrium points $E_0^* = (0,0), E_1^* = (\gamma ,0),$ we obtain,

$$\begin{aligned}&\displaystyle J_{(0,0)} = \left( \begin{array}{cc} 1 &{}\quad 0 \\ 0 &{}\quad \frac{\beta \xi }{1 + \alpha \xi } - \delta \\ \end{array} \right) , \end{aligned}$$

(36)

$$\begin{aligned}&\displaystyle J_{(\gamma ,0)} = \left( \begin{array}{cc} g^{'}(\gamma )f(\gamma ) &{}\quad -f(\gamma ) \\ 0 &{}\quad \beta \left[ \frac{\gamma + \xi (\omega \gamma ^2 + 1)}{(1 + \alpha \xi )(\omega \gamma ^2 + 1) + \gamma } \right] - \delta \\ \end{array} \right) . \end{aligned}$$

(37)

From $J_{(0,0)}$, the determinant is $\frac{\beta \xi }{1 + \alpha \xi } - \delta$, which shows that $E_0^* = (0,0)$ is a saddle node, whenever $(\beta \xi - \delta (1+\alpha \xi )) < 0$ and unstable otherwise.

From $J_{(\gamma ,0)}$, the determinant is $g^{'}(\gamma )f(\gamma )\left( \beta \left[ \frac{\gamma + \xi (\omega \gamma ^2 + 1)}{(1 + \alpha \xi )(\omega \gamma ^2 + 1) + \gamma } \right] - \delta \right)$. This implies that the determinant is positive if $\left( \beta \left[ \frac{\gamma + \xi (\omega \gamma ^2 + 1)}{(1 + \alpha \xi )(\omega \gamma ^2 + 1) + \gamma } \right] - \delta \right) < 0$, since $g^{'}(\gamma ) = \frac{-1}{\gamma }((1+\alpha \xi )(\omega \gamma ^2+ 1) + \gamma ) <0$ and $f(\gamma )= \frac{\gamma }{(1+\alpha \xi )(\omega \gamma ^2+ 1) + \gamma } >0$. Evaluating the community matrix at the interior equilibria point $E_2^* = (x_1^*,y_1^*)$ and $E_3^* = (x_2^*,y_2^*)$, we obtain,

$$\begin{aligned} J_{(x_1^*,y_1^*)}= & {} \left( \begin{array}{cc} g^{'}(x_1^*)f(x_1^*) &{} -f(x_1^*) \\ \left( \beta f^{'}(x_1^*)(1 + \frac{\xi }{x_1^*}(\omega {x_1^*}^2 + 1)) + \beta f(x_1^*) \frac{\xi }{{x_1^*}^2}(\omega {x_1^*}^2 - 1) \right) y_1^* &{} 0 \\ \end{array} \right) , \nonumber \\ \end{aligned}$$

(38)

$$\begin{aligned} J_{(x_2^*,y_2^*)}= & {} \left( \begin{array}{cc} g^{'}(x_2^*)f(x_2^*) &{} -f(x_2^*) \\ \left( \beta f^{'}(x_2^*)\left( 1 + \frac{\xi }{x_2^*}(\omega {x_2^*}^2 + 1)\right) + \beta f(x_2^*) \frac{\xi }{{x_2^*}^2}(\omega {x_2^*}^2 - 1) \right) y_2^* &{} 0 \\ \end{array} \right) . \nonumber \\ \end{aligned}$$

(39)

Now, let ${h}(x) = \beta f(x)\left( 1 + \frac{\xi }{x}(\omega x^2 + 1)\right) - \delta ,$ i.e., ${h}(x) = \frac{(\beta \xi -\delta (1+\alpha \xi ))( \omega x^2+1)+(\beta -\delta )x}{(1+\alpha \xi )(\omega x^2 + 1)+ x}$. Clearly, for $\omega > \frac{(\beta -\delta )^2}{4(\beta \xi -\delta (1+\alpha \xi ))^2}, \ h(x) < 0,$ for all $x > 0.$ It can be seen that the predator isoclines, $x_1^* \ \& \ x_2^*$ are the roots of h(x) and the necessary condition for the existence of $x_1^*$ and $x_2^*$ is $\beta \xi - \delta (1+ \alpha \xi ) < 0.$ Hence

$$\begin{aligned} {h}(x) > 0, \ x_1^*< x < x_2^* \end{aligned}$$

(40)

and

$$\begin{aligned} {h}(x)< 0, 0< x < x_1^* \text { or } x > x_2^*. \end{aligned}$$

(41)

Inequalities (40) and (41) imply that

$$\begin{aligned} {h}^{'}(x_1^*) > 0, \ {h}^{'}(x_2^*) < 0. \end{aligned}$$

(42)

From definition of h(x),  we see that ${h}^{'}(x) = \beta f^{'}(x )\left( 1 + \frac{\xi }{x }(\omega {x }^2 + 1)\right) + \beta f(x ) \frac{\xi }{{x }^2}(\omega {x_1 }^2 - 1),$ implying that,

$$\begin{aligned} \beta f^{'}(x_1^*)\left( 1 + \frac{\xi }{x_1^*}(\omega {x_1^*}^2 + 1)\right) + \beta f(x_1^*) \frac{\xi }{{x_1^*}^2}(\omega {x_1^*}^2 - 1) > 0, \end{aligned}$$

(43)

$$\begin{aligned} \beta f^{'}(x_2^*)\left( 1 + \frac{\xi }{x_2^*}(\omega {x_2^*}^2 + 1)\right) + \beta f(x_2^*) \frac{\xi }{{x_2^*}^2}(\omega {x_2^*}^2 - 1) < 0. \end{aligned}$$

(44)

Now, the characteristic equation associated with the community matrix evaluated at the interior equilibrium $E_2^{*} = (x_1^*,y_1^*)$ is given by

$$\begin{aligned} \lambda ^2 - Tr J|_{(x_1^*,y_1^*)} \lambda + Det J|_{(x_1^*,y_1^*)} = 0. \end{aligned}$$

(45)

The determinant $Det J|_{(x_1^*,y_1^*)}$ is given by $\beta {f}(x_1^*)\left( \beta f^{'}(x_1^* )\left( 1 + \frac{\xi }{x_1^* }(\omega {x_1^* }^2 + 1)\right) \right. \left. + \beta f(x_1^* ) \frac{\xi }{{x_1^* }^2}\left( \omega {x_1^* }^2 - 1\right) \right)$. From (43), we conclude that $Det J|_{(x_1^*,y_1^*)} > 0,$ as ${f}({x_1}^*) = \frac{{x_1}^*}{(1+\alpha \xi )(\omega {{x_1}^*}^2 + 1)+ {x_1}^*} > 0.$ Hence by Routh–Hurwitz criterion [18], $(x_1^*,y_1^*)$ is locally asymptotically stable if $Tr J|_{(x_1^*,y_1^*)} < 0$ and unstable if $Tr J|_{(x_1^*,y_1^*)} > 0.$ We have

$$\begin{aligned} Tr J|_{(x_1^*,y_1^*)} = \left( 3\omega {x_1^*}^2(1 + \alpha \xi ) + 2x_1^*(1 -\omega \gamma (1 + \alpha \xi )) + (1 + \alpha \xi ) - \gamma \right) \left( \frac{-1}{\gamma }\right) f(x_1^*) \end{aligned}$$

(46)

to be negative whenever the slope of the prey isocline is negative (as the term in the brackets of R.H.S. of (46) represents the slope of the prey isocline $(= g^{'}(x))$ at $(x_1^{*},y_1^{*})$. Now, let $H(x) =\left( 3\omega {x}^2(1 + \alpha \xi ) + 2x(1 -\omega \gamma (1 + \alpha \xi )) + (1 + \alpha \xi ) - \gamma \right) .$ Hence the interior equilibrium $(x_1^{*},y_1^{*})$ is locally asymptotically stable if $H(x_1^*) > 0$ and unstable if $H(x_1^*) < 0.$

Conjecture 2

The interior equilibrium $E_2^* = (x_1^*,y_1^*)$ loses its stability through Hopf bifurcation when $Tr J|_{(x_1^*,y_1^*)} = 0$ with respect to the bifurcation parameter $\xi$- quantity of additional food(while the other parameters are fixed). This can be seen from figures 4, 6, 8 and Table 3 which deal with the global dynamics of the additional food provided system with respect to the variation of $\xi$. Also, a necessary condition for the occurrence of Hopf bifurcation can be obtained from the following equation.

$$\begin{aligned} H(x_1^*) = (3\omega {x_1^*}^2(1 + \alpha \xi ) + 2x_1^*(1 -\omega \gamma (1 + \alpha \xi )) + (1 + \alpha \xi ) - \gamma ) = 0. \end{aligned}$$

(47)

Substituting for $x_1^*$ in the above equation, we obtain the following parametric relation

$$\begin{aligned}&3w(1+ \alpha \xi )\left[ \frac{(\beta - \delta ) - \sqrt{{(\beta - \delta )}^2 - 4 \omega {[\delta (1 + \alpha \xi ) - \beta \xi ]}^2}}{2 \omega [\delta (1 + \alpha \xi ) - \beta \xi ]} \right] ^2 \\&\quad +\; (2-2w\gamma (1+ \alpha \xi ))\left[ \frac{(\beta - \delta ) - \sqrt{{(\beta - \delta )}^2 - 4 \omega {[\delta (1 + \alpha \xi ) - \beta \xi ]}^2}}{2 \omega [\delta (1 + \alpha \xi ) - \beta \xi ]} \right] \\&\quad + \;(1+ \alpha \xi ) - \gamma = 0 \end{aligned}$$

which is a necessary condition for the occurrence of Hopf bifurcation.

Now, from (44), we see that $Det J|_{(x_2^*,y_2^*)} < 0,$ which implies that the product of eigen values is negative. Hence, interior equilibrium $E_3 = (x_2^*,y_2^*)$ continues to remain as saddle through out its existence.

As seen in the initial system (7)–(8), for the additional food provided system (33)–(34) also, the nature of the interior equilibrium depends upon the shape of the prey isocline. This is discussed below in four different cases.

• If the equation $H(x) = 0$ has both positive roots ($H_1, H_2$ with $0< H_1 < H_2$), then $(x_1^*,y_1^*)$ is stable whenever $x_1^*$ does not belong to $(H_1,H_2)$(region wherein $g^{'}(x_1^*) < 0$) and is unstable if $x_1^*$ belongs to $(H_1,H_2)$(region wherein $g^{'}(x_1^*) > 0$).

• If the equation $H(x) = 0$ has a positive root and a negative root ($H_1, H_2$ with $H_1< 0 < H_2$), then $(x_1^*,y_1^*)$ is stable whenever $x_1^*$ does not belong to $(0,H_2)$(region wherein $g^{'}(x_1^*) < 0$) and is unstable if $x_1^*$ belongs to $(0,H_2)$(region wherein $g^{'}(x_1^*) > 0$) in the positive quadrant.

• If the equation $H(x) = 0$ has both negative roots ($H_1, H_2$ with $H_1< H_2 < 0$), then, $(x_1^*,y_1^*)$ is always asymptotically stable (since, $g^{'}(x_1^*) < 0$ always).

• If the equation $H(x) = 0$ does not admit any real root, then as in previous case, $(x_1^*,y_1^*)$ is always asymptotically stable.

The instability of the interior equilibrium $E_2^*$ in above cases induces a locally asymptotically stable limit cycle into the system.

Global Dynamics and Controllability for the Additional Food Provided System with Respect to Region I of the Initial System

From $J_{(0,0)},J_{(\gamma ,0)}$ and $J_{(x_1^*,y_1^*)}$, we infer that the nature of the equilibrium points $(0,0), (\gamma , 0)$ and $(x_1^*,y_1^*)$ depends on the signs of the expressions $\frac{\beta \xi }{1 + \alpha \xi } - \delta$ (an eigen value of $J_{(0,0)}$), $\beta \left( \frac{\gamma + \xi (w \gamma ^2 + 1)}{(1 + \alpha \xi )(w \gamma ^2 + 1) + \gamma }\right) - \delta$ (an eigen value of $J_{(\gamma ,0)}$) and $g'(x_1^*) = 0$ (Hopf bifurcation indicator). The second interior equilibrium $(x_2^*,y_2^*)$ continues to remain saddle throughout its existence. We see that the necessary condition for the interior equilibria to exist is ${(\beta - \delta )}^2 - 4w{(-\beta \xi + \delta (1 + \alpha \xi ))}^2 > 0.$

Hence, we consider the following curves (related to the expressions mentioned above) in the positive quadrant of the $(\alpha ,\xi )$ space:

$$\begin{aligned} \beta \xi - \delta (1 + \alpha \xi ) = 0 \end{aligned}$$

(48)

Prey elimination curve (PEC) at (0, 0)

$$\begin{aligned} \beta (\gamma + \xi (w \gamma ^2 + 1)) - \delta ((1 + \alpha \xi )(w \gamma ^2 + 1) + \gamma ) = 0 \end{aligned}$$

(49)

Transcritical bifurcation curve (TBC) at $(\gamma ,0)$

$$\begin{aligned}&3w(1+ \alpha \xi )\left[ \frac{(\beta - \delta ) - \sqrt{{(\beta - \delta )}^2 - 4 \omega {[\delta (1 + \alpha \xi ) - \beta \xi ]}^2}}{2 \omega [\delta (1 + \alpha \xi ) - \beta \xi ]} \right] ^2 \nonumber \\&\quad + (2-2w\gamma (1+ \alpha \xi ))\left[ \frac{(\beta - \delta ) - \sqrt{{(\beta - \delta )}^2 - 4 \omega {[\delta (1 + \alpha \xi ) - \beta \xi ]}^2}}{2 \omega [\delta (1 + \alpha \xi ) - \beta \xi ]} \right] \nonumber \\&\quad + (1+ \alpha \xi ) - \gamma = 0 \end{aligned}$$

(50)

Hopf bifurcation curve (HBC) at $(x_1^*,y_1^*)$

$$\begin{aligned} {(\beta - \delta )}^2 - 4w{(-\beta \xi + \delta (1 + \alpha \xi ))}^2 = 0 \end{aligned}$$

(51)

Discriminant curve (DISC)

We see that each of the curves (48)–(51) divide the positive quadrant of $(\alpha ,\xi )$ space into two regions which characterize the nature of the associated equilibrium point of (33)–(34). Equation (51) gives the region of existence of the predator isoclines(possible region of existence of interior equilibria). It can be observed that $\alpha = \frac{\beta }{\delta }$ is an asymptote for the curves (48), (49) and (51).

In this paper, we study the consequences of providing additional food to the region I(comprising of regions I-1, I-2 and I-3) of the initial system (7)–(8) and derive conclusions basing on the global dynamics of the additional food provided system (33)–(34).

In this regard, we study, the dynamics of the additional food provided system (33)–(34) through the curves (48)–(51) under the conditions I-1, I-2, I-3 in Table 1. For the sake of brevity, the dynamics of the additional food provided system for the remaining conditions((Con-II)-(Con-VI)) will be discussed in the future continuation work.

On provision of additional food to the region I of the initial system, we observe the following dynamics, depicted in Figs. 4, 6, and 8. In the first scenario there is a possibility that the system can undergo a single Hopf bifurcation(under condition I-1), in the second the system can undergo double Hopf bifurcation(under condition I-2) whereas in the third(under condition I-3), the system does not undergo Hopf bifurcation.

Fig. 4

Additional food provided system (33)–(34) for $\beta = 2.2, \ \delta = 0.4, \ \omega = 8.0, \ and \ \gamma = 1.2.$ The parameters chosen satisfy the condition ${I-1}$ in Table 1. This figure represents the division of control parameter space by the discriminant curve (DISC) (51), the prey elimination curve (PEC) (48), the Hopf bifurcation curve (HBC) (50), the transcritical bifurcation curve (TBC) (49) and the curve $\alpha = \frac{\beta }{\delta }$

Fig. 5

Isoclines for additional food provided system (33)–(34) for $\beta = 2.2, \ \delta = 0.4, \ \omega = 8.0, \ \& \ \gamma = 1.2,$ under condition $I-1$

Fig. 6

Additional food provided system (33)–(34) for $\beta = 2.2, \ \delta = 0.4, \ \omega = 7, \ and \ \gamma = 0.63.$ The parameters chosen satisfy the condition ${I-2}$ in Table 1. This figure represents the division of control parameter space by the discriminant curve (DISC) (51), the prey elimination curve (PEC) (48), the Hopf bifurcation curve (HBC) (50), the transcritical bifurcation curve (TBC) (49) and the curve $\alpha = \frac{\beta }{\delta }$

We now discuss the significance of each of the regions presented in Fig. 4.

• Region A1 of Fig. 4

  For a fixed $\alpha (< \frac{\beta }{\delta })$ as $\xi$ increases from zero, we enter the region A1 of Fig. 4. The system dynamics can be seen form the behavior of the isoclines which are shown in the frame A of Fig. 5. Clearly the system does not even admit predator isoclines and all the solutions tend to the axial equilibrium $(\gamma ,0).$ Here the equilibrium (0, 0) coexists with saddle nature.

• Region A2 of Fig. 4

  By further provision of additional food, the predator isoclines come into existence as soon as the system touches the discriminant curve (i.e., when $\ \xi = \frac{\beta - (1-2\sqrt{w})\delta }{2\sqrt{w}(\beta - \delta \alpha )})$ and an unstable interior equilibrium is born. On this discriminant curve, all the solutions of the system goes to either interior equilibrium or the axial equilibrium $(\gamma ,0)$ depending on the initial value. (0, 0) continues to remain as saddle. On further provision of additional food (i.e., for, $\ \xi > \frac{\beta - (1-2\sqrt{w})\delta }{2\sqrt{w}(\beta - \delta \alpha )}),$ we move to the region A2. The system dynamics can be seen from the behavior of isoclines as depicted in frame B of Fig. 5. Two interior equilibria $E_2^*$ and $E_3^*$ tend to exist. The interior equilibrium $E_2^*$ is unstable whereas the second interior equilibrium $E_3^*$ has a saddle nature. The latter equilibrium continues to remain saddle throughout its existence. The instability of $E_2^*$ induces a stable limit cycle. Due to this there exists a separatrix such that the solution trajectories that lie above this manifold converge to the stable limit cycle surrounding $E_2^*$ and the trajectories which lie below converge to stable equilibrium $E_1^*.$ On further increase of $\xi$ the limit cycle runs into the saddle point $E_3^*$ and forms a homoclinic orbit. After the disappearance of the limit cycle all the solutions tend toward $E_1^*.$

  Increasing $\xi$ further, the second interior equilibrium $E_3^*$ vanishes by undergoing transcritical bifurcation with $(\gamma ,0),$ at $\xi = \frac{\delta (w\gamma ^2 + 1) - \gamma (\beta - \delta )}{(w\gamma ^2 + 1)(\beta - \alpha \delta )}.$ Upon further increase in $\xi ,$ enter region A3.

• Region A3 of Fig. 4

  The system dynamics for this region can be understood from frame C of Fig. 5. In this region all the solutions of the system goes to the stable limit cycle induced due to the instability of interior equilibrium $E_2^*$. The axial equilibrium $E_1^*$ becomes saddle and $E_0^*$ continues to remain as saddle. Further provision of additional food leads to Hopf bifurcation of $E_2^*$ and the system moves to the region A4.

• Region A4 of Fig. 4

  The behavior of the system isoclines for this region can be seen from frame D of Fig. 5. The interior equilibrium point $E_2^*$ becomes stable. The solution trajectories will tend to the stable interior point $E_2^*.$ The axial equilibria, $E_0^*$ and $E_1^*$ continue to remain as saddle. Continuous supply of additional food in this region leads us to touch the prey elimination curve (i.e., $\ \text {when} \$) and the prey goes to zero and we move into region A5.

• Region A5 of Fig. 4

  We have very interesting dynamics happening in this region. From frame E of Fig. 5, it can be seen that the system does not admit a positive interior equilibrium and also there is an unbounded growth for the predators in this region. The predators in this region survive only on the additional food provided. Withdrawal of additional food drives the predator population to zero.

• Region A6 of Fig. 4

  For a fixed $\alpha (> \frac{\beta }{\delta })$ as $\xi$ increases from zero, we enter the region A6 of Fig. 4. The system dynamics can be seen form the behavior of the isoclines which are shown in the frame F of Fig. 5. As in region A1, the system does not even admit predator isoclines and all the solutions tend to the axial equilibrium $E_1^*.$ Here the equilibrium $E_0^*$ coexists with saddle nature.

Fig. 7

Isoclines for additional food provided system (33)–(34) for $\beta = 2.2, \ \delta = 0.4, \ \omega = 8.0, \ \& \ \gamma = 1.2,$ under condition $I-2$

Fig. 8

Additional food provided system (33)–(34) for $\beta = 2.2,\ \delta = 0.4, \ \omega = 6.7, \ and \ \gamma = 0.42.$ The parameters chosen satisfy the condition ${I-3}$ in Table 1. This figure represents the division of control parameter space by the discriminant curve (DISC) (51), the prey elimination curve (PEC) (48), the transcritical bifurcation curve (TBC) (49) and the curve $\alpha = \frac{\beta }{\delta }$

We now discuss the significance of the region B2(which exhibits interesting dynamics) presented in Fig. 6. The dynamics for the remaining regions B1, B3–B8 will be similar to that of the regions A1–A6 of Fig. 4.

• Region B2 of Fig. 6

  On provision of additional food in region B1, the predator isoclines come into existence as soon as the system touches the discriminant curve and an stable interior equilibrium is born, which can be seen from frame B of Fig. 7. On this discriminant curve, all the solutions of the system goes to either interior equilibrium or the axial equilibrium $E_1^*$ depending on the initial value. $E_0^*$ continues to remain as saddle. On further provision of additional food, we move to the region B2. The system dynamics can be seen from the behavior of isoclines as depicted in frame C of Fig. 7. Two interior equilibria $E_2^*$ and $E_3^*$ tend to exist. The interior equilibrium $E_2^*$ is stable whereas the second interior equilibrium $E_3^*$ has a saddle nature. This interior equilibrium continues to remain saddle throughout its existence. The stable manifold of the saddle point $E_3^*$ separates the phase plane into two domains of attraction. The solution trajectories that lie above this manifold converge to $E_2^*$ and the trajectories which lie below converge to $E_1^*.$ Increasing $\xi$ further, there exists a critical value of $\alpha$, denoted by $\alpha ^{'}$, where, both TBC and HBC intersect.

Conjecture 3

For $0< \alpha < \alpha ^{'}$, the interior equilibrium $E_2^*$ undergoes Hopf bifurcation with respect to the bifurcation parameter $\xi$ - quantity of additional food(while the other parameters are fixed) and we enter region B3 or it can happen that for $\alpha \ge \alpha ^{'}$ the second interior equilibrium $E_3^*$ can vanish by undergoing transcritical bifurcation(with respect to the bifurcation parameter $\xi$) with $(\gamma ,0),$ at $\xi = \frac{\delta (w\gamma ^2 + 1) - \gamma (\beta - \delta )}{(w\gamma ^2 + 1)(\beta - \alpha \delta )}.$ In this situation, there exists another critical value of $\alpha (< \frac{\beta }{\delta })$ given by $\alpha ^*,$ such that if $\alpha ^{'}<\alpha < \alpha ^*,$ we enter region B4. For all $\alpha > \alpha ^*,$ we move to the region B6.

Similar dynamics can be discussed for regions C1–C5 of Fig. 8.

The global dynamics of the additional food provided system for the different scenarios discussed above is summarized in the Table 3. The space and time complexity analysis for the border cases are shown in Table 5 in Appendix.

Table 3 Global dynamics of the Additional food provided system under Condition-I

The analysis presented above helps us to study some of the controllability aspects pertaining to the system (33)–(34) with respect to the control parameters $\alpha$ and $\xi$. The analysis suggests that, for an appropriate choice of additional food, the system can either be driven to a desired equilibrium level or to a limit cycle surrounding the desired equilibrium. If $(\tilde{x},\tilde{y})$ is the desired equilibrium state for the system, then $(\tilde{x},\tilde{y})$ can become an equilibrium point of the system (33)–(34), provided $\alpha > 0$ and $\xi > 0$ are chosen to satisfy

$$\begin{aligned} {\tilde{x}}= & {} \frac{(\beta - \delta ) - \sqrt{{(\beta - \delta )}^2 - 4 \omega {[\delta (1 + \alpha \xi ) - \beta \xi ]}^2}}{2 \omega [\delta (1 + \alpha \xi ) - \beta \xi ]}, \end{aligned}$$

(52)

$$\begin{aligned} { \tilde{y}}= & {} \left( (1 + \alpha \xi )(\omega {\tilde{x}}^2 + 1) + {\tilde{x}}\right) \left( 1 - \frac{{\tilde{x}}}{\gamma }\right) . \end{aligned}$$

(53)

If $H(\tilde{x}) <0$ then this equilibrium $(\tilde{x},\tilde{y})$ can be reached asymptotically. On the other hand, if $H(\tilde{x}) > 0$ then the equilibrium would be unstable, as a result, solutions in the vicinity of this equilibrium approach a limit cycle surrounding $(\tilde{x},\tilde{y})$. For the given system parameters $\beta , \delta$ and $\gamma$ and the desired equilibrium $(\tilde{x},\tilde{y})$, the components of intersection of these two curves (52)–(53) give us the values of $\alpha$ and $\xi$ for which the considered system admits $(\tilde{x},\tilde{y})$ as its equilibrium.

The analysis also suggests that, for an appropriate choice of additional food, the equilibrium $(\tilde{x},\tilde{y})$ will remain as a saddle throughout its existence, provided, the values of $\alpha$ and $\xi$ are chosen to satisfy the following equations(for a given choice of $\beta , \delta ,$ $\gamma$ and $(\tilde{x},\tilde{y}),$

$$\begin{aligned} {\tilde{x}}= & {} \frac{(\beta - \delta ) + \sqrt{{(\beta - \delta )}^2 - 4 \omega {[\delta (1 + \alpha \xi ) - \beta \xi ]}^2}}{2 \omega [\delta (1 + \alpha \xi ) - \beta \xi ]}, \end{aligned}$$

(54)

$$\begin{aligned} { \tilde{y}}= & {} ((1 + \alpha \xi )(\omega {\tilde{x}}^2 + 1) + {\tilde{x}})\left( 1 - \frac{{\tilde{x}}}{\gamma }\right) . \end{aligned}$$

(55)

Consequences of Providing Additional Food to Predators

In this section, we discuss the consequences of providing additional food to the predators, when they exhibit type IV functional response towards the available food. It can be seen from the above discussions that the quality of additional food $\alpha$ and its position with respect to $\frac{\beta }{\delta }$ plays a crucial role in determining the eventual state of the system. In fact it is interesting to note that the system takes two different directions basing on the relationship between $\alpha$ and $\frac{\beta }{\delta }.$ As defined in [23, 31], we characterize the additional food to be of high quality if $\alpha < \frac{\beta }{\delta }$ and it is of low quality if $\alpha > \frac{\beta }{\delta }$. Here quality reflects the ability of the predators to control the prey by consuming the additional food. From the expressions of $\alpha , \beta$ and $\delta ,$ we observe that the additional food is of high (low) quality if the maximum growth rate of the predators due to consumption of additional food ($\frac{\epsilon _2}{h_2}$) is greater (less) than the natural death rate (m) of the predators.

If the system (7)–(8) does not support the predator–prey coexistence initially (i.e., the system does not admit an interior equilibrium in the absence of additional food), then coexistence cannot be achieved by providing low quality additional food to predators. Whereas provision of additional food of high quality with supply level satisfying $\frac{\beta - (1-2\sqrt{w})\delta }{2\sqrt{w}(\beta - \delta \alpha )}< \xi < {\frac{\delta }{\beta - \delta \alpha }}$, brings coexistence into the system.

On further increase of additional food supply from ${\frac{\delta }{\beta - \delta \alpha }}$, the prey ceases to exist and the predators survive only on the additional food provided to them. Thus provision of additional food of high quality helps the predators to overcome the inhibitory effect of the prey, there by getting the coexistence of predator–prey system. Thus, initially even though the eco system is prey dominated, provision of additional food of high quality to the predators gets in the coexistence of the predator and prey. And also, the eradication of the prey can be realized by further provision of high quality additional food.

When $\alpha = \frac{\beta }{\delta },$ if the system does not admit any interior equilibrium in the absence of additional food then the system will not admit any interior equilibrium by providing any amount of additional food of the considered quality.

We observe from the control parameter space analysis that characteristics (quality) of additional food (which is the ratio of maximum growth rates of the predator due to consuming the prey and the additional food) plays a crucial role in the controllability of the considered ecosystem. This system can be steered to either prey dominated or predator dominated system for a suitable choice of food supply (subject to the parameters satisfying certain conditions).

Upon the extinction of prey from the ecosystem the predator can also be eliminated completely by with drawing the additional food from the ecosystem.

Discussion and Conclusions

The study of predator–prey dynamics in presence of additional food to predators and consequences of such provision on the interacting species in the ecosystem has off late been a topic of interest in the fields of theoretical as well as practical biological control [4, 5, 13, 22, 26, 28,29,30,31, 34, 36]. The aim and goal of these studies is to derive strategies for biological control of pests (treated as prey) using their natural enemies (treated as predators) or biological conservation of either of the interacting species. From some of the recent theoretical works [23, 27,28,29,30,31], we see that the quality and quantity of additional food supplied to the predators play an important role in controlling the pest in the agro-ecosystems and also in the conservation of the interacting species. In these works the functional response of predators towards available food was assumed to be of Holling types II and III. The outcomes of the study have confirmed some of the observations made by the experimental scientists. Some limitation of the study presented in [31] include the unbounded growth for predators and also maintaining the predators at any level with the same amount of additional food supply. This limitation was overcome when mutual interference was assumed among predators [23].

In this work, a detailed study is done on the dynamics of a predator–prey model wherein the predator is provided with additional food and the Holling type IV functional response has been assumed for the predator towards the available food, where initially the system is prey dominated due to inhibitory effect of the prey. As in [23, 27,28,29,30,31], we make no distinction (such as complementary, substitutable, essential or alternative) for the additional food provided to the predators. The quality of the additional food is characterized by its nutritive value and handling time. It is termed as low quality if the maximum growth rate of the predator due to consumption of additional food is less than the natural death rate of the predator and it is of high quality if the above mentioned relation reverses. The study undertaken in this work indicates that the considered system exhibits apparent competition only when the predators are provided with high quality additional food. The system analysis bifurcates the qualitative study into three significant cases that depend on the quality of the additional food as presented below.

Case 1 (Low Quality Additional Food)

First, let us consider the case where the maximum growth rate of the predator due to consuming additional food is less than the natural death rate of the predator(low quality additional food).

In this case, we clearly have either the handling time for the predator of the additional food to be higher or the nutritive value the additional food to be lower than that of the target prey. In this case we find that, if initially the predators are unable to survive due to the group defense(inhibitory effect) of the prey, then providing any amount of additional food of low quality can not bring in coexistence between the prey and the predator. This is due to the fact that, if in the absence of additional food itself the predators are not able to predate on the prey, then providing additional food of lower quality will not improve the sustenance of the predators. Moreover the presence of additional food distracts the predators (from the target prey) which are time limited. So in this situation controlling the prey using biological means cannot be achieved.

Case 2 (High Quality Additional Food)

Now let us consider the case where the maximum growth rate of the predator due to consuming additional food is greater than the natural death rate of the predator(high quality additional food). The system admits three different behaviors basing on the initial value chosen in the region I of the $(\omega ,\gamma )$ parameter space(refer Fig. 2).

If the system does not support coexistence between the prey and predator in the absence of additional food due to the inhibitory effect of the prey, then coexistence(either stable or unstable) can be brought into the system by providing additional food of high quality.

On supply of additional food if the system admits a stable interior equilibrium point, then the stable coexistence can continue to remain with increased additional food level till the prey vanishes from the system. Or this stable coexistence can depend on the quality and quantity of the additional food. If the quality of additional food is greater than a critical $\alpha ^*$ then the stable coexistence will continue to remain with increased additional food level till the prey vanishes from the system. On the other hand, if the quality of the additional food is less than the said critical value $\alpha ^*,$ provision of additional food, induces oscillations into the system. With further increase in the quantity of additional food, the system once again stabilizes at low prey equilibrium density. While retaining the stability, this low equilibrium value of the prey continues to decrease with increase in the additional food quantity and the prey goes to extinction for a specific level of additional food supply. This behavior may be attributed to the fact that provision of additional food of very high quality increases the fecundity of the predators which in turn increases the predation pressure on the prey. Also, the abundance of predators in the environment and their dependence on both additional food as well as prey brings in oscillations into the system. Beyond a certain level of food supply, the predator fails to track the prey due to its low density and at this stage the system gets stabilized. Further increase in the quantity of additional food increases the predators which in turn leads to the extinction of the prey population. Thus the prey can be controlled biologically in this case.

In the other case if the system admits an unstable interior equilibrium with initial supply of additional food, then on further increase in the quantity the oscillations in the system can be subdued and stable coexistence can be achieved. Continuous supply of additional food further, will extinct the prey, thereby achieving the biological control. The initial oscillations in the system can be attributed to the relatively high carrying capacity of the system with respect to the earlier cases. Due to the continuous supply of high quality additional food from hereon, the predators fecundity and ferocity increases thereby getting the stable coexistence. As in the earlier situation further increase in the quantity of additional food leads to the extinction of the prey population.

Case 3 (Borderline Case)

Finally, we consider the case where the maximum growth rate of the predator due to consuming additional food is equal to the natural death rate of the predator. If initially in the absence of additional food the system does not admit any interior equilibrium then providing any amount of such additional food will not bring the coexistence into the system. This behavior can be attributed to the group defense(inhibitory effect) of the prey.

In summary we see that the modified version of predator–prey model with Holling type IV functional response with provision of additional food exhibits very interesting dynamics. We see that, by providing additional food of a appropriate choice, it is possible to drive both the prey and predator population to a desired level thus allowing to biologically control the system. The quality and supply level of the additional food plays an important role in the control of the system. It is possible to eliminate the oscillations or oscillations can be brought in by providing additional food of appropriate choice and supply level. Also, the predators can be eliminated by providing them with low quality additional food, which essentially reduces the per capita growth rate of the predators compared to its natural death rate, there by relieving the prey from predation pressure. While the prey can be eliminated from the system by providing high quality additional food, care must be taken in the choice of the quality. Providing additional food of very high quality can destabilize the system and bring in oscillations which can be avoided by an appropriate choice on the quality of the additional food.

We conclude that with provision of additional food as a tool, a predator–prey system (with inhibitory effect of the prey towards predator) can be controlled and steered to a desirable state. With appropriate choice on the quality and quantity of additional food, the predator–prey system can be stabilized at a state with low prey and high predator densities or high prey and low predator densities. It is also possible to eliminate either of the interacting species through provision of suitable additional food to predators. This analysis offers eco-friendly strategies to manage a predator–prey system. The vital role of the quality and quantity of the additional food in the system dynamics cautions the manager on the choice of the additional food for realizing the goal in the biological control programme. An arbitrary choice of the additional food can result in completely opposite results to the desired ones.

Appendix

See Tables 4 and 5.

Table 4 Space and time complexity analysis for the border cases of the initial system (7)–(8)

Table 5 Space and time complexity analysis for the border cases of the additional food provided system (33)–(34)