Achieving Minimum-Time Biological Conservation and Pest Management for Additional Food provided Predator–Prey Systems involving Inhibitory Effect: A Qualitative Investigation

Abstract

Theoretical and experimental studies on prey–predator systems where predator is supplied with alternate sources of food have received significant attention over the years due to their relevance in achieving biological conservation and biological control. Some of the outcomes of these studies suggest that with appropriate quality and quantity of additional food, the system can be steered towards any desired state eventually with time. One of the limitations of previous studies is that the desired state is reached asymptotically, which makes the outcomes not easily applicable in practical scenarios. To overcome this limitation, in this work, we formulate and study optimal control problems to achieve the desired outcomes in minimum (finite) time. We consider two different models of additional food provided prey–predator systems involving Holling type IV functional response (with inhibitory effect of prey). In the first scenario, additional food is incorporated implicitly into the predator’s functional response with a possibility of achieving biological conservation through co-existence of species and biological control by maintaining prey at a level that is least harmful to the system. In the second, the effect of additional food is incorporated explicitly into the predator’s compartment with the goal of pest management by maintaining prey density at a very minimal damaging level. For both cases, appropriate optimal control strategies are derived and the theoretical findings are illustrated by numerical simulations. We also discuss the ecological significance of the theoretical findings for both models.

1 Introduction

Provision of additional food to the predators and its impact on predator–prey system dynamics has become one of the active and important areas of research for biologists, ecologists (both theoretical and experimental), statisticians, and mathematicians (Beltrà et al. 2017; Elkinton et al. 2004; Ghasemzadeh et al. 2017; Gurubilli et al. 2017; Harwood et al. 2004, 2005; Hik 1995; Kozak et al. 1994; Landis et al. 2000; Putman and Staines 2004; Redpath et al. 2001; Soltaniyan et al. 2020; Van Baalen et al. 2001). This is because of the applicability of outcomes of these studies in achieving both biological conservation of species and biological control (bio-control) of harmful/invasive species. Provision of additional food to the generalist predators not only facilitates depredation on prey species by diverting the predator but also provides means to sustain the predator density when the target prey species are low in density (Beltrà et al. 2017; Elkinton et al. 2004; Harwood et al. 2005; Kozak et al. 1994, 1995; Redpath et al. 2001). However, lack of adequate care while providing additional food could lead to undesired outcomes (Putman and Staines 2004; Robb et al. 2008). On the other hand, to achieve bio-control of harmful pests in the ecosystem, habitat management and integrated pest management schemes (Landis et al. 2000) provide additional food supplements to generalist natural enemies for increasing their survival, oviposition rate, longevity, fecundity and predation rate thereby resulting in effective control of the pests (Ghasemzadeh et al. 2017; Messelink et al. 2014; Sabelis and Van Rijn 2006; Urbaneja-Bernat et al. 2013; Vandekerkhove and De Clercq 2010; Wade et al. 2008).

Some of the observations from field studies and greenhouse experiments by ecologists show that the quality of additional food plays a vital role in determining the eventual state of the system by affecting its global dynamics (Blackburn et al. 2016; Calixto et al. 2013; Magro and Parra 2004; Marcarelli et al. 2011; Putman and Staines 2004; Wakefield et al. 2010). Quality of additional food is generally measured in terms of the nutritional value of the additional food item and the growth rate of the predator on consumption of the additional food relative to the consumption of prey. The mirid predator Macrolophus pygmaeus, which is a widely used natural enemy to control whiteflies and arthropod pests in Mediterranean Europe, is reared on eggs of Ephestia kuehniella for their production and development. Bee pollen was found to be nutritionally adequate for M. pygmaeus as an alternative source of food for improving its fitness (Vandekerkhove and De Clercq 2010). On the other hand, results from (Magro and Parra 2004) show that the additional food composed of holotissue of Diatraea saccharalis pupae, fetal bovine serum, egg yolk lactoalbumin hydrolysate etc. is a low quality food for rearing Bracon hebetor Say (Hymenoptera: Braconidae) because 60% of the larvae failed to produce a protective cocoon during pupal phase. The study on responses to sugar (additional food) by the parasitoid Diadegma semiclausum which is a natural enemy of Plutella xylostella showed that the predator showed response only to the nutritional content irrespective of the quantity of sugar in the solution (Winkler et al. 2005). Also, it was seen that not all sugars were of high quality for the parasitoid. The effects of providing high quality and low quality additional food to predator species have been discussed in (Putman and Staines 2004; Kozak et al. 1994) and the review articles (Blackburn et al. 2016 and Lu et al. 2014 and references therein).

Some of the mathematical studies involving additional food provided prey–predator systems include (Das and Samanta 2018; Gurubilli et al. 2017; Ghosh et al. 2017; Prasad and Prasad 2018, 2019; Srinivasu et al. 2007). One of the key features of these mathematical studies is the Functional response, defined as the rate at which the predator captures prey (Kot 2001). Among various functional responses displayed by different taxa in nature, the Holling type IV functional response is one where the catchability of predator reduces at high densities of prey as a consequence of prey toxicity or interference. The prey species tend to exhibit group defense against their predator when in large numbers as a survival mechanism (Caro 2005; Collings 1997; Wilcox and Larsen 2008). This is also called as inhibitory effect of the prey. For example, spider mites reduce the predation rate of their natural enemy (predatory mite) Euseius sojaensis by living in groups of large numbers and sharing the web rather than building new webs (Yano 2012). Also, experimental outcomes of the work (McClure and Despland 2011) show that the group defense exhibited by the caterpillar species Malacosoma disstria reduced the predation risk by their natural enemy parasitoids in spite of multiple attacks due to increasing difficulty of attacking defense groups.

Recently, the authors in (Srinivasu et al. 2018a) and (Vamsi et al. 2019) have studied an additional food provided predator–prey system involving type IV functional response. Findings from these studies reveal that for an appropriate choice of quality and quantity of additional food, stable coexistence of both species can be achieved. It is also possible to eliminate either of the interacting species through provision of suitable choice of additional food. These findings are in accordance with the field outcomes presented in (Kozak et al. 1994, 1995; Putman and Staines 2004) and (Winkler et al. 2005). Though the findings of (Srinivasu et al. 2018a) and (Vamsi et al. 2019) are very helpful in the context of biological conservation and bio-control, they may not be of good help in practical scenarios owing to their asymptotic nature. To overcome these limitations, we wish to study the controllability aspects of the additional food system involving type IV response in order to achieve the desired outcomes in minimum (finite) time.

Motivated by the aforementioned observations and limitations, in this paper, we study two optimal control problems dealing with additional food provided systems involving type IV functional response with quality of additional food as the control parameter keeping the quantity of additional food fixed. The objective of these studies is to reach the desired state of the system in minimum (finite) time. Since quantity of additional food consumed by the predator is constrained by the gut volume of the predator, it is relevant to study the controllabilty aspects of the additional food system with respect to the quality of additional food for a fixed quantity. The study of controllability of additional food system with respect quantity has its own significance and can be found in the author’s work (Ananth and Vamsi 2021).

In this paper, we consider two models of additional food provided systems involving type IV functional response: In the first scenario, we consider the additional food implicitly incorporated into the predator’s functional response with predator exhibiting type II response with respect to the additional food. With the quality as the control parameter, we formulate and study a time optimal control problem. We use Filippov’s Existence Theorem to prove the existence of optimal solution and Pontryagin’s Maximum Principle to obtain the characteristics of the optimal solutions. In the second scenario, we model the additional food provision by explicitly incorporating it into the predator’s compartment thereby directly influencing the rate of change of predators. This makes the predator density vary linearly with respect to the additional food in contrast to the former case where additional food has a non-linear influence on the predator’s rate of change of population. This implies that in the second scenario, there is a possibility of obtaining linear feedback control which is very relevant in cases of inundative bio-control (Blackburn et al. 2016). Thus we model an error system and formulate a feedback control problem in this case. Numerical illustrations validate the theoretical results for both these studies. The findings from both studies find applications in the context of biological conservation and pest management. The results from the study of implicit control system suggest a possibility of achieving biological conservation and bio-control (achieved by maintaining the prey at a minimal damaging level). On the other hand, results from explicit control system suggest strategies for only bio-control.

The section-wise division of this article is as follows: In the next section, for the sake of providing clarity to the reader, we briefly discuss the type IV initial system and the corresponding additional food provided system. Later, in Sect. 3, we discuss the role of quality of additional food in the dynamics of the system. The next Sect. 4 is devoted to the time optimal control studies for the additional food provided system with quality as implicit control. Further, in Sect. 5 we present the optimal control studies with quality as explicit control. We first define the error system and later formulate a linear feedback control optimal control problem and study its optimal solutions and factors that affect the optimal solutions. We briefly study the role of inhibitory effect of prey in a subsection at the end of this section. Finally, we present the discussion and conclusions in Sect. 6.

2 The Type IV Predator–Prey System

The predator–prey systems involving type IV functional response in the absence of additional food (called as initial system) and in the presence of additional food have been derived in (Srinivasu et al. 2018a). To make it easier for the reader to understand the later sections of this paper, in this section, we provide a glimpse of the dynamics of initial system and additional food provided system involving Type IV functional response as discussed in (Srinivasu et al. 2018a). For detailed analysis of stability of the equilibria admitted by both the systems and details of the local and global dynamics of the systems, readers are requested to refer to the works (Srinivasu et al. 2018a; Vamsi et al. 2019)

Consider the predator–prey system involving type IV functional response given by the system of equations (with the time variable here indicated by T)

$$\begin{aligned} \dot{N}= & {}\, rN\bigg ( 1-\dfrac{N}{k}\bigg ) - \dfrac{cN}{a(bN^2 +1 ) + N}P \end{aligned}$$

(1)

$$\begin{aligned} \dot{P}= & {} \dfrac{eN}{a(bN^2 + 1) + N}P - mP \end{aligned}$$

(2)

where N is the prey population and P the predator population. The biological meaning of the parameters have been provided in the table below:

Parameters	Biological meaning
r	Intrinsic growth rate of the prey
k	Prey carrying capacity
m	Mortality rate of predators in the absence of prey
c	Maximum rate of predation in the absence of inhibitory effect
a	Half-saturation rate of predators in the absence of inhibitory effect
e	Maximum growth rate of predators due to consumption of prey
b	Inhibitory effect of the prey on predators’ foraging

Let $N = ax;\ t = rT; \text { and } P = y \frac{ra}{c}$; which implies, $dN = a dx$; $\frac{dt}{r} = dT$; $dP = \frac{ra}{c}dy$. Now, using the following transformations $\gamma = \frac{k}{a},\;\; \omega = ba^2, \;\;\; \beta = \frac{e}{r}, \;\;\; \delta = \frac{m}{r},$ we get the corresponding non-dimensionalized system as follows:

$$\begin{aligned} \dot{x}= & {} x\bigg ( 1-\dfrac{x}{\gamma } \bigg )- \bigg ( \dfrac{xy}{\omega x^2 + x + 1}\bigg ) \end{aligned}$$

(3)

$$\begin{aligned} \dot{y}= & {} \bigg ( \dfrac{\beta xy}{(\omega x^2 + 1) + x} \bigg ) - \delta y \end{aligned}$$

(4)

In the non-dimensional system, $\gamma$ and $\omega$ are parameters that represent the carrying capacity and inhibitory effect respectively. Now, consider the additional food of biomass A constantly supplied to the predators. The predator–prey system (1)–(2) now becomes

$$\begin{aligned} \dot{N}= & {} rN\bigg (1-\dfrac{N}{k}\bigg ) - \bigg (\dfrac{cN}{(A\eta \alpha + a)[bN^2+1] + N}\bigg )P, \end{aligned}$$

(5)

$$\begin{aligned} \dot{P}= & {} e\bigg (\dfrac{N+\eta A(bN^2+1)}{(A\eta \alpha + a)[bN^2+1] + N}\bigg )P - mP. \end{aligned}$$

(6)

Here, the parameter $\alpha$ is the ratio of the growth rate of predator when it consumes prey to the growth rate when it consumes additional food. In other words, $\alpha$ stands for the relative efficiency of the predator to convert either of the food available into predator biomass. $\alpha$ is inversely proportional to the nutritional value of the additional food and directly proportional to the handling time of the additional food. Since the conversion factor for prey can be treated as constant (obtained naturally from the ecosystem), we see that when the parameter $\alpha$ increases, handling time of additional food also increases. This does not favour bio-control and may also lead to prey outbreaks (Srinivasu et al. 2007, 2018a, b). In this study, we use the parameter $\alpha$ to represent the Quality of additional food provided to the predators. Additional food is termed high quality if $\alpha < \frac{\beta }{\delta }$ and low quality otherwise. The parameter $\eta$ denotes the ratio of nutritional value of prey perceptible to the predator to that of the additional food.

Now, using the same transformations as above and taking $\xi = \eta \frac{A}{a}$, the system (5)–(6) gets reduced to the non-dimensionalised system given below:

$$\begin{aligned} \dfrac{dx}{dt}= & {} x\bigg (1-\dfrac{x}{\gamma }\bigg ) - \bigg [\dfrac{xy}{(1+\alpha \xi )(\omega x^2 + 1) + x}\bigg ] \end{aligned}$$

(7)

$$\begin{aligned} \dfrac{dy}{dt}= & {} \beta \bigg [\dfrac{x+\xi (\omega x^2 + 1)}{(1+\alpha \xi )(\omega x^2 + 1) + x}\bigg ]y - \delta y \end{aligned}$$

(8)

Let $f(x) = \dfrac{x}{(1+\alpha \xi )(\omega x^2 + 1) + x}$ and $g(x) = \bigg (1-\dfrac{x}{\gamma }\bigg ) ((1+\alpha \xi )(\omega x^2 + 1) + x)$. Then, the system (7)–(8) can be written as

$$\begin{aligned} \dfrac{dx}{dt}= & {} (g(x) - y)f(x) \end{aligned}$$

(9)

$$\begin{aligned} \dfrac{dy}{dt}= & {} \bigg ( \beta f(x) \bigg [ 1 + \dfrac{\xi }{x}(\omega x^2 + 1) \bigg ] - \delta \bigg )y \end{aligned}$$

(10)

In this study, the parameter $\xi$ represents the Quantity of additional food provided to the predators. In the additional food system (7)–(8), the parameters $\beta ,\;\delta ,\;\gamma$ and $\omega$ are regarded as system parameters whereas the parameters $\alpha$ and $\xi$ are considered control parameters. This is because the former are obtained from the ecosystem while the latter are under the control of eco-managers/experimental ecologists who supply additional food to the predators. (Note: The Control Parameters are not to be mistakenly treated as the control variables (functions) of an optimal control problem in the mathematical sense. We will formulate the optimal control problems in later sections).

The system (7)–(8) admits four equilibrium points: the trivial equilibrium $E^{\ast}_0 = (0,0)$, the axial equilibrium point $E^{\ast}_1 = (\gamma ,0)$, and two interior equilibria $E^{\ast}_2 = (x^{\ast}_1(\alpha ,\xi ),y^{\ast}_1(\alpha ,\xi ))$ and $E^{\ast}_3 = (x^{\ast}_2(\alpha ,\xi ),y^{\ast}_2(\alpha ,\xi ))$ given by

$$\begin{aligned} E_2^{\ast}&=(x_1^{\ast},y_1^{\ast})=&\bigg (\dfrac{(\beta -\delta )-\sqrt{(\beta -\delta )^2 - 4\omega [\delta (1+\alpha \xi )-\beta \xi ]^2}}{2\omega [\delta (1+\alpha \xi )-\beta \xi ]},g(x_1^{\ast})\bigg ),\\ E_3^{\ast}&=(x_2^{\ast},y_2^{\ast})=&\bigg (\dfrac{(\beta -\delta )+\sqrt{(\beta -\delta )^2 - 4\omega [\delta (1+\alpha \xi )-\beta \xi ]^2}}{2\omega [\delta (1+\alpha \xi )-\beta \xi ]},g(x_2^{\ast})\bigg ). \end{aligned}$$

The interior equilibria are admitted only when $x_1^{\ast}<\gamma$ and $x_2^{\ast}<\gamma$. The outcomes of the studies (Srinivasu et al. 2018a; Vamsi et al. 2019) show that the dynamics of the system (7)–(8) depend on the dynamics of the initial system (3) - (4) and nature of its isoclines. As in (Srinivasu et al. 2018a), we too consider the additional food provided to the initial system under the Condition I where the initial system does not admit any interior equilibria. We provide the summary of global dynamics of the additional food system under condition I in Appendix 1.

3 Role of Quality in the Dynamics of the Additional Food System

The stability analysis and global dynamics of the system (7)–(8) (refer to Appendix 1) can be applied to both biological conservation of species and bio-control (pest eradication) of harmful species. In this paper, we wish to reach these outcomes in finite time and to that end, we want to formulate and study an optimal control problem with quality of additional food ($\alpha$) as the control parameter. With this as the objective, henceforth we shall assume that the quantity of additional food provided is a constant and keep it fixed ($\xi > 0$). Also, due to the saddle nature of the second interior equilibrium $E_3^{\ast} = (x_2^{\ast},y_2^{\ast})$ throughout its existence, in this paper, we will focus only on reaching the first interior equilibrium $E_2^{\ast} = (x_1^{\ast},y_1^{\ast})$ for achieving co-existence of species and this equilibrium point will be denoted by $E^{\ast}_2=(x^{\ast}(\alpha ),y^{\ast}(\alpha ))$. The dynamics of the system in terms of parameter $\alpha$ can be seen from the Table 1. The terms P, Q and R in Table 1 are obtained by solving the three bifurcation curves (PEC, TBC and HBC mentioned above) for $\alpha$.

Table 1 Global dynamics of the system (7)—(8) w.r.t. the parameter $\alpha$

Since this study is based on the quality of additional food, let us consider $[\alpha _{\min },\alpha _{\max }]$ to be the range of parameter $\alpha$. Since $\alpha$ depends inversely on the nutritional values of the additional food, we see that $\alpha _{\min }(\alpha _{\max })$ represents the highest (lowest) quality of additional food. From the analysis presented above, we see that in order to eliminate the harmful species (pest which are in the form of prey) eventually with time, the additional food supplements provided to natural enemies must be of high quality. This implies that we need to have $\alpha _{\min } < \frac{\beta \xi - \delta }{\delta \xi }$, so that the trajectories which emerge from below the prey isocline curve move towards y-axis to the desired state sufficiently close to $x = 0$. Otherwise, there is no possibility of any trajectory that moves towards the predator axis (y-axis). The outcomes of a recent study (Parshad et al. 2020) state that for predator–prey systems of the form (7) - (8), prey elimination $(x^{\ast} = 0)$ cannot be achieved in finite time T (with $T<\infty$). Thus, for achieving bio-control, we choose a terminal state such that $x^{\ast}(T) = \epsilon < x_d$ where $x_d$ denotes the prey density level below which the damage caused to the system is minimal. In some natural systems, to achieve bio-control, it is preferred that the prey (pest) continue to exist minimally exist and not get eliminated from the system because predator tends to damage the crops of the ecosystem after their target prey gets eliminated (Calvo et al. 2009; Urbaneja-Bernat et al. 2013). Thus, maintaining the prey at low densities such that they do not damage crops is desirable.

On the other hand, to achieve biological conservation, we need to achieve co-existence of species. Mathematically, this means that we must drive the system to the interior equilibrium. To that end, we will now obtain the set of all admissible interior equilibria that could be reached, followed by control strategies to reach the same depending on the species to be conserved. If the objective is to conserve the prey (predator) species and maintain their density at a certain level $\tilde{x} (\bar{y})$, then we must reach the admissible equilibrium with the corresponding prey (predator) component and possibly maintain the state at that level from then on by providing appropriate quality of additional food. From the practical view point, an adaptive approach is necessary to continue to maintain that state of co-existence. As the predators in such cases are usually generalists in nature, if need be, the eco-managers could alternate between feasible and low cost additional food of appropriate quality to maintain the state of the system as is done in cases of conservation bio-control (Blackburn et al. 2016).

Consider the interior equilibrium $E^{\ast}_2=(x^{\ast}(\alpha ),y^{\ast}(\alpha ))$ for a fixed $\xi >0$. The prey and predator component are given by

$$\begin{aligned} x^{\ast}(\alpha )= & {} \dfrac{(\beta -\delta )-\sqrt{(\beta -\delta )^2 - 4\omega [\delta (1+\alpha \xi )-\beta \xi ]^2}}{2\omega [\delta (1+\alpha \xi )-\beta \xi ]} \end{aligned}$$

(11)

$$\begin{aligned} y^{\ast}= & {} \bigg (1 - \dfrac{x^{\ast}(\alpha )}{\gamma }\bigg ) (x^{\ast}(\alpha ) + (1 + \alpha \xi )(1 + \omega (x^{\ast}(\alpha ))^2)) \end{aligned}$$

(12)

Now, solving (11) for $\alpha$, we get

$$\begin{aligned} \alpha = \dfrac{(\beta \xi - \delta ) (1 + \omega (x^{\ast}(\alpha ))^2) + (\beta - \delta )x^{\ast}(\alpha ) }{\delta \xi (1 + \omega (x^{\ast}(\alpha ))^2)} \end{aligned}$$

(13)

Now, substituting $\alpha$ from (13) in (12), we get

$$\begin{aligned} y^{\ast}(\alpha ) = \dfrac{\beta }{\delta } \bigg ( 1 - \dfrac{x^{\ast}(\alpha )}{\gamma }\bigg )(x^{\ast}(\alpha ) + \xi (1 + \omega (x^{\ast}(\alpha ))^2)) \end{aligned}$$

(14)

Equation (14) gives the set of all admissible equilibrium points for the system (7)–(8). This curve intersects the $y-axis$ at $y = \frac{\beta \xi }{\delta }$. To know if a given point $(x^{\ast}(\alpha ),y^{\ast}(\alpha ))$ on the curve of admissible equilibrium points is stable or not, we consider the analysis of the prey isocline curve of the system (7)–(8) as given in (Srinivasu et al. 2018a). We provide the details of stability of an admissible equilibrium in Appendix 2. This analysis helps in determining the terminal state of the system to which we want to drive the state in minimum time. Depending on the terminal state, we obtain the admissible control using which we fix the range for the parameter $\alpha$.

4 Time Optimal Control Studies for Additional Food System with Quality as Implicit Control

In this section, we formulate and study a time optimal control problem for the system (7)–(8) that drives the state trajectory from the initial state $(x_0,y_0)$ to the desired terminal state $(\bar{x},\bar{y})$ in minimum time using optimal quality of additional food provided to the predator species, with quantity of additional food as constant.

4.1 Formulation of the Time Optimal Control Problem and Existence of Optimal Control

We assume $\xi > 0$ is fixed and the quality parameter $\alpha$ varies in the interval $[\alpha _{\min },\alpha _{\max }]$. Then the time optimal control problem (a Mayer Problem of Optimal Control (Cesari 2012)) with respect to the system (7)–(8) is formulated as follows:

$$\begin{aligned} \left. \begin{array}{ll} &{} \displaystyle {\min _{\alpha _{\min } \le \alpha (\mathbf{t}) \le \alpha _{\max }} T} \\ &{} \text {subject to:} \\ &{} \dot{x} = f_1(x,y,\alpha ) \\ &{} \dot{y} = f_2(x,y,\alpha ) \\ &{} (x(0),y(0)) = (x_0,y_0) \ \text {and} \ (x(T),y(T)) = (\bar{x},\bar{y}). \end{array}\right\} \text {Optimal Control Problem} \end{aligned}$$

(15)

where $f_1(x,y,\alpha )= x\bigg (1 - \frac{x}{\gamma }\bigg ) - \bigg (\frac{x y}{ x + (1 + \alpha \xi ) (\omega x^2 + 1)}\bigg ) \text { and } f_2(x,y,\alpha ) = \beta \bigg (\frac{x + \xi (\omega x^2 + 1)}{x + (1 + \alpha \xi ) (\omega x^2 + 1)} \bigg )y - \delta y.$ Using the equations (9)–(10), we have

$$\begin{aligned} f_1(x,y,\alpha )= & {} (g(x) - y)f(x) \\ f_2(x,y,\alpha )= & {} \bigg ( \beta f(x) \bigg [ 1 + \dfrac{\xi }{x}(\omega x^2 + 1) \bigg ] - \delta \bigg )y \end{aligned}$$

where $f(x) = \dfrac{x}{(1+\alpha \xi )(\omega x^2 + 1) + x}$ and $g(x) = \bigg (1-\dfrac{x}{\gamma }\bigg ) ((1+\alpha \xi )(\omega x^2 + 1) + x)$.

Comparing this problem with the general form of Mayer time optimal control problem, we have $n = 2$, $m = 1$ and $\mathbf{x}(t) = (x(t),y(t))$, $\mathbf{u}(t) = \alpha (t)$ with $\mathbf{f} (t,\mathbf{x} (t),\mathbf{u} (t)) = (f_1(x,y,\alpha ),f_2(x,y,\alpha ))$. The boundary conditions are $e[\mathbf{x} ] = (0,x_0,y_0,T,\bar{x},\bar{y})$.

The set A for the problem (15) is the subset of $t\mathbf{x}$ - space ($\mathbb {R}^{1+2}$), i.e., $A \subset \mathbb {R}^{1+2}$ from which we get the state variables. For the control problem (15), the set A can be represented as $A = [0,T] \times \mathbf{B}$ where $\mathbf{B}$ is the solution space for the system (7)–(8) to which all trajectories belong. We must note here that $\mathbf{B}$ depends on the terminal state that is chosen and the corresponding trajectory of the system. We see that whenever $\frac{\beta \xi - \delta }{\delta \xi } > 0$, using the positivity and boundedness theorem (Vamsi et al. 2019), we can define $\mathbf{B}$ as $\mathbf{B} = \left\{ (x,y) \in \mathbb {R}^{2}_+ : 0\le x\le \gamma ,\; 0\le x + \frac{1}{\beta }y \le \frac{M}{\eta } ,\; \eta >0 \right\}$ with $M = \frac{\gamma (1+\eta )^2 }{4}$.

On the other hand, we know that when $\alpha < \frac{\beta \xi - \delta }{\delta \xi }$ the solution trajectories tend towards the predator axis asymptotically. From the discussion in previous sections, we see that the terminal state $(0,y^{\ast}(T))$ cannot be reached for $T<\infty$ based on a recent study on additional food provided systems (Parshad et al. 2020). Thus, choosing the terminal state as $x^{\ast}(T) = \epsilon < x_d$, we can define the set $\mathbf{B} = \left\{ (x,y) \in \mathbb {R}^{2}_+ : 0\le x\le \gamma ,\; 0 \le y \le \frac{\beta }{\delta }(\epsilon + \xi (1 - \epsilon )),\; 0<\epsilon <x_d \right\}$ where $x_d$ is a threshold pest level below which there is least damage to the system.

Now, we define the set of all admissible solutions to the above problem (15) as

$$\begin{aligned} \Omega := \big \{ (\mathbf{x} ,\alpha ) = (x,y,\alpha ) : (x,y)\text { is a solution of the system }(7)--(8) \forall \alpha \;\in [\alpha _{\min },\alpha _{\max }] \big \} \end{aligned}$$

We now wish to obtain a solution from the set $\Omega$ which minimizes the time to reach the terminal state (x(T), y(T)) that in turn becomes the optimal solution for (15). We establish this in the next theorem by proving the existence of an optimal control using Filippov’s Existence Theorem (refer to Appendix 3).

Theorem 1

If the desired terminal state of the system $(\bar{x},\bar{y})$ is admissible and satisfies the conditions in Proposition 2 (refer to Appendix 2), then there exists an optimal control $\alpha ^{\ast}(t)$ that drives the system from an initial state $(x_0,y_0)$ to the desired terminal state $(\bar{x},\bar{y})$ in minimum (finite) time for the time optimal control problem (15) provided the set of admissible solutions $\Omega$ is non-empty.

Proof

We will use Filippov’s Existence Theorem to prove the existence of an optimal control by showing that all the conditions in the theorem are satisfied by the considered problem. Using that, it is enough to show that the considered problem satisfies the following conditions to prove the existence of optimal control.

• 1. The set A is compact.

• 2. The set of all controls $[\alpha _{\min },\alpha _{\max }]$ is compact.

• 3. The set of boundary points $\partial \mathbf{B} = \{0,x_0,y_0,T,\bar{x},\bar{y}\}$ is compact and objective function is continuous on $\mathbf{B}$.

• 4. For every $(x,y) \in A$ the sets $Q(x,y) := \{(z_1,z_2) | z_1 = f_1(x,y,\alpha ), z_2 = f_2(x,y,\alpha ), \alpha \; \in \; [\alpha _{min},\alpha _{max}]\}$ are convex.

   We will now show that the considered control problem (15) satisfies all the properties above.

• (i) From the discussion above, we see that the set A can be written as $A = [0,T] \times \mathbf{B}$ where the set $\mathbf{B}$ gets defined according to the terminal state and the inequality satisfied by the parameter $\alpha$. We know that [0, T] is compact by definition. We need to show that the set $\mathbf{B}$ is compact in both the following cases:

  Case (a) Whenever $\frac{\beta \xi - \delta }{\delta \xi } < 0$, we know from the system analysis that the solution trajectories of the system (7 )–(8) reach $y-axis$ eventually with time. Since we have chosen the terminal state in this case as $(\bar{x},\bar{y}) = (\epsilon , y^{\ast}(T))$ close to the predator axis, the solutions space defined by $\mathbf{B} = \left\{ (x,y) \in \mathbb {R}^{2}_+ : 0\le x\le \gamma ,\; 0 \le y \le \frac{\beta }{\delta }(\epsilon + \xi (1 - \epsilon )) \right\}$ with $0<\epsilon <x_d$ becomes closed and bounded.

  Case (b) Whenever $\frac{\beta \xi - \delta }{\delta \xi } > 0$, we have from the positivity and boundedness theorem (Vamsi et al. 2019) that the solutions belong to $\mathbf{B} = \left\{ (x,y) \in \mathbb {R}^{2}_+ : 0\le x\le \gamma ,\; 0\le x + \frac{1}{\beta }y \le \frac{M}{\eta } ,\; \eta >0 \right\}$ with $M = \frac{\gamma (1+\eta )^2 }{4}$ which is also closed and bounded. Thus, we can conclude that A is compact and this proves condition 1.

• (ii) Conditions 2 and 3 are satisfied from the definitions of the respective sets $[\alpha _{\min },\alpha _{\max }]$ and $\partial \mathbf{B} = \{0,x_0,y_0,T,\bar{x},\bar{y}\}$ and also by definition of the objective function $J[\alpha ] = T$

• (iii) To prove condition 4, we need to show that the sets Q(x, y) are convex. To that end, consider $z_1 = f_1(x,y,\alpha ) = x\bigg (1 - \frac{x}{\gamma }\bigg ) - \bigg (\frac{x y}{ x + (1 + \alpha \xi ) (\omega x^2 + 1)}\bigg )$. Rearranging the terms, we get

  $$\begin{aligned} \bigg (\frac{x y}{ x + (1 + \alpha \xi ) (\omega x^2 + 1)}\bigg ) = x\bigg (1 - \frac{x}{\gamma }\bigg ) - z_1 \end{aligned}$$

  Cancelling the extra terms, we get

  $$\begin{aligned} \bigg (\frac{y}{ x + (1 + \alpha \xi ) (\omega x^2 + 1)}\bigg ) = \bigg (1 - \frac{x}{\gamma }\bigg ) - \dfrac{z_1}{x} \end{aligned}$$

  (16)

  Now consider

  $$\begin{aligned} z_2 = f_2(x,y,\alpha ) = \beta \bigg (\frac{x + \xi (\omega x^2 + 1)}{x + (1 + \alpha \xi ) (\omega x^2 + 1)} \bigg )y - \delta y \end{aligned}$$

  Replacing the term $\dfrac{y}{ x + (1 + \alpha \xi ) (\omega x^2 + 1)}$ in the above expression using equation (16), we get

  $$\begin{aligned} z_2= & {} \beta (x + \xi (\omega x^2 + 1)) \bigg ( \bigg (1 - \frac{x}{\gamma }\bigg ) - \dfrac{z_1}{x} \bigg ) - \delta y\\= & {} -\beta \bigg ( 1 + \dfrac{\xi }{x}(\omega x^2 + 1) \bigg ) z_1 + \beta (x + \xi (\omega x^2 + 1)) \bigg (1 - \frac{x}{\gamma }\bigg ) - \delta y \end{aligned}$$

  By rearranging the last expression, we get

  $$\begin{aligned} \beta \bigg ( 1 + \dfrac{\xi }{x}(\omega x^2 + 1) \bigg ) z_1 + z_2 = \beta (x + \xi (\omega x^2 + 1)) \bigg (1 - \frac{x}{\gamma }\bigg ) - \delta y \end{aligned}$$

  (17)

  From the equation (17), we see that the sets Q(x, y) are linear segments of its components which are convex. This proves Condition 4.

Hence, the time optimal control problem (15) admits an optimal solution provided the set of admissible solutions $\Omega$ is non-empty. $\square$

4.2 Characteristics of Optimal Control

Let us assume that the optimal solution exists for the control problem (15) and obtain the characteristics of such a solution using the necessary conditions for optimal solutions given by the Pontryagin’s Maximum Principle (Liberzon 2011).

We first define the Hamiltonian Function associated with the Control Problem (15):

$$\begin{aligned} \mathbb {H}(x,y,\alpha ,\lambda ,\mu ) := \lambda \dfrac{dx}{dt} + \mu \dfrac{dy}{dt} \end{aligned}$$

Here, $\lambda$ and $\mu$ are called the Co-state variables or Adjoint variables. Using the expressions for $\frac{dx}{dt}$ and $\frac{dy}{dt}$ from the system (7)–(8), we get

$$\begin{aligned}\mathbb {H}(x,y,\alpha ,\lambda ,\mu ) &= \lambda \bigg [ x\bigg (1 - \frac{x}{\gamma }\bigg ) - \bigg (\dfrac{x y}{ x + (1 + \alpha \xi ) (\omega x^2 + 1)}\bigg ) \bigg ] \nonumber \\&\quad + \mu \bigg [ \beta \bigg (\dfrac{x + \xi (\omega x^2 + 1)}{x + (1 + \alpha \xi ) (\omega x^2 + 1)} \bigg )y - \delta y\bigg ] \end{aligned}$$

(18)

Rearranging the above expression, we get

$$\begin{aligned}\mathbb {H}(x,y,\alpha ,\lambda ,\mu ) &= \bigg ( \lambda x\bigg (1 - \frac{x}{\gamma }\bigg ) - \mu \delta y\bigg ) \nonumber \\&\quad - \dfrac{y}{(x + (1 + \alpha \xi ) (\omega x^2 + 1))} (\lambda x - \mu \beta [x + \xi (\omega x^2 + 1)]) \end{aligned}$$

(19)

Using the modified system (9)–(10), the Hamiltonian Function can also be written as

$$\begin{aligned}\mathbb {H}(x,y,\alpha ,\lambda ,\mu ) &= \lambda \bigg [ (g(x,\alpha ,\xi ) - y) f(x,\alpha ,\xi ) \bigg ] \nonumber \\&\quad + \mu \bigg [ \beta f(x,\alpha ,\xi )\bigg (1 + \dfrac{\xi }{x} (\omega x^2 + 1) \bigg )-\delta \bigg ]y \end{aligned}$$

(20)

According to the maximum principle, the Co-state variables satisfy the canonical equations (adjoint system) given by $\frac{d\lambda }{dt} = -\frac{\partial \mathbb {H}}{dx},\; \frac{d\mu }{dt} = -\frac{\partial \mathbb {H}}{dy}$. Using (20), the canonical equations become

$$\begin{aligned} \dfrac{d\lambda }{dt}= & {} -\lambda \{ g_x(x,\alpha ,\xi )f(x,\alpha ,\xi ) + (g(x,\alpha ,\xi ) - y)f_x(x,\alpha ,\xi ) \} \nonumber \\&- \mu \{ \beta f_x(x,\alpha ,\xi ) (1 + \frac{\xi }{x} (\omega x^2 + 1)) + \frac{\beta \xi }{x^2} f(x,\alpha ,\xi ) (\omega x^2 - 1) \}y \end{aligned}$$

(21)

$$\begin{aligned} \dfrac{d\mu }{dt}= & {} \lambda f(x,\alpha ,\xi ) - \mu \{\beta f(x,\alpha ,\xi )(1 + \frac{\xi }{x} (\omega x^2 + 1)) - \delta \} \end{aligned}$$

(22)

Now, to obtain the characteristics of the optimal control, we differentiate the Hamiltonian function (19) with respect to the control parameter $\alpha .$ We see that

$$\begin{aligned} \dfrac{\partial \mathbb {H}}{\partial \alpha } = \dfrac{y\xi (\omega x^2 + 1)}{(x + (1 + \alpha \xi ) (\omega x^2 + 1))^2} (\lambda x - \mu \beta [x + \xi (\omega x^2 + 1)]) \end{aligned}$$

(23)

We observe that the optimal control $\alpha ^{\ast}(t)$ cannot be explicitly obtained from the above equation. Thus, differentiating the Hamiltonian function twice with respect to the control parameter $\alpha$, we get

$$\begin{aligned} \dfrac{\partial ^2\mathbb {H}}{\partial \alpha ^2} = \dfrac{-2y\xi (\omega x^2 + 1)}{(x + (1 + \alpha \xi ) (\omega x^2 + 1))} \dfrac{\partial \mathbb {H}}{\partial \alpha } \end{aligned}$$

(24)

From the above equation we see that the Hamiltonian function is a monotone with respect to the parameter $\alpha$ provided the quantity $\frac{\partial \mathbb {H}}{\partial \alpha } \ne 0$. Using the Hamiltonian maximization condition of the maximum principle (which becomes a minimization condition in our problem owing to the objective function) (Liberzon 2011), we see that

$$\begin{aligned} \mathbb {H}(x^{\ast}(t),y^{\ast}(t),\alpha ^{\ast}(t),\lambda ^{\ast}(t),\mu ^{\ast}(t)) \le \mathbb {H}(x^{\ast}(t),y^{\ast}(t),\alpha ,\lambda ^{\ast}(t),\mu ^{\ast}(t)) \end{aligned}$$

(25)

$\forall \alpha \in [\alpha _{\min },\alpha _{\max }]$ and $\forall t \in [0,T]$. Also, since (15) is a time optimal control problem, the Hamiltonian function turns out to be a constant along the optimal trajectory and in particular, it assumes value -1 (Clark 1974). Hence,

$$\begin{aligned} \mathbb {H}(x(t),y(t),\alpha ,\lambda (t),\mu (t)) = -1 \end{aligned}$$

(26)

Now, using equation (19), the condition (25), and the monotonicity property of Hamiltonian function with respect to $\alpha$, we can conclude that the optimal control might be of bang–bang type provided singular solution does not exist. This means that optimal control function would assume the form:

$$\begin{aligned} \alpha ^{\ast}(t) = {\left\{ \begin{array}{ll} \alpha _{\max }, &{}\text { if\quad } \frac{\partial \mathbb {H}}{\partial \alpha } < 0\\ \alpha _{\min }, &{}\text { if \quad } \frac{\partial \mathbb {H}}{\partial \alpha } > 0\\ ?&{}\text { if \quad } \frac{\partial \mathbb {H}}{\partial \alpha } = 0 \end{array}\right. } \end{aligned}$$

When $\frac{\partial \mathbb {H}}{\partial \alpha } = 0$ for an interval in [0, T], the optimal control function cannot be obtained using the Hamiltonian maximization condition and the monotonicity property. This is the case of singularity. In order to show that the optimal solution is of bang–bang type only, we must prove that the the solution does not exhibit singular arc in some interval $(t_1,t_2),\subseteq [0,T]$. Thus, to know the exact nature of the optimal control, we assume that singular solution exists and analyse the optimal solution.

Let us assume that the singular solution exists, that is, $\frac{\partial \mathbb {H}}{\partial \alpha } = 0$ at some time $t \in [0,T]$. This implies

$$\begin{aligned} \lambda (t) x(t) - \beta \mu (t) [x(t) + \xi (\omega x^2(t) + 1)] = 0 \end{aligned}$$

(27)

Rearranging the terms, we get

$$\begin{aligned} \dfrac{\lambda (t)}{\mu (t)} = \dfrac{(x(t) + \xi (\omega x^2(t) + 1))}{x(t)} \end{aligned}$$

which means that when singularity occurs, the co-state variables $\lambda$ and $\mu$ both have the same sign and cannot become zero simultaneously. Otherwise, (26) would not hold along the optimal trajectory. To obtain the characteristics of the singular solution, we differentiate equation (23) with respect to time along the singular solution. This gives

$$\begin{aligned} \dfrac{d}{dt} \dfrac{\partial \mathbb {H}}{\partial \alpha }= & {} \dfrac{d}{dt} \bigg [ \dfrac{y\xi (\omega x^2 + 1)}{(x + (1 + \alpha \xi ) (\omega x^2 + 1))^2} (\lambda x - \mu \beta [x + \xi (\omega x^2 + 1)]) \bigg ] = 0\\= & {} \dfrac{d}{dt} \bigg ( \dfrac{y\xi (\omega x^2 + 1)}{(x + (1 + \alpha \xi ) (\omega x^2 + 1))^2} \bigg ) (\lambda x - \mu \beta [x + \xi (\omega x^2 + 1)]) \\&+ \dfrac{y\xi (\omega x^2 + 1)}{(x + (1 + \alpha \xi ) (\omega x^2 + 1))^2} \dfrac{d}{dt} [\lambda x - \mu \beta [x + \xi (\omega x^2 + 1)]] = 0 \end{aligned}$$

Since (27) holds along singular solution, the first term on the right hand side in the above expression vanishes and as a result we get

$$\begin{aligned} \dfrac{d}{dt} \dfrac{\partial \mathbb {H}}{\partial \alpha } = \dfrac{y\xi (\omega x^2 + 1)}{(x + (1 + \alpha \xi ) (\omega x^2 + 1))^2} \dfrac{d}{dt} [\lambda x - \mu \beta [x + \xi (\omega x^2 + 1)]] = 0 \end{aligned}$$

(28)

Now consider

$$\begin{aligned}\dfrac{d}{dt} [\lambda x - \mu \beta [x + \xi (\omega x^2 + 1)]] &= x \dfrac{d\lambda }{dt} - \beta [x + \xi (\omega x^2 + 1)] \dfrac{d\mu }{dt} \nonumber \\&\quad + [\lambda - \mu \beta (1 + 2\xi \omega x)] \dfrac{dx}{dt} = 0 \end{aligned}$$

(29)

Using the canonical equations (21)–(22), the system (7 )–(8), and equation (27) along singular solution, (29) becomes

$$\begin{aligned} \dfrac{d}{dt} \dfrac{\partial \mathbb {H}}{\partial \alpha } = \dfrac{\mu \beta y\xi (\omega x^2 + 1)}{\gamma (x + (1 + \alpha \xi ) (\omega x^2 + 1))^2} \left\{ 3 \omega \xi x^3 + (2 - \gamma \xi \omega \delta ) x^2 + (\xi - \delta \gamma )x - \xi \gamma \delta \right\} = 0 \end{aligned}$$

(30)

which essentially means that

$$\begin{aligned} 3 \omega \xi x^3 + (2 - \gamma \xi \omega \delta ) x^2 + (\xi - \delta \gamma )x - \xi \gamma \delta = 0 \end{aligned}$$

(31)

along the singular solution. The equation in (31) is a cubic equation with one real root $\hat{x}$. This shows that singularity occurs at points which are the roots of the above equation (provided the roots are positive). To understand more, we differentiate (30) again with respect to time along the singular solution (by substituting $\hat{x}$ and using (27)) and get

$$\begin{aligned}\dfrac{d^2}{dt^2} \dfrac{\partial \mathbb {H}}{\partial \alpha } = \dfrac{\mu \beta y \xi (\omega \hat{x}^2+ 1)}{(\hat{x} + (1 + \alpha \xi ) (\omega \hat{x^2} + 1))^2} \bigg ( 9 \omega \xi \hat{x^2} + 2 (2 - \gamma \xi \omega \delta ) \hat{x} + \xi - \delta \gamma \bigg ) (g(\hat{x},\alpha ,\xi ) - y) f(\hat{x},\alpha ,\xi ) = 0 \end{aligned}$$

(32)

which implies that

$$\begin{aligned} \hat{y} = g(\hat{x},\alpha ,\xi ) \end{aligned}$$

(33)

and this means that the if singularity occurs, then it occurs at specific points $(\hat{x},\hat{y})$ on the prey isocline. Using the analysis and discussion presented above, we state the result

Theorem 2

The optimal control solution for the problem (15) is a combination of bang–bang controls only, with possibility of switches occurring in the optimal trajectory. The Optimal control is given by

$$\begin{aligned} \alpha ^{\ast}(t) = {\left\{ \begin{array}{ll} \alpha _{\max }, &{}\text { if \quad } \frac{\partial \mathbb {H}}{\partial \alpha } < 0\\ \alpha _{\min }, &{}\text { if \quad } \frac{\partial \mathbb {H}}{\partial \alpha } > 0 \end{array}\right. } \end{aligned}$$

(34)

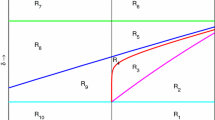
Now, in order to understand the characteristics of the optimal trajectory and nature of the switches (assuming singularity occurs), we divide the phase plane into four regions based on the curve of admissible equilibrium points (14) and the line passing through the point $\hat{x}$, which is the solution of the equation (31). The regions are given below and are depicted in the Fig. 1.

$$\begin{aligned} \text {Region I }&:= \biggl \{(x,y)\;\bigg |\; y<\dfrac{\beta }{\delta } \bigg ( 1 - \dfrac{x^{\ast}(\alpha )}{\gamma }\bigg )(x^{\ast}(\alpha ) + \xi (1 + \omega (x^{\ast}(\alpha ))^2)) \; \text {and} \; x< \hat{x}\biggr \} \\ \text {Region II }&:= \biggl \{(x,y)\;\bigg |\; y< \dfrac{\beta }{\delta } \bigg ( 1 - \dfrac{x^{\ast}(\alpha )}{\gamma }\bigg )(x^{\ast}(\alpha ) + \xi (1 + \omega (x^{\ast}(\alpha ))^2)) \; \text {and} \; x> \hat{x}\biggr \}\\ \text {Region III }&:= \biggl \{(x,y)\;\bigg |\; y> \dfrac{\beta }{\delta } \bigg ( 1 - \dfrac{x^{\ast}(\alpha )}{\gamma }\bigg )(x^{\ast}(\alpha ) + \xi (1 + \omega (x^{\ast}(\alpha ))^2)) \; \text {and} \; x> \hat{x}\biggr \}\\ \text {Region IV }&:= \biggl \{(x,y)\;\bigg |\; y > \dfrac{\beta }{\delta } \bigg ( 1 - \dfrac{x^{\ast}(\alpha )}{\gamma }\bigg )(x^{\ast}(\alpha ) + \xi (1 + \omega (x^{\ast}(\alpha ))^2)) \; \text {and} \; x < \hat{x}\biggr \} \\ \end{aligned}$$

Since the optimal strategy is of bang–bang type, switches occur when the optimal control switches its values from $\alpha_{\min }$ to $\alpha_{\max }$ and vice–versa. We know that when such a switch occurs, the singular solution occurs at an instant of time where $\frac{\partial \mathbb {H}}{\partial \alpha } = 0$. Thus, at that instant we have

$$\begin{aligned} \dfrac{y\xi (\omega x^2 + 1)}{(x + (1 + \alpha \xi ) (\omega x^2 + 1))^2} (\lambda x - \mu \beta [x + \xi (\omega x^2 + 1)]) = 0 \end{aligned}$$

Let us define the function $\sigma (t) = \lambda (t) x(t) - \mu (t) \beta (x(t) + \xi (\omega x^2(t) + 1))$. Then, we see that $\sigma (t) = 0$ when switch occurs. Also, and being optimal solution, Eq. (26) holds. Thus, denoting the instant of time of switch to be $\tau$ and using (19), (26) and (27), we get the equations

$$\begin{aligned} \lambda (\tau ) x(\tau ) - \mu (\tau ) \beta [x(\tau ) + \xi (\omega x^2(\tau ) + 1)]= & {} 0\end{aligned}$$

(35)

$$\begin{aligned} \lambda (\tau ) x(\tau ) \bigg (1 - \dfrac{x(\tau )}{\gamma }\bigg ) - \mu (\tau ) \delta y(\tau )= & {} -1 \end{aligned}$$

(36)

Using both the equations above, we get

$$\begin{aligned} \mu (\tau ) = \dfrac{-1}{\bigg (1 - \dfrac{x(\tau )}{\gamma }\bigg )\beta \;[x(\tau ) + \xi (1 + \omega (x(\tau ))^2)] - \delta y(\tau )} \end{aligned}$$

(37)

We know that the along the singular solutions, both $\lambda (t)$ and $\mu (t)$ have the same sign. Thus, using the definitions of the Regions I, II, III and IV and from the equations (35) and (37), we conclude that both $\lambda (\tau )$ and $\mu (\tau )$ are positive (negative) if the switch occurs in the regions I and II (III and IV).

Fig. 1

This figure depicts the regions $I,\; II,\;III,\; \text {and} \;IV$ based on the curve of admissible equilibria (14) and the positive cubic root $\hat{x}$ of Eq. (31)

Now, differentiating $\sigma (t)$ with respect to time and using state system (7)–(8) and adjoint system (21)–(22) at time $t = \tau$, with $\sigma (\tau ) = 0$, we get

$$\begin{aligned} \dfrac{d\sigma }{dt}\bigg |_{t = \tau } = \beta \mu \bigg [ 3 \omega \xi x^3 + (2 - \gamma \xi \omega \delta ) x^2 + (\xi - \delta \gamma )x - \xi \gamma \delta \bigg ]_{t = \tau } \end{aligned}$$

(38)

From the definition of $\sigma (t)$ and using the optimal control strategy (34), we see that when the control switches from $\alpha _{\max }$ to $\alpha _{\min }$ (or $\alpha _{\min }$ to $\alpha _{\max }$) at $t = \tau$, then $\frac{\partial \mathbb {H}}{\partial \alpha }$ increases from negative to positive (positive to negative). Thus, $\frac{d\sigma }{dt} > 0 \;(<0)$ at $t = \tau$ for the switch $\alpha _{\max }$ to $\alpha _{\min }$ (or $\alpha _{\min }$ to $\alpha _{\max }$).

Also, we know that $\hat{x}$ is the root of the Eq. (31). This is the same expression in (38). From this and the definitions of the regions, we conclude that the switch $\alpha _{\max }$ to $\alpha _{\min }$ ($\alpha _{\min }$ to $\alpha _{\max }$) can happen in Regions I and III (II and IV) only. Summarizing the discussion above we have the following result that gives the characteristics of optimal control when switching occurs.

Proposition 1

The optimal solution of the time optimal control problem (15) switches from $\alpha _{\max }$ to $\alpha _{\min }$ ($\alpha _{\min }$ to $\alpha _{\max }$) in the regions I and III (II and IV) only along the optimal trajectory. Moreover, the co-state variables $\lambda$ and $\mu$ are negative (positive) at the switch points occurring in the regions I and II (III and IV).

Note The optimal control strategy is given by the Eq. (34) with the term $\frac{\partial \mathbb {H}}{\partial \alpha }$ given by (23). Also, since (15) is a time optimal control problem, the state and the co-state variables satisfy (26) along the optimal path. The trajectory of the state variables is given by the system (7)–(8) and that of the co-state variables is given by the system (21)–(22). Now, to construct the optimal path from the given initial state $(x_0,y_0)$, we must choose appropriate initial values for the co-state variables, denoted by $(\lambda _0,\mu _0)$, so that the system with initial values $(x_0,y_0,\lambda _0,\mu _0)$ reaches the desired terminal state $(\bar{x},\bar{y})$ by implementing the optimal control strategy (34) in minimum time satisfying (26) all through the optimal path. Mathematically, we can conclude that with appropriate initial values for the co-state variables, we can reach any desired state from a given initial state. However, obtaining the initial values $(\lambda _0,\mu _0)$ that are suitable to the optimal control problem could involve a lot of trial and error work. The result 1 stated above indicates that if the terminal state is an interior equilibrium, then the optimal strategy could involve multiple switches between the extremum values $\alpha _{\min }$ and $\alpha _{\max }$ of the control $\alpha (t)$.

4.3 Application of Optimal Strategy in the context of Pest Management

In this section, we apply the results obtained on the characteristics of the optimal strategy in the context of pest management. Consider the predator–prey system where prey species denote the pests and the predators are their natural enemies that do not harm the crops. We aim to obtain ways of achieving the goal of pest eradication by controlling the quality of additional food supplied to the predators in order to eliminate the prey. As per the dynamics of the system (7 )–(8), we want to achieve the prey elimination case as stated in Table 4. In the context of the optimal control problem (15), we wish to reach the terminal state (0, y(T)) from a given initial state in minimum time by providing optimal quality of additional food to the predator species. The following result gives the existence of optimal solution and characteristics of the co-state variables and the optimal control at terminal time in the case of pest eradication.

Lemma 1

The time optimal control problem (15) with $x(T) = \epsilon < x_d$ admits an optimal solution if $\alpha _{min} < \frac{\beta \xi - \delta }{\delta \xi }$ and $\lambda (T) > \frac{-1}{\epsilon }$. Moreover, $\alpha ^{\ast}(T) = \alpha _{min}$ with $\mu (T) < 0$.

Proof

Let $\alpha _{\min } < \frac{\beta \xi - \delta }{\delta \xi }$. Then, we know from the dynamics of the system (7)–(8) as given in Table 1 that the prey get eliminated eventually as the trajectories move towards the $y-axis.$ However, for the optimal control problem, we choose the terminal state with $x(T) = \epsilon < x_d$ such that there is least damage caused to the system. From the outcomes of the recent work (Parshad et al. 2020), we see that for the systems of the form

$$\begin{aligned} \dot{x} = f_1(x,y,\alpha ),\; \dot{y} = f_2(x,y,\alpha ) \end{aligned}$$

the terminal state $x^{\ast}(T) = 0$ cannot be reached in finite time $T<\infty$. Thus, choosing $x(T) = \epsilon < x_d$ will make the terminal state admissible which could be reached in finite time.

This implies that the admissible solution set $\Omega \ne \phi$ and thus, we conclude from result on the existence of optimal solution that the control problem (15) with $x(T) = \epsilon$ indeed admits an optimum if $\alpha _{\min } < \frac{\beta \xi - \delta }{\delta \xi }$ and drives the system to minimal pest density $(\epsilon ,y(T))$ in minimum time T.

From (27), we know that

$$\begin{aligned} \mathbb {H}(\epsilon ,y(T),\alpha ^{\ast}(T),\lambda (T),\mu (T)) = -1 \end{aligned}$$

Substituting the terminal state values $(\epsilon ,y(T))$ in the above equation, using the fact that $\epsilon$ is close to 0 and from (19), we get

$$\begin{aligned} \lambda (T)\epsilon + \mu (T) \bigg (\dfrac{\beta \xi }{1 + \alpha ^{\ast}\xi } - \delta \bigg ) y(T) = -1 \end{aligned}$$

Rearranging the above equation, we get

$$\begin{aligned} \mu (T) = \dfrac{-1 - \lambda (T)\epsilon }{\bigg (\dfrac{\beta \xi }{1 + \alpha ^{\ast}\xi } - \delta \bigg ) y(T)} \end{aligned}$$

(39)

From the hypothesis of the lemma, we have $\lambda (T) > \frac{-1}{\epsilon }$. This implies that $(1 + \lambda (T) \epsilon ) > 0$ Since $\alpha ^{\ast}(T) < \frac{\beta \xi - \delta }{\delta \xi }$, we get $\frac{\beta \xi }{1 + \alpha ^{\ast}(T)\xi } - \delta > 0$. Thus, using (39), we conclude that $\mu (T) < 0$.

Also, since $\alpha ^{\ast}(t) = \alpha _{min}$ whenever $\frac{\partial \mathbb {H}}{\partial \alpha } > 0$, using the fact that $\mu (T) < 0$, using (23), we see that $\frac{\partial \mathbb {H}}{\partial \alpha }\big |_{t = T} > 0$ and thus we conclude that

$$\begin{aligned} \alpha ^{\ast}(T) = \alpha _{\min } \end{aligned}$$

(40)

This proves the lemma. $\square$

The above result states that at the instant when the terminal state is reached, the optimal quantity is $\alpha _{\min }$ and the co-state variable $\mu$ is negative for $\lambda (T) > \frac{-1}{\epsilon }$. The following theorem gives a more stronger property of the optimal strategy in the context of pest management.

Theorem 3

If $\alpha _{\min } < \frac{\beta \xi - \delta }{\delta \xi }$, then the optimal solution of the time optimal control problem (15) with $x(T) = \epsilon < x_d$ is given by $\alpha ^{\ast}(t) = \alpha _{\min }$ for all $t \in [0,T]$.

Proof

Let us assume that $\alpha _{\min } < \frac{\beta \xi - \delta }{\delta \xi }$. Now we re-write the canonical equations (21)–(22) as

$$\begin{aligned} \begin{aligned} \dfrac{d \lambda }{dt}&= -\lambda \bigg ( 1 - \dfrac{2x}{\gamma } - \dfrac{(1 + \alpha \xi ) (1 - \omega x^2)y}{[x + (1 + \alpha \xi )(\omega x^2 + 1)]^2}\bigg )\\&- \mu \bigg ( \dfrac{\beta y (1 + \alpha \xi - \xi ) (\omega x^2 + 1)}{[x + (1 + \alpha \xi )(\omega x^2 + 1)]^2} \bigg ) \end{aligned} \end{aligned}$$

(41)

and

$$\begin{aligned} \dfrac{d\mu }{dt} = \bigg ( \dfrac{\lambda x}{[x + (1 + \alpha \xi )(\omega x^2 + 1)]} \bigg ) - \mu \bigg ( \dfrac{\beta \; (x + \xi (\omega x^2 + 1))}{[x + (1 + \alpha \xi )(\omega x^2 + 1)]} - \delta \bigg ) \end{aligned}$$

(42)

To prove this theorem, we will use the zero solution of the linear system formed by the system of canonical equations (41)–(42) which can be expressed in a matrix form as given below:

$$\begin{aligned} \begin{pmatrix} \dfrac{d\lambda }{dt}\\ \dfrac{d\mu }{dt} \end{pmatrix} = \begin{pmatrix} -a_1(t) &{} -b_1(t)\\ &{}\\ a_2(t) &{} -b_2(t) \end{pmatrix} \begin{pmatrix} \lambda (t)\\ \mu (t) \end{pmatrix} \end{aligned}$$

(43)

where

$$\begin{aligned} a_1(t)= & {} 1 - \dfrac{2x}{\gamma } - \dfrac{(1 + \alpha \xi ) (1 - \omega x^2)y}{[x + (1 + \alpha \xi )(\omega x^2 + 1)]^2}\\ b_1(t)= & {} \dfrac{\beta y (1 + \alpha \xi - \xi ) (\omega x^2 + 1)}{[x + (1 + \alpha \xi )(\omega x^2 + 1)]^2} \\ a_2(t)= & {} \dfrac{x}{[x + (1 + \alpha \xi )(\omega x^2 + 1)]}\\ b_2(t)= & {} \dfrac{\beta \; (x + \xi (\omega x^2 + 1))}{[x + (1 + \alpha \xi )(\omega x^2 + 1)]} - \delta \end{aligned}$$

From the above expressions, we observe that

• $a_2(t) > 0$.

• The sign of $b_1(t)$ depends on the sign of the term $1 + \alpha \xi - \xi$.

• If $\alpha (t) = \alpha _{\min }$, then $b_2(t) > 0$ by the hypothesis of the theorem.

• $a_1(t)$ can either be negative or positive given the values of the state variables and parameters.

To know the nature of the zero solution of the system (43) qualitatively, we consider its characteristic equation given below:

$$\begin{aligned} m^2 + (a_1(t) + b_2(t)) m + (a_1(t)b_2(t) + a_2(t)b_1(t)) = 0 \end{aligned}$$

(44)

Since the system (43) admits (0, 0) as its equilibrium, it is sufficient to study the properties of the functions $(a_1(t)+b_2(t))$ and $(a_1(t)b_2(t) + a_2(t)b_1(t))$ to understand the nature of the zero solution (0, 0). If we assume that $\frac{-1}{\epsilon }<0<\lambda (T)$, then using the Lemma - 1 and from the continuity of the functions $(a_1(t) + b_2(t))$ and $(a_1(t)b_2(t) + a_2(t)b_1(t))$, we see that there exists an interval $[a,T] \subset [0,T]$ in which $\lambda (t)>0$ and $\mu (t) < 0$. The proof of this theorem is done if we can show that $a = 0$ because $a = 0$ will imply that $\frac{\partial \mathbb {H}}{\partial \alpha } > 0$ throughout [0, T] and this will result in $\alpha ^{\ast}(t) = \alpha _{\min }\; \forall t \in [0,T]$.

Using the qualitative behaviour of the zero solution of the system (43), we will now discuss below how to choose initial values for $\lambda$ and $\mu$ such that they maintain their signs $\lambda (t)>0$ and $\mu (t) < 0$ throughout the interval [0, T]. Let $I = (a_1(t)+b_2(t))$ and $J = (a_1(t)b_2(t) + a_2(t)b_1(t))$. Then the characteristic equation (44) becomes $m^2 + Im + J = 0$, whose discriminant is given by $D = I^2 - 4J$. J plays a major role in determining the sign of the discriminant. Now, let us consider two cases based on the sign of the function $b_1(t)$ that determines the nature of the J:

Case 1 $1 + \alpha \xi - \xi \ge 0$

In this case, $b_1(t) \ge 0$ in the system (43). On evaluating the discriminant of the characteristic equation (44), in this case it turns out to be positive for all $t \in [0,T]$. This implies that the solution trajectories with initial values for $\lambda$ and $\mu$ chosen such that $\lambda (0) > 0$ and $\mu (0) < 0$ will remain in the fourth quadrant of the $\lambda \mu -$ space and do not move to any other quadrant. This will ensure that the sign of the switching function remains the same throughout [0, T] leading to the desired outcome.

Case 2 $1 + \alpha \xi - \xi < 0$

In this case, $b_1(t) < 0$. Thus, we observe that D can change its sign depending on $a_1(t)$. Consequently, we observe that if a trajectory (of the state $(\lambda (t),\mu (t))$) starts from fourth quadrant of the $\lambda \mu$ space, it may leave the quadrant as time progresses. Also, it is important to note that at the terminal time T, $x(T) = \epsilon$ and as a result, using the curve of admissible equilibria (14) we get $y(T) > 1 + \alpha _{\min } \xi$. This means that the zero solution of the system (41)–(42) behaves like a saddle as t nears T.

Thus, we need to choose initial values $(\lambda _0,\mu _0)$ with $\mu _0$ far from the origin on the negative $\mu$ - axis and $\lambda _0 > 0$, such that the Hamiltonian is $-1$ at $t = 0$. This will ensure at that as t increases, when the co-state trajectory approaches the positive $\lambda$ - axis, then under the influence of the saddle nature of (0, 0) it does not leave the fourth quadrant. This will help achieve our objective.

Therefore, by choosing initial values as suggested, we have $\sigma (t) > 0 \; \forall \; t \in \; [0,T]$ and thus,

$$\begin{aligned} \alpha ^{\ast}(t) = \alpha _{\min } \; \forall \; t \in \; [0,T] \end{aligned}$$

This completes the proof of the theorem. $\square$

4.4 Numerical Illustrations

In this section, we perform numerical simulations to validate the theory presented in the previous sub-sections and discuss the findings. We consider four examples depicting different cases. The numerical simulations were run on MATLAB software. The figures illustrating each example display the optimal trajectory of the state variables, the co-state variables, the optimal control function $\alpha (t)$ and the switching function $\frac{\partial \mathbb {H}}{\partial \alpha }$. To obtain the optimal strategy, we first fixed the initial and terminal states. Using the parameter values and the terminal state of the system, we obtained the optimal control value at the terminal state $\alpha ^{\ast}(T)$ which is required to maintain the system at the terminal state for all future times. Using this, we fixed the range of the control parameter $[\alpha _{\min },\alpha _{\max }]$. Then, using the equation (26) along with various combinations of trial-error guesses with the objective of reaching the terminal state, we obtained the initial values for the co-state variables. Then we used Runge-Kutta $4^{\text {th}}$ order routine to simulate the systems (7)–(8) and (21)–(22) and switched the control accordingly as per (34) which finally gave us the desired trajectories. The Hamiltonian function was monitored throughout the process. The step size used for the simulations is $h= 0.01$ based on which the time units obtained at the end of simulations are re-scaled by multiplying $T\times 10^{-2}$.

Example 1

This example illustrates the possibility of steering the system (15) from the initial state (1.39, 3.62) to the terminal state (6.15, 1.17) with $\alpha ^{\ast}(T) = 1.76$ with the initial values for co-states being $(2,-0.75)$. The parameters values are taken to be $\gamma = 6.5\;\beta = 0.4,\;\delta = 0.2,\;\xi = 1,\;\omega = 0.2,\; \alpha _{\min } = 1,\; \text {and }, \alpha _{\max } = 2$. We see that this system takes $T = 4222 \times 10^{-2} = 42.2$ units of time to reach the desired state. Once the system reaches the desired state, the quality of additional food is maintained at $\alpha ^{\ast}(T)$. Figure 2 illustrates this example. This examples is a case with one switch. This is applicable in the context of biological conservation of the prey species and we see that prey density increases from $x(0) = 1.38$ to $x(T) = 6.15$ by feeding the predators with high-quality additional food initially and then reducing the quality of additional food later.

Fig. 2

This figure depicts the optimal trajectory of the time optimal control problem (15) from the initial state (1.39, 3.62) to the terminal state (6.15, 1.17) with the parameters values $\gamma = 6.4\;\beta = 0.4,\;\delta = 0.2,\;\xi = 1,\;\omega = 0.2,\; \alpha _{\min } = 1,\; \text {and } \alpha _{\max } = 2.$

Example 2

This example illustrates the possibility of steering the system (15) from the initial state (5.17, 4.78) to the terminal state (0.58, 4.8) with $\alpha ^{\ast}(T) = 1.76$ and the initial values for co-states being $(1,-3.90904)$. The parameters values are taken to be $\gamma = 6\;\beta = 0.4,\;\delta = 0.2,\;\xi = 2,\;\omega = 0.26,\; \alpha _{\min } = 1,\; \text {and }, \alpha _{\max } = 3$. We see that this system takes $T = 1712 \times 10^{-2} = 17.12$ units of time to reach the desired state. Figure 3 illustrates this example. This examples is also a case with one switch. This is an illustration of the case where there is reduction of the prey species from $x(0) = 5.17$ to $x(T) = 0.58$ by feeding the predators with high-quality additional food initially and then low-quality additional food with the initial and terminal predator densities almost same.

Fig. 3

This figure depicts the optimal trajectory of the time optimal control problem (15) from the initial state (5.17, 4.78) to the terminal state (0.58, 4.8). The parameters values are taken to be $\gamma = 6\;\beta = 0.4,\;\delta = 0.2,\;\xi = 2,\;\omega = 0.26,\; \alpha _{\min } = 1,\; \text {and }, \alpha _{\max } = 3$

Example 3

This example illustrates the possibility of steering the system (15) from the initial state (5.17, 4.78) to the terminal state (0.04, 12.2) with the initial values for co-states being $(0.56170,-6.80)$. The parameters values are taken to be are same as that of the previous example. We see that this system takes $T = 1050 \times 10^{-2} = 10.5$ units of time to reach the desired state. Figure 4 illustrates this example. This examples is a case without any switch. This case is an illustration of pest management with minimal prey density. This is also an illustration of the Theorem 3 where $\lambda (t) > 0\; \forall t \in [0,T]$ and $\mu (t) < 0\; \forall t \in [0,T]$ along with $\alpha ^{\ast}(t) = \alpha _{\min }, \; \forall t \in [0,T]$. This example also shows that if the eco-manager or the experimental ecologist does not switch the additional food to low quality at the specified time, then the system could tend towards prey elimination eventually.

Fig. 4

This figure depicts the optimal trajectory of the time optimal control problem (15) from the initial state (5.17, 4.78) to the terminal state (0.04, 12.2). The parameters values are taken to be $\gamma = 6\;\beta = 0.4,\;\delta = 0.2,\;\xi = 2,\;\omega = 0.26,\; \alpha _{\min } = 1,\; \text {and }, \alpha _{\max } = 3$

Example 4

This example illustrates the possibility of steering the system (15) from the initial state (0.2, 0.1) to the terminal state (0.4, 3.77) with $\alpha ^{\ast}(T) = 1.69$ and the initial values for co-states being (7.07, 23). The parameters values are taken to be $\gamma = 0.9\;\beta = 0.2,\;\delta = 0.1,\;\xi = 2,\;\omega = 0.26,\; \alpha _{\min } = 1,\; \text {and }, \alpha _{\max } = 2$. We see that this system takes $T = 11477 \times 10^{-2} = 114.77$ units of time to reach the desired state. Figure 5 illustrates this example. This examples is a case with multiple switches. This is an illustration of the case where there is an increase in the predator species from $y(0) = 0.1$ to $y(T) = 3.37$ by feeding the predators with optimal quality additional food and with the initial and terminal prey densities almost same. This is applicable in the Biological conservation of the predator species.

Fig. 5

This figure depicts the optimal trajectory of the time optimal control problem (15) from the initial state (0.2, 0.1) to the terminal state (0.4, 3.77). The parameters values are taken to be $\gamma = 0.9\;\beta = 0.2,\;\delta = 0.1,\;\xi = 2,\;\omega = 0.26,\; \alpha _{\min } = 1,\; \text {and }, \alpha _{\max } = 2$

4.5 Ecological Significance

It can be inferred from the above theoretical findings of the implicit control system that to achieve prey elimination, it is sufficient to provide the predator with high quality additional food ($\alpha _{\min }$). This is in line with the outcomes of the work (Toft 2005) which states that the optimal availability of high quality of alternative food sources to the generalist predators maximize the control of the aphids that attack on cereal fields. This is also observed from the outcomes of experimental studies by Calixto et al. (2013), where the natural enemy Orius insidiosus is provided with various combinations of additional food supplements like pollen, Anagasta kuesniella eggs and nymphs of its target prey Frankliniella occidentalis. F. occidentalis are thrips whose adult stages damage agro-ecosystems. In this study, it is observed that A. kuehniella eggs are an excellent factitious food for rearing O. insidiosus were found to be of high nutritional value compared to both pollen and nymphs of the target prey. The predation on F. occidentalis thrips was found to be maximum when the predators O. insidiosus were supplemented with A. kuehniella eggs which increased their longevity and fecundity. This shows that the mathematical findings are in accordance with the experimental observations. Figure 4 illustrates this case of eliminating pest.

One of the aims of providing additional food is to reduce depredation. From the illustrations above it can be observed from Fig. 2 that initially when additional food is provided, the predators consume both prey and additional food and hence increase in density with reduction in prey. But as the predators increase, competition among predators also increases. This demonstrates the case of apparent competition (Muller and Godfray 1997) when high-quality of additional food is provided.

5 Optimal Control Studies for Type IV System (3)–(4) with Quality as Explicit Control

In this section, we will define another additional food provided system with Type IV functional response where the additional food is explicitly provided as a linear component added to the predator’s compartment of the initial system (1)-(2).

5.1 Explicit Control System and the Error System

Let U represent the additional food term with $U = AB$, where A represents the quality of additional food and B represents the quantity of additional food. Since our aim is to study the influence of quality of additional food, we assume the quantity to be fixed $B>0$ and henceforth we shall consider U to represent the quality of additional food. When additional food is provided explicitly, the initial system (1)–(2) becomes

$$\begin{aligned} \dfrac{dN}{dT}= & {} rN\bigg (1 - \frac{N}{K}\bigg ) - \dfrac{cN}{a(bN^2 +1 ) + N}P \end{aligned}$$

(45)

$$\begin{aligned} \dfrac{dP}{dT}= & {} \dfrac{eN}{a(bN^2 + 1) + N}P - mP + U \end{aligned}$$

(46)

Using the same transformations as performed before, and letting $u = \frac{U}{r}$, the non-dimensionalised explicit additional food system is given by the system of equations

$$\begin{aligned} \dot{x}= & {} x\bigg (1 - \frac{x}{\gamma }\bigg ) - \bigg ( \dfrac{xy}{\omega x^2 + x + 1}\bigg ) \end{aligned}$$

(47)

$$\begin{aligned} \dot{y}= & {} \beta \bigg ( \dfrac{\beta xy}{(\omega x^2 + 1) + x} \bigg ) - \delta y + u \end{aligned}$$

(48)

The goal of this study is to maintain the prey (pest population) at the level $x^{\ast} = x_c < x_d$ by providing additional food to the predator which is of optimal quality $u^{\ast}$, where $x_d$ is the threshold level below which there is no damage by pests to the ecosystem. To ensure that the state $(x^{\ast},y(x^{\ast}))$, is admissible, we consider the isoclines of the system (47)–(48) with $x^{\ast} = x_c$ fixed and solve for $y^{\ast}$ and $u^{\ast}$. We must also ensure that $x^{\ast}$ that is chosen satisfies the condition $x^{\ast} < \gamma$. Choosing such an $x^{\ast}$, using equation (47), we get $y^{\ast}$ as follows:

$$\begin{aligned} x^{\ast}\bigg ( 1 - \dfrac{x^{\ast}}{\gamma } \bigg ) - \bigg ( \dfrac{x^{\ast}y^{\ast}}{1 + x^{\ast}+\omega (x^{\ast})^2} \bigg ) = 0\\ \dfrac{y^{\ast}}{1 + x^{\ast}+\omega (x^{\ast})^2} = \bigg ( 1 - \dfrac{x^{\ast}}{\gamma } \bigg ) \end{aligned}$$

Rearranging the above expression, we get

$$\begin{aligned} y^{\ast} = \bigg ( 1 - \dfrac{x^{\ast}}{\gamma } \bigg )(1 + x^{\ast} + \omega (x^{\ast})^2) \end{aligned}$$

(49)

Now, using equations (48) and (49), we get

$$\begin{aligned} \dfrac{\beta x^{\ast} y^{\ast}}{1 + x^{\ast} + \omega (x^{\ast})^2} - \delta y^{\ast} + u^{\ast} = 0 \end{aligned}$$

Solving for $u^{\ast}$, we get

$$\begin{aligned} u^{\ast} = \bigg ( \delta - \dfrac{\beta x^{\ast}}{1 + x^{\ast} + \omega (x^{\ast})^2} \bigg )y^{\ast} \end{aligned}$$

To obtain the expression using $x^{\ast}$, we substitute for $y^{\ast}$ and get

$$\begin{aligned} u^{\ast} = \dfrac{\delta (1 + x^{\ast} + \omega (x^{\ast})^2) - \beta x^{\ast}}{1 + x^{\ast} + \omega (x^{\ast})^2} \bigg ( 1 - \dfrac{x^{\ast}}{\gamma } \bigg )(1 + x^{\ast} + \omega (x^{\ast})^2) \end{aligned}$$

Cancelling and rearranging the terms in the above expression, we get

$$\begin{aligned} u^{\ast} = \bigg ( 1 - \dfrac{x^{\ast}}{\gamma } \bigg ) (1 - (\beta - \delta )x^{\ast} + \omega (x^{\ast})^2 ) \end{aligned}$$

(50)

The desired state is $(x^{\ast},y^{\ast})$ controlled by $u^{\ast}$ may not be stable always because the value $x_d$ is chosen based on the damage caused to the ecosystem. Since the goal of the study is to drive the system (49)–(50) optimally to the state $(x^{\ast},y^{\ast})$, we will carry out the following steps to that end:

• 1. Define an error system (also called perturbed system) using linearization of the system (49)–(50) with respect to the desired terminal state $(x^{\ast},y^{\ast})$.

• 2. Formulate a linear feedback control optimal control problem with respect to the error system that drives the system to the origin.

• 3. Once the running cost of the control problem is shown to be positive definite, then using the results of an infinite horizon LQR problem the optimal solution can be shown as a feedback control that minimizes the objective and also ensures the asymptotic stability of the terminal state of the error system.

• 4. Using the feedback control, control for the system (49)–(50) can be obtained, which will make the terminal state stable.

• 5. Translating back to the original system, the terminal state would be reached optimally.

We will now implement the above mentioned procedure to reach the desired state optimally. We define the variables for the error system as follows:

$$\begin{aligned} v = \begin{bmatrix} v_1\\ v_2 \end{bmatrix} = \begin{bmatrix} x - x^{\ast}\\ y - y^{\ast} \end{bmatrix} ,\; \alpha = u - u* \end{aligned}$$

(51)

Using the isoclines of the system (49)–(50), the first order Taylor’s expansion of the state variables x and y around $x^{\ast}$ and $y^{\ast}$, and the new variables, we get the error system as

$$\begin{aligned} \dot{v} = Mv + h(v) + N\alpha \end{aligned}$$

(52)

where

$$\begin{aligned} M = \begin{bmatrix} 1 - \dfrac{2x^{\ast}}{\gamma } - \dfrac{y^{\ast}(1 - \omega (x^{\ast})^2)}{1 +x^{\ast} + \omega (x^{\ast})^2} &{} - \dfrac{x^{\ast}}{(1 + x^{\ast} + \omega (x^{\ast})^2)}\\ \dfrac{\beta y^{\ast} (1 - \omega (x^{\ast})^2)}{(1 + x^{\ast} +\omega (x^{\ast})^2)^2} &{} \dfrac{\beta x^{\ast}}{1 + x^{\ast} + \omega (x^{\ast})^2} - \delta \end{bmatrix} ,\; N = \begin{bmatrix} 0\\ 1 \end{bmatrix} \end{aligned}$$

and

$$\begin{aligned} h(v) = \begin{bmatrix} h_1(v)\\ h_2(v) \end{bmatrix} = \begin{bmatrix} h_1(v_1,v_2)\\ h_2(v_1,v_2) \end{bmatrix} =\begin{bmatrix} \dfrac{-v_1^2}{\gamma } - \dfrac{v_1^2 v_2}{1 + v_1 + \omega v_1^2}\\ \dfrac{\beta v_1 v_2}{1 + v_1 + \omega v_1^2} \end{bmatrix} \end{aligned}$$

5.2 The Linear Feedback Control Optimal Control Problem and Optimal Solution

The linear feedback control optimal control problem involving error system (52) is defined as follows:

$$\begin{aligned} \left. \begin{array}{l} \text {Minimize: } \\ J = \int _{0}^{\infty } \big (l(v) + \alpha ^T R \alpha \big ) dt\\ \text {Subject to :}\\ \dot{v} = Mv + h(v) + N\alpha \\ (v_1(\infty ),v_2(\infty )) = (0,0) \end{array}\right. \end{aligned}$$

(53)

with l(v) defined as

$$\begin{aligned} l(v) = [v^T Q v - h^T(v)Pv-v^TPh(v)] \end{aligned}$$

(54)

The control system (54) and the associated optimal control problem (53) is a special case of the general perturbed non-linear system $\frac{dX}{dt} = A'X + g(X) + B'U$ and its associated control problem studied in Rafikov and Limeira (2012), where $A' \in \mathbb {R}^{n\times n}$ is a constant matrix, g a vector whose elements are continuous non-linear functions, $U \in \mathbb {R}^m$ is the control vector, and $B' \in \mathbb {R}^{n\times m}$ is a constant matrix. Thus, the results proved for the general system in Rafikov and Limeira (2012) can be applied to obtain the optimal solution. The l(v) of the objective function in (53) is a variation of the linear quadratic regulator defined for strictly linear systems (Liberzon 2011). Since the error system (52) is based on feedback control, the objective function J in (53) makes the control problem similar to the infinite horizon LQR control problem.

Theorem 4

For any matrix P and

$$\begin{aligned} Q = \begin{bmatrix} q_{11} &{} 0\\ 0&{}q_{22} \end{bmatrix}, \ h(v) = \begin{bmatrix} \dfrac{-v_1^2}{\gamma } - \dfrac{v_1^2 v_2}{1 + v_1 + \omega v_1^2}\\ \dfrac{\beta v_1 v_2}{1 + v_1 + \omega v_1^2} \end{bmatrix} \end{aligned}$$

the function l(v) defined in the Eq. (54) is positive definite in a neighbourhood $\Gamma _0$ of the origin (0, 0).

Proof

Letting the matrix P to be $\begin{bmatrix} p_{11}&{}p_{12}\\ p_{21}&{}p_{22} \end{bmatrix}$, using Q and h(v) from the hypothesis of the theorem, and expanding the function l(v) we get

$$\begin{aligned}&l(v) = l(v_1,v_2) = q_{11} v_1^2 + q_{22} v_2^2 + \dfrac{2 p_{11} v^3_1}{\gamma } + \dfrac{2 (p_{11} - \beta p_{12}) v^2_1 v_2}{1 + v_1 + \omega v^2_1} \nonumber \\&\quad + \dfrac{2 p_{12} v^2_{1}v_2}{\gamma } + \dfrac{2 (p_{12} - \beta p_{22})\beta v_1 v^2_2}{1 + v_1 + \omega v^2_1} \end{aligned}$$

(55)

The first partial derivatives of l(v) are given by

$$\begin{aligned} \dfrac{\partial l}{\partial v_1}= & {} 2 q_{11} v_1 + \dfrac{6p_{11}v^2_1}{\gamma } + \dfrac{4 p_{12} v_1 v_2}{\gamma } + 2 (p_{11} - \beta p_{12}) \dfrac{2 v_1 v_2 + v^2_1 v_2}{(1 + v_1 + \omega v^2_1)^2} \nonumber \\&+ 2 (p_{12} - \beta p_{22}) \dfrac{v^2_2 (1 - \omega v^2_1)}{(1 + v_1 + \omega v^2_1)^2}\\ \dfrac{\partial l}{\partial v_2}= & {} 2 q_{22} v_2 + \dfrac{2(p_{11} - \beta p_{12}) v^2_1}{1 + v_1 + \omega v^2_1} + \dfrac{4(p_{12} - \beta p_{22})v_1 v_2}{1 + v_1 + \omega v^2_1} + \dfrac{2p_{12}v^2_1}{\gamma } \\ \end{aligned}$$

It is obvious from the above equations that

$$\begin{aligned} \dfrac{\partial l}{\partial v_1}(0,0) = \dfrac{\partial l}{\partial v_2}(0,0) = 0 \end{aligned}$$

and the Hessian of l(v) at the origin is given by

$$\begin{aligned} H(0) = \begin{bmatrix} 2q_{11} &{} 0\\ 0 &{} 2q_{22} \end{bmatrix} \end{aligned}$$

which is clearly positive definite. This implies that the origin is the strict local minimum of function l(v) and that this function is positive definite at the neighbourhood $\Gamma _0$ of the origin. This completes the proof of the theorem. $\square$

The following theorem from Rafikov and Limeira (2012) shows that the feedback control $\alpha$ for the error system (52) minimizes the objective functional defined above and also ensures that the desired terminal state is asymptotically stable.

Theorem 5

If there exist constant matrices Q and R, positive definite, Q begin symmetric, such that the function l(v) as defined in (54) is positive definite, then the linear feedback control

$$\begin{aligned} \alpha = -R^{-1} N^T P(t)v \end{aligned}$$

(56)

is optimal, in order to drive the non-linear system (52) from an initial state to the final state

$$\begin{aligned} (v_1(\infty ),v_2(\infty )) = (0,0) \end{aligned}$$

(57)

minimizing the functional

$$\begin{aligned} J = \int _{0}^{\infty } \big (l(v) + \alpha ^T R \alpha \big ) dt \end{aligned}$$

(58)

where P the symmetric, positive definite matrix is the solution of the Algebraic Riccati Equation

$$\begin{aligned} PM + M^T P - PNR^{-1}N^TP + Q = 0 \end{aligned}$$

(59)

Moreover, with the feedback control given by (56), there exists a neighbourhood $\Gamma _0 \subset \Gamma \subset \mathbb {R}^2$, of the origin such that if $v_0 = (v_1(0),v_2(0)) \in \Gamma _0$, then the solution $v(t) = 0, \ t \ge 0$ of the controlled error system (52) is locally asymptotically stable, and $J_{\min } = v^T_0P(0)v_0$ (Liberzon 2011). Finally, if $\Gamma = \mathbb {R}^2$, then the solution $v(t) = 0, \ t \ge 0$ becomes globally asymptotically stable.

From the theorems 4 and 5, we can now conclude that the optimal control problem (53) admits an optimal solution and the error system (52) controlled by linear feedback control $\alpha$ as given in (56) is locally asymptotically stable. Hence the system (49)–(50), controlled by

$$\begin{aligned} u = u^{\ast} + \alpha \end{aligned}$$

(60)

tends to the desired equilibrium $(x^{\ast},y^{\ast})$.

5.3 Numerical Simulations

In this section, we numerically illustrate the application of the control strategy in equation (60). We apply this to the explicit control system (47)–(48) by defining the error system (52) for a specific desired terminal state $(x^{\ast},y^{\ast})$ and implementing the feedback control (56) for the same, thereby obtaining the optimal strategy for pest management in finite time. The terminal state is obtained by choosing $x^{\ast} = x_c < s_d$ such that the prey (pest) population is no longer harmful to the ecosystem.

We know from Srinivasu et al. (2018a) that the initial system (1)–(2) admits two interior equilibrium points $E^{\ast}_2$ and $E^{\ast}_3$ provided the parameters of the system satisfy certain conditions. The stability of these equilibria (if they exist) depend in the position of the prey component and the nature of the prey isocline curve, which is given by $y = g(x)$, where

$$\begin{aligned} g(x) = \bigg ( 1 - \dfrac{x}{\gamma }\bigg ) (1 + x + \omega x^2) \end{aligned}$$

(61)

Since the system (47)–(48) is obtained by incorporating additional food explicitly to the predator component of the initial system (3 )–(4), we see that the dynamics of the initial system could play a crucial role in the implementation of control strategy, depending on the choice of the terminal state with respect to the nature of the prey isocline. We want to quantitatively obtain this relation and also see how the control strategy is affected with the variation of inhibitory effect.

5.3.1 Nature of the Prey Isocline

Consider the prey isocline curve $y = g(x)$. To obtain the nature of the curve, we consider the equation $g'(x) = 0$:

$$\begin{aligned} \dfrac{d}{dx}\bigg [ \bigg ( 1 - \dfrac{x}{\gamma }\bigg ) (1 + x + \omega x^2) \bigg ] = 0 \end{aligned}$$

Simplifying the above equation we get the quadratic equation

$$\begin{aligned} 3\omega x^2 + (1 + \omega \gamma ) x + (1-\gamma ) = 0 \end{aligned}$$

Depending on the nature of roots of the above equation, which in turn is based on the values of the parameters $\beta ,\; \delta ,\;\gamma$ and $\omega$, we obtain the following cases:

• (i) Case I $(1-\omega \gamma )^2 - 3\omega (1-\gamma )>0,\; 1-\gamma > 0$ and $1-\omega \gamma < 0$

• (ii) Case II $(1-\omega \gamma )^2 - 3\omega (1-\gamma ) >0,\; 1-\gamma < 0$

• (iii) Case III $(1-\omega \gamma )^2 - 3\omega (1-\gamma )>0,\; 1-\gamma > 0$ and $1-\omega \gamma > 0$

• (iv) Case IV$(1-\omega \gamma )^2 - 3\omega (1-\gamma ) <0$

The Fig. 6 shows the various cases depicting the nature of prey isocline. $E^{\ast}_2$ is the first interior equilibrium. Since $\gamma < E^{\ast}_3$, the second interior equilbrium is not admitted by the system. The values chosen for the parameters and resulting equilibrium points for all the cases of the prey isocline of initial system have been listed in the Table 2.

Fig. 6

This figure shows the nature of the curve $y = g(x)$ given in the Eq. (61) under the four cases mentioned above

Table 2 Parameter values and equilibrium points for various cases of prey isocline behavior

First, we numerically simulate the trajectory of the state variables in the absence of the control from the initial point (4.5, 3). This is depicted in Fig. 7. We observe that in all the cases, the system undergoes initial oscillations and tends to stabilize eventually. However, the desired state is not reached in the absence of the control.

Fig. 7

This figure shows the trajectory of the state variables from the initial state (4.5, 3) without application of any control for all the four cases. The system undergoes oscillations initially but becomes stable over a period of time in Case IV but in other cases oscillations persist. Also, in all the cases, the system does not reach the desired terminal state

Let us consider the desired prey (pest) population to be $x^{\ast} = 0.01$ such that there is almost no harm caused to the ecosystem. Then, using Eqs. (49) and (50), we obtain the values for $y^{\ast}$ and $u^{\ast}$ respectively. Using $(x^{\ast},y^{\ast}(x^{\ast}))$ and $u^{\ast}$ we define the error system (52) and formulate the optimal control problem (53) for each case. Choosing the matrices

$$\begin{aligned} Q = \begin{bmatrix} 0.01 &{} 0\\ 0&{} 0.01 \end{bmatrix}, \ R = [1] \end{aligned}$$

and solving the Algebraic Riccati Equation (59) using the LQR command of MATLAB, we get the solution matrix P for each case using which we obtain the feedback control for the error system. Then using equation (60), we get the optimal control for the explicit control system (47)–(48). The optimal trajectory of the state variables is depicted in Fig. 8. We observe that in all the cases, the optimal control drives the system from the same initial point (4.5, 3) to the desired terminal state in finite time.

Fig. 8

This figure shows the optimal trajectory of the state variables from the initial state (4.5, 3) to the desired terminal State with the application of control for all the four cases. In all the cases, the system reaches the desired terminal state in finite time

Figures 9 and 10 depict the local definiteness of the function l(v) and the trajectory of the optimal control u in each case. We see that the local definiteness of the function l(v) ensures the asymptotic stability of the terminal state of the system.

Fig. 9

This figure shows the local definiteness of the function $l(v) = l(v_1,v_2)$ around the origin (0, 0)

Fig. 10

This figure shows the trajectory of the Optimal Control function (60) for all the four cases

Now, we will simulate the trajectories of the state variables under the application of the control (60) for each case but with the terminal prey population chosen to be $x^{\ast} = E^{\ast}_2 + 0.05$, where $E^{\ast}_2$ is the respective first interior equilibrium point for each case. The resulting terminal states for all cases have been listed in Table 3. Under ideal circumstances, we will expect the system to reach the desired terminal state under the application of the control. However, we observe that does not happen in this case. We see from Fig. 11 that in none of the cases the system reaches the desired state. Moreover, the system becomes unstable with predator density becoming negative in all cases. This in feasibility is attributed to the chosen prey component of the terminal state $x^{\ast}$.

Fig. 11

This figure shows the trajectory of the state variables under the application of control when the prey component of the terminal state is chosen to be greater than the equilibrium of the initial system $x^{\ast} > E^{\ast}_2$ for all the four cases

Table 3 This tables shows the values of the chosen terminal states for all cases

We know from the dynamics of the initial system (3)–(4) that when the equilibria $E^{\ast}_2$ alone exists, it is either stable or there is an asymptotically stable limit cycle which is formed and the axial equilibrium $(\gamma ,0)$ is always saddle. Thus, when we choose $x^{\ast} > E^{\ast}_2$, the resulting point on the prey isocline curve $(x^{\ast},y^{\ast}(x^{\ast}))$ lies on the unstable manifold of $(\gamma ,0)$. This results in the unexpected behavior of the system. Thus, we conclude that the control can drive the system only when the prey component of the terminal state $x^{\ast}$ is chosen sufficiently close to zero. Thus, the control strategy provided by the explicit control system is applicable only for the pest management applications with feedback optimal control mechanism.

5.3.2 Inhibitory Effect of the System

In this section, we consider the variation of inhibitory effect (represented by the parameter $\omega$) in the optimal strategies by keeping other parameters fixed to $\beta = 2.2,\;\delta = 0.4,\;$ and $\gamma = 0.9$. By considering $x^{\ast} = 0.2$, we consider 7 cases with $\omega$ varying from 0 to 8.

Figures 12 and 13 represent the optimal trajectories of the prey and predator respectively with the application of feedback control as the parameter $\omega$ varies. For the cases where $\omega$ takes the values $0,\; 0.5$ and 1, we see that the system is driven by the control to the corresponding terminal state. However, as the parameter increases starting from from $\omega = 2$ the states start oscillating instead of reaching the desired state and as $\omega$ further increases, oscillations also increase. When $\omega = 6$, the prey population increases out of the range as compared to its desired level and correspondingly the predator population becomes too negative. When $\omega = 8$, then prey start to grow exponentially and predators behavior becomes more unpredictable.

Fig. 12

This figure shows the optimal trajectory of the prey (pest) with the application of feedback control as the parameter $\omega$ varies

Fig. 13

This figure shows the optimal trajectory of the predator with the application of feedback control as the parameter $\omega$ varies

5.4 Ecological Significance

The theoretical findings of the explicit control system show that bio-control of species can be achieved using feedback control by maintaining the pest at minimal levels without causing damage to the systems. This type of control strategy is applicable when additional food needs to be provided at regular intervals as feed back apart from the usual optimally regulated supply (Wade et al. 2008). In particular, when the goal is to achieve inundative bio-control (Blackburn et al. 2016), the natural enemies are mass reared and released into eco-systems which are not natural for them. Thus, providing additional food in a feedback fashion helps them to sustain in the ecosystem.

We also see from the numerical illustrations that the increase in inhibitory effect in the system can de-stabilize the system and even the controlled system need not be driven to the desired state. Ecological experimental findings from McClure and Despland (2011) reveal similar outcomes when the inhibitory effect of social caterpillar is studied against three of its natural enemies: spiders, parasitoids and stinkbugs. In all cases the results show that as the number of fourth instar caterpillars increase, the capture by the predator starts to drastically reduce. In particular, for a group of two fourth instar caterpillars, for 0.8 mean number of attacks by stinkbugs, 0.6 were captured where as for a group of 30 caterpillars, for every 0.8 mean number of attacks, only 0.2 were captured. Not just being together as a group, the caterpillars also used techniques such as jerking away, thrashing and even biting. It is stated in McClure and Despland (2011) that: “When stinkbugs were used as predators, evasive behaviours were the most efficient in creasing survival". Similarly, when in large groups, caterpillars also employed head flicking and biting against parasitoids. The authors also state that: “In general. the fourth instar caterpillars showed more varied defensive responses, including falling off the bridge and biting the aggressor, and were more successful against all the three natural enemies". These findings show that the mathematical results obtained are in line with the ecological field observations and that the inhibitory effect plays a major role in foraging of the predator especially in high prey densities.

6 Discussion and Conclusions

Studies on providing additional food to the predators have been receiving attention over the years by theoretical and experimental scientists (Harwood et al. 2004, 2005; Redpath et al. 2001; Sabelis and Van Rijn 2006; Soltaniyan et al. 2020; Van Baalen et al. 2001; van Rijn et al. 2002; Wade et al. 2008) in the contexts of both biological conservation and bio-control. The role of quality of additional food to predators and its impact on the system is discussed in Redpath et al. (2001), Sabelis and Van Rijn (2006), Wade et al. (2008), Winkler et al. (2005). A detailed study involving qualitative properties and asymptotic controllability of the additional food provided system involving type IV response has been done in Srinivasu et al. (2018a) and Vamsi et al. (2019). The findings reveal that the system admits either an asymptotically stable equilibrium or a limit cycle surrounding an unstable equilibrium. It is also observed that the system could be asymptotically driven to any of the two states under certain conditions. Most importantly, it is shown that providing additional food need not always result in successful achievement of biological conservation or bio-control. This, in fact, is supported by the experimental findings in Harwood et al. (2004, 2005); Putman and Staines (2004), Toft (2005). The extent of achieving the desired objective depends on the choice of quality and quantity of additional food provided (Marcarelli et al. 2011, Soltaniyan et al. 2020).

Though the findings of Srinivasu et al. (2018a), Vamsi et al. (2019) are useful, they cannot be practically implemented because of the asymptotic nature of the results. In practice, achieving the objective of reaching the terminal state in finite time is highly desirable. In that context, the focus of this article has been to use the available control parameters to optimally reach the desired terminal state in finite time. Two optimal control problems involving type IV functional response have been considered: one with the additional food system where quality of additional food is an implicit control and other, with the quality of additional food as explicit control. Mathematically, the rate of change of the predator density is linear with respect to the explicit control and non-linear with respect to the implicit control. Accordingly, in the first case, a time optimal control problem is formulated and studied using the Maximum Principle approach. In the second, a linear feedback control optimal control problem is formulated and studied using the Dynamic Programming approach. The outcomes of these studies are applicable in both biological conservation and bio-control.

6.1 Study 1: Time Optimal Control Problem

The objective of this study is to drive the system from a given initial state to the desired terminal state in minimum time by varying the quality of additional food. Using the characteristics of the optimal solution provided by Pontryagin’s Maximum Principle, the optimal strategy turned out to be of bang–bang type with possibility of multiple switches. One of the significant findings of this work is that both biological conservation and bio-control can be achieved in finite time. In the case of biological conservation, the terminal state is one of the points in the curve of admissible equilibria. Depending on the nature of the admissible curve and the prey component of the desired state, the terminal state is either stable or unstable. The advantage of this optimal strategy is that the system is driven to the terminal state even if it is unstable. Once the terminal state is reached, the optimal strategy suggests that the additional food of constant quality needs to be provided so as to maintain the system in the same state for all future times. However, there is a need to employ a cost effective technique to provide additional food especially on a long term basis. One such technique is to grow some suitable alternate sources of food to predator in the ecosystem itself (Landis et al. 2000).

On the other hand, if the objective of the study is to control the pest (prey) at a minimal level, then the results indicate that the predators must be constantly supplied with high-quality additional food. As a result, there would be no switches in the optimal strategy. This will lead to an increase in predator population and leads to a minimal level of the prey (pest) that exist in the ecosystem with the predator species feeding predominantly on additional food (Srinivasu et al. 2018a). These results are in agreement with the experimental findings of Calixto et al. (2013); Soltaniyan et al. (2020). Numerical illustrations validate these theoretical results for specific examples.

In the case of biological conservation, switching in optimal strategy (Proposition 1) is very pertinent because outcomes of ecological studies show that constant provision of high quality additional food not only leads to apparent competition (Holt 1977) leading to reduction of prey but could also eventually eliminate prey (Srinivasu et al. 2018a; Vamsi et al. 2019). On the other hand, providing predator constantly with low quality additional food leads to the reduction in survival, fecundity and predation capacity (Magro and Parra 2004; Putman and Staines 2004; Redpath et al. 2001). If the predators are not optimal foraging species, then feeding low quality additional food could lead to adverse effects. The findings of Putman and Staines (2004) state that “the red deer Cervus elaphus may develop a reliance on the food supplement provided, reducing intake of natural forages to near zero; where feed provided is less than 100 percent of daily requirement, these animals may regularly lose, rather than gain condition. Also, it is stated that provision of low quality food supplements such as grain, root crops which are deficient in fiber may adversely affect the water balance of predators. It has been observed that winter feeding did not produce calves with greater birth weights than those reported for animals which are not given supplementary feed.”

6.2 Study 2: Linear feedback control Optimal Control Problem

For this study, additional food is explicitly incorporated into the functional response by linear addition into the predator compartment. Here, the desired terminal state is chosen based on the threshold pest density such that there is least or no damage to the ecosystem. This is motivated from the ecological findings that have shown that the predators could damage the ecosystem by feeding on the crops (Calvo et al. 2009; Urbaneja-Bernat et al. 2013) in the absence of prey. In some of the ecological experiments by Hamdi et al. (2013), it was seen that once the pest were eradicated from the system, the predators displayed cannibalistic behaviour when there was a reduction in the supply of high quality additional food. These results show that it is better to sometimes not eliminate the pest completely but sustain them at low densities such that there is no damage to the crops and at the same time predators also have their target prey.

Using the steady states of the system, the corresponding predator density and the control are obtained. The disadvantage of this control is that the terminal state may not be asymptotically stable. Thus, to overcome this limitation, an error system is defined and an linear feedback control optimal control problem is formulated based on the error system to drive the state to the origin. This would drive the actual system to the desired state. The optimal control is shown to be a feedback control that ensures asymptotically stability of the terminal state. The optimal strategy obtained suggests to the experimental ecologists a way of maintaining the pest at the least harmful level without eradicating them completely. This is shown to be reached within finite time. Numerical illustrations validate the above results.

The numerical simulations when performed by taking the terminal prey value greater than the prey component of the interior equilibrium of the initial system showed that the desired state could not be reached with the control strategy. This could be attributed to the inherent instability of the system. In fact, this is one major difference between both the studies undertaken in this work. While the time optimal control strategy can steer the system even to unstable interior equilibrium, the feedback control fails to do so. Similar simulations were also carried out by varying the inhibitory effect of the prey. The results showed that on increase of the inhibitory effect, the system could not be driven to prey control (pest management) state. These theoretical findings validate the experimental outcomes in Collings (1997) where spider mites display group defense when in large densities.

The outcomes of the implicit control system studies are qualitatively similar to the findings of optimal control studies (Srinivasu and Prasad 2010) involving the type II additional food provided system (Srinivasu et al. 2007). Recently, it has been pointed out by Parshad et al. (2020) that some of the results of the work (Srinivasu et al. 2007) have flaws pertaining to elimination of prey in finite time. Thus, in this work, we have modified the terminal state to a minimal prey density to achieve bio-control rather than eliminating prey from the system. This work can also be seen in a more general manner as we consider Holling type IV response which is a generalization of Holling type II response. In the present work we also model the control in the explicit fashion that helps us to have a feedback mechanism which is suited for adaptive studies. We also discuss the role and effect of inhibitory effect.

In conclusion, the outcomes of these studies show that the additional food provided predator–prey systems involving type IV functional response can be driven to a desired state in finite time with quality of additional food as implicit and explicit control parameter. The analysis shows the vital role played by the quality of additional food provided to the predators, emphasizing the importance of switching the quality from high to low or vice–versa depending on the objective. Due care must be taken while doing so because arbitrary choice of quality could lead to adverse effects.

Appendices

Appendix: 1

1.1 Global Dynamics of the Additional Food System (7)–(8)

We will now briefly describe the global dynamics of the additional food provided system (7)–(8). Let us consider the following condition holding true for the initial system (3)–(4):

$$\begin{aligned} \omega - \dfrac{(\beta - \delta )^2}{4\delta ^2} > 0 \end{aligned}$$

Under this condition, when additional food is provided to the initial system (3)–(4) we get three different cases depending on the behavior of the prey isocline of the initial system (3)–(4). The Fig. 14 depicts the different types of the prey isocline that occur under the condition - I.

Fig. 14

This figure shows the nature of prey isocline curve of the initial system under the three sub-cases I-1, I-2 and I-3 of condition—I. These are plotted for the values of parameters $\beta = 2.2$ and $\delta = 0.4$

Along with the nature of the prey isocline curve (as shown in Fig. 14), the dynamics of the additional food provided system (7)–(8) also depend on the values that the parameters $\alpha$ and $\xi$ take with respect to the following four curves where the first three determine the stability of equilibria while the fourth determines the existence of interior equilibrium points (for the additional food system):

The Prey Elimination Curve (PEC)

$$\begin{aligned} \beta \xi - \delta (1+\alpha \xi ) = 0 \end{aligned}$$

the Transcritical Bifurcation Curve (TBC)

$$\begin{aligned} \beta (\gamma + \xi (\omega \gamma ^2 + 1)) - \delta ((1+\alpha \xi )(\omega \gamma ^2 + 1) + \gamma ) = 0 \end{aligned}$$

the Hopf Bifurcation Curve (HBC)

$$\begin{aligned} \begin{aligned}&3\omega (1+\alpha \xi )\bigg [\dfrac{(\beta -\delta ) - \sqrt{(\beta -\delta )^2 - 4\omega [\delta (1+\alpha \xi )-\beta \xi ]}}{2\omega [\delta (1+\alpha \xi )-\beta \xi ]}\bigg ]^2\\&\quad +(2-2\omega \gamma (1+\alpha \xi ))\bigg [\dfrac{(\beta -\delta ) - \sqrt{(\beta -\delta )^2 - 4\omega [\delta (1+\alpha \xi )-\beta \xi ]}}{2\omega [\delta (1+\alpha \xi )-\beta \xi ]}\bigg ] \\&\quad + (1+\alpha \xi ) - \gamma = 0 \end{aligned} \end{aligned}$$

and the Discriminant Curve (DISC)

$$\begin{aligned} (\beta -\delta )^2-4\omega (-\beta \omega +\delta (1+\alpha \xi ))^2=0 \end{aligned}$$

The Figs. 15, 16, and 17 (called bifurcation diagrams) show the division of the $(\alpha ,\xi )$ - space based on the four curves mentioned above and the curve $\alpha = \frac{\beta }{\delta }$ for each of the sub-conditions I-1, I-2 and I-3 respectively. Table 4 summarizes the global dynamics of the system (7)–(8).

Fig. 15

This figure represents the division of control parameter space by the discriminant curve (DISC), the prey elimination curve (PEC), the Hopf bifurcation curve (HBC), the transcritical bifurcation curve (TBC) and the curve $\alpha = \frac{\beta }{\delta }$. The parameter values chosen are $\beta = 2.2,\; \delta = 0.4,\; \gamma = 1.2,\;$ and $\omega = 8$, satisfying the condition I-1

Fig. 16

This figure represents the division of control parameter space by the discriminant curve (DISC), the prey elimination curve (PEC), the Hopf bifurcation curve (HBC), the transcritical bifurcation curve (TBC) and the curve $\alpha = \frac{\beta }{\delta }$. The parameter values chosen are $\beta = 2.2,\; \delta = 0.4,\; \gamma = 0.63,\;$ and $\omega = 7$, satisfying the condition I-2

Fig. 17

This figure represents the division of control parameter space by the discriminant curve (DISC), the prey elimination curve (PEC), the transcritical bifurcation curve (TBC) and the curve $\alpha = \frac{\beta }{\delta }$. The parameter values chosen are $\beta = 2.2,\; \delta = 0.4,\; \gamma = 0.42,\;$ and $\omega = 6.4$, satisfying the condition I-3

Table 4 Global dynamics of the additional food provided system (7)–(8)

Appendix: 2

1.1 Stability of the Admissible Equilibria (14)

The study reveals that the possibility of instability in the interior equilibrium occurs only if one or more positive critical points exist for the derivative of the prey isocline of the system (7)–(8). The quadratic equation obtained by equating the derivative of the prey isocline to zero is given by

$$\begin{aligned} 3 \omega (1 + \alpha \xi ) x^2 + 2(1 - \omega \gamma (1 + \alpha \xi )) x + (1+\alpha \xi ) - \gamma = 0 \end{aligned}$$

From the above equation we observe that for the prey isocline to have a positive real critical point, the sum of the roots of the equation, must satisfy the inequality $-\frac{2(1 - \omega \gamma (1 + \alpha \xi ))}{3 \omega (1 + \alpha \xi )} \ge 0$ along with the discriminant being positive. This implies that we must have

$$\begin{aligned} (\omega \gamma (1 + \alpha \xi ) - 1)\le & {} 0\\ \omega \gamma + \omega \gamma \alpha \xi\le & {} 1\\ \omega \gamma \alpha \xi\le & {} 1 - \omega \gamma \\ \end{aligned}$$

Rearranging the expression, we get

$$\begin{aligned} \alpha \le \dfrac{1 - \omega \gamma }{\omega \gamma \xi } \end{aligned}$$

(62)

Now, we apply this result to the curve of admissible equilibrium points by substituting for $\alpha$ from Eq. (13). Then, the above inequality (62) becomes

$$\begin{aligned} \dfrac{(\beta \xi - \delta ) (1 + \omega (x^{\ast}(\alpha ))^2) + (\beta - \delta ) x^{\ast}(\alpha )}{\delta \xi (1 + \omega (x^{\ast}(\alpha ))^2 }\le & {} \dfrac{1 - \omega \gamma }{\omega \gamma \xi }\\ ((\beta \xi - \delta ) (1 + \omega (x^{\ast}(\alpha ))^2) + (\beta - \delta ) x^{\ast}(\alpha )) (\omega \gamma \xi )\le & {} (1 - \omega \gamma ) \delta \xi (1 + \omega (x^{\ast}(\alpha ))^2 \end{aligned}$$

The last expression contains a quadratic polynomial in $x^{\ast}(\alpha )$. Solving for $x^{\ast}(\alpha )$, we get

$$\begin{aligned} (x^{\ast}(\alpha ) - \hat{x}_1)(x^{\ast}(\alpha ) - \hat{x}_2) \le 0 \end{aligned}$$

(63)

where $\hat{x}_1$ and $\hat{x}_2$ are the roots of the quadratic equation

$$\begin{aligned} ((\beta \xi - \delta ) (1 + \omega (x^2)) + (\beta - \delta ) x) (\omega \gamma \xi ) - (1 - \omega \gamma ) \delta \xi (1 + \omega x^2) = 0 \end{aligned}$$

and they are given by

$$\begin{aligned} \hat{x}_1= & {} \dfrac{-(\beta - \delta ) \gamma \omega - \sqrt{(\beta - \delta )^2\gamma ^2\omega ^2 - 4\omega (\delta - \beta \xi \omega )^2}}{2 \omega (\beta \gamma \xi \omega - \delta )} \end{aligned}$$

(64)

$$\begin{aligned} \hat{x}_2= & {} \dfrac{-(\beta - \delta ) \gamma \omega + \sqrt{(\beta - \delta )^2\gamma ^2\omega ^2 - 4\omega (\delta - \beta \xi \omega )^2}}{2 \omega (\beta \gamma \xi \omega - \delta )} \end{aligned}$$

(65)

Clearly, from the above expressions, $\hat{x}_1 < \hat{x}_2$ depending on the existence of these roots. If they exist, then using the inequalities (62) and (63), we conclude that instability occurs in the admissible equilibria only if the prey component $x^{\ast}(\alpha )$ lies between the two, i.e., if $\hat{x}_1< x^{\ast}(\alpha ) < \hat{x}_2$. In other words, whenever $x^{\ast}(\alpha ) < \hat{x}_1$ and $x^{\ast}(\alpha ) > \hat{x}_2$, the admissible equilibrium point $(x^{\ast}(\alpha ),y^{\ast}(\alpha ))$ is stable. Thus, the existence of the points $\hat{x}_1$ and $\hat{x}_2$ determine the nature of the admissible equilibrium curve and thus the stability of the equilibrium point. The existence is determined by the sign of the discriminant $D = (\beta - \delta )^2\gamma ^2\omega ^2 - 4\omega (\delta - \beta \xi \omega )^2$. Based on this we have the following cases:

• Case Ia: $D \ge 0,\; \hat{x}_1 < 0 \; \text {and } \hat{x}_2 > 0$

  In this case, the admissible equilibrium has a positive local maximum and hence a crest. Thus for points between $x^{\ast}(\alpha ) = 0$ and $x^{\ast}(\alpha ) = \hat{x}_2$, the corresponding equilibrium points are unstable. The relationship between the admissible equilibria and the control parameter $\alpha$ for this case is depicted in two-quadrant plot in the Fig. 18. The dotted lines on the curve from A till $y_{max}$ represent the unstable branch $x^{\ast}y^{\ast}$ - plane. The point $A = \frac{\beta \xi }{\delta }$ represents the curve touching the $y-axis$. We also see from the figure that whenever we choose predator density between 0 and A (represented by point B in the figure), there are two choices of the prey component for admissible equilibria. The one that lies to the left of $\hat{x}_2$ on the $x-axis$ would be unstable and the other would be stable. On the other hand, for the choice of predator population less than $A =\frac{\beta \xi }{\delta }$ (represented by C in the figure) there exits a unique prey density and control and the resulting admissible equilibrium is stable.

  Fig. 18

  

  Admissible equilibria and control—Case Ia

• Case Ib: $D> 0,\; \hat{x}_1> 0 \; \text {and } \hat{x}_2 > 0$

  In this case, the admissible equilibrium curve has both local maximum and local minimum in the positive quadrant and hence there is both trough and crest. Here the admissible equilibria is unstable between the two points $\hat{x}_1$ and $\hat{x}_2$ as discussed before but stable elsewhere. The relationship between the admissible equilibria and the control parameter $\alpha$ for this case is depicted in two-quadrant plot in the Fig. 19. The dotted lines on the curve from $y_{\min }$ till $y_{\max }$ represent the unstable branch in the $x^{\ast}y^{\ast}$ - plane. The points B and C represent the same quantities as discussed in the above case.

• Case II: $D > 0,\; \hat{x}_1< 0 \; \text {and } \hat{x}_2 < 0$ or $D < 0$

  In this case, either the two points $\hat{x}_1$ and $\hat{x}_2$ exist and are negative or they are not real numbers. This means that there are no positive critical points for the admissible equilibrium curve and thus the admissible equilibrium curve is monotonically decreasing. As a result, any equilibrium point on the curve is stable. This case is depicted in two-quadrant plot in Fig. 20.

  Fig. 19

  

  Admissible equilibria and control—Case Ib

  Fig. 20

  

  Admissible equilibria and control—Case II

The following proposition summarizes the discussion above and can be applied to the case of biological conservation:

Proposition 2

For Prey Species Conservation:

For $0< \bar{x} < \gamma$, there exists a unique $\bar{\alpha }$ such that $(\bar{x},\bar{y}(\bar{\alpha }))$ is an admissible interior equilibrium for the system (7)–(8). Further, this equilibrium is asymptotically stable provided $\hat{x}_1< \bar{x} < \hat{x}_2$ and unstable otherwise (see Figs. 18, 19 and 20)

For Predator Species Conservation:

• 1. For every $\tilde{y}$ below the crest (in Fig. 18) and between the crest and trough (in Fig. 19), there exist two values of quality, $\alpha _1$ and $\alpha _2$ such that $(x(\alpha _1),\tilde{y})$, $(x(\alpha _2),\tilde{y})$ are admissible equilibria for the system (7)–(8). Moreover, $(x(\alpha _1),\tilde{y})$ is unstable since $\hat{x}_1< x(\alpha _1) < \hat{x}_2$ and $(x(\alpha _2),\tilde{y})$ is stable since $\hat{x}_2 < x(\alpha _2)$.

• 2. For $\tilde{y}$ below the point A (see Figs. 18, 19 and 20) with $\tilde{y} < A$, there exists a unique $\tilde{\alpha }$ such that $(\tilde{x}(\tilde{\alpha },\tilde{y})$ is an admissible equilibria for the system (7)–(8). Moreover this equilibrium is asymptotically stable.

• 3. For $\tilde{y}$ above the crest with $\tilde{y} > y_{\max }$ (see Figs. 18 and 19), there exists no admissible equilibrium point for the system (7)–(8).

Appendix: 3

1.1 General form of Mayer Problem of Optimal Control

We will present here the general form of Mayer Problem of Optimal Control as stated in Cesari (2012). Let $A = [t_1,t_2] \times \mathbf{B}$ be a subset of the $t\mathbf{x}$ - space $\mathbb {R}^{1 + n}$, let U be a given subset of the $\mathbf{u}$ - space $\mathbb {R}^m$. Let $\mathbf{f} (t,\mathbf{x} ,\mathbf{u} ) = (f_1,f_2,...,f_n)$ be a given function on $A \times U$. For every $(t,\mathbf{x} ) \in A$, let $Q(t,\mathbf{x} ) = \mathbf{f} (t,\mathbf{x} ,U) \subset \mathbb {R}^n$ be the set of all $z = (z_1,z_2,...,z_n)$ with $z_i = f_i(t,\mathbf{x} ,\mathbf{u} ),\; i = 1,2,...,n$ for some $\mathbf{u} \in U$. Let E be a given subset of $t_1\mathbf{x} _1t_2\mathbf{x} _2$ - space $\mathbb {R}^{2n+2}$. The Mayer problem of optimal control is to find the optimal solution, usually to minimize the functional

$$\begin{aligned} I[\mathbf{x} ,\mathbf{u} ] = g(t_1,\mathbf{x} (t_1)t_2\mathbf{x} (t_2)) \end{aligned}$$

(66)

for pairs of functions $\mathbf{x} (t) = (x_1,x_2,...,x_n)$, $\mathbf{u} (t) = (u_1,u_2,...,u_m)$, $t_1 \le t \le t_2$, x absolutely continuous, u measurable satisfying

$$\begin{aligned} \dfrac{d\mathbf{x} }{dt} = \mathbf{f} (t,\mathbf{x} (t),\mathbf{u} (t)),\; t_1 \le t \le t_2 \end{aligned}$$

(67)

boundary conditions

$$\begin{aligned} e[\mathbf{x} ] = (t_1,\mathbf{x} (t_1)t_2\mathbf{x} (t_2)) \in E \end{aligned}$$

(68)

and constraints

$$\begin{aligned} (t,\mathbf{x} (t))\in & {} A,\; t_1 \le t \le t_2, \end{aligned}$$

(69)

$$\begin{aligned} \mathbf{u} (t)\in & {} U\; t_1 \le t \le t_2. \end{aligned}$$

(70)

in the class $\Omega$ of all admissible pairs $(\mathbf{x} ,\mathbf{u} )$. By an admissible pair for the problem (66)–(70) we mean a pair $(\mathbf{x} (t),\mathbf{u} (t)),\; t_1 \le t \le t_2$, x absolutely continuous, u measurable, satisfying all the requirements (66)–(70). Here, x and u are also called an admissible trajectory and admissible control respectively.

We will now state the Filippov’s Existence Theorem which is used to prove the existence of an optimal solution to the optimal control problem (66)–(70).

Theorem 6

(The Filippov existence Theorem for Mayer problem of optimal control) If A and U are compact, E closed, $\mathbf{f}$ is continuous on $A \times U$, g is continuous on E, $\Omega \ne \Phi$, and for every $(t,\mathbf{x} ) \in A$ the set $Q(t,\mathbf{x} ) = \mathbf{f} (t,\mathbf{x} ,U) \subset \mathbb {R}^n$ is convex, then the objective functional $I[\mathbf{x} ,\mathbf{u} ]$ has an absolute minimum in $\Omega$.