Integrated deployment of local urban relief teams in the first hours after mass casualty incidents

Abstract

This paper develops scenario-based stochastic optimization model to choose optimal policies for the integrated deployment of local urban relief teams in the early aftermath of sudden-onset mass casualty incidents. The deployment of local relief teams in an urban area with several affected sites, allocation of casualties to casualty treatment centres, and assignment of medical teams to casualty treatment centres and triage groups are simultaneously determined. Seven strategies under “streaming” and “pooling” groups of treatment strategies are linked to the activity of relief teams. Based on realistic data, our model is analysed for 1750 random samples of the disaster field and 35 instances of a hypothetical earthquake. The results show the integration of SAR and on-field treatment operations can increase the number of survivors. The robust model results in a less number of survivors because it tries to maintain the optimal solution under given scenarios close to its expected value.

1 Introduction

Statistics show that frequency and magnitude of natural and man-made disasters/mass casualty incidents (MCIs), are increasing all over the world over time (Gupta et al. 2016). The vulnerability of societies to disastrous events, particularly in terms of fatalities and injuries, is increasing as a result of urbanization and population growth. The situation may worsen in the case of sudden-onset disasters that happen with short notice or without warning. This fact is evident in the number of casualties and fatalities in recent severe earthquakes in Japan (Tōhoku, 2011), Nepal (Gorkha, 2015), Chile (Illapel, 2015), Iran (Sarpol-e Zahab, 2017), and Indonesia (2018) (Doocy et al. 2013). The same trend is observed for man-made disasters, particularly urban terrorism, in London (2005), Boston (2013), and Syria (2018). These tragic events urge the necessity for better decision making on the coordination and allocation of relief resources during the response phase of MCIs (D’Andrea et al. 2013), comprising operations such as evacuation, debris clearing, resource dispatching, and casualty management (Çelik et al. 2015). As an attempt to improve the situation, this research focuses on casualty management. More specifically, it studies the problem of deploying the limited number of urban search and rescue (USAR¹) and medical teams (known as relief teams) in the first hours after the occurrence of a sudden-onset MCI to increase the expected number of survivors (ENS). The relief teams, introduced below, play important roles in casualty management right after MCIs.

USAR teams USAR teams, supported by national agencies like Red Cross, Red Crescent, and governmental emergency management, consist of specially-trained personnel, supplied with heavy and light rescue equipment (Alexander 2002; Chen and Miller-Hooks 2012). Teir responsibility is to find casualties, extricate the trapped ones, and transfer them to the nearby casualty treatment stations (CTSs). The first day, particularly the first hours after a disaster, plays a vital role in search and rescue (SAR) operations. For example, in the 1980 earthquake in southern Italy, 94% of people were rescued during the first 24 h (McGuigan et al. 2002); in the 1976 earthquake in Tangshan (China), 81% of the affected people were rescued in the first day (Olson and Olson 1987).

Medical teams A medical team, dispatched from hospitals/medical centres, consists of health professionals (physician, nurse, paramedic, etc.) who provide emergency care services like on-field triage and treatment for serious casualties in the scene of disaster. Affected people in a disaster field are usually divided into four triage groups: red (immediate), yellow (observation), green (wait, walking wounded) and black (expectant, deceased). Casualties in red triage group require immediate life-saving procedures whereas yellow-group ones need surgical or medical intervention within the next 2–4 h (Smith and Wallis 2012).

When an urban area is struck by a sudden-onset MCI of high magnitude like earthquake, many people, trapped in affected sites of municipal districts, will be in need of extrication and emergency care services. Yet, in such situations, local authorities usually do not have sufficient number of relief teams to fulfil the shocked post-disaster demands. Therefore, secondary relief teams from national and sometimes international organizations are called. But, it usually takes a relatively long time for them to arrive at the affected sites. Therefore, the efficient management of the limited local relief teams in the first post-disaster hours is a very challenging task (Rodriguez-Espindola et al. 2018).

Coordination is a challenge in the response phase of disasters (Bahadori et al. 2015). In the 2003 earthquake in Bam, Iran, lack of coordination among responder units in SAR operations resulted in a large number of deaths (Ramezankhani and Najafiyazdi 2008). Rodriguez-Espindola et al. (2018) emphasized the necessity of coordination among prepositioning, allocation and distribution of relief resources. They stated that Operations Research (OR) and optimization methods could provide a support to increase coordination in response operations.

SAR and on-field treatment are two sequential inter-related activities of casualty management. Therefore, the deployment of both USAR and medical teams should simultaneously be addressed for increasing the number of rescued casualties. Moreover, because of the inherent dynamics in post-disaster conditions, choosing the best policy to deploy relief teams is not straightforward and must frequently be altered based on the last updated data. Hence, our purpose is to recommend the best policies for deploying local relief teams right after a sudden-onset MCI when the time is scarce. Here, policy means a set of allocation decisions on relief teams and casualties corresponding to a given treatment strategy. Moreover, our objective is to optimize the number of survivors which is considered to be the most important aim in casualty management operations (Wilson et al. 2013; Farahani et al. 2020).

The paper is organized as follows. In Sect. 2, the relevant body of literature is reviewed. Section 3 describes the research problem. In Sect. 4, we formulate the stochastic optimization models and robust models. Section 5 explains the details of secondary data for our statistical analysis. In Sect. 6, we present a numerical analysis and some managerial implications, based on i) the 50 randomly generated test problems and ii) primary and secondary real-life data for a hypothetical earthquake in Tehran, capital of Iran, as a large populated city. The primary data was mainly gathered by conducting phone interviews with the experts in local authorities. The results of robust models are presented in Sect. 6.5. Discussion of the findings is provided in Sect. 6.6. Section 7 is devoted to concluding remarks and directions for future research.

2 Literature review

While there is an extensive literature on disaster operations management (Altay and Green 2006; Caunhye et al. 2012; Galindo and Batta 2013; Abidi et al. 2014; Anaya-Arenas et al. 2014; Leiras et al. 2014; Hoyos et al. 2015; Özdamar and Ertem 2015; Alem et al. 2016; and Gupta et al. 2016 are some review papers in this area), casualty management, particularly, in the first hours after disasters, has received little attention. In a comprehensive review paper, Farahani et al. (2020) categorized the research in the field of casualty management as resource dispatching/ search and rescue, on-site triage, on-site medical assistance, transportation to hospital, and triage and treatment in hospital categories. They analysed all papers in a micro level and reported insights and future directions. Casualty management is comprised of three operations: (I) SAR; (II) on-field treatment; and (III) in-hospital treatment. In-hospital treatment falls outside the scope of this paper. In this section, a review of the literature on SAR and on-field treatment is presented in terms of the related research streams as follows. The papers which integrated these two operations are reviewed as the coordination/ integration.

SAR Chen and Miller-Hooks (2012) proposed a stochastic model to allocate USAR teams to affected sites in the first hours after disasters for maximizing the expected number of rescued casualties. Wex et al. (2013) formulated the same problem; but, their objective was to minimize the completion time of SAR operations.

Zhang et al. (2017) proposed a multi-stage non-linear model for the allocation of rescue teams to affected sites in secondary disasters. Their objectives were to minimize the maximum arrival times and to maximize the allocations’ satisfaction. Bravo et al. (2018) proposed a Markov decision model, using unmanned aerial vehicles to find casualties. Rauchecker and Schryen (2019) proposed a model for allocating the limited number of multi-capability rescue units to several disasters. They minimized the weighted sum of the rescue completion times for all units. Ahmadi et al. (2020) introduce a two-stage allocation-routing model for SAR operations after disaster. The model maximizes the demand coverage in first stage and minimizes the completion time in second stage.

On-field treatment Rescued casualties with serious injuries are transferred to nearby CTSs to prioritize and receive stable emergency services (Frykberg 2005). Sacco et al. (2005, 2007), Mills et al. (2013), Dean and Nair (2014), Mills (2015), and Kamali et al. (2017) developed optimization models for prioritization and triage of casualties for treatment and transportation to hospitals. Sacco et al. (2005) developed an on-field treatment model in which a historical-based survival probability function was introduced considering deterioration in patients’ condition over time. Mills et al. (2013) and Mills (2015) also developed some intuitive heuristics for prioritizing the transportation of casualties to hospitals considering transportation time, available vehicles, and triage group distribution. Both Sacco et al. (2005) and Mills et al. (2013) considered the same treatment times for all casualty groups. Dean and Nair (2014) proposed a model for dispatching victims to hospitals and compared it with the other heuristics used in practice. Kamali et al. (2017) optimized service order for casualties with multiple servers and several casualty types.

Li and Glazebrook (2010) investigated casualties’ misclassification. They considered a scheduling system with one server and multiple jobs, having uncertain service time and lifetime. Jacobson et al. (2013), considering resource limitations, categorized casualties based on service time and fix survival probability distributions. Salman and Gul (2014) proposed a deterministic multi-period model to optimize the location and casualty transportation decisions aiming at minimizing the weighted sum of total travel and waiting times of casualties and the total costs of locating new facilities. Triage was ignored in this paper. Jin et al. (2015) developed a resource allocation model to maximize the number of survivors in a network of disaster sites, on-site clinics, and hospitals. They considered limitations on medical resources, the number of physicians, and operating rooms as well as capacity constraints in clinics and hospitals. Sun et al. (2017) considered a job scheduling problem with two classes of casualties. One medical provider can choose a person randomly for treatment or spend some time for triage before treatment. The goal was to balance the time spent on triage and service. Niessner et al. (2017) proposed an optimization-simulation approach for allocating physicians and medics to patients in Austrian advanced medical posts. Minimizing the total rescue time and the total number of patients was investigated. Gu et al. (2018) developed a single-period model to determine the location of medical shelters and to distribute medical supplies with budget limitation, and the severity and location of casualties. Caunhye et al. (2018) developed a three-stage stochastic model to locate medical centres and allocate casualties to medical centres and hospitals in which the total transportation time was minimized. Sabouhi et al. (2019) proposed a model to locate shelters, transport casualties to hospitals and distribute relief supplies. Liu et al. (2019) proposed a model to optimize the location of CTSs and the distribution of casualties in CTSs with the objectives of maximizing the ENS and minimizing the total operational costs. Alizadeh et al. (2019) formulated a two-stage robust stochastic optimization model for network design decisions and multi-period response operational decisions under uncertainty in the number of various-injured casualties at affected sites and transportation capacity. Sample average approximation was used to solve the model. Oksuz and Satoglu (2020) proposed two-stage stochastic model to determine the number and location of medical centres in the disaster response. The model minimized the total setup of medical centres and transportation costs of casualties.

Literature review shows that scholars have applied optimization and job scheduling as two major approaches to solve on-field treatment problems. Those who applied job scheduling approach (like Li and Glazebrook, 2011; Jacobson et al. 2013; Sun et al. 2017) have assumed that all casualties, considered individually, were available at time zero in a specific area. Such models become difficult to solve and inapplicable to speed-demanding post-disaster cases. On the other hand, optimization-based papers have not studied treatment strategies explicitly.

Coordination/integration The performance of USAR teams will determine the number of saved casualties and survival probability of them in CTSs. These will, in turn, affect the triage process and determine the best treatment strategies. As Table 1 shows, few recent papers have studied some types of coordination/integration among casualty management operations. Wilson et al. (2013, 2016) proposed a static flexible job scheduling problem to allocate casualties to a set of responder units, involved in transportation, pre-transportation treatment, rescue and pre-rescue treatment. Rezapour et al. (2018), which is directly related to this research, developed a single-period model for deploying relief units in multiple affected sites to maximize ENS. They considered extrication task, on-field triage, and on-field treatment simultaneously, but only addressed the streaming strategy with/without overflow. They assumed all casualties were available on the field right after the disaster. Although they emphasized coordination among casualty management operations, no experimental analysis was reported in this regard. Sun et al. (2021a) considered two types of casualties (mild and serious clusters) in a rescue chain to determine the location of CTSs and hospitals as well as to transport casualties to them. They minimized an Injury Severity Score for all casualties. The model was extended to a bi-objective model by Sun et al. (2021b). They also addressed the distribution of medical supplies. These two papers did not consider the allocation of USAR teams and the treatment strategies.

Table 1 The details of reviewed papers

Contribution In Table 1, we compare our research with the relevant body of literature. The proposed approaches for on-field treatment are classified into two categories. The first one studies the scheduling and routing of individual teams and casualties. Such an approach leads to complex models. Therefore, its application in MCIs is mainly limited to a single temporary location. The second category applies optimization to make decisions for groups of teams, casualties, relief items, and temporary locations. In brief, our contribution to the field is as follows:

Stochastic optimization models are proposed to integrate SAR and on-field treatment operations. Table 1 indicates that only Wilson et al. (2013, 2016) and Rezapour et al. (2018) addressed the operations simultaneously. Wilson et al. (2013, 2016) focused on individuals, whereas our problem is inherently for casualty groups. Note that Rezapour et al. (2018) did not address the allocation of extricated casualties to CTSs as a key decision linking SAR and on-field treatment operations. This variable also implicitly determines near which affected sites the CTSs should be located.

• (1) Policy making is embedded in model formulations by proposing various combinations of treatment strategies and linking them to the allocation of relief teams. In fact, the operations of relief teams are optimized in line with any treatment strategy. According to Table 1, only Rezapour et al. (2018) addressed this issue. They considered “streaming” strategies with/without overflows, while we propose different “pooling” strategies and compare them with streaming strategies.

• (2) Practical implications are reached by analysing different test problems and a case study. In dynamic speed-demanding post-disaster conditions, required accurate data is updated gradually; but, due to the severe time limitation, the models may not be solved with any update of data. Therefore, relief teams need to be equipped with the effective if–then rules beforehand. We generate insights on the performance of treatment strategies and the related allocation policy considering variations in triage group distribution and strategy choice in preparedness phase which can be implemented in response phase.

3 Problem definition

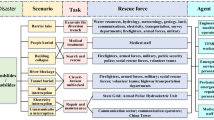
By developing stochastic optimization models to provide insights under some plausible scenarios, we figure out the best policy to allocate (1) local USAR teams to affected sites, (2) extricated casualties to CTSs, (3) Local medical teams to CTSs and (4) local medical teams to serious casualty groups in CTSs. We focus on several treatment strategies; the triage group and prioritization of casualties are assumed to be known. Our research scope is illustrated by a dotted rectangle in Fig. 1. These sequence of tasks referred to as casualty processing by some scholars (e.g., Wilson et al. 2013). Casualties are extricated by USAR teams and sent to nearby CTSs for on-field treatment by medical teams. The ultimate objective is to maximize ENS. Dispatching sufficient number of USAR and medical teams in the first hours after a sudden-onset MCI is impossible. Thus, the optimal deployment of limited local relief teams in the immediate aftermath of disasters is critical.

Fig. 1

Casualty processing after a disaster strike

Various strategies may be applied to allocate medical teams for treating casualty groups. Two widely-used extreme strategies at emergency departments of hospitals are “Streaming Strategy (SS)” and “Pooling Strategy (PS)” (Saghafian et al. 2012). In SS, medical teams are divided into two classes: one serves the red group, referred to as red class medical team, and the other serves the yellow group, referred to as yellow class medical team. In PS, medical teams serve both red and yellow groups according to the dictated priorities. Situations in the disaster field differ mainly from those in emergency departments (Venkat et al. 2015). Proposed strategies are as follows:

I. Four strategies are considered under SS:

SS-Regular: Medical teams are classified into two classes; i.e., red and yellow. Each casualty group is treated by its own dedicated medical team.

SS with red class overflow (SSR): Only red class medical teams overflow to treat yellow group when they are idle. It means red class medical teams may treat the yellow group, with priority given to red group.

SS with yellow class overflow (SSY): Only yellow class medical teams overflow to treat red group when they are idle. It means yellow class medical teams may treat red group, with priority given to yellow group.

SS with both classes overflow (SSB): Both red and yellow class medical teams are allowed to overflow in their idleness.

II. Three strategies are considered under PS:

PS with priority given to red triage casualties (PSR): Medical teams keep servicing the red group as long as there is any casualty in the red group. They only serve the yellow group when the red group is empty.

PS with priority given to yellow triage casualties (PSY): Medical teams keep servicing the yellow group as long as there is any casualty in the yellow group. They only serve the red group when the yellow group is empty.

PS with dynamic priority (PSD): PSR and PSY lead to a low service level for one of the triage groups. PSD improves the drawback by changing dynamically the priority of casualty groups over time according to the number of casualties.

The survival probability of casualties in CTSs depends on their waiting times, which in turn depend not only on the implemented treatment strategy, but also on the workload. The workload of a given CTS depends on (1) the treatment rates of allocated medical teams and (2) the casualty inflow rate determined by the USAR team allocation. This confirms the need for coordination between SAR and on-field treatment (see Fig. 2).

Fig. 2

The proposed decision framework

In the first post-disaster hours, the flow of volunteers and relief teams from other regions as well as changes in the existing local relief teams, as the main sources of supply side uncertainty, are not significant. However, the uncertainty in some demand side parameters including the number of affected people, the ratio of injured people in triage groups, the availability of transportation links, and the flow of casualties between nodes are taken into account by defining plausible scenarios with corresponding probabilities. The plausible scenarios will be made by the severity level and the time of occurring disasters. Three levels of severity (low, medium and high) and two time intervals (day and night) generate six scenarios whose probabilities are known.

4 Problem formulation

In this section, seven mathematical models are formulated to show the problem under different casualty treatment strategies. In Sect. 4.1 and 4.2, the formulation of SS-related and PS-related strategies are presented. In 4.3, the robust formulation is developed for SSB and PSD as two representatives of both types of treatment strategies.

SAR and on-field treatment operations are undertaken after a sudden-onset MCI during a finite planning horizon. We discretize the planning horizon by short time periods in which a reasonable number of casualties can be searched, rescued and treated in the field. $T$ is set of time periods indexed by $t$, $t \in T$. Set $S$ shows all the plausible scenarios and $s$ is index of scenarios, $s \in S$.

• There are some nodes, N, to represent affected sites (and CTSs as a subset of them) struck by the sudden-onset disaster. Allocation decisions in different periods are made by movements among different nodes through the transportation links. Rescued casualties are transferred from affected sites to CTSs with the rate proportional to the corresponding number of allocated USAR teams. In each CTS, arrived casualties are treated with the rate proportional to the corresponding number of allocated medical teams.

• Extricated casualties at the affected site $m$ arrived at a CTS located at the node $n \ne m$ (if there is any CTS at this node) in time period $t = d^{s}_{m,n} + 1$ where $d^{s}_{m,n}$ is the number of time periods (travel time) it takes to transport casualties from $m$ to $n$ under scenario s. Then, it takes $d^{s}_{m,n}$ time periods to return to node $m$ and move new casualties to node $n$. Therefore, new casualties will arrive at node $n$ in time period $t = 3.d^{s}_{m,n} + 1$. This means the casualty flow is only possible between $m$ and $n$ in time periods $t = d^{s}_{m,n} + 1$, $3.d^{s}_{m,n} + 1$, $5.d^{s}_{m,n} + 1$, etc. Hence, binary parameters are defined as follows:

  $$\beta_{m,n,t}^{s} = {\text{1 if}}\;t = \left( {2r + 1} \right).d^{s}_{m,n} + 1{ }\left( {r = 0,{ }1,{ }2,{ } \ldots {\text{ and }}n \ne m} \right);{\text{ and }}0{\text{ otherwise}}.$$

Where $\beta_{m,n,t}^{s}$ is a binary parameter which used for the allocation of relief teams to affected sites and CTSs.

If variable $x_{m,n,t}^{s}$ represents the casualty flow from $m$ to $n$ under scenario s, then we need the following expression ($M$ is a big value) which means the extricated casualties are passed only through the accessible routes and periods.

$$x_{m,n,t}^{s} \le M.\beta_{m,n,t}^{s}$$

4.1 Formulation of SS treatment strategies

As a result of deploying SS treatment strategies, yellow casualties with shorter service times will not be awaiting red casualties with long service times because they are served by a separate class of medical teams. Consequently, ENS in yellow triage group is improved. Usually, the number of yellow casualties is significantly higher than the red ones; therefore, SS treatment strategies may increase ENS. We develop four mathematical models corresponding to the considered SS treatment strategies.

Model SS-Regular Medical teams allocated to the red group do not deal with those allocated to the yellow group and vice versa. For example, assume that 20% of casualties, needing emergency services, belong to the red group; hence, 20% of the allocated medical teams are dedicated to the red group and 80% to the yellow one.

Sets and indices
N	Set of affected sites and CTSs indexed by $m$ and $n$ respectively
T	Set of time periods indexed by $t$
I	Set of USAR teams which can be allocated to each node indexed by $i$
J	Set of medical teams which can be allocated to each node indexed by $j$
S	Set of scenarios indexed by $s$
Parameters
${TC}_{m}^{s}$	Total number of casualties in red and yellow groups at node $m\in N$ under scenario $s$
${{d}^{s}}_{m,n}$	Time (in time periods) from node $m$ to node $n$ ($n, m\in N$) under scenario $s$
${\beta }_{m,n,t}^{s}$	A binary parameter which is equal to 1 under scenario $s$ if route from node $m$ and $n$ accessible and time period $t$ equals to $\left(2j+1\right).{{d}^{s}}_{m,n}+1 \left(j=0, 1, 2, \dots and n,m\in N\right)$
${\gamma }^{s}$	Ratio of red-group casualties to all casualties under scenario $s$
$v$	Average capacity of a given USAR team
${m}^{r}$	Average capacity of a given medical team for treating red-group casualties
${m}^{y}$	Average capacity of a given medical team for treating yellow-group casualties
${pr}_{t}^{r}$	Survival probability of red-group casualties if treated at $t$ (i.e., $t$ time periods after injury)
${pr}_{t}^{y}$	Survival probability of yellow-group casualties if treated at $t$ (i.e., $t$ time periods after injury)
$CU$	Total number of local USAR teams available in the first hours
$CM$	Total number of local medical teams available in the first hours
${P}^{s}$	Probability of scenario $s$
$M$	A sufficiently large number
Variables
${WU}_{m}^{i}$	A binary variable which is equal to 1 if i USAR teams is allocated to node $m$
${WM}_{n}^{j}$	A binary variable which is equal to 1 if j medical teams is allocated for node $n$
${x}_{m,n,t}^{s}$	Casualty flow between $m$ and $n$ in time period $t$ under scenario $s$
${x}_{m,n,t}^{r,s}$	Red-group casualty flow between $m$ and $n$ in time period $t$ under scenario $s$
${x}_{m,n,t}^{y,s}$	Yellow-group casualty flow between $m$ and $n$ in time period $t$ under scenario $s$
${y}_{n,t}^{r,s}$	Number of non-treated red-group casualties at node $n$ in time period $t$ under scenario $s$
${y}_{n,t}^{y,s}$	Number of non-treated yellow-group casualties at node $n$ in time period $t$ under scenario $s$
${z}_{n,t}^{r-r,s}$	Number of red-group casualties at node $n$ in time period $t$, treated by red class medical teams under scenario $s$
${z}_{n,t}^{y-y,s}$	Number of yellow-group casualties at node $n$ in time period $t$, treated by yellow class medical teams under scenario $s$

Below, we develop a mathematical model to determine the best deployment policy and to manage casualty flow through the relief network when the treatment strategy in CTSs is SS-Regular.

$$Max\;Z_{SS - Regular} = \mathop \sum \limits_{s} P^{s} \cdot \left\{ {\mathop \sum \limits_{t} \mathop \sum \limits_{n} \left( {z_{n,t}^{r - r,s} \cdot pr_{t}^{r} + z_{n,t}^{y - y,s} \cdot pr_{t}^{y} } \right)} \right\}$$

(1)

$$\begin{gathered} S.T. \hfill \\ \mathop \sum \limits_{t} \mathop \sum \limits_{n} x_{m,n,t}^{s} \le TC_{m}^{s} \left( {\forall m \in N; \forall s \in S} \right) \hfill \\ \end{gathered}$$

(2)

$$\mathop \sum \limits_{{\varvec{n}}} x_{m,n,t}^{s} \le v.\mathop \sum \limits_{i} WU_{m}^{i} .i\left( {\forall m \in N; \forall t \in T; \forall s \in S} \right)$$

(3)

$$\mathop \sum \limits_{i} WU_{m}^{ i} = 1 \left( {\forall m \in N} \right)$$

(4)

$$x_{m,n,t}^{s} \le M.\beta_{m,n,t }^{s} \left( {\forall n,m \in N; \forall t \in T; \forall s \in S} \right)$$

(5)

$$x_{m,n,t}^{r,s} = \gamma^{s} .x_{m,n,t}^{s} \left( {\forall n,m \in N;\forall t \in T;\forall s \in S} \right)$$

(6)

$$x_{m,n,t}^{y,s} = \left( {1 - \gamma^{s} } \right).x_{m,n,t}^{s} \left( {\forall n,m \in N; \forall t \in T; \forall s \in S} \right)$$

(7)

$$\mathop \sum \limits_{m} x_{m,n,t}^{r,s} + y_{n,t - 1}^{r,s } = z_{n,t}^{r - r,s} + y_{n,t}^{r,s } \left( {\forall n \in N; \forall t \in T; \forall s \in S} \right)$$

(8)

$$\mathop \sum \limits_{m} x_{m,n,t}^{y,s} + y_{n,t - 1}^{y,s } = z_{n,t}^{y - y,s} + y_{n,t}^{y,s} \left( {\forall n \in N; \forall t \in T; \forall s \in S} \right)$$

(9)

$$z_{n,t}^{r - r,s} \le m^{r} .\gamma^{s} .\left( {\mathop \sum \limits_{j} WM_{n}^{j} .j} \right)\left( {\forall n \in N; \forall t \in T; \forall s \in S} \right)$$

(10)

$$z_{n,t}^{y - y,s} \le m^{y} .\left( {1 - \gamma^{s} } \right).\left( {\mathop \sum \limits_{j} WM_{n}^{j} .j} \right)\left( {\forall n \in N; \forall t \in T; \forall s \in S} \right)$$

(11)

$$\mathop \sum \limits_{j} WM_{n}^{j} = 1 \left( {\forall n \in N} \right)$$

(12)

$$\mathop \sum \limits_{n} \mathop \sum \limits_{j} WM_{n}^{j} .j \le CM$$

(13)

$$\mathop \sum \limits_{m} \mathop \sum \limits_{i} WU_{m}^{ i} .i \le CU$$

(14)

$$z_{n,t}^{r - r,s} ,z_{n,t}^{y - y,s} ,x_{m,n,t}^{s} ,x_{m,n,t}^{r,s} ,x_{m,n,t}^{y,s} ,y_{n,t}^{r,s }, y_{n,t}^{y,s} \ge 0 \quad \left( {\forall m,n \in N; \forall t \in T; \forall s \in S} \right)$$

(15)

$$WU_{m}^{i} ,WM_{n}^{j} \in \left\{ {0,1} \right\}\left( {\forall m,n \in N; \forall i \in I; \forall j \in J} \right)$$

(16)

The objective function (1), calculate ENS in red and yellow groups under all scenarios. Based on (2), the total outflow from each affected site, cannot be more than its casualty number. Constraints (3) ensure that the outflow from each affected site does not violate the capacity of allocated USAR teams. Constraints (4) ensure that only one option of allocating USAR teams can be selected for each node. Constraints (5) consider the transportation time of casualties among nodes. Constraints (6) and (7) determine the percentage of extricated casualties in red and yellow triage groups $\left(0\le {\gamma }^{s}\le 1\right)$. Constraints (8) and (9) ensure the inflow and outflow balance on red- and yellow-group casualties, respectively, in CTSs. In each CTS, the sum of untreated casualties from the previous time period and the newly arrived extricated casualties should be equal to the sum of treated casualties in the current time period and the untreated casualties left for the next time period. In constraints (10) and (11), the capacity of red and yellow class medical teams, respectively, allocated to a given CTS should not be violated by the number of treated casualties. Constraints (12) are for the selection of only one option of allocating medical teams for each node. Constraints (13) and (14) impose that the allocation is limited to the available number of local teams. Constraints (15) are for non-negative variables and constraints (16) show binary variables.

Model SSR: Only idle red class medical teams have permission to treat the yellow group. Below, model SS-Regular is customized for SSR. We define a new variable as follows.

$z_{n,t}^{r - y,s}$ Yellow-group casualties treated by red class teams at node $n$ in time period $t$ under scenario s.

The objective function (1) should be modified as follows:

$$Max\;Z_{SSR} = \mathop \sum \limits_{s} P^{s} \cdot \left\{ {\theta_{1} \cdot \left( {\mathop \sum \limits_{t} \mathop \sum \limits_{n} \left( {z_{n,t}^{r - r,s} \cdot pr_{t}^{r} + z_{n,t}^{y - y,s} \cdot pr_{t}^{y} } \right)} \right) + \theta_{2} \cdot \left( {\mathop \sum \limits_{t} \mathop \sum \limits_{n} z_{n,t}^{r - y,s} .pr_{t}^{y} } \right)} \right\}$$

(17)

The first term in (17) is the expected number of casualties treated by the corresponding class of medical teams while the second one gives the expected number of yellow-group casualties treated by idle red class medical teams. ${\theta }_{1}$ and ${\theta }_{2}$ are the weights assigned to prioritized and non-prioritized casualties, respectively. With ${\theta }_{1}$ much greater than ${\theta }_{2}$ (i.e., ${\theta }_{1}\gg {\theta }_{2}$), we can ensure that red class medical teams serve the red group prior to the yellow-group. In SSR strategy, some of yellow-group casualties are treated by yellow class of medical teams while some others are treated by red class of medical teams; hence, constraints (9) and (10) should be modified as follows:

$$\mathop \sum \limits_{m} x_{m,n,t}^{y,s} + y_{n,t - 1}^{y,s } = z_{n,t}^{y - y ,s} + z_{n,t}^{r - y,s } + y_{n,t}^{y,s } \left( {\forall n \in N; \forall t \in T; \forall s \in S} \right)$$

(18)

$$z_{n,t}^{r - r,s } + \frac{{m^{r} }}{{m^{y} }}.z_{n,t}^{r - y,s } \le m^{r} .\gamma^{s} .\left( {\mathop \sum \limits_{j} WM_{n}^{j} .j} \right)\left( {\forall n \in N; \forall t \in T; \forall s \in S} \right)$$

(19)

Model SSY: Only idle yellow class medical teams are allowed to treat the red group. Below, model SS-Regular is customized for SSY. We define a new variable as follows.

$z_{n,t}^{y - r,s}$ Red-group casualties treated by yellow class teams at node $n$ in time period $t$ under scenario s.

The objective function (1) should be modified as follows:

$$Max\;Z_{SSY} = \mathop \sum \limits_{s} P^{s} \cdot \left\{ {\theta_{1} \cdot \left( {\mathop \sum \limits_{t \in T} \mathop \sum \limits_{n} \left( {z_{n,t}^{r - r,s} \cdot pr_{t}^{r} + z_{n,t}^{y - y,s} \cdot pr_{t}^{y} } \right)} \right) + \theta_{2} \cdot \left( {\mathop \sum \limits_{t} \mathop \sum \limits_{n} z_{n,t}^{y - r,s} \cdot pr_{t}^{r} } \right)} \right\}$$

(20)

The first term in (20) is the same as that in (17) while the second one gives the expected number of red-group casualties, treated by idle yellow class teams. Constraints (8) and (11) should be modified as follows:

$$\mathop \sum \limits_{m} x_{m,n,t}^{r,s} + y_{n,t - 1}^{r,s } = z_{n,t}^{r - r,s } + z_{n,t}^{y - r,s } + y_{n,t}^{r } \left( {\forall n \in N; \forall t \in T; \forall s \in S} \right)$$

(21)

$$z_{n,t}^{y - y,s } + \frac{{m^{y} }}{{m^{r} }} \cdot z_{n,t}^{y - r,s} \le m^{y} \cdot \left( {1 - \gamma^{s} } \right) \cdot \left( {\mathop \sum \limits_{j} WM_{n}^{j} \cdot j} \right)\left( {\forall n \in N; \forall t \in T; \forall s \in S} \right)$$

(22)

Model SSB: Red and yellow class medical teams that are idle are allowed to treat one another. Below, model SS-Regular is customized for SSB. We need all types of variable in the previous models to represent treated casualties. The objective function (1) should be modified as follows:

$$Max\;Z_{SSB} = \mathop \sum \limits_{s \in S} P^{s} \cdot \left\{ {\theta_{1} \cdot \left( {\mathop \sum \limits_{t} \mathop \sum \limits_{n} \left( {z_{n,t}^{r - r,s} \cdot pr_{t}^{r} + z_{n,t}^{y - y,s} \cdot pr_{t}^{y} } \right)} \right) + \theta_{2} \cdot \left( {\mathop \sum \limits_{t} \mathop \sum \limits_{n} (z_{n,t}^{y - r,s} \cdot pr_{t}^{r} + z_{n,t}^{r - y,s} \cdot pr_{t}^{y} )} \right)} \right\}$$

(23)

The first term in (23) is the same as those in (17) and (20) while the second one is the total expected number of casualties, treated by another idle class of medical teams. Furthermore, constraints (8)-(11) should be replaced with (21), (18), (19), and (22), respectively.

4.2 Formulation of PS treatment strategies

As a result of deploying PS treatment strategies, medical teams serve both triage groups simultaneously. Consequently, compared to SS, effectiveness is enhanced. Below, the mathematical model for the Regular-PS strategy is presented.

Variables
${z}_{n,t}^{r1,s}$	Prioritized red-group casualties treated at node $n$ in time period $t$ under scenario s
${z}_{n,t}^{y1,s}$	Prioritized yellow-group casualties treated at node $n$ in time period $t$ under scenario s
${z}_{n,t}^{r2,s}$	Non-prioritized red-group casualties treated by idle teams at node $n$ in time period $t$ under scenario $s$
${z}_{n,t}^{y2,s}$	Non-prioritized yellow-group casualties treated by idle teams at node $n$ in time period $t$ under scenario $s$
New Parameter
${\vartheta }_{t}^{s}=\left\{\begin{array}{ll}1; & \text{if}\; \text{the}\; \text{treatment}\; \text{priority}\; \text{at}\; t\; \text{is}\; \text{given}\; \text{to}\; \text{red}\; \text{group}\; \text{under}\; \text{scenario}\; s\\ 0; &\text{If}\; \text{the}\; \text{treatment}\; \text{priority}\; \text{at}\; t\; \text{is}\; \text{given}\; \text{to}\; \text{yellow}\; \text{group}\; \text{under}\; \text{scenario}\; s\end{array}\right\}$

Below, the mathematical model for the Regular-PS strategy is presented.

$$Max\;Z_{PS} = \mathop \sum \limits_{s} P^{s} .\left\{ \theta_{1} .\left(\mathop \sum \limits_{t \in T} \mathop \sum \limits_{n} \left( {z_{n,t}^{r1,s} .pr_{t}^{r} + z_{n,t}^{y1,s} .pr_{t}^{y} } \right)\right) + \theta_{2} .\left( {\mathop \sum \limits_{t} \mathop \sum \limits_{n} (z_{n,t}^{r2,s} .pr_{t}^{r} + z_{n,t}^{y2,s} .pr_{t}^{y} )} \right)\right\}$$

(24)

$$\begin{gathered} S.T. \hfill \\ z_{n,t}^{r1,s} \le M.\vartheta_{t}^{s} \left( {\forall n \in N; \forall t \in T; \forall s \in S} \right) \hfill \\ \end{gathered}$$

(25)

$$z_{n,t}^{y2,s} \le M.\vartheta_{t}^{s} \left( {\forall n \in N; \forall t \in T; \forall s \in S} \right)$$

(26)

$$z_{n,t}^{y1,s} \le M.\left( {1 - \vartheta_{t} } \right)\left( {\forall n \in N; \forall t \in T; \forall s \in S} \right)$$

(27)

$$z_{n,t}^{r2,s} \le M.\left( {1 - \vartheta_{t} } \right)\left( {\forall n \in N; \forall t \in T; \forall s \in S} \right)$$

(28)

$$\mathop \sum \limits_{m} x_{m,n,t}^{r,s} + y_{n,t - 1}^{r,s} = z_{n,t}^{r1,s} + z_{n,t}^{r2,s} + y_{n,t}^{r,s} \left( {\forall n \in N; \forall t \in T; \forall s \in S } \right)$$

(29)

$$\mathop \sum \limits_{m} x_{m,n,t}^{y,s} + y_{n,t - 1}^{y,s } = z_{n,t}^{y1,s} + z_{n,t}^{y2,s} + y_{n,t}^{y,s} \left( {\forall n \in N; \forall t \in T; \forall s \in S} \right)$$

(30)

$$z_{n,t}^{r1,s} + z_{n,t}^{r2,s} + \frac{{m^{r} }}{{m^{y} }}.\left( {z_{n,t}^{y1,s} + z_{n,t}^{y2,s} } \right) \le m^{r} .\left( {\mathop \sum \limits_{j} WM_{n}^{j} .j} \right)\left( {\forall n \in N; \forall t \in T; \forall s \in S} \right)$$

(31)

$$z_{n,t}^{r1,s} ,z_{n,t}^{y1,s} ,z_{n,t}^{r2,s} ,z_{n,t}^{y2,s} ,x_{m,n,t}^{s} ,x_{m,n,t}^{r,s} ,x_{m,n,t}^{y,s} ,y_{n,t}^{r,s} ,y_{n,t}^{y,s } \ge 0 \left( {\forall m,n \in N; \forall t \in T; \forall s \in S} \right)$$

(32)

According to the weights assigned to prioritized and non-prioritized casualties ($\theta_{1} \gg \theta_{2}$), objective function (24) maximizes ENS. Based on constraints (25)-(28), treatment variables of casualties obtain positive values when priority is given to the corresponding triage groups, using parameter ${\vartheta }_{t}^{s}$. Constraints (29) and (30) are similar to (8) and (9) in model SS-Regular. Constraint (31) ensures that the capacity of medical teams allocated to a given CTS should not be violated by the number of treated casualties. Constraint (32) is for non-negative variables. Constraints (2)-(7), (12)-(14) and (16) in model SS-Regular are considered in the model PS-Regular directly.

Model PSR Medical teams serve the yellow group only when the red group is empty. PSR gives priority to the red group whose fatality probability (probability of moving to the black group) increases more rapidly than the yellow one. Therefore, we need to set ${\vartheta }_{t}^{s}=1$ ($\forall t\in T$) in model Regular-PS to customize it for PSR.

Model PSY Medical teams serve the red group only when the yellow group is empty. PSY gives priority to the yellow group because they naturally have higher survival probabilities and shorter emergency care times. Therefore, we need to set ${\vartheta }_{t}^{s}=0$ ($\forall t\in T$) in model Regular-PS to customize it for PSY.

Model PSD We dynamically change group priorities in proportion to their corresponding casualty numbers. For example, if 20% of serious casualties belong to the red group (i.e., ${\gamma }^{s}=0.2$) under a given scenario, then priority is given to the red group in the first time period of each five time periods till the end of planning horizon. To customize Regular-PS for PSD, we need to set ${\vartheta }_{t}^{s}=1$ in the ${\gamma }^{s}\%$ of time periods and ${\vartheta }_{t}^{s}=0$ in the remaining $(1-{\gamma }^{s})\%$.

Notably, all the proposed models are mixed integer programming (MIP). The number of binary variables is equal to $\left(\left|I\right|+\left|J\right|\right).\left|N\right|$ which can be tackled in reasonable computation times by commercial optimization software packages. The number of constraints is equal to $(3{\left|N\right|}^{2}+8\left|N\right|).\left|T\right|.\left|S\right|+\left|N\right|.(\left|S\right|+2)+2$. We use GAMS win 64 24.1.2 optimization package to solve the models.

4.3 Robust model

Uncertainty is inevitable for optimization models in the disaster management. Among approaches to handle uncertainty of input parameters, only robust optimization guarantees the optimization of satisfaction levels and the reliability of output results. Robust optimization considers the risk attribution of decision-makers and reduces the risk of dispersion of the objective function value. When there are discrete uncertain parameters such as the number of casualties, the scenarios are defined by different possible values with corresponding probabilities. Because we formulate uncertainties via the discrete scenarios, the method in Mulvey et al. (1995) is chosen. They defined two main concepts in robust optimization: model robustness and solution robustness. Model robustness makes the solution almost feasible for any occurrence of a scenario. Solution robustness guarantees the optimal solution remains close to the optimum for any occurrence of a scenario. We consider the robust model for following reasons:

• To address a high level of uncertainty involved in the response phase of disaster management

• To consider the risk attribute of decision makers

• To consider the risk of dispersion of the objective function value

• To overcome the shortage in historical data.

In this method, the traditional expected objective function is replaced by the one that explicitly addresses the objective function variability. The variability term is simply added to the main objective function via a weighting parameter representing the risk tolerance of the decision. In fact, this parameter captures the decision makers’ preference. The variables are categorized into design and control groups. Design variables are decided before the realization of stochastic parameters and control variables are subject to the adjustment when a specific occurrence of uncertain parameters is realized. Mulvey et al. (1995) considered the following model:

$$Min c^{T} x + d^{T} y$$

(33)

$$\begin{gathered} {\text{S}}.{\text{T}}. \hfill \\ Ax = b \hfill \\ \end{gathered}$$

(34)

$$Bx + Cy = e$$

(35)

$$x,y \ge 0$$

(36)

Let x and y denote the vectors of design variables and control variables, respectively. $A$ and $b$ are the matrix of parameters in constraint (34) and $B,C$ and $e$ the uncertain coefficient matrix in constraint (35). The first term in the objective function defines the solution robustness and the second term defines the model robustness if there is a finite set of scenarios $S=\{\mathrm{1,2},..,s\}$ and ${p}_{s}$ denotes the probability of scenario s ($\sum_{s\in S}{p}_{s}$=1). Also, the control variable y, which is subject to the adjustment when one scenario is realized, can be denoted as ${y}_{s}$ for scenario s. The model may be infeasible for some scenarios due to the uncertainty in some parameters. Therefore, the infeasibility of the model under scenario s is denoted as $\eta_{s}$. A robust model is formulated as follows:

$$Min \sigma \left( {x,y_{1} , y_{2} , \ldots ,y_{s} } \right) + \delta \rho \left( {\eta_{1} ,\eta_{1} , \ldots ,\eta_{s} } \right)$$

(37)

$$\begin{gathered} {\text{S}}.{\text{T}}. \hfill \\ Ax = b \hfill \\ \end{gathered}$$

(38)

$$\begin{gathered} B_{s} x + C_{s} y_{s} + \eta_{s} = e_{s} \quad (\forall s \in S) \hfill \\ x,y_{s} ,\eta_{s} \ge 0\quad (\forall s \in S) \hfill \\ \end{gathered}$$

(39)

$B_{s} ,C_{s}$ and $e_{s}$ are the uncertain coefficient matrix in constraint (35). The first term in the objective function defines the solution robustness and the second term defines the model robustness weighted by $\delta$. Let $\xi_{s}$ = $f\left( {x,y_{s} } \right)$ denotes the objective function for scenario s. The solution robustness is

$$\sigma \left( \cdot \right) = \mathop \sum \limits_{s \in S} p_{s} \xi_{s} + \omega \mathop \sum \limits_{s \in S} p_{s} \left( {\xi_{s} - \mathop \sum \limits_{s \in S} p_{s} \xi_{s} } \right)^{2}$$

(40)

Yu and Li (2000) discussed the required computational effort due to a quadratic term and proposed an absolute deviation instead of the quadratic term, which is shown as follows:

$$\sigma \left( \cdot \right) = \mathop \sum \limits_{s \in S} p_{s} \xi_{s} + \omega \mathop \sum \limits_{s \in S} p_{s} \left| {\xi_{s} - \mathop \sum \limits_{s \in S} p_{s} \xi_{s} } \right|$$

(41)

For the linearization, two nonnegative variables namely $Q_{s}^{ + }$ and $Q_{s}^{ - }$ are introduced:

$$\sigma \left( \cdot \right) = \mathop \sum \limits_{s \in S} p_{s} \xi_{s} + \omega \mathop \sum \limits_{s \in S} p_{s} \left( {Q_{s}^{ + } + Q_{s}^{ - } } \right)$$

(42)

$$\xi_{s} - \mathop \sum \limits_{s \in S} p_{s} \xi_{s} = Q_{s}^{ + } - Q_{s}^{ - }$$

(43)

We aim to investigate the robust optimization approach for SSB and PSD models. Therefore, the objective function is changed and a new constraint is added based on Mulvey et al. (1995) and linearization approach proposed by Yu and Li (2000). The objective function of robust model for SSB, replaced with (23), is as follows:

$$\begin{aligned} Max\;Z_{Robust - SSB} & = \mathop \sum \limits_{s} P^{s} \{ \theta_{1} \cdot \mathop \sum \limits_{t} \mathop \sum \limits_{n} \left( {z_{n,t}^{r - r,s} \cdot pr_{t}^{r} + z_{n,t}^{y - y,s} \cdot pr_{t}^{y} } \right) \\ & \quad + \theta_{2} \cdot \mathop \sum \limits_{t} \mathop \sum \limits_{n} (z_{n,t}^{y - r,s} \cdot pr_{t}^{r} + z_{n,t}^{r - y,s} \cdot pr_{t}^{y} )\} - \delta \cdot \mathop \sum \limits_{s} P^{s} \cdot \left( {Q_{1}^{s} + Q_{2}^{s} } \right) \\ \end{aligned}$$

(44)

$$\begin{gathered} \theta_{1} .\mathop \sum \limits_{t} \mathop \sum \limits_{n} \left( {z_{n,t}^{r - r,s} .pr_{t}^{r} + z_{n,t}^{y - y,s} .pr_{t}^{y} } \right) + \theta_{2} .\mathop \sum \limits_{t} \mathop \sum \limits_{n} (z_{n,t}^{y - r,s} .pr_{t}^{r} + z_{n,t}^{r - y,s} .pr_{t}^{y} ) \hfill \\ - \mathop \sum \limits_{s} P^{s} \left\{ \theta_{1} .\mathop \sum \limits_{t} \mathop \sum \limits_{n} \left( {z_{n,t}^{r - r,s} .pr_{t}^{r} + z_{n,t}^{y - y,s} .pr_{t}^{y} } \right) + \theta_{2} .\mathop \sum \limits_{t} \mathop \sum \limits_{n} (z_{n,t}^{y - r,s} .pr_{t}^{r} + z_{n,t}^{r - y,s} .pr_{t}^{y} )\right\} = Q_{1}^{s} - Q_{2 }^{s} \forall s \in \in S \hfill \\ \end{gathered}$$

(45)

Therefore, the robust model for SSB strategy is including (44), (45), (2)–(7), (12)–(16), (18), (19), (21) and (22). The objective function of robust model for PSD, replaced with (24), is as follows:

$$Max\;Z_{Robust - PSD} = \mathop \sum \limits_{s} P^{s} \{ \theta_{1} .\mathop \sum \limits_{t} \mathop \sum \limits_{n} \left( {z_{n,t}^{r1,s} .pr_{t}^{r} + z_{n,t}^{y1,s} .pr_{t}^{y} } \right) + \theta_{2} .\mathop \sum \limits_{t} \mathop \sum \limits_{n} (z_{n,t}^{r2,s} .pr_{t}^{r} + z_{n,t}^{y2,s} .pr_{t}^{y} )\} - \delta .\mathop \sum \limits_{s} P^{s} .\left( {Q_{1}^{s} + Q_{2}^{s} } \right)$$

(46)

$$\begin{gathered} \theta_{1} .\mathop \sum \limits_{t} \mathop \sum \limits_{n} \left( {z_{n,t}^{r1,s} .pr_{t}^{r} + z_{n,t}^{y1,s} .pr_{t}^{y} } \right) + \theta_{2} .\mathop \sum \limits_{t} \mathop \sum \limits_{n} (z_{n,t}^{r2,s} .pr_{t}^{r} + z_{n,t}^{y2,s} .pr_{t}^{y} ) \hfill \\ - \mathop \sum \limits_{s} P^{s} \{ \theta_{1} .\mathop \sum \limits_{t} \mathop \sum \limits_{n} \left( {z_{n,t}^{r1,s} .pr_{t}^{r} + z_{n,t}^{y1,s} . pr_{t}^{y} } \right) + \theta_{2} .\mathop \sum \limits_{t} \mathop \sum \limits_{n} (z_{n,t}^{r2,s} .pr_{t}^{r} + z_{n,t}^{y2,s} .pr_{t}^{y} )\} = Q_{1}^{s} - Q_{2}^{s} \quad \forall s \in S \hfill \\ \end{gathered}$$

(47)

The robust model for PSD strategy is including (46), (47), (2)-(7), (12)-(14), (16) and (25)-(32).

5 Experimental setting

We explain details of experimental data, including secondary sources. We also use some secondary data, previously gathered by Rezapour et al. (2018). They are used as the basis for constructing numerical experiments in Sect. 6.

5.1 SAR (v) and on-field treatment (${{\varvec{m}}}^{{\varvec{r}}}$, ${{\varvec{m}}}^{{\varvec{y}}}$) rates, and time periods

The average performance rate of USAR teams ($v$) and the average treatment rates of medical teams for red and yellow groups (${m}^{r}$ and ${m}^{y}$, respectively) are estimated. As proposed by Wilson et al. (2013), time period is assumed to be 15 min. The length of planning horizon is considered to be 12 h. In other words, there are 48 time periods.

We use the RPM index (Respiration, Perfusion, and Mental status), proposed by Sacco et al. (2005) to score victims. RPM is calculated based on the respiratory rate, pulse rate, and motor response. Table 2 shows twelve RPM values according to the severity of injuries (Sacco et al. 2005) and the processing times in CTSs (Jin et al. 2015). Red-coloured columns show the scores and treatment times of the red triage group and yellow-coloured columns are those for the yellow triage group. Dean and Nair (2014) proposed three distribution patterns for the RPM in MCIs: uniform, left-skewed, and right-skewed. For each triage group, the expected treatment time of each distribution pattern is determined. Then, the average of the three expected treatment times for each triage group is computed and considered as its average treatment time. Accordingly, the average treatment time for the red and yellow groups is equal to 3.3 and 2.5 min, respectively. Therefore, the corresponding treatment rates in a given time period are 4.5 (i.e. ${m}^{r}$=4.5 casualties per time period) and 6 (i.e., ${m}^{y}$=6 casualties per time period), respectively.

Table 2 RPM scores of casualties and corresponding on-field treatment times

There is very little real data on the performance of USAR teams. During the 2004 Indian Ocean earthquake, 44 USAR teams were sent to Banda Aceh in Indonesia and in five days, 150,000 lives were saved (Amateur Seismic Centre 2004). Hence, the average performance rate of USAR teams is denoted as 7.1 casualties per period.

5.2 Survival probability of red (${pr}_{t}^{r}$) and yellow (${pr}_{t}^{y}$) casualties

To predict the survival probability of casualties, we model the extrication of casualties according to their triage group as a discrete time Markov chain of casualty health states (Wilson et al. 2013). The state space S = {Green, Red, Yellow, Black} illustrates four triage groups before treatment. Having the initial triage group, we calculate the survival probabilities at time period $t$. The Markov chain and transition probabilities are shown in Fig. 3 (Wilson et al. 2013):

Fig. 3

Markov chain representing health state transition probabilities of trapped casualties

For the Markov chain in Fig. 3, the corresponding transition matrix, $A$, can be drawn as follows:

$$A = \left[ {\begin{array}{cccc} {0.983} & {0.017} &0&0\\0&0.97&0.03&0\\0&0&0.93&0.07\\0&0&0&1 \end{array} } \right]$$

Using the transition matrix $A^{t}$, we can estimate the survival probability of red and yellow casualties, i.e., $pr_{t}^{r}$ and $pr_{t}^{y}$, respectively. The probabilities are calculated as $pr_{t}^{r} = 1 - A_{{}}^{t} \left[ {3,4} \right]$ and $pr_{t}^{y} = 1 - A_{{}}^{t} \left[ {2,4} \right]$.

6 Numerical analysis

In this section, the investigation of model performance is considered through different experimental analyses. In Sect. 6.1, we describe how to generate 50 random test problems to provide useful post-disaster insights to be implemented by relief teams right after a sudden-onset MCI. In Sect. 6.2, we run optimization models based on realistic data, related to a hypothetical earthquake in Tehran, the capital of Iran, as a large populated city. Next, in Sect. 6.3, we give generalized insights for the implementation of treatment strategies. Moreover, the results of integrating SAR and on-field treatment operations are presented in Sect. 6.4. The results of robust models for SSB and PSD strategies are illustrated in 6.5. Finally, a discussion of the necessity and importance of our findings is provided in Sect. 6.6.

6.1 Analysis of random instances

To make useful observations and insights regarding the deployment of relief teams in sudden-onset MCIs, and to see whether they are dependent on different data realizations or not, we analyse the optimization models for 50 test problems. Because the number of nodes in the relief network is the major determinant of our problem size (the planning horizon is fixed), we classify our problem sizes based on it. We consider three levels of disaster severity, namely low (lower than 6 Richter), medium (between 6 and 7 Richter) and high (more than 7 Richter) and two times of occurring the disaster, day and night. Uncertain parameters are generated randomly in the specific intervals. Table 3 shows the uncertain parameters and their generation ranges for different test problems. Moreover, ${{d}^{s}}_{m,n}$ is generated based on the uniform random numbers in different intervals. Then, ${{\beta }^{s}}_{m,n,t}$ are caclulated based on ${{d}^{s}}_{m,n}$. Table 4 shows the scenario-independent parameters.

Table 3 Plausible scenarios and scenario-dependent parameters

Table 4 Details of generating random values

The sensitivity analysis of the models will give us reliable insights. In post-disaster chaotic circumstances, the following factors are very difficult to be estimated or controlled:

• Incomplete implementation of the best treatment strategy We cannot ensure that the advised treatment strategy will completely be implemented by medical teams. It is always likely that they deviate from the advised strategy.

• Error in estimation of ${\varvec{\gamma}}^{{\varvec{s}}}$ ($\hat{\varvec{\gamma }}^{{\varvec{s}}}$) The estimated ratio of casualties in the red triage group may not be accurate; it may vary from the estimated value.

We consider five error intervals for $\gamma^{s}$, including $\gamma^{s}$ = $\hat{\gamma }^{s} - 0.2$, $\gamma^{s}$ = $\hat{\gamma }^{s} - 0.1$, $\gamma^{s}$ = $\hat{\gamma }^{s}$, $\gamma^{s}$ = $\hat{\gamma }^{s} + 0.1$ and $\gamma^{s}$ = $\hat{\gamma }^{s} + 0.2$. Therefore, the total number of random instances based on the 50 test problems is 1750, i.e., 50 test problems, 7 treatment strategies and 5 values of $\gamma^{s}$. In SS models, medical teams are divided among triage groups by replacing $\gamma^{s}$ with $\hat{\gamma }^{s}$ in constraints (10), (11), (19), and (22). However, the extricated casualties are divided among triage groups by embedding $\gamma^{s}$ in constraints (6) and (7). The priority of triage groups in PSD changes according to ${\widehat{\gamma }}^{s}$ over time. The extricated casualties are divided among triage groups by inserting ${\widehat{\gamma }}^{s}$ in constraints (37) and (38). We use the ratio of ENS to the total number of seriously-injured population as the objective (namely RENS) to be able to compare the results of different test problems. The results of numerical analysis for different problem sizes are given in Figs. 4, 5, 6, 7. Although running times depend mainly on the number of nodes and the treatment strategies, they are solved in 1, 10, 30 and about 60 min for 5, 10, 15 and 20 nodes, respectively. In order to examine the performance of different treatment strategies for 5 nodes, we present the results in Figs. 4a, b. The results for other test problems of 10, 15, and 20 node sizes, as illustrated in Figs. 5, 6, 7.

Fig. 4

RENS versus deviations around ${\widehat{\gamma }}^{s}$ (5 nodes)

Fig. 5

RENS versus deviations around ${\widehat{\gamma }}^{s}$ (10 nodes)

Fig. 6

RENS versus deviations around ${\widehat{\gamma }}^{s}$ (15 nodes)

Fig. 7

RENS versus deviations around ${\widehat{\gamma }}^{s}$ (20 nodes)

6.1.1 Performance of SS strategies

As can be seen in Fig. 4a, SS treatment strategies are not significantly different in terms of RENS where ${\gamma }^{s}$ matches its estimation. However, when ${\gamma }^{s}$ deviates from its estimation, RENS decreases in SS-Regular strategy in positive deviations of ${\gamma }^{s}$; i.e., for ${\gamma }^{s}>{\widehat{\gamma }}^{s}$. SSY shows almost the same behaviour though its performance is much better than SS-Regular in positive deviations of ${\gamma }^{s}$. This happens because the number of red-group casualties increases in positive deviations and SSY allows the idle yellow class teams to treat this group. As Fig. 4(a) depicts, the performance of SSR is higher than that of both SS-Regular and SSY in negative deviations of ${\gamma }^{s}$; i.e., for ${\gamma }^{s}<{\widehat{\gamma }}^{s}$. This is because the number of yellow-group casualties increases in negative deviations and SSR allows the idle red class teams to treat this group. However, the performance of SS-Regular and SSR is similar in positive deviations of ${\gamma }^{s}$. In positive deviations, SSY performs better than SSR because of the existence of a large number of red-group casualties. The performance of SSB, as the combination of SSR and SSY, coincides with SSR in negative deviations and SSY in positive deviations. It performs better than SSY and SSR in negative and positive deviations, respectively. The results are summarized in the following observations.

Observation 1 SSB performs better than SS-Regular and SSY, and the same as SSR in negative deviations. It performs better than SS-Regular and SSR, and the same as SSY in positive deviations.

Observation 2 Since the estimation of ${\gamma }^{s}$ is a difficult task in the uncertain conditions after the sudden-onset MCIs, continuous negative and positive deviations of ${\gamma }^{s}$ from ${\widehat{\gamma }}^{s}$ are inevitable. Therefore, SSB has the best performance among the SS-related strategies.

Observation 3 The effect of incomplete implementation of SS strategies in terms of RENS is shown by arrows in the range of ${\gamma }^{s}={\widehat{\gamma }}^{s}$±0.1 in Fig. 4(a). As can be observed, SS strategies are robust in terms of the inappropriateness for implementation. The more the actual ${\gamma }^{s}$ deviates from ${\widehat{\gamma }}^{s}$, the more the distance becomes among SS strategies.

6.1.2 Performance of PS strategies

According to Figs. 4b, the performance of PSR and PSY is independent of ${\widehat{\gamma }}^{s}$, as they usually have the same behaviour for different values of ${\widehat{\gamma }}^{s}$. Notably, the performance of PSY in terms of RENS is much better than that of PSR because yellow-group casualties inherently have higher survival probabilities and shorter treatment times.

Therefore, PSY, giving priority to the yellow group, significantly improves RENS. However, it is not ethical to leave red-group casualties for the last only because of their lower survival probabilities. The performance of PSD with dynamic priority always falls between the two thresholds denoted as PSR and PSY.

Observation 4 The performance of PSD is always between PSY and PSR, as the upper and lower thresholds for PS models, respectively. The performance of PSD is closer to that of PSR for ${\gamma }^{s}<{\widehat{\gamma }}^{s}$ while it is closer to that of PSY for ${\gamma }^{s}>{\widehat{\gamma }}^{s}$. While there are less red-group casualties than estimated ones for ${\gamma }^{s}<{\widehat{\gamma }}^{s}$, a more number of time periods are dedicated to the red group in PSD. Therefore, it behaves like PSR for these values. In contrast, there are more red-group casualties than estimated ones for ${\gamma }^{s}>{\widehat{\gamma }}^{s}$, and a less number of time periods are dedicated to red group. Therefore, PSD behaves like PSY for this case.

Observation 5 The effect of incomplete implementation of PS strategies in terms of RENS is represented by arrows in range of ${\gamma }^{s}={\widehat{\gamma }}^{s}$±0.1 in Figs. 4(a) and 4(b). The upper threshold corresponds to PSY and the lower one to PSR. The thresholds are not close even for ${\gamma }^{s}$ values very close to ${\widehat{\gamma }}^{s}$. Therefore, PS strategies are very sensitive to variations in the strategy implementation.

6.1.3 Comparing SS and PS strategies

In Fig. 4a, b, the performance of SS and PS strategies with respect to our two critical factors is compared. It was demonstrated that SSB and PSD have the highest performance among the SS and PS strategies, respectively. Therefore, the following observations may be made:

Observation 7 The performance of SS strategies is more robust than PS ones with respect to variations in the strategy implementation by medical teams.

Observation 8 In terms of RENS, PSD performs moderately better than SSB with respect to the error in the estimation of ${\gamma }^{s}$. However, the difference between them is not too much to be considered significant.

All the proposed observations will be the same for the other test problems of 10, 15, and 20 node sizes, as illustrated in Figs. 5–7.

6.2 Empirical data for a hypothetical earthquake

Rapid expansion, high population density, and old structure have made Tehran, the capital of Iran, potentially as one of the most vulnerable urban areas. As mentioned in Sect. 4.3, very little primary data regarding the early response of past MCIs is recorded and published in details. Also, historical data for key parameters in the first hours of past disasters is not valid for the other disasters with different magnitude, location and time occurrence. Therefore, we used multiple-source data gathering (mainly primary and secondary data) to make sure our data is realistic. The primary data are summarized in Tables 5, 6 and 7.

Table 5 The number of population by districts in Tehran

Table 6 Number of rescue teams currently available by IFRC societies in Tehran

Table 7 Number of available medical teams in Tehran

Tehran has 22 municipal districts with administrative centres. According to studies in the year 2000 census, for a 0.35 g² scenario around 640,000 buildings out of 1,100,000 in Tehran would collapse or seriously be damaged; 1,450,000 people would be killed and about 4,300,000 would be injured (Nateghi-A, 2001). Usually, 10 to 20 percent of the casualties need serious emergency care services (Borden Institute 2013). The archival data, based on the research conducted by Japan International Cooperation Agency (JICA, 2000), confirms mainly different levels of vulnerability in various municipal districts of Tehran. The population of 22 districts are reported in Table 5 and the injured population of casualties in red and yellow groups in each scenario is generated based upon them.

In Table 6, we summarize the number of rescue teams of IFRC's (International Federation of Red Cross and Red Crescent Societies) agencies, being available either inside or geographically close to our case study that can operate rapidly right after the disaster strike. We received the initial list and the contact details from archival data; but in order to get the number of rescue teams, we conducted a brief phone interview with all the IFRC branches. According to the archival data, the emergency centres being available either inside the city or geographically close to it and the corresponding number of medical teams to provide service in CTSs are summarized in Table 7.

The results of running optimization models for 35 instances, i.e., 7 treatment strategies and 5 values of ${\gamma }^{s}$, related to the hypothetical earthquake in Tehran are depicted in Fig. 8. Computation time of the model is equal to 300 min which seems to be high for such a problem with a 12-h time horizon. However, this should not be considered a limitation because the proposed model is run in the preparedness stage, when sufficient time is available, to extract some simple yet effective if–then rules for the implementation in response phase. As can be seen, all the eight observations made on the 50 random instances in Sect. 6.1 are confirmed when we apply the empirical data of the case study. Because the number of relief teams is few in case study, the difference among SS-strategies are not specific.

Fig. 8

RENS versus deviations around ${\widehat{\gamma }}^{s}$ for our case study

6.2.1 Incremental increase in the number of relief teams

As the number of available local USAR and medical teams is insufficient, it should be increased to improve the response to sudden-onset disasters, particularly the earthquakes. To efficiently increase the number of local USAR and medical teams, we conducted another experiment for 440 instances (20 options for the number of USAR teams and 22 options for the number of medical teams). There are three major regions (I, II, and III) in Fig. 9, and each corresponds to the best choice to increase the number of relief teams. We gradually increased the number of USAR and medical teams and computed the corresponding ENS values. The number of USAR and medical teams are changed between 30 and 60 and between 45 and 100, respectively. For each number of USAR teams, the model is solved for all the number of medical teams. For example, the number of USAR is set to 35 and the number of medical teams is changed from 45 to 100. Compared the objective function values of these combinations of relief teams, we found that RENS is incresed for the number of medical teams between 45 and 90 while after that, it does not changed significantly. Therefore, the combination (35,90) for the number of USAR and medical teams, respectively, is a treshhold for region 3. Similarly, the combination (35,51) is a treshhold for region 1. Finally, region 2 is known as the area between region 1 and region 3. The regions and their corresponding choices are as follows:

• Region I If the current combination of USAR and medical teams falls within this region, then adding more medical teams is recommended to increase ENS. Adding more USAR teams does not make a significant improvement. The boundary of Regions I and II determines the maximum number of recommended medical teams.

• Region II If the current combination of USAR and medical teams falls within this region, then adding both more medical and USAR teams is recommended to increase ENS. The boundaries of Region II with Regions I and III determine, respectively, the maximum number of USAR and medical teams to be efficient.

• Region III If the current combination of USAR and medical teams falls within this region, then adding more USAR teams is recommended to increase ENS. Adding more medical teams does not make any significant change.

Fig. 9

Different combinations of relief teams for our case study

Figure 9 illustrates that the optimal choice to improve response to disaster depends on the current combination of local relief teams in the field. Such an analysis can similarly be presented for any other case.

6.3 Strategy implementation

According to the numerical results in Sects. 6.1 and 6.2, among streaming strategies, SSB is the best one to maximize ENS. On the other hand, PSY is the best among pooling strategies. Though the performance of PSY is higher than that of PSD and SSB, it may not be ethically attractive. Our recommended pooling strategy; i.e., PSD, makes an appropriate balance between ethics (i.e., giving an equal attention to all triage groups) and ENS (i.e., providing service for the greatest number of people). PSD and SSB yield almost the same ENS values and are the same ethically. Hence, we compare their performance in rescuing the greatest number of casualties in all the possible scenarios in terms of robustness. The results are given in Fig. 10 according to the two critical factors: (1) variations in treatment strategy implementation and (2) error in estimating the ratio of red-group casualties.

Fig. 10

Best treatment strategy

6.4 Integration of SAR and on-field treatment operations

We aim to compare the integrated optimization approach to the case in which SAR and on-field treatment decisions are made in distinct models. First, the objective function (51), as the maximization of the number of rescued people, and constraints (2), (3), (4), (5), and (14) are considered as SAR model. It is solved to determine the inflow of casualties to CTSs. Then, the outputs are used as parameters in SSB and PSD models to determine the allocation of medical teams to CTSs and casualty groups. As an example, the results of SSB and PSD strategies for our instances and case study are given in Table 8. Consequently, the integrated models are suggested for two reasons: 1) they are not complex and time-consuming to solve, and 2) little improvements are also significant, as the objective function is the expected number of survivors.

$$Max\quad Z_{SAR} = \mathop \sum \limits_{s} \mathop \sum \limits_{t} \mathop \sum \limits_{m} \mathop \sum \limits_{n} P^{s} .x_{m,n,t}^{s}$$

(51)

Table 8 Percent improvement (%) of integrated models over non-integrated case in terms of RENS for $\gamma =\widehat{\gamma }$

6.5 Robust approach

In this subsection, the performance of robust models for SSB and PSD strategies is compared. Based on the formulation presented in 4.3 and considering $\delta =10$, the results are illustrated in Fig. 11 for problems with 5 nodes. The robust and stochastic models are compared in this figure. As can be seen, the robust model has less RENS values because the worst case is considered and the solution of each scenario tends to be close to its average. It is useful for risk averse decision makers who consider a worst case scenario.

Fig. 11

RENS versus variations around ${\widehat{\gamma }}^{s}$ (5 nodes)

This is true for other problem sizes.

6.6 Discussion

The proposed observations and insights, supported by a comprehensive numerical study, are important from the following perspectives:

• (1) They recommend the best policy for the allocation of relief teams over the time horizon corresponding to a given treatment strategy, implemented by relief teams.

  They are useful to choose the best treatment strategy before a disaster and to be implemented right after the disaster. Fig. 10 introduces PSD and SSB as the best strategies in terms of robustness in rescuing the greatest number of casualties in different field scenarios.

• (2) They help to revise the decision on strategy implementation appropriately based on the last updated data on the distribution of casualty types. No treatment strategy is dominant in all conditions.

Our work may be used by a disaster commander in a centralized manner or as a way for coordination and inter-relation among several agents/organizations which are in service in a decentralized manner.

The most relevant paper to our research is Rezapour et al. (2018) which considered only streaming strategy with and without overflow. They noted that “emergency units should be allocated to affected sites proportional to their casualty populations. This strategy is not optimal, but yields a good expected number of survivors that is very close to the optimal solution.” They compared ENS in two cases with and without casualty overflow and reported “casualty overflow does not make a significant increase in ENS if medical teams are divided fairly (NOT optimally) between red and yellow groups of casualties.”. In fair allocation, red and yellow class teams have the same workload. Our results are not in contradiction with the above recommendations. Table 9 compares our research with Rezapour et al. (2018) in details.

Table 9 Comparing our research to Rezapour et al. (2018)

7 Conclusion

In this research, we have developed seven stochastic MILP models corresponding to different on-field relief strategies to figure out the best policies before a disaster and to implement them in the response phase of disaster when we lack time to solve optimization problems. The uncertainty in demand-side parameters is taken into account through some plausible scenarios while the supply capacity relies basically on the known local relief teams. The policies are supposed to be implemented efficiently for the integrated deployment of USAR and medical teams right after an urban mass-casualty incident. The models simultaneously allocated USAR teams to the affected sites, medical teams and extricated casualties to the CTSs, and medical teams to the casualty groups with the aim of improving the expected number of survivors. A comprehensive numerical study was established by generating 50 random instances to evaluate the performance of the proposed optimization models in 1750 field scenarios. Then, a hypothetical but realistic earthquake in Tehran, as one of the most vulnerable cities in the world, was investigated. Next, the performance of our models in terms of two critical parameters was examined: (1) variations in treatment strategy implementation, and (2) error estimation in the estimation of the ratio of red-group casualties. Additionally, we reported findings for the best deployment of relief teams in the event of earthquake which can be established similarly for the other cases. The results confirmed that the integration of SAR and on-field treatment operations can increase the number of survivors. The robust model that tries to maintain the optimal solution under given scenarios close to its expected value results in less survivors. Based on the above mentioned experiments, some observations and insights were provided and discussed. Enriching the proposed treatment strategies, considering the transportation of casualties to hospitals for comprehensive treatment, and evaluating the impact of treatment operations on the performance of USAR teams can be important directions for future research.