1 Introduction

Stationarity of hedge ratios indicates a stable relationship between spot and Future prices. Since hedgers seek for reducing the risk of their investments, reliable dynamics of hedge ratios are expected. If not, Future mark may lose its usefulness to hedgers since the risk diversification can be hard to achieve. The property of stationarity motivates investors to use diversification strategies and can be utilised by policy makers to stabilize financial mark.

A hedge is a spread between a spot asset and a Future position that reduces risk.Footnote 1 Thus, the hedge ratio is defined as the number of Future contracts bought or sold divided by the number of spot contracts whose risk is being hedged. A considerable amount of research has focused on modelling the distribution of spot and Future prices and applies the results to estimate the optimal hedge ratio using various type of models (see Chen et al. 2003; Floros and Vougas 2004; Salvador and Arago 2014; Wang et al. 2014; Dai et al. 2017). Although most of the previous studies on optimal hedge ratios are successful in capturing the time-varying covariance-variances, almost all of them focus only on the estimate of the hedge ratios. The main purpose of this paper is to further examine and understand the stationarity of hedge ratios over time, as the literature provides limited information about it.Footnote 2

Stationarity of hedge ratios indicates a stable relationship between spot and Future prices. Since hedgers seek for reducing the risk of their investments, reliable dynamics of hedge ratios are expected. If not, Future mark may lose its usefulness to hedgers since the risk diversification can be hard to achieve. The property of stationarity motivates investors to use diversification strategies and can be utilised by policy makers to stabilize financial mark.

The analysis of stationarity of hedge ratios can be viewed as a first step for portfolio hedging in any asset or market. Hedge ratios represent the sensitivity of spot prices to changes in Future prices, and measure how changes in the Future market affect spot mark. If this sensitivity is stationary, we are confident that the predictions we make lie into reasonable bounds. As a stationary process, the mean value of this sensitivity is constant and the variance is finite, so deviations of the predicted sensitivity to the observed sensitivity will be due to short-term corrections. On the other hand, if the sensitivity of spot and Future returns is not stationary it will represent a burden to the successful implementation of a hedging strategy since accurate predictions of this sensitivity will be hard to achieve.

The potential deviations from stationarity for the sensitivity between spot and Future returns can be due to two main reasons. First, during crisis periods it is possible that the dynamics of the relationship between spot and Future mark follow different dynamics. This would lead to periods where the expected values for the sensitivities differ, casting doubts on the predictability of the hedge ratios. Second, the investment horizon considered might not capture completely the stationary characteristics of the relationship between spot and Future returns. This can be the case when we look at this relationship at a very high frequency. If deviations from the expected hedge ratio take too long to revert (due to the presence of short-term traders), focusing the analysis at high frequency observations over short horizons may blur the stationary characteristics of this sensitivity between spot and Future mark.

Early studies, such as Ederington (1979) and Anderson and Danthine (1981), assume a constant optimal hedge ratio which can be obtained as the slope coefficient of an OLS regression. When the optimal hedge ratios depend on the conditional distributions of spot and Future price movements, then the hedge ratios vary over time as this distribution changes. Subsequent studies show the variability of hedge ratios over time, and support the hypothesis that optimal hedge ratios are time-varying and non-stationary (see Baillie and Myers 1991). These studies report that hedge ratios contain a unit root and therefore behave much like a random walk.

Grammatikos and Saunders (1983) were the first to examine the stability of hedge ratios. They concluded that hedge ratio stability (stationarity) in currencies could not be rejected. Furthermore, Malliaris and Urrutia (1991) examined the random walk hypothesis and concluded that hedge ratios of selected indices and currencies follow a random walk. However, Ferguson and Leistikow (1998) report that Future hedge ratios are stationary using a simple OLS regression approach. They argue that hedge ratios in previous studies appear to follow a random walk due to small sample size of data and hedge ratio calculation overlap. Lien et al. (2002) reject the null hypothesis that the optimal GARCH hedge ratios have a unit root. Further, Brooks et al. (2002) show that optimal hedge ratio series obtained through the estimation of the asymmetric MGARCH model appears stationary. They argue that optimal hedge ratio may be linked to the arrival of news to the market and the relevant Future price and covariance news impact surfaces. Recently, Lai and Sheu (2010) propose a new class of multivariate volatility models encompassing realized volatility (RV) estimates to obtain risk-minimizing hedge ratios. Their results show that hedging improvement is substantial when switching from daily to intraday frequencies. They also report that the ADF test on the RV-based hedge ratios (intraday) rejects a unit root, except for their results based on (daily) OLS and ECT-GARCH-CCC models for the post-crisis period of 2008.

Leistikow et al. (2019) present a Bias Adjustment Multiplier (BAM) calculated from a prior period’s data as (the prior period’s traditional Future hedge ratio)/(the prior period’s new ex ante hedge ratio based on the underlying spot asset’s carry cost rate). They test if BAM is stationary, and find empirical support for the hypothesis. Further, Leistikow and Chen (2019) test whether the traditional Future hedge ratio (hT) and the carry cost rate Future hedge ratio (hc) vary as predicted both within and across spot asset carry cost rate (c) regimes. They report that the BAM is not statistically significant different from low and high c periods.

The contribution of our article is to examine whether time-varying hedge ratios, calculated from a set of European stock indices (German DAX30, British FTSE100, French CAC40 and Spanish IBEX35), are stationary over time. The novelty of the paper lays on the analysis of the hedge ratio stationarity from a state-dependent perspective. A hedger expects that her strategy allows her to reduce risk all the time, but especially during periods of financial distress. During periods of market instability, positions in the spot market are likely to lose value and hedgers rely on Future mark position to minimise losses. Thus, analysing hedge ratio stationarity in both states (low and high volatility) is a crucial topic which shows evidence on the usefulness of Future mark as hedging mark.

The studies we mentioned previously about HR stationarity do not make this distinction among states, and this can lead to misleading conclusions about the stationarity of hedge ratios series across volatility regimes. There are several papers from other areas of economics or financial economics that report mixed evidence on the stationarity hypothesis, depending on the volatility regime. See, for example, Holmes (2010) for the long-run purchasing power, Kanas and Genius (2005) for the US/UK real exchange rate, and Camacho (2011) for the US real GDP. Recently, Cotter and Salvador (2015) analyze the relationship between expected return and risk in the US market, and find that market volatility follows non-stationary dynamics during period of high instability. However, since the volatility process will eventually come back to the tranquil state, the whole process remains stationary.

Given the evidence reported in previous papers when analysing the stationarity properties of economic/financial time-series from a state-dependent perspective, we support that it is necessary to re-examine the stationarity properties of Future hedge ratios. The non-stationary volatility in spot mark during these high-volatility states may have a negative effect on the stationarity of the hedge ratios and on the hedging effectiveness of hedging ratios. Therefore, we test for state-dependent stationarity to verify the usefulness of Future mark as hedging mark in both states (especially during periods of financial instability).

The results in this paper provide empirical evidence that time-varying hedge ratios are stationary over time. Thus, we confirm the stable relationship between Future and spot returns across time. If we take a closer look at the evolution of spot and Future dynamics, and analyse stationarity across states, we find that hedge ratios are described better as a combination of two different mean-reverting stationary processes, which depend on the state of the market. Our state-dependent analysis confirms the existence of Future mark as hedging mark. In both states, the hedge ratios follow stable and predictable processes, which can be used to manage investors’ risk. However, although correlations follow a stable stationary process in both states, during periods of financial turmoil the correlations between spot and Future are different from the ones during calm periods.

This last result can provide an explanation to the controversy caused by the evidence of greater hedging effectiveness using static hedge ratios than using simple dynamics ones, and as why there have been several recent papers which both theoretically (Lien 2012) and empirically (Alizadeh et al. 2008; Salvador and Arago 2014) showed a greater effectiveness of regime-switching models. The intuition is that omitting the regime-switching specification leads to inefficient hedges compared not only to the ones considering state-dependence, but also to the static ones.

Finally, we also analyse the dynamics of optimal hedge ratios at intraday level (we extend the study by Lai and Sheu 2010). Since executing an intraday hedging strategy would be very expensive, we focus on providing new insights about the dynamics of the spot and Future mark at ultra-high frequency.

Our results display a similar picture in the dynamics of spot-Future returns at this intraday frequency. The evidence suggests that intraday movements in the hedge between spot asset and Future position are driven mainly by market participants, with similar perspectives of investment horizon. Even if there are different types of traders at this frequency, they do not have a significant impact on the hedge between spot and Future positions.

The rest of the paper is organised as follows. Section 2 provides a description of the database. Section 3 develops the model used to obtain the dynamic hedge ratios. Section 4 analyses time-series stationarity of estimated hedge ratios using both a standard perspective and the regime-switching framework. In Sect. 5, we take a closer look at stationarity properties of hedge ratios using intraday data and Sect. 6 concludes.

2 Data description

The dataset contains daily data (spot and Future closing prices) from the main stock indices and their corresponding Future contracts in Germany (DAX30), France (CAC40), United Kingdom (FTSE100) and Spain (IBEX35). The time horizon includes observations from May 2000Footnote 3 to November 2013. Within this sample period we have two different contexts, i.e. before (under several years of stability and sustained growth) and after the global financial crisis and the Eurozone debt problems started in 2008.

The stock mark analysed are the most traded European financial mark and all of them are traded on an electronic trading system. The time-series for the indices, and their near-time delivery (nearby) Future contract,Footnote 4 are provided by Datastream®.

Table 1 presents the statistical properties of the price and returns series. The returns of spot and Future prices follow all stylized facts of financial time series such as leptokurtosis, volatility clustering, and leverage effects (see Bollerslev et al. 1994). We estimate time-varying hedge ratios using GARCH models, which are very popular in the literature to capture the stylized facts of financial time series (see, for example, Degiannakis and Floros 2010; Floros and Salvador 2016). In the next section, we develop the empirical models to obtain dynamic hedge ratios and we describe their patterns.

Table 1 Summary statistics for log-returns and prices of spot and Future on the selected European indices
Full size table

3 Estimating time-varying hedge ratios

3.1 Methodology

In more traditional hedge-ratio estimation methodology, the covariance matrix of spot and Future prices (and therefore the hedge ratio) is assumed constant through time. However, according to Lee (1999), given the time-varying nature of the covariance in financial mark, the OLS assumption is inappropriate when estimating optimal hedge ratios. There has been a large body of research that has applied the GARCH framework to infer time-varying hedge ratios (Cecchetti et al. 1988; Kroner and Sultan 1993; Park and Switzer 1995). In the GARCH model,Footnote 5 the conditional variance of a time-series depends on the squared residuals of the process (Bollerslev 1986). It also captures the tendency for volatility clustering in financial data, and utilises the information in one market own history (univariate GARCH) or uses information from more than one mark history (multivariate GARCH). According to Conrad et al. (1991), multivariate GARCH models provide more precise estimates of the parameters because they utilise information in the entire variance–covariance matrix of the errors and allow the variance and covariance to depend on the information set in a vector of the ARMA manner (Engle and Kroner 1995).Although GARCH models are useful for estimating time-varying optimal hedge ratios, a time-varying covariance matrix of spot and Future prices is not sufficient to establish that the optimal hedge ratio is time-varying.Footnote 6

In this study we use a bivariate model with GARCH errors, the Diag-BEKK (p, q) model, to estimate the dynamic variance–covariance matrix of spot and Future log-returns. The Diag-BEKK (p,q) framework of log-spot (s) and log-Future (f) is estimated in the form

$$ \begin{gathered} {\mathbf{Y}}_{t} = \left( {\begin{array}{*{20}c} {\left( {1 - L} \right)\log \left( {s_{t} } \right)} \\ {\left( {1 - L} \right)\log \left( {f_{t} } \right)} \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {a_{0} } \\ {b_{0} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {\varepsilon_{s,t} } \\ {\varepsilon_{f,t} } \\ \end{array} } \right) \\ {{\varvec{\upvarepsilon}}}_{t} \equiv \left( {\begin{array}{*{20}c} {\varepsilon_{s,t} } \\ {\varepsilon_{f,t} } \\ \end{array} } \right)|\Psi_{t - 1} \sim N\left( {0,{\mathbf{H}}_{t} } \right) \\ \end{gathered} $$
(1)
$$ {\mathbf{H}}_{t} = \left( {\begin{array}{*{20}c} {\sigma _{{s,t}}^{2} } & {\sigma _{{sf,t}} } \\ {\sigma _{{sf,t}} } & {\sigma _{{f,t}}^{2} } \\ \end{array} } \right) = C_{{\mathbf{0}}} C^{\prime}_{{\mathbf{0}}} + \sum\limits_{{i = 1}}^{{\tilde{q}}} {\left( {{\mathbf{A}}_{i} {\mathbf{\varepsilon }}_{{t - i}} {\mathbf{\varepsilon ^{\prime}}}_{{t - i}} {\mathbf{A^{\prime}}}_{i} } \right)} + \sum\limits_{{j = 1}}^{q} {\left( {{\mathbf{B}}_{j} {\mathbf{H}}_{{t - j}} {\mathbf{B^{\prime}}}_{j} } \right)} $$

where \(\Psi_{t - 1}\) is the information at time \(t - 1\) and the variance–covariance matrix specification, \({\mathbf{H}}_{t}\), is the BEKK model of Baba et al. (1990). The matrices \({\mathbf{A}}_{i}\) and \({\mathbf{B}}_{j}\) are restricted to be diagonal. The Diag-BEKK(\(q,\tilde{q}\)) model is guaranteed to be positive definite and requires the estimation of fewer parameters compared to other multivariate models; i.e. Diag-VECH, BEKK.

This multivariate specification allows us obtain time-varying hedge ratios through the conditional covariance matrix

$$ HR_{t} = \frac{{\sigma_{sf,t} }}{{\sigma_{f,t}^{2} }} $$
(2)

where the dynamic hedge ratios are computed as the quotient between the conditional spot-Future covariance and the Future variance.

Recent studies on HR estimation include Lai and Lien (2017) and Lai et al. (2017). Lai and Lien (2017) examine the usefulness of high-frequency data for estimating hedge ratios for different hedging horizons, while Lai et al. (2017) propose a multivariate Markov regime-switching high-frequency-based volatility model for modeling the covariance structure of S&P 500 spot and Future returns, and estimating the associated hedge ratios. Qu et al. (2019) investigate the dynamic hedging performance of the high frequency data based realized minimum-variance hedge ratio approach using data from China’s CSI 300 market. Lien et al. (2020) argue that when looking into high- and low-volatility states, quantile hedge ratios show different results compared with conventional models. For recent studies on the Future Minimum Variance Hedge Ratios, see Chen et al. (2019), Cui and Feng (2020), Wang et al. (2019), and Chiou-Wei et al. (2020).

3.2 Empirical results

The estimation of the model is conducted using conditional quasi maximum likelihood estimation.Footnote 7 Diagnostic tests and information criteria were employed to determine the lag orders, the validation of the assumptions concerning symmetry and diagonality. The results from the Diag-BEKK(1,1) model (Eq. 1) are presented in Table 2. The coefficients are all statistically significant and imply volatility clustering. Both spot and Future log-returns exhibit strong persistence in volatility, but it is the Future market that shows the strongest persistence.

Table 2 Parameters estimations of the Diag-BEKK (1, 1) model
Full size table

Figure 1 shows the estimated variances over time for the DAX30, FTSE100, CAC40 and IBEX35 spot and Future indices. We observe several peaks in the volatility measures common to all mark; e.g. around 2003, in latest 2008 coinciding with global financial crisis, and one covering end 2011–beginning 2012 with the worst part of the Eurozone debt problems which reflected in the stock mark. Also for Spain, there is a peak during the beginning of 2013 showing further problems with the stability of that market.

Fig. 1
figure 1

Conditional variances. This Figure plots the conditional spot (\(\sigma_{s,t}^{2}\)) (black line) and Future (\(\sigma_{f,t}^{2}\)) variances (green line) for the log-returns of the DAX30, FTSE100, CAC40 and IBEX35 indices (sample period May 2000–November 2013)

Full size image

Figure 2 shows the plot of time-varying hedge ratios obtained from Eq. 2. The DAX hedge ratios are quite volatile during the first part of the sample, but they seem to stabilise after 2005. Despite the evident peaks in volatilities in all countries, the hedge ratios follow a smooth pattern along the sample period where they seem to return always to a predetermined value. As from visual description of the hedge ratios, we cannot infer about their stationarity. Next section provides a formal study of the hedge ratio stationarity and the implications for optimal hedging.

Fig. 2
figure 2

Hedge ratios. This Figure plots the estimated HRs according to Eq. 2 for the spot and Future stock indices in Germany, United Kingdom, France and Spain. Shaded areas correspond to periods of high volatility based on the filtered probabilities of Eq. 4

Full size image

4 Analysing the (non) stationarity of the hedge ratios

The purpose of the paper is to distinguish hedge ratios series that appear to have a unit root from those that appear to be stationary over time. For this purpose, we employ two well-known unit root tests,Footnote 8 i.e. the Augmented Dickey Fuller (ADF) and Phillips and Perron (PP) tests, which test the hypotheses:

Ho: there is a unit root

Ha: there is stationarity

4.1 Unit root theory

The ADF test assumes that series \(y_{t}\) follows an AR(p) process

$$ \Delta y_{t} = ay_{t - 1} + x_{t}^{{\prime}} \delta + \beta_{1} \Delta y_{t - 1} + \cdots + \beta_{p} \Delta y_{t - p} + u_{t} $$
(3)

where \(\Delta y_{t}\) defines the first difference of hedge ratios, and \(u_{t} \sim N\left( {0,\sigma_{u}^{2} } \right)\), with \(H_{0} :a = 0\) and \(H_{1} :a < 0\).

Phillips and Perron (1998) propose a nonparametric method to control for serial correlation when testing for a unit root (this test is popular in the analysis of financial time series). The PP test estimates the equation, \(\Delta y_{t} = ay_{t - 1} + x_{t}^{^{\prime}} \delta + u_{t}\), and modifies the t-ratio of the \(a\) coefficient; hence, the serial correlation does not affect the asymptotic distribution of the test statistic.Footnote 9

4.2 Regime-switching ADF test

Regime switching models are an important methodology to model nonlinear dynamics and widely applied to economic data including business cycles, bull and bear mark, interest rates and inflation. There are two common features of these models. First, past states can recur over time. Second, the number of states is finite and small (it is usually two and at most four). In contrast to the regime switching models, structural break models can capture dynamic instability by assuming an infinite or a much larger number of states at the cost of extra restrictions. If there is a change in the data dynamics, it will be captured by a new state. The restriction in these models is that the parameters in a new state are different from those in the previous ones. This condition is imposed for estimation tractability. However, it prevents the data divided by breakpoints from sharing the same model parameters, and could incur some loss in estimation precision.

Did hedge ratios have distinct dynamics or revert to a historical state with the same dynamics during the sample period analysed? Existing econometric models have difficulty answering such questions. In our paper we took the first assumption where past states can recur over time (in terms of bull and bear mark) instead of being considered new states. For more information about the regime switching models, see Samitas and Armenatzoglou (2014) and Billio et al. (2018).

Recent literature has questioned the asymptotic power and statistical properties of traditional ADF tests; e.g. Chortareas et al. (2002) and Sollis et al. (2002). In this paper, we are interested in the stationarity properties of hedge ratios conditioned to volatility levels (regimes) in the mark (low and high volatility regimes), i.e. if the hedge ratios are (non)stationary within high and low volatility periods independently of which is its stationarity in the long-run (assuming a single regime in the long-run). This allows us to identify if there is any state of the market where hedging with Future contracts is not useful.

We can test this hypothesis by applying the methodology developed in Kanas and Genius (2005) and Camacho (2011), extending Hall et al. (1999). These authors extend the ADF regression by allowing both the autoregressive parameters and the volatility of the hedge ratios to change over time, following a first-order Markov process. Hence, the regime-switching ADF, or RS-ADF, specification test for the (non-)stationarity of hedge ratios, under different states of volatility, is.

$$ \Delta y_{t} = a_{{0,s_{t} }} + \sum\limits_{k = 1}^{p} {a_{{k,s_{t} }} } \Delta y_{t - k} + b_{{s_{t} }} y_{t - 1} + u_{t} ,\,u_{t} \sim N\left( {0,\sigma_{{s_{t} }}^{2} } \right) $$
(4)

where \(a_{{0,s_{t} }} ,...,a_{{k,s_{t} }} ,b_{{s_{t} }}\) are regime-switching parameters, \(s_{t}\) is the unobservable regime, and \(u_{t}\) are normal innovations with state-dependent variances.Footnote 10

4.3 Empirical results

Table 3 shows the results from the ADF and PP tests applied to the estimated hedge ratios under three cases: (i) a simple AR(p) process (Panel A), (ii) an AR(p) with intercept only (Panel B) and (iii) an AR(p) with intercept and linear trend. The tests presented in Panel B and C show that the hedge ratios are stationary. This does not hold, however, when we do not employ an intercept, or an intercept and linear trend (Panel A). This shows the importance of employing deterministic components when testing for unit roots in hedge ratios. Our results are in line with previous papers, Ferguson and Leistikow (1998) and Lien et al. (2002), who found that time-varying hedge ratios are stationary over time.

Table 3 Unit-root tests for HRs series
Full size table

The implication of this result is that optimal hedges on stock indices tend to fluctuate around a mean-reverting value. This stable relationship, between correlations of spot and Future mark, can be exploited by hedgers to reduce risk of their investments. This result of stationarity in the hedge ratios can be viewed as good news, since it implies a reliable relationship between the spot and Future prices and a confirmation that Future mark are useful for hedgers.

Besides this first analysis, we also examine the stationarity of hedge ratios by looking at low and high volatile periods. The advantage of our approach is that we do not need to assume which periods correspond to low/high volatility states. The estimation procedure makes this classification (regime-switching methodology).

Table 4 shows the estimates of the RS-ADF model presented in Eq. 4. Two volatility regimes have been employed. We observe that all constant drift coefficients are statistically significant, and the same is true for the autoregressive ones. The most relevant coefficient in Table 4 is \(b_{{s_{t} }}\) which indicates existence of a unit root in the state-dependent process. Our results are noteworthy and need further discussion.

Table 4 RS-ADF test with drift
Full size table

First, in both states, the coefficients\(b_{{s_{t} }}\) are negative and significant, which implies stationarity of the process in both states/regimes. For all countries and for the first state St = 1 autoregressive coefficients are more negative than those of the second state St = 2. Our results of stationarity confirm similar findings of Francq and Zakoian 2001; Timmerman 2000; and Yang 2000. Here we have two different mean-reverting processes, one when the process is in low-volatility periods, and another one when the process is in high-volatility periods.Footnote 11 Within each state, hedge ratios tend to fluctuate around different state-dependant values, instead of just one common value independent of state. The good news for hedgers is that hedge ratios follow stationary processes in both states, which implies that they can use these mark to manage their risk at any time (even under the most needful times of market turmoil).

Figure 3 shows the probability of being in a state of low volatility and complements Fig. 2 which shows, in shaded areas, the observations that correspond to high volatility periods when compared to the estimated hedge ratios.

Fig. 3
figure 3

Filtered probabilities for low volatility states. This Figure plots the probability of being in a low volatility state [P(St = 1|Ψt−1)] for the RS-ADF test of Eq. 4. In these plots we use the estimated HRs from Eq. 2 using the returns on the spot and Future stock indices in Germany, United Kingdom, France and Spain as the main input for the regime-switching stationarity test

Full size image

The hedge-ratios process changes continuously among regimes. Nevertheless, the hedge-ratios within each regime are stationary, and the dynamics of the correlation in the different regimes are not the same. Thus, if we are interested in shorter horizons hedges, not considering different states can be a cause of a worse hedging performance.

These differences among regimes can be observed more clearly in Fig. 4. For all mark there are obvious differences in the distributions of the hedge ratios during LV states and HV states. During HV states the optimal HRs are consistently higher than during LV states. Based on the way the HRs are computed, this suggests that the covariance between spots and Future mark is higher during these periods of uncertainty.

Fig. 4
figure 4

Hedge ratios for intraday data. This figure plots the distribution of the optimal HRs during different states (defined by the RS-stationarity test). The first two plots represent the HRs in Germany and UK during high volatility states with the corresponding plots for the high-volatility states below. The plots in the bottom part of the figure correspond to the HRs in UK and Spain both for low and high volatility states

Full size image

This result can provide an explanation to very recent evidence, which shows, both theoretically and empirically, that hedge ratios obtained from regime switching models outperform the rest of strategies (both static and dynamic). Lien (2012) characterizes conditions under which the regime-switching hedge strategy performs better than the OLS hedge strategy and where the GARCH effects prevail. These conditions would allow the RS-GARCH hedge strategy to dominate both OLS and GARCH hedge strategies.

Recently, Alizadeh et al. (2008), for commodities, and Salvador and Arago (2014), for stock indices, report a greater performance of (multiple-) regime-switching strategies than those obtained through single-regime models. Our results about this state-dependent stationarity of hedge ratios support this previous evidence. When analysing the performance of hedging strategies, we usually look at shorter horizons and we tend to follow the false dynamics. Neglecting the switching of HRs' regimes causes a worse hedging effectiveness. Given that both states are stationary, optimal hedging can be exploited in any volatility regime. However, we need to identify the proper dynamics for each one of the regimes.

In Table 5, we repeat the estimations of the RS-ADF model, and we do not consider a drift in the model. Here we obtain an interesting result. The coefficient \(b_{{s_{t} }}\) in the low volatility state is negative and significant providing evidence of stationarity of hedge ratios during this low volatility state. However, if we look at high volatility states it seems that the process followed by optimal hedge ratios is non-stationary. This result highlights the importance of modelling the trend of the time series properly. Similar results apply when using standard unit-root tests. Wrong trend specification leads into wrong/incorrect conclusions about the stationarity of hedge ratios. We recommend the use of a state dependent drift when testing the stationarity of HRs.

Table 5 RS-ADF test with no drift
Full size table

5 Hedge ratio stationarity for intraday data

Dynamic hedging is usually expensive to implement since it involves transaction costs any time the hedged portfolio is re-balanced. Therefore, hedging is more rational at low frequencies. However, if investors conduct the hedging, the hedge dynamics will not differ across different sampling frequencies. On the other hand, if both investors and short-term traders conduct the hedging (i.e. swap trading between Future and spot for speculation), then the hedge dynamics will differ across different sampling frequencies. In this section, we try to unmask this hypothesis by looking at the stationarity patterns of intraday hedge ratios.

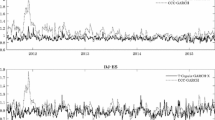
The dataset is comprised by hourly observations of the DAX index and its corresponding Fut contract from 3rd of January, 2000 to 30th of December, 2010 (25,138 observations).Footnote 12 As in the previous datasets, we first compute the dynamic hedge ratios based on eqs.1 and 2. A plot of the estimated intraday hedge ratios is displayed in Fig. 4. The hedge ratios seem to follow a smooth pattern although it is not possible to draw any conclusion about its stationarity from this figure. Therefore, we run the corresponding stationarity tests to provide new insights (Fig. 5).

Fig. 5
figure 5

Hedge ratios for intraday data. This figure plots the estimated HRs according to Eq. 2 using the intraday (hourly) returns on the spot and Future stock indices in Germany

Full size image

Table 6 displays the unit-root tests when we consider the regime-switching approach and distinguish between high and low volatility regimes. The empirical results show that we do reject the unit root for both regimes, when a switching intercept is employed.

Table 6 RS-ADF test with drift
Full size table

If we had found evidence in favour of unit root presence, then we should have obtained a more complex picture for the distributions of spot and Future returns at this intraday frequency. That would have implied that, looking at longer horizons, the spot-Future correlations would have seemed to follow a stationary process, although when looking at intra-day horizons, the dynamics of the spreads between these two mark would have followed unpredictable dynamics. Nevertheless, there is no such discrepancy in our findings. There is no evidence that the dynamics of hedge ratios vary across different sampling frequencies. There is no evidence that the agents driving the spread of these mark at intraday level are mainly short-term traders. Even if market participants have different perspectives of their investment horizon, this is not evident in regime-switching unit root testing. Our results suggest evidence of investors prevailing at both daily and intra-day frequencies. The impact of the short-term traders do not affect significantly the dynamics of the hedge between spot and Future at the intra-day frequency.

It is also unclear how transaction costs affect rebalancing the optimal hedge position, although it may discourage speculators in general. On the other hand, professional speculators may employ day trading or speculation in securities. In line with Tse and Williams (2013) we do support that spot-Future mark need to be fully examined using high frequency intraday data.

6 Conclusion

Static and dynamic models of various forms have been employed in the literature to calculate hedge ratios. However, there is to date no definite conclusion concerning stationarity of the dynamic hedge ratios. We focus on the characteristics of optimal hedge ratios for the DAX30 (Germany), FTSE100 (UK), CAC40 (France), and IBEX35 (Spain) indices over the period 2000–2013. We estimate dynamic hedge ratios by a bivariate diagonal multivariate GARCH-type model and we examine stationarity of hedge ratios by employing standard econometric methods of unit root tests and a new state-dependent approach following the RS-ADF test.

We find that dynamic hedge ratios are stationary over time when the entire sample is considered. This result implies a stable relationship in spot-Future correlations that can be used by hedgers to reduce the risk in their investments. However, when we consider shorter horizons and distinguish between volatility states (i.e. high and low volatile periods), we show that the dynamic hedge ratios follow different stationary processes during periods of calm and periods of financial turmoil. These results support evidence in previous studies that report a greater hedging performance of dynamic strategies using regime-switching models.

The different processes followed by the hedge ratios for volatile periods are associated with changes in the variances and the covariance between spot and Fut returns. This has important implications for hedgers. First, financial analysts and hedgers must determine the effect of this unexpected change in the risk on their position. Second, they should determine the factors causing this shifted stationarity. The good news for investors is that Future mark can be seen as a hedging market at any time or state of the market (even for the most necessary periods of market turmoil).

The results for the dynamic hedge ratios at intraday level are also in line with the high frequency results. There is no clear evidence that the spreads are distorted by short-term market participants. Our conclusion is that the role of speculators in the determination of intra-day spot-Future stock dynamics is not as relevant as the one taken by hedgers. Further research should consider structural breaks tests in both spot and Future returns, and examine if hedging effectiveness change when HRs are stationary or not.