Keywords

1 Introduction

The application of financial derivative stock index futures in capital market is more and more extensive , mainly because of its hedging function in the solution of systemic risk has a superiority [1]. By combing the development of hedging theory, we found that the researchers have conducted a thorough and comprehensive study of the optimal hedging model and the effectiveness of hedging. The research theory has had a profound impact. Ederington [2] (1979) used the General Least Squares Estimator (OLS) to do the hedging of the US Treasury futures market and found that the hedging ratio was less than 1. He also raised the degree of reduction in the variance of the yield before and after hedging as a criterion for hedging. Engle [3] (1982) proposed an autoregressive Heteroscedastic Model (ARCH) and a generalized autoregressive Heteroscedastic Model (GARCH) . And compared with the traditional valuation model, he found that GARCH model is more suitable for stock index futures hedge rate estimates. Holmes [4] (1996) conducted a study on the effectiveness of stock index futures contracts after hedging operations, and the results show that the risk of hedging portfolio without hedging is far greater than the hedging effect of the optimal hedging rate derived from the regression of OLS model . Wu Xianzhi [5] (2008) employed the hedging model to estimate the hedging ratio within a sample data, and on the basis of which the effectiveness of hedging is checked. However, this static analysis method is defective, mainly due to the existence of time-varying and dynamic characteristics of the impact index and the fluctuation of the stock index. In view of the multi-sample and dynamic hedging ratio, Zhang Hua et al. [6] (2014) proposed the method of estimating the dynamic hedging rate of grain futures based on GARCH model. The results show that both the data in the sample and the data outside the sample are better than the static estimation method in the dynamic estimation.

Follow the development of this theory, we assume that the joint distribution of the spot market and the futures market is fixed, thus taking into account the typical OLS model of static analysis. Simultaneously, the impact of new information on the market and expected changes will change the joint distribution of futures and spot markets. Then the time-dependent GARCH model can capture the dynamic characteristics of futures and spot market more accurately [7]. Therefore, this paper introduces OLS and GARCH hedging model. First of all, we lies in the selection of the longest futures and spot sample data from the last 4 years CSI 300 stock index futures contract as the analysis object, and a total of four sets of sample data were obtained. Next, we estimate the hedge ratio in the OLS and GARCH models and calculate the average of the hedge ratios. Then we compare the hedging ratio between the average of the hedge ratio and the hedging ratio of the single sample on the basis of the hedging portfolio outside the construction sample. The purpose is to avoid the problem that the hedging rate caused by the single sample is not significant in the actual hedging operation. Finally, the paper summarizes the full text and analyzes the future research direction.

2 Hedging Ratio Determination and Model Construction

2.1 Optimal Hedging Ratio Determination

The hedge ratio based on the minimum variance is the hedging ratio that the volatility minimizes of the constructed hedging portfolio by hedging tools [8].The investor adopts a long or short hedging strategy, where the price of the hedged asset portfolio changes to ΔS − hΔF or hΔF − ΔS. No matter whether the investor adopts long hedging strategy or short hedging strategy, the variance of the hedging portfolio price is:

$$ {\sigma}^2={\sigma}_s^2-2h{\rho \sigma}_s{\sigma}_f+{h}^2{\sigma}_f^2 $$
(30.1)

In (30.1) formula, σ s 2 is the variance of spot asset price variation △S, σ F 2 is the variance of futures asset price variation △F. Simultaneously, σ sf is the covariance of ΔS and ΔF, ρ is the correlation coefficients of ΔS and ΔF. According to the minimum variance of the hedging ratio connotation, we make \( \frac{d{\sigma}^2}{dh}=0 \) to get the hedging ratio of the minimum variance of portfolio return volatility. Therefore, optimal hedge ratio is:

$$ h=\rho \frac{\sigma_S}{\sigma_F} $$
(30.2)

Therefore, the key of estimate the hedging ratio is using the hedging model to estimate h.

2.2 Hedging Model Construction and Effect Evaluation

2.2.1 Hedging Model Construction

  1. 1.

    OLS Hedging model Construction

When estimating the optimal hedging ratio based on the spot and Futures Portfolio, the general practice is to minimize the variance of the portfolio volatility (risk) of the spot and futures assets [9]. We assume that there is a linear relationship between the price of the goods and the price of the futures asset, and a linear function is introduced. Then, this paper construct the bivariate linear regression model:

$$ \ln \left(\frac{S_{t+1}}{S_t}\right)=\alpha +\beta \ln \left(\frac{F_{t+1}}{F_t}\right)+{\mu}_t $$
(30.3)

In (30.3) formula, \( \ln \left(\frac{S_{t+1}}{S_t}\right) \) is the daily logarithmic yield of spot index stock at t time, \( \ln \left(\frac{F_{t+1}}{F_t}\right) \) is the daily logarithmic yield of t time stock index futures. Simultaneously, α is the intercept of the equation, μ t is the disturbance term, and β is slope of the equation (that is, the optimal hedge ratio under the OLS model).

  1. 2.

    GARCH Hedging model Construction

The implicit condition of the OLS model is that the variance of the random error is constant, but the actual financial time series mostly has heteroscedasticity. Therefore, the autoregressive conditional heteroscedasticity model is used to solve heteroscedasticity problems and to capture more time series financial information. Then, the generalized autoregressive conditional heteroscedasticity model is derived on the basis of the ARCH model. In addition, the GARCH model is not only related to the squared u 2 t − q of the random error in the previous Q period, but also related to the variance σ 2 t − p of the random error in the previous P period [10]. Therefore, the GARCH (p, q) model of under the daily logarithmic yield sample data of the CSI300 stock index futures and spot is:

$$ \left\{\begin{array}{l}\ln \left(\frac{S_{t+1}}{S_t}\right)=C+\beta \ln \left(\frac{F_{t+1}}{F_t}\right)+{\varepsilon}_t\\ {}{\sigma}_t^2={\alpha}_0+\sum \limits_{i=1}^q{\alpha}_i{u}_{t-i}^2+\sum \limits_{j=1}^p{\gamma}_j{\sigma}_{t-j}^2\end{array}\right. $$
(30.4)

In the (30.4) formula, ε t is a random error and obeys the GARCH (p, q) process, \( \ln \left(\frac{S_{t+1}}{S_t}\right) \) is the daily logarithmic yield of spot index stock at t time, and \( \ln \left(\frac{F_{t+1}}{F_t}\right) \) is the daily logarithmic yield of at time stock index futures . In addition, \( {\sigma}_t^2 \) is the variance of the random error, \( {\varepsilon}_{t-j}^2 \) is the square lag term of the lag J period residual, and \( {\sigma}_{t-i}^2 \) is the variance lag term of the lag I period residual.

Here consider the leverage effect is to solve the future multi-step forecast when the volatility is negative situation, and the asymmetric effect of market information is reflected in the EGARCH model [11]. Therefore, a common EGARCH (1,1) model is established here:

$$ \Big\{{\displaystyle \begin{array}{l}\ln \left(\frac{S_{t+1}}{S_t}\right)=C+\beta \ast \ln \left(\frac{F_{t+1}}{F_t}\right)+{\varepsilon}_t\\ {}\ln \left({\sigma}_t^2\right)=\omega +\alpha \mid \frac{u_{t-1}}{\sigma_{t-1}}\mid +\gamma \frac{u_{t-1}}{\sigma_{t-1}}+\lambda \ln {\sigma}_{t-1}^2\end{array}}\operatorname{} $$
(30.5)

EGARCH model of leverage effect can be judged by γ is not equal to 0. When u t − 1 > 0 represents the presence of good information can bring α + γ times the impact; and u t − 1 < 0 on behalf of the negative information can bring α − γ times the impact [12]. So, β is the optimal hedging ratio for GARCH and EGARCH models.

2.2.2 Evaluation Criteria for Hedging Effect

The most common way to measure the hedging effect under different models is to examine the increase or decrease of the variance of the portfolio return before and after the hedging operation [13]. The formula for calculating the yield of our stock portfolio without risk avoidance is as follows:

$$ V\mathrm{ar}\left({X}_t\right)=V\mathrm{ar}\left(\ln \left(\frac{S_t}{S_{t-1}}\right)\right)=V\mathrm{ar}\left(\ln {S}_t\hbox{-} \ln {S}_{t-1}\right)={\sigma}_x^2 $$
(30.6)

In the (30.6) formula, X t and σ x 2 represent the variance of the daily logarithmic yield of stock index spot and the daily logarithmic yield. The variance of the yield of the portfolio after hedging operations is:

$$ V\mathrm{ar}\left(\Pi \right)=V\mathrm{ar}\left[\ln \left(\frac{S_{\mathrm{t}}}{S_{\mathrm{t}\hbox{-} 1}}\right)\right]+{h}^2V\mathrm{ar}\left[\ln \left(\frac{F_{\mathrm{t}}}{F_{\mathrm{t}\hbox{-} 1}}\right)\right]-2 hCov\left[\ln \left(\frac{S_{\mathrm{t}}}{S_{\mathrm{t}\hbox{-} 1}}\right),\ln \left(\frac{F_{\mathrm{t}}}{F_{\mathrm{t}\hbox{-} 1}}\right)\right]={\sigma^2}_{\Pi} $$
(30.7)

In the (30.7) formula, Π stands for the constructed hedging portfolio, the \( {\sigma}_{\Pi}^2 \) hedging portfolio’s yield variance, and the h as the hedging ratio . The measure of the minimum variance hedging effect is the percentage reduction in the risk of the return on the portfolio after the hedging rate relative to the non-hedged spot rate of return [14]. In combination with (30.6) and (30.7), the measure of hedging effectiveness is:

$$ {e}^{\ast }=\frac{\sigma_x^2\hbox{-} {\sigma}_{\prod}^2}{\sigma_x^2}=\frac{2 hCov\left[\ln \left(\frac{S_{\mathrm{t}}}{S_{\mathrm{t}\hbox{-} 1}}\right),\ln \left(\frac{F_{\mathrm{t}}}{F_{\mathrm{t}\hbox{-} 1}}\right)\right]-{h}^2V\mathrm{ar}\left[\ln \left(\frac{F_{\mathrm{t}}}{F_{\mathrm{t}\hbox{-} 1}}\right)\right]}{V\mathrm{ar}\left[\ln \left(\frac{S_t}{S_{t-1}}\right)\right]} $$
(30.8)

In the formula , e ∗ represents the proportion of the risk of the hedging portfolio to the original risk. The greater the e ∗, the better the effect of the hedging [15].

3 Empirical Analysis

3.1 Sample Data Selection and Processing

3.1.1 CSI 300 Stock Index Sample Data Selection

This paper lies in the selection of the longest futures and spot sample data from the last 4 years CSI 300 stock index futures contract as the analysis object, and a total of four sets of sample data were obtained. The contract varieties are IF1412, IF1512, IF1612 and IF1703. Moreover, a set of spot price sequences corresponding to the futures price series is generated. Through the CSI 300 stock index futures trading chart and the correlation coefficient of 0.95566, we can get a high consistency between the daily logarithmic price of CSI300 stock index futures and the daily logarithmic price of the spot, so it will avoid the basis risk to a certain extent.

3.1.2 Descriptive Statistics Analysis of Sample Data

This paper uses Eviews software to make a descriptive statistical analysis of the daily logarithmic yield of the CSI 300 stock index futures(See Figs. 30.1 and 30.2). As can be seen from the figure, first of all, the average daily yield of CSI300 stock index futures and spot contracts is −0.000182 and −0.000173, the results are less than 0 and fluctuate around 0. Secondly, the standard deviations are 0.015195 and 0.018430, indicating that both fluctuations are not large, that is, the degree of dispersion is relatively stable. Then, the P value of the J-B statistic is close to 0, indicating that the daily return of the spot is rejected to the normal distribution. At last, by the kurtosis 8.468, 10.904 and skewness −0.706, −0.313, we can see that the daily logarithmic yield of CSI300 stock index futures contracts and share index spot follows the left skewed spike tail distribution.

Fig. 30.1
figure 1

Descriptive statistics of stock index spot

Full size image
Fig. 30.2
figure 2

Descriptive statistics of stock index futures

Full size image

3.1.3 Processing and Checking of Sample Data

In order to avoid the phenomenon of pseudo regression , this paper uses Eviews software to do the unit root test for the sample data of CSI 300 stock index futures and spot stock. CSI 300 stock index futures and spot daily closing price logarithm sequence and first-order difference sequence ADF test results shown in Table 30.1.

Table. 30.1 Unit root test results
Full size table

Table 30.1 shows the original data by ADF test P value in the range of 0.0488–0.9894 and more than 0.01 significant level under, so accept the null hypothesis, that is, indicating that these contracts data is not stationary. In addition, the P values of the ADF tests for first difference sequences are all 0 and are less than the significant level of 0.05 and 0.01, that is, rejecting the original hypothesis. Therefore, the two column data are a stationary sequence and are the first order single integral sequence, that is, ln(S t )~I(1) and ln(F)~I(1). This paper selected the sample data for cointegration test and Granger causality test (See Figs. 30.3 and 30.4).

Fig. 30.3
figure 3

Cointegration test results

Full size image
Fig. 30.4
figure 4

Granger causality test results

Full size image

As can be seen from Fig. 30.3, the P value of the T statistic is 0 in the cointegration test and less than the significant level of 0.05. Therefore, the original hypothesis is rejected and there is a long-term equilibrium relation between the two variables. According to Fig. 30.4, “spot is not the cause of futures,” the hypothesis that the P value of the F statistic is 0.2843 and it is greater than 0.05 of the significance level, that is, inspection passed. However, “futures do not cause spot”, the hypothesis that the P value of the assumed F statistic is 0.0261 and less than the significant level of 0.05, that is, the test does not pass. To sum up, the CSI 300 stock index futures is “because”, the spot is “fruit”.

3.2 Hedging Ratios Analysis

3.2.1 OLS Model Empirical Analysis

This paper use the OLS model to do empirical analysis and find that the P value of the T statistic of the constant term in the partial sample fitting is greater than 0.05, that is, accepting the original hypothesis shows that the constant term is not significant. Therefore, the regression of the OLS model does not include the constant term. Then the regression results of OLS model were tested by residual difference test and autocorrelation test, and found that there was no heteroskedasticity in the regression results of all samples. However, we found that the regression results of some samples had residual first-order autocorrelation. Therefore, we use the Cochrane Orcutt method to eliminate the original model of the first-order autocorrelation [16]. Finally, we do a residual autocorrelation test on the adjusted fitting results and found that there is no autocorrelation, as shown in Table 30.2 below.

Table. 30.2 Empirical analysis results and their tests based on OLS model
Full size table

From Table 30.2, The P values of the T statistics of the 4 sets of samples under the OLS model are 0, and R 2 are close to 1, which shows that the OLS model fits well. The P values of the White test and the LM test were greater than the significant level of 0.05, and indicating that there was no residual heteroscedasticity and autocorrelation in the fitting results . Therefore, the β value is the optimal hedging ratio and calculate the average hedge ratio under the OSL model is 0.7532.

3.2.2 Empirical Analysis Based on GARCH Model

According to the requirements of the GARCH model, the ARCH effect of the sample data is checked and the independent Q test is used to determine the lag order. Moreover, a common GARCH (1,1) GARCH (1,2) GARCH (2,1) GARCH (2,2) model is established here. We selected the appropriate model by comparing the fitting degree, coefficient significance, AIC and SC criteria, and found that the IF1612 and IF1703 sample data did not meet the GARCH modeling requirements. Therefore, the EGARCH model is established and then the ARCH LM test of the fitting results ensures that there is no autocorrelation of the fitting residuals. According to the sample data, the GARCH and EGARCH models are established, and the fitting results are shown in Tables 30.3 and 30.4.

Table. 30.3 Fitting regression results based on GARCH model
Full size table
Table. 30.4 Fitting regression results based on EGARCH model
Full size table

As can be seen from Table 30.3, the P values of the ARCH effect tests for the contract IF1412 and the IF1512 samples are less than the significant level of 0.05 and indicates the existence of ARCH effect. Here, according to the nature of the coefficient significance test and the sum of the variance equation coefficients of the GARCH model is less than 1 and the coefficient is greater than 0, the GARCH (1,1) model (the mean equation does not include the constant term) is established. In the fitting result, the P value of coefficient significance is 0 and shows that the coefficient is remarkable. Moreover, the sum of coefficients of the variance equation is less than 1 and the R 2 is close to 1, which shows that the model fitting is better. In this paper, the residual value of GARCH (1,1) model to do ARCH LM test and we found that the P values of the F statistics are greater than the significant level of 0.05, that is, there is no autocorrelation of the residuals. Therefore, the β value can be the optimal hedging ratio.

As can be seen from Table 30.4, the P values of the ARCH effect tests for the contract IF1612 and the IF1703 samples are less than the significant level of 0.05 and indicates the existence of ARCH effect. Since the variance equation coefficient is negative and the GARCH model can not be established. Therefore, the EGARCH (1,1) model is established and the P value of the coefficient T statistic is 0, and indicating that the coefficient is significant. The values of AIC and SC are relatively small and R 2 is close to 1, which shows that the model fits well. Finally, the residual of the EGARCH model is tested by ARCH LM and the P value of the F statistic is greater than 0.05, which indicates that the original assumption is accepted, that is, there is no autocorrelation. Therefore, the β value is the optimal hedging ratio and calculate the average hedge ratio under the GARCH model is 0.838.

3.3 Hedging Effects Comparative Analysis

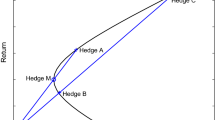
In this paper, we use the OLS and GARCH model to estimate the hedge ratio and construct the futures and spot investment portfolio outside the sample. Here with the hedging performance formula for hedging the effect of comparative analysis(See Fig. 30.5). As shown in Fig. 30.5 and Table 30.5, the average of the hedging ratios under the GARCH model constructs the portfolio outside the sample and the hedging effect is better than the hedge ratio under a single sample.Similarly, this paper using the average of the hedging ratios under the OLS model to build a portfolio outside the sample and the hedging effect is better than that the hedge ratio obtained under IF1512 and IF1703 samples, but slightly lower than the hedge ratio of IF1412 and IF1612 samples. Thus, the average of the hedging ratios in the two models is superior to the estimated hedging ratio estimated in most individual historical samples in terms of hedging effectiveness.

Fig. 30.5
figure 5

Hedging effect of different hedging ratios outside the sample

Full size image
Table. 30.5 Hedging effects of different hedging ratios outside of sample
Full size table

This paper is based on the theory of portfolio hedging, the minimum variance method is used to estimate the average of the optimal hedging ratio under the OLS and GARCH hedging models. The results show that the average of the hedging ratios is better than the hedging ratios estimated by most individual historical samples in terms of hedging effectiveness . Therefore, the analysis processing method by calculating the average hedge ratio optimization can adapt to different market conditions.

This paper suggests that investors can select several continuous historical contracts at the moment of hedging as the object of study. Then, we estimate the hedge ratio in the optimal hedging model and calculate the average of the hedge ratios. At the same time, this paper only uses the average value of the hedging ratio to construct a hedge portfolio outside the sample and the future needs a lot of empirical data validation. In addition, the average of the hedging ratio should be dynamically adjusted on the basis of multiple tests as the future research direction.