Dynamic hedging with futures: a copula-based GARCH model with high-frequency data

Abstract

Modeling the joint distribution of spot and futures returns is crucial for establishing optimal hedging strategies. This paper proposes a new class of dynamic copula-GARCH models that exploits information from high-frequency data for hedge ratio estimation. The copula theory facilitates constructing a flexible distribution; the inclusion of realized volatility measures constructed from high-frequency data enables copula forecasts to swiftly adapt to changing markets. By using data concerning equity index returns, the estimation results show that the inclusion of realized measures of volatility and correlation greatly enhances the explanatory power in the modeling. Moreover, the out-of-sample forecasting results show that the hedged portfolios constructed from the proposed model are superior to those constructed from the prevailing models in reducing the (estimated) conditional hedged portfolio variance. Finally, the economic gains from exploiting high-frequency data for estimating the hedge ratios are examined. It is found that hedgers obtain additional benefits by including high-frequency data in their hedging decisions; more risk-averse hedgers generate greater benefits.

1 Introduction

Modeling the joint distribution of spot and futures returns is crucial for optimal futures hedging because the optimal hedge ratio is obtained as the ratio of the covariance between spot and futures returns to the variance of futures returns (Ederington 1979). According to Engle (1982) and Bollerslev (1986), the conditional variances of many asset returns change over time. Consequently, bivariate generalized autoregressive conditional heteroskedasticity (GARCH) models enabling time-dependent covariances are commonly applied to estimate dynamic hedge ratios (Baillie and Myers 1991; Brooks et al. 2002; Cecchetti et al. 1988; Kroner and Sultan 1993; Park and Switzer 1995). It is found that the GARCH hedge ratios are superior essentially because they account for the conditional heteroskedasticity in the distribution of spot and futures returns.

Most aforementioned studies model the conditional distribution under a bivariate normality assumption. Recent studies indicate that bivariate normality fails to account for the distribution’s higher moments or for the tail dependence between spot and futures returns (Hsu et al. 2008; Lai 2012; Lee 2009; Park and Jei 2010). In this situation, standard GARCH estimators attach too much weight to extreme observations, leading to the estimation of the optimal hedge ratio being generally inefficient (Harris and Shen 2003).

In addition, standard GARCH models use low frequency (LF) returns to determine current covariance levels. Squared (or cross-product) returns, however, offer limited information regarding the estimation of return covariation, compared with realized (co-)variances computed using high-frequency (HF) data (Andersen and Bollerslev 1998; Andersen et al. 2001; Barndorff-Nielsen and Shephard 2004). Based on this, high-frequency-based volatility models have been developed recently (Hansen et al. 2012, 2014; Noureldin et al. 2012; Shephard and Sheppard 2010). It is shown that GARCH models using HF data can more quickly adjust to changes in volatility than can standard GARCH models.

This study improves the effectiveness of dynamic hedging by specifying the joint distribution using the features of flexible density function and shorter response time, rendering it more flexible and effective than the prevailing methods of modeling the dynamic structures are. On the basis of conditional Sklar’s theorem, Patton (2006) demonstrated a conditional joint distribution can be decomposed into its conditional marginal distributions and its conditional copula function. This provides full flexibility in specifying the conditional joint distribution, which is thus more realistic in capturing many of the observed features in spot and futures returns that may affect the hedge ratio estimation. Moreover, copula forecasts using HF data can more swiftly adapt to changing markets than forecasts using only daily data can (Salvatierra and Patton 2015).

Herein, the performance of the proposed copula-based GARCH model with HF data (copula-GARCH-X) is compared with the competing models in two respects: First, in terms of goodness-of-fit, the estimation results indicate that the improvement caused by switching from the conventional models to the proposed copula-GARCH-X model can be substantial for the equity index markets. Second, when investigating out-of-sample performance, the forecasting results illustrate that the copula-GARCH-X model can substantially reduce the (estimated) conditional hedged portfolio variance, translating into pronounced expected utility gains particular for hedgers with higher risk aversion attitudes.

The remainder of this paper is organized as follows: the second section presents the copula-GARCH-X model for hedge ratio estimation, the third section provides the data and preliminary analysis results, the forth section describes the conditional hedging performance measure, the fifth section describes the model’s forecasting performance, and the final section concludes.

2 Methodology

Consider a hedger who desires an underlying spot asset and seeks to hedge the price risk of the asset by shorting its own futures contracts. The optimal hedge ratio given by

$$ \delta_{t}^{*} = \frac{{\sigma_{sf,t} }}{{\sigma_{f,t}^{2} }} = \rho_{sf,t} \frac{{\sigma_{s,t} }}{{\sigma_{f,t} }} $$

(1)

determines the optimal futures position per unit underlying spot asset at time $t$, where $\sigma_{sf,t}$ and $\rho_{sf,t}$ denote the conditional covariance and correlation of spot and futures returns, and $\sigma_{s,t}$ and $\sigma_{f,t}$ denote the conditional spot and futures volatility, respectively.¹ The empirical estimation of the hedge ratio clearly depends on how the joint distribution of spot and futures returns is modeled and thus how the conditional covariance matrix of assets is estimated.

Denote ${\mathbf{r}}_{t} \equiv [r_{s,t} ,r_{f,t} ]^{\prime}$ as a $2 \times 1$ vector consisting of spot and futures returns at time $t$. Let ${\mathbf{F}}_{t} :{\mathbb{R}}^{2} \to [0,1]$ be the conditional distribution of ${\mathbf{r}}_{t}|{\mathcal{F}}_{t - 1}$, where ${\mathcal{F}}_{t - 1}$ denotes some information set at time $t - 1$. The conditional Sklar’s theorem of Patton (2006) suggests that the conditional distribution can be split into conditional marginal distributions $F_{i,t} :{\mathbb{R}} \to [0,1]$, and a unique conditional copula ${\mathbf{C}}_{t} :[0,1]^{2} \to [0,1]$ such that

$$ {\mathbf{r}}_{t} |{\mathcal{F}}_{t - 1} \sim{\mathbf{F}}_{t} (r_{s,t} ,r_{f,t} ) = {\mathbf{C}}_{t} (F_{s,t} (r_{s,t} ),F_{f,t} (r_{f,t} )) $$

(2)

Write $v_{i,t} \equiv F_{i,t} (r_{i,t} )$ and ${\mathbf{v}}_{t} \equiv [v_{s,t} ,v_{f,t} ]^{\prime }$. The conditional copula of ${\mathbf{r}}_{t}$ can be expressed as the conditional joint distribution of the probability integral transforms (PIT) of the random variables:

$$ {\mathbf{C}}_{t} (v_{s,t} ,v_{f,t} ) = {\mathbf{F}}_{t} \left( {F_{s,t}^{ - 1} (v_{s,t} ),F_{f,t}^{ - 1} (v_{f,t} )} \right),\quad \forall (v_{s,t} ,v_{f,t} ) \in [0,1]^{2} $$

(3)

where $F_{i,t}^{ - 1}$ is the quantile function of $F_{i,t}$. This copula contains the information regarding the dependence structure of spot and futures returns through the dependence parameter implied by a copula function.

The most prominent hedging model is provided by Kroner and Sultan (1993), who employ the following bivariate error correction model with a constant conditional correlation GARCH (CCC-GARCH) structure for describing the conditional distribution of spot and futures returns:

$$ r_{i,t} = \alpha_{0i} + \alpha_{1i} \left( {s_{t - 1} - \lambda f_{t - 1} } \right) + u_{i,t} ,\quad i = s,f $$

(4)

$$ {\mathbf{u}}_{t} = \left[ {\begin{array}{*{20}c} {u_{s,t} } \\ {u_{f,t} } \\ \end{array} } \right]|{\mathcal{F}}_{t - 1} \sim N({\mathbf{0}},{\mathbf{H}}_{t} ) $$

(5)

$$ {\mathbf{H}}_{t} = D_{t} RD_{t} $$

(6)

$$ h_{i,t} = \beta_{0i} + \beta_{1i} h_{i,t - 1} + \beta_{2i} u_{i,t - 1}^{2} $$

(7)

where $s_{t - 1} - \lambda f_{t - 1}$ denotes the error-correction term for modeling the long-run relationship between spot and futures prices, ${\mathbf{u}}_{t}$ denotes the return innovation vector, ${\mathbf{H}}_{t}$ denotes a conditional covariance matrix, $D_{t} = {\text{diag}}(h_{s,t}^{1/2} ,h_{f,t}^{1/2} )$ denotes a diagonal matrix containing the information of conditional standard deviations of spot and futures returns, and $R = (\rho_{sf} )$ denotes a constant correlation matrix.² Note that this CCC-GARCH model corresponds to the case of conditional bivariate normality, where the marginal distributions (Eq. 2) and the conditional copula (Eq. 3) are both normal (Jondeau and Rockinger 2006; Patton 2006).

The normality of the innovations for financial asset returns is usually rejected on the basis of daily or weekly data, illustrating that the bivariate normality seems too restrictive to jointly model the spot and futures distribution. To relax this restriction, Hsu et al. (2008) extended the CCC-GARCH model by suggesting a copula-GARCH approach for specifying the joint distribution. To illustrate, denote $m_{i,t} \equiv \alpha_{0i} + \alpha_{1i} (s_{t - 1} - \lambda f_{t - 1} )$, the conditional mean equation, and $\varepsilon_{i,t} \equiv h_{i,t}^{ - 1/2} (r_{i,t} - m_{i,t} )$, the standardized error, satisfying $E[\varepsilon_{i,t} ] = 0$ and $\text{var} [\varepsilon_{i,t} ] = 1$, for $i = s,f$. Assume the standardized errors $\varepsilon_{i,t}$ follow the skew-t distribution of Hansen (1994) given as follows:

$$ f_{{\varepsilon_{i} }} (\varepsilon_{i,t} ;\phi ,\eta ) = \left\{ {\begin{array}{*{20}c} {bc\left( {1 + \tfrac{1}{\eta - 2}\left( {\tfrac{{b\varepsilon_{t} + a}}{1 - \phi }} \right)^{2} } \right)^{{ - {{(\eta + 1)} \mathord{\left/ {\vphantom {{(\eta + 1)} 2}} \right. \kern-0pt} 2}}} ,\quad \varepsilon_{i,t} < - \tfrac{a}{b}} \\ {bc\left( {1 + \tfrac{1}{\eta - 2}\left( {\tfrac{{b\varepsilon_{t} + a}}{1 + \phi }} \right)^{2} } \right)^{{ - {{(\eta + 1)} \mathord{\left/ {\vphantom {{(\eta + 1)} 2}} \right. \kern-0pt} 2}}} ,\quad \varepsilon_{i,t} \ge - \tfrac{a}{b}} \\ \end{array} } \right. $$

(8)

where

$$ a \equiv 4\phi c\frac{\eta - 2}{\eta - 1},\quad b \equiv \sqrt {1 + 3\phi^{2} - a^{2} } ,\quad c \equiv \frac{{\Gamma \left( {\tfrac{\eta + 1}{2}} \right)}}{{\sqrt {\pi \left( {\eta - 2} \right)} \Gamma \left( {\tfrac{\eta }{2}} \right)}} $$

$\phi \in ( - 1,1)$ denotes the skewness parameter and $\eta \in (2,\infty )$ denotes the degree of freedom parameter; subsequently the marginal distributions can be obtained as follows:

$$ F_{i,t} (r_{i,t} ) = F_{{\varepsilon_{i} ,t}} \left( {h_{i,t}^{ - 1/2} (r_{i,t} - m_{i,t} )} \right),\quad i = s,f $$

(9)

The rationality of using this skew-t density function is that the standardized errors filtered using a GARCH model may still be asymmetric and/or leptokurtic, and thus some non-normal distributions must be considered for the PIT usage.

To capture the dependence structure between spot and futures returns, firstly consider the normal-copula

$$ {\mathbf{C}}_{t}^{N} \left( {v_{s,t} ,v_{f,t} ;\rho_{sf,t} } \right) = \Phi_{{\rho_{t} }} \left( {\Phi^{ - 1} (v_{s,t} ),\Phi^{ - 1} (v_{f,t} )} \right) $$

(10)

and the t-copula

$$ {\mathbf{C}}_{t}^{T} \left( {v_{s,t} ,v_{f,t} ;\rho_{sf,t} ,\nu } \right) = T_{{\rho_{t} ,\nu }} \left( {T_{\nu }^{ - 1} (v_{s,t} ),T_{\nu }^{ - 1} (v_{f,t} )} \right) $$

(11)

where $\Phi^{ - 1}$ and $T_{\nu }^{ - 1}$ represent the quantile functions of a standardized univariate normal distribution and a univariate Student’s t distribution, respectively, and $\nu$ denotes the degree of freedom parameter. The dependence parameter $\rho_{sf,t}$ captures the time-varying dependence relation implied by the copulas, dynamics of which can be specified, as suggested by Tse and Tsui (2002):

$$ \rho_{sf,t} = (1 - \kappa_{1} - \kappa_{2} )\bar{\rho }_{sf} + \kappa_{1} \rho_{sf,t - 1} + \kappa_{2} \frac{{\sum\nolimits_{j = 1}^{2} {u_{s,t - j} u_{f,t - j} } }}{{\sqrt {\left( {\sum\nolimits_{j = 1}^{2} {u_{s,t - j}^{2} } } \right)\left( {\sum\nolimits_{j = 1}^{2} {u_{f,t - j}^{2} } } \right)} }} $$

(12)

where $\kappa_{1}$ and $\kappa_{2}$ are nonnegative with $\kappa_{1} + \kappa_{2} \le 1$. Both copulas have U-shape tail dependence, implying that the comovements of spot and futures strength in turbulent periods.³ The difference between the copulas is that the t-copula function captures both the linear correlation and tail dependence between spot and futures returns, whereas the normal-copula having zero tail dependence captures only the linear correlation. The second copulas that will be considered are the Gumbel copula

$$ {\mathbf{C}}_{t}^{G} \left( {v_{s,t} ,v_{f,t} ;\vartheta_{t}^{G} } \right) = \exp \left\{ { - \left( {( - \ln v_{s,t} )^{{\vartheta_{t}^{G} }} + ( - \ln v_{f,t} )^{{\vartheta_{t}^{G} }} } \right)^{{1/\vartheta_{t}^{G} }} } \right\} $$

(13)

and the Clayton copula

$$ {\mathbf{C}}_{t}^{C} \left( {v_{s,t} ,v_{f,t} ;\vartheta_{t}^{C} } \right) = \left( {v_{s,t}^{{ - \vartheta_{t}^{C} }} + v_{f,t}^{{ - \vartheta_{t}^{C} }} - 1} \right)^{{ - 1/\vartheta_{t}^{C} }} $$

(14)

where the associated dependence parameters are defined as $\vartheta_{t}^{G} = 1/(1 - \tau_{t} )$ and $\vartheta_{t}^{C} = 2\tau_{t} /(1 - \tau_{t} )$, respectively; and, the time-varying Kendall’s tau is given by a monotone transformation, $\tau_{t} = \tfrac{2}{\pi }\arcsin (\rho_{t} )$ (see, e.g., Chen 2007; Hsu et al. 2008; Lee 2009). The difference between the asymmetric copulas is that a Gumbel (Clayton) copula implies a higher dependence at the right (left) tails of the marginal distributions. Hsu et al. (2008) reported that for the case of a direct hedge, a model based on Gaussian copula density outperforms those based on Gumbel and Clayton copula densities in terms of variance reduction size.

The copula-GARCH model suggested by Hsu et al. (2008) is specified conditioning on historical return information ${\mathcal{F}}_{t - 1}^{\text{LF}}$. Alternatively, this paper specifies a copula-GARCH-X model conditioning on HF information set ${\mathcal{F}}_{t - 1}^{\text{HF}}$ for the bivariate futures hedge.⁴

Assume that $2 \times 1$ return vector ${\mathbf{r}}_{t}$ conditioning on ${\mathcal{F}}_{t - 1}^{\text{HF}}$ follows the joint distribution

$$ {\mathbf{r}}_{t} |{\mathcal{F}}_{t - 1}^{\text{HF}} \sim{\mathbf{F}}_{t} \left( {r_{s,t} ,r_{f,t} } \right) = {\mathbf{C}}_{t} \left( {v_{s,t} ,v_{f,t} } \right) $$

(15)

similar to that of Eqs. (2) and (3) and that it has marginal distributions similar to those of Eqs. (8) and (9). The copula function ${\mathbf{C}}_{t} ( \cdot )$ may be interpreted as the copulas provided in Eqs. (10), (11), (13) and (14), respectively. After specifying the mean equations, marginal distributions, and copulas, the remaining step for extending the conventional copula-GARCH model is to specify the dynamic process of conditional variances and dependence by encompassing realized variance (RV) and realized correlation (RCorr) measures, respectively, into the second-order moment equations, given as follows:

$$ h_{i,t} = \beta_{0i} + \beta_{1i} h_{i,t - 1} + \beta_{2i} {\text{RV}}_{i,t - 1} ,\quad i = s,f $$

(16)

$$ \rho_{sf,t} = (1 - \kappa_{1} - \kappa_{2} )\bar{\rho }_{sf} + \kappa_{1} \rho_{sf,t - 1} + \kappa_{2} {\text{RCorr}}_{sf,t - 1} $$

(17)

Given the aforementioned specification, the hedge ratio in Eq. (1) is estimated through one-step-ahead forecasts of the conditional variances that are obtained from the univariate variance equations and the (transformed) dependence parameters obtained from the conditional copulas.

The density function equivalent of Eq. (2) provides benefits in estimating conditional copula-GARCH models (Patton 2006). This paper estimates the unknown parameters for the copula-GARCH-X models follows a three-stage method such as that of Chen (2007), because it is difficult in practice to achieve a simultaneous estimation for large number of parameters in a model system (Hsu et al. 2008; Patton 2006).⁵ In the first stage, the conditional mean and variance equations for each asset are estimated separately by maximizing the likelihood function $L_{1i} (\alpha_{i} ,\beta_{i} ) = - \tfrac{1}{2}\ln 2\pi - \tfrac{1}{2T}\sum\nolimits_{t = 1}^{T} {\ln h_{i,t} } - \tfrac{1}{2T}\sum\nolimits_{t = 1}^{T} {h_{i,t}^{ - 1} (r_{i,t} - m_{i,t} )^{2} }$ by using the Gaussian quasi-maximum likelihood estimator. In the second stage, the skewness and degree of freedom parameters for each asset are obtained by maximizing the likelihood function $L_{2i} (\phi ,\eta |\hat{\alpha }_{i} ,\hat{\beta }_{i} ) = \tfrac{1}{T}\sum\nolimits_{t = 1}^{T} {\ln f_{{\varepsilon_{i} }} (\hat{\varepsilon }_{i,t} ;\phi ,\eta )}$ of the unconditional skew-t distribution on the basis of the parameter estimates in the first stage. After obtaining the PIT for each marginal distribution, in the third stage, the copula parameters are then obtained by maximizing the copula likelihood function $L_{3i} (\rho ,\nu |\hat{\theta }) = \tfrac{1}{T}\sum\nolimits_{t = 1}^{T} {\ln c_{t} (\hat{v}_{t} ;\rho ,\nu )}$, where $\theta \equiv (\alpha_{i} ,\beta_{i} ,\phi ,\eta )$, $v_{t} \equiv (v_{s,t} ,v_{f,t} )$, and $c_{t} (v_{s,t} ,v_{f,t} ) \equiv \partial^{2} {\mathbf{C}}_{t} (v_{s,t} ,v_{f,t} )/\partial v_{s,t} ,\partial v_{f,t}$.

3 Data and preliminary analysis

This paper investigates the performance of alternative hedge ratio estimates by using data on S&P 500 e-mini futures (symbol ES) with their underlying S&P 500 equity index (symbol SP), and the correlated Dow index (symbol DJ). The HF prices for the assets are obtained from Tick Data, Inc., spanning the period of July 1, 2003 to June 30, 2015. The filtered prices are used to construct daily returns and realized volatility measures.⁶ Daily returns are calculated as the logarithmic difference between the last and first prices of a day, illustrating that this paper focuses on modeling the variation of daily open-to-close returns.⁷ For daily realized volatility measures, the multivariate realized kernel estimator is adopted with the use of 1-min returns and the Parzen kernel function.⁸ The single bandwidth parameter is selected each day on the basis of the procedure reported in Barndorff-Nielsen et al. (2011). For the sample period, the mean (standard deviation) of the bandwidth parameters for the SP–ES and DJ–ES assets is approximately 15.03 (1.47) and 15.13 (1.49), respectively.

Panels A and B of Table 1 present the descriptive statistics of daily open-to-close returns and realized volatility measures, respectively. The daily returns are skewed with excess kurtosis and are supported by the Jarque–Bera statistics. In other words, the (unconditional) univariate distribution of spot/futures is asymmetric and fat-tailed. In addition, the volatility/correlation of returns differs in terms of the estimation using LF data (Panel A) relative to that using HF data (Panel B). Because squared (cross-product) returns are a rather noisy proxy for the true conditional (co)variance, a superior better realized (co)variance estimator creates a more precise proxy in measuring the return (co)variation (Andersen and Bollerslev 1998; Andersen et al. 2001; Barndorff-Nielsen and Shephard 2004). Overall, the preliminary analysis might provide an initial insight into the rationality of including precise realized volatility/correlation measures into conditional copulas for modeling the dynamics of LF returns (Salvatierra and Patton 2015).

Table 1 Summary statistics of daily returns and realized measures of volatility

Tables 2 and 3 present the estimation results of the copula-GARCH models for the SP–ES and DJ–ES assets, respectively, using in-sample data from July 1, 2003, to June 30, 2011. First, focusing on the parameter estimates employing LF data, Panel A of Tables 2 and 3 presents the parameter estimates for the conditional mean and variance equations. As shown in Table 2, the coefficient on the error-correction term for the spot and futures is negative and positive, respectively. In other words, in response to a positive deviation at time $t - 1$ (i.e., $s_{t - 1} > f_{t - 1}$), the SP price in the subsequent period declines, whereas the ES price increases to restore the long-term relationship.⁹ For the conditional variance estimates, the results indicate that the GARCH coefficients are all greater than 0.90 with significant coefficients on the ARCH term, clearly indicating that the conditional heteroskedasticity is revealed in the data.¹⁰ In Panel B of Tables 2 and 3, we present the parameter estimates on the standardized residuals using the unconditional skew-t distribution. The results indicate that the skewness parameters are all negative and the degree of freedom parameters are all positive, showing that the standardized residuals remain asymmetric and leptokurtic even after considering the GARCH effects. To examine whether the specification of the marginal distribution is adequate, the Kolmogorov–Smirnov (KS) statistics with p values are reported to check whether the conditional PIT data is uniformly distributed. Because the statistics are all insignificant at a 1% level, showing the skew-t transformation on the standardized residuals should be adequate for all assets examined.

Table 2 Estimation of the copula-GARCH models for the SP–ES assets

Table 3 Estimation of the copula-GARCH models for the DJ–ES assets

Subsequently, we focus on estimations by using HF data (Tables 2, 3); Panel A shows that the estimates employing HF data can differ from those employing LF data. The coefficients on the error-correction terms for SP–ES are both positive, showing that in response to a positive deviation, the spot price in the subsequent period raises, whereas the futures price raises more to restore the long-term relationship. The GARCH coefficients employing HF data are approximately 0.70–0.75, whereas the corresponding estimates employing LF data are approximately 0.90. Obviously, the decrease in the GARCH weight translates into the increase in the ARCH weight. The higher weights on the ARCH term given HF data against LF data clearly illustrate that HF data are more informative in forecasting future volatility (Hansen et al. 2012; Shephard and Sheppard 2010). In Panel B, the estimates for the marginal distribution using HF data indicate that the standardized residuals remain skewed and leptokurtic, implying that employing the skewed-t density for modeling purpose is crucial.

After obtaining the PIT data, Panel C of Tables 2 and 3 show the parameter estimates of the dynamic copulas. In measuring the degree of persistence in conditional dependence process, the estimates obtained from the HF data can differ from the corresponding estimates obtained from the LF data. Considering SP–ES with the normal-copula as an example, the persistence in conditional dependence employing LF and HF data is 0.0138 and 0.9921, respectively, showing that the estimates obtained from LF and HF data support the constant and time-varying conditional correlation hypothesis, respectively. On comparing the estimates employing HF data, the sample mean (standard deviation) of the conditional correlations interpreted by the normal- and t-copulas is approximately 0.9026 (0.0064) and 0.9083 (0.0077), respectively, showing that the estimates that further consider the tail dependence can be higher in both level and variation.¹¹ Regarding to the dynamics of Kendall’s tau generated by the asymmetric copulas, the sample mean (standard deviation) of the estimates interpreted by the Gumbel- and Clayton-copula is approximately 0.6950 (0.0132) and 0.6439 (0.0120), respectively, showing there are substantial differences in determining the dependence level and variation.

In terms of model fitting, the log-likelihood (LogL) functions indicate that switching from LF to HF data can substantially increase the total LogL scores. To test the significance of the improvement, the non-nested likelihood ratio test of Vuong (1989) is performed. All the statistics exceed 1.96 (5% significance level), confirming the usefulness of HF data in the modeling.

4 Measuring conditional hedging performance

Recall that the hedge ratio in Eq. (1) is derived by minimizing the conditional variance of hedged portfolio return,

$$ {\mathbf{w}}_{t}^{*} = \mathop {\arg \hbox{min} }\limits_{{{\mathbf{w}}_{t} }} \;{\mathbf{w}}_{t} \Sigma_{t} {\mathbf{w}}_{t}^{\prime } $$

(18)

where ${\mathbf{w}}_{t}^{*} \equiv [1, - \delta_{t}^{*} ]$, comprising the weights on spot and futures assets, represents the weight vector constructed from the true conditional covariance matrix of returns $\Sigma_{t} \equiv \text{cov} [{\mathbf{r}}_{t} |{\mathcal{F}}_{t - 1} ]$. To compare the performance of two competing hedged portfolios with the corresponding weight ${\tilde{\mathbf{w}}}_{t}$, constructed in terms of forecasts of the conditional covariance matrix, ${\tilde{\mathbf{H}}}_{t}$, the result of Patton and Sheppard (2009) given by

$$ {\mathbf{w}}_{t}^{*} \Sigma_{t} {\mathbf{w}}_{t}^{\prime *} < {\tilde{\mathbf{w}}}_{t} \Sigma_{t} {\tilde{\mathbf{w}}}_{t}^{\prime } $$

(19)

can be applied, showing that the conditional variance of the hedged portfolio that is based on the weight ${\tilde{\mathbf{w}}}_{t}$ estimated by any model’s forecast must be larger than that based on the true weight ${\mathbf{w}}_{t}^{*}$ constructed from the true covariance matrix. Consequently, the superior hedged portfolio approaches the lower bound when the estimated weight ${\tilde{\mathbf{w}}}_{t}$ approaches its true counterpart, ${\mathbf{w}}_{t}^{*}$.

To test the significance of switching from the benchmark model to the alternative model on the basis of the null hypothesis,

$$ H_{0} :E\left[ {L\left( {\Sigma_{t} ;{\tilde{\mathbf{w}}}_{t}^{\text{b}} } \right)} \right] = E\left[ {L\left( {\Sigma_{t} ;{\tilde{\mathbf{w}}}_{t}^{\text{a}} } \right)} \right] $$

(20)

a Diebold–Mariano and West (henceforth DMW) forecast comparison test, given by Diebold and Mariano (1995) and West (1996), is adopted, where $L(\Sigma_{t} ;{\tilde{\mathbf{w}}}_{t} ) \equiv {\tilde{\mathbf{w}}}_{t} \Sigma_{t} {\tilde{\mathbf{w}}}_{t}^{\prime }$ denotes the loss function defined over the true conditional covariance matrix $\Sigma_{t}$, and ${\tilde{\mathbf{w}}}_{t}^{\text{b}}$ and ${\tilde{\mathbf{w}}}_{t}^{\text{a}}$ denote the weight vectors constructed from the benchmark model and the alternative model, respectively. Define

$$ d_{t} \equiv \;{\tilde{\mathbf{w}}}_{t}^{\text{b}} \Sigma_{t} {\tilde{\mathbf{w}}}_{t}^{{\prime {\text{b}}}} - {\tilde{\mathbf{w}}}_{t}^{\text{a}} \Sigma_{t} {\tilde{\mathbf{w}}}_{t}^{{\prime {\text{a}}}} ; $$

(21)

then, the DMW test statistic is computed using

$$ {\text{DMW}} = \frac{{\sqrt T \bar{d}_{T} }}{{\sqrt {{\text{avar}}\left[ {\sqrt T \bar{d}_{T} } \right]} }} $$

(22)

where $\bar{d}_{T} \equiv T^{ - 1} \sum\nolimits_{t = 1}^{T} {d_{t} }$, and ${\text{avar}}\left[ {\sqrt T \bar{d}_{T} } \right]$ represents the Newey–West estimator of the asymptotic variance of the re-scaled average $\sqrt T \bar{d}_{T}$. Under the null hypothesis, the DMW statistic is asymptotically normally distributed, and the hedged portfolio constructed using the alternative model is superior to that constructed using the benchmark model if the mean of $d_{t}$ is significantly positive.

In addition to statistical evaluation, hedgers may be concerned regarding the economic benefits of a copula hedge using HF returns. Kroner and Sultan (1993) derived the optimal hedge ratio by maximizing the expected utility function,

$$ E_{t} U(r_{p,t + 1} ) = E_{t} (r_{p,t + 1} ) - \gamma \text{var}_{t} (r_{p,t + 1} ) $$

(23)

where $\gamma > 0$ measures the degree of risk aversion of a hedger and risk is measured using conditional variances.¹² To compare the performance economically across different hedged portfolios, the economic value (EV) approach of Fleming et al. (2001) is considered for evaluating the economic benefits of switching from the benchmark model to the alternative models, where the EV can be estimated by solving the following equation:

$$ \hat{E}_{n} U\left( {r_{p,t + 1}^{\text{b}} ;\gamma } \right) = \hat{E}_{n} U\left( {r_{p,t + 1}^{\text{a}} - {\text{EV;}}\gamma } \right) $$

(24)

where $\hat{E}_{n}$ denotes the sample average operator, and $r_{p,t + 1}^{\text{b}}$ and $r_{p,t + 1}^{\text{a}}$ represent the hedged portfolio returns obtained by the benchmark and alternative models, respectively. In this paper, EV is represented in annualized basis points, with the levels of risk aversion equals to 1, 4, and 20 to assess the performance gains across hedgers (Kroner and Sultan 1993; Lai 2016).¹³ A positive EV indicates that the alternative model outperforms the benchmark model, which can aid hedgers when they consider switching from the benchmark model to the alternative model.

5 Empirical results

The third section shows that HF data can substantially improve the goodness-of-fit of the dynamic copulas. Because hedgers are more concerned regarding the model’s performance in the future, but not in the past, whether the HF data might provide valuable information regarding hedge ratio prediction must be judged by their empirical performances. Hence, the model’s parameters are re-estimated each day by using a rolling-over approach with a fixed in-sample size.¹⁴ The period from July 1, 2011, to June 30, 2015, is regarded as the out-of-sample data. The hedged portfolios are recursively constructed each day by using the hedge ratio estimates obtained from one-step-ahead forecasts of conditional variances and correlations predicted by the model.

The out-of-sample conditional hedging performance of the hedged portfolios is measured using the loss function $L(\Sigma_{t} ;{\tilde{\mathbf{w}}}_{t} ) \equiv {\tilde{\mathbf{w}}}_{t} \Sigma_{t} {\tilde{\mathbf{w}}}_{t}^{\prime }$. Because the true conditional covariance matrix $\Sigma_{t}$ is unobservable, the usual realized covariance matrix estimator $\hat{\Sigma }_{t}^{(m)} = \sum\nolimits_{i = 1}^{m} {r_{i,t} r_{i,t}^{\prime } }$ computed using uniformly spaced vector of returns $r_{i,t}$ with the corresponding sampling frequency (e.g., 5-, 15-, and 30-min) is employed for calculations. According to Patton (2011), using precise RV, rather than squared return, in the construction of volatility proxy can be more efficient when performing the comparison test; and the degree of distortion on measuring the conditional expected loss function should be eliminated when using 5-min returns.

The results are provided in Table 4; the CCC-GARCH model of Kroner and Sultan (1993) is considered the benchmark model in the comparison. The percentage risk reduction size of switching from the benchmark model to the normal-copula-GARCH-X (normal-copula-GARCH) ranges from 8.13% (1.71%) to 11.24% (3.00%) and from 3.30% (1.78%) to 5.21% (2.75%) for the SP–ES and DJ–ES, respectively. Alternatively, if hedgers adopt a t-copula density, the associated risk reduction size ranges from 8.10% (1.34%) to 11.10% (2.50%) and from 3.36% (1.66%) to 5.24% (2.58%) for the SP–ES and DJ–ES, respectively. When considering the asymmetric copulas, the associated percentage risk reduction size can range from 7.77% (0.95%) to 12.05% (6.28%) for the SP–ES, and can range from 1.31% (0.98%) to 5.09% (3.23%) for the DJ–ES. To test whether the conditional variances constructed from the alternative models are statistically different from the benchmark model, the DMW test using Eq. (22) is performed. All statistics are positive and statistically significant at the 5% level (except Clayton-copula in DJ–ES), indicating the importance of considering a flexible copula-GARCH model for hedge ratio estimation. Figure 1 plots optimally performing hedge ratios for the assets, showing that the estimates can depart from those obtained from the benchmark CCC-GARCH model during some periods.

Table 4 Out-of-sample hedging performance comparison

Fig. 1

This figure compares the optimally performing hedge ratios obtained from the copula-GARCH-X model with those obtained from the benchmark CCC-GARCH model

To further investigate the performance of dynamic copulas switching from LF to HF data, the DMW tests are applied again. On the basis of normal (t) copulas, the DMW statistics using 5-, 15-, and 30-min volatility proxies are 2.60 (2.60), 2.46 (2.45), and 2.63 (2.63) for the SP–ES, and 1.68 (1.74), 2.23 (2.28), and 2.03 (2.13) for the DJ–ES. On the basis of Gumbel (Clayton) copulas, the associated DMW statistics are 2.59 (2.62), 2.57 (2.69), and 2.71 (2.86) for the SP–ES, and 1.47 (1.25), 2.09 (1.21), and 1.53 (0.45) for the DJ–ES. Rejection of the null hypothesis shows that the hedged portfolios constructed from the copula-GARCH-X model are superior to those constructed from the copula-GARCH model, in terms of their estimated conditional hedged portfolio variances.¹⁵ On comparing the performance difference between normal- and t-copula functions employing HF data, the associated DMW statistics are − 6.54 (1.30), − 4.31 (2.25), and − 1.19 (1.99) for the SP–ES (DJ–ES) assets, respectively. The DJ–ES case illustrates that permitting tail dependence when modeling dynamic copulas might further reduce conditional variance in hedged portfolios. The SP–ES case further illustrates that permitting asymmetric tail dependence when modeling dynamic copulas improves the out-of-sample hedging performance. Overall, the comparisons using 5-min realized covariances conclude that the Clayton (t) copula provide the best performance for the SP–ES (DJ–ES) hedging.

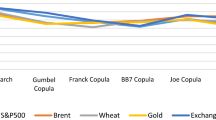
In terms of economic benefits, Table 5 presents the switching fees for the direct and cross hedges. Evidently, the EV can further increase as the level of risk aversion raises. For the case of a higher risk aversion (e.g., 20), the estimated EV employing HF data for the SP–ES (DJ–ES) ranges from 119.45 (22.18) to 216.72 (89.21) basis points per annum, compared with the benchmark CCC-GARCH model. Alternatively, the associated EV employing LF data ranges from 14.62 (16.63) to 112.90 (54.94) basis points per annum. This illustrates that switching from LF- to HF-based dynamic copulas for the SP–ES (DJ–ES) assets can engender extra benefits ranging from 64.51 (5.55) to 170.86 (45.36) basis points per annum. Figure 2 compares the hedge ratios estimated using LF- and HF-data, also showing substantial differences in the estimates.

Table 5 Basis point fees for switching from CCC-GARCH to the copula-GARCH models

Fig. 2

This figure compares the hedge ratios obtained from the copula-GARCH-X model with those obtained from the copula-GARCH model

The above comparison primarily focuses on a period of stable and upward trending markets. Since the sample data covers the period of 2008 subprime crisis, this allows to investigate the model’s performance when the market is in turmoil. This is especially important when effective hedging tools are needed the most. To do this, the sample period from July 2003 to June 2007 (1007 trading days) is reserved for in-sample estimation of the model; the sample period from July 2007 to April 2009 (462 trading days) is regarded as the crisis period for out-of-sample analysis. Table 6 reports the percentage risk reduction size of the model for the crisis period, showing that the asymmetric Clayton (symmetric t) copula specification with HF data provides the best performance for the SP–ES (DJ–ES) hedges. Table 7 further reports the basis point fees of switching from the benchmark CCC-GARCH model to the copula-GARCH models. Compared with those reported in Table 5, it is found that the switching fees of the proposed copula-GARCH-X model over the CCC-GARCH model can enlarge when the market is in turmoil. For the case of a higher risk aversion, the estimated EV employing HF data with Clayton (t) copula for the SP–ES (DJ–ES) ranges from 260.57 (145.15) to 352.80 (199.08) basis points per annum. Meanwhile, the associated EV employing LF data ranges from 180.94 (36.79) to 216.72 (71.57) basis points per annum. This illustrates that switching from LF- to HF-based dynamic Clayton (t) copulas for the SP–ES (DJ–ES) assets can engender extra benefits ranging from 72.57 (92.73) to 136.08 (127.51) basis points per annum for the crisis period. Overall, the finding of this paper offers an economic inference that supports the copula-GARCH-X model more capably than can the CCC-GARCH and copula-GARCH models for establishing optimal hedging strategies.

Table 6 Hedging performance comparison for the crisis period

Table 7 Basis point fees for the crisis period

6 Conclusions

In optimal futures hedging, the task of modeling and forecasting the joint distribution of spot and futures returns is a critical issue that has attracted the interest of academic researchers and practical investors. This paper extends the conventional hedging models by augmenting the copula-GARCH model with realized measures of volatility and covolatility for effectively managing the risk exposure of portfolios because the hedging decisions that are based on the estimated hedge ratio can not only be more realistic in capturing much of the observed behavior in spot and futures returns but can also efficiently exploit the information from HF data. Applying the model to equity index data shows that including HF data for dynamic copula-GARCH modeling can substantially improve goodness-of-fit of spot and futures distribution; this finding is robust across the copula functions and markets that are considered.

Furthermore, we examine whether HF data regarding the modeling can produce statistical and economic gains for hedgers from dynamic hedging strategies. In particular, the out-of-sample comparisons are conducted on the basis of conditionally unbiased volatility proxies. The results reveal that the hedged portfolios constructed from the copula-GARCH-X model can be superior to those constructed from the copula-GARCH model; thus hedgers, especially those with pronounced risk aversions, would willingly pay substantial switching fees ranging from 64.51 (5.55) to 170.86 (45.36) annualized basis points to switch their strategies from the copula-GARCH model to the copula-GARCH-X model for the SP–ES (DJ–ES) assets. When the market is in turmoil, our results further indicate that switching from LF- to HF-based dynamic asymmetric Clayton (symmetric t) copulas for the SP–ES (DJ–ES) assets can engender extra benefits ranging from 72.57 (92.73) to 136.08 (127.51) basis points per annum. Our empirical evidences clearly illustrates the value of a copula-GARCH futures hedge employing HF data and provides relevant information for hedgers to exercise their strategies when achieving their trading goals. These findings have crucial financial and economic implications for risk management practice.