Natural Convection Non-Newtonian EMHD Dissipative Flow Through a Microchannel Containing a Non-Darcy Porous Medium: Homotopy Perturbation Method Study

Abstract

Non-Newtonian thermal processing in microchannel systems, is emerging as a major area of interest in modern thermal engineering. Motivated by these developments, in the current paper, a mathematical model is developed for laminar, steady state fully developed viscoelastic natural convection electro-magnetohydrodynamic (EMHD) flow in a microchannel containing a porous medium. Transverse magnetic field and axial electrical field are considered. A modified Darcy–Brinkman–Forchheimer model is deployed for porous media effects. Viscous dissipation and Joule heating effects are included. The primitive conservation equations are rendered into dimensionless coupled ordinary differential equations with associated boundary conditions. The nonlinear ordinary differential boundary value problem is then solved using He’s powerful homotopy perturbation method (HPM). Validation with the MATLAB bvp4c numerical scheme is included for Nusselt number. Graphical plots are presented for velocity, temperature and Nusselt number for the influence of emerging parameters. Increment in thermal Grashof number and electric field parameter enhance velocity. Increasing Brinkman number and magnetic interaction number boost temperatures and a weak elevation is also observed in temperatures with increment in third-grade non-Newtonian parameter and Forchheimer number. Nusselt number is also elevated with thermal Grashof number, Forchheimer number, third-grade fluid parameter, Darcy parameter, Brinkman number and magnetic number.

1 Introduction

Natural convection is a significant process that plays an important role in a wide range of industrial applications, including heat exchangers, nuclear reactor transport phenomena, electronic devices, building insulation, solar collectors. Furthermore, natural convective flows arise in geothermal energy, metallurgy, semiconductor fabrication, coating flows and chemical engineering processes. As a result, natural convection has attracted a substantial amount of attention from various researchers in recent years. In particular, many theoretical and computational studies have been reported addressing both internal and external flows. Senapti et al. [1] discussed natural convection across an annular finned horizontal cylinder using numerical simulation. Shirvan et al. [2] focused on how a wavy surface interacts with natural convection in a corrugated square cavity filled with nanofluid. Rahimi et al. [3] conducted a comprehensive review on natural convection heat transfer in a diverse range of engineering geometries. Haghighi et al. [4] investigated the natural convection from a new plate-fin-based configuration with heat sinks. Mohebbi et al. [5] studied natural convection in a nanofluid within a Γ-Shaped geometry in the presence of a rectangular hot impediment. The solutions were obtained by the use of the lattice Boltzmann method. Roy et al. [6] presented a computational analysis on the natural convection and heat transfer over an inclined plate finned channel. Natural convection with entropy generation over a multiple structured heated cylinder in the presence of non-uniform temperature along the walls were investigated by Bhowmick et al. [7]. Recently, Ding et al. [8] investigated the natural convection heat transfer for three-dimensional extrinsic finned tubes using both experimental and numerical methods. These studies have all demonstrated the significant influence of thermal buoyancy force on transport phenomena in natural convection heat transfer.

Microfluidic channels also have technical significance in various fields such as fuel cells, heat exchangers [9, 10], separation of physical particles and biomedical and biochemical processes. This is due to the higher ratio of surface to volume that exists in microfluidic channels and this feature can be used to improve heat transfer rates. The deployment of pressure gradients, electric field and /or magnetic field, porous media and other effects can all be used to efficiently mobilize fluid motion in microchannels. Electro-magnetohydrodynamics micro-pumps have been addressed [11, 12] in several pumping designs due to their potential applications in microfluidics systems. The working mechanism of electro-magnetohydrodynamic (EMHD) micropumps is based on Lorentz magnetohydrodynamic and electrical body forces generated by extrinsic imposed electric and magnetic fields between parallel plates containing electro-conductive fluids [13, 14]. Additionally heat transfer in the presence of electrical and magnetic fields is significant in a variety of applications in the metallurgical industry [15] i.e., liquid metal flows. They also arise in thermal duct process control [16], smart lubrication [17, 18], energy generators [19] and smart micropumps in biomedicine [20, 21].

Heat transfer through microchannels containing porous media also has a wide range of engineering applications, including heat pipes, thermal management in microelectronics, thermal ducts in process engineering, nuclear waste disposal and radiators [22]. Furthermore, porous media are also applicable in hydrogen storage system, membrane-based water desalination via converse osmosis, electrokinetic energy converting devices, shale reservoirs and biofilters. Microchannel systems are also useful for effective heat removal in cooling systems in aerospace electronics devices with significant small dimensions [23, 24]. Micro-radiators, which are employed in thermal control, assist in the reduction of temperature gradients and the absolute highest temperature on the surface of equipment that is subjected to a high heat flux [25]. Porous media may be simulated in a variety of ways including hierarchy models, spatially periodic models, tortuous geometric models among others. A simpler approach is to use drag force models of which the Darcy model and Darcy–Brinkman–Forhchheimer model are popular. The Darcy model is valid for low velocity transport (i. e. pore Reynolds numbers less than 10) [26]. For higher velocity flows, the Darcy–Forchheimer and Darcy–Brinkman–Forchheimer model [27] are used which include a quadratic term for the inertial drag experienced at higher Reynolds numbers. The Brinkman model also accounts for vorticity diffusion and channeling effects near the boundary [28].

Many studies have examined natural convection in porous media for both Newtonian and non-Newtonian fluids. Aksoy and Pakdemirili [29] proposed approximations for third- grade fluid flow between parallel plates with porous material. In particular, constant viscosity, Vogel's model viscosity, and Reynold's model viscosity were explored. Kairi et al. [30] investigated heat and mass transfer in a vertical cone using non-Newtonian fluid flow. They took into account the non-Darcy model with viscous dissipation implications and natural convection. Zhao et al. [31] studied unsteady natural convection with heat transmission through a porous medium saturated with Oldroyd-B fluid. The solutions were obtained using a finite difference approach with the L1-algorithm. Ahmed et al. [32] studied magnetized squeezed flow through a non-Darcy medium with joule heating and viscous dissipation implications. Dutta et al. [33] used a porous quadrantal cavity to study natural convection and entropy generation and reported a numerical result. Ewis [34] applied a novel differential transformation method to investigate magnetized non-Darcy flow using a Newtonian fluid model. Gopal et al. [35] analyzed the performance of magnetized nanofluid flow on high order chemical reactions and viscous dissipation using the Darcy–Brinkmann–Forchheimer model. Saha et al. [36] studied natural convection across a complex wavy wall reactor to a non-Darcy porous material. The combined effect of MHD, porosity, and viscous dissipation on periodic convective heat transport through a cone was addressed by Ashraf et al. [37]. This study's major contribution is composed of non-oscillating component solutions, which are then utilized to analyze periodic behavior of rate of heat transfer, shear stress, and rate of current density in the influence of viscous dissipation. Abbas et al. [38] addressed the chemical reaction with Lorentz force on fluid flow in the third grade across an exponentially stretched surface. They investigated the consequences of the modified Darcy model with mass and heat transport.

Inspection of the literature has revealed that so far, no study has addressed the simultaneous electro-magnetohydrodynamic (EMHD) dissipative natural convection in a micro-channel containing a porous medium saturated with a viscoelastic fluid. This is the focus of the present study. The Reiner-Rivlin third grade viscoelastic model is utilized for non-Newtonian effects. Transverse magnetic field and axial electrical field are considered. The Darcy–Brinkmann–Forchheimer model is deployed for porous media effects. Viscous dissipation and Joule heating effects are also included. The primitive conservation equations are rendered into dimensionless coupled ordinary differential equations with associated boundary conditions. The nonlinear ordinary differential boundary value problem is solved using He’s powerful HPM. Validation with the MATLAB bvp4c numerical scheme is included for Nusselt number. Graphical plots are presented for velocity, temperature and Nusselt number for the influence of emerging parameters including thermal Grashof number, electric field parameter, Brinkman number and magnetic parameter. The simulations are relevant to smart electromagnetic non-Newtonian micro-duct flows in nuclear engineering and EMHD micropumps in bio-chemical engineering systems [39].

2 EMHD Non-Newtonian Microchannel Flow Model

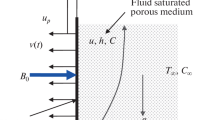
Consider the third-grade viscoelastic fluid flow under the presence of electrical and magnetic body force and natural convection, propagating through a non-Darcian porous medium in a micro-channel. The fluid is electrically conducting, incompressible and irrotational. A Cartesian coordinate system ($X^{\prime},$$Y^{\prime},$$Z^{\prime}$) is adopted. The physical model is depicted in Fig. 1 where the $X^{\prime}-$ and $Z^{\prime} -$ axes are in the plane of the plates and the $Y^{\prime} -$ axis is perpendicular to the plane of the plates. The space between the micro-parallel plates is filled with a Darcy–Brinkmann–Forchheimer porous medium. The presence of homogenous magnetic field $\overrightarrow {{\text{B}}}$ and externally imposed electric field $\overrightarrow {{\text{E}}}$ in $Y^{\prime}$ and negative $Z^{\prime}$ directions, respectively, produces a Lorentz force in $X^{\prime} -$ direction which induces the fluid motion. The length of the micro-channel along the $X^{\prime} -$ axis is represented by $\lambda$; the height is represented by $2\mathchar'26\mkern-10mu\lambda$ (usually, the height $2\mathchar'26\mkern-10mu\lambda$ is $10^{2} - 2 \times 10^{2} {{\upmu {\rm m}}}$); and width towards the $Z^{\prime} -$ axis is represented by $\omega$.

Fig. 1

Geometrical configuration of electro-magnetohydrodynamics (EMHD) third-grade fluid flow through micro-parallel plates a three-dimensional view b two-dimensional cross-section view

It is assumed that with $\omega$ and the height $2\mathchar'26\mkern-10mu\lambda$ of the channel is smaller than the length $\lambda$ of the channel i.e., [39] $\omega << \lambda$ and $2\mathchar'26\mkern-10mu\lambda << \lambda$. Hall current and magnetic induction effects are neglected. In view of the afore-mentioned assumptions, the two-dimensional rectangular flow reduces to one-dimensional fully developed steady flow through micro-parallel plates and the velocity will be independent of the $Z^{\prime} -$ axis. Therefore, the equation of continuity (mass conservation) may be defined in vectorial form as:

$$ \nabla \cdot \overrightarrow {{\text{V}}} = 0, $$

(1)

Deploying the Darcy–Brinkmann–Forchheimer model for porous media and Ohm’s law, the momentum conservation equation takes the vectorial form [37, 40]:

$$\begin{aligned} \rho \left( {\overrightarrow {{\text{V}}} \cdot \nabla \overrightarrow {{\text{V}}} + \frac{{\partial \overrightarrow {{\text{V}}} }}{{\partial t^{\prime}}}} \right) &= - \nabla \cdot p^{\prime} + \nabla \cdot \chi + \overrightarrow {{\text{J}}} {\mathbf{ \times }}\overrightarrow {{\text{B}}} - R \\ &\quad+ \rho \beta \left[ {T_{s} \left( {X^{\prime}} \right) - T\left( {X^{\prime},Y^{\prime}} \right)} \right]g,\end{aligned} $$

(2)

Here the stress tensor is denoted by $\chi$, dynamic viscosity is denoted by $\mu$, pressure is denoted by $p^{\prime}$, $R$ represents the Darcy resistance, $g$ is gravity, thermal expansion coefficient is denoted by $\beta$, $T$ is the temperature, $s$ in the subscript represents the surface (wall), density is denoted by $\rho$, time is denoted by $t^{\prime}$, magnetic field is denoted by $\overrightarrow {{\text{B}}}$. The local current density vector is denoted by $\overrightarrow {{\text{J}}}$ and is defined following [41, 42] as:

$$ \overrightarrow {{\text{J}}} = \sigma \left( {\overrightarrow {{\text{V}}} {\mathbf{ \times }}\overrightarrow {{\text{B}}} + \overrightarrow {{\text{E}}} } \right), $$

(3)

Here electrical conductivity is denoted by $\sigma$, and electrical field is denoted by $\overrightarrow {{\text{E}}}$.

The mathematical form of the third-grade viscoelastic fluid model is defined following [43]:

$$ \chi = - p{\text{I}} + \mu \hbar_{1} + \tau_{1} \hbar_{2} + \tau_{2} \hbar_{1}^{2} + \overline{\tau }_{1} \hbar_{3} + \overline{\tau }_{2} \left( {\hbar_{1} \hbar_{2} + \hbar_{2} \hbar_{1} } \right) + \overline{\tau }_{3} \left( {{\text{tr}}\hbar_{1}^{2} } \right)\hbar_{1} , $$

(4)

where $\tau_{1} ,\tau_{2} ,\overline{\tau }_{1} ,\overline{\tau }_{2} ,\overline{\tau }_{3}$ represent the material constants, and the kinematical tensors $\hbar_{1} ,\hbar_{2} ,\hbar_{3}$ are expressed as follows:

$$ \left[ \begin{aligned} & \hbar_{1} = {\rm X} + {\rm X}^{{\text{t}}} , \, {\rm X} = {\text{grad}}\overrightarrow {{\text{V}}} , \hfill \\ & \hbar_{n} = \frac{{{\text{d}}\hbar_{n - 1} }}{{{\text{d}}t^{\prime}}} + {\rm X}^{{\text{t}}} \hbar_{n - 1} + \hbar_{n - 1} {\rm X}{, }\,\,\,\,\,\,n = 2,3, \ldots \hfill \\ \end{aligned} \right. $$

(5)

The energy equation with viscous dissipation and Joule heating effects takes the form:

$$ \rho C_{h} \frac{{{\text{d}}T}}{{{\text{d}}t^{\prime}}} = \chi :{\text{grad }}\overrightarrow {{\text{V}}} + \frac{{\overrightarrow {{\text{J}}} \cdot \overrightarrow {{\text{J}}} }}{\sigma } + R\overrightarrow {{\text{V}}} - \nabla \cdot h_{f} , $$

(6)

In the above equation $C_{h}$ denotes the specific heat,$h_{f}$ represents the heat flux vector, and the symbols “$\cdot$” and “$:$” represents the single and double dot products.

For the current microchannel electromagnetohydrodynamic viscoelastic fully developed flow configuration, the velocity along $X^{\prime} -$ axis and is expressed as:

$$ \overrightarrow {{\text{V}}} = \left[ {U\left( {Y^{\prime}} \right),0,0} \right]. $$

(7)

For non-Newtonian fluid flow through porous media [44], the Darcy term will be modified with the third-grade fluid model, and the Forchheimer term be left unchanged (since it is independent of the viscosity). They are defined following [41]:

$$ R = \frac{\mu }{k}\left[ {\mu + 2\left( {\overline{\tau }_{2} + \overline{\tau }_{3} } \right)\left( {\frac{{{\text{d}}U}}{{{\text{d}}Y^{\prime}}}} \right)^{2} } \right]U + \frac{{\rho C_{F} }}{{k^{1/2} }}U^{2} , $$

(8)

where the permeability of the homogenous, isotropic porous medium is denoted by $k$, and Forchheimer coefficient is denoted by $C_{F}$.

Using Eq. (7) in the momentum conservation Eq. (2), leads to the following set of equations:

$$ \begin{aligned} \frac{{\partial p^{\prime}}}{{\partial X^{\prime}}} & = \mu \frac{{{\text{d}}^{2} U}}{{{\text{d}}Y^{{\prime}{2}} }} + 6\left( {\overline{\tau }_{2} + \overline{\tau }_{3} } \right)\frac{{{\text{d}}^{2} U}}{{{\text{d}}Y^{{\prime}{2}} }}\left( {\frac{{{\text{d}}U}}{{{\text{d}}Y^{\prime}}}} \right)^{2} - \sigma B^{2} U + \sigma BE \\ \,& \quad - \frac{1}{k}\left[ {\mu + 2\left( {\overline{\tau }_{2} + \overline{\tau }_{3} } \right)\left( {\frac{{{\text{d}}U}}{{{\text{d}}Y^{\prime}}}} \right)^{2} } \right]U \hfill \\ \,& \quad - \frac{{\rho C_{F} }}{{k^{1/2} }}U^{2} + \rho \beta \left[ {T_{s} \left( {X^{\prime}} \right) - T\left( {X^{\prime},Y^{\prime}} \right)} \right]g, \hfill \\ \end{aligned} $$

(9)

$$ \frac{{\partial p^{\prime}}}{{\partial Y^{\prime}}} = \left( {2\tau_{1} + \tau_{2} } \right)\frac{{\text{d}}}{{{\text{d}}Y^{\prime}}}\left[ {\left( {\frac{{{\text{d}}U}}{{{\text{d}}Y^{\prime}}}} \right)^{2} } \right], $$

(10)

$$ \frac{{\partial p^{\prime}}}{{\partial Z^{\prime}}} = 0. $$

(11)

It is evident from these equations that the pressure function is dependent on the $Y^{\prime} -$ coordinate. It follows that:

$$ \begin{aligned} & \mu \frac{{{\text{d}}^{2} U}}{{{\text{d}}Y^{{\prime}{2}} }} + 6\left( {\overline{\tau }_{2} + \overline{\tau }_{3} } \right)\frac{{{\text{d}}^{2} U}}{{{\text{d}}Y^{{\prime}{2}} }}\left( {\frac{{{\text{d}}U}}{{{\text{d}}Y^{\prime}}}} \right)^{2} - \sigma B^{2} U + \sigma BE \\ & \quad - \frac{1}{k}\left[ {\mu + 2\left( {\overline{\tau }_{2} + \overline{\tau }_{3} } \right)\left( {\frac{{{\text{d}}U}}{{{\text{d}}Y^{\prime}}}} \right)^{2} } \right]U \\ & \quad - \frac{{\rho C_{F} }}{{k^{1/2} }}U^{2} + \rho \beta \left[ {T_{s} \left( {X^{\prime}} \right) - T\left( {X^{\prime},Y^{\prime}} \right)} \right]g = 0, \\ \end{aligned} $$

(12)

The boundary conditions are defined as follows, in accordance with the microchannel geometry:

$$ U\left( { \pm{ \mathchar'26\mkern-10mu\lambda } } \right) = 0, $$

(13)

The energy equation for the electroconductive fluid may be written as [45]:

$$ \begin{aligned} \rho C_{h} U\frac{\partial T}{{\partial X^{\prime}}} & = k_{T} \left( {\frac{{\partial^{2} T}}{{\partial X^{{\prime}{2}} }} + \frac{{\partial^{2} T}}{{\partial Y^{{\prime}{2}} }}} \right) + \mu \left( {\frac{{{\text{d}}U}}{{{\text{d}}Y^{\prime}}}} \right)^{2} + 2\left( {\overline{\tau }_{2} + \overline{\tau }_{3} } \right)\left( {\frac{{{\text{d}}U}}{{{\text{d}}Y^{\prime}}}} \right)^{4} \\ & \quad + \sigma \left( {B^{2} U^{2} + E^{2} - 2BEU} \right)\\ &\quad + \frac{1}{k}\left[ {\mu + 2\left( {\overline{\tau }_{2} + \overline{\tau }_{3} } \right)\left( {\frac{{{\text{d}}U}}{{{\text{d}}Y^{\prime}}}} \right)^{2} } \right]U^{2} + \frac{{\rho C_{F} }}{{k^{1/2} }}U^{3} . \\ \end{aligned} $$

(14)

Here thermal conductivity of the electroconductive fluid is denoted by $k_{T}$. The Joule heating and volumetric heat generation owing to viscous dissipation are represented by the last terms in the preceding equation.

The dimensionless form of the temperature is defined as:

$$ T = \frac{{T_{s} \left( {X^{\prime}} \right) - T\left( {X^{\prime},Y^{\prime}} \right)}}{{T_{s} \left( {X^{\prime}} \right) - T_{m} \left( {X^{\prime}} \right)}}, $$

(15)

where $T_{m}$ represents the mean temperature.

The temperature profile, in the fully developed natural convection flow is solely dependent on the $Y^{\prime} -$ direction. As a result, we have the following condition:

$$ \frac{\partial }{{\partial X^{\prime}}}\left( {\frac{{T_{s} \left( {X^{\prime}} \right) - T\left( {X^{\prime},Y^{\prime}} \right)}}{{T_{s} \left( {X^{\prime}} \right) - T_{m} \left( {X^{\prime}} \right)}}} \right) = 0. $$

(16)

The following expressions for the heat flux boundary conditions are applied:

$$ \frac{\partial T}{{\partial X^{\prime}}} = \frac{{{\text{d}}T_{m} }}{{{\text{d}}X^{\prime}}} = {\text{Const}}{\text{., and }}\frac{{\partial^{2} T}}{{\partial X^{{\prime}{2}} }} = 0. $$

(17)

According to the stated assumptions, the energy Eq. (13) and the associated boundary conditions effectively assume the form:

$$ \begin{aligned} \rho C_{h} U\frac{{\partial T_{m} }}{{\partial X^{\prime}}} & = k_{T} \frac{{\partial^{2} T}}{{\partial Y^{{\prime}{2}} }} + \mu \left( {\frac{{{\text{d}}U}}{{{\text{d}}Y^{\prime}}}} \right)^{2} + 2\left( {\overline{\tau }_{2} + \overline{\tau }_{3} } \right)\left( {\frac{{{\text{d}}U}}{{{\text{d}}Y^{\prime}}}} \right)^{4} \\ & \quad + \sigma \left( {B^{2} U^{2} + E^{2} - 2BEU} \right) \\ &\quad+ \frac{1}{k}\left[ {\mu + 2\left( {\overline{\tau }_{2} + \overline{\tau }_{3} } \right)\left( {\frac{{{\text{d}}U}}{{{\text{d}}Y^{\prime}}}} \right)^{2} } \right]U^{2} + \frac{{\rho C_{F} }}{{k^{1/2} }}U^{3} . \\ \end{aligned} $$

(18)

$$ f_{h} = \left. {k_{T} \frac{\partial T}{{\partial Y^{\prime}}}} \right|_{{Y^{\prime} = \pm { \mathchar'26\mkern-10mu\lambda } }} {\text{ or }}\left. T \right|_{{_{{Y^{\prime} = \pm { \mathchar'26\mkern-10mu\lambda } }} }} = T_{s} \left( {X^{{\prime}{2}} } \right), $$

(19)

Here the heat flux is denoted by $f_{h}$(constant). Incorporating an overall energy balance into the design of an elemental control volume along the length of a duct ${\text{d}}X^{\prime}$:

$$ \begin{aligned} \rho C_{h} U_{m} { \mathchar'26\mkern-10mu\lambda } {\text{d}}T_{m} = & f_{h} {\text{d}}X^{\prime} + \sigma E^{2} { \mathchar'26\mkern-10mu\lambda } {\text{d}}X^{\prime} + \sigma \int\limits_{0}^{{ \mathchar'26\mkern-10mu\lambda } } {\left( {B^{2} U^{2} - 2EBU} \right){\text{d}}Y^{\prime}{\text{d}}X^{\prime}}\\&\quad + \mu \int\limits_{0}^{{ \mathchar'26\mkern-10mu\lambda } } {\left( {\frac{{{\text{d}}U}}{{{\text{d}}X^{\prime}}}} \right)^{2} {\text{d}}Y^{\prime}{\text{d}}X^{\prime}} \\ & \quad + 2\left( {\overline{\tau }_{2} + \overline{\tau }_{3} } \right)\int\limits_{0}^{{ \mathchar'26\mkern-10mu\lambda } } {\left( {\frac{{{\text{d}}U}}{{{\text{d}}Y^{\prime}}}} \right)^{4} {\text{d}}Y^{\prime}{\text{d}}X^{\prime}} \\&\quad+ \int\limits_{0}^{{ \mathchar'26\mkern-10mu\lambda } } {\left( {\frac{{\rho C_{F} }}{{k^{1/2} }}U^{3} + \frac{1}{k}\left[ {\mu + 2\left( {\overline{\tau }_{2} + \overline{\tau }_{3} } \right)\left( {\frac{{{\text{d}}U}}{{{\text{d}}Y^{\prime}}}} \right)^{2} } \right]U^{2} } \right){\text{d}}Y^{\prime}{\text{d}}X^{\prime}} . \\ \end{aligned} $$

(20)

The mean temperature is obtained in the following form:

$$ \frac{{{\text{d}}T_{m} }}{{{\text{d}}X^{\prime}}} = \frac{{c_{0} }}{{\rho C_{h} }} = {\text{Const}}{., } $$

(21)

Here $c_{0}$ is defined as:

$$ \begin{aligned} c_{0} = & \frac{{f_{h} }}{{c_{1} }} + \frac{{\sigma E^{2} { \mathchar'26\mkern-10mu\lambda } }}{{c_{1} }} + \frac{{\sigma B^{2} c_{2} }}{{c_{1} }} + \frac{{\mu c_{3} }}{{c_{1} }} + \frac{{2\left( {\overline{\tau }_{2} + \overline{\tau }_{3} } \right)c_{4} }}{{c_{1} }} \\ &\quad + \frac{1}{{c_{1} }}\frac{{\left[ {\mu c_{2} + 2\left( {\overline{\tau }_{2} + \overline{\tau }_{3} } \right)c_{6} } \right]}}{k} + \frac{{\rho C_{F} }}{{k^{1/2} }}c_{5} - 2EB\sigma . \\ \end{aligned} $$

(22)

The coefficients in the above Eq. (22) take the following definitions:

$$ \begin{aligned} c_{1} & = \int\limits_{0}^{{ \mathchar'26\mkern-10mu\lambda } } {U{\text{d}}Y^{\prime}} ,\,c_{2} = \int\limits_{0}^{{ \mathchar'26\mkern-10mu\lambda } } {U^{2} {\text{d}}Y^{\prime}} ,\,c_{3} = \int\limits_{0}^{{ \mathchar'26\mkern-10mu\lambda } } {\left( {\frac{{{\text{d}}U}}{{{\text{d}}Y^{\prime}}}} \right)^{2} {\text{d}}Y^{\prime}} , \\ c_{4} & = \int\limits_{0}^{{ \mathchar'26\mkern-10mu\lambda } } {\left( {\frac{{{\text{d}}U}}{{{\text{d}}Y^{\prime}}}} \right)^{4} {\text{d}}Y^{\prime},\,c_{5} = \int\limits_{0}^{{ \mathchar'26\mkern-10mu\lambda } } {U^{3} {\text{d}}Y^{\prime},\,c_{6} = \int\limits_{0}^{{ \mathchar'26\mkern-10mu\lambda } } {U^{2} \left( {\frac{{{\text{d}}U}}{{{\text{d}}Y^{\prime}}}} \right)^{2} {\text{d}}Y^{\prime}} } .} \\ \end{aligned} $$

(23)

Next, the derived equations are rendered into dimensionless form by employing the following scaling variables and non-dimensional numbers:

$$ \begin{aligned} u & = \frac{U}{{{\upsilon \mathord{\left/ {\vphantom {\upsilon { \mathchar'26\mkern-10mu\lambda } }} \right. \kern-\nulldelimiterspace} { \mathchar'26\mkern-10mu\lambda } }}},\,y = \frac{{Y^{\prime}}}{{ \mathchar'26\mkern-10mu\lambda } },\,D_{a} = \frac{{{ \mathchar'26\mkern-10mu\lambda }^{2} }}{k},D_{F} = \frac{{C_{F} { 2\mathchar'26\mkern-10mu\lambda } }}{\sqrt k },\,H_{a} = B{ 2\mathchar'26\mkern-10mu\lambda } \sqrt {\frac{\sigma }{\rho }} , \\ G_{r} & = \frac{{g\beta { 2\mathchar'26\mkern-10mu\lambda }^{3} \left( {T_{m} - T_{s} } \right)}}{{\upsilon^{2} }},\,E_{h} = \frac{{\sigma BE{ 2\mathchar'26\mkern-10mu\lambda }^{3} }}{\mu \upsilon },\,\xi = \frac{{\upsilon^{2} \left( {\overline{\tau }_{2} + \overline{\tau }_{3} } \right)}}{{\mu { 2\mathchar'26\mkern-10mu\lambda }^{4} }}, \\ B_{r} & = \frac{{\mu \upsilon^{2} }}{{{ 2\mathchar'26\mkern-10mu\lambda }^{2} k_{T} \left( {T_{m} - T_{s} } \right)}},\,\xi_{1} = \frac{{\upsilon { 2\mathchar'26\mkern-10mu\lambda } \left( {c_{0} + 2\sigma BE} \right)}}{{\left( {T_{m} - T_{s} } \right)k_{T} }},\, \xi_{2} = \frac{{\sigma { 2\mathchar'26\mkern-10mu\lambda }^{2} E^{2} }}{{\left( {T_{m} - T_{s} } \right)k_{T} }}. \\ \end{aligned} $$

(24)

Using Eqs. (15) & (24), the dimensionless form of Eqs. (12) & (14) along with their associated boundary conditions emerge as:

$$ \frac{{{\text{d}}^{2} u}}{{{\text{d}}y^{2} }} + 6\xi \left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{2} \frac{{{\text{d}}^{2} u}}{{{\text{d}}y^{2} }} - H_{a}^{2} u + E_{h} - D_{a} \left[ {1 + 2\xi \left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{2} } \right]u - D_{F} u^{2} + G_{r} T = 0, $$

(25)

$$ \begin{aligned} \frac{{{\text{d}}^{2} T}}{{{\text{d}}y^{2} }} &+ B_{r} \left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{2} + 2B_{r} \xi \left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{4} + B_{r} H_{a}^{2} u^{2} - \xi_{1} u + \xi_{2} \\ & + B_{r} D_{a} \left[ {1 + 2\xi \left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{2} } \right]u^{2} + B_{r} D_{F} u^{3} = 0, \end{aligned}$$

(26)

The boundary conditions are as follows:

$$ u\left( { \pm 1} \right) = 0, \,\,\, T\left( { \pm 1} \right) = 0, \, $$

(27)

Here kinematic viscosity is denoted by $\upsilon$, magnetic interaction number is denoted by $H_{a}$, dimensionless parameter related to electrical strength is denoted by $E_{h}$, third-grade fluid parameter is denoted by $\xi$, Darcy parameter is denoted by $D_{a}$, Forchheimer (non-Darcian porous medium) number is denoted by $D_{F}$, thermal Grashof number is denoted by $G_{r}$,$B_{r}$ represents the Brinkman number, which indicates the ratio of heat created by viscous dissipation to heat transferred by molecular conduction, the effects of heat generation owing to the interaction of magnetic and electric fields on heat conduction is denoted by $\xi_{1}$ and the ratio of Joule heating to heat conduction is represented by $\xi_{2}$. We note that $D_{a}$ is inversely proportional to permeability and has values ranging from 0 (pure fluid i. e. infinite permeability) to infinity (pure solid i.e. zero permeability). It is also noteworthy that the present non-Darcy model features modified terms also in the energy Eq. (26).

The Nusselt number provides an estimation of the convective heat transfer relative to conduction heat transfer at a boundary (microchannel plate inner surfaces) and also the temperature gradient at the wall. It is determined by the following expression:

$$ N_{u} = \frac{{D_{{ 2\mathchar'26\mkern-10mu\lambda } } h_{c} }}{{k_{T} }} = \frac{{D_{{ 2\mathchar'26\mkern-10mu\lambda } } f_{h} }}{{k_{T} \left( {T_{s} - T_{m} } \right)}}, $$

(28)

Here the convective heat transfer coefficient is denoted by $h_{c}$ and $f_{h} = \left( {T_{s} - T_{m} } \right)h_{c} .$ $D_{{ 2\mathchar'26\mkern-10mu\lambda } }$ is the hydraulic diameter and $D_{{ 2\mathchar'26\mkern-10mu\lambda } } = { 2\mathchar'26\mkern-10mu\lambda }$ is the semi-height of the microchannel. The final definition required for Nusselt number at the upper plate is obtained by using Eqs. (19) and (28), which is emerges as:

$$ N_{u} = \left. { - \frac{{{\text{d}}T}}{{{\text{d}}y}}} \right|_{y = 1} . $$

(29)

3 Solutions Using Homotopy Perturbation Method (HPM)

To obtain the solution of the resulting nonlinear differential Eqs. (25)–(26) with associated boundary conditions (27), we have used He’s HPM. This method is very accurate and exceptionally fast at converging compared with other perturbation methods [46] and uses higher order power series solutions. It has been utilized in many nonlinear non-Newtonian fluid dynamics problems including Jeffreys viscoelastic flows [47] and Maxwell rheological flows [48]. The HPM formulation for the coupled ordinary differential momentum and energy Eqs. (25)–(26) are defined in the following form:

$$\begin{aligned} h\left( {v,\varepsilon } \right) &= \left( {1 - \varepsilon } \right)\left[ {L_{{{\text{op}}}} \left( v \right) - L_{{{\text{op}}}} \left( {\tilde{v}_{0} } \right)} \right] + \varepsilon \left[ {L_{{{\text{op}}}} \left( v \right) + 2\xi \frac{{\text{d}}}{{{\text{d}}y}}\left( {\frac{{{\text{d}}v}}{{{\text{d}}y}}} \right)^{3} - H_{a}^{2} v }\right. \\ & \quad \left.{+ E_{h} - D_{a} \left[ {1 + 2\xi \left( {\frac{{{\text{d}}v}}{{{\text{d}}y}}} \right)^{2} } \right]v - D_{F} v^{2} + G_{r} T} \right],\end{aligned} $$

(30)

$$ \begin{aligned} h\left( {\vartheta ,\varepsilon } \right) & = \left( {1 - \varepsilon } \right)\left[ {L_{{{\text{op}}}} \left( \vartheta \right) - L_{{{\text{op}}}} \left( {\tilde{\vartheta }_{0} } \right)} \right] + \varepsilon \left[ {L_{{{\text{op}}}} \left( \vartheta \right) + B_{r} \left( {\frac{{{\text{d}}v}}{{{\text{d}}y}}} \right)^{2} + 2B_{r} \xi \left( {\frac{{{\text{d}}v}}{{{\text{d}}y}}} \right)^{4} } \right. \\ & \quad \left. { + B_{r} H_{a}^{2} v^{2} - \xi_{1} v + \xi_{2} + B_{r} \left[ {1 + 2\xi \left( {\frac{{{\text{d}}v}}{{{\text{d}}y}}} \right)^{2} } \right]v^{2} + B_{r} D_{F} v^{3} } \right], \\ \end{aligned} $$

(31)

In the above equations $L_{{{\text{op}}}}$ is the linear operator and $\tilde{v}_{0} ,\tilde{\vartheta }_{0}$ are the initial guesses, and they are defined as:

$$ L_{{{\text{op}}}} = \frac{{{\text{d}}^{2} }}{{{\text{d}}y^{2} }},\tilde{v}_{0} = \tilde{\vartheta }_{0} = \frac{{y^{2} - 1}}{2}, $$

(32)

To proceed further, let us define series expansions for Eqs. (29)-(31):

$$ \begin{aligned} v & = v_{0} + \varepsilon v_{1} + \varepsilon^{2} v_{2} + \ldots , \\ \vartheta & = \vartheta_{0} + \varepsilon \vartheta_{1} + \varepsilon^{2} \vartheta_{2} + \ldots , \\ \end{aligned} $$

(33)

Applying Eq. (33), in Eqs. (29)--(31), we obtain a set of linear differential equations for each order, which are defined next.

3.1 Zeroth Other System $\varepsilon^{0}$

At zeroth order we obtain the following set of differential equations with their boundary conditions:

$$ \begin{aligned} & L_{{{\text{op}}}} \left( {v_{0} } \right) - L_{{{\text{op}}}} \left( {\tilde{v}_{0} } \right) = 0, \\ & v_{0} \left( { \pm 1} \right) = 0, \\ \end{aligned} $$

(34)

$$ \begin{aligned} & L_{{{\text{op}}}} \left( {\vartheta_{0} } \right) - L_{{{\text{op}}}} \left( {\tilde{\vartheta }_{0} } \right) = 0, \\ & \vartheta_{0} \left( { \pm 1} \right) = 0, \\ \end{aligned} $$

(35)

The solution at the zeroth order is obtained as:

$$ \begin{gathered} v_{0} = \frac{{y^{2} - 1}}{2}, \hfill \\ \vartheta_{0} = \frac{{y^{2} - 1}}{2}, \hfill \\ \end{gathered} $$

(36)

3.2 First Order System $\varepsilon^{1}$

The first order system is obtained in the following form:

$$ \begin{aligned} & L_{{{\text{op}}}} \left( {v_{1} } \right) + L_{{{\text{op}}}} \left( {v_{0} } \right) + 2\xi \frac{{\text{d}}}{{{\text{d}}y}}\left( {\frac{{{\text{d}}v_{0} }}{{{\text{d}}y}}} \right)^{3} - H_{a}^{2} v_{0} \\ & \quad+ E_{h} - D_{a} \left[ {1 + 2\xi \left( {\frac{{{\text{d}}v_{0} }}{{{\text{d}}y}}} \right)^{2} } \right]v_{0} - D_{F} v_{0}^{2} + G_{r} \vartheta_{0} , \\ & v_{1} \left( { \pm 1} \right) = 0, \\ \end{aligned} $$

(37)

$$ \begin{aligned} & \left\{ \begin{aligned}& L_{{{\text{op}}}} \left( {\vartheta_{1} } \right) + L_{{{\text{op}}}} \left( {\vartheta_{0} } \right) + B_{r} \left( {\frac{{{\text{d}}v_{0} }}{{{\text{d}}y}}} \right)^{2} + 2B_{r} \xi \left( {\frac{{{\text{d}}v_{0} }}{{{\text{d}}y}}} \right)^{4} + B_{r} H_{a}^{2} v_{0}^{2} - \xi_{1} v_{0} + \xi_{2} \hfill \\ &+ B_{r} D_{a} \left[ {1 + 2\xi \left( {\frac{{{\text{d}}v_{0} }}{{{\text{d}}y}}} \right)^{2} } \right]v_{0}^{2} + B_{r} D_{F} v_{0}^{3} , \hfill \\ \end{aligned} \right. \\ & \vartheta_{1} \left( { \pm 1} \right) = 0, \\ \end{aligned} $$

(38)

The solution of the first order system is obtained as:

$$\begin{aligned} v_{1}& = \frac{1}{120}\left( { - 1 + y^{2} } \right)\\ &\quad \times\left( \begin{gathered} D_{F} \left( {11 - 4y^{2} + y^{4} } \right) + D_{a} \left( { - 25 + y^{2} \left( {5 - 6\xi } \right) - 6\xi + 4y^{4} \xi } \right) \hfill \\ - 5\left( {G_{r} \left( { - 5 + y^{2} } \right) - H_{a}^{2} \left( { - 5 + y^{2} } \right) + 12\left( {1 + E_{h} + \xi + y^{2} \xi } \right)} \right) \hfill \\ \end{gathered} \right)\end{aligned} $$

(39)

$$\begin{aligned} \vartheta_{1} &= - \frac{1}{6720}\left( { - 1 + y^{2} } \right)\\ & \quad \times\left[ \begin{aligned} & Br\left( \begin{aligned} & 56D_{a} \left( {11 - 4y^{2} + y^{4} } \right) + 3D_{F} \left( { - 93 + 47y^{2} - 23y^{4} + 5y^{6} } \right) \hfill \\ &+ 4D_{a} \left( {29 + 29y^{2} - 41y^{4} + 15y^{6} } \right)\xi \hfill \\ & + 56\left( {10\left( {1 + y^{2} } \right) + H_{a}^{2} \left( {11 - 4y^{2} + y^{4} } \right) + 8\left( {1 + y^{2} + y^{4} } \right)\xi } \right) \hfill \\ \end{aligned} \right) \hfill \\ &- 280\left( {\left( { - 5 + y^{2} } \right)\xi_{1} - 12\left( {1 + \xi_{2} } \right)} \right) \hfill \\ \end{aligned} \right],\end{aligned} $$

(40)

3.3 Second Order System $\varepsilon^{2}$

The second order system is obtained as:

$$ \begin{aligned} & \left\{ \begin{aligned} &L_{{{\text{op}}}} \left( {v_{2} } \right) + 6\xi \left[ {2\frac{{{\text{d}}v_{0} }}{{{\text{d}}y}}\frac{{{\text{d}}^{2} v_{0} }}{{{\text{d}}y^{2} }}\frac{{{\text{d}}v_{1} }}{{{\text{d}}y}} + \frac{{{\text{d}}^{2} v_{1} }}{{{\text{d}}y^{2} }}\left( {\frac{{{\text{d}}v_{0} }}{{{\text{d}}y}}} \right)^{2} } \right] - H_{a}^{2} v_{1} - D_{a} v_{1} \hfill \\ & - 2\xi \left[ {v_{1} \left( {\frac{{{\text{d}}v_{0} }}{{{\text{d}}y}}} \right)^{2} + 2v_{0} \frac{{{\text{d}}v_{1} }}{{{\text{d}}y}}\frac{{{\text{d}}v_{0} }}{{{\text{d}}y}}} \right] - 2D_{F} v_{1} v_{0} + G_{r} \vartheta_{1} , \hfill \\ \end{aligned} \right. \\ & v_{2} \left( { \pm 1} \right) = 0, \\ \end{aligned} $$

(41)

$$ \begin{aligned} & \left\{ \begin{aligned} & L_{{{\text{op}}}} \left( {\vartheta_{1} } \right) + 2B_{r} \frac{{{\text{d}}v_{0} }}{{{\text{d}}y}}\frac{{{\text{d}}v_{1} }}{{{\text{d}}y}} + 8B_{r} \xi \frac{{{\text{d}}v_{1} }}{{{\text{d}}y}}\left( {\frac{{{\text{d}}v_{0} }}{{{\text{d}}y}}} \right)^{3} + 2B_{r} H_{a}^{2} v_{1} v_{0} - \xi_{1} v_{1} + 2B_{r} D_{a} v_{1} v_{0} \hfill \\& + 2\xi B_{r} D_{a} \left( {v_{0}^{2} \frac{{{\text{d}}v_{0} }}{{{\text{d}}y}}\frac{{{\text{d}}v_{1} }}{{{\text{d}}y}} + v_{0} v_{1} \left( {\frac{{{\text{d}}v_{0} }}{{{\text{d}}y}}} \right)^{2} } \right) + 3B_{r} D_{F} v_{0}^{2} v_{1} , \hfill \\ \end{aligned} \right. \\ & \vartheta_{1} \left( { \pm 1} \right) = 0, \\ \end{aligned} $$

(42)

The solution of the second order system is obtained as:

$$ v_{1} = v_{1,0} + v_{1,1} y^{2} + v_{1,2} y^{4} + v_{1,3} y^{6} + v_{1,4} y^{8} + v_{1,5} y^{10} , $$

(43)

$$ \vartheta_{1} = \vartheta_{1,0} + \vartheta_{1,1} y^{2} + \vartheta_{1,2} y^{4} + \vartheta_{1,3} y^{6} + \vartheta_{1,4} y^{8} + \vartheta_{1,5} y^{10} + \vartheta_{1,6} y^{12} , $$

(44)

The constants $v_{1,n} ,\vartheta_{1,n} ;\left( {n = 0,1 \ldots ,6} \right)$ mentioned in the above equations are algebraically rigorous and are therefore omitted for brevity. They can, however, be easily determined through the use of regular computations in the symbolic software, Mathematica.

Using the HPM property, we may derive the final form of the solutions as:

$$ u = \mathop {\lim }\limits_{\varepsilon \to 1} v = v_{0} + v_{1} + v_{2} + \ldots , $$

(45)

$$ T = \mathop {\lim }\limits_{\varepsilon \to 1} \vartheta = \vartheta_{0} + \vartheta_{1} + \vartheta_{2} + \ldots , $$

(46)

Finally, they can be written as:

$$ \begin{aligned} u &= \frac{{y^{2} - 1}}{2} + \frac{1}{120}\left( { - 1 + y^{2} } \right)\\ & \quad \times\left( \begin{gathered} D_{F} \left( {11 - 4y^{2} + y^{4} } \right) + D_{a} \left( { - 25 + y^{2} \left( {5 - 6\xi } \right) - 6\xi + 4y^{4} \xi } \right) \hfill \\ - 5\left( {G_{r} \left( { - 5 + y^{2} } \right) - H_{a}^{2} \left( { - 5 + y^{2} } \right) + 12\left( {1 + E_{h} + \xi + y^{2} \xi } \right)} \right) \hfill \\ \end{gathered} \right) \\ & \quad { + }v_{1,0} + v_{1,1} y^{2} + v_{1,2} y^{4} + v_{1,3} y^{6} + v_{1,4} y^{8} + v_{1,5} y^{10} , \\ \end{aligned} $$

(47)

$$ \begin{aligned} T &= \frac{{y^{2} - 1}}{2} - \frac{1}{6720}\left( { - 1 + y^{2} } \right)\\&\quad \times\left[ {Br\left( \begin{aligned} & 56D_{a} \left( {11 - 4y^{2} + y^{4} } \right) + 3D_{F} \left( { - 93 + 47y^{2} - 23y^{4} + 5y^{6} } \right) \hfill \\ & + 4D_{a} \left( {29 + 29y^{2} - 41y^{4} + 15y^{6} } \right)\xi \hfill \\& + 56\left( {10\left( {1 + y^{2} } \right) + H_{a}^{2} \left( {11 - 4y^{2} + y^{4} } \right) + 8\left( {1 + y^{2} + y^{4} } \right)\xi } \right) \hfill \\ \end{aligned} \right)} \right. \\ & \quad \left. { \vphantom{\left( \begin{aligned} & 56D_{a} \left( {11 - 4y^{2} + y^{4} } \right) + 3D_{F} \left( { - 93 + 47y^{2} - 23y^{4} + 5y^{6} } \right) \hfill \\ & + 4D_{a} \left( {29 + 29y^{2} - 41y^{4} + 15y^{6} } \right)\xi \hfill \\& + 56\left( {10\left( {1 + y^{2} } \right) + H_{a}^{2} \left( {11 - 4y^{2} + y^{4} } \right) + 8\left( {1 + y^{2} + y^{4} } \right)\xi } \right) \hfill \\ \end{aligned} \right)}- 280\left( {\left( { - 5 + y^{2} } \right)\xi_{1} - 12\left( {1 + \xi_{2} } \right)} \right)} \right] + \vartheta_{1,0} + \vartheta_{1,1} y^{2} + \vartheta_{1,2} y^{4} \\ &\quad+ \vartheta_{1,3} y^{6} + \vartheta_{1,4} y^{8} + \vartheta_{1,5} y^{10} + \vartheta_{1,6} y^{12} . \\ \end{aligned} $$

(48)

4 HPM and Numerical bvp4c Results and Discussion

In this section, graphical results are presented based on the HPM solutions. Additionally, solutions have been obtained using the numerical shooting quadrature available in the bvp4c command in MATLAB. The following parametric values were chosen to carry out the computational formulation such as: $D_{a} = 1.5;\,$ $\xi = 0.2;\,$ $B_{r} = 0.2;\,$ $E_{h} = 1;$ $H_{a} = 2;\,$ $D_{F} = 1;\,$ $G_{r} = 0.2;\,$ $\xi_{1} = 0.5;\,$ $\xi_{2} = 0.5.$ These values have been adopted from references [10, 14, 39, 40] and represent realistic scenarios in microchannel electromagnetic non-Newtonian heat transfer systems. A comparison between the proposed results and a numerical technique based on the built-in command bvp4c in Matlab to ensure that the results are valid (see Table 1). According to this table, it is evident the HPM solutions correlate very closely with the MATLAB bvp4c numerical results, which verifies that the current results are correct.

Table 1 Numerical comparison of the Nusselt number using numerical and perturbation solutions

Figures 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 and 16 illustrate the influence of key parameters on the velocity, temperature and Nusselt number distributions.

Fig. 2

Behavior of $\xi$ on velocity profile

Fig. 3

Behavior of $G_{r}$ on velocity profile

Fig. 4

Behavior of $D_{a}$ on velocity profile

Fig. 5

Behavior of $D_{F}$ on velocity profile

Fig. 6

Behavior of $H_{a}$ on velocity profile

Fig. 7

Behavior of $B_{r}$ on velocity profile

Fig. 8

Behavior of $E_{h}$ on velocity profile

Fig. 9

Behavior of $\xi$ on temperature profile

Fig. 10

Behavior of $B_{r}$ on temperature profile

Fig. 11

Behavior of $D_{a}$ on temperature profile

Fig. 12

Behavior of $D_{F}$ on temperature profile

Fig. 13

Behavior of $\xi_{2}$ on temperature profile

Fig. 14

Behavior of $\xi_{1}$ on temperature profile

Fig. 15

Behavior of $H_{a}$ on temperature profile

Fig. 16

Effect of multiple parameters on Nusselt number profile

Figures 2, 3, 4, 5, 6, 7 and 8 show the evolution in velocity profile in relation to several parameters such as the third-grade fluid parameter $\xi$, the thermal Grashof number $G_{r}$, the Darcy number $D_{a}$, the Forchheimer number $D_{F}$, the magnetic number $H_{a}$, the Brinkman number $B_{r}$, and the electric strength $E_{h}$.

Figure 2 shows how increasing the third-grade fluid parameter (ξ) causes significant reduction in the velocity magnitude. When the third-grade fluid parameter is set to zero, however, the case of a Newtonian fluid is retrieved, and this corresponds to the maximum velocity i. e. greatest flow acceleration in the micro-channel. The third-grade fluid parameter (ξ) arises in the momentum Eq. (25) in the term,$6\xi {\left(\frac{du}{dy}\right)}^{2}\frac{{d}^{2}u}{d{y}^{2}}$. Since $\xi =\frac{{\upsilon }^{2}\left({\overline{\tau }}_{2}+{\overline{\tau }}_{3}\right)}{\mu {{ 2\mathchar'26\mkern-10mu\lambda }}^{4}}$ the parameter is dominated by viscosity and not elasticity of the non-Newtonian fluid. Higher values will therefore imply greater viscous resistance which will lead to a depletion in velocity across the micro-channel. Strongly viscoelastic fluids will therefore flow slower than the classical Newtonian case. There is no cross-over in velocity profiles and a consistent deceleration is induced across the micro-channel span with higher third-grade fluid parameter (ξ) values.

Figure 3 demonstrates that the thermal Grashof number induces a considerable enhancement in the velocity profile. The buoyancy force, $+{G}_{r}T$ in Eq. (25) increases as the thermal Grashof number increases. This intensifies natural convection currents which amplifies the velocity magnitude. Again, this behaviour is maintained across the micro-channel span. The case of forced convection is retrieved for G_r <  < 1 and this corresponds to the lowest velocity computed. The velocity profiles are symmetrical about the centreline of the micro-channel (y = 0).

The effects of Darcy number on the velocity profile are depicted in Fig. 4. In this illustration, it can be seen that increasing the Darcy number causes the velocity profile to decline drastically. The Darcy parameter, ${D}_{a}=\frac{{\lambda}^{2}}{k}$ and is inversely proportional to porous medium permeability, k. This is distinct from the classical Darcy number which is directly proportional to permeability. ${D}_{a}$ features in the Darcian drag force term i.e. $-{D}_{a}u$ in the momentum conservation Eq. (25). As ${D}_{a}$ is elevated, the permeability is reduced and this decelerates the flow since greater resistance is generated to the percolating viscoelastic fluid. The velocity is therefore maximized for ${D}_{a}$ = 0 which corresponds to vanishing permeability (infinite) implying there are no solid matrix fibers and the regime is purely viscoelastic fluid. The significant damping effect of small permeability of the porous medium is clearly demonstrated, confirming the excellent control mechanism offered in electromagnetic micro-channel flows via the presence of a porous matrix.

The effects of the Forchheimer number ${D}_{F}$ on velocity distribution across the micro-channel span are depicted in Fig. 5. $D_{F} = \frac{{C_{F} { 2\mathchar'26\mkern-10mu\lambda } }}{\sqrt k }$ and enables an assessment of non-Darcian inertial drag forces on the viscoelastic flow in the porous medium. A significant decrease in the velocity profile is observed with increment in Forchheimer number. As Forchheimer number increases, the second order (quadratic) inertial drag is boosted i. e. the term, $-{D}_{F}{u}^{2}$ is enhanced and this decelerates the flow across the micro-channel. For ${D}_{F}$ = 0, Forchheimer effects are negated and the classical Darcian model is retrieved. Symmetric profiles are sustained at all values of ${D}_{F}$ across the microchannel. At the plate boundaries, in accordance with the no-slip boundary conditions, velocities vanish. The strong damping achieved with inertial (Forchheimer) drag is clearly demonstrated. These findings concur with many other non-Darcy studies including Saha et al. [36] and Ashraf et al. [37].

Figure 6 shows that increasing values of the magnetic interaction parameter, ${H}_{a}$. $H_{a} = B{ 2\mathchar'26\mkern-10mu\lambda } \sqrt {\frac{\sigma }{\rho }}$ and an increment in this parameter enhances the Lorentzian magnetic drag force, $-{H}_{a}^{2}u$, in Eq. (24). This damps the flow and reduces velocity across the micro-channel. The non-magnetic case is retrieved for ${H}_{a}$= 0 and this achieves the maximum velocity. A significant deceleration in the flow is clearly achieved with greater magnetic parameter which corresponds to a stronger transverse magnetic field presence in the regime. Peak velocity is always computed at the centre line ($y = 0$) and again the profiles are symmetric. In all cases magnitudes of velocity are positive indicating that back flow is never induced in the regime, even at maximum magnetic parameter of ${H}_{a}$ = 2.5.

It is seen in Fig. 7 that there is a slight increase in velocity owing to an increment in Brinkman number, but the impacts are minimal. $B_{r} = \frac{{\mu \upsilon^{2} }}{{{ 2\mathchar'26\mkern-10mu\lambda }^{2} k_{T} \left( {T_{m} - T_{s} } \right)}}$ and describes the viscous dissipation effect. Ordinarily this parameter which features in the viscous heating term, $+{B}_{r}{\left(\frac{du}{dy}\right)}^{2}$ in Eq. (26) will convert kinetic energy into thermal energy. However in the present case, Br also appears in many other terms in the energy conservation Eq. (26), viz, a non-Newtonian term, $+2{B}_{r}\xi {\left(\frac{du}{dy}\right)}^{4}$, the Joule heating term, $+{B}_{r}{H}_{a}^{2}{u}^{2}$, and additionally the modified non-Darcian dissipative terms, $+{B}_{r}{D}_{a}{u}^{2}$ and $+{B}_{r}{D}_{F}{u}^{3}$. The collective contribution of these multiple terms however modifies the action of the Brinkman number and leads to a slight acceleration in the flow across the micro-channel.

The impact of electric field parameter, ${E}_{h}$, on velocity evolution across the micro-channel span is depicted in Fig. 8. $E_{h} = \frac{{\sigma BE{ 2\mathchar'26\mkern-10mu\lambda }^{3} }}{\mu \upsilon }$ is directly proportional to the electrical field strength, E. It arises in the single axial electrical body force term, $+{E}_{h}$ u in Eq. (25) which unlike the magnetic Lorentzian force, is an assistive body force. Increment in electrical field parameter therefore magnifies this electrohydrodynamic body force which assists the flow and induces strong acceleration in the regime. There is therefore a significant boost in axial velocity across the micro-channel span with stronger electrical field strength effect. The electrohydrodynamic body force therefore can be utilized to balance the magnetic Lorentzian drag effect and together these two body forces provide a dual mechanism for regulating the micro-channel flow distribution. The simultaneous presence of electromagnetohydrodynamic (EMHD) effects i. e. H_a > 0 and E_h > 0, therefore offers improved control of the microchannel regime compared to only electrohydrodynamic (EHD) (for which H_a = 0) or magnetohydrodynamic (MHD) designs (for which E_h = 0).

Figure 9 depicts the third-grade fluid parameter ($\xi$) impact on temperature profile. A very slight heating effect is induced with a large increment in$\xi$. The non-Newtonian third grade viscoelastic parameter, $\xi =\frac{{\upsilon }^{2}\left({\overline{\tau }}_{2}+{\overline{\tau }}_{3}\right)}{\mu {{ 2\mathchar'26\mkern-10mu\lambda }}^{4}}$. It features in both the momentum Eq. (25) in the term, $+6\xi {\left(\frac{du}{dy}\right)}^{2}\frac{{d}^{2}u}{d{y}^{2}}$ and also in the energy Eq. (26) in the term,$+2{B}_{r}\xi {\left(\frac{du}{dy}\right)}^{4}$. As observed earlier, higher values of $\xi$ lead to a deceleration in the flow. This enables a faster thermal diffusion rate in the viscoelastic liquid which increases temperature magnitudes. Also, the term, $+2{B}_{r}\xi {\left(\frac{du}{dy}\right)}^{4}$ is also increased with greater $\xi$ which also contributes to a heating effect.

Figure 10 shows that as the Brinkman number $B_{r}$ increases, the temperature profile is very strongly enhanced. Increment in Brinkman number greatly amplifies the viscous heating (and Joule heating) effect. It also magnifies the non-Darcy dissipation effects simulated in the supplementary terms in the energy Eq. (26). This contributes to an accentuation in the viscous heating relative to the heat conduction process. Temperatures are therefore strongly modified. It is noteworthy that inclusion of the viscous dissipation (and associated effects) is very important since it achieves significantly different temperature values (they are much higher) than when viscous heating is neglected (B_r = 0). As with the velocity profiles computed earlier, there is symmetry in the temperature profiles across the micro-channel and the peak temperature always arises at the centre (y = 0). At the plate boundaries, temperatures vanish in accordance with the boundary conditions prescribed in Eq. (27).

Figure 11 illustrates that increasing the Darcy parameter, $D_{a}$ increases the temperature profile, although the impacts are minimal. A slight elevation in temperature is induced with greater Darcy parameter, which is maximized at the centre of the micro-channel. As noted earlier, when ${D}_{a}$ is elevated, the permeability is reduced. There are therefore less solid matric fibers in the regime. However thermal conduction is still greater than for the case of ${D}_{a}$ = 0 and the latter is associated with the lowest temperatures since there are no solid matrix fibers present for infinite permeability (purely viscoelastic fluid in the regime). Temperature is also influenced by the dissipative Darcian term in the energy conservation Eq. (26), $+{B}_{r}{D}_{a}{u}^{2}$, which has been included in the modified formulation adopted, and is usually neglected in simpler models of porous media.

The impact of Forchheimer number $D_{F}$ i.e. non-Darcian effect on the temperature profile is depicted in Fig. 12. Here, it should be noticed that the temperature profile is enhanced weakly with Forchheimer number. There is a direct contribution of Forchheimer number to the temperature field via the term, $+{B}_{r}{D}_{F}{u}^{3}$ in the energy Eq. (26). This induces a slight heating effect in the regime which is also associated with viscous dissipation. Clearly for the Darcian case (D_F = 0) temperature is minimized.

Figure 13 shows the behavior of $\xi_{2}$ on temperature profile. In terms of physics, this parameter describes the relationship between Joule heating and heat conduction. As can be seen in this graph, increasing this parameter results in a significant increase in the temperature profile along the entire channel length. $\xi_{2} = \frac{{\sigma { 2\mathchar'26\mkern-10mu\lambda }^{2} E^{2} }}{{\left( {T_{m} - T_{s} } \right)k_{T} }}$ arises in the term, $+{\xi }_{2}$ in the energy Eq. (26). This assists the thermal diffusion field and indicates that the transverse magnetic field (Joule dissipation) generates strong heating in the regime which dominates thermal conduction.

Figure 14 demonstrates that by increasing the value of $\xi_{1}$ there is a decrement in the temperature profile. This parameter arises in the negative term, $- \xi_{1} u$ in the energy Eq. (26) which inhibits thermal diffusion. Physically, $\xi_{1} = \frac{{\upsilon { 2\mathchar'26\mkern-10mu\lambda } \left( {c_{0} + 2\sigma BE} \right)}}{{\left( {T_{m} - T_{s} } \right)k_{T} }}$ represents the effects of heat generation on heat conduction due to the interaction of magnetic and electric fields. When this parameter is absent i. e. $\xi_{1}$ = 0, the heat generation effect on thermal conduction due to the combined electromagnetohydrodynamic effect vanishes and temperatures are a maximum. The implication is that the parameter $\xi_{1}$ has a cooling effect on the regime since when it is increased there is a suppression in the thermal conduction modification by dual electrical and magnetic field action.

Figure 15 shows that with increment in the magnetic interaction parameter, $H_{a}$ there is a strong elevation in temperatures across the micro-channel. This behaviour is primarily due to the term, $+{B}_{r}{H}_{a}^{2}{u}^{2}$ in the energy Eq. (25) i. e. Joule dissipation, also known as Ohmic heating. The supplementary work expended in dragging the viscoelastic fluid against the action of the transverse magnetic field is dissipated as thermal energy. This heats the fluid and elevates the temperature. Again, the maximum temperatures are observed at the centre-line of the micro-channel and are inverse parabolic profiles, with symmetry.

Figure 16 shows the Nusselt number magnitudes tabulated for selected parameters. The Nusselt number is the ratio of convective to conductive heat transfer at the upper plate of the micro-channel. It also quantifies the temperature gradient at the upper plate and is a measure of the rate of heat transfer from the inner viscoelastic EMHD fluid to the upper plate. Diffusion (conduction) and advection (fluid motion) are both involved in convection. Due to an increase in the thermal Grashof number, Forchheimer number, third-grade fluid parameter, Darcy number, Brinkman number, and magnetic interaction number, the Nusselt number magnitude is observed to increase. Therefore, stronger thermal buoyancy, higher quadratic porous drag, stronger viscoelasticity, lower permeability, higher viscous heating and stronger magnetic field all enhance the rate of heat transfer to the upper plate boundary.

5 Conclusions

A theoretical study of laminar, steady state fully developed viscoelastic natural convection electro-magnetohydrodynamic (EMHD) flow in a microchannel containing a porous medium has been presented Transverse magnetic field and axial electrical field are considered. A modified Darcy–Brinkmann–Forchheimer model is deployed for porous media effects. Viscous dissipation and Joule heating effects are included. The primitive conservation equations are rendered into dimensionless coupled ordinary differential equations with associated boundary conditions. The nonlinear ordinary differential boundary value problem has been solved using He’s powerful HPM. Validation with the MATLAB bvp4c numerical scheme has been included for Nusselt number. Graphical plots are presented for velocity, temperature and Nusselt number for the influence of emerging parameters. The computations show that:

• (i) Increment in thermal Grashof number and electric field parameter enhance velocity whereas increment in magnetic interaction parameter, third grade viscoelastic parameter, Darcy parameter and Forchheimer number inhibit the flow.

• (ii) Increasing Brinkman number and magnetic interaction number boost temperatures and a weak elevation is also observed in temperatures with increment in third-grade non-Newtonian parameter and Forchheimer number.

• (iii) Increasing magnetic field slightly heats the regime as does an increase in electrical parameter relating the Joule heating and heat conduction. However, there is a reduction in temperatures across the micro-channel with the combined electromagnetic parameter relating heat generation to heat conduction due to the interaction of magnetic and electric fields.

• (iv) Nusselt number is also elevated with thermal Grashof number, Forchheimer number, third-grade fluid (viscoelastic) parameter, Darcy parameter, Brinkman number and magnetic number.

• (v) The simultaneous presence of electromagnetohydrodynamic (EMHD) effects i. e. H_a $>0$ and ${E}_{h} > 0$, enables improved control of the microchannel regime compared to only electrohydrodynamic (EHD) (for which H_a = 0) or magnetohydrodynamic (MHD) designs (for which E_h = 0).

• (vi) The fluid motion is significantly opposed by the strong influence of magnetic field, and the third-grade fluid.

The present investigation has revealed some intriguing features of electromagnetohydrodynamic non-Newtonian microchannel flows of relevance to for example microscale thermal ducts. Future studies may consider alternative non-Newtonian models such as the upper convected Maxwell (UCM) viscoelastic model or Eringen micropolar model and will be communicated imminently.