1 Introduction

The applications of non-Newtonian fluids can be discussed in two ways: (i) flow geometry and its boundary conditions and (ii) viscoelastic nature. Viscoelastic fluids are used in a variety of industrial applications, such as cooling metallic plates, making sticky tapes and extruding plastic sheets aerodynamically. Most liquids do not reveal linear relation between the stress and strain rates, making the study of non-Newtonian fluids more complicated. Liquids such as oil and some polymers exhibit close resemblance with elastico-viscous fluid. The constitutive equations of certain fluids not obeying Newton’s law of stress to strain are studied by Oldroyd [1]. Fluids having small elasticity or small relaxation time are termed Walters’ liquid B. Boundary layer flow of the Walters’ liquid B near stagnation point was investigated by Beard and Walters [2]. A similar problem of fluctuating flow past a porous flat plate of elastico-viscous fluid has been discussed by Kaloni [3]. Fluctuating flow past an infinite plate of an elastico-viscous fluid with variable suction has been examined by Soundalgekar and Puri [4]. The velocity of the free stream fluid was found to be less than that of the velocity of the fluid layer in an analysis concluded by Frater [5] where the elastic parameters were taken to be small, which is physically unacceptable. These solutions are valid adjacent to the bounding surface. Frater used the exact result of the characteristic equation in a steady state. The characteristic equation obtained in this problem is a cubic one. For the evaluation of unknown constants, Frater proposed one condition. As per the condition, suitable roots are only those that have a Taylor series expansion in viscoelastic parameter (\(k_{1}\)). This new approach is the same as that of the condition \(k_{1}\rightarrow 0\) (in the case of Newtonian fluid). Puri and Kulshrestha [6] investigated the problem of elastico-viscous fluid past a plate moving with a velocity that is time-dependent on its plane. Heat transfer stagnation point flow of an elastico-viscous fluid with variable temperature was studied by Soundalgekar and Vighnesan [7]. Later on, elastico-viscous fluid flow over a semi-infinite flat plate was investigated by Soundalgekar and Murty [8, 9]. Foote et al [10] discussed some exact solutions for the Stokes problem of an elastico-viscous fluid. They pointed out that the limitations on the solution for flow problem obtained by researchers [2,3,4, 7] can be solved if we extend the solution to include \(k_{1}\). There is a natural limit on the values of \(k_{1}\) (\(0\le k_{1}\le 0.25\)) for which we can get the perturbation solution from exact solutions with the help of Taylor series expansion. In a series of papers, Ariel [11,12,13,14,15] discussed the exact solution of the viscoelastic flow problem through the porous channel. Ariel considered various aspects of the flow problem together with the hybrid method for studying viscoelastic fluid flow. In these papers, Ariel was able to point out the whole scenario of the exact solution and its advantages. He finally concluded that the perturbation technique is not guaranteed to produce the correct results qualitatively or quantitatively; hence, exact solutions (whether analytical or numerical) must be considered for solving the original set of equations. Lawrence and Rao [16] obtained a closed-form solution for elastico-viscous fluid through an infinite plate comprising suction and constant heat flux. Lawerence and Rao [17] obtained two closed-form solutions for the governing fourth-order nonlinear ODE. Helmy [18] obtained an exact solution to the oscillatory flow of elastico-viscous liquid. An incompressible conducting fluid and Taylor’s series expansion is employed in powers of \(k_1\) to obtain the solution. Siddique et al [19] discussed some exact solutions of elastico-viscous fluid. The flow of non-Newtonian fluid over an expanding surface in conjunction with variable viscosity was studied by Abel et al [20]. Comment regarding this paper has been published by Pantokratoras [21]. Khan et al [22] studied an electrically conducting viscoelastic fluid over an expanding sheet considering various approaches. Khan [23] examined viscoelastic fluid flow with thermal radiation. Cortell [24] studied mass transfer along with chemical reaction on two classes of viscoelastic fluid flow over a porous stretching sheet. Heat and mass transfer in elastico-viscous fluid with Hall effect has been discussed by Chaudhury and Jha [25]. Shit and Haldar [26] studied the thermal radiation effect on MHD viscoelastic fluid flow. The fluid flow was considered to be over a stretching sheet with variable viscosity. Stokes’s second problem for a second-grade fluid has been studied by Ali et al [27] considering the fluid flow in a porous medium and derived an exact solution for the proposed model.

Hamza et al [28] have studied free convection with slip effect on elastico-viscous fluid through a porous medium in conjunction with the heat source. The spectral homotopy analysis approach was used by Fagbade et al [29] to study the free convection of viscoelastic liquid. The flow was considered to be passed on an accelerating permeable surface with thermal radiation. Krishna [30] has analysed Hall and ion slip effects on an elastico-viscous fluid via a circular cylinder. Again, Hall and ion slip effects on MHD rotating flow of elastico-viscous fluid through a porous medium have been investigated by Krishna et al [31]. The effects of thermal radiation and viscous dissipation on MHD slip Darcy flow of viscoelastic fluid over a stretching sheet has been studied by Wahid et al [32]. Heat transport phenomena of non-Newtonian MHD fluid flow in a vertical surface with magnetic and thermal diffusion are explored by Singh and Seth [33]. Several researchers have used different methods of solutions. The exact solution to the problem of the time-dependent flow of elastico-viscous liquid embedded in a porous medium within two parallel plates was reported by Kulkarni [34]. Later on, unsteady MHD elastico-viscous fluid flow of second-order type in a tube of hyperbolic cross-section in porous boundary has been solved by Kulkarni [35] using the exact solution. The same exact solution was used by Ali and Khan [36] to study magnetohydrodynamic (MHD) slip flow and heat transfer over an oscillating and translating porous plate. The study of MHD unsteady viscoelastic fluid flow past an infinite vertical plate using an exact solution was reported by Kumaresan and Kumar [37], in the presence of thermal radiation. Raju et al [38] also used a closed analytical method to solve the problem designed for a non-Newtonian liquid past a vertical plate in connection with radiation and chemical reaction. EL-Shehawey et al [39] have obtained an exact solution to the MHD flow of an elastico-viscous fluid using Laplace and Hankel transform. Jafeer and Mustafa [40] have discussed Von Karman’s problem of the infinite disk in an elastico-viscous fluid. The present study focusses on the flow of electrically conducting oscillatory viscoelastic fluid embedded within a porous medium with a transverse magnetic field. Moreover, the flow medium is considered optically thin because the effect of radiative heat transfer is considered in the energy equation. Thus, the absence of additional body force terms in the momentum equation and heat energy terms in the heat equation reduces the present discussion to Helmy [18]. Comparison of the solutions obtained from Cardan’s method and perturbation method as well as with available results (Helmy [18]) in a particular case provides consistency of the solutions and conformity of the effects of the emerging parameters. Regarding applications of such unsteady boundary value problems, there are many; problems ranging from the motion of greatly influenced liquids.

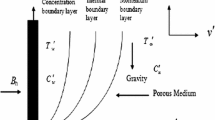
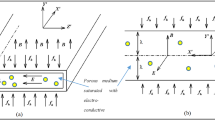
2 Mathematical formulation of the problem

The oscillatory flow of a conducting viscoelastic fluid embedded in a porous material has been investigated in the presence of a transverse magnetic field. The x-axis runs along the direction of the plate, and the y-axis, which is perpendicular to the plate, represents the transverse direction. If the plate is infinite, all flow variables are just functions of time t and space variable y, and the motion is autonomous along the x-axis. The governing equations for MHD viscoelastic fluid flow are as follows:

$$\begin{aligned} \frac{\partial { v}}{\partial { y}} = 0 \quad (\text {continuity equation}). \end{aligned}$$
(1)

Neglecting the pressure gradient term, momentum equation can be written as

$$\begin{aligned} \frac{\partial u}{\partial t} + { v}\frac{\partial u}{\partial y}= & {} \nu \frac{\partial ^2 u}{\partial y^2} - \frac{k_{0}}{\rho } \left[ \frac{\partial ^3 u}{\partial y^2 \partial t} + { v} \frac{\partial ^3u}{\partial y^3}\right] \nonumber \\&+\frac{F_{x}}{\rho }-\frac{\nu }{k_{p}^{'}}u, \end{aligned}$$
(2)

where u and \({ v}\) are the velocity components along and normal to the plate, \(\nu \) is the kinematic viscosity, \(k_{0}\) is the viscoelastic parameter, \(\rho \) is the density and \(k'_{p}\) is the permeability parameter. The x-component of the magnetic force F in the absence of excess charge may be written as

$$\begin{aligned} F_{x} = \left( J\times B\right) _{x}, \end{aligned}$$
(3)

where J and B are current density and magnetic induction vector, respectively. According to the generalised Ohm’s law

$$\begin{aligned} J = \sigma \left( E+V\times B\right) , \end{aligned}$$
(4)

where \(\sigma \) and E are the electric conductivity and the electric field, respectively.

In the absence of electric field, eq. (4) can be written as

$$\begin{aligned} J = \sigma \left( V\times B\right) . \end{aligned}$$
(5)

The magnetic Reynolds number is considered to be small because the induced magnetic field is negligible and insignificant in comparison to the applied field. In particular, low velocity free convective flow (\(B=i_zB_0\)) makes this condition physically acceptable for terrestrial applications. Thus, the final form of eq. (3) can be written as

$$\begin{aligned} F_{x} = -\sigma u B_{0}^{2}. \end{aligned}$$
(6)

It is considered that the plate velocity normal to the flow is fluctuating with constant non-zero value \({ v}_{0}\). Integrating continuity equation (1) yields

$$\begin{aligned} { v} = -{ v}_{0}(1+\epsilon A \mathrm {e}^{i\omega t}), \end{aligned}$$
(7)

where A is a real positive constant, \(\epsilon \) is a small parameter such that \(\epsilon A\ll 1\), \({ v}_{0}>0\) is the suction velocity and \({ v}_{0}<0\) represents the blowing velocity. The symbol i stands for the complex imaginary number.

Substituting eqs (6) and (7) in eq. (2) we obtain,

$$\begin{aligned}&\frac{\partial u}{\partial t} - { v}_{0}( 1 + \epsilon A \mathrm {e}^{i \omega t}) \frac{\partial u}{\partial y} = \nu \frac{\partial ^2 u}{\partial y^2}\nonumber \\&\quad - \frac{k_{0}}{\rho }\left[ \frac{\partial ^3u}{\partial y^2 \partial t}- { v}_{0}(1 + \epsilon A \mathrm {e}^{i \omega t})\frac{\partial ^3u}{\partial y^3}\right] \nonumber \\&\quad - \frac{\sigma B_{0}^2 u}{\rho } - \frac{\nu u}{k_{p}^{'}} \end{aligned}$$
(8)

subject to the boundary conditions

$$\begin{aligned} u&=U(t)=U_{0}(1+\epsilon \mathrm {e}^{i \omega t}) \quad \text {at}\quad y=0 \nonumber \\ u&=0 \quad \text {as}\quad y \rightarrow \infty , \end{aligned}$$
(9)

in which only real parts have physical meaning.

Introducing non-dimensional quantities

$$\begin{aligned}&\tilde{u} = \frac{u}{U_{0}},\; \tilde{t} = \frac{{ v}_{0}^{2}t}{\nu },\; \tilde{\omega }=\frac{\nu \omega }{{ v}_{0}^{2}}, \; \tilde{y}= \frac{{ v}_0 y}{\nu },\;\tilde{U}=\frac{U}{U_{0}}, \nonumber \\&k_{1}= \frac{k_{0}{} { v}_{0}^{2}}{\rho \nu ^2}, \; M = \frac{\sigma B_{0}^{2}\nu }{\rho { v}_{0}^{2}}, \; k_{p} = \frac{\nu ^2}{k_{p}^{'}{} { v}_{0}^{2}}, \end{aligned}$$
(10)

and plugging eq. (10) in eq. (8) and dropping tilde we have

$$\begin{aligned}&\frac{\partial u}{\partial t} - ( 1 + \epsilon A \mathrm {e}^{i \omega t}) \frac{\partial u}{\partial y} = \frac{\partial ^2 u}{\partial y^2}\nonumber \\&\quad - k_{1}\left[ \frac{\partial ^3 u}{\partial y^2 \partial t}- (1 + \epsilon A \mathrm {e}^{i \omega t})\frac{\partial ^3 u}{\partial y^3}\right] - (M+k_{p})u, \end{aligned}$$
(11)

where \(k_{1}\) is the elastico-viscous parameter. The term \((M+k_{p})\) is a combined parameter due to the inclusion of permeability of porous medium and magnetic field. Here \(k_{p}=0\) corresponds to electrical conductivity of the fluid and \(M=0\) is a problem in a porous medium.

The corresponding boundary conditions are

$$\begin{aligned} u&= 1 + \epsilon \mathrm {e}^{i \omega t}, \quad \text {at}\; y =0 \nonumber \\ u&= 0, \quad \text {when}\quad y\rightarrow \infty . \end{aligned}$$
(12)

3 Solution for the velocity field

In order to find solution to eq. (11), we consider

$$\begin{aligned} u(y,t) = u_{1}(y) + \epsilon u_{2}(y)\mathrm {e}^{i \omega t} + O(\epsilon ^2). \end{aligned}$$
(13)

Substituting eq. (13) in eq. (11) and ignoring \((\epsilon ^2)\) terms, we obtain equations for \(u_{1}(y)\) and \(u_{2}(y)\).

$$\begin{aligned}&k_{1}u'''_{1} + u''_{1} + u'_{1} -(M + k_{p}) u_{1} = 0 \end{aligned}$$
(14)
$$\begin{aligned}&k_{1}u'''_{2} + \left( 1-iw k_{1}\right) u''_{2} + u'_{2} -(M + k_{p}+iw) u_{2}\nonumber \\&\quad = -A\left( k_{1}u'''_{1} + u'_{1}\right) . \end{aligned}$$
(15)

The prime indicates differentiation with respect to y. The boundary conditions for eqs (14) and (15) are

$$\begin{aligned} u_{1}&=1,\; u_{2}=1 \quad \text {at}\; y=0 \nonumber \\ u_{1}&\rightarrow 0, \; u_{2} \rightarrow 0 \quad \text {as}\; y \rightarrow \infty \end{aligned}$$
(16)

and the physical condition that the non-Newtonian fluid reduces to Newtonian under limiting elastic condition, i.e. for \(k_{1}=0\), the model eqs (14) and (15) reduce to the Newtonian model. We obtain exact solution for eqs (14) and (15) for any value of \(k_{1}\) using Cardan’s technique [18]. The approximate solutions for the small elastic parameter \(k_{1}\) are also obtained in Beard and Walters [2].

3.1 Exact solution for any value of \(k_{1}\)

Following Cardan’s technique [18], the exact solution for the velocity fields \(u_{1}\) and \(u_{2}\) satisfying the boundary conditions (eqs (16)) can be written as

$$\begin{aligned}&u_{1}(y) = \mathrm {e}^{-(a_{2}+b_{2}k_{1})y} \end{aligned}$$
(17)
$$\begin{aligned}&u_{2}(y) = \frac{iA}{\omega }\left( a_{2}+b_{2}k_{1}\right) \mathrm {e}^{-(a_{2}+b_{2}k_{1})y}\nonumber \\&\quad + \left( 1-\frac{iAa_{2}}{\omega }\right) \mathrm {e}^{-(b+nk_{1})y} - \frac{i A b_{2}k_{1}}{\omega }\mathrm {e}^{-by}, \end{aligned}$$
(18)

where

$$\begin{aligned} a_{2}&= \frac{1}{2}\left( 1 + \sqrt{1+4M+4k_{p}}\right) , \\ b_{2}&=\frac{a_{2}^{3}}{2a_{2}-1},\quad n = \frac{b^2(b+i\omega )}{2b-1} \end{aligned}$$

and

$$\begin{aligned} b&= \frac{1}{2}\left( 1+ \sqrt{1+4M + 4 k_{p} + 4i\omega }\right) . \end{aligned}$$

Although exact solution is in complex form, velocity being real quantity, and the real component of velocity has been considered for discussion.

3.2 The approximate solution for a small elastic parameter \(k_{1}\)

To solve eqs (14) and (15) with boundary conditions (eq. (16)) we follow Beard and Walters [2] and seek the solution in the following form for small values of \(k_{1}\):

$$\begin{aligned} u_{1}(y)= & {} u_{10}(y) + k_{1} u_{11}(y) + O(k_{1}^2) \end{aligned}$$
(19)
$$\begin{aligned} u_{2}(y)= & {} u_{20}(y) + k_{1} u_{21}(y) + O(k_{1}^2). \end{aligned}$$
(20)

Using eqs (19) and (20) in eqs (14) and (15), and equating the corresponding coefficient of \(k_{1}\) up to first order, the following set of perturbation relations are obtained:

Zero order

$$\begin{aligned}&u''_{10} + u'_{10} - (M+k_{p})u_{10}=0 \end{aligned}$$
(21)
$$\begin{aligned}&u''_{20} + u'_{20} - (M+k_{p}+iw)u_{20}=-A u'_{10}. \end{aligned}$$
(22)

First order

$$\begin{aligned}&u''_{11} + u'_{11} - (M+k_{p})u_{11}=-u'''_{10} \end{aligned}$$
(23)
$$\begin{aligned}&u''_{21} + u'_{21} - (M+k_{p}+iw)u_{21} \nonumber \\&\quad = -Au'''_{10} -A u'_{11} + iw u''_{20} - u'''_{20}. \end{aligned}$$
(24)

From eqs (19) and  (20), it follows that the boundary conditions for eqs (21)–(24) are:

$$\begin{aligned}&u_{10}=u_{20}=1 \quad \text {and}\quad u_{11}=u_{21}=0, \quad \nonumber \\&\quad \text {at}\;\; y=0 \nonumber \\&u_{10}\rightarrow 0, u_{11}\rightarrow 0, u_{20}\rightarrow 0\; \text {and}\; u_{21}\rightarrow 0, \nonumber \\&\text {as} \;\; y \rightarrow \infty . \end{aligned}$$
(25)

4 Solution of energy equation

The energy equation for a fluid flow over a flat plate in the presence of transverse magnetic field with unsteady injection, heat source and radiation parameter, can be written as

$$\begin{aligned}&\frac{\partial T}{\partial t} - { v}_{0}(1 + \epsilon A \mathrm {e}^{i \omega t}) \frac{\partial T}{\partial y} \nonumber \\&\qquad + \tau \frac{\partial }{\partial t}\left[ \frac{\partial T}{\partial t} - { v}_{0}(1+\epsilon A \mathrm{e}^{i \omega t}) \frac{\partial T}{\partial y}\right] \nonumber \\&\quad = \alpha \frac{\partial ^2 T}{\partial y^2} - \frac{1}{\rho c_{p}}\frac{\partial q_{r}}{\partial y} + \frac{Q}{\rho c_{p}}\left( T_{\infty } - T\right) . \end{aligned}$$
(26)

We employ the following boundary conditions

$$\begin{aligned} T&=T_{w} \quad \text {at} \quad y =0 \nonumber \\ T&\rightarrow T_{\infty } \quad \text {as} \quad y\rightarrow \infty , \end{aligned}$$
(27)

where the subscripts \(\omega \) and \(\infty \) refer to wall and ambient condition respectively.

Using Rosseland’s approximation for radiation, we have

$$\begin{aligned} q_{r}= - \frac{4 \sigma }{3 \alpha _{0}} \frac{\partial T^{4}}{\partial y}. \end{aligned}$$
(28)

The constant term Q in eq. (26) can have either positive or negative values when the wall temperature \(T_{w}\) exceeds the free stream temperature \(T_{\infty }\). When \(Q<0\), then the third term of eq. (26) represents heat source and heat sink when \(Q>0\). The opposite relationship is also true. The symbol \(\sigma \) is the Stefan–Boltzmann constant, and \(\alpha _{0}\) is the absorption coefficient. Temperature difference within the flow is such that \(T^{4}\) may be expanded in a Taylor series. Expanding \(T^{4}\) about \(T_{\infty }\) and neglecting higher-order terms, we have

$$\begin{aligned} T^{4} = 4T_{\infty }^{3}T - 3T_{\infty }^{4}. \end{aligned}$$
(29)

On account of eqs (28) and (29), eq. (26) reduces to

$$\begin{aligned}&\frac{\partial T}{\partial t} - { v}_{0}(1 + \epsilon A \mathrm {e}^{i\omega t}) \frac{\partial T}{\partial y} \nonumber \\&\qquad + \tau \frac{\partial }{\partial t}\left[ \frac{\partial T}{\partial t} - { v}_{0}(1+\epsilon A \mathrm {e}^{i \omega t}) \frac{\partial T}{\partial y}\right] \nonumber \\&= \alpha \frac{\partial ^2 T}{\partial y^2} + \frac{1}{\rho c_{p}} \frac{4 \sigma }{ 3 \alpha _{0}}4 T_{\infty }^{3}\frac{\partial ^2 T}{\partial y^2}\nonumber \\&\qquad + \frac{Q}{\rho c_{p}}\left( T_{\infty } - T \right) . \end{aligned}$$
(30)

Let us introduce the dimensionless variables

$$\begin{aligned} \tilde{\theta }&= \frac{T-T_{\infty }}{T_{w}-T_{\infty }}, \quad Pr = \frac{\nu }{\alpha }, \quad \tilde{\tau } = \frac{{ v}_{0}^{2}\tau }{\nu }, \nonumber \\ \beta&= \frac{Q}{\rho c_{p}{} { v}^{2}/\nu }, \quad \text {heat source}/\text {sink parameter}, \nonumber \\ N&= \frac{3 k \alpha _{0}}{16 \sigma T_{\infty }^{3}}, \quad \text {radiation parameter}. \end{aligned}$$
(31)

Using relation (31) and dropping the tilde, eq. (30) yields

$$\begin{aligned}&\frac{\partial \theta }{\partial t} - (1 + \epsilon A \mathrm {e}^{i \omega t}) \frac{\partial \theta }{\partial y}\nonumber \\&\quad + \tau \frac{\partial }{\partial t}\left[ \frac{\partial \theta }{\partial t} - (1+\epsilon A \mathrm{e}^{i \omega t}) \frac{\partial \theta }{\partial y}\right] \nonumber \\&\quad = \left( \frac{N+1}{ \Pr N}\right) \frac{\partial ^2 \theta }{\partial y^2} - \beta \theta . \end{aligned}$$
(32)

The corresponding boundary conditions are

$$\begin{aligned} \theta&= 1 \quad \text {at} \quad y=0\nonumber \; \nonumber \\ \theta&= 0 \quad \text {as} \quad y\rightarrow \infty . \end{aligned}$$
(33)

We solve eq. (32) by assuming that

$$\begin{aligned} \theta (y, t) = \theta _{1}(y) + \epsilon \theta _{2}(y) \mathrm {e}^{i\omega t} \end{aligned}$$
(34)

subject to the boundary conditions

$$\begin{aligned} \theta _{1}&=1,\; \theta _{2}=0 \quad \text {at}\; y=0 \nonumber \; \nonumber \\ \theta _{1}&=0,\; \theta _{2}=0 \quad \text {as}\; y\rightarrow \infty . \end{aligned}$$
(35)

Substituting eq. (34) in eq. (32) gives the equation for \(\theta _{1}(y)\) and \(\theta _{2}(y)\).

$$\begin{aligned}&\theta ''_{1}(y) + p \theta '_{1}(y) - r \theta _{1}(y) =0 \end{aligned}$$
(36)
$$\begin{aligned}&\theta ''_{2}(y) + p\left( 1+i\omega \tau \right) \theta '_{2}(y) \nonumber \\&\qquad - i\omega p \left( 1+i\omega \tau - \frac{i \beta }{\omega }\right) \theta _{2}(y) \nonumber \\&\quad = -A p\left( 1+ i \omega \tau \right) \theta '_{1}, \end{aligned}$$
(37)

where

$$\begin{aligned} p=\frac{Pr N}{N+1} \quad \hbox {and}\quad r=\beta p. \end{aligned}$$

Solution of eq. (36) for \(\theta _{1}\) is

$$\begin{aligned} \theta _{1}(y) = \mathrm {e}^{-\xi y}, \quad \text {where}\; \xi = \frac{p+\sqrt{p^2 +4r}}{2} \end{aligned}$$
(38)

Substituting \(\theta _{1}\) in eq. (37) and using boundary condition (35), we get

$$\begin{aligned} \theta _{2}(y) = C_{1} [ \mathrm {e}^{- \xi y} - \mathrm {e}^{-\lambda y}], \end{aligned}$$
(39)

where

$$\begin{aligned}&C_{1} = \frac{c}{\xi ^2 -d \xi -e} \quad \text {and}\quad \lambda = \frac{d + \sqrt{d^2 + 4 e}}{2}, \end{aligned}$$

with

$$\begin{aligned}&d = p(1+i \omega \tau ), \nonumber \\&e = i \omega p\left( 1 + i\omega \tau -\frac{i \beta }{\omega }\right) \quad \end{aligned}$$

and

$$\begin{aligned} c= & {} \xi A p( 1 + i \omega \tau ). \end{aligned}$$
(40)

5 Results and discussion

The solutions of many fluid mechanics problem are based on the understanding of the dynamic behaviour of unsteady boundary layer. Therefore, the effects of magnetic field, viscoelastic parameter, porosity, suction parameter, radiation parameter and source parameter have been calculated and depicted in diagrams. Moreover, the variation of temperature profiles with relaxation time have been depicted pictorially. Velocities and temperature are real quantities. Hence, real components of velocity and temperature profile are depicted for the physical interpretation of different parameters on the flow pattern.

We now discuss about the consequences of each parameter separately. It should be mentioned that, in conjunction with the shooting approach, the Runge–Kutta fourth-order method is used to numerically solve the perturbation equations for the velocity field.

The Lorentz force, which results from the interaction of the magnetic field and current in a viscoelastic fluid, is illustrated in figure 1.

Fig. 1
figure 1

Effect of magnetic parameter on velocity profiles u(y, t) with \(\omega =3\), \(A=1\), \(\epsilon =0.1\), \(\omega t=\pi \), \(k_{1} = 0.1\) and \(k_{p}=0\).

Full size image
Fig. 2
figure 2

Effect of elastic parameter on velocity profiles u(y, t) with \(\omega =3\), \(A=1\), \(\epsilon =0.1\), \(\omega t=\pi \), \(k_{1} = 0.1\), \(M=2\) and \(k_{p}=0.1\).

Full size image

It is evident that Lorentz force opposes the motion of the fluid and as a result, the velocity decreases at all points. The effect is more pronounced near the solid boundary resulting in a two-layer structure. The layer where viscosity is significant is governed by Navier–Stokes equations and the other layer, where viscosity is not significant is governed by Bernoulli equation. The important feature of figure 1 is that perturbation solutions obtained using viscoelastic parameter as perturbed quantity coincides well with the closed-form solution obtained using Cardan’s technique [18, 41]. This is in good agreement with the results obtained by Helmy [18]. At last, the consistency of the solution and conformity of the results are established.

From figure 2, it is evident that the viscoelastic parameter characterising the viscoelastic property of the fluid reduces the velocity field. Helmy [18] made a similar observation, which gives us confidence that the numerical approach is being applied correctly. When a viscoelastic liquid flows, the material’s stored energy overshoots in the form of strain energy due to the additional dissipative heat energy, which is why there is a drop in velocity in relation to the elastic parameter. Although the strain rate in a viscoelastic liquid is small, it is still not a good idea to ignore it, but in a viscous inelastic liquid, we can ignore it. The strain resulting from the withdrawal of stress that results in the drop in velocity is what causes the flow to reverse and return to its original state.

The influence of permeability of the porous medium is depicted in figure 3. It is noticed that permeability of the medium increases with decreasing porosity. Physically, the drag force tends to increase by decreasing the velocity field. Again, in all the profiles, the velocity field decreases smoothly as point of investigation shifts into the fluid.

Fig. 3
figure 3

Effect of porosity parameter on velocity profiles u(y, t) with \(\omega =3\), \(A=1\), \(\epsilon =0.1\), \(\omega t=\pi \), \(k_{1} = 0.1\) and \(M=2\).

Full size image
Fig. 4
figure 4

Effect of suction parameter on temperature profiles \(\theta (y,t)\) with \(\omega =3\), \(\epsilon =0.1\), \(\omega t=\pi /2\), \(Pr = 2\), \(N=0\) and \(\beta =0\).

Full size image

This resists the motion that causes the boundary layer to become thin. In addition, a detailed examination of figure 4, which depicts the temperature variation caused by suction at the plate, reveals that fluctuations with a larger amplitude result in a more gradual decrease in temperature than velocity profiles. This is due to the fact that, in contrast to small fluctuation, or steady suction, high fluctuation causes heat energy cease to exist in the fluid layers, resulting in a drop in temperature.

In figure 5 the radiation parameter shows decrease in temperature and thermal boundary layer thickness with an increase in the value of radiation parameter N. It is observed that energy transport into the fluid is decreasing due to the increase in radiation. This is due to the presence of the extra term in the thermal boundary layer.

Fig. 5
figure 5

Effect of radiation parameter on temperature profiles \(\theta (y,t)\) with \(\omega =3\), \(\epsilon =0.1\), \(\omega t=\pi /2\), \(Pr = 2\), \(A=1\) and \(\beta =0\).

Full size image

Figure 6 is related to the effect of heat source/sink on the temperature distribution in the presence of radiation associated with fluctuating suction.

Fig. 6
figure 6

Effect of source parameter on temperature profiles \(\theta (y,t)\) with \(\omega =3\), \(\epsilon =0.1\), \(\omega t=\pi /2\), \(Pr = 2\), \(A=1\) and \(N=1\).

Full size image

By looking at the graph, it is clear that while temperature decreases with increasing heat source strength, it rises with increasing heat sink strength. Since it depends on the suction velocity and kinematic viscosity, it is obvious from the definition that it does not simply exhibit the material attribute. The profiles in figure 6 match the numerical solution to the energy eq. (32). In the free stream, the dimensionless temperature value drops to zero from unity at the wall. By taking into account two factors, physical interpretation can be provided: (i) \(T_w>T_{\infty }\) and \(\beta >0\) suggests a heat sink. There is a rapid drop of temperature as the heat flowing from the wall is absorbed, (ii) when \(T_w>T_{\infty }\) and \(\beta <0\), the heat source causes a rise in temperature in the entire boundary layer.

Figure 7 shows the variation of fluid temperature with relaxation time. The energy equation considered here is a manifestation of the relaxation effects introduced by a simple modification of Gibbs relation. The effect of relaxation time is significant for small values of \(\tau \) and the effect has no significance for large values of \(\tau \). On close observation, it is seen that for a few layers, the temperature increases slightly, then decreases and again increases. Thus, relaxation time induces an oscillatory temperature variation. The oscillation has been reduced due to the presence of the sink term. The oscillation obtained by Helmy [18] is slightly larger due to the absence of the sink term in the temperature equation.

Fig. 7
figure 7

Effect of relaxation time on temperature profiles \(\theta (y,t)\) with \(\omega =3\), \(\epsilon =0.1\), \(\omega t=\pi /2\), \(Pr = 4\), \(A=1\), \(\beta =0.1\) and \(N=1\).

Full size image

6 Concluding remarks

Non-Newtonian fluid in the presence of viscoelastic parameter yields a third-order differential equation. However, \(k_{1}=0\) (Newtonian fluid) resulted in second-order differential equation. Even then the flow solution is presented by using Cardan’s technique. The solutions are physically significant in the sense that a slightly elastic fluid (\(k_{1}\ll 1\)) produces a boundary layer slightly different from the viscous fluid. As a consequence of the above discussion, it is observed that

  • Fluctuating suction increases the velocity field and reduces the temperature distribution.

  • The Lorentz force, i.e., the magnetic field parameter M offers a resistance to the flow. Therefore, the velocity field decreases.

  • Increase in relaxation time causes fluctuation in temperature distribution.

  • Presence of radiation parameter transfer energy into the fluid, and consequently, temperature across the boundary layer decreases.

  • Heat sink parameter reveals a rapid fall in temperature with the absorption of heat whereas heat source parameter brings about an increase in temperature of the entire boundary layer.

  • More pores in the medium establish thinning of the boundary layer.