1 INTRODUCTION

Flow, heat and mass transfer with chemical action have numerous applications in many areas of chemical engineering such as the molecular evaporator [1], polymer processing [2], catalytic slab systems [3], electrochemical phenomena [4], and adsorption processes [5]. These studies have also been materialized in porous medium flow owing to potential applications in drying technologies, distribution of temperature and moisture over agricultural fields, energy transfer in wet cooling towers, flow in desert coolers and drying. Ulson de Souza and Whitaker [6] studied mass transfer in a packed-bed reactor with heterogeneous chemical reaction.

Many such studies have been done within boundary layer theory. Gatica et al. [7] studied free convection boundary layer flow in a porous medium with chemical reaction. Prud’homme and Jasmin [8] studied biochemical free convection flow through porous medium with internal heat generation from microbial oxidation, for Rayleigh numbers equal to 0.25 and 25. Beg et al. [9] analyzed the effects of chemical reaction rate on buoyancy-driven micropolar free convective heat and mass transfer in a Darcian porous regime. Ibrahim et al. [10] studied the effects of chemical reaction and radiation absorption on transient hydromagnetic natural convection flow with wall transpiration and heat source. Zueco et al. [11] examined the impact of chemical reaction on the hydromagnetic boundary layer flow from a horizontal cylinder in a Darcy–Forchheimer regime using network simulation. Rashad et al. [12] studied the effect of chemical reaction and thermal radiation on MHD micropolar fluid in a rotating frame of reference. Shateyi [13] examined the steady MHD flow of Maxwell fluid past of vertical stretching sheet through Darcian porous medium in the presence of thermophoresis and chemical reaction. Tripathy et al. [14] discussed the effect of chemical reaction over a vertical moving plate in porous medium. The effects of chemical reaction on MHD stagnation point flow of nanofluids in porous medium with radiation and viscous dissipation effect was examined by Mabood et al. [15]. The modified form of homogeneous and heterogeneous chemical reactions was examined by Khan et al. [16] by considering MHD stagnation point flow with Joule heating and viscous dissipation. Hayat et al. [17] studied the impacts of chemical reactions in MHD flow of Jeffrey liquid over a nonlinear radially stretching surface. Tripathi and Sharma [18] examined the effect of variable viscosity on MHD flow of blood with chemical reaction. Seth et al. [19] analyzed the effect of nth order chemical reaction with Newtonian heating on Casson fluid flow in porous medium. Sharma and Kumawat [20] discussed the impact of temperature dependent viscosity and thermal conductivity on the MHD blood flow with ohmic heating and chemical reaction over a vertical stretching surface. Recently, Meena et al. [21] examined the combined effect of heat source/sink and chemical reaction on mixed convection flow across a vertical cone.

The relations between the fluxes and the driving potentials may be of a more intricate nature as heat and mass transfer occur simultaneously in a moving fluid. An energy flux can be generated by composition gradients and this embodies the Dufour or diffusion-thermo effect. On the other hand, by temperature gradients, mass fluxes can also be created and is termed as the Soret or thermal-diffusion effect. Such effects occur simultaneously when density differences exist in the flow regime. For example, when species are introduced at the surface in fluid domain, with a different density than the surrounding fluid, both thermo-diffusion (Soret) and diffuso-thermal (Dufour) effects can become significant. The Soret and Dufour effects are important for intermediate molecular weight gases in coupled heat and mass transfer in fluid binary systems, often encountered in chemical process engineering and also in high-speed aerodynamics. Dursunkaya and Worek [22] have studied Soret/Dufour effects on transient and steady natural convection from vertical surface. Anghel et al. [23] have discussed the composite Dufour and Soret effects on free convection boundary layer flow over a vertical surface embedded in a Darcian porous medium. Postelnicu [24] has presented numerical solutions for the effect of magnetic field on buoyancy-driven heat and mass transfer from a vertical surface in a porous medium including Soret and Dufour effects. The free as well as forced convection boundary layer flows with Soret and Dufour effects have been addressed by Abreu et al. [25]. Beg et al. [26] studied coupled heat and mass transfer in a micropolar fluid-saturated Darcy–Forchheimer porous medium with Soret and Dufour effects. Beg et al. [27] analyzed chemically reacting mixed convective heat and mass transfer from an inclined plate with Soret/Duofur effects with the applications in solar energy collector systems. Vempati and Laxmi-Narayana-Gari [28] explored, the consolidated effect of Soret and Dufour effect with thermal radiation on unsteady MHD boundary layer fluid flow on an infinite vertical plate. Hayat and Nawaz [29] examined the influence of Soret and Dufour effects on the mixed convection flow of a second-grade fluid subject to Hall and ion-slip currents. Ram Reddy et al. [30] examined the Soret effect on mixed convection flow of nanofluid under convective boundary condition. Ojjella and Kumar [31] studied the Soret and Dufour effects on chemically reacting micropolar fluid flow between expanding or contracting walls with ion slip. Reddy and Chamkha [32] discussed the impact of Soret and Dufour effect on convective MHD flow of Al2O3–water and TiO2–water nanofluids in porous media past a stretching sheet with heat generation/absorption. Gbadeyan et al. [33] explored the effect of Soret and Dufour effects on heat and mass transfer in chemically reacting MHD flow through a wavy channel. Shojaei et al. [34] examined the Dufour and Soret effect on the second-grade fluid flow on a radiative stretching cylinder. Shehzad et al. [35] studied the dynamics of fluid flow subject to upward and downward motion of rotating disk through Soret–Dufour impacts.

Nomenclature

  

μ

Dynamic viscosity

c s

Concentration susceptibility

ε

Porosity of medium

F

Forchheimer inertial drag parameter

ρ

Density of the fluid

k l

Chemical rate parameter

x

Distance along the plate

h m

Mean fluid temperature

y

Distance normal to the plate

\({{{v}}_{0}}\)

Suction velocity \({v}\)

u

Velocity components in x directions

U

Dimensionless X direction velocity

h

Temperature

θ

Dimensionless temperature

C

Concentration

ϕ

Dimensionless concentration

u p

Plate velocity

X

Dimensionless distance along the plate

h w

Surface temperature

Y

Dimensionless distance normal to the plate

h ∞

Fluid free-stream temperature

T

Dimensionless time

C w

Surface concentration

U p

Dimensionless plate velocity

C ∞

Free-stream concentration

Pr

Prandtl number

t

Time

Sc

Schmidt number

ν

Kinematic viscosity

Q

Dimensionless heat absorption parameter

βT

Coefficient of thermal expansion

Ec

Eckert number

βC

Coefficient of species expansion

Sc

Schmidt number

M

Magnetic field parameter

Du

Dufour number

Da

Darcy number

Sr

Soret number

Fr

Forchheimer number

χ

Dimensionless chemical rate parameter

Gr

Grashof number

C f

Skin friction coefficient

Gc

Species Grashof number

Nux

Nusselt number

k p

Permeability of the porous medium

Shx

Sherwood number

k h

Thermal diffusion ratio

Rex

Reynolds number

α

Thermal diffusivity

Γ

Penalty parameter

D

Mass diffusivity

Subscripts

σ

Electrical conductivity

w

Surface conditions

B 0

Strength of magnetic field

∞

Conditions far away from the surface

Q 0

Heat absorption coefficient

Superscripts

g

Gravitational acceleration

T

Transpose

c p

Specific heat at constant pressure

'

Derivative

The main objective of the present analysis is to investigate simultaneously the effect of heat and mass transfer through fluid saturated porous medium in the presence of heat absorption and first order homogeneous chemical action with Soret and Dufour effects. The coupled non-linear partial differential equations governing the flow have been solved numerically using element free Galerkin method. Such a study constitutes an important addition to multiphysical chemical engineering transport phenomena modeling.

2 MATHEMATICAL MODEL

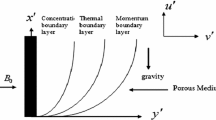
Consider the transient boundary layer flow of fluid along the semi-infinite porous vertical plate embedded in Darcy–Forchheimer porous medium in the presence of homogenous chemical reaction and heat absorption with Soret and Dufour effects. The fluid is considered as incompressible, Newtonian, vi-scous and electrically-conducting with uniform properties. The \(x\)-axis is directed along the plate, and \(y\)-axis is transverse to this axis. The magnetic field of uniform strength \({{B}_{0}}\) is applied along \(y\)-axis. Magnetic field is sufficiently weak to produce induction effects. It is assumed that there is negligible heat release by the chemical action. For \(t \geqslant 0\), the plate starts moving impulsively in its own plane with constant velocity \({{u}_{p}}\), and the plate temperature is elevated to \(T\) and the concentration level of the mass particle at the plate is raised to \(C.\) The physical model and geometrical coordinates are shown in Fig. 1. A heat sink is placed within the flow to allow possible heat absorption effects. Under these assumptions, the physical variables are functions of space (\(y\)) and time (\(t\)) coordinates only. With the usual boundary layer and Boussinesq approximations, the problem can be governed by the following set of equations:

Fig. 1.
figure 1

Flow configuration and coordinate system.

Full size image

Continuity equation:

$$\frac{{\partial {v}}}{{\partial y}} = 0.$$
(1)

Momentum conservation equation:

$$\rho \left( {\frac{{\partial u}}{{\partial t}} + {v}\frac{{\partial u}}{{\partial y}}} \right) = \mu \frac{{{{\partial }^{2}}u}}{{\partial {{y}^{2}}}} - \left( {\sigma B_{0}^{2} + \frac{{\mu \varepsilon }}{{{{k}_{p}}}} + \frac{{F\rho {{\varepsilon }^{2}}}}{{k_{p}^{{1/2}}}}u} \right)u + {{\beta }_{T}}\rho g\left( {h - {{h}_{\infty }}} \right) + {{\beta }_{C}}\rho g\left( {C - {{C}_{\infty }}} \right).$$
(2)

Energy conservation equation:

$$\frac{{\partial h}}{{\partial t}} + {v}\frac{{\partial h}}{{\partial y}} = \alpha \frac{{{{\partial }^{2}}h}}{{\partial {{y}^{2}}}} + \frac{1}{{\rho {{c}_{p}}}}\left( {\frac{{\mu \varepsilon }}{{{{k}_{p}}}}{{u}^{2}} + \frac{{F\rho {{\varepsilon }^{2}}}}{{k_{p}^{{1/2}}}}{{u}^{3}} + \mu {{{\left( {\frac{{\partial u}}{{\partial y}}} \right)}}^{2}}} \right) - \frac{{{{Q}_{0}}}}{{\rho {{c}_{p}}}}\left( {h - {{h}_{\infty }}} \right) + \frac{{D{{k}_{h}}}}{{{{c}_{s}}{{c}_{p}}}}\frac{{{{\partial }^{2}}C}}{{\partial {{y}^{2}}}}.$$
(3)

Species diffusion equation:

$$\frac{{\partial C}}{{\partial t}} + {v}\frac{{\partial C}}{{\partial y}} = D\frac{{{{\partial }^{2}}C}}{{\partial {{y}^{2}}}} - {{k}_{l}}\left( {C - {{C}_{\infty }}} \right) + \frac{{D{{k}_{h}}}}{{{{h}_{m}}}}\frac{{{{\partial }^{2}}h}}{{\partial {{y}^{2}}}}.$$
(4)

The initial and boundary conditions are:

$$t < 0{\kern 1pt} :\quad u = 0,\quad h = {{h}_{\infty }},\quad C = {{C}_{\infty }}\quad {\text{for}}\;{\text{all}}\;y,$$
(5)
$$t \geqslant 0{\kern 1pt} :\;\;\left\{ \begin{gathered} u = {{u}_{p}},\quad {v} = {v}(t),\quad h = {{h}_{w}} + \delta ({{h}_{w}} - {{h}_{\infty }}){{e}^{{nt}}},\quad C = {{C}_{w}} + \delta ({{C}_{w}} - {{C}_{\infty }}){{e}^{{nt}}}\quad {\text{at}}\;y = 0 \hfill \\ u = 0,\quad h \to {{h}_{\infty }},\quad C \to {{C}_{\infty }}\quad {\text{as}}\;y \to \infty . \hfill \\ \end{gathered} \right.$$
(6)

The last terms on the right-hand side of the energy equation (3) and concentration equation (4) signify the Dufour or diffusion-thermo effect and the Soret or thermo diffusion effect respectively. The second term on the right-hand side of concentration equation (4) is the chemical action term.

It is assumed that the solution of Eq. (1) takes the following form:

$${v} = {v}(t) = - {{{v}}_{0}}\left( {1 + \delta {{A}_{0}}{{e}^{{nt}}}} \right),$$
(7)

where \({{A}_{0}}\) is a real positive constant, \(\delta \) is constant, and \({{{v}}_{0}}\) is the suction velocity at the plate surface.

To obtain the nondimensional form of the governing equations, the following dimensionless variables are introduced:

$$U = \frac{u}{{{{{v}}_{0}}}},\quad Y = \frac{{{{{v}}_{0}}y}}{\nu },\quad T = \frac{{{v}_{0}^{2}t}}{\nu },\quad {{U}_{p}} = \frac{{{{u}_{p}}}}{{{{{v}}_{0}}}},\quad n^* = \frac{{n\nu }}{{{v}_{0}^{2}}},\quad \theta = \frac{{h - {{h}_{\infty }}}}{{{{h}_{w}} - {{h}_{\infty }}}},\quad \phi = \frac{{C - {{C}_{\infty }}}}{{{{C}_{w}} - {{C}_{\infty }}}}.$$
(8)

Substituting the relation (8) into Eqs. (2) to (4), the following dimensionless partial differential equations are obtained:

$$\frac{{\partial U}}{{\partial T}} - (1 + \delta A{{e}^{{n^*T}}})\frac{{\partial U}}{{\partial Y}} = \frac{{{{\partial }^{2}}U}}{{\partial {{Y}^{2}}}} - \left( {M + \frac{1}{{\operatorname{Da} \operatorname{Re} _{x}^{2}}} + \frac{{\operatorname{Fr} }}{{\operatorname{Da} {{{\operatorname{Re} }}_{x}}}}U} \right)U + \operatorname{Gr} \theta + \operatorname{Gm} \phi ,$$
(9)
$$\frac{{\partial \theta }}{{\partial T}} - \left( {1 + \delta A{{e}^{{n^*T}}}} \right)\frac{{\partial \theta }}{{\partial Y}} = \frac{1}{{\Pr }}\frac{{{{\partial }^{2}}\theta }}{{\partial {{Y}^{2}}}} + \operatorname{Ec} \left[ {\frac{1}{{\operatorname{Da} \operatorname{Re} _{x}^{2}}}{{U}^{2}} + \frac{{\operatorname{Fr} }}{{\operatorname{Da} {{{\operatorname{Re} }}_{x}}}}{{U}^{3}} + {{{\left( {\frac{{\partial U}}{{\partial Y}}} \right)}}^{2}}} \right] - Q\theta + \operatorname{Du} \frac{{{{\partial }^{2}}\phi }}{{\partial {{Y}^{2}}}},$$
(10)
$$\frac{{\partial \phi }}{{\partial T}} - \left( {1 + \delta A{{e}^{{n^*T}}}} \right)\frac{{\partial \phi }}{{\partial Y}} = \frac{1}{{\operatorname{Sc} }}\frac{{{{\partial }^{2}}\phi }}{{\partial {{Y}^{2}}}} - \chi \phi + \operatorname{Sr} \frac{{{{\partial }^{2}}\theta }}{{\partial {{y}^{2}}}},$$
(11)

where \(M = \frac{{\sigma B_{0}^{2}\nu }}{{\rho {v}_{0}^{2}}}\) magnetic field parameter, \(\operatorname{Da} = \frac{{{{k}_{p}}}}{{\varepsilon {{x}^{2}}}}\) is the Darcy number, \({\text{Fr}} = \frac{{F\varepsilon k_{p}^{{1/2}}}}{x}\) is the Forchheimer number, \({{\operatorname{Re} }_{x}} = \frac{{{{{v}}_{0}}x}}{\nu }\) is the Reynolds number, Gr = \(\frac{{\nu g{{\beta }_{T}}\left( {{{h}_{w}} - {{h}_{\infty }}} \right)}}{{{v}_{0}^{3}}}\) is the Grashof number, Gc = \(\frac{{\nu g{{\beta }_{C}}\left( {{{C}_{w}} - {{C}_{\infty }}} \right)}}{{{v}_{0}^{3}}}\) is the species Grashof number, \(\Pr = \frac{\nu }{\alpha }\) is the Prandtl number, \(Q = \frac{{{{Q}_{0}}\nu }}{{\rho {{c}_{p}}{v}_{0}^{2}}}\) heat absorption parameter, Ec = \(\frac{{{v}_{0}^{2}}}{{{{c}_{p}}\left( {{{h}_{w}} - {{h}_{\infty }}} \right)}}\) is the Eckert number, \(\operatorname{Sc} = \frac{\nu }{D}\) is the Schmidt number, \(\chi = \frac{{{{k}_{l}}\nu }}{{{v}_{0}^{2}}}\) is the chemical rate parameter, Du = \(\frac{{D{{k}_{h}}\left( {{{C}_{w}} - {{C}_{\infty }}} \right)}}{{{{c}_{s}}{{c}_{p}}\left( {{{h}_{w}} - {{h}_{\infty }}} \right)}}\) is the Dufour number, Sr = \(\frac{{D{{k}_{h}}\left( {{{h}_{w}} - {{h}_{\infty }}} \right)}}{{\nu {{h}_{m}}\left( {{{C}_{w}} - {{C}_{\infty }}} \right)}}\) is the Soret number.

The corresponding transformed initial and boundary conditions are

$$T < 0{\kern 1pt} :\quad U = 0,\quad \theta \to 0,\quad \phi = 0\quad {\text{for}}\;{\text{all}}\;Y,$$
(12)
$$T \geqslant 0{\kern 1pt} :\;\;\left\{ \begin{gathered} U = {{U}_{p}},\quad \theta = 1 + \delta {{e}^{{n^*T}}},\quad \phi = 1 + \delta {{e}^{{n^*T}}}\quad {\text{at}}\;Y = 0 \hfill \\ U \to 0,\quad \theta \to 0,\quad \phi \to 0\quad {\text{as}}\;Y \to \infty . \hfill \\ \end{gathered} \right.$$
(13)

The coefficient of skin friction at the plate is defined as

$$\begin{gathered} {{C}_{f}} = \frac{{{{\tau }_{w}}}}{{\rho u_{p}^{2}}},\quad {\text{where}}\quad {{\tau }_{w}} = {{\left. {\mu \frac{{\partial u}}{{\partial y}}} \right|}_{{y = 0}}} = \rho V_{0}^{2}{{\left. {\frac{{\partial U}}{{\partial Y}}} \right|}_{{Y = 0}}}, \\ {\text{i}}{\text{.e}}.,\quad {{C}_{f}} = 4{{\left. {\frac{{\partial U}}{{\partial Y}}} \right|}_{{Y = 0}}}. \\ \end{gathered} $$
(14)

The local Nusselt number/heat transfer rate at wall is defined as

$$\begin{gathered} {\text{N}}{{{\text{u}}}_{x}} = \frac{{{{q}_{w}}x}}{{({{h}_{w}} - {{h}_{\infty }}){{k}_{0}}}},\quad {\text{where}}\quad {{q}_{w}} = - {{k}_{0}}{{\left. {\frac{{\partial h}}{{\partial y}}} \right|}_{{y = 0}}}, \\ {\text{i}}{\text{.e}}.,\quad {\text{N}}{{{\text{u}}}_{x}} = - {{\operatorname{Re} }_{x}}{{\left. {\frac{{\partial \theta }}{{\partial Y}}} \right|}_{{Y = 0}}}, \\ \end{gathered} $$
(15)

and the local Sherwood number/mass transfer rate at wall is defined as

$$\begin{gathered} {\text{S}}{{{\text{h}}}_{x}} = \frac{{{{q}_{m}}x}}{{D({{C}_{w}} - {{C}_{\infty }})}},\quad {\text{where}}\quad {{\left. {{{q}_{m}} = - D\frac{{\partial C}}{{\partial y}}} \right|}_{{y = 0}}}, \\ {\text{i}}{\text{.e}}.,\quad {{S}_{h}}(x) = - {{\operatorname{Re} }_{x}}{{\left. {\frac{{\partial \phi }}{{\partial Y}}} \right|}_{{Y = 0}}}. \\ \end{gathered} $$
(16)

3 NUMERICAL SOLUTION

The initial boundary value problem defined by (9)–(11) under initial condition (12) and boundary conditions (13) are solved using the element free Galerkin method as described by Liu [36]. If \({{Y}_{\infty }}\) is taken to be more than 8, the unknown functions do not change up to desired order of accuracy. Therefore, \({{Y}_{\infty }}\) has been taken as 8 in present simulation. The whole domain is discretized by uniform 81 nodal points. The time step has been taken as 0.0001. The fundamental steps comprising the method are as follows.

3.1 Variational Formulation

The variational formulation associated with Eqs. (9)–(11) over entire domain \(\left( {0,\,{{Y}_{\infty }}} \right)\) is given by:

$$\int\limits_0^{{{Y}_{\infty }}} {{{w}_{1}}\left( {\frac{{\partial U}}{{\partial T}} - \left( {1 + \delta A{{e}^{{n^*T}}}} \right)\frac{{\partial U}}{{\partial Y}} - \frac{{{{\partial }^{2}}U}}{{\partial {{Y}^{2}}}} + \left( {M + \frac{1}{{\operatorname{Da} {{{\operatorname{Re} }}_{x}}^{2}}} + \frac{{\operatorname{Fr} }}{{\operatorname{Da} {{{\operatorname{Re} }}_{x}}}}U} \right)U - \operatorname{Gr} \theta - \operatorname{Gm} \phi } \right)dY = 0} ,$$
(17)
$$\begin{gathered} \int\limits_0^{{{Y}_{\infty }}} {{{w}_{2}}\left( {\frac{{\partial \theta }}{{\partial T}} - \left( {1 + \delta A{{e}^{{n^*T}}}} \right)\frac{{\partial \theta }}{{\partial Y}} - \frac{1}{{\Pr }}\frac{{{{\partial }^{2}}\theta }}{{\partial {{Y}^{2}}}}} \right.} \\ \left. { - \;\operatorname{Ec} \left[ {\frac{1}{{\operatorname{Da} \operatorname{Re} _{x}^{2}}}{{U}^{2}} + \frac{{\operatorname{Fr} }}{{\operatorname{Da} {{{\operatorname{Re} }}_{x}}}}{{U}^{3}} + {{{\left( {\frac{{\partial U}}{{\partial Y}}} \right)}}^{2}}} \right] + Q\theta - \operatorname{Du} \frac{{{{\partial }^{2}}\phi }}{{\partial {{Y}^{2}}}}} \right)dY = 0, \\ \end{gathered} $$
(18)
$$\int\limits_0^{{{Y}_{\infty }}} {{{w}_{3}}\left( {\frac{{\partial \phi }}{{\partial T}} - \left( {1 + \delta A{{e}^{{n^*T}}}} \right)\frac{{\partial \phi }}{{\partial Y}} - \frac{1}{{\operatorname{Sc} }}\frac{{{{\partial }^{2}}\phi }}{{\partial {{Y}^{2}}}} + \chi \phi - \operatorname{Sr} \frac{{{{\partial }^{2}}\theta }}{{\partial {{Y}^{2}}}}} \right)} dY = 0,$$
(19)

where \({{w}_{1}}\), \({{w}_{2}}\), and \({{w}_{3}}\) are arbitrary test functions and may be viewed as the variation in \(U,\theta \), and \(\phi \), respectively.

3.2 Essential Boundary Conditions

To enforce essential boundary conditions, the penalty method in accordance with Zhu and Atluri [37] is applied in Eqs. (17)–(19) as follows:

$$\begin{gathered} \int\limits_0^{{{Y}_{\infty }}} {\left( {{{w}_{1}}\frac{{\partial U}}{{\partial T}} - \left( {1 + \delta A{{e}^{{n^*T}}}} \right){{w}_{1}}\frac{{\partial U}}{{\partial Y}} + \frac{{\partial {{w}_{1}}}}{{\partial Y}}\frac{{\partial U}}{{\partial Y}}} \right.} \\ \left. { + \;{{w}_{1}}\left( {M + \frac{1}{{\operatorname{Da} \operatorname{Re} _{x}^{2}}} + \frac{{\operatorname{Fr} }}{{\operatorname{Da} {{{\operatorname{Re} }}_{x}}}}\bar {U}} \right)U - \operatorname{Gr} {{w}_{1}}\theta - \operatorname{Gm} {{w}_{1}}\phi } \right)dY + {{\left. {\Gamma {{w}_{1}}(U - {{U}_{0}})} \right|}_{{Y = 0}}} = 0, \\ \end{gathered} $$
(20)
$$\begin{gathered} \int\limits_0^{{{Y}_{\infty }}} {\left( {{{w}_{2}}\frac{{\partial \theta }}{{\partial T}} - \left( {1 + \delta A{{e}^{{n^*T}}}} \right){{w}_{2}}\frac{{\partial \theta }}{{\partial Y}} + \frac{1}{{\Pr }}\frac{{\partial {{w}_{2}}}}{{\partial Y}}\frac{{\partial \theta }}{{\partial Y}} - \operatorname{Ec} {{w}_{2}}\left[ {\frac{1}{{\operatorname{Da} {{{\operatorname{Re} }}_{x}}^{2}}}\bar {U}U + \frac{{\operatorname{Fr} }}{{\operatorname{Da} {{{\operatorname{Re} }}_{x}}}}{{{\bar {U}}}^{2}}U + \left( {\frac{{\partial \bar {U}}}{{\partial Y}}} \right)\left( {\frac{{\partial U}}{{\partial Y}}} \right)} \right]} \right.} \\ \left. { + \;Q{{w}_{2}}\theta + {\text{Du}}\frac{{\partial {{w}_{2}}}}{{\partial Y}}\frac{{\partial \phi }}{{\partial Y}}} \right)dY + {{\left. {\Gamma {{w}_{2}}(\theta - {{\theta }_{0}})} \right|}_{{Y = 0}}} + {{\left. {\Gamma {{w}_{2}}(\theta - {{\theta }_{\infty }})} \right|}_{{Y = \infty }}} = 0, \\ \end{gathered} $$
(21)
$$\begin{gathered} \int\limits_0^{{{Y}_{\infty }}} {\left( {{{w}_{3}}\frac{{\partial \phi }}{{\partial T}} - \left( {1 + \delta A{{e}^{{n^*T}}}} \right){{w}_{3}}\frac{{\partial \phi }}{{\partial Y}} + \frac{1}{{\operatorname{Sc} }}\frac{{\partial {{w}_{3}}}}{{\partial Y}}\frac{{\partial \phi }}{{\partial Y}} + \chi {{w}_{3}}\phi + \operatorname{Sr} \frac{{\partial {{w}_{3}}}}{{\partial Y}}\frac{{\partial \theta }}{{\partial Y}}} \right)} dY \\ + \;{{\left. {\Gamma {{w}_{3}}(\phi - {{\phi }_{0}})} \right|}_{{Y = 0}}} + {{\left. {\Gamma {{w}_{3}}(\phi - {{\phi }_{\infty }})} \right|}_{{Y = \infty }}} = 0. \\ \end{gathered} $$
(22)

Finally, the problem is reduced to Eqs. (20)–(22) instead of Eqs. (17)–(19), which are solved using element-free Galerkin method.

3.3 Element-Free Galerkin Model

Element-free Galerkin model is obtained by substituting MLS approximations for \(U(Y),\theta (Y)\), and \(\phi (Y)\) in Eqs. (20)–(22), which can be written globally in the matrix form as follows:

$$\left[ {\begin{array}{*{20}{c}} {\left[ {{{K}^{{11}}}} \right]}&{\left[ {{{K}^{{12}}}} \right]}&{\left[ {{{K}^{{13}}}} \right]} \\ {\left[ {{{K}^{{21}}}} \right]}&{\left[ {{{K}^{{22}}}} \right]}&{\left[ {{{K}^{{23}}}} \right]} \\ {\left[ {{{K}^{{31}}}} \right]}&{\left[ {{{K}^{{32}}}} \right]}&{\left[ {{{K}^{{33}}}} \right]} \end{array}} \right]\left[ \begin{gathered} \left[ U \right] \\ \left[ \theta \right] \\ \left[ \phi \right] \\ \end{gathered} \right] + \left[ {\begin{array}{*{20}{c}} {\left[ {{{M}^{{11}}}} \right]}&{\left[ {{{M}^{{12}}}} \right]}&{\left[ {{{M}^{{13}}}} \right]} \\ {\left[ {{{M}^{{21}}}} \right]}&{\left[ {{{M}^{{22}}}} \right]}&{\left[ {{{M}^{{23}}}} \right]} \\ {\left[ {{{M}^{{31}}}} \right]}&{\left[ {{{M}^{{32}}}} \right]}&{\left[ {{{M}^{{33}}}} \right]} \end{array}} \right]\left[ \begin{gathered} \left[ {\dot {U}} \right] \\ \left[ {\dot {\theta }} \right] \\ \left[ {\dot {\phi }} \right] \\ \end{gathered} \right] = \left[ \begin{gathered} \left[ {{{F}_{1}}} \right] \hfill \\ \left[ {{{F}_{2}}} \right] \hfill \\ \left[ {{{F}_{3}}} \right] \hfill \\ \end{gathered} \right],$$
(23)

where \(\left[ {{{K}_{{lm}}}} \right]\), \(\left[ {{{M}_{{lm}}}} \right]\), and \(\left[ {{{F}_{l}}} \right]\) (\(l\), \(m\) = 1, 2, 3) are the matrices of order \(81 \times 81\), \(81 \times 81\), and \(81 \times 1\). \(\left[ U \right],\left[ \theta \right]\), and \(\left[ \phi \right]\) are matrices of order \(81 \times 1\). Here \(\dot {U},\dot {\theta }\), and \(\dot {\phi }\) are derivatives of \(U,\theta \), and \(\phi \) with respect to \(T\). These matrices are defined as follows:

$${{({{K}_{{11}}})}_{{IJ}}} = - \int\limits_0^{{{Y}_{\infty }}} {\left( {\Phi _{I}^{T}\left( {1 + \delta A{{e}^{{n^*T}}}} \right)\Phi _{J}^{'} - \Phi {{{_{I}^{'}}}^{T}}\Phi _{J}^{'} - \Phi _{I}^{T}\left( {M + \frac{1}{{\operatorname{Da} \operatorname{Re} _{x}^{2}}} + \frac{{\operatorname{Fr} }}{{\operatorname{Da} {{{\operatorname{Re} }}_{x}}}}\bar {U}} \right){{\Phi }_{J}}} \right)dY} ,$$
(24)
$${{({{K}_{{12}}})}_{{IJ}}} = - \operatorname{Gr} \int\limits_0^{{{Y}_{\infty }}} {\Phi _{I}^{T}\Phi _{J}^{'}dY} ,\quad {{({{K}_{{13}}})}_{{IJ}}} = - \operatorname{Gm} \int\limits_0^{{{Y}_{\infty }}} {\Phi _{I}^{T}\Phi _{J}^{'}dY} ,$$
(25)
$${{({{K}_{{21}}})}_{{IJ}}} = - \int\limits_0^{{{Y}_{\infty }}} {\Phi _{I}^{T}\left( {\frac{1}{{\operatorname{Da} \operatorname{Re} _{x}^{2}}}\bar {U}{{\Phi }_{J}} + \frac{{\operatorname{Fr} }}{{\operatorname{Da} {{{\operatorname{Re} }}_{x}}}}{{{\bar {U}}}^{2}}{{\Phi }_{J}} + \frac{{\partial \bar {U}}}{{\partial Y}}\Phi _{J}^{'}} \right)dY} ,$$
(26)
$${{({{K}_{{22}}})}_{{IJ}}} = - \int\limits_0^{{{Y}_{\infty }}} {\left( {\Phi _{I}^{T}\left( {1 + \delta A{{e}^{{n^*T}}}} \right)\Phi _{J}^{'} - \Phi {{{_{I}^{'}}}^{T}}\frac{1}{{\Pr }}\Phi _{J}^{'} - \Phi _{I}^{T}Q{{\Phi }_{J}}} \right)dY} ,$$
(27)
$${{({{K}_{{23}}})}_{{IJ}}} = \operatorname{Du} \int\limits_0^{{{Y}_{\infty }}} {\Phi {{{_{I}^{'}}}^{T}}\Phi _{J}^{'}dY} ,\quad {{({{K}_{{31}}})}_{{IJ}}} = 0,\quad {{({{K}_{{32}}})}_{{IJ}}} = \operatorname{Sr} \int\limits_0^{{{Y}_{\infty }}} {\Phi {{{_{I}^{'}}}^{T}}\Phi _{J}^{'}dY} ,$$
(28)
$${{({{K}_{{33}}})}_{{IJ}}} = - \int\limits_0^{{{Y}_{\infty }}} {\left( {\Phi _{I}^{T}\left( {1 + \delta A{{e}^{{n^*T}}}} \right)\Phi _{J}^{'} - \Phi {{{_{I}^{'}}}^{T}}\frac{1}{{\operatorname{Sc} }}\Phi _{J}^{'} - \Phi _{I}^{T}\chi {{\Phi }_{J}}} \right)dY} ,$$
(29)
$${{({{M}_{{11}}})}_{{IJ}}} = {{({{M}_{{22}}})}_{{IJ}}} = {{({{M}_{{33}}})}_{{IJ}}} = \int\limits_0^{{{Y}_{\infty }}} {\left( {\Phi _{I}^{T}{{\Phi }_{J}}} \right)dY} ,$$
(30)
$${{({{M}_{{12}}})}_{{IJ}}} = {{({{M}_{{13}}})}_{{IJ}}} = {{({{M}_{{21}}})}_{{IJ}}} = {{({{M}_{{31}}})}_{{IJ}}} = {{({{M}_{{32}}})}_{{IJ}}} = 0,$$
(31)
$${{({{F}_{1}})}_{I}} = {{U}_{0}}\Gamma \Phi _{I}^{'},\quad {{({{F}_{2}})}_{I}} = {{\theta }_{0}}\Gamma \Phi _{I}^{'} + {{\theta }_{\infty }}\Gamma \Phi _{I}^{'},\quad {{({{F}_{3}})}_{I}} = {{\phi }_{0}}\Gamma \Phi _{I}^{'} + {{\phi }_{\infty }}\Gamma \Phi _{I}^{'},$$
(32)

where

$$\bar {U} = \sum\limits_{I = 1}^n {\overline {{{U}_{I}}} {{\Phi }_{I}}.} $$
(33)

The domain is represented by a set of 81 uniform nodal points. At each node, 3 functions need to be evaluated; therefore, a set of 243 equations is obtained. The system of equations is nonlinear, therefore an iterative scheme is employed to solve it at each time step. The initial guess has been taken at each nodal point. The system of equations is then linearized by incorporating function \(\bar {U},\) which is assumed to be known value of function U. After applying given six boundary conditions, the system of 237 equations is solved using the Gauss elimination method, which give the values of unknowns for next iteration. This process is repeated till the absolute differences in values of two successive iterations become less than the desired accuracy.

4 RESULT AND DISCUSSION

The primarily interest in this study is to examine the effect of thermal-diffusion and diffusion-thermo effects, i.e., Soret number (Sr) and Dufour number (Du) on the fluid variables. Additionally, the influence of the chemical rate parameter (\(\chi \)), magnetic parameter (\(M\)), Eckert number (Ec), heat absorption parameter (\(Q\)), and Schmidt number (Sc) have been computed. The values of other parameters are taken to be fixed as follows:\(A = 0.5\), \(\delta = 0.2\), \(n^* = 0.1\), \({{U}_{p}} = 0.5\), \(\operatorname{Da} = 1.0\), \(\operatorname{Fr} = 0.5\), \({{\operatorname{Re} }_{x}} = 1.0\), \(\Pr = 0.71\) (air), \(\operatorname{Sc} = 0.22\) (hydrogen at 25°C and 1 atm pressure), \(\operatorname{Gr} = 2\) and \(\operatorname{Gm} = 2\). It is simulated that \(T = 6\) is the time when steady state is obtained. Therefore, all the computations have been done at \(T = 6\). The values of Sr and Du have been selected to ensure that the product SrDu remains constant, assuming constant mean temperature.

The variation of skin friction, heat transfer rate and mass transfer rate with respect to the Soret number (Sr) and Dufour number (Du), Eckert number (Ec), chemical rate parameter (\(\chi \)) and heat absorption parameter (\(Q\)) are presented in Tables 1–3. Table 1 indicates that the skin friction coefficient {\(U{\kern 1pt} '(0)\)} decreases with the decrease in Sr from 2.0 to 0.12 (i.e., increase in Du); subsequently it starts increasing. The rate of heat transfer {\( - \theta {\kern 1pt} '(0)\)} increases as Sr decreases from 2.0 to 1.0; thereafter however it decreases with a subsequent lowering in Sr from 1.0 to 0.06. The rate of mass transfer {\( - \phi {\kern 1pt} '(0)\)} increases continuously with the decrease in Sr, i.e., the maximum mass transfer rate corresponds to the minimum Sr value of 0.06 (and the maximum value of Du, i.e., 1.00). Tables 2 and 3 indicate that the skin friction increases with an increase in Ec, but decreases with a rise in \(\chi \) and \(Q\). Heat transfer rate however decreases with the increase in Ec, but increases with the increase in \(\chi \) and \(Q\). The increase in Eckert number implies more thermal energy is added to the fluid which causes a decrease in heat transfer at the wall. The rate of mass transfer {\( - \phi {\kern 1pt} '(0)\)} increases with the increase in Ec and \(\chi \), but decreases markedly with an increase in \(Q\). table 4

Table 1. Skin friction, heat transfer rate and mass transfer rate for different Sr (or Du) (M = 0.3, Da = 0.01, Rex = 10, Fr = 0.05, Ec = 0.2, Q = 1.0, χ = 1.0, Sc = 0.22)
Full size table
Table 2. Skin friction, heat transfer rate and mass transfer rate for different \(\chi \) (M = 0.3, Da = 0.01, Rex = 10, Fr = 0.05, Ec = 0.2, Q = 1.0, Sc = 0.22, Sr = 1.00, Du = 0.06)
Full size table
Table 3. Skin friction, heat transfer rate and mass transfer rate for different \(Q\) (M = 0.3, Da = 0.01, Rex = 10, Fr = 0.05, Ec = 0.2, χ = 1.0, Sc = 0.22, Sr = 1.00, Du = 0.06)
Full size table
Table 4. Skin friction, heat transfer rate and mass transfer rate for different Ec (M = 0.3, Da = 0.01, Rex = 10, Fr = 0.05, Q = 1.0, χ = 1.0, Sc = 0.22, Sr = 1.00, Du = 0.06)
Full size table

The effect of chemical rate parameter on the velocity, temperature and concentration in the boundary layer is depicted in Figs. 2–4 keeping other parameters fixed (M = 0.3, Ec = 0.2, Q = 1.0, Sc = 0.22, Sr = 1.00, Du = 0.06). Velocity (\(U\)) is clearly boosted with weak chemical action as shown in Fig. 2, i.e., as the parameter, \(\chi \) decreases from 15 to 1 (slow rate), profiles are lifted continuously throughout the boundary layer transverse to the plate. A distinct velocity escalation occurs near the wall. After this, profiles decay smoothly to the stationary value in the free stream. Thus, a weak chemical action reduces the momentum transfer, i.e., decelerates the flow. A similar response for the magnetohydrodynamic case (without porous media, viscous heating and Soret/Dufour effects) has been documented by Ibrahim et al. [10]. Temperature (\(\theta \)) and concentration (\(\phi \)) likewise decreases in Figs. 3 and 4, respectively, with an increase in the value of the parameter \(\chi \). The profiles in both the cases are monotonically decreasing, from a maximum at the wall (plate surface) to zero in the free stream. It is thus concluded that the chemical action is therefore obstructive to momentum, heat and mass transfer processes in the regime.

Fig. 2.
figure 2

Velocity distribution for different χ.

Full size image
Fig. 3.
figure 3

Temperature distribution for different χ.

Full size image
Fig. 4.
figure 4

Concentration distribution for different χ.

Full size image

The variation of velocity and temperature with the effects of heat absorption parameter \(Q\) with fixed values other parameters (M = 0.3, Ec = 0.2, χ = 1.0, Sc = 0.22, Sr = 1.00, Du = 0.06) is illustrated in Figs. 5–6. Velocity values are clearly reduced with the increase in \(Q\). An overshoot is computed close to the plate both in the presence and absence of heat absorption. Heat absorption however suppresses the overshoot. The temperature continuously decreases with the increase in \(Q\) as shown in Fig. 6. The presence of heat sink absorbs energy of fluid which causes the decrease of fluid temperature. This decrease in temperature reduces the thermal buoyancy effects, which reduce the flow velocity. Hence, our results are consistent with the physics also.

Fig. 5.
figure 5

Velocity distribution for different Q.

Full size image
Fig. 6.
figure 6

Temperature distribution for different Q.

Full size image

The temperature and concentration distributions with collective variation in Soret number Sr and Dufour number Du keeping constant values of other variables (M = 0.3, Ec = 0.2, Q = 1.0, χ = 1.0, Sc = 0.22) is presented in Figs. 7–8. Sr represents the effect of temperature gradients on mass (species) diffusion. Du simulates the effect of concentration gradients on thermal energy flux in the flow domain. It is observed from Fig. 7 that a rise in Du from 0.06 to 1.00 boost up the influence of species gradients on the temperature so that temperature values are clearly enhanced, i.e., the fluid in the porous medium is heated up. The Sr values fall from 1.0 to 0.06 over this range so that the product of Sr and Du must remain constant, i.e., 0.06. Temperature continuously decreases in the boundary layer from wall to free stream. Concentration in the flow domain is increased as Sr increases from 0.06 to 1.0 as shown in Fig. 8. Thus, the mass transfer is boosted up with the increase of temperature gradients. These results concur with the trends in Anghel et al. [23], who solved the nonmagnetic Darcian case and also with Postelnicu [24], who considered the magnetic Darcian case.

Fig. 7.
figure 7

Temperature distribution for different Sr and Du.

Full size image
Fig. 8.
figure 8

Concentration distribution for different Sr and Du.

Full size image

The effect of Eckert number Ec on temperature is shown in Fig. 9 with fixed values of other parameters (M = 0.3, Q = 1.0, χ = 1.0, Sc = 0.22, Sr = 1.00, Du = 0.06). It is observed that an increase in Ec, from 0 (no viscous heating) to 1.0 (high viscous heating) clearly boosts temperature in the porous regime. Eckert number signifies the quantity of mechanical energy converted into thermal energy via internal friction, which is known as heat dissipation. Thus, the increase in Ec values will therefore cause an increase in thermal energy contributing to the flow; thereby the fluid will heat up.

Fig. 9.
figure 9

Temperature distribution for different Ec.

Full size image

The variation of velocity and temperature with the magnetic field parameter \(M\) keeping fixed values of other parameters (Ec = 0.2, Q = 1.0, χ = 1.0, Sc = 0.22, Sr = 1.00, Du = 0.06) is shown in Figs. 10–11. The presence of magnetic field in an electrically conducting fluid creates a drag-like force called the Lorentz force. This type of resistive force tends to slow down the motion of the fluid in the boundary layer, i.e., decelerates the flow, as shown in Fig. 10, where velocity (\(U\)) clearly decrease as \(M\) rises from 0 (electrically nonconducting case) to \(M = 2\). The relative influence of magnetic field on the fluid temperature has also been investigated in Fig. 11. The results show that the temperature is slightly increased as \(M\)increases. Hence, magnetic field retards the flow and heat the fluid in the porous regime.

Fig. 10.
figure 10

Velocity distribution for different M.

Full size image
Fig. 11.
figure 11

Temperature distribution for different M.

Full size image

The temperature and concentration with transverse coordinate for different Schmidt number Sc with constant values of other variables (M = 0.3, Ec = 0.2, Q = 1.0, χ = 1.0, Sr = 1.00, Du = 0.06) is illustrated in Figs. 12 and 13. An increase in Sc causes a considerable reduction in temperature as well as in the concentration. A greater reduction is observed in concentration than temperature. An increase in Sc will suppress concentration in the boundary layer regime. Higher Sc implies a decrease of molecular diffusivity (\(D\)), which causes a reduction in concentration boundary layer thickness. For \(\operatorname{Sc} = 1\), the momentum and concentration boundary layer thicknesses are approximately of same value, i.e., both species and momentum will diffuse at the same rate in the boundary layer.

Fig. 12.
figure 12

Temperature distribution for different Sc.

Full size image
Fig. 13.
figure 13

Concentration distribution for different Sc.

Full size image

5 CONCLUSIONS

On the basis of work presented in this chapter, the following observations are made:

(1) The velocity of fluid flow is boosted with weak chemical action. Thus, a weak chemical action reduces the momentum transfer, i.e., decelerates the flow.

(2) The increase in the heat absorption parameter reduces both velocity and temperature. Hence, a desired temperature can be sustained by controlling the heat absorption effect in practical chemical engineering applications.

(3) The increase in Dufour number (and simultaneously reducing Soret number) increases the temperature of the fluid, and the increase in Soret number (and simultaneously reducing the Dufour number) increases the concentration values, i.e., reduces the species diffusion from the wall.

(4) The increase in the magnetic parameter decreases the velocity in the regime.

(5) The increase in Eckert number heats up the porous regime, i.e., increases the temperature.

(6) The increase in Schmidt number reduces both temperature and concentration values in the porous regime.

(7) The skin friction coefficient decreases with a decrease in Soret number (and increase in Dufour number). It decreases with the increase in chemical action parameter as well as heat absorption parameter but increases with an increase in Eckert number.

(8) The rate of heat transfer increases initially as Soret number decreases, and then decreases with a subsequent lowering it. It decreases with a rise in Eckert number but increases with higher chemical action parameter values and also with an increase in heat absorption parameter. Thus, fast chemical reaction rate and heat absorption parameter can be used to enhance heat transfer rate in many industrial problems.

(9) The rate of mass transfer increases continuously with a decrease in Soret number (and an increase in Dufour number), and is also increased with a rise in Eckert number and chemical reaction parameter; however it decreases with an increase in heat absorption parameter.