Analysis of a delayed malaria transmission model including vaccination with waning immunity and reinfection

Abstract

To study the impact of infection delays in human and mosquito populations, vaccination with waning immunity and reinfection on the malaria transmission process, a malaria transmission model with these factors is developed and investigated. The local stability of disease-free and endemic equilibria have been discussed explicitly. By taking the delay as the bifurcation parameter, the existence of Hopf bifurcation is analyzed in four cases. Using normal form theory and center manifold theorem, direction and stability of Hopf bifurcation are discussed. Numerically, the bifurcation diagrams show that both delays can destabilize the endemic equilibrium and cause Hopf bifurcation and irregular oscillations, and that stability switches can occur mainly because of the delay in human. In addition, the malaria transmission case of Nigeria is studied. Numerical analysis reveals that ignoring the waning of immunity and reinfection may underestimate the infection risk and enlarge the critical value of Hopf bifurcation. Moreover, combined with sensitivity analysis, we can see that even though vaccination is not so effective in reducing the basic reproduction number, it is efficient for controlling the disease.

1 Introduction

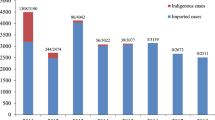
Malaria, caused by protozoan parasites, is a mosquito-borne disease affecting health systems and economies greatly. The World Health Organization (WHO) reports that 249 million cases of malaria and 608 thousand malaria deaths occurred globally in 2022 [1]. There are five parasite species that induce malaria in human: Plasmodium falciparum (P. falciparum), Plasmodium vivax (P. vivax), Plasmodium malariae (P. malariae), Plasmodium ovale (P. ovale), and Plasmodium knowlesi (P. knowlesi). Of which P. falciparum and P. vivax pose the greatest threat. In the WHO African Region, P. falciparum accounts for 99.7% of estimated malaria cases, while P. vivax is responsible for 74.1% of malaria cases in the WHO Region of Americas. Besides, a large proportion of malaria deaths worldwide is in four African countries in 2021: Nigeria (31.3%), the Democratic of the Congo (12.6%), United Republic of Tanzania (4.1%) and Niger (3.9%). Take Nigeria, for example. The death rate caused by malaria of this country is about 0.04% in 2021, and the number of population infected with malaria keeps increasing from 4% in 2014 to about 10% in 2021 (See Table 1 and Fig. 1).

Table 1 Reported cases (from [1]) and the population (from [2]) of Nigeria

We know that malaria is transmitted to human through the bitten by an infected female anopheline mosquito. And a susceptible mosquito get infected after it takes a blood meal from an infectious human. There are incubation periods in the two transmission processes [4,5,6]. In general, the time needed for mosquito to get infected is described as extrinsic incubation period (EIP) [7]. And the period for host population to get infected is intrinsic incubation period (IIP) [8].

To prevent and control the transmission of infectious diseases, vaccination is an effective way [9, 10]. Since October 2021, the WHO recommend the broad use of, RTS,S/AS01, the first malaria vaccine, among children living in regions with moderate to high P. falciparum malaria transmission [1]. In October 2023, the WHO recommended a second vaccine, R21/Matrix-M. Both are shown to be safe and effective and expected to have high health influence when implemented broadly. In fact, the immunity acquisition process is not easy and years or decades may be needed [11]. And waning of immunity and reinfection may happen since the immunity may waning over time in some extent. Therefore, it is necessary to investigate the influence of the extrinsic incubation period, intrinsic incubation period, vaccination with waning immunity and reinfection on malaria transmission process.

Mathematical modelling have being an important way for investigating the dynamics of infectious diseases long time ago. The first mathematical model depicting the transmission process of malaria was introduced by Ross [3], and refined by MacDonald [4]. From then on, the malaria transmission models were developed extensively [12,13,14,15,16]. In [17], considered waning immunity of vaccination and treatment, the authors established an ordinary malaria transmission model and studied the optimal control. Considering the reinfection of recovered class, Xu and Zhou [18] developed a malaria model with EIP and studied the Hopf bifurcation and stability. Wan and Cui [19] studied a malaria model with both EIP and IIP. Zhang et. al. extended their result by adding the reinfection effect in [8]. However, the influence of the vaccinated class wasn’t considered in these delayed models.

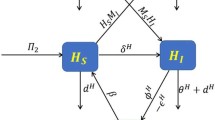
In this paper, we divide the human population into four classes: the susceptible $S_h(t)$, vaccinated V(t), infected $I_h(t)$, recovered $R_h(t)$ and divide the mosquito population into two classes: susceptible $S_m(t)$, infected $I_m(t)$. Taking the delays of malaria in human and mosquito, vaccination with waning of immunity and reinfection into account, we construct model (see Fig. 2)

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{dS_{h}(t) }{dt}=b_h(1-p)-\beta _hS_h(t-\tau _h)I_m(t-\tau _h)-(\mu _h+\eta )S_h(t),\\ \displaystyle \frac{d V(t) }{dt}= b_hp+\eta S_h(t)-\epsilon \beta _hV(t-\tau _h)I_m(t-\tau _h)-\mu _h V(t),\\ \displaystyle \frac{d I_h(t)}{dt}=\beta _h( S_h(t-\tau _h)+\epsilon V(t-\tau _h)+\sigma R_h(t-\tau _h))I_m(t-\tau _h)\\ \qquad -(\mu _h+\alpha +\gamma )I_h(t), \\ \displaystyle \frac{d R_h(t)}{dt}=\gamma I_h(t)-\sigma \beta _h R_h(t-\tau _h) I_m(t-\tau _h)-\mu _h R_h(t),\\ \displaystyle \frac{d S_m(t) }{dt}=b_m-\beta _m S_m(t-\tau _m)I_h(t-\tau _m)-\mu _m S_m(t),\\ \displaystyle \frac{d I_m(t) }{dt}=\beta _m S_m(t-\tau _m)I_h(t-\tau _m)- \mu _m I_m(t), \end{array} \right. \end{aligned}$$

(1.1)

where all parameters are positive and their meanings are described as follows: $\tau _h$: the incubation period in human (IIP), $\tau _m$: the incubation period in mosquito (EIP), $b_h$: recruitment rate of the human population, $b_m$: recruitment rate of the mosquito population, $\beta _h$: human transmission rate, $\beta _m$: mosquito transmission rate, $\mu _h$: natural death rate of human, $\mu _m$: natural death rate of mosquitoes, $\gamma$: recovery rate of infected human, $\alpha$: disease induced death rate, $\sigma \ (0\le \sigma \le 1)$: degree of partial protection for recovered individuals, $\epsilon \ (0\le \epsilon \le 1)$: the efficacy of vaccine, $p\ (0\le p\le 1)$: vaccination proportion of new borns, $\eta$: vaccination rate for susceptible class.

From the last two equations of model (1.1) we obtain that $N_m=S_m+I_m$ satisfies $\frac{dN_m}{dt}=b_m-\mu _mN_m.$ This implies that $\lim _{t\rightarrow \infty }N_m(t)=\frac{b_m}{\mu _m}$. Therefore, we can assume that $N_m(t)=S_m(t)+I_m(t)\equiv \frac{b_m}{\mu _m}$. Thus, by the limit system theory of differential equations [21], the dynamical behavior of model (1.1) is equivalent to the following model

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \frac{dS_{h}(t) }{dt}=b_h(1-p)-\beta _hS_h(t-\tau _h)I_m(t-\tau _h)-(\mu _h+\eta )S_h(t),\\ \displaystyle \frac{d V(t) }{dt}= b_hp+\eta S_h(t)-\epsilon \beta _hV(t-\tau _h)I_m(t-\tau _h)-\mu _h V(t),\\ \displaystyle \frac{d I_h(t)}{dt}=\beta _h( S_h(t-\tau _h)+\epsilon V(t-\tau _h)\\ \qquad +\sigma R_h(t-\tau _h))I_m(t-\tau _h)-(\mu _h+\alpha +\gamma )I_h(t), \\ \displaystyle \frac{d R_h(t)}{dt}=\gamma I_h(t)-\sigma \beta _h R_h(t-\tau _h) I_m(t-\tau _h)-\mu _h R_h(t),\\ \displaystyle \frac{d I_m(t) }{dt}=\beta _m(\frac{b_m}{\mu _m}- I_m(t-\tau _m))I_h(t-\tau _m)- \mu _m I_m(t). \end{array} \right. \end{aligned}$$

(1.2)

Fig. 1

The reported cases of malaria normalized by the population and the death rate during 2014–2021

Fig. 2

Schematic diagram for the transmission of malaria

This paper is arranged as follows. Basic properties are presented in Sect. 2. In Sect. 3, the local asymptotic stability of disease-free and endemic equilibria is established firstly. Then existence of Hopf bifurcation is investigated in four cases: (1) $\tau _h=0$ and $\tau _m>0$; (2) $\tau _h>0$ and $\tau _m=0$; (3) $\tau _h=\tau _m:=\tau >0$; and (4) $\tau _h\in (0,\tau ^*_h)$ and $\tau _m>0$, where (2)-(4) are studied under special condition. What’s more, direction and stability of Hopf bifurcation also are examined. In Sect. 4, Hopf bifurcation of these four cases for original model and special case are both simulated numerically. Besides, we apply our model to the transmission of malaria in Nigeria numerically. Finally, conclusions are summarized in Sect. 5.

2 Basic properties

Let $\mathbb {R}_{+}^5=\{(x_1,x_2,x_3,x_4,x_5): x_i\ge 0, i=1,2,3,4,5\}$ and $\tau =\max \{\tau _h,\tau _m\}$. For Banach space $C_{+}:=C([-\tau ,0],\mathbb {R}_{+}^5)$ consist of continuous functions from $[-\tau ,0]$ to $\mathbb {R}_{+}^5$, define the norm of $\phi =(\phi _1,\phi _2,\phi _3,\phi _4,\phi _5)\in C_{+}$ by $\Vert \phi \Vert =\max _{s\in [-\tau ,0]}\left( \sum _{i=1}^5|\phi _i|^2\right) ^{\frac{1}{2}}.$ Define $\mathbb { X}=\{\phi \in C_{+}:\phi _i(0)> 0,\ i=1,2,3,4,5\}.$ For any continuous function $u:[-\tau ,\sigma )\rightarrow \mathbb {R}_{+}^5$ with $\sigma >0$, define $u_t\in C_{+}$ for $t\in [0,\sigma )$ as $u_t(\theta )=u(t+\theta ),\forall \theta \in [-\tau ,0]$. From the fundamental theory of functional differential equations [22], we have the following well-posedness result of system (1.2), and the proof is presented in Appendix A.

Theorem 2.1

For any $\phi \in \mathbb { X}$, system (1.2) admits a unique solution $u(t,\phi )$ with $u_0=\phi$ and $u_t(\cdot ,\phi )\in \mathbb {X}$ for all $t\ge 0$, and solutions are uniformly and ultimately bounded.

Obviously, system (1.2) always has a disease-free equilibrium $P^0(S_h^0,V^0,0,0,0)$ with $S_h^0=\frac{b_h(1-p)}{\mu _h+\eta },\ V^0=\frac{b_h(\mu _h p+\eta )}{\mu _h(\mu _h+\eta )}.$ By linearizing the equations of $I_h$ and $I_m$ of model (1.2) at point $P_0$, we can obtain the Jacobia matrices as follows

$$\begin{aligned} F= \begin{pmatrix} 0 &{}\beta _hS_h^0+\epsilon \beta _hV^0 \\ \beta _m\frac{b_m}{\mu _m}&{} 0 \end{pmatrix},\;V= \begin{pmatrix} \mu _h+\alpha +\gamma &{} 0 \\ 0 &{} \mu _m \end{pmatrix}. \end{aligned}$$

According to [23], define the basic reproduction number by

$$\begin{aligned} R_0=\rho (FV^{-1})=\sqrt{\frac{\beta _hb_h\beta _mb_m\left( \mu _h(1-p)+\epsilon (\mu _hp+\eta )\right) }{\mu _m^2\mu _h(\mu _h+\eta )(\mu _h+\alpha +\gamma )}}, \end{aligned}$$

where $\rho (\cdot )$ presents the spectral radius of matrix.

Assume that $P^*(S_h^*,V^*,I_h^*,R_h^*,I_m^*)$ is the endemic equilibrium of system (1.2). Then we have

$$\begin{aligned} \begin{aligned} S_h^*&=\frac{b_h(1-p)}{\beta _h I_m^*+\mu _h+\eta },\; V^*=\frac{b_hp\beta _h I_m^*+b_hp\mu _h+b_h\eta }{(\epsilon \beta _hI_m^*+\mu _h)(\beta _hI_m^*+\mu _h+\eta )},\ R_h^*=\frac{\gamma I_h^*}{\sigma \beta _h I_m^*+\mu _h},\\ I_h^*&=\frac{(\epsilon \beta _h^2b_hI_m^*+\beta _hb_h\left( \mu _h(1-p)+\epsilon (p\mu _h+\eta )\right) )(\sigma \beta _hI_m^*+\mu _h)I_m^*}{(\epsilon \beta _h I_m^*+\mu _h)(\beta _h I_m^* +\mu _h+\eta )\left( (\mu _h+\alpha )(\sigma \beta _hI_m^*+\mu _h)+\mu _h\gamma \right) },\ \\&I_m^*=\frac{\beta _mb_m I_h^*}{ \beta _m b_mI_h^*+\mu _m^2}. \end{aligned} \end{aligned}$$

Substituting the expression of $I_m^*$ into $I_h^*$, we can get:

$$\begin{aligned} F_1(I_h^*)=F_2(I_h^*) \end{aligned}$$

(2.1)

with

$$\begin{aligned} \begin{aligned} F_1(y)&=\beta _m\left( \epsilon \beta _h^2 b_h y+\beta _hb_h(\mu _h(1-p)+\epsilon (p\mu _h+\eta ))\right) (\sigma \beta _h y+\mu _h)(b_m-\mu _m y),\\ F_2(y)&=\mu _m^2(\epsilon \beta _hy+\mu _h)(\beta _hy+\mu _h+\eta )\left( (\mu _h+\alpha )\sigma \beta _h y+\mu _h(\mu _h+\alpha +\gamma )\right) . \end{aligned} \end{aligned}$$

Fig. 3

Sketch profiles for $F_1(y)$ and $F_2(y)$

Therefore, the existence of endemic equilibrium of system (1.2) is equivalent to the existence of positive intersection point of functions $F_1(y)$ and $F_2(y)$. From the sketches in Fig. 3, we can see that there is a positive intersection point if $F_1(0)>F_2(0)$, and there is no positive intersection if $F_1(0)\le F_2(0)$. Moreover, $F_1(0)>F_2(0)\Leftrightarrow R_0> 1$. Thus, there is a unique endemic equilibrium when $R_0>1$ and there is no endemic equilibrium when $R_0\le 1$.

3 Stability and Hopf bifurcation

3.1 Stability of equilibria

The community matrix of system (1.2) at $P=(S_h,V,I_h,R_h,I_m)$ is given by $J(P)=L(P)+H(P)e^{-\lambda \tau _h}+M(P)e^{-\lambda \tau _m},$ where

$$\begin{aligned}&\small L(P)= \begin{pmatrix} l_{11} &{} 0 &{} 0 &{} 0 &{} 0\\ l_{21} &{} l_{22} &{} 0 &{} 0 &{}0\\ 0 &{} 0 &{} l_{33} &{} 0 &{} 0\\ 0 &{} 0 &{} l_{43} &{} l_{44} &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} l_{55} \end{pmatrix},\; H(P)= \begin{pmatrix} h_{11} &{} 0 &{} 0 &{} 0 &{} h_{15}\\ 0 &{} h_{22} &{} 0 &{} 0 &{}h_{25}\\ h_{31} &{} h_{32} &{} 0 &{} h_{34} &{} h_{35}\\ 0 &{} 0 &{} 0 &{} h_{44} &{} h_{45}\\ 0 &{} 0 &{} 0 &{} 0&{} 0 \end{pmatrix},\\&M(P)= \begin{pmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{}0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} m_{53} &{} m_{55} \end{pmatrix} \end{aligned}$$

with $l_{11}=-\mu _h-\eta ,\; l_{21}=\eta ,\; l_{22}=-\mu _h,\; l_{33}=-(\mu _h+\alpha +\gamma ),\; l_{43}=\gamma ,\; l_{44}=-\mu _h,\ l_{55}=-\mu _m,\;h_{11}=-\beta _h I_m,\; h_{15}=-\beta _h S_h,\; h_{22}=-\epsilon \beta _h I_m,\; h_{25}=-\epsilon \beta _h V,\ h_{31}=\beta _h I_m,\; h_{32}=\epsilon \beta _h I_m,\; h_{34}=\sigma \beta _h I_m,\; h_{35}=\beta _h(S_h+\epsilon V+\sigma R_h),\ h_{44}=-\sigma \beta _h I_m,\; h_{45}=-\sigma \beta _h R_h,\; m_{53}=\beta _m (\frac{b_m}{\mu _m}-I_m),\; m_{55}=-\beta _m I_h.$ The characteristic equation of J(P) is $|J(P)-\lambda E|=0$, i.e.,

$$\begin{aligned} \left| \begin{matrix} a_{11}-\lambda &{} 0 &{} 0 &{} 0 &{} h_{15}e^{-\lambda \tau _h}\\ l_{21} &{} a_{22}-\lambda &{} 0 &{} 0 &{}h_{25}e^{-\lambda \tau _h}\\ h_{31}e^{-\lambda \tau _h} &{} h_{32}e^{-\lambda \tau _h} &{} l_{33}-\lambda &{} h_{34}e^{-\lambda \tau _h} &{} h_{35}e^{-\lambda \tau _h}\\ 0 &{} 0 &{} l_{43} &{} a_{44}-\lambda &{} h_{45}e^{-\lambda \tau _h}\\ 0 &{} 0 &{} m_{53}e^{-\lambda \tau _m}&{} 0 &{} a_{55}-\lambda \end{matrix}\right| =0, \end{aligned}$$

where $a_{ii}=l_{ii}+h_{ii}e^{-\lambda \tau _h}\;(i=1,2,4)$ and $a_{55}=l_{55}+m_{55}e^{-\lambda \tau _m}$. For the disease-free equilibrium $P^0$, the characteristic equation is

$$\begin{aligned} (l_{11} -\lambda ) (l_{22} -\lambda )(l_{44} -\lambda )\left( \lambda ^2-(l_{33} +l_{55} )\lambda +l_{55} l_{33} (1-R_0^2e^{-\lambda \tau _h}e^{-\lambda \tau _m})\right) =0.\nonumber \\ \end{aligned}$$

(3.1)

For the endemic equilibrium $P^*(S_h^*,V^*,I_h^*,R_h^*,I_m^*)$, the characteristic equation is

$$\begin{aligned}&\lambda ^5 +\sum _{j=4}^0u_{ 0j}\lambda ^j+ \sum _{j=4}^0u_{ 1j}\lambda ^je^{-\lambda \tau _m} +\sum _{j=4}^0u_{ 2j}\lambda ^je^{-\lambda \tau _h}\nonumber \\ {}&\displaystyle +\sum _{j=3}^0u_{ 3j}\lambda ^je^{-\lambda (\tau _h+\tau _m)} +\sum _{j=3}^0u_{ 4j}\lambda ^je^{-2\lambda \tau _h} +\sum _{j=2}^0u_{ 5j}\lambda ^je^{-\lambda (\tau _m+2\tau _h)}\nonumber \\ {}&\displaystyle +\sum _{j=2}^0u_{ 6j}\lambda ^je^{-3\lambda \tau _h}+\sum _{j=1}^0u_{ 7j}\lambda ^je^{-\lambda (\tau _m+3\tau _h)}\ +u_{80}e^{-\lambda (\tau _m+4\tau _h)}=0, \end{aligned}$$

(3.2)

where coefficients $u_{kj}\;(k=0,1,2,3,\ j=0,1,2,3,4)$, $u_{71}$, $u_{70}$ and $u_{80}$ are given in Appendix B.

Remark 3.1

On account of the appearance of two efficient malaria vaccine RTS,S/AS01 and R21/Matrix-M, the vaccinated component is considered. Besides, factors of vaccination with waning immunity, reinfection and delays in human and mosquitoes are taken into consideration in our malaria model, which extends previous malaria models [8, 18]. In fact, he form of the characteristic equation (3.2) is quite different and generalizes previous ones, and therefore, Theorems 3.2–3.6 in the following are generalizations of corresponding results in [8, 18].

According to the characteristic equations (3.1) and (3.2), we have the following stability results for the disease-free and endemic equilibria, respectively.

Theorem 3.2

• (i) For any $\tau _m\ge 0$ and $\tau _h\ge 0$, if $R_0<1$, then disease-free equilibrium $P^0$ is locally asymptotically stable.

• (ii) When $\tau _h=\tau _m=0$, if $R_0> 1,$ then endemic equilibrium $P^*$ is locally asymptotically stable if $D_j>0\;(j=1,2,3,4)$, where $D_j\;(j=1,2,3,4)$ are presented in Appendix B.

The proof of Theorem 3.2 is given in Appendix C.

3.2 Existence of Hopf bifurcation

We know that all zero points of Eq. (3.1) have negative real parts if $R_0<1$. Roots of Eq. (3.1) are continuously dependent on delays [24], and only when a root crossing the imaginary axis its real part of a root can become positive. On account of $\lambda =0$ is not a root of Eq. (3.1), the real part of roots for Eq. (3.1) can become positive when $\lambda =i\kappa , \kappa \ne 0$.

For various delays $\tau _m$ and $\tau _h$, we have the following theorems about the existence of Hopf bifurcation.

Theorem 3.3

Assume the delay $\tau _h=0$ in model (1.2). When $R_0> 1,$ then there is a $\tau _m^*>0$ such that (1) $P^*$ is locally asymptotically stable if $\tau _m\in [0,\tau _{m}^*)$; (2) system (1.2) undergoes a Hopf bifurcation at $P^*$ when $\tau _m=\tau _{m}^*$, and a family of periodic solutions bifurcate from $P^*$.

The proof of Theorem 3.3 is given in Appendix C.

However, for the cases $\tau _h>0,\ \tau _m=0$ and $\tau _h>0,\ \tau _m>0$, characterization Eq. (3.2) is too complicated to analyze. Therefore, we suppose $\epsilon =\sigma =0$ for simple. When $\epsilon =\sigma =0$, we have $h_{25}=h_{22}=h_{32}=h_{34}=h_{44}=h_{45}=0$. And then characteristic equation (3.2) is reduced to

$$\begin{aligned} \begin{array}{lll} \displaystyle \lambda ^5 +\sum _{j=4}^0p_{ 0j}\lambda ^j+ \sum _{j=4}^0p_{ 1j}\lambda ^je^{-\lambda \tau _m} +\sum _{j=4}^0p_{ 2j}\lambda ^ie^{-\lambda \tau _h} +\sum _{j=3}^0p_{ 3j}\lambda ^je^{-\lambda (\tau _h+\tau _m)}=0, \end{array}\nonumber \\ \end{aligned}$$

(3.3)

where $p_{kj}\;(k=0,1,2,~ j=0,1,2,3,4)$ and $p_{3j}\;(j=0,1,2,3)$ are presented in Appendix B.

Theorem 3.4

Assume $\epsilon =\sigma =0$ and $\tau _m=0$ in model (1.2). When $R_0> 1$, then there is a $\tau _h^*>0$ such that (1) $P^*$ is locally asymptotically stable if $\tau _h\in [0,\tau _{h}^*)$; (2) system (1.2) undergoes a Hopf bifurcation at $P^*$ when $\tau _h=\tau _{h}^*$, and a family of periodic solutions bifurcate from $P^*$.

Theorem 3.5

Assume $\epsilon =\sigma =0$ and $\tau _m=\tau _h:=\tau >0$ in model (1.2). When $R_0> 1$, then there is a $\tau ^*>0$ such that (1) $P^*$ is locally asymptotically stable if $\tau \in [0,\tau ^*)$; (2) system (1.2) undergoes a Hopf bifurcation at $P^*$ when $\tau =\tau ^*$, and a family of periodic solutions bifurcate from $P^*$.

Theorem 3.6

Assume $\epsilon =\sigma =0$ and a fixed $\tau _h\in (0,\tau _h^*)$ in model (1.2). When $R_0> 1$, then there is a $\hat{\tau }_m>0$ such that (1) $P^*$ is locally asymptotically stable if $\tau _m\in [0,\hat{\tau }_{m} )$; (2) system (1.2) undergoes a Hopf bifurcation at $P^*$ when $\tau _m=\hat{\tau }_{m}$, and a family of periodic solutions bifurcate from $P^*$.

The proofs of Theorems 3.4-3.6 are given in Appendix C.

3.3 Direction and stability of Hopf bifurcation

Previously, we have proved that system (1.2) admits a family of periodic solutions bifurcating from the endemic equilibrium $P^*$ in various critical values of delay parameters. In this subsection, we derive explicit formula to determine the direction as well as stability of Hopf bifurcation at critical value $\hat{\tau }_m$ applying the normal form theory and the center manifold theorem by Hassard et al. [25]. In the following, for special case $\epsilon =\sigma =0$, we assume $\tau _h\in (0,\tau _h^*)$ with $\tau _h^*<\hat{\tau }_m$ and.

Theorem 3.7

(i) The direction of the Hopf bifurcation is determined by the sign of $\mu _2$. If $\mu _2>0$ $(\mu _2<0)$, then it is a supercritical (subcritical) bifurcation. (ii) The stability of the bifurcated periodic solution is determined by $\beta _2$. The periodic solution is stable (unstable) if $\beta _2<0$ $(\beta _2>0)$. (iii) The period of bifurcated periodic solutions is determined by $T_2$. The size of period increases (decreases) if $T_2>0$ $(T_2<0)$.

The expressions of parameters $\mu _2$, $\beta _2$ and $T_2$ in Theorem 3.7, and the proof of Theorem 3.7 are given in Appendix B.

4 Numerical simulatons

In this section, we first simulate the phenomenon of Hopf bifurcation in four cases. Then we simulate the reported cases of Nigeria with model (1.2). Based on the estimated parameters, we get that the basic reproduction number of Nigeria is about 5.1448. Therefore, the disease in Nigeria will be endemic. To present some control suggestions for Nigeria, sensitivity analysis is shown by partial rank correlation coefficient (PRCC).

4.1 Simulations of Hopf bifurcation

Choosing $\beta _h=0.01$, $\beta _m=0.01$, $b_h=70$, $b_m=10$, $\alpha =0.1$, $\mu _h=0.4$, $\mu _m=0.1$, $\gamma =1$, $\eta =0.1$, $p=0.02$, $\sigma =0.2$ and $\epsilon =0.2,$ then $P^*=(53.51,12.13,35.89,64.5,78.21)$ and $R_0=3.1066>1$. When $\sigma =\epsilon =0$, then $P^*=( 55.73,17.43,27.16,67.89, 73.08)$ and $R_0=3.0243>1$.

Fig. 4

Case (1): the first column is for $\epsilon ,\sigma >0$, the second column is for $\epsilon =\sigma =0$

Fig. 5

Case (2): the first column is for $\epsilon ,\sigma >0$, the second column is for $\epsilon =\sigma =0$

Fig. 6

Case (3): the first column is for $\epsilon ,\sigma >0$, the second column is for $\epsilon =\sigma =0$

Fig. 7

Case (4): the first column is for $\epsilon ,\sigma >0$, the second column is for $\epsilon =\sigma =0$

Fig. 8

Left is the MCMC analysis of parameters $\beta _h,\beta _m,\gamma ,\sigma ,\epsilon ,p,\eta$; Right is the simulation and prediction of of the reported malaria cases for Nigeria from 2014 to 2021

Fig. 9

Solution curves of system (1.2) for $R_0>1$ and $R_0<1$

Fig. 10

Partial rank correlation coefficients (PRCCs) for $R_0$

Fig. 11

The dependence of $R_0$ on $\beta _h,\beta _m,\mu _m,\gamma ,b_m,p,\eta$

Fig. 12

The dependence of $p,\eta ,\epsilon ,\sigma$ on $I_h(t)$

In Sect. 3.2, we have shown the existence of Hopf bifurcation for cases (1): $\tau _h=0$, $\tau _m>0$; (2): $\tau _h>0, \tau _m=0$; (3): $\tau _h=\tau _m=\tau >0;$ (4): $\tau _h\in (0,\tau _h^*), \tau _m>0$, where cases (2)-(4) are analyzed under special condition $\epsilon =\sigma =0$. In this subsection, we demonstrate the Hopf bifurcation theorems through numerical simulations in four different cases. In particular, we also simulate the dynamical behaviors of cases (1)-(4) for $\epsilon ,\sigma >0$ and $\epsilon =\sigma =0$.

Case (1): $\tau _h=0,\ \tau _m>0$. By calculating, we obtain $\nu _0=0.081,\ \kappa _0=0.29$ and $\tau _m^*=6.71$, $\mathcal {L}^{'}(\nu _0)=0.49\ne 0$. We can see from the first column of Fig. 4 that $P^*$ is locally asymptotically stable when $\tau _m\in [0,\tau _m^*)$, and unstable for larger $\tau _m$, leading to irregular oscillations. In addition, system (1.2) undergoes a Hopf bifurcation when $\tau _m$ cross $\tau _m^*$ and a family of periodic solutions bifurcate from $P^*$ near $\tau _m^*$. Last but not the least, comparing the first column and second column in Fig. 4, we can obtain that when $\epsilon$ and $\sigma$ go to zero, the critical value of $\tau _m^*$ becomes larger.

Case (2): $\tau _m=0,\ \tau _h>0$. We can see from Fig. 5 that $P^*$ is locally asymptotically stable when $\tau _h\in [0,\tau _h^*)$, and unstable for larger $\tau _h$. In addition, system (1.2) undergoes a Hopf bifurcation when $\tau _h=\tau _h^*$ and a family of periodic solutions bifurcate from $P^*$ near $\tau _h^*$. Similarly, comparing the first column and second column we can obtain that when $\epsilon$ and $\sigma$ go to zero, the critical value becomes larger.

Case (3): $\tau _h=\tau _m=\tau >0$. When $\epsilon =\sigma =0$, we obtain $\kappa _2=0.56$ and $\tau ^*=2.69$, $e_2e_3-e_1e_4=0.45\ne 0$. We can see from Fig. 6 that $P^*$ is locally asymptotically stable when $\tau \in [0,\tau ^*)$, and unstable for larger $\tau$. In addition, system (1.2) undergoes a Hopf bifurcation when $\tau =\tau ^*$, and a family of periodic solutions bifurcate from $P^*$ near $\tau ^*$. Similarly, when $\epsilon$ and $\sigma$ go to zero, the critical value of $\tau ^*$ becomes larger.

Case (4): $\tau _h\in (0,\tau _h^*),\ \tau _m>0$. When $\tau _h=2.8$, Eq. (5.16) has three positive roots $\hat{\kappa }_1=0.89$, $\hat{\kappa }_2=0.625$, $\hat{\kappa }_3=0.20$. When $\hat{\kappa }=\hat{\kappa }_1=0.89$, we get three critical values $\hat{\tau }_{m1} =0.55$, $\hat{\tau }_{m2} =5.03$, and $\hat{\tau }_{m3} =9.99$ with $q_1q_4-q_2q_3$ equals 2.84, 2.42, 0.019 nonzero respectively. Under this condition, stability switches occur see second column of Fig. 7. Similarly, comparing the first row with second row in Fig. 7, we can obtain that when $\epsilon$ and $\sigma$ go to zero, the critical values becomes larger. In addition, we can see from Fig. 7 that the delay in human has great influence on behaviors of the infected class and vaccinated class. Besides, from the first two rows and the third row one can see that influences of human delays on infected class and vaccinated class are different and that with the increase of incubation period of human the dynamical behaviors of both classes become more complex. Finally, if compare Fig. 7 with Fig. 4, 5, we know the delays in mosquito and human are both non-negligible for malaria transmission model (1.2).

4.2 Application to Nigeria

In this subsection, model (1.2) is used to simulate the reported malaria cases in Nigeria [1]. Some parameters values are chosen based on references and some are to match the data. We explain part of them in the following.

The Birth rate of Nigeria is 3.38% [26], and the total population of Nigeria in 2021 is $2.134\times 10^8$. Therefore, the recruitment is taken by $6.06\times 10^6$ year$^{-1}$. We assume the birth rate of mosquitoes is $10^6$. The Life span of human in Nigeria is 61–64 [27]. So the corresponding death rate $\mu _h$ is taken 0.016. The average disease induced death rate is $7.39\times 10^{-4}$ by data in Table 1. The average life expectancy of adult mosquito is about 15 to 20 days. Here we take $\mu _m$ to be 22 year$^{-1}$. Incubation period in human beings is 7–15 days [7], here we take $\tau _h$ to be 0.027. Incubation period in mosquito is 10-30 days [7], here we take $\tau _m$ to be 0.082.

We choose 2014 as the initial time, and suppose initial value to be $(2\times 10^8,2\times 10^7,8572322,10^7,3\times 10^5)$. Based on these parameter values and data in Table 1, applying Markov-chain Monte-Carlo (MCMC), we can obtain, $\beta _h=1.1139\times 10^{-6},\ \beta _m=5.0381\times 10^{-7},\ \gamma =0.0997,\ \sigma =0.0201,\ \epsilon =0.4233,\ p=0.0505$ and $\eta =0.0033$ respectively (see Fig. 8). Besides, there is an appropriate match between malaria cases of Nigeria and model (1.2) (see Fig. 8).

Based on the estimated parameters, we get that the basic reproduction number of Nigeria is about 5.1448 and there is an endemic equilibrium $P^*=(2.2644\times 10^7,3.2996\times 10^6,6.0226\times 10^7,2.8980\times 10^8, 2.108\times 10^5)$. Besides, we have coefficients in Theorem 3.2 are $D_1=0.2203,D_2=0.7652,D_3=15.8331,D_4=833.92>0$. Therefore, $P^*$ is locally asymptotically stable when $\tau _m=\tau _h=0$, as shown in Fig. 9. In addition, when $\beta _h=1.1139\times 10^{-8}$, then $R_0=0.5145<1$ and the disease-free equilibrium is locally asymptotically stable, see Fig. 9.

4.3 Sensitivity analysis

To investigate the sensitivity of the basic reproduction number $R_0$ with respect to parameters, we calculate the partial rank correlation coefficient (PRCC), which reflects the dependence correlation between each parameter and $R_0$. We take a normal distribution for each of the six parameters: $\beta _h,\beta _m,p,\epsilon ,\eta ,\gamma$. Every parameters is sampled 3000 times. The correlation between input parameter and output values of $R_0$ is significant if $p<0.01$. The PRCC bar chart is in Fig. 10, which indicates that parameters $\beta _h,\beta _m,\epsilon$ are positively correlated with $R_0$ and parameters $p,\eta ,\gamma$ are negatively correlated with $R_0$. Therefore, reducing contact rate between human and mosquito, waning of immunity as well as increase vaccination rate and treatment of infected humans can reduce the value of $R_0$ effectively. In addition, from Fig. 11, we can see the influence of parameters $\beta _h,\beta _m,b_m,\mu _m,\gamma ,p$ on the basic reproduction number more directly.

The influence of vaccinated rate of newborns and susceptible as well as the reinfection rate and waning of immunity rate on the disease can be seen more directly in Fig. 12. It shows that neglecting the reinfection rate and immunity rate, the risk will be underestimated. and that the vaccination strategy should be enforced regardless of its direct efficacy in reducing the basic reproduction number.

5 Conclusions and discussions

In this paper, a malaria transmission model with delays, vaccination with waning immunity and reinfection is developed and investigated. Dynamical behaviors including stability of equilibria, the existence of Hopf bifurcations and direction and stability of delay induced Hopf bifurcation are analyzed. As an example, our model is used to simulate the reported cases of malaria in Nigeria. Based on our analysis, some suggestions are given on the control of malaria in Nigeria. (i) Using the long-lasting insecticide-treated mosquito net extensively; (ii) Using indoor spraying, biocontrol (such as Wolbachia) [28, 29] to control the mosquito population; (iii) Make sure infected people treated timely; (iv) Screening the recovered and vaccine class regularly; (v) Let newborns and susceptible class inoculate malaria vaccine in the country.

However, how to allocate the limited vaccine resources in the country isn’t studied in this paper. We will consider this problem in the future.

Appendices

Proof of Theorem 3.3

For any $\phi \in \mathbb {X}$, define a functional $g(\phi ):=(g_1(\phi ),g_2(\phi ),g_3(\phi ),g_4(\phi ),g_5(\phi ))^T:\mathbb {X}\rightarrow \mathbb {R}^5$ as

$$\begin{aligned} g(\phi )= \begin{pmatrix} \displaystyle b_h(1-p)-\beta _h\phi _1(-\tau _h)\phi _5(-\tau _h)-(\mu _h+\eta )\phi _1(0) \\ \displaystyle b_hp+\eta \phi _1(0)-\epsilon \beta _h\phi _2(-\tau _h)\phi _5(-\tau _h)-\mu _h \phi _2(0) \\ \displaystyle \beta _h( \phi _1(-\tau _h)+\epsilon \phi _2(-\tau _h)+\sigma \phi _4(-\tau _h))\phi _5(-\tau _h)-(\mu _h+\alpha +\gamma )\phi _3(0)\\ \displaystyle \gamma \phi _3(0)-\sigma \beta _h \phi _4(-\tau _h) \phi _5(-\tau _h)-\mu _h \phi _4(0)\\ \displaystyle \beta _m(\frac{b_m}{\mu _m}- \phi _5(-\tau _m))\phi _3(-\tau _m)- \mu _m \phi _5(0) \end{pmatrix}. \end{aligned}$$

Since $g(\phi )$ is continuous and Lipschitz in each compact set in $\mathbb {X}$, it follows from Theorems 2.2.1 and 2.2.3 in [22] that there exists a unique solution $u(t,\phi )=(S_h(t,\phi ),V(t,\phi ),I_h(t,\phi ),R_h(t,\phi ), I_m(t,\phi ))$ with respect to initial value $\phi$. So the system (1.2) has a unique solution $u(t,\phi )$ on its maximal existence interval $[0,\sigma _\phi )$. It is easy to see that $g_i(\phi )\ge 0$ if $\phi _i(0)\ge 0$, for $i=1,2,3,4,5$. Therefore, we can get the unique solution $u(t,\phi )$ on $\forall t\in [0,\sigma _\phi )$ which is non-negative.

Furthermore, let $N_h(t):=S_h(t)+V(t)+I_h(t)+R_h(t)$, it is easy to get from system (1.2) that $\frac{dN_h(t)}{dt}=b_h-\mu _hN_h-\alpha I_h$, which implies $\limsup _{t\rightarrow \infty }N_h(t)\le \frac{b_h}{\mu _h}$. Besides, $\limsup _{t\rightarrow \infty }N_m(t)=\frac{b_m}{\mu _m}$. Therefore, $u(t,\phi )$ is bounded. And then $\sigma _\phi =\infty$ by Theorem 2.3.1 in [22]. The proof is completed.

Coefficients of the characteristic equations

$$\begin{aligned} u_{04}&=- l_{11} - l_{22} - l_{33} - l_{44} - l_{55},\\ u_{03}&= l_{11} l_{22} + l_{11} l_{33} + l_{11} l_{44} + l_{22} l_{33} + l_{11} l_{55} + l_{22} l_{44} + l_{22} l_{55} + l_{33} l_{44} + l_{33} l_{55} + l_{44} l_{55},\\ u_{02}&=- l_{11} l_{22}( l_{33} + l_{44} + l_{55}) - l_{11} l_{33} ( l_{44} + l_{55} ) - l_{22} l_{55}(l_{33} + l_{44} )\\&\quad - l_{44} l_{55} (l_{33}+ l_{11})- l_{22} l_{33} l_{44},\\ u_{01}&= l_{11} l_{22} l_{33} l_{44} + l_{11} l_{22} l_{33} l_{55} + l_{11} l_{22} l_{44} l_{55} + l_{11} l_{33} l_{44} l_{55} + l_{22} l_{33} l_{44} l_{55},\\ u_{00}&=- l_{11} l_{22} l_{33} l_{44} l_{55},\; u_{14}=- m_{55},\; u_{13}= l_{11} m_{55} + l_{22} m_{55} + l_{33} m_{55} + l_{44} m_{55},\\ u_{12}&=-m_{55} ( l_{11} l_{22} + l_{11} l_{33} + l_{11} l_{44} + l_{22} l_{33} + l_{22} l_{44} + l_{33} l_{44}),\\ u_{11}&=m_{55} ( l_{11} l_{22} l_{33} + l_{11} l_{22} l_{44} + l_{11} l_{33} l_{44} + l_{22} l_{33} l_{44}),\\ u_{10}&=- l_{11} l_{22} l_{33} l_{44} m_{55},\; u_{24}=- h_{11} - h_{22} - h_{44},\\ u_{23}&=h_{11} ( l_{22} + l_{33}+ l_{44}+ l_{55} ) + h_{22} ( l_{11} + l_{33} + l_{44}+ l_{55})\\&\quad + h_{44} ( l_{11} + l_{22}+ l_{33} + l_{55}) - h_{34} l_{43},\\ u_{22}&= - h_{11} ( l_{22} ( l_{44}+ l_{33}+ l_{55})+ l_{33} ( l_{44}+ l_{55}) + l_{44} l_{55}) - h_{22} ( l_{33} (l_{44}+ l_{55})\\&\quad + l_{44} l_{55}+ l_{11} ( l_{33} + l_{44} + l_{55}))\\&\quad - h_{44} ( l_{11} ( l_{22} + l_{33}+ l_{55}) - l_{33} (l_{55} + l_{22} )- l_{22} l_{55}) + h_{34} l_{43} (l_{22} + l_{55} + l_{11}), \\ u_{21}&= h_{11} l_{22} ( l_{33} l_{44} + l_{33} l_{55}+ l_{44}l_{55} )+ l_{33} l_{44} l_{55}(h_{11}+ l_{33} l_{44} l_{55}) \\ {}&\quad + h_{22} l_{11} ( l_{33} l_{44} + l_{33} l_{55}+ l_{44} l_{55})\\&\quad - h_{34} l_{11}l_{43} ( l_{22} - l_{55}) - h_{34} l_{22} l_{43} l_{55}+ h_{44} l_{11} l_{22} ( l_{33} + l_{55} )\\ {}&\quad + h_{44} l_{33} l_{55}(l_{11}+ l_{22} ),\\ u_{20}&= h_{34} l_{11} l_{22} l_{43} l_{55} - h_{22} l_{11} l_{33} l_{44} l_{55} - h_{11} l_{22} l_{33} l_{44} l_{55}- h_{44} l_{11} l_{22} l_{33} l_{55},\\ u_{33}&= h_{11} m_{55} + h_{22} m_{55} - h_{35} m_{53} + h_{44} m_{55},\\ u_{32}&= -h_{11} m_{55}(l_{22} + l_{33} + l_{44} ) - h_{22} m_{55}(l_{11} + l_{33} + l_{44} )+ h_{34} l_{43} m_{55}\\&\quad - h_{44} m_{55}( l_{11}+ h_{44} m_{55}+ l_{33} )+ h_{35} m_{53}(l_{44} + l_{11} + l_{22} ),\\ u_{31}&= h_{11} m_{55} (l_{22} l_{33}+ l_{22} l_{44} + l_{33} l_{44} )+ h_{22}m_{55} (l_{11} l_{33} + l_{11} l_{44} + l_{33} l_{44} )\\&\quad - h_{35}m_{53} (l_{11} l_{22} + l_{11} l_{44} + l_{22} l_{44} )\\&\quad + h_{44} m_{55}(l_{11} l_{22}+ l_{11} l_{33} + l_{22} l_{33} ) - h_{34} l_{43} m_{55}(l_{11} + l_{22}),\\ u_{30}&=- ( l_{33} l_{44} m_{55}(h_{11} l_{22} + h_{22} l_{11} ) - h_{34} l_{11} l_{22} l_{43} m_{55} - h_{35} l_{11} l_{22} l_{44} m_{53}\\ {}&\quad + h_{44} l_{11} l_{22} l_{33} m_{55}),\\ u_{43}&= h_{11} h_{22} + h_{11} h_{44} + h_{22} h_{44},\\ u_{42}&= h_{11} (h_{34} l_{43} - h_{22} ( l_{44}+ l_{55} + l_{33})- h_{44} (l_{22} + l_{33}+ l_{55}))\\&\quad +h_{22}( h_{34} l_{43} - h_{44} ( l_{33}+ l_{11}+ l_{55})),\\ u_{41}&= h_{11} h_{22} l_{44} (l_{33}+ l_{55}) - h_{11} h_{34} l_{43}(l_{22} + l_{55}) + h_{11} l_{33} l_{55} (h_{44} + h_{22}) \\ {}&\quad + h_{11} h_{44} l_{22} ( l_{33}+ l_{55})\\&\quad - h_{22} h_{34} l_{43}(l_{11} + l_{55})+ h_{22} h_{44} l_{11} ( l_{33} + l_{55})+ h_{22} h_{44} l_{33} l_{55},\\ u_{40}&=h_{11} l_{55} ( h_{34} l_{22} l_{43} - h_{22} l_{33} l_{44} ) - h_{11} h_{44} l_{22} l_{33} l_{55} \\ {}&\quad + h_{22} h_{34} l_{11} l_{43} l_{55} - h_{22} h_{44} l_{11} l_{33} l_{55},\\ u_{52}&= -h_{11}(m_{55}(h_{22} + h_{44} )- h_{35} m_{53} ) - m_{53} ( h_{15} h_{31}- h_{35}( h_{22}+ h_{44}) \\&\quad + h_{25} h_{32} + h_{34} h_{45} )- h_{22} h_{44} m_{55},\\ u_{51}&= m_{53}(- h_{11} h_{35}( l_{22} + l_{44})+ h_{15} h_{31} ( l_{22} + l_{44} ) - h_{15} h_{32} l_{21} - h_{22} h_{35}( l_{11} + l_{44}),\\&\quad + h_{25} h_{32} ( l_{11} + l_{44}) + h_{34} h_{45} l_{11} - h_{35} h_{44} ( l_{11} + l_{22}) + h_{34} h_{45} l_{22} )+ m_{55}( h_{11} h_{22} ( l_{33} + l_{44} ), \\&\quad + h_{11} ( h_{44} l_{22} - h_{34} l_{43} + h_{44} l_{33})+ h_{22} (h_{44} l_{11}- h_{34} l_{43} + h_{44} l_{33} ) ),\\ u_{50}&= - h_{11} m_{55} (h_{22} l_{33} l_{44} - h_{34} l_{22} l_{43} + h_{44} l_{22} l_{33} )+ m_{53}(h_{11} h_{35} l_{22} l_{44}\\&\quad + h_{25} h_{32} l_{11} l_{44}- h_{35} h_{44} l_{11} l_{22} )\\&\quad - h_{15} l_{44} m_{53}( h_{31} l_{22}- h_{32} l_{21} ) + h_{22} l_{44} m_{53}(h_{35} l_{11}- h_{44} l_{33})\\&\quad - h_{34} ( h_{45} l_{11} l_{22} m_{53} - h_{22} l_{11} l_{43} m_{55}),\\ u_{62}&=- h_{11} h_{22} h_{44},\; u_{61}= h_{11} h_{22} h_{44} l_{33} - h_{11} h_{22} h_{34} l_{43} + h_{11} h_{22} h_{44} l_{55},\\ u_{60}&= h_{11} h_{22} h_{34} l_{43} l_{55} - h_{11} h_{22} h_{44} l_{33} l_{55},\\ u_{71}&= h_{11} h_{25} h_{32} m_{53} - h_{11} h_{22} h_{35} m_{53} + h_{15} h_{22} h_{31} m_{53} + h_{11} h_{22} h_{44} m_{55} \\ {}&\quad + h_{11} h_{34} h_{45} m_{53}\\&\quad - h_{11} h_{35} h_{44} m_{53} + h_{15} h_{31} h_{44} m_{53} + h_{22} h_{34} h_{45} m_{53} \\ {}&\quad - h_{22} h_{35} h_{44} m_{53} + h_{25} h_{32} h_{44} m_{53},\\ u_{70}&= - h_{11} h_{22} ( h_{44} l_{33} m_{55} - h_{35} l_{44} m_{53}- h_{34} l_{43} m_{55}) - h_{11} m_{53} (h_{25} h_{32} l_{44}\\&\quad + h_{34} h_{45} l_{22}- h_{35} h_{44} l_{22}) \\&\quad - h_{15} m_{53}( h_{22} h_{31} l_{44} + h_{31} h_{44} l_{22} - h_{32} h_{44} l_{21} )\\&\quad - h_{22} l_{11} m_{53}( h_{34} h_{45} - h_{35} h_{44} ) + h_{25} h_{32} h_{44} l_{11} m_{53},\\ u_{80}&=-m_{53} ( h_{11} h_{22} h_{34} h_{45} - h_{11} h_{22} h_{35} h_{44} + h_{11} h_{25} h_{32} h_{44} + h_{15} h_{22} h_{31} h_{44}).\\ p_{04}&=- l_{11} - 2 l_{22} - l_{33} - l_{55},\; p_{03}= 2 l_{11} l_{22} + l_{11} l_{33} + 2 l_{22} l_{33} + l_{11} l_{55} \\&\quad + 2 l_{22} l_{55} + l_{33} l_{55} + l_{22}^2,\\ p_{02}&=- l_{11} l_{22}^2 - l_{22}^2 l_{33} - l_{22}^2 l_{55} - l_{22}^2 m_{55} - 2 l_{11} l_{22} l_{33} - 2 l_{11} l_{22} l_{55} - l_{11} l_{33} l_{55} - 2 l_{22} l_{33} l_{55},\\ p_{01}&= l_{11} l_{22}^2 l_{33} + l_{11} l_{22}^2 l_{55} + l_{22}^2 l_{33} l_{55} + 2 l_{11} l_{22} l_{33} l_{55},\ p_{00}=- l_{11} l_{22}^2 l_{33} l_{55},\\ p_{14}&=- m_{55},\; p_{13}= l_{11} m_{55} + 2 l_{22} m_{55} + l_{33} m_{55},\; p_{12}=- 2 l_{11} l_{22} m_{55} \\&\quad - l_{11} l_{33} m_{55} - 2 l_{22} l_{33} m_{55},\\ p_{11}&= l_{11} l_{22}^2 m_{55} + l_{22}^2 l_{33} m_{55} + 2 l_{11} l_{22} l_{33} m_{55},\; p_{10}=- l_{11} l_{22}^2 l_{33} m_{55},\\ p_{24}&=-h_{11},\; p_{23}=2 h_{11} l_{22} + h_{11} l_{33} + h_{11} l_{55},\; p_{22}=- h_{11} l_{22}^2 - 2 h_{11} l_{22} l_{33} \\&\quad - 2 h_{11} l_{22} l_{55} - h_{11} l_{33} l_{55},\\ p_{21}&=h_{11} l_{22}^2 l_{33} + h_{11} l_{22}^2 l_{55} + 2 h_{11} l_{22} l_{33} l_{55},\; p_{20}=- h_{11} l_{22}^2 l_{33} l_{55},\\ p_{33}&= h_{11} m_{55} + h_{15} m_{53},\; p_{32}=- h_{15} l_{11} m_{53} - 2 h_{11} l_{22} m_{55} - 2 h_{15} l_{22} m_{53} - h_{11} l_{33} m_{55},\\ p_{31}&= h_{11} l_{22}^2 m_{55} + h_{15} l_{22}^2 m_{53} + 2 h_{15} l_{11} l_{22} m_{53} + 2 h_{11} l_{22} l_{33} m_{55},\\ p_{30}&= - h_{15} l_{11} l_{22}^2 m_{53} - h_{11} l_{22}^2 l_{33} m_{55}. \end{aligned}$$

Proofs of Theorems 3.2–3.7

Proof of Theorem 3.2

When $R_0\le 1,$ and $\tau _h=\tau _m=0$, the disease-free equilibrium $P^0$ is locally asymptotically stable. When $\tau _h>0,\tau _m>0$, it is obvious that Eq. (3.1) has roots with positive real part if and only if equation

$$\begin{aligned} \lambda ^2+a_1\lambda +a_2(1-R_0^2e^{-\lambda \tau _h}e^{-\lambda \tau _m})=0 \end{aligned}$$

(5.1)

with $a_1=-(l_{33}+l_{55}),a_2=l_{55}l_{33}$ has roots with positive real part. By substituting $\lambda =i\kappa$ into Eq. (5.1) and separating the real and imaginary parts, we have

$$\begin{aligned} \begin{array}{l} a_1\kappa =-a_2R_0^2\sin \kappa (\tau _h+\tau _m),\ -\kappa ^2+a_2=a_2R_0^2\cos \kappa (\tau _h+\tau _m). \end{array} \end{aligned}$$

(5.2)

Squaring and taking the sum of Eq. (5.2) yields $\kappa ^4+(a_1^2-2a_2)\kappa ^2+a_2^2(1-R_0^4)=0,$ with $a_1^2-2a_2= (l_{33})^2+(l_{55})^2>0$ and $1-R_0^4>0$ since $R_0<1$. Hence, all roots of Eq. (3.1) have negative real parts. Here completes the proof. $\square$

When $R_0>1,$ for $\tau _m=\tau _h=0$, Eq. (3.2) reduced to the following equation

$$\begin{aligned} \lambda ^5+ n_4\lambda ^4+n_3\lambda ^3+n_2\lambda ^2+n_1\lambda +n_0=0 \end{aligned}$$

with $n_4=\sum _{j=0}^2u_{j4},\ n_3=\sum _{j=0}^4u_{j3},\ n_2=\sum _{j=0}^6u_{j2},\ n_1=\sum _{j=0}^7u_{j1},\ n_0=\sum _{j=0}^8u_{j0}.$ According to the Routh-Hurwitz criteria gives $Re(\lambda )<0$ if and only if

$$\begin{aligned} \small D_1=n_1>0,\ D_2=\begin{vmatrix} n_1&n_0 \\ n_3&n_2 \end{vmatrix}>0,\ D_3=\begin{vmatrix} n_1&n_0&0 \\ n_3&n_2&n_1\\ 1&n_4&n_3 \end{vmatrix}>0,\ D_4=\begin{vmatrix} n_1&n_0&0&0\\ n_3&n_2&n_1&n_0\\ 1&n_4&n_3&n_2\\ 0&0&1&n_4 \end{vmatrix}>0. \end{aligned}$$

Proof of Theorem 3.3

For $\tau _h=0$, Eq. (3.2) reduced to the following equation

$$\begin{aligned}{} & {} \lambda ^5+ E_4\lambda ^4+E_3\lambda ^3+E_2\lambda ^2+E_1\lambda +E_0+\left( W_4\lambda ^4+W_3\lambda ^3+W_2\lambda ^2+W_1\lambda +W_0\right) \nonumber \\{} & {} \quad e^{-\lambda \tau _m}=0 \end{aligned}$$

(5.3)

with $E_4=u_{04}+u_{24},\ E_3=u_{03}+u_{23}+u_{43},\ E_j=u_{0j}+u_{2j}+u_{4j}+u_{6j}\;( j=0,1,2),\ W_4=u_{14},\ W_3=u_{13}+u_{33},\ W_2=u_{12}+u_{32}+u_{52}, W_1=u_{11}+u_{31}+u_{51}+u_{71},\ W_0=u_{10}+u_{30}+u_{50}+u_{70}+u_{80}.$ Suppose that $\lambda =i\kappa$ is a root of Eq. (5.3), then we have

$$\begin{aligned} \begin{array}{l} b_{11}(\kappa )\sin \kappa \tau _m+b_{12}(\kappa )\cos \kappa \tau _m=b_{13}(\kappa ),\ b_{12}(\kappa )\sin \kappa \tau _m-b_{11}(\kappa )\cos \kappa \tau _m\\ \qquad =b_{23}(\kappa ), \end{array} \end{aligned}$$

(5.4)

where $b_{11}(\kappa )=W_4\kappa ^4-W_2\kappa ^2+W_0,\ b_{12}(\kappa )=W_3\kappa ^3-W_1\kappa ,\ b_{13}(\kappa )=\kappa ^5-E_3\kappa ^3+E_1\kappa ,\ b_{23}(\kappa )=E_4\kappa ^4-E_2\kappa ^2+E_0,$ which implies

$$\begin{aligned} \kappa ^{10}+c_4\kappa ^8+c_3\kappa ^6+c_2\kappa ^4+c_1\kappa ^2+c_0=0 \end{aligned}$$

(5.5)

with $c_4=-2E_3+E_4^2-W_4^2,\ c_3=2E_1+E_3^2-2E_4E_2+2W_4W_2-W_3^2,\ c_2=E_2^2-W_2^2-2E_3E_1+2E_4E_0-2W_4W_0+2W_3W_1,\ c_1=E_1^2-2E_0E_2+2W_2W_0-W_1^2,\ c_0=E_0^2-W_0^2.$ For simplicity denote $\nu =\kappa ^2$, then Eq. (5.5) turns into

$$\begin{aligned} \mathcal {L}(\nu ):=\nu ^{5}+c_4\nu ^4+c_3\nu ^3+c_2\nu ^2+c_1\nu +c_0=0. \end{aligned}$$

(5.6)

If the assumption: $({\textbf {H}}_1):$ Eq. (5.6) has a positive root $\nu _0$ is satisfied, then, Eq. (5.5) has a positive root $\kappa _0=\sqrt{\nu _0}$. Eliminating $\sin \kappa \tau _m$ in Eq. (5.4) and letting $\kappa =\kappa _0$, we can obtain that

$$\begin{aligned} \tau _{m}^*=\frac{1}{\kappa _0}\arccos \left( \frac{b_{13}(\kappa _0)b_{12}(\kappa _0)-b_{23}(\kappa _0)b_{11}(\kappa _0)}{b_{12}^2(\kappa _0)+b_{11}^2(\kappa _0)}\right) . \end{aligned}$$

Substituting $\lambda (\tau _m)$ into Eq. (5.3), taking derivative with respect to $\tau _m$, we obtain

$$\begin{aligned}{} & {} \left( 5\lambda ^5+\sum _{j=4}^1jE_j\lambda ^{j-1} +(\sum _{j=4}^1jW_j\lambda ^{j-1}-\tau _m\sum _{j=4}^0W_j\lambda ^j)e^{-\lambda \tau _m}\right) \frac{d\lambda }{dt} \\{} & {} \quad =\lambda \sum _{j=4}^0W_j\lambda ^je^{-\lambda \tau _m} \end{aligned}$$

Therefore,

$$\begin{aligned} \left( \frac{d\lambda }{d\tau _m}\right) ^{-1}=\frac{(5\lambda ^4+\sum _{j=4}^1jE_j\lambda ^{j-1})e^{\lambda \tau _m}+\sum _{j=4}^1jW_j\lambda ^{j-1}}{\lambda \sum _{j=4}^0W_j\lambda ^j} -\frac{\tau _m}{\lambda }. \end{aligned}$$

Thus, when $\lambda =i\kappa _0$, we can get $\text {Re}\left( \frac{d\lambda }{d\tau _m}\right) ^{-1}_{\lambda =i\kappa _0}=\frac{g^{'}(\nu _0)}{b_{12}^2(\nu _0^2)+b_{11}^2(\nu _0^2)}.$ It can be seen that $\text {Re}\left( \frac{d\lambda }{d\tau _m}\right) ^{-1}_{\lambda =i\kappa _0}\ne 0$ if the assumption: $({\textbf {H}}_2): \mathcal {L}^{'}(\nu _0)=\frac{d\mathcal {L}(\nu )}{d\nu }|_{\nu =\nu _0}\ne 0$ is satisfied. Therefore, by the Hopf bifurcation theorem [25], Theorem 3.2 can be obtained if $({\textbf {H}}_1)$ and $({\textbf {H}}_2)$ hold. $\square$

Proof of Theorem 3.4

For $\tau _m=0$, Eq. (3.3) reduced to the following equation

$$\begin{aligned}{} & {} \lambda ^5+ F_4\lambda ^4+F_3\lambda ^3+F_2\lambda ^2+F_1\lambda +F_0+\left( X_4\lambda ^4+X_3\lambda ^3+X_2\lambda ^2+X_1\lambda +X_0\right) \nonumber \\{} & {} \quad e^{-\lambda \tau _h}=0 \end{aligned}$$

(5.7)

with $F_j=p_{0j}+p_{1j}\;(j=0,1,2,3,4),\; X_4=p_{24},\; X_j=p_{2j}+p_{3j}\;(j=0,1,2,3).$

Suppose that $\lambda =i\kappa$ is a root of Eq. (5.7), then we have

$$\begin{aligned} \begin{array}{l} d_{11}(\kappa )\sin \kappa \tau _h+d_{12}(\kappa )\cos \kappa \tau _h=d_{13}(\kappa ),\ d_{12}(\kappa )\sin \kappa \tau _h-d_{11}(\kappa )\cos \kappa \tau _h=d_{23}(\kappa ), \end{array}\nonumber \\ \end{aligned}$$

(5.8)

where $d_{11}(\kappa )=X_4\kappa ^4-X_2\kappa ^2+X_0,\ d_{12}(\kappa )=X_3\kappa ^3-X_1\kappa ,\ d_{13}(\kappa )=\kappa ^5-F_3\kappa ^3+F_1\kappa ,\ d_{23}(\kappa )=F_4\kappa ^4-F_2\kappa ^2+F_0,$ which implies

$$\begin{aligned} \kappa ^{10}+r_4\kappa ^8+r_3\kappa ^6+r_2\kappa ^4+r_1\kappa ^2+r_0=0 \end{aligned}$$

(5.9)

with $r_4=-2F_3+F_4^2-X_4^2,\ r_3=2F_1+F_3^2-2F_4F_2+2X_4X_2-X_3^2,\ r_2=F_2^2-X_2^2-2F_3F_1+2F_4F_0-2X_4X_0+2X_3X_1,\ r_1=F_1^2-2F_0F_2+2X_2X_0-X_1^2,\ r_0=F_0^2-X_0^2.$ For simplicity denote $\nu =\kappa ^2$, then Eq. (5.9) turns into

$$\begin{aligned} \mathcal {L}_1(\nu ):=\nu ^{5}+r_4\nu ^4+r_3\nu ^3+r_2\nu ^2+r_1\nu +r_0=0. \end{aligned}$$

(5.10)

If the assumption: $({\textbf {H}}_3):$ Eq. (5.10) has a positive root $\nu _1$ is satisfied, then, Eq. (5.9) has a positive root $\kappa _1=\sqrt{\nu _1}$. Eliminating $\sin \kappa \tau _h$ in Eq. (5.8) and letting $\kappa =\kappa _1$, we can obtain that $\tau _h^*=\frac{1}{\kappa _1}\arccos \left( \frac{d_{13}(\kappa _1)d_{12}(\kappa _1)-d_{23}(\kappa _1)d_{11}(\kappa _1)}{d_{12}^2(\kappa _1)+d_{11}^2(\kappa _1)}\right) .$

Similar to the proof of Theorem 3.3, differentiating Eq. (5.7) with respect $\tau _h$ and substituting $\lambda =i\kappa _1$, we can get $\text {Re}\left( \frac{d\lambda }{d\tau _h}\right) ^{-1}_{\lambda =i\kappa _1}=\frac{\mathcal {L}_1^{'}(\nu _1)}{d_{12}^2(\nu _1^2)+d_{11}^2(\nu _1^2)}.$ Thus, $\text {Re}\left( \frac{d\lambda }{d\tau _h}\right) ^{-1}_{\lambda =i\kappa _1}\ne 0$ if the assumption: $({\textbf {H}}_4): \mathcal {L}_1^{'}(\nu _1)=\frac{d\mathcal {L}_1(\nu )}{d\nu }|_{\nu =\nu _1}\ne 0$ is satisfied. Therefore, by the Hopf bifurcation theorem [25], Theorem 3.4 can be obtained if $({\textbf {H}}_3)$ and $({\textbf {H}}_4)$ hold. $\square$

Proof of Theorem 3.5

For $\tau _m=\tau _h=\tau >0$, Eq. (3.3) reduced to the following equation

$$\begin{aligned} \lambda ^5+ \sum _{j=4}^0g_j\lambda ^j+\sum _{j=4}^0y_{1j}\lambda ^je^{-\lambda \tau }+\sum _{j=3}^0y_{2j}\lambda ^je^{-2\lambda \tau }=0 \end{aligned}$$

(5.11)

with $g_j=p_{0j},\ y_{1j}=p_{1j}+p_{2j},j=0,\cdots ,4,\ y_{2j}=p_{3j},\ j=0,\cdots ,3.$

Multiplying $e^{\lambda \tau }$ on both sides of Eq. (5.11), we can get

$$\begin{aligned} \left( \lambda ^5+ \sum _{j=4}^0g_j\lambda ^j\right) e^{\lambda \tau }+\sum _{j=4}^0y_{1j}\lambda ^j+\sum _{j=3}^0y_{2j}\lambda ^je^{-\lambda \tau }=0 \end{aligned}$$

(5.12)

Let $\lambda =i\kappa$ be a root of Eq. (5.12), then we have $e_{11}(\kappa )\sin \kappa \tau +e_{12}(\kappa )\cos \kappa \tau =e_{13}(\kappa ),\ e_{21}(\kappa )\sin \kappa \tau +e_{22}(\kappa )\cos \kappa \tau =e_{23}(\kappa ),$ with $e_{11}(\kappa )=g_4\kappa ^4+(-g_2+y_{22})\kappa ^2+g_0-y_{20},\ e_{12}(\kappa )=\kappa ^5-(g_3+y_{23})\kappa ^3+(g_1+y_{21})\kappa ,\ e_{21}=-\kappa ^5+(g_3-y_{23})\kappa ^3-(g_1-y_{21})\kappa ,\ e_{22}=g_4\kappa ^4-(g_2+y_{22})\kappa ^2+g_0+y_{20},\ e_{13}(\kappa )=y_{13}\kappa ^3-y_{11}\kappa ,\ e_{23}(\kappa )=-y_{14}\kappa ^4+y_{12}\kappa ^2-y_{10},$ which implies

$$\begin{aligned} \sin \kappa \tau =\frac{e_{13}e_{22}-e_{12}e_{23}}{e_{11}e_{22}-e_{12}e_{21}},\ \cos \kappa \tau =\frac{e_{11}e_{23}-e_{13}e_{21}}{e_{11}e_{22}-e_{12}e_{21}}. \end{aligned}$$

(5.13)

Consequently, the following equation with respect to $\kappa$ is obtained

$$\begin{aligned} \kappa ^{20}+\sum _{j=9}^0s_j\kappa ^{2j}=0 \end{aligned}$$

(5.14)

with

$$\begin{aligned} s_9&= - 2g_4^2 - y_{14}^2 - 4g_3 ,\ s_8= 4g_1 + 2g_4(g_2 - y_{22}) + (g_4^2 + 2g_3)^2 - (y_{13} \\&\quad - g_4y_{14})^2 + 2y_{14}(y_{12} + g_4y_{13}\\&\quad + y_{14}(g_3 + y_{23})),+ 2g_4(g_2 + y_{22}) + 2(g_3 + y_{23})(g_3 - y_{23}),\\ s_7&= 2(y_{13} - g_4y_{14})(y_{11} - g_4y_{12} - y_{14}(g_2 - y_{22}) + y_{13}(g_3 - y_{23})) - 2g_4(g_0 - y_{20})\\&\quad - 2(g_4^2 + 2g_3)(2g_1 + g_4(g_2 - y_{22}) + g_4(g_2 + y_{22}) + (g_3 + y_{23})(g_3 - y_{23}))\\&\quad - 2y_{14}(y_{10} + g_4y_{11} + y_{14}(g_1 + y_{21}) + y_{13}(g_2 + y_{22}) + y_{12}(g_3 + y_{23})) \\&\quad - 2g_4(g_0 + y_{20}) - 2(g_1 + y_{21})(g_3 - y_{23}) - 2(g_2 + y_{22})(g_2 - y_{22})\\&\quad - 2(g_3 + y_{23})(g_1 - y_{21}) - (y_{12} + g_4y_{13} + y_{14}(g_3 + y_{23}))^2 ,\\ s_6&= 2(g_4^2 + 2g_3)(g_4(g_0 - y_{20}) + g_4(g_0 + y_{20}) + (g_1 + y_{21})(g_3 - y_{23})+ (g_2 + y_{22})(g_2 - y_{22}) ,\\&\quad + (g_3 + y_{23})(g_1 - y_{21})) - (y_{11} - g_4y_{12} - y_{14}(g_2 - y_{22})+ y_{13}(g_3 - y_{23}))^2\\&\quad + 2(y_{12} + g_4y_{13} + y_{14}(g_3 + y_{23}))(y_{10} + g_4y_{11} + y_{14}(g_1 + y_{21})\\&\quad + y_{13}(g_2 + y_{22}) + y_{12}(g_3 + y_{23})) + 2(g_0 + y_{20})(g_2 - y_{22}) + 2(g_1 + y_{21})(g_1 - y_{21})\\&\quad + 2(g_2 + y_{22})(g_0 - y_{20}) + (2g_1 + g_4(g_2 - y_{22}) + g_4(g_2 + y_{22}) + (g_3 + y_{23})(g_3 - y_{23}))^2 \\&\quad + 2(y_{13} - g_4y_{14})(g_4y_{10} + y_{14}(g_0 - y_{20}) - y_{13}(g_1 - y_{21}) + y_{12}(g_2 - y_{22}) - y_{11}(g_3 - y_{23}))\\&\quad + 2y_{14}(y_{13}(g_0 + y_{20}) + y_{12}(g_1 + y_{21}) + y_{11}(g_2 + y_{22}) + y_{10}(g_3 + y_{23})),\\ s_5&=- 2(y_{11} - g_4y_{12} - y_{14}(g_2 - y_{22}) + y_{13}(g_3 - y_{23}))(g_4y_{10} + y_{14}(g_0 - y_{20})\\&\quad - y_{13}(g_1 - y_{21}) + y_{12}(g_2 - y_{22}) - y_{11}(g_3 - y_{23})) \\&\quad - 2(y_{12} + g_4y_{13} + y_{14}(g_3 + y_{23}))(y_{13}(g_0 + y_{20}) \\&\quad + y_{12}(g_1 + y_{21}) + y_{11}(g_2 + y_{22}) + y_{10}(g_3 + y_{23})) \\&\quad - 2(2g_1 + g_4(g_2 - y_{22}) + g_4(g_2 + y_{22})\\&\quad + (g_3 + y_{23})(g_3 - y_{23}))(g_4(g_0 - y_{20}) + g_4(g_0 + y_{20}) + (g_1 + y_{21})(g_3 - y_{23})\\&\quad + (g_2 + y_{22})(g_2 - y_{22}) + (g_3 + y_{23})(g_1 - y_{21})) - (y_{10} + g_4y_{11} \\&\quad + y_{14}(g_1 + y_{21}) + y_{13}(g_2 + y_{22})\\&\quad + y_{12}(g_3 + y_{23}))^2- 2y_{14}(y_{11}(g_0 + y_{20}) + y_{10}(g_1 + y_{21})) \\&\quad - 2(g_4^2 + 2g_3)((g_0 + y_{20})(g_2 - y_{22}) \\&\quad + (g_1 + y_{21})(g_1 - y_{21})+ (g_2 + y_{22})(g_0 - y_{20})) - 2(g_0 + y_{20})(g_0 - y_{20}) \\&\quad - 2(y_{13} - g_4y_{14})(y_{12}(g_0 - y_{20}) - y_{11}(g_1 - y_{21}) + y_{10}(g_2 - y_{22})), \end{aligned}$$

$$\begin{aligned} s_4&=2((g_0 + y_{20})(g_2 - y_{22}) + (g_1 + y_{21})(g_1 - y_{21}) \\&\quad + (g_2 + y_{22})(g_0 - y_{20}))(2g_1 + g_4(g_2 - y_{22})\\&\quad + g_4(g_2 + y_{22}) + (g_3 + y_{23})(g_3 - y_{23})) - (g_4y_{10} + y_{14}(g_0 - y_{20}) \\&\quad - y_{13}(g_1 - y_{21}) + y_{12}(g_2 - y_{22}) ,\\&\quad - y_{11}(g_3 - y_{23}))^2 + 2(y_{13}(g_0 + y_{20}) + y_{12}(g_1 + y_{21}) \\&\quad + y_{11}(g_2 + y_{22}) + y_{10}(g_3 + y_{23}))(y_{10} \\&\quad + g_4y_{11} + y_{14}(g_1 + y_{21})+ y_{13}(g_2 + y_{22}) + y_{12}(g_3 + y_{23}))\\&\quad + 2(y_{11}(g_0 + y_{20}) + y_{10}(g_1 + y_{21}))(y_{12} \\&\quad + g_4y_{13} + y_{14}(g_3 + y_{23}))+ (g_4(g_0 - y_{20}) + g_4(g_0 + y_{20}) + (g_1 + y_{21})(g_3 - y_{23})\\&\quad + (g_2 + y_{22})(g_2 - y_{22})+ (g_3 + y_{23})(g_1 - y_{21}))^2+ 2(y_{12}(g_0 - y_{20}) - y_{11}(g_1 - y_{21}) \\&\quad + y_{10}(g_2 - y_{22}))(y_{11} - g_4y_{12} - y_{14}(g_2 - y_{22}) + y_{13}(g_3 - y_{23}))\\&\quad + 2(g_0 + y_{20})(g_0 - y_{20})(g_4^2 + 2g_3)\\&\quad + 2y_{10}(g_0 - y_{20})(y_{13} - g_4y_{14}),\\ s_3&= 2(y_{12}(g_0 - y_{20}) - y_{11}(g_1 - y_{21}) + y_{10}(g_2 - y_{22}))(g_4y_{10} + y_{14}(g_0 - y_{20}) - y_{13}(g_1 - y_{21})\\&\quad + y_{12}(g_2 - y_{22}) - y_{11}(g_3 - y_{23})) - 2((g_0 + y_{20})(g_2 - y_{22}) + (g_1 + y_{21})(g_1 - y_{21}) \\&\quad + (g_2 + y_{22})(g_0 - y_{20}))(g_4(g_0 - y_{20}) + g_4(g_0 + y_{20}) + (g_1 + y_{21})(g_3 - y_{23})\\&\quad + (g_2 + y_{22})(g_2 - y_{22}) + (g_3 + y_{23})(g_1 - y_{21})) - (y_{13}(g_0 + y_{20}) + y_{12}(g_1 + y_{21})\\&\quad + y_{11}(g_2 + y_{22}) + y_{10}(g_3 + y_{23}))^2 - 2(y_{11}(g_0 + y_{20}) \\&\quad + y_{10}(g_1 + y_{21}))(y_{10} + g_4y_{11} + y_{14}(g_1 + y_{21})\\&\quad + y_{13}(g_2 + y_{22}) + y_{12}(g_3 + y_{23})) - 2y_{10}(g_0 - y_{20})(y_{11} - g_4y_{12} \\&\quad - y_{14}(g_2 - y_{22}) + y_{13}(g_3 - y_{23})) \\&\quad - 2(g_0 + y_{20})(g_0 - y_{20})(2g_1 + g_4(g_2 - y_{22}) + g_4(g_2 + y_{22}) + (g_3 + y_{23})(g_3 - y_{23})),\\ s_2&= 2(y_{11}(g_0 + y_{20}) + y_{10}(g_1 + y_{21}))(y_{13}(g_0 + y_{20}) + y_{12}(g_1 + y_{21}) + y_{11}(g_2 + y_{22})\\&\quad + y_{10}(g_3 + y_{23})) - (y_{12}(g_0 - y_{20}) - y_{11}(g_1 - y_{21}) \\&\quad + y_{10}(g_2 - y_{22}))^2 + ((g_0 + y_{20})(g_2 - y_{22}) \\&\quad + (g_1 + y_{21})(g_1 - y_{21}) + (g_2 + y_{22})(g_0 - y_{20}))^2 + 2(g_0 + y_{20})(g_0 - y_{20})(g_4(g_0 - y_{20}) \\&\quad + g_4(g_0 + y_{20})+ (g_1 + y_{21})(g_3 - y_{23}) + (g_2 + y_{22})(g_2 - y_{22}) + (g_3 + y_{23})(g_1 - y_{21})) \\&\quad -2y_{10}(g_0 - y_{20})(g_4y_{10} + y_{14}(g_0 - y_{20}) - y_{13}(g_1 - y_{21}) \\&\quad + y_{12}(g_2 - y_{22}) - y_{11}(g_3 - y_{23})),\\ s_1&=2y_{10}(g_0 - y_{20})(y_{12}(g_0 - y_{20}) - y_{11}(g_1 - y_{21}) + y_{10}(g_2 - y_{22})) \\&\quad - 2(g_0 + y_{20})(g_0 - y_{20})((g_0 + y_{20})(g_2 - y_{22})+ (g_1 + y_{21})(g_1 - y_{21}) \\&\quad + (g_2 + y_{22})(g_0 - y_{20})) \\&\quad - (y_{11}(g_0 + y_{20}) + y_{10}(g_1 + y_{21}))^2,\ s_0=(g_0 + y_{20})^2(g_0 - y_{20})^2 - y_{10}^2(g_0 - y_{20})^2. \end{aligned}$$

For simplicity denote $\nu =\kappa ^2$, then Eq. (5.14) turns into

$$\begin{aligned} g(\nu ):=\nu ^{10}+\sum _{j=9}^0s_j\nu ^{j}=0. \end{aligned}$$

(5.15)

If the assumption: $({\textbf {H}}_5):$ Eq. (5.15) has a positive root $\nu _2$ is satisfied. then Eq. (5.14) has a positive root $\kappa _2=\sqrt{\nu _2}$. Letting $\kappa =\kappa _2$ in Eq. (5.13), we can obtain that

$$\begin{aligned} \tau ^*=\frac{1}{\kappa _2}\arccos \left( \frac{e_{13}(\kappa _2)e_{21}(\kappa _2)-e_{11}(\kappa _2)e_{23}(\kappa _2)}{e_{11}(\kappa _2)e_{22}(\kappa _2)-e_{12}(\kappa _2)e_{21}(\kappa _2)}\right) . \end{aligned}$$

Similar to the proof of Theorem 3.3, differentiating Eq. (5.11) with respect $\tau$ and substituting $\lambda =i\kappa _2$, we can get

$$\begin{aligned} \text {Re}\left( \frac{d\lambda }{d\tau }\right) ^{-1}_{\lambda =i\kappa _2}=\frac{e_2e_3-e_1e_4}{\kappa _2(e_3^2+e_4^2)}, \end{aligned}$$

where $e_1=-3y_{13}\kappa _2^3+y_{11}+(5\kappa _2^4-3g_3\kappa _2^2+g_1-3y_{23}\kappa _2^2+y_{21})\cos \kappa _2\tau ^*\ +(2y_{22}\kappa _2+4g_4\kappa _2^3-2g_2\kappa _2)\sin \kappa _2\tau ^*,\ e_2=-4y_{14}\kappa _2^3+2y_{12}\kappa _2+(5\kappa _2^4-3g_3\kappa _2^2+g_1+3y_{23}\kappa _2^2-y_{21})\sin \kappa _2\tau ^*\ +(2y_{22}\kappa _2-4g_4\kappa _2^3+2g_2\kappa _2)\sin \kappa _2\tau ^*,\ e_3=e_{11}(\kappa _2)\cos \kappa _2\tau ^*-e_{21}(\kappa _2)\sin \kappa _2\tau ^*,\;e_4=e_{12}(\kappa _2)\cos \kappa _2\tau ^*+e_{22}(\kappa _2)\sin \kappa _2\tau ^*.$ Therefore, $\text {Re}\left( \frac{d\lambda }{d\tau }\right) ^{-1}_{\lambda =i\kappa _2}\ne 0$ if the assumption: $({\textbf {H}}_6): e_2e_3-e_1e_4\ne 0$ is satisfied. Consequently, by the Hopf bifurcation theorem [25], Theorem 3.4 can be obtained if $({\textbf {H}}_5)$ and $({\textbf {H}}_6)$ hold. $\square$

Proof of Theorem 3.6

For $\tau _m>0$ and $\tau _h\in (0,\tau _h^*)$, Eq. (3.3) can be written as

$$\begin{aligned} \begin{array}{lll} \displaystyle \lambda ^5 +\sum _{j=4}^0\left( p_{ 0j}+p_{ 2j}e^{-\lambda \tau _h}\right) \lambda ^j +\left( p_{14}\lambda ^4+\sum _{j=3}^0\left( p_{ 1j}+p_{ 3j}e^{-\lambda \tau _h}\right) \lambda ^j\right) e^{-\lambda \tau _m}=0. \end{array} \end{aligned}$$

Considering $\tau _h$ as a parameter and letting $\lambda =i\kappa$, we can obtain

$$\begin{aligned} \begin{array}{l} f_{11}(\kappa )\sin \kappa \tau _m+f_{12}(\kappa )\cos \kappa \tau _m=f_{13}(\kappa ),\ f_{12}(\kappa )\sin \kappa \tau _m-f_{11}(\kappa )\cos \kappa \tau _m=f_{23}(\kappa ), \end{array} \end{aligned}$$

with $f_{11}(\kappa )= -p_{13}\kappa ^3+p_{11}\kappa -(p_{33}\kappa ^3-p_{31}\kappa )\cos \kappa \tau _h-(-p_{32}\kappa ^2+p_{30})\sin \kappa \tau _h,\$ $f_{12}(\kappa )= p_{14}\kappa ^4-p_{12}\kappa ^2+p_{10}-(p_{33}\kappa ^3-p_{31}\kappa )\sin \kappa \tau _h+(-p_{32}\kappa ^2+p_{30})\cos \kappa \tau _h,\ f_{13}(\kappa )= -(p_{04}\kappa ^4-p_{02}\kappa ^2+p_{00})+(p_{23}\kappa ^3-p_{21}\kappa )\sin \kappa \tau _h-(p_{24}\kappa ^4-p_{22}\kappa ^2+p_{20})\cos \kappa \tau _h,\ f_{23}(\kappa )= (\kappa ^5-p_{03}\kappa ^3+p_{01}\kappa )-(p_{23}\kappa ^3-p_{21}\kappa )\cos \kappa \tau _h-(p_{24}\kappa ^4-p_{22}\kappa ^2+p_{20})\sin \kappa \tau _h,$ which implies

$$\begin{aligned} \kappa ^{10}+\sum _{i=4}^0q_{0j}\kappa ^{2j}+\left( \sum _{i=4}^0q_{1j}\kappa ^{2j}\right) \cos \kappa \tau _h+\left( \sum _{i=4}^0q_{2j}\kappa ^{2j}\right) \kappa \sin \kappa \tau _h=0\nonumber \\ \end{aligned}$$

(5.16)

with

$$\begin{aligned} q_{04}&= p_{04}^2 - p_{14}^2 + p_{24}^2 - 2p_{03},\ q_{03}=p_{03}^2 - p_{13}^2 + p_{23}^2 - p_{33}^2 + 2p_{01} \\&\quad - 2p_{02}p_{04} + 2p_{12}p_{14} - 2p_{22}p_{24},\\ q_{02}&=p_{02}^2 - p_{12}^2 + p_{22}^2 - p_{32}^2 + 2(p_{00}p_{04} - p_{01}p_{03} - p_{10}p_{14} + p_{11}p_{13} \\&\quad + p_{20}p_{24} - p_{21}p_{23} + p_{31}p_{33}),\\ q_{01}&= p_{01}^2 - p_{11}^2 + p_{21}^2 -p_{31}^2 - 2p_{00}p_{02} + 2p_{10}p_{12} - 2p_{20}p_{22} + 2p_{30}p_{32},\\ q_{00}&= p_{00}^2 - p_{10}^2 + p_{20}^2 - p_{30}^2,\ q_{14}=2p_{04}p_{24} - 2p_{23},\\ q_{13}&=2p_{21} - 2p_{02}p_{24} + 2p_{03}p_{23} - 2p_{04}p_{22} - 2p_{13}p_{33} + 2p_{14}p_{32},\\ q_{12}&=2p_{00}p_{24} - 2p_{01}p_{23} + 2p_{02}p_{22} - 2p_{03}p_{21} + 2p_{04}p_{20} + 2p_{11}p_{33} \\&\quad - 2p_{12}p_{32} + 2p_{13}p_{31} - 2p_{14}p_{30},\\ q_{11}&= 2(p_{01}p_{21} - p_{00}p_{22} - p_{02}p_{20} + p_{10}p_{32} - p_{11}p_{31} + p_{12}p_{30}),\\ q_{10}&= 2p_{00}p_{20} - 2p_{10}p_{30},\ q_{24}= - 2p_{24},\ q_{23}= 2p_{22} + 2p_{03}p_{24} - 2p_{04}p_{23} + 2p_{14}p_{33},\\ q_{22}&= 2p_{02}p_{23} - 2p_{01}p_{24} - 2p_{20} - 2p_{03}p_{22} + 2p_{04}p_{21} - 2p_{12}p_{33} + 2p_{13}p_{32} - 2p_{14}p_{31},\\ q_{21}&=2p_{01}p_{22} - 2p_{00}p_{23} - 2p_{02}p_{21} + 2p_{03}p_{20} + 2p_{10}p_{33} - 2p_{11}p_{32} + 2p_{12}p_{31} - 2p_{13}p_{30},\\ q_{20}&= 2p_{00}p_{21} - 2p_{01}p_{20} - 2p_{10}p_{31} + 2p_{11}p_{30}. \end{aligned}$$

If the assumption: $({\textbf {H}}_7):$ Eq. (5.16) has a positive root $\hat{\kappa }$ is satisfied, then, from Eq. (5.8) we can obtain that $\hat{\tau }_m =\frac{1}{\hat{\kappa }}\arccos \left( \frac{f_{13}(\hat{\kappa })f_{12}(\hat{\kappa })-f_{23}(\hat{\kappa })f_{11}(\hat{\kappa })}{f_{12}^2(\hat{\kappa })+f_{11}^2(\hat{\kappa })}\right) .$

Similar to the proof of Theorem 3.3, differentiating Eq. (5.7) with respect $\tau _m$ and substituting $\lambda =i\hat{\kappa }$, we can get $\text {Re}\left( \frac{d\lambda }{d\tau _m}\right) ^{-1}_{\lambda =i\hat{\kappa }}=\frac{q_1q_4-q_2q_3}{\hat{\kappa }(q_1^2+q_2^2)},$ where $q_1=(p_{14}\hat{\kappa }^4-p_{12}\hat{\kappa }^2+p_{10}+p_{30}-p_{32}\hat{\kappa }^2)\cos \hat{\kappa }\hat{\tau }_m+(p_{11}\hat{\kappa }-p_{13}\hat{\kappa }^3 + p_{33}\hat{\kappa }^3-p_{31}\hat{\kappa })\sin \hat{\kappa }\hat{\tau }_m,\ q_2=-(p_{14}\hat{\kappa }^4-p_{12}\hat{\kappa }^2+p_{10}+p_{30}-p_{32}\hat{\kappa }^2)\sin \hat{\kappa }\hat{\tau }_m+(p_{11}\hat{\kappa }-p_{13}\hat{\kappa }^3 +p_{33}\hat{\kappa }^3-p_{31}\hat{\kappa })\cos \hat{\kappa }\hat{\tau }_m,\ q_3=5\hat{\kappa }^4-3p_{03}\hat{\kappa }^2+p_{01}+(p_{21}-3p_{23}\hat{\kappa }^2-\tau _h((p_{24}\hat{\kappa }^4-p_{22}\hat{\kappa }^2+p_{20})))\cos \hat{\kappa }\tau _h +(2p_{22}\hat{\kappa }-4p_{24}\hat{\kappa }^3-\tau _h(p_{23}\hat{\kappa }^3-p_{21}\hat{\kappa }))\sin \hat{\kappa }\tau _h +(p_{11}-3p_{13}\hat{\kappa }^2)\cos \hat{\kappa }\hat{\tau }_m +(2p_{12}\hat{\kappa }-4p_{14}\hat{\kappa }^3)\sin \hat{\kappa }\hat{\tau }_m +(p_{31}-3p_{33}\hat{\kappa }^2-\tau _h(-p_{32}\hat{\kappa }^2+p_{30}))\cos \hat{\kappa }(\tau _h+\hat{\tau }_m) +(2p_{32}\hat{\kappa }-\tau _h(p_{31}\hat{\kappa }-p_{33}\hat{\kappa }^3))\sin \hat{\kappa }(\tau _h+\hat{\tau }_m),\ q_4=-4p_{04}\hat{\kappa }^3+2p_{02}\hat{\kappa }+(3p_{23}\hat{\kappa }^2-p_{21}+\tau _h(p_{24}\hat{\kappa }^4-p_{22}\hat{\kappa }^2+p_{20}))\sin \hat{\kappa }\tau _h +(2p_{22}\hat{\kappa }-4p_{24}\hat{\kappa }^3-\tau _h(p_{23}\hat{\kappa }^3-p_{21}\hat{\kappa }))\cos \hat{\kappa }\tau _h +(3p_{13}\hat{\kappa }^2-p_{11})\sin \hat{\kappa }\hat{\tau }_m$

$+(2p_{12}\hat{\kappa }-4p_{14}\hat{\kappa }^3)\cos \hat{\kappa }\hat{\tau }_m +(3p_{33}\hat{\kappa }^2-p_{31}+\tau _h(p_{30}-p_{32}\hat{\kappa }^2))\sin \hat{\kappa }(\tau _h+\hat{\tau }_m) +(2p_{32}\hat{\kappa }-\tau _h(p_{31}\hat{\kappa }-p_{33}\hat{\kappa }^3))\cos \hat{\kappa }(\tau _h+\hat{\tau }_m).$ Thus, $\text {Re}\left( \frac{d\lambda }{d\tau _m}\right) ^{-1}_{\lambda =i\hat{\kappa }}\ne 0$ if the assumption: $({\textbf {H}}_8): q_1q_4-q_2q_3\ne 0$ is satisfied. Therefore, by the Hopf bifurcation theorem [25], Theorem 3.4 can be obtained if $({\textbf {H}}_7)$ and $({\textbf {H}}_8)$ hold. $\square$

Proof of Theorem 3.7

Define $C= C([-1,0],\mathbb {R}^5)$ the space of continuous real valued functions. Let $\tau _m=\hat{\tau }_m+\varrho$ and make time-scaling $t\rightarrow t/{\hat{\tau }_m}$. Let $x_1(t)=S_h(t)-S_h^*$, $x_2(t)=V(t)-V^*$, $x_3(t)=I_h(t)-I_h^*$, $x_4(t)=R_h(t)-R_h^*$, $x_5(t)=I_m(t)-I_m^*$, then model (1.2) is transformed into

$$\begin{aligned} \frac{dx(t)}{dt}=L_{ \varrho }(x_t)+F(\varrho ,x_t), \end{aligned}$$

(5.17)

where $x(t)=(x_1(t),x_2(t),x_3(t),x_4(t),x_5(t))^T\in \mathbb {R}^5$ and $x_t(\theta )=x(t+\theta )\in C([-1,0],\mathbb {R}^5)$. In (5.17), $L_{\varrho }: C \rightarrow \mathbb {R}^5$ and $F:\mathbb { R}\times C \rightarrow \mathbb {R}^5$ are given by

$$\begin{aligned} L_{\varrho }(\varphi )= (\hat{\tau }_m+\varrho )\left( A^{'}\varphi (0)+C^{'}\varphi (-\frac{\tau _h^*}{\hat{\tau }_m})+B^{'}\varphi (-1)\right) , \end{aligned}$$

where

$$\begin{aligned} \small A^{'}= \begin{pmatrix} a_{11} &{} 0 &{} 0 &{} 0 &{} 0\\ a_{21} &{} a_{22} &{} 0 &{} 0 &{}0\\ 0 &{} 0 &{} a_{33} &{} 0 &{} 0\\ 0 &{} 0 &{} a_{43} &{} a_{22} &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} a_{55} \end{pmatrix},B^{'}= \begin{pmatrix} b_{11} &{} 0 &{} 0 &{} 0 &{} b_{15}\\ 0 &{} 0 &{} 0 &{} 0 &{}0\\ b_{31} &{} 0 &{} 0 &{} 0 &{} b_{35}\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{pmatrix}, C^{'}= \begin{pmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{}0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} c_{53} &{} 0 &{} c_{55} \end{pmatrix}. \end{aligned}$$

with $a_{11}=-\mu _h-\eta ,\ a_{21}=\eta ,\ a_{22}=-\mu _h,\ a_{33}=-(\mu _h+\alpha +\gamma ),\ a_{43}=\gamma ,\ \ a_{55}=-\mu _m,\ b_{11}=-\beta _h I_m^*,\ b_{15}=-\beta _h S_h^*,\ b_{31}=\beta _h I_m^*,\ b_{35}=\beta _hS_h^*,\ c_{53}=\beta _m (\frac{b_m}{\mu _m}-I_m^*),\ c_{55}=-\beta _m I_h^*,$ and

$$\begin{aligned} \small F= \begin{pmatrix} \displaystyle -\beta _hx_1(-\frac{\tau _h^*}{\hat{\tau }_m})x_5(-\frac{\tau _h^*}{\hat{\tau }_m}) \\ \displaystyle 0 \\ \displaystyle \beta _hx_1(-\frac{\tau _h^*}{\hat{\tau }_m})x_5(-\frac{\tau _h^*}{\hat{\tau }_m})\\ \displaystyle 0\\ \displaystyle -\beta _mx_3(-1)x_5(-1) \end{pmatrix}. \end{aligned}$$

According to the Riesz representation theorem, there exists a bounded variation function $\zeta (\theta ,\mu )$ in $\theta \in [-1,0]$ such that $\small L_{\varrho }(\varphi )=\int _{-1}^0d\zeta (\theta ,\varrho )\varphi (\theta ),\quad \varphi \in C.$ We select

$$\begin{aligned} \zeta (\theta ,\varrho )= {\left\{ \begin{array}{ll} \displaystyle (\hat{\tau }_m+\varrho )(A^{'}+B^{'}+C^{'}) ,&{}\theta =0, \\ \displaystyle (\hat{\tau }_m+\varrho )(B^{'}+C^{'}) ,&{}\theta \in [-\frac{\hat{\tau }_m}{\tau _h^*},0),\\ \displaystyle (\hat{\tau }_m+\varrho )B^{'} ,&{}\theta \in (-1,-\frac{\hat{\tau }_m}{\tau _h^*}),\\ \displaystyle 0 ,&{}\theta =-1,\\ \end{array}\right. } \end{aligned}$$

For $\varphi \in C$, define

$$\begin{aligned} \small A(\varrho )\varphi = {\left\{ \begin{array}{ll} \displaystyle \frac{d{\varphi }(\theta )}{d\theta } ,&{}\theta \in [-1,0), \\ \displaystyle \int _{-1}^0d\zeta (\varrho ,\theta )\varphi (\theta ) ,&{}\theta =0, \end{array}\right. } \end{aligned}$$

(5.18)

and $\small R(\mu )\varphi = {\left\{ \begin{array}{ll} 0,&{} \theta \in [-1,0) \\ F(\varrho ,\varphi ),&{} \theta =0 \end{array}\right. }.$ Then model (5.17) is equivalent to

$$\begin{aligned} \small \frac{dx_t}{dt}=A(\varrho )x_t+R(\varrho )x_t, \end{aligned}$$

(5.19)

where $x_t=u(t+\theta )$ for $\theta \in [-1,0]$.

For $\psi \in C^1([0,1],(\mathbb {R}^5)^*)$, being the conjugated space of $C^1([0,1],\mathbb {R}^5)$, define

$$\begin{aligned} \small A^*\psi (s)= {\left\{ \begin{array}{ll} \displaystyle -\frac{d{\psi }(s)}{ds},&{} s\in (0,1], \\ \displaystyle \int _{-1}^0d\zeta ^T(t,0)\psi (-t),&{} s=0, \end{array}\right. } \end{aligned}$$

and the bilinear inner product

$$\begin{aligned} \langle \psi ,\varphi \rangle =\bar{\psi }(0)\varphi (0) -\int _{-1}^0\int _{\xi =0}^{\theta }\bar{\psi }(\xi -\theta )d\zeta (\theta )\varphi (\xi )d\xi , \end{aligned}$$

(5.20)

where $\zeta (\theta )=\zeta (\theta ,0)$. From the discussion in Sect. 4, we know that $\pm i\hat{\kappa }\hat{\tau }_m$ are eigenvalues of A(0). Thus, $\pm i\hat{\kappa }\hat{\tau }_m$ are also eigenvalues of $A^*(0)$. We will calculate the eigenvectors of A(0) and $A^*(0)$ with respond to $\pm i\hat{\kappa }\hat{\tau }_m$.

Assume $q(\theta )=(1,q_2,q_3,q_4,q_5)^Te^{i\hat{\kappa }\hat{\tau }_m\theta }$ is the eigenvector of A(0) corresponding to $i\hat{\kappa }$, namely, $A(0)q(\theta )=i\hat{\kappa }\hat{\tau }_m q(\theta )$ and let $q^*(s)=D(1,q_1^*,q_2^*,q_3^*,q_4^*)^T e^{i\hat{\kappa }\hat{\tau }_ms }$ is the eigenvector corresponding to $-i\hat{\kappa }$, then we have

$$\begin{aligned} \begin{aligned} q_1&=\frac{a_{21}+b_{25}e^{-i\hat{\kappa }\tau _h^*}q_4}{i\hat{\kappa }-a_{22}},\ q_2=\frac{(i\hat{\kappa }-c_{55}e^{-i\hat{\kappa }\hat{\tau }_m})q_4}{c_{53}e^{-i\hat{\kappa }\hat{\tau }_m}},\\ q_3&=\frac{a_{43}(i\hat{\kappa }-c_{55}e^{-i\hat{\kappa }\hat{\tau }_m})}{c_{53}e^{-i\hat{\kappa }\hat{\tau }_m}}q_4,\ q_4=\frac{b_{15}e^{-i\hat{\kappa }\tau _h^*}}{i\hat{\kappa }-a_{11}-b_{11}e^{-i\hat{\kappa }\tau _h^*}},\\ q_1^*&=0,\ q_2^*=\frac{-i\hat{\kappa }-a_{11}-b_{11}e^{-i\hat{\kappa }\tau _h^*} }{b_{31}e^{-i\hat{\kappa }\tau _h^*}},\ q_3^*=0,\\ q_4^*&=\frac{(-i\hat{\kappa }-a_{33})(-i\hat{\kappa }-a_{11}-b_{11}e^{-i\hat{\kappa }\tau _h^*}) }{c_{53}b_{31}e^{-i\hat{\kappa }(\tau _h^*+\hat{\tau }_m)}}, \end{aligned} \end{aligned}$$

where D is a constant satisfying $\langle q^*(s),q(\theta )\rangle =1$. By (5.20), we get

$$\begin{aligned} \begin{aligned} \displaystyle&\langle q^*(s),q(\theta )\rangle \\ \displaystyle&={\bar{D}}(1+q_2{\bar{q}}_2^*+q_4\bar{q}_4^*+\tau _h^*e^{-i\hat{\kappa }\tau _h^*}(b_{11}+b_{31}q_2^*+q_1b_{32}q_2^* +q_4(b_{15}+b_{35}q_2^*))\\&\quad +\hat{\tau }_me^{-i\hat{\kappa }\hat{\tau }_h}q_4^*(c_{53}q_2+c_{55}q_4)) \end{aligned} \end{aligned}$$

Therefore, we can choose

$$\begin{aligned} {\bar{D}}{} & {} =(1+q_2{\bar{q}}_2^*+q_4\bar{q}_4^*+\tau _h^*e^{-i\hat{\kappa }\tau _h^*}(b_{11}+b_{31}q_2^*+q_1b_{32}q_2^* +q_4(b_{15}+b_{35}q_2^*)) \\ {}{} & {} \quad +\hat{\tau }_me^{-i\hat{\kappa }\hat{\tau }_h}q_4^*(c_{53}q_2+c_{55}q_4))^{-1} \end{aligned}$$

such that $\langle q^*,q \rangle =1$ and $\langle q^*,{\bar{q}} \rangle =0$.

To compute the center manifold $C_0$ at $\varrho =0$. Define

$$\begin{aligned} z(t)=\langle q^*, x_t \rangle ,\quad W(t,\theta )=x_t(\theta )-z(t)q(\theta )-{\bar{z}}(t){\bar{q}}(\theta ). \end{aligned}$$

(5.21)

On $C_0$, we have

$$\begin{aligned} W(t,\theta )=W(z,\bar{z},\theta )=W_{20}(\theta )\frac{z^2}{2}+W_{11}(\theta )z\bar{z}+W_{02}(\theta )\frac{{\bar{z}}^2}{2}+\cdots . \end{aligned}$$

(5.22)

Note that W is real if $x_t$ is real, so we deal the real solutions only. For solution $x_t\in C_0$ with $\zeta =0$, we have

$$\begin{aligned} \begin{aligned} \displaystyle \frac{dz(t)}{dt}&= i\omega z+{\bar{q}}^*(0)f(0,W(z(t),\bar{z}(t),0))+z(t)q(\theta )+{\bar{z}}(t){\bar{q}}(\theta )) \triangleq i\omega z\\&\quad +{\bar{q}}^*(0) f_0(z,{\bar{z}}). \end{aligned}\qquad \end{aligned}$$

(5.23)

Denote $f_0(z,{\bar{z}})\triangleq f_{z^2}\frac{z^2}{2}+f_{z\bar{z}}z{\bar{z}}+f_{z^2{\bar{z}}} z^2{\bar{z}}+\cdots ,$ and write equation (5.23) as $\frac{dz(t)}{dt}=i\omega z+g(z,{\bar{z}}).$ Besides, denote

$$\begin{aligned} g(z,{\bar{z}})={\bar{q}}^*(0)f_0(z,{\bar{z}})=g_{20}\frac{z^2}{2}+g_{11} z{\bar{z}}+g_{02}\frac{{\bar{z}}^2}{2}+g_{21}\frac{ z^2{\bar{z}}}{2}+\cdots . \end{aligned}$$

(5.24)

Then we have

$$\begin{aligned} g_{20}={\bar{q}}^*(0)f_{z^2},\ g_{11}={\bar{q}}^*(0)f_{z{\bar{z}}},\ g_{02}={\bar{q}}^*(0)f_{{\bar{z}}^2},\ g_{21}={\bar{q}}^*(0)f_{z^2{\bar{z}}}. \end{aligned}$$

(5.25)

From (5.21) and (5.22), it follows that

$$\begin{aligned} \begin{aligned} x_t(\theta )&=(1,q_1,q_2,q_3,q_4)^Te^{i\hat{\kappa }\hat{\tau }_m \theta }z+(1,{\bar{q}}_1,{\bar{q}}_2,{\bar{q}}_3,\bar{q}_4)^Te^{-i\hat{\kappa }\hat{\tau }_m \theta }{\bar{z}}\\&\quad +W_{20}(\theta )\frac{z^2}{2}+W_{11}(\theta )z\bar{z}+W_{02}(\theta )\frac{{\bar{z}}^2}{2}+\cdots . \end{aligned} \end{aligned}$$

We have

$$\begin{aligned} \begin{aligned} x_{1t}(-\frac{\tau _h^*}{\hat{\tau }_m})&=\displaystyle ze^{-i\hat{\kappa }\tau _h^*}+\bar{z}e^{i\hat{\kappa }\tau _h^*}+W_{20}^{(1)}(-\frac{\tau _h^*}{\hat{\tau }_m})\frac{z^2}{2}+W_{11}^{(1)}(-\frac{\tau _h^*}{\hat{\tau }_m})z\bar{z}+W_{02}^{(1)}(-\frac{\tau _h^*}{\hat{\tau }_m})\frac{\bar{z}^2}{2}+\cdots ,\\ x_{5t}(-\frac{\tau _h^*}{\hat{\tau }_m})&=\displaystyle q_4ze^{-i\hat{\kappa }\tau _h^*}+{\bar{q}}_4\bar{z}e^{i\hat{\kappa }\tau _h^*}+W_{20}^{(5)}(-\frac{\tau _h^*}{\hat{\tau }_m})\frac{z^2}{2}+W_{11}^{(5)}(-\frac{\tau _h^*}{\hat{\tau }_m})z\bar{z}+W_{02}^{(5)}(-\frac{\tau _h^*}{\hat{\tau }_m})\frac{\bar{z}^2}{2}+\cdots ,\\ x_{3t}(-1)&=\displaystyle q_2ze^{-i\hat{\kappa }\hat{\tau }_m}+\bar{q}_2\bar{z}e^{i\hat{\kappa }\hat{\tau }_m}+W_{20}^{(3)}(-1)\frac{z^2}{2}+W_{11}^{(3)}(-1)z\bar{z}+W_{02}^{(3)}(-1)\frac{{\bar{z}}^2}{2}+\cdots ,\\ x_{5t}(-1)&=\displaystyle q_4ze^{-i\hat{\kappa }\hat{\tau }_m}+\bar{q}_4\bar{z}e^{i\hat{\kappa }\hat{\tau }_m}+W_{20}^{(5)}(-1)\frac{z^2}{2}+W_{11}^{(5)}(-1)z\bar{z}+W_{02}^{(5)}(-1)\frac{{\bar{z}}^2}{2}+\cdots , \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{array}{lll} f_{z^2}= \begin{pmatrix} \displaystyle -\beta _hq_4e^{-2i\hat{\kappa }\tau _h^*} \\ \displaystyle 0 \\ \displaystyle \beta _hq_4e^{-2i\hat{\kappa }\tau _h^*}\\ \displaystyle 0\\ \displaystyle -\beta _mq_2q_4e^{-2i\hat{\kappa }\hat{\tau }_m} \end{pmatrix},\ f_{z{\bar{z}}}= \begin{pmatrix} \displaystyle -\beta _h(q_4+{\bar{q}}_4) \\ \displaystyle 0 \\ \displaystyle \beta _h(q_4+{\bar{q}}_4)\\ \displaystyle 0\\ \displaystyle -\beta _m(q_2q_4+{\bar{q}}_2{\bar{q}}_4) \end{pmatrix},\ f_{{\bar{z}}^2}= \begin{pmatrix} \displaystyle -\beta _h{\bar{q}}_4 e^{2i\hat{\kappa }\tau _h^*} \\ \displaystyle 0 \\ \displaystyle \beta _h{\bar{q}}_4e^{2i\hat{\kappa }\tau _h^*} \\ \displaystyle 0\\ \displaystyle -\beta _m{\bar{q}}_2{\bar{q}}_4 e^{2i\hat{\kappa }\hat{\tau }_m} \end{pmatrix},\\ f_{z^2{\bar{z}}}= \begin{pmatrix} \displaystyle -\beta _h(\frac{1}{2} {W_{20}^{(1)}(-\frac{\tau _h^*}{\hat{\tau }_m} )} {\bar{q}}_4e^{i\hat{\kappa }\tau _h^*} + W_{11}^{(5)}(-\frac{\tau _h^*}{\hat{\tau }_m} )e^{-i\hat{\kappa }\tau _h^*} +\frac{1}{2} {W_{20}^{(5)}(-\frac{\tau _h^*}{\hat{\tau }_m} )} e^{-i\hat{\kappa }\tau _h^*}) \\ \displaystyle 0 \\ \displaystyle \beta _h(\frac{1}{2} {W_{20}^{(1)}(-\frac{\tau _h^*}{\hat{\tau }_m} )} e^{i\hat{\kappa }\tau _h^*}{\bar{q}}_4+ W_{11}^{(5)}( -\frac{\tau _h^*}{\hat{\tau }_m})e^{-i\hat{\kappa }\tau _h^*} +\frac{1}{2} {W_{20}^{(5)}(-\frac{\tau _h^*}{\hat{\tau }_m} } ){\bar{q}}_4 e^{-i\hat{\kappa }\tau _h^*}) \\ \displaystyle 0\\ \displaystyle -\beta _m(\frac{1}{2} {W_{20}^{(3)}(-1 )} \bar{q}_4e^{i\hat{\kappa }\hat{\tau }_m} + W_{11}^{(3)}( -1)q_4 e^{-i\hat{\kappa }\hat{\tau }_m}+\frac{1}{2}{W_{20}^{(5)}( -1)} {\bar{q}}_2 e^{-i\hat{\kappa }\hat{\tau }_m}) \end{pmatrix}. \end{array} \end{aligned}$$

(5.26)

In order to get $g_{11}$, we still need to compute $W_{20}(\theta )$ and $W_{11}(\theta )$. From (5.19) and (5.21), we have

$$\begin{aligned} \begin{aligned} \dot{W}&=\displaystyle \dot{x}_t-\dot{z} q(\theta ) -\dot{{\bar{z}}} {\bar{q}}(\theta )\\&=\displaystyle {\left\{ \begin{array}{ll} A(0)W- {\bar{g}}{\bar{q}}(\theta )- gq(\theta ), &{} \theta \in [-1,0), \\ A(0)W- gq(0)- {\bar{g}} q(0) +f_0(z,{\bar{z}}),&{} \theta =0. \end{array}\right. } \end{aligned} \end{aligned}$$

(5.27)

On the other hand, in $C_0$, we can write (5.27) as

$$\begin{aligned} \begin{aligned} \dot{W}&=W_z\dot{z}+W_z\dot{{\bar{z}}}\\&=[W_{20}(\theta )z+W_{11}(\theta ){\bar{z}}](i\hat{\kappa }\hat{\tau }_m+g(z,{\bar{z}}))+[W_{11}(\theta )z+W_{02}(\theta )\bar{z}]\\&\quad (-i\hat{\kappa }\hat{\tau }_m+{\bar{g}}(z,{\bar{z}})). \end{aligned} \end{aligned}$$

(5.28)

Then substituting (5.22) and (5.24) into (5.27) and (5.28), comparing the coefficients of $\frac{z^2}{2}$ and $z{\bar{z}}$, one can get

$$\begin{aligned} (2i\hat{\kappa }\hat{\tau }_mI-A)W_{20}(\theta )= {\left\{ \begin{array}{ll} \displaystyle -g_{20}q(\theta )-{\bar{g}}_{02}{\bar{q}}(\theta ),&{} s\in [-1,0), \\ \displaystyle -g_{20}q(0)-{\bar{g}}_{02}{\bar{q}}(0)+f_{z^2},&{} s=0, \end{array}\right. } \end{aligned}$$

(5.29)

$$\begin{aligned} -AW_{11}(\theta )= {\left\{ \begin{array}{ll} \displaystyle -g_{11}q(\theta )-{\bar{g}}_{11}{\bar{q}}(\theta ),&{} s\in [-1,0), \\ \displaystyle -g_{11}q(0)-{\bar{g}}_{11}{\bar{q}}(0)+f_{z{\bar{z}}},&{} s=0, \end{array}\right. } \end{aligned}$$

(5.30)

From (5.18) and (5.29) we can see that when $\theta \in [-1,0),$ $W_{20}^{'}(\theta )=2i\hat{\kappa }\hat{\tau }_mW_{02}(\tau )+g_{20}q(\theta )+\bar{g}_{02}{\bar{q}}(\theta ),$ which has the solution

$$\begin{aligned} W_{20}(\theta )=\frac{ig_{02}}{\hat{\kappa }\hat{\tau }_m}q(0)e^{i\hat{\kappa }\hat{\tau }_m\theta } +\frac{i{\bar{g}}_{02}}{3\hat{\kappa }\hat{\tau }_m}\bar{q}(0)e^{-i\hat{\kappa }\hat{\tau }_m\theta } +\mathcal {E}_1e^{2i\hat{\kappa }\hat{\tau }_m\theta }. \end{aligned}$$

(5.31)

When $\theta =0$

$$\begin{aligned} \int _{-1}^0d\zeta (\theta )W_{20}(\theta )=2i\hat{\kappa }\hat{\tau }_mW_{20}+g_{02}q(0)+\bar{g}_{02}{\bar{q}}(0)-f_{z^2}. \end{aligned}$$

(5.32)

Substituting equation (5.31) into (5.32), one can obtain

$$\begin{aligned} \mathcal {E}_1=\left( 2i \hat{\kappa }\hat{\tau }_m I- \int _{-1}^0e^{2i\hat{\kappa }\hat{\tau }_m\theta }d\zeta (\theta )\right) f_{z^2}. \end{aligned}$$

(5.33)

From (5.18) and (5.30) we can see that when $\theta \in [-1,0),$ $W_{11}^{'}(\theta )= g_{11}q(\theta )+{\bar{g}}_{11}\bar{q}(\theta ),$ which has the solution

$$\begin{aligned} W_{11}(\theta )=-\frac{ig_{11}}{\hat{\kappa }\hat{\tau }_m}q(0)e^{i\hat{\kappa }\hat{\tau }_m\theta } +\frac{i{\bar{g}}_{11}}{\hat{\kappa }\hat{\tau }_m}\bar{q}(0)e^{-i\hat{\kappa }\hat{\tau }_m\theta } +\mathcal {E}_2. \end{aligned}$$

(5.34)

When $\theta =0$

$$\begin{aligned} \int _{-1}^0d\zeta (\theta )W_{11}(\theta )= g_{11}q(0)+{\bar{g}}_{11}\bar{q}(0)-f_{z{\bar{z}}}. \end{aligned}$$

(5.35)

Substituting equation (5.34) into (5.35) one can obtain

$$\begin{aligned} \mathcal {E}_2=\left( \int _{-1}^0d\zeta (\theta )\right) f_{z{\bar{z}}}. \end{aligned}$$

(5.36)

Therefore, from (5.25), (5.26), (5.33), (5.36) we can obtain

$$\begin{aligned} g_{20}&=2\hat{\tau }_m{\bar{D}}((-\beta _h q_4+{\bar{q}}_2^*\beta _h q_4)e^{-2\hat{\kappa }\tau _h^*}-\beta _m {\bar{q}}_4^*q_2q_4e^{-2\hat{\kappa }\hat{\tau }_m}),\\ g_{11}&=\hat{\tau }_m{\bar{D}}(\beta _h({\bar{q}}_4+q_4)(-1+{\bar{q}}_2^*) e^{-2\hat{\kappa }\tau _h^*}-\beta _m {\bar{q}}_4^*(q_2{\bar{q}}_4+{\bar{q}}_2q_4)e^{-2\hat{\kappa }\hat{\tau }_m}),\\ g_{02}&=2\hat{\tau }_m{\bar{D}}((-\beta _h {\bar{q}}_4+{\bar{q}}_2^*\beta _h q_4)e^{-2\hat{\kappa }\tau _h^*}-\beta _m {\bar{q}}_4^*{\bar{q}}_2{\bar{q}}_4e^{-2\hat{\kappa }\hat{\tau }_m})\\ g_{21}&=2\hat{\tau }_m{\bar{D}}[-\beta _h(\frac{1}{2}{W_{20}^{(1)}(-\frac{\tau _h^*}{\hat{\tau }_m} )} {\bar{q}}_4e^{i\hat{\kappa }\tau _h^*} + W_{11}^{(5)}(-\frac{\tau _h^*}{\hat{\tau }_m} )e^{-i\hat{\kappa }\tau _h^*} +\frac{1}{2} {W_{20}^{(5)}(-\frac{\tau _h^*}{\hat{\tau }_m} )} e^{-i\hat{\kappa }\tau _h^*}) \\&\quad +{\bar{q}}_2^*\beta _h(\frac{1}{2} {W_{20}^{(1)}(-\frac{\tau _h^*}{\hat{\tau }_m} )} e^{i\hat{\kappa }\tau _h^*}{\bar{q}}_4+ W_{11}^{(5)}( -\frac{\tau _h^*}{\hat{\tau }_m})e^{-i\hat{\kappa }\tau _h^*} +\frac{1}{2} {W_{20}^{(5)}(-\frac{\tau _h^*}{\hat{\tau }_m} } ){\bar{q}}_4 e^{-i\hat{\kappa }\tau _h^*})\\&\quad -{\bar{q}}_4^*\beta _m( \frac{1}{2}{W_{20}^{(3)}(-1 )} \bar{q}_4e^{i\hat{\kappa }\hat{\tau }_m} + W_{11}^{(3)}( -1)q_4 e^{-i\hat{\kappa }\hat{\tau }_m}+\frac{1}{2} {W_{20}^{(5)}( -1)} {\bar{q}}_2 e^{-i\hat{\kappa }\hat{\tau }_m})]. \end{aligned}$$

After analysis and computation, we have the following quantities:

$$\begin{aligned} \begin{aligned} C_1(0)&=\displaystyle \frac{i}{2\omega }\big (g_{20}g_{11}-2|g_{11}|^2-\frac{1}{3}|g_{02}|^2\big )+\frac{g_{21}}{2},\ \displaystyle \mu _2=\displaystyle -\frac{Re\{C_1(0)\}}{Re\{\lambda '(\hat{\tau }_m)\}},\\ \beta _2&=\displaystyle 2Re\{C_1(0)\},\ \displaystyle T_2=\displaystyle -\frac{Im(C_1(0))+\mu _2Im\{\lambda '(\hat{\tau }_m)\}}{\omega }. \end{aligned} \end{aligned}$$

$\square$