1 Introduction

Malaria is an acute febrile illness caused by protozoan parasites of genus Plasmodium spread by infectious female Anopheles mosquitoes when they seek blood meal for production of their eggs. There are five species of the parasites that cause malaria in humans. These parasites include: Plasmodium falciparum; Plasmodium vivax; Plasmodium malariae; Plasmodium ovale; Plasmodium knowlesi, of which Plasmodium falciparum and Plasmodium vivax pose the greatest threat. Malaria remains one of the major public health challenges and life-threatening diseases worldwide [1]. Currently, an estimated 228 million people is at risk of malaria and mortality rate stands at 405,000 worldwide. The disease is characterized by symptoms such as fever, headache, sweats, muscle aches, chills, tiredness, nausea, vomiting, diarrhea, anaemia, jaundice, seizures [2] and malaria symptoms in individuals usually appear about 10-15 days after the infected mosquito has taken its blood meal [3]. Malaria can be cured, but symptoms may recur if the disease is not efficiently treated and properly controlled.

Recurrent malaria is referred to as the subsequent parasitaemic episodes occurring not later than seven days after receiving anti-malaria treatment. Recurrent malaria constitutes greatest challenge to the total extinction of malaria in our community [4]. Recurrence of malaria can be caused by recrudescence, relapse and re-infection. Recrudescence is the recurrence of malaria symptoms due to the survival of malaria parasites in the blood. Relapse refers to the situation whereby symptoms reappear due to reactivation of dormant hypnozoites in the liver cells after the total clearance of the parasites from the blood. In contrast, re-infection is the reappearance of malaria symptoms due to infection from new mosquito bite [5,6,7,8].

A number of contemporary mathematical models have been developed after the pioneer works of Ross [9], Macdonald [10], and Anderson and May [11] to assess the dynamical spread of malaria in human population (see, e.g., [5, 12,13,14,15,16,17,18,19] and some of the references therein). In [12], the author studied the bifurcation analysis of a mathematical model for malaria transmission using a system of ordinary differential equation via the modification of models from literature and then incorporated some more realistic features. Anguelov et al. [5] established a nonpolluting technique of curtailing the prevalence of female anopheles mosquito through the release of sterile males using compartmental model. Olaniyi and Obabiyi [17] explored the implication of nonlinear incidence function on the transmission dynamics of malaria in human population. The model incorporated the rate at which recovered humans returned back to the susceptible and their infectious states due to lack of complete acquired immunity. Mbogo et al. [15] proposed a mathematical model which is a modification of [22], where the disease dynamics of deterministic and stochastic models were compared basically to determine the effect of randomness in malaria transmission dynamics. In [16], the authors formulated a mathematical model to investigate the global stability of malaria transmission dynamics with vigilant compartment, where a normalized system of ordinary differential equation with the concept that human may not have equal likelihood of being infected with malaria parasites was considered. Traoré et al. [18] developed a system of retarded functional differential equations to investigate transmission of malaria dynamics with maturation delay of a vector population in a periodic environment.

A limited number of studies have been presented on the mathematical analysis of recurrent malaria featuring relapse and re-infection. Niger and Gumel [20] focused on the mathematical modelling of assessing the role of repeated exposure on the transmission dynamics of malaria disease in human population by formulating a comprehensive mathematical model. Li et al. [21] studied the fast and slow dynamics of malaria model with relapse by considering two distinct mathematical models where the first dynamic model was based on constant vector population and the second dynamic model was based on variable vector population sizes. Huo and Qui [22] formulated a mathematical model to assess the stability of malaria transmission with relapse. In a related development, Ghosh et al. [23] explored the analysis of recurrent malaria by considering only two of the phenomena of recurrent malaria representing relapse and re-infection. The model presented in this study extends the features considered in [23]. Till date, and to the best of our knowledge, the mathematical assessment of malaria transmission dynamics detailing all components of recurrent malaria has not been studied in the literature.

Therefore, in this study, recovered human population is stratified into pseudo-recovered humans population with relapse, recovered humans with possibility of re-infection, and recovered humans with recrudescence. Keeping this in mind, a more robust mathematical model of malaria featuring all the classes of recurrent malaria is analysed using stability theory of differential equations. The organization of the remaining aspects of the study is as follows: Sect. 2 presents the mathematical formulation and fundamental properties of the recurrent malaria model. The possibility of existence of bifurcation and global stability analysis of the malaria model around equilibria are presented in Sects. 3 and 4, respectively. Section 5 gives the concluding remarks of the study.

2 Formulation of the model

To develop the transmission dynamics of malaria model with recrudescence, relapse, and re-infection, the following six classes of human population are considered: susceptible human class, denoted by \(S_{h}(t)\); exposed human class, denoted by \(E_h(t)\); infectious human class \(I_h(t)\); pseudo-recovered human with possible reactivation of infection (relapse), denoted by \(R_{1h}(t)\); recovered human with re-infection possibility \(R_{2h}(t)\); and recovered human with possibility of recrudescence, denoted by \(R_{3h}(t)\). Hence, the total human population at time t, denoted by \(N_h(t)\), is given by

\(N_h(t)=S_h(t)+E_h(t)+I_h(t)+R_{1h}(t)+R_{2h}(t)+R_{3h}(t)\).

On the other hand, the mosquito population is stratified into three classes, namely, susceptible \(S_m(t)\); exposed \(E_m(t)\); and infectious \(I_m(t)\), so that the total mosquito population \(N_m(t)\) becomes

\(N_m(t)=S_m(t)+E_m(t)+I_m(t)\).

The susceptible human class is increased by the recruitment of humans, assumed susceptible, at a rate given by \(\Lambda _{h}\). However, due to effective contact with infectious mosquito \(I_m(t)\), the susceptible human class is reduced by the standard incidence of infection, \(\beta _h b S_h I_m/N_h\), where \(\beta _h\) and b are infection transmission probability in humans and biting rate of mosquitoes, respectively. The population of susceptible human is further decreased by the natural mortality rate \(\mu _h\). Hence, the susceptible human class changing with respect to time is given by

$$\begin{aligned} \dfrac{dS_h}{dt}=\Lambda _h-\dfrac{\beta _h b S_h I_m}{N_h}-\mu _hS_h \end{aligned}$$
(1)

Following the infection of the susceptible human class and the re-infection of the recovered human class, the population of exposed human class is increased by \(\beta _h b S_h I_m/N_h\) and \(\varepsilon \beta _h b R_{2h} I_m/N_h\), where \(\varepsilon \in (0, 1)\) is the modification parameter responsible for the reduced transmission probability of re-infection, which is due to the prior infection-acquired immunity by recovered individuals [20, 23]. Moreover, the population of exposed humans is increased by the relapse of pseudo-recovered human (at a rate \(\theta \)) and decreased by both progression rate of exposed humans to the infectious class \((I_h(t))\) (at a rate \(\alpha _h\)) and natural mortality (at a rate \(\mu _h\)). Hence, the exposed human class changing with time is given by

$$\begin{aligned} \dfrac{dE_{h}}{dt}=\frac{\beta _{h}bI_{m}(S_{h}+\varepsilon R_{2h})}{N_{h}}+\theta R_{1h}-(\alpha _{h}+\mu _{h})E_{h} \end{aligned}$$
(2)

The infectious human class, \((I_h(t))\) increases following progression of the exposed humans at a rate \(\alpha _h\). This class is further increased due to recrudescence at a rate \(\tau \), while the class is reduced due to both recovery from infectious state at per capita rate \(\gamma \) and the natural mortality rate \(\mu _h\). Therefore, the rate of change of the infectious human class with time is given by

$$\begin{aligned} \dfrac{dI_{h}}{dt}=\alpha _{h} E_{h}+\tau R_{3h}-(\gamma +\mu _{h})I_{h} \end{aligned}$$
(3)

Following the relapse of recovered infectious humans, the population of pseudo-recovered humans with infection at the dormant liver stage is generated by a fraction \(\sigma _1\) of the per capita recovery rate of infectious human. The population is reduced by relapse (at a rate \(\theta \)) and the natural mortality rate \(\mu _h\). Therefore, the rate of change of the pseudo-recovered human class with time is given by

$$\begin{aligned} \dfrac{dR_{1h}}{dt}=\sigma _{1}\gamma I_{h}-(\theta +\mu _{h})R_{1h} \end{aligned}$$
(4)

The population of recovered human with re-infection possibility (\(R_{2h}(t)\)) is increased by a fraction \(\sigma _2\) of the per capita recovery rate of infectious human. Following effective re-infection from infectious mosquito, this population is diminished by the standard incidence \(\beta _h b \varepsilon R_{2h}/N_h\) and the natural mortality (at a rate \(\mu _h\)). Thus, the rate of change of \(R_{2h}(t)\) is given by

$$\begin{aligned} \dfrac{dR_{2h}}{dt}=\sigma _{2}\gamma I_{h}-\frac{\varepsilon \beta _{h}bR_{2h}I_{m}}{N_{h}}-\mu _{h}R_{2h} \end{aligned}$$
(5)

The population of recrudescent human is increased by the remaining fraction \((1-(\sigma _1+\sigma _2))\) of the per capita recovery rate of infectious human. Following incomplete treatment of the disease, this population is downsized at per capita recrudescent rate \(\tau \), and also reduced by the natural mortality rate \(\mu _h\). This translates to the equation specified by

$$\begin{aligned} \dfrac{dR_{3h}}{dt}=(1-(\sigma _{1}+\sigma _{2}))\gamma I_{h}-(\tau +\mu _{h})R_{3h} \end{aligned}$$
(6)

Moreover, the susceptible mosquito class is generated by the recruitment rate, \(\Lambda _m\), assumed susceptible and is decreased due to effective contact with both infectious human and recrudescent human via standard incidences of the form \(\beta _m b S_m I_h/N_h\) and \(\beta _m b \phi S_m R_{3h}/N_h\), where \(\beta _m\) is the probability of transmission of infection in mosquitoes and \(\phi \in (0, 1)\) is the modification parameter reflecting the reduced infectiousness of recrudescent humans when compared to the infectious humans. The susceptible mosquito population is further reduced by natural per capita death rate \(\mu _m\), so that

$$\begin{aligned} \dfrac{dS_{m}}{dt}=\Lambda _{m}-\dfrac{\beta _{m}bS_{m}(I_{h}+\phi R_{3h})}{N_{h}}-\mu _{m}S_{m} \end{aligned}$$
(7)

Following effective contact with both infectious human and recrudescent human, the class of exposed mosquito is increased by the standard incidences \(\beta _mbS_mI_h/N_h\) and \(\beta _mb\phi S_m R_{3h}/N_h\). The exposed mosquito population is reduced both at the progression rate \(\alpha _m\) and natural per capita death rate \(\mu _m\). Therefore, the rate of change of the population yields

$$\begin{aligned} \dfrac{dE_{m}}{dt}=\frac{\beta _{m}bS_{m}(I_{h}+\phi R_{3h})}{N_{h}}-(\alpha _{m}+\mu _{m})E_{m} \end{aligned}$$
(8)

The population of infectious mosquito class is increased as a result of progression from the exposed class at the rare \(\alpha _h\). However, the population is downsized at the natural mortality rate \(\mu _m\), so that

$$\begin{aligned} \dfrac{dI_{m}}{dt}=\alpha _{m} E_{m}-\mu _{m}I_{m} \end{aligned}$$
(9)

In what follows, the mathematical model describing the transmission of malaria with recrudescence, relapse, and re-infection is given by combining all the aforementioned equations to form the following system.

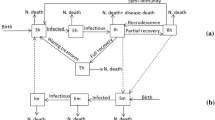
$$\begin{aligned} \begin{array}{ccl} \dfrac{dS_{h}}{dt}&{}=&{}\Lambda _{h}-\dfrac{\beta _{h}bS_{h}I_{m}}{N_{h}}-\mu _{h}S_{h}\\ \ \\ \dfrac{dE_{h}}{dt}&{}=&{}\dfrac{\beta _{h}bI_{m}(S_{h}+\varepsilon R_{2h})}{N_{h}}+\theta R_{1h}-(\alpha _{h}+\mu _{h})E_{h}\\ \ \\ \dfrac{dI_{h}}{dt}&{}=&{}\alpha _{h} E_{h}+\tau R_{3h}-(\gamma +\mu _{h})I_{h}\\ \ \\ \dfrac{dR_{1h}}{dt}&{}=&{}\sigma _{1}\gamma I_{h}-(\theta +\mu _{h})R_{1h}\\ \ \\ \dfrac{dR_{2h}}{dt}&{}=&{}\sigma _{2}\gamma I_{h}-\dfrac{\varepsilon \beta _{h}bR_{2h}I_{m}}{N_{h}}-\mu _{h}R_{2h}\\ \ \\ \dfrac{dR_{3h}}{dt}&{}=&{}(1-(\sigma _{1}+\sigma _{2}))\gamma I_{h}-(\tau +\mu _{h})R_{3h}\\ \ \\ \dfrac{dS_{m}}{dt}&{}=&{}\Lambda _{m}-\dfrac{\beta _{m}bS_{m}(I_{h}+\phi R_{3h})}{N_{h}}-\mu _{m}S_{m}\\ \ \\ \dfrac{dE_{m}}{dt}&{}=&{}\dfrac{\beta _{m}bS_{m}(I_{h}+\phi R_{3h})}{N_{h}}-(\alpha _{m}+\mu _{m})E_{m}\\ \ \\ \dfrac{dI_{m}}{dt}&{}=&{}\alpha _{m} E_{m}-\mu _{m}I_{m} \end{array} \end{aligned}$$
(10)

A schematic diagram representing the formulation of the model (10) is given in Fig. 1, while the descriptions of the variables and parameters of the model (10) are provided in Tables 1 and 2, respectively.

Fig. 1
figure 1

Schematic diagram for the full recurrent malaria dynamics (10)

Full size image
Table 1 The description of variables of the malaria model (10)
Full size table
Table 2 The description of parameters of the malaria model (10)
Full size table

2.1 Fundamental properties

To begin with, since the parameters of the model governed by system (10) address the interaction between humans and mosquitoes, then, it is worthy of mentioning that, all the associated parameters and state variables of the model are non-negative for all times. Hence, it is cogent to show that all the variables of the model are also non-negative for \(t>0\).

2.1.1 Invariant region and positivity of solutions

Lemma 1

The feasible region of the malaria model (10), given by \(\mathfrak {D}=\mathfrak {D}_{h}\times \mathfrak {D}_{m}\subset \mathbb {R}^{6}_{+}\times \mathbb {R}^{3}_{+}\), where

$$\begin{aligned} \mathfrak {D}_h= & {} \left\{ (S_{h}, E_{h}, I_{h}, R_{1h}, R_{2h}, R_{3h})\in {\mathbb {R}^{6}_{+}}:S_{h}+E_{h}+I_{h}+R_{1h}+R_{2h}+R_{3h}\le \frac{\Lambda _h}{\mu _h}\right\} and\\ \mathfrak {D}_m= & {} \left\{ (S_{m}, E_{m}, I_{m})\in \mathbb {R}^{3}_{+}: S_{m}+E_{m}+I_{m} \le \frac{\Lambda _{m}}{\mu _{m}}\right\} , \end{aligned}$$

is positively-invariant and attracting.

Proof

It is straightforward from the rates of change of the total human population \(N_{h}(t)\) and total mosquito population \(N_{m}(t)\), respectively, that

$$\begin{aligned} N_{h}(t)\le N_{h}(0)\exp (-\mu _{h}t)+\frac{\Lambda _{h}}{\mu _{h}}(1-\exp (-\mu _{h}t)) \end{aligned}$$

and

$$\begin{aligned} N_{m}(t)\le N_{m}(0)\exp (-\mu _{m}t)+\frac{\Lambda _{m}}{\mu _{m}}(1-\exp (-\mu _{m}t)). \end{aligned}$$

Therefore, if \(N_{h}(0) \le \frac{\Lambda _{h}}{\mu _{h}}\) and \(N_{m}(0) \le \frac{\Lambda _{m}}{\mu _{m}}\), then, \(N_{h}(t) \le \frac{\Lambda _{h}}{\mu _{h}}\) and \(N_{m}(t) \le \frac{\Lambda _{m}}{\mu _{m}}\). Thus, the region \(\mathfrak {D}\) is positively-invariant. Further, if \(N_{h}(0)\ge \frac{\Lambda _{h}}{\mu _{h}}\) and \(N_{m}(0)\ge \frac{\Lambda _{m}}{\mu _{m}}\), then the solution either enters \(\mathfrak {D}\) in finite time or both \(N_{h}\) approaches \(\frac{\Lambda _{h}}{\mu _{h}}\) and \(N_{m}\) approaches \(\frac{\Lambda _{m}}{\mu _{m}}\) asymptotically as \(t\rightarrow \infty \). Hence, the region \(\mathfrak {D}\) attracts all solutions in \(\mathbb {R}_{+}^{9}\).

On this note, it is therefore suffices to consider the dynamics of malaria transmission governed by a system of differential equation (10) in the biologically feasible region \(\mathfrak {D}\), where the model is epidemiologically and mathematically well posed. \(\square \)

Theorem 1

The solution set, \(\left\{ (S_{h}, E_{h}, I_{h}, R_{1h}, R_{2h}, R_{3h}, S_{m}, E_{m}, I_{m})\right\} \) of the malaria model (10) with positive initial data \(S_{h}(0)\), \(E_{h}(0)\), \(I_{h}(0)\), \(R_{1h}(0)\), \(R_{2h}(0)\), \(R_{3h}(0)\), \(S_{m}(0)\), \(E_{m}(0)\), and \(I_{m}(0))\) in \(\mathfrak {D}\), remain positive in \(\mathfrak {D}\) for all time, \(t>0\).

Proof

The first equation of the model (10) gives rise to the following differential inequality

$$\begin{aligned} \frac{dS_{h}}{dt}\ge -\left( \frac{\beta _{h}bI_{m}}{N_{h}}+\mu _{h}\right) S_{h}. \end{aligned}$$

so that,

$$\begin{aligned} \dfrac{d}{dt}\left[ S_h(t)\exp \left( -\int _{0}^{t} \frac{\beta _{h}bI_{m}(\psi )}{N_{h}(\psi )}d\psi +\mu _{h}t\right) \right] >0 \end{aligned}$$

It therefore follows that,

$$\begin{aligned} S_{h}(t) \ge S_{h}(0)\exp \left[ -\int _{0}^{t} \frac{\beta _{h}bI_{m}(\psi )}{N_{h}(\psi )}d\psi +\mu _{h}t\right]>0, \quad \text {for all}\quad t >0. \end{aligned}$$

The remaining state variables \(E_{h}\), \(I_{h}\), \(R_{1h}\), \(R_{2h}\), \(R_{3h}\), \(S_{m}\), \(E_{m}\), \(I_{m}\) can also be shown in a similar manner. Hence, the solution set \({(S_{h}, E_{h}, I_{h}, R_{1h}, R_{2h}, R_{3h}, S_{m}, E_{m}, I_{m})}\) is non-negative \(\forall \) \(t>0\). \(\square \)

3 Equilibrium points and bifurcation analysis

This section explores the existence of equilibrium points and the type of bifurcation the model (10) exhibits.

3.1 Disease-free equilibrium

At malaria-free equilibrium, it is assumed that there is no infection, such that, all the infection related variables in the malaria model (10) are set to zero. Therefore, the disease-free equilibrium of the malaria model (10), designated by \(\mathcal {E}_{0}\), is given by

$$\begin{aligned} \mathcal {E}_{0}=(S_h^{*},E_h^{*},I_h^{*},R_{1h}^{*},R_{2h}^{*},R_{3h}^{*},S_{m}^{*},E_{m}^{*},I_{m}^{*})=\left( \dfrac{\Lambda _h}{\mu _h}, 0, 0, 0, 0, 0, \dfrac{\Lambda _m}{\mu _m}, 0, 0\right) \end{aligned}$$
(11)

The basic reproduction number, \(\mathcal {R}_{0}\), of the malaria model (10) can be obtained using the well-known next generation operator approach as described in [24]. Evaluating the matrices F (of the new infection terms) and V (of the transition terms) at the given point \(\mathcal {E}_{0}\) (11), respectively, gives

$$\begin{aligned} F=\left( \begin{array}{cccccc} 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \beta _{h}b\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad \dfrac{\beta _{m}b\Lambda _{m}\mu _{h}}{\Lambda _{h}\mu _{m}}&{}\quad 0&{}\quad \dfrac{\beta _{m}b\phi \Lambda _{m}\mu _{h}}{\Lambda _{h}\mu _{m}}&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{array}\right) \end{aligned}$$

and

$$\begin{aligned} V=\left( \begin{array}{cccccc} k_1&{}\quad 0&{}\quad -\theta &{}\quad 0&{}\quad 0&{}\quad 0\\ -\alpha _{h}&{}\quad k_{2}&{}\quad 0&{}\quad -\tau &{}\quad 0&{}\quad 0\\ 0&{}\quad -\sigma _{1}\gamma &{}\quad k_{3}&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad x&{}\quad 0&{}\quad k_{4}&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad k_{5}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -\alpha _{m}&{}\quad \mu _{m} \end{array}\right) , \end{aligned}$$

where \(k_1=(\alpha _{h}+\mu _{h})\), \(k_2=(\gamma +\mu _{h})\), \(k_3=(\theta +\mu _{h})\), \(k_4=(\tau +\mu _{h})\), \(k_5=(\alpha _{m}+\mu _{m})\) and \(x=[1-(\sigma _{1}+\sigma _{2})]\gamma \). It follows that the spectral radius of \(FV^{-1}\), denoted by \(\rho (FV^{-1})\), is the basic reproduction number given by

$$\begin{aligned} \mathcal {R}_{0}=\sqrt{\frac{\beta _h b^2 \alpha _m \beta _m\mu _h\Lambda _m\alpha _hk_3(k_4+\phi x)}{\mu _m^2\Lambda _hk_5[{k_1k_3(k_2k_4-\tau x)-\theta \alpha _h\sigma _1\gamma k_4}]}}. \end{aligned}$$
(12)

Keeping in mind that the denominator in (12) is positive by algebraic simplification. Thus, it follows that

$$\begin{aligned} \mu _m^2\Lambda _hk_5[{k_1k_3(k_2k_4-\tau x)-\theta \alpha _h\sigma _1\gamma k_4}]= & {} \mu _m^2\Lambda _hk_5[\mu _h k_3 [\tau k_1+\mu _h k_2+\tau (\sigma _1+\sigma _2)\gamma ]\nonumber \\&+ \alpha _{h}\mu _h[\mu _h(\theta +k_2)+\tau (\sigma _1+\sigma _2)\gamma ]+ \theta \alpha _h[\mu _h(1-\sigma _1)+\tau \sigma _2]] \end{aligned}$$
(13)

The basic reproduction number, \(\mathcal {R}_0\), of the malaria model (10) is the threshold parameter that determines the spread potential of the disease when an infectious individual enters a completely susceptible population.

The local asymptotic stability of the disease-free equilibrium (DFE) (11) follows from Theorem 2 in [24]. Hence, the following result is claimed.

Lemma 2

The DFE, denoted by \(\mathcal {E}_0\), of the malaria model (10) is locally asymptotically stable in \(\mathfrak {D}\) if \(\mathcal {R}_0 <1\) and unstable otherwise.

The epidemiological implication of Lemma 2 is that malaria can be effectively curtailed in the population if the initial sizes of the infected individuals (humans and mosquitoes) of the malaria model (10) are in the basin of attraction of the DFE, such that \(\mathcal {R}_{0}<1\).

3.2 Endemic equilibrium

The endemic equilibrium point of the malaria model (10) is a non-trivial steady state where the disease is present in the population. Due to the complexity of the model which incorporates the features of recurrent malaria, the analytical expression of the endemic equilibrium point is not shown, as multiple endemic equilibria could be obtained. This possibility leads to the investigation of bifurcation property of the malaria model (10) in the next section.

3.3 Bifurcation property

The center manifold theory made popular by Castillo-Chavez and Song [25] is employed to show the type of bifurcation that the malaria model (10) will exhibit. To apply this theory, it is convenient to perform the following changes of variables.

Let the malaria model (10) be written in the vector form \(dX/dt=F(X)\), where \(X=(x_1, x_2,\ldots , x_9)^{\intercal }\) and \(F=(f_1, f_2,\ldots , f_9)^{\intercal }\), so that \(S_h=x_1\), \(E_h=x_2\), \(I_h=x_3\), \(R_{1h}=x_4\), \(R_{2h}=x_5\), \(R_{3h}=x_6\), \(S_m=x_7\), \(E_m=x_8\), \(I_m=x_9\). Then, the malaria model (10) becomes:

$$\begin{aligned} \begin{array}{ccl} \dfrac{dx_{1}}{dt}\equiv f_1&{}=&{}\Lambda _{h}-\dfrac{\beta _{h}bx_{1}x_{9}}{\sum _{i=1}^{6} x_i}-\mu _{h}x_{1}\\ \ \\ \dfrac{dx_{2}}{dt}\equiv f_2&{}=&{}\dfrac{\beta _{h}bx_{9}(x_{1}+\varepsilon x_{5})}{\sum _{i=1}^{6}{ x_i}}+\theta x_{4}-(\alpha _{h}+\mu _{h})x_{2}\\ \ \\ \dfrac{dx_{3}}{dt}\equiv f_3&{}=&{}\alpha _{h} x_{2}+\tau x_{6}-(\gamma +\mu _{h})x_{3}\\ \ \\ \dfrac{dx_{4}}{dt}\equiv f_4&{}=&{}\sigma _{1}\gamma x_{3}-(\theta +\mu _{h})x_{4}\\ \ \\ \dfrac{dx_{5}}{dt}\equiv f_5&{}=&{}\sigma _{2}\gamma x_{3}-\dfrac{\varepsilon \beta _{h}bx_{5}x_{9}}{\sum _{i=1}^{6}{ x_i}}-\mu _{h}x_{5}\\ \ \\ \dfrac{dx_{6}}{dt}\equiv f_6&{}=&{}(1-(\sigma _{1}+\sigma _{2}))\gamma x_{3}-(\tau +\mu _{h})x_{6}\\ \ \\ \dfrac{dx_{7}}{dt}\equiv f_7&{}=&{}\Lambda _{m}-\dfrac{\beta _{m}bx_{7}(x_{3}+\phi x_{6})}{\sum _{i=1}^{6}{ x_i}}-\mu _{m}x_{7}\\ \ \\ \dfrac{dx_{8}}{dt}\equiv f_8&{}=&{}\dfrac{\beta _{m}bx_{7}(x_{3}+\phi x_{6})}{\sum _{i=1}^{6}{ x_i}}-(\alpha _{m}+\mu _{m})x_{8}\\ \ \\ \dfrac{dx_{9}}{dt}\equiv f_9&{}=&{}\alpha _{m} x_{8}-\mu _{m}x_{9} \end{array} \end{aligned}$$
(14)

Consider the case when \(\beta _h=\beta _{h}^{*}\) is chosen as the bifurcation parameter. Solving for \(\beta _h=\beta _{h}^{*}\) at \(\mathcal {R}_{0}=1\) in (12) yields

$$\begin{aligned} \beta _{h}^{*}=\dfrac{\mu _m^2\Lambda _hk_5[{k_1k_3(k_2k_4-\tau x)-\theta \alpha _h\sigma _1\gamma k_4}]}{b^2 \alpha _m \beta _m\mu _h\Lambda _m\alpha _hk_3(k_4+\phi [1-(\sigma _1+\sigma _2)]\gamma )} \end{aligned}$$

The Jacobian matrix of (14) evaluated at disease-free equilibrium \((\mathcal {E}_{0})\) with \(\beta _h=\beta _{h}^{**}\), is given by

$$\begin{aligned} \mathcal {J}(\mathcal {E}_{0})\mid _{\beta _h^{*}}=\left( \begin{array}{ccccccccc} -\mu _h&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -\beta _h^{*}b\\ 0&{}\quad -k_1&{}\quad 0&{}\quad \theta &{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \beta _h^{*}b\\ 0&{}\quad \alpha _{h}&{}\quad -k_{2}&{}\quad 0&{}\quad 0&{}\quad \tau &{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad \sigma _{1}\gamma &{}\quad -k_{3}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad \sigma _2\gamma &{}\quad 0&{}\quad -\mu _h&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad x&{}\quad 0&{}\quad 0&{}\quad -k_{4}&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad -y&{}\quad 0&{}\quad 0&{}\quad -z&{}\quad -\mu _m&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad y&{}\quad 0&{}\quad 0&{}\quad z&{}\quad 0&{}\quad -k_5&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \alpha _m&{}\quad -\mu _m \end{array}\right) , \end{aligned}$$
(15)

where \(k_1=(\alpha _{h}+\mu _{h})\), \(k_2=(\gamma +\mu _{h})\), \(k_3=(\theta +\mu _{h})\), \(k_4=(\tau +\mu _{h})\), \(k_5=(\alpha _{m}+\mu _{m})\), \(x=[1-(\sigma _{1}+\sigma _{2})]\gamma \), \(y=(\beta _mb\mu _h\Lambda _m)/\Lambda _h\mu _m\), \(z=(\phi \beta _mb\mu _h\Lambda _m)/\Lambda _h\mu _m\).

Solving for the eigenvalues of the Jacobian matrix (15) gives simple zero eigenvalue and the other eight eigenvalues having negative real part. It follows that a right eigenvector corresponding to the simple zero eigenvalue is given by \(\mathbf{w} =(w_1, w_2, w_3, w_4, w_5, w_6, w_7, w_8, w_9)^{\intercal }\), where

$$\begin{aligned} w_1= & {} -\left[ \dfrac{\beta _h^{*}b^{2}\alpha _m\beta _m\mu _h\Lambda _m (k_4+\phi [1-(\sigma _1+\sigma _2)]\gamma )}{\Lambda _h\mu _h\mu _m^{2}k_4k_5}\right] w_3,\nonumber \\ w_2= & {} \dfrac{\theta \sigma _1\gamma \Lambda _h\mu _m^{2}k_4k_5+\alpha _m\beta _h^{*}b^{2}\beta _m\mu _h\Lambda _m(k_4+\phi [1-(\sigma _1+\sigma _2)]\gamma )}{\Lambda _h\mu _m^{2}k_1k_3k_4k_5}w_3,\nonumber \\ w_3= & {} w_3>0,\ \ \ \ \ w_4=\dfrac{\sigma _1\gamma }{k_3}w_3,\nonumber \\ w_5= & {} \dfrac{\sigma _2\gamma }{\mu _h}w_3\ \ \ \ \ \ w_6=\dfrac{[1-(\sigma _1+\sigma _2)]\gamma }{k_4}w_3,\nonumber \\ w_7= & {} -\left[ \dfrac{\beta _m b \mu _h\Lambda _m(k_4+\phi [1-(\sigma _1+\sigma _2)]\gamma )}{\Lambda _h\mu _m^{2}k_4}\right] w_3,\nonumber \\ w_8= & {} \dfrac{\beta _m b \mu _h\Lambda _m(k_4+\phi [1-(\sigma _1+\sigma _2)]\gamma )}{\Lambda _h\mu _m k_4k_5}w_3,\nonumber \\ w_9= & {} \dfrac{\alpha _m\beta _m b \mu _h\Lambda _m(k_4+\phi [1-(\sigma _1+\sigma _2)]\gamma )}{\Lambda _h\mu _m^{2}k_4k_5}w_3. \end{aligned}$$
(16)

In addition to the right eigenvectors, the Jacobian matrix has a left eigenvector \(\mathbf{v} =(v_1, v_2, v_3, v_4, v_5, v_6, v_7, v_8, v_9)^{\intercal }\), where

$$\begin{aligned} \begin{array}{lll} v_1=0,\ \ \ \ \ \ v_2=\dfrac{\alpha _h}{k_1}v_3,\\ \ \\ v_3=v_3>0,\ \ \ \ \ v_4=\dfrac{\theta \alpha _h}{k_1k_3}v_3,\ \ \ \ v_5=0,\\ \ \\ v_6=\dfrac{\tau \Lambda _h\mu _m^{2}k_1k_5+\phi \alpha _h\beta _h^{*}\alpha _m\beta _m b^{2}\mu _h\Lambda _m}{\Lambda _h\mu _m^{2}k_1k_4k_5} v_3,\\ \ \\ v_7=0,\ \ \ \ \ v_8=\dfrac{\alpha _h\alpha _m\beta _h^{*}b}{\mu _mk_1k_5}v_3,\\ \ \\ v_9=\frac{\alpha _h\beta _h^{*}b}{\mu _mk_1}v_3. \end{array} \end{aligned}$$
(17)

Noting that \(\mathbf{v}.w =1\) as required in [25]. The non-varnishing partial derivatives (evaluated at \(\mathcal {E}_{0}\) with \(\beta _h=\beta _h^{*}\)) of the right hand side of the system (14) are given by

$$\begin{aligned} \begin{array}{llll} \frac{\partial ^{2} f_2}{\partial x_5 \partial x_9}= \frac{\varepsilon \beta _h^{*}b\mu _h }{\Lambda _h},\ \ \ \ \ \ \ \ \ \frac{\partial ^{2} f_5}{\partial x_5 \partial x_9}=-\frac{\varepsilon \beta _h^{*}b\mu _h }{\Lambda _h},\\ \ \\ \frac{\partial ^{2} f_7}{\partial x_3 \partial x_7}=-\frac{\beta _m b\mu _h }{\Lambda _h},\ \ \ \ \ \ \ \ \frac{\partial ^{2} f_7}{\partial x_6 \partial x_7}=-\frac{\phi \beta _m b\mu _h }{\Lambda _h},\\ \ \\ \frac{\partial ^{2} f_8}{\partial x_3 \partial x_7}=\frac{\beta _m b\mu _h }{\Lambda _h},\ \ \ \ \ \ \ \ \ \ \frac{\partial ^{2} f_8}{\partial x_6 \partial x_7}=\frac{\phi \beta _m b\mu _h }{\Lambda _h},\\ \ \\ \frac{\partial ^{2} f_1}{\partial x_9 \partial \beta _h}=-b,\ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\partial ^{2} f_2}{\partial x_9 \partial \beta _h}=b.\\ \end{array} \end{aligned}$$
(18)

Using the partial derivatives in (18), the bifurcation coefficient a is computed as follows

$$\begin{aligned} \begin{array}{lllll} \mathbf{a} &{}=&{}\displaystyle \sum _{k,i,j=1}^{9} {v_k w_i w_j} \frac{\partial ^{2}f_k}{\partial x_i \partial x_j} (\mathcal {E}_{0})\\ \ \\ &{}=&{}\dfrac{\alpha _h\sigma _2\gamma \varepsilon \beta _h^{*}b\mu _hA}{\Lambda _h^{2}\mu _h\mu _m^{2}k_1k_4k_5}v_3w_3^{2}-\dfrac{\alpha _h\beta _h^{*}b^{2}\beta _m\mu _hA}{\Lambda _h^{2}\mu _m^{3}k_1k_4}(1+\phi xk_4)v_3w_3^{2}, \end{array} \end{aligned}$$
(19)

where \(A=\alpha _m\beta _mb\mu _h\Lambda _m(k_4+\phi x)\) and \(x=[1-(\sigma _1+\sigma _2)]\gamma \). Further, the bifurcation coefficient b is obtained by

$$\begin{aligned} \begin{array}{llllll} \mathbf{b} &{}=&{}\displaystyle \sum _{k,i=1}^{9} {v_k w_i} \frac{\partial ^{2}f_k}{\partial x_i \partial \beta _h} (\mathcal {E}_{0})\\ \ \\ &{}=&{} \left[ \dfrac{\alpha _h\alpha _m\beta _mb^{2}\mu _h\Lambda _m(k_4+\phi x)}{\Lambda _h\mu _m^{2}k_1k_4k_5}\right] v_3w_3. \end{array} \end{aligned}$$
(20)

Since the parameters of the model are positive, then it is expected that the bifurcation coefficient b is positive. Therefore, the sign of the bifurcation coefficient a determines the type of bifurcation to be exhibited by the malaria model (10). The following results is then established using the Theorem 4.1 in [25].

Theorem 2

The malaria model (10) exhibits backward bifurcation as \(\mathcal R_{0}\) crosses unity whenever the bifurcation coefficient a in (19) is positive. That is,

$$\begin{aligned} \frac{\alpha _h\sigma _2\gamma \varepsilon \beta _h^{*}b\mu _hA}{\Lambda _h^{2}\mu _h\mu _m^{2}k_1k_4k_5}v_3w_3^{2}>\frac{\alpha _h\beta _h^{*}b^{2}\beta _m\mu _hA}{\Lambda _h^{2}\mu _m^{3}k_1k_4}(1+\phi xk_4)v_3w_3^{2}. \end{aligned}$$
(21)

The occurrence of backward bifurcation in epidemiological models makes the disease control difficult. In other words, the necessary requirement of having \(\mathcal R_{0}<1\), when backward bifurcation occurs, is not sufficient to control malaria effectively in the community (see, [20, 23]). Thus, the implication of Theorem 2 is that the possibility of controlling malaria when \(\mathcal R_{0}<1\) would be dependent on the initial sizes of the infected sub-populations of the malaria model (10). Now, to rule out the occurrence of this backward bifurcation, the next analysis is carried out.

3.3.1 Non-existence of backward bifurcation

The malaria model (10) may not undergo a backward bifurcation property if an endemic equilibrium does not exist at \(\mathcal R_{0}<1\). To ensure the non-existence of endemic equilibrium when \(\mathcal R_{0}<1\), let the modification parameter due to re-infection, denoted by \(\varepsilon \), be set to zero, i.e. \(\varepsilon =0\). Thus, the malaria model (10) with \(\varepsilon =0\) will possess unique endemic equilibrium when \(\mathcal R_{0}>1\). This result is summarized as follows.

Theorem 3

The malaria model (10) in the absence of re-infection \((\varepsilon =0)\) has no endemic equilibrium whenever \(\mathcal R_{0}<1\), and a unique endemic equilibrium point exists whenever \(\mathcal R_{0}>1\).

It is worthy of note that the presence or absence of both relapse rate, \(\theta \), and recrudescence rate, \(\tau \), does not affect the backward bifurcation property of the malaria model (10). Thus, Theorem 3 indicates that the possibility of backward bifurcation can only be ruled out when re-infection seizes to occur. This result is further confirmed by setting \(\varepsilon =0\) in (19), so that the bifurcation coefficient a becomes

$$\begin{aligned} \mathbf{a}=-\frac{\alpha _h\beta _h^{*}b^{2}\beta _m\mu _hA}{\Lambda _h^{2}\mu _m^{3}k_1k_4}(1+\phi xk_4)v_3w_3^{2}<0. \end{aligned}$$
(22)

Since \(\mathbf{a}<0\), it follows that the malaria model (10) with \(\varepsilon =0\) will not undergo backward bifurcation property at \(\mathcal R_{0}=1\). Hence, the following result, which is equivalent to Theorem 3 is claimed.

Theorem 4

The malaria model (10) in the absence of re-infection rate, (i.e., when \(\varepsilon =0)\), exhibits forward bifurcation as \(\mathcal R_{0}\) crosses unity.

The epidemiological implication of Theorem 4 is that the disease will only persist at the basic reproduction number above the unity. It also implies that the unique endemic equilibrium of the malaria model is locally asymptotically stable, meaning that a small influx of infected humans or mosquitoes will cause malaria to persist in the population. This endemism is, however, dependent on the initial sizes of the infected individuals in the population.

4 Global asymptotic dynamics of the model

In this section, the global asymptotic dynamics of the malaria model (10) around the disease-free equilibrium \((\mathcal {E}_{0})\) and endemic equilibrium \((\varepsilon _{e})\) are explored to show the behaviour of the model regardless of the initial sizes of the infected individuals in the population.

4.1 Global asymptotic stability of \(\mathcal {E}_{0}\)

Theorem 5

The disease-free equilibrium point \(\mathcal {E}_{0}\), given in (11), of the model (10) in the absence of re-infection rate \(\varepsilon \), is globally asymptotically stable if the basic reproduction \(\mathcal R_{0}\) is less than one.

Proof

Consider the continuously differentiable linear Lyapunov function [26,27,28,29] given by

$$\begin{aligned} V=v_1E_h+v_2I_h+v_3R_{1h}+v_4R_{3h}+v_5E_m+v_6I_m, \end{aligned}$$
(23)

where

$$\begin{aligned} \begin{array}{l} v_1=\dfrac{\alpha _hk_3(k_4+\phi x)}{B},\; v_2=\dfrac{k_1k_3(k_4+\phi x)}{B},\; v_3=\dfrac{\theta \alpha _h(k_4+\phi x)}{B},\\ \ \\ v_4=\dfrac{\tau k_1k_3+\phi (k_4+\phi x-\theta \alpha _h\sigma _1\gamma )}{B},\; v_5=\sqrt{\dfrac{\Lambda _h\beta _h\alpha _m\alpha _h k_3(k_4+\phi x)}{\beta _m\mu _h\Lambda _m k_5 B}},\\ \ \\ v_6=\sqrt{\dfrac{\Lambda _h\beta _h\alpha _h k_3 k_5(k_4+\phi x)}{\alpha _m\beta _m\mu _h\Lambda _m B}}, \end{array} \end{aligned}$$

and where \(B=[{k_1k_3(k_2k_4-\tau x)-\theta \alpha _h\sigma _1\gamma k_4}]>0\) as shown in (13). The time derivative of the Lyapunov function (23), denoted by V̇, along the solution path of (10) with \(\varepsilon =0\), is given by

$$\begin{aligned} \begin{aligned} \dot{V}=&\frac{\alpha _hk_3(k_4+\phi x)}{B}\left[ \frac{\beta _{h}bI_{m}S_{h}}{N_{h}}+\theta R_{1h}-(\alpha _{h}+\mu _{h})E_{h}\right] +\frac{k_1k_3(k_4+\phi x)}{B}\\ \ \\&\times \left[ \alpha _{h} E_{h}+\tau R_{3h}-(\gamma +\mu _{h})I_{h}\right] +\frac{\theta \alpha _h(k_4+\phi x)}{B}\left[ \sigma _{1}\gamma I_{h}-(\theta +\mu _{h})R_{1h}\right] \\ \ \\&+\frac{\tau k_1k_3+\phi (k_4+\phi x-\theta \alpha _h\sigma _1\gamma )}{B}\left[ (1-(\sigma _{1}+\sigma _{2}))\gamma I_{h}-(\tau +\mu _{h})R_{3h}\right] \\ \ \\&+\sqrt{\frac{\Lambda _h\beta _h\alpha _m\alpha _h k_3(k_4+\phi x)}{\beta _m\mu _h\Lambda _m k_5 B}}\left[ \frac{\beta _{m}bS_{m}(I_{h}+\phi R_{3h})}{N_{h}}-(\alpha _{m}+\mu _{m})E_{m}\right] \\ \ \\&+\sqrt{\frac{\Lambda _h\beta _h\alpha _h k_3 k_5(k_4+\phi x)}{\alpha _m\beta _m\mu _h\Lambda _m B}}\left[ \alpha _{m} E_{m}-\mu _{m}I_{m}\right] \end{aligned} \end{aligned}$$
(24)

Algebraic simplification of (24) gives

$$\begin{aligned} \begin{aligned} \dot{V}=&\left( \dfrac{\alpha _h\beta _h bk_3(k_4+\phi x)S_h}{BN_h}-\sqrt{\dfrac{\mu _{m}^{2}\Lambda _h\beta _h\alpha _h k_3 k_5(k_4+\phi x)}{\alpha _m\beta _m\mu _h\Lambda _m B}}\right) I_m-I_{h}-\phi R_{3h}\\ \ \\ {}&+ \frac{\beta _m b S_m}{N_h}\sqrt{\dfrac{\Lambda _h\beta _h\alpha _m\alpha _h k_3(k_4+\phi x)}{\beta _m\mu _h\Lambda _m k_5 B}}(I_h+\phi R_{3h}), \end{aligned} \end{aligned}$$

which, after substituting the limiting value \(N_h=\Lambda _h/\mu _h\) together with the bounds \(S_h\le \Lambda _h/\mu _h\) and \(S_m\le \Lambda _m/\mu _m\) in \(\mathfrak {D}\), becomes

$$\begin{aligned} \begin{aligned} \dot{V} \le&\left( \dfrac{\alpha _h\beta _h bk_3(k_4+\phi x)}{B}-\sqrt{\dfrac{\mu _{m}^{2}\Lambda _h\beta _h\alpha _h k_3 k_5(k_4+\phi x)}{\alpha _m\beta _m\mu _h\Lambda _m B}}\right) I_m\\&+\left( \dfrac{\beta _m b\Lambda _m\mu _m}{\mu _m\Lambda _h}\sqrt{\dfrac{\Lambda _h\beta _h\alpha _m\alpha _h k_3(k_4+\phi x)}{\beta _m\mu _h\Lambda _m k_5 B}} -1\right) I_{h}\\&+ \left( \dfrac{\beta _m b\Lambda _m\mu _m}{\mu _m\Lambda _h}\sqrt{\dfrac{\Lambda _h\beta _h\alpha _m\alpha _h k_3(k_4+\phi x)}{\beta _m\mu _h\Lambda _m k_5 B}}-1 \right) \phi R_{3h}\\ =&\left( \sqrt{\frac{\mu _{m}^{2}\Lambda _h\beta _h\alpha _h k_3 k_5(k_4+\phi x)}{\alpha _m\beta _m\mu _h\Lambda _m B}}(\mathcal R_{0}-1)\right) I_m +\left( \mathcal R_{0}-1\right) I_{h} + \phi \left( \mathcal R_{0}-1\right) R_{3h} \end{aligned} \end{aligned}$$
Fig. 2
figure 2

Simulations showing global asymptotic behaviour of the recurrent malaria model (25) with different initial conditions. Parameter values used include \(b=0.3\), \(\beta _h=0.05\), \(\beta _m=0.15\), \(\Lambda _h=2.5\), \(\Lambda _m=1000\), \(\mu _h=0.0000548\), \(\mu _m=0.066\), \(\sigma _1=0.25\), \(\sigma _{2}=0.5\), \(\varepsilon =0\), \(\theta =0.0028\), \(\gamma =0.01\), \(\phi =0.75\), \(\alpha _m=1/18\), \(\alpha _h=1/17\), \(\tau =0.2\), so that \(\mathcal {R}_{0}=0.5537<1\)

Full size image

This shows that \(\dot{V}<0\) for \(\mathcal R_{0}<1\), and \(\dot{V}=0\) provided that \(I_h=I_m=R_{3h}=0\). Then, it follows that \((S_h^{*},E_h^{*},I_h^{*},R_{1h}^{*},R_{2h}^{*},R_{3h}^{*},S_{m}^{*},E_{m}^{*},I_{m}^{*})=\left( \Lambda _h/\mu _h, 0, 0, 0, 0, 0, \Lambda _m/\mu _m, 0, 0\right) \) as \(t\rightarrow \infty \). Accordingly, by LaSalle’s invariance principle [30], the largest compact invariant set for which \(\dot{V}=0\) is the singleton {\(\mathcal {E}_{0}\)}. Hence, the disease-free equilibrium, \(\mathcal {E}_{0}\), of the model (10) is globally-asymptotically stable.\(\square \)

The asymptotic behaviour of the model (10) is quantitatively illustrated at different initial sizes of the sub-population of the model (see, Fig. 2).

4.2 Global asymptotic stability of endemic equilibrium

Following the non-existence of backward bifurcation of the model (10) without re-infection as shown in Theorem 3 and Theorem 4, a special case of the malaria model (10), in the absence of the re-infection compartment \(R_{2h}\), is hereby presented as follows.

$$\begin{aligned} \frac{dS_{h}}{dt}= & {} \Lambda _{h}-\frac{\beta _{h}bS_{h}I_{m}}{N_{h}}-\mu _{h}S_{h}\nonumber \\ \ \nonumber \\ \frac{dE_{h}}{dt}= & {} \frac{\beta _{h}bI_{m}S_{h}}{N_{h}}+\theta R_{1h}-(\alpha _{h}+\mu _{h})E_{h}\nonumber \\ \ \nonumber \\ \frac{dI_{h}}{dt}= & {} \alpha _{h} E_{h}+\tau R_{3h}-(\gamma +\mu _{h})I_{h}\nonumber \\ \nonumber \ \\ \frac{dR_{1h}}{dt}= & {} \sigma _{1}\gamma I_{h}-(\theta +\mu _{h})R_{1h}\nonumber \\ \nonumber \ \\ \frac{dR_{3h}}{dt}= & {} (1-\sigma _{1})\gamma I_{h}-(\tau +\mu _{h})R_{3h}\nonumber \\ \nonumber \ \\ \frac{dS_{m}}{dt}= & {} \Lambda _{m}-\frac{\beta _{m}bS_{m}(I_{h}+\phi R_{3h})}{N_{h}}-\mu _{m}S_{m}\nonumber \\ \nonumber \ \\ \frac{dE_{m}}{dt}= & {} \frac{\beta _{m}bS_{m}(I_{h}+\phi R_{3h})}{N_{h}}-(\alpha _{m}+\mu _{m})E_{m}\nonumber \\ \nonumber \ \\ \dfrac{dI_{m}}{dt}= & {} \alpha _{m} E_{m}-\mu _{m}I_{m} \end{aligned}$$
(25)

Let the unique endemic equilibrium of the model (25) be arbitrarily given by

$$\begin{aligned} \varepsilon _{e}=(S_{h}^{**},E_{h}^{**},I_{h}^{**},R_{1h}^{**},R_{3h}^{**},S_{m}^{**},E_{m}^{**},I_{m}^{**}). \end{aligned}$$

Since the model (25) is obtained by setting \(\sigma _2\) and \(\varepsilon \) to zero, the corresponding basic reproduction number for the special case model (25) is now given by

$$\begin{aligned} \mathcal {R}_{0}|_{\sigma _{2}=0}=\sqrt{\frac{\beta _h b^2 \alpha _m \beta _m\mu _h\Lambda _m\alpha _hk_3(k_4+\phi (1-\sigma _{1})\gamma )}{\mu _m^2\Lambda _hk_5[{k_1k_3(k_2k_4-\tau (1-\sigma _{1})\gamma ))-\theta \alpha _h\sigma _1\gamma k_4}]}} \end{aligned}$$
(26)

Therefore, the global asymptotic stability of the model  (25) around the endemic equilibrium \(\varepsilon _{e}\) is investigated next.

Theorem 6

The endemic equilibrium point of system (25), denoted by \(\varepsilon _{e}\), is globally-asymptotically stable when \(\mathcal R_{0}|_{\sigma _{2}=0}>1\) with \(S_{m}^{**}E_m\le S_mE_{m}^{**}\) and \(R_{1h}\le R_{1h}^{**}\).

Proof

Consider the following nonlinear Lyapunov function of Goh-Volterra type [31,32,33,34]

$$\begin{aligned} D= & {} d_1\left( S_h-S_h^{**}-S_h^{**}\ln \frac{S_h}{S_h^{**}}\right) +d_2\left( E_h-E_h^{**}-E_h^{**}\ln \frac{E_h}{E_h^{**}}\right) \nonumber \\ \nonumber \ \\&+ d_3\left( I_h-I_h^{**}-I_h^{**}\ln \frac{I_h}{I_h^{**}}\right) +d_4\left( R_{1h}-R_{1h}^{**}-R_{1h}^{**}\ln \frac{R_{1h}}{R_{1h}^{**}}\right) \nonumber \\ \nonumber \ \\&+ d_5\left( R_{3h}-R_{3h}^{**}-R_{3h}^{**}\ln \frac{R_{3h}}{R_{3h}^{**}}\right) +d_6\left( S_m-S_m^{**}-S_m^{**}\ln \frac{S_m}{S_m^{**}}\right) \nonumber \\ \nonumber \ \\&+ d_7\left( E_m-E_m^{**}-E_m^{**}\ln \frac{E_m}{E_m^{**}}\right) +d_8\left( I_m-I_m^{**}-I_m^{**}\ln \frac{I_m}{I_m^{**}}\right) , \end{aligned}$$
(27)

where \(d_1=d_2=\frac{\beta _m S_{m}^{**}(I_{h}^{**}+\phi R_{3h}^{**})}{\beta _{h}S_{h}^{**}I_{m}^{**}}\), \(d_3=\frac{\beta _m S_{m}^{**}(I_{h}^{**}+\phi R_{3h}^{**})}{\alpha _h E_{h}^{**}}\left[ \frac{b\mu _h}{\Lambda _h}+\frac{\theta R_{1h}^{**}}{\beta _h S_{h}^{**}I_{m}^{**}}\right] \),

\(d_4=\frac{\beta _m S_{m}^{**}(I_{h}^{**}+\phi R_{3h}^{**})}{\sigma _{1}\gamma I_{h}^{**}\alpha _h E_{h}^{**}}\left[ \frac{b\mu _h}{\Lambda _h}+\frac{\theta R_{1h}^{**}}{\beta _h S_{h}^{**}I_{m}^{**}}\right] \tau R_{3h}^{**}+\frac{\beta _m b \mu _h S_{m}^{**}(I_{h}^{**}+\phi R_{3h}^{**})}{2\sigma _{1}\gamma I_{h}^{**}\Lambda _h}+\frac{\beta _m S_{m}^{**}(I_{h}^{**}+\phi R_{3h}^{**})\theta R_{1h}^{**}}{\sigma _{1}\gamma I_{h}^{**}\beta _h S_{h}^{**}I_{m}^{**}}\),

\(d_5=\frac{\beta _m S_{m}^{**}(I_{h}^{**}+\phi R_{3h}^{**})}{(1-\sigma _{1})\gamma I_{h}^{**}\alpha _h E_{h}^{**}}\left[ \frac{b\mu _h}{\Lambda _h}+\frac{\theta R_{1h}^{**}}{\beta _h S_{h}^{**}I_{m}^{**}}\right] \tau R_{3h}^{**}+\frac{\beta _m b \mu _h S_{m}^{**}(I_{h}^{**}+\phi R_{3h}^{**})}{2(1-\sigma _{1})\gamma I_{h}^{**}\Lambda _h}\), \(d_6=d_7=1,\)

\(d_8=\frac{\beta _m b \mu _h S_{m}^{**}(I_{h}^{**}+\phi R_{3h}^{**})}{\alpha _{m}E_{m}^{**}\Lambda _h}\).

The time derivative of D in (27) is given by

$$\begin{aligned} \begin{array}{lll} \dfrac{dD}{dt}=&{} d_1\left( 1-\frac{S_h^{**}}{S_h}\right) \frac{dS_h}{dt}+d_2\left( 1-\frac{E_h^{**}}{E_h}\right) \frac{dE_h}{dt}+d_3\left( 1-\frac{I_h^{**}}{I_h}\right) \frac{dI_h}{dt}\\ \ \\ {} &{}+d_4\left( 1-\frac{R_{1h}^{**}}{R_{1h}}\right) \frac{dR_{1h}}{dt}+ d_5\left( 1-\frac{R_{3h}^{**}}{R_{3h}}\right) \frac{dR_{3h}}{dt}+d_6\left( 1-\frac{S_m^{**}}{S_m}\right) \frac{dS_m}{dt}\\ \ \\ {} &{}+ d_7\left( 1-\frac{E_m^{**}}{E_m}\right) \frac{dE_m}{dt}+d_8\left( 1-\frac{I_m^{**}}{I_m}\right) \frac{dI_m}{dt} \end{array} \end{aligned}$$
(28)

Substituting the expressions on the right hand sides of the model (25) into (28) gives

$$\begin{aligned} \dfrac{dD}{dt}= & {} d_1\left( 1-\frac{S_h^{**}}{S_h}\right) \left( \Lambda _{h}-\frac{\beta _{h}bS_{h}I_{m}}{N_{h}}-\mu _{h}S_{h}\right) +d_2\left( 1-\frac{E_h^{**}}{E_h}\right) \nonumber \\&\times \left( \frac{\beta _{h}bI_{m}S_{h}}{N_{h}}+\theta R_{1h}-(\alpha _{h}+\mu _{h})E_{h}\right) + d_3\left( 1-\frac{I_h^{**}}{I_h}\right) \nonumber \\&\times \left( \alpha _{h} E_{h}+\tau R_{3h}-(\gamma +\mu _{h})I_{h}\right) +d_4\left( 1-\frac{R_{1h}^{**}}{R_{1h}}\right) \left( \sigma _{1}\gamma I_{h}-(\theta +\mu _{h})R_{1h}\right) \nonumber \\&+d_5\left( 1-\frac{R_{3h}^{**}}{R_{3h}}\right) \left( (1-\sigma _{1})\gamma I_{h}-(\tau +\mu _{h})R_{3h}\right) \nonumber \\&+d_6\left( 1-\frac{S_m^{**}}{S_m}\right) \left( \Lambda _{m}-\frac{\beta _{m}bS_{m}(I_{h}+\phi R_{3h})}{N_{h}}-\mu _{m}S_{m}\right) + d_7\left( 1-\frac{E_m^{**}}{E_m}\right) \nonumber \\&\times \left( \frac{\beta _{m}bS_{m}(I_{h}+\phi R_{3h})}{N_{h}}-(\alpha _{m}+\mu _{m})E_{m}\right) +d_8\left( 1-\frac{I_m^{**}}{I_m}\right) \left( \alpha _{m} E_{m}-\mu _{m}I_{m}\right) \end{aligned}$$
(29)

Clearly, it can be shown from (25) that the following equilibrium relations hold.

$$\begin{aligned}&\Lambda _{h}=\frac{\beta _{h}b\mu _hS_{h}^{**}I_{m}^{**}}{\Lambda _{h}}+\mu _{h}S_{h}^{**}, \; \; \quad \; \; (\alpha _{h}+\mu _{h})=\frac{\beta _{h}b\mu _hI_{m}^{**}S_{h}^{**}}{\Lambda _{h}E_{h}^{**}}+\frac{\theta R_{1h}^{**}}{E_{h}^{**}},\nonumber \\&(\gamma +\mu _{h})=\frac{\alpha _{h} E_{h}^{**}}{I_{h}^{**}}+\frac{\tau R_{3h}^{**}}{I_{h}^{**}},\; \; \quad \; \; (\theta +\mu _{h})=\frac{\sigma _{1}\gamma I_{h}^{**}}{R_{1h}^{**}},\nonumber \\&(\tau +\mu _{h})=\frac{(1-\sigma _{1})\gamma I_{h}^{**}}{R_{3h}^{**}},\; \; \quad \; \; \Lambda _{m}=\frac{\beta _{m}b\mu _hS_{m}^{**}(I_{h}^{**}+\phi R_{3h}^{**})}{\Lambda _{h}}+\mu _{m}S_{m}^{**},\nonumber \\&(\alpha _{m}+\mu _{m})=\frac{\beta _{m}b\mu _hS_{m}^{**}(I_{h}^{**}+\phi R_{3h}^{**})}{\Lambda _{h}E_{m}^{**}}, \; \; \quad \; \; \mu _{m}=\frac{\alpha _{m} E_{m}^{**}}{I_{m}^{**}}. \end{aligned}$$
(30)

Further algebraic simplification of (29) using (30) yields

$$\begin{aligned} \begin{array}{llll} \dfrac{dD}{dt}=&{} u_{1} \left( 8-\frac{S_{h}^{**}}{S_h}-\frac{S_hI_mE_{h}^{**}}{S_{h}^{**}I_{m}^{**}E_h}+\frac{I_h}{I_{h}^{**}}-\frac{I_{h}^{**}E_h}{I_hE_{h}^{**}}-\frac{S_{m}^{**}}{S_m} +\frac{I_h+\phi R_{3h}}{I_{h}^{**}+\phi R_{3h}^{**}} \left( 1-\frac{S_mE_{m}^{**}}{S_{m}^{**}E_m}\right) \right. \\ &{}\left. -\frac{I_{m}^{**}E_m}{I_mE_{m}^{**}}-\frac{R_{1h}}{R_{1h}^{**}}-\frac{R_{1h}^{**}I_{h}}{R_{1h}I_{h}}-\frac{R_{3h}}{R_{3h}^{**}}-\frac{R_{3h}^{**}I_{h}}{R_{3h}I_{h}^{**}}\right) \\ \ \\ {} &{} +u_{2}\left( 2-\frac{S_h}{S_{h}^{**}}-\frac{S_{h}^{**}}{S_h}\right) +u_{3}\left( 3-\frac{R_{1h}E_{h}^{**}}{R_{1h}^{**}E_h}-\frac{I_{h}^{**}E_h}{I_hE_{h}^{**}}-\frac{R_{1h}^{**}I_{h}}{R_{1h}I_{h}^{**}}\right) \\ \ \\ {} &{} +u_{4}\left( 3-\frac{I_{h}^{**}R_{3h}}{I_hR_{3h}^{**}}-\frac{R_{3h}^{**}I_h}{R_{3h}I_{h}^{**}}+\frac{I_{h}}{I_{h}^{**}}-\frac{R_{1h}}{R_{1h}^{**}}-\frac{R_{1h}^{**}I_{h}}{R_{1h}I_{h}^{**}}\right) \\ \ \\ &{} +u_5\left( 3-\frac{I_{h}^{**}R_{3h}}{I_hR_{3h}^{**}}-\frac{R_{3h}^{**}I_h}{R_{3h}I_{h}^{**}}+\frac{I_{h}}{I_{h}^{**}}-\frac{R_{1h}}{R_{1h}^{**}}-\frac{R_{1h}^{**}I_{h}}{R_{1h}I_{h}^{**}}\right) +\mu _{m}S_{m}^{**}\left( 2-\frac{S_m}{S_{m}^{**}}-\frac{S_{m}^{**}}{S_m}\right) , \end{array} \end{aligned}$$
(31)

where

$$\begin{aligned} \begin{array}{ll} u_1=\frac{\beta _{m}b\mu _hS_{m}^{**}(I_{h}^{**}+\phi R_{3h}^{**})}{\Lambda _h},&{}\ \ \ u_2=\frac{\beta _{m}S_{m}^{**}(I_{h}^{**}+\phi R_{3h}^{**})}{\beta _h I_{m}^{**}},\ \ \ u_3=\frac{\beta _{m}S_{m}^{**}(I_{h}^{**}+\phi R_{3h}^{**})\theta R_{1h}^{**}}{\beta _hS_{h}^{**}I_{m}^{**}},\\ \ \\ u_4=\frac{\beta _{m}b\mu _{h}S_{m}^{**}(I_{h}^{**}+\phi R_{3h}^{**})\tau R_{3h}^{**}}{\Lambda _{h}\alpha _hE_{h}^{**}},&{}\ \ \ u_5=\frac{\beta _{m}S_{m}^{**}(I_{h}^{**}+\phi R_{3h}^{**})\theta R_{1h}^{**}\tau R_{3h}^{**}}{\alpha _hE_{h}^{**}\beta _{h}S_{h}^{**}I_{m}^{**}}. \end{array} \end{aligned}$$
Fig. 3
figure 3

Simulations showing global asymptotic behaviour of the recurrent malaria model (25) with different initial conditions. The parameter values used are the same as in Fig. 2, except that \(\sigma _2=0\), so that \(\mathcal {R}_{0}=3.8581>1\)

Full size image

Thus, using the given inequality conditions \(S_{m}^{**}E_m\le S_mE_{m}^{**}\) and \(R_{1h}\le R_{1h}^{**}\), then, \(\left( 1-\frac{S_mE_{m}^{**}}{S_{m}^{**}E_{m}}\right) \le 0\) and \(\left( 1-\frac{R_{1h}^{**}}{R_{1h}}\right) \le 0\) with equalities if and only if \(\frac{S_{m}^{**}}{S_m}=\frac{E_{m}^{**}}{E_m}\) and \(R_{1h}=R_{1h}^{**}\). As a consequence,

$$\begin{aligned} \dfrac{dD}{dt}= & {} u_{1} \left( 7-\frac{S_{h}^{**}}{S_h}-\frac{S_hI_mE_{h}^{**}}{S_{h}^{**}I_{m}^{**}E_h}-\frac{I_{h}^{**}E_h}{I_hE_{h}^{**}}-\frac{S_{m}^{**}}{S_m}-\frac{R_{3h}}{R_{3h}^{**}}-\frac{R_{3h}^{**}I_{h}}{R_{3h}I_{h}^{**}}-\frac{I_{m}^{**}E_m}{I_mE_{m}^{**}}\right) \nonumber \\ \nonumber \ \\&+u_{2}\left( 2-\frac{S_h}{S_{h}^{**}}-\frac{S_{h}^{**}}{S_h}\right) +u_{3}\left( 3-\frac{E_{h}^{**}}{E_h}-\frac{I_{h}^{**}E_h}{I_hE_{h}^{**}}-\frac{I_h}{I_{h}^{**}}\right) \nonumber \\ \nonumber \ \\&+u_{4}\left( 2-\frac{I_{h}^{**}R_{3h}}{I_hR_{3h}^{**}}-\frac{R_{3h}^{**}I_h}{R_{3h}I_{h}^{**}}\right) \nonumber \\ \nonumber \ \\&+u_{5}\left( 2-\frac{I_{h}^{**}R_{3h}}{I_hR_{3h}^{**}}-\frac{R_{3h}^{**}I_h}{R_{3h}I_{h}^{**}}\right) +\mu _{m}S_{m}^{**}\left( 2-\frac{S_m}{S_{m}^{**}}-\frac{S_{m}^{**}}{S_m}\right) \end{aligned}$$
(32)

By AM-GM inequality: the arithmetic mean is greater than or equal to the geometric mean, it follows that

$$\begin{aligned}&\left( 7-\frac{S_{h}^{**}}{S_h}-\frac{S_hI_mE_{h}^{**}}{S_{h}^{**}I_{m}^{**}E_h}-\frac{I_{h}^{**}E_h}{I_hE_{h}^{**}}-\frac{S_{m}^{**}}{S_m}-\frac{R_{3h}}{R_{3h}^{**}}-\frac{R_{3h}^{**}I_{h}}{R_{3h}I_{h}^{**}}-\frac{I_{m}^{**}E_m}{I_mE_{m}^{**}}\right) \le 0,\nonumber \\ \nonumber \ \\&\left( 2-\frac{S_h}{S_{h}^{**}}-\frac{S_{h}^{**}}{S_h}\right) \le 0,\ \quad \left( 3-\frac{E_{h}^{**}}{E_h}-\frac{I_{h}^{**}E_h}{I_hE_{h}^{**}}-\frac{I_h}{I_{h}^{**}}\right) \le 0,\nonumber \\ \nonumber \ \\&\left( 2-\frac{I_{h}^{**}R_{3h}}{I_hR_{3h}^{**}}-\frac{R_{3h}^{**}I_h}{R_{3h}I_{h}^{**}}\right) \le 0,\ \quad \left( 2-\frac{S_m}{S_{m}^{**}}-\frac{S_{m}^{**}}{S_m}\right) \le 0. \end{aligned}$$
(33)

Hence, \(dD/dt\le 0\) with \(dD/dt=0\) if and only if \(S_{h}=S_{h}^{**}\), \(E_{h}=E_{h}^{**}\), \(I_{h}=I_{h}^{**}\), \(R_{1h}=R_{1h}^{**}\), \(R_{3h}=R_{3h}^{**}\), \(S_{m}=S_{m}^{**}\), \(E_{m}=E_{m}^{**}\), \(I_{m}=I_{m}^{**}\), which indicates that

$$\begin{aligned} (S_h, E_h, I_h, R_{1h}, R_{3h}, S_{m}, E_{m}, I_{m})\rightarrow (S_{h}^{**}, E_{h}^{**}, I_{h}^{**}, R_{1h}^{**}, R_{3h}^{**}, S_{m}^{**}, E_{m}^{**}, I_{m}^{**}) \end{aligned}$$

as \(t\rightarrow \infty \). Thus, by Lasalle’s invariance principle [30], the endemic equilibrium of the system (25) is globally-asymptotically stable. \(\square \)

The quantitative illustration of Theorem 6 at various initial sizes of the sub-populations of the system (25) is given in Fig. 3.

5 Concluding remarks

A mathematical model representing the time-evolution of malaria spread with a nine-dimensional system of ordinary differential equations is presented. The model takes into account all the three classes of recurrent malaria, which are relapse, re-infection and recrudescence. Theoretical analysis of the model is performed to understand the behaviour of the system, and the following major findings are obtained.

  1. i.

    The model reveals backward bifurcation property, which is due to the existence of re-infection of recovered humans in the population. However, the presence of both relapse and recrudescence in malaria dynamics do not cause the phenomenon of backward bifurcation. Hence, the possibility of backward bifurcation can only be ruled out when re-infection seizes to occur.

  2. ii.

    The global asymptotic dynamics of the model without re-infection is established; showing that the resulting model has a globally-asymptotically stable disease-free equilibrium point whenever the basic reproduction number is below one, and a globally-asymptotically stable unique endemic equilibrium point if the basic reproduction number is above one.

  3. iii.

    Simulations of the recurrent malaria model are done to support the theoretical results; showing the convergence of solutions at various initial sizes of sub-populations of the model to the equilibrium points.

Since the occurrence of backward bifurcation driven by re-infection shows how hard it is to control or eliminate the transmission of malaria even when the basic reproduction is below one, it is, therefore, imperative to scale up efforts or measures toward interrupting malaria re-infection in the community. More attention should be given to the control of recurrent malaria in order to achieve a malaria-free community.