Bifurcations in a modified Leslie–Gower predator–prey discrete model with Michaelis–Menten prey harvesting

Abstract

In this paper, a modified Leslie–Gower predator–prey discrete model with Michaelis–Menten type prey harvesting is investigated. It is shown that the model exhibits several bifurcations of codimension 1 viz. Neimark–Sacker bifurcation, transcritical bifurcation and flip bifurcation on varying one parameter. Bifurcation theory and center manifold theory are used to establish the conditions for the existence of these bifurcations. Moreover, existence of Bogdanov–Takens bifurcation of codimension 2 (i.e. two parameters must be varied for the occurrence of bifurcation) is exhibited. The non-degeneracy conditions are determined for occurrence of Bogdanov–Takens bifurcation. The extensive numerical simulation is performed to demonstrate the analytical findings. The system exhibits periodic solutions including flip bifurcation and Neimark–Sacker bifurcation followed by the wide range of dense chaos.

1 Introduction

The resource-consumer species interaction is one of the most common and focal research area in the field of mathematical biology. The dynamics of population models is concerned with population size, age distribution and many other natural factors. In biological systems, there are a number of models in which time is taken as a continuous function [13, 19, 24]. For population models, this could be seen as a overlapping situation which implies a continuous series of birth and death processes and these models are usually performed by ordinary differential equations. But there are so many other species, e.g. semelparous animals and monocarpic plants in which this continuous time criteria is quite unsatisfactory as their birth occurs in regular breeding season. These interactions are performed by difference equations and can depicts much more complex behavior as compared to the continuous models [25, 35, 37, 41, 45].

The discrete time population models are pertinent for non-overlapping generation models [1, 18, 36] and thus seems to be more realistic than continuous one. Many researchers investigated discrete-time models which give interesting dynamics in the system by exploring several type of bifurcations [14, 17, 40, 43, 44].

Generally, the discrete-time resource-consumer interaction models consist of only three fixed points that correlates with the extermination of both species together, existence of resource upto its carrying capacity that corresponds the extinction of consumer species and lastly the coexistence of both interacting species.

The Lotka-Volterra prey-predator model with discrete time was firstly introduced by Maynard Smith [45] and studied by Levine [34] and Liu and Xiao [37]. It has been shown that these discrete time models undergo several bifurcations such as fold bifurcation, flip bifurcation and Neimark–Sacker bifurcation. Moreover, Hadelar and Gerstmann [23] were the first who derives a discrete time model involving Holling type-II functional response using continuous time model. Also the complete discussion for the bifurcations of codimension 1 and parametric restriction for non-hyperbolicity has been done by Li and Zhang [35]. In another study, the authors discussed the chaotic dynamics of a discrete prey-predator model with Holling type-II functional response [1]. Singh and Deolia investigated a discrete-time prey-predator model with Leslie–Gower functional response [44]. In their study the system exhibited Neimark–Sacker bifurcation, flip bifurcation and fold bifurcation under certain conditions. In another work, a modified Leslie–Gower prey-predator model with harvesting in prey population is investigated. The authors explored rich dynamics of the model viz. period-doubling bifurcation and Neimark–Sacker bifurcation by using bifurcation theory and center-manifold theorem [2].

From last decade, high-codimensional bifurcation have been got great attention in dynamical systems because they may exhibit more complex dynamical behavior. Bogdanov–Takens bifurcation is one of the most important high-codimensional bifurcation in nonlinear dynamics. Bogdanov [5, 6] and Takens [46, 47] independently and simultaneously studied and described this bifurcation of codimension two and hence this bifurcation was coined after their name. Other researcher also studied Bogdanov–Takens bifurcation, see, for example, Chow and Hale [10], Dumortier et al. [16], Arnold [3], Chow et al. [11], Guckenheimer and Holmes [21], Kuznetsov [33], Xiao and Ruan [48, 49]. Huang et al. [26] explored Bogdanov–Takens bifurcation in a predator-model with constant-yield predator harvesting. They exhibited saddle node-bifurcation, repelling and attracting Bogdanov–Takens bifurcation and supercritical and subcritical Hopf bifurcation. In another study, the authors investigated a discrete predator–prey model in which a nonmonotonic functional response is considered. The codimension-2 bifurcation associated with 1:2, 1:3 and 1:4 resonance are analyzed using bifurcation theory [9]. In another study, Xiang et al. [50] studied a prey-predator model host-parasitoid model with Holling type-II functional response. They discussed sequence of bifurcations viz. cusp, focus and Bogdanov–Takens bifurcations of codimension 3 and Hopf bifurcation. Kong and Zhu [31] explored Bogdanov–Takens bifurcations of codimension 2 and 3 in a Leslie–Gower predator–prey model with prey harvesting. There are number of studies in which different bifurcations of higher codimension have been investigated [22, 27, 38, 39].

2 Mathematical model

Aziz-Alaoui and Daher Okiye [4] proposed the following two-dimensional prey-predator model with modified version of Leslie–Gower and Holling type II functional response:

$$\begin{aligned} \frac{dX}{dT}= & {} \left( r_{1}-b_{1}X-\frac{a_{1}Y}{k_{1}+X}\right) X \nonumber \\ \frac{dY}{dT}= & {} \left( r_{2}-\frac{a_{2}Y}{k_{2}+X}\right) Y \end{aligned}$$

(1)

with positive initial conditions $X(0)\ge 0$ and $Y(0)\ge 0$ where X(T) and Y(T) represent the population densities at time T. Here $r_{1}$ denotes growth rate of prey and $b_{1}$ represents strength of competition among individuals in prey. The parameter $k_{1} (k_{2})$ signifies the extent of protection provided by environment to the prey (predator) and $r_{2}$ describes the growth rate of Y. $a_{1} (a_{2})$ measures the maximum value per capita reduction rate of prey X (predator Y). All the parameters are assumed to be positive.

The model (1) has been widely studied by many researchers. In particular, Aziz-Alaoui and Okiye established boundedness of the solutions and global stability of the interior equilibrium point [4]. Under some certain conditions, permanence and global stability of the diffusive system has been discussed by Du et al. [15]. In another study, Ji et al. investigated the model with stochastic perturbation and determined long term behavior and persistence conditions [29, 30]. The effect of discrete delays on this model has been discussed by Gakkhar and Singh [20]. They resulted that otherwise stable non zero equilibria undergoes Hopf bifurcation with respect to discrete delays. In another work, feedback linearization (approximate and exact linearization) is applied to stabilize the complexity in the system [42].

The harvesting is a conservation strategy among population f or commercial or recreational value. Due to such important contribution of harvesting in population dynamics, it becomes very crucial for bioeconomics. Michaelis–Menten type harvesting is considered to be most realistic in biological and economic points of view [12, 32]. The model (1) with Michaelis–Menten type harvesting under the assumption that same extent ($k_{1}=k_{2}=k$) to which environment provided protection to both the predator and prey [29, 30], is given by:

$$\begin{aligned} \frac{dX}{dT}= & {} \left( r_{1}-b_{1}X-\frac{a_{1}Y}{k+X}\right) x-\frac{cEX}{m_{1}E+m_{2}X} \nonumber \\ \frac{dY}{dT}= & {} \left( r_{2}-\frac{a_{2}Y}{k+X}\right) Y. \end{aligned}$$

(2)

Here c signifies catchability coefficient and E denotes harvesting effort in prey species. Where $m_{1}$ and $m_{2}$ are suitable constants. All the parameters are assumed to be positive and similar meaning as of (1).

To investigate the dynamics of the system (2), the following non-dimensional scheme is taken:

$$\begin{aligned} x= & {} \frac{r_{1}X}{b_{1}},~~~ t=\frac{T}{r_{1}},~~~ y=\frac{r_{1}^{2}Y}{ab_{1}^2} \\ p= & {} \frac{1}{b_{1}},~~ \alpha =\frac{cEb_{1}}{m_{2}r_{1}^{2}},~~ \gamma =\frac{b_{1}k}{r_{1}},~~ \delta =\frac{m_{1}Eb_{1}}{m_{2}r_{1}}, ~~\beta =\frac{r_{2}}{r_{1}},~ q=\frac{a_{2}}{a_{1}b_{1}}{.} \end{aligned}$$

Using the above scheme, we get the following non-dimensional system:

$$\begin{aligned} \frac{dx}{dt}= & {} x\left( 1-x-\frac{p y}{\gamma +x}-\frac{\alpha }{\delta +x}\right) \nonumber \\ \frac{dy}{dt}= & {} \beta y\left( 1-\frac{qy}{\gamma +x}\right) \end{aligned}$$

(3)

with the initial conditions $x(0)=x_{0}\ge 0$,    $y(0)=y_{0}\ge 0$.

Gupta and Chandra [22] investigated the continuous-time model (3) and determined several local bifurcations viz. Hopf bifurcation, saddle-node bifurcation, transcritical bifurcation and Bogdanov–Takens bifurcation.

In order to derive discrete time model from the system (3), employing forward Euler scheme and taking $\epsilon$ is the step size. Letting $\epsilon \rightarrow 1$ then $(n+1)$th generation of the prey-predator population is governed by following set of equations:

$$\begin{aligned} x_{n+1}= & {} x_{n}+x_{n}\left( 1-x_{n}-\frac{py_{n}}{\gamma +x_{n}}-\frac{\alpha }{\delta +x_{n}}\right) \nonumber \\ y_{n+1}= & {} y_{n}+\beta y_{n}\left( 1-\frac{q y_{n}}{\gamma +x_{n}}\right) \end{aligned}$$

(4)

with initial conditions $x(0)=x_{0}$, and $y(0)=y_{0}$.

Now, the discrete time prey-predator model can be defined by a mapping

$$\begin{aligned} G:\left( \begin{array}{c} x \\ y \\ \end{array} \right) \rightarrow \left( \begin{array}{c} x+x\left( 1-x-\frac{py}{\gamma +x}-\frac{\alpha }{\delta +x}\right) \\ y+\beta y\left( 1-\frac{q y}{\gamma +x}\right) \end{array}\right) \end{aligned}$$

(5)

The map (5) is considered for the region $\Omega =\mathbb {R_{+}}^{2}=\{(x,y):x\ge 0, y\ge 0\}$.

Now an interesting question arises whether discrete-time version of the system (3) still shows Bogdanov–Takens bifurcation (codimension-two bifurcation). Broer et al. [7, 8] and Kuznetsov [33] explained the theory on Bogdanov–Takens bifurcation for generic diffeomorphisms. The results discussed by Broer et al. [7, 8], Kuznetsov [33] and techniques given by Yagasaki [51] will be used to show existence of Bogdanov–Takens bifurcation and calculate the expressions for bifurcation curves in the system (4). To the best of our knowledge very few study [28] has been done for showing Bogdanov–Takens bifurcation in a discrete-time model. Huang et al. [28] studied bifurcations in a discrete-time predator–prey model with nonmonotone functional response. A simplified type Holling-IV functional response has been taken in the interaction term. The system exhibited various bifurcations of codimension 1 including fold bifurcation, transcritical bifurcation, flip bifurcation and Neimark–Sacker bifurcation. The authors established the existence of Bogdanov–Takens bifurcation and calculate the expressions for bifurcation curves.

In this paper, Sect. 3 discusses the existence as well as dynamical behavior of the fixed points of map (5). Then different types of bifurcations of codimension 1 including transcritical bifurcation, flip bifurcation, fold bifurcation and Neimark–Sacker bifurcation (NSB) under certain conditions are discussed in Sect. 4. In Sect. 5, existence of Bogdanov–Takens (BT) bifurcation of codimension 2 in the discrete-system is established. The Sect. 6 illustrates extensive numerical simulation for the theoretical results.

3 Existence and stability of fixed points

This section illustrates the existence and stability of the fixed points of the map (5).

The fixed points of the map (5) are summarized as follows:

• 1. The trivial fixed point is $E_{0}(0,0)$.

• 2. The semitrivial fixed points are $E_{x_{1 }}(x_{1}, 0)$ and $E_{x_{2 }}(x_{2}, 0)$ where

  $$\begin{aligned} x_{1}=\frac{1}{2} \left( 1-\delta +\sqrt{(1-\delta )^2-4(\alpha -\delta )}\right) \end{aligned}$$

  and

  $$\begin{aligned} x_{2}=\frac{1}{2} \left( 1-\delta -\sqrt{(1-\delta )^2-4(\alpha -\delta )}\right) \end{aligned}$$

  respectively, $\delta <1$ and $(\delta +1)^2>4\alpha .$ Alternatively, The two fixed points can be written as

  $$\begin{aligned} E_{x_{1,2}}=(x_{1, 2},0)=\left( \frac{1}{2} \left( 1-\delta \pm \sqrt{(1-\delta )^2-4(\alpha -\delta )}\right) ,0\right) . \end{aligned}$$

  • If $\alpha >\delta$ then $E_{x_{1}}(x_{1},0)$ and $E_{x_{2}}(x_{2}, 0)$ both exist provided $(\delta +1)^2>4\alpha$, $\delta <1.$

  • If $\alpha <\delta$ then $E_{x_1}$ exists only.

• 3. Another semitrivial fixed point is $E_{y}(0,\frac{\gamma }{q}).$

• 4. The positive fixed points are $E_{xy_1}=(x_{1}^{*}, y_{1}^{*})$ and $E_{xy_2}=(x_{2}^{*}, y_{2}^{*})$ where $y_{1}^{*}=\frac{\gamma +x_{1}^{*}}{q}$ and $y_{2}^{*}=\frac{\gamma +x_{2}^{*}}{q}$ respectively. The first component of $E_{xy_1}$ and $E_{xy_2}$ gives

  $$\begin{aligned} x_{1}^{*}=\frac{1}{2}\left( \left( 1-\delta -\frac{p}{q}\right) +\sqrt{\left( 1-\delta -\frac{p}{q}\right) ^{2}-4\delta \left( \frac{p}{q}+\frac{\alpha }{\delta }-1\right) }\right) \end{aligned}$$

  and

  $$\begin{aligned} x_{2}^{*}=\frac{1}{2}\left( \left( 1-\delta -\frac{p}{q}\right) -\sqrt{\left( 1-\delta -\frac{p}{q}\right) ^{2}-4\delta \left( \frac{p}{q}+\frac{\alpha }{\delta }-1\right) }\right) \end{aligned}$$

  respectively where $\frac{p}{q}+\frac{\alpha }{\delta }>1$. In an alternate way, the above two fixed points can be written as

  $$\begin{aligned}&E_{(xy)_{1,2}}=(x_{1,2}^*, y_{1,2}^*)=\\&\quad \left( \frac{1}{2}\left( (1-\delta -\frac{p}{q})\pm \sqrt{(1-\delta -\frac{p}{q})^{2}-4\delta (\frac{p}{q}+\frac{\alpha }{\delta }-1)}\right) , \frac{\gamma +x_{1,2}^{*}}{q} \right) . \end{aligned}$$

  • $E_{xy_1}$ and $E_{xy_2}$ both exist when $\frac{p}{q}+\delta <1$ and $\left( 1-\delta -\frac{p}{q}\right) ^{2}>4\delta \left( \frac{p}{q}+\frac{\alpha }{\delta }-1\right) .$

  • If $\left( 1-\delta -\frac{p}{q}\right) ^{2}=4\delta \left( \frac{p}{q}+\frac{\alpha }{\delta }-1\right)$ then ${\bar{E}}({\bar{x}},{\bar{y}})$ exists where ${\bar{x}}=\frac{1}{2}\left( 1-\delta -\frac{p}{q}\right)$ and ${\bar{y}}=\frac{\gamma +{\bar{x}}}{q}$.

  • If $\left( 1-\delta -\frac{p}{q}\right) ^{2}<4\delta \left( \frac{p}{q}+\frac{\alpha }{\delta }-1\right)$, no positive fixed point exists.

The conditions for existence of all fixed points are outlined also in Table 1.

The Jacobian matrix for the discrete map (5) at arbitrary fixed point $({\widehat{x}}, {\widehat{y}})$ is given as

$$\begin{aligned} J(E)=\left( \begin{array}{cc} 2-\left( 2{\widehat{x}}+\frac{p\gamma {\widehat{y}}}{(\gamma +{\widehat{x}})^2}+\frac{\alpha \delta }{(\delta +{\widehat{x}})^2}\right) &{} -\frac{p{\widehat{x}}}{\gamma +{\widehat{x}}} \\ \frac{q\beta {\widehat{y}}^2}{(\gamma +{\widehat{x}})^2} &{} 1+\beta \left( 1-\frac{2q{\widehat{y}}}{\gamma +{\widehat{x}}}\right) \\ \end{array} \right) . \end{aligned}$$

The corresponding characteristic equation is written as

$$\begin{aligned} \lambda ^{2}-Tr\lambda +Det=0 \end{aligned}$$

(6)

where

$$\begin{aligned} Tr= & {} 3+\beta -2{\widehat{x}}-\frac{p\gamma {\widehat{y}}}{(\gamma +{\widehat{x}})^2}-\frac{\alpha \delta }{(\delta +{\widehat{x}})^2}-\frac{2\beta q {\widehat{y}}}{\gamma +{\widehat{x}}}\\ Det= & {} \left( 2-2{\widehat{x}}-\frac{p\gamma {\widehat{y}}}{(\gamma +{\widehat{x}})^2}-\frac{\alpha \delta }{(\delta +{\widehat{x}})^2}\right) \left( 1+\beta -\frac{2\beta q {\widehat{y}}}{\gamma +{\widehat{x}}}\right) +\frac{p q\beta {\widehat{x}} {\widehat{y}}^2}{(\gamma +{\widehat{x}})^3} \end{aligned}$$

The dynamical behavior of the fixed points can be classified by the following lemma:

Lemma 1

Consider a polynomial $\tau (\lambda )=\lambda ^{2}-Tr\lambda +Det$, $\lambda _{1}$ and $\lambda _{2}$ be the eigenvalues. Suppose $\tau (1)>0$ then

• 1. $|\lambda _{1}|<1$ and $|\lambda _{2}|<1$ if and only if $\tau (-1)>0$ and $Det<1$;

• 2. $|\lambda _{1}|<1$ and $|\lambda _{2}|>1$ (or $|\lambda _{1}|>1$ and $|\lambda _{2}|<1$) if and only if $\tau (-1)<0$;

• 3. $|\lambda _{1}|>1$ and $|\lambda _{2}|>1$ if and only if $\tau (-1)>0$ and $Det>1$;

• 4. $\lambda _{1}=-1$ and $\lambda _{2}\ne 1$ if and only if $\tau (-1)=0$ and $Tr\ne 0,2$;

• 5. $\lambda _{1}$ and $\lambda _{2}$ are complex conjugate and $|\lambda _{1}|= |\lambda _{2}|$ if and only if $(Tr)^{2}-4Det<0$ and $Det=1$.

3.1 Dynamical behavior around the trivial fixed point $E_{0}(0,0)$

The Jacobian of (5) has eigenvalues $\lambda _{1}=2-\frac{\alpha }{\delta }$ and $\lambda _{2}=1+\beta$ at trivial fixed point $E_{0}$. The fixed point $E_{0}$ is a saddle when $\alpha >\delta$, a source when $\alpha <\delta$ and non-hyperbolic for both conditions $\alpha =\delta$ and $\alpha =3\delta$. These results are listed in the Table 2.

3.2 Dynamical behavior around the semitrivial fixed points

• (a) The eigenvalues of the Jacobian of the map (5) are $\lambda _{1}=2-2x_{1,2}-\frac{\alpha \delta }{(\delta +x_{1,2})^2}$ and $\lambda _{2}=1+\beta$ at semitrivial fixed point $E_{x_{1,2}}(x_{1,2},0)$. $E_{x_{1,2}}$ is a saddle point if $1<2x_{1,2}-\frac{\alpha \delta }{(\delta +x_{1,2})^2}<3$, a source if $0\le 2x_{1,2}-\frac{\alpha \delta }{(\delta +x_{1,2})^2}<1$ and non-hyperbolic for both the conditions $2x_{1,2}-\frac{\alpha \delta }{(\delta +x_{1,2})^2}=1$ and $2x_{1,2}-\frac{\alpha \delta }{(\delta +x_{1,2})^2}=3$. These results are summarized in the Table 3.

• (b) The eigenvalues are $\lambda _{1}=2-\frac{p}{q}-\frac{\alpha }{\delta }$ and $\lambda _{2}=1-\beta$ at semitrivial fixed point $E_{y}(0,\frac{\gamma }{q})$. The dynamical behavior $E_{y}$ is summarized in the Table 4.

Table 1 Existence of fixed points

Table 2 Properties of trivial fixed point $E_{0}$

3.3 Dynamical behavior at positive fixed point $E_{(xy)_{1, 2}}(x_{1, 2}^{*}, y_{1, 2}^{*})$

The characteristic polynomial at $E_{(xy)_{1, 2}}(x_{1, 2}^{*}, y_{1, 2}^{*})$ is obtained as

$$\begin{aligned} \tau (\lambda )=\lambda ^{2}-\left( 3-\beta -A\right) \lambda +\left( 2-A+\beta (B-2)\right) \end{aligned}$$

(7)

where $A(x_{1,2}^*)=2x_{1,2}^*+\frac{p\gamma }{q(\gamma +x_{1,2}^*)}+\frac{\alpha \delta }{(\delta +x_{1,2}^*)^2}$ and $B(x_{1,2}^*)=2x_{1,2}^*+\frac{p}{q}+\frac{\alpha \delta }{(\delta +x_{1,2}^*)^2}$. The stability of the positive fixed point $E_{(xy)_{1, 2}}$ can be discussed by using the following results. The positive fixed point $E_{(xy)_{1,2}}(x_{1,2}^{*}, y_{1,2}^{*})$ is said to be stable if:

$$\begin{aligned} \begin{array}{l} Tr(J(E_{(xy)_{1,2}})-Det(J(E_{(xy)_{1,2}})<1\\ Tr(J(E_{(xy)_{1,2}})+Det(J(E_{(xy)_{1,2}})>-1\\ Det(J(E_{(xy)_{1,2}})<1.\\ \end{array} \end{aligned}$$

(8)

Theorem 1

The dynamical behavior of the map (5) at positive fixed point $E_{(xy)_{1, 2}} (x_{1, 2}^*, y_{1, 2}^*)$ is concluded as follows:

• 1. Sink when $\frac{2(A-3)}{B-3}<\beta <\frac{A-1}{B-2}$;

• 2. Source when $\beta >\max \left\{ \frac{A-1}{B-2},\frac{2(A-3)}{B-3}\right\}$ or $\beta <\frac{2(A-3)}{B-3}$;

• 3. Non-hyperbolic if one of the following condition holds:

  • (a) $\beta =\frac{2(A-3)}{B-3}$, $\beta \ne \frac{A-2}{B-2}$ and $\beta \ne \frac{A}{B-2}$;

  • (b) $\beta =\frac{A-1}{B-2}$ and $(1+\beta +A)^2<4B\beta +8$.

For the details, see Table 5.

Table 3 Properties of semitrivial fixed point $E_{x_{1,2}}$

Table 4 Properties of semitrivial fixed point $E_{y}$

Table 5 Properties of positive fixed point $E_{(xy)_{1, 2}}$

4 Bifurcation of codimension 1

This section discusses bifurcation of codimension 1 of map (5) at the fixed points.

4.1 Bifurcation around trivial fixed point $E_{0}{(0,0)}$

Theorem 2

The map (5) undergoes transcritical bifurcation with respect to bifurcation parameter $\alpha =\delta$ and flip bifurcation for bifurcation parameter $\alpha =3\delta$ at the trivial fixed point $E_{0}(0,0)$.

Proof

From the Table 2, it can be seen that the map (5) is non-hyperbolic (i.e. $\lambda _{1}=1$ and $\lambda _{1}\ne 1$) at $E_{0}(0,0)$, when $\alpha =\delta$. We take $\alpha$ as a bifurcation parameter and $\alpha =\delta +\mu$, where $\mu$ is sufficiently small. Then the center manifold of G is $y=0$, if $\alpha =\delta$ and G is restricted to the map $x\rightarrow (1-\frac{\mu }{\delta })x+\frac{\mu }{\delta ^2}x^2-x^2+O(|x,\mu |^3)$. Hence, the map (5) undergoes transcritical bifurcation at fixed point $E_{0}(0,0)$, if $\alpha =\delta$. In similar manner, the map (5) undergoes flip bifurcation around bifurcation parameter $\alpha =3\delta$ at $E_{0}$, (refer Table 2 for eigenvalues $\lambda _{1}=-1$ and $\lambda _{1}\ne 1$). The manifold of G is restricted to the map $x\rightarrow (-1-\frac{\mu }{\delta })x-x^2+\frac{3}{\delta }x^2-\frac{\mu }{\delta ^2}x^2+O(|x,\mu |^3)$. $\square$

4.2 Bifurcation around semitrivial fixed point $E_{x_{1}}(x_{1},0)$

Theorem 3

The map (5) undergoes (i) transcritical bifurcation when the semitrivial fixed point $E_{x_1}(x_{1},0)$ is non hyperbolic for $\alpha =\frac{(2x_{1}-1)(x_{1}+\delta )^2}{\delta }$ and (ii) flip bifurcation for bifurcation parameter $\alpha =\frac{(2x_{1}-3)(x_{1}+\delta )^2}{\delta }$ at semitrivial fixed point $E_{x_1}(x_{1},0)$.

Proof

(i) From the Table 3, it is evident that for non-hyperbolicity of $E_{x_1}$, $|\lambda _{1}|= 1$ and $|\lambda _{2}|\ne 1$ for $\alpha =\frac{(2x_{1}-1)(x_{1}+\delta )^2}{\delta }$.

Assuming $u=x-x_{1}$, $v=y-0$ and $\mu =\alpha -\left( \frac{(2x_{1}-1)(x_{1}+\delta )^2}{\delta }\right)$, where $\mu$ is a new variable and sufficiently small. The fixed point $E_{x_1}(x_{1},0)$ is shifted to the origin and expansion of right-hand side of map (5) is given as

$$\begin{aligned} \left( \begin{array}{l} u \\ v \end{array}\right) \rightarrow \left\{ \begin{array}{l} (3-4x_{1})u-\frac{px_{1}}{\gamma +x_{1}}v-\frac{x_{1}}{\delta +x_{1}} \mu -\frac{\delta }{(\delta +x_{1})^2}\mu u-\frac{p\gamma }{(\gamma +x_{1})^2}uv\\ +\left( 1-\frac{1+2\delta }{\delta +x_{1}}\right) u^2+\frac{p\gamma }{(\gamma +x_{1})^2}u^2v+O(|u,v|^4) \\ (1+\beta )v-\frac{q\beta }{\gamma +x_{1}}v^2+\frac{q\beta }{(\gamma +x_{1})^2}uv^2+O(|u,v|^4). \end{array} \right. \end{aligned}$$

(9)

The associated variational matrix at (0, 0) is

$$\begin{aligned} {J_{(0,0)}}=\left( \begin{array}{ccc} 3-4x_{1} &{} -\frac{px_{1}}{\gamma +x_{1}} &{} -\frac{x_{1}}{(\delta +x_{1})} \\ 0 &{} 1+\beta &{} 0 \\ 0&{} 0&{}1 \end{array} \right) . \end{aligned}$$

Let $T=\left( \begin{array}{ccc} 1 &{} -a &{} -b \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right)$, $a=\frac{px_{1}}{(\gamma +x_{1})(\beta -2+4x_{1})}$, $b=\frac{x_1}{2(\delta +x_{1})(2x_{1}-1)}$ and under the transformation $\left( \begin{array}{c} u \\ v \\ \mu \end{array}\right) =T \left( \begin{array}{c} X \\ Y \\ w \end{array}\right) ,$ the map (9) yields

$$\begin{aligned} \left( \begin{array}{c} X \\ Y \\ w \end{array}\right) = \left( \begin{array}{ccc} 1 &{} 0 &{} 0\\ 0 &{} 1+\beta &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right) \left( \begin{array}{c} X \\ Y \\ w \end{array} \right) + \left( \begin{array}{c} F_{1}(X, Y, w) \\ G_{1}(X,Y, w) \\ 0 \end{array} \right) \end{aligned}$$

(10)

where

$$\begin{aligned} F_{1}(X,Y,w)= & {} -\left( \frac{\delta }{(\delta +x_{1})^2}+2b\left( 1-\frac{1+2\delta }{\delta +x_{1}}\right) \right) w X+\left( 1-\frac{1+2\delta }{\delta +x_{1}}\right) X^2\\&+\left( \frac{a\delta }{(\delta +x_1)^2}+2ab\left( 1-\frac{1+2\delta }{\delta +x_{1}}\right) +\frac{pb\gamma }{(\gamma +x_1)^2}\right) w Y\\&-\left( 2a\left( 1-\frac{1+2\delta }{\delta +x_{1}}\right) +\frac{p\gamma }{(\gamma +x_1)^2}\right) X Y +\left( \frac{b\delta }{(\delta +x_1)^2}\right. \\&+\left. \left( 1-\frac{1+2\delta }{\delta +x_{1}}\right) b^2\right) w^2 +\left( \frac{pa\gamma }{(\gamma +x_{1})^2}+a^2\left( 1-\frac{1+2\delta }{\delta +x_{1}}\right) \right) Y^2\\&+O(|X,Y|^3){,}\\ G_{1}(X,Y,w)= & {} -\frac{q\beta }{(\gamma +x_{1})^2}Y^2+\frac{q\beta }{(\gamma +x_{1})^2}XY^2-\frac{qb\beta }{(\gamma +x_{1})^2}wY^2+O(|X,Y|^3). \end{aligned}$$

From the center manifold theory, a one-parameter family of reduced equations restricted on a center manifold determines the stability of $(X,Y)=(0,0)$ in the neighborhood of $w=0$ which can be written as

$$\begin{aligned} Z^{c}(0)=\{(X,Y,w)\in R^{3}| Y=S(X,w), S(0,0)=0, DS(0,0)=0\}, \end{aligned}$$

here X and w are sufficiently small. Further, consider a center manifold as follows:

$$\begin{aligned} S(X,w)=S_{1}w^{2}+S_{2}w X+S_{3}X^{2}+O(|X,w|^{3}). \end{aligned}$$

(11)

The manifold S(X, w) must satisfy the relation

$$\begin{aligned}&\kappa (S(X,w),w)=S(X+F_{1}(X,S(X,w),w))\nonumber \\&-(1+\beta )S(X,w)-G_{1}(X,S(X,w),w)=0. \end{aligned}$$

(12)

From (11) and (12), getting $S_{1}=S_{2}=S_{3}=0$. Therefore the map restricted to the center manifold is given by

$$\begin{aligned} X\sim \widetilde{F_{1}}(X,w)= & {} X-\left( \frac{\delta }{(\delta +x_{1})^2}+2b\left( 1-\frac{1+2\delta }{\delta +x_{1}}\right) \right) w X+\left( 1-\frac{1+2\delta }{\delta +x_{1}}\right) X^2\\&+\left( \frac{b\delta }{(\delta +x_1)^2}+\left( 1-\frac{1+2\delta }{\delta +x_{1}}\right) b^2\right) w^2+O(|X,w|^4). \end{aligned}$$

It is easily concluded that

$\widetilde{F_{1}}(0,0)=0$, $\frac{\partial \widetilde{F_{1}}}{\partial X}(0,0)=1$, $\frac{\partial \widetilde{F_{1}}}{\partial w}(0,0)=0$, $\frac{\partial ^2\widetilde{F_{1}}}{\partial X^2}(0,0)=2\left( 1-\frac{1+2\delta }{\delta +x_{1}}\right) \ne 0$, ${\frac{\partial ^2\widetilde{F_{1}}}{\partial X\partial w}(0,0)}=-\frac{\delta }{(\delta +x_{1})^2}-2b\left( 1-\frac{1+2\delta }{\delta +x_{1}}\right) \ne 0$.

Hence by [28, 33], the map (5) occurs transcritical bifurcation at the semitrivial fixed point $E_{x_1}(x_{1},0)$ with respect to bifurcation parameter $\alpha =\frac{(2x_{1}-1)(\delta +x_{1})^2}{\delta }.$

(ii) When $\alpha =\frac{(2x_{1}-3)(x_{1}+\delta )^2}{\delta }$, $E_{x_1}(x_{1},0)$ is non-hyperbolic because $J(E_{x_{1}})$ has eigenvalues $|\lambda _{1}|=-1$ and $|\lambda _{2}|\ne 1$.

Let $u=x-x_{1}$, $v=y-0$ and $\mu =\alpha -\left( \frac{(2x_{1}-3)(x_{1}+\delta )^2}{\delta }\right)$, where $\mu$ is a new variable and sufficiently small. On transforming the fixed point $E_{x_{1}}(x_{1},0)$ to the origin and expanding the right-hand side of map (5) at origin, it is obtained

$$\begin{aligned} \left( \begin{array}{c} u \\ v \end{array}\right) \rightarrow \left\{ \begin{array}{l} (5-4x_{1})u-\frac{px_{1}}{\gamma +x_{1}}v-\frac{x_{1}}{\delta +x_{1}}\mu -\frac{\delta }{(\delta +x_{1})^2}\mu u-\frac{p\gamma }{(\gamma +x_{1})^2}uv\\ +\left( 1-\frac{3+2\delta }{\delta +x_{1}}\right) u^2+\frac{p\gamma }{(\gamma +x_{1})^2}u^2v+\frac{3-2x_{1}}{(\delta +x_{1})^2}u^3+O|u,v|^4 \\ (1+\beta )v-\frac{q\beta }{\gamma +x_{1}}v^2+\frac{q\beta }{(\gamma +x_{1})^2}uv^2+O|u,v|^4. \end{array} \right. \end{aligned}$$

(13)

Linearizing map (13) at (0, 0), the associated Jacobian matrix at origin is given by

$$\begin{aligned} J(0,0)=\left( \begin{array}{ccc} 5-4x_{1} &{} -\frac{px_{1}}{\gamma +x_{1}} &{} -\frac{x_{1}}{\delta +x_{1}} \\ 0 &{} 1+\beta &{} 0 \\ 0&{} 0&{}1 \end{array} \right) . \end{aligned}$$

Let

$$\begin{aligned} T=\left( \begin{array}{ccc} 1 &{} -a &{} -b \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right) , \end{aligned}$$

where $a=\frac{px_{1}}{(\gamma +x_{1})(\beta -4+4x_{1})}$ and $b=\frac{x_1}{4(\delta +x_{1})(x_{1}-1)}$.

Under the transformation $\left( \begin{array}{c} u \\ v \\ \mu \end{array}\right) =T \left( \begin{array}{c} X \\ Y \\ w \end{array}\right) ,$ the map (13) becomes

$$\begin{aligned} \left( \begin{array}{c} X \\ Y \\ w \end{array}\right) = \left( \begin{array}{ccc} -1 &{} 0 &{} 0\\ 0 &{} 1+\beta &{} 0 \\ 0 &{} 0 &{} 1 \end{array} \right) \left( \begin{array}{c} X \\ Y \\ w \end{array} \right) + \left( \begin{array}{c} F_{1}(X, Y, w) \\ G_{1}(X,Y, w) \\ 0 \end{array} \right) \end{aligned}$$

(14)

where

$$\begin{aligned} F_{1}(X,Y,w)= & {} \left( 1-\frac{3+2\delta }{\delta +x_{1}}\right) X^2-\left( \frac{\delta }{(\delta +x_{1})^2}+2b\left( 1-\frac{3+2\delta }{\delta +x_{1}}\right) \right) w X\\&+\left( \frac{a\delta }{(\delta +x_1)^2}+2ab\left( 1-\frac{3+2\delta }{\delta +x_{1}}\right) +\frac{pb\gamma }{(\gamma +x_1)^2}\right) w Y\\&-\left( 2a\left( 1-\frac{3+2\delta }{\delta +x_{1}}\right) +\frac{p\gamma }{(\gamma +x_1)^2}\right) XY\\&+\left( \frac{b\delta }{(\delta +x_1)^2}+\left( 1-\frac{3+2\delta }{\delta +x_{1}}\right) b^2\right) w^2+\frac{3-2x_{1}}{(\delta +x_{1})^2}X^3\\&+\left( \frac{pa\gamma }{(\gamma +x_{1})^2}+a^2\left( 1-\frac{3+2\delta }{\delta +x_{1}}\right) \right) Y^2+O(|X,Y|^4)\\ G_{1}(X,Y,w)= & {} -\frac{q\beta }{(\gamma +x_{1})^2}Y^2+\frac{q\beta }{(\gamma +x_{1})^2}XY^2-\frac{qb\beta }{(\gamma +x_{1})^2}wY^2+O(|X,Y|^4). \end{aligned}$$

Once again from the center manifold theory, the stability of $(X,Y)=(0,0)$ near $w=0$ can be obtained by studying a one-parameter family of equations restricted on a center manifold, which can be represented as follows

$$\begin{aligned} Z^{c}(0)=\{(X,Y,w)\in R^{3}| Y=S(X,w), S(0,0)=0, DS(0,0)=0\}, \end{aligned}$$

here X and w are sufficiently small. Further, consider a center manifold

$$\begin{aligned} S(X,w)=S_{1}w^{2}+S_{2}w X+S_{3}X^{2}+O(|X,w|^{3}). \end{aligned}$$

(15)

The manifold S(X, w) must satisfy the relation

$$\begin{aligned} \kappa (S(X,w),w)=S(-X+F_{1}(X,S(X,w),w))-(1+\beta )S(X,w)-G_{1}(X,S(X,w),w)=0. \end{aligned}$$

(16)

From (15) and (16), we get $S_{1}=S_{2}=S_{3}=0$. Therefore the map is restricted to the center manifold, given as

$$\begin{aligned} X\sim \widetilde{F_{1}}(X,w)= & {} -X-\left( \frac{\delta }{(\delta +x_{1})^2}+2b\left( 1-\frac{3+2\delta }{\delta +x_{1}}\right) \right) w X +\left( 1-\frac{3+2\delta }{\delta +x_{1}}\right) X^2\\&\quad +\left( \frac{b\delta }{(\delta +x_1)^2}+\left( 1-\frac{+2\delta }{\delta +x_{1}}\right) b^2\right) w^2+\frac{3-2x_{1}}{(\delta +x_{1})^2}X^3+O(|X,w|^4). \end{aligned}$$

Here, $\widetilde{F_{1}}(0,0)=0$, $\frac{\partial \widetilde{F_{1}}}{\partial X}(0,0)=-1$, $\frac{\partial \widetilde{F_{1}}}{\partial w}(0,0)=0$, $\frac{\partial ^2\widetilde{F_{1}}}{\partial X^2}(0,0)=2\left( 1-\frac{3+2\delta }{\delta +x_{1}}\right) ,$ ${\frac{\partial ^2\widetilde{F_{1}}}{\partial X\partial w}(0,0)}=-\frac{\delta }{(\delta +x_{1})^2}-2b\left( 1-\frac{3+2\delta }{\delta +x_{1}}\right)$ and $\frac{\partial ^3\widetilde{F_{1}}}{\partial X^3}(0,0)=\frac{6(3-2x_{1})}{(\delta +x_{1})^2}.$

The existence conditions for flip bifurcation, given in  [28, 33, 47] are

$$\begin{aligned} \varrho _{1}= & {} \left( \frac{1}{2}\frac{\partial \widetilde{F_{1}}}{\partial w}\frac{\partial ^2\widetilde{F_{1}}}{\partial X^2}+{\frac{\partial ^2 \widetilde{F_{1}}}{\partial X \partial w}}\right) ,\nonumber \\ \varrho _{2}= & {} \left( \left( \frac{1}{2}\frac{\partial ^2\widetilde{F_{1}}}{\partial X^2}\right) ^2+\frac{1}{6}\frac{\partial ^3\widetilde{F_{1}}}{\partial X^3}\right) , \end{aligned}$$

(17)

$\varrho _{1}=-\frac{\delta }{(\delta +x_{1})^2}-2b\left( 1-\frac{3+2\delta }{\delta +x_{1}}\right) \ne 0$ and $\varrho _{2}=\left( 1-\frac{3+2\delta }{\delta +x_{1}}\right) ^2+\frac{(3-2x_{1})}{(\delta +x_{1})^2}\ne 0$.

Hence the map (5) undergoes flip bifurcation at the semitrivial fixed point $E_{x_1}$ around the bifurcation parameter $\alpha =\frac{(2x_{1}-3)(\delta +x_{1})^2}{\delta }.$

Theorem 4

The map (5) occurs (i) transcritical bifurcation at $E_{{x_2}}(x_{2},0)$ for $\alpha =\frac{(2x_{2}-1)(x_{2}+\delta )^2}{\delta }$ and (ii) flip bifurcation for $\alpha =\frac{(2x_{2}-3)(x_{2}+\delta )^2}{\delta }$.

Proof

The proof is with similar lines of Theorem 4, we can omit it. $\square$

4.3 Bifurcation around another fixed point $E_{y}(0,\frac{\gamma }{q})$

Theorem 5

(i) At another semitrivial fixed point $E_{y}(0,\frac{\gamma }{q})$, the map (5) occurs (i) flip bifurcation at bifurcation parameter $\beta =2$. (ii) transcritical bifurcation with respect to bifurcation parameter $\alpha =\delta \left( \frac{q-p}{q}\right)$ and $\beta \ne 2$.

Proof

(i): From the Table 4, the eigenvalues of the Jacobian matrix J are $|\lambda _{1}|\ne 1$ and $\lambda _{2}=-1$ for $\beta =2$ and $\frac{p}{q}+\frac{\gamma }{q}\ne 1,3$. Then the semitrivial fixed point $E_{y}$ is non-hyperbolic.

Assuming $u=x-0$, $v=y-\frac{\gamma }{q}$ and $\mu =\beta -2$, $\mu$ is sufficiently small.

The expansion of right-hand side of map (5) at semitrivial fixed point $E_{y}(0,\frac{\gamma }{q})$ is given by

$$\begin{aligned} \left( \begin{array}{l} u \\ v \end{array}\right) \rightarrow \left\{ \begin{array}{l} (2-\frac{p}{q}-\frac{\gamma }{q})u-\frac{p}{\gamma }uv-\left( 1-\frac{p}{q\gamma }-\frac{\alpha }{\gamma ^2}\right) u^2+\frac{p}{\gamma ^2}u^2v\\ -\left( \frac{p}{q\gamma ^2}+\frac{\alpha }{\delta ^3}\right) u^3+O|u,v|^4 \\ -v-\mu v-\frac{(\mu +2)q}{\gamma }u+\frac{2(\mu +2)}{\gamma }uv-\frac{(\mu +2)}{q\gamma }u^2-\frac{(\mu +2)q}{\gamma }v^2\\ +\frac{(2+\mu )q}{\gamma ^2}uv^2-\frac{2(2+\mu )}{\gamma ^2}u^2v+O|u,v|^4. \end{array} \right. \end{aligned}$$

(18)

The associated variational matrix at origin is written as

$$\begin{aligned} {J_{(0,0)}}=\left( \begin{array}{cc} (2-\frac{p}{q}-\frac{\gamma }{q}) &{} 0 \\ \frac{2}{q} &{} -1 \end{array} \right) . \end{aligned}$$

Assuming $T=\left( \begin{array}{cc} 1 &{} 1 \\ 0 &{} A_{1} \end{array} \right)$, where $A_{1}=3q\gamma -p\gamma -q\alpha$ and the transformation is taken as

$$\begin{aligned} \left( \begin{array}{c} u \\ v \end{array}\right) =T \left( \begin{array}{c} X \\ Y \end{array}\right) . \end{aligned}$$

The map (18) becomes

$$\begin{aligned} \left( \begin{array}{c} X \\ Y \end{array}\right) = \left( \begin{array}{cc} 2-\frac{p}{q}-\frac{\alpha }{\delta } &{} 0 \\ 0 &{} -1 \end{array} \right) \left( \begin{array}{c} X \\ Y \end{array} \right) + \left( \begin{array}{c} F_{1}(X, Y) \\ G_{1}(X,Y) \end{array} \right) \end{aligned}$$

(19)

where

$$\begin{aligned} F_{1}(X,Y)= & {} \left( 2\left( \frac{\alpha }{\gamma ^2}+\frac{p}{q\gamma }-1\right) -\frac{pA_{1}}{\gamma }\right) XY+\left( \left( \frac{\alpha }{\gamma ^2}+\frac{p}{q\gamma }-1\right) -\frac{pA_{1}}{\gamma }\right) Y^2\\&+\left( \frac{\alpha }{\gamma ^2}+\frac{p}{q\gamma }-1\right) X^2+O(|X,Y|^3),\\ G_{1}(X,Y)= & {} \frac{1}{q}\mu X+\left( \frac{1-qA_{1}}{q}\right) \mu Y+\frac{2(2+\mu )}{\gamma }\left( 1-\frac{\gamma }{q}\right) XY-\left( \frac{2+\mu }{q}\right) X^2\\&+\frac{2+\mu }{\gamma }\left( 2-q^2A_{1}^2-\frac{\gamma }{q}\right) Y^2+\frac{(2+\mu )qA_{1}^{2}}{\gamma ^2}Y^3+O(|X,Y|^3). \end{aligned}$$

From the center manifold theory, a one-parameter family of reduced equations restricted on a center manifold determines the stability of $(X,Y)=(0,0)$ in the neighborhood of $\mu =0$, which can be represented as

$$\begin{aligned} Z^{c}(0)=\{(X,Y,\mu )\in R^{3}| X=S(Y,\mu ), S(0,0)=0, DS(0,0)=0\}, \end{aligned}$$

for sufficiently small Y and $\mu$. Further, a center manifold is taken as

$$\begin{aligned} S(Y,\mu )=S_{1}{\mu }^{2}+S_{2}\mu Y+S_{3}Y^{2}+O(|Y,\mu |^{3}). \end{aligned}$$

(20)

The manifold $S(Y,\mu )$ must satisfy the relation

$$\begin{aligned} \kappa (S(Y,\mu ))=S(-Y+G_{1}(S(Y,\mu ),Y,\mu )) -\left( 2-\frac{p}{q}-\frac{\alpha }{\delta }\right) S(Y,\mu )-F_{1}(S(Y,\mu ),Y,\mu )=0.\qquad \end{aligned}$$

(21)

From (20) and (21), $S_{1}=S_{2}=0$ and $S_{3}=\frac{\left( 1-\frac{\alpha }{\gamma ^2}-\frac{p}{q\gamma }\right) }{\left( {\frac{p}{q}+\frac{\alpha }{\delta }-1}\right) }\ne 0$.

Therefore the map restricted to the center manifold is given as

$$\begin{aligned} Y\sim \widetilde{G_{1}}(Y,\mu )= & {} -Y+\frac{S_{3}}{q}\mu Y^2+\left( \frac{1-qA_{1}}{q}\right) \mu Y+\frac{2+\mu }{\gamma }\left( 2-q^2A_{1}^2-\frac{\gamma }{q}\right) Y^2\\&+\frac{2S_{3}(2+\mu )}{\gamma }\left( 1-\frac{\gamma }{q}\right) Y^3+\frac{(2+\mu )qA_{1}^{2}}{\gamma ^2}Y^3+O(|Y,\mu |^4). \end{aligned}$$

It is easily concluded that

$\widetilde{G_{1}}(0,0)=0$, $\frac{\partial \widetilde{G_{1}}}{\partial Y}(0,0)=-1$, $\frac{\partial \widetilde{G_{1}}}{\partial \mu }(0,0)=0$, $\frac{\partial ^2\widetilde{G_{1}}}{\partial Y^2}(0,0)=-\left( \frac{4q^2A_{1}^2}{\gamma }+\frac{8}{\gamma }\right) \ne 0$, ${\frac{\partial ^2\widetilde{G_{1}}}{\partial Y\partial \mu }}(0,0)=-A_{1}+\frac{1}{q}\ne 0$ and $\frac{\partial ^3\widetilde{G_{1}}}{\partial Y^3}(0,0)=-\frac{24S_{3}}{\gamma }+\frac{12qA_{1}^{2}}{\gamma ^2}$.

By using existence conditions of flip bifurcation (17), $\varrho _{1}\ne 0$, $\varrho _{2}\ne 0$ at $E_{y}(0,\frac{\gamma }{q})$. Hence the map (5) undergoes flip bifurcation at $E_{y}$ when $\beta =2$ and $\frac{p}{q}+\frac{\alpha }{\delta }\ne 1,3$.

(ii) The Jacobian matrix J at $E_{y}(0,\frac{\gamma }{q})$ has eigenvalues ($|\lambda _{1}|= 1$ and $|\lambda _{2}|\ne 1$) for $\alpha =\delta \left( \frac{q-p}{q}\right)$ and $\beta \ne 2$. For this, the fixed point $E_{y}$ is non-hyperbolic also.

Let $u=x-0$, $v=y-\frac{\gamma }{q}$ and $\mu =\alpha -\delta \left( \frac{q-p}{q}\right)$. The fixed point $E_{y}(0,\frac{\gamma }{q})$ is shifted to origin and expanding the right-hand side of map (5) at origin, it gives

$$\begin{aligned} \left( \begin{array}{c} u \\ v \end{array}\right) \rightarrow \left\{ \begin{array}{c} u-\frac{\mu }{\delta }u-\frac{p}{\gamma }uv+\left( -1+\frac{1}{\delta }-\frac{p(\delta -\gamma )}{q\delta \gamma }+\frac{\mu }{\delta ^2}\right) u^2+\frac{p}{\gamma ^2}u^2v+O|u,v|^4 \\ \frac{\beta }{q}u+(1-\beta )v+\frac{2\beta }{\gamma }uv-\frac{\beta }{q\gamma }u^2-\frac{q\beta }{\gamma }v^2+\frac{q\beta }{\gamma ^2}uv^2-\frac{2\beta }{\gamma ^2}u^2v+O|u,v|^4. \end{array}\right. \end{aligned}$$

(22)

The associated variational matrix at origin is given by

$$\begin{aligned} {J_{(0,0)}}= \left( \begin{array}{cc} 1 &{} 0 \\ \frac{\beta }{q} &{} 1-\beta \end{array} \right) . \end{aligned}$$

Let $T=\left( \begin{array}{cc} 1 &{} 1 \\ 0 &{} q \end{array} \right)$ and use the transformation $\left( \begin{array}{c} u \\ v \end{array}\right) =T \left( \begin{array}{c} X \\ Y \end{array}\right) .$

The map (22) transforms as

$$\begin{aligned} \left( \begin{array}{c} X \\ Y \end{array}\right) = \left( \begin{array}{cc} 1 &{} 0 \\ 0 &{} 1-\beta \end{array} \right) \left( \begin{array}{c} X \\ Y \end{array} \right) + \left( \begin{array}{c} F_{1}(X, Y) \\ G_{1}(X,Y) \end{array} \right) \end{aligned}$$

(23)

where

$$\begin{aligned} F_{1}(X,Y)= & {} -\frac{\mu X}{\delta }-\frac{\mu Y}{\delta }+\left( 2\left( -1+\frac{1}{\delta }-\frac{p(\delta -\gamma )}{q\delta \gamma } +\frac{\mu }{\delta ^2}\right) -\frac{pq}{\gamma }\right) XY\\&+\frac{pq}{\gamma ^2}X^2Y+\left( -1+\frac{1}{\delta }-\frac{p(\delta -\gamma )}{q\delta \gamma }+\frac{\mu }{\delta ^2}\right) X^2\\&+\left( -1-\frac{pq}{\gamma }+\frac{1}{\delta }-\frac{p(\delta -\gamma )}{q\delta \gamma }+\frac{\mu }{\delta ^2}\right) Y^2+O(|X,Y|^4),\\ G_{1}(X,Y)= & {} \frac{2\beta (q^2-1)}{q\gamma }XY-\frac{\beta }{q\gamma }X^2+\left( \frac{2q\beta }{\gamma }-\frac{q^3\beta }{\gamma }-\frac{\beta }{q\gamma }\right) Y^2 -\frac{2q\beta }{\gamma ^2}X^2Y\\&+\left( \frac{q^3\beta }{\gamma ^2}-\frac{4q\beta }{\gamma ^2}\right) XY^2+O(|X,Y|^4). \end{aligned}$$

Once again, the stability of $(X,Y)=(0,0)$ near $\mu =0$, can be determined as follows:

$$\begin{aligned} Z^{c}(0)=\{(X,Y,\mu )\in R^{3}| Y=S(X,\mu ), S(0,0)=0, DS(0,0)=0\}, \end{aligned}$$

for sufficiently small X and $\mu$. Now assume

$$\begin{aligned} S(X,\mu )=S_{1}{\mu }^{2}+S_{2}\mu X+S_{3}X^{2}+O(|X,\mu |^{3}). \end{aligned}$$

(24)

Then it is obtained

$$\begin{aligned} \kappa (S(X,\mu ),\mu )=S(X+F_{1}(X,S(X,\mu ),\mu ))-(1-\beta )S(X,\mu )-G_{1}(X,S(X,\mu ),\mu )=0. \end{aligned}$$

(25)

Substituting (24) into (25) and comparing the coefficients of (25), we get $S_{1}=S_{2}=0$ and $S_{3}=\frac{\beta }{q\gamma \left( \frac{2\mu }{\delta }-\frac{\mu ^2}{\delta ^2}-\beta \right) }\ne 0$.

Thus the map restricted to the center manifold is given as

$$\begin{aligned} X\sim \widetilde{F_{1}}(X,\mu )= & {} X-\frac{\mu X}{\delta }-\frac{S_{3}\mu X^2}{\delta }+\left( -1+\frac{1}{\delta }-\frac{p(\delta -\gamma )}{q\delta \gamma } +\frac{\mu }{\delta ^2}\right) X^2\\&+S_{3}\left( -\frac{pq}{\gamma }+2\left( -1+\frac{1}{\delta }-\frac{p(\delta -\gamma )}{q\delta \gamma }+\frac{\mu }{\delta ^2}\right) \right) X^3+O(|X,\mu |^4). \end{aligned}$$

We can see that $\widetilde{F_{1}}(0,0)=0$, $\frac{\partial \widetilde{F_{1}}}{\partial X}(0,0)=1$, $\frac{\partial \widetilde{F_{1}}}{\partial \mu }(0,0)=0$, ${\frac{\partial ^2\widetilde{G_{1}}}{\partial X\partial \mu }(0,0)}=-\frac{1}{\delta }\ne 0$, $\frac{\partial ^2\widetilde{F_{1}}}{\partial X^2}(0,0)=2\left( -1+\frac{1}{\delta }-\frac{p(\delta -\gamma )}{q\delta \gamma }+\frac{\mu }{\delta ^2}\right) \ne 0$.

Therefore the map (5) undergoes transcritical bifurcation around fixed point $E_{y}$ at bifurcation parameter $\alpha =\delta \left( \frac{q-p}{q}\right)$ and $\beta \ne 2$. $\square$

4.4 Bifurcation around first positive fixed point

This subsection determines the conditions of occurrence of flip bifurcation and Neimark–Sacker bifurcation at positive fixed point $E_{(xy)_1}(x_1^*,y_1^*)$.

Theorem 6

(i) The flip bifurcation is occurred at $\beta =\frac{2(A-3)}{B-3}$ (ii) Neimark–Sacker bifurcation is occurred at $\beta =\frac{A-1}{B-2}$ around the positive fixed point ${E_{(xy)_1}(x_1^*,y_1^*)}$ in the map (5).

Proof

It is clear from the Table 5, the Jacobian J has eigenvalues $|\lambda _{1}|\ne 1$ and $\lambda _{2}=-1$ at the positive fixed point ${E_{(xy)_1}(x_1^*,y_1^*)}$ for $\beta =\frac{2(A-3)}{B-3}$. i.e. ${E_{(xy)_1}}$ is non-hyperbolic. Let $u=x-x_1^{*}$, $v=y-y_1^{*}$ and $\mu =\beta -\beta _{1}$, where $\beta _{1}=\frac{2(A-3)}{B-3}$. The fixed point ${E_{(xy)_1}(x_1^{*},y_1^{*})}$ is shifted to the origin and expanding the right-hand side of map (5), it yields

$$\begin{aligned} \left( \begin{array}{c} u \\ v \end{array}\right) \rightarrow \left\{ \begin{array}{l} a_{11}u+a_{12}v+a_{13}uv+a_{14}u^2+a_{15}u^2v+O(|u,v|^4)\\ b_{11}u+b_{12}v+b_{13}\mu +b_{14}v^2+b_{15}\mu v+b_{16}u^2+b_{17}\mu u\\ +b_{18}uv+b_{19}uv^2+O(|u,v|^4). \end{array} \right. . \end{aligned}$$

(26)

where

${a_{11}\ =\ 2\,-\,2x_1^*\,-\,\frac{\alpha \delta }{(\delta \,+\,x_1^*)^2}\,-\,\frac{p\gamma y_1^*}{(\gamma \,+\,x_1^*)^2}}$, ${a_{12}\,=\,-\,\frac{px_1^*}{\gamma +x_1^*}}$, ${a_{13}=-\frac{p\gamma }{(\gamma +x_1^*)^2}}$,

${a_{14}=\left( \frac{\alpha \delta }{(\delta +x_1^*)^3}+\frac{p\gamma y_1^*}{(\gamma +x_1^*)^3}-1\right) }$, ${a_{15}=\frac{p\gamma }{(\gamma +x_1^*)^3}}$, ${b_{11}=\frac{q\beta _1 (y_1^*)^2}{(\gamma +x_1^*)^2}}$, ${b_{12}=1+\beta _{1} \left( 1-\frac{2q y^*}{\gamma +x^*}\right) }$, ${b_{13}=y^*\left( 1-\frac{q y^*}{\gamma +x_1^*}\right) }$, ${b_{14}=-\frac{q\beta _{1}}{\gamma +x_1^*}}$, ${b_{15}=\left( 1-\frac{2q y_1^*}{\gamma +x_1^*}\right) }$, ${b_{16}=-\frac{q\beta _1 (y_1^*)^2}{(\gamma +x_1^*)^3}}$, ${b_{17}=\frac{q(y_1^*)^2}{(\gamma +x_1^*)^2}}$, ${b_{18}=\frac{2q\beta _1 y_1^*}{(\gamma +x_1^*)^2}}$ and ${b_{19}=-\frac{q\beta _{1}(y_1^*)^2}{(\gamma +x_1^*)^3}.}$

Now linearizing the map (26) at (0, 0) and forming an invertible matrix,

$$\begin{aligned} T=\left( \begin{array}{ccc} \lambda _{1}-a_{11} &{} -a_{11}-1 &{} 0\\ a_{12} &{} a_{12} &{} 0\\ 0 &{} 0 &{} 1 \end{array}\right) . \end{aligned}$$

By using the transformation $\left( \begin{array}{c} u \\ v \\ \mu \end{array}\right) =T\left( \begin{array}{c} X \\ Y \\ w \end{array}\right) ,$ the map (26) turns into

$$\begin{aligned} \left( \begin{array}{c} X \\ Y \\ w \end{array}\right) \rightarrow \left( \begin{array}{ccc} \lambda _{1} &{} 0 &{} 0\\ 0 &{} -1 &{} 0 \\ 0 &{} 0 &{} 1 \end{array}\right) \left( \begin{array}{c} X \\ Y \\ w \end{array}\right) + \left( \begin{array}{c} F_{1}(X,Y,w) \\ G_{1}(X,Y,w) \\ 0 \end{array}\right) \end{aligned}$$

where

$$\begin{aligned} F_{1}(X,Y,w) &\,= k_{1}X^2+k_{2}Y^2+k_{3}XY+k_{4}X^2 Y+k_{5}XY^2+k_{6}X^3+O(|X,Y|^4),\\ G_{1}(X,Y,w) &\,= e_{1}Y^2+e_{2}wY+k_{3}wX+e_{4}X Y+e_{5}X^2+e_{6}X^3+e_{7}Y^3+O(|X,Y|^4). \end{aligned}$$

Here $k_{1}=a_{12}a_{13}(\lambda _{1}-a_{11})+a_{14}(\lambda _{1}-a_{11})^2$, $k_{2}=a_{14}(1+a_{11})^2-a_{12}a_{13}(1+a_{11})$, $k_{3}=a_{12}a_{13}(\lambda _{1}-a_{11})-a_{12}a_{13}(1+a_{11})-2a_{14}(\lambda _{1}-a_{11})(1+a_{11})$, $k_{4}=a_{15}(\lambda _{1}-a_{11})^2-2a_{15}(\lambda _{1}-a_{11})(1+a_{11})$, $k_{5}=2a_{15}(1+a_{11})^2-2(\lambda _{1}-a_{11})(1+a_{11})$, $k_{6}=a_{15}(\lambda _{1}-a_{11})^2$, $e_{1}=b_{14}+b_{16}(1+a_{11})^2-b_{18}(1+a_{11})$, $e_{2}=b_{15}-b_{17}(1+a_{11})$, $e_{3}=b_{15}+b_{17}(\lambda _{1}-a_{11})$, $e_{4}=2b_{14}-2b_{16}(\lambda _{1}-a_{11})(1+a_{11})+b_{18}(\lambda _{1}-a_{11})-b_{18}(1+a_{11})$, $e_{5}=b_{14}+b_{16}(\lambda _{1}-a_{11})^2+b_{18}(\lambda _{1}-a_{11})$, $e_{6}=a_{12}^2(\lambda _{1}-a_{11})$ and $e_{7}=-a_{12}^2(1+a_{11}).$

To discuss the stability of $(X,Y)=(0,0)$ near $w=0$, the center manifold is considered as

$$\begin{aligned} Z^{c}(0)=\{(X,Y,w)\in R^{3}| X=S(Y,w), S(0,0)=0, DS(0,0)=0\}, \end{aligned}$$

here X and w are sufficiently small. Let

$$\begin{aligned} S(Y,w)=S_{1}w^{2}+S_{2}w Y+S_{3}Y^{2}+O(|Y,w|^{3}). \end{aligned}$$

(27)

Then

$$\begin{aligned} \kappa (S(Y,w),w)=S(-Y+G_{1}(S(Y,w),Y,w))-\lambda _{1}S(Y,w)-F_{1}(S(Y,w),Y,w)=0. \end{aligned}$$

(28)

Substituting (27) into (28) and comparing the coefficients of (28), we obtain $S_{1}=S_{2}=0$ and $S_{3}=\frac{k_{2}}{1-\lambda _{1}}$.

Then the map (26) restricted to the center manifold is given by

$$\begin{aligned} Y\sim \widetilde{G_{1}}(Y,w)= & {} e_{1}Y^2-Y+e_{2}wY+e_{3}S_{3}wY^2+e_{4}S_{3}Y^{3}+e_{5}S_{3}^{2}Y^{4}\\&+e_{7}Y^{3}+O|Y,w|^5. \end{aligned}$$

It can be seen that $\widetilde{G_{1}}(0,0)=0$, $\frac{\partial \widetilde{G_{1}}}{\partial Y}(0,0)=-1$, $\frac{\partial \widetilde{G_{1}}}{\partial w}(0,0)=0$, $\frac{\partial ^2\widetilde{G_{1}}}{\partial Y^2}(0,0)=2e_{1}\ne 0$, ${\frac{\partial ^2\widetilde{G_{1}}}{\partial Y\partial w}(0,0)}=e_{2}\ne 0$ and $\frac{\partial ^3\widetilde{F_{1}}}{\partial Y^3}(0,0)=6(e_{4}S_{3}+e_{7})$.

From (17), $\varrho _{1}=e_{2}\ne 0$ and $\varrho _{2}=e_{4}S_{3}+e_{1}^2\ne 0$.

Therefore, the map (5) occurs flip bifurcation at fixed point ${E_{(xy)_1}}$ for bifurcation parameter $\beta =\frac{2(A-3)}{B-2}$.

(ii) Now we discuss Neimark–Sacker bifurcation at fixed point ${E_{(xy)_1}}$ is non-hyperbolic at $\beta =\frac{A-1}{B-2}$ for $|\lambda _{1}|=1$, $|\lambda _{2}|=1$ (see Table 5).

We transform the fixed point ${E_{(xy)_1}(x_1^*,y_1^*)}$ to the origin and expand the right-hand side of map (5) around the origin by using following translation $u=x-x_1^{*}$, $v=y-y_1^{*}$ and $\beta =\beta _{1}=\frac{A-1}{B-2}$. The map (5) yields

$$\begin{aligned} \left( \begin{array}{c} u \\ v \end{array}\right) \rightarrow \left\{ \begin{array}{l} a_{11}u+a_{12}v+a_{13}uv+a_{14}u^2+a_{15}u^2v+O(|u,v|^4)\\ b_{11}u+b_{12}v+b_{13}uv+b_{14}u^2+b_{15} v^2+b_{16}u^2v+b_{17}uv^2+O(|u,v|^4) \end{array} \right. \qquad \end{aligned}$$

(29)

where $a_{11}=2-2x_1^*-\frac{\alpha \delta }{(\delta +x_1^*)^2}-\frac{p\gamma y_1^*}{(\gamma +x_1^*)^2}$, $a_{12}=-\frac{px_1^*}{\gamma +x_1^*}$, $a_{13}=-\frac{p\gamma }{(\gamma +x_1^*)^2}$, $a_{14}=\left( \frac{\alpha \delta }{(\delta +x_1^*)^3}+\frac{p\gamma y_1^*}{(\gamma +x_1^*)^3}-1\right)$, $a_{15}=\frac{p\gamma }{(\gamma +x_1^*)^3}$, $b_{11}=\frac{q\beta (y_1^*)^2}{(\gamma +x_1^*)^2}$, $b_{12}=1+\beta \left( 1-\frac{2q y_1^*}{\gamma +x_1^*}\right)$, $b_{13}=\frac{2q\beta y_1^*}{(\gamma +x_1^*)^2}$, $b_{14}=-\frac{q\beta (y_1^*)^2}{(\gamma +x_1^*)^3}$, $b_{15}=-\frac{q\beta }{\gamma +x_1^*}$, $b_{16}=-\frac{2q\beta y_1^*}{(\gamma +x_1^*)^3}$, $b_{17}=\frac{q\beta }{(\gamma +x_1^*)^2}$.

Let us consider the following set of complex eigenvalues, obtained by linearizing the map (29) at (0, 0)

$$\begin{aligned} \lambda _{1,2}=\frac{m(\beta )\pm \iota \sqrt{4n(\beta )-(m(\beta ))^{2}}}{2} \end{aligned}$$

with $|\lambda _{1,2}|=\sqrt{n(\beta )}$, followed by the transversality condition

$$\begin{aligned} \left( \frac{d|\lambda _{1,2}|}{d\beta }\right) _{\beta =\beta _1=\frac{A-1}{B-2}}=\frac{-1}{2\sqrt{n\left( \frac{A-1}{B-2}\right) }}\ne 0. \end{aligned}$$

It is required to verify nondegeneracy condition ${{\lambda ^{j}}_{1,2}}\ne 1, j=1,2,3,4$ which is equivalent to $m(\beta )\ne 0,-1$ i.e. $A\ne \frac{4}{B-1}$ and $A\ne \frac{B+2}{B-1}$.

Now we assume an invertible matrix

$$\begin{aligned} T=\left[ \begin{array}{cc} a_{12} &{} 0 \\ M-a_{11} &{} N \end{array}\right] \end{aligned}$$

$M=\frac{m(\beta )}{2}$, $N=\sqrt{4n(\beta )-(m(\beta ))^2}$.

The map (29) becomes

$$\begin{aligned}&\left( \begin{array}{c} X \\ Y \end{array} \right) \rightarrow \left( \begin{array}{cc} M &{} -N \\ N &{} M \end{array} \right) \left( \begin{array}{c} X \\ Y \end{array} \right) + \left( \begin{array}{c} F_1(X,Y) \\ G_{1}(X,Y) \end{array} \right) \nonumber \\&F_{1}(X,Y) = k_{11}X^2+K_{22}X^3+k_{33}XY+k_{44}X^2Y+O(|X,Y|^4) \nonumber \\&G_{1}(X,Y) = e_{11}X^2+e_{22}Y^2+e_{33}XY+e_{44}X^2Y+e_{55}X^3+O(|X,Y|^4) ,\qquad \end{aligned}$$

(30)

$k_{11}=a_{12}a_{13}(M-a_{11})+a_{12}^2a_{14}$, $k_{22}=a_{12}^{2}a_{15}(M-a_{11})$, $k_{33}=-a_{12}a_{13}N$, $k_{44}=-a_{12}^2a_{15}N$, $e_{11}=a_{12}b_{13}(M-a_{11})+a_{12}^2b_{14}+b_{15}(M-a_{11})^2+a_{12}b_{17}(M-a_{11})^2$, $e_{22}=(b_{15}+a_{12}b_{17})N^2$, $e_{33}=-N(a_{12}b_{13}+2b_{15}(M-a_{11})+2a_{12}b_{17}(M-a_{11}))$, $e_{44}=-a_{12}^2b_{16}N$ and $e_{55}=b_{16}a_{12}^2(M-a_{11})$.

It is easily noticed that (30) is exactly in the form of center manifold, the non-degeneracy condition for the Neimark–Sacker bifurcation is given by

$$\begin{aligned} {\hat{\beta }}=-Re\left( \frac{(1-2\lambda ){\bar{\lambda }}^{2}}{1-\lambda }\Phi _{11}\Phi _{20}\right) -\frac{1}{2}|\Phi _{11}|^{2}-|\Phi _{02}|^{2}+Re({\bar{\lambda }}\Phi _{21}) \end{aligned}$$

(31)

where

$$\begin{aligned} \Phi _{20}= & {} \frac{1}{4}\left[ k_{11}+e_{33}+i(e_{11}-e_{22}-k_{33})\right] _{(0,0)},\\ \Phi _{11}= & {} \frac{1}{2}\left[ k_{11}+i(e_{11}+e_{22})\right] _{(0,0)},\\ \Phi _{02}= & {} \frac{1}{4}\left[ k_{11}-e_{33}+i(e_{11}-e_{22}+k_{33})\right] _{(0,0)},\\ \Phi _{21}= & {} \frac{1}{8}\left[ 3k_{22}+e_{44}+i(3e_{55}-k_{44})\right] _{(0,0)}. \end{aligned}$$

Thus, the aforementioned argument provides following theorem for the occurrence of Neimark–Sacker bifurcation [21, 26, 33].

Theorem 7

The map (5) undergoes Neimark–Sacker bifurcation if the both conditions $\beta \ne 3-A$ and $\beta \ne 4-A$ holds and ${\hat{\beta }}\ne 0$ at fixed point ${E_{(xy)_1}}$. Moreover, if ${\hat{\beta }}<0$ $( {\hat{\beta }}>0)$ then a unique closed invariant curve bifurcates at $\beta =\beta _1=\frac{A-1}{B-2}$ which is supercritical (subcritical) and asymptotically stable (unstable).

4.5 Bifurcation around unique positive fixed point

Theorem 8

The map (5) undergoes fold bifurcation at bifurcation parameter $\alpha =\frac{\left( p-q(1+\delta )\right) ^2}{4q^{2}}$ around unique positive fixed point ${\bar{E}}({\bar{x}},{\bar{y}})$.

Proof

The eigenvalues of the Jacobian J at positive fixed point ${\bar{E}}$ are $\lambda _{1}=1$ and $|\lambda _{2}|\ne 1$ for $\alpha =\frac{\left( p-q(1+\delta )\right) ^2}{4q^{2}}$.

The map (5) gives

$$\begin{aligned} \left( \begin{array}{c} u \\ v \end{array}\right) \rightarrow \left\{ \begin{array}{l} a_{11}u+a_{12}v+a_{13}\mu +a_{14}uv+a_{15}\mu u+a_{16}u^2+a_{17}u^2v+O(|u,v|^4)\\ b_{11}u+b_{12}v+b_{13}uv+b_{14}v^2+b_{15} u^2+b_{16}uv^2+b_{17}u^2v+O(|u,v|^4) \end{array} \right. \end{aligned}$$

(32)

where $a_{11}={\bar{x}}\left( \frac{p{\bar{y}}}{(\gamma +{\bar{x}})^2}+\frac{\alpha ^*}{(\delta +{\bar{x}})^2}-2\right) -\frac{p{\bar{y}}}{\gamma +{\bar{x}}}+\frac{2\delta +2{\bar{x}}-\alpha ^*}{\delta +{\bar{x}}}$, $a_{12}=\frac{-p{\bar{x}}}{\gamma +{\bar{x}}}$, $a_{13}=\frac{-{\bar{x}}}{\delta +{\bar{x}}}$, $a_{14}=\frac{-p\gamma }{(\gamma +{\bar{x}})^2}$, $a_{15}=\frac{-\delta }{(\delta +{\bar{x}})^2}$, $a_{16}=\frac{\alpha ^*\delta }{(\delta +{\bar{x}})^3}+\frac{p\gamma {\bar{y}}}{(\gamma +{\bar{x}})^3}-1$, $a_{17}=\frac{p\gamma }{(\gamma +{\bar{x}})^3}$, $b_{11}=\frac{q\beta ({\bar{y}})^2}{(\gamma +{\bar{x}})^2}$, $b_{12}=1+\beta \left( 1-\frac{2q {\bar{y}}}{\gamma +{\bar{x}}}\right)$, $b_{13}=\frac{2q\beta {\bar{y}}}{(\gamma +{\bar{x}})^2}$, $b_{14}=-\frac{q\beta }{\gamma +{\bar{x}}}$, $b_{15}=-\frac{q\beta ({\bar{y}})^2}{(\gamma +{\bar{x}})^3}$, $b_{16}=\frac{q\beta }{(\gamma +{\bar{x}})^2}$, $b_{17}=-\frac{2q\beta {\bar{y}}}{(\gamma +{\bar{x}})^3}.$

Constructing an invertible martix

$$\begin{aligned} T=\left( \begin{array}{ccc} a_{12} &{} a_{12} &{} 0 \\ -(1+a_{11}) &{} \lambda _{2}-a_{11} &{} 0 \\ 0 &{} 0 &{} a_{13} \end{array}\right) \end{aligned}$$

and linearizing the map (32) at (0, 0) as

$$\begin{aligned}&\left( \begin{array}{c} X \\ Y \\ w \end{array}\right) \rightarrow \left( \begin{array}{ccc} 1 &{} 1 &{} 0\\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \end{array}\right) \left( \begin{array}{c} X \\ Y \\ w \end{array}\right) + \left( \begin{array}{c} F_{1}(X,Y,w) \\ G_{1}(X,Y,w) \\ 0 \end{array}\right) , \nonumber \\&F_{1}(X, Y) = k_{1}X^2+K_{2}wX+k_{3}wY+k_{4}XY+k_{5}Y^2+O(|X,Y|^3) \nonumber \\&G_{1}(X,Y)= e_{1}X^2+e_{2}XY+e_{3}Y^2+O(|X,Y|^3) \end{aligned}$$

(33)

$k_{1}=a_{12}^2a_{16}-a_{12}a_{14}(1+a_{11})$, $k_{2}=k_{3}=a_{12}a_{13}a_{15}$, $k_{4}=a_{12}a_{14}((\lambda _{2}-a_{11})- (1+a_{11}))+2a_{12}^2a_{16}$, $k_{5}=a_{12}a_{14}(\lambda _{2}-a_{11})+a_{12}^2a_{16}$, $e_{1}=a_{12}^2b_{15}+b_{14}(1+a_{11})^2-a_{12}b_{13}(1+a_{11})$, $e_{2}=a_{12}b_{13}\left( (\lambda _{2}-a_{11})-(1+a_{11})\right) +2a_{12}^2b_{15}-2b_{14}(1+a_{11})(\lambda _{2}-a_{11})$, and $e_{3}=a_{12}b_{13}(\lambda _{2}-a_{11})+a_{12}^2b_{15}+(\lambda _{2}-a_{11})^2.$

A one-parameter family of equations on a center manifolds gives stability of $(X,Y)=(0,0)$ around $w=0$, which can be written as

$$\begin{aligned} Z^{c}(0)=\{(X,Y,w)\in R^{3}| Y=S(x,w), S(0,0)=0, DS(0,0)=0\}, \end{aligned}$$

for small X and w. Further, consider a center manifold

$$\begin{aligned} S(X,w)=S_{1}w^{2}+S_{2}w X+S_{3}X^{2}+O(|X,w|^{3}). \end{aligned}$$

(34)

Then

$$\begin{aligned} \kappa (S(X,w),w)= & {} S(X+w+F_{1}(X,S(X,w),w))-\lambda _{2}S(X,w)\nonumber \\&-G_{1}(X,S(X,w),w)=0. \end{aligned}$$

(35)

From (34) and (35), we get $S_{1}=\frac{e_{1(1+\lambda _{2})}}{(1-\lambda _{2})^3}$, $S_{2}=\frac{-e_{1}}{(1-\lambda _{2})^2}$ and $S_{3}=\frac{e_{1}}{1-\lambda _{2}}$.

Thus the map restricted to the center manifold is given as

$$\begin{aligned}&X\sim \widetilde{F_{1}}(Y,w)=X+w+k_{1}X^2+k_{2}wX\\&+k_{3}w\left( S_{1}w^{2}+S_{2}w X+S_{3}X^{2}\right) +O(|X,w|^4). \end{aligned}$$

We have $\widetilde{F_{1}}(0,0)=0$, $\frac{\partial \widetilde{F_{1}}}{\partial X}(0,0)=1$, $\frac{\partial \widetilde{F_{1}}}{\partial w}(0,0)=1$, $\frac{\partial ^2\widetilde{F_{1}}}{\partial X^2}(0,0)=2k_{1}\ne 0$.

Therefore the map (5) undergoes the fold bifurcation around the bifurcation parameter $\alpha =\frac{\left( p-q(1+\delta )\right) ^2}{4q^{2}}$ at the positive fixed point ${\bar{E}}({\bar{x}},{\bar{y}})$ (see also [8, 26]). $\square$

Theorem 9

The Jacobian of the map (5) has eigenvalues 1 and -1 under the conditions $\beta =3-2{\bar{x}}-\frac{p\gamma }{q(\gamma +{\bar{x}})}-\frac{\alpha \delta }{(\delta +{\bar{x}})^2}$ and $2{\bar{x}}+\frac{p}{q}+\frac{\alpha \delta }{(\delta +{\bar{x}})^2}$=1 at positive fixed point ${\bar{E}}({\bar{x}},{\bar{y}})$. Therefore, the fold-flip bifurcation may occur for these conditions at ${\bar{E}}$.

5 Bifurcation of codimension 2

5.1 Bogdanov–Takens bifurcation at unique fixed point ${\bar{E}}({\bar{x}},{\bar{y}})$

From the Sect. 3 and Table 1, when $\left( 1-\delta -\frac{p}{q}\right) ^2=4\delta \left( \frac{p}{q}+\frac{\alpha }{\delta }-1\right)$, the map (5) has an unique fixed point ${\bar{E}}({\bar{x}},{\bar{y}})$. And $J({\bar{E}})$ has an eigenvalue 1 with multiplicity 2 if $\alpha =\frac{\left( p-q(1+\delta )\right) ^2}{4q^{2}}$ and $\beta =\delta +\frac{p}{q}-\frac{4\alpha \delta q^2}{(p-q(1+\delta ))^2}+\frac{2pq\gamma }{p+q(\delta -2\gamma -1)}$. Thus Bogdanov–Takens bifurcation may occur at ${\bar{E}}$.

First we discuss some results about Bogdanov–Takens bifurcation for diffeomorphisms (see Yagasaki [51], Kuznetsov [33], Broer et al. [7]).

For an analytic family of planar diffeomorphisms $G_{\xi }:{\mathbb {R}}^2\rightarrow {\mathbb {R}}^2$, $G_{\xi }$ has a fixed point $u=0$ at $\xi =0$ such that the Jacobian matrix $D_{u}G_{0}(0)$ has two repeated unit eigenvalues but not identity (1:1 resonance); that is, $D_{u}G_{0}(0)$ has the nilpotent form

$$\begin{aligned} D_{u}G_{0}(0)=\left( \begin{array}{cc} 1 &{} 1 \\ 0 &{} 1 \end{array}\right) . \end{aligned}$$

In suitable coordinates, $G_{\xi }$ has the normal form

$$\begin{aligned} G_{\xi }(u)=\left( \begin{array}{cc} 1 &{} 1 \\ 0 &{} 1 \end{array}\right) u+ \left( \begin{array}{c} g_{1}(u,\xi ) \\ g_{2}(u,\xi ) \end{array} \right) + O(|u|^3), \end{aligned}$$

(36)

where $u=(u_{1},u_{2})^T$, $\xi =(\xi _{1},\xi _{2})$ and

$$\begin{aligned} \begin{array}{l} g_{1}(u,\xi )=a_{00}(\xi )+a_{10}(\xi )u_{1}+a_{01}(\xi )u_{2}+\frac{1}{2}a_{20}(\xi )u_{1}^2+a_{11}(\xi )u_{1}u_{2}+\frac{1}{2}a_{02}(\xi )u_{2}^2 \\ g_{2}(u,\xi )=b_{00}(\xi )+b_{10}(\xi )u_{1}+b_{01}(\xi )u_{2}+\frac{1}{2}b_{20}(\xi )u_{1}^2+b_{11}(\xi )u_{1}u_{2}+\frac{1}{2}b_{02}(\xi )u_{2}^2 \\ \end{array} \end{aligned}$$

(37)

with $a_{00}(0)=a_{10}(0)=a_{01}(0)=b_{00}(0)=b_{10}(0)=b_{01}(0)=0$.

The diffeomorphism (36) can be approximated by the time-one flow of the planar vector field, which has a singularity with nilpotent linear part. Here is the following lemma refereed from Yagasaki [51], [see also Kuznetsov [33] and Broer et al. [7]].

Lemma 2

The diffeomorphism (36) can be written for sufficiently small $|\xi |$ as follows:

$$\begin{aligned} u\mapsto \omega _{\xi }^{1}(u)+O((|u|)^3), \end{aligned}$$

(38)

where $\omega _{\xi }^{1}(u)$ is the time–one flow of the following planar vector field

$$\begin{aligned} {\dot{u}}=\left( \begin{array}{cc} 0 &{} 1 \\ 0 &{} 0 \end{array} \right) u+\left( \begin{array}{c} f_{1}(u,\xi ) \\ f_{2}(u,\xi ) \end{array}\right) \end{aligned}$$

(39)

and

$$\begin{aligned} \begin{array}{lll} f_{1}(u,\xi )=c_{00}(\xi )+c_{10}(\xi )u_{1}+c_{01}(\xi )u_{2}+\frac{1}{2}c_{20}(\xi )u_{1}^2+c_{11}(\xi )u_{1}u_{2}+\frac{1}{2}c_{02}(\xi )u_{2}^2 \\ f_{2}(u,\xi )=d_{00}(\xi )+d_{10}(\xi )u_{1}+d_{01}(\xi )u_{2}+\frac{1}{2}d_{20}(\xi )u_{1}^2+d_{11}(\xi )u_{1}u_{2}+\frac{1}{2}d_{02}(\xi )u_{2}^2 \\ \end{array}\qquad \end{aligned}$$

(40)

in which the coefficients can be expressed by those in (37) as follows

$$\begin{aligned} c_{00}(\xi )= & {} a_{00}(\xi )-\left( \frac{1}{2}a_{10}(\xi )-\frac{1}{3}b_{10}(\xi )\right) a_{00}(\xi )\\&-\left( \frac{1}{2}-\frac{1}{3}a_{10}(\xi )+\frac{1}{2}a_{01}(\xi )+\frac{1}{4}b_{10}(\xi )-\frac{1}{3}b_{01}(\xi )\right) b_{00}(\xi ),\\ c_{10}(\xi )= & {} a_{10}(\xi )-\frac{1}{2}b_{10}(\xi ),\\ c_{01}(\xi )= & {} a_{01}(\xi )-\frac{1}{2}a_{10}(\xi )+\frac{1}{3}b_{10}(\xi )-\frac{1}{2}b_{01}(\xi ),\\ c_{20}(\xi )= & {} a_{20}(\xi )-\frac{1}{2}b_{20}(\xi ),\\ c_{11}(\xi )= & {} a_{11}(\xi )-\frac{1}{2}a_{20}(\xi )+\frac{1}{3}b_{20}(\xi )-\frac{1}{2}b_{11}(\xi ), \\ c_{02}(\xi )= & {} a_{02}(\xi )+\frac{1}{6}a_{20}(\xi )-a_{11}(\xi )-\frac{1}{6}b_{20}(\xi )+\frac{2}{3}b_{11}(\xi )-\frac{1}{2}b_{02}(\xi ),\\ d_{00}(\xi )= & {} b_{00}(\xi )-\frac{1}{2}b_{10}(\xi )a_{00}(\xi )+\left( \frac{1}{3}b_{10}(\xi )-\frac{1}{2}b_{01}(\xi )\right) b_{00}(\xi ), \\ d_{10}(\xi )= & {} b_{10}(\xi ), \\ d_{01}(\xi )= & {} b_{01}-\frac{1}{2}b_{10}(\xi ), \\ d_{20}(\xi )= & {} b_{20}(\xi ), \\ d_{11}(\xi )= & {} b_{11}-\frac{1}{2}b_{20}(\xi ), \\ d_{02}(\xi )= & {} b_{02}(\xi )+\frac{1}{6}b_{20}(\xi )-b_{11}(\xi ) \end{aligned}$$

In particular, $c_{00}(\xi )=c_{10}(\xi )=c_{01}(\xi )=d_{00}(\xi )=d_{10}(\xi )=d_{01}(\xi ).$

For certain nondegeneracy and transversality conditions, the system (39) can be written as versal unfolding of a Bogdanov–Takens singularity of codimension 2 by a series of near-identity transformations. Subsequently, the diffeomorphism (36) can be transformed to the versal unfolding of a Bogdanov–Takens bifurcation of codimension 2. See in details (Lemma 3.2 and proposition in Yagasaki [51]).

Lemma 3

Consider that the non-degeneracy conditions

$$\begin{aligned} \begin{array}{cc} d_{20}(0)\ne 0 (i.e. b_{20}(0)\ne 0) \\ c_{20}(0)+d_{11}(0)\ne 0 (i.e.a_{20}(0)+b_{11}(0)-b_{20}(0)\ne 0) \end{array} \end{aligned}$$

(41)

are satisfied, then under analytic near-identity transformations of coordinates and scaling of time (40) (and in turn system (37)) converts as (up to second order of coordinates)

$$\begin{aligned} \dot{x_{1}}=x_{2} {} and \dot{x_{2}}=\eta _{1}(\xi )+\eta _{2}(\xi )x_{1}+x_{1}^{2}+sx_{1}x_{2} \end{aligned}$$

(42)

where

$$\begin{aligned} s=sign\left[ b_{20}(0)\left( a_{20}(0)+b_{11}(0)-b_{20}(0)\right) \right] =\pm 1, \end{aligned}$$

and $\eta _{1}(\xi )$ and $\eta _{2}(\xi )$ can be expressed by the coefficients in (40) [and in turn by those in (37)] as given as:

$$\begin{aligned} \eta _{1}(\xi )= & {} \frac{8\zeta _{0}^{4}}{b_{20}^{3}(0)}\zeta _{1}(\xi )-\frac{8\zeta _{0}^{3}}{b_{20}^{3}(0)}\zeta _{2}(\xi )\zeta _{3}(\xi )+ \frac{4\zeta _{0}^{2}}{b_{20}^{2}(0)}\zeta _{2}^{2}(\xi ),\\ \eta _{2}(\xi )= & {} \frac{4\zeta _{0}^{2}}{b_{20}^{2}(0)}\zeta _{4}(\xi )-\frac{4\zeta _{0}}{b_{20}(0)}\zeta _{2}(\xi ) , \end{aligned}$$

in which

$$\begin{aligned} \zeta _{0}(\xi )= & {} a_{20}(0)+b_{11}(0)-b_{20}(0), \\ \zeta _{1}(\xi )= & {} b_{00}(\xi )+\frac{1}{2}\left( \frac{1}{6}b_{20}(0)-b_{11}(0)+b_{02}(0)\right) a_{00}^{2}(\xi ) \\&-\left( \frac{1}{6}a_{20}(0)-a_{11}(0)+a_{02}(0)-\frac{1}{12}b_{20}(0)+\frac{1}{6}b_{11}(0)\right) a_{00}(\xi )b_{00}(\xi ) \\&+\frac{1}{2}\left( \frac{1}{6}a_{20}(0)-a_{11}(0)+a_{02}(0)-\frac{1}{8}b_{20}(0)+\frac{5}{12}b_{11}(0)-\frac{1}{4}b_{02}(0)\right) b_{00}^{2}(\xi ) \\&-a_{00}(\xi )b_{01}(\xi )-\frac{1}{2}a_{10}(\xi )b_{00}(\xi )+a_{01}(\xi )b_{00}(\xi )+\frac{5}{12}b_{00}(\xi )b_{10}(\xi )-\frac{1}{2}b_{00}(\xi )b_{01}(\xi ),\\ \zeta _{2}(\xi )= & {} a_{10}(\xi )-b_{10}(\xi )+b_{01}(\xi )+\left( \frac{1}{2}a_{20}(0)-a_{11}(0)-\frac{1}{2}b_{20}(0)+\frac{3}{2}b_{11}(0)-b_{02}(0) \right) a_{00}(\xi ) \\&-\left( \frac{1}{12}a_{20}(0)+\frac{1}{2}a_{11}(0)-a_{02}(0)-\frac{1}{12}b_{20}(0)+\frac{1}{12}b_{11}(0)\right) b_{00}(\xi )\\ \zeta _{3}(\xi )= & {} b_{10}(\xi )+\left( \frac{1}{2}b_{20}(0)-b_{11}(0)\right) a_{00}(\xi )-\left( \frac{1}{2}a_{20}(0)-a_{11}(0)-\frac{1}{12} b_{20}(0)\right) b_{00}(\xi ), \\ \zeta _{4}(\xi )= & {} b_{10}(\xi )+\left( \frac{1}{2}b_{20}(0)-b_{11}(0)\right) a_{00}(\xi )\\&+\left( \frac{1}{2}a_{20}(0)-a_{11}(0)-\frac{3}{4}b_{20}(0)+2b_{11}(0)-b_{02}(0)\right) b_{00}(\xi ). \end{aligned}$$

Furthermore, if the transversality condition

$$\begin{aligned} det D_{\xi }\eta (0)\ne 0 \end{aligned}$$

(43)

is satisfied, then system (42) is the versal unfolding of the Bogdanov–Takens singularity of codimension 2.

Theorem 10

The diffeomorphism (5) undergoes Bogdanov–Takens bifurcation around the unique fixed point ${\bar{E}}({\bar{x}},{\bar{y}})$ varies as $(\alpha ,\beta )$ where $\alpha =\frac{\left( p-q(1+\delta )\right) ^2}{4q^{2}}$ and $\beta =\delta +\frac{p}{q}-\frac{4\alpha \delta q^2}{(p-q(1+\delta ))^2}+\frac{2pq\gamma }{p+q(\delta -2\gamma -1)}$.

Proof

The unique interior fixed point ${\bar{E}}({\bar{x}},{\bar{y}})$ of map (5) is a nilpotent fixed point when $\alpha =\frac{\left( p-q(1+\delta )\right) ^2}{4q^{2}}$ and $\beta =\delta +\frac{p}{q}-\frac{4\alpha \delta q^2}{(p-q(1+\delta ))^2}+\frac{2pq\gamma }{p+q(\delta -2\gamma -1)}$, then the Jacobian $J({\bar{E}})$ has an eigenvalue 1 of multiplicity 2.

Fig. 1

Stable time series at $\beta =0.25$

Fig. 2

Bifurcation diagram with respect to $\beta$ at $\alpha =0.095$

Fig. 3

Maximal Lyaupnov exponent with respect to $\beta$

Fig. 4

Neimark–Sacker bifurcation diagram with respect to $\beta$

Fig. 5

Phase portrait corresponding to Fig. 4 at $\beta =0.24$

Fig. 6

Phase portrait corresponding to Fig. 4 at $\beta =0.23$

Fig. 7

Phase portrait corresponding to Fig. 4 at $\beta =0.25$

Fig. 8

Bogdanov–Takens bifurcation with respect to $(\alpha ,\beta )$

For existence of Bogdanov–Takens bifurcation, we have to determine the bifurcation curves of diffeomorphism (5). Let us choose two parameters $\alpha$ and $\beta$ as bifurcation parameters and taking unfolding map

$$\begin{aligned} G_{\xi }:\left( \begin{array}{c} x \\ y \\ \end{array} \right) \rightarrow \left[ \begin{array}{c} x+x\left( 1-x-\frac{py}{\gamma +x}-\frac{\alpha _{0}+\xi _{1}}{\delta +x}\right) \\ y+(\beta _{0}+\xi _{2}) y\left( 1-\frac{q y}{\gamma +x}\right) \end{array}\right] . \end{aligned}$$

(44)

Let $u=x-{\bar{x}}$, $v=y-{\bar{y}}$ and two bifurcation parameter $\xi _{1}=\alpha -\alpha _{0}$, $\xi _{2}=\beta -\beta _{0}$, where $\alpha _{0}=\frac{\left( p-q(1+\delta )\right) ^2}{4q^{2}}$ and $\beta _{0}=\delta +\frac{p}{q}-\frac{4\alpha \delta q^2}{(p-q(1+\delta ))^2}+\frac{2pq\gamma }{p+q(\delta -2\gamma -1)}$ and $\xi _{1}$, $\xi _{2}$ are in small neighborhood of origin (0, 0).

Now, Taylor expansion of the map (44) in the small neighborhood of the origin (0, 0) gives

$$\begin{aligned} \left( \begin{array}{c} u \\ v \end{array}\right) \rightarrow \left\{ \begin{array}{l} k_{1}(\xi )u+5k_{2}(\xi )v+k_{3}(\xi )+k_{4}(\xi )uv+k_{5}(\xi )u^2+k_{6}(\xi )\\ \quad +\chi _{i}(\xi _{1})+O(|u,v|^3)\\ e_{1}{(\xi )}u+e_{2}(\xi )v+e_{3}(\xi )+e_{4}(\xi )uv+e_{5}(\xi ) u^2+e_{6}(\xi )v^2\\ \quad +\chi _{j}(\xi _{2})+O(|u,v|^3) \end{array} \right. \end{aligned}$$

(45)

where $k_{1}(\xi )=2-2{\bar{x}}-\frac{\delta (\alpha _0+\xi _{1})}{(\delta +{\bar{x}})^2}-\frac{p\gamma {\bar{y}}}{(\gamma +{\bar{x}})^2}$, $k_{2}(\xi )=\frac{-p{\bar{x}}}{\gamma +{\bar{x}}}$, $k_{3}(\xi )=\frac{-{\bar{x}}\xi _{1}}{\delta +{\bar{x}}}$, $k_{4}(\xi )=\frac{-p\gamma }{(\gamma +{\bar{x}})^2}$, $k_{5}(\xi )=\frac{\delta (\alpha _{0}+\xi _{1})}{(\delta +{\bar{x}})^3} +\frac{p\gamma {\bar{y}}}{(\gamma +{\bar{x}})^3}-1$, $k_{6}(\xi )=0$, $e_{1}(\xi )=\frac{q(\beta _{0}+\xi _{2}) {\bar{y}}^2}{(\gamma +{\bar{x}})^2}$, $e_{2}(\xi )=1+(\beta _{0}+\xi _{2})\left( 1-\frac{2q {\bar{y}}}{\gamma +{\bar{x}}}\right)$, $e_{3}(\xi )={\bar{y}}\xi _{2}$, $e_{4}(\xi )=\frac{2q(\beta _{0}+\xi _{2}){\bar{y}}}{(\gamma +{\bar{x}})^2}$, $e_{5}(\xi )=-\frac{q(\beta _{0}+\xi _{2}){\bar{y}}^{2}}{(\gamma +{\bar{x}})^3}$, $e_{6}(\xi )=-\frac{q(\beta _{0}+\xi _{2}){\bar{y}}}{\gamma +{\bar{x}}}$ and $\chi _{i}(\xi )$, $\chi _{j}(\xi )$ $(i=j=1,2,3)$ are the functions of at least second order in $\xi _{1}$, $\xi _{2}$.

Using affine translation $k_{1}(\xi )u=X$ and $e_{1}(\xi )u+e_{2}(\xi )v=Y$ and taking series of transformations, the equation (45) becomes

$$\begin{aligned} \left( \begin{array}{c} X \\ Y \end{array}\right) \rightarrow \left\{ \begin{array}{l} X+Y+c_{1}(\xi )+c_{2}(\xi )XY+c_{3}(\xi )X^{2}+O(|X,Y|^3)\\ Y+c_{4}(\xi )+c_{5}(\xi )XY+c_{6}(\xi ) X^2+c_{7}(\xi )Y^2+O(|X,Y|^3) \end{array} \right. \end{aligned}$$

(46)

where $c_{1}(\xi )=k_{3}(\xi )$, $c_{2}(\xi )=\frac{e_{2}k_{4}}{(k_{1}e_{2}-k_{2}e_{1})}$, $c_{3}(\xi )=\frac{e_{2}(e_{2}k_{5}-e_{1}e_{4}k_{2})}{(k_{1}e_{2}-k_{2}e_{1})^2}$, $c_{4}(\xi )=\frac{k_{2}e_{3}\xi _{2}}{e_{2}}$, $c_{5}(\xi )=\frac{(e_{2}e_{4}-2e_{1}k_{2}^2)}{e_{2}(k_{1}e_{2}-k_{2}e_{1})}$, $c_{6}(\xi )=\frac{(e_{2}^{2}e_{5}-e_{1}e_{2}e_{4}+e_{1}^{2}k_{2}^{2})}{(k_{1}e_{2}-k_{2}e_{1})^2}$ and $c_{7}(\xi )=\frac{k_{2}^{2}}{e_{2}^{2}}.$

Rewriting the above map (46) in the following normal form,

$$\begin{aligned} G_{\xi }\left( \begin{array}{c} X \\ Y \end{array} \right) =\left( \begin{array}{cc} 1 &{} 1 \\ 0 &{} 1 \\ \end{array} \right) \begin{array}{c} X \\ Y \end{array}+ \left( \begin{array}{c} F_{1}(X,Y,\xi ) \\ F_{2}(X,Y,\xi ) \end{array} \right) +O(|X,Y,\xi |^3) \end{aligned}$$

(47)

where

$$\begin{aligned} F_{1}(X,Y,\xi ) = a_{00}(\xi )+a_{10}(\xi )X+a_{01}(\xi )Y+\frac{1}{2}a_{20}(\xi )X^2+a_{11}(\xi )XY+\frac{1}{2}a_{02}(\xi )y^2, \\ F_{2}(X,Y,\xi ) = b_{00}(\xi )+b_{10}(\xi )X+b_{01}(\xi )Y+\frac{1}{2}b_{20}(\xi )X^2+b_{11}(\xi )XY+\frac{1}{2}b_{02}(\xi )y^2. \end{aligned}$$

On comparing the equation (46) and (47), we get $a_{00}(\xi )=k_{3}(\xi )$, $a_{10}(\xi )=a_{01}(\xi )=0$, $a_{20}(\xi )=2c_{3}(\xi )$, $a_{11}(\xi )=c_{2}(\xi )$, $a_{02}(\xi )=0$, $b_{00}(\xi )=c_{4}(\xi )$, $b_{10}(\xi )=b_{01}=0$, $b_{20}(\xi )=2c_{6}(\xi )$, $b_{11}(\xi )=c_{5}(\xi )$ and $b_{02}(\xi )=2c_{7}(\xi )$.

From lemma 3, the non-degeneracy conditions

$$\begin{aligned} d_{20}(0)=b_{20}(0)=2c_{6}(0)\ne 0 \end{aligned}$$

and

$$\begin{aligned} c_{20}(0)+d_{11}(0)=a_{20}(0)+b_{11}(0)-b_{20}(0)=2c_{3}(0)+c_{5}(0)-2c_{5}(0)\ne 0, \end{aligned}$$

the transversality condition

$$\begin{aligned} det D_{\xi }\eta (0)= & {} \frac{-32{\bar{x}}\beta _{0}^5}{(\delta +{\bar{x}})b_{20}^{4}(0)}\left[ \frac{{\bar{x}}\beta _{0}(\frac{1}{2}b_{20}(0)-b_{11}(0))}{(\delta +{\bar{x}})b_{20}(0)}\right. \\&\left. -\left( \frac{1}{2}a_{20}(0)-a_{11}(0)-\frac{1}{2}b_{20}(0)+\frac{3}{2}b_{11}(0)-b_{02}(0)\right) {\bar{y}}\right] \ne 0{.} \end{aligned}$$

By proposition in [51] and corresponding result in Broer et al. [7, 8] and Kuznetsov [33], the diffeomorphism map (5) undergoes Bogdanov–Takens bifurcation in a small neighborhood of the unique second fixed positive point ${\bar{E}}({\bar{x}},{\bar{y}})$ around the two bifurcation parameters $\alpha =\frac{\left( p-q(1+\delta )\right) ^2}{4q^{2}}$ and $\beta =\delta +\frac{p}{q}-\frac{4\alpha \delta q^2}{(p-q(1+\delta ))^2}+\frac{2pq\gamma }{p+q(\delta -2\gamma -1)}$. $\square$

6 Numerical simulation

In order to substantiate the obtained results and explore the complex dynamics in the map (5), the numerical simulation is performed for the following set of parameters [22]:

$$\begin{aligned} p=0.40,~~q=1.0,~~ \alpha =0.10,~~ \gamma =0.10,~~ \delta =0.05,~~ \beta =0.25 {.} \end{aligned}$$

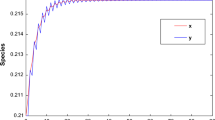
For these set of parameters, the stability conditions of the fixed point ${E_{(xy)_1}(x_1^{*},y_1^{*})}$, mentioned in Table 5, are satisfied. Figure 1 shows the stable dynamics in the system (5). It confirms that both species coexist and converge to fixed point ${E_{(xy)_1}}(0.35,0.45)$.

For these parameters, the results of first part of Theorem 6 holds i.e. $\varrho _{1}=-3.13426$, $\varrho _{2}=2741.9$, hence the system (5) undergoes flip bifurcation at $E_{xy}$ and as $\varrho _{2}>0$ which shows period-2 point and its stability. Figure 2 gives bifurcation diagram for the parameter $\beta$ at $\alpha =0.095$ (without changing other parameters). The system (5) exhibits flip bifurcation followed by chaos (period doubling route to chaos) at the parameter $\beta$. The system shows a stable window upto $\beta =2.3$, followed by a cascade of period doubling. Further a dense chaotic region is occurred for $\beta \in (2.862,3.012)$ along with intermittent quasi periodic window at (2.94, 2.952) which ends to a stable window beyond $\beta =3.012$. The maximal Lyapunov exponent (MLE) for the same values is plotted in Fig. 3. The positive value of Lyapunov exponent confirms the presence of chaos in the system.

Further for substantiating the results of theorem 6(ii), we choose the new set of parameters

$$\begin{aligned} p=0.9,~~q=2.0,~~ \alpha =0.1695,~~ \gamma =0.10,~~ \delta =0.3 \end{aligned}$$

The value of nondegeneracy condition for Neimark–Sacker bifurcation is ${\hat{\beta }}=-0.13563<0$. According to theorem 7, the fixed point ${E_{(xy)_1}}$ is stable when $\beta <\beta _{1}$, ${E_{(xy)_1}}$ loses its stability and becomes unstable, a closed invariant curve appears when $\beta >\beta _{1}$. And ${\hat{\beta }}<0$, supercritical NSB is occurred. The bifurcation diagram is plotted in $(\beta , x)$ plane at $\beta _{1}=0.245$ in Fig. 4, a closed invariant curve appeared. The corresponding phase portraits are given in Figs. 5, 6 and 7.

Now we take a new set of parameters

$$\begin{aligned} p=0.403,~~q=2.2~~ \gamma =0.10,~~ \delta =0.055,~~\alpha =0.19,~~ \beta =0.0993. \end{aligned}$$

The unique fixed point ${\bar{E}}$ has unit eigenvalues with multiplcity 2 for two bifurcation parameters $\alpha$ and $\beta$. The map (5) satisfies non-degeneracy conditions and transversality condition for Bogdanov–Takens bifurcation i.e.

$$\begin{aligned} d_{20(0)}=b_{20}(0)=-0.15229\ne 0~~ and ~~ a_{20}(0)+b_{11}(0)-b_{20}(0)=0.493912\ne 0 \end{aligned}$$

and

$$\begin{aligned} Det_{\xi }\zeta (0)=321.980659\ne 0 \end{aligned}$$

Thus, the map (5) undergoes Bogdanov–Takens bifurcation for parameters $(\alpha , \beta )$. The bifurcation diagram for B–T bifurcation is plotted in Fig. 8.

7 Conclusion

In this paper, the discretized form of a modified Leslie–Gower prey-predator model with Michaelis–Menten type harvesting in prey, has been studied. The continuous-time version of this model has been investigated by many researchers (see [12, 22, 32] ). Gupta and Chandra [22] explored local bifurcations, Hopf bifurcation, Saddle-node bifurcation, transcritical bifurcation and Bogdanov–Takens bifurcation in continuos-time model. In our work, we employ bifurcation theory and center manifold theory to exhibit various bifurcations of codimension 1 viz. Neimark–Sacker bifurcation, flip bifurcation, fold bifurcation, fold-flip bifurcation and transcritical bifurcation in the discrete-time model. By using results of Broer et al. [7, 8], Kuznetsov [33] and Yagasaki [51], the existence of Bogdanov–Takens bifurcation (bifurcation of codimension 2) in the discretized model is established under non-degeneracy and transversality conditions. The approximate expressions of bifurcation curves are also determined. The numerical simulation gives an extensive presentation about occurrence of different bifurcation and chaos.