1 Introduction

Consider the following VIE of the second kind

$$\begin{aligned} u(x)=f(x)+\lambda \int _a^x k(x,t,u(t))dt,\quad x\in I:=\left[ a, b\right] , \end{aligned}$$
(1.1)

where \(\lambda \) is a non-zero constant, the right hand side function f, and the kernel k are several times continuously differentiable with respect to x on the interval I, and u is the unknown solution of the problem.

VIEs of type (1.1) frequently appear in the diffusion problems [1], heat conduction [2], electroelastic [3], electromagnetics [4], and many other areas of science, engineering, economics, medicine, etc [5,6,7,8,9,10]. Consider, for instance, the problem of scattering of a electromagnetic wave with a kerr type nonlinear layer, which is an important problem in the nonlinear optics. Suppose that a plane wave of frequency \(\omega _0\) encounters a dielectric film of thickness \(d_0\) at angle \(\varphi \).The film is between two semi-infinite media and all the layers are assumed to be non-magnetic and homogenous. Considering a kerr-like nonlinearity inside the film, the permittivity function can be formulated as [8]

$$\begin{aligned} \varepsilon (y)=\left\{ \begin{aligned}&\varepsilon _1,\quad y>d,\\&\varepsilon _2 =\varepsilon _2^0+{\tilde{\varepsilon }}_2(y)+a_0E^2(y),\quad 0<y<d,\\&\varepsilon _3,\quad y<0, \end{aligned}\right. \end{aligned}$$

where \(a_0\), \(\varepsilon _1\), \(\varepsilon _2^0\), \(\varepsilon _3\) are real constants.

Utilizing the Maxwell equations, the problem can be modelled by the following nonlinear Helmholtz equations for each of the layers (\(j=1, 2, 3\)) [8, 11]

$$\begin{aligned} \frac{\partial ^2 {\tilde{E}}_j(x,y)}{\partial x^2}+\frac{\partial ^2 {\tilde{E}}_j(x,y)}{\partial y^2}+k_0^2\varepsilon _j{\tilde{E}}_j(x,y)=0,\quad j=1, 2, 3, \end{aligned}$$

where \(k_0^2=\omega _0^2/c^2\) and \({\tilde{E}}_j(x,y)\) is the time-independent part of the fields.

In order to investigate the field intensity inside the film, it is helpful to reduce the Helmholtz equation for the film (\(j=2\)) into a nonlinear VIE as follows [8]:

$$\begin{aligned} I(y)=f(y)+\int _0^y k\left( y,t,I(t)\right) I(t)dt, \end{aligned}$$

where

$$\begin{aligned} f(y)= & {} A\cos (2\kappa y)+B\sin (2\kappa y)+\frac{c_2}{2\kappa ^2}\sin ^2(\kappa y),\\ k\left( y,t,I(t)\right)= & {} -\frac{\sin (2\kappa (y-t))}{\kappa }\left( 8\pi ^2{\tilde{\varepsilon }}_2(t)+6\pi ^2a_0I(t)\right) \\&\quad -2\pi ^2\frac{\cos (2\kappa (y-t))-1}{\kappa ^2}\frac{d{\tilde{\varepsilon }}_2(t)}{dt},\\ \kappa ^2= & {} 4\pi ^2\varepsilon _2^0-p^2,\quad p=\sqrt{\varepsilon _1}k_0\sin (\varphi ). \end{aligned}$$

As another important problem, we present here the susceptible–infective–susceptible (SIS) epidemic model which can be formulated as a VIE. This formulation can be advantageous to analyse the reproduction number of the disease and the methods for disease control. Let I(t) and \(S(t)=1-I(t)\) be the fraction of the infective and susceptible individuals, respectively. Suppose that \(\lambda (I)\) is the contact rate, which represents the number of encounters per unit time between an infective person and another person in the population [12]. All the individuals that are not infective at time t belong to the susceptible population at this time. The rate \(\lambda (I(t))I(t)S(t)\) shows the probability for a susceptible person to become infective. Let the fraction of the individuals that were infective from time zero to time t and survive to this time be denoted by P(t), and let \(b_0\) denote the death rate which is independent of infection. The mean time that a person remains infective can be computed as [13]

$$\begin{aligned} \tau =\int _0^{\infty } P(u)e^{-b_0u}du. \end{aligned}$$

Under the above assumptions, the fraction of infective individuals can be formulated by the following VIE [13]

$$\begin{aligned} I(t)=I_0(t)+\int _0^t\lambda \left( I(u)\right) I(u)\left( 1-I(u)\right) P(t-u)e^{-b_0(t-u)}du, \end{aligned}$$

where \(I_0(t)\) is the fraction of individuals that were infective from time zero to time t.

Since most of such problems can not be solved analytically, presenting and improving numerical techniques for solving VIEs have been an important branch of the numerical analysis in the last decades. Several researchers have attempted to present some efficient schemes to approximate the solution of VIEs. Conte and Paternoster in [14] proposed the multistep collocation methods for solving VIEs and generated stable solutions with low computational costs. Cherruault and Zitoun in [15] presented a simple and accurate method based on the Taylor expansion and the Faà di Bruno’s formula to approximate the solution of VIEs of the second and third kind. Maleknejad et al. [16] employed the fixed point method (FPM) with the cubic B-spline scaling functions as basis functions to solve nonlinear VIEs. Also, Maleknejad and Najafi [17] combined the idea of quasilinearization with the Lagrange collocation method (LCQM) in the piecewise continuous space to solve nonlinear VIEs. In their presented method, nonlinear VIEs are solved indirectly with solving the related sequences of linear VIEs. The quasilinearization technique was employed later with non-polynomial spline functions (NPSQM) in [18] and gave more accurate results in comparison to the LCQM. Mirzaee and Hoseini utilized a combination of Bernstein polynomials and block-pulse functions to present a numerical method for solving a class of VIEs of the second kind [19]. Also, Mirzaee and Hadadiyan in [20] used the modified block-pulse functions method to approximate the solution of VIEs. The Nyström interpolation formula was utilized to solve VIE (1.1) by Baratella [1]. The Adomian decomposition method [21], homotopy analysis method [22], Galerkin method [23,24,25,26], radial basis functions method [27,28,29,30,31], Bernoulli collocation method [32], Fibonacci collocation method [33], Euler matrix method [34], two-dimensional delta functions method [35], least squares method [36, 37], trapezoidal quadrature iterative method [38], implicit Runge–Kutta method [39], reproducing kernel method [40], successive approximations method [41,42,43], modified Newton method [44], hat functions method [45,46,47,48,49], and Chebyshev cardinal functions method [50] can also be addressed as some effective methods which have been applied for solving VIEs in recent years. We refer the interested reader to [51,52,53,54,55,56,57] for more details about VIEs and their applications.

The main aim of this article is to present a simple and fast numerical method to solve linear and nonlinear VIEs. The proposed scheme is based upon a special type of Hermite interpolation method. In this interpolation problem, the needed data to construct the polynomial interpolant of an arbitrary function over each interval are the values of the function and its derivatives up to an adequate order at the endpoints of the interval. This interpolation problem is called the two-point Hermite interpolant or two-point Taylor formula (TTF). Phillips in [58] obtained an explicit form of the two-point Hermite interpolant over \(\left[ 0, 1\right] \). This kind of interpolation was applied later to solve ordinary differential equations [59,60,61]. However, according to the authors knowledge, the utility of this method for solving Volterra integral equations has not been investigated before. The TTF uses a set of 2n data to construct a \((2n-1)\)th degree polynomial as an approximate solution of a VIE. Since the structure of the problem provides us the half of the needed data, the solution of the VIE reduces to the solution of a system of n algebraic equations. The constructed system can be solved by using a suitable iterative method. Furthermore, we present the multistep TTF which is a reliable method to solve VIEs of type (1.1), especially in large domains, where the TTF may take difficulty to obtain accurate results. The main feature of the multistep TTF is that it uses in each step the data of the previous step. Therefore, in each step, only the half of the needed data remain unknown. Also, this property keeps the continuity of the solution. Since in this method the large intervals are divided into small subintervals, the multistep TTF can provide high accurate approximations without the need to increase the number of bases. Although many of the methods in the literature encounter difficulties for solving VIEs over large intervals, the multistep TTF gives acceptable results in such intervals. The error bound and the convergence analysis of the proposed method are studied. The capability of the method is inspected by applying it to solve different examples of VIEs of form (1.1). All the obtained results verify the analytical studies.

The next sections of this article are organized as follows. In Sect. 2, the TTF and its multistep form for solving VIEs of type (1.1) are explained. The convergence analysis of the proposed TTF is discussed in Sect. 3. The numerical results of applying the method for solving several VIEs are reported in Sect. 4. Finally, we finish this article with the conclusion of this study.

2 The TTF for solving VIEs

2.1 Construction of the TTF

Suppose that the values of a function \(f\in C^{2n}\left[ 0, 1\right] \), and its derivatives up to \((n-1)\)th order are given at \(x=0\) and \(x=1\). The TTF generates a polynomial \(\mathrm {P}\in {\mathbb {P}}_{2n-1}\) which satisfies the following given data:

$$\begin{aligned} \left\{ \begin{array}{ll} \mathrm {P}^{(q)}(0)=f^{(q)}(0), \\ \mathrm {P}^{(q)}(1)=f^{(q)}(1), \end{array} \right. \quad q=0,1,2,\ldots ,n-1. \end{aligned}$$
(2.1)

An explicit form of \(\mathrm {P}(x)\) based on interpolation conditions (2.1) is illustrated in the following theorem.

Theorem 2.1

[58] Suppose that \(f\in C^{2n}\left[ 0,1\right] \), then f can be approximated by using the following polynomial interpolant

$$\begin{aligned} \mathrm {P}_{2n-1}\left( f;x\right) =\sum _{j=0}^{n-1}\sum _{s=0}^{1}{(-1)}^{js}\phi _{n,j}(s+(-1)^s x)f^{(j)}(s), \end{aligned}$$
(2.2)

where \(\phi _{n,j}(x), j=0,\ldots ,n-1\) are the nonnegative basis functions on the interval [0, 1] and defined as

$$\begin{aligned} \phi _{n,j}(x)=\frac{x^j}{j!}{(1-x)}^n\sum _{k=0}^{n-j-1}{n+k-1\atopwithdelims ()k}x^k. \end{aligned}$$

Furthermore, there exists a number \(\xi _x\in (0,1)\) such that

$$\begin{aligned} \mathrm {R}_n\left( f;x\right) := f(x)-\mathrm {P}_{2n-1}\left( f;x\right) =\frac{f^{(2n)}(\xi _x)}{(2n)!}x^n{(1-x)}^n. \end{aligned}$$

In order to obtain the TTF over a general interval \(\left[ a, b\right] \), and approximate an arbitrary function \(f\in C^{2n}\left[ a, b\right] \), we can follow [58] and define the linear mapping \(\psi :=[a,b]\rightarrow [0,1]\) as

$$\begin{aligned} \psi (x)=\frac{x-a}{b-a}. \end{aligned}$$

Now, the basis functions \({\tilde{\phi }}_{n,j}, j=0\ldots , n-1\), can be constructed such that

$$\begin{aligned} \frac{d^q}{dx^q}{\tilde{\phi }}_{n,j}(x)=0,\quad \text {at} x=b,\quad q=0,1,2,\ldots ,n-1, \end{aligned}$$

and

$$\begin{aligned} \frac{d^q}{dx^q}{\tilde{\phi }}_{n,j}(x)=\delta _{jq},\quad \text {at} x=a,\quad q=0,1,2,\ldots ,n-1, \end{aligned}$$

where \(\delta _{jq}\) is the Kronecker delta function. Therefore, we can state the following corollary.

Corollary 2.1

Let \(f\in C^{2n}\left[ a, b\right] \), then

$$\begin{aligned} f(x)=\mathrm {P}_{2n-1}(f;x)+\mathrm {R}_n( f;x), \end{aligned}$$

where

$$\begin{aligned} \mathrm {P}_{2n-1}\left( f;x\right) =\sum _{j=0}^{n-1}\sum _{s=0}^{1}{(-1)}^{js}{\tilde{\phi }}_{n,j}\Big ((a+b)s+(-1)^s x\Big )f^{(j)}\Big ((b-a)s+a\Big ),\qquad \end{aligned}$$
(2.3)
$$\begin{aligned} {\tilde{\phi }}_{n,j}(x)=\left( b-a\right) ^j(\phi _{n,j}\circ \psi )(x),~~~j=0\ldots , n-1, \end{aligned}$$
$$\begin{aligned} \mathrm {R}_n\left( f;x\right) =\frac{f^{(2n)}(\xi _x)}{(2n)!}(x-a)^n{(b-x)}^n,\quad \xi _x \in (a,b). \end{aligned}$$
(2.4)

Polynomial (2.3) satisfies the following interpolation conditions

$$\begin{aligned} \left\{ \begin{array}{ll} \mathrm {P}_{2n-1}^{(q)}(f;a)=f^{(q)}(a), \\ \mathrm {P}_{2n-1}^{(q)}(f;b)=f^{(q)}(b), \end{array} \right. \quad q=0,1,2,\ldots ,n-1, \end{aligned}$$

and gives an approximation to f for every point \(x\in \left[ a, b\right] \).

2.2 Implementation of the TTF for VIEs

Now, suppose that \(u\in C^{2n}\left[ a, b\right] \) is the exact solution of VIE (1.1). According to the description in the previous subsection, the TTF (2.3) can provide a \((2n-1)\)th degree approximation to u as

$$\begin{aligned} u(x)\simeq \mathrm {P}_{2n-1}\left( u;x\right) =\sum _{j=0}^{n-1}\sum _{s=0}^{1}{(-1)}^{js}{\tilde{\phi }}_{n,j}\Big ((a+b)s+(-1)^s x\Big )u^{(j)}\Big ((b-a)s+a\Big ).\qquad \end{aligned}$$
(2.5)

The only needed data to construct (2.5) are \(u^{(j)}(a)\) and \(u^{(j)}(b)\) for \( j=0, 1, \ldots ,n-1\). In order to obtain them, we follow the idea of [15] and define the nonlinear Volterra integral operator \({\mathscr {K}}:C^{n-1}[a,b]\rightarrow C^{n-1}[a,b] \) as follows:

$$\begin{aligned} ({\mathscr {K}}u)(x)=\int _a^x k(x,t,u(t))dt. \end{aligned}$$

Now, by j times differentiating both sides of VIE (1.1) with respect to x, we can deduce

$$\begin{aligned} u^{(j)}(x)=f^{(j)}(x)+\lambda ({\mathscr {K}}u)^{(j)}(x),\quad j=0,1,2,\ldots ,n-1, \end{aligned}$$
(2.6)

where

$$\begin{aligned} ({\mathscr {K}}u)^{(j)}(x)=\sum _{i=0}^{j-1}\left( {\mathscr {D}}_{j-i-1}u\right) ^{(i)}(x)+\int _a^x\frac{\partial ^j}{\partial x^j}k(x,t,u(t))dt, \end{aligned}$$

and

$$\begin{aligned} \left( {\mathscr {D}}_ju\right) (x)=\left. \frac{\partial ^j}{\partial x^j}k(x,t,u(t))\right| _{t=x},\quad j=0, 1, \ldots , n-1. \end{aligned}$$

The values of \(u^{(j)}(a), j=0, 1, \ldots ,n-1\) can be calculated directly from (2.6) as

$$\begin{aligned} \left\{ \begin{aligned}&u(a)=f(a),\\&u^{(j)}(a)=f^{(j)}(a)+\lambda \sum _{i=0}^{j-1}\left( {\mathscr {D}}_{j-i-1}u\right) ^{(i)}(a) ,\quad j=1,2,\ldots ,n-1. \end{aligned}\right. \end{aligned}$$
(2.7)

Therefore, polynomial interpolant (2.5) includes only n unknowns \(u^{(j)}(b), j=0, 1, \ldots ,n-1\). Note that by substituting polynomial approximation (2.5) into (2.6), we get

$$\begin{aligned} u^{(j)}(x)\simeq f^{(j)}(x)+\lambda ({\mathscr {K}}\mathrm {P}_{2n-1})^{(j)}(x),\quad j=0,1,2,\ldots ,n-1. \end{aligned}$$
(2.8)

If \({\tilde{u}}^{(j)}(b)\) is the estimation of the exact value \(u^{(j)}(b)\), an approximation to \(\mathrm {P}_{2n-1}(u; x)\) can be determined as

$$\begin{aligned} \tilde{\mathrm {P}}_{2n-1}(u;x)=\sum _{j=0}^{n-1}\sum _{s=0}^{1}{(-1)}^{js}{\tilde{\phi }}_{n,j}\Big ((a+b)s+(-1)^s x\Big ){\tilde{u}}^{(j)}\Big ((b-a)s+a\Big ), \end{aligned}$$
(2.9)

where

$$\begin{aligned} \left\{ \begin{array}{l} {\tilde{u}}^{(j)}(a)= u^{(j)}(a), \\ {\tilde{u}}^{(j)}(b)\simeq u^{(j)}(b), \end{array} \right. ~~~j=0,1,\ldots ,n-1. \end{aligned}$$
(2.10)

Indeed, the approximate values \({\tilde{u}}^{(j)}(b),j=0, 1, \ldots , n-1\) can be obtained by solving the following system of n equations

$$\begin{aligned} {\tilde{u}}^{(j)}(b)=f^{(j)}(b)+\lambda ({\mathscr {K}}\tilde{\mathrm {P}}_{2n-1})^{(j)}(b),\quad j=0,1,2,\ldots ,n-1. \end{aligned}$$
(2.11)

The obtained approximations from (2.11) can then be utilized to calculate polynomial (2.9) as an approximation to the exact solution of VIE (1.1).

Remark 2.1

The integrals which appeared in (2.11) can be accurately estimated by using the Gauss–Legendre quadrature formula as

$$\begin{aligned} \left. \int _a^b\frac{\partial ^j}{\partial x^j}k\left( x, t, \tilde{\mathrm {P}}_{2n-1}(u;t)\right) \right| _{x=b}dt\simeq \frac{b-a}{2}\left. \sum _{j=0}^{m}w_j\frac{\partial ^j}{\partial x^j}k\left( x,\tau _j,\tilde{\mathrm {P}}_{2n-1}\quad \left( u;\tau _j\right) \right) \right| _{x=b}, \end{aligned}$$
(2.12)

where

$$\begin{aligned} \left\{ \begin{array}{l} \tau _j=\frac{b-a}{2}t_j+\frac{b+a}{2}, \\ w_j=\frac{2}{(1-t_j^2)\left( L'_{m+1}(t_j)\right) ^2}, \end{array} \right. \quad j=0, 1, \ldots , m, \end{aligned}$$

and \(\lbrace t_j\rbrace _{j=0}^m\) are the zeros of the Legendre polynomial \(L_{m+1}(t)\) .

2.3 The multistep TTF for VIEs

The presented TTF method only uses the data at the endpoints of the domain. This may increase the error of the approximation over large intervals. Therefore, in what follows, we explain the multistep form of the TTF for solving VIEs of the second kind.

Let us discretize the interval I by using the uniform mesh \(I_h:=\{ x_i:=a+ih, i=0, 1,\ldots , N\} \), where \(h=\frac{b-a}{N}\) is the mesh size and N is a positive integer. Consider again the nonlinear VIE (1.1) with the exact solution u(x). Let \(u_r, r=1, 2 , \ldots , N\), be the exact solution of problem (1.1) over the interval \(\sigma _r:=\left[ x_{r-1}, x_r\right] \), then this problem can be divided into a set of N problems as follows:

$$\begin{aligned} u_r(x)= & {} f(x)+\lambda \sum _{i=1}^{r-1}\int _{x_{i-1}}^{x_i}k\left( x,t,u_i(t)\right) dt\nonumber \\&+\lambda \int _{x_{r-1}}^xk\left( x,t,u_r(t)\right) dt,\quad r=1, 2, \ldots , N. \end{aligned}$$
(2.13)

Now, in each step, we can estimate the solution by using the TTF as

$$\begin{aligned}&u_r(x)\simeq \mathrm {P}_{2n-1}^{[r]}\left( u;x\right) =\sum _{j=0}^{n-1}\\&\quad \sum _{s=0}^{1}{(-1)}^{js}{\tilde{\phi }}^{[r]}_{n,j} \Big ((x_{r-1}+x_r)s+(-1)^s x\Big )u^{(j)}\Big (hs+x_{r-1}\Big ),\quad x\in \sigma _r, \end{aligned}$$

where

$$\begin{aligned} \psi ^{[r]}(x)= & {} \frac{1}{h}(x-x_{r-1}),~~~r=1,2,\ldots ,N,\\ {\tilde{\phi }}^{[r]}_{n,j}(x)= & {} h^j(\phi _{n,j}\circ \psi ^{[r]})(x),~~~j=0\ldots , n-1,~~~r=1,2,\ldots ,N. \end{aligned}$$

Differentiating both sides of (2.13) with respect to x leads to

$$\begin{aligned} u_r^{(j)}(x)= f^{(j)}(x)+\lambda \sum _{i=1}^{r-1}\int _{x_{i-1}}^{x_i}\frac{\partial ^j}{\partial x^j}k\left( x,t,u_i(t)\right) dt+\lambda \left( {\mathscr {K}}_ru\right) ^{(j)}(x), \end{aligned}$$
(2.14)

where

$$\begin{aligned} \left( {\mathscr {K}}_ru\right) ^{(j)}(x)=\sum _{i=0}^{j-1}\left( {\mathscr {D}}_{j-i-1}u_r\right) ^{(i)}(x)+\int _{x_{r-1}}^x\frac{\partial ^j }{\partial x^j}k\left( x,t,u_r(t)\right) dt. \end{aligned}$$

In the first step, we require \(u_1^{(j)}(x_0)\) and \(u_1^{(j)}(x_1)\) for \(j=0, 1, \ldots , n-1\), to obtain the TTF on \(\sigma _1\). Similar to (2.7), the values of \(u_1^{(j)}(x_0), j=0, 1, \ldots , n-1\), can be exactly calculated from (2.14). Thus, the only unknowns in this step are \(u_1^{(j)}(x_1), j=0, 1, \ldots , n-1\). Furthermore, it can be concluded from (2.13) that

$$\begin{aligned} u_1^{(j)}(x_1)=u_2^{(j)}(x_1),\quad j=0, 1, \ldots , n-1. \end{aligned}$$

Therefore, if we compute the values of \(u_1^{(j)}(x_1), j=0, 1, \ldots , n-1\) in the first step, they can be utilized again in the second step to obtain the TTF on \(\sigma _2\). Since generally we have

$$\begin{aligned} u_r^{(j)}(x_{r})=u_{r+1}^{(j)}(x_{r}),\quad r=1, 2, \ldots , N-1, \end{aligned}$$

this process is continued for all the steps. Consequently, in each step, we have n unknowns which can be estimated by solving the following system of n equations

$$\begin{aligned} {\tilde{u}}_r^{(j)}(x_r)= & {} f^{(j)}(x_r)+\lambda \sum _{i=1}^{r-1}\left. \int _{x_{i-1}}^{x_i}\frac{\partial ^j}{\partial x^j}k\left( x,t,\tilde{\mathrm {P}}_{2n-1}^{[i]}(u;t)\right) \right| _{x=x_r}dt\nonumber \\&\quad +\lambda \left( {\mathscr {K}}_r\tilde{\mathrm {P}}^{[r]}_{2n-1}\right) ^{(j)}(x_r) ,\quad j=0, 1, \ldots , n-1,\quad r=1, 2, \ldots , N,\nonumber \\ \end{aligned}$$
(2.15)

where \(\tilde{\mathrm {P}}_{2n-1}^{[r]}(u;x), r=1, 2, \ldots , N\), are approximations of \(\mathrm {P}_{2n-1}^{[r]}(u;x), r=1, 2, \ldots , N\), and defined as

$$\begin{aligned} \tilde{\mathrm {P}}_{2n-1}^{[r]}\left( u;x\right)= & {} \sum _{j=0}^{n-1}\sum _{s=0}^{1}{(-1)}^{js}{\tilde{\phi }}^{[r]}_{n,j}\nonumber \\&\quad \Big ((x_{r-1}+x_r)s+(-1)^s x\Big ){\tilde{u}}^{(j)}\Big (hs+x_{r-1}\Big ),\quad x\in \sigma _r,\quad r=1, 2, \ldots , N. \end{aligned}$$

It should be noted that, similar to (2.10) we have

$$\begin{aligned} \left\{ \begin{array}{l} {\tilde{u}}^{(j)}(x_0)= u^{(j)}(x_0), \\ {\tilde{u}}^{(j)}(x_r)\simeq u^{(j)}(x_r),~~~r=1,2,\ldots ,N, \end{array} \right. ~~~j=0,1,\ldots ,n-1. \end{aligned}$$

Finally, the N-step TTF can approximate the solution of nonlinear VIE (1.1) over the interval \(\left[ a, b\right] \) as

$$\begin{aligned} u(x)\simeq {\mathscr {P}}_{2n-1}^N(u;x)=\left\{ \begin{aligned}&\tilde{\mathrm {P}}_{2n-1}^{[1]}(u;x),\quad x\in \sigma _1,\\&\tilde{\mathrm {P}}_{2n-1}^{[2]}(u;x),\quad x\in \sigma _2,\\&\vdots \\&\tilde{\mathrm {P}}_{2n-1}^{[N]}(u;x),\quad x\in \sigma _N. \end{aligned}\right. \end{aligned}$$

Note that the one-step TTF (\(N=1\)) is exactly the method that was explained in the previous subsection. Also, the integrals in (2.15) can be estimated using the Gauss–Legendre quadrature formula (2.12).

3 Convergence analysis

In the current section, we study the error estimate of the TTF method in solving VIE (1.1). Let us firstly recall a discrete inequality of Gronwall type which is useful in the selected method to inspect the convergence analysis of the presented method.

Lemma 3.1

[62] Suppose that \(\lbrace a_n\rbrace _{n=n_0}^{\infty }\) and \(\lbrace b_n\rbrace _{n=n_0}^{\infty }\) are two given sequences and

$$\begin{aligned} a_n\le c+\displaystyle {\sum _{k=n_0}^{n-1}}a_kb_k,\quad n=n_0,n_0+1, \ldots , \end{aligned}$$

where \(n_0\in {\mathbb {N}}\cup \{0\}\) and \(c\ge 0\) is a real constant, also let \(b_n\ge 0\) for \(n=n_0,n_0+ 1, \ldots ,\) then

$$\begin{aligned} a_n\le c\prod _{k=n_0}^{n-1}[1+b_k],\quad n=n_0,n_0+ 1, \ldots . \end{aligned}$$

Now, consider the following linear VIE of the second kind

$$\begin{aligned} u(x)=f(x)+{\lambda }\int _a^x k(x,t)u(t)dt,\quad x\in I. \end{aligned}$$
(3.1)

Similar to what described before for nonlinear case (1.1), to derive the TTF approximation of u, the exact solution of Eq. (3.1), we need different orders of derivatives of u at \(x=a\) and \(x=b\), which can be calculated as

$$\begin{aligned} u^{(j)}(x)= & {} f^{(j)}(x)+\sum _{i=0}^{j-1}\left( h_{j-i-1}(x)u(x)\right) ^{(i)}\nonumber \\&\quad +{\lambda }\int _a^x\frac{\partial ^jk(x,t)}{\partial x^j}u(t)dt,\quad j=0,1,\ldots ,n-1, \end{aligned}$$
(3.2)

where

$$\begin{aligned} h_i(x)={\lambda }\left. \frac{\partial ^ik(x,t)}{\partial x^i}\right| _{t=x}. \end{aligned}$$

Applying the general Leibniz rule, (3.2) can be reformulated as

$$\begin{aligned} u^{(j)}(x)= & {} f^{(j)}(x)+\sum _{i=0}^{j-1}\sum _{k=0}^{i}H_{i,j,k}(x)u^{(k)}(x)\nonumber \\&\quad +{\lambda }\int _a^x\frac{\partial ^jk(x,t)}{\partial x^j}u(t)dt,\quad j=0,1 ,\ldots ,n-1, \end{aligned}$$
(3.3)

in which

$$\begin{aligned} H_{i,j,k}(x)={i\atopwithdelims ()k}\left( h_{j-i-1}(x)\right) ^{(i-k)}. \end{aligned}$$

Equation (3.3) can be rewritten as

$$\begin{aligned} u^{(j)}(x)= & {} f^{(j)}(x)+\sum _{k=0}^{j-1}{\mathscr {H}}_{i,j,k}(x)u^{(k)}(x)\nonumber \\&+{\lambda }\int _a^x\frac{\partial ^jk(x,t)}{\partial x^j}u(t)dt,\quad j=0,1 ,\ldots ,n-1, \end{aligned}$$
(3.4)

where

$$\begin{aligned} {\mathscr {H}}_{i,j,k}(x)=\sum _{i=k}^{j-1}H_{i,j,k}(x),\quad j=0,1 ,\ldots ,n-1. \end{aligned}$$

Although \(u^{(j)}(a), j=0,1,\ldots , n-1\) can be exactly computed from (3.4), the values of \(u^{(j)}(b), j=0,1,\ldots , n-1\) are not generally available. Therefore, the TTF (2.9) is constructed by applying \({\tilde{u}}^{(j)}(b), j=0,1,\ldots , n-1\), which are the obtained estimations of different orders of derivatives of u at \(x=b\) by solving the following system of algebraic equations

$$\begin{aligned} {\tilde{u}}^{(j)}(b)= & {} f^{(j)}(b)+\sum _{k=0}^{j-1}{\mathscr {H}}_{i,j,k}(b)\tilde{\mathrm {P}}_{2n-1}^{(k)}(u;b)\nonumber \\&\quad +{\lambda }\int _a^b\frac{\partial ^jk(x,t)}{\partial x^j}\Big |_{x=b}\tilde{\mathrm {P}}_{2n-1}(u;t)dt,\quad j=0,1 ,\ldots ,n-1. \end{aligned}$$
(3.5)

We can deduce from (3.4), (3.5) and interpolation conditions \(\tilde{\mathrm {P}}_{2n-1}^{(j)}(u;b)={\tilde{u}}^{(j)}(b),~j=0,1 ,\ldots ,n-1\) that

$$\begin{aligned} \begin{aligned} \left| u^{(j)}(b)-{\tilde{u}}^{(j)}(b)\right|&\le \sum _{k=0}^{j-1}\left| {\mathscr {H}}_{i,j,k}(b)\right| \left| u^{(k)}(b)-{\tilde{u}}^{(k)}(b)\right| +{\vert \lambda \vert \int _a^b\left| \frac{\partial ^jk(x,t)}{\partial x^j}\Big |_{x=b}\right| } \\&\quad \left| u(t)-\tilde{\mathrm {P}}_{2n-1}(u;t)\right| dt\\&\le \sum _{k=0}^{j-1}\left| {\mathscr {H}}_{i,j,k}(b)\right| \left| u^{(k)}(b)-{\tilde{u}}^{(k)}(b)\right| +{\vert \lambda \vert \int _a^b\left| \frac{\partial ^jk(x,t)}{\partial x^j}\Big |_{x=b}\right| } \\&\quad \left| u(t)-\mathrm {P}_{2n-1}(u;t)\right| dt\\&\quad +{\vert \lambda \vert \int _a^b\left| \frac{\partial ^jk(x,t)}{\partial x^j}\Big |_{x=b}\right| } \left| \mathrm {P}_{2n-1}(u;t)-\tilde{\mathrm {P}}_{2n-1}(u;t)\right| dt, \end{aligned} \end{aligned}$$
(3.6)

and subsequently, from (2.4) we have

$$\begin{aligned}&\left| u^{(j)}(b)-{\tilde{u}}^{(j)}(b)\right| \le \sum _{k=0}^{j-1}\left| {{\mathscr {H}}}_{i,j,k}(b)\right| \left| u^{(k)}(b)-{\tilde{u}}^{(k)}(b)\right| +{\vert \lambda \vert }\left( b-a\right) \\&\quad M_n\left( E_n+\left\| \mathrm {P}_{2n-1}(u;t)-\tilde{\mathrm {P}}_{2n-1}(u;t)\right\| _{\infty }\right) , \end{aligned}$$

where

$$\begin{aligned} M_n=\max _{0\le j\le n-1}\left\{ \max _{a\le x,t\le b}\left\{ \left| \frac{\partial ^jk(x,t)}{\partial x^j}\right| \right\} \right\} ,\quad E_n=\frac{(b-a)^{2n}\Vert u^{(2n)}(t)\Vert _\infty }{2^{2n}(2n)!}. \end{aligned}$$
(3.7)

Thus, Lemma 3.1 implies

$$\begin{aligned}&\left| u^{(j)}(b)-{\tilde{u}}^{(j)}(b)\right| \le {\vert \lambda \vert }\left( b-a\right) M_n\left( E_n+\left\| \mathrm {P}_{2n-1}(u;t)-\tilde{\mathrm {P}}_{2n-1}(u;t)\right\| _{\infty }\right) \nonumber \\&\quad \prod _{k=0}^{j-1}\left[ 1+\left| {\mathscr {H}}_{i,j,k}(b)\right| \right] . \end{aligned}$$
(3.8)

This result allows us to derive an upper bound to the error of the proposed method for solving linear VIE (3.1).

Theorem 3.1

Let \(\mathrm {P}_{2n-1}\left( u;x\right) \) obtained by (2.5) be the polynomial interpolant of the exact solution of linear VIE (3.1), and let polynomial \(\tilde{\mathrm {P}}_{2n-1}\left( u;x\right) \) defined in (2.9) be its approximation. Also suppose that the following condition holds:

$$\begin{aligned} m_n\Delta _nM_n(b-a)<1, \end{aligned}$$

where

$$\begin{aligned} m_n=\max _{a\le x\le b}\left\{ \sum _{j=0}^{n-1}{\tilde{\phi }}_{n,j}(x)\right\} , \quad \Delta _n=\max _{0\le j\le n-1}\left\{ \prod _{k=0}^{j-1}\left[ 1+\left| {\mathscr {H}}_{i,j,k}(b)\right| \right] \right\} , \end{aligned}$$

and \(M_n\) is as introduced before. Then, we have

$$\begin{aligned} \left\| \mathrm {P}_{2n-1}\left( u;x\right) -\tilde{\mathrm {P}}_{2n-1}\left( u;x\right) \right\| _{\infty }\le \frac{m_n\Delta _nM_nE_n{\vert \lambda \vert }(b-a)}{1-m_n\Delta _nM_n{\vert \lambda \vert }(b-a)}, \end{aligned}$$
(3.9)

where \(E_n\) is as introduced in (3.7).

Proof

Since \(u^{(j)}(a), j=0, 1, \ldots , n-1\), can be calculated exactly by substituting \(x=a\) into (3.4), from (2.5), (2.9) and (3.8) we get

$$\begin{aligned} \begin{aligned} \left| \mathrm {P}_{2n-1}\left( u;x\right) -\tilde{\mathrm {P}}_{2n-1}\left( u;x\right) \right|&\le \sum _{j=0}^{n-1} {\tilde{\phi }}_{n,j}(a+b-x)\left| u^{(j)}(b)-{\tilde{u}}^{(j)}(b)\right| \\&\le {\vert \lambda \vert }\left( b-a\right) M_n\left( E_n+\left\| \mathrm {P}_{2n-1}(u;t)-\tilde{\mathrm {P}}_{2n-1}(u;t)\right\| _{\infty }\right) \\&\quad \prod _{k=0}^{j-1}\left[ 1+\left| {\mathscr {H}}_{i,j,k}(b)\right| \right] \sum _{j=0}^{n-1} {\tilde{\phi }}_{n,j}(a+b-x). \end{aligned}\nonumber \\ \end{aligned}$$
(3.10)

The symmetry of \({\tilde{\phi }}_{n,j}(x)\) and \({\tilde{\phi }}_{n,j}(a+b-x)\) with respect to \(x=\frac{a+b}{2}\) implies that

$$\begin{aligned} m_n=\max _{a\le x\le b}\left\{ \sum _{j=0}^{n-1}{\tilde{\phi }}_{n,j}(a+b-x)\right\} . \end{aligned}$$

Subsequently, it can be deduced from (3.10) that

$$\begin{aligned}&\left| \mathrm {P}_{2n-1}\left( u;x\right) -\tilde{\mathrm {P}}_{2n-1}\left( u;x\right) \right| \le m_n\Delta _nM_n{\vert \lambda \vert }(b-a)\\&\quad \left( E_n+\left\| \mathrm {P}_{2n-1}(u;t)-\tilde{\mathrm {P}}_{2n-1}(u;t)\right\| _{\infty }\right) , \end{aligned}$$

and therefore

$$\begin{aligned} \left( 1-m_n\Delta _nM_n{\vert \lambda \vert }(b-a)\right) \left\| \mathrm {P}_{2n-1}\left( u;x\right) -\tilde{\mathrm {P}}_{2n-1}\left( u;x\right) \right\| _{\infty }\le m_n\Delta _nM_nE_n{\vert \lambda \vert }(b-a), \end{aligned}$$

which implies (3.9). \(\square \)

Theorem 3.2

Suppose that \(u\in C^{2n}\left[ a,b\right] \) is the exact solution of linear VIE (3.1). Then, under the assumptions of Theorem 3.1, we have

$$\begin{aligned} \Vert u(x)-\tilde{\mathrm {P}}_{2n-1}(u;x)\Vert _{\infty } \le \frac{E_n}{1-m_n\Delta _nM_n{\vert \lambda \vert }(b-a)}, \end{aligned}$$

where \(E_n\) has been introduced in (3.7).

Proof

Corollary 2.1 and Theorem 3.1 imply that

$$\begin{aligned} \begin{aligned} \Vert u(x)-\tilde{\mathrm {P}}_{2n-1}(u;x)\Vert _{\infty }&\le \Vert u(x)-\mathrm {P}_{2n-1}(u;x)\Vert _{\infty }\\&+\Vert \mathrm {P}_{2n-1}(u;x)-\tilde{\mathrm {P}}_{2n-1}(u;x)\Vert _{\infty } \\&\le \frac{\Vert u^{(2n)}(x)\Vert _\infty }{(2n)!}\Vert (x-a)^n(b-x)^n\Vert _{\infty }\\&+\frac{m_n\Delta _nM_nE_n{\vert \lambda \vert }(b-a)}{1-m_n\Delta _nM_n{\vert \lambda \vert }(b-a)} \\&\le E_n\left( 1+\frac{m_n\Delta _nM_n{\vert \lambda \vert }(b-a)}{1-m_n\Delta _nM_n{\vert \lambda \vert }(b-a)}\right) \\&=\frac{E_n}{1-m_n\Delta _nM_n{\vert \lambda \vert }(b-a)}. \end{aligned} \end{aligned}$$

\(\square \)

Remark 3.1

It should be emphasized that the error analysis for nonlinear VIE (1.1) is considerably more complicated than linear case (3.1). Nevertheless, in what follows, we try to present the outline of the error estimate of the proposed method for nonlinear VIEs. For \(j=0, 1,\ldots , n-1\), we can get from (2.6) and (2.8) that

$$\begin{aligned} \begin{aligned} \left| u^{(j)}(b)-{\tilde{u}}^{(j)}(b)\right|&=\vert \lambda \vert \left| \left( {\mathscr {K}}u\right) ^{(j)}(b)-\left( {\mathscr {K}}\tilde{\mathrm {P}}_{2n-1}\right) ^{(j)}(b)\right| \\&\le \vert \lambda \vert \sum _{i=0}^{j-1}\left| \left( {\mathscr {D}}_{j-i-1}u\right) ^{(i)}(b)-\left( {\mathscr {D}}_{j-i-1}\tilde{\mathrm {P}}_{2n-1}\right) ^{(i)}(b)\right| \\&\quad +\vert \lambda \vert \int _a^b\left| \frac{\partial ^j}{\partial x^j}\left( k(x,t,u(t))-k(x,t,\tilde{\mathrm {P}}_{2n-1}(u;t)\right) \right| _{x=b} dt. \end{aligned} \end{aligned}$$
(3.11)

Note that \(\left( {\mathscr {D}}_ju\right) (x)\) is generally a function of x and u(x). Therefore, the i-th derivative of this function with respect to x, which we denote by \(\left( {\mathscr {D}}_ju\right) ^{(i)}(x)\), includes x, u(x), and the first i derivatives of u. Now, suppose that \(\left( {\mathscr {D}}_ju\right) (x), j=0, 1, \ldots , n-1\) and their derivatives satisfy the following Lipschitz conditions

$$\begin{aligned} \left| \left( {\mathscr {D}}_ju_1\right) ^{(i)}(x)-\left( {\mathscr {D}}_ju_2\right) ^{(i)}(x)\right| \le \sum _{k=0}^{i}L_k\left| u_1^{(k)}-u_2^{(k)}\right| ,\quad i=0, 1, \ldots , n-2.\nonumber \\ \end{aligned}$$
(3.12)

Also suppose that the kernel \(k:\left[ a, b\right] ^2\times {\mathbb {R}}\rightarrow {\mathbb {R}}\) and its derivatives are Lipschitz continuous in u, that is

$$\begin{aligned} \left| \frac{\partial ^j}{\partial x^j}k(x,t,u_1)-\frac{\partial ^j}{\partial x^j}k(x,t,u_2)\right| \le {\bar{L}}_j\left| u_1-u_2\right| ,\quad j=0, 1, \ldots , n-1.\nonumber \\ \end{aligned}$$
(3.13)

Then inequality (3.11) implies that

$$\begin{aligned} \begin{aligned} \left| u^{(j)}(b)-{\tilde{u}}^{(j)}(b)\right|&\le L\vert \lambda \vert \sum _{i=0}^{j-1}\sum _{k=0}^{i}\left| u^{(k)}(b)-{\tilde{u}}^{(k)}(b)\right| \\&\quad +{\bar{L}}\vert \lambda \vert \int _a^b\left| u(t)-\tilde{\mathrm {P}}_{2n-1}(u;t)\right| dt\\&\le L\vert \lambda \vert \sum _{k=0}^{j-1}\left( j-k\right) \left| u^{(k)}(b)-{\tilde{u}}^{(k)}(b)\right| \\&\quad +{\bar{L}}\vert \lambda \vert (b-a)\left\| u(t)-\tilde{\mathrm {P}}_{2n-1}(u;t)\right\| _{\infty }, \end{aligned} \end{aligned}$$

where \(L=\displaystyle \max _{0\le k\le n-2}\lbrace L_k\rbrace \) and \({\bar{L}}=\displaystyle \max _{0\le j\le n-1}\lbrace {\bar{L}}_j\rbrace \). The continuation of the procedure is similar to the linear case.

We present now the matrix form of system (2.11) in order to investigate the existence and uniqueness of its solution. Let us define

$$\begin{aligned} U= & {} \left[ {\tilde{u}}(b), {\tilde{u}}'(b),\ldots , {\tilde{u}}^{(n-1)}(b)\right] ^T,\\ F_0= & {} \left[ f(b), f'(b), \ldots ,f^{(n-1)}(b)\right] ^T,\\ D(U)= & {} \left[ d_0, d_1, \ldots , d_{n-1}\right] ^T, \\ G(U)= & {} \left[ g_0, g_1, \ldots , g_{n-1}\right] ^T, \end{aligned}$$

where

$$\begin{aligned} \left\{ \begin{aligned} d_0&=0,\\ d_j&=\sum _{i=0}^{j-1}\left( {\mathscr {D}}_{j-i-1}\tilde{\mathrm {P}}_{2n-1}\right) ^{(i)}(b),\quad j=1,2, \ldots ,n-1, \end{aligned}\right. \end{aligned}$$

and

$$\begin{aligned} g_j=\int _a^b\frac{\partial ^j}{\partial x^j}\left. k\left( x,t,\tilde{\mathrm {P}}_{2n-1}(u;t)\right) \right| _{x=b}dt,\quad j=0, 1, \ldots , n-1. \end{aligned}$$

Then, system (2.11) can be formulated in the matrix form

$$\begin{aligned} U=F_0+\lambda \left( D(U)+G(U)\right) , \end{aligned}$$

which can be solved by using the following iterative method

$$\begin{aligned} U^{\left[ \upsilon +1\right] }=F_0+\lambda \left( D(U^{\left[ \upsilon \right] })+G(U^{\left[ \upsilon \right] })\right) ,\quad \upsilon =0, 1, \ldots , \end{aligned}$$
(3.14)

with the starting value \(U^{\left[ 0\right] }\).

Remark 3.2

Suppose that the Lipschitz conditions (3.12) and (3.13) are satisfied and the iterative procedure (3.14) is utilized to solve system (2.11). We can get from (3.14) that

$$\begin{aligned} \begin{aligned}&\left\| U^{\left[ \upsilon +1\right] }-U^{\left[ \upsilon \right] }\right\| _{\infty }=\vert \lambda \vert \left\| \left( D\left( U^{\left[ \upsilon \right] }\right) -D\left( U^{\left[ \upsilon -1\right] }\right) \right) +\left( G\left( U^{\left[ \upsilon \right] }\right) -G\left( U^{\left[ \upsilon -1\right] }\right) \right) \right\| _{\infty }\\&\quad \le \vert \lambda \vert \left( \left\| D\left( U^{\left[ \upsilon \right] }\right) -D\left( U^{\left[ \upsilon -1\right] }\right) \right\| _{\infty } +\left\| G\left( U^{\left[ \upsilon \right] }\right) -G\left( U^{\left[ \upsilon -1\right] }\right) \right\| _{\infty }\right) . \end{aligned}\nonumber \\ \end{aligned}$$
(3.15)

The Lipschitz condition (3.12) and the interpolation conditions \(\tilde{\mathrm {P}}_{2n-1}^{(j)}(u;t)={\tilde{u}}^{(j)}(b), j=0, 1, \ldots , n-1\) imply that each element of the vector \(D\left( U^{\left[ \upsilon \right] }\right) -D\left( U^{\left[ \upsilon -1\right] }\right) \) satisfies the following inequality:

$$\begin{aligned} \begin{aligned} \left| d_j^{\left[ \upsilon \right] }-d_j^{\left[ \upsilon -1\right] }\right|&\le \sum _{i=0}^{j-1}\left| \left( {\mathscr {D}}_{j-i-1}\tilde{\mathrm {P}}_{2n-1}^{\left[ \upsilon \right] }\right) ^{(i)}(b)-\left( {\mathscr {D}}_{j-i-1}\tilde{\mathrm {P}}_{2n-1}^{\left[ \upsilon -1\right] }\right) ^{(i)}(b)\right| \\&\le \sum _{i=0}^{j-1}\sum _{k=0}^{i}L_k\left| \left( \tilde{\mathrm {P}}_{2n-1}^{\left[ \upsilon \right] }\right) ^{(k)}(b)-\left( \tilde{\mathrm {P}}_{2n-1}^{\left[ \upsilon -1\right] }\right) ^{(k)}(b)\right| \\&=\sum _{i=0}^{j-1}\sum _{k=0}^{i}L_k\left| \left( {\tilde{u}}^{(k)}\right) ^{\left[ \upsilon \right] }(b)-\left( {\tilde{u}}^{(k)}\right) ^{\left[ \upsilon -1\right] }(b)\right| \\&=\sum _{k=0}^{j-1}(j-k)L_k\left| \left( {\tilde{u}}^{(k)}\right) ^{\left[ \upsilon \right] }(b)-\left( {\tilde{u}}^{(k)}\right) ^{\left[ \upsilon -1\right] }(b)\right| ,\\&\quad j=0, 1, \ldots , n-1. \end{aligned} \end{aligned}$$
(3.16)

Since generally we have

$$\begin{aligned} \left| \left( {\tilde{u}}^{(k)}\right) ^{\left[ \upsilon \right] }(b)-\left( {\tilde{u}}^{(k)}\right) ^{\left[ \upsilon -1\right] }(b)\right| \le \left\| U^{\left[ \upsilon \right] }-U^{\left[ \upsilon -1\right] }\right\| _{\infty },\quad k=0, 1, \ldots , j-1, \end{aligned}$$

inequality (3.16) signifies that

$$\begin{aligned} \left| d_j^{\left[ \upsilon \right] }-d_j^{\left[ \upsilon -1\right] }\right|\le & {} \sum _{k=0}^{j-1}(j-k)L_k\left\| U^{\left[ \upsilon \right] }-U^{\left[ \upsilon -1\right] }\right\| _{\infty }\\\le & {} \frac{j(j+1)}{2}L\left\| U^{\left[ \upsilon \right] }-U^{\left[ \upsilon -1\right] }\right\| _{\infty },\quad j=0, 1, \ldots , n-1, \end{aligned}$$

where L is as introduced before. Therefore, we can write

$$\begin{aligned} \left\| D\left( U^{\left[ \upsilon \right] }\right) -D\left( U^{\left[ \upsilon -1\right] }\right) \right\| _{\infty }\le \frac{n(n-1)}{2}L\left\| U^{\left[ \upsilon \right] }-U^{\left[ \upsilon -1\right] }\right\| _{\infty }. \end{aligned}$$
(3.17)

Furthermore, from the Lipschitz condition (3.13), it can be concluded that

$$\begin{aligned} \left\| G\left( U^{\left[ \upsilon \right] }\right) -G\left( U^{\left[ \upsilon -1\right] }\right) \right\| \le {\bar{L}}(b-a)\left\| \tilde{\mathrm {P}}_{2n-1}^{\left[ \upsilon \right] }(u;t)-\tilde{\mathrm {P}}_{2n-1}^{\left[ \upsilon -1\right] }(u;t)\right\| _{\infty }. \end{aligned}$$
(3.18)

As mentioned before, the polynomial \(\tilde{\mathrm {P}}_{2n-1}(u;t)\) is constructed by using the exact values \(u^{(j)}(a)\) and the approximate values \({\tilde{u}}^{(j)}(b)\) for \( j=0,1, \ldots , n-1\). Thus, by introducing

$$\begin{aligned} {\mathscr {C}}(t)=\left[ {\tilde{\phi }}_{n,0}(a+b-t), -{\tilde{\phi }}_{n,1}(a+b-t),\ldots , (-1)^{n-1}{\tilde{\phi }}_{n,n-1}(a+b-t)\right] ^T, \end{aligned}$$

we can deduce

$$\begin{aligned} \left| \tilde{\mathrm {P}}_{2n-1}^{\left[ \upsilon \right] }(u;t)-\tilde{\mathrm {P}}_{2n-1}^{\left[ \upsilon -1\right] }(u;t)\right|= & {} \left| {\mathscr {C}}^T(t)\left( U^{\left[ \upsilon \right] }-U^{\left[ \upsilon -1\right] }\right) \right| \\\le & {} n\left\| {\mathscr {C}}^T(t)\right\| _{\infty }\left\| U^{\left[ \upsilon \right] }-U^{\left[ \upsilon -1\right] }\right\| _{\infty }, \end{aligned}$$

which together with (3.15), (3.17) and (3.18) yields

$$\begin{aligned} \left\| U^{\left[ \upsilon +1\right] }-U^{\left[ \upsilon \right] }\right\| _{\infty }\le & {} \vert \lambda \vert \left( \frac{n(n-1)}{2}L\left\| U^{\left[ \upsilon \right] }-U^{\left[ \upsilon -1\right] }\right\| _{\infty }\right. \\&\quad \left. +n{\bar{L}}(b-a)\left\| {\mathscr {C}}^T(t)\right\| _{\infty }\left\| U^{\left[ \upsilon +1\right] }-U^{\left[ \upsilon \right] }\right\| _{\infty }\right) . \end{aligned}$$

Therefore, if \(\vert \lambda \vert \left( \frac{n(n-1)}{2}L+n{\bar{L}}(b-a)\left\| {\mathscr {C}}^T(t)\right\| _{\infty }\right) <1\), then it follows from the contraction mapping theorem [63] that the iterative method (3.14) has a unique solution.

The convergence of the proposed method for solving both the linear and nonlinear VIEs is analysed numerically in the next section.

4 Illustrative examples

In this section, the precision of the presented TTF and its multistep form for solving integral equation (1.1) is investigated during the numerical experiments. In order to ensure the competence of the method, we applied it to solve several VIEs. The obtained results for nine examples are reported in this section. To confirm the accuracy of the method, we compute and report the absolute errors of the approximations. Also, the obtained results are compared with the results of the other existing methods in the literature. We employ the TTF method for Example 4.1, both the TTF and multistep TTF methods for Examples 4.2–4.6, and only the multistep TTF method for Examples 4.7–4.9. The accuracy of the multistep TTF for the examples is investigated by computing the \(L_{\infty }\) error, which is defined as

$$\begin{aligned} L_{\infty }=\left\| u_{ex}(x)-{\mathscr {P}}_{2n-1}^N(u;x)\right\| _{\infty }, \end{aligned}$$

where \(u_{ex}(x)\) is the exact solution of each problem. In order to increase the speed of the algorithm, the Gauss–Legendre quadrature rule is utilized for estimating the integrals which appeared in the method. In the reported results, the quadrature formula is constructed by taking \(m=15\) for Examples 4.2, 4.3, 4.4, and \(m=10\) for the other examples. The used computational time for each problem is also reported. In order to solve systems (2.11) and (2.15) for the examples, we utilize the fsolve command in Maple software. All the computations are written in Maple 2016 software and run on a Core (TM) i7 PC with 2.70 GHz of CPU and 16 GB of RAM.

Example 4.1

As the first example, consider the nonlinear VIE [64]

$$\begin{aligned} u(x)=2-\cos (x)-\int _0^x\sin (xu(t)-t)dt,\quad x\in \left[ 0, 5\right] . \end{aligned}$$

with the exact solution \(u_{ex}(x)=1\),

Taking \(n=1\), the TTF approximates the exact solution of this problem as

$$\begin{aligned} \tilde{\mathrm {P}}_1(u;x)=1- 6.0550704156\times 10^{-20}x, \end{aligned}$$

which implies that the method can calculate the exact solution of VIEs with polynomial solutions. The result has been obtained in only 0.359 s of computational time.

Fig. 1
figure 1

a Comparison between the exact and approximate solutions for Example 4.2, b the absolute error of the TTF for Example 4.2

Full size image

Example 4.2

Now, consider the nonlinear problem [17, 18]

$$\begin{aligned} u(x)=\sin (x)-e^{\sin (x)}+1+\int _0^x\cos (t)e^{u(t)}dt,\quad x\in \left[ 0, 1\right] , \end{aligned}$$

with the exact solution \(u_{ex}(x)=\sin (x)\).

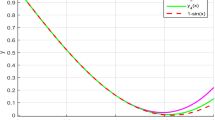
We have utilized the TTF with \(n=10\) to solve this problem. The exact and approximate solutions and the absolute error of the TTF for solving this example are plotted in Fig. 1. As can be seen, the TTF gives accurate approximation to the solution of this problem over interval \(\left[ 0, 1\right] \). Table 1 is provided to compare the TTF results with the reported results of LCQM [17] and NPSQM [18]. It indicates the accuracy of the proposed method in comparison to the other two methods. The used CPU time in this case is 1.248 s. We have also utilized the multistep TTF to obtain an appropriate estimation of the solution over large intervals. The obtained \(L_{\infty }\) errors and the used CPU times are reported in Table 2. The table shows the acceptable speed and accuracy of the method over large intervals and the influence of increasing n on the precision of the approximation.

Table 1 Absolute errors for Example 4.2
Full size table
Table 2 Results of the multistep TTF with \(N=10\) for Example 4.2
Full size table
Fig. 2
figure 2

Comparison between a the real, b the imaginary parts of the exact and approximate solutions for Example 4.3

Full size image

Example 4.3

In this example, we consider the following nonlinear VIE in the complex plane [65]

$$\begin{aligned} u(x)=f_1(x)+if_2(x)+\frac{1}{50}\int _0^x x^2t^2u^2(t)dt,\quad x\in \left[ 0, 1\right] , \end{aligned}$$

where

$$\begin{aligned} f_1(x)= & {} \sin (2\pi x)\\&+\frac{x^2\left( 8\pi ^2x^2\cos (2\pi x)\sin (2\pi x)+4\pi x\cos ^2(2\pi x) -2\pi x-\cos (2\pi x)\sin (2\pi x)\right) }{800\pi ^3},\\ f_2(x)= & {} \cos (2\pi x)\\&+\frac{x^2\left( 8\pi ^2 x^2\cos ^2(2\pi x)-4\pi ^2x^2-4\pi x\cos (2\pi x)\sin (2\pi x)+\sin ^2(2\pi x)\right) }{800\pi ^3}. \end{aligned}$$

The exact solution of this problem is

$$\begin{aligned} u_{ex}(x)=\sin (2\pi x)+i\cos (2\pi x). \end{aligned}$$

The TTF by using \(n=15\) is determined and its real and imaginary parts are compared with the exact solution in Fig. 2. In order to separately investigate the accuracy of the real and imaginary parts of the approximation, we define the following error functions

$$\begin{aligned} \mathrm {E}_1(x)=\left| \mathrm {Re}\left( \tilde{\mathrm {P}}_{2n-1}(u;x)\right) -\sin \left( 2\pi x\right) \right| ,\quad \mathrm {E}_2(x)=\left| \mathrm {Im}\left( \tilde{\mathrm {P}}_{2n-1}(u;x)\right) -\cos \left( 2\pi x\right) \right| . \end{aligned}$$

These functions are displayed in Fig. 3. Also the absolute error which is defined as

$$\begin{aligned} \text {Absolute Error}=\sqrt{\left( \mathrm {E}_1(x)\right) ^2+\left( \mathrm {E}_2(x)\right) ^2}, \end{aligned}$$

is calculated in some selected points and compared with the results of the RH wavelet method (RHWM) [65] in Table 3. The used CPU times of the proposed method and the RHWM are also compared in this table. In order to investigate the accuracy of the multistep TTF for solving this problem, we have employed it by taking \(N=30\) over intervals \(\left[ 0, 1\right] \) and \(\left[ 0, 5\right] \). The obtained \(L_{\infty }\) errors and the used CPU times are reported in Table 4. It can be concluded from the results that the TTF and its multistep form are dependable methods for solving VIEs in the complex plane.

Fig. 3
figure 3

The error of approximating a the real, b the imaginary part of the solution for Example 4.3

Full size image
Table 3 Absolute errors for Example 4.3
Full size table
Table 4 Results of the multistep TTF with \(N=30\) for Example 4.3
Full size table

Example 4.4

Consider the following VIE of the first kind [66]

$$\begin{aligned} \int _0^x\frac{e^{x-t}}{1+x^2}u(t)dt=-\frac{4\pi \cos (4\pi x)+\sin (4\pi x)-4\pi e^x}{\left( 1+x^2\right) \left( 1+16\pi ^2\right) }, \end{aligned}$$
(4.1)

where the exact solution is

$$\begin{aligned} u_{ex}(x)=\sin (4\pi x). \end{aligned}$$

Applying differentiation with respect to x on both sides of (4.1), the following second kind VIE is obtained:

$$\begin{aligned} u(x)= & {} \frac{-1}{1+16\pi ^2}\left( -16\pi ^2\sin (4\pi x)+4\pi \cos (4\pi x)-4\pi e^x\right) \\&-\int _0^x e^{x-t}u(t)dt,\quad x\in \left[ 0, 1\right] . \end{aligned}$$

Now, the TTF (2.9) can be used to approximate the solution of this problem. The exact and approximate solutions and the absolute error of the TTF by using \(n=15\) are displayed in Fig. 4. Also, we compare the TTF with the Haar wavelets method (HWM) [66], Daubechies wavelets method (DWM) [66], and Coifman wavelets method (CWM) [66] in Table 5. The listed absolute errors and computational times indicate that the proposed TTF is fast and can achieve more accurate results in comparison to the other mentioned methods. Also, the multistep TTF with \(N=10\) and different choices of n has been utilized to estime the solution of this problem over intervals \(\left[ 0, 1\right] \) and \(\left[ 0, 5\right] \). The obtained results are reported in Table 6. This table shows that by choosing suitable values of n and N, the method can provide acceptable results in short computational times.

Fig. 4
figure 4

a Comparison between the exact and approximate solutions for Example 4.4, b the absolute error of the TTF for Example 4.4

Full size image
Table 5 Absolute errors for Example 4.4
Full size table
Table 6 Results of the multistep TTF with \(N=10\) for Example 4.4
Full size table
Fig. 5
figure 5

The absolute error of a \(u_1(x)\), b \(u_2(x)\) for Example 4.5

Full size image
Table 7 Absolute errors for Example 4.5
Full size table

Example 4.5

Now, consider the following system of linear VIEs of the second kind [67, 68]

$$\begin{aligned} \left\{ \begin{aligned}&u_1(x)=\cosh (x)+x\sin (x)-\int _0^x \left( e^{x-t}u_1(t)+\cos (x-t)u_2(t)\right) dt,\\&u_2(x)=2\sin (x)+x\left( \sin ^2(x)+e^x\right) -\int _0^x \left( e^{x+t}u_1(t)+x\cos (t)u_2(t)\right) dt, \end{aligned}\right. \quad x\in \left[ 0, 1\right] , \end{aligned}$$

with the exact solutions \(u_1(x)=e^{-x}\) and \(u_2(x)=2\sin (x)\). The absolute errors of the TTF by taking \(n=10\) for approximating \(u_1(x)\) and \(u_2(x)\) are plotted in Fig. 5. The TTF results are compared with the results of the biorthogonal systems method (BSM) [67] and the block by block method (BBM) [68] in Table 7. The obtained results reveal the acceptable agreement between the TTF approximations and the exact solutions of the problem over interval \(\left[ 0, 1\right] \). The used CPU time to earn these results is only 1.560 s. Taking \(N=4\), the multistep TTF has been utilized to approximate the solution of the problem over intervals \(\left[ 0, 5\right] \) and \(\left[ 0, 10\right] \). The \(L_{\infty }\) errors of approximating \(u_1(x)\) and \(u_2(x)\) and also the used computational times are presented in Table 8. As expected, the accuracy of the results increases by increasing n.

Table 8 \(L_{\infty }\) errors of the multistep TTF with \(N=4\) for Example 4.5
Full size table

Example 4.6

Consider the following system of nonlinear VIEs of the second kind [68, 69]

$$\begin{aligned} \left\{ \begin{aligned}&u_1(x)=\cos (x)-\frac{1}{2}\sin ^2(x)+\int _0^x u_1(t)u_2(t)dt,\\&u_2(x)=\sin (x)-x+\int _0^x \left( u_1^2(t)+u_2^2(t)\right) dt, \end{aligned}\right. \quad x\in \left[ 0, 1\right] , \end{aligned}$$

with the exact solutions \(u_1(x)=\cos (x)\) and \(u_2(x)=\sin (x)\).

We have employed the TTF with \(n=10\) to approximate the solutions of this problem. The obtained absolute errors of the method for estimating \(u_1(x)\) and \(u_2(x)\) are plotted in Fig. 6. The TTF results are compared with the results of the single-term Walsh series method (STWSM) [69] and the BBM [68] in Table 9. The used computational time in this case is 5.086 s. We have also implemented the multistep TTF with \(N=15\) to obtain accurate approximations to the solutions of this problem over intervals \(\left[ 0, 5\right] \) and \(\left[ 0, 10\right] \). The \(L_{\infty }\) errors and the used computational times for three choices of n are presented in Table 10. The reported results confirm the acceptable accuracy and speed of the algorithm over large intervals.

Fig. 6
figure 6

The absolute error of a \(u_1(x)\), b \(u_2(x)\) for Example 4.6

Full size image
Table 9 Absolute errors for Example 4.6
Full size table
Table 10 \(L_{\infty }\) errors of the multistep TTF with \(N=15\) for Example 4.6
Full size table

Example 4.7

Now, consider the nonlinear VIE [70]

$$\begin{aligned} u(x)=e^{-x}+\int _0^x e^{t-x}\left( u(t)+e^{-u(t)}\right) dt,\quad x\in \left[ 0, 20\right] , \end{aligned}$$

with the exact solution \(u_{ex}(x)=\ln (x+e)\).

Since the problem is defined over a large interval, we employ the multistep TTF with \(n=4\) and \(N=20\) steps to approximate its solution. The exact and approximate solutions and the absolute error of the presented method are plotted in Fig. 7. This figure shows that by applying the multistep TTF, we can accurately approximate the solution of this problem over \(\left[ 0, 20\right] \). The used CPU time in this case is 8.705 s. Also, the influence of increasing n and N on the precision of the approximation has been investigated by computing the \(L_{\infty }\) error of the method. The results are reported in Table 11. This table shows clearly that how we can get better results by increasing n or N.

Fig. 7
figure 7

a Comparison between the exact and approximate solutions for Example 4.7 and b the absolute error of the multistep TTF for Example 4.7

Full size image
Table 11 \(L_{\infty }\) errors of the multistep TTF with different values of n and N for Example 4.7
Full size table

Example 4.8

In this example, we consider the stiff VIE [71]

$$\begin{aligned} u(x)=f(x)-\int _0^x \left( 100+1500(x-t)\right) u^3(t)dt,\quad x\in \left[ 0, 10\right] , \end{aligned}$$

where f has been chosen so that the exact solution of the problem is

$$\begin{aligned} u_{ex}(x)=2-e^{-x}. \end{aligned}$$

The multistep TTF with \(n=9\) and \(N=5\) has been utilized to approximate the solution of this problem. The used computational time in this case is 20.857 s. The agreement between the obtained approximation and the theoretical solution is displayed in Fig. 8a. The Log-plots of the absolute errors of the presented method with \(N=5\) and different choices of n over \(\left[ 0, 10\right] \) are plotted in Fig. 8b. This figure indicates that we can reduce the error of the approximation by increasing n. In Table 12, we present the absolute values of the error of the multistep TTF with a fixed n and three choices of N to confirm the influence of increasing N on the precision of the approximation.

Fig. 8
figure 8

a Comparison between the exact and approximate solutions for Example 4.8 and b log-plots of absolute errors of the multistep TTF for Example 4.8

Full size image
Table 12 Absolute errors of the multistep TTF with \(n=5\) for Example 4.8
Full size table
Fig. 9
figure 9

a The approximate solution of Example 4.9 and b The residual error of the multistep TTF for Example 4.9

Full size image

Example 4.9

As the last example, we investigate the nonlinear VIE [70, 72, 73]

$$\begin{aligned} u(x)=1+\int _0^x (x-t)^3(4-x+t)e^{t-x}\frac{u^4(t)}{1+2u^2(t)+2u^4(t)}dt,\quad t\in \left[ 0, 10\right] , \end{aligned}$$
(4.2)

which arises in the analysis of neural networks with post-inhibitory rebound [72]. The exact solution of this problem at \(x=10\) is \(u(10)=1.25995582337233\) [73]. We have utilized the multistep TTF with \(n=4\) and \(N=20\) to estimate the solution of this problem. The obtained estimation is presented in Fig. 9a. In order to study the accuracy of the multistep TTF, we plot in Fig. 9b the residual error based on VIE (4.2) which is defined as

$$\begin{aligned} \mathrm {Res}(x)= & {} {\mathscr {P}}_{2n-1}^N(u;x)-1-\int _0^x (x-t)^3(4-x+t)e^{t-x}\\&\frac{\left( {\mathscr {P}}_{2n-1}^N(u;t)\right) ^4}{1+2\left( {\mathscr {P}}_{2n-1}^N(u;t)\right) ^2+2\left( {\mathscr {P}}_{2n-1}^N(u;t)\right) ^4}dt. \end{aligned}$$

The results were obtained in 18.829 s of computational time. We also display the influence of increasing n and N on the accuracy of the presented approximation in Table 13.

Table 13 Absolute errors of the multistep TTF with different values of n and N for Example 4.9 at \(x=10\)
Full size table

5 Conclusion

Integral equations are applicable tools in the modeling of many physical phenomena. Therefore, several numerical techniques have been applied to approximate the solution of them. In this article, we presented the TTF to solve linear and nonlinear VIEs of the second kind and systems of such equations. The proposed method can achieve smooth approximations of the solution of VIEs without the need of any collocation points. We investigated the convergence analysis of the presented method. The accuracy of the approximation can be controlled by the number of the basis functions. We also presented the multistep form of the TTF to increase the precision of the approximation over large intervals. This method reduces the solution of a VIE over a large interval into the solution of a set of VIEs over small subintervals. Moreover, This method utilizes in each step the computed results of the previous step. Subsequently, there is no need to increase the number of bases and find a large number of unknowns in each step. In order to increase the speed of the implemented algorithm, we estimated the integrals which appeared in the approximations by using the Gauss–Legendre quadrature formula. The obtained algorithm can provide accurate approximations to the solution of VIEs of the second kind in acceptable computational times. The method can compute the exact solution of the problems which have polynomial analytical solutions. It can also give accurate approximation to the solution of the other VIEs. The capability of the method confirmed by employing it to solve several illustrative examples. Future work will involve the development of this method for solving nonlinear integro-differential equations and nonstandard Volterra integral equations. Also, we intend to extend the proposed idea by employing the general form of the Hermite interpolation.