Bernstein approximation technique for numerical solution of Volterra integral equations of the third kind

Abstract

We propose a numerical scheme based upon the Bernstein approximation method for computational solution of a new class of Volterra integral equations of the third kind (3rdVIEs). Construction of the technique and its practicality for proposed equations have been introduced. Furthermore we have examined the numerability and convergence analysis of the proposed scheme. Finally, we demonstrate a series of numerical examples demonstrating the effectiveness of this new technique for solving 3rdVIEs.

1 Introduction and preliminaries

In the early 1900s, Vito Volterra developed new types of equations for his work on the phenomenon of population growth and called these equations integral equations. In more detail, the integral equation is the equation that contains the unknown function under the integral sign. Integral equations; arise in chemistry, biology, physics and engineering applications modelled with initial value problems for a finite closed interval (Wazwaz 1997). There are three basic kinds of integral equations, but in this study we focus on the third kind due to the its characteristic properties than the others.

The Volterra integral equations of the third kind (3rdVIEs) can be expressed in the literature as follows:

$$\begin{aligned} x^{\beta }f(x)=x^{\beta }g(x)+\lambda \int _{0}^{x}\dfrac{1}{(x-t)^{\alpha }}{\mathcal {K}}(x,t)f(t)\mathrm{{d}}t,\quad x\in [0,\tau ], \end{aligned}$$

(1.1)

where $\lambda$ is constant, $\alpha \in [0,1)$, $\beta >0$, $\alpha +\beta \ge 1$. In addition to these, g(x) is a continuous function on $[0,\tau ]$ and ${\mathcal {K}}(x,t)$ is continuous on the domain,

$$\begin{aligned} \Delta = \lbrace (x,t)\,\, \vert \,\,\, 0 \le t < x \le \tau \rbrace , \end{aligned}$$

such that

$$\begin{aligned} {\mathcal {K}}(x,t)= t^{\alpha + \beta -1} {\mathcal {K}}^{*}(x,t), \end{aligned}$$

where ${\mathcal {K}}^{*}(x,t)$ is a continuous function on $\Delta$ and $f(\cdot )$ is unknown function to be determined. As it can be easily seen that the coefficient of the f(x) on the left-hand side of (1.1), which causes to be 3rdVIEs different from the Volterra integral equations of the first and second kind (denoted by 1stVIEs and 2ndVIEs, respectively), gives the characteristic feature to the 3rdVIEs. Therefore, they help us understand why this equations are called the third kind in the literature. As a consequence of these, over the past century, there has been a dramatic increase in the studies of the above-mentioned equations.

The existence and uniqueness theorems and regularity properties of the computational solutions to the 3rdVIEs, including equations associated with for both weakly singular kernels ($0<\alpha <1$) and smooth kernel ($\alpha =0$) have been presented in Allaei et al. (2015) for $\beta >1$ and $\beta \in [0,1)$. Additionally, at the same study, the authors have provided the conditions for g and ${\mathcal {K}}$ to obtain the cordial Volterra integral equations (cVIEs), for detailed information about cVIEs see Vainikko (2009, 2010). Therefore, this enabled to apply to Eq. (1.1) some derived consequences known for cordial equations. In addition these, the case of $\alpha +\beta >1$ has a special significance with regard to compactness. In more detail, if ${\mathcal {K}}^{*}(x,t)>0$, the integral operator related to third kind Volterra integral equations in (1.1) is not compact. In the circumstances, the classical computational techniques can not guarantee the solvability of the third kind Volterra integral equations.

As it is understood, it follows from Allaei et al. (2015), that under certain conditions on ${\mathcal {K}}(x,t)$, $\alpha$ and $\beta$ the integral operator in the (1.1) is compact and then the algebraical system resulting from the collocation technique is uniquely solvable for entire adequately small mesh sizes. However, in the non-compact circumstances, generally, the solvability of the algebraical system with equally distanced or graded mesh is not guaranteed. That is to say, computational approaches to obtain numerical solution of 3rdVIEs take an important place in the literature. In Allaei et al. (2017), the authors have presented the spline collocation technique in the piece-wise polynomial spaces directly to 3rdVIEs with noncompact operator. Additionally, in this study, the authors show that the operator associated the equivalent 2ndVIEs is compact under specific conditions which led the resultant system is uniquely computable for all adequately small size mesh diameters. In addition to these, classical and adapted version of collocation technique for solving 3rdVIEs for both linear and non-linear cases is explained, analysed and tested detailed in Shayanfard et al. (2019, 2020) and Song et al. (2019). Moreover, a spectral collocation technique, based upon the generalized Jacobi wavelets accompanied by the Gauss–Jacobi numerical integration formula has been presented in Nemati et al. (2021). Another approach for solving 3rdVIEs has been presented in Nemati and Lima (2018) by an operational matrix. All these studies show that the 3rdVIEs is worth studying and researches on this subject will increase day by day.

In addition to these, polynomials are one of the most widely used mathematical tools since they are easy to define, can be calculated quickly in the modern computer system and used to express functions in a simple form. Therefore, they played a significant role in approximation theory and numerical analysis for many years. Studies in approximation theory began when Weierstrass proved that it is possible to approximate continuous functions with the help of polynomials. In 1912, Bernstein defined new polynomials called Bernstein polynomials in the method used in the proof of the Weierstrass approximation theory Bernstein (1913). In more detailed, for each bounded function on [0, 1] , $n\ge 1$ and $x\in [0,1]$, Bernstein approximations are defined as

$$\begin{aligned} {\mathfrak {B}}_n(f;x)=\sum _{k=0}^{n} {\mathcal {P}}_{n,k}(x) f\left( k/n \right) , \end{aligned}$$

(1.2)

where and is binomial coefficient. A number of different operators have been introduced and different generalizations have been made on the basis of the linear and positive Bernstein operators that produced by Bernstein polynomials. Today, studies are still carried out using these operators, Altomare and Leonessa (2006), Altomare (2010), Altomare and Rasa (1999) and Usta (2020).

Throughout this and next sections, C[0, 1] is the space of whole continuous real valued functions on [0, 1] , endowed with the supremum norm $\Vert \cdot \Vert _{\infty }$ and the natural point-wise ordering. In addition to these, if $m\in {\mathbb {N}}$, the symbol $C^m[0,1]$ denote by the space of whole continuously m-times differentiable functions on [0, 1] .

Theorem 1

Let $f\in C[0,1]$. Then, ${\mathfrak {B}}_n(f)$ converges to f uniformly on [0, 1] .

Proof

For detailed proof, see Powel (1981). $\square$

Furthermore, the well-recognized Voronovskaya type theorem for the classical Bernstein operators $({\mathfrak {B}}_n)_{n\ge 1}$ was expressed as follows.

Theorem 2

Let $f\in C^2[0,1]$, $n\in {\mathbb {N}}$ and $0\le x \le 1$. Then, the following inequality holds;

$$\begin{aligned} \left| n({\mathfrak {B}}_n(f;x)-f(x)) -\dfrac{1}{2}x(1-x)f''(x) \right| \le \dfrac{1}{2}x(1-x){\tilde{\omega }}\left( f'';\sqrt{\dfrac{nx(1-x)+1}{n^2}} \right) , \end{aligned}$$

where ${\tilde{\omega }}$ is the least concave limit superior of the first order modulus of continuity denoted by $\omega$, satisfying for $\epsilon \ge 0$

$$\begin{aligned} \omega (f;\epsilon )\le {\tilde{\omega }}(f;\epsilon ) \le 2\omega (f;\epsilon ). \end{aligned}$$

Proof

For detailed proof, see DeVore and Lorentz (1993). $\square$

In other words, one can state the above-mentioned theorem as follows, Bustamante (2017)

$$\begin{aligned} \left| {\mathfrak {B}}_n(f;x)-f(x)\right| \le \dfrac{1}{2n}x(1-x)\Vert f'' \Vert , \end{aligned}$$

(1.3)

which means the rate of convergence of the Bernstein operators is at least $n^{-1}$ for $f\in C^2[0,1]$.

In this direction, Maleknejad et al. (2011) introduced the new method for solving 1stVIEs and 2ndVIEs using the Bernstein approximation method. In this work, they presented the convergence analysis for the introduced methods using the Voronovskaja type theorem for classical Bernstein approximation. Additionally, Usta et al. (2021) have extended this work using the Szasz–Mirakyan operators to solve 1stVIEs and 2ndVIEs and presented convergence properties of the introduced method.

In this study, motivated by the above studies, we construct a numerical scheme to solve 3rdVIEs by means of Bernstein approximation method. We will then give convergence analysis results to prove that the solution technique we proposed is theoretically consistent. Finally we will strengthen our claim with numerical results.

The rest of the presented manuscript is constructed as follows: in Sect. 2, the construction of the technique is presented, along with the Bernstein approximation method. In Sect. 3, the convergence analysis of introduced methods is given with the help of Voronovskaja type theorem of Bernstein operators. Numerical examples are presented in Sect. 4, while some concluding remarks and farther directions of study are discussed in Sect. 5.

2 Construction of the numerical scheme

The main goal in this part is to construct a numerical scheme to solve 3rdVIEs with the aid of Bernstein approximation method in a simple one dimensional setting. In line with this objective, we tackle the 3rdVIEs given in (1.1). To solve 3rdVIEs computationally, firstly, we need to approximate the unknown function f(x) which need to be determined, as follows,

$$\begin{aligned} f(x)\approx {\mathfrak {B}}_n(f(x))=\sum _{k=0}^{n} {\mathcal {P}}_{n,k}(x) f\left( k/n \right) , \end{aligned}$$

(2.1)

where ${\mathcal {P}}_{n,k}$ given as above. Since Bernstein approximation is valid for the functions defined on [0, 1] , let us consider the following third kind Volterra integral equation, that is to say,

$$\begin{aligned} x^{\beta }f(x)=x^{\beta }g(x)+\lambda \int _{0}^{x}\dfrac{1}{(x-t)^{\alpha }}{\mathcal {K}}(x,t)f(t)\mathrm{{d}}t,\quad x\in [0,1]. \end{aligned}$$

For computationally solving of this kind of integral equation, we approximate the unknown function f by (2.1). In other words, by direct substitution of the expansions for f(x) into 3rdVIEs, we deduce that,

$$\begin{aligned} x^{\beta }{\mathfrak {B}}_n(f(x))=x^{\beta }g(x)+\lambda \int _{0}^{x}\dfrac{1}{(x-t)^{\alpha }}{\mathcal {K}}(x,t){\mathfrak {B}}_n(f(t))\mathrm{{d}}t, \end{aligned}$$

(2.2)

then we have

$$\begin{aligned} x^{\beta }\sum _{k=0}^{n} {\mathcal {P}}_{n,k}(x) f\left( k/n \right) =x^{\beta }g(x)+\lambda \int _{0}^{x}\dfrac{1}{(x-t)^{\alpha }}{\mathcal {K}}(x,t)\sum _{k=0}^{n} {\mathcal {P}}_{n,k}(t) f\left( k/n \right) \mathrm{{d}}t, \end{aligned}$$

which yields,

$$\begin{aligned} \sum _{k=0}^{n}f\left( k/n \right) \left[ x^{\beta } {\mathcal {P}}_{n,k}(x) -\lambda \int _{0}^{x}\dfrac{1}{(x-t)^{\alpha }}{\mathcal {K}}(x,t) {\mathcal {P}}_{n,k}(t) \mathrm{{d}}t\right] =x^{\beta }g(x). \end{aligned}$$

It is outstanding to emphasise here that it is required to change x with $x_i=i/n+\varepsilon$, where $\varepsilon$ is arbitrary small number, before one determines the unknown coefficients $f\left( k/n \right)$, $k=0,1, \ldots , n$. In other words, in order to avoid from singularity problem, we can select for $x_i$, $i=0,1,2,\ldots ,n$ any other distinct values in [0, 1] except singular values of our integral equation, that is to say, $x_i=i/n+\varepsilon$, $i=0,1,2,\ldots ,n-1$ and $x_n=1-\varepsilon$. So we can express in matrix notation the fully discretized 3rdVIEs as follows,

$$\begin{aligned}{}[\varvec{\alpha }][\mathbf{X} ]=[\varvec{\beta }], \end{aligned}$$

where

$$\begin{aligned} {[}\varvec{\alpha }]= & {} \left[ x_i^{\beta } {\mathcal {P}}_{n,k}(x_i) -\lambda \int _{0}^{x_i}\dfrac{1}{(x_i-t)^{\alpha }}{\mathcal {K}}(x_i,t) {\mathcal {P}}_{n,k}(t) \mathrm{{d}}t\right] _{n\times n},\qquad i,k=0,1,\cdots , n,\nonumber \\ {[}\varvec{\beta }]= & {} \left[ \begin{array}{c} x_0^{\beta }g(x_0) \\ x_1^{\beta }g(x_1) \\ \vdots \\ \vdots \\ x_n^{\beta }g(x_n) \end{array} \right] _{n \times 1},\quad [\mathbf{X} ]= \left[ \begin{array}{c} f\left( 0 \right) \\ f\left( 1/n \right) \\ \vdots \\ \vdots \\ f\left( 1 \right) \end{array} \right] _{n \times 1}, \end{aligned}$$

(2.3)

where $\varvec{\alpha }$ is a $n \times n$ matrix and $\varvec{\beta }$ and $\mathbf{X}$ are $n \times 1$ vectors. These are the matrices that will be the essential part in the Matlab implementation. Then, in an effort to compute the array of $\mathbf{x}$, first of all, we are in need of to calculate matrix $\varvec{\alpha }$ and vector $\varvec{\beta }$ computationally. By the end of this process, accordingly, we will deduce $\mathbf{X}$ vector with n components. Eventually, when we specify the vector $\mathbf{X}$ we can obtain the approximate computational solution of 3rdVIEs.

It is note that, we can show f(k/n) , $k=0,1,2,\ldots ,n$ by $f_n(k/n)$, $k=0,1,2,\ldots ,n$ that are our solution in nodes k/n, $k=0,1,2,\ldots ,n$ and by substituting them in (1.2), we can find ${\mathfrak {B}}_n(f_n(x_k))$, $k=0,1,2,\ldots ,n$ that is a solution for the third kind Volterra integral equation (1.1).

Now we provide an error bound for the scheme presented above in the following theorem.

3 Convergence analysis

Now, we focus on the converge analysis of the proposed solution technique to validate it theoretically. In parallel with this purpose, we need to find an upper bound for $\sup _{x_i\in [0,1]}\vert f(x_i)-{\mathfrak {B}}_n(f_n(x_i)) \vert$ where it must go to zero in limit case. The following theorem show that the numerical solution of the 3rdVIEs convergence the exact one with larger n.

Theorem 3

Consider the 3rdVIEs given in (1.1). Assume that ${\mathcal {K}}(x,t)$ is continuous kernel on the square $[0,1]^2$ and $\varvec{\alpha }$ is a matrix given in (2.3). Then assume that the numerical solution of 3rdVIEs given in (1.1) belong to $(C \cap L^2)([0,1])$. If the matrix $\varvec{\alpha }$ is invertible, then the following inequality holds,

$$\begin{aligned} \sup _{x_i\in [0,1]}\vert f(x_i)-{\mathfrak {B}}_n(f_n(x_i))\vert \le \dfrac{1}{8n}\Vert f^{''}\Vert \left[ 1+(1+\nabla ) \Vert \varvec{\alpha }^{-1}\Vert ) \right] , \end{aligned}$$

where

$$\begin{aligned} \nabla = \sup _{x_i,t\in [0,1]}\left| \lambda \dfrac{1}{(x_i-t)^{\alpha }}{\mathcal {K}}(x_i,t)\right| , \end{aligned}$$

and f(x) is the exact solution, ${\mathfrak {B}}_n(f_n(x))$ is the numerical solution of the introduced technique, $x_i=i/n$ for $i=0,1,\ldots , n$.

Proof

Thanks to the well-known triangular inequalities, we have

$$\begin{aligned} \sup _{x_i\in [0,1]}\vert f(x_i)-{\mathfrak {B}}_n(f_n(x_i))\vert\le & {} \sup _{x_i\in [0,1]}\vert f(x_i)-{\mathfrak {B}}_n(f(x_i))\vert +\sup _{x_i\in [0,1]}\vert {\mathfrak {B}}_n(f(x_i))\nonumber \\- & {} {\mathfrak {B}}_n(f_n(x_i))\vert , =:{\mathcal {A}}_1+{\mathcal {A}}_2. \end{aligned}$$

(3.1)

So, finding an upper limit for ${\mathcal {A}}_1$ and ${\mathcal {A}}_2$ will be enough to conclude the proof. Let begin with ${\mathcal {A}}_1$. With the aid of the Voronovskaya type theorem given in (1.3), we obtain the following upper bound for ${\mathcal {A}}_1$.

$$\begin{aligned} {\mathcal {A}}_1=\sup _{x\in [0,1]}\vert f(x)-{\mathfrak {B}}_n(f(x))\vert \le \dfrac{1}{2n}x(1-x)\Vert f'' \Vert \le \dfrac{1}{8n}\Vert f'' \Vert . \end{aligned}$$

(3.2)

Then it is enough to find an upper bound for ${\mathcal {A}}_2$ to finalize the proof of theorem. If we replace $f(\cdot )$ with ${\mathfrak {B}}_n(f(\cdot ))$ in the equation

$$\begin{aligned} x^{\beta }g(x) =x^{\beta }f(x)-\lambda \int _{0}^{x}\dfrac{1}{(x-t)^{\alpha }}{\mathcal {K}}(x,t)f(t)\mathrm{{d}}t, \end{aligned}$$

(3.3)

then the function g(x) in the left hand side of the above equation is switch by a new function which we denote by h(x) . So we get

$$\begin{aligned} x^{\beta }h(x) =x^{\beta }{\mathfrak {B}}_n(f(x))-\lambda \int _{0}^{x}\dfrac{1}{(x-t)^{\alpha }}{\mathcal {K}}(x,t){\mathfrak {B}}_n(f(t))\mathrm{{d}}t. \end{aligned}$$

(3.4)

Using the (3.3) and (3.4), we deduce the following inequality,

$$\begin{aligned} x^{\beta }[g(x)-h(x)] =x^{\beta }[f(x)-{\mathfrak {B}}_n(f(x))]-\lambda \int _{0}^{x}\dfrac{1}{(x-t)^{\alpha }}{\mathcal {K}}(x,t)[f(t)-{\mathfrak {B}}_n(f(t))]\mathrm{{d}}t. \end{aligned}$$

(3.5)

Then using (3.5) and (1.3), we obtain that

$$\begin{aligned} \sup _{x_i\in [0,1]}\vert x_i^{\beta }[g(x_i)-h(x_i)] \vert&=\sup _{x_i,t\in [0,1]}\left| x_i^{\beta }[f(x_i)-{\mathfrak {B}}_n(f(x_i))]\right. \nonumber \\&\quad -\left. \lambda \int _{0}^{x_i}\dfrac{1}{(x_i-t)^{\alpha }}{\mathcal {K}}(x_i,t)[f(t)-{\mathfrak {B}}_n(f(t))]\mathrm{{d}}t\right| ,\nonumber \\&\le \sup _{x_i\in [0,1]}\left| x_i^{\beta }[f(x_i)-{\mathfrak {B}}_n(f(x_i))] \right| \nonumber \\&\quad + \sup _{x_i,t\in [0,1]} \left| \lambda \int _{0}^{x_i}\dfrac{1}{(x_i-t)^{\alpha }}{\mathcal {K}}(x_i,t)[f(t)-{\mathfrak {B}}_n(f(t))]\mathrm{{d}}t \right| ,\nonumber \\&\le \sup _{x_i\in [0,1]}\left| x_i^{\beta }[f(x_i)-{\mathfrak {B}}_n(f(x_i))] \right| \nonumber \\&\quad + \sup _{x_i,t\in [0,1]}\ \left| \lambda \dfrac{1}{(x_i-t)^{\alpha }}{\mathcal {K}}(x_i,t)[f(t)-{\mathfrak {B}}_n(f(t))]\right| ,\nonumber \\&\le \sup _{x_i\in [0,1]}\left| x_i^{\beta }[f(x_i)-{\mathfrak {B}}_n(f(x_i))] \right| \nonumber \\&\quad + \sup _{x_i,t\in [0,1]}\left| \lambda \dfrac{1}{(x_i-t)^{\alpha }}{\mathcal {K}}(x_i,t)\right| \sup _{x_i\in [0,1]}\left| [f(t)-{\mathfrak {B}}_n(f(t))]\right| ,\nonumber \\&\le \frac{1}{8n} \Vert f^{''}\Vert +\nabla \frac{1}{8n} \Vert f^{''}\Vert ,\nonumber \\&= (1+\nabla )\frac{1}{8n} \Vert f^{''}\Vert . \end{aligned}$$

(3.6)

On the other hand, we have $[\varvec{\alpha }][\mathbf{X} ]=[\varvec{\beta }]$ and $[\varvec{\alpha }][\tilde{\mathbf{X }}]=[\tilde{\varvec{\beta }}]$, where

$$\begin{aligned} {[}{} \mathbf{X} ]=[{\mathfrak {B}}_n(f_n(x_i))], \quad [\varvec{\beta }]=[x^{\beta }g(x_i)], \quad [\tilde{\mathbf{X }}]=[{\mathfrak {B}}_n(f(x_i))], \quad [\tilde{\varvec{\beta }}]=[x^{\beta }h(x_i)], \end{aligned}$$

therefore using (3.6), we have

$$\begin{aligned} {\mathfrak {B}}_n(f(x))-{\mathfrak {B}}_n(f_n(x))=\varvec{\alpha }^{-1}x^{\beta }[h(x)-g(x)], \end{aligned}$$

which yields,

$$\begin{aligned} {\mathcal {A}}_2=\sup _{x_i\in [0,1]}\left| [{\mathfrak {B}}_n(f(x_i))-{\mathfrak {B}}_n(f_n(x_i))] \right|\le & {} \Vert \varvec{\alpha }^{-1} \Vert \sup _{x_i\in [0,1]}\left| x_i^{\beta }[g(x_i)-h(x_i)]\right| ,\nonumber \\\le & {} (1+\nabla )\frac{1}{8n} \Vert \varvec{\alpha }^{-1} \Vert \cdot \Vert f^{''}\Vert . \end{aligned}$$

(3.7)

Finally, by substituting (3.7) and (3.2) into (3.1), we get the desired results thus the proof is completed. $\square$

The drawback of the Theorem 3 is the error bound of the scheme contains the quantity $\Vert \alpha ^{-1} \Vert$. Hence, in the following Lemma using extra condition, we found a bound for $\Vert \alpha ^{-1} \Vert$ and condition number of $\alpha$.

Lemma 1

Suppose that the same circumstances in previous theorem hold. Let $\mathbf{I}$ is the $n\times n$ identity matrix and $\Vert \cdot \Vert$ is the maximum norm of rows. In the given circumstances, we have

$$\begin{aligned} \text{ cond }( \varvec{\alpha }) \le \dfrac{1+\nabla _1}{1-\nabla _2}, \end{aligned}$$

such that

$$\begin{aligned} \Vert \varvec{\alpha }-\mathbf{I} \Vert =\nabla _2<1, \end{aligned}$$

where $\nabla _1=\max \nolimits _{i} \vert \lambda \vert \int _{0}^{x_i}\dfrac{1}{(x_i-t)^{\alpha }}\vert {\mathcal {K}}(x_i,t)\vert \mathrm{{d}}t$.

Proof

Let us begin with finding an upper bound $\Vert \varvec{\alpha } \Vert$ utilizing (2.3), as follows

$$\begin{aligned} \Vert \varvec{\alpha }\Vert= & {} \max _{i}\sum _{k=0}^n\left| x_i^{\beta } {\mathcal {P}}_{n,k}(x_i) -\lambda \int _{0}^{x_i}\dfrac{1}{(x_i-t)^{\alpha }}{\mathcal {K}}(x_i,t) {\mathcal {P}}_{n,k}(t) \mathrm{{d}}t\right| ,\\= & {} \max _{i}\left| x_i^{\beta } -\lambda \int _{0}^{x_i}\dfrac{1}{(x_i-t)^{\alpha }}{\mathcal {K}}(x_i,t) \mathrm{{d}}t\right| ,\\\le & {} \max _{i} \left[ 1+\vert \lambda \vert \int _{0}^{x_i}\dfrac{1}{(x_i-t)^{\alpha }}\vert {\mathcal {K}}(x_i,t)\vert \mathrm{{d}}t \right] ,\\\le & {} (1+\nabla _1). \end{aligned}$$

Then, we need to find another upper bound for $\Vert \varvec{\alpha }^{-1} \Vert$. For that, we have

$$\begin{aligned} \Vert \varvec{\Lambda } \Vert = \Vert \varvec{\alpha }-\mathbf{I} \Vert =\nabla _2<1. \end{aligned}$$

Due to the geometric series theorem, we conclude that

$$\begin{aligned} \Vert \varvec{\alpha }^{-1} \Vert = \Vert (\mathbf{I} +\varvec{\Lambda })^{-1} \Vert \le \dfrac{1}{1-\Vert \varvec{\Lambda } \Vert }=\dfrac{1}{1-\nabla _2}. \end{aligned}$$

Therefore,

$$\begin{aligned} \text{ cond }( \varvec{\alpha })=\Vert \varvec{\alpha }\Vert \Vert \varvec{\alpha }^{-1}\Vert \le \dfrac{1+\nabla _1}{1-\nabla _2}, \end{aligned}$$

thus the desired result has been obtained. $\square$

4 Numerical results

So far this manuscript has focused on the construction of the numerical solution procedure of 3rdVIEs and the convergence analysis. In this section we will present and test various constructive computational experiments to demonstrate the proficiency of our numerical algorithm for solving 3rdVIEs. Henceforward, Max-Err stands for the maximum modulus error, i.e., $\Vert f(x)-{\mathcal {B}}_n(f_n(x))\Vert$, and Rms-Err stands for the standard root mean squared error, i.e.

$$\begin{aligned} \sqrt{\dfrac{\sum \nolimits _{i=1}^{\text {Neval}}\vert f(x_i)-{\mathcal {B}}_n(f_n(x_i)) \vert }{\text {Neval}}}, \end{aligned}$$

where f(x) is the exact solution 3rdVIEs, ${\mathcal {B}}_n(f_n(x))$ is the approximate solution 3rdVIEs, and Neval is the number of the test points. Time represents the CPU time consumed in each numerical examples. All these examples have been performed in MATLAB because it is convenient for our algorithm.

4.1 Experiment 1

(Nemati et al. 2021) We first consider the following 3rdVIEs,

$$\begin{aligned} x^{1/2}f(x)=x^2-B\left( \dfrac{1}{2},\dfrac{9}{2}\right) x^4+\int _{0}^x \dfrac{1}{(x-t)^{1/2}}t^2 f(t)\mathrm{{d}}t, \quad 0\le x \le 1, \end{aligned}$$

where B(p, q) is the Beta function defined by,

$$\begin{aligned} B(p,q)=\int _0^1 r^{p-1}(1-r)^{q-1}dr, \end{aligned}$$

for $p,q>0$. The exact solution of the above 3rdVIEs here is $f(x)=x^{3/2}$, and $\varepsilon =0.01$.

Table 1 Bernstein approximation results for 3rdVIEs with $\varepsilon =0.01$ for different values of n

Fig. 1

Numerical solution of 3rdVIEs via Bernstein approximation technique: exact solution (blue-line), Bernstein approximation technique of 3rdVIEs (red-circle) (colour figure online)

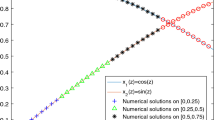
In Table 1, we present the maximum error, root mean square error and the CPU time for the solution of the first experiment for different values of n. Additionally, in Fig. 1, we draw the exact solution and approximate solution of 3rdVIEs at the same Figure. Both Table and Figure show that, the proposed method provide the reliable numerical solution method for 3rdVIEs. Additionally, the last column of Table 1 shows the computational time of algorithm.

4.2 Experiment 2

(Nemati et al. 2021) Now, let consider another example given as below,

$$\begin{aligned} x^{2/3}f(x)=x^{47/12}\left( 1-\dfrac{\Gamma \left( 1/3 \right) \Gamma \left( 55/12 \right) }{\pi \sqrt{3}\Gamma \left( 59/12 \right) } \right) +\int _{0}^x \dfrac{\sqrt{3}}{3\pi }t^{1/3}\dfrac{1}{(x-t)^{2/3}} f(t)\mathrm{{d}}t, \quad 0\le x \le 1. \end{aligned}$$

The exact solution of the above 3rdVIEs here is $f(x)=x^{13/4}$, and $\varepsilon =0.001$.

Table 2 Bernstein approximation results for 3rdVIEs with $\varepsilon =0.001$ for different values of n

Similarly, in the first round of the second experiment, in Table 2, we present the maximum error, root mean square error and the CPU time for the solution of the second experiment for different values of n. In addition to this, in Fig. 2, we plot the exact solution and approximate solution of 3rdVIEs at the same figure.

It can be easily seen that it is immediately obvious from these results, both table and figure show that, the proposed method provide the reliable numerical solution method for 3rdVIEs.

Fig. 2

Numerical solution of 3rdVIEs via Bernstein approximation technique: exact solution (blue-line), Bernstein approximation technique of 3rdVIEs (red-circle) (colour figure online)

4.3 Experiment 3

(Shayanfard et al. 2019) Finally, we present the last experiment to show the reliability of the method as follows

$$\begin{aligned} xf(x)=x^2\left( 1-\dfrac{x}{3} \right) +\int _{0}^x t f(t)\mathrm{{d}}t, \quad 0\le x \le 1. \end{aligned}$$

The exact solution of the above 3rdVIEs here is $f(x)=x$, and $\varepsilon =0.01$.

Table 3 Bernstein approximation results for 3rdVIEs with $\varepsilon =0.01$ for different values of n

Finally, in Table 3, we present the maximum error, root mean square error and the CPU time for the solution of the first experiment for different values of n. Furthermore, in Fig. 3, we draw the exact solution and approximate solution of 3rdVIEs at the same figure. We see from the table and figure that the proposed method provide the reliable numerical solution method for 3rdVIEs. Again, the last column of Tables 2 and 3 demonstrate the CPU time of algorithm.

In this section, it has been provided a series of the numerical experiments and these show that the proposed method can be applied successfully for solving 3rdVIEs. Especially, this method provide good results in the small number of iteration.

Fig. 3

Numerical solution of 3rdVIEs via Bernstein approximation technique: exact solution (blue-line), Bernstein approximation technique of 3rdVIEs (red-circle) (colour figure online)

5 Concluding remarks

In the existing paper, we proposed and tested a numerical scheme based upon the Bernstein approximation technique for solving a new class of 3rdVIEs. Construction of the technique and its practicality for presented equations have been introduced. in additional to these, we have examined the numerability and convergence analysis of the proposed scheme. At the end of the paper, we tested a series of numerical examples demonstrating the effectiveness of this new technique for solving 3rdVIEs.