Matching numbers in fuzzy graphs

Abstract

The present study aims to introduce new methods to achieve optimal matching in fuzzy graphs and classify the fuzzy sizes of the edges and vertices of a matching called “matching number”. Matching numbers in a fuzzy graph are not only a direct tool in improving existing matching optimization algorithms, but also can be used to build optimization algorithms based on the vertices of a matching. Thus, introduce the properties of matching numbers which are useful in constructing and solving edge-fuzzy and vertex-fuzzy maximization problems.

1 Introduction

Conflict between co-workers in a workplace is a part of employees’ daily work lives. From a problem-oriented perspective, any conflict situation is a problem which should be addressed. Therefore, the first step of conflict resolution is to understand that the current situation does not correspond to the ideal situation. The second stage of problem-solving is related to the production of alternative solutions by available information. Finally, the decision made about each of the alternative solutions and its implementation is considered as the end of the process. March and Simon [14] considered conflict as a failure of standard decision-making mechanisms, where an individual or group has difficulty in choosing the optimal reciprocal alternative. The problems of task assignment is a part of the organizational conflict, and the disruptive nature of the conflict can be resolved by selecting and introducing an algorithm which employs fair standards and procedure. Matching theory in crisp graphs can provide impartially solutions to such problems [10, 18, 30]. The clash of goals, ideas, attitudes, and behaviors produces different types of conflict situations. The evaluation of these parameters is not accurate for employees in the workplace with the criteria of crisp graphs. Therefore, the graph displaying the value of such relationships is a fuzzy graph. Further, deciding on the positions of employees in the workplace which, can result in the least amount of work conflict between individuals is consistent with the valuation of uncertain criteria. New patterns in decision-making theory are modeled with fuzzy graph infrastructures [27, 28]. Thus, we propose a model for resolving conflict problem in the workplace and deciding on the most appropriate partner in the present study.

Kaufmann first introduced the concept of fuzzy graphs to express uncertainty in networks [13]. However the definition of a fuzzy graph was officially introduced by Rosenfeld [23]. Additional discussions on fuzzy graph theory were provided by Mordeson et al. [16]. Applied and new developments of fuzzy graph theory were reported [3, 7, 8, 15, 25, 26]. Although the adjacency of vertices is important in graph models, separate edges with special properties are considered in some cases. Matching is considered as one of the main topics studied in graph theory and computer science. Today, some scholars consider the definition of independent domination by Sumosandaram [31], who first introduced matching in fuzzy graphs [29]. Actually, an independent domination is a matching like in crisp graphs with effective edges. A domination may not include many nonadjacent edges. Innovative and new work was done on domination, independent of the concept of matching [4, 24]. Ramakrishnan and Vaidyanathan [22] introduced matching for fuzzy graphs by using the concept of fractional matching. The definition of matching in a fuzzy graph, based on the fractional matching, uses the inherent functions attributed to the edges, and compares the above sum with the value of each vertex (instead of comparing with 1). Thus, in this paper, in addition to maintaining the concept of matching in a crisp graph, we present a definition which can highlight the diversity of matching by looking at the characteristics of edges and vertices fuzzy values. Consequently, classical problems are reconstructed in optimizing matching from edge and vertex value perspectives, and the methods are introduced for these optimization.

2 Preliminaries

In this section, we introduce some preliminary definitions and results which are used in this paper. Let $G^{*}=(V,E)$ is a simple crisp graph (no loops and duplicate edges). Let’s have a brief overview of the concepts related to matching in crisp graphs. A matching M in a graph $G^{*}$ is a set of pairwise nonadjacent edges. An M-alternating path or cycle in $G^{*}$ is a path or cycle whose edges are alternately in M and $E \setminus M$. In an M-alternating path if neither its origin nor its terminus is covered by M the path is called an M-augmenting path. The two ends of each edge of M are matched under M, and each vertex incident with an edge of M are covered by M. A perfect matching is the one which covers every vertex of the graph $G^{*}$ and a maximum matching is the one which covers as many vertices as possible. The number of edges in a maximum matching of a graph $G^*$ is called matching number of $G^*$ and is denoted by $\alpha '(G^*)$. A matching M in a graph $G^{*}$ is a maximum matching if and only if $G^{*}$ contains no M-augmenting path (Berge’s Theorem). See [2, 5, 6] for more information.

Let V be a set. A fuzzy relation $\mu$ on V is a fuzzy subset of $E=V\times V$. From now on, for all $u, v \in V$ , we use uv instate of $(u, v)\in E=V\times V$. A fuzzy graph $G=(V, \sigma , \mu )$ is a triple consisting of a nonempty set V, a fuzzy subset $\sigma$ and a fuzzy relation $\mu$ on V such that for all $u, v \in V$, $\mu (uv) \le \sigma (u) \wedge \sigma (v)$ [16, 23].

We often refer to values of these two functions as degrees of membership and can talk about the support of these fuzzy subsets. In other words, $\sigma ^*=\{v\in V |\sigma (v)>0\}$ and $\mu ^*=\{uv\in E |\mu (uv)>0\}$.

Definition 2.1

[20, 21]. Let $G=(V,\sigma ,\mu )$ be a fuzzy graph. Then,

• (i) The degree of a vertex $u\in V$ is defined as $(fd)(u) = \sum _{\begin{array}{c} v \in V \\ v\ne u \end{array}}\mu (uv)$.

• (ii) The degree of an edge $uv \in E$ is defined as $(fd)(uv)= \sum _{x\in V}\mu (ux)+\sum _{x\in V}\mu (xv)-2\mu (uv)$.

A path P in a fuzzy graph $G= (\sigma , \mu )$ is a sequence of distinct vertices $u_0, u_1, \ldots , u_n$ (except possibly $u_0$ and $u_n$) such that $\mu (u_{i-1}u_i) > 0$ for any $i = 1, \ldots , n$. The strength of P is defined to be $\wedge _{i=1}^n\mu (u_{i-1}u_i)$. In other words, the strength of a path is defined to be the weight of the weakest edge. We denote the strength of a path P by s(P). The strength of connectedness between two vertices u and v is defined as the maximum of the strengths of all paths between u and v and is denoted by $\mu ^\infty (u, v)$ or $CONN_G(u, v)$. The strongest path joining any two vertices u and v has strength $\mu ^\infty (u, v)$ [16].

Definition 2.2

[16]. Let $G= (V, \sigma ,\mu )$ be a fuzzy graph. Then, a fuzzy graph $H=(V,\tau ,\nu )$ is called a partial subgraph of G if $\tau \subseteq \sigma$ and $\nu \subseteq \mu$. Similarly, the fuzzy graph $H = (P, \tau , \nu )$ is called a subgraph of G induced by P, if $P \subseteq V$, $\tau (x) = \sigma (x)$ for all $x \in P$, and $\nu (xy) = \mu (xy)$ for all $x, y \in P$. We write $\langle P \rangle$ to denote the subgraph induced by P.

Note From now on, $G= (V, \sigma ,\mu )$ or G is a fuzzy graph; otherwise, it is state.

3 Matching in fuzzy graphs

In this section, we introduce the notation of matching which can preserve its main concepts and properties in crisp graphs and are considered as the characteristics of fuzzy graphs, namely, the degrees of membership for the vertices and edges. First, with a simple change, there is a definition similar to what is for crisp graphs. In this definition, the edges (the fuzzy value of the edges) are considered. Then, the vertices are highlighted and the topic continues with a focus on the edges and vertices values, along with a background of the number of edges (the classical concept).

Definition 3.1

A subgraph of G such as $M=(W,\sigma _M,\mu _M)$ is called a matching in G if only one $v \in W$ can be found for all $u \in W$ such that $u \ne v$ and $\mu _M(uv)>0$.

If M is a matching in G, we denote vertices set and edges set of M by $V_s(M)$ and $E_s(M)$, respectively. A matching M in G is a covering matching if $V=V_s(M)$.

Example 3.2

Figure 1 shows a fuzzy graph G and a sample matching of G.

$$\begin{aligned} V_s(M)=\{v_1, v_2, v_4, v_5\}, E_s(M)=\{e_4, e_6\}. \end{aligned}$$

Fig. 1

A fuzzy graph and a sample matching

We denote the collection of all matchings in G by ${\mathscr {M}}(G)$. Since we can assume $\mu (e)=1$ in a crisp graph $G^{*}=(V,E)$ for all $e\in E$, we have:

Corollary 3.3

Every matching in $G^{*}=(V,E)$ induces a matching in G.

Because we consider the vertices in our definitions, we consider a matching as a set of triples in the form $\left\langle \ldots , v_ie_jv_k, \ldots \right\rangle$ wherever we need to mention the edges and vertices specifically. Thus, the matching M in Example 3.2 can be represented as $\left\langle v_1e_6v_5, v_2e_4v_4\right\rangle$.

Proposition 3.4

If M is a matching on G, then $\mu ^{\infty }(u,v)=\mu (uv)$ for all $u, v\in V_s(M)$.

Proof

Let $u, v\in V_s(M)$. If there is a path P to join u to v, this path is a single edge uv and $s(P)=\mu (uv)$. Otherwise, $s(P)=\mu (uv)=0$. Thus, $\mu ^{\infty }(u,v)=\mu (uv)$ in any case. $\square$

Theorem 3.5

If $M=(V_s(M),\sigma _M,\mu _M)$ is a matching of G, $(fd)(u)=(fd)(v)=\mu (uv)$ and $(fd)(uv)=0$ for any $uv \in \mu _M^*$.

Proof

Since for all $v\in V_s(M)$, only one $u\in V_s(M)$ is available such that $\mu (uv)>0$, we get

$$\begin{aligned} (fd)(u) = \sum _{\begin{array}{c} x \in V_s(M) \\ x\ne u \end{array}} \mu (ux)=\sum _{x = v }\mu (ux)=\mu (uv). \end{aligned}$$

and

$$\begin{aligned} (fd)(uv)&= \sum _{x\in V_s(M)}\mu (ux)+\sum _{x\in V_s(M)}\mu (xv)-2\mu (uv)\\&= \sum _{x=v}\mu (ux)+\sum _{x=u}\mu (xv)-2\mu (uv)\\&= \mu (uv)+\mu (uv)-2\mu (uv)\\&=0. \end{aligned}$$

$\square$

Based on graph theory, increasing the number of edges is considered as a matching problem [6]. In fuzzy graphs, depending on its applications, we are interested in knowing when the fuzzy values of the entire edges and vertices of the matching are maximum or minimum. For example, in a job assignment problem, increasing the fuzzy value of a job allocation results in higher costs (maximizing the value of matching edges) if rating the amount of income per person in the target job is the fuzzy value of the edges, while allocating jobs with the lowest fuzzy value reduces costs (minimizing the value of matching edges). Therefore, a job allocation can be tailored to the financial strength of the organization, as well as in the status of importance of the needs of business in order to attract the highest possible value for the bidders. An optimal job allocation based on the value of fuzzy graph vertices is that, professional occupations are assigned to individuals with a better capability (matching vertex value maximization) in a matching. Further, in a situation in which some professions do not require professional expertise, people with less work experience can take those jobs (minimizing the value of matching vertices). Now, we describe the definitions, concepts, and theorems for the matching numbers.

Definition 3.6

Let M be a matching on G. Then,

• (i) The matching edge-fuzzy number of M is defined by:

  $$\begin{aligned} \lambda _{E}(M)=\sum _{e \in E_s(M)}\mu (e). \end{aligned}$$

• (ii) The matching vertex-fuzzy number of M is defined as follows.

  $$\begin{aligned} \lambda _{V}(M)=\sum _{v \in V_s(M)}\sigma (v). \end{aligned}$$

• (iii) The matching crisp number of M is defined as follows.

  $$\begin{aligned} \lambda _C(M)=|E_s(M)|. \end{aligned}$$

We refer to $\lambda _{E}(M)$, $\lambda _{V}(M)$, and $\lambda _C(M)$ as matching fuzzy principal numbers (MFPNs) of M.

Example 3.7

The MFPNs for matching M in Example 3.2, are as follows:

$$\begin{aligned} \lambda _{E}(M)=0.8\ \ , \ \ \lambda _{V}(M)=2.7 \ \ , \ \ \lambda _C(M)=2. \end{aligned}$$

Definition 3.8

Let M be a matching on G. Then, we have:

• (i) The matching maximum edge-fuzzy number of G is defined by:

  $$\begin{aligned} \lambda _E^{max}=Max\{\lambda _{E}(M):M\in {\mathscr {M}}(G)\}. \end{aligned}$$

• (ii) The matching maximum vertex-fuzzy number of G is defined by:

  $$\begin{aligned} \lambda _V^{max}=Max\{\lambda _{V}(M):M\in {\mathscr {M}}(G)\}. \end{aligned}$$

• (iii) The matching maximum crisp number of G is defined by:

  $$\begin{aligned} \lambda _C^{max}=Max\{\lambda _{C}(M):M\in {\mathscr {M}}(G)\}. \end{aligned}$$

We refer to these numbers as MMEF, MMVF, and MMC numbers, respectively.

In a crisp graph, several matchings with MMC number can be obtained, the importance of which are the same. However, in the fuzzy sense, we differentiate between these matchings in terms of fuzzy value. For example, the graph has the greatest number of edges in the optimal state of a matching in crisp graph, the matching of which is not unique. However, we seek to optimize the values of a matching in the context of fuzzy sense. In this case, two matchings having the same MMC number, cannot be considered as the same.

Example 3.9

In Fig. 2 we show a fuzzy graph and all of its matchings with MMC number. By considering the matching principal numbers, we will get a fuzzy ranking for these matchings. All of the matching principal numbers of $G=(\mu ,\sigma )$ are listed in Table 1. Then, by routine calculation, we have $\lambda _C^{max}=2$, $\lambda _E^{max}=1$ and $\lambda _V^{max}=2.7$.

Fig. 2

A fuzzy graph and all its matching with MMC number

Table 1 Matching principal numbers of $G=(\mu ,\sigma )$

Based on the Example 3.9, only one of the matchings ($M^1$) has the MMEF number. In addition, if a matching has the MMEF number, its crisp number is not necessarily the maximum.

Example 3.10

Figure 3 shows a fuzzy graph, in which a matching with MMEF number has only one edge, while the MMC number of this graph is 2. Table 2 indicates all the matching principal numbers. As shown, $\lambda _C^{max}=2$, $\lambda _E^{max}=0.7$ and $\lambda _V^{max}=2.6$ (Table 2).

Fig. 3

A fuzzy graph and its matchings with MMEF number and MMC number

Table 2 Matching principal numbers

Proposition 3.11

Let M be a matching on G. Then, for all $M \in {\mathscr {M}}(G)$, $\lambda _{E}(M)<\lambda _{V}(M)$.

Proof

Suppose $M \in {\mathscr {M}}(G)$. Since G is a fuzzy graph, $\mu (uv)\le \sigma (u)\wedge \sigma (v)$ for all $e=uv \in M$. Then, we have:

$$\begin{aligned} \lambda _{E}(M)= \sum \limits _{uv\in M}\mu (uv) \leqslant \sum \limits _{u,v\in V_s(M)}\{\sigma (u)\wedge \sigma (v) \} < \sum \limits _{v\in V_s(M)}\sigma (v)=\lambda _{V}(M). \end{aligned}$$

$\square$

Definition 3.12

Let M be a matching of G. A fuzzy M-augmenting path in G is an M-alternating path including distinct vertices $v_0, v_1, \ldots , v_m, v_{m+1}$. Thus we have:

• (i) $\mu (v_{i-1}v_i) > 0$, $i = 1, \ldots , m+1$,

• (ii) $\{v_1, \ldots , v_m\}\subseteq V_s(M)$,

• (iii) None of $v_0$ and $v_{m+1}$ are in $V_s(M)$.

Corollary 3.13

If P is a fuzzy M-augmenting path in G, it is M-augmenting path in $G^*$.

Let M be a matching of G, P be a fuzzy M-augmenting path and $\oplus$ indicates the symmetric difference. Since $M\oplus P$ is a collection of nonadjacent edges and $\mu (e)>0$ for all $e\in M\cap P$, we conclude that $M\oplus P$ is a matching. Now, we compare matching numbers of $M\oplus P$ and M.

Theorem 3.14

Let M be a matching of G. $\lambda _{V}(M\oplus P)>\lambda _{V}(M)$ if P is a fuzzy M-augmenting path.

Proof

Let $m\in N$ and P be the sequence of vertices in the form of $v_0, v_1, \ldots , v_m, v_{m+1}$. Then, by Definition 3.12, we have:

$$\begin{aligned} V_s(M\oplus P)=V_s(M)\bigcup \{v_0,v_{m+1}\}. \end{aligned}$$

So, by Definition 3.8, we have:

$$\begin{aligned} \lambda _V(M\oplus P)= & {} \sum _{v\in V_s(M\oplus P)}\sigma (v)\\= & {} \sum _{v\in V_s(M)}\sigma (v)+\sigma (v_0)+\sigma (v_1)=\lambda _V(M)+\sigma (v_0)+\sigma (v_1). \end{aligned}$$

$\square$

In the following example, we show that in Theorem 3.14, there is no increase in matching edge-fuzzy number.

Example 3.15

In Fig. 4, we see the matching $M=\left\langle v_4e_5v_3\right\rangle$ and the fuzzy M-augmenting path $P=v_1v_4v_3v_5$. By constructing the matching $M\oplus P=\left\langle v_1e_3v_4, v_3e_4v_5\right\rangle$, $\lambda _E(M\oplus P)<\lambda _E(M)$. Comparison of M and $M_{\oplus }$ P principal numbers is given in Table 3.

Fig. 4

A matching M, its augmenting path P and expansion of M to $M\oplus P$

Table 3 Comparing the principal numbers of M and $M\oplus P$

Since there is no dependence between the MMC and MMEF number, there is a relatively strong dependence between the MMC and MMVF number. Theorem 3.16 is the first step in introducing such a relationship and we continue to explain more affiliations.

Theorem 3.16

If M is a matching with MMVF number, M accepts MMC number.

Proof

Let M be a matching with MMVF number. Then, it is sufficient to show that M is a matching which has the maximum number of edges. Since M is a matching in $G^*$, if there is at least one M-augmenting path P, then the symmetric difference $M\oplus P$ increases the matching vertex-fuzzy number by Theorem 3.14. Thus the maximal condition of MMVF number of M holds. Hence, there is no M-augmenting path, and M has the maximum number of edges by Berge’s Theorem. $\square$

Since a fuzzy covering matching contains all vertices of a fuzzy graph, each fuzzy covering matching admits MMVF number, and the following corollary is obtained.

Corollary 3.17

If M is a fuzzy covering matching, then M accepts the MMVF number.

By Theorem 3.16, every matching with MMVF number has MMC number. However, sufficient condition can be found. To this aim, we need a definition. For a fuzzy graph $G=(\mu ,\sigma )$ we assume that each vertex has distinct labels from 1 to |V|. The label assigned to vertex v is denoted by l(v).

Definition 3.18

• (i) For arbitrary two vertices $v_1, v_2\in V$, we say $v_1$ is fuzzy prior to $v_2$ and is denoted by $v_1\prec v_2$ if and only if $\sigma (v_1)<\sigma (v_2)$ or $\sigma (v_1)=\sigma (v_2)$ and $l(v_1)<l(v_2)$.

• (ii) Let $M^1$ and $M^2$ be two matchings of G such that $| V_s(M^1) | = | V_s(M^2)|$. Then, $M^1$ is called a fuzzy prior to $M^2$ and denoted by $M^1 \prec M^2$ if and only if $\lambda _V(M^1) < \lambda _V(M^2)$.

• (iii) In the set $\{M^i | 1\le i \le k\}$, including all matchings in G with MMC number, a matching such as $M^L$ is called a fuzzy strong-vertex matching, if $M^i \prec M^L$, $i=1, \ldots , k$.

Accordance to Definition 3.18(ii) and (iii), each pair of subgraphs can be compared for more general term, and thus the fuzzy strong-vertex subgraph is identified.

Proposition 3.19

If $M^L$ is a fuzzy strong-vertex matching on G, then $\lambda _V(M^L)=\lambda _V^{max}$.

Proof

If $M^*$ is a matching that $\lambda _V(M^*)=\lambda _V^{max}$, then $\lambda _V(M^L)\le \lambda _V(M^*)$. Hence, by Theorem 3.16, $M^{*}$ admits the MMC number and $\lambda _V(M^*)\le \lambda _V(M^L)$ by definition of fuzzy strong-vertex matching. $\square$

To complete the preparations for finding the matchings with maximum principal numbers, we are going to redesign the Mendelsohn–Dulmage Theorem [17] for fuzzy graphs. First, we construct pseudo-fuzzy restrictions of bipartite fuzzy graphs. Assume that $G=(\mu ,\sigma )$ is a fuzzy bipartite graph, the set of vertices is considered to be $V = S\cup T$. We consider the pseudo-fuzzy restriction $G^S = (\mu ,\sigma _S)$. Thus we have:

$$\begin{aligned} E(G^S )=E(G),\quad V(G^S )=V(G)=V\quad \text {and} \quad \sigma _S(v)={\left\{ \begin{array}{ll} \sigma (v) &{} \quad v \in S \\ l(v) &{} \quad v \in T \end{array}\right. }. \end{aligned}$$

Similarly, we consider the pseudo-fuzzy restriction $G^T=(\mu ,\sigma _T)$ as follows.

$$\begin{aligned} E(G^T )=E(G),\quad V(G^T )=V(G)=V \quad \text {and} \quad \sigma _T(v)={\left\{ \begin{array}{ll} \sigma (v) &{} \quad v \in T \\ l(v) &{} \quad v \in S \end{array}\right. }. \end{aligned}$$

We use this in the methods for finding a matching with maximum principal numbers.

Now, we can present a remake of Mendelsohn–Dulmage Theorem.

Theorem 3.20

Given two matchings $M^S$ and $M^T$, respectively, in the pseudo-fuzzy restrictions $G^S$ and $G^T$ of a bipartite fuzzy graph $G = (\mu ,\sigma )$ with $V=(S\cup T)$ as vertices set. There is a new matching $M^*\subseteq M^S\cup M^T$, which matches all of the vertices covered by $M^S$ and $M^T$.

Proof

The details of the proof, are completely compatible with the proof of Mendelsohn–Dulmage’s Theorem. $\square$

4 Matching maximum principal number problems

In this section matching maximum principal number problems are discussed. Before focusing on general states, it is easy to find the matching maximum principal number for paths and cycles. In fact, we can obtain a matching by alternating selection the edges for paths and cycles. Among two situations the matching with a larger number ($\lambda _E$ or $\lambda _V$) makes the maximum principal number. Regarding the general cases of fuzzy graphs, we consider the problems of finding the matching maximum principal numbers as follows:

• (i) Matching Maximum Edge-Fuzzy Number Problem (MME-FN)

• (ii) Matching Maximum Vertex-Fuzzy Number Problem (MMV-FN)

In this section, we provide methods for solving any of the above issues. In all of the methods, a matching is found with maximum principal number. Matching methods and their correctness for general graphs are considerably more complicated than bipartite graphs. The main question raised is whether this complexity is inevitable or not? By comparing the proposed methods for the bipartite graph and those for general graphs, the answer is “yes” [33]. First, we introduce the method of finding the maximum matching principal number in a bipartite fuzzy graph. In all of the discussions in this section, it is assumed that the fuzzy graphs are connected. Obviously, methods are valid in each component of unconnected fuzzy graph. Before describing the methods, we introduce a notation which is used here. The largest fuzzy value of the edges in G, is denoted by ${\mathscr {M}}_{max}(G)$. For a vertex u, we denote the largest fuzzy value of the edges connected to the vertex u by ${\mathscr {M}}_{max}(u)_G$. In other words, we have:

$$\begin{aligned} {\mathscr {M}}_{max}(G)=\underset{e\in E}{\text {max }} \mu (e) \quad \text {and}\quad {\mathscr {M}}_{max}(u)_G=\underset{e=uv}{\text {max }} \mu (e). \end{aligned}$$

Similarly, the largest fuzzy value of the vertices is denoted by ${\mathscr {S}}_{max}(G)$. Regarding a vertex u, the largest fuzzy value of its adjacent vertices is denoted by ${\mathscr {S}}_{max}(u)_G$. Thus, we have:

$$\begin{aligned} {\mathscr {S}}_{max}(G)=\underset{v\in V}{\text {max }} \sigma (v) \quad \text {and}\quad {\mathscr {S}}_{max}(u)_G=\underset{e=uv}{\text {max }} \sigma (v). \end{aligned}$$

4.1 MME-FN problem in a bipartite fuzzy graph

Let $G=(V,\sigma ,\mu )$ be a bipartite fuzzy graph and $V = S\cup T$. For any $v\in V$, there is just one adjacent edge of v which is involved in matching construction. We define $x:E\rightarrow \{0,1\}$ called an incidence vector, which indicates the existence or nonexistence of an edge in the matching. Thus $\sum _{e=uv \in E}x(e)=1$ in a matching for all $v\in V$. The MME-FN problem in a bipartite fuzzy graph can be expressed as the following integer linear program.

$$\begin{aligned} \begin{array}{lr} \quad \text {Maximize:} &{} z=\displaystyle \sum _{e \in E}\mu (e)x(e)\\ \\ \text {Subject to:} &{} \displaystyle \sum _{e=uv \in E}x(e)=1, \, \forall v \in V.\\ \\ &{} x(e)\in \{0,1\}, \forall e \in E. \end{array} \end{aligned}$$

Example 4.1

For the fuzzy graph shown in Fig. 5a, we can write the linear programming problem as follows.

Maximize:

$$\begin{aligned}&0.3x(e_1 )+0.4x(e_2 )+0.6x(e_3 )+0.4x(e_4 )+0.3x(e_5 )\\&\quad +\,0.4x(e_6 ) +0.2x(e_7 )+0.7x(e_8 )+0.4x(e_9 ) \end{aligned}$$

Subject to:

$$\begin{aligned}&x(e_1 )+x(e_2 )=1\\&x(e_1 )+x(e_3 )+x(e_6 )=1\\&x(e_3 )+x(e_4 )+x(e_5 )=1\\&x(e_2 )+x(e_4 )+x(e_7 )=1\\&x(e_6 )+x(e_7 )+x(e_8 )+x(e_9 )=1\\&x(e_5 )+x(e_8 )=1\\&x(e_i )\in \{0,1\},\quad 1\le i\le 9. \end{aligned}$$

This linear programming problem can be solved using the simplex method. The optimal answer to this problem triggered during the seven steps of the simplex method, is shown in Table 4. Then, the matching M, is obtained based on Fig. 5b, where, $\lambda _E(M)=\lambda _E^{max}=1.7$.

Table 4 The optimal answer of simplex method

Fig. 5

A bipartite fuzzy graph, and its matching with MMEF number

4.2 MME-FN problem in an arbitrary fuzzy graph

In this section, we introduce a method for obtaining a matching with MMEF number in an arbitrary fuzzy graph. This method was originated from the Wattenhofer and Wattenhofer [34] method for weighted graphs. In this method, is obtained all the subgraphs of a fuzzy graph $G=(\mu ,\sigma )$, which are paths or cycle. Then, the maximal matching is extracted in these subgraphs. Finally, the condition of Berge’s Theorem is examined for new matchings, in which $\lambda _E$ is the largest.

Description of the method Suppose $M^*$ is the matching with MMEF number, which is obtained from this method. The steps are as follows.

Step 1 (Default ${{M}}^*$) Consider $M^*=\emptyset$ and $G^1=G$ by default.

Step 2 (Making subgraph ${{H}}^{{{j}}}$ of ${{G}}^{{{j}}}$): The edge $e = uv$ is called the elected edge for $H^j$, if $\sigma (u) \geqslant \frac{1}{2}{\mathscr {M}}_{max} (u)_{G_j}$ and $\sigma (v) \geqslant \frac{1}{2} {\mathscr {M}}_{max}(v)_{G^j}$. All of the elected edges make subgraph $H^j$ of $G^j$. It is worth noting that the subgraph $H^1$ of $G^1$ is made first.

Step 3 (Making paths and cycles in ${{H}}^{{{j}}}$) Weak subgraphs of $H^j$ (paths and cycles) are made with the process of deletion and selection (we call these subgraphs $P_k ^ j$).

• Selection process Each vertex selects an adjacent edge randomly. For each vertex u, we show the selected edge as sele and the other adjacent edges of the vertex u are named as imposed, and is represented by imp.

• Deletion process For each vertex, imposed edge randomly selected and the other edges are removed, except the selected edge.

• Making ${{P}}_{{{i}}}^{{{j}}}$ The result of selection and deletion process is a union of paths and cycles ($deg(v)\le 2$). Depending on the number of modes (k modes) for the selected and imposed edges, the resulted subgraph is named $P_i^j$.

Do Step 4 to 6 for all $1\leqslant i\leqslant k$.

Step 4 (Making matchings in each ${{P}}_{{{i}}}^{{{j}}}$) Extract all paths from each $P_i^j$, which is done in common ways of finding paths in a graph. Make the matching with MMEF number for each path and cycle (there are two ways to choose the edges alternately). Call each of this matching $M_{l}^{ij}$, where l changes depending on the number of paths. Make all possible unions of these matching. Denote the strongest union, which is a matching, as $M_{ij}^{*}$.

Step 5 (First expansion of ${{M}}^*$) Check out $M^*\cup M_{ij}^*$. The first union of this kind, which is a matching, is the first expansion of $M^*$, which is set as new $M^*$ ($M^*\hookleftarrow M^*\cup M_{i}^*$).

Step 6 (Second expansion of ${{M}}^*$) Make $M^*\oplus P$ for each possible fuzzy $M^*$-augmenting path P and calculate $\lambda _E(M^*\oplus P)$. If this value increases ($\lambda _E(M^*\oplus P)\ge \lambda _E( M^*)$), then consider $M^*\hookleftarrow M^*\oplus P$. Otherwise repeat this step until there is no augmenting path increasing $\lambda _E$ number.

Step 7 (Making ${{G}}^{{{i}}+{{1}}}$) We consider $G^{j+1}=G^j\ominus H^j$ as a subgraph of G. Thus, we have:

$$\begin{aligned} {\left\{ \begin{array}{ll} E(G^j\ominus H^j)=E(G^j)-E(H^j), \\ V(G^j\ominus H^j)=V(G^j). \end{array}\right. } \end{aligned}$$

Step 8 (Stop condition) If $G^{j+1}=\emptyset$ stop, otherwise go to step 2.

Example 4.2

Assume that G is a fuzzy graph, we obtain a matching with MMEF number for this graph (Fig. 6).

Fig. 6

A fuzzy graph and its matching with MMEF number

4.3 MMV-FN problem in a bipartite fuzzy graph

Similar to weighted graphs, the complexity of a MMV-FN Problem is very close to the crisp graphs. Here we present the method for finding the matching with MMVF number in a fuzzy bipartite graph (Fig. 6).

Some studies that examined the vertex matching in weighted graphs by assuming that the weight of an edge is equal to the sum of the vertices weights and have linked the maximum vertex problem to the maximum edge problem. Based on the MMV-FN problem is considerably simpler than the MME-FN state and is very close to the general graph. In Theorems 3.16, 3.19 and Corollary 3.17, we provided preliminary steps for this fact. The vertex maximization of matchings in the weighted graphs was studied by Spencer and Mayer [32]. In addition, Mulmuley, Umesh Vazirani, and Vijay Vazirani proposed vertex matching maximization of weighted graphs [19]. Now based on the above-mentioned issues for weighted graphs, we discuss the problem for fuzzy graphs.

Description of the method Assume $G = (\mu , \sigma )$ is a bipartite fuzzy graph whose vertices are considered to be $V = S\cup T$.

Step 1 (Fuzzy vertex ordering) Arrange the vertices of S and T sets in accordance with the fuzzy vertex ordering.

Step 2 (Making pseudo-fuzzy restricts) Make $G^S=(\mu ,\sigma _S)$ and $G^T=(\mu ,\sigma _T)$.

Step 3 (Making matching in pseudo-fuzzy restricts) Let u be the vertex in $G_S$ that $\sigma (u)={\mathscr {S}}_{max}(G_S)$. First, consider $M_S^1=uv$ to be a single-edged matching, which is obtained with an edge connected to u, and v is the strongest adjacent of u.

Step 4 (Expansion of ${{M}}_{{{S}}}^{{{i}}}$) Consider $P^i$ the strong-vertex fuzzy $M_S^i$-augmenting path (Definition 3.18). Start from $P^1$, as the strong-vertex fuzzy $M_S^1$-augmenting path, and construct $M_S^{i+1}=M_S^i\oplus P^i$ as a new matching. Obviously, according to the Theorem 3.14, $\lambda _{V}(M_S^{i+1})\ge \lambda _{V}(M_S^{i})$. In other words, $M_S^{i+1}\succ M_S^{i}$. Continue this process until there are augmenting paths.

Step 5 (Choosing strong-vertex matching in pseudo-fuzzy restrict): Select the strong-vertex matching from the $M_S^{i}$ matchings, shown as $M_S^*$. Thus, such a matching as the last matching is made in the previous step.

Step 6 (Checking Point) If $\sigma (v)={\mathscr {S}}_{max}(G_T)$ (vertex v in step 3), stop ($M^*=M_S^*$). Otherwise, go to the next step.

Step 7 (Making strong-vertex matching in ${{G}}^{{{T}}}$): Repeat steps 3 to 6 for $G^T$ and call the strong-vertex matching of $G_T$ to $M_T^*$.

Step 8 (Making strong-vertex matching in G): Given the various states occurring for the $M_S^*$ and $M_T^*$ matchings (in accordance with the conditions of Theorem 3.20), construct such a matching which is a subset of $M_S^*\cup M_T^*$ and covers all the vertices in $M_S^*$ and $M_T^*$ (call it $M^*$). Such a matching, due to its construction process, is stronger than all matchings made in this way. Therefore, by Theorem 3.19, $\lambda _V(M^*)=\lambda _V^{max}$.

Example 4.3

We consider the bipartite graph as in Example 4.1 (Fig. 5), and get the matching with MMVF number. Note that in this fuzzy graph the strongest vertex in S is connected to the strongest vertex in T. Thus, the method stops in step 6 (Fig. 7).

Example 4.4

As shown in Fig. 8, we consider a bipartite fuzzy graph that the strongest vertex in S is not connected to the strongest vertex in T. Therefore, the execution of the method in step 6 will not stop. Here, we construct two matchings in pseudo-fuzzy restricts subgraphs ($G^S$ and $G^T$).

Fig. 7

The strongest vertex in S is connected to the strongest vertex in T

Fig. 8

The strongest vertex in S is not connected to the strongest vertex in T

4.4 MMV-FN problem in an arbitrary fuzzy graph

For an arbitrary fuzzy graph, the structure of the augmenting paths should be considered. We distinguish between the first and last vertex of such paths. The first and last vertex of an augmenting path are the corresponding vertices of each other, and this pairing is uniquely determined in our method. The fundamental idea to make a matching with MMVF number is to find an augmenting path and develop the matching via the difference of the augmenting path and the current matching. In this section, we refer to a simple method for obtaining a matching with MMVF number in an arbitrary fuzzy graph. The process is very similar to non-fuzzy graphs and we use the expansion of augmenting paths. By considering the vertex fuzzy value involved in the augmenting paths, we maximize the matching value.

Description of the method Assume that $G=(V,\sigma ,\mu )$ is a fuzzy graph:

Step 1 (Vertices fuzzy ordering) Arrange all vertices of G in accordance with the vertices fuzzy ordering. Consider the strongest vertex $V^1_M$.

Step 2 (Making basic matching) Consider the first vertex which is connected to $V^1_M$ and weaker than it. Call it $V^1_{M-1}$. Let a separate edge, except $V^1_MV^1_{M-1}$, connected to $V^1_{M-1}$, the first matching ($M^1$). If such an edge is not found, start with $V^1_MV^1_{M-1}$.

Step 3 (Finding augmenting paths) Obtain all possible fuzzy $M^1$-augmenting paths starting from $V^1_M$ ($P_{V^1_M}=\{P^1_1,P^1_2,P^1_3,\cdots \})$.

Step 4 (Making new matching) Choose the strong-vertex $M^1$-augmenting path ($P^1_{strog}$), and select $M^1\oplus P^1_{strog}$ as the new matching.

Step 5 (Expanding matching) Continue the matching development process by finding the possible augmenting paths, until there is no any augmenting path.

Step 6 (Reduction of vertices set) Draw $V^1_M$ from the vertices fuzzy ordering and repeat the steps (1) to (5) for the other vertices until all vertices of the graph are removed from the order.

Step 7 (Choosing maximum vertex-matching) The strong vertex matching after completing the process is a matching with MMVF number.

It is worth noting that $M^j\oplus P^j_{strog}$ should be made for all of the paths (step 3) if we find strong-vertex augmenting paths ($P_i^j$), having the same fuzzy value. In each stage of implementing the method, if we get matching covering all graph vertices, it is the matching with MMVF number by Corollary 3.17. In the following example, we find a matching with MMVF number for an arbitrary fuzzy graph.

Example 4.5

Let G be a fuzzy graph as in Example 4.2. We want to find a matching with MMVF number. This process is displayed in Fig. 9.

Fig. 9

A fuzzy graph and its matching with MMVF number

5 The best co-workers’ problem (BCP)

Conflict is an inevitable fact for any organization. Leaders should understand and apply various conflict management techniques and conflict resolution styles in order to form strong relationships with subordinates [11]. Hyde et al. [12] examined the relationship between conflict management in the workplace and self-reported measures of stress, poor general health, exhaustion and sickness absence due to overstrain or fatigue. Many attempts have been made to design stable algorithms based on the concept of matching [1, 9]. In this section, we present a proposed model based on matching in fuzzy graphs to reduce workplace conflict.

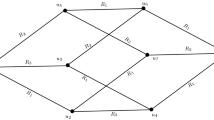
Consider a company with 7 employees ($h_i$), in which employees are given two types of grades (name these grades $\mu$ and $\sigma$) based on their backgrounds and capabilities. One grade is based on individual abilities ($\sigma (h_i)$), and another grade is based on the level of interaction of two employees having a joint work history $\mu (h_i,h_j)$ (Fig. 10). Suppose that the company intends to make the placement of individuals in order to increase the efficiency of work so that each person can co-operate with the one having the highest degree of interaction in the workplace. Figure 11a displays the individual and interaction privileges of the employees in this company.

Fig. 10

Employee rating functions

Fig. 11

A BCP fuzzy graph and its solution

Choosing the best partner for each individual, that achieves maximum efficiency, is a matching with the highest edge-fuzzy value. By implementing the method presented in Sect. 4.2, we arrive at a matching with MMEF number as shown in Fig. 11b. In general graph theory, Berge’s Theorem suggests a natural approach to finding a maximum matching in a graph. We start with some matchings M and search for an M-augmenting path. If such a path P is found, we replace M by $M\oplus P$. We repeat the procedure until no augmenting path can be found with respect to the current matching. This final matching is then a maximum matching (APS method) [6]. This method is used for finding the maximum matching, as displayed in Fig. 12. We start APS method with the strongest edge (as a matching) leading to two matchings. As shown, none of them are the matching with MMEF number.

Fig. 12

Two implementations of the APS method from the same starting point

6 Conclusions

Matching in a fuzzy graph implies its meaning for crisp graphs. Matching numbers, result in classifying the concept of matching in fuzzy graphs in addition to being tools for stabilizing methods of achieving optimal matching. Structuring the introduced methods in solving optimization problems based on vertex or edge numbers leads to a unique answer, unlike classical methods in crisp graphs giving multiple optimal solutions depending on the starting point, although approximation is considered in the implementation method. In this paper, after introducing, classifying, and customized readings of optimization problems (maximization state) in fuzzy graphs, the results, theorems, and properties of the numbers related to the matching were explaind. A decision-making model which can reduce conflict in the workplace was presented by achieving a maximum consistency between employees. More work can be done in this regard by considering the construction conditions of the optimization problems in the minimization state. Finally it is important to examine and generalize the concept of matching to other types of specific fuzzy graphs which results in related application problems such as a multi-parameter decision-making.