Certain fuzzy graph structures

Abstract

A fuzzy graph structure is an extension of a fuzzy graph. In this research paper, we present certain notions, including semi strong min-product of fuzzy graph structures, regular fuzzy graph structures, strong and complete fuzzy graph structures. Moreover, we discuss degree and total degree of a vertex in semi strong min-product of fuzzy graph structures and investigate some of their properties. Furthermore, we present an application of fuzzy graph structures in decision-making, that is, identification of best traveling service. In last, we develop an algorithm explaining general procedure of our application.

1 Introduction

Zadeh [21] introduced the fuzzy set on universal set A, which can accommodate “degrees of membership”. The notion of fuzzy set differs from classical concept of bivalent set called crisp set, whose boundary is precise, that is, crisp set is collection of objects about which it is clear that whether any object is inside it or not. Zadeh generalized the notion of crisp set by extending valuation set {0, 1} (definitely out or definitely in) to real valued interval between 0 and 1, that is, [0, 1]. Degree of membership of an element of fuzzy set denotes the degree of camaraderie of that element with concept presented by fuzzy set. It means fuzzy set F contains an element a of degree $\sigma (a)$, i.e., $\sigma (a) = Degree(a \in A)$ and mapping $\sigma : A \rightarrow \{Membership Degrees\}$ is called membership function or set function. The fuzzy set F can be expressed as $F = \{(a, \sigma (a)), a \in A \}$ and it imposes elastic constrain of possible values of elements $a \in A$ called possibility distribution. Fuzzy set captures vagueness exclusively by membership function that is mapping from given universe of discourse to interval of real values.

Graph theory initiated with finding a walk connecting seven bridges of Königsberg. Later on, this field developed meticulously in all domains of sciences and humanities with large number of applications. It is an important tool representing many real world phenomena. There are many systems which can not be properly represented because haziness or uncertainty of attributes of systems exists naturally. Various real life phenomena, provided a strong motivation to define the fuzzy graphs. Kauffman [8] introduced the fuzzy graphs on the bases of Zadeh’s fuzzy relations [22]. Fuzzy graph theory has many applications in various areas, including, data mining, networking, image segmentation, clustering, communication, planning, image capturing and scheduling. Rosenfeld [16] discussed fuzzy analogue of different graph theoretical notions. Later on, Bhattacharya [5] gave some remarks on fuzzy graphs. Mordeson and Nair [9] defined some fuzzy graphs and fuzzy hypergraphs. Mordeson and Chang-Shyh [10] discussed some operations on the fuzzy graphs. Sunitha and Vijayakumar [18, 20] defined complement of the fuzzy graphs and discussed some characterization of fuzzy trees. Nagoor Gani and Radha [11, 12] defined some properties of regular fuzzy graphs and degree of vertex in some fuzzy graphs.

Sampathkumar [17] introduced the concept of generalized graph structures. Graph structures are the generalization of graphs and widely useful in study of some structures like, graphs, semi graphs, signed graphs, edge colored graphs and edge labeled graphs. Graph structures are much advantageous in study of different domains of computer science and computational intelligence. Dinesh [6] described the notion of fuzzy graph structures and defined some related notions. Fuzzy graph structures are much advantageous than graph structures, because they deal with impreciseness and ambiguity of various real life phenomena. Ramakrishnan and Dinesh [13,14,15] worked on generalized fuzzy graph structures. Harinath and Lavanya described fuzzy graph structures for wheel, star and Helm graphs [7]. Akram et al [1, 2] introduced certain notions of m-polar fuzzy graph structures. For further notions and applications, readers are referred to [3, 4, 19, 23, 24]. In this research article, we introduce semi strong min-product of fuzzy graph structures, regular fuzzy graph structures, strong and complete fuzzy graph structures. Moreover, we define degree of a vertex in semi strong min-product of fuzzy graph structures. We also discuss total degree of vertex in semi strong min-product of fuzzy graph structures and explain some properties of all these concepts with detailed examples. Furthermore, we present an application of fuzzy graph structures in decision-making, that is, identification of best traveling service.

2 Concepts of fuzzy graph structures

Definition 2.1

[17] A graph structure(GS)$G=(V,R_{1},\ldots ,R_{n})$ consists of a non-empty set V together with relations $R_{1},R_{2},\ldots ,R_{n}$ on V which are mutually disjoint such that each $R_{i}$, $1 \le i \le n$, is symmetric and irreflexive.

One can represent a graph structure $G^{*}=(V,R_{1},\ldots ,R_{n})$ in the plane just like a graph where each edge is labeled as $R_{i}$, $1 \le i \le n$.

Example 2.2

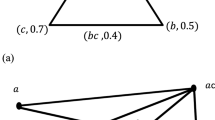
Consider a set $V = \{u_{1}, u_{2}, u_{3}, u_{4}, u_{5}, u_{6}, u_{7}, u_{8}\}$, and define three relations $R_{1}=\{u_{1}u_{2}, u_{2} u_{7}, u_{4}u_{8}, u_{6}u_{8}, u_{5}u_{6}, u_{3}u_{4}\}$, $R_{2}=\{u_{1}u_{5}, u_{5}u_{7}, u_{3}u_{6}, u_{7}u_{8}\}$, $R_{3}=\{u_{1}u_{3}, u_{2}u_{4}\}$. We can check that $R_{1}$, $R_{2}$ and $R_{3}$ are mutually disjoint, symmetric and irreflexive relations. Hence $G^{*}= (V, R_{1}, R_{2}, R_{3})$ is a graph structure and is shown in Fig. 1.

Fig. 1

Graph Structure $G^{*}= (V, R_{1}, R_{2}, R_{3})$

In this graph structure each edge is labeled as $R_{1}$, $R_{2}$ or $R_{3}$.

Definition 2.3

[6] Let $\sigma$ be the fuzzy set on set V and $\mu _{1}, \mu _{2},\ldots , \mu _{n}$ be fuzzy sets on $R_{1}, R_{2},\ldots , R_{n}$, respectively. If $0 \le \mu _{i}(uv) \le \sigma (u) \wedge \sigma (v)$ for all $u,v \in V$, $i = 1,2,\ldots ,n$, then ${G}= (\sigma ,\mu _{1},\mu _{2}, \ldots ,\mu _{n})$ is called fuzzy graph structure(FGS) of graph structure $G^{*}$. If $uv \in supp(\mu _{i})$, then uv is named as $\mu _{i}$-edge of FGS G.

Example 2.4

Consider a graph structure $G^{*}= (V, R_{1}, R_{2}, R_{3})$ shown in Fig. 1. Let $\sigma$ be a fuzzy set on set V given in Table 1 and $\mu _{1}$, $\mu _{2}$, $\mu _{3}$ be fuzzy sets on the relations $R_{1}$, $R_{2}$, $R_{3}$ shown in Tables 2, 3 and 4, respectively.

Table 1 Fuzzy set $\sigma$ on vertex set V

Table 2 Fuzzy set $\mu _{1}$ on relation $R_{1}$

Table 3 Fuzzy set $\mu _{2}$ on relation $R_{2}$

Table 4 Fuzzy set $\mu _{3}$ on relation $R_{3}$

Fuzzy set $\sigma$ with fuzzy relations $\mu _{1}$, $\mu _{2}$ and $\mu _{3}$ is a fuzzy graph structure $G= (\sigma ,\mu _{1},\mu _{2},\mu _{3})$ and is shown in Fig. 2.

Fig. 2

Fuzzy graph structure $G=(\sigma ,\mu _{1},\mu _{2},\mu _{3})$

Definition 2.5

Let $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ be two fuzzy graph structures with underlying crisp graph structures $G^{*}_{1}= (V_{1}, R'_{1}, R'_{2}, \ldots ,R'_{n})$ and $G^{*}_{2}= (V_{2}, R''_{1}, R''_{2}, \ldots ,R''_{n})$, respectively.

Define $G = (\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ with underlying crisp graph structure $G^{*}= (V, R_{1}, R_{2}, \ldots ,R_{n})$, where $V = V_{1} \times V_{2}$ and $R_{i} = \{ (u_{1}, v_{1}) (u_{2}, v_{2})/ u_{1} = u_{2}, v_{1}v_{2} \in R''_{i}$ or $u_{1}u_{2} \in R'_{i} \}$ by $\sigma (u,v) = \sigma _{1}(u) \vee \sigma _{2}(v)$, for all $(u,v) \in V = V_{1} \times V_{2}$ and

$$\begin{aligned} \mu _{i}((u_{1}, v_{1}) (u_{2}, v_{2})) = \left\{ \begin{array}{ll} \mu '_{i}(u_{1}u_{2}), \,\ u_{1}u_{2} \in R'_{i}\\ \sigma _{1}(u_{1})\wedge \mu ''_{i}(v_{1}v_{2}),\,\ u_{1} = u_{2}, v_{1}v_{2} \in R''_{i}\\ \end{array}\right. \end{aligned}$$

$i= 1,2,\ldots ,n$.

$G = (\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ is called semi strong min-product of $G_{1}$ and $G_{2}$ and is denoted by $G_{1}[G_{2}]_{min}$.

Example 2.6

Consider two fuzzy graph structures ${G}_{1}= (\sigma _{1},\mu '_{1},\mu '_{2})$ and ${G}_{2}= (\sigma _{2},\mu ''_{1},\mu ''_{2})$ with underlying crisp GSs ${G}^{*}_{1}= (V_{1},R'_{1},R'_{2})$ and ${G}^{*}_{2}= (V_{2},R'_{1},R''_{2})$, respectively, as shown in Fig. 3, where $R'_{1} = \{u_{1}u_{2}\}$, $R'_{2} = \{u_{3}u_{4}\}$, $R''_{1} = \{v_{1}v_{2}\}$, $R''_{2} = \{v_{2}v_{3}\}$. Semi strong min-product of ${G}_{1} = (\sigma _{1},\mu '_{1},\mu '_{2})$ and ${G}_{2} = (\sigma _{2},\mu ''_{1},\mu ''_{2})$ is shown in Fig. 4. In semi strong min-product, $\mu '_{i}$ and $\mu ''_{i}$ edges belong to $\mu _{i}$ fuzzy set.

Fig. 3

Two fuzzy graph structures ${G}_{1} = (\sigma _{1},\mu '_{1},\mu '_{2})$ and ${G}_{2} = (\sigma _{2},\mu ''_{1},\mu ''_{2})$

Fig. 4

Semi strong min-product of two FGSs

Theorem 2.7

If $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2} = (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are two strong fuzzy graph structures with underlying crisp graph structures $G^{*}_{1} = (V_{1}, R'_{1}, R'_{2}, \ldots ,R'_{n})$ and $G^{*}_{2} = (V_{2}, R''_{1}, R''_{2}, \ldots ,R''_{n})$, respectively, such that $\sigma _{2} \le \sigma _{1}$, $\mu '_{i}$ and $\mu ''_{i}$ are constant functions of same value, then semi strong min-product of $G_{1}$ and $G_{2}$ is a strong fuzzy graph structure.

Proof

Let $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ be two strong fuzzy graph structures with underlying crisp graph structures $G^{*}_{1}= (V_{1}, R'_{1}, R'_{2}, \ldots ,R'_{n})$ and $G^{*}_{2}= (V_{2}, R''_{1}, R''_{2}, \ldots ,R''_{n})$, respectively, such that $\sigma _{2} \le \sigma _{1}$, $\mu '_{i}$ and $\mu ''_{i}$ are constant functions of same value, according to definition of semi strong min-product:

Case 1: :

$u_{1}u_{2} \in R'_{i}$

$$\begin{aligned} \mu _{i}(u_{1},v_{1})(u_{2}, v_{2})= & {} \mu '_{i}(u_{1}u_{2})= \sigma _{1}(u_{1})\wedge \sigma _{1}(u_{2})\\= & {} (\sigma _{1}(u_{1})\vee \sigma _{2}(v_{1})) \wedge (\sigma _{1}(u_{2})\vee \sigma _{2}(v_{2}))\\ {}= & {} \sigma (u_{1}, v_{1}) \wedge \sigma (u_{2}, v_{2}). \end{aligned}$$

Case 2: :

$u_{1} = u_{2},\,\ v_{1}v_{2} \in R''_{i}$

$$\begin{aligned} \mu _{i}(u_{1},v_{1})(u_{2}, v_{2})= & {} \mu ''_{i}(v_{1}v_{2})\\= & {} \mu '_{i}(u_{1}u_{2}) = \sigma _{1}(u_{1})\wedge \sigma _{1}(u_{2})\\= & {} (\sigma _{1}(u_{1})\vee \sigma _{2}(v_{1})) \wedge (\sigma _{1}(u_{2})\vee \sigma _{2}(v_{2}))\\ {}= & {} \sigma (u_{1}, v_{1}) \wedge \sigma (u_{2}, v_{2}). \end{aligned}$$

Thus $\mu _{i}(u_{1},v_{1})(u_{2}, v_{2}) = \sigma (u_{1}, v_{1}) \wedge \sigma (u_{2}, v_{2})$ for all edges.

Hence $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ is strong fuzzy graph structure. $\square$

Example 2.8

Consider two fuzzy graph structures ${G}_{1} = (\sigma _{1},\mu '_{1},\mu '_{2})$ and ${G}_{2} = (\sigma _{2},\mu ''_{1},\mu ''_{2})$, which are shown in Fig. 5.

Fig. 5

Two fuzzy graph structures

It is clear from Fig. 5 that,

$$\begin{aligned}&\mu '_{1}(u_{1}u_{2})= \sigma _{1}(u_{1})\wedge \sigma _{1}(u_{2})= 0.5 \wedge 0.5 = 0.5,\\&\mu '_{2}(u_{3}u_{4})=\sigma _{1}(u_{3})\wedge \sigma _{1}(u_{4})= 0.5 \wedge 0.5 = 0.5,\\&\mu ''_{1}(v_{1}v_{2})= \sigma _{2}(v_{1})\wedge \sigma _{2}(v_{2})= 0.5 \wedge 0.5 = 0.5,\\&\mu ''_{2}(v_{2}v_{3})= \sigma _{2}(v_{2})\wedge \sigma _{2}(v_{3})= 0.5 \wedge 0.5 = 0.5. \end{aligned}$$

Hence ${G}_{1} = (\sigma _{1},\mu '_{1},\mu '_{2})$ and ${G}_{2} = (\sigma _{2},\mu ''_{1},\mu ''_{2})$ are strong fuzzy graph structures. Moreover, $\sigma _{1}=\sigma _{2}$, $\mu '_{1}$, $\mu '_{2}$, $\mu ''_{1}$, $\mu ''_{2}$ are constant functions of same value, that is, 0.5. Semi strong min-product of ${G}_{1}= (\sigma _{1},\mu '_{1},\mu '_{2})$ and ${G}_{2}= (\sigma _{2},\mu ''_{1},\mu ''_{2})$ is shown in Fig. 6.

Fig. 6

Semi strong min-product($G_{1}[G_{2}]_{min}$) of two FGs

It is clear from Fig. 6, that,

$$\begin{aligned} \mu '_{1}((u_{1},v_{1})(u_{2},v_{1}))= & {} \sigma (u_{1},v_{1})\wedge \sigma (u_{2},v_{1})= 0.5 \wedge 0.5 = 0.5,\\ \mu ''_{1}((u_{1},v_{1})(u_{1},v_{2}))= & {} \sigma (u_{1},v_{1})\wedge \sigma (u_{1},v_{2})= 0.5 \wedge 0.5 = 0.5,\\ \mu '_{1}((u_{1},v_{1})(u_{2},v_{2}))= & {} \sigma (u_{1},v_{1})\wedge \sigma (u_{2},v_{2})= 0.5 \wedge 0.5 = 0.5,\\ \mu '_{1}((u_{1},v_{1})(u_{2},v_{3}))= & {} \sigma (u_{1},v_{1})\wedge \sigma (u_{2},v_{3})= 0.5 \wedge 0.5 = 0.5,\\ \mu ''_{1}((u_{4},v_{1})(u_{4},v_{2}))= & {} \sigma (u_{4},v_{1})\wedge \sigma (u_{4},v_{2})= 0.5 \wedge 0.5 = 0.5,\\ \mu '_{2}((u_{4},v_{1})(u_{3},v_{1}))= & {} \sigma (u_{4},v_{1})\wedge \sigma (u_{3},v_{1})= 0.5 \wedge 0.5 = 0.5,\\ \mu '_{2}((u_{4},v_{1})(u_{3},v_{2}))= & {} \sigma (u_{4},v_{1})\wedge \sigma (u_{3},v_{2})= 0.5 \wedge 0.5 = 0.5,\\ \mu '_{2}((u_{4},v_{1})(u_{3},v_{3}))= & {} \sigma (u_{4},v_{1})\wedge \sigma (u_{3},v_{3})= 0.5 \wedge 0.5 = 0.5,\\ \mu '_{1}((u_{2},v_{1})(u_{1},v_{2}))= & {} \sigma (u_{2},v_{1})\wedge \sigma (u_{1},v_{2})= 0.5 \wedge 0.5 = 0.5,\\ \mu ''_{1}((u_{2},v_{1})(u_{2},v_{2}))= & {} \sigma (u_{2},v_{1})\wedge \sigma (u_{2},v_{2})= 0.5 \wedge 0.5 = 0.5,\\ \end{aligned}$$

$$\begin{aligned} \mu '_{1}((u_{2},v_{1})(u_{1},v_{3}))= & {} \sigma (u_{2},v_{1})\wedge \sigma (u_{1},v_{3})= 0.5 \wedge 0.5 = 0.5,\\ \mu ''_{1}((u_{3},v_{1})(u_{3},v_{2}))= & {} \sigma (u_{3},v_{1})\wedge \sigma (u_{1},v_{2})= 0.5 \wedge 0.5 = 0.5,\\ \mu '_{2}((u_{3},v_{1})(u_{4},v_{3}))= & {} \sigma (u_{3},v_{1})\wedge \sigma (u_{4},v_{3})= 0.5 \wedge 0.5 = 0.5,\\ \mu '_{2}((u_{3},v_{1})(u_{4},v_{2}))= & {} \sigma (u_{3},v_{1})\wedge \sigma (u_{4},v_{2})= 0.5 \wedge 0.5 = 0.5,\\ \mu ''_{2}((u_{1},v_{2})(u_{1},v_{3}))= & {} \sigma (u_{1},v_{2})\wedge \sigma (u_{1},v_{3})= 0.5 \wedge 0.5 = 0.5,\\ \mu '_{1}((u_{1},v_{2})(u_{2},v_{2}))= & {} \sigma (u_{1},v_{2})\wedge \sigma (u_{2},v_{2})= 0.5 \wedge 0.5 = 0.5,\\ \mu '_{1}((u_{1},v_{2})(u_{2},v_{3}))= & {} \sigma (u_{1},v_{2})\wedge \sigma (u_{2},v_{3})= 0.5 \wedge 0.5 = 0.5,\\ \mu '_{1}((u_{2},v_{2})(u_{1},v_{3}))= & {} \sigma (u_{2},v_{2})\wedge \sigma (u_{1},v_{3})= 0.5 \wedge 0.5 = 0.5,\\ \mu ''_{2}((u_{2},v_{2})(u_{2},v_{3}))= & {} \sigma (u_{2},v_{2})\wedge \sigma (u_{2},v_{3})= 0.5 \wedge 0.5 = 0.5,\\ \mu '_{1}((u_{2},v_{3})(u_{1},v_{3}))= & {} \sigma (u_{2},v_{3})\wedge \sigma (u_{1},v_{3})= 0.5 \wedge 0.5 = 0.5. \end{aligned}$$

Similarly, we can calculate for all remaining edges. Hence $G_{1}[G_{2}]_{min}$ shown in Fig. 6 is a strong fuzzy graph structure. This example shows that semi strong min-product $G_{1}[G_{2}]_{min}$ of two strong fuzzy graph structures is a strong fuzzy graph structure.

Remark 2.9

If in $G_{1}[G_{2}]_{min}$ condition $\sigma _{2} \le \sigma _{1}$ is replaced by $\sigma _{2} \ge \sigma _{1}$ then semi strong min-product of $G_{1}$ and $G_{2}$ is $G_{2}[G_{1}]_{min}$.

Theorem 2.10

If $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are two complete fuzzy graph structures with underlying crisp graph structures $G^{*}_{1}= (V_{1}, R'_{1}, R'_{2}, \ldots ,R'_{n})$ and $G^{*}_{2}= (V_{2}, R''_{1}, R''_{2}, \ldots ,R''_{n})$, respectively, such that $\sigma _{2} \le \sigma _{1}$, $\mu '_{i}$ and $\mu ''_{i}$ are constant functions of same value, then semi strong min-product of $G_{1}$ and $G_{2}$ is a complete fuzzy graph structure.

Proof

Proof of this theorem is similar to that of theorem 2.7. $\square$

Theorem 2.11

The semi strong min-product $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ of two fuzzy graph structures $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ is connected fuzzy graph structure if and only if $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ is connected fuzzy graph structure.

Proof

Assume that $G_{1}$ is connected fuzzy graph structure. According to the definition of semi strong min-product $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$, there are as many copies of $G_{1}$ as number of vertices in $G_{2}$ i.e, for every vertex of $G_{2}$ there exists a copy of graph structure $G_{1}$ in semi strong min-product $G_{1}[G_{2}]_{min}$. Since $G_{1}$ is connected, so $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ is connected fuzzy graph structure.

Conversely, suppose that $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ is a fuzzy graph structure, and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ is connected fuzzy graph structure such that $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ is connected fuzzy graph structure. To prove that $G_{1}$ is connected, on contrary suppose that $G_{1}$ is not connected. Then there are at least two vertices in $V_{1}$ such that there does not exist any path between them. Since $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ is connected, there exists at least one path between any two vertices of $V_{1} \times V_{2}$. This implies that there will be at least one path between vertices of $G_{1}$. This is contradiction. Hence $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ is connected fuzzy graph structure. $\square$

Theorem 2.12

Connected components in semi strong min-product $G_{1}[G_{2}]_{min}$ of two fuzzy graph structures $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ is equal in number to that of $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$.

Proof

Let $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ be a connected fuzzy graph structure and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ be a fuzzy graph structure. Then according to the theorem 2.11, semi strong min-product $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ is connected. This implies, both $G_{1}$ = $(\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ are connected and hence theorem. Suppose that $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ is not connected fuzzy graph structure having ‘m’ distinct connected components. We rename vertices of fuzzy graph structure $G_{1}$ such that $\{u_{1},u_{2},\ldots ,u_{k1}\}$, $\{u_{k1+1},u_{k1+2},\ldots ,u_{k2}\}, \ldots \{u_{km+1},u_{km+2},\ldots ,u_{km+n}\}$ are vertex sets of m distinct connected components of $G_{1}$.

If $\{v_{1},v_{2},\ldots ,v_{n}\}$ are vertices of $G_{2}$, then corresponding to each vertex of $G_{2}$ there is a copy of every connected component of $G_{1}$ in semi strong min-product $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$. No edge exists between all these components . Because for an edge between $u_{1}v_{i}$ and $u_{k1+1}v_{i}$, there will be an edge between $u_{1}$ and $u_{k1+1}$ of $G_{1}$. Which is contradiction. Thus every component of semi strong min-product $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ is distinct from any other and hence the theorem. $\square$

Definition 2.13

Degree of a vertex in semi strong min-product $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ of fuzzy graph structures $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ is defined as:

$$\begin{aligned} d_{G_{1}[G_{2}]_{min}}(u_{i},v_{j})= & {} \sum _{u_{i}u_{k} \in R'_{i}, v_{l} \in V_{2} }\mu '_{i}(u_{i}u_{k}) + \sum _{v_{j}v_{l} \in R''_{j}, u_{i}= u_{k} }\mu ''_{j}(v_{j}v_{l}) \wedge \sigma _{1}(u_{i}). \end{aligned}$$

$\mu _{i}-$ degree of a vertex in semi strong min-product $G_{1}[G_{2}]_{min}$ is defined as:

$$\begin{aligned} \mu _{i}-d_{G_{1}[G_{2}]_{min}}(u_{i},v_{j})= & {} \sum _{u_{i}u_{k} \in R'_{i}, v_{l} \in V_{2} }\mu '_{i}(u_{i}u_{k}) + \sum _{v_{j}v_{l} \in R''_{i}, u_{i}= u_{k} }\mu ''_{i}(v_{j}v_{l}) \wedge \sigma _{1}(u_{i}). \end{aligned}$$

Fig. 7

Two fuzzy graph structures

Fig. 8

Semi strong min-product of ${G}_{1}= (\sigma _{1},\mu '_{1},\mu '_{2})$ and ${G}_{2}= (\sigma _{2},\mu ''_{1},\mu ''_{2})$

Example 2.14

Consider two fuzzy graph structures ${G}_{1}= (\sigma _{1},\mu '_{1},\mu '_{2})$ and ${G}_{2}= (\sigma _{2},\mu ''_{1},\mu ''_{2})$, which are shown in Fig. 7. Semi strong min-product of ${G}_{1}= (\sigma _{1},\mu '_{1},\mu '_{2})$ and ${G}_{2}= (\sigma _{2},\mu ''_{1},\mu ''_{2})$ is shown in Fig. 8. To calculate degree of vertex in semi strong min-product, we will use following formula:

$$\begin{aligned} d_{G_{1}[G_{2}]_{min}}(u_{i},v_{j})= & {} \sum _{u_{i}u_{k} \in R'_{i}, v_{l} \in V_{2} }\mu '_{i}(u_{i}u_{k}) + \sum _{v_{j}v_{l} \in R''_{j}, u_{i}= u_{k} }\mu ''_{j}(v_{j}v_{l}) \wedge \sigma _{1}(u_{i}).\\ d_{G_{1}[G_{2}]_{min}}(u_{1},v_{1})= & {} \mu '_{1}(u_{1}u_{2}) +\mu '_{1}(u_{1}u_{2}) +\mu '_{1}(u_{1}u_{2}) + (\mu ''_{1}(v_{1}v_{2}) \wedge \sigma _{1}(u_{1}))\\= & {} 0.6 + 0.6 +0.6 + (0.3\wedge 0.6)\\= & {} 1.8+ 0.3\\= & {} 2.1,\\ d_{G_{1}[G_{2}]_{min}}(u_{2},v_{1})= & {} \mu '_{1}(u_{2}u_{1}) + \mu '_{1}(u_{2}u_{1}) +\mu '_{1}(u_{2}u_{1}) + (\mu ''_{1}(v_{1}v_{2}) \wedge \sigma _{1}(u_{2}))\\= & {} 0.6 +0.6 +0.6 + (0.3\wedge 0.8)\\= & {} 1.8+ 0.3\\= & {} 2.1,\\ d_{G_{1}[G_{2}]_{min}}(u_{1},v_{3})= & {} \mu '_{1}(u_{1}u_{2}) + \mu '_{1}(u_{1}u_{2}) +\mu '_{1}(u_{1}u_{2}) +(\mu ''_{2}(v_{3}v_{2}) \wedge \sigma _{1}(u_{1})) \\= & {} 0.6 + 0.6 +0.6 +(0.4\wedge 0.6)\\= & {} 1.8+ 0.4\\= & {} 2.2,\\ d_{G_{1}[G_{2}]_{min}}(u_{2},v_{3})= & {} \mu '_{1}(u_{2}u_{1}) + \mu '_{1}(u_{2}u_{1}) +\mu '_{1}(u_{2}u_{1}) +(\mu ''_{2}(v_{3}v_{2}) \wedge \sigma _{1}(u_{2})) \\= & {} 0.6 +0.6 +0.6 + (0.4\wedge 0.8)\\= & {} 1.8+ 0.4\\= & {} 2.2,\\ \end{aligned}$$

$$\begin{aligned} d_{G_{1}[G_{2}]_{min}}(u_{4},v_{1})= & {} \mu '_{2}(u_{4}u_{3}) + \mu '_{2}(u_{4}u_{3}) +\mu '_{2}(u_{4}u_{3}) + (\mu ''_{1}(v_{1}v_{2}) \wedge \sigma _{1}(u_{4}))\\= & {} 0.4 +0.4 +0.4 + (0.3\wedge 0.6)\\= & {} 1.2+ 0.3\\= & {} 1.5,\\ d_{G_{1}[G_{2}]_{min}}(u_{3},v_{1})= & {} \mu '_{2}(u_{3}u_{4}) + \mu '_{2}(u_{3}u_{4}) +\mu '_{2}(u_{3}u_{4}) + (\mu ''_{1}(v_{1}v_{2}) \wedge \sigma _{1}(u_{3}))\\= & {} 0.4 + 0.4 +0.4 + (0.3\wedge 0.4)\\= & {} 1.2+ 0.3\\= & {} 1.5,\\ d_{G_{1}[G_{2}]_{min}}(u_{4},v_{3})= & {} \mu '_{2}(u_{4}u_{3}) + \mu '_{2}(u_{4}u_{3}) + \mu '_{2}(u_{4}u_{3}) +(\mu ''_{2}(v_{3}v_{2}) \wedge \sigma _{1}(u_{4})) \\= & {} 0.4 + 0.4 +0.4 + (0.4\wedge 0.6)\\= & {} 1.2+ 0.4\\= & {} 1.6,\\ d_{G_{1}[G_{2}]_{min}}(u_{3},v_{3})= & {} \mu '_{2}(u_{3}u_{4}) + \mu '_{2}(u_{3}u_{4}) + \mu '_{2}(u_{3}u_{4}) + (\mu ''_{2}(v_{3}v_{2}) \wedge \sigma _{1}(u_{3})) \\= & {} 0.4 +0.4 +0.4 + (0.4\wedge 0.4)\\= & {} 1.2+ 0.4\\= & {} 1.6,\\ d_{G_{1}[G_{2}]_{min}}(u_{3},v_{2})= & {} \mu '_{2}(u_{3}u_{4}) + \mu '_{2}(u_{3}u_{4}) +\mu '_{2}(u_{3}u_{4}) + (\mu ''_{1}(v_{2}v_{1}) \wedge \sigma _{1}(u_{3})) \\&+\, (\mu ''_{2}(v_{2}v_{3}) \wedge \sigma _{1}(u_{3}))\\= & {} 0.4 +0.4 +0.4 + (0.3\wedge 0.4)+ (0.4\wedge 0.4)\\= & {} 1.2+ 0.3+ 0.4\\= & {} 1.9,\\ \end{aligned}$$

$$\begin{aligned} d_{G_{1}[G_{2}]_{min}}(u_{4},v_{2})= & {} \mu '_{2}(u_{4}u_{3}) + \mu '_{2}(u_{4}u_{3}) +\mu '_{2}(u_{4}u_{3}) + (\mu ''_{1}(v_{2}v_{1}) \wedge \sigma _{1}(u_{4}))\\&+\, (\mu ''_{2}(v_{2}v_{3}) \wedge \sigma _{1}(u_{4}))\\= & {} 0.4 + 0.4 +0.4 + (0.3\wedge 0.6)+ (0.4\wedge 0.6)\\= & {} 1.2+ 0.3+ 0.4\\= & {} 1.9,\\ d_{G_{1}[G_{2}]_{min}}(u_{1},v_{2})= & {} \mu '_{1}(u_{1}u_{2}) + \mu '_{1}(u_{1}u_{2}) +\mu '_{1}(u_{1}u_{2}) + (\mu ''_{1}(v_{2}v_{1}) \wedge \sigma _{1}(u_{1})) \\&+\, (\mu ''_{2}(v_{2}v_{3}) \wedge \sigma _{1}(u_{1}))\\= & {} 0.6 +0.6 +0.6 + (0.3\wedge 0.6)+ (0.4\wedge 0.6)\\= & {} 1.8+ 0.3+ 0.4\\= & {} 2.5,\\ d_{G_{1}[G_{2}]_{min}}(u_{2},v_{2})= & {} \mu '_{1}(u_{2}u_{1}) + \mu '_{1}(u_{2}u_{1}) +\mu '_{1}(u_{2}u_{1}) + (\mu ''_{1}(v_{2}v_{1}) \wedge \sigma _{1}(u_{2})) \\&+\, (\mu ''_{2}(v_{2}v_{3}) \wedge \sigma _{1}(u_{2}))\\= & {} 0.6 + 0.6 +0.6 + (0.3\wedge 0.8)+ (0.4\wedge 0.8)\\= & {} 1.8+ 0.3+ 0.4\\= & {} 2.5. \end{aligned}$$

$\mu _{i}-$ degree of a vertex of semi strong min-product $G_{1}[G_{2}]_{min}$ is given by:

$$\begin{aligned} \mu _{i}-d_{G_{1}[G_{2}]_{min}}(u_{i},v_{j})= & {} \sum _{u_{i}u_{k} \in R'_{i}, v_{l} \in V_{2} }\mu '_{i}(u_{i}u_{k}) + \sum _{v_{j}v_{l} \in R''_{i}, u_{i}= u_{k} }\mu ''_{i}(v_{j}v_{l}) \wedge \sigma _{1}(u_{i}). \end{aligned}$$

Using this formula, we calculate $\mu _{i}-$degree of vertices in $G_{1}[G_{2}]_{min}$ as:

$$\begin{aligned} \mu _{1}-d_{G_{1}[G_{2}]_{min}}(u_{1},v_{1})= & {} \mu '_{1}(u_{1}u_{2}) +\mu '_{1}(u_{1}u_{2}) +\mu '_{1}(u_{1}u_{2}) + (\mu ''_{1}(v_{1}v_{2}) \wedge \sigma _{1}(u_{1}))\\= & {} 0.6 + 0.6 +0.6 + (0.3\wedge 0.6)\\= & {} 1.8+ 0.3\\= & {} 2.1,\\ \mu _{1}-d_{G_{1}[G_{2}]_{min}}(u_{2},v_{1})= & {} \mu '_{1}(u_{2}u_{1}) + \mu '_{1}(u_{2}u_{1}) +\mu '_{1}(u_{2}u_{1}) + (\mu ''_{1}(v_{1}v_{2}) \wedge \sigma _{2}(u_{2}))\\= & {} 0.6 +0.6 +0.6 + (0.3\wedge 0.8)\\= & {} 1.8+ 0.3\\= & {} 2.1,\\ \mu _{1}- d_{G_{1}[G_{2}]_{min}}(u_{1},v_{2})= & {} \mu '_{1}(u_{1}u_{2}) + \mu '_{1}(u_{1}u_{2}) +\mu '_{1}(u_{1}u_{2}) + (\mu ''_{1}(v_{2}v_{1}) \wedge \sigma _{1}(u_{1})) \\= & {} 0.6 +0.6 +0.6 + (0.3\wedge 0.6)\\= & {} 1.8+ 0.3\\= & {} 2.1,\\ \end{aligned}$$

$$\begin{aligned} \mu _{1}- d_{G_{1}[G_{2}]_{min}}(u_{2},v_{2})= & {} \mu '_{1}(u_{2}u_{1}) + \mu '_{1}(u_{2}u_{1}) +\mu '_{1}(u_{2}u_{1}) + (\mu ''_{1}(v_{2}v_{1}) \wedge \sigma _{1}(u_{2})) \\= & {} 0.6 + 0.6 +0.6 + (0.3\wedge 0.8)\\= & {} 1.8+ 0.3\\= & {} 2.1,\\ \mu _{2}- d_{G_{1}[G_{2}]_{min}}(u_{4},v_{3})= & {} \mu '_{2}(u_{4}u_{3}) + \mu '_{2}(u_{4}u_{3}) + \mu '_{2}(u_{4}u_{3}) +(\mu ''_{2}(v_{3}v_{2}) \wedge \sigma _{1}(u_{4})) \\= & {} 0.4 + 0.4 +0.4 + (0.4\wedge 0.6)\\= & {} 1.2+ 0.4\\= & {} 1.6,\\ \mu _{2}- d_{G_{1}[G_{2}]_{min}}(u_{3},v_{3})= & {} \mu '_{2}(u_{3}u_{4}) + \mu '_{2}(u_{3}u_{4}) + \mu '_{2}(u_{3}u_{4}) + (\mu ''_{2}(v_{3}v_{2}) \wedge \sigma _{1}(u_{3})) \\= & {} 0.4 +0.4 +0.4 + (0.4\wedge 0.4)\\= & {} 1.2+ 0.4\\= & {} 1.6,\\ \mu _{2}- d_{G_{1}[G_{2}]_{min}}(u_{3},v_{2})= & {} \mu '_{2}(u_{3}u_{4}) + \mu '_{2}(u_{3}u_{4}) +\mu '_{2}(u_{3}u_{4})+(\mu ''_{2}(v_{2}v_{3}) \wedge \sigma _{1}(u_{3}))\\= & {} 0.4 +0.4 +0.4 + (0.4\wedge 0.4)\\= & {} 1.2+ 0.4\\= & {} 1.6,\\ \end{aligned}$$

$$\begin{aligned} \mu _{2}- d_{G_{1}[G_{2}]_{min}}(u_{4},v_{2})= & {} \mu '_{2}(u_{4}u_{3}) + \mu '_{2}(u_{4}u_{3}) +\mu '_{2}(u_{4}u_{3}) + (\mu ''_{2}(v_{2}v_{3}) \wedge \sigma _{1}(u_{4}))\\= & {} 0.4 + 0.4 +0.4 + (0.4\wedge 0.6)\\= & {} 1.2+ 0.4\\= & {} 1.6,\\ \mu _{1}- d_{G_{1}[G_{2}]_{min}}(u_{1},v_{3})= & {} \mu '_{1}(u_{1}u_{2}) + \mu '_{1}(u_{1}u_{2}) +\mu '_{1}(u_{1}u_{2}) \\= & {} 0.6 + 0.6 +0.6 \\= & {} 1.8,\\ \mu _{1}- d_{G_{1}[G_{2}]_{min}}(u_{2},v_{3})= & {} \mu '_{1}(u_{2}u_{1}) + \mu '_{1}(u_{2}u_{1}) +\mu '_{1}(u_{2}u_{1}) \\= & {} 0.6 +0.6 +0.6 \\= & {} 1.8,\\ \mu _{2}- d_{G_{1}[G_{2}]_{min}}(u_{4},v_{1})= & {} \mu '_{2}(u_{4}u_{3}) + \mu '_{2}(u_{4}u_{3}) +\mu '_{2}(u_{4}u_{3}) \\= & {} 0.4 +0.4 +0.4 \\= & {} 1.2,\\ \mu _{2}-d_{G_{1}[G_{2}]_{min}}(u_{3},v_{1})= & {} \mu '_{2}(u_{3}u_{4}) + \mu '_{2}(u_{3}u_{4}) +\mu '_{2}(u_{3}u_{4}) \\= & {} 0.4 + 0.4 +0.4 \\= & {} 1.2,\\ \end{aligned}$$

$$\begin{aligned} \mu _{1}- d_{G_{1}[G_{2}]_{min}}(u_{4},v_{2})= & {} \mu ''_{1}(v_{2}v_{1}) \wedge \sigma _{1}(u_{4})=0.3\wedge 0.6= 0.3,\\ \mu _{1}- d_{G_{1}[G_{2}]_{min}}(u_{3},v_{2})= & {} \mu ''_{1}(v_{2}v_{1}) \wedge \sigma _{1}(u_{3})=0.3\wedge 0.4= 0.3,\\ \mu _{1}-d_{G_{1}[G_{2}]_{min}}(u_{3},v_{1})= & {} \mu ''_{1}(v_{1}v_{2}) \wedge \sigma _{1}(u_{3})=0.3\wedge 0.4= 0.3,\\ \mu _{1}-d_{G_{1}[G_{2}]_{min}}(u_{4},v_{1})= & {} \mu ''_{1}(v_{1}v_{2}) \wedge \sigma _{1}(u_{4})=0.3\wedge 0.6= 0.3,\\ \mu _{2}- d_{G_{1}[G_{2}]_{min}}(u_{2},v_{2})= & {} \mu ''_{2}(v_{2}v_{3}) \wedge \sigma _{1}(u_{2})=0.4\wedge 0.8=0.4,\\ \mu _{2}- d_{G_{1}[G_{2}]_{min}}(u_{1},v_{2})= & {} \mu ''_{2}(v_{2}v_{3}) \wedge \sigma _{1}(u_{1})=0.4\wedge 0.6=0.4,\\ \mu _{2}- d_{G_{1}[G_{2}]_{min}}(u_{2},v_{3})= & {} \mu ''_{2}(v_{3}v_{2}) \wedge \sigma _{1}(u_{2})=0.4\wedge 0.8= 0.4,\\ \mu _{2}- d_{G_{1}[G_{2}]_{min}}(u_{1},v_{3})= & {} \mu ''_{2}(v_{3}v_{2}) \wedge \sigma _{1}(u_{1}) = 0.4\wedge 0.6 = 0.4. \end{aligned}$$

Theorem 2.15

If $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are two fuzzy graph structures such that $\mu ''_{i} \le \sigma _{1}$, $i= 1,2,\ldots ,n$, then degree of any vertex in semi strong min-product $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ of fuzzy graph structures $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ is given by: $d_{G_{1}[G_{2}]_{min}}(u_{i},v_{j}) = d_{G_{2}}(v_{j}) + d_{G_{1}}(u_{i})|V_{2}|$.

Proof

Let $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ be two fuzzy graph structures such that $\mu ''_{i} \le \sigma _{1}$, then $\mu ''_{i} \wedge \sigma _{1} = \mu ''_{i}$, $i= 1,2,\ldots ,n$. Then degree of any vertex in $G_{1}[G_{2}]_{min}$ (semi strong min-product) is given by:

$$\begin{aligned} d_{G_{1}[G_{2}]_{min}}(u_{i},v_{j})= & {} \sum _{u_{i}u_{k} \in R'_{i}, v_{l} \in V_{2} }\mu '_{i}(u_{i}u_{k}) + \sum _{v_{j}v_{l} \in R''_{i}, u_{i}= u_{k} }\mu ''_{i}(v_{j}v_{l}) \wedge \sigma _{1}(u_{i})\\= & {} |V_{2}|\sum _{u_{i}u_{k} \in R'_{i}, v_{j}= v_{l} }\mu '_{i}(u_{i}u_{k}) + \sum _{v_{j}v_{l} \in R''_{i}, u_{i}= u_{k} }\mu ''_{i}(v_{j}v_{l})\\= & {} |V_{2}| d_{G_{1}}(u_{i})+ d_{G_{2}}(v_{j}). \end{aligned}$$

$\square$

Fig. 9

Two fuzzy graph structures

Fig. 10

Semi strong min-product of two FGSs

Example 2.16

Consider two fuzzy graph structures ${G}_{1}= (\sigma _{1},\mu '_{1},\mu '_{2})$ and ${G}_{2}= (\sigma _{2},\mu ''_{1},\mu ''_{2})$ with underlying crisp graph structures ${G}^{*}_{1}= (V_{1},R'_{1},R'_{2})$ and ${G}^{*}_{2}= (V_{2},R'_{1},R''_{2})$, respectively, as shown in Fig. 9, where $R'_{1} = \{u_{1}u_{2}\}$, $R'_{2} = \{u_{3}u_{4}\}$, $R''_{1} = \{v_{1}v_{2}\}$, $R''_{2} = \{v_{2}v_{3}\}$. It is clear from Fig. 9, $\mu ''_{i} \le \sigma _{1}$. Semi strong min-product of ${G}_{1}= (\sigma _{1},\mu '_{1},\mu '_{2})$ and ${G}_{2}= (\sigma _{2},\mu ''_{1},\mu ''_{2})$ is shown in Fig. 10. According to theorem 2.15, formula to calculate degree of vertex in semi strong min-product is:

$$\begin{aligned} d_{G_{1}[G_{2}]_{min}}(u_{i},v_{j})= & {} |V_{2}| d_{G_{1}}(u_{i})+ d_{G_{2}}(v_{j}).\\ d_{G_{1}[G_{2}]_{min}}(u_{1},v_{1})= & {} |V_{2}| d_{G_{1}}(u_{1})+ d_{G_{2}}(v_{1})\\= & {} (3)(0.6)+ 0.3\\= & {} 1.8 + 0.3 \\= & {} 2.1,\\ d_{G_{1}[G_{2}]_{min}}(u_{1},v_{2})= & {} |V_{2}| d_{G_{1}}(u_{1})+ d_{G_{2}}(v_{2})\\= & {} (3)(0.6)+ 0.7\\= & {} 1.8 + 0.7 \\= & {} 2.5,\\ d_{G_{1}[G_{2}]_{min}}(u_{1},v_{3})= & {} |V_{2}| d_{G_{1}}(u_{1})+ d_{G_{2}}(v_{3})\\= & {} (3)(0.6)+ 0.4\\= & {} 1.8 + 0.4 \\= & {} 2.2,\\ d_{G_{1}[G_{2}]_{min}}(u_{2},v_{1})= & {} |V_{2}| d_{G_{1}}(u_{2})+ d_{G_{2}}(v_{1})\\= & {} (3)(0.6)+ 0.3\\= & {} 1.8 + 0.3 \\= & {} 2.1,\\ d_{G_{1}[G_{2}]_{min}}(u_{2},v_{2})= & {} |V_{2}| d_{G_{1}}(u_{2})+ d_{G_{2}}(v_{2})\\= & {} (3)(0.6)+ 0.7\\= & {} 1.8 + 0.7 \\= & {} 2.5,\\ d_{G_{1}[G_{2}]_{min}}(u_{2},v_{3})= & {} |V_{2}| d_{G_{1}}(u_{2})+ d_{G_{2}}(v_{3})\\= & {} (3)(0.6)+ 0.4\\ \end{aligned}$$

$$\begin{aligned}= & {} 1.8 + 0.4 \\= & {} 2.2,\\ d_{G_{1}[G_{2}]_{min}}(u_{3},v_{1})= & {} |V_{2}| d_{G_{1}}(u_{3})+ d_{G_{2}}(v_{1})\\= & {} (3)(0.4)+ 0.3\\= & {} 1.2 + 0.3 \\= & {} 1.5,\\ d_{G_{1}[G_{2}]_{min}}(u_{3},v_{2})= & {} |V_{2}| d_{G_{1}}(u_{3})+ d_{G_{2}}(v_{2})\\= & {} (3)(0.4)+ 0.7\\= & {} 1.2 + 0.7 \\= & {} 1.9,\\ d_{G_{1}[G_{2}]_{min}}(u_{3},v_{3})= & {} |V_{2}| d_{G_{1}}(u_{3})+ d_{G_{2}}(v_{3})\\= & {} (3)(0.4)+ 0.4\\= & {} 1.2 + 0.4 \\= & {} 1.6,\\ d_{G_{1}[G_{2}]_{min}}(u_{4},v_{1})= & {} |V_{2}| d_{G_{1}}(u_{4})+ d_{G_{2}}(v_{1})\\= & {} (3)(0.4)+ 0.3\\= & {} 1.2 + 0.3 \\= & {} 1.5,\\ d_{G_{1}[G_{2}]_{min}}(u_{4},v_{2})= & {} |V_{2}| d_{G_{1}}(u_{4})+ d_{G_{2}}(v_{2})\\= & {} (3)(0.4)+ 0.7\\= & {} 1.2 + 0.7 \\= & {} 1.9,\\ d_{G_{1}[G_{2}]_{min}}(u_{4},v_{3})= & {} |V_{2}| d_{G_{1}}(u_{4})+ d_{G_{2}}(v_{3})\\= & {} (3)(0.4)+ 0.4\\= & {} 1.2 + 0.4 \\= & {} 1.6. \end{aligned}$$

By direct calculations we found that:

$$\begin{aligned} d_{G_{1}[G_{2}]_{min}}(u_{1},v_{1})= & {} 0.6+0.6+0.6+0.3=2.1,\\ d_{G_{1}[G_{2}]_{min}}(u_{4},v_{3})= & {} 0.4+0.4+0.4+0.4=1.6,\\ d_{G_{1}[G_{2}]_{min}}(u_{1},v_{3})= & {} 0.6+0.6+0.6+0.4=2.2,\\ d_{G_{1}[G_{2}]_{min}}(u_{2},v_{1})= & {} 0.6+0.6+0.6+0.3=2.1,\\ d_{G_{1}[G_{2}]_{min}}(u_{2},v_{3})= & {} 0.6+0.6+0.6+0.4=2.2,\\ d_{G_{1}[G_{2}]_{min}}(u_{3},v_{1})= & {} 0.4+0.4+0.4+0.3=1.5,\\ d_{G_{1}[G_{2}]_{min}}(u_{4},v_{1})= & {} 0.4+0.4+0.4+0.3=1.5,\\ d_{G_{1}[G_{2}]_{min}}(u_{3},v_{3})= & {} 0.4+0.4+0.4+0.4=1.6,\\ d_{G_{1}[G_{2}]_{min}}(u_{3},v_{2})= & {} 0.4+0.4+0.4+0.4+0.3=1.9,\\ d_{G_{1}[G_{2}]_{min}}(u_{2},v_{2})= & {} 0.6+0.6+0.6+0.4+0.3=2.5,\\ d_{G_{1}[G_{2}]_{min}}(u_{4},v_{2})= & {} 0.4+0.4+0.4+0.4+0.3=1.9,\\ d_{G_{1}[G_{2}]_{min}}(u_{1},v_{2})= & {} 0.6+0.6+0.6+0.4+0.3=2.5. \end{aligned}$$

This shows that degrees calculated by both methods are same.

Corollary 2.17

If $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are two fuzzy graph structures such that $\mu ''_{i} \le \sigma _{1}$ and $\mu ''_{i}$ is constant function having value c , $i= 1,2,\ldots ,n$, then degree of any vertex in semi strong min-product $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ of fuzzy graph structures $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ is given by: $d_{G_{1}[G_{2}]_{min}}(u_{i},v_{j}) = d_{G^{*}_{2}}(v_{j})c + d_{G_{1}}(u_{i})|V_{2}|$.

Proof

Let $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ be two fuzzy graph structures such that $\mu '_{i}$ is constant function having value c and $\mu ''_{i} \le \sigma _{1}$, then $\mu ''_{i} \wedge \sigma _{1} = \mu ''_{i}$, $i= 1,2,\ldots ,n$.

Then degree of any vertex in $G_{1}[G_{2}]_{min}$ (semi strong min-product) is given by:

$$\begin{aligned} d_{G_{1}[G_{2}]_{min}}(u_{i},v_{j})= & {} \sum _{u_{i}u_{k} \in R'_{i}, v_{l} \in V_{2} }\mu '_{i}(u_{i}u_{k}) + \sum _{v_{j}v_{l} \in R''_{j}, u_{i}= u_{k} }\mu ''_{j}(v_{j}v_{l}) \wedge \sigma _{1}(u_{i})\\= & {} |V_{2}|\sum _{u_{i}u_{k} \in R'_{i}, v_{j}= v_{l} }\mu '_{i}(u_{i}u_{k}) + \sum _{v_{j}v_{l} \in R''_{j}, u_{i}= u_{k} }\mu ''_{j}(v_{j}v_{l})\\= & {} |V_{2}| d_{G_{1}}(u_{i})+ d_{G^{*}_{2}}(v_{j})c . \end{aligned}$$

$\square$

Theorem 2.18

If $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are two fuzzy graph structures such that $\mu ''_{i} \ge \sigma _{1}$, $i= 1,2,\ldots ,n$, then degree of any vertex in semi strong min-product $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ of fuzzy graph structures $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ is given by: $d_{G_{1}[G_{2}]_{min}}(u_{i},v_{j}) = d_{G^{*}_{2}}(v_{j})\sigma _{1}(u_{i}) + d_{G_{1}}(u_{i})|V_{2}|$.

Proof

Let $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ be two fuzzy graph structures such that $\mu ''_{i} \ge \sigma _{1}$, then $\mu ''_{i} \wedge \sigma _{1} =\sigma _{1}$, $i= 1,2,\ldots ,n$. Then degree of any vertex in $G_{1}[G_{2}]_{min}$ (semi strong min-product) is given by:

$$\begin{aligned} d_{G_{1}[G_{2}]_{min}}(u_{i},v_{j})= & {} \sum _{u_{i}u_{k} \in R'_{i}, v_{l} \in V_{2} }\mu '_{i}(u_{i}u_{k}) + \sum _{v_{j}v_{l} \in R''_{i}, u_{i}= u_{k} }\mu ''_{i}(v_{j}v_{l}) \wedge \sigma _{1}(u_{i})\\= & {} |V_{2}| d_{G_{1}}(u_{i}) + \sum _{v_{j}v_{l} \in R''_{i}, u_{i}= u_{k} }\sigma _{1}(u_{i})\\= & {} |V_{2}| d_{G_{1}}(u_{i})+ d_{G^{*}_{2}}(v_{j})\sigma _{1}(u_{i}). \end{aligned}$$

$\square$

Corollary 2.19

If $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are two fuzzy graph structures such that $\mu ''_{i} \ge \sigma _{1}$, $i= 1,2,\ldots ,n$ and $\sigma _{1}$ is constant function having value $`c'$ then degree of any vertex in semi strong min-product $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ of fuzzy graph structures $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ is given by: $d_{G_{1}[G_{2}]_{min}}(u_{i},v_{j}) = d_{G^{*}_{2}}(v_{j})c + d_{G_{1}}(u_{i})|V_{2}|$.

Proof

Let $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ be two fuzzy graph structures such that $\mu ''_{i} \ge \sigma _{1}$, then $\mu ''_{i} \wedge \sigma _{1} =\sigma _{1}$, $i= 1,2,\ldots ,n$. Moreover, $\sigma _{1}$ is constant function having value c. Then degree of any vertex in $G_{1}[G_{2}]_{min}$ (semi strong min-product) is given by:

$$\begin{aligned} d_{G_{1}[G_{2}]_{min}}(u_{i},v_{j})= & {} \sum _{u_{i}u_{k} \in R'_{i}, v_{l} \in V_{2} }\mu '_{i}(u_{i}u_{k}) + \sum _{v_{j}v_{l} \in R''_{j}, u_{i}= u_{k} }\mu ''_{j}(v_{j}v_{l}) \wedge \sigma _{1}(u_{i})\\= & {} |V_{2}| d_{G_{1}}(u_{i}) + \sum _{v_{j}v_{l} \in R''_{j}, u_{i}= u_{k} }\sigma _{1}(u_{i})\\= & {} |V_{2}| d_{G_{1}}(u_{i})+ d_{G^{*}_{2}}(v_{j})\sigma _{1}(u_{i})\\= & {} |V_{2}| d_{G_{1}}(u_{i})+ d_{G^{*}_{2}}(v_{j})c. \end{aligned}$$

$\square$

Remark 2.20

If $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are partially regular fuzzy graph structures, then both semi strong min-products $G_{1}[G_{2}]_{min}$ and $G_{2}[G_{1}]_{min}$ are partially regular fuzzy graph structures since $G^{*}_{1}= (V_{1}, R'_{1}, R'_{2}, \ldots ,R'_{n})$ and $G^{*}_{2}= (V_{2}, R''_{1}, R''_{2}, \ldots ,R''_{n})$ are regular fuzzy graph structures.

Theorem 2.21

If $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are two fuzzy graph structures such that $\mu ''_{i} \le \sigma _{1}$, then semi strong min-product $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ is regular fuzzy graph structure if and only if $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are regular fuzzy graph structures.

Proof

Let $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ be two fuzzy graph structures such that $\mu ''_{i} \le \sigma _{1}$. Then degree of a vertex in semi strong min-products $G_{1}[G_{2}]_{min}$ is given by:

$$\begin{aligned} d_{G_{1}[G_{2}]_{min}}(u_{i},v_{j}) = d_{G_{2}}(v_{j}) + d_{G_{1}}(u_{i})|V_{2}|. \end{aligned}$$

Assume that $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are two regular fuzzy graph structures of degree $k_{1}$ and $k_{2}$, respectively then

$$\begin{aligned} d_{G_{1}[G_{2}]_{min}}(u_{i},v_{j}) = k_{2} + k_{1}|V_{2}|. \end{aligned}$$

Since $k_{1}$, $k_{2}$ and $|V_{2}|$ are constants, so $d_{G_{1}[G_{2}]_{min}}$ is constant for all vertices of $V_{1} \times V_{2}$. Thus semi strong min-product $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots , \mu _{n})$ of fuzzy graph structures $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ is regular fuzzy graph structure.

Conversely, suppose that $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are two fuzzy graph structures such that $\mu ''_{i} \le \sigma _{1}$, and semi strong min-product $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ is regular fuzzy graph structure. We have to prove that $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are regular fuzzy graph structures.

Then degrees of any two vertices $(u_{1},u_{2})$ and $(v_{1},v_{2})$ in $V_{1} \times V_{2}$ are equal, that is,

$$\begin{aligned} d_{G_{1}[G_{2}]_{min}}(u_{1},u_{2})= & {} d_{G_{1}[G_{2}]_{min}}(v_{1},v_{2}),\\ d_{G_{2}}(u_{2}) + d_{G_{1}}(u_{1})|V_{2}|= & {} d_{G_{2}}(v_{2}) + d_{G_{1}}(v_{1})|V_{2}|. \end{aligned}$$

Fix $u \in V_{2}$ and consider $(u_{1},u)$ and $(v_{1},u)$ in $V_{1} \times V_{2}$, where $u_{1},v_{1}$ are arbitrary elements of $V_{1}$, then above equation becomes

$$\begin{aligned} d_{G_{2}}(u) + d_{G_{1}}(u_{1})|V_{2}|= & {} d_{G_{2}}(u) + d_{G_{1}}(v_{1})|V_{2}|,\\ d_{G_{1}}(u_{1})|V_{2}|= & {} d_{G_{1}}(v_{1})|V_{2}|,\\ d_{G_{1}}(u_{1})= & {} d_{G_{1}}(v_{1}). \end{aligned}$$

This holds for all vertices $u_{1}$ and $v_{1}$ of $V_{1}$.

Thus $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ is regular fuzzy graph structure. Now Fix $u' \in V_{1}$ and consider $(u',u_{2})$ and $(u',v_{2})$ in $V_{1} \times V_{2}$, where $u_{2},v_{2}$ are arbitrary elements of $V_{1}$, then above equation becomes

$$\begin{aligned} d_{G_{2}}(u_{2}) + d_{G_{1}}(u')|V_{2}|= & {} d_{G_{2}}(v_{2}) + d_{G_{1}}(u')|V_{2}|,\\ d_{G_{2}}(u_{2})= & {} d_{G_{2}}(v_{2}). \end{aligned}$$

This holds for all vertices $u_{2}$ and $v_{2}$ of $V_{2}$. Thus $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ is regular fuzzy graph structure. $\square$

Theorem 2.22

If $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ is regular fuzzy graph structure and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ is partially regular fuzzy graph structure such that $\mu ''_{i} \wedge \sigma _{1}$ is constant, then semi strong min-product $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ of $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ is regular fuzzy graph structure.

Proof

Let $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ be $k_{1}-$regular fuzzy graph structure and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ be partially regular FGS such that $G^{*}_{2}= (V_{2}, R''_{1}, R''_{2}, \ldots ,R''_{n})$ (underlying graph structure) is $r_{1}-$regular graph structure. Moreover $\mu ''_{i} \wedge \sigma _{1}$ is constant, that is, $\mu ''_{i} \wedge \sigma _{1} = c$, where c is constant.

Then degree of a vertex in semi strong min-product $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ of fuzzy graph structures $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ is given by:

$$\begin{aligned} d_{G_{1}[G_{2}]_{min}}(u_{i},v_{j})= & {} d_{G^{*}_{2}}(v_{j}) (\mu ''_{i} \wedge \sigma _{1}) + d_{G_{1}}(u_{i})|V_{2}| \\= & {} d_{G^{*}_{2}}(v_{j}) c + d_{G_{1}}(u_{i})|V_{2}| \\= & {} r_{1} c + k_{1}|V_{2}|. \end{aligned}$$

Since c, $k_{1}$, $r_{1}$ and $|V_{2}|$ are constants, so $d_{G_{1}[G_{2}]_{min}}$ is constant for all vertices of $V_{1} \times V_{2}$. Thus semi strong min-product $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots , \mu _{n})$ of fuzzy graph structures $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ is regular fuzzy graph structure. $\square$

Theorem 2.23

If $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are two fuzzy graph structures such that $\mu '_{i} \le \sigma _{2}$, then semi strong min-product $G_{2}[G_{1}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ is regular fuzzy graph structure if and only if $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are regular fuzzy graph structures.

Proof

Let $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ be two fuzzy graph structures such that $\mu '_{i} \le \sigma _{2}$. Then degree of a vertex in semi strong min-products $G_{1}[G_{2}]_{min}$ is given by:

$$\begin{aligned} d_{G_{2}[G_{1}]_{min}}(u_{i},v_{j}) = |V_{1}| d_{G_{2}}(v_{j}) + d_{G_{1}}(u_{i}). \end{aligned}$$

Assume that $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are two regular fuzzy graph structures of degree $k_{1}$ and $k_{2}$, respectively then

$$\begin{aligned} d_{G_{2}[G_{1}]_{min}}(u_{i},v_{j}) = |V_{1}| k_{2} + k_{1}. \end{aligned}$$

Since $k_{1}$, $k_{2}$ and $|V_{1}|$ are constants, so $d_{G_{2}[G_{1}]_{min}}$ is constant for all vertices of $V_{1} \times V_{2}$. Thus semi strong min-product $G_{2}[G_{1}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots , \mu _{n})$ of fuzzy graph structures $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ is regular fuzzy graph structure.

Conversely, suppose that $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are two fuzzy graph structures such that $\mu '_{i} \le \sigma _{2}$, and semi strong min-product $G_{2}[G_{1}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ is regular fuzzy graph structure. We have to prove that $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are regular fuzzy graph structures.

Then degrees of any two vertices $(u_{1},u_{2})$ and $(v_{1},v_{2})$ in $V_{1} \times V_{2}$ are equal, that is,

$$\begin{aligned} d_{G_{2}[G_{1}]_{min}}(u_{1},u_{2})= & {} d_{G_{2}[G_{1}]_{min}}(v_{1},v_{2}),\\ |V_{1}| d_{G_{2}}(u_{2}) + d_{G_{1}}(u_{1})= & {} |V_{1}|d_{G_{2}}(v_{2}) + d_{G_{1}}(v_{1}). \end{aligned}$$

Fix $u \in V_{2}$ and consider $(u_{1},u)$ and $(v_{1},u)$ in $V_{1} \times V_{2}$, where $u_{1},v_{1}$ are arbitrary elements of $V_{1}$, then above equation becomes

$$\begin{aligned} |V_{1}| d_{G_{2}}(u) + d_{G_{1}}(u_{1})= & {} |V_{1}|d_{G_{2}}(u) + d_{G_{1}}(v_{1}),\\ d_{G_{1}}(u_{1})= & {} d_{G_{1}}(v_{1}). \end{aligned}$$

This holds for all vertices $u_{1}$ and $v_{1}$ of $V_{1}$.

Thus $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ is regular fuzzy graph structure. Now Fix $u' \in V_{1}$ and consider $(u',u_{2})$ and $(u',v_{2})$ in $V_{1} \times V_{2}$, where $u_{2},v_{2}$ are arbitrary elements of $V_{1}$, then above equation becomes

$$\begin{aligned} |V_{1}| d_{G_{2}}(u_{2}) + d_{G_{1}}(u')= & {} |V_{1}| d_{G_{2}}(v_{2}) + d_{G_{1}}(u'),\\ |V_{1}| d_{G_{2}}(u_{2})= & {} |V_{1}| d_{G_{2}}(v_{2}),\\ d_{G_{2}}(u_{2})= & {} d_{G_{2}}(v_{2}). \end{aligned}$$

This holds for all vertices $u_{2}$ and $v_{2}$ of $V_{2}$. Thus $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ is regular fuzzy graph structure. $\square$

Definition 2.24

Total degree of a vertex in semi strong min-product $G_{1}[G_{2}]_{min} = (\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ of fuzzy graph structures $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ is defined as:

$$\begin{aligned} td_{G_{1}[G_{2}]_{min}}(u_{i},v_{j})= & {} \sum _{u_{i}u_{k} \in R'_{i}, v_{l} \in V_{2} }\mu '_{i}(u_{i}u_{k}) + \sum _{v_{j}v_{l} \in R''_{j}, u_{i}= u_{k} }\mu ''_{j}(v_{j}v_{l}) \wedge \sigma _{1}(u_{i})\\&+ \sigma (u_{i},v_{j}). \end{aligned}$$

Example 2.25

Consider two fuzzy graph structures ${G}_{1}= (\sigma _{1},\mu '_{1},\mu '_{2})$ and ${G}_{2}= (\sigma _{2},\mu ''_{1},\mu ''_{2})$, which are shown in Fig. 11.

Fig. 11

Two fuzzy graph structures

Semi strong min-product of ${G}_{1}= (\sigma _{1},\mu '_{1},\mu '_{2})$ and ${G}_{2}= (\sigma _{2},\mu ''_{1},\mu ''_{2})$ is shown in Fig. 12.

Fig. 12

Semi strong min-product of ${G}_{1}= (\sigma _{1},\mu '_{1},\mu '_{2})$ and ${G}_{2}= (\sigma _{2},\mu ''_{1},\mu ''_{2})$

To calculate total degree of vertex in semi strong min-product, we will use following formula:

$$\begin{aligned} td_{G_{1}[G_{2}]_{min}}(u_{i},v_{j})= & {} \sum _{u_{i}u_{k} \in R'_{i}, v_{l} \in V_{2} }\mu '_{i}(u_{i}u_{k}) + \sum _{v_{j}v_{l} \in R''_{j}, u_{i}= u_{k} }\mu ''_{j}(v_{j}v_{l}) \wedge \sigma _{1}(u_{i}) \\&+\, \sigma (u_{i},v_{j}) .\\ td_{G_{1}[G_{2}]_{min}}(u_{1},v_{1})= & {} \mu '_{1}(u_{1}u_{2}) +\mu '_{1}(u_{1}u_{2}) +\mu '_{1}(u_{1}u_{2}) \\&+ (\mu ''_{1}(v_{1}v_{2}) \wedge \sigma _{1}(u_{1})) + \sigma (u_{1},v_{1})\\= & {} 0.7 + 0.7 +0.7 + (0.4\wedge 0.7)+0.7\\= & {} 2.1+ 0.4+0.7\\= & {} 3.2,\\ td_{G_{1}[G_{2}]_{min}}(u_{2},v_{1})= & {} \mu '_{1}(u_{2}u_{1}) + \mu '_{1}(u_{2}u_{1}) +\mu '_{1}(u_{2}u_{1}) \\&+\, (\mu ''_{1}(v_{1}v_{2}) \wedge \sigma _{2}(u_{2}))+ \sigma (u_{2},v_{1})\\= & {} 0.7 +0.7 +0.7 + (0.4\wedge 0.9)+0.9\\= & {} 2.1+ 0.4+0.9\\= & {} 3.4,\\ td_{G_{1}[G_{2}]_{min}}(u_{1},v_{3})= & {} \mu '_{1}(u_{1}u_{2}) + \mu '_{1}(u_{1}u_{2}) +\mu '_{1}(u_{1}u_{2}) \\&+\,(\mu ''_{2}(v_{3}v_{2}) \wedge \sigma _{1}(u_{1})) + \sigma (u_{1},v_{3}) \\= & {} 0.7 + 0.7 +0.7 +(0.5\wedge 0.7)+0.7\\= & {} 2.1+ 0.5+0.7\\= & {} 3.3,\\ td_{G_{1}[G_{2}]_{min}}(u_{2},v_{3})= & {} \mu '_{1}(u_{2}u_{1}) + \mu '_{1}(u_{2}u_{1}) +\mu '_{1}(u_{2}u_{1}) \\&+\,(\mu ''_{2}(v_{3}v_{2}) \wedge \sigma _{1}(u_{2}))+ \sigma (u_{2},v_{3}) \\= & {} 0.7 +0.7 +0.7 + (0.5\wedge 0.9)+0.9\\= & {} 2.1+ 0.5+0.9\\= & {} 3.5,\\ td_{G_{1}[G_{2}]_{min}}(u_{4},v_{1})= & {} \mu '_{2}(u_{4}u_{3}) + \mu '_{2}(u_{4}u_{3}) +\mu '_{2}(u_{4}u_{3}) \\&+\, (\mu ''_{1}(v_{1}v_{2}) \wedge \sigma _{1}(u_{4}))+ \sigma (u_{4},v_{1})\\= & {} 0.5 +0.5 +0.5 + (0.4\wedge 0.7)+0.7\\= & {} 1.5+ 0.4+0.7\\ \end{aligned}$$

$$\begin{aligned}= & {} 2.6,\\ td_{G_{1}[G_{2}]_{min}}(u_{3},v_{1})= & {} \mu '_{2}(u_{3}u_{4}) + \mu '_{2}(u_{3}u_{4}) +\mu '_{2}(u_{3}u_{4}) \\&+\, (\mu ''_{1}(v_{1}v_{2}) \wedge \sigma _{1}(u_{3}))+ \sigma (u_{3},v_{1})\\= & {} 0.5 + 0.5 +0.5 + (0.4\wedge 0.5)+0.5\\= & {} 1.5+ 0.4+0.5\\= & {} 2.4,\\ td_{G_{1}[G_{2}]_{min}}(u_{4},v_{3})= & {} \mu '_{2}(u_{4}u_{3}) + \mu '_{2}(u_{4}u_{3}) + \mu '_{2}(u_{4}u_{3}) \\&+\,(\mu ''_{2}(v_{3}v_{2}) \wedge \sigma _{1}(u_{4}))+ \sigma (u_{4},v_{3}) \\= & {} 0.5 + 0.5 +0.5 + (0.5\wedge 0.7)+0.7\\= & {} 1.5+ 0.5+0.7\\= & {} 2.7,\\ td_{G_{1}[G_{2}]_{min}}(u_{3},v_{3})= & {} \mu '_{2}(u_{3}u_{4}) + \mu '_{2}(u_{3}u_{4}) + \mu '_{2}(u_{3}u_{4}) \\&+\, (\mu ''_{2}(v_{3}v_{2}) \wedge \sigma _{1}(u_{3})) + \sigma (u_{3},v_{3})+0.6\\= & {} 0.5 +0.5 +0.5 + (0.5\wedge 0.5)+0.6\\= & {} 1.5+ 0.5+0.6\\ \end{aligned}$$

$$\begin{aligned}= & {} 2.6,\\ td_{G_{1}[G_{2}]_{min}}(u_{3},v_{2})= & {} \mu '_{2}(u_{3}u_{4}) + \mu '_{2}(u_{3}u_{4}) +\mu '_{2}(u_{3}u_{4}) + (\mu ''_{1}(v_{2}v_{1}) \wedge \sigma _{1}(u_{3})) \\&+\, (\mu ''_{2}(v_{2}v_{3}) \wedge \sigma _{1}(u_{3}))+ \sigma (u_{3},v_{2})\\= & {} 0.5 +0.5 +0.5 + (0.4\wedge 0.5)+ (0.5\wedge 0.5)+0.5\\= & {} 1.5+ 0.4+ 0.5+0.5\\= & {} 2.9,\\ td_{G_{1}[G_{2}]_{min}}(u_{4},v_{2})= & {} \mu '_{2}(u_{4}u_{3}) + \mu '_{2}(u_{4}u_{3}) +\mu '_{2}(u_{4}u_{3}) + (\mu ''_{1}(v_{2}v_{1}) \wedge \sigma _{1}(u_{4})) \\&+\, (\mu ''_{2}(v_{2}v_{3}) \wedge \sigma _{1}(u_{4}))+ \sigma (u_{4},v_{2})\\= & {} 0.5 + 0.5 +0.5 + (0.4\wedge 0.7)+ (0.5\wedge 0.7)+0.7\\= & {} 1.5+ 0.4+ 0.7+0.7\\= & {} 3.3,\\ td_{G_{1}[G_{2}]_{min}}(u_{1},v_{2})= & {} \mu '_{1}(u_{1}u_{2}) + \mu '_{1}(u_{1}u_{2}) +\mu '_{1}(u_{1}u_{2}) + (\mu ''_{1}(v_{2}v_{1}) \wedge \sigma _{1}(u_{1})) \\&+\, (\mu ''_{2}(v_{2}v_{3}) \wedge \sigma _{1}(u_{1}))+ \sigma (u_{1},v_{2})\\= & {} 0.7 +0.7 +0.7 + (0.4\wedge 0.7)+ (0.5\wedge 0.7)+0.7\\= & {} 2.1+ 0.4+ 0.5+0.7\\= & {} 3.7,\\ td_{G_{1}[G_{2}]_{min}}(u_{2},v_{2})= & {} \mu '_{1}(u_{2}u_{1}) + \mu '_{1}(u_{2}u_{1}) +\mu '_{1}(u_{2}u_{1}) + (\mu ''_{1}(v_{2}v_{1}) \wedge \sigma _{1}(u_{2})) \\&+\, (\mu ''_{2}(v_{2}v_{3}) \wedge \sigma _{1}(u_{2}))+ \sigma (u_{2},v_{2})\\= & {} 0.7 + 0.7 +0.7 + (0.4\wedge 0.9)+ (0.5\wedge 0.7)+0.9\\= & {} 2.1+ 0.4+ 0.5+0.9\\= & {} 3.9. \end{aligned}$$

Theorem 2.26

If $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are two fuzzy graph structures such that $\mu ''_{i} \le \sigma _{1}$, then semi strong min-product $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ is totally regular FGS if and only if $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are totally regular FGS.

Proof

Let $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ be two fuzzy graph structures such that $\mu ''_{i} \le \sigma _{1}$. Then total degree of a vertex in semi strong min-product $G_{1}[G_{2}]_{min}$ is given by:

$$\begin{aligned} td_{G_{1}[G_{2}]_{min}}(u_{i},v_{j}) = td_{G_{2}}(v_{j}) + td_{G_{1}}(u_{i})|V_{2}|. \end{aligned}$$

Assume that $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are two totally regular fuzzy graph structures of degree $k_{1}$ and $k_{2}$, respectively then

$$\begin{aligned} td_{G_{1}[G_{2}]_{min}}(u_{i},v_{j}) = k_{2} + k_{1}|V_{2}|. \end{aligned}$$

Since $k_{1}$, $k_{2}$ and $|V_{2}|$ are constants, so $d_{G_{1}[G_{2}]_{min}}$ is constant for all vertices of $V_{1} \times V_{2}$. Thus semi strong min-product $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots , \mu _{n})$ of fuzzy graph structures $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ is totally regular FGS.

Conversely, suppose that $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are two fuzzy graph structures such that $\mu ''_{i} \le \sigma _{1}$, and semi strong min-product $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ is totally regular fuzzy graph structure. We have to prove that $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are totally regular fuzzy graph structures.

Then total degrees of any two vertices $(u_{1},u_{2})$ and $(v_{1},v_{2})$ in $V_{1} \times V_{2}$ are equal, that is,

$$\begin{aligned} td_{G_{1}[G_{2}]_{min}}(u_{1},u_{2})= & {} td_{G_{1}[G_{2}]_{min}}(v_{1},v_{2}),\\ td_{G_{2}}(u_{2}) + td_{G_{1}}(u_{1})|V_{2}|= & {} td_{G_{2}}(v_{2}) + td_{G_{1}}(v_{1})|V_{2}|. \end{aligned}$$

Fix $u \in V_{2}$ and consider $(u_{1},u)$ and $(v_{1},u)$ in $V_{1} \times V_{2}$, where $u_{1},v_{1}$ are arbitrary elements of $V_{1}$, then above equation becomes

$$\begin{aligned} td_{G_{2}}(u) + td_{G_{1}}(u_{1})|V_{2}|= & {} td_{G_{2}}(u) + td_{G_{1}}(v_{1})|V_{2}|,\\ td_{G_{1}}(u_{1})|V_{2}|= & {} td_{G_{1}}(v_{1})|V_{2}|,\\ td_{G_{1}}(u_{1})= & {} td_{G_{1}}(v_{1}). \end{aligned}$$

This holds for all vertices $u_{1}$ and $v_{1}$ of $V_{1}$.

Thus $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ is totally regular FGS. Now Fix $u' \in V_{1}$ and consider $(u',u_{2})$ and $(u',v_{2})$ in $V_{1} \times V_{2}$, where $u_{2},v_{2}$ are arbitrary elements of $V_{1}$, then above equation becomes

$$\begin{aligned} td_{G_{2}}(u_{2}) + td_{G_{1}}(u')|V_{2}|= & {} td_{G_{2}}(v_{2}) + td_{G_{1}}(u')|V_{2}|,\\ td_{G_{2}}(u_{2})= & {} td_{G_{2}}(v_{2}). \end{aligned}$$

This holds for all vertices $u_{2}$ and $v_{2}$ of $V_{2}$. Thus $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ is totally regular FGS. $\square$

Theorem 2.27

If $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are two fuzzy graph structures such that $\mu ''_{i} \le \sigma _{1}$, then semi strong min-product $G_{1}[G_{2}]_{min}$ = $(\sigma , \mu _{1}, \mu _{2}, \ldots \mu _{n})$ is regular FGS on complete graph structure if and only if $G_{1}= (\sigma _{1}, \mu '_{1}, \mu '_{2}, \ldots ,\mu '_{n})$ and $G_{2}= (\sigma _{2}, \mu ''_{1}, \mu ''_{2}, \ldots ,\mu ''_{n})$ are regular FGSs on complete graph structures $G^{*}_{1}= (V_{1}, R'_{1}, R'_{2}, \ldots ,R'_{n})$ and $G^{*}_{2}= (V_{2}, R''_{1}, R''_{2}, \ldots ,R''_{n})$, respectively .

Proof

The proof of this theorem is similar to the proof of theorem 2.26. $\square$

3 Application

Identification of Best Traveling Service: Traveling sources are need of human beings in all times. In ancient times people used to travel on foot. With the passage of time, man tried to make traveling a little bit convenient. When wheel was invented traveling became convenient than before. Man made carts with help of wheels due to which time and energy consuming in traveling were saved to some extent. As time passed, man made engines and prepare vehicles with help of wheels and engine. Firstly, coal engines were invented, after that man made engines working with petrol and gas. Man invented trains, which saved a lot of traveling time. After this man made aeroplane much better and convenient source of traveling. Due to aeroplanes traveling from one country to other country has become much convenient. There are many airlines working in every country which provide very quick and convenient international traveling. In a country airports are in big cities, rather than this, every one can not afford traveling by air, so mostly people travel by road or train. There are many traveling agencies working in any country which provide road traveling. When a person travel from one city to other city, in selection of a traveling source he has to consider many things, including, fair, traveling time, traveling facilities, environment of bus station, conveyance available near that bus stop etc. To travel from one city to other city there are many traveling agencies, on the basis of above factors he will choose best traveling service for him.

A FGS of travel agencies can be used to show which travel agency is best to travel from one city to other, in accordance to fair, traveling time, traveling facilities, environment of bus station, conveyance available near that bus stop etc. This FGS can also show that in a region of a country which travel agency is best. A FGS of travel agencies of a particular region can be very helpful for the passengers of that region. By looking at this FGS, he can choose the best travel agency. It can also show that which travel agency is becoming popular. By looking at it, other travel agencies can also know, any agency is at which level and it will tell them which services are not good and they should improve their services to be popular.

Consider a set C of eight cities.

$$\begin{aligned} C= & {} \{\textit{Lahore}, \textit{Faisalabad}, \textit{Sialkot}, \textit{Dera Ghazi Khan}, \textit{Multan}, \\&\textit{Qasoor}, \textit{Rawalpindi}, \textit{Lyyaah}\}. \end{aligned}$$

Let $\sigma$ be a fuzzy set on set C, defined in Table 5.

Table 5 Fuzzy set $\sigma$ of eight cities

In Table 5, membership value of a city depicts strength of that city in accordance to educational facilities, economical progress, health facilities and peace.

In Tables 6, 7, 8, 9, 10, 11, 12, 13 and 14, we have mentioned membership values of travel agencies among each pair of cities.

Table 6 Fuzzy set of travel agencies providing service from Rawalpindi to other cities

Table 7 Fuzzy set of travel agencies providing service from Dera Ghazi Khan to other cities

Table 8 Fuzzy set of travel agencies providing service from Faisalabad to other cities

Table 9 Fuzzy set of travel agencies providing service from Sialkot to other cities

Table 10 Fuzzy set of travel agencies providing service from Qasoor to other cities

Table 11 Fuzzy set of travel agencies providing service from Multan to other cities

Table 12 Fuzzy set of travel agencies providing service from Lahore to other cities

Table 13 Fuzzy set of travel agencies providing service from Lyyaah to other cities

Table 14 Fuzzy set of travel agencies providing service among some cities

On set C many relations may be defined, let’s define following relations on C:

$R_{1} = \hbox {Daewoo Express}$, $R_{2} = \hbox {Niazi Express}$, $R_{3} = \hbox {Faisal Movers}$, $R_{4} = \hbox {Train}$, $R_{5} = \hbox {Subhan Travels}$, $R_{6} = \hbox {Local Times}$, such that $(C, R_{1}, R_{2}, R_{3}, R_{4}, R_{5}, R_{6})$ is graph structure. Every element in any relation demonstrates particular kind of best traveling service among those two cities.

As $(C, R_{1}, R_{2}, R_{3}, R_{4}, R_{5}, R_{6})$ is graph structure, that’s why a pair of cities appears in only one relation. Hence it will be considered an element of that particular relation, for which its membership value is high than that of other relations.

Using above data, elements in relations are paired with their membership values, resulting sets are fuzzy sets on $R_{1}$, $R_{2}$, $R_{3}$, $R_{4}$, $R_{5}$, $R_{6}$, respectively. These fuzzy sets are named as: $\mu _{1}$, $\mu _{2}$, $\mu _{3}$, $\mu _{4}$, $\mu _{5}$, $\mu _{6}$, respectively. Let

• $R_{1}= \{(\textit{Faisalabad},\textit{Lahore}), (\textit{Faisalabad}, \textit{Multan})$,

  $(\textit{Lahore}, \textit{Qasoor}), (\textit{Dera Ghazi Khan},\textit{Lahore})\}$,

• $R_{2}=\{(\textit{Dera Ghazi Khan}, \textit{Faisalabad})\}$,

• $R_{3}=\{(\textit{Dera Ghazi Khan}, \textit{Rawalpindi}),(\textit{Lyyaah}, \textit{Rawalpindi})\}$,

• $R_{4}=\{(\textit{Faisalabad}, \textit{Qasoor})$, $(\textit{Sialkot}, \textit{Lahore})\}$,

• $R_{5}= \{(\textit{Multan}, \textit{Rawalpindi}), (\textit{Lyyaah}, \textit{Sialkot})\}$,

• $R_{6}= \{(\textit{Faisalabad}, \textit{Lyyaah})\}$.

And corresponding fuzzy sets are:

• $\mu _{1}=\{((\textit{Faisalabad},\textit{Lahore}),0.7),((\textit{Faisalabad}, \textit{Multan}),0.6)$,

  $((\textit{Lahore}, \textit{Qasoor}),0.7), ((\textit{Dera Ghazi Khan},\textit{Lahore}),0.7) \}$,

• $\mu _{2}=\{(\textit{Dera Ghazi Khan}, \textit{Faisalabad}),0.7)\}$

• $\mu _{3}=\{((\textit{Dera Ghazi Khan}, \textit{Rawalpindi}), 0.7),((\textit{Lyyaah}, \textit{Rawalpindi}),0.4) \}$,

• $\mu _{4}=\{(\textit{Faisalabad}, \textit{Qasoor}),0.8)$,$((\textit{Sialkot}, \textit{Lahore}),0.6) \}$,

• $\mu _{5}=\{((\textit{Multan}, \textit{Rawalpindi}),0.6),$$((\textit{Lyyaah}, \textit{Sialkot}),0.4) \}$,

• $\mu _{6}=\{((\textit{Faisalabad}, \textit{Lyyaah}), 0.4) \}$.

Clearly, $(\sigma , \mu _{1}, \mu _{2}, \mu _{3}, \mu _{4}, \mu _{5}, \mu _{6})$ is a FGS and is shown in Fig. 13.

Fig. 13

Fuzzy graph structure showing best traveling service among different cities

In FGS shown in Fig. 13 each edge demonstrate best traveling service among corresponding cities. For example: best traveling service among Faisalabad and Lahore is Daewoo Express. It is noted that the vertex Faisalabad has highest degree of relation Daewoo Express, it means that Faisalabad has Daewoo Express as best traveling service. Moreover, according to above FGS, Dera Ghazi Khan and Rawalpindi has Faisal Movers as best traveling service at this time. Furthermore, to travel from Lahore to Sialkot best traveling service is train. We can also observe that Daewoo Express is best traveling service at this time in this region of eight cities.

We now present the general procedure of our method which is used in this application in the following algorithm.

Algorithm

Step 1 :

Input the set $C= \{c_{1}, c_{2}, \ldots , c_{n}\}$ of cities(vertices) and the fuzzy set $\sigma$ defined on set C.

Step 2 :

Input the fuzzy set of travel agencies providing services from one city to other cities and compute its degree of membership using, $\mu (c_{i}c_{j}) \le \sigma (c_{i})\wedge \sigma (c_{j})$.

Step 3 :

Repeat Step 2 for all cities in set C.

Step 4 :

Develop mutually disjoint, irreflexive and symmetric relations $R_{1}, R_{2}, \ldots , R_{n}$ on set of cities C and give the name each relation as a travel agency.

Step 5 :

Select a travel agency as best travel agency to travel from one city to other, whose membership value is high than that of other agencies.

Step 6 :

Construct a graph structure on set of cities with relations, select those pairs of cities having same kind of best travel agency as elements of same relation.

Step 7 :

Write all elements of relations with their membership values, resulting relations $\mu _{1}, \mu _{2}, \ldots , \mu _{n}$ are fuzzy sets on $R_{1}, R_{2}, R_{3}, \ldots , R_{n}$, respectively and $(\sigma , \mu _{1}, \mu _{2}, \ldots , \mu _{n} )$ is a fuzzy graph structure.

Step 8 :

Draw the fuzzy graph structure whose every edge identify best traveling service among corresponding cities.

4 Conclusions

Graph structures are widely useful in studying some structures, including graphs, labeled graphs, signed graphs, edge colored graphs and have numerous applications in various domains. In some cases, certain aspects of graph-theoretical systems may be ambiguous. Use of fuzzy methods in dealing vague notions and uncertainty is quite natural. Fuzzy graph structures have many advantages to cope with vagueness and uncertainty. In this paper, we have introduced semi strong min-product of fuzzy graph structures, regular fuzzy graph structures, strong and complete regular fuzzy graph structures. Moreover, we have defined degree of a vertex in semi strong min-product of fuzzy graph structures. We have also discussed total degree of a vertex in semi strong min-product of fuzzy graph structures and explained some properties of all these concepts with detailed examples. Furthermore, we have presented an application of fuzzy graph structures in decision-making, that is, identification of best traveling service. We aim to extend our work to: (1) Pythagorean fuzzy graph structures, (2) Bipolar fuzzy graph structures, (3) Soft fuzzy graph structures, (4) Rough fuzzy graph structures, (5) Rough fuzzy soft graph structures, and (6) Fuzzy soft graph structures.