Abstract
Decision-making is an ongoing process for humankind. Many of these real-world decisions can be modeled using the problems contained in the generalized area of combinatorial optimization. Another area with recent advancements is fuzzy logic.
This chapter is concerned about the fuzzy solution approaches of combinatorial optimization problems. First section presents the fuzzy graph theory. Fuzzy linear programming and fuzzy integer programming are explained in second and third sections. Fuzzy spanning trees, fuzzy shortest path, fuzzy network flows, and the fuzzy minimum cost flow problems are introduced at Sects. 4–7. Fuzzy matching algorithm, fuzzy matroids, and fuzzy approximation algorithm are discussed in Sects. 8–10. Basic information on fuzzy knapsack and fuzzy bin-packing problems is given in Sects. 11 and 12. Fuzzy multicommodity flows and edge-disjoint paths are explained in Sect. 13 in detail with four subsections. Fuzzy network design problems and fuzzy traveling salesman problem are provided in Sects. 14 and 15 respectively. Finally, fuzzy facility location is presented in the last section.
Access provided by Autonomous University of Puebla. Download reference work entry PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Fuzzy Graph
A pair G = (V, E) with \(E \subseteq E(V )\) is called a graph (on V ). The elements of V are the vertices of G, and those of E the edges of G. The vertex set of a graph G is denoted by V G and its edge set by E G . Therefore, \(G = (V _{G},E_{G})\).
In the literature, graphs are also called simple graphs; vertices are called nodes or points; edges are called lines or links. More extensive information on graph theory can be found at [1, 2].
Fuzzy graph theory was introduced by Rosenfeld in 1975 [3], and some important definitions about this theory are as follows [3–10]:
Definition 1
A fuzzy graph G which is a pair of functions can be denoted by \(G : (\sigma,\mu )\) where \(\sigma\) is a fuzzy subset of set V (a nonempty set) and \(\mu\) is a symmetric fuzzy relation on \(\sigma\). The underlying crisp graph of \(G : (\sigma,\mu )\) is denoted by \({G}^{{\ast}}(V,E)\) where \(E \subseteq V \times V\). A fuzzy graph G is complete if \(\mu (uv) =\sigma (u) \wedge \sigma (v)\) for all \(u,v \in V\) where uv stands for the edge between u and v.
Definition 2
A fuzzy graph G denoted by \(G : (\sigma,\mu )\). The degree of a vertex u is \(d_{G(u)} =\sum _{u\neq V }\mu (uv)\). As \(\mu (uv)> 0\) for \(uv \in E\) and \(\mu (uv) = 0\) for \(uv\notin E\), this is equivalent to \(d_{G(u)} =\sum _{uv\in E}\mu (uv)\). Then the minimum degree of G is \(\delta (G) = \Lambda \{d(v)/v \in V \}\), and the maximum degree of G is \(\Delta (G) = \vee \{d(v)/v \in V \}\).
Definition 3
The strength of connectedness between two vertices u and v is \({\mu }^{\infty }(u,v) = \mathrm{sup}\{{\mu }^{k}(u,v)/k = 1,2\ldots.\}\) where
Definition 4
An edge uv is a fuzzy bridge of \(G : (\sigma,\mu )\) if deletion of uv reduces the strength of connectedness between pair of vertices.
Definition 5
A vertex u is a fuzzy cut vertex of \(G : (\sigma,\mu )\) if deletion of u reduces the strength of connectedness between some other pair of vertices.
Definition 6
Let \(G : (\sigma,\mu )\) be a fuzzy graph such that \({G}^{{\ast}}(V,E)\) is a cycle. Then G is a fuzzy cycle if and only if there does not exist a unique edge xy such that \(\mu (\mathit{xy}) = \vee \{\mu (\mathit{uv})/(\mathit{uv})> 0\}\).
Definition 7
The order of a fuzzy graph G is \(O(G) =\sum _{u\in V }\sigma (u)\). The size of a fuzzy graph G is \(S(G) =\sum _{\mathit{uv}\in E}\mu (\mathit{uv})\).
Definition 8
Let \(G : (\sigma,\mu )\) be a fuzzy graph on \({G}^{{\ast}}(V,E)\). If d G (v) = k for all \(v \in V\), that is, if each vertex has some degree k, then G is said to be a regular fuzzy graph of degree k or a k-regular fuzzy graph. This is analogous to the definition of regular graphs in crisp graph theory.
Definition 9
Let \(G : (\sigma,\mu )\) be a fuzzy graph on \({G}^{{\ast}}(V,E)\). The total degree of a vertex \(u \in V\) is defined by \(\mathit{td}_{G}(u) =\sum _{u\neq v}\mu (\mathit{UV }) +\sigma (u) =\sum _{\mathit{uv}\in E}\mu (\mathit{UV }) +\sigma (u) = d_{G}(u) +\sigma (u)\). If each vertex G has the same total degree k, then G is said to be a totally regular fuzzy graph of total degree k or a k-totally regular fuzzy graph.
The most important areas for the application of fuzzy graphs and fuzzy relations are logic, topology, pattern recognition, information theory, control theory, artificial intelligence, neural networks, operations research, planning, and systems analysis.
Bhattacharya [4] established some connectivity concepts regarding fuzzy cut nodes and fuzzy bridges. The author also introduced the notions of eccentricity and center.
Moreover, Bhattacharya and Suraweera [11] introduced an algorithm to find the connectivity of a pair of nodes in a fuzzy graph [4].
Furthermore, Tong and Zheng [12] presented an algorithm to find the connectedness matrix of a fuzzy graph. While, Xu [13] introduced connectivity parameters of fuzzy graphs to problems in chemical structures, Sunitha and Vijayakumar [7] focused on characterizing fuzzy trees using its unique maximum spanning tree. In addition, a sufficient condition for a node to be a fuzzy cut node is presented in [14]. Also, center problems in fuzzy graphs [15], blocks in fuzzy graphs [16], and properties of self-complementary fuzzy graphs [17] were introduced by the same authors. Therefore, using the concept of the strongest paths, they have obtained a characterization for blocks in fuzzy graphs [15]. Bhutani and Rosenfeld have focused on the concepts of strong arcs [18], fuzzy end nodes [19], and geodesics in fuzzy graphs [20]. In [17], the authors have defined the concepts of strong arcs and strong paths. They have pointed out the existence of a strong path between any two nodes of a fuzzy graph and have studied the strong arcs of a fuzzy tree. In [15], the concepts of fuzzy end nodes and multimin and locamin cycles are studied. The concept of strong arc in maximum spanning trees [21] and its applications in cluster analysis and neural networks were presented by Sameena and Sunitha [21, 22]. According to Mathew and Sunitha, there are different types of arcs in fuzzy graphs and they have obtained an arc identification procedure [14].
2 Fuzzy Linear Programming
Linear programming is one of the most widely used decision-making tools for solving real-world problems. Many researchers focus on the area of fuzzy linear programming because of the fact that the real-world situations are characterized by imprecision rather than exactness. In order to have a clear understanding, few of such researches are discussed/shown below.
Gupta and Mehlawat studied a pair of fuzzy primal–dual linear programming problems and calculate duality results using an aspiration level approach. They use an exponential membership function, which is in contrast to the earlier works that relied on a linear membership function. As the fuzzy environment causes a duality gap, they investigate how choosing the exponential membership function impacts the gap [23].
Amiria and Nasseria applied a linear ranking function to order trapezoidal fuzzy numbers. Then, they establish the dual problem of the linear programming problem with trapezoidal fuzzy variables and hence deduce some duality results. In particular, they prove that the auxiliary problem is indeed the dual of the linear programming problems with trapezoidal fuzzy variables (FVLP). Having established the dual problem, the results will then follow as natural extensions of duality results for linear programming problems with crisp data. Finally, using the results, they develop a new dual algorithm for solving the FVLP problem directly, making use of the primal simplex tableau [24].
In his paper, Ramik introduced a broad class of FLP problems firstly and defined the concepts of \(\beta\)-feasible and \((\alpha,\beta )\)-maximal and minimal solutions of FLP problems. The class of classical LP problems can be embedded into the class of FLP ones. Furthermore, he defines the concept of duality and proves the weak and strong duality theorem generalizations of the classical ones for FLP problems [25].
On the other hand, Inuiguchi treats fuzzy linear programming problems with uncertain parameters whose ranges are specified as fuzzy polytopes in his study. The problem is formulated as a necessity measure optimization model. It is shown that the problem can be reduced to a semi-infinite programming problem and solved by a combination of a bisection method and a relaxation procedure. An algorithm in which the bisection method and the relaxation procedure converge simultaneously is proposed. A simple numerical example is given to illustrate the solution procedure [26].
Wua et al. present an efficient method to optimize such a linear fractional programming problem. First, some theoretical results are developed based on the properties of max-Archimedean t-norm composition. Then, the result is used to reduce the feasible domain. The problem can thus be simplified and converted into a traditional linear fractional programming problem and eventually optimized in a small search space. A numerical example is provided to illustrate the procedure [27].
In addition to above-mentioned studies, a new method to find the fuzzy optimal solution of same type of fuzzy linear programming problems is proposed by Kumar et al. It is easier to apply the proposed method, compared to the existing method in order to solve the fully fuzzy linear programming problems with equality constraints occurring in real-life situations. To illustrate, the proposed method numerical examples are solved, and the obtained results are discussed [28]. Additionally, Lotfi et al. discussed full fuzzy linear programming (FFLP) problems of which all parameters and variables are triangular fuzzy numbers. They use the concept of the symmetric triangular fuzzy number and introduce an approach to defuzzify a general fuzzy quantity [29].
By proposing the fuzzy multiobjective linear programming (FMOLP) model with triangular fuzzy numbers, Zenga et al., transformed the FMOLP model and its corresponding fuzzy goal programming (FGP) problem to crisp ones. These can be solved by the conventional programming methods. The FMOLP model was applied to crop area planning of Liang Zhou region, Gansu province of northwest China, and then the optimal cropping patterns were obtained under different water-saving levels and satisfaction grades for water resources availability of the decision-makers (DM) [30].
Further, Liang developed an interactive fuzzy multiobjective linear programming (i-FMOLP) method for solving the fuzzy multiobjective transportation problems with piecewise linear membership function. Proposed i-FMOLP method aims to simultaneously minimize the total distribution costs and the total delivery time. i-FMOLP method also has reference to fuzzy available supply and total budget at each source and fuzzy forecast demand with maximum warehouse space at each destination. Additionally, the above-mentioned method describes a systematic framework that facilitates the fuzzy decision-making process, enabling a decision-maker (DM) to interactively modify the fuzzy data and related parameters until a set of satisfactory solutions are obtained. An industrial case is presented to demonstrate the feasibility of applying such proposed method to real transportation problems [31].
Peidro et al. modeled supply chain (SC) uncertainties by fuzzy sets and develop a fuzzy linear programming model for tactical supply chain planning in a multi-echelon, multiproduct, multilevel, multi-period supply chain network in their study. In this approach, the demand, process, and supply uncertainties are jointly considered. The aim is to centralize multi-node decisions simultaneously to achieve the best use of the available resources along the time horizon so that customer demands are met at a minimum cost. With this intention, Peidro et al.’s proposal is tested by using data from a real automobile SC. Thus, fuzzy model provides the decision-maker (DM) with alternative decision plans with different degrees of satisfaction [32].
Other solutions are found by Bucley and Feuring to the fully fuzzified linear program where all the parameters and variables are fuzzy numbers in their study. First, they change the problem of maximizing a fuzzy number, the value of the objective function, into a multiobjective fuzzy linear programming problem. Then, they prove that fuzzy flexible programming can be used to explore the whole nondominated set to the multiobjective fuzzy linear program. Hence, an evolutionary algorithm is designed to solve the fuzzy flexible program, and they apply this program to two applications to generate good solutions [33].
Comparatively, Chanas and Zielinski analyzed the linear programming problem with fuzzy coefficients in the objective function. The set of nondominated (ND) solutions with respect to an assumed fuzzy preference relation, according to Orlovsky’s concept, is supposed to be the solution of the problem. Special attention is paid to unfuzzy nondominated (UND) solutions (the solutions which are nondominated to the degree 1). The main results of their paper are sufficient conditions on a fuzzy preference relation which allows reducing the problem of determining UND solutions to that of determining optimal solutions of a classical linear programming problem. These solutions can thus be determined by means of classical linear programming methods [34].
Another major study is by Stanciulescu et al., modeling a multiobjective decision-making process by a multiobjective fuzzy linear programming problem with fuzzy coefficients for the objectives and the constraints. Moreover, the decision variables are linked together because they have to sum up to a constant. Most of the time, the solutions of a multiobjective fuzzy linear programming problem are crisp values. Thus, the fuzzy aspect of the decision is partly lost, and the decision-making process is constrained to crisp decisions. However, they propose a method that uses fuzzy decision variables with a joint membership function instead of crisp decision variables. First, they consider lower-bounded fuzzy decision variables that set up the lower bounds of the decision variables. Second, the method is generalized to lower–upper-bounded fuzzy decision variables that also set up the upper bounds of the decision variables. The results are closely related to the special type of the problem they are coping with, since they embed a sum constraint in the joint membership function of the fuzzy decision variables. Numerical examples are presented in order to illustrate their method [35].
By the same token, as a case study, Sadeghi and Hosseini tried to demonstrate the method of application of FLP for optimization of supply energy system in Iran. They used FLP model comprises fuzzy coefficients for investment costs. Following the mentioned purpose, it is realized that FLP is an easy and flexible approach that can be a serious competitor for other confronting uncertainties approaches, that is, stochastic and minimax regret strategies [36].
On the other hand, Liu proposed a new kind of method for solving fuzzy linear programming problems based on the satisfaction (or fulfillment) degree of the constraints. Using a new ranking method of fuzzy numbers, the fulfillment of the constraints can be measured. Then the properties of the ranking index are discussed. With this ranking index, the decision-maker can make the constraints tight or loose based on his optimistic or pessimistic attitude and get the optimal solution from the fuzzy constraint space. The corresponding value of objective distribution function therefore can be obtained. A numerical example illustrates the merits of the approach [37].
Chen and Ko proposed fuzzy linear programming models to determine the fulfillment levels of PCs under the requirement to achieve the determined contribution levels of design requirements (DRs) for customer satisfaction. In addition, by considering the design risk, they incorporate failure modes and effect analysis (FMEA) into quality function deployment (QFD) processes, which are treated as the constraint in the models. In order to cope with the vague nature of product development processes, fuzzy approaches are used for both FMEA and QFD. The illustration of the suggested models is performed with a numerical example to indicate the applicability in practice [38].
Eventually, Katagiri et al. considered multiobjective linear programming problems with fuzzy random variables coefficients. A new decision-making model is proposed to maximize both possibility and probability, which is based on possibilistic programming and stochastic programming. An interactive algorithm is constructed to obtain a satisficing solution satisfying at least weak Pareto optimality [39].
3 Fuzzy Integer Programming
The linear programming models that have been discussed thus far all have been continuous, in the sense that decision variables are allowed to be fractional.
Often this is a realistic assumption. For instance, we might easily produce 102 3/4 gallons of a divisible good such as wine. It might also be reasonable to accept a solution giving an hourly production of automobiles at 58 1/2 if the models were based upon average hourly production, and the production had the interpretation of production rates.
At other times, however, fractional solutions are not realistic, and we must consider the optimization problem:
subject to
This problem is called the (linear) integer programming problem. It is said to be a mixed-integer program when some, but not all, variables are restricted to be integer and is called a pure integer program when all decision variables are integers.
The implications of fuzzy set theory in optimal decision-making were first recognized by Bellman and Zadeh [40] and were later extended to linear programming problems with fuzzy constraints and multiple objectives by Zimmermann [41]. The latter formulation was subsequently extended to integer programming problems [42–45]. Fuzzy techniques have recently been applied to the analysis and optimization [46, 47]. Also, linear and integer linear programming are known to capture well optimization problems relevant to high-speed networks [48].
The fuzzy integer programming (FIP) methods provide another type of potentially useful approach for integer programming under uncertainty. Major shortcomings with the FIP methods are that, firstly, it may be difficult to obtain membership information for all system components in practical problems; secondly, FIP methods may lead to more complicated submodels that are computationally difficult for practical applications; and thirdly, most of the FIP solution algorithms are indirect approaches containing intermediate control variables or parameters, which are difficult to determine by certain criteria. They are thus unable to communicate uncertainty directly into the optimization processes and resulting specific solutions [49].
Tan et al. present integer programming optimization models for planning the retrofit of power plants at the regional or national level at their study. In addition to the base case (i.e., non-fuzzy or crisp) formulation, two fuzzy extensions are given to account for the inherent conflict between environmental and economic goals, as well as parametric uncertainties pertaining to the emerging carbon capture technologies. Case studies are shown to illustrate the modeling approach [50].
Asratian and Kuzjurin considered covering programs with 0–1 variables and cost function of the form \(\sum _{j}x_{j}\) under the assumption that they know a pattern of coefficients in constraints, which are nonzero and only those coefficients can vary in some interval [1, M] (zero elements do not change their value). As their main result, they found some sufficient conditions guaranteeing the variation of integral optimum in the average case (over all zero–nonzero patterns) is close to 1 as the number of variables tends to infinity. This means that for typical patterns the values of nonzero elements in A can vary without affecting significantly the value of the optimum of the integer program (i.e., the optimum value depends mostly on the pattern but not on the values of nonzero elements) [48].
Gharehgozli et al. present a new mixed-integer goal programming (MIGP) model for a parallel-machine scheduling problem with sequence-dependent setup times and release dates. Two objectives are considered in the model to minimize the total weighted flow time and the total weighted tardiness simultaneously. Due to the complexity of the above model and uncertainty involved in real-world scheduling problems, it is sometimes unrealistic or even impossible to acquire exact input data. Hence, they consider the parallel-machine scheduling problem with sequence-dependent setup times under the hypothesis of fuzzy processing time’s knowledge and two fuzzy objectives as the MIGP model [51].
Li et al. developed a two-stage fuzzy robust integer programming (TFRIP) method for planning environmental management systems under uncertainty. Their approach integrates techniques of robust programming and two-stage stochastic programming within a mixed-integer linear programming framework. It can facilitate dynamic analysis of capacity-expansion planning for waste-management facilities within a multistage context. The TFRIP method is applied to a case study of long-term waste-management planning under uncertainty. Generated solutions for continuous and binary variables can provide desired waste-flow allocation, capacity-expansion plans with a minimized system cost, and maximized system feasibility [52].
Allahviranloo and Afandizadeh formulated an investment model to find the optimum investment steps by application of operational research science and fuzzy logic concept to model the available uncertainties. Fuzzy integer linear programming models are used to determine the optimum investment and development of a port [53].
Also, Emam studied a bi-level integer nonlinear programming problem [54] with linear or nonlinear constraints, where nonlinear objective function at each level is maximized. The bi-level integer nonlinear programming (BLI-NLP) problem can be thought as a static version of the Stackelberg game, which is used as a leader–follower game. A Stackelberg game is used by the leader, or the higher-level decision-maker (HLDM), given the rational reaction of the follower, or the lower-level decision-maker (LLDM). He proposed a two-planner integer model and a solution method for solving this problem. This method uses the concept of tolerance membership function and the branch-and-bound technique to develop a fuzzy max–min decision model for generating Pareto optimal solution for this problem; an illustrative numerical example is given to represent the obtained results [53].
4 Fuzzy Spanning Trees
In classical mathematical programming, the coefficients of objective functions or constraints in problems are assumed to be completely known. However, in real systems, they are uncertain than constant. In order to deal with such uncertainty, stochastic programming [55] and fuzzy programming [56] were considered. Both are useful tools for the decision-making under a stochastic environment or a fuzzy environment, respectively [57].
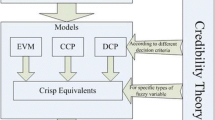
In parallel Gao and Lu formulated a fuzzy quadratic minimum spanning tree problem as expected value model, chance-constrained programming, and dependent-chance programming according to different decision criteria in their study. Then the crisp equivalents are derived when the fuzzy costs are characterized by trapezoidal fuzzy numbers. Furthermore, a simulation-based genetic algorithm using Prüfer number representation is designed for solving the proposed fuzzy programming models as well as their crisp equivalents, and a numerical example is displayed to illustrate the effectiveness of the genetic algorithm at the end of the study [57].
Katagiri et al. [58] investigated bottleneck spanning tree problems where each cost attached to the edge in a given graph is represented with a fuzzy random variable. The problem is to find the optimal spanning tree that maximizes a degree of possibility or necessity under some chance constraint. After transforming the problem into the deterministic equivalent one, they introduce the subproblem which has close relations to the deterministic problem. Utilizing fully the relations, they give a polynomial order algorithm for solving the deterministic problem.
Additionally, Katagiri et al. [59] studied minimum spanning tree problems where each edge weight is a fuzzy random variable. A fuzzy goal for the objective function is defined to capture the imprecise judgment of the decision-maker. They also proposed a decision-making model based on a possibilistic programming model and the expectation optimization model in stochastic programming.
5 Fuzzy Shortest Path
The shortest path problem (SPP) is one of the most fundamental and well-known combinatorial optimization problem that appears in many applications, including communications, transportation, routing, supply chain management, or models involving agents as a subproblem [60].
The problem of finding the shortest path from a specified source node to the other nodes is a fundamental matter in graph theory and one that is currently being greatly studied [61–68].
The classical problem seeks to select a path with minimum length from a finite set of paths. In real-world problems, arc lengths represent traveling time, cost, distance, or other variables. However, in practice, uncertainty cannot be avoided, and usually, the arc lengths cannot be determined precisely. For instance, on road networks, for several reasons, that is, traffic, accidents, or weather condition, arc lengths representing the vehicle travel time are subject to uncertainty. In such situations, a fuzzy shortest path problem (FSPP) seems to be more realistic and reliable.
According to Hernandes et al., an iterative algorithm assumes a generic ranking index for comparing the fuzzy numbers involved in the problem, in such a way that each time in which the decision-maker wants to solve a concrete problem(s) he/she can choose (or propose) the ranking index that best suits that problem. Hernandes et al.’s algorithm is based on the Ford–Moore–Bellman algorithm for classical graphs. In concrete, it can be applied in graphs with negative parameters, and it can detect whether there are negative circuits. For the sake of illustrating the performance of the algorithm in the study, it has been developed using only certain order relations. However, it is not restricted at all to use these comparison relations exclusively. As the theoretical base of a decision support system’s concern is to solve this kind of problems, the proposed iterative algorithm is easy to understand [69].
Tajdin et al. concerned with the design of a model and an algorithm for computing a shortest path in a network having various types of fuzzy arc lengths. Firstly, to obtain membership functions for the considered additions, they developed a new technique for the addition of various fuzzy numbers in a path using \(\alpha\)-cuts by proposing a linear least squares model. Then, using a recently proposed distance function for comparison of fuzzy numbers, they present a dynamic programming method for finding a shortest path in the network [70].
Moazeni discussed the shortest path problem in his study. A positive fuzzy quantity is assigned to each arc as its arc length on a network. He defines an order relation between fuzzy quantities with finite supports. Then by applying Hansen’s multiple labeling method together with Dijkstra’s shortest path algorithm, he proposes a new algorithm for finding the set of nondominated paths with respect to the extension principle. Moreover, he shows that the only existing approach for this problem, Klein’s algorithm, may lead to a dominated path in the sense of extension principle [60].
Keshavarz and Khorram concentrated on a shortest path problem on a network where arc lengths (costs) are not deterministic numbers, but imprecise ones in their study. Here, costs of the shortest path problem are fuzzy intervals with increasing membership functions, whereas the membership functions of the total cost of the shortest path are a fuzzy interval with a decreasing linear membership function. By the max–min criterion suggested in [71], the fuzzy shortest path problem can be treated as a mixed-integer nonlinear programming problem. They pointed out that this problem can be simplified into a bi-level programming problem that is very solvable. In order to solve the bi-level programming problem, they propose an efficient algorithm based on the parametric shortest path problem. An illustrative example is used to denote their algorithm [72].
In a network, the arc lengths may represent time or cost. In practical situations, it is reasonable to assume that each arc length is a discrete fuzzy set. It is called the discrete fuzzy shortest path problem. There are several methods reported to solve this kind of problem in the literature. In these methods, they can obtain either the fuzzy shortest length or the shortest path. In their study, Chuang and Kung claimed a new algorithm which can obtain both of them. The discrete fuzzy shortest length method is proposed to find the fuzzy shortest length, and the fuzzy similarity measure is utilized to get the shortest path. An illustrative example represents their proposed algorithm [62].
Ji et al. considers the shortest path problem with fuzzy arc lengths in their study. According to different decision criteria, the concepts of expected shortest path, \(\alpha\)-shortest path, and the shortest path in fuzzy environment are originally introduced, and three types of models are formulated. In order to solve these models, a hybrid intelligent algorithm integrating simulation and genetic algorithm are asserted and numerous examples illustrate its effectiveness [73].
Okada deals with a shortest path problem on a network in which a fuzzy number, instead of a real number, is assigned to each arc length in his study. Such a problem is “ill-posed” because each arc cannot be identified as being either on the shortest path or not. Therefore, based on the possibility theory, he introduces the concept of “degree of possibility” that an arc is on the shortest path. Every pair of distinct paths from the source node to any other node is implicitly assumed to be noninteractive in the conventional approaches. This assumption is unrealistic and also involves inconsistencies. To overcome this drawback, he defines a new comparison index between the sums of fuzzy numbers by considering interactivity among fuzzy numbers. An algorithm is presented to determine the degree of possibility for each arc on a network. This algorithm is evaluated by means of large-scale numerical examples. Consequently, this approach is found efficient even for real-world practical networks [66].
The fuzzy shortest path (SP) problem aims at providing decision-makers with the fuzzy shortest path length (FSPL) and the SP in a network with fuzzy arc lengths. In their study, Chuand and Kung represent each arc length a triangular fuzzy set and propose a new algorithm to deal with the fuzzy SP problem. First, they proposed a heuristic procedure to find the FSPL among all possible paths in a network. It is based on the idea that a crisp number is a minimum number if and only if any other number is larger than or equal to it. It owns a firm theoretic base in fuzzy sets theory and can be implemented effectively. Second, they propose a way to measure the similarity degree between the FSPL and each fuzzy path lengths. The path with the highest similarity degree is the SP. An illustrative example is added to display their proposed approach [61].
6 Fuzzy Network Flows
Network flow problems have a wide range of engineering and management applications such as analyses and design of computer networks, cable television networks, transportation systems, communication networks, project schedules, queuing systems, inventory systems, and manpower allocation [74].
In parallel, Liu and Kao [74] studied the network flow problems in that the arc lengths of the network and the objective value are fuzzy numbers. The illustrative example is on the problem of multimedia transmission over Internet.
Flows in networks provide very useful models in a number of practical contexts. The major techniques in the area revolve around celebrated max-flow min-cut theorem (MFMCT) and associated algorithms. In this context, Diamond develops analogues of the MFMCT and Karp–Edmonds algorithm for networks with fuzzy capacities and flows in their study. The principal difference between fuzzified and traditional crisp versions is that although the maximum fuzzy flow corresponds to a minimum fuzzy capacity, the latter may incorporate a number of network cuts. Preliminary results are for interval-valued flows and capacities which, in themselves, provide robustness and estimates for flows in an uncertain environment. In turn, a fuzzy theorem and algorithm are obtained by regarding these intervals as level sets of fuzzy numbers [75].
Georgiadis considered a general class of optimization problems regarding spanning trees in directed graphs (arborescence). In his study, Georgiadis considered the following optimization problem. He assumed that edge costs take values in a set U endowed with a dyadic relation and a dyadic operation. He sought to find the directed spanning tree whose cost (with respect to the dyadic operation) is minimal with respect to the dyadic relation. Then, he provided an algorithm for solving the problem, which can be considered as generalization of Edmonds’ special cases of this problem provide algorithms for the minimum sum, bottleneck and lexicographically optimal arborescence, as well as the widest-minimum sum spanning arborescence problem [76].
7 Fuzzy Minimum Cost Flow Problems
Minimal cost flow problem (MCFP) is an important problem in combinatorial optimization and network flows and has many applications in practical problems, such as communication, transportation, urban design, and job scheduling models [77].
The aim of the minimal cost flow problem (MCFP) in fuzzy nature, denoted with FMCFP, is to find the least cost of the shipment of a commodity through a capacitated network in order to satisfy imprecise concepts in supply or demand of network nodes and capacity or cost of network links [78].
Ghatee and Hashemi presented a model in which the supply and demand of nodes and the capacity and cost of edges are represented as fuzzy numbers. For easier reference, they refer to this group of problems as fully fuzzified MCFP. Hukuhara’s difference and approximated multiplication are used to represent their model. Thereafter, they sort fuzzy numbers by an order using a ranking function and show that it is a total order, that is, a reflexive, antisymmetric, transitive, and complete binary relation. Utilizing the proposed ranking function, they transform the fully fuzzified MCFP into three crisp problems solvable in polynomial time [79].
Also, Ghatee and Hashemi deal with fuzzy quantities and relations in multi-objective minimum cost flow problem in their study. When t-conorms and t-conorms are available, the goal programming is applied to minimize the deviation among the multiple costs of fuzzy flows and the given targets. To obtain the most optimistic and the most pessimistic satisficing solutions of the problem, two different polynomial time algorithms are introduced by applying some network transformations. To verify the performance of this approach in actual substances, network design under fuzziness is considered, and an efficient scheme is proposed including genetic algorithm including fuzzy minimum cost flow problem [80].
Similarly, Ghatee et al. study the minimal cost flow problem (MCFP) with fuzzy link costs, say fuzzy MCFP, to understand the effect of uncertain factors in applied shipment problems. With respect to the most possible case, the worst case, and the best case, the fuzzy MCFP can be converted into a three-objective MCFP. Applying a lexicographical ordering on the objective functions of derived problem, two efficient algorithms are provided to find the preemptive priority-based solution(s), namely, p-successive shortest path algorithm and p-network simplex algorithm. In both of them, lexicographical comparison is used which is a natural ordering in many real problems especially in hazardous material transportation where transporting through some links jeopardizes people’s lives. Presented schemes maintain the network structure of the problem, and so, they are efficiently implementable. A sample network is added to illustrate the procedure and to compare the computational experiences with those of previously established works. Finally, the above-presented approach is applied to find an appropriate plan to transit hazardous materials in Khorasan roads network using annual data of accidents [81].
8 Fuzzy Matching Algorithm
Matching problem is one of the most important optimization problems. The model is widely used in practice such as pattern recognizing, system optimization, and job assignment problem. A matching of a graph is an independent subset M of edge set. In other words, a matching is a set of pairwise disjoint edges.
To explain this algorithm, first, we will explain fuzzy maximum matching algorithms. A maximum matching has as many edges in it as possible. Another version of this general problem is called the maximum weighted matching problem, and significantly more difficult will be captured in the second subsection of this section.
A maximum weighted matching problem is to choose a maximum matching in a given graph so that the sum of weight of the edges in it is at the maximum level. Nonbipartite weighted matching appears to be one of the “hardest” combinatorial optimization problems that can be solved in polynomial time.
Another version of weighted matching algorithms is a well-known problem called the assignment problem (AP). It can also be called as the minimum weight perfect matching problem in bipartite graphs. The fuzzy assignment problem (FAP) is also introduced at the Sect. 8.2.1.
There are several other inexact matching methods based on continuous optimization that have been proposed in the recent years. Among them we can cite the fuzzy graph matching (FGM) that is a simplified version of weighted graph matching (WGM) problem and based on fuzzy logic. In FGM, as the cost of matching two nodes does not depend on the matching of the other nodes of the graph, the objective function is considerably simpler than the objective function in WGM problem [82].
Medasani et al. [83] provided a relaxation approach to graph matching based on a fuzzy assignment matrix. Hence, the authors are able to derive that iterative FGM algorithm, which has a matching accurate than the graduated assignment algorithm.
Medasani and Krishnapuram [84] introduced a fuzzy approach to content-based retrieval of segmented images using fuzzy attributed relational graphs (FARGs) and an efficient FGM. In sum, the FGM algorithm is of the order O\(({n}^{2}{m}^{2})\) and hence suitable for image retrieval.
8.1 Fuzzy Maximum Matching Algorithms
The maximum matching model is also called cardinality matching problem. An independent subset of the edges set is called a matching of a graph, and a matching with as many edges in it as possible is called a maximum matching.
Matching problems with fuzzy weights arise when the decision-maker has some vague information about some data of the real-world system. In other words, the parameters of a system can be characterized by fuzzy variables.
Essentially, Liu et al. initialized the concepts of expected maximum fuzzy weighted matching, the \(\alpha\)-maximum fuzzy weighted matching, and the most maximum fuzzy weighted matching. According to various decision criteria, by using the credibility theory, with crisp equivalents are also given, the maximum fuzzy weighted matching problem is formulated as expected value model, chance-constrained programming, and dependent-chance programming. Furthermore, a hybrid genetic algorithm is designed to solve the proposed fuzzy programming models. Finally, a numerical example is given. The weights of the edges are trapezoidal fuzzy variables in the numerical example [85].
Liu and Gao [86] suggested concepts of the maximum random fuzzy weighted matching problem: (a) the expected maximum random fuzzy weighted matching, (b) the \((\alpha,\beta )\)-maximum random fuzzy weighted matching, and (c) the most maximum random fuzzy weighted matching. Later they formulated the maximum random fuzzy weighted matching problem as an expected value model, chance-constrained programming, and dependent-chance programming. To get the expected maximum random fuzzy weighted matching, the expected maximum random fuzzy weighted matching problem can be formulated as follows:
Later a knowledge-based hybrid genetic algorithm is designed for solving the problem.
8.2 Fuzzy Weighted Matching Algorithm
Main goal of the algorithm is to find a matching in a given graph such that sums the weights of the edges at its maximum level. The sum of the weights of the edges in a matching is called the weight of matching. Sometimes, instead of a matching maximum weighted matching problem is used to find a maximum matching with maximum weight.
When the decision-maker has some vague information about some data of a real-life system, the matching model with fuzzy weighted is used. In other words, fuzzy variables are used for the parameters of a system.
In recent years, a lot of researches on matching have been conducted. A quite compact and flexible search-based artificial algorithm that makes use of relations based on representation of the graph is proposed by Balakrishnarajan and Venuvanaligam [87] to find all the perfect matching on a general graph.
An extension of the bipartite weighted matching problem is studied by Hsieh et al. [88]. A reduction algorithm reducing the matching problem to the assignment problem is proposed. Also, three examples are used to illustrate the process of the proposed method and its applications. As a result of the reduction to assignment problem on a larger graph, exact solution can be found at polynomial time.
Hsieh et al. [89] studied the weighted matching problem for on-line handwritten Chinese character recognition. The Hungarian method and a greedy algorithm based on the Hungarian method are proposed to solve the matching problem by a reduction algorithm. For each iteration of the greedy algorithm, a matched pair is deleted, and if the relation of their neighbors does not match, a new matching is then found by applying Hungarian method.
Lamb [90] studied the weighted matching with penalty and showed that bipartite weighted matching with penalty problem can be reduced to a bipartite maximum weight matching problem. The reduction to a maximum weight matching problem is not only easier than the reduction of Hsieh et al. [88, 89] to an AP, but also produces a smaller problem.
By using the appropriate data structures, Steiner and Yeomans [91] designed a linear time algorithm for maximum matching in convex, bipartite graphs and showed that the maximum matching problem can be efficiently transformed into an off-line minimum problem. This algorithm finds a maximum matching in less time complexity which is less than the graph size.
Kim and Wormal [92] studied the matching problem as an extension of matching problem, in random regular graphs, which are showing a random d-regular graph for even d asymptotically, almost surely (a.a.s.), has an edge decomposition into Hamilton cycles.
Zito [93] also studied bipartite and d-regular random graphs, and proved that with high probability, ratio between the sizes of any two maximal matchings approaches one in dense random graphs and random bipartite graphs. According to their findings, weaker bounds hold for sparse random graphs and random d-regular graphs.
For this model primarily, some preliminary knowledge of credibility theory and notations could be used. Let \(\xi\) be a fuzzy variable with membership function \(\mu (x)\) and r a real number. Then, the possibility measure [94] and the necessity measure of fuzzy event \(\leq \{\xi \quad r\}\) are defined as
respectively.
The credibility measure of fuzzy event \(\{\xi \leq r\}\) is defined by Liu and Liu [95] as
It can easily verified that \(\mathrm{Cr}\{\xi \leq r\} +\mathrm{ Cr}\{\xi> r\} = 1\) for any fuzzy event \(\{\xi \leq r\}\). Liu [96] also presented two critical values, say \(\alpha\)-optimistic value which was defined as
and a pessimistic value which was defined as
which serve as roles to rank fuzzy variables, where \(\alpha \epsilon (0,1]\) and \(\xi\) is a fuzzy variable. The expected value of a fuzzy variable \(\xi\) is defined as
provided that at least one of the two integrals is finite.
For more detailed properties of credibility measure, the interested reader may consult Liu [97].
For this model, it is thought that all the graphs are undirected and simple. Let \(G(V,E,\xi )\) be a graph, where V, E, and \(\xi\) are the vertices set, edges set, and weights vector of the graph G. Sometimes, we employ E(G) and V(G) to denote the edges set and the vertices set of graph G, respectively. The degree and the set of incident edges of the vertex v \(\epsilon \) V are denoted by dG(v) and Ne[v], respectively. For a subset S of E or V, G[S] denotes the subgraph induced by the subset S. The weight of edge \((i,j)\epsilon E\) is denoted by a fuzzy variable \(\xi _{\mathit{ij}}\), where
Let \(M \subseteq E\) be a matching of \(G(V,E,\xi )\). Let
Then the matching M can also be denoted by such a vector x, and the cost function of matching x can be defined as
where x and \(\xi\) denote the vectors consist of \(x_{\mathit{ij}}\) and \(\xi _{\mathit{ij}},(i,j)\epsilon E\), respectively.
Definition 10
The \(\alpha\)-cost of \(f(x,\xi )\) is defined as the cost value \(\bar{f}\) such that
where \(\alpha\) is a predetermined confidence level between 0 and 1.
It is clear that the cost function \(f(x,\xi )\) is also a fuzzy variable when the vector \(\xi\) is a fuzzy vector. In order to rank \(f(x,\xi )\), different ideas are employed in different situations. If the decision-maker wants to find a maximum weighted matching with maximum expected value of the cost function \(f(x,\xi )\), then the following concept is induced.
Definition 11
A maximum matching \({x}^{{\ast}}\) is called the expected maximum fuzzy weighted matching if
for any maximum matching x.
In other situation, the decision-maker hopes to maximize the a-cost value \(\bar{f}\) with
For this case, we propose the concept of a-maximum fuzzy weighted matching as follows:
Definition 12
A maximum matching \({x}^{{\ast}}\) is called a-maximum fuzzy weighted matching if
for any maximum matching x, where a is a predetermined confidence level.
Furthermore, the most maximum weighted matching arises when the decision-maker gives a cost value \(\bar{f}\) and hopes that the credibility of the cost value exceeding \(\bar{f}\) will be as maximized as possible
Definition 13
A maximum matching \({x}^{{\ast}}\) is called the most maximum fuzzy weighted matching if
for any maximum matching x, where \(\bar{f}\) is a predetermined cost value.
Based upon these, we will recast the maximum fuzzy weighted matching problem as multiobjective expected value model, chance-constrained programming, and dependent-chance programming, respectively.
Liu and Liu [95] initialized the fuzzy expected value model. Its main idea is to optimize the expected value of the objective function subjected to some expected constraints. Therefore, the expected maximum fuzzy weighted matching problem can be formulated as
With respect to stochastic chance-constrained programming [98], Liu and Iwamura [99] offered the concept of fuzzy chance-constrained programming. When the decision-maker wants to optimize the critical value of the cost function subjected to some chance-constraints, the chance-constrained programming is employed. Therefore, the \(\alpha\)-maximum fuzzy weighted matching problem can be formulated as follows:
Liu [100] proposed the dependent-chance programming in which the goal is to optimize a fuzzy event’s chance in an uncertain environment, such as possibility, necessity, or credibility. According to this model, the problem to find a most maximum fuzzy weighted matching with given cost value \(\bar{f}\) can be formulated as follows:
8.2.1 Fuzzy Assignment Problem
Assignment problem (AP) is a special type of linear programming problem and widely used in both manufacturing and service systems. AP can also be called as the minimum weight perfect matching problem in bipartite graphs.
In this model the objective is to assign n number of jobs to n number of persons at a minimum cost or time. The problem’s mathematical formulation suggests that this is a 0–1 programming problem and is highly degenerate. It is applicable for transportation problems in which all the algorithms developed to find optimal solution.
The AP parameters are imprecise numbers instead of fixed real numbers because time or cost for doing a job by a firm (machine or person) might vary due to a lot of reasons. Assigning men to jobs, drivers to buses, trucks to delivery routes, etc. are some examples over the past 50 years for this matter.
Here, it is aimed to find such an assignment, in which the total costs or sum of the single assignments is to become a minimum ratio [101]. The Hungarian method [102], which is the most popular algorithm for AP, carries through the algorithm directly on the nxn cost matrix \([c_{\mathit{ij}}]\), where \(c_{\mathit{ij}}\) represents the cost associated with worker \(i(i = 1,2,\ldots..n)\) who has performed job \(j(j = 1,2,\ldots.n)\) as seen in Fig. 1.
In this model, all \(c_{\mathit{ij}}\)’s are deterministic numbers.
The AP also could be modeled as a 0–1 integer programming problem:
However, many real-world application costs are not deterministic. For example, a consultant company provides different services to their customers for predetermined charges in each case. The job or case quality (may be the satisfaction of the customer or the job performance of the worker) may assume to be positively correlated to the input time or cost of the worker. Highest quality of the case is different because of the difference among individual workers. Furthermore, the manager of the company usually restricts the total labor hours or costs to a range as his fuzzy goal.
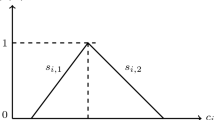
Hence, a minimum personnel cost is assumed to perform a job, and bigger spending costs to get result for higher quality until it reaches an upper bound, but it has to be thought that an increase in cost does not increase the quality. In this case, the costs are no longer deterministic numbers, and they will be denoted as c ij ’s, \(\alpha _{ij}\) as the least cost associated with the worker i performing the job j and \(\beta _{ij}\) as the least cost associated with worker i performing the job j at the highest quality (it is assumed that \(\beta _{ij}\ j>,\alpha _{ij}> 0\)). Also the quality matrix [q ij ] that represents the highest quality associated with the worker i performing the job \(j(0 < q_{ij} \leq 1)\) is defined. In most real cases, \(0 < q_{ij} < 1\) and then c ij is a subnormal fuzzy interval. The membership function of c ij is defined as the linear monotone increasing function shown in Fig. 2, which suggests that any expense exceeding \(\beta _{ij}\) is useless since the quality (worker’s job performance or customer’s satisfaction) can no longer be increased at its upper limit q ij condition.
\(x_{\mathit{ij}} = 1\) is added to (13) because there is no real expense if \(x_{\mathit{ij}} = 0\) in any feasible solution x of (12).
The notation \(\alpha _{ij},\beta _{ij}\) is used to denote c ij (all the \(\alpha _{ij}\)’s form the matrix \([\alpha _{ij}]\) and \(\beta _{ij}\)’s form the matrix \([\beta _{ij}]\)).
Matrix [\(c_{\mathit{ij}}\)] is shown as follows:
In addition to this model, let c T denote the total cost that is related to the job performance of the manager, and for the upper and lower bounds of the total cost, numbers a and b are defined. The membership function of c T is defined as the linear monotonically decreasing function in (15) and uses the notation (a;b) to denote fuzzy interval c T . The manager chooses a and b numbers as constant values. Then Werners [103] fuzzy linear programming in which taking a number less than or equal to the minimum assignment of matrix [\(\alpha _{\mathit{ij}}\)] as a, and a number larger than or equal to the maximum assignment of matrix [\(\beta _{\mathit{ij}}\)] as b could be used:
The performance of worker i, denoted as \(\mu _{i}\), based on the solution x will be
Here Bellman–Zadeh’s criterion [71] was chosen that maximizes the minimum of the membership functions corresponding to which solution, to equally emphasize the performance of workers and manager, that is,
or
where \(x_{\mathit{ij}}\) is an element of a feasible solution x of (9). Then we can represent the fuzzy AP as follows:
The cost of worker i performing job j is restricted to be less than or equal to \(\beta _{\mathit{ij}}\) since any expense exceeding \(\beta _{\mathit{ij}}\) is useless. By membership functions of (13) and (15), the following model (20) could be showed:
where \(C_{\mathit{ij}}^{\lambda }\) denotes the \(\alpha\)-cut of \(c_{\mathit{ij}}\), and \(\sum _{i=1}^{n}\sum _{j=1}^{n}c_{\mathit{ij}}^{n}x_{\mathit{ij}}\) is the corresponding total cost \(c_{T}^{\lambda }\). In (26), since \(x_{\mathit{ij}},c_{\mathit{ij}}^{\lambda }\) and \(\lambda\) all are decision variables, it can be treated as a mixed-integer nonlinear programming model.
In recent years, both fuzzy transportation and fuzzy assignment problems have received major attention. Many have been developed to advance numerous methodologies and applications to various decision problems. To deal with imprecision, and vagueness in real-life situations, Zadeh [104] introduced the concept of fuzzy sets.
Chen [105] presented a fuzzy assignment model that did not consider the differences of individuals. Similarly, Wang [106] solved a model by graph theory.
Dubois and Fortemps [107] proposed a flexible assignment problem, which combines with fuzzy theory, multiple criteria decision-making, and constraint-directed methodology. They survey refinements of the ordering of solutions supplied by the max–min formulation, namely, the discrimin partial ordering and the leximin complete preordering. Additionally, they have given a general algorithm which computes all maximal solutions in the sense of these relations. They also demonstrated and solved an example of fuzzy assignment problem.
On the other hand, Sakawa et al. [108] dealt with actual problems on production and work force assignment in a housing material manufacturer and a subcontract firm and formulated two-level linear and linear fractional programming problems according to profit and profitability maximization respectively. By applying interactive fuzzy programming for two-level linear and linear fractional programming problems, they derived satisfactory solutions to the problems.
Chanas et al. [109] solved transportation problems with fuzzy supply and demand values. Tada and Ishii [110] and Chanas and Kuchta [111] added an integer restriction to that fuzzy transportation problem and solved it. Also they suggested a specific definition for an optimal solution to the transportation problem using fuzzy cost coefficients and proposed an algorithm [112].
Lin and Wen [113] solved the assignment problem with fuzzy interval number costs by a labeling algorithm. The algorithm begins with primal feasibility and proceeds to obtain dual feasibility while maintaining complementary slackness until the primal optimal solution is found.
Feng and Yang [114] investigated a two-objective-cardinality assignment problem. A chance-constrained goal programming model is constructed for the problem, and tabu search algorithm based on fuzzy simulation is used to solve the problem.
Majumdar and Bhunia [115] proposed an elitist genetic algorithm with interval-valued fitness function to solve generalized assignment problem with imprecise cost/time. In their study, the coefficient of the interval-valued assignment problem’s objective function has been considered as interval-valued number. Also, they represented the impreciseness of cost(s)/time(s) with interval-valued numbers.
Ye and Xu [116] proposed an effective method on priority-based genetic algorithm to solve fuzzy vehicle routing assignment when there is no genetic algorithm which can give clearly procedure of solving it.
Liu and Gao [117] proposed an equilibrium optimization problem using genetic algorithm. Then they extended the assignment problem to the equilibrium multi-job assignment problem and equilibrium multi-job quadratic assignment problem.
Kumar et al. [118] proposed a new method to find the fuzzy optimal solution of fuzzy assignment problems by representing all the parameters as triangular fuzzy numbers. In their method, decision-maker takes the final results as fuzzy numbers, and if there is no uncertainty about the cost, their method gives the same result as in crisp assignment problem.
Mukherjee and Basu [119] introduced a mathematical model of the assignment problem considering the restrictions on job cost and person cost based on his/her efficiency/qualification. Under these conditions, both the cost and the restriction of qualification are considered as triangular or trapezoidal fuzzy numbers. They also considered the case where a person without certain qualification/efficiency should not be assigned a particular job.
However, Nagarajan and Solairaju [120] considered the assignment costs as imprecise numbers described by fuzzy numbers. They transformed the fuzzy assignment problem to a crisp assignment problem using Robust’s ranking indices.
9 Fuzzy Matroids
In combinatorial optimization, matroid means independence structure which is a structure that generalizes linear independence in vector spaces. Many real-world problems can be defined and solved using matroids theory. Matroids are precisely the structures for which the very simple and efficient greedy algorithm works.
When we take as E the set of all edges in graph G and consider a set of edges independent if and only if it does not contain a simple cycle, this edge set is called a forest in graph theory. It can also be called the cycle matroid or graphic matroid of G; it is usually written M(G). The graphic matroid of G can also be defined as the column matroid of any oriented incidence matrix of G. A base can be called a spanning tree in G, and a circuit is a subset of edges creating a simple cycle in G.
When we want to find an object A composed of the elements of a given finite set E, a real weight w(e) is associated with every element e of E, and we seek an object A for which the total weight \(w(A) =\sum _{e\in A}w(e)\) is minimal or maximal. A classical example is finding the minimum spanning tree or a shortest path in a given graph, where E is the set of edges of this graph [121].
A system is called weighted if there is a nonnegative weight w(e) given for every element \(e \in E\) [122].
In the matroidal combinatorial optimization problem, a nonnegative weight w(e) is given for every element \(e \in E\), and we seek a base B, for which the cost \(F(B) =\sum _{e\in E}w_{e}\) is maximal (or minimal) [123].
In classical problem, it is assumed that all the weights are precisely known. However, this assumption may be a serious restriction since in many practical applications, the exact values of the weights are not known in advance. A typical example is traveling time between two cities in the shortest path problems or activity durations in scheduling problems. One of the simplest methods of modeling the imprecise weights is to define them as closed intervals. It is then assumed that the value of each weight may fall within a given range, independently on the values taken by the other weights. Classical intervals can be generalized into so-called fuzzy numbers, which are actually fuzzy intervals, and are richer in information [120].
In [121, 122, 124, 125], when all values of a weight function are closed intervals or fuzzy numbers, the optimality of solutions and the optimality of elements are characterized by means of a family of interval matroids \(\{(E,I_{a}) : a \in [0,1]\}\). Because of the varying nature of the world, they used fuzzy intervals to model the not precisely known element weights.
Another use of fuzzy sets is in a matroid problem solved by Goetschel and Voxman where a group of independent fuzzy sets was defined as a crisp family of fuzzy subsets of a finite set satisfying certain set of axioms [126]. Their closed regular fuzzy matroid can be shown as follows: [155] if w is a weight function on E and A is a fuzzy subset of E, it could be defined as:
The question asked is whether we can find an object \(B \in {[0,1]}^{E}\) for which the total weight w(B) is minimal or maximal?
For Goetschel–Voxman fuzzy matroids, we can refer to studies [127–131].
Defining a fuzzy subset of a finite set E as a subset of E x (0, 1], we obtain fuzzy matroids by fuzzifying independence spaces on E x (0, 1]. Instead, by defining fuzzy subsets of E as functions from E into [0, 1], we can obtain fuzzy matroids from polymatroids associated with “real” rank functions [132].
The concepts of fuzzy pre-matroid and hereditary fuzzy pre-matroid are introduced and investigated. The property “to be perfect” for hereditary fuzzy pre-matroids is also considered. It is shown that Goetschel and Voxman fuzzy matroids coincide with perfect hereditary fuzzy pre-matroids. The fuzzy rank function of a Goetschel–Voxman fuzzy matroid (E, I) was defined by a map \(R : {[0,1]}^{E} \rightarrow N\). But in general, a Goetschel–Voxman fuzzy matroid and its fuzzy rank function are not one-to-one corresponding [133].
Also in the literature, Shi [121] proposed a closed fuzzy pre-matroid as a fuzzifying matroid and generalized it to L-fuzzy set theory. They showed that an L-fuzzifying matroid can be characterized by means of its L-fuzzifying rank function which is one-to-one corresponding with the L-fuzzifying matroid.
10 Fuzzy Approximation Algorithms
In Sect. 10.1 we focus on the quite general problem called the minimum weight set cover problem. The minimum weight edge cover problem is also a special case of the minimum weight set cover problem. In Sect. 10.2 we discuss a strongly NP-hard problem, the maximum weight cut problem. The edge coloring and the vertex coloring in planar graphs will be defined in Sect. 10.3.
10.1 Fuzzy Set Covering
Hwang et al. [134] proposed the fuzzy set-covering model which uses auxiliary 0–1 variables and a system of inequalities. Model is obtained by taking logarithm of the inequalities constraints and using the nature of the Boolean variables of this fuzzy set-covering model.
Given two subsets \(I =\{ 1,2,\ldots,m\}\) and \(J =\{ 1,2,\ldots,n\}\) of integers, let \(\tilde{p}_{j} =\{ (i,\mu _{j}(i)) : i \in I\}\) be a fuzzy subset of I and \((\mu _{j}(i)) \in [0,1]\) be the membership grade of \(i \in I\), using the membership function \(\mu _{j}\) of fuzzy set p j .
The model is proposed as
In this model \(\alpha\) is a given real number (level degree) that represents the desired level (each \(i \in I\) and the membership grade of i is no less than the level degree \(\alpha\)). According to Theorem 1 in [135], Problem (P 1) can be transformed to Problem (P 2) by replacing the product of 0–1 variables in constraints (30) with auxiliary variables and a system of linear inequalities. The details can be found in [135].
The mentioned formulation is mathematically appropriate and also elegant, but solutions are difficult to find because of the fact that the number of decision variables is proportion to the number of auxiliary variables and extra constraints that usually grows exponentially [135] as the number of variables increases.
10.2 Fuzzy Max-Cut Problem
The max-cut problem is a combinatorial optimization problem and is one of the first problems proved to be NP-hard [136], because it determines the maximum cut of a graph. Its goal is to find a division of a vertex set into two parts, maximizing the sum of weights over all the edges across the two vertex subsets in a given edge-weighted graph. For an unweighted graph, the weights over the edges are equal to 1. Such a division is called a maximum cut.
This problem has many applications in various fields, that is, network design, circuit layout design [137], and data clustering [138]. The weight of the cut in the max-cut problem has real and concrete implications when applied in real life due to the fact that parameters are not so deterministic owing to the effects of many factors. For example, for network design, the weight may represent the cost of some infrastructure.
There are many optimization problems that are based on this theory, and several optimization models in stochastic models [95] and also including various fuzzy programming models [139], fuzzy shortest path problems [66], and fuzzy max-flow problems [75] have been studied. Recently, Liu [140] developed a credibility theory where the expected value criterion, the optimistic value criterion, and the credibility criterion are used as fuzzy ranking methods.
10.2.1 The Max-Cut Problem with Fuzzy Coefficients
The max-cut problem is widely used in practical applications. When applied in real life, the weights of a graph have real and concrete implications. They are often not so deterministic. The weights on edges can be formulated as fuzzy variables and are more proper to describe the quantities in the real world since decision-makers are often faced with some uncertain situations due to the vagueness or subjective nature of these parameters.
To compute this problem with fuzzy coefficients, let G = (V, E) be an undirected edge-weighted graph with nonnegative weights \(\xi : E \rightarrow {R}^{+}\). A cut C of G is any nontrivial subset of V, and the weight of a cut is the sum of weights of edges crossing C and \(\bar{C}\), where
Then a max-cut is defined as a cut of G with maximum weight. The max-cut problem’s goal is to find such a cut.
Assume that the vertices in V are labeled as \((v_{1},v_{2},\ldots,v_{n})\) and the edges in E are labeled as
\(\xi _{\mathit{ij}}\) is the weight associated with the edge \(e_{\mathit{ij}}\). We define a binary variable x i for each vertex v i to denote whether it is in a cut
C or not:
Then any cut of the graph G can be denoted by an n-dimensional binary vector \({(x_{1},x_{2},\ldots,x_{n})}^{T}\) over {1, − 1}. Similarly, any n-dimensional binary vector \({x_{1},x_{2},\ldots,x_{n}}^{T}\) over {1, − 1} corresponds to a cut of G. So the weight of a cut \({(x_{1},x_{2},\ldots,x_{n})}^{T}\) can be denoted as
Obviously, if and only if v i and v j respectively belong to two parts of the vertex set \(V (x_{i}x_{j} = -1)\), the weight of the edge (if any) linking them is considered. Let \(\beta\) be the set of all cuts of G. Then a cut \({x}^{{\ast}}\) is called a maximum cut if and only if \(W({x}^{{\ast}},\xi ) \geq W(x,\xi )\) for any \(x \in B\).
10.3 Fuzzy Coloring
A vertex coloring of graph G is defined as an assignment of colors to the vertices of G. So, no adjacent vertices get the same color. An edge coloring of graph G is an assignment of colors to the edges of G so that no adjacent edges have the same color.
A total coloring of a graph G is a coloring of the vertices and edges of G in such a way that no two adjacent elements have the same color. More information on coloring graphs can be found in [141].
The smallest possible total over all vertices that can occur among all colorings of G using natural numbers for the colors is called the chromatic sum of a graph G [142].
Munoz et al. [143] discussed two different approaches to the graph coloring problem of a fuzzy graph with crisp nodes and fuzzy edges. The traffic lights problem and a timetabling problem are studied according to these two different approaches. They also provided the concept of chromatic number of fuzzy graphs.
Chaudhuri and De [144] also introduced a timetabling problem called the university course timetable problem. Fuzzy genetic heuristic for this problem is discussed. There is a considerable amount of uncertainty involved in objectives which comprises of different aspects of real-life data. This uncertainty is handled by formulating some parameters using fuzzy membership functions.
The class of quasi-line graphs and more specifically fuzzy circular interval graphs gained a lot of attention recently. Eisenbrand and Niemeier [145] introduced a combinatorial algorithm that calculates weighted colorings and the weighted coloring number for fuzzy circular interval graphs efficiently.
11 Fuzzy Knapsack Problems
Knapsack problem (KP) has m different objects to choose from to put into the knapsack. Each object has a weight (w i ) and benefit (p i ). Aim of the problem is to choose the objects giving the maximum benefit without exceeding the total knapsack capacity. There are many real-life problems that can be modeled as the KP, such as cargo loading, capital budgeting, cutting stock, and economic, and network planning. Basic model for the crisp KP is as follows:
Indices
i : object indice(m)
Decision Variables
Parameters
p i : benefit of project i
w i : cost of project i
c: capacity of knapsack not to be exceeded
Objective Function
Constraints
Kuchta [146] discussed a fuzzy multiple choice KP where the total risk is minimized while staying in the budget. Each project has a risk and cost where each of these is represented with fuzzy numbers.
In Kasperski and Kulej [147], the concept of using fuzzy weights and fuzzy profits for the KP is used. This is different than the classical problem where it is assumed that all the item profits and weights are deterministic, because in practice many knapsack-type problems involve items whose weights or profits are not precisely known which is a useful extension. One of the methods of dealing with imprecision in real-world data is applying the fuzzy sets theory; they used the concept of a fuzzy interval to model the imprecise profits and the imprecise weights of items.
Lin and Yao [148] introduced a fuzzy KP where all weight coefficients are fuzzy numbers to model the imprecise weights in practical situations. They find it easier for the decision-maker to decide the value of the weight of an object as a range rather than a crisp value. After defuzzyfying the fuzzy number, they use the same methodology to solve the problem as the crisp version.
On the other hand, Lin [149] provided a genetic algorithm methodology to solve imprecise weight coefficients in KPs.
In addition, Sakawa et al. [150] introduced an interactive fuzzy satisficing method for multiobjective multidimensional 0–1 KPs by using both the interactive fuzzy programming methods and genetic algorithms. By considering the imprecise nature of decision-maker (DM) judgments, fuzzy goals of the objective functions are quantified by using linear membership functions.
Chen [151] proposed a parametric programming approach to the continuous knapsack problem with fuzzy objective weights. The fuzzy maximum total return is analyzed. In this model, when the object weights are fuzzy, the maximal total profit also becomes fuzzy.
The mathematical model of the crisp continuous KP is as follows: Lin and Yao [152],
The continuous KP with fuzzy object weights is of the following form Chen [153]:
For this model there are some example studies. One is Nezhad et al. [154], introducing a fuzzy capital budgeting model for selecting an optimum portfolio of projects. A real-world extension of all parameters of the projects was assumed to be imprecise.
Verdegay and Moreno’s work [155] focused on the advantage of a fuzzy termination criterion providing results with low errors and with very short times with respect to both the exact and approximate solutions especially when the number of objects increases. The fuzzy-rule based systems and mathematical programming models and methods are used to solve the conventional KP.
Kato and Sakawa [156] provided a genetic algorithm with decomposition structures for large-scale multidimensional 0–1 KPs with block angular structures.
Lin [157] introduced a generalized fuzzy multiconstraint KP model, and extend it to another fuzzy multiobjective programming model. The multiconstraint 0–1 KPs are solved with imprecise weight coefficients.
Hasuike et al. [158] proposed a new model of random fuzzy 0–1 KPs where the objectives are represented with fuzzy goals and expected returns assumed as random fuzzy numbers.
Shih [159] focused on fuzzy multiobjective and multilevel KPs and proposed a solution procedure.
12 Fuzzy Bin Packing
Within a given rectangular area, finding an efficient packing has much relevance to operating systems, operations research, and manufacturing industries [160, 161]. For example, in a given time to operating systems or in steelworks, the problem is related with the allocation of resources. The task is cutting the roll of raw steel to make components of products. As these are mentioned, such can be formulated as bin-packing (BP) problems. BP is a problem that has long been studied by many researchers to better formulate and efficiently solve practical problems [162].
The problem is known to be NP-hard [163], while its description seems to be simple; it is very difficult to solve this problem precisely. In order to simplify the formulations of the problem, we have to concentrate on finding more efficient heuristics. Most formulations, therefore, assume rigidity, orientation, and orthogonality of the pieces [164, 165].
Suppose that there is a bin B = (W, H) and a set of pieces \(P =\{ p_{1},\ldots,p_{n}\}\). We can represent each piece in the following manner: \(p_{i} = (w_{i},h_{i})\) because the piece is rigid and oriented (we cannot change the size of a piece or its orientation). Letting \((x_{i},y_{i})\) denote the center position of a piece p i , we can also obtain the height of the packing as \(\max _{i}(y_{i} + h_{i}/2)\) because of the orthogonality assumption [166]. The bin-packing problem’s goal is to minimize the height of the packing \(\max _{i}(y_{i} + h_{i}/2)\) by choosing appropriate center positions \((x_{i},y_{i})\)’s, which also satisfy the two following constraints: (1) all pieces should be contained within the bin and (2) no two pieces should overlap. By applying simple arithmetic, we can convert the two constraints as a set of inequalities.
However, assuming that the heights are rigid, that is, a constraint becomes too strong in many applications. When facing strong conflicting requirements, we should trade-off between the efficiency and the satisfaction. If we want to pay additional costs for decreasing the designer’s satisfaction, then we could degrade the satisfaction because of the reduction.
However, in above-mentioned issue, we are not supposing the long-term cost such as deterioration of production quality or customer dissatisfactions. Long-term cost is due reducing the heights of pieces; thus, we call the cost as reduction cost. In fuzzy bin-packing problems, the model formulates the height of a piece as a fuzzy number. So, its goal is to minimize the height cost and the reduction cost. From these costs combining, the total cost emerges.
The fuzzy bin packing problem alleviates the rigidity constraint of the conventional bin-packing problem. In the conventional bin-packing problem, a piece p i is represented as an ordered pair of two real numbers, \((w_{i},h_{i})\) in which w i stands for the width, and h stands for the height. In the fuzzy bin-packing problem, we represent the piece as an ordered pair of a real number and a fuzzy number, \((w_{i},h_{i}^{\sim })\).
We define the fuzzy bin-packing problem N as a tuple with three components, \(N = (B,P,\Psi )\), where B is the bin, P is the set of pieces, and W is the reduction cost function. The bin B is a rectangle which has a limited width (W) and an unlimited height \((H = \infty )\). The set of pieces P is a collection of rectangular pieces \(p_{i} = (w_{i},h_{i}^{\sim })\), where h is a fuzzy number. Therefore, we can get a membership degree for a reduced height h i . At the initial height \(h_{i}^{0}\), the membership degree is 1. This degree is called as the satisfaction degree. As a trade-off for reducing the height of a piece, the reduction cost function W is also given to evaluate the additional cost due to reduction. It is a function of the satisfaction degree and the initial height.
Yet, the conventional bin-packing problems’ two constraints are not changed in the fuzzy bin-packing problem. Unlike in the conventional bin-packing problem, these constraints cannot be represented by a set of inequalities because the height is a fuzzy number. Therefore, we define the two constraints using the a-cut operation of fuzzy sets. The fuzzy set A is usually represented by a mapping \(\mu _{A} : U \rightarrow [0,\ldots,1]\). The \(\alpha\)-cut of a fuzzy set A at the given membership degree n produces a crisp set, \(\alpha (A,\mu ) =\{ x\vert \mu _{A}(x)\} \geq \mu.\)
In this model \(\alpha\)-cut of a fuzzy number always becomes an interval because the fuzzy number is a convex and normal fuzzy set. If we have two \(\alpha\)-cuts of two fuzzy numbers \(\tilde{a}\) and \(\tilde{b}\), that is, if we have \(\alpha (\tilde{a},\mu _{a})\) and \(\alpha (\tilde{b},\mu _{b})\), \(\alpha\)-cut can be defined as follows:
If the below constraints satisfy these conditions, it could be stated that the piece p i is contained within the bin at the satisfaction degree \(\mu _{i}\).
And also if below constraints satisfy the two conditions, it could be said that the two pieces p i and p j are nonoverlapping at satisfaction degree \(\mu _{i}\) and \(\mu _{j}\).
It can be said that, the packing is feasible with the satisfaction degrees \((\mu _{1},\ldots,\mu _{n})\), if the bin contains all the pieces and no overlapping occurs with satisfaction degrees \((\mu _{1},\ldots,\mu _{n})\).
Because a piece’s height can be reduced by sacrificing satisfaction, the objective of the fuzzy bin-packing problem is defined by minimizing the total cost \(\hat{X}\) for a feasible fuzzy bin-packing.
-
The total cost is defined as the sum of the height costX h.
-
The reduction costX r .
-
The height cost X h represents the maximum height of the packing, which is similar to the conventional bin-packing problem.
-
The reduction cost X r represents the extra cost due to the decrease in satisfaction.
From these expressions, the total cost can be formulated as
The height cost and the reduction cost can be defined in algebraic forms. Suppose a piece p i is located at the top of packing.
The upper edge \(\hat{y}_{i}\) of the piece p i can be represented as \(\hat{y}_{i} =\max [\alpha (y_{i} + (\tilde{h}_{\tilde{i}}/2),\mu _{i})]\).
Therefore, we can represent the height cost as follows: \(X_{h} = (\hat{y}_{i})\). Also, the reduction costX r can be defined in an algebraic form. If all the functions sum taken, we get the reduction cost of the fuzzy bin-packing as follows:
where \(h_{i}^{0}\) is the initial height of the piece and \(\Psi (\mu _{i},h_{i}^{0})\) should be defined according to the problem.
13 Fuzzy Multicommodity Flows and Edge-Disjoint Paths
In optimization techniques, we have to well define the given precise data because these problems do not include inexact and unsure data. But using the fuzzy sets as a technology coping with granular information is useful [167]. Also, generally speaking, information granules are collections of entities that usually originate at the numeric level and are arranged together due to their similarity, functional adjacency, indistinguishability, coherency, or the like [168]. As a theoretical perspective, it encourages an approach to data that recognizes and exploits the knowledge present in data at various levels of resolution or scales. In this sense, it encompasses all methods which provide flexibility and adaptability in the resolution where knowledge or information is extracted and represented, see Bargiela and Pedrycz [169] for details.
While solving optimization problems, following the principle of information granulation is important [170]. Fuzzy data, which are various in the literature [79], are used as a concept of the solution of these programs. Fuzzy network solutions, for example, fuzzy shortest path problem [171] or fuzzy minimal cost flow problem [172], are limited when compared to the classical fuzzy optimization programming problems. These problems can be stated as the minimal cost multicommodity flow problem (MCMFP).
A fuzzy number is a convex normalized fuzzy set of the real line R, whose membership function is piecewise continuous. The set of fuzzy numbers on \(\mathbb{R}\) is denoted with \(\mathcal{F}(\mathbb{R})\). An LR type flat fuzzy number [171] is denoted as \(\tilde{a} = (a_{1},a_{2},a_{3},a_{4})_{LR}\), if
where the symmetric nonincreasing function \(L : [0,\infty ]\mapsto [0,1]\) is the left shape function, that is, L(0) = 1. Naturally a right shape function R(.) is similarly defined as L(.) (see Fig. 3). We denote the LR type flat fuzzy numbers on real line with \(\mathcal{L}\mathcal{R}(\mathbb{R})\).
According to the extension principle, the binary operation \({}^{{\ast}} \in \{\mathop{ +}^{\sim } -^{\sim } \times ^{\sim } \div ^{\sim }\}\) on fuzzy number \(\tilde{a}\) and \(\tilde{b}\) with the membership functions \(\mu _{\tilde{a}}(x)\) and \(\mu _{\tilde{b}}(x)\) with the following:
Also the fuzzy scalar product of two fuzzy vectors \(\tilde{x} = (\tilde{x}_{1},\ldots,\tilde{x}_{n})\) and \(\tilde{y} = (\tilde{y}_{1},\ldots,\tilde{y}_{n})\) in \(\mathcal{F}({\mathbb{R}}^{n})\) is defined [23] as follows:
Let \(\tilde{a} = (a_{1},a_{2},a_{3},a_{4})_{LR}\) belong to \(\mathcal{L}\mathcal{R}(\mathbb{R})\). The exact formula for the extended addition and approximated formula for the extended multiplication are as follows:
where \(\tilde{a} \geq 0\) and \(\tilde{b} \geq 0\).
LR fuzzy number could not be attained with multiplication of two LR fuzzy numbers. In a situation like this, interpolation methods to get a fuzzy number could be used, whose some \(\alpha\)-cuts are equal to the multiplication of two \(\mu\)-cuts of corresponding operands. The details of this idea [173] and scalar multiplication are derived as follows:
where \(\lambda \geq 0\).
\(\tilde{b}\tilde{ -}\tilde{ a}\) is not really a difference and is rather unnatural with respect to a linear structure. For example, \(\tilde{b}\tilde{ +} (-1)\tilde{a}\) is not compatible with the difference in the function space. But the Hukuhara difference [174], defined as the solution for \(\tilde{x}\) in the equation \(\tilde{a}\tilde{ +}\tilde{ x} =\tilde{ b}\) if it exists, does coincide with the difference in the function space. This property justifies the application of this difference instead of the fuzzy number, \(\tilde{b}\tilde{ +} (-1)\tilde{a}\).
Hukuhara [174], Diamond and Korner [175], and Ghatee et al. [176] entitled as Hukuhara difference is observed to identify these differences as follows:
Definition 14
For \(\tilde{a}\) and \(\tilde{b}\) belong to \(\mathcal{L}\mathcal{R}(\mathbb{R})\) if the Hukuhara difference \(\tilde{b} \ominus _{H}\tilde{a}\) exists, it is given by
where \(\pm \) in the above equation for two sets \(\bar{X}\) and \(\bar{Y }\) means as follows:
For some cases, it can be proved that
where
From this definition it can be said that Zadeh’s difference is not true because \(\tilde{a} \ominus _{H}\tilde{a}\) is zero.
Therefore, this operator for solving systems seems to be more accurate and reasonable results in comparison with Zadeh’s difference.
Definition 15
For \(\tilde{a}\) and \(\tilde{a}\) belong to \(\mathcal{L}\mathcal{R}(\mathbb{R})\), we have:
13.1 Minimal Cost Multicommodity Flow Problem
The minimal cost multicommodity flow problem (MCMFP) which transships the flows of the commodities by minimal cost has been evaluated in this section.
The MCMFP satisfies the demand for each commodity at each vertex without violating the constraints imposed by the supply–demand and capacity.
Let N and A be the sets of nodes and links, and for a given network \(G = (N,A)\): general MCMFP can be expressed:
The notations are as follows:
-
\(x_{\mathit{ij}}^{t}\) is a positive integral regarding the amount of flow from tth commodity which streams through link (i,j).
-
\(u_{\mathit{ij}}\) is the capacity of link (i,j).
-
T is the number of commodities.
-
Moreover, for commodity t, \(c_{\mathit{ij}}^{t}\) and \(b_{t}^{t}\) are the unit cost of flow through link (i,j).
-
The supply or demand of node i.
If not change the variables, it can be assumed that each commodity has one resource and one customer without loss of generality [177]. Also \({r}^{t},{s}^{t}\), and d t denote the resource node, the customer node, and the travel demand for a given commodity t, respectively. Then, the following model regarding the path-flow variables is met:
where the flow of commodity t along the path p is denoted by \(f_{p}^{t}\).
Additionally, \(\delta _{p} = (\delta _{p}^{i,j})(i,j) \in A\) is link-path incident vector and assigns 1 when the link (i,j) shares in path p and 0 otherwise. p t includes all of the directed paths joining r t and s t.
From the first constraint, it can be said that the demand for each commodity is supplied by the path flows activated for that commodity. Including the link (i,j), \(x_{\mathit{ij}}\) denotes the sum of flow of individual paths, and the other constraint shows the total flow is less than its capacity.
Equally important, vast majority of this classic model is deterministic. While this problem is influenced by social and economic interactions and is dependent on users’ perceived information and granular information, one assumes the travel cost and demand to be known a priori for the entire links and nodes [177]. On the other hand, granular computing offers a landmark change from the current machine-centric to human-centric approach in information and knowledge and is an emerging conceptual and computing paradigm of information processing. It has been motivated by the urgent need for intelligent processing of empirical data that is now commonly available in vast quantities, into a humanly manageable abstract knowledge.
In other words, the granular computing’s theoretical foundations involve fuzzy sets, rough sets, and random sets that linked together in a highly comprehensive treatment of this emerging paradigm [178]. In transportation concepts, due to granular information and the different provision of traffic information, the different types of transportation might be deduced. Now, we consider a case that the data of MCMFP have been exhibited with \(\mathcal{L}\mathcal{R}(\mathbb{R})\) numbers, which handle vagueness as an important category of uncertainty. So, first, we elaborate the origin of fuzziness in real problems. In the next section, two extended variants to take uncertain travel cost, and uncertain travel demand into account will be explained.
13.2 Fuzziness in Real Transportation Problems
In uncertainty modeling, transportation models adopted with fuzzy relations and quantities can contribute stochastic versions. In other words, since the classical random utility-based approach is not sufficient for uncertainty handling, some alternate solution to probability-based models, for example, Ghatee and Hashemi [179], may be obtained with possibility-based methods. Initially Das et al. [180] applied fuzzy logic tools to transportation problems. Then, many researches are conducted particularly on this problem. From a high level categorization, in real networks, such as urban networks, we face the following three uncertainty sources:
-
Unsure network topology (a network with fuzzy nodes and fuzzy links)
-
Inexact travel cost (a network with fuzzy link cost)
-
Imprecise travel demand (a network whose nodes include fuzzy excess or fuzzy deficit)
When the supply and demand of nodes and the capacity and cost of links are represented as fuzzy numbers, finding the lowest transportation cost of some commodities through a capacitated network is the aim of fuzzy transportation. This problem is a new branch in combinatorial optimization and network flow problems [79]. Some applications of such standpoint were presented in industries [181] such as the one we will discuss in the next section.
13.3 MCMFP in Fuzzy Environment
MCMFP is widely used in engineering and economics contexts. In urban transportation systems problems and production–distribution problems, this method emerges. Also, in designing telecommunication networks, it also has an important role. In all of aforementioned problems, finding the lowest transportation cost of some commodities through a capacitated network in order to satisfy demands at certain nodes, using available supplies at other nodes, is crucial.
Since this model is influenced by complex social and political interactions, this problem is dependent on user perception of information and nondeterministic factors of the network. Considering fuzzy numbers as the amount of supplies, demands, capacities, and costs provides a reasonable infrastructure is used to handle vagueness as an important category of uncertainty. Such an implementation of MCMFP can be applied to recognize the appropriate models of traffic assignment with intelligent agents; see, for example, [179] for details.
Ghatee and Hashemi treat with the minimal cost multi commodity flow problem (MCMFP) in the setting of fuzzy sets, by forming a coherent algorithmic framework, referred to as a fuzzy MCMFP. Given the character of granular information captured by fuzzy sets, the objective is to find multiple flows satisfying the demands of commodities, by using available supplies consuming the least possible cost. Having this aim in mind, the supply and demand of nodes may be presented linguistically; the travel cost and capacity of links can be defined under uncertainty as well. Then, to solve the problem, two efficient algorithms are motivated. In the first algorithm, they utilize fuzzy shortest paths and K-shortest paths to generate preferred and absorbing paths, and then they find the flow on them by solving a classic MCMFP. Coupled with the first, the second algorithm exhibits with fuzzy supply–demand and employs a total order on trapezoidal fuzzy numbers to reduce the fuzzy MCMFP into four classic MCMFPs [182].
13.4 MCMFP with Uncertain Travel Cost
Under traffic conditions, it is necessary to reflect a driver’s perception of link travel time. For this purpose fuzzy sets of perceived link travel time are developed due the fuzziness of a driver’s perception over link travel time.
There are various traffic conditions such as congestion and construction or incident, so for most frequent traffic conditions, it is necessary to construct fuzzy sets. To show these fuzzy set, Liu et al. [183] used linguistic descriptions. Obviously, if necessary, more fuzzy sets can be constructed to show other traffic conditions. Additionally, Henn [184] considered the meaning of fuzzy costs in fuzzy traffic assignment models.
In this chapter, assume that the cost, the length, or the travel time of a link (i,j) for commodity t is given by
Then for shipping T commodities through the network, we can write:
where \(\tilde{c}_{p}^{t} =\sum _{ (i,j)\in p}^{\pm }\tilde{c}_{i,j}^{t}\) for each \(p \in {p}^{t}\).
This problem has an important concept that is the way of generating the absorbing and preferred pathsp t. Usually, the column generation approach [185] is used for solving the classic MCMFP. But we can take path enumeration techniques, which include a great number of algorithms with the capability of finding reasonable and preferred paths through a network, to understand p t. In this method, the preference can be defined in terms of time, cost, distance, or some combination of these items. These reasonable paths are the base of problems consisting of path-flow variables.
14 Fuzzy Network Design Problems
In recent years, with the advance of computation evolutionary, new methods such as the optimal design of neural networks and fuzzy systems have been represented in the literature. For solving more complex real-world problems, computation evolutionary provides more robust and efficient approaches.
Network design is a combinatorial optimization problem involving optimization of several objectives such as cost, average delay, and reliability of network. Similarly, search space of the problem is huge even for small number of computers and is intractable for nonevolutionary approaches. A network is basically a graph G of a set of nodes N and a set of links L. The links denote the connections between the nodes and are assumed to be directional.
In formulating and solving engineering or management problems, network flow models provide a rich and powerful framework. For problems such as transportation systems, communication networks, project schedules, inventory systems and man/machine allocation, there have been studies in the literature [185]. In theory and practice, this model is particularly important and it is considered in uncertain environment by many researchers [186]. Transportation models adopted with fuzzy relations and quantities can contribute stochastic versions in uncertainty modeling. More specifically, since the classical random utility-based approach is not sufficient for uncertainty handling, some alternate solution to probability-based models may be obtained with possibility-based methods; see, for example, Ghatee and Hashemi [179]. However, in order to refer their historical background, fuzzy logic tools have initially been applied to transportation problems by Das et al. [187]. Then, great attention has been focused on this problem. From a high-level categorization, in real networks, such as urban networks, there are three uncertainty sources:
-
Unsure network topology (a network with fuzzy nodes and fuzzy links)
-
Inexact travel cost (a network with fuzzy link cost)
-
Imprecise travel demand (a network whose nodes include fuzzy excess or fuzzy deficit)
The aim of fuzzy transportation is to find the lowest transportation cost of some commodities through a capacitated network when the supply and demand of nodes, capacity, and cost of links are represented as fuzzy numbers. Given the character of granular information captured by fuzzy sets (where one could capitalize on the nonbinary character of their membership functions), such methods are capable of handling the decision-maker’s risk taking. This problem is a new branch in combinatorial optimization and network flow problems [79, 179]. Some applications of such standpoint were presented in industries [188].
Furthermore, the network design problem is one of the most important problems in combinatorial optimization, which has been considered by many researchers and engineers [189]. The aim of this problem is to design a network to satisfy the demand of users who wish to travel through the network by consuming minimum construction cost. Steiner tree is the traditional variants of this problem, which have been applied to design communication and water networks [185]. In some cases, a network exists, and the management wishes to extend the network to satisfy future demand. The extension of a network can also be considered by interchanging the objectives such as cost, reliability, mobility, and accessibility. To consider such concepts, the designer needs to consider a great number of concepts. One important point in this problem is the granular information about this problem, because designing is done for a long-term period and the future statues cannot to be considered in a clear manner. It is worth reporting the sources of uncertainty in measurement of data in this problem [190]:
-
The demand for transportation of each node, which is dependent on many items such as time, season, and weather conditions
-
Linguistic definition of important travel
-
Imperfect realization of the definition of important travel
-
Nonrepresentative sampling (the sample measured may not represent the defined travels)
-
Inadequate knowledge of the effects of environmental conditions on the measurement or imperfect measurement of environmental conditions.
-
Personal bias in reading analogue instruments
-
Finite instrument resolution or discrimination threshold
-
Inexact values of measurement standards
-
Inexact values of traffic constants and other parameters obtained from external sources and used in the data-reduction algorithm
-
Approximations and assumptions incorporated in the measurement method and procedure
-
Variations in repeated observations of travel under apparently identical conditions
-
The minimum cost flow problem (MCFP) as mentioned before is a general structure in these models which provides a unified approach to many applications.
To design a network after processing these granular information, one can consider fuzzy numbers as transportation and construction costs, and with respect to these parameters, the following model may be expressed:
where \(\tilde{x}_{\mathit{ij}}^{t}\) is the fuzzy flow of commodity t and variables \(z_{\mathit{ij}}\epsilon \{0,1\}\) are associated with the construction of link \((i,j)\epsilon A.;z_{\mathit{ij}} = 1\), if (i,j) belongs to the final solution; otherwise, \(z_{\mathit{ij}} = 0\). The objective function (Eq. 70) is the sum of variable and fixed fuzzy costs. In this function c is the linear fuzzy cost associated with fuzzy flow of tth commodity through link (i,j), and \(\tilde{\mu }_{\mathit{ij}}\) is the fixed fuzzy cost associated with the selection of link (i,j) in the final solution. \(\theta\) is a control parameter implying the trade-off between two objective functions.
14.1 Steiner Tree Problem
One of the most basic versions of finding a subgraph that optimizes some global cost function is known as the minimum weight. Steiner tree [191] (or the minimum Steiner tree problem, MST) is a problem in combinatorial optimization, which may be formulated in a number of settings, with the common part being that it is required to find the shortest interconnect for a given set of objects.
Given an undirected graph with positive weights on the edges, the MST problem consists in finding a connected subgraph of minimum weight that contains a selected set of “terminal” vertices [192]. Such construction may require the inclusion of some nonterminal nodes which are called Steiner nodes. Clearly, an optimal subgraph must be a tree. Solving MST is a key component of many optimization problems involving real networks. Concrete examples are network reconstruction in biology (phylogenetic trees and regulatory subnetworks), Internet multicasting, circuit design, and power or water distribution networks design, just to mention few famous ones. MST is also a beautiful mathematical problem in itself which lies at the root of computer science being both NP complete [193] and difficult to approximate [194]. In physics the Steiner tree problem has similarities with many basic models such as polymers, self-avoiding walks, or transport networks (e.g., [195]) with a nontrivial interplay between local an global frustration. The Steiner tree problem has applications in circuit layout or network design. Most versions of the Steiner tree problem are NP complete.
The Steiner tree problem is superficially similar to the minimum spanning tree problem: given a set V of points (vertices), interconnect them by a network (graph) of shortest length, where the length is the sum of the lengths of all edges. Difference between the Steiner tree problem and the minimum spanning tree problem is that, in the Steiner tree problem, extra intermediate vertices and edges may be added to the graph in order to reduce the length of the spanning tree. These new vertices introduced to decrease the total length of connection are known as Steiner points or Steiner vertices. It has been proved that the resulting connection is a tree, known as the Steiner tree. There may be several Steiner trees for a given set of initial vertices.
The fuzzy steiner tree (FST) problem on a graph is the version of the classical ST problem where edge weights are defined as fuzzy numbers. Seda [196] provided a modification of the shortest paths approximation for solving FST problem. Linear triangular fuzzy numbers as the edge weights and Cheng’s centroid point fuzzy ranking method were used in his study [196].
15 Fuzzy Traveling Salesman Problem
Traveling salesman problem (TSP) is finding the shortest route for a given number of cities. It is one of the most widely studied combinatorial optimization problems [197]. Main characteristics of TSP are that every city has to be visited and no profit is associated to the cities.
TSP is one of the most widely studied combinatorial optimization problems. This has led to numerous extensions and modifications of the basic TSP.
A variant of TSP where a profit value is associated to each city and cities are selected depending on their profit is proposed in the literature. Feillet et al. [198] define these kinds of problems as TSP with profit [198].
The problem in which cities are selected to be visited depending on the profit associated with them is called traveling salesman problem with profit (TSP with profit). TSP with profit is encountered in many different situations. For instance, it may not be possible to visit every city in a TSP application. In this kind of application, some constraints can enforce selection of cities to be visited. Balas and Martin [199] introduce the scheduling of daily operations of a steel rolling mill, which is an application of TSP with profit. This problem gives rise to a prize collecting traveling salesman problem (prize collecting TSP) with penalty terms in the objective function.
In the literature, TSP with profit is studied as a single-objective problem. The only attempt to solve TSP with profit as a biobjective problem is studied by Keller and Goodchild [200]. The main difference of biobjective approach compared to a single-objective approach is finding not only one but Pareto optimal solutions. By finding more solutions, the trade-off among them can be analyzed to make better decision. The purpose of this study is to develop a multiobjective approach for the biobjective TSP with profit in order to obtain the Pareto optimal solutions.
The TSP can be described as follows:
In the graph G = (V, E), V is the set of nodes, or cities, and E is the set of edges, \(E =\{ (a,b) : a,b \in V \}\). The Euclidean distance between a and b is \(D_{\mathit{ab}}\), supposing that \(D_{\mathit{ab}} = D_{\mathit{ba}}\). The object of TSP is to find a minimal-length closed tour that visits each city once and only once, and the closed tour is also called Hamiltonian cycle. TSP has been proven to be an NP complete problem.
15.1 Fuzzy Matrix to Represent TSP Solution
When domains X, Y are finite sets, fuzzy relation can be expressed by fuzzy matrix. Suppose \(X =\{ X_{1},X_{2}\ldots,X_{m}\};Y =\{ Y _{1},Y _{2},\ldots,Y _{n}\}\), then the fuzzy relation from X to Y can be expressed as follows:
Here \(r_{ij} \in [0,1]\) represents the degree of membership of the ith element X i in domain X and the jth element Y i in domain Y to relation R. First we introduce the following definitions:
Definition 16
Set S is a sequence of a TSP solution,
if \(S =\{ S_{1},S_{2},\ldots,S_{n}\}\), n is the number of the cities, \(S_{i}(i \in \{ 1,2,\ldots,n\})\) is the ith node in the visit tour (TSP solution).
Definition 17
Set N is the serial number of a TSP,
if \(N =\{ N_{1},N_{2},\ldots,N_{n}\}\}\), n is the number of the cities, \(N_{i}(i \in \{ 1,2,\ldots N\})\) represents the concrete node (city) in a TSP problem.
Explanation: For each element in Set S, S i means that current tour has visited i–1 nodes and will visit the ith nodes. The state space can be expressed as S s ,
The fuzzy relation R of S and N has the following meaning: for each element in the matrix R,
\(\mu _{R}\) is the membership function; the value of \(r_{\mathit{ij}}\) means the degree of membership that the ith node S i in the feasible solution S “choose” the node with the serial number of N j in a concrete problem.
15.1.1 Fuzzy Branch-and-Bound Algorithm
In this algorithm, each node is a particular schedule and tree structure is used in this model. The strategy of “breath first search” is used to determine the best partial schedule node to branch, the lower-bound values for completion times of whole partial schedule limits are calculated, and the node having the least value is chosen. Branching from lowest bound, the procedure is repeated at each time. The nodes having highest values of the lower bounds than the completion time of this schedule are fathomed after obtaining an order where all jobs are scheduled.
As shown below, A indicates the set of scheduled jobs. In Eq. 2, the lower-bound value of fuzzy completion time of each schedule beginning with A is calculated.
In this equation:
-
\(r_{\mathit{ij}}\): Fuzzy operation time of \(i\mathrm{th}\) job on jth workstation
-
U : The set of jobs which are not scheduled
-
\(\tilde{\alpha }_{A}\): Completion time of the last job in schedule A on the first machine
-
\(\tilde{\beta }_{A}\): Completion time of the last job in schedule A on the second machine
-
\(\tilde{\gamma }_{A}\): Completion time of the last job in schedule A on the third machine
In this model, firstly the first machine assumed to operate first and third machine as last.
The completion times of the jobs on the machines are calculated by using Eqs.3 and 4. If there is only one job in the set of A, then the completion times are computed by Eq. 3. If there is more than one job, then Eq. 4 is used.
After fuzzy lower-bound values for nodes are calculated, branching from the lowest bound to form new nodes for all jobs is not scheduled yet. This process is continued until all jobs are scheduled. Addition and maximum operations are fuzzy operations in this computation process.
Lee and Li’s [201] approach is used for ranking in the maximum operation. They propose the use of generalized mean and standard deviation based on the probability measures of fuzzy events to rank fuzzy number. Let us assume that two fuzzy sets, where each member is a number,
are given. The dimensions of the fuzzy numbers can be various. By using the extension principle, the addition of \(\tilde{\alpha }_{1}\) and \(\tilde{\alpha }_{2}\) is calculated as follows:
If there are more than one \((x_{i} + y_{j})\) having the same value, then only the one having the largest membership degree is kept.
According to Agin [202], branch and bound is a powerful method capable of solving combinatorial problems with nonlinear, discontinuous, or nonmathematically defined objective functions and under several types of constraints. In branch-and-bound method, a tree structure which consists of properly connected nodes is established. Throughout the search, constraints imposed by the problem should be taken into account. Agin [202] divides these into two groups, namely, implicit and explicit constraints. In a successfully developed branch-and-bound algorithm, implicit constraints are satisfied by the manner in which the search tree is established. Explicit constraints, however, are to be considered in each step of the search. An example to implicit constraints might be given as the precedence relations, whereas explicit constraints might be exemplified by resource limitations in RCPSP [203]. A feasible solution to the problem, therefore, has to assign numerical values to the set of decision variables (e.g., start dates of all activities in RLP and RCPSP) so that both implicit and explicit constraints are satisfied.
Nodes, of which a search tree consists of, are subsets of the set of all solutions of the combinatorial problem. Branching, on the other hand, is the partitioning of any set of feasible solutions into separate subsets [202].
Branching process starts from the root node (the node in the uppermost level of the tree) which represents the set of all solutions. In some instances during the search, there might be nodes from which no branching has occurred yet. These nodes which are to be discovered further are called intermediate nodes. On the contrary to intermediate nodes which imply a partial solution, final nodes represent a complete solution. In order to reach a final node (leaf), all decisions required to establish a valid solution set have to be made. In RLP, for example, a leaf stores start dates of all noncritical activities. Obviously final nodes are located in the lowermost level of the search tree.
Two main characteristics of branch-and-bound algorithms presented by Agin [202] are branching characteristic and bounding characteristic. According to the definitions provided, branching characteristic ensures that an optimal solution is going to be reached at the end of the search since all possible combinations are going to be considered, whereas bounding characteristic implies a possibility to reach the optimal solution without visiting each node by pruning some parts of the tree.
Finally definition of the lower bound should be given since this concept is in the very heart of the branch-and-bound logic. Lower bound is a value of the objective function for all solutions included in a specific node such that none of the solutions that could be branched from that node will have a better objective function value than that bound. As this definition implies, there is no use to branch a node any further if its lower-bound value is worse than the objective function value of one of the explored final nodes (complete solutions). Objective function value of the best complete solution explored so far, that is, upper bound, is used to decide whether a node is promising or not. Obviously, upper bound at the end of the search provides the optimal solution to the problem.
According to Agin [202], a branch-and-bound algorithm might be said to consist of rules for:
-
1.
Deciding on how to continue the search given an intermediate node (branching rule)
-
2.
Deciding on how to calculate lower bounds on each established node
-
3.
Deciding on the intermediate node from which to branch next
-
4.
Recognizing when a node contains only infeasible or nonoptimal solutions
-
5.
Recognizing optimal solutions encountered on final nodes
16 Fuzzy Facility Location
In earlier studies in location problems literature, we saw that this area firstly related to industrial contexts, referring to the supply of a single commodity from a set of potential locations, where facilities may be placed, to clients of known locations and demands, at minimum cost. Location problems consist of determining the locations of the facilities and the flows of the commodity from facilities to clients at a minimum cost.
Facility location selection that exhibits a significant impact on market share and profitability is critical and also has strategic issues in supply chain design and management [204, 205].
Solving the problems in which the demands and the costs are deterministic, many efficient methods are used. In the literature there are some examples such as the following: Akinc and Khumawala [206] used a branch- and-bound algorithm for a capacitated warehouse location problem. Dearing and Newruck [207] developed an implicit enumeration algorithm with Lagrange relaxation for a capacitated bottleneck facility location problem. Badri [208] used analytic hierarchy process with multiobjective goal programming methods for a facility location. Dupont [209] introduced a new type of facility location model with a concave global cost function and proposed a branch-and-bound algorithm for this model. For other types of methods also some examples in the literature, for example, Drezner and Hamacher [210], Ernst and Krishnamoorthy [211], Lozano et al. [212], and Misra et al. [213].
Facility location problem copes with the imprecise or qualitative nature of the linguistic assessment in real applications. Also this problem processes imprecise, uncertain, or vague data, such as the imprecise experience-based demands of the clients or the costs of operating the facilities. The imprecise nature of these data is due to the fact that the precise and complete historical data are usually unavailable in real situations. To the former, fuzzy sets and fuzzy logic [104, 214–216] are suitable methods of dealing with the linguistic assessment.
For example, Batanovi et al. [217] discussed a class of fuzzy maximum covering location problems in networks by assuming that the relative weights of demand nodes are imprecise and described by linguistic expressions and developed algorithms for choosing the best facility locations based on comparison operations on discrete fuzzy sets. Bhattacharya et al. [218] considered facilities located under multiple fuzzy criteria and proposed a fuzzy goal programming approach to deal with the problem. Ishii et al. [219] developed a location model by considering the customer satisfaction degree with respect to the distance of each customer from the facility. Kahraman et al. [220] solved facility location problems by using four different approaches to fuzzy multiattribute group decision-making, that is, fuzzy model of group decision, fuzzy synthetic evaluation, Yager’s weighted goals method, and a fuzzy analytic hierarchy process.
Uncertainty is closely related to risks that include environmental and organiza- tional. For the companies it is important to reduce risks that involves in their location decisions in order to enhance customer service and improve their business processes, to result increasing competitiveness and profitability. Uncertain parameters based on fuzzy set theory [95, 221–223] have been developed, which aim to deal with the cases of imprecise or vague data. For instance, Bhattacharya et al. [224] considered facilities located under multiple fuzzy criteria and proposed a fuzzy goal programming approach to deal with the problem. Ishii et al. [225] developed a location model by considering the satisfaction degree with respect to the distance from the facility for each customer. Assuming that demands of customers are represented as fuzzy variables, Wen and Iwamura [226] presented a continuous \(\alpha\)-cost facility location model employing Hurwicz criterion, while Zhou and Liu [227] presented three types of continuous capacitated location–allocation problem with different decision criteria.
Stochastic problems deal with the cases where the parameters are treated as random variables. In real applications, randomness and fuzziness may coexist in a facility location problem. Due to the fact that there are some variables such as subjective judgment, imprecise human knowledge and perception in capturing statistical data may embrace randomness and fuzziness at the same time or some data that belong to the history for the location problems may be insufficient. Therefore, the experience-based fuzzy information can be incorporated into the originally available statistic data. In both cases, there is a genuine need to deal with a hybrid uncertainty containing simultaneously randomness and fuzziness. The concept of fuzzy random variables [228–230] was introduced to quantify and deal with the phenomena in which vagueness and randomness appear at the same time. This formalism serves as a basic tool to construct a framework of decision-making models operating in a fuzzy and random environment.
17 Cross-References
Recommended Reading
R. Diestel, Graph Theory (Springer, New York, 1997)
H. Korte, J. Vygen, Combinatorial Optimization Theory and Algorithms, 4th edn. (Springer, Berlin, 2008)
A. Rosenfeld, Fuzzy graphs, in Fuzzy Sets and Their Applications, ed. by L.A. Zadeh, K.S. Fu, M. Shimura (Academic, New York, 1975), pp. 77–95
P. Bhattacharya, Some remarks on fuzzy graphs. Pattern Recognit. Lett. 6, 297–302 (1987)
F. Harary, Graph Theory, Indian Student Edition, (Narosa/Addison Wesley, New Delhi, 1988)
K.R. Bhutani, On automorphism of fuzzy graphs. Pattern Recognit. Lett. 12, 413–420 (1991)
M.S. Sunitha, A.A. Vijayakumar, Characterization of fuzzy trees. Inf. Sci. 113, 293–300 (1999)
J.N. Mordeson, P.S. Nair, Fuzzy Graphs and Fuzzy Hypergraphs (Physica, Heidelberg, 2000)
A. NagoorGani, M. BasheerAhamed, Order and size in fuzzy graph. Bull. Pure Appl. Sci. 22E(1), 145–148 (2003)
A.N. Gani, K. Radha, On regular fuzzy graphs. J. Phys. Sci. 12, 33–40 (2008)
P. Bhattacharya, F. Suraweera, An algorithm to compute the max–min powers and a property of fuzzy graphs. Pattern Recognit. Lett. 12, 413–420 (1991)
Z. Tong, D. Zheng, An algorithm for finding the connectedness matrix of a fuzzy graph. Congr. Numer. 120, 189–192 (1996)
J. Xu, The use of fuzzy graphs in chemical structure research, in Fuzzy Logic in Chemistry, ed. by D.H. Rouvry (Academic, San Diego, 1997), pp. 249–282
S. Mathew, M.S. Sunitha, Types of arcs in a fuzzy graph. Inf. Sci. 179, 1760–1768 (2009)
M.S. Sunitha, A. Vijayakumar, Some metric aspects of fuzzy graphs, in Proceedings of the Conference on Graph Connections, ed. by R. Balakrishna, H.M. Mulder, A. Vijayakumar (CUSAT, Allied Publishers, New Delhi, 1999), pp. 111–114
M.S. Sunitha, A. Vijayakumar, Blocks in fuzzy graphs. J. Fuzzy Math. 13(1), 13–23 (2005)
M.S. Sunitha, A. Vijayakumar, Complement of a fuzzy graph. Indian J. Pure Appl. Math. 33(9), 1451–1464 (2002)
K.R. Bhutani, A. Rosenfeld, Fuzzy end nodes in fuzzy graphs. Inf. Sci. 152, 323–326 (2003)
K.R. Bhutani, A. Rosenfeld, Geodesics in fuzzy graphs. Electron. Notes Discret. Math. 15, 51–54 (2003)
K. Sameena, M.S. Sunitha, Strong arcs and maximum spanning trees in fuzzy graphs. Int. J. Math. Sci. 5(1), 17–20 (2006)
K. Sameena, M.S. Sunitha, Characterisation of g-self centered fuzzy graphs. J. Fuzzy Math. 16(4), 787–792 (2008)
K. Sameena, M.S. Sunitha, Distance in fuzzy graphs. Ph.D. Thesis, National Institute of Technology Calicut, India, 2008
P. Gupta, M. KumarMehlawat, Bector–Chandra type duality in fuzzy linear programming with exponential membership functions. Fuzzy Sets Syst. 160, 3290–3308 (2009)
N. Mahdavi-Amiria, S.H. Nasseria, Duality results and a dual simplex method for linear programming problems with trapezoidal fuzzy variables. Fuzzy Sets Syst. 158, 1961–1978 (2007)
J. Ramík, Duality in fuzzy linear programming with possibility and necessity relations. Fuzzy Sets Syst. 157, 1283–1302 (2006)
M. Inuiguchi, Necessity measure optimization in linear programming problems with fuzzy polytopes. Fuzzy Sets Syst. 158, 1882–1891 (2007)
Y.K. Wua, S.M. Guub, J.C. Liu, Reducing the search space of a linear fractional programming problem under fuzzy relational equations with max-Archimedean t-norm composition. Fuzzy Sets Syst. 159, 3347–3359 (2008)
A. Kumar, J. Kaur, P. Singh, A new method for solving fully fuzzy linear programming problems. Appl. Math. Model. 35, 817–823 (2011)
H. Lotfi, T. Allahviranloo, M.A. Jondabeh, L. Alizadeh, Solving a full fuzzy linear programming using lexicography method and fuzzy approximate solution F. Appl. Math. Model. 33, 3151–3156 (2009)
X. Zenga, S. Kanga, F. Li, L. Zhang, P. Guo, Fuzzy multi-objective linear programming applying to crop area planning. Agric. Water Manage. 98, 134–142 (2010)
T. Liang, Distribution planning decisions using interactive fuzzy multi-objective linear programming. Fuzzy Sets Syst. 157, 1303–1316 (2006)
D. Peidro, J. Mula, M. Jimenez, M. Botella, A fuzzy linear programming based approach for tactical supply chain planning in an uncertainty environment. Eur. J. Oper. Res. 205, 65–80 (2010)
J.J. Buckley, T. Feuring, Evolutionary algorithm solution to fuzzy problems: fuzzy linear programming. Fuzzy Sets Syst. 109, 35–53 (2000)
S. Chanas, P. Zielinski, On the equivalence of two optimization methods for fuzzy linear programming problems. Eur. J. Oper. Res. 121, 56–63 (2000)
C. Stanciulescu, Ph. Fortemps, M. Instale, V. Wertz, Multi objective fuzzy linear programming problems with fuzzy decision variables. Eur. J. Oper. Res. 149, 654–675 (2003)
M. Sadeghi, H.M. Hosseini, Energy supply planning in Iran by using fuzzy linear programming approach (regarding uncertainties of investment costs). Energy Policy 34, 993–1003 (2006)
X. Liu, Measuring the satisfaction of constraints in fuzzy linear programming. Fuzzy Sets Syst. 122, 263–275 (2001)
L.H. Chen, W.C. Ko, Fuzzy linear programming models for new product design using QFD with FMEA. Appl. Math. Model. 33, 633–647 (2009)
H. Katagiri, M. Sakawa, K. Kato, I. Nishizaki, Interactive multi objective fuzzy random linear programming: maximization of possibility and probability. Eur. J. Oper. Res. 188, 530–539 (2008)
R. Bellman, L.A. Zadeh, Decision making in a fuzzy environment. Manage. Sci. 17B, 141–164 (1970)
H.J. Zimmermann, Fuzzy programming and linear programming with several objective functions. Fuzzy Sets Syst. 1, 45–55 (1978)
F. Herrera, J.L. Verdegay, H.J. Zimmermann, Boolean programming with fuzzy constraints. Fuzzy Sets Syst. 55, 285–293 (1993)
M.S. Osman, O.M. Saad, A.G. Hasan, Solving a special class of large-scale fuzzy multi objective integer linear programming problems. Fuzzy Sets Syst. 107, 289–297 (1999)
J.J. Buckley, L.J. Jowers, Monte Carlo Methods in Fuzzy Optimization (Springer, Berlin, 2008)
K. Eshghi, J. Nematian, Special classes of fuzzy integer programming models with all-different constraints. Sci. Iran. Trans. E 16, 1–10 (2009)
R.R. Tan, Using fuzzy numbers to propagate uncertainty in matrix-based LCI.LCI. Int. J. Life Cycle Assess. 13, 585–593 (2008)
R.R. Tan, A.B. Culaba, K.B. Aviso, A fuzzy linear programming extension of the general matrix-based life cycle model. J. Clean. Prod. 16, 1358–1367 (2008)
A.S. Asratian, N.N. Kuzjurin, Two sensitivity theorems in fuzzy integer Programming. Discret. Appl. Math. 134, 129–140 (2004)
G.H. Huang, W. Baetz, G. Patry, Grey fuzzy integer programming: an application to regional waste management planning under uncertainty. Socio-Econ. Plan. Sci. 29(1), 17–38 (1995)
R.R. Tan, D.K.S. Ng, D.C.Y. Foo, K.B. Aviso, Crisp and fuzzy integer programming models for optimal carbon sequestration retrofit in the power sector. Chem. Eng. Res. Des. 88, 1580–1588 (2010)
A.H. Gharehgozli, R.T. Moghaddam, N. Zaerpour, A fuzzy-mixed-integer goal programming model for a parallel-machine scheduling problem with sequence-dependent set up times and release dates. Robot. Comput.-Integr. Manuf. 25, 853–859 (2009)
Y.P. Li, G.H. Huang, X.H. Nie, S.L. Nie, A two-stage fuzzy robust integer programming approach for capacity planning of environmental management systems. Eur. J. Oper. Res. 189, 399–420 (2008)
M. Allahviranloo, S. Afandizadeh, Investment optimization on port’s development by fuzzy integer programming. Eur. J. Oper. Res. 186, 423–434 (2008)
O.E. Emam, A fuzzy approach for bi-level integer non-linear programming problem. Appl. Math. Comput. 172, 62–71 (2006)
S. Vajda, Probabilistic Programming (Academic, New York, 1972)
M. Sakawa, Fuzzy Sets and Interactive Optimization (Plenum, New York, 1993)
J. Gao, M. Lu, Fuzzy quadratic minimum spanning tree problem. Appl. Math. Comput. 164, 773–788 (2005)
H. Katagiri, M. Sakawaa, H. Ishii, Fuzzy random bottleneck spanning tree problems using possibility and necessity measures. Eur. J. Oper. Res. 152, 88–95 (2004)
H. Katagiri, E.B. Mermri, M. Sakawa, K. Kato, A study on fuzzy random minimum spanning tree problems through possibilistic programming and the expectation optimization model, in The 47th IEEE International Midwest Symposium on Circuits and Systems, Hiroshima, Japan, (2004), pp. III-49–52
S. Moazeni, Fuzzy shortest path problem with finite fuzzy quantities. Appl. Math. Comput. 183, 160–169 (2006)
T.N. Chuang, J.Y. Kung, The fuzzy shortest path length and the corresponding shortest path in a network. Comput. Oper. Res. 32, 1409–1428 (2005)
T.-N. Chuang, J.Y. Kung, A new algorithm for the discrete fuzzy shortest path problem in a network. Appl. Math. Comput. 174, 1660–1668 (2006)
F. Hernandes, A. Yamakami, Um algoritmopara o problema de caminhomínimoemgrafos com custosnos arcos fuzzy, in XV CongressoBrasileiro de Automática, Gramado, RS, 2004
J.A. Moreno, J.M. Moreno, J.L. Verdegay, Fuzzy location problems on networks. Fuzzy Sets Syst. 142, 393–405 (2004)
S.M.A. Nayeem, M. Pal, Shortest path problem on a network with imprecise edge weight. Fuzzy Optim. Decis. Mak. 4, 293–312 (2005)
S. Okada, Fuzzy shortest path problems incorporating interactivity among paths. Fuzzy Sets Syst. 142(3), 335–357 (2004)
A. Sengupta, T.K. Pal, Solving the shortest path problem with intervals arcs. Fuzzy Optim. Decis. Mak. 5, 71–89 (2006)
M.T. Takahashi, Contribuiçõesaoestudo de grafos fuzzy: Teoria e algoritmos. Ph.D. Thesis, Faculdade de EngenhariaElétrica e de Computação, UNICAMP, 2004
F. Hernandes, M.T. Lamata, J.L. Verdegay, A. Yamakami, The shortest path problem on networks with fuzzy parameters. Fuzzy Sets Syst. 158, 1561–1570 (2007)
A. Tajdin, I. Mahdavi, N. Mahdavi-Amiri, B. Sadeghpour-Gildeh, Computing a fuzzy shortest path in a network with mixed fuzzy arc lengths using \(\alpha\)-cuts. Comput. Math. Appl. 60, 989–1002 (2010)
R.E. Bellman, L.A. Zadeh, Decision-making in a fuzzy environment. Manage. Sci. 17B, 141–164 (1970)
E. Keshavarz, E. Khorram, A fuzzy shortest path with the highest reliability. J. Comput. Appl. Math. 230, 204–212 (2009)
X.K. Iwamura, Z. Shao, New models for shortest path problem with fuzzy arc lengths. Appl. Math. Model. 31, 259–269 (2007)
ST. Liu, C. Kao, Network flow problems with fuzzy arc lengths. IEEE Trans. Syst. Man Cybern. B 34(1), 765–769 (2004)
P. Diamond, A fuzzy max-flow min-cut theorem. Fuzzy Sets Syst. 119, 139–148 (2001)
L. Georgiadis, Arborescence optimization problems solvable by Edmonds’ algorithm. Theor. Comput. Sci. 301, 427–437 (2003)
M. Ghatee, S.M. Hashemi, Generalized minimal cost flow problem in fuzzy nature: an application in bus network planning problem. Appl. Math. Model. 32, 2490–2508 (2008)
S.M. Hashemi, M. Ghatee, E. Nasrabadi, Combinatorial algorithms for the minimum interval cost flow problem. Appl. Math. Comput. 175, 1200–1216 (2006)
M. Ghatee, S.M. Hashemi, Ranking function-based solutions of fully fuzzified minimal cost flow problem. Inf. Sci. 177, 4271–4294 (2007)
M. Ghatee, S.M. Hashemi, Application of fuzzy minimum cost flow problems to network design under uncertainty. Fuzzy Sets Syst. 160, 3263–3289 (2009)
M. Ghatee, S.M. Hashemi, M. Zarepisheh, E. Khorram, Preemptive priority-based algorithms for fuzzy minimal cost flow problem: an application in hazardous materials transportation. Comput. Ind. Eng. 57, 341–354 (2009)
D. Conte, P. Fogg\(\imath \)ay, X.C. Sansoney, M. Vento, Thirty years of graph matching in pattern recognition. Int. J. Pattern Recognit. Artif. Intell. 18(3), 265–298 (2004)
S. Medasani, R. Krishnapuram, Y.S. Choi, Graph matching by relaxation of fuzzy assignments. IEEE Trans. Fuzzy Syst. 9, 173–182 (2001)
S. Medasani, R. Krishnapuram, A fuzzy approach to content-based image retrieval, in FUZZ-IEEE ’99: IEEE International Fuzzy Systems Conference Proceedings, Seoul, Korea, 22-25 Aug 1999 (IEEE, Piscataway, 1999), pp. 1251–1260
L. Liu, Y. Li, L. Yang, The maximum fuzzy weighted matching models and hybrid genetic algorithm. Appl. Math. Comput. 181, 662–674 (2006)
L. Liu, X. Gao, Maximum random fuzzy weighted matching models and hybrid genetic algorithm, http://orsc.edu.cn/’’xfgao/
M. Balakrishnarajan, P. Venuvanaligam, An artificial intelligence approach for the generation and enumeration of perfect matching on graphs. Comput. Math. Appl. 29, 115–121 (1995)
A. Hsieh, C. Ho, K. Fan, An extension of the bipartite weighted matching problem. Pattern Recognit. Lett. 16, 347–353 (1995)
A. Hsieh, K. Fan, T. Fan, Bipartite weighted matching for on-line handwritten Chinese character recognition. Pattern Recognit. 28, 143–151 (1995)
J. Lamb, A note on the weighted matching with penalty problem. Pattern Recognit. Lett. 19, 261–263 (1998)
G. Steiner, G. Yeomans, A linear time algorithm for maximum matching in convex, bipartite graphs. Comput. Math. Appl. 31, 91–96 (1996)
J. Kim, N. Wormal, Random matchings which induce Hamilton cycles and Hamiltonian decompositions of random regular graphs. J. Combin. Theory B 81, 20–44 (2001)
M. Zito, Small maximal matchings in random graphs. Theor. Comput. Sci. 297, 487–507 (2003)
D. Dubois, H. Prade, Possibility Theory: An Approach to Computerized Processing of Uncertainty (Plenum, New York, 1988)
B. Liu, Y.K. Liu, Expected value of fuzzy variable and fuzzy expected value models. IEEE Trans. Fuzzy Syst. 10, 445–450 (2002)
B. Liu, Theory and Practice of Uncertain Programing (Physica, New York, 2002)
B. Liu, Uncertainty Theory: An Introduction to Its Axiomatic Foundations (Springer, Berlin, 2004)
A. Charnes, W.W. Copper, Chance-constrained programming. Manage. Sci. 6, 73–79 (1959)
B. Liu, K. Iwamura, A note on chance constrained programming with fuzzy coefficients. Fuzzy Sets Syst. 100, 229–233 (1998)
B. Liu, Dependent-chance programming with fuzzy decisions. IEEE Trans. Fuzzy Syst. 7(3), 354–360 (1999)
H. Haken, M. Schanz, J. Starke, Treatment of combinatorial optimization problems using selection equations with cost terms. Part I. Two-dimensional assignment problems. Phys. D 134, 227–241 (1999)
H.W. Kuhn, The Hungarian method for the assignment problem. Nav. Res. Logist. Quart. 2, 253–258 (1996)
B. Werners, Interactive multiple objective programming subject to Kexible constraints. Eur. J. Oper. Res. 31, 342–349 (1987)
L.A. Zadeh, Fuzzy sets. Inf. Control 8, 338–353 (1965)
M.S. Chen, On a fuzzy assignment problem. Tamkang J. 22, 407–411 (1985)
X. Wang, Fuzzy optimal assignment problem. Fuzzy Math. 3, 101–108 (1987)
D. Dubois, P. Fortemps, Computing improved optimal solutions to max - min flexible constraint satisfaction problems. Eur. J. Oper. Res. 118, 95–126 (1999)
M. Sakawa, I. Nishizaki, Y. Uemura, Interactive fuzzy programming for two-level linear and linear fractional production and assignment problems: a case study. Eur. J. Oper. Res. 135, 142–157 (2001)
S. Chanas, W. Kolodziejczyk, A. Machaj, A fuzzy approach to the transportation problem. Fuzzy Sets Syst. 13, 211–221 (1984)
M. Tada, H. Ishii, An integer fuzzy transportation problem. Comput. Math. Appl. 31, 71–87 (1996)
S. Chanas, D. Kuchta, Fuzzy integer transportation problem. Fuzzy Sets Syst. 98, 291–298 (1998)
S. Chanas, D. Kuchta, A concept of the optimal solution of the transportation problem with fuzzy cost coefficients. Fuzzy Sets Syst. 82, 299–305 (1996)
C.J. Lin, U.P. Wen, A labeling algorithm for the fuzzy assignment problem. Fuzzy Sets Syst. 142, 373–391 (2004)
Y. Feng, L. Yang, A two-objective fuzzy k-cardinality assignment problem. J. Comput. Appl. Math. 197, 233–244 (2006)
J. Majumdar, A.K. Bhunia, Elitist genetic algorithm for assignment problem with imprecise goal. Eur. J. Oper. Res. 177, 684–692 (2007)
X. Ye, J. Xu, A fuzzy vehicle routing assignment model with connection network based on priority-based genetic algorithm. World J. Model. Simul. 4, 257–268 (2008)
L. Liu, X. Gao, Fuzzy weighted equilibrium multi-job assignment problem and genetic algorithm. Appl. Math. Model. 33, 3926–3935 (2009)
A. Kumar, A. Gupta, A. Kaur, Method for solving fully fuzzy assignment problems using triangular fuzzy numbers. Int. J. Comput. Inf. Eng. 3:4, 231–234 (2009)
S. Mukherjee, K. Basu, A more realistic assignment problem with fuzzy costs and fuzzy restrictions. Adv. Fuzzy Math. 5(3), 395–404 (2010)
R. Nagarajan, A. Solairaju, Computing improved fuzzy optimal Hungarian assignment problems with fuzzy costs under Robust ranking techniques. Int. J. Comput. Appl. 6(4), 6–13 (2010)
F.G. Shi, A new approach to the fuzzification of matroids. Fuzzy Sets Syst. 160, 696–705 (2009)
A. Kasperski, P. Zielinski, On combinatorial optimization problems on matroids with uncertain weights. Eur. J. Oper. Res. 177, 851–864 (2007)
A. Kasperski, P. Zielinski, A possibilistic approach to combinatorial optimization problems on fuzzy-valued matroids, in Fuzzy Logic and Applications, 6th International Workshop, WILF, Crema, Italy, ed. by I. Bloch, A. Petrosino, A. Tettamanzi (Springer-Verlag, Berlin, Heidelberg, 2006), pp. 46–52
J. Fortin, A. Kasperski, P. Zielinski, Efficient methods for computing optimality degrees of elements in fuzzy weighted matroids, in Fuzzy Logic and Applications, 6th International Workshop, WILF, Crema, Italy, ed. by I. Bloch, A. Petrosino, A. Tettamanzi (Springer, Berlin, Heidelberg, 2006), pp. 99–107
A. Kasperski, P. Zielinski, Using gradual numbers for solving fuzzy-valued combinatorial optimization problems, in Foundations of Fuzzy Logic and Soft Computing, 12th International Fuzzy Systems Association World Congress, Cancun, Mexico, ed. by P. Melin, O. Castillo, L.T. Aguilar, J. Kacprzyk, W. Pedrycz (Springer, Berlin, Heidelberg, 2007), pp. 656–665
R. Goetschel, W. Voxman, Fuzzy matroids. Fuzzy Sets Syst. 27, 291–302 (1998)
R. Goetschel, W. Voxman, Bases of fuzzy matroids. Fuzzy Sets Syst. 31, 253–261 (1989)
R. Goetschel, W. Voxman, Fuzzy matroids and a greedy algorithm. Fuzzy Sets Syst. 37, 201–214 (1990)
I.-C. Hsueh, On fuzzication of matroids. Fuzzy Sets Syst. 53, 319–327 (1993)
L.A. Novak, A comment on ‘Bases of fuzzy matroids’. Fuzzy Sets Syst. 87, 251–252 (1997)
L.A. Novak, On Goetschel and Voxman fuzzy matroids. Fuzzy Sets Syst. 117, 407–412 (2001)
R. Goetschel, W. Voxman, Fuzzy matroids. Fuzzy Sets Syst. 27, 291–302 (1998)
R. Goetschel, W. Voxman, Fuzzy matroids and a greedy algorithm. Fuzzy Sets Syst. 37, 201–214 (1990)
M.J. Hwang, C.I. Chiang, Y.H. Liu, Solving a fuzzy set covering problem. Math. Comput. Model. 40(7/8), 861–865 (2004)
G.L. Nemhauser, L.A. Wolsey, Integer and Combinatorial Optimization (Wiley, New York, 1988)
R.M. Karp, Reducibility among combinatorial problems, in Complexity of Computer Computations, ed. by R. Miller, J. Thatcher (Plenum, New York, 1972), pp. 85–103
F. Barahona, M. Grotschel, M. Junger, G. Reinelt, An application of combinatorial optimization to statistical physics and circuit layout design. Oper. Res. 36, 493–513 (1998)
J. Poland, T. Zeugmann, Clustering pairwise distances with missing data: maximum cuts versus normalized cuts. Lect. Notes Comput. Sci. 4265, 197–208 (2006)
H.F. Wang, M.L. Wang, A fuzzy multi-objective linear programming. Fuzzy Sets Syst. 86, 61–72 (1997)
B. Liu, Uncertainty Theory, 2nd edn. (Springer, Berlin, 2007)
P.M. Pardalos, T. Mavridou, J. Xue, The graph coloring problem: a bibliographic survey, in Handbook of Combinatorial Optimization, vol. 2, ed. by D.Z. Du, P.M. Pardalos (Kluwer Academic, Boston, 1998), pp. 331–395
C. Eslahchi, B.N. Onagh, Vertex strength of fuzzy graphs. Int. J. Math. Math. Sci. 2006, 1–9 (2006)
S. Munoz, T. Ortuno, J. Ramirez, J. Yanez, Coloring fuzzy graphs. Omega 32, 211–221 (2005)
A. Chaudhuri, K. De, Fuzzy genetic heuristic for university course timetable problem. Int. J. Adv. Soft Comput. Appl. 2(1), 100–123 (2010)
F. Eisenbrand, M. Niemeier, European Conference on Combinatorics, Graph Theory and Applications, Coloring fuzzy circular interval graphs. Electron. Notes Discret. Math. 34, 543–548 (2009)
D. Kuchta, A generalisation of an algorithm solving the fuzzy multiple choice knapsack problem. Fuzzy Sets Syst. 127(2), 131–140 (2002)
A. Kasperski, M. Kulej, The 0–1 knapsack problem with fuzzy data. Fuzzy Optim. Decis. Mak. 6, 163–172 (2007)
F.T. Lin, J.S. Yao, Using fuzzy number in knapsack problem. Eur. J. Oper. Res. 135(1), 158–176 (2001)
F.T. Lin, Solving the imprecise weight coefficients Knapsack problem by genetic algorithms, in 2006 IEEE International Conference on Systems, Man, and Cybernetics, Taipei, Taiwan, 8–11 Oct 2006
M. Sakawa, K. Kato, T. Shibano, An interactive fuzzy satisficing method for multiobjective multidimensional 0–1 knapsack problems through genetic algorithms, in Proceedings of IEEE International Conference on Evolutionary Computation, Nagoya University, Japan, 20–22 May, 1996 (Institute of Electrical and Electronics Engineers, Piscataway, 1996), pp. 243–246
S.P. Chen, Analysis of maximum total return in the continuous knapsack problem with fuzzy object weights. Appl. Math. Model. 33, 2927–2933 (2009)
F.T. Lin, J.S. Yao, Using fuzzy number in knapsack problem. Eur. J. Oper. Res. 135(1), 158–176 (2001)
S.P. Chen, Analysis of maximum total return in the continuous knapsack problem with fuzzy object weights. Appl. Math. Model. 33, 2927–2933 (2009)
S. Sadi-Nezhad, K.K. Damghani, N. Pilevari, Application of 0–1 fuzzy programming in optimum project selection. World Acad. Sci. Eng. Technol. 64, 335–339 (2010)
J.L. Verdegay, E. Vergara-Moreno, Fuzzy termination criteria in Knapsack problem algorithms. Mathw. Soft Comput. 7, 89–97 (2000)
K. Kato, M. Sakawa, Genetic algorithms with decomposition procedures for multidimensional 0–1 knapsack problems with block angular structures. IEEE Trans. Syst. Man Cybern. B 33(3), 410–419 (2003)
F.T. Lin, On the generalized fuzzy multiconstraint 0–1 knapsack problem, in Proceedings of 2006 IEEE International Conference on Fuzzy Systems Sheraton Vancouver Wall Centre Hotel, Vancouver, BC, Canada 16–21 July 2006
T. Hasuike, H. Katagiri, H. Ishii, Probability maximization model of 0–1 Knapsack problem with random fuzzy variables, in Proceedings of 2008 IEEE International Conference on Fuzzy Systems, Hong Kong, China, 2008. FUZZ
H. Shih, Fuzzy approach to multilevel Knapsack problems. Comput. Math. Appl. 49, 1157–1176 (2005)
J.D. Ullman, Complexity of sequencing problems, in Computer and Job-Shop Scheduling Theory, ed. by E.G. Coffman (Wiley, New York, 1975)
C.B. Kim, K.A. Seong, H. Lee-Kwang, J.O. Kim, Design and implementation of FEGCS. IEEE Trans. Syst. Man Cybern. A 28(3) (1998)
B.S. Baker, E.G. Coffman, R.L. Rivest, Orthogonal packing in two dimensions. SIAM J. Comput. 9, 846–855 (1980)
B.S. Baker, D.J. Brown, H.P. Katsef, A 5=4 algorithm for two-dimensional packing. J. Algorithm 2, 348–368 (1981)
H. Dyckho, A typology of cutting and packing problems. Eur. J. Oper. Res. 44, 145–159 (1990)
M. Adamowicz, A. Albano, Nesting two-dimensional shapes in rectangular modules. Comput. Aided Des. 8(1), 27–33 (1976)
B. Chazelle, The bottom-left bin packing heuristic: an efficient implementation. IEEE Trans. Comput. C-32(8), 697–707 (1983)
R. Dong, W. Pedrycz, A granular time series approach to long-term forecasting and trend forecasting. Phys. A 387, 3253–3270 (2008)
J.N. Choi, S.K. Oh, W. Pedrycz, Identification of fuzzy models using a successive tuning method with a variant identification ratio. Fuzzy Sets Syst. 159, 2873–2889 (2008)
A. Bargiela, W. Pedrycz, Granular Computing: An Introduction (Kluwer Academic, Dordrecht, 2002)
W. Pedrycz, K. Hirota, Fuzzy vector quantization with the particle swarm optimization: a study in fuzzy granulation_degranulation information processing. Signal Process. 87, 2061–2074 (2007)
S. Okada, T. Soper, A shortest path problem on a network with fuzzy arc lengths. Fuzzy Sets Syst. 109, 129–140 (2000)
H.S. Shih, E.S. Lee, Fuzzy multi-level minimum cost flow problems. Fuzzy Sets Syst. 107, 159–176 (1999)
M. Dehghan, M. Ghatee, B. Hashemi, Inverse of a fuzzy matrix of fuzzy numbers. Int. J. Comput. Math. (2008). doi:10.1080/00207160701874789
M. Hukuhara, Intégration des applications measurable dont la valeurest un compact convexe. FunkcialajEkvacioj 10, 205–223 (1967)
P. Diamond, R. Korner, Extended fuzzy linear models and least squares estimates. Comput. Math. Appl. 33, 15–32 (1997)
M. Ghatee, S.M. Hashemi, B. Hashemi, M. Dehghan, The solution and duality of imprecise network problems. Comput. Math. Appl. 55, 2767–2790 (2008)
R.K. Ahuja, T.L. Magnanti, J.B. Orlin, Network Flows (Prentice-Hall, Englewood Cliffs, 1993)
A. Bargiela, W. Pedrycz, Granular Computing: An Introduction (Kluwer Academic, Dordrecht, 2002)
M. Ghatee, S.M. Hashemi, Traffic assignment model with fuzzy level of travel demand: an efficient algorithm based on quasi-Logit formulas. Eur. J. Oper. Res. (2008). doi:10.1016/j.ejor.2007.12.023
S.K. Das, A. Goswami, S.S. Alam, Multiobjective transportation problem with fuzzy interval cost, source and destination parameters. Eur. J. Oper. Res. 117, 100–112 (1999)
P. Ekel, W. Pedrycz, R. Schinzinger, A general approach to solving a wide class of fuzzy optimization problems. Fuzzy Sets Syst. 97, 49–66 (1998)
M. Ghatee, S. Mehdi Hashemi, Some concepts of the fuzzy multi commodity flow problem and their application in fuzzy network design. Math. Comput. Model. 49, 1030–1043 (2009)
H. Liu, X. Ban, B. Ran, P.B. Mirchandani, A formulation and solution algorithm for fuzzy dynamic traffic assignment model. Transp. Res. Rec. 178 (2003)
V. Henn, What is the meaning of fuzzy costs in fuzzy traffic assignment models? Transp. Res. C 13, 107–119 (2005)
R.K. Ahuja, T.L. Magnanti, J.B. Orlin, Network Flows (Prentice-Hall, Englewood Cliffs, 1993)
P.R. Bhave, R. Gupta, Optimal design of water distribution networks for fuzzy demands. Civil Eng. Environ. Syst. 21, 229–245 (2004)
S.K. Das, A. Goswami, S.S. Alam, Multiobjective transportation problem with fuzzy interval cost, source and destination parameters. Eur. J. Oper. Res. 117, 100–112 (1999)
P. Ekel, W. Pedrycz, R. Schinzinger, A general approach to solving a wide class of fuzzy optimization problems. Fuzzy Sets Syst. 97, 49–66 (1998)
A.M. Costa, A survey on benders decomposition applied to fixed-charge network design problems. Comput. Oper. Res. 32, 1429–1450 (2005)
M. Ghatee, S.M. Hashemi, Some concepts of the fuzzy multicommodity flow problem and their application in fuzzy network design. Math. Comput. Model. 49, 1030–1043 (2009)
D.Z. Du, J.M. Smith, J.H. Rubinstein, Advances in Steiner Trees (Kluwer Academic, Dordrecht, 2000)
F.K. Hwang, D.S. Richards, P. Winter, The Steiner Tree Problem (North-Holland, Amsterdam, 1992)
R. Karp, in Complexity of Computer Computations, ed. by R.E. Miller, J.W. Thatcher. IBM Research Symposia Series, vol. 43 (Plenum, New York, 1972), p. 85
G. Robins, A. Zelikovsky, in Proceedings of the Eleventh Annual ACM-SIAM Symposium on Discrete Algorithms (SIAM, San Francisco, 2000), pp. 770–779
M. Durand, Phys. Rev. Lett. 98, 088701 (2007)
M. Seda, Fuzzy shortest paths approximation for solving the fuzzy steiner tree problem in graphs. Int. J. Math. Comput. Sci. 1:3, 22–26 (2005)
G. Gutin, A. Punnen (eds.), Traveling Salesman Problem and Its Variations (Kluwer Academic, Dordrecht, 2002); C. Helmberg, The m-cost ATSP. Lect. Notes Comput. Sci. 1610, 242–258 (1999)
D. Feillet, P. Dejax, M. Gendreau, Traveling salesman problems with profits. Transp. Sci. 39(2), 188–205 (2005)
E. Balas, G. Martin, Roll-a-Round: Software Package for Scheduling the Rounds of a Rolling Mill (Balas and Martin Associates, Pittsburgh, 1965)
C.P. Keller, M. Goodchild, The multiobjective vending problem: a generalization of the traveling salesman problem. Environ. Plan. B 15, 447–460 (1988)
E.S. Lee, R.J. Li, Comparison of fuzzy numbers based on probability measure of fuzzy events. Comput. Math. Appl. 15, 887–896 (1988)
N. Agin, Optimum seeking with branch and bound. Manage. Sci. 13(4), B-176–B-185 (1996)
E. Demeulemeester, W. Herroelen, Project Scheduling: A Research Handbook (Kluwer Academic, Boston, 2002)
S.H. Owen, M.S. Daskin, Strategic facility location: a review. Eur. J. Oper. Res. 111(3), 423–447 (1998)
D.J. van der Zee, J.G.A.J. van der Vorst, A modeling framework for supply chain simulation: Opportunities for improved decision making. Decis. Sci. 36(1), 65–95 (2005)
U. Akinc, B.M. Khumawala, An efficient branch and bound algorithm for the capacitated warehouse location problem. Manage. Sci. 23(6), 585–594 (1977)
P.M. Dearing, F.C. Newruck, A capacitated bottleneck facility location problem. Manage. Sci. 25(11), 1093–1104 (1979)
M.A. Badri, Combining the analytic hierarchy process and goal programming for global facility location-allocation problem. Int. J. Prod. Econ. 62(3), 237–248 (1999)
L. Dupont, Branch and bound algorithm for a facility location problem with concave site dependent costs. Int. J. Prod. Econ. 112(1), 245–254 (2008)
Z. Drezner, W. Hamacher (eds.), Facility Location: Applications and Theory (Springer, New York, 2004)
A.T. Ernst, M. Krishnamoorthy, Solution algorithms for the capacitated single allocation hub location problem. Ann. Oper. Res. 86(1–4), 141–159 (1999)
S. Lozano, F. Guerrero, L. Onieva, J. Larrañeta, Kohonen maps for solving a class of location-allocation problems. Eur. J. Oper. Res. 108(1), 106–117 (1998)
A. Misra, A. Roy, S.K. Das, Information-theory based optimal location management schemes for integrated multi-system wireless networks. IEEE/ACM Trans. Netw. 16, 525–538 (2008)
W. Pedrycz, F. Gomide, An Introduction to Fuzzy Sets; Analysis and Design (MIT, Cambridge MA, 1998)
W. Pedrycz, F. Gomide, Fuzzy Systems Engineering: Toward Human-Centric Computing (Wiley, Hoboken, 2007)
L.A. Zadeh, Is there a need for fuzzy logic? Inf. Sci. 178(13), 2751–2779 (2008)
V. Batanovic, D. Petrovic, R. Petrovic, Fuzzy logic based algorithms for maximum covering location problems. Inf. Sci. 179(1–2), 120–129 (2009)
U. Bhattacharya, J.R. Rao, R.N. Tiwari, Fuzzy multi-criteria facility location problem. Fuzzy Sets Syst. 51(3), 277–287 (1992)
H. Ishii, Y.L. Lee, K.Y. Yeh, Fuzzy facility location problem with preference of candidate sites. Fuzzy Sets Syst. 158(17), 1922–1930 (2007)
C. Kahraman, D. Ruan, I. Dogan, Fuzzy group decision-making for facility location selection. Inf. Sci. 157, 135–153 (2003)
D. Dubois, H. Prade, Possibility Theory (Plenum, New York, 1988)
W. Pedrycz, F. Gomide, Fuzzy Systems Engineering: Toward Human- Centric Computing (Wiley, Hoboken, 2007)
L.A. Zadeh, Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1(1), 3–28 (1978)
U. Bhattacharya, J.R. Rao, R.N. Tiwari, Fuzzy multi-criteria facility location problem. Fuzzy Sets Syst. 51(3), 277–287 (1992)
H. Ishii, Y.L. Lee, K.Y. Yeh, Fuzzy facility location problem with preference of candidate sites. Fuzzy Sets Syst. 158(17), 1922–1930 (2007)
M. Wen, K. Iwamura, Fuzzy facility location-allocation problem under the Hurwicz criterion. Eur. J. Oper. Res. 184(2), 627–635 (2008)
J. Zhou, B. Liu, Modeling capacitated location-allocation problem with fuzzy demands. Comput. Ind. Eng. 53(3), 454–468 (2007)
R. Kruse, K.D. Meyer, Statistics with Vague Data (D. Reidel, Dordrecht, 1987)
H. Kwakernaak, Fuzzy random variables–I. Definitions and theorems. Inf. Sci. 15, 1–29 (1978)
Y.K. Liu, B. Liu, Fuzzy random variable: a scalar expected value operator. Fuzzy Optim. Decis. Mak. 2, 143–160 (2003)
R. Goetschel, W. Voxman, Fuzzy matroids and a greedy algorithm. Fuzzy Sets Syst. 37, 201–214 (1990)
D. Kuchta, A generalisation of an algorithm solving the fuzzy multiple choice knapsack problem. Fuzzy Sets Syst 127(2), 131–140 (2002)
F.T. Lin, J.S. Yao, Using fuzzy number in knapsack problem. Eur. J. Oper. Res. 135(1), 158–176 (2001)
L.A. Zadeh, Fuzzy sets. Inf. Control 8(3), 338–353 (1965)
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer Science+Business Media New York
About this entry
Cite this entry
Pardalos, P.M., Aydogan, E.K., Gurbuz, F., Demirtas, O., Bakirli, B.B. (2013). Fuzzy Combinatorial Optimization Problems. In: Pardalos, P., Du, DZ., Graham, R. (eds) Handbook of Combinatorial Optimization. Springer, New York, NY. https://doi.org/10.1007/978-1-4419-7997-1_68
Download citation
DOI: https://doi.org/10.1007/978-1-4419-7997-1_68
Published:
Publisher Name: Springer, New York, NY
Print ISBN: 978-1-4419-7996-4
Online ISBN: 978-1-4419-7997-1
eBook Packages: Mathematics and StatisticsReference Module Computer Science and Engineering