1 Introduction

Cognitive radios (CRs) aim to mitigate the scarcity of spectral resources by using the same frequency spectrum allocated to primary users, as long as the CR users do not cause harmful interference to primary users (PUs) in an underlay scenario [1, 2]. In order to reduce interference in wireless communications, one of the best methods is power control. Much research effort has been devoted to distributed power control problems in cognitive radio networks from different aspects and different system models. For example, to satisfy the interference temperature constraint at the PUs and maximize the CR users’ throughput, the authors propose a power allocation strategy to dynamically allocate the transmitted power to CR users in [3]. In [4] a transmitted power control scheme for a CR user is proposed in fading environment, which maximizes the capacity of the CR users subject to the interference threshold constraint at the PUs . This constraint can be in the form of either a hard or a soft threshold. At any time, we should not violate the hard threshold [5], whereas for a soft threshold, it can be maintained in a probabilistic manner [6–8].

All these works depend on the assumption that the constraints and objective function of the optimization problem can be obtained precisely. However, in practical situations, the parameters are imperfectly known, and they are uncertain or time varying. The solutions of the nominal optimization may be infeasible when some parameters are inaccurate. Hence, robust optimization has been utilized to deal with the uncertainty parameters [9, 10]. Robust optimization research is to seek a proper set to describe the uncertainty parameters. Usually, it is transformed to be convex optimization problem and preserves its tractability. In [11], to apply the worst-case interference control in CR networks, the uncertainty region is defined by utilizing the probability distribution function. The worst case robust optimization algorithm is proposed in [13] to minimize the total transmitted power of all users, given signal-to-interference-plus-noise ratio(SINR) constraints at each CR user and PU with the uncertain channel gains. To tackle uncertainty, the authors also use the Bayesian approach in wireless networks [14]. The main idea of Bayesian approach and the worst case robust optimization algorithm is to convert the uncertain parameters and constraints into the certain ones. In [15], the author applies the worst case, D-norm and Bayesian robust algorithm in orthogonal frequency-division multiplexing CRs network, however, only the uncertainty channel gains from CR’s transmitter to PU receiver are considered. The worst case and D-norm algorithm are used to maximize the social utility of CR users by Lagrange dual decomposition in [16]. However, the high-loading networks or poor channel may be cause the optimal power control infeasible. In [17], the robust probabilistic distributed power control algorithm is proposed to minimize the total transmitted power of users, with SINR requirement at CR users and interference limitation at base station respectively. However, in the CRs network, the PUs’ interference should be taken into consideration.

In this paper, we research the distributed robust power control problem in cognitive radio networks when the interference channels, including that from cognitive transmitters (CR-Txs) to primary receiver (PU-Rx) and from CR-Txs to cognitive receivers (CR-Rxs), are uncertain. Our objective is to minimize the transmission powers of all the cognitive users for energy-saving, subject to the outage probability of all CR users and PU below their predefined thresholds. We consider jointly the standard interference function algorithm and adjustment of maximum transmission power, while keeping the outage probability constraints of CR users and PU with uncertainty channel gains. In order to improve resource utilization, admission control is introduced.

The rest of the paper is organized as follows. Section 2 introduces the system model and robust problem formulation. The chance constraint robust power control allocation algorithm in a distributed way is presented in Section 2. In Section 3, the simulations are provided to demonstrate the performance of the proposed schemes. Finally, Section 4 makes the concluding remarks.

2 System model and problem formulation

2.1 A. Problem statement

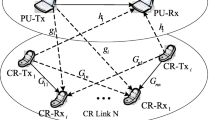
Considering a CRs network as shown in Fig. 1, there is no central control node and there are N cognitive user links and one primary user link. We investigate the scenario where all CR users share the same frequency resource with the PU, but, the total interference generated by CR users does not exceed the threshold that PU-Rx can tolerate. In particular, CRs can’t obtain system information from PU very well, when PU are not obliged to provide any information to CRs. That can cause undesired interference at PU-Rx. So, to avoid such instances, we restrict the outage probability of PU below a threshold.

$$\begin{array}{@{}rcl@{}} Pr\left\{\sum\limits_{i=1}^{N}h_{i}p_{i}\geq I\right\}\leq \varepsilon, \end{array} $$
(1)

where \(p_{i}\in [p_{i}^{\min }, p_{i}^{\max }]\) denotes CR-Tx’s transmitted power of link i (i=1,2,...,N), \(p_{i}^{\min }\) and \(p_{i}^{\max }\) are the minimum and the maximum transmitted power of CR-Tx of link i, respectively. h i denotes the channel gain from the CR-Tx to the PU-Rx. Let I be the interference threshold at PU-Rx. ε∈(0,1) denotes the desired upper-bound of the probability that the total interference is beyond of given threshold.

Fig. 1
figure 1

The model of cognitive radio networks

Full size image

To guarantee the normal uplink communication and meet the QoS requirements of all CR users, the SINR of each cognitive user should be greater than or equal to the target SINR. Similarly, when the uncertain channel gains from a CR-TX to a CR-RX that does not match with the CR-TX are considered, the uncertainty can cause the SINR below the target SINR. Then, the outage probability constraint of CR user in link i is given

$$\begin{array}{@{}rcl@{}} Pr\left\{r_{i}\leq {\hat{r_{i}}}\right\}\leq \xi_{i},\forall i. \end{array} $$
(2)

where the SINR of the i th CR user can be described as

$$\begin{array}{@{}rcl@{}} r_{i}=\frac{p_{i}G_{ii}}{\sum\limits_{k\neq i,k=1}^{N}p_{k}G_{ki}+\sigma^{2}+p_{o}g_{i}}, \end{array} $$
(3)

where g i represents the channel gain between the PU-Tx and the i th CR-Rx, and G i i , G k i are channel gains from the i th CR-Tx to the i th CR-Rx and from the k th CR-Tx to the i th CR-Tx, respectively. Besides, the transmitted power of the PU-Tx is p o . Assume that the background noise at the CR-Rxs of all links are σ 2. For simplicity, we denote N i as the interference caused by the PU-Tx and the noise at the i th CR-Rx, i.e., N i =σ 2+p o g i . Thus, (3) can be rewritten as

$$\begin{array}{@{}rcl@{}} r_{i}=\frac{p_{i}G_{ii}}{\sum\limits_{k\neq i,k=1}^{N}p_{k}G_{ki}+N_{i}}. \end{array} $$
(4)

2.2 B. Bernstein approximation

We apply a useful class of approximation techniques for chance- constraint known as Bernstein approximation, which can convert the uncertain problem to a deterministic problem. Bernstein approximation is briefly reviewed in [18, 19]. Consider a chance constraint

$$\begin{array}{@{}rcl@{}} Pr\left\{f_{0}(\textbf{p})+\sum\limits_{i=1}^{N}\zeta_{n}f_{n}(\textbf{p})<0\right\}\geq 1-\epsilon, \end{array} $$
(5)

where p is a deterministic parameter vector, and {ζ n } are random variables with marginal distributions denoted as {π n }. Suppose that one desires to meet this constraint for a given family of {ζ n } distributions under the following assumptions.

  • 1) f n (p) are affine in p for n=0,1,...,N.

  • 2) {ζ n } are independent of each other.

  • 3) {π n } have a common bounded support of [-1,1], that is, −1≤ζ n ≤1 for all n=1,...,N.

Under these assumptions, we can obtain a convex conservative surrogate for Eq. 5, which is proven in [18, 19].

$$\begin{array}{@{}rcl@{}} f_{0}(\textbf{p})&+&\sum\limits_{n=1}^{N}\max\{\mu_{n}^{-}f_{n}(\textbf{p}),\mu_{n}^{+}f_{n}(\textbf{p})\}\\ &+&\sqrt{2\log\frac{1}{\epsilon}}\left(\sum\limits_{n=1}^{N}{\sigma_{n}^{2}}f_{n}(\textbf{p})^{2}\right)^{\frac{1}{2}}\geq 0, \end{array} $$
(6)

where \(-1\leq \mu _{n}^{-}\leq \mu _{n}^{+}\leq 1\) and σ n ≥0, n∈{0,1,...,N} are constants that depend on the given families of probability distributions.

In the preceding discussion, we analyze the distributed robust power control problem in cognitive radio networks when the interference links’ channel gains are uncertain. For CR users, the influence of the channel gains g i between primary transmitter (PU-Tx) and cognitive receiver (CR-Rxs) is small, so, the uncertainty of channel gains g i can be neglected.

We denote that the uncertain channel gains form the CR-Tx of link i to the PU-Rx as \(h_{i}=\bar {h_{i}}+\hat {h_{i}}\), where \(\bar {h_{i}}\) is the nominal value, and \(\hat {h_{i}}\) is the perturbation part. We assume \(\hat {h_{i}}\) belongs to a general class of probability distribution, and is bounded in \(\hat {h_{i}}\in [-\varphi _{i},\varphi _{i}]\). For simplicity, \(\varphi _{i}=\varrho \bar {h_{i}}\), ϱ has a bonded support of [-1,1], which is consistent with assumption 3). So, h i can be rewritten as \(h_{i}=\bar {h_{i}}\pm \varrho \bar {h_{i}}\). h i is independent of each other and the probability distribution for all channels are same. Under above assumptions, we let \(f_{0}(p)=\sum \limits _{i=1}^{N}\bar {h_{i}}p_{i}-I_{}\) and \(f_{n}(p)=\varrho \bar {h_{i}}p_{i}\) for all i∈N. Substituting the parameters into Eq. 6, the constraint (1) can be reformulated by the Bernstein approximations as

$$\begin{array}{@{}rcl@{}} \sum\limits_{i=1}^{N}\bar{h_{i}}p_{i}\,+\,\sum\limits_{i=1}^{N}u^{+}\varrho\bar{h_{i}}p_{i}\,+\,\sqrt{2\eta\ln\varepsilon^{-1}}\left(\sum\limits_{i=1}^{N}(\varrho\bar{h_{i}}p_{i})^{2}\right)^{\frac{1}{2}}\! \leq \! I. \end{array} $$
(7)

Similarly, for the uncertain channel gain G k i , we model it as \(G_{ki}=\bar {G_{ki}}+\hat {G_{ki}}\), where \(\bar {G_{ki}}\) is the estimated channel gain, and \(\hat {G_{ki}}\) is uncertain part. \(\hat {G_{ki}}\) belongs to a general class of probability distribution, and is bounded in \(\hat {G_{ki}}\in [-\epsilon _{ki},\epsilon _{ki}]\), \(\epsilon _{ki}=\delta \bar {G_{ki}}\) with δ∈[−1,1]. G k i is expressed by \(G_{ki}=\bar {G_{ki}}\pm \delta \bar {G_{ki}}\) and independent of each other. Now, let \(f_{0}(p)= \frac {p_{i}G_{ii}}{\hat {r_{i}}}-(N_{i}+\sum \limits _{k\neq i,k=1}^{N}p_{k}\bar {G_{ki}})\) and \(f_{n}(p)=\delta \bar {G_{ki}}p_{k}\) for all i∈N. They meet the three conditions of the Bernstein approximation. Then, we rewrite the constraint (2) by the Bernstein approximation as

$$\begin{array}{@{}rcl@{}} \frac{p_{i}G_{ii}}{\hat{r_{i}}}&-& \left(N_{i}+\sum\limits_{k\neq i,k=1}^{N}p_{k}\bar{G_{ki}}\right) - \sum\limits_{k\neq i}^{N}u^{+}\delta\bar{G_{ki}} p_{k}\\ &-&\sqrt{2\eta\ln\xi_{i}^{-1}} \left(\sum\limits_{k\neq i,k=1}^{N}(p_{k}\delta\bar{G_{ki}})^{2}\right)^{\frac{1}{2}}\geq 0, \end{array} $$
(8)

where u + and η depend on the probability distribution. In [17], three typical families of probability distribution are given. In this paper, we adopt the Case II in [17].

2.3 C. Standard interference function algorithm

With the outage probability constraint of cognitive users, we can obtain the optimal power by a distributed algorithm. The formula (8) is rewritten as

$$\begin{array}{@{}rcl@{}} && p_{i}\geq\frac{\hat{r_{i}}}{G_{ii}}\left[\left(N_{i}+(1+u^{+}\delta)\sum\limits_{k\neq i,k=1}^{N}p_{k}\bar{G_{ki}}\right) \right.\\ &&\left. + \sqrt{2\eta\ln\xi_{i}^{-1}}\left(\sum\limits_{k\neq i,k=1}^{N}(p_{k}\delta\bar{G_{ki}})^{2}\right)^{\frac{1}{2}}\right],(i=1,2,...,N) \\ \end{array} $$
(9)

The matrix form of the formula (8) is

$$\begin{array}{@{}rcl@{}} \textbf{p}\geq \textbf{I}(\textbf{p}) \end{array} $$
(10)

Denote vector p and I(p) as p=[p 1,p 2,...,p N ], I(p)=[I 1(p),I 2(p),...,I N (p)], where \(I_{i}(\textbf {p})=\frac {\hat {r_{i}}}{G_{ii}}[(N_{i}+(1+u^{+}\delta )\sum \limits _{k\neq i,k=1}^{N}p_{k}\bar {G_{ki}})+\beta _{i}(\sum \limits _{k\neq i,k=1}^{N}(p_{k}\bar {G_{ki}})^{2})^{\frac {1}{2}}],(i=1,2,...,N) \) and β=[β 1,β 2,...,β N ], \(\beta _{i}=\delta \sqrt {2\eta \ln \xi _{i}^{-1}}\). I(p) is a standard interference function, if it meets three conditions:

  • 1) positivity I(p)>0,

  • 2) monotonicity \(\textbf {p}^{\prime }>\textbf {p}\Rightarrow \textbf {I}(\textbf {p}^{\prime })> \textbf {I}(\textbf {p})\),

  • 3) scalability α I(p)>I(α p), which is investigated in [20].

Proposition 1

I(p) is a standard interference function.

Proof

1) positivity: It clear that I(p) > 0, since I i (p) is nonnegative.

2) monotonicity: When p′> p

$$\begin{array}{@{}rcl@{}} \textbf{I}(\textbf{p}^{\prime})-\textbf{I}(\textbf{p})&=&\frac{\hat{r_{i}}}{G_{ii}}\left[\left(N_{i}+(1+u^{+}\delta)\sum\limits_{k\neq i,k=1}^{N}p_{k}^{\prime}\bar{G_{ki}}\right) \right.\\ &+&\left. \beta_{i} \left(\sum\limits_{k\neq i,k=1}^{N}(p_{k}^{\prime}\bar{G_{ki}})^{2}\right)^{\frac{1}{2}}\right]\\ &-&\frac{\hat{r_{i}}}{G_{ii}}\left[\left(N_{i}+(1+u^{+}\delta)\sum\limits_{k\neq i,k=1}^{N}p_{k}\bar{G_{ki}}\right)\right.\\ &+&\left.\beta_{i} \left(\sum\limits_{k\neq i,k=1}^{N}(p_{k}\bar{G_{ki}})^{2}\right)^{\frac{1}{2}}\right]\\ &=&u^{+}\delta\sum\limits_{k\neq i,k=1}^{N} \left(p_{k}^{\prime}-p_{k}\right) \bar{G_{ki}}\\ &+&\beta_{i} \left[\left(\sum\limits_{k\neq i,k=1}^{N} \left(p_{k}^{\prime}\bar{G_{ki}}\right)^{2}\right)^{\frac{1}{2}} \right.\\ &-& \left.\left(\sum\limits_{k\neq i,k=1}^{N}(p_{k}\bar{G_{ki}})^{2}\right)^{\frac{1}{2}}\right]\geq0 \end{array} $$
(11)

3) scalability:

$$\begin{array}{@{}rcl@{}} \alpha\textbf{I}(\textbf{p})-\textbf{I}(\alpha \textbf{p})&=&\alpha\frac{\hat{r_{i}}}{G_{ii}}\left[\left(N_{i}+(1+u^{+}\delta)\sum\limits_{k\neq i,k=1}^{N}p_{k}\bar{G_{ki}}\right)\right.\\ &+&\left. \beta_{i}(\sum\limits_{k\neq i,k=1}^{N}(p_{k}\bar{G_{ki}})^{2})^{\frac{1}{2}}\right]\\ &-&\frac{\hat{r_{i}}}{G_{ii}}\left[\left(N_{i}+(1+u^{+}\delta)\sum\limits_{k\neq i,k=1}^{N}\alpha p_{k}\bar{G_{ki}}\right)\right.\\ &+&\left. \beta_{i}\left(\sum\limits_{k\neq i,k=1}^{N}(p_{k}\bar{G_{ki}})^{2}\right)^{\frac{1}{2}}\right] \\ &=&(\alpha-1)\frac{\hat{r_{i}}}{G_{ii}}N_{i} \end{array} $$
(12)

Since α > 1, we have α I(p) > I(α p) □

In conclusion, we know that I(p) is a standard interference function. Hence, the iterative distributed algorithm is presented to get optimal power allocation with the outage probability constraint of CR users. The power control iterative algorithm converges to the fixed point, which is unique. The power-update rule is

$$\begin{array}{@{}rcl@{}} \textbf{p}(t+1)=\textbf{I}(\textbf{p}(t)), \end{array} $$
(13)

where t is the iteration number. the power updates for the i th CR user can be summarized as

$$\begin{array}{@{}rcl@{}} p_{i}(t+1)&=&\frac{\hat{r_{i}}}{G_{ii}}\left[\left(N_{i}+(1+u^{+}\delta)\sum\limits_{k\neq i,k=1}^{N}p_{k}(t)\bar{G_{ki}}\right) \right. \\ &+&\left. \sqrt{2\eta\ln\xi_{i}^{-1}}\left(\sum\limits_{k\neq i,k=1}^{N}(p_{k}(t)\delta\bar{G_{ki}})^{2}\right)^{\frac{1}{2}}\right]. \end{array} $$
(14)

By taking the minimum and maximum power constraints into consideration, CR user i updates its power level by

$$\begin{array}{@{}rcl@{}} p_{i}(t+1)&=&\min\left\{\left[\frac{\hat{r_{i}}}{G_{ii}}\left[\left(N_{i}+(1+u^{+}\delta)\sum\limits_{k\neq i,k=1}^{N}p_{k}\bar{G_{ki}}\right)\right.\right.\right.\\ &+&\left.\left.\left.\sqrt{2\eta\ln\xi_{i}^{-1}}(\sum\limits_{k\neq i,k=1}^{N}(p_{k}\delta\bar{G_{ki}})^{2})^{\frac{1}{2}}\right]\right]^{+},p_{i}^{\max}\right\}\\ \end{array} $$
(15)

where [x]+=max (0,x).

2.4 D. Power iteration process and admission control

Now, we take the constraint (1) into consideration. the interference threshold that PU can tolerate is set to I. Based on the inequality (1), the aggregate interference obtained by the optimal power allocation from all CR users should be no greater than ε. Mathematically, this can be written as

$$\begin{array}{@{}rcl@{}} Pr\left\{\sum\limits_{i=1}^{N}h_{i}p_{i}^{\ast}\geq I\right\}\leq \varepsilon. \end{array} $$
(16)

It is transformed into a deterministic setting by Bernstein’s approximation as

$$\begin{array}{@{}rcl@{}} I^{\ast}\leq I, \end{array} $$
(17)

where \(I^{\ast }=\sum \limits _{i=1}^{N}(1+u^{+})\varrho \bar {h_{i}}p_{i}^{\ast } +\sqrt {2\eta \ln \varepsilon ^{-1}}(\sum \limits _{i=1}^{N}(\varrho \bar {h_{i}}p_{i}^{\ast })^{\frac {1}{2}}\). \(p_{i}^{\ast }\) is the optimal power obtained from the standard interference function algorithm.

When we take into account the constraint (1), the interference I ∗ caused by all CR users may be beyond the interference threshold. In this case, the power of CR users should be readjusted. The process is as follows: Firstly, the PU users set the threshold I and the initial maximum power \(\textbf {p}_{\max }^{(1)}\) for all CR users, where \(\textbf {p}_{\max }^{(1)}=\{p_{1, \max }^{(1)}, p_{2,\max }^{(1)},..., p_{N,\max }^{(1)}\}\) and we assume \(p_{1,\max }^{(1)}=p_{2,\max }^{(1)}=...=p_{N,\max }^{(1)}\). Secondly, the optimal power vector \(\textbf {p}^{(n)^{\ast }}=\{p_{1}^{(n)^{\ast }},p_{2}^{(n)^{\ast }},...,p_{N}^{(n)^{\ast }}\}\) is updated by the standard interference function algorithm. With \(p_{i}^{(n)^{\ast }}\), the value of I ∗ at the PU-Rx is calculated. Finally, the PU-Rx judges whether I ∗ surpasses its threshold I. If I ∗ is greater than I, the CR users maximum power is adjusted to decrease the interference to PU users, i,e., \(\textbf {p}_{\max }^{(n+1)}=\textbf {p}_{\max }^{(n)}-{\Delta } \textbf {p}\) with pre-specified Δp and the system goes to next adaption. Otherwise, the optimal power is \(p_{i}^{(n)^{\ast }}\).

Under the above analysis, we give the following algorithm to achieve the optimal power of problem to satisfy the outage probability constraint of all CR users and PU users.

Remark 1

The algorithm presented in our work only requires limited amount of signal to be exchanged among the CRs and the PUs. In Algorithm 1, the power updates of the CRs can be executed in a distributed manner, based on the information available at local links. On one hand, each CR-Rx of link i can estimate G i i and h i , for instance, exploiting the pilot channel. On the other hand, the CR-Rx can also measure the total received power, and then subtract its own received power to obtain the aggregated interference I i (p −i ), i.e., \(I_{i}(\textbf {p}_{-i})=\sum p_{j}G_{ij}-p_{i}G_{ii}\) assuming that noise can be ignored. When the optimal transmission power is obtained, the CR-Rx transmits it to the PU-Rxs through the backhaul channel. Then, the PU-Rxs calculate their total interference based on the optimal power of all CR users, and decide whether adapt the maximum power constraint or not. The control information is transmitted to each CR-Tx through the backhaul channel.

figure f

From the above scheme, the optimal SINR \(r_{i}^{\ast }=\frac {p_{i}^{\ast }G_{ii}}{\sum \limits _{k\neq i, k=1}^{N}(1+\delta )\bar {G_{ki}}p_{k}^{\ast }+N_{i}}\) can be obtained after determining the optimal power \(p_{i}^{\ast }\) of cognitive user i.

It is natural to realize that the obtained \(r_{i}^{\ast }\) may be below the minimum SINR \(\hat {r_{i}}\) for the outage probability constraint with the uncertainty channel gains. So, we can remove the CR uesrs whose optimal SINR is smaller than the target SINR. By the application of admission control, the inferior CR users are removed to improve the admitted CR users performance and also make full use of the limited network resources.

The admission control is implement as follows:

  • (1) Based on CRs optimal SINRs \(r_{i}^{\ast }\) obtained from Algorithm 1, each CR user compares its optimal SINR with the target SINR \(\hat {r_{i}}\).

  • (2) If \(r_{i}^{\ast }< \hat {r_{i}}\), the CR-Tx sends a request for terminating transmission to the CR-Rx of link i, otherwise, the CR-Tx sends the request for transmission.

  • (3) The admitted CR users recalculate the optimal SINRs.

The following Algorithm is the admission control in detail.

figure g

3 Simulation results and performance analysis

In this section, we provide simulation results to examine the convergence and effectiveness of the proposed robust power control algorithm. The PU-Rx is located at the center of the area of 1000m×1000m rectangle, and both the CR-Txs and CR-Rxs are randomly located in primary user’s coverage area. It is assumed that channel gains follow a path loss model, which is relevant with the distance. The channel gain models are independent of each other. Set I=10−6W, \(\hat {r_{i}}=9.5\)dB, \(p_{i,\max }=0.5\)W and N i =10−8W for all CR users.

First, we show the convergence of the proposed robust power control algorithm. We consider the situation that there are N(N=25) cognitive links. The parameters of uncertain channel gains are set as δ=ϱ=0.01, and the bound of outage probability are ε=ξ i =0.01. Fig. 2 shows the power allocation convergence of CR users under the proposed power update rule.

Fig. 2
figure 2

The power convergence of CR users

Full size image

Next, the effectiveness of admission control is shown in Figs. 3 and 4. From Fig. 3, we can clearly see that the CR user 6 and user 9 can not meet the target SINR. When we introduce the admission control, all of the rest CR users SINR can satisfy the target SINR and are greater than that without admission control. Since, the interference \(I_{_{i}}(\textbf {p}_{-i})\) from other CR users decreases if some CR users drop out. This proves that the admission control is effective. When the uncertainty sets of channel gains from CR-Txs to PU-Rx and the outage probability of all CR users are fixed, i.e., for ϱ=0.01,ε=ξ i =0.01, we present CR users’ average SINR with and without admission control, respectively in Fig. 4. It is clear that the average SINR is larger than the target SINR with the admission control for small values of δ. This strongly proves the admission control scheme can improve the average SINR of the CR users.

Fig. 3
figure 3

The comparison of the SINRs of CR users

Full size image
Fig. 4
figure 4

Average SINR of CR users versus δ with and without admission control

Full size image

Then, we investigate the average power of CR users for different values of ξ and δ. In Fig. 5, with the increasing of δ, the average transmitted power of CR users increases. The reason is that for larger value of δ, it needs more power to meet the the outage probability constraints of all CR users. With same δ, the average power decreases with increasing of ξ, as we relax the SINR requirements of CR users.

Fig. 5
figure 5

The average power of CR users versus δ

Full size image

Figure 6 shows the robust power control approach’s impact on the maximum transmitted power of CR users. We can find that, as the values of ϱ increases, the maximum transmitted power of CR users decreases. It is due to the channel gains uncertain, the maximum transmitted power should be decreased in order to reducing the primary users’ interference power caused by CR-Txs. Because the outage probability constraint is strict, the maximum transmitted power will be smaller for a smaller value ε.

Fig. 6
figure 6

The maximum transmitted power of CR users versus ε

Full size image

Next we evaluate the performance of outage probability with uncertain channel gains. The parameters are set as follows, N=5, ρ=0.4, ε and ξ i are same. The outage probability of PU and CR users are shown in Fig. 7. It can be seen that all outage probabilities of users are below the given threshold.

Fig. 7
figure 7

The outage probability of all users

Full size image

4 Conclusions

In this paper, we propose a robust power control algorithm for CRs network by considering CR users’ energy efficiency. In order to guarantee the QoS of the CR users, the outage probability is introduced by considering uncertain channel gains. Also, for interference suppression, we maintain the outage probability of PU users below a predefined threshold. The chance constraint robust approach is formulated, and a distributed power control algorithm is introduced to find CR users’ optimal power. The admission control algorithm is adopted to effectively improve CR users’ performance. However, in reality, there are other uncertain parameters such as the channel gains between PU-Tx and CR-Rx, between PU-Tx and PU-Rx, which may cause that the cognitive users’ target SINRs are violated and PUs fail to connect the network. So, the future work is to solve the power control problem under such circumstances.