1 Introduction

The demand for the spectrum resource has increased with the emergence of various wireless services in recent years. A number of studies show that spectrum is used inefficiently both in space and time. Hence, Cognitive Radios (CRs) has been considered as a very promising technology to improve the unsatisfied spectrum utilization [1]. To mitigate the scarcity of spectral resources, one way is that CR users use the same frequency spectrum allocated to primary users, as long as the CR users do not cause unacceptable interference to primary users (PUs) in an underlay scenario [2,3,4]. Therefore, in the underlay scenario, the challenge is how to maximize CR users’ sum-utility while keeping the condition on interference to PUs. Much research efforts have been devoted to the problem of power allocation to the CR users [5, 6]. Most of the existing works depend on the assumption that the constraints and objective function of the optimization problem can be obtained precisely. However, in practical situations, for the reason that PUs do not have the obligation to provide any information to CR users, the dynamic information of channel status is difficult to obtain. In Ref. [7], with the assumption that the statistics of channel gains between transmitter of CR users and receiver of PUs are known, a power control approach is proposed to maximize the ergodic capacity of the CR users links. Due to the imperfect channel information, the situation, where only partial Channel State Information (CSI) is available to the CR users, is considered and the CR users’ outage capacity is investigated in Ref. [8].

Robust optimization is an emerging methodology for dealing with the optimization problems, which takes the non-stochastic “uncertain-but-bounded” parameter perturbations into account. The basic idea is that the optimization problem remains feasible with the parameter perturbations. Robust optimization research needs to seek a proper set to describe the uncertain parameters and keeps the robust problems are still convex optimization problems. There are some models to describe uncertain parameters, for example, general polyhedron, D-norm and ellipsoid. These models are applied to solve rate control problem in wireless networks in Ref. [9].

Most of the existing works addressing the application of robust optimization into cognitive radio networks concentrate on the robust beamforming design [10,11,12,13]. In Ref. [11], the authors design robust and distributed power control algorithm in wireless communications. The worst case robust optimization algorithm is proposed in Ref. [12] for minimizing the total transmitted power of users, which keeps the Signal-to-Interference noise ratio (SINR) of CR user receiver above the desired threshold with the uncertainty of channel gains. To tackle uncertainty, the researchers also use the Bayesian approach in wireless networks [14, 15]. The main idea of Bayesian approach and the worst case robust optimization method is to convert the uncertain parameters into the certain ones. When the optimization problem contain uncertain parameters, they are satisfied statistically in the Bayesian approach [16]. Due to the fact that the parameter variations are stochastic, the worst case robust method, although which is conservative, is more benefit of PUs to make PUs interference threshold within the given region for any uncertainty [17]. In Ref. [18], the worst case robust algorithm is applied, which is at cost of CR users’ sum-utility. Therefore, D-norm robust algorithm as a tradeoff mechanism between the robustness and CR users’ sum-utility is proposed. In this paper, we relax the constraint conditions, i.e., keeping the outage probability of all CR users and PUs below a given threshold. Then, the chance-constraint robust approach is adopted to overcome the uncertain channel gains. The feasible region of the optimal problem with chance-constraint robust approach is better than that of the worst case robust approach. Also, the chance-constraint approach is superior to D-norm approach for both CR users and PUs’ perspective.

The rest of this paper is organized as follows. Section 2 introduces the system model and robust problem formulation. The distributed robust power allocation algorithm based on Lagrange dual decomposition is presented in Section 3. Section 4 contains sensitivity analysis and simulations to demonstrate the performance of the proposed power control schemes. Finally, section V makes the concluding remarks.

2 System model and problem formulation

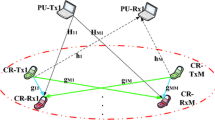
Considering a cognitive radio network as shown in Fig. 1, there is no central control node and there are N CR user links and one PU links, where the users are distributed randomly. We investigate the scenario in the underlay where all CR users can share the same frequency resource with PU under the constraint that the total interference generated by cognitive users does not exceed a threshold that PU-Rx can tolerate.

Fig. 1
figure 1

A cognitive radio network is composed of N CR links and one PU link

Full size image

The Signal-to-Interference-Noise-Ratio (SINR) of the ith CR user receiver (CR-Rx) is

$$\begin{array}{@{}rcl@{}} r_{i}=\frac{p_{i}G_{ii}}{{\sum}_{k\neq i,k = 1}^{N}p_{k}G_{ki}+\sigma^{2}+p_{o}g_{i}}. \end{array} $$
(1)

where \(p_{i}\in [p_{i}^{\min }, p_{i}^{\max }]\) denotes the transmitted power of CR user transmitters (CR-Txs) of link i(i = 1,2,...,N), \(p_{i}^{\min }\) and \(p_{i}^{\max }\) are the minimum and the maximum transmitted power of CR user transmitter (CR-Tx) of link i, respectively. gi represents the channel gain from the PU transmitter (PU-Tx) to the ith CR-Rx, and the channel gains from the ith CR-Tx to the ith CR-Rx and from the kth CR-Tx to the ith CR-Tx are denoted as Gii and Gki, respectively. Besides, the transmitted power of the PU-Tx is p0. We further assume that the background noise at the CR-Rxs of all links are σ2. For simplify, the SINR of each CR-Rx can be rewritten as:

$$\begin{array}{@{}rcl@{}} r_{i}=\frac{p_{i}}{{\sum}_{k\neq i,k = 1}^{N}p_{k}F_{ki}+\frac{N_{i}}{G_{ii}}}. \end{array} $$
(2)

where Ni denotes the interference caused by the PU-Tx and the noise at the ith CR-Rx, i.e., Ni = σ2 + pogi, F = [F1i,...,FNi] is the gain vector of cognitive users with

$$\begin{array}{@{}rcl@{}} &&\hspace{0.5cm}F_{ki}=\left\{\begin{array}{ccc} \frac{G_{ki}}{G_{ii}},& i\neq k,\\ 0, & i=k. \end{array} \right. \end{array} $$

So as to guarantee the QoS requirements of cognitive users with the uncertainty of channel gains, the outage probability of each CR-Rx doesn’t exceed the predefined level ζi.

$$\begin{array}{@{}rcl@{}} Pr\left\{r_{i}\leq \hat{r_{i}}\right\}\leq \zeta_{i},\quad\forall i. \end{array} $$
(3)

where \(\hat {r_{i}}\) is the desired SINR of user i.

Also, the QoS requirements of the PU should be satisfied under the uncertainty of channel gains, i.e, the probability of violating the interference threshold doesn’t exceed a predefined value ξ.

$$\begin{array}{@{}rcl@{}} Pr\left\{\sum\limits_{i = 1}^{N}h_{i}p_{i}\geq I\right\}\leq\xi. \end{array} $$
(4)

where hi denotes the channel gain from the CR-Tx of link i to the PU-Rx. I is the interference threshold at PU-Rx.

Denote ui(ri) as the utility function of the ith CR user, which will be illustrated in next subsection in detail. With the con0straints (3) and (4), we formulate the power control allocation framework that aims at maximizing the sum-utility of CR users. Mathematically, the optimization problem can be formulated as follows:

$$\begin{array}{@{}rcl@{}} && \max\limits_{p_{i}^{\min}\leq p_{i}\leq p_{i}^{\max}} \sum\limits_{i = 1}^{N} u_{i}(r_{i})\\ &&\qquad\ s.t.\ \left\{\begin{array}{ccc} C1 &Pr(r_{i}\leq \hat{r_{i}})\leq \zeta_{i}\quad\forall i.\\ C2 &Pr({\sum}_{i = 1}^{N}p_{i}h_{i}\geq I)\leq\xi \end{array} \right. \end{array} $$
(5)

2.1 Chance-constraint robust algorithm

In our problem formulation, uncertainties are considered which are related to interference channel gains from CR-TXs to PU-RX (i.e., hi), and from one CR-TX to other CR-RX (i.e., Gki). From the formula (1), we know the influence of the channel gains gi from PU-Tx to CR-Rx of link i is small, so, the uncertainty of channel gains gi can be neglected. To track such uncertainties, we use the Bernstein’s approximation of chance-constraint affine function to derive optimal problem (5) to a deterministic formulation.

We suppose that the channel gain Gki is uncertain, so Fki also is uncertain and it can be modeled by \(F_{ki}=\bar {F_{ki}}+\hat {F_{ki}}\), where \(\bar {F_{ki}}\) is the estimated channel gain, and \(\hat {F_{ki}}\) is uncertain part. \(\hat {F_{ki}}\) belongs to a general class of probability distribution, and is bounded in \(\hat {F_{ki}}\in [-\epsilon _{ki}, \epsilon _{ki}]\), \(\epsilon _{ki}=\alpha _{ki}\bar {F_{ki}}\) with αki ∈ [− 1, 1]. Fki can be expressed by \(F_{ki}\in [\bar {F_{ki}}- \alpha _{ki}\bar {F_{ki}}, \bar {F_{ki}}+ \alpha _{ki}\bar {F_{ki}}]\) and they are independent.

Referring to [19], the following lemma is introduced based on Bernstein approximations.

Lemma 1

Consider a chance constraint of the form of

$$\begin{array}{@{}rcl@{}} Pr \left\{ {f_{0}(y)+\sum\limits_{i = 1}^{n}\zeta_{i} f_{i}(y)\leq0} \right\} \geq 1-\varepsilon, \end{array} $$

where ζi is the random variable and it is known to vary in the range [− 1, 1]. Then for every ε ∈ (0, 1), the above probability constraint can be converted to the following approximation of the chance constraint with variable substitution and appropriately chosen parameter \(-1\leq \mu _{i}^{-}\leq \mu _{i}^{+}\leq 1, \sigma \geq 0\).

$$\begin{array}{@{}rcl@{}} &&{} f_{0}(y)+\sum\limits_{i = 1}^{n}|z_{i}|+\sum\limits_{i = 1}^{n}\max[\mu^{-} w_{i},\mu^{+}w_{i}]\,+\,\sqrt{2\ln{(1/\varepsilon)}}\left( \sum\limits_{i = 1}^{n}{\sigma_{i}^{2}} {w_{i}^{2}}\right)^{1/2}\\ &&{}f_{i}(y)=z_{i}+w_{i}, i = 1,...,n \end{array} $$

Then, we can get the following theorem.

Theorem 1

The outage probability constraint (3) can be reformulated by the following affine function:

$$\begin{array}{@{}rcl@{}} \frac{{\sum}_{k\neq i,k = 1}^{N}\bar{F_{ki}}p_{k}+{\sum}_{k\neq i}^{N}u^{+}\hat{F_{ki}}p_{k}+ \sqrt{2\sigma^{2}\ln\zeta_{i}^{-1}}({\sum}_{k\neq i,k = 1}^{N}(\hat{F_{ki}}p_{k})^{2})^{\frac{1}{2}} +\frac{N_{i}}{G_{ii}}}{p_{i}}\leq\frac{1}{\hat{r_{i}}}\quad\forall i. \end{array} $$
(6)

Proof

Comparing with the formula of uncertain channel gain mentioned above, it is found that the formulated problem satisfies the conditions of the Bernstein approximations in lemma 1. The probability constraint (3) is equivalent to the following formula,

$$\begin{array}{@{}rcl@{}}Pr\left\{r_{i}\leq \hat{r_{i}}\right\}\geq 1-\zeta_{i},\quad\forall i. \end{array} $$

Considering \(r_{i}=\frac {p_{i}}{{\sum }_{k\neq i,k = 1}^{N}p_{k}F_{ki}+\frac {N_{i}}{G_{ii}}}\), \(F_{ki}=\bar {F_{ki}}+\hat {F_{ki}}\) and \(\hat {F_{ki}}\in [-\epsilon _{ki}, \epsilon _{ki}]\), \(\epsilon _{ki}=\alpha _{ki}\bar {F_{ki}}\) with αki ∈ [− 1, 1], we can get the following expression according to the lemma 1.

$$\begin{array}{@{}rcl@{}} \frac{N_{i}}{G_{ii}}-\frac{p_{i}}{\hat{r_{i}}}&&\,+\,\sum\limits_{k\neq i,k = 1}^{N}\bar{F_{ki}}p_{k}\\&&+\sum\limits_{k\neq i}^{N}\max{[u^{-}\hat{F_{ki}}p_{k},u^{+}\hat{F_{ki}}p_{k}]}\\&&\!+ \sqrt{2\sigma^{2}\ln\zeta_{i}^{-1}}\left( {\sum}_{k\neq i,k = 1}^{N}(\hat{F_{ki}}p_{k})^{2}\right)^{\frac{1}{2}} \!\leq\!0 \quad\forall i. \end{array} $$

Also, with the parameter \(-1\leq \mu _{i}^{-}\leq \mu _{i}^{+}\leq 1, \sigma \geq 0, \hat {F_{ki}}p_{k} \geq 0\), we get

$$\begin{array}{@{}rcl@{}} \frac{N_{i}}{G_{ii}}-\frac{p_{i}}{\hat{r_{i}}}&&+\sum\limits_{k\neq i,k = 1}^{N}\bar{F_{ki}}p_{k}+\sum\limits_{k\neq i}^{N}u^{+}\hat{F_{ki}}p_{k}\\&&+ \sqrt{2\sigma^{2}\ln\zeta_{i}^{-1}}\left( \sum\limits_{k\neq i,k = 1}^{N}(\hat{F_{ki}}p_{k})^{2}\right)^{\frac{1}{2}} \leq0 \quad\forall i, \end{array} $$

which is equivalent to Eq. 6, where u+ is bounded parameter satisfying 0 < u+ ≤ 1, and the typical upper bound is 1 and \(1/\sqrt {2}\) [19].

The proof is finished. □

In further, referring to the ref. [19], we also have the following conclusion, which is not proved duo to the limited space. If 0 < ζi < 1, another deterministic setting of Eq. 3 is

$$\begin{array}{@{}rcl@{}} \frac{{\sum}_{k\neq i,k = 1}^{N}\bar{F_{ki}}p_{k}+{\sum}_{k\neq i}^{N}u^{+}\hat{F_{ki}}p_{k}+ \sqrt{2N\sigma^{2}\ln\zeta_{i}^{-1}}\max(\hat{F_{ki}}p_{k}) +\frac{N_{i}}{G_{ii}}}{p_{i}}\leq\frac{1}{\hat{r_{i}}}\quad\forall i. \end{array} $$
(7)

Similarly, we also consider that the uncertain channel gains from the CR-Tx of link i to the PU-Rx as \(h_{i}=\bar {h_{i}}+\hat {h_{i}}\), where \(\bar {h_{i}}\) is the nominal value, and \(\hat {h_{i}}\) is the perturbation part. We assume \(\hat {h_{i}}\) belongs to a general class of probability distribution, and is bounded in \(\hat {h_{i}}\in [-\varphi _{i},\varphi _{i}]\). For simplicity, \(\varphi _{i}=\beta _{i}\bar {h_{i}}\), βi has a bonded support of [-1, 1]. So, hi can be rewritten as \(h_{i}\in [\bar {h_{i}}-\beta _{i}{\bar {h_{i}}}, \bar {h_{i}}+\beta _{i}{\bar {h_{i}}}]\). hi is independent of each other and the probability distribution for all channels are the same. Thus, outage constraint (4) can be reformulated by the following affine function:

$$\begin{array}{@{}rcl@{}} \sum\limits_{i = 1}^{N}p_{i}\bar{h_{i}}+\sum\limits_{i = 1}^{N}u^{+}\hat{h_{i}}p_{i} +\sqrt{2\sigma^{2}\ln\xi^{-1}}\left( \sum\limits_{i = 1}^{N}(\hat{h_{i}}p_{i})^{2}\right)^{\frac{1}{2}}\leq I. \end{array} $$
(8)

If 0 < ξ < 1, another deterministic setting of Eq. 4 is

$$\begin{array}{@{}rcl@{}} \sum\limits_{i = 1}^{N}p_{i}\bar{h_{i}}+\sum\limits_{i = 1}^{N}u^{+}\hat{h_{i}}p_{i} +\sqrt{2N\sigma^{2}\ln\xi^{-1}}\max(\hat{h_{i}}p_{i}))\leq I. \end{array} $$
(9)

where u+ and η depend on the probability distribution and they are presented in Ref. [19] for typical families of probability distribution.

With the formula (6) and (8), the optimal problem (5) is called the chance-constraint problem I, while optimal problem (5) under the formula (7) and (9), is called the chance-constraint problem II. Due to limited space, we focus on the chance-constraint problem I. It is noted that the solving process of two optimization problems are similar. The robust counterpart of optimization problem (5) by Bernstein approximations of chance constraints is

$$\begin{array}{@{}rcl@{}} && \max\limits_{p_{i}^{\min}\leq p_{i}\leq p_{i}^{\max}} \sum\limits_{i = 1}^{N} u_{i}(r_{i})\\ &&\quad s.t.\ \left\{ \begin{array}{lll} C1 &\frac{{\sum}_{k\neq i,k = 1}^{N}\bar{F_{ki}}p_{k}+{\sum}_{k\neq i}^{N}u^{+}\hat{F_{ki}}p_{k}+ \sqrt{2\sigma^{2}\ln\zeta_{i}^{-1}}({\sum}_{k\neq i,k = 1}^{N}(\hat{F_{ki}}p_{k})^{2})^{\frac{1}{2}}+\frac{N_{i}}{G_{ii}}}{p_{i}}\leq\frac{1}{\hat{r_{i}}}\quad\forall i.\\ C2 &{\sum}_{i = 1}^{N}p_{i}\bar{h_{i}}+{\sum}_{i = 1}^{N}u^{+}\hat{h_{i}}p_{i} +\sqrt{2\sigma^{2}\ln\xi^{-1}}({\sum}_{i = 1}^{N}(\hat{h_{i}}p_{i})^{2})^{\frac{1}{2}}\leq I \end{array} \right. \end{array} $$
(10)

Since the parameters of optimization problem (10) are certain, the problem (5) is solvable. Compared with problem (5), problem (10) has the protection function against uncertain channel gains. From Eqs. 6 and 8, we can see the protection values for uncertainty of Fki and hi are

$$\begin{array}{@{}rcl@{}} {\Delta}_{i}\,=\,\sum\limits_{k\neq i,k = 1}^{N}u^{+}\hat{F_{ki}}p_{k}\,+\, \sqrt{2\sigma^{2}\ln\zeta_{i}^{-1}}\left( \sum\limits_{k\neq i,k = 1}^{N}(\hat{F_{ki}}p_{k})^{2}\right)^{\frac{1}{2}}, \end{array} $$
(11)

and

$$\begin{array}{@{}rcl@{}} {\Delta}=\sum\limits_{i = 1}^{N}u^{+}\hat{h_{i}}p_{i} +\sqrt{2\sigma^{2}\ln\xi^{-1}}\left( \sum\limits_{i = 1}^{N}(\hat{h_{i}}p_{i})^{2}\right)^{\frac{1}{2}}. \end{array} $$
(12)

It can be found that the robustness against uncertain channel gain depends on both the uncertain boundary and the outage threshold. Moreover, the parameter u+, which is determined according to the probability distribution of uncertainties, also affects the ability of protection.

2.2 The changing of convex problems

We can find that Eqs. 6 and 8 are second order cone programming (SOCP) problems, which belong to convex optimization. But, generally speaking, the problem (10) is non-convex in pi if the selection of {ui(⋅)} is inappropriate and hence difficult to solve. According to the methods in Ref. [20], to solve (10) efficiently, the {ui(⋅)} should be chosen to simultaneously satisfy the following two conditions:

  • (a) {ui(⋅)} is strictly increasing and twice continuously differentiable over (0,∞).

  • (b) \(-r_{i}u_{i}^{\prime \prime }(r_{i})/u_{i}^{\prime }(r_{i})\geq 1\) (indicates differentiation).

Considering the above conditions, let wi is the bandwidth for user i, the utility function of user i is chosen as

$$\begin{array}{@{}rcl@{}} u_{i}(r_{i})=w_{i}\ln r_{i}. \end{array} $$
(13)

which can indicate the achievable rate of user.

Now, the suitable relaxation of problem (10) is introduced to make the problem be the convex problem, which is easy to obtain the optimization solution. An auxiliary variable qi is introduced associated with the link i, upper-bounding the ratio between interference at CR-Rx and the channel gain Gii. Then, the problem (10) can be rewritten as

$$\begin{array}{@{}rcl@{}} &&\hspace{0.5cm} \max\limits_{p_{i}^{\min}\leq p_{i}\leq p_{i}^{\max}} \sum\limits_{i = 1}^{N} u_{i}(p_{i}q_{i}^{-1})\\ &&\hspace{0.5cm}s.t.\ \left\{ \small\begin{array}{lll} C1: \ q_{i}\hat{r_{i}}\leq p_{i}\\ C2:\ {\sum}_{k\neq i,k = 1}^{N}p_{k}\bar{F_{ki}}+\frac{N_{i}}{G_{ii}}+{\sum}_{k\neq i,k = 1}^{N}u^{+}\hat{F_{ki}}p_{k}+ \sqrt{2\sigma^{2}\ln\zeta_{i}^{-1}}({\sum}_{k\neq i,k = 1}^{N}(\hat{F_{ki}}p_{k})^{2})^{\frac{1}{2}}+\frac{N_{i}}{G_{ii}}\leq q_{i}.\\ C3:\ {\sum}_{i = 1}^{N}\bar{h_{i}}p_{i}+{\sum}_{i = 1}^{N}u^{+}\hat{h_{i}}p_{i} +\sqrt{2\sigma^{2}\ln\xi^{-1}}({\sum}_{i = 1}^{N}(\hat{h_{i}}p_{i})^{2})^{\frac{1}{2}}\leq I \end{array} \right. \end{array} $$
(14)

Clearly, if the left-hand side and right-hand side of constraint C2 are equivalent, Eq. 14 is equivalent to Eq. 10. Even if the optimality of the relaxation is established, the solution of Eq. 14 is also a solution of Eq. 10. However, to make the problem (14) be efficiently solvable, the problem (14) is converted to a convex optimization by applying the one-to-one change of variables \(p_{i}=e^{y_{i}}\) and \(q_{i}=e^{z_{i}}\). The transformed constraints are convex in y = [y1,...,yN] and z = [z1,...,zN], since all left sides of the inequalities can be changed to the nonnegative sum of exponentials, which are concave functions [21]. So the objective function of Eq. 14 is also concave in y, z. Since the objective function is a nonnegative sum of \(u_{i}(e^{y_{i}-z_{i}})\) terms, it suffices for ui(ex) to meet both of (a) and (b) constrains. In conclusion, the problem (14) becomes a convex problems by variable substitution. Next, we can use the convex optimization and give the distributed power allocation algorithm based on the converted problem (14).

3 Robust distributed algorithm

In this section, we present the solution to the proposed robust power control problem in detail. Firstly, we investigate the robust power allocation problem feasible conditions.

The robust problem (14) is feasible, if and only if it satisfies the following conditions.

  1. (1)

    \(\|\bar {\textbf {M}}\|_{2}(1+\alpha u^{+}+\|\textbf {L}\|_{2})<1\), where \(\bar {\textbf {M}}\) is the N × N matrix, whose element \(M_{ki}=\hat {r_{i}}\bar {F_{ki}}\). Assume that the varies of all channel gains Fki are the same, i.e., αki = α, and \(\textbf {L}=[L_{1},L_{2},...,L_{N}], L_{i}=\sqrt {2\sigma ^{2}\alpha ^{2}\ln \zeta _{i}^{-1}}\).

  2. (2)

    p△≤pmax, where \(\textbf {p}^{\max }=[p_{1}^{\max },...,p_{N}^{\max }]\), and \(\textbf {p}_{\triangle }=(\textbf {I}-\bar {\textbf {M}})^{-1}(\textbf {v}+\textbf {k})\). The vector of v and k are expressed as \(\textbf {v}=[\frac {\hat {r_{1}}N_{i}}{G_{11}},...,\frac {\hat {r_{N}}N_{i}}{G_{NN}}]^{T}\), \(\textbf {k}=[\hat {r_{1}}{\Delta }_{1},...,\hat {r_{i}}{\Delta }_{i}]\), respectively.

  3. (3)

    \((1+u^{+}\beta )\bar {h_{i}}\textbf {p}_{\triangle }^{T}+\varepsilon \|\hat {h_{i}}\textbf {p}\|_{2}\leq \textbf {I}\), where \(\varepsilon =\sqrt {2\sigma ^{2}\beta ^{2}\ln \xi ^{-1}}\). Also, we assume that the varies of all channel gains hi are the same, i.e., βi = β.

The condition (1) and condition (2) implies that there exists a positive power vector \(\textbf {p}_{\triangle }=(\textbf {I}-\bar {\textbf {M}})^{-1}(\textbf {v}+\textbf {k})\), which satisfies the outage probability bound and the maximum transmitting power constraint of each CR user. If further, the condition (3) is holden, each CR user can increase their power by some factor, which decreases the outage probability for every CR user. Hence, there are another p△ ≤p∗≤pmax, which can meet all constraint conditions of problem (14), and maximize the objective function.

When the above conditions are satisfied, there will be a feasible power allocation for the CR users, otherwise, only a subset of the CR users can access to the networks. Because of convexity of the problem, transmitted power levels can be obtained by Lagrangian dual function as follows.

$$\begin{array}{@{}rcl@{}} &&\hspace{1.5cm}L(\lambda_{i},\nu_{j},\mu_{i},e^{z_{i}},e^{y_{i}})= -\sum\limits_{i = 1}^{N}u_{i}(e^{y_{i}-z_{i}})+\sum\limits_{i = 1}^{N}\lambda_{i}(\hat{r_{i}}e^{z_{i}-y_{i}}-1)\\ &&\hspace{1.5cm}+\sum\limits_{i = 1}^{N}\mu_{i}\left( e^{-z_{i}}\left( \sum\limits_{k\neq i,k = 1}^{N}e^{y_{k}}\bar{F_{ki}} +\frac{N_{i}}{G_{ii}}+\sum\limits_{k\neq i,k = 1}^{N}u^{+}\hat{F_{ki}}e^{y_{k}}+\sqrt{2\sigma^{2}\ln\zeta_{i}^{-1}}\left( {\sum}_{k\neq i,k = 1}^{N}(\hat{F_{ki}}e^{y_{k}})^{2}\right)^{\frac{1}{2}} \right) -1\right)\\ &&\hspace{1.5cm}+\nu\left( \frac{{\sum}_{i = 1}^{N}\bar{h_{i}}e^{y_{i}}+{\sum}_{i = 1}^{N}u^{+}\hat{h_{i}}e^{y_{i}} +\sqrt{2\sigma^{2}\ln\xi^{-1}}({\sum}_{i = 1}^{N}(\hat{h_{i}}e^{y_{i}})^{2})^{\frac{1}{2}}}{I}-1\right). \end{array} $$
(15)

where λi, μi, and ν are the Lagrangian multipliers for C1, C2, and C3 in Eq. 14, respectively. Problem (14) is solved via the following first-order algorithm that utilizes the subgradient of \(L(\lambda _{i},\nu _{j},\mu _{i},e^{z_{i}},e^{y_{i}})\) to simultaneously update the primal and dual variables. \(\beta _{y_{i}}\), \(\beta _{z_{i}}\), \(\beta _{\lambda _{i}}\), \(\beta _{\mu _{i}}\), βν are small step size for Lagrange multipliers. Let \(y_{i}^{\max }=\ln p_{i}^{\max }\), \(y_{i}^{\min }=\ln p_{i}^{\min }\), \([.]^{y_{i}^{\max }}_{y_{i}^{\min }}\) denotes the projection onto \([y_{i}^{\min },y_{i}^{\max }]\), and [x]+ = max{0,x}. Then, the algorithm converges to the optimal value at the optimal Lagrange multipliers by gradient projection iterations (indexed by t):

$$\begin{array}{@{}rcl@{}} y_{i}(t + 1)=\left[y_{i}(t)-\beta_{y_{i}}\frac{\partial L}{\partial y_{i}}\right]_{y_{i}^{\min}}^{y_{i}^{\max}}. \end{array} $$
(16)
$$\begin{array}{@{}rcl@{}} z_{i}(t + 1)=\left[z_{i}(t)-\beta_{z_{i}}\frac{\partial L}{\partial z_{i}}\right]^{+}. \end{array} $$
(17)
$$\begin{array}{@{}rcl@{}} \lambda_{i}(t + 1)=\left[\lambda_{i}(t)+\beta_{\lambda_{i}}(\hat{r_{i}}e^{z_{i}-y_{i}}-1)\right]^{+}. \end{array} $$
(18)
$$\begin{array}{@{}rcl@{}} \mu_{i}(t + 1)&=&[\mu_{i}(t)+\beta_{\mu_{i}}(e^{-z_{i}}(\sum\limits_{i = 1}^{N}\lambda_{i}(\hat{r_{i}}e^{z_{i}-y_{i}}-1)+\sum\limits_{i = 1}^{N}\mu_{i}(e^{-z_{i}}(\sum\limits_{k\neq i,k = 1}^{N}e^{y_{k}}\bar{F_{ki}} +\frac{N_{i}}{G_{ii}}+\sum\limits_{k\neq i,k = 1}^{N}u^{+}\hat{F_{ki}}e^{y_{k}}\\ &&+\sqrt{2\sigma^{2}\ln\zeta_{i}^{-1}}(\sum\limits_{k\neq i,k = 1}^{N}(\hat{F_{ki}}e^{y_{k}})^{2})^{\frac{1}{2}}) -1)]^{+}. \end{array} $$
(19)
$$\begin{array}{@{}rcl@{}} \nu(t + 1)=\left[\nu(t)+\beta_{\nu_{i}}\left( \frac{{\sum}_{i = 1}^{N}\bar{h_{i}}e^{y_{i}}+{\sum}_{i = 1}^{N}u^{+}\hat{h_{i}}e^{y_{i}} +\sqrt{2\sigma^{2}\ln\xi^{-1}}({\sum}_{i = 1}^{N}(\hat{h_{i}}e^{y_{i}})^{2})^{\frac{1}{2}}}{I}-1\right)\right]^{+}. \end{array} $$
(20)

Now, let the derivative of Lagrangian dual function with yi and zi be

$$\begin{array}{@{}rcl@{}} &&\partial L/\partial y_{i}=-u_{i}^{\prime}(e^{y_{i}-z_{i}})e^{y_{i}-z_{i}}-\lambda_{i}\hat{r_{i}}e^{z_{i}-y_{i}}+\frac{\nu}{I}\left( \bar{h_{i}}e^{y_{i}}+u^{+}\hat{h_{i}}e^{y_{i}}+\sqrt{2\sigma^{2}\ln\xi^{-1}}\frac{(\hat{h_{i}}e^{y_{i}})^{2}}{\sqrt{{\sum}_{i = 1}^{N}(\hat{h_{i}}e^{y_{i}})^{2}}}\right)\\ &&+\sum\limits_{k\neq i,k = 1}^{N}\mu_{k}e^{-z_{k}}\left( e^{y_{i}}\bar{F_{ik}}+u^{+}\hat{F_{ik}}e^{y_{i}}+\sqrt{2\sigma^{2}\ln\zeta_{k}^{-1}}\frac{(\hat{F_{ik}}e^{y_{i}})^{2}}{\sqrt{{\sum}_{i\neq k,i = 1}^{N}(\hat{F_{ik}}e^{y_{i}})^{2}}}\right). \end{array} $$
(21)
$$\begin{array}{@{}rcl@{}} &&\hspace{1cm}\partial L/\partial z=u_{i}^{\prime}(e^{y_{i}-z_{i}})e^{y_{i}-z_{i}}+\lambda_{i}\hat{r_{i}}e^{z_{i}-y_{i}}\\ &&\hspace{1cm}-\mu_{i}\left( e^{-z_{i}}\left( \sum\limits_{k\neq i,k = 1}^{N}e^{y_{k}}\bar{F_{ki}}+\frac{N_{i}}{G_{ii}} +\sum\limits_{k\neq i,k = 1}^{N}u^{+}\hat{F_{ki}}e^{y_{k}}+\sqrt{2\sigma^{2}\ln\zeta_{i}^{-1}}\left( \sum\limits_{k\neq i,k = 1}^{N}(\hat{F_{ki}}e^{y_{k}})^{2}\right)^{\frac{1}{2}}\right)\right). \end{array} $$
(22)

There are two global scalar variables denoted as \(w_{1}(t)=\sqrt {{\sum }_{i = 1} ^{N}e^{2y_{i}(t)}}\) and \(w_{2}(t)={\sum }_{i = 1}^{N}\mu _{i}e^{-z_{i}(t)}\bar {F_{ki}}\), respectively, which update both primal and dual local variables. The global dual variable ν is updated at the CR-Rxs, as it is needed to know all the values of CR-Txs’ power levels, channel gains hi, and I. To void large amount of information exchanging, distributed power control algorithm based on Lagrange dual decomposition is introduced as follows.

figure e

The uncertainties of channel gains involved in C2 and C3 of Eq. 14 affect the CR-Txs’ transmitted power levels in opposite tendency. On one hand, the CR-Txs’ transmitted power levels should be decreased to satisfy PU-Rx’ outage probability threshold because of the uncertainty in hi. On the other hand, they should be increased to meet the CR-Rxs’ outage probability constraint due to uncertainty in Fki. So there is tradeoff and balance. It is known the worst case approach, which increases the power levels in the presence of uncertainty, leads to increment of interference to primary user. And for a smaller value of violated constraint conditions, the robust problem may become infeasible. Moreover, in reality, the worst case scenario is not realized all the time, which forces all CR users to consume more power, and that may result in excessive energy consumption. Therefore, to moderate the worst-case effect, one of suitable schemes to overcome uncertainty is D-norm approach proposed in Ref. [18]. In this paper, we propose the chance-constraint approach, and compare performance with D-norm approach and worst-case approach with the same objective of maximizing sum-utility of CR users in the next section.

4 Simulation results

We provide simulation results to examine the convergence and effectiveness of the proposed robust power control algorithms, and compare the performance of different robust power control algorithms. Assume that there are three cognitive links and one primary link, where they are distributed randomly. Some parameters used in the simulations as set as follows, I = 2.5 × 10− 3, \(\hat {r_{i}}= 18\), wi = 1 and Ni = 10− 4W.

First, we examine the convergence of the proposed chance-constraint robust power control algorithm. Figure 2 shows the convergence of the powers and Lagrangian multipliers, when the value of uncertain channel gains is α = β = 10%, and the threshold of outage probability of CR users and PU is ξ = ζ = 0.01. It can be seen that the optimal problem Eq. 10 is feasible. The optimal Lagrange multipliers \(\mu _{i}^{*}>0\), so, the constraint C2 holds as equality at the optimal primal variables, i.e., \({\sum }_{k\neq i,k = 1}^{N}p_{k}^{*}\bar {F_{ki}}+\frac {N_{i}}{G_{ii}}+\delta _{i}\sqrt {{\sum }_{k\neq i,k = 1}^{N}}p_{k}^{*2}= q_{i}^{*}\), which indicates that the optimal power allocations as well as the optimal objective values of Eqs. 10 and 14 coincide. It is validated that the relaxation incurs no loss of optimality. Constraint C2 is active for user 2, when \(p_{2}^{*}\) satisfy \({\sum }_{i = 1}^{N}\bar {h_{i}}p_{2}^{*}+\varepsilon \sqrt {{\sum }_{i = 1}^{N}(p_{2}^{*})^{2}}=I\), the outage probability of CR user 2 is less than the given threshold.

Fig. 2
figure 2

The convergence of powers and the Lagrangian multipliers

Full size image

In Figs. 3 and 4, the effect of robustness on the sum-utility of cognitive users in chance-constraint robust approach for different values of α, β and I are shown. If the allowable interference constraint is relaxed, the total utility of SUs is increased. With the increasing α and β, the sum-utility obtained of cognitive users is smaller than that achieved under the α = 0 and β = 0, as shown in Figs. 5 and 6. Clearly, we can see that the reduction in the sum-utility via increasing the values α is greater than the reduction compared with increasing β. For example, when I = 2 × 10− 3W, α = 10%, the sum-utility is about 4.2, while it is about 4.3 for β = 10%. The reason is that for larger values of α, we need to allocate more power to cognitive users, that leads to the interference threshold violated and makes the power allocation problem infeasible. Because a smaller interference threshold I means that the constraint C3 shrinks the feasible region of power, the sum-utility is reduced with the decreasing I. Also, we can see that the sum-utility increment is larger for hi uncertainty than that for Fki uncertainty, when the value of interference threshold I varies from 2 × 10− 3W to 2.5 × 10− 3W. This denotes hi is very sensitive to the values of the interference threshold I.

Fig. 3
figure 3

The sum-utility of cognitive users versus α

Full size image
Fig. 4
figure 4

The sum-utility of cognitive users versus β

Full size image
Fig. 5
figure 5

The sum-utility of cognitive users versus α and ζ

Full size image
Fig. 6
figure 6

The sum-utility for chance constrained approach versus β and ξ

Full size image

Then, we investigate how the chance constrained approach influences the sum-utility via varying the values of ζ and ξ. In Fig. 5, we only consider the uncertainty of Fki. When ζ increases, it means the constraint C1 in Eq. 10 is relaxed. So, the sum-utility is larger when ζi is a relative smaller value. Also, with small ζ, especially ζ < 0.2, the sum-utility is sensitive to ζ, that is also validated in Ref. [22].

Meanwhile, the sum-utility versus uncertainty regions are depicted. When the values of α is smaller, the sum-utility is more closed to the values of perfect channels. Similarly, in Fig. 6, we analyze the sum-utility of CR users by considering the uncertainty of hi. When ξ increases, it means the constraint C2 in Eq. 10 is relaxed. Therefore, the sum-utility is larger for a smaller value of ξ. For ξ > 0.2, the variation of the sum-utility decreases, as it subjects to other conditions. Again, for a smaller values of β, the sum-utility is more close to the values of perfect channels.

Then, we compare the sum-utility for chance constrained approach and D-norm approach with different values of ξ. In Fig. 7, the sum-utility of the D-norm approach is lower than that of chance-constrain algorithm. From the protection function, we know the chance-constrain algorithm has better protection function to deal with the uncertain parameters, which is benefit for PU.

Fig. 7
figure 7

The sum-utility for chance constrained approach versus ξ

Full size image

Next, some simulations are carried out to evaluate the outage performance. With different outage probability thresholds, we run Monte-Carlo simulations to simulate the average outage probabilities of the users when the channels vary. It is noted that the results are the average of 3000 independent operations. The outage occur if the instantaneous SINR of user is lower than the desired value as shown in Eq. 3. The outage threshold is set from 0.05 to 0.5, from Fig. 8, it can be found that all the real statistics outage probability of users are bounded. Hence, it is concluded that the constraints in Eq. 3 are satisfied.

Fig. 8
figure 8

The outage probabiltiy of users versus ξ

Full size image

We also compare the utility and transmitting power of three users with the existing power allocation scheme in [11]. In the simulation, the related parameters are set as α = 0.1,β = 0.1,I = 2 × 10− 3W. Under the same topology and uncertain channel gains, the simulated results of utility and transmitting power are given in Figs. 9 and 10, respectively. We can see that the average utility of the proposed scheme, which can be regarded as the transmitting rate based on the definition of utility in Eq. 13, is higher than that of Ref. [11] as shown in Fig. 9. While the consuming power is a little lower than Ref. [11] as shown in Fig. 10. It is concluded that the proposed power allocation scheme shows better energy efficiency.

Fig. 9
figure 9

The utility comparsion

Full size image
Fig. 10
figure 10

The transmitting power comparsion

Full size image

To evaluate the performance of the proposed scheme under more complex topology, the texts are made further in the scenarios where there are 5 to 10 cognitive users (CRs) distributed randomly in the region of interest, respectively. The comparison results of power consumption are given in Table 1. We can see that the proposed method in this paper behaves the best performance in aspect of energy saving. It is pointed that the distributed power control scheme proposed in Ref. [12] is based on the worst case, i.e. it is assumed that the uncertain channel gain is bounded, and only the boundary is used to determine the transmitting power. Hence it behaves conservation in aspect of energy consumption, although it can achieve lower outage probability. As mentioned above, under the proposed scheme in this paper, all the outage performance of users can also be guaranteed with pre-given outage threshold.

Table 1 The comparison of transmitting power with different number of CUs (unit: dBm)
Full size table

5 Conclusions

In this paper, we propose a chance-constraint robust power control scheme in cognitive radio networks by considering the uncertainties of channel gains. We formulate a power control problem that attempts to maximize the the sum-utility of the CR users, with the outage probability constraints of the cognitive users and primary users. In order to transform the uncertainty region into the established one, a protection function is introduced to make the optimization problem solvable by the Bernstein approach. Via a relaxation, the convex problem is achieved. Then, we can acquire the optimal power of the robust problem with the Lagrange dual decomposition. Due to the uncertainty, the sum-utility of cognitive users is reduction compared to the normal problem. The numerical results verify the proposed robust power control algorithm can approach the solution of the original problem without the relaxation, and it is superior to the D-norm and worst case approaches in aspect of utility of users and energy consumption.