Abstract
In this work, a systematic approach is proposed to estimate the disturbance trajectory using a new generalized Lyapunov matrix valued function of the joint angle variables and the robot’s physical parameters using the maximum likelihood estimate (MLE). It is also proved that the estimated disturbance error remains bounded over the infinite time interval. Here, the manipulator is excited with a periodic torque and by the position and velocity data collected at discrete time points construct an ML estimator of the parameters at time \( t + dt \). This process is carried over hand in hand in a recursive manner, thus resulting in a novel unified disturbance rejection and parameter estimation in a general frame work. These parameter estimates are then analyzed for mean and covariance and compared with the Cramer Rao Lower Bound (CRLB) for the parametric statistical model. Using the Lyapunov method, convergence of the “disturbance estimation error” to zero is established. We assume that a Lyapunov matrix dependent on the link angle and form the energy corresponding to this matrix as a quadratic function of the disturbance estimate error. Using the dynamics of the disturbance observer, the rate of change of the Lyapunov energy is evaluated as a quadratic form in the disturbance error. This quadratic form is negative definite for the angular velocity in a certain range and for a certain structured form of the Lyapunov energy matrix. The most general form of the Lyapunov matrix is obtained that guarantees negative rate of increase of the energy and a better bound on the disturbance estimation error convergence rate to zero. This is possible only because we have used the most general form of the Lyapunov energy matrix.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Robot manipulators are subjected to different types of disturbances such as joint frictions, unknown payloads, and unmodeled dynamics. To estimate disturbance tracking, nonlinear disturbance observer (NDO) is one of the techniques to achieve the desired performance. In general, the main objective of the use of NDO is to deduce external unknown disturbance torque without the use of an additional sensor. A disturbance observer has been designed in [1] based on measurements of only the angular variables q of the robot and its angular velocity \( q. \) The design involves the contraction of an auxiliary signal \( z_{t} \) that satisfies first order differential equation involving \( q\left( t \right) \) and \( q\left( t \right). \) The asymptotic convergence of the disturbance estimate to the true disturbance is proved in [1], using a Lyapunov energy function which is a quadratic form in the disturbance estimate error, and which depends on the instantaneous value of \( q\left( t \right). \) The rate of change of this energy function with time is shown to be not only negative, but upper bounded by a negative definite quadratic form, provided that a certain matrix in the Lyapunov energy is chosen approximately.We have in our paper considered a Lyapunov energy function for the same disturbance observer as in [1], but with an additional degree of freedom in the choice of a certain matrix F, in the construction of the Lyapunov function. This This additional degree of freedom F satisfies a constraint that the Lyapunov energy metric be symmetric and positive definite. The advantage of using this additional degree of freedom is that we can prove faster convergence rate of the disturbance estimate error to zero. In an article [2], an NDO for multi-DOF robotic manipulator was designed by selecting the observer gain functions and global convergence was guaranteed based on Lyapunov theory. This work was extended in [3] for -link serial manipulator. Although in both the articles, the proposed observer is designed for very slow varying disturbances while in the present work we bounded the rate of disturbance. Both used explicit formula for the inertia matrices of a particular class of manipulators to solve the disturbance observer design. In [4] the system has been linearized by removing the centrifugal-Coriolis- gravitational components regarded as disturbance and by using frequency selective properties of LTI filters, this disturbance estimates has been achieved. Our philosophy however has been to treat the nonlinear centrifugal-Coriolis- gravitational torque components as parts of the system and to estimate disturbance only present in the control input. While in [5] to improve robust stability without compromising the performance of NDO, nominal plant model in the NDO was manipulated and the parameters of the discretized nominal model are optimized to improve robust stability in the discrete time domain. This method is applicable for linear model. In [6], the system is a motor modeled using a second order linear equation. Inertia and torque coefficient are uncertain and hence are expressed as nominal values. The applied method is applicable to LTI system and to apply this method to nonlinear system like robot, this method needs to be modified. Stability of this closed loop system is established by standard root locus techniques. In [7] robust stability of a closed loop LTI system has been dealt. Specifically a NDO is constructed and this depends on a time constant parameter τ. The author proves that there exists a \( n \tau^{ *} > 0 \) such that if \( \tau \le \tau^{ *} \), then the closed loop system is stable. It would be interesting to see whether such a result can be proved for nonlinear robotic systems. In [8], the robustness and stability of a disturbance observer and a reactio n torque observer (RTOB)-based robust motion control systems was analyzed. The desired acceleration, external disturbance and noise of velocity measurement are passed through filters. All these are LTI system based techniques and need to be modified for our application. In [9], a class of stabilizing decentralized proportional integral derivative (PID) controllers for an n-link robot manipulator system is proposed. In [10], the relative position control can be performed by a disturbance observer as well as a position controller. Here, the disturbance does not exist in reality but it is assumed as position error. In [11], a new method is introduced to address the decoupling problem for system with large uncertainty of internal dynamics and unknown external disturbances. When the accurate plant model is unknown, an external state observer is designed which estimate the states using only knowledge of the system output. Convergence of the state estimates to the true state is established. It is a question whether this technique can be applied even to nonlinear system with several states and few outputs. In robotics it is used to estimate the system parameters rather than the states and we have followed this approach. In [12], control with multiple plant disturbances has been surveyed. First the author discuss standard disturbance observer techniques then they survey problem in which system nonlinearities are also regarded as disturbances so that linear design methods can be used. Then they discussed nonlinear methods. Finally the composite method is surveyed involving two models, a disturbance observer and a controller. Disturbances modeled as random processes have also been surveyed. These involve methods like Kalman filtering for state estimates followed by controller design. Minimum variance issue is also surveyed for minimizing the output variance in the presence of Gaussian noise. In [13], the control of a damped harmonic oscillator with external disturbance in the input force and output measurement noise has been proposed. The effect of the overall controller is to produce the plant output i.e. position as a linear combination of filtered version of desired position, external disturbance and measurements noise. This technique also after some modification can be applied by means of nonlinear filters for nonlinear robotic system. In [14], the nonlinear system is modeled using parameters that describe the unmodeled dynamics and parameters that describe the unknown parameter vector.
The authors then design an observer with the output y(t) and input u(t) to estimate the system states. The observer is designed using the output error as feedback. In our approach, we directly estimate the unknown system parameters from the available output data by assuming a random disturbance and then using the unknown parameter estimates, we estimate the disturbance using the disturbance observer. The algorithm in [14] is more appropriate when we wish directly to estimate the state (angular position and velocities) without having to estimate the system parameters. In the case of stochastic disturbances when the system parameters to be estimated, our MLE based algorithm appears to be superior. In [15], a disturbance observer for discrete time linear system has been proposed. The idea is same as the standard construction of the disturbance observer in the literature but is carried out in discrete time using recursive difference equations expressing the disturbance estimate in terms of an auxiliary variable ‘z’ which satisfies a difference equation driven by the state and the input processes. The state is then replaced by the output with a pseudo inverse operation and of the disturbance observer is then proved. The method does not work if there are unknown system parameters and then one has to use a statistical approach to estimate these parameters from input-output data. Our algorithm for ML estimation of unknown system parameters can be combined with the disturbance observer in [15] when the system is discrete time linear with unknown parameters. In [16], the parameters of a motor are estimated for a first order linear differential equation using least square technique. Using these parameter estimates, a plant (motor) is constructed, an error signal generated which when passed through a filter yields the estimated disturbance. In [17], an algorithm based on the least square method is used to estimate the two time constants of a second order LTI system from discrete output measurements.
This is essentially an ML method if we assume that the output measurement noises are iid Gaussian. Then based on the second order partial derivatives of the measurement error energy w.r.t. the parameters, an iterative scheme are proposed to obtain a Newtonian iterative algorithm for parameter estimation.
The method will however require modification if the system is nonlinear as it is in robotics problems. One way to use the technique in [17] for nonlinear systems is to expand the nonlinear terms in the dynamical system as a power series in the state variables and then apply perturbation theory to obtain an approximate solution to the system in terms of the parameters. After that the measurement in error energy can be minimized by the Newton-iteration algorithm. In [18], the extended Kalman filter (EKF) has been used to estimate \( \dot{\text{q}}\), variation in physical parameter, and the environment force with noisy state measurements. But this technique cannot be used for estimation of disturbance and physical parameters.
As disturbance is neither can be modeled as a component of the machine torque nor it is a random noise, it is some where in between. Also EKF is suboptimal technique as it does not give the minimum mean square state estimate error (MMSE). Although Kushner filter is the optimal MMSE but it is not implementable as it is infinite dimensional filter. Least square method to linear system is applied in [19]; we have applied LS to nonlinear system followed by linearizion. Both methods give optimal ML estimates provided that the disturbance is assumed to be WGN. In [20], multi-variable systems parameters estimation and control is discussed for moving average noise. This is a linear system and both control inputs and noise are present. The moving average disturbance is transferred into an auto regressive disturbance and then a least square algorithm is proposed to identify the system parameters.
This technique can be adapted to nonlinear system after some modification. Results of [21] are used for the comparison of the proposed method. In [22], synchronization issues of two non-identical hyper chaotic master/slave systems were investigated. In [23], the unknown system output is modeled using a parametric function of time and the errors between (a) the unknown system output and the parametric model output (modeling error), (b) between the measured observation and the parametric model output are computed. These two errors are combined to compute the modeling error plus error due to measurement noise. The resultant error magnitude is then minimized by parameter adjustment. To get an initial guess for the parameter model in the robotic case, we can apply perturbation theory. Moreover, in the presence of stochastic disturbance, we can use perturbation theory to derive a parameter model for the state perturbation due to noise and parametric error. The parameter θ may be determined by the least square method to this linearized model. Essentially, the methodology of [24] needs to be modified slightly when the disturbance is stochastic using the ergodic hypothesis. The system model in [25] is described by a nonlinear differential equation expressed in state variable form. The nonlinear system terms and the external disturbance are then clubbed into a total disturbance term and a linear generalized proportional integral (GPI) observer based on output error feedback is designed to estimate the state. The authors prove convergence of the output error estimates to zero under sufficiently several conditions. This method of linear GPI observer may not be approximate when the nonlinear system terms are not treated as disturbances. Our method will work in such cases. Most noticeably, the proposed approach offers the following contribution compared to the previous work: 1) More generalized Lyapunov function and the Lyapunov energy is bounded. 2) Simultaneous parameter and disturbance estimation using disturbance observer and MLE.
MLE of parameter at time \( t +\Delta \) is obtained based on data collected up to time \( t \) and then disturbance estimate at time \( t +\Delta \) is also derived. 3) Bounded disturbance instead of slow-varying disturbance. 4) The model involves assuming the difference between the disturbance process and its estimate as a WGN stochastic process thus resulting in an improved performance ML estimator. 5) It enables us to use “estimation theory for stochastic process” with improved results. 6) Performance analysis of the estimator by CRLB evaluation using perturbation theory. The remaining part of the article is organized as follows: In section 2, dynamics of the manipulator with disturbance and parameter estimation is formulated. In section 3, Parameter Estimation by MLE is derived. In section 4, Nonlinear Disturbance Observer with parameter estimation is modeled. In section 5, the method for stability analysis is proposed. In section 6, convergence rate of the NDO is proposed. In section 7, performance analysis of the proposed parameter estimation is proposed. Then the validity of the proposed technique is verified by simulation results in section 8. This article ends with the conclusion given in the last section.
2 Dynamic model in the presence of disturbance and parameter uncertainty
The Robot dynamics can be described as
where \( \left( {\theta_{0} } \right) \) is the true parametric vector \( (\theta_{0} = \left( {{\mathbf{m}}_{1} ,{\mathbf{m}}_{2} ,{\mathbf{L}}_{1} ,{\mathbf{L}}_{2} )^{{\mathbf{T}}} } \right) \) and
where \( {\mathbf{M}}\left( {{\mathbf{q}},\theta_{0} } \right), \) is the inertia matrix. \( {\mathbf{N}}\left( {{\mathbf{q}},{\dot{\mathbf{q}}},\theta } \right) \) is the vector of Coriolis and centrifugal forces. \( \theta_{0} \) is the true parametric vector and represents physical parameters like mass, length or inertia of the links. \( {\mathbf{d}}_{{\mathbf{i}}} \left( {\mathbf{t}} \right) \) is the disturbance.
3 Parameter estimation by MLE
Here, \( {\mathbf{d}}_{{\mathbf{i}}} \left( {\mathbf{t}} \right) \) is the disturbance corrupting the dynamics of the robot. \( \hat{d}_{t} \) is its estimate based on the past data. It is well known in signal processing that if \( {\mathbf{X}}_{{\mathbf{t}}} \) is a stochastic process and \( {\hat{\mathbf{X}}}_{{{\mathbf{t}}|{\mathbf{t}} - 1}} = \left( {{\mathbf{X}}_{{\mathbf{t}}} |{\mathbf{X}}_{{{\mathbf{t}} - 1}} ,{\mathbf{X}}_{{{\mathbf{t}} - 2}} , \ldots } \right) \) is its estimate based on past data, then the estimation error \( {\mathbf{X}}_{{\mathbf{t}}} - {\hat{\mathbf{X}}}_{{{\mathbf{t}}|{\mathbf{t}} - 1}} \equiv {\mathbf{e}}_{{\mathbf{t}}} \) is an uncorrelated process. This is the orthogonal projection theory. \( {\text{If }}\theta_{0} \) is unknown, and \( {\mathbf{d}}_{{\mathbf{i}}} \left( {\mathbf{t}} \right) - {\hat{\mathbf{d}}}_{{\mathbf{i}}} \left( {\mathbf{t}} \right) \) is white-Gaussian noise (WGN), then the MLE of \( \theta_{0} \) based on data \( {\mathbf{q}}\left( \cdot \right) \) collected up to time \( t \) is least square and is given by
This is a highly nonlinear optimization problem. A more practical algorithm is to assume an initial given estimator \( \hat{\theta } \,{\text{for}}\,\theta_{0} \) and define \( \delta \theta = \hat{\theta } - \theta_{0} . \) Linearising (1) about \( \hat{\theta } \) gives
where \( {\mathbf{O}}\left( {\delta \theta \cdot {\mathbf{d}}_{{\mathbf{i}}} \left( {\mathbf{t}} \right)} \right) \) terms have been neglected since both are small quantities. Then, the MLE based on Least Square Estimation of \( \delta \theta \), based on data collected position data is
Then the improved estimates of \( \theta_{0} \) is
4 NDO with parameter estimation
The estimates \( \hat{\theta }\left( {\mathbf{t}} \right) \) is used to obtained the disturbance estimate \( {\hat{\mathbf{d}}}_{{\mathbf{i}}} \left( {{\mathbf{t}} + {\varvec{\Delta}}} \right) \) using the standard equation:
The equations are based on the continuous time versions
Here,
Which guarantees that
on using the equation of motion.
These equations that constitute the disturbance observer guarantee (1) the dynamics of the disturbance estimate depends only on measurement of \( {\mathbf{q}}\left( {\mathbf{t}} \right),{\mathbf{q}}^{0} \left( {\mathbf{t}} \right) \) and \( \tau \left( {\mathbf{t}} \right) \) and does not involve measurement of \( {\ddot{\mathbf{q}}}\left( {\mathbf{t}} \right). \) Indeed, if \( {\ddot{\mathbf{q}}}\left( {\mathbf{t}} \right) \) is also measured, then \( {\mathbf{d}}_{{\mathbf{i}}} \left( {\mathbf{t}} \right) \) could be directly estimated using Eq. (1). Having this obtained \( {\hat{\mathbf{d}}}_{{\mathbf{i}}} \left( {{\mathbf{t}} + {\varvec{\Delta}}} \right), \) we can determine \( \delta \hat{\theta }\left( {{\mathbf{t}} + {\varvec{\Delta}}} \right) \) using \( {\mathbf{q}}\left( {{\mathbf{t}} + {\varvec{\Delta}}} \right),{\dot{\mathbf{q}}}\left( {{\mathbf{t}} + {\varvec{\Delta}}} \right),{\ddot{\mathbf{q}}}\left( {{\mathbf{t}} + {\varvec{\Delta}}} \right) \) as with these quantities satisfying
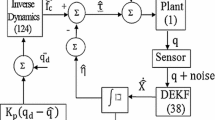
This is the forward dynamics equation of the robot (actual plant) as shown in figure 1. Then
The improved parameter estimate at time \( t +\Delta \) is then
By subtracting the disturbance estimates \( {\hat{\mathbf{d}}}_{{\mathbf{i}}} \left( {{\mathbf{t}} + {\varvec{\Delta}}} \right) \) at time \( {\mathbf{t}} + {\varvec{\Delta}} \) from the dynamics, the effect of the disturbance on the robot reduces and with this reduced error, our updated parameter estimate \( \hat{\theta }\left( {{\mathbf{t}} + {\varvec{\Delta}}} \right) \) gives better results using MLE for less noise variance. The integrals are in practice replaced by discrete summations.
5 Stability analysis of the NDO
The choice of \( {\mathbf{C}} \) in the disturbance dynamics observer is based on the Lyapunov energy method. The construction of the new generalized Lyapunov matrix for proving boundedness of the disturbance estimation error is based on the following principle. We assume that it is a positive definite matrix \( {\mathbf{J}}\left( {\mathbf{q}} \right) \) and compute the rate of change of the disturbance error energy with respect to this matrix, i.e., dynamics of the disturbance observer in terms of the matrix \( {\mathbf{L}} \) that is used in the disturbance observer construction. The condition for this rate of change to be negative is then imposed on \( {\mathbf{J}} \) and this yields a very general form for \( {\mathbf{J}} \) in terms of the mass moment of inertia matrix and a matrix \( {\mathbf{F}} \) that gives us additional degrees of freedom to establish faster convergence of the disturbance error to zero or more generally, a smaller bound on the error energy. We have in the ideal case when \( \theta_{0} \) is exactly known,
Or
where
For simplicity, here we are considering the case of two degree of freedom robot. Procedure for n degree of freedom robot is also discussed in Appendix A. Let \( {\mathbf{J}}\left( {{\mathbf{q}}_{2} } \right)\,{\text{be}}\,{\text{a}}\,{\text{positive}}\,{\text{definite}}\, 2 \times 2 \) Jacobin matrix of the robot and V is the Lyapunov energy function.Then
Then
For \( {\mathbf{V}} \) to be bounded (stability), we require
in a given range and
Writing \( {\mathbf{L}} = {\mathbf{CM}}^{ - 1} \left( {{\mathbf{q}}_{2} } \right) \) gives
Here \( {\varvec{\Gamma}} \) is a constant \( 2 \times 2 \) positive definite matrix.The above equation guarantees that the rate of change of the Lyapunov energy \( {\mathbf{V}}\left( {{\mathbf{e}},{\mathbf{q}}} \right) \) will be strictly negative and hence the disturbance estimates error will reduce nearly to zero after a sufficiently long duration.We now give a general method of constructing the symmetric Lyapunov matrix \( {\mathbf{J}}\left( {{\mathbf{q}}_{2} } \right) \) that guarantees that will hold for all \( {\mathbf{q}}_{2} \left[ {0,2\pi } \right] \) and all the angular velocities, \( {\dot{\mathbf{q}}}_{2} \) bounded above by a finite positive constant. Indeed this condition guarantee that the first component of
and the last component of \( \dot{V} \) is bounded by \( {\mathbf{K}},{\mathbf{J}}\,{\text{and}}\,{\mathbf{e}}. \) Later we shall used this inequality to rigorously establish the asymptotic boundedness of \( {\mathbf{V}}\left( {\mathbf{t}} \right) \) and hence of \( {\mathbf{e}}\left( {\mathbf{t}} \right). \) If as in the literature we take \( {\mathbf{F}} = {\mathbf{I}}, \) then \( {\mathbf{A}} = {\mathbf{C}}^{{ - {\mathbf{T}}}} \) and \( {\mathbf{J}} = {\mathbf{C}}^{{ - {\mathbf{T}}}} {\mathbf{MC}}^{ - 1} . \) This shows that C affects the Lyapunov matrix as well as its rate of decrease. In other words, \( {\mathbf{C}} \) has control over the eigenvalues of \( {\mathbf{J}} \) and hence can be manipulated to get approximate rate of error energy decreases. This implies in turn that the disturbance estimate will converge to the true disturbance at a faster rate.
To simplify matters, we shall assume that
(\( {\mathbf{A}} \) is a constant matrix) i.e.,
This condition that \( {\mathbf{JCM}}^{ - 1} \) be a constant matrix, guarantees that the range of \( {\dot{\mathbf{q}}}_{2} \) for asymptotically stability can be derived easily as we presently investigate.
\( {\mathbf{J}}^{{\mathbf{T}}} = {\mathbf{J}} \) is required, we have
or
Let \( {\mathbf{A}}^{{\mathbf{T}}} {\mathbf{C}} = {\mathbf{F}} \). Then the above reduces to
or
Or
or
Here more generalized Inertia matrix \( M \) is considered as compared to [2] with more degree of freedom for better results. Thus,
or
and
The most general form of \( {\mathbf{F}}\,{\text{that}}\,{\text{guarantees}} \)
\( {\dot{\mathbf{J}}}\left( {{\mathbf{q}}_{2} } \right)\,{\text{be}}\,{\text{symmetric}}\,\forall \,{\mathbf{q}}_{2} \) is therefore
or
where
We have
and thus,
In the special case where \( {\mathbf{f}}_{22} = 0\,{\text{and}}\,{\mathbf{f}}_{22} = 1 \), we get
Which is the standard Lyapunov matrix used in the literature. We now require
or equivalently,
6 Convergence rate of the NDO
In this section, we use standard matrix norm inequalities and a well-known inequality in (Gronwall’s inequality) to derive an improved convergence rate for the error in the disturbance tracking. We are free to choose \( {\mathbf{f}}_{12} ,{\mathbf{f}}_{22} \) so that (48) holds. Then
(where \( \parallel {\dot{\mathbf{d}}}_{{\mathbf{i}}} \left( {\mathbf{t}} \right)\parallel \le \rho_{1} < \infty \,is\,assumed\,for\,all\,t \)).
Now
where
and hence
where
Now
where
Thus,
Also,
where
We get
Write
Then
So setting
or
It follows that
In particular \( \forall \delta > 0\exists {\mathbf{T}} > 0 \) s.t.,
Then
and so we get the least upper bound
This equation guarantees that asymptotically, the disturbance estimate error can not go out of bounds. Therefore it is a partial stability result. Note that
and the condition (48) \( {\text{for }}{\dot{\mathbf{V}}} = 0 \) can be guaranteed if
Alternatively, (48) holds if
and this is guaranteed if
These conditions are stronger than \( {\dot{\mathbf{V}}} < 0. \)
They ensure that if the disturbance error estimate falls on a sphere of radius R, then \( {\dot{\mathbf{V}}} \) will be upper bounded by a negative number which increases with R. The two extra degree of freedom \( {\mathbf{f}}_{11} ,{\mathbf{f}}_{22} \,{\text{in}}\,{\mathbf{F}} \) gives us more flexibility in the choice of the Lyapunov matrix which in terms enable us to derive smaller upper bounds on the asymptotic value of the Lyapunov function \( V\left( t \right) \). This in turn leads us to smaller upper bounds on the disturbance error energy as compared to the existing bounds in the literature. Remark. Let \( {\mathbf{A}},{\mathbf{B}} > 0. \) Then a necessary sufficient condition for \( \left[ {\begin{array}{*{20}l} {\mathbf{A}} \hfill & {\mathbf{C}} \hfill \\ {{\mathbf{C}}^{{\mathbf{T}}} } \hfill & {\mathbf{B}} \hfill \\ \end{array} } \right] \) is thus
i.e.
Minimum is attained when
i.e.,
Thus
if
Remark
Adaptive update of \( \delta \hat{\theta } \):
We can update \( \delta \theta \) adoptively using the algorithm (LMS) \( \delta \hat{\theta }\left( {{\mathbf{t}} + {\varvec{\Delta}}} \right) = \delta \hat{\theta }\left( {\mathbf{t}} \right) - \mu \frac{\partial }{{\partial \delta \hat{\theta }\left( {\mathbf{t}} \right)}}\parallel {\mathbf{G}}\left( {{\mathbf{q}},\hat{\theta }\left( {\mathbf{t}} \right)} \right)({\ddot{\mathbf{q}}}\left( {\mathbf{t}} \right) \)
This equation ensures that at each time step, the parameter estimate is changed so that the equation of motion with \( \theta_{0} \,{\text{replaced}}\,{\text{by}}\,\hat{\theta }\left( {\mathbf{t}} \right) \), is satisfied to a better degree of approximation.
7 Performance analysis of the proposed parameter estimator
7.1 CRLB for parameter estimation \( \left( {\partial \hat{\theta }\left( t \right)} \right) \)
The CRLB sets a lower bound on the variance of any unbiased estimator. We can find a minimum variance unbiased estimator and it achieves the lower bound. The bound states that the variance of any unbiased estimator is at least as high as the inverse of the Fisher information. The CRLB for the parametric uncertainty \( \partial \theta \) has been obtained by linearizing the dynamic system about \( \hat{\theta }\,{\text{when}}\,\hat{\theta } \) is the given value of the parameter and \( \theta_{0} = \hat{\theta } - \partial \theta \) is the true parameter vector. The log-likelihood function of the given measurements \( {\mathbf{q}}\left( {\mathbf{t}} \right) \) over a given time range, is thus obtained as a linear quadratic form in \( \partial \theta \) assuming white Gaussian noise present in the dynamical system.The Fisher information matrix for, \( \partial \theta \) is easily computed from the log-likelihood function with the exceptions evaluated using a linearized theory in which the trajectory perturbations \( \partial {\mathbf{q}}\left( {\mathbf{t}} \right) \) in the presence of noise follow a linear differential equation with coefficients being functions of the noiseless trajectory. \( \partial {\mathbf{q}}\left( {\mathbf{t}} \right) \) is therefore a Gaussian process and its mean and covariance are easily determined from the linearized dynamical equations. The fisher information matrix is thus easily obtained. The approximate CRLB parameter here is only for the sake of completeness. Assuming that the disturbance observe is not incorporated we have
and hence assuming \( \left\{ {{\mathbf{d}}_{{\mathbf{i}}} \left( {\mathbf{t}} \right)} \right\} \) to be zero mean. While Gaussian with spectral density \( \sigma_{{\mathbf{d}}}^{2} {\mathbf{I}}_{2} , \) we get the log-likelihood function for \( \delta \hat{\theta } \) based on \( \left\{ {q\left( t \right):0 \le t \le T} \right\} \) as
The Fisher information matrix for \( \delta \hat{\theta }\left( {\mathbf{T}} \right) \) is thus
To evaluate this expectation approximately, we assume that \( \left\{ {{\mathbf{q}}_{{0\left( {\mathbf{t}} \right)}} ,0 \le {\mathbf{t}} \le {\mathbf{T}}} \right\} \) is the solution with
\( \delta \theta = \hat{\theta } - \theta_{0} \quad {\text{and}}\quad {\mathbf{d}}_{{\mathbf{i}}} \left( {\mathbf{t}} \right) \equiv 0 \), i.e.
Let \( \Delta{\mathbf{q}}\left( {\mathbf{t}} \right) = {\mathbf{q}}\left( {\mathbf{t}} \right) - {\mathbf{q}}_{0} \left( {\mathbf{t}} \right)\,{\text{be}}\,{\text{the}}\,{\text{change}}\,{\text{is}}\,{\mathbf{q}}\,{\text{due}}\,{\text{to}}\,{\text{noise}}\,{\mathbf{d}}_{{\mathbf{i}}} \,\left( {\mathbf{t}} \right) \). Then we have approximately that
or equivalently
where
Let \( \phi \left( {{\mathbf{t}},\tau } \right)\,{\text{denote}}\,{\text{the}}\,{\text{state}}\,{\text{transition}}\,{\text{matrix}}\,{\text{of }} \) (98). Then
Writing
Then
The condition \( {{\mathbb{E}}\Delta }q_{\alpha } \left( t \right)\Delta q_{\beta } \left( t \right),{{\mathbb{E}}\Delta }\dot{q}_{\alpha } \left( t \right)\Delta \dot{q}_{\beta } \left( t \right) \) and \( {{\mathbb{E}}\Delta }q_{\alpha } \left( t \right),\Delta \dot{q}_{\beta } \left( t \right) \) in the expression can easily be evaluated by solving the linear differential equation (98) which in term involves evaluating the time varying state transition matrix corresponding to \( \left[ {\begin{array}{*{20}l} {0_{2} } \hfill & {{\mathbf{I}}_{2} } \hfill \\ {{\mathbf{P}}\left( {\mathbf{t}} \right)} \hfill & {{\mathbf{Q}}\left( {\mathbf{t}} \right)} \hfill \\ \end{array} } \right] \) using the Dyson series, So
So
In order to evaluate the expectations approximately in the CRLB, we require expressions for the statistical correlations in the position deviations and velocity deviations from the non-random components of the positions and angular velocities. In what follows, we evaluate these correlations using a linearized state variable model for the robot dynamics.
7.2 General comparison of MLE variance with CRLB
Consider the dynamical system
where \( \theta_{0} \,{\text{is}}\,{\text{an}}\,{\text{unknown}}\,{\text{parameter}}\,{\text{vector}}\,{\text{and}}\,{\mathbf{d}}_{{\mathbf{i}}} \left( {\mathbf{t}} \right) - {\hat{\mathbf{d}}}_{{\mathbf{i}}} \left( {\mathbf{t}} \right)\,{\text{is}}\,{\text{WGN}} .\,{\text{Then}}\,{\text{MLE}}\,{\text{of}}\,\theta_{0} \) is:
Our algorithm determines an adaptive scheme for computing \( \hat{\theta }_{{{\mathbf{ML}}}} \left( {\mathbf{T}} \right) \) or detecting with T. Suppose we use \( \hat{\theta } \) as an inherent sense and write \( \theta_{0} \approx \hat{\theta } - \delta \theta \), thus from the dynamics
To estimate \( \theta_{0} \,{\text{better}}\,{\text{we}}\,{\text{need}}\,{\text{to}}\,{\text{estimate}}\,\delta \theta_{0} \) and this is obtained from
This minimization leads to a linear equation for \( \delta \theta \) which we have solved above. On the other hand, the CRLB for \( \delta \theta \) is given by
We need to compare this with the covariance of \( \delta \hat{\theta }_{{{\mathbf{ML}}}} \left( {\mathbf{T}} \right) \) which is given by
Under the ergodic hypothesis, time average can be replaced by ensemble averages and hence
Also
so
Again under the ergodic hypothesis this becomes
and hence
And
Which is the CRLB. Thus under the ergodic hypothesis, we have proved that our ML estimates (112) performs effectively in accordance with the CRLB (125), i.e., ergodic hypothesis \( {\mathbf{Cov}}\left\{ {\delta \hat{\theta }_{{\mathbf{M}}} {\mathbf{L}}\left( {\mathbf{T}} \right)} \right\} \approx {\mathbf{CRLB}}\,{\text{for}}\,{\text{all}}\,{\text{estimates}}. \) In order to evaluate the exceptions approximately in the CRLB, we require expressions for the statistical correlations in the position deviations and velocity deviations from the non-random components of the position and velocity.
8 Simulation and results
For ease of simplicity, a two link revolute joint robot with mass \( \left( m \right)\,{\text{and}}\,{\text{length}}\,\left( a \right) \) is considered in this study. The dynamics of this manipulator is as below: \( M = \left[ {m_{11} m_{12} ;m_{21} m_{22} } \right]; N = \left[ {N_{1} , N_{2} } \right] \)
Where \( m_{11} = \left( {m_{1} + m_{2} } \right) \times a_{1}^{2} + m_{2} \times a_{2}^{2} + 2 \times m_{2} \times a_{1} \times a_{2} \times \text{cos}\left( {q_{2} } \right) \);
\( m_{12} = m_{2} \times a_{2}^{2} + m_{2} \times a_{1} \times a_{2} \times \text{cos}\left( {q_{2} } \right);m_{21} = m_{12} ;m_{22} = m_{2} \times a_{2}^{2} \); \( N_{1} = - m_{2} \times a_{1} \times a_{2} \times \left( {2 \times \dot{q}_{1} \times \dot{q}_{2} + \dot{q}_{2}^{2} } \right) \times \text{sin}\left( {q_{2} } \right) + \left( {m1 + m2} \right) \times g \times a1 \times \text{cos}\left( {q_{1} } \right) + m2 \times g \times a2 \times \text{cos}\left( {q_{1} + q_{2} } \right)m_{2} \times a_{1} \times a_{2} \times \dot{q}_{1}^{2} \times \text{sin}\left( {q_{2} } \right) + m2 \times g \times a2 \times \text{cos}\left( {q_{1} + q_{2} } \right); \) \( {\text{Here }}\theta_{0} = m. \)
Two types of disturbances are exerted on the robot, namely Normal Sinusoidal tracking disturbance corrupted by noise whose distribution is Gaussian (Normally distributed pseudorandom; randn function in Matlab®) as shown in figures 2 and 3. This is more generalized form of the disturbances as compared to[1,2,3]. \( di_{1} = 0.03 \times sin\left( {\pi \times t} \right) + 0.003 \times randn; \) \( di_{2} = 0.03 \times sin\left( {\pi \times t} \right) + 0.003 \times randn; \) The reference trajectory provided for the joints of robots are given by (126) and shown in figures 3 and 4 respectively.
For joint tracking acceleration controller is applied and is designed as
It is evident by figures 4 and 5 that the actual trajectory is following the desired trajectory by the proposed method. As per figures 3 and 5 the joint tracking error RMS values are in the range of \( 10^{ - 4} \) by the proposed method. Initially, this error is very high due to error in mass estimation but after some time it stabilized after correct mass estimation.
Table 3 of [1] depicts the simulation results of SCARA industrial robot while table 6 of [1] depicts the experimental results of Phantom Robot. As per these tables, the minimum tracking error is in the range of \( 10^{ - 3} \).
These errors as mentioned in [1] is also without white Gaussian noise. So the results of the proposed method are superior compared to the three methods as mentioned above. It is evident by figures 6 and 7 that estimated disturbance trajectory is successfully following the actual disturbance trajectory with white Gaussian noise by the proposed method.
As per figures 8 and 9 the disturbance trajectory error RMS values are in the range of \( 10^{ - 3} \) by the proposed method. As proposed method is also simultaneously estimating the mass of the link, initially the error is high but after some time it stabilized.
Table 4 of [1] depicts the simulation results of SCARA industrial robot while table 7 of [1] depicts the experimental results of Phantom Robot. As per these tables the minimum error is in the range of \( 10^{ - 3} \).
Also this error is without mass estimation and random noise. So results of the proposed method are superior compare to the three methods as mentioned above.
The reason being that at each time step t, we estimate \( {\text{d}}_{\text{i}} ( {\text{t)}}\,{\text{as}}\, {\hat{\text{d}}}_{\text{i}} ( {\text{t) }} \)using the disturbance observer. Then we subtract it from the input control torque.
This is equivalent to giving a torque \( \uptau{\text{ + d}}_{\text{i}} ({\text{t}}) - \hat{\text{d}}_{\text{i}} ( {\text{t)}} \) for the next iteration and the robot moves to \( {\text{q(t + dt)}} \) based on this disturbance torque.
Figures 10 and 11 depict the actual and estimated mass of link 1 and link 2, respectively. From these figures it is clear that the proposed MLE technique with disturbance observer is correctly estimating the mass of the links. So the proposed method successfully simultaneously tracking the position trajectory and disturbance trajectory with mass estimation.
9 Conclusion
A new systematic disturbance observer design method for manipulators has been proposed in this paper. The nonlinear disturbance observers with convergence and unknown parameter estimation unified in the proposed general framework. The proposed design method guarantees convergence of the observer tracking error to the origin with an exponential rate in the case of bounded disturbances. The parameter estimation was achieved using MLE with internal disturbance and white Gaussian noise and in addition, the CRLB for this statistical model has been evaluated for comparison with the proposed ML estimator. The MLE is for the parameter error is equivalent to the least squares estimator in view of the white Gaussianity of the noise. Simulation study on a manipulator demonstrated the superior performance of the developed novel approach as compare to other methods from literature. While the performance of the proposed method has been verified through simulation, the experimental verification will be the goal of future work. To get more accurate tracking, we can introduce a nonlinearity in the feedback loop in the form of second order Volterra feedback. Then the error energy to be optimized will be a function of the input forcing signal and the first and second order feedback kernels.
References
Mohammadi A, Tavakoli M, Marquez H J and Hashemzadeh F 2013 Nonlinear disturbance observer design for robotic manipulators. Control Engineering Practice 21: 253–267
Wen-Hua Chen, Ballance D J, Gawthrop P J and O’ Reilly J 2000 A nonlinear disturbance observer for robotic manipulators. IEEE Transactions on Industrial Electronics 47: 932–938
Nikoobin A and Haghighi R 2009 Lyapunov-based nonlinear disturbance observer for serial n-link manipulators. Journal of Intelligent and Robotic Systems 55: 135–153
Seok Jinwook, Woojong Yoo and Sangchul Won 2012 Inertia-related Coupling Torque Compensator for Disturbance Observer based Position Control of Robotic Manipulator. International Journal of Control, Automation, and Systems 10(4): 753–760
Kong Kyoungchul and Tomizuka Masayoshi 2013 Nominal Model Manipulation for Enhancement of Stability Robustness for Disturbance Observer-Based Control Systems. International Journal of Control, Automation and Systems 11(1): 12–20
Kobayashi Hideyuki Kobayashi, Seiichiro Katsura and Kouhei Ohnishi 2007 An analysis of parameter variations of disturbance observer for motion control. IEEE Transactions on Industrial Electronics 54(6): 3413–3421
Shim H and Jo N H 2009 An almost necessary and sufficient condition for robust stability of closed loop systems with disturbance observer. Automatica 45(1): 296–299
Emre and Ohnishi Kouhei 2015 Stability and Robustness of Disturbance-Observer-Based MotionControl Systems. IEEE Trans. on Industrial Electronics 62(1): 414–422
Leena G and Ray G 2012 A set of decentralized PID controllers for an n-link robot manipulator Sadhana 37(3): 405–423
Yoon Young-Doo, Eunsoo Jung and Seung-Ki Sul 2008 Application of a Disturbance Observer for a Relative Position Control System. IEEE Transactions on Industrial Electronics 46(2): 849–856
Zheng Qing Chen, Zhongzhou and Gao Zhiqiang 2009 A practical approach to disturbance decoupling control. Control Engineering Practice 17: 1016–1025
Guo Lei and Cao Songyin 2014 Anti-disturbance control theory for systems with multiple disturbances: A survey. ISA Transactions 53: 846–849
Liu Chao, Jianhua Wu, Jia Liu and Zhenhua Xiong 2014 High acceleration motion control based on a time-domain identification method and the disturbance observer. Mechatronics 24: 672–678
Zhang Zhengqiang and Xu Shengyuan 2015 Observer design for uncertain nonlinear systems with unmodeled dynamics. Automatica 51: 80–-84
Kim Kyung-Soo and Rew Keun-Ho 2013 Reduced order disturbance observer for discrete-time linear systems. Automatica 49: 968–975
Kapun A, Curkovic M, Ales Hace and Jezernik K 2008 Identifying dynamic model parameters of a BLDC motor. Simulation Modelling Practice and Theory 16: 1254–1265
Xu Ling, Lei Chen and Weili Xiong 2015 Parameter estimation and controller design for dynamic systems from the step responses based on the Newton iteration. Nonlinear Dynamics 79(3): 2155–2163
Chan Linping, Fazel Naghdy and David Stirling 2013 Extended active observer for force estimation and disturbance rejection of robotic manipulators. Robotics and Autonomous Systems 61: 1277–1287
Pan Yi-Ren, Yi-Ti Shih, Rong-Hwang Horng and An-Chen Lee 2009 Advanced Parameter Identification for a Linear-Motor-Driven Motion System Using Disturbance Observer. International Journal of precision Engineering and Manufacturing 10(4): 35–47
Wang Dongqing, Feng Ding and Xinzhuang Dong 2012 Iterative Parameter Estimation for a Class of Multivariable Systems Based on the Hierarchical Identification Principle and the Gradient Search. Circuits Systems Signal Process 31: 2167–2177
Liu C S and Peng H 2000 Disturbance observer based tracking control. ASME Transactions of the Dynamic Systems Measurement and Control 122: 332–335
Shahi M and Mazinan A H 2015 Automated adaptive sliding mode control scheme for a class of real complicated systems. Sadhana 40(1): 51–74
Karkar N, Benmhammed K and Bartil A 2014 Parameter Estimation of Planar Robot Manipulator Using Interval Arithmetic Approach. Arabian Journal for Science and Engineering 39: 5289–5295
Cazalilla J, Marina Vallés, Vicente Mata and Ángel Valera 2014 Adaptive control of a 3-DOF parallel manipulator considering payload handling and relevant parameter models. Robotics and Computer-Integrated Manufacturing 30: 468–477
JohnCorts-Romero, Germán A Ramos and HoracioCoral-Enriquez 2014 Generalized proportional integral control for periodic signals under active disturbance rejection approach. ISA Transactions 53: 1901–1909
Acknowledgements
This work was supported by grant (SR/CSI/24/2011(C and G)) from the Department of Science and Technology, Government of India.
Author information
Authors and Affiliations
Corresponding author
Appendix A
Appendix A
We have derived the general form of the Lyapunov matrix for the 2 link case which it can analytically be generalized to the n \( \ge \) 2 link case as follows:
Then
Therefore, we require for stability
or
We chose J such that
a constant matrix of size n \( \times \) n then
So, we require to solve \( {\mathbf{A}} \) such that
1. \( {\mathbf{J}}^{{\mathbf{T}}} = {\mathbf{J}} \) i.e
2.
for all \( \left| {{\dot{\mathbf{q}}}_{\alpha } } \right| \le {\dot{\mathbf{q}}}_{{{\mathbf{max}}}} ,{\dot{\mathbf{q}}}_{\alpha } \in \left[ {0,\pi } \right]. \) The general solution to this for A will then give the general form of the Lyapunov matrix \( {\mathbf{J}}\left( {\mathbf{q}} \right). \)
Rights and permissions
About this article
Cite this article
AGARWAL, V., PARTHASARATHY, H. Simultaneous estimation of parameter uncertainties and disturbance trajectory for robotic manipulator. Sādhanā 44, 109 (2019). https://doi.org/10.1007/s12046-019-1092-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12046-019-1092-2