Disturbance estimator as a state observer with extended Kalman filter for robotic manipulator

Abstract

In most of the existing literature, disturbance observer theory has been developed only for constant disturbance, while in the present work, by defining the disturbance as a state observer, we are able to track and reject disturbances varying with time. This is possible with only joint position variables unlike other works where derivative of position variables is also needed. In the novel technique proposed by us, the standard disturbance observer output is treated as a part of the state variable of a nonlinear system. The disturbance estimation error is treated as a white Gaussian noise (WGN) independent of the WGN in the dynamics of the robot. The extended Kalman filter (EKF) is then applied based on noisy measurements of the position to obtain estimates of the angular coordinate and the disturbance. Superior estimates of the disturbance are possible because we are first using the nonlinear disturbance observer to produce a new state and then we are applying the EKF to remove the residual noise in the disturbance estimate. Stability and convergence analysis of the EKF is established using linearization of the state equations around the estimated state. Using the Lyapunov method, we also establish convergence of the disturbance estimation error to zero. Finally, robustness of the EKF to uncertainty is established by linearizing the dynamical equation w.r.t the parametric uncertainty and the dynamics w.r.t the state estimation error, thereby yielding an upper bound for the error variance in terms of the norm square of the parametric uncertainty. The proposed technique is applied to an Omni®Robot Manipulator. The results are encouraging and demonstrate better disturbance rejection ability of the proposed scheme as compared to other techniques available in the literature.

1 Introduction

Positional accuracy and trajectory control of the surgical tools at the end effector of the manipulator are crucial for medical robot applications [1, 2]. However, this highly nonlinear system is always affected by different types of internal and external disturbances like environmental forces [3, 4]. Such disturbances, when unaccounted for, result in the instability and performance degradation of the closed loop system. Therefore, several methods have been developed for stability analysis and robust control design of systems with disturbances over the past several years. Various effective techniques and their applications have been proposed, and their properties such as stability have been rigorously established. An exhaustive survey is available in [5].

In [6], a disturbance observer has been proposed which dynamically estimates the disturbances based on instantaneous angular measurement of the position and velocity $[\varvec{q}(t),\varvec{\dot{q}}(t)]$. However, if the measurements are corrupted by noise, this procedure will fail. Also most of the industrial robots are equipped with position encoders only. So the available feedback signals are only the angular positions. In this case, the EKF proposed in [7] has to be used. Further in [7], the authors model the environment force (disturbance) as a constant direct current (dc) signal and treating it as a parameter, estimate it along with the state $[\varvec{q}(t),\varvec{\dot{q}(t)}]$ using the EKF. This method may not perform well if the disturbance is rapidly time-varying because it takes a finite settling time for the EKF estimate to converge close to the true state. Further in both [6] and [7], it is assumed that the rate of change of disturbance is negligible while we are proposing a technique applicable to situations in which the disturbance may be rapidly varying with time.

Hence, in the present work the shortcomings of both the works are addressed by assuming the disturbance estimate $\varvec{\hat{d}}(t)$ to be a state variable like $\varvec{q}(t),\varvec{\dot{q}}(t)$ and the disturbance itself to be such that $\varvec{d}_i(t)-\varvec{\widehat{d}}_i(t)$ can be modeled as a WGN of known variance.

In this work, the EKF is applied to the enlarged system consisting of the robot dynamics and disturbance observer and therefore we produce superior disturbance estimates when both process noise and measurement noise are accounted for.

If the disturbance consists of a nonrandom component ($\varvec{d}_i(t)$) plus a small random component ($\varvec{\tilde{w}}(t)$), then the disturbance observer will be able to estimate the nonrandom component well and we denote this estimate by $\varvec{\widehat{d}}_i(t)$. Then, $\varvec{\epsilon }= \varvec{d}_i(t)-\varvec{\widehat{d}}_i(t)$ will be pure noise and it may be assumed to be WGN.

Thus, in this work the EKF estimate of $\varvec{\widehat{d}}_i(t)$ is subtracted from $\varvec{d}_i(t)$ + $\varvec{\tilde{w}}(t)$, where $\varvec{\widehat{d}}_i(t)$ satisfies a state variable equation involving the other states $\varvec{q}(t),\varvec{\dot{q}}(t)$ and is driven by WGN.

We have assumed an appropriate power spectral density for WGN and developed an EKF with disturbance observer as part of the state $[\varvec{q}(t),\varvec{\dot{q}}(t),\varvec{\widehat{d}}_i(t)]$.

On the other hand, in [7] the model used is $\varvec{\dot{d}}_i(t)=$ WGN or $\varvec{d}_i(t)=$ Brownian motion which is unrealistic since the variance of Brownian motion keeps increasing with time. In [7], the external disturbance has been modeled as a constant force or equivalently as an unknown parameter vector whose differential is therefore zero+ a differential of Brownian motion. We have considered a more general model for the disturbance with unknown amplitudes, frequencies and phases (AFP). The case of dc disturbance is a special case of our model.

Finally, coming to the convergence aspect of the algorithm [7], a generalized active state observer is suggested which is based on replacing the Kalman gain matrix by an arbitrary matrix and then computing, using the state equation and the state observer equations, a stochastic differential equation for the state estimation error and proving boundedness of this error energy asymptotically.

We have on the other hand considered the full nonlinear state variable equations and state observer using EKF and have derived an approximate stochastic differential equation for the state estimation error by linearizing the nonlinear state driving force as well as the measurement function about the state estimate. We then derive an upper bound for the stochastic Lyapunov average energy and using some techniques of linear algebra, obtain a Gronwall inequality for the mean square error. As $t \rightarrow \infty$, this gives an upper bound for this error energy in terms of the state and measurement noise energy and an assumed lower bound on the Lyapunov matrix.

The proposed method works well even for nonlinear state measurement in contrast to [7].

Adaptive controllers like [1–6, 8–10] are suboptimal. The error does not converge to zero, but rather fluctuates about zero in the limit. EKF is a direct approximation to the optimal Kushner equation which is the minimum mean square error (MMSE) filter. So EKF will produce better results than adaptive methods although computational cost will be higher. A discrete time Lyapunov energy difference is derived between successive error samples in [11]. The conditional expectations of the Lyapunov energy at a given time sample given the previous error sample is evaluated and is shown apart from multiplicative and additive constants to be smaller than the energy at the previous time instant, thus settling the stability issue. Our analysis of the stability of the continuous time EKF is directed toward linearizing the dynamics of the state evolution and using that to establish conditions under which the expected value of the Lyapunov energy will decrease with time. We make use of Ito’s formulation for this purpose unlike [11]. Since we directly work with the continuous time dynamical system rather than its discretized version, the proposed method is less crude.

In [12], analysis of robustness is applied to the specific motor model chosen. Our stability analysis is based on the most general EKF for the most general nonlinear stochastic differential equation (SDE).

In [13], three new methods are discussed for linearization of EKF.

In summary, the proposed approach offers the following contributions compared to the previous work in the literature:

• 1. A new disturbance observer is proposed which needs only measurable joint signals unlike [6] which also needs measurable velocity signals.

• 2. A new disturbance observer is proposed where disturbance estimation error is equal to WGN and this error can be minimized by treating the disturbance observer as extra state variables and applying the EKF to these extra state variables without any computational cost.

• 3. If joint positions are measured with noise, direct implementation of disturbance observer would not work because measurement noise is not differentiable so a new technique “DO with EKF” (DEKF) is proposed with estimated disturbance as state variable.

• 4. $\varvec{d}(t)-\varvec{\hat{d}}_i(t)$ is treated as WGN in the state model for $[\varvec{q}(t),\varvec{\dot{q}}(t),\varvec{ \widehat{d}}_i(t)]$, and this enables us to construct the estimate of the disturbance observer using EKF. This works even for time-varying disturbance $(\varvec{d}_i(t))$. The analysis for the extended active observer (EAOB) in [7] assumes a dc disturbance, but can also be applied for time-varying disturbance like random walks, but our method may work better because a two-stage filter is used: first a DO and then an EKF.

• 5. We choose a Lyapunov matrix V and obtain an inequality for $\frac{ d}{dt} \mathbb {E}[\varvec{e}(t)^T V\varvec{e}(t)]$, where $\varvec{e}(t)$ is the disturbance estimation error. Using this, we derive a Gronwall inequality for $\mathbb {E}[\Vert \varvec{e}(t) \Vert ^2]$ which converges to an upper bound.

• 6. This justifies the construction of the disturbance observer with disturbance estimate as a separate state variable, and it must be estimated using EKF.

• 7. Robust performance for uncertainty $\varvec{\theta }(t)$ is also analyzed for the proposed technique, and it is proved that the proposed technique is robust for any type of uncertainty.

The remaining part of the paper is organized as follows: The dynamic model of a robotic manipulator is proposed with disturbances in Sect. 2. In Sect. 3, a new disturbance observer is proposed based on the dynamic model. This will be followed by presenting the proposed extended Kalman filter with disturbance observer (DEKF) in Sect. 4. In Sect. 5, the stability and convergence analysis is discussed. In Sect. 6, robustness for uncertainty is analyzed. Section 7 details the experimental setup, procedure and results. Section 8 provides observations and conclusions.

2 Problem formulation

The dynamic model of a robotic manipulator without disturbance can be represented by

$$\begin{aligned} \varvec{M(q)\ddot{q}} + \varvec{N(q,\dot{q})}=\varvec{\tau }(t) \end{aligned}$$

(1)

The dynamic model of a robotic manipulator with disturbance can be represented by

$$\begin{aligned} \varvec{M(q)\ddot{q}} + \varvec{N(q,\dot{q})}=\varvec{\tau }(t) +\varvec{d}_i(t)+\varvec{\widetilde{w}}(t) \end{aligned}$$

(2)

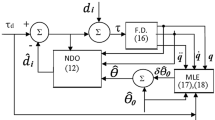
as shown in Fig. 1. Here $\varvec{d}_i(t)$ is the nonrandom component of the disturbance and $\varvec{\widetilde{w}}(t)$ is random component of the disturbance present in the plant. $\varvec{\tau }(t)$ is the control signal torque. $\varvec{M(q)}$ is the inertia matrix, and $\varvec{N(q,\dot{q})}$ is the vector of Coriolis, centrifugal forces and the gravity vector.

Here $\varvec{\tau }(t)$is generated from a desired trajectory $q_d(t)$ using inverse dynamics, state error feedback and disturbance component, i.e.,

$$\begin{aligned}&\tau (t)=M(q_d)\left( \ddot{q}_d+K_p(q_d-\hat{q}\right) +K_d\left( \dot{q}_d-\hat{\dot{q}}\right) \\&\qquad \quad +N(q_d,{\dot{q}})-\hat{\eta _t} \end{aligned}$$

Here $\varvec{q}(t),\varvec{\dot{q}}(t),\varvec{{\ddot{q}}}(t)$ is joint’s position, velocity and acceleration, respectively.

Here $\hat{\eta }(t)$ is an estimate of the disturbance $d_i(t)$. Figure 1 takes into account the EKF and DO in the torque generation. The DEKF disturbance estimate has been subtracted from the dynamics. However, we shall, to start with, assume $\tau (t)$ to be just the torque generated by inverse dynamics, i.e., $\tau (t)=M(\varvec{q}_d)\varvec{\ddot{q}_d}+N(\varvec{q}_d, \dot{q}_d)$ because we are yet to design the EKF and so $(\hat{q},\hat{\dot{q}},\hat{\eta })$ are as yet not available to us.

If $\varvec{\varepsilon }(t)=\varvec{d}_i(t)-\varvec{\widehat{d}}_i(t)$= WGN, then the extended state model is

$$\begin{aligned} \varvec{M(q)\ddot{q}}+\varvec{N(q,\dot{q} )}\,=\varvec{\tau }(t) +\varvec{\widehat{d}}_i(t)+\varvec{\varepsilon }(t) +\varvec{\tilde{w}}(t) \end{aligned}$$

(3)

Here $\varvec{w}(t)=\varvec{\varepsilon }(t) +\varvec{\widetilde{w}}(t)$ is WGN with spectral density $\sigma _w^2=\sigma _{\varepsilon }^2+\sigma _{\widetilde{w}}^2$. Thus, if $\varvec{B}(t)$ is Brownian motion

$$\begin{aligned} \varvec{w}(t)=\sigma _w\frac{{\hbox {d}}\varvec{B}(t)}{{\hbox {d}}t} \end{aligned}$$

(4)

So from (3)

$$\begin{aligned} \varvec{M(q)\ddot{q}} + \varvec{N(q,\dot{q})}=\varvec{\tau }(t) +\varvec{\widehat{d}}_i(t) + \varvec{w}(t) \end{aligned}$$

(5)

Fig. 1

Block diagram Inverse dynamics (computation), plant (forward dynamics) and DEKF

If $\varvec{\widehat{d}}_i(t)$ is projection of $\varvec{d}_i(t)$ on its past, then $\varvec{d}_i(t)-\varvec{ \widehat{d}}_i(t)$ is WGN by innovation process theory [14–16] . Thus, we can model

$$\begin{aligned} \varvec{\varepsilon }(t)=\varvec{d}_i(t)-\varvec{\widehat{d}}_i(t)= \varvec{w}(t)-\varvec{\tilde{w}}(t) = WGN. \end{aligned}$$

(6)

Specifically, if

$$\begin{aligned} \varvec{\widehat{d}}_i{(t+\delta t)}=\mathbb {E}[\varvec{{d}}_i{(t+\delta t)}|\varvec{d}\tau ,\tau \le t] \end{aligned}$$

then as per orthogonality property of conditional expectation [16]:

$$\begin{aligned} \mathbb {E} [(\varvec{{d}}_i{(t+\delta t)}-\varvec{\widehat{d}}_i{(t+\delta t)} )f(\varvec{d}_i(\tau ),\tau \le t )]=0 \end{aligned}$$

which means that $(\varvec{{d}}_i{(t+\delta t)}-\varvec{\widehat{d}}_i{(t+\delta t)})$ is uncorrelated with any Borel function [17] of the past $[\varvec{d}\tau ,\tau \le t]$. So the performance of the controller $\varvec{\tau }(t)$ depends on the accurate estimation of $\varvec{d}_i(t)$. In the majority of current research [6], $\varvec{\widehat{d}}_i(t)$ is estimated as observer with measurable $\varvec{q}$ and $\varvec{\dot{q}}$.

3 Nonlinear disturbance observer (NDO)

The basic idea is the design of a new observer assuming only joint position $(\varvec{q}(t))$ measurements are available instead of $\varvec{q}(t)$ and $\varvec{\dot{q}}(t)$ as reported in [1–3, 6]. Since (2) can be written as

$$\begin{aligned} \varvec{d}_i(t)=\varvec{M(q)\ddot{q} }+ \varvec{N(q},\varvec{\dot{q})}-\varvec{\tau }(t) -\varvec{\widetilde{w}}(t) \end{aligned}$$

(7)

so that $\varvec{\widehat{d}}_i(t)$ increases when $\varvec{\widehat{d}}_i(t)<\varvec{d}_i(t)$ and $\varvec{d}_i(t)$ decreases when $\varvec{\widehat{d}_i}(t)>\varvec{d}_i(t)$, a NDO is proposed as:

$$\begin{aligned} \varvec{\dot{\widehat{d}}_i}(t)=-\varvec{L(q) (\widehat{d}}_i(t)- \varvec{d}_i(t) -\varvec{\widetilde{w}}(t)) \end{aligned}$$

(8)

From (7)

$$\begin{aligned} \varvec{\dot{\widehat{d}}}_i(t)=&-\varvec{L(q)}(\varvec{\widehat{d}}_i(t))+ \varvec{L(q)}(\varvec{M(q)\ddot{q}})\nonumber \\&+\varvec{L(q)}(\varvec{(N(q,\dot{q})}-\varvec{\tau }(t)) \end{aligned}$$

(9)

Here $\varvec{L(q)}$ is the observer gain matrix and $\varvec{\ddot{q}}$ signal is not available. So we have to propose a modified disturbance observer. For this purpose, the auxiliary variable $\varvec{d_z}(t)$ is proposed as the solution to the following differential equation:

$$\begin{aligned}&\varvec{\dot{\widehat{d}_z}}(t)\equiv -\varvec{L(q)(\widehat{d}_i(t))}+\varvec{0}+\varvec{L(q)(N(q,\dot{q})}-\varvec{\tau (t))} \end{aligned}$$

(10)

$$\begin{aligned}&= -\varvec{L(q)(\widehat{d}_z(t)}+\varvec{p(\dot{q}))}+\varvec{ L(q)(N(q,\dot{q})}-\varvec{\tau (t))} \end{aligned}$$

(11)

Here

$$\begin{aligned} p\equiv \varvec{M(q)}\ddot{q} \end{aligned}$$

(12)

From (10) and (11),

$$\begin{aligned}&\varvec{\widehat{d}}_i(t)= \varvec{\widehat{d}_z}(t) + \varvec{p(\dot{q})} \end{aligned}$$

(13)

$$\begin{aligned}&\Rightarrow \quad \varvec{\dot{\widehat{d}}}_i(t)= \varvec{\dot{\widehat{d}}_z}(t)+\varvec{ p'(\dot{q})\ddot{q}} \end{aligned}$$

(14)

Here the construction of DO depends only on measurement of $\varvec{q}(t)$ and $\varvec{\dot{q}}(t)$ and not on $\varvec{\ddot{q}}(t)$.

Eqs. (9)–(10)

$$\begin{aligned} \varvec{\dot{\widehat{d}}_i(t)}-\varvec{\dot{\widehat{d}}_z}(t) = \varvec{L(q) M(q) \ddot{q}} \end{aligned}$$

(15)

From (14) and (15),

$$\begin{aligned}&\varvec{L(q) M(q) \ddot{q}}=\varvec{(p^{\prime } (\dot{q}))\ddot{q}} \end{aligned}$$

(16)

$$\begin{aligned}&\Rightarrow \quad \varvec{L(q)}=\varvec{p^{\prime }(\dot{q})} \varvec{M^{-1} (q)} \end{aligned}$$

(17)

$$\begin{aligned}&\Rightarrow \quad \varvec{p^{\prime }(\dot{q})} =\varvec{L(q)M(q)} \end{aligned}$$

(18)

where the function $\varvec{p}(\varvec{\dot{q}})$ in the observer (11) and (13) is chosen as

$$\begin{aligned} \varvec{p}(\varvec{\dot{q}})=\varvec{c}*\varvec{\dot{q}} \end{aligned}$$

(19)

Here $\varvec{c}$ is a constant matrix and then

$$\begin{aligned} \varvec{p^{\prime }(\dot{q})}=\varvec{c}\quad \text {and}\quad \varvec{L(\varvec{q})}=\varvec{c {M(q)}^{-1}} \end{aligned}$$

(20)

Also from (8) and (6),

$$\begin{aligned}&\varvec{\dot{\widehat{d}}_i}(t) = \varvec{L(q(t))} \times \varvec{w} (t) \end{aligned}$$

(21)

Expression (21) is a new finding not reported in the literature so far. Also we are able to calculate $\varvec{\dot{\widehat{d}}_i}(t)$ in measurable signal $\varvec{q}(t)$ only.

Remark 1

The common method of constructing the disturbance observer is:-

$$\begin{aligned} \varvec{\dot{d}_z}(t)&=\varvec{L}(t)(-\varvec{\tau }(t)+\varvec{N(q},\varvec{\dot{q})}-\varvec{\widehat{d}_i}(t)) \end{aligned}$$

(22)

$$\begin{aligned} \varvec{\widehat{d}_i}(t)&=\varvec{d_z}(t)+\varvec{p}(\varvec{\dot{q}}(t)) \end{aligned}$$

(23)

(see (20)) where $\varvec{p^{\prime }} (\dot{q}(t))=C$ is a constant matrix so that $\varvec{L}(t)=\varvec{C}(\varvec{M} (q))^{-1}.$ It follows that

$$\begin{aligned} \frac{d}{dt} \varvec{\widehat{d}_i}(t)&=\varvec{\dot{d}_z}(t)+\varvec{ p^{\prime }}\varvec{\dot{q}}(t)\varvec{\ddot{q}}(t) \end{aligned}$$

(24)

$$\begin{aligned}&=\varvec{L}(t)(-\varvec{\tau }(t)+\varvec{N(q,\dot{q})} -\varvec{\widehat{d}}_i(t))+\varvec{C\ddot{q}}(t)\end{aligned}$$

(25)

$$\begin{aligned}&=\varvec{L}(t)(-\varvec{\tau }(t)+\varvec{N(q,\dot{q})} -\varvec{\widehat{d}}_i(t)+\varvec{M(q)\ddot{q}}) \end{aligned}$$

(26)

and since

$$\begin{aligned} \varvec{M \ddot{q}}+\varvec{N(q},\varvec{\dot{q})}=\varvec{\tau (t)+d_i}(t)+\varvec{\tilde{w}}(t) \end{aligned}$$

(27)

(according to 2), we see $\varvec{\dot{\widehat{d}}_i}(t)=\varvec{L( d}(t)-\varvec{\widehat{d}_i}(t)+\varvec{\tilde{w}})$.

The extra term $\tilde{w}$ appears in our work because we have decomposed the whole disturbance into a purely random component $\tilde{w}$ and a predictable component $\varvec{d}_i(t)$.

The fundamental assumption of this work is that the disturbance prediction error $\varvec{d}(t)-\varvec{\widehat{d}}_i(t)=\varvec{\epsilon }(t)$ behaves like white noise that is independent of $\varvec{\tilde{w}}(t)$ the purely random component of the disturbance.

Although we cannot directly prove that $\varvec{\epsilon }(t)$ is white, we can heuristically make this postulate based on the well-known fact that if $[d_n]_{n=1}^{\infty }$ is a random sequence, then with $\varvec{\widehat{d}_n}=\mathbb {E}[d_n,|d_{n-1},d_{n-2},\ldots \ldots ]$, it follows that $\mathbb {E}[(d_n-\widehat{d_n})f(d_{n-1},d_{n-2},\ldots )]=0$ for any Borel function f. Hence, $d_n-\widehat{d}_n$ is uncorrelated with any function of $\{d_k-\widehat{d}_k,|k\le n-1\}$. Thus, $\{d_n-\widehat{d}_n\}$ is white noise. Our heuristic assumption is based on this fact, and this is confirmed by our simulation success.

Remark 2

The disturbance observer differential equation $\varvec{\dot{\widehat{d}}_i}(t)=\varvec{L}(t)(\varvec{d_i}(t)-\varvec{\widehat{d}_i}(t)+\varvec{\tilde{w}}(t))$ defines a time-varying system, and hence, it is difficult to talk of a frequency domain analysis. However, we can give an argument as follows, which justifies somewhat that $d_i(t)-\widehat{d}_i(t)$ behaves like white noise in the sense that it contains almost all the frequencies in its spectrum.

Since $\varvec{\tilde{\sigma }_w}^2$ is very small, we have approximately

$$\begin{aligned} \varvec{\dot{\widehat{d}}_i}(t)=\varvec{L}(t)(d_i(t)-\varvec{\widehat{d}}_i(t)) \end{aligned}$$

and with $\epsilon (t)=d_i(t)-\widehat{d}_i(t),$ we get $\varvec{\dot{\epsilon }}(t)=\varvec{\dot{d}_i}(t)-\varvec{L}(t)\varvec{\epsilon }(t).$

The solution to this differential equation is the infinite series (Dyson series)

$$\begin{aligned} \varvec{\epsilon }_t=&d_t+\sum _{n=1}^{\infty }(-1)^n\nonumber \\&\times \int _{0<t_n< \cdots t_1<t}L(q(t_1)) \ldots L(q(t_n))d_i(t_1)\nonumber \\&\ldots d_i(t_n) dt_1 \ldots dt_n \end{aligned}$$

(28)

If L(t) consists of a discrete set of frequencies (or is periodic with a Fourier series)$, \omega _1, \ldots ,\omega _k$ and $d_i(t)$ also consist of a discrete set of frequencies, say $\omega _1^{\prime } \ldots \omega _m^{\prime },$ then the integral

$$\begin{aligned}&\int _{0<t_n< \cdots t_1<t} L(q(t_1)) \nonumber \\&\quad \ldots L(q(t_n))d_i(t_1) \ldots d_i(t_n) dt_1 \ldots dt_n \end{aligned}$$

(29)

will contain the frequencies $\theta _1+\theta _2+ \cdots \cdots \theta _{2n}$ where each $\theta _i \epsilon \{\pm \omega _1, \ldots \ldots ,\pm \omega _k,\pm \omega _1^{\prime }, \ldots ,\pm \omega _n^{\prime } \}$; hence, the Dyson series (28) shows that $\epsilon (t)$ will contain almost all the frequencies obtained as infinite integer linear combination of $\omega _1, \ldots ,\omega _k, \omega _1^{\prime }, \ldots ,\omega _n$ and hence $\epsilon (t)$ can be justified as being white noise.

Remark 3

If

$$\begin{aligned} \varvec{q}(t)=\varvec{q}^{(0)}+\varvec{q}^{(1)}(t)+\varvec{q}^{(2)}(t) \end{aligned}$$

where $\varvec{q}^{(0)}$ is a dc vector (constant), $\varvec{q}^{(1)}(t)$ is a linear time-varying vector, and $\varvec{q}^{(2)}(t)$ consists of sinusoidal oscillating term.

Then by Taylor’s series,

$$\begin{aligned} L(t)= & {} L(\varvec{q}^{(0)}+\varvec{q}^{(1)}(t)+\varvec{q}^{(2)}(t)+\varvec{\dot{q}}^{(1)}(t)+\varvec{\dot{q}}^{(2)}(t))\\= & {} \varvec{L}_0+\varvec{L}_1(t) \end{aligned}$$

where $\varvec{L}_0=L(\varvec{q}^{(0)}, \varvec{q}^{(1)})$ is a constant matrix, and $\varvec{L}_1(t)$ comes from Taylor expansion of L around $(\varvec{q}^{(0)},\varvec{q}^{(1)})$.

$\varvec{L}_1(t)$ consists of harmonic terms. Then

$$\begin{aligned} \dot{\epsilon }(t)= & {} \dot{d}_i(t)-(\varvec{L}_0+\varvec{L}_1(t))(\epsilon (t)+\tilde{w}(t)) \approxeq \dot{d}_i(t)\\&\quad -(L_0+L_1(t))\epsilon (t)-L_0\tilde{w}(t) \end{aligned}$$

If we further neglect $\tilde{w}(t)$, we get $\dot{\epsilon }(t)=\dot{d}_i(t)-(\varvec{L}_0+\varvec{L}_1(t))(\epsilon (t))$.

Which has the Dyson series solution

$$\begin{aligned} \epsilon =&d_i(t)+\sum \limits _{n=1}^{\infty }(-1)^n\int (L_0+L_1(t_1)) \ldots \ldots \\&(L_0+L_1(t_n))d(t_1) \ldots d(t_n)(dt_1 \ldots \ldots dt_n) \end{aligned}$$

This expression contains terms

$$\begin{aligned}&d_i(t)+\sum _{n=1}^{\infty }L_0^n(-1)^n\int d(t_1) \ldots d(t_n)0<t_n\nonumber \\&\quad< \cdots <dt_1 \ldots dt_n \end{aligned}$$

which contains not only the frequency of $d_i(t)$, but also linear combination of the frequencies of $d_i(t)$. The frequencies of $d_i(t)$ appear in $\epsilon (t)$ however, with a suppressed amplitude. This can be seen by taking the Fourier transform of the approximate equation $\dot{\epsilon }(t)=\dot{d}_i(t)-L_0\epsilon (t)$ which gives

$$\begin{aligned} (\mathcal {F}\epsilon )(\omega )=(j\omega I+\varvec{L}_0)^{-1}j\omega \mathcal {F}(di)(\omega ) \end{aligned}$$

where $\mathcal {F}$ denotes the Fourier transform operator.

Thus, if $\varvec{L}_0$ is chosen so that for $\omega$ falling in the band of

$$\begin{aligned} d_i(t)(i.e., (\mathcal {F}ds(\omega ))) \end{aligned}$$

$|\omega |<<||\varvec{L}_0||$, then $|(\mathcal {F}(.)(\omega ))$ will be small and hence then frequencies of $d_i(t)$ will be suppressed in $\epsilon (t)$.

$\tilde{w}(t)$ is white processes noise independent of d(t). Suppose we include its effects in this linear analysis. Then we get $\dot{\epsilon }(t)=\dot{d}_i(t)-L_0(\epsilon (t)+\tilde{w}(t))$ which gives on taking Fourier transforms $(\mathcal {F}\epsilon )(\omega )=\frac{[j\omega \mathcal {F}(d_i)(\omega )-L_0\mathcal {F}\{\tilde{w}\}(\omega )]}{(j\omega I+L_0)}$ so if $\omega$ falls in a range of $\mathcal {F}\{d\}$ such that $|\omega |<<||L_0||$, then in this range, $(\mathcal {F}\epsilon )(\omega )\approxeq -\mathcal {F}\{\tilde{w}\}(\omega )$ which means that again $\epsilon (t)$ will behave like white noise.

4 The proposed disturbance extended Kalman filter (DEKF)

We begin by defining the state vector:

$$\begin{aligned} X=[\varvec{q}(t) \ \varvec{\omega }(t) \ \varvec{\eta }(t)]^T \end{aligned}$$

Here $\varvec{\eta }(t) =\varvec{\widehat{d}}_i(t)$, $\dot{\varvec{\eta }}(t) =\varvec{\dot{\widehat{d}}}_i(t)$ as shown in (21), and $\varvec{\omega }(t) =\varvec{\dot{q}}(t)$.

The robot system model in (5) will be extended as follows:

$$\begin{aligned} \varvec{\dot{q}}&= \varvec{\omega } \end{aligned}$$

(30)

$$\begin{aligned} \varvec{\dot{\omega }}&=\varvec{F(q,\omega ,t)}+\varvec{G(q)(\eta }+\varvec{w)}\end{aligned}$$

(31)

$$\begin{aligned} \varvec{\dot{\eta }}&=\varvec{L(q)w} \end{aligned}$$

(32)

Here

$$\begin{aligned}&\varvec{F(q,\omega ,t)}=\varvec{G(q)(\tau }-\varvec{N(q,\dot{q}))} \end{aligned}$$

(33)

$$\begin{aligned}&\varvec{G(q)}=\varvec{M(q)^{-1} } \end{aligned}$$

(34)

Introduction of disturbance observer as a state variable is the one of the major contributions of this work.

So

$$\begin{aligned}&\dot{X} = \frac{d}{{dt}}\left[ {\begin{array}{lll} q \\ \omega \\ \eta \\ \end{array} } \right] \nonumber \\&\quad = \left[ {\begin{array}{lll} \omega \\ {F(q,\omega ,t) + G(q)\eta } \\ 0 \\ \end{array} } \right] + \left[ {\begin{array}{lll} 0 \\ {G(q)} \\ {L(q)} \\ \end{array} } \right] \varvec{w} \end{aligned}$$

(35)

$$\begin{aligned}&\Rightarrow \quad \varvec{\dot{X}} = \varvec{f(t,X)}+\varvec{g}(\varvec{q})\varvec{w} \end{aligned}$$

(36)

For nonlinear system,

$$\begin{aligned}&\varvec{\dot{z}}=\varvec{h} (t,\varvec{X})+\varvec{\eta }_X \end{aligned}$$

(37)

Here $\varvec{\eta }_X=\sigma _v \frac{d\varvec{v}(t)}{dt}$ is Gaussian measurement noise. From Kushner filter theory [18], extended nonlinear disturbance observer is constructed along with plant dynamics as below:

$$\begin{aligned} \varvec{\dot{\widehat{X}}} = \varvec{f( {t,\widehat{X}})}+\varvec{P}\varvec{\widehat{h}}^{\prime T} \varvec{\sigma }_v^{-2}(\varvec{\dot{z}}- \varvec{\widehat{h}}) \end{aligned}$$

(38)

and

$$\begin{aligned} \varvec{\dot{P}}= \varvec{\widehat{f}}^{\prime } \varvec{P}+\varvec{P}\varvec{\widehat{f}}^{\prime T}+\varvec{\sigma }_w\varvec{\widehat{g}}\varvec{\widehat{g}} ^T - \varvec{P} \varvec{\widehat{h}}^{\prime T}\varvec{\sigma }_v^{-1} \varvec{\widehat{h}^{\prime } P} \end{aligned}$$

(39)

So for a linear measurement system:

$$\begin{aligned}&\dot{\widehat{\varvec{X}}} = \varvec{f(t,\widehat{X})}+\varvec{PH}^T \varvec{\sigma }_v^{-2} (\varvec{\dot{z}}-\varvec{H}\varvec{ \widehat{X}}) \end{aligned}$$

(40)

$$\begin{aligned}&= \varvec{f(t,\varvec{\widehat{X}})}+\varvec{PH}^T \varvec{\sigma }_v^{-2} (\varvec{\dot{z}}-\varvec{\widehat{q}}) \end{aligned}$$

(41)

$$\begin{aligned}&\varvec{\dot{P}}= \varvec{\widehat{f}}^{\prime } \varvec{P}+\varvec{P}\varvec{\widehat{f}}^{\prime T}\nonumber \\&\quad +\varvec{\sigma }_w\varvec{\widehat{g}}\varvec{\widehat{g}} ^T - \varvec{P} \varvec{H}^{T}\varvec{\sigma }_v^{-1} \varvec{H P} \end{aligned}$$

(42)

$$\begin{aligned}&\varvec{h} (t,\varvec{X})=\varvec{HX} \end{aligned}$$

(43)

$$\begin{aligned}&\implies \varvec{\dot{z}}=\varvec{HX} + \varvec{\eta }_X \end{aligned}$$

(44)

Here $\varvec{\dot{z}}$ is the measurable output of the plant. $\varvec{H}$ is the state observation matrix. For a robot with optical encoder:

$$\begin{aligned}&\varvec{H} =[I:0] \ \ \text {so that} \ \ \varvec{HX}=\varvec{q}\,. \end{aligned}$$

(45)

$$\begin{aligned}&\varvec{\sigma }_v = covariance (\varvec{\eta _x}) \end{aligned}$$

(46)

$$\begin{aligned}&\varvec{\sigma }_w= \left[ {\begin{array}{lll} 0 &{} 0 &{} 0 \\ 0 &{} {cov.(w)} &{} 0 \\ 0 &{} 0 &{} {cov.(w)} \\ \end{array} } \right] \end{aligned}$$

(47)

$$\begin{aligned}&\varvec{P}=\varvec{\widehat{h}},_\beta ^T \varvec{P}_{\alpha ,\beta } = \left[ {\begin{array}{lll} {P_{q} } &{} {P_{{q,\omega }} } &{} {P_{{q,\eta }} } \\ {P_{{\omega ,q}} } &{} {P_{\omega } } &{} {P_{{\omega ,\eta }} } \\ {P_{{\eta ,q}} } &{} {P_{{\eta ,\omega }} } &{} {P_{\eta } } \\ \end{array} } \right] \end{aligned}$$

(48)

$$\begin{aligned}&\varvec{g(\widehat{X})}=\varvec{g(\widehat{q})} = \left[ {\begin{array}{lll} 0 \\ {G(\hat{q})} \\ {L(\hat{q})} \\ \end{array} } \right] \end{aligned}$$

(49)

5 Stability and convergence analysis of DEKF

In the previous section, we have written down the nonlinear state equation in SDE form and the nonlinear noisy measurement equations with additional WGN. We then write down the EKF for the state estimate and its error covariance matrix with driving force provided by the difference between the actual measurements and the estimated measurements. The EKF can in some sense be looked upon as a nonlinear version of the active observer with gain dependent on the error covariance and the measurement Jacobian evaluated at the current state estimates. In this section, we shall form using the difference of the state and EKF equation an approximate linear SDE for the state estimation error and calculate its mean square error w.r.t a Lyapunov matrix. Conditions on the noise coefficients (both state and measurements) for this mean square error to remain bounded with time are then derived. Here we derive a generalized form of sensitivity analysis which may be applied using Gronwall’s inequality [19] not addressed so far in the literature.

State model In what follows, we consider the general model for the state vector defined by a general multivariate stochastic differential equation driven by a multivariate standard Brownian motion with time-dependent drift and diffusion coefficients and we have also considered the measurement model as general as possible, i.e., given by a nonlinear time-dependent function of the state plus white Gaussian noise. We then develop a theory for calculating the EKF-based estimation error and upper bounds for this. The state model is:

$$\begin{aligned} d\varvec{X}_t=\varvec{f}(t,\varvec{X}_t)dt+\varvec{g} (t,\varvec{X}_t)d\varvec{B}_t \end{aligned}$$

(50)

and the measurement model is:

$$\begin{aligned} d\varvec{z}_t = \varvec{h} (t,\varvec{X}_t)dt+\sigma _V d\varvec{V}_t \end{aligned}$$

(51)

EKF

$$\begin{aligned}&d\widehat{\varvec{X}}_t = \varvec{f}(t, \widehat{\varvec{X}}_t)dt+\sigma _V^{-2} \varvec{P}_t \varvec{h}^{\prime }(t, \widehat{\varvec{X}}_t)^T\nonumber \\&\quad (d\varvec{z}_t-h(t,\widehat{\varvec{X}}_t)dt) \end{aligned}$$

(52)

$$\begin{aligned}&\dfrac{d\varvec{P}_t}{dt} =\varvec{f}^{\prime }(t,\widehat{\varvec{X}}_t)\varvec{P}_t+\varvec{P}_t \varvec{f}^{\prime }(t, \widehat{\varvec{X}}_t)^T \nonumber \\&- \varvec{P}_t \varvec{h}^{\prime }(t,\widehat{\varvec{X}_t})^T \varvec{h}^{\prime }(t, \widehat{\varvec{X}_t})P_t+(\varvec{g} \varvec{g}^T)(t,\widehat{\varvec{X}}_t) \end{aligned}$$

(53)

Let

$$\begin{aligned}&\varvec{g} \varvec{g}^T (t, \varvec{x}) = \varvec{a}(t, \varvec{x}) \end{aligned}$$

(54)

$$\begin{aligned}&\varvec{e}_t =\varvec{X}_t - \widehat{\varvec{X}}_t \end{aligned}$$

(55)

$$\begin{aligned}&d \varvec{e_t} = d\varvec{X_t}- d\widehat{\varvec{X_t}} \end{aligned}$$

(56)

After linearization around $\widehat{\varvec{X_t}}$,

$$\begin{aligned}&d \varvec{e} _t=f^{\prime }(t,\widehat{\varvec{X}}_t)\varvec{e_t}dt + g(t, \widehat{\varvec{X}}_t)d \varvec{B}_t \nonumber \\&\quad - \sigma _V^{-2}\varvec{P}_t \varvec{h}^{\prime }(t, \widehat{\varvec{X}}_t)^T (\varvec{h}^{\prime }(t, \widehat{\varvec{X}}_t)\varvec{e}_tdt +\sigma _V d \varvec{V}_t) \end{aligned}$$

(57)

$$\begin{aligned}&=[\varvec{f}^{\prime }(t, \widehat{\varvec{X}}_t)-\sigma _V^{-2}\varvec{P}_t \varvec{h}^{\prime }(t, \widehat{\varvec{X}}_t)^T \varvec{h}^{\prime }(t,\varvec{X}_t)]\varvec{e}_t dt\nonumber \\&\quad +\varvec{g} (t, \widehat{\varvec{X}}_t)d\varvec{B}_t- \sigma _V^{-1}\varvec{P}_t \varvec{h}^{\prime } (t, \widehat{\varvec{X}}_t)^T d\varvec{V}_t \end{aligned}$$

(58)

Let

$$\begin{aligned} \varvec{F}_t=\varvec{f}^{\prime }(t, \widehat{\varvec{X}}_t)-\varvec{P}_t \varvec{h}^{\prime }(t, \widehat{\varvec{X}}_t)^T \varvec{h}^{\prime }(t, \widehat{\varvec{X}}_t) \end{aligned}$$

(59)

and

$$\begin{aligned} \varvec{G}_t&= \varvec{g}(t, \widehat{\varvec{X}}_t), \end{aligned}$$

(60)

$$\begin{aligned} \varvec{H}_t&=-\varvec{\sigma }_V^{-1} \varvec{P}_t \varvec{h}^{\prime }(t, \widehat{\varvec{X}}_t)^T \end{aligned}$$

(61)

Then (58) can be expressed as:,

$$\begin{aligned} d \varvec{e}_t&= \varvec{F}_t \varvec{e}_t dt + \varvec{G}_t d\varvec{B}_t+\varvec{H}_t d\varvec{V}_t \end{aligned}$$

(62)

with solution

$$\begin{aligned} \varvec{e}_t&=\int _0^T \varvec{\phi }_F(t,\tau ) (\varvec{G}_\tau d\varvec{B}_\tau + \varvec{H}_\tau d\varvec{V}_\tau ) \end{aligned}$$

(63)

where $\varvec{\phi }_F(t,\tau )$ is the state transition matrix satisfying:

$$\begin{aligned} \dfrac{\partial \varvec{\varPhi } _F(t,\tau )}{\partial t}&=\varvec{F}_t \varvec{\varPhi }_F (t,\tau ),\quad t\ge \tau , \end{aligned}$$

(64)

with the initial condition:

$$\begin{aligned} \varvec{\varPhi } _F(\tau ,\tau )&=I \end{aligned}$$

(65)

Theorem 1

Assuming that

$$\begin{aligned} \max _{t\ge 0}\mathbb {E}[Tr(\varvec{G}_t \varvec{G}_t^T)+Tr (\varvec{H}_t \varvec{H}_t^T)]=K^{\prime }<\infty \end{aligned}$$

We have that $\mathbb {E}||e_t||^2$ is a bounded function of time.

Proof

We have from (63)

$$\begin{aligned}&\mathbb {E} [\Vert \varvec{e}_t\Vert ^2]=\,\mathbb {E}\int _0^T Tr(\varvec{\varPhi }_F(t,\tau ) \varvec{G}_\tau \varvec{G}_\tau ^T\varvec{\varPhi }_F(t,\tau ))d\tau \nonumber \\&\quad + \mathbb {E}\int _0^T Tr (\varvec{\varPhi }_F (t,\tau ) \varvec{H}_\tau \varvec{H}_\tau ^{T}\varvec{\varPhi }_F^T (t,\tau ))d\tau \ \end{aligned}$$

(66)

More generally, let the Lyapunov energy matrix $V>0$. Then

$$\begin{aligned}&d\ (\mathbb {E} [e_t^T V e_t]) = \mathbb {E} (d(\varvec{e}_t^T \varvec{V}\varvec{e}_t))=\mathbb {E} (\varvec{e}_t^T V d\varvec{e}_t)\nonumber \\&\quad +Tr[V\,\mathbb {E}(d\varvec{e}_t d \varvec{e}_t^T)] \end{aligned}$$

(67)

$$\begin{aligned}&= \mathbb {E} [\varvec{e}_t^T (\varvec{F}_t^T \varvec{V}+\varvec{V}\varvec{F}_t^T)\varvec{e}_t]dt \nonumber \\&\quad + \mathbb {E}[Tr (\varvec{G}_t \varvec{G}_t^T)+Tr (\varvec{H}_t \varvec{H}_t^T)]dt \end{aligned}$$

(68)

$\square$

The rate of change of the mean square state estimation error energy is obtained for the EKF using the stochastic Lyapunov method, and using this expression, we derive an inequality for the mean square error which resembles the Gronwall inequality. This inequality is used to show that as $t \rightarrow \infty$ under sufficiently general conditions on the noise coefficients $\varvec{G}_t$ and $\varvec{H}_t$, the mean square error remains bounded.

If rate of change of error energy:

$$\begin{aligned} \varvec{F}_t^T \varvec{V}+V\varvec{F}_t^T \le -\varvec{\varGamma }<0 \forall t \end{aligned}$$

(69)

Then

$$\begin{aligned} \dfrac{d}{dt}\mathbb {E} [\varvec{e}_t^T\varvec{V} \varvec{e}_t]\le \mathbb {E}[\varvec{e}_t^T \varvec{\varGamma } \varvec{e}_t]+\eta _t \end{aligned}$$

(70)

where

$$\begin{aligned} \eta _t=\mathbb {E}\left[ Tr(\varvec{G}_t \varvec{G}_t^T)+Tr (\varvec{H}_t \varvec{H}_t^T)\right] \end{aligned}$$

(71)

So,

$$\begin{aligned} \mathbb {E} \left[ \varvec{e}_t^T\varvec{V} \varvec{e}_t^T\right] \le -\int _0^t \mathbb {E} \left[ \varvec{e}^{\prime T}_t \varvec{\varGamma } \varvec{e}^{\prime }_t\right] \mathrm{d}t^{\prime } +\int _0^t \eta _t^{\prime } \mathrm{d}t^{\prime } \end{aligned}$$

(72)

Suppose $V\ge KI$. Then

$$\begin{aligned} \mathbb {E} \left[ \Vert \varvec{e}_t\Vert ^2\right] \le -K^{-1} \int _0^t \mathbb {E} \left[ \varvec{e}_s^T \varvec{\varGamma } \varvec{e}_s\right] \mathrm{d}s+K^{-1} \int _0^t \eta _s \mathrm{d}s \end{aligned}$$

(73)

Let $\varvec{\varGamma } \ge K_0 I$.

Then we get

$$\begin{aligned} \mathbb {E}[\Vert \varvec{e}_t\Vert ^2]\le -\dfrac{K_0}{K}\int _0^t \Vert \varvec{e}_s\Vert ^2 \mathrm{d}s +K^{-1} \int _0^ t \eta _s \mathrm{d}s \end{aligned}$$

(74)

Put

$$\begin{aligned} \int _0^t \Vert \varvec{e}_s\Vert ^2 \mathrm{d}s =\xi _t \end{aligned}$$

(75)

and then Gronwall’s inequality can be applied to (74), which is then same as

$$\begin{aligned} \dfrac{{\hbox {d}}\xi _t}{{\hbox {d}}t}\le -\alpha \xi _t+\beta _t \end{aligned}$$

(76)

where $\alpha =K_0/K$ and $\beta _t=K^{-1}\int _0^t \eta _s \mathrm{d}s$.

Thus,

$$\begin{aligned} \xi _t\le e^{-\alpha t} \xi _0+\int _0^t e^{-\alpha (t-s)}\beta _s \mathrm{d}s \end{aligned}$$

(77)

Hence, if

$$\begin{aligned} e^{-\alpha t}\int _0^t e^{\alpha s} \beta _s \mathrm{d}s\rightarrow 0,\quad t\rightarrow \infty , \end{aligned}$$

(78)

then

$$\begin{aligned} \mathbb {E} \Vert \varvec{e}_t\Vert ^2 \rightarrow 0; t\rightarrow \infty , \end{aligned}$$

(79)

Since it is assumed that

$$\begin{aligned}&\max _{t\ge 0}\mathbb {E}[Tr(\varvec{G}_t \varvec{G}_t^T)+Tr (\varvec{H}_t \varvec{H}_t^T)]=K^{\prime }<\infty , \end{aligned}$$

(80)

$$\begin{aligned}&i.e., \qquad \max _{t\ge 0}(\eta _t)=K^{\prime }<\infty \end{aligned}$$

(81)

It follows that

$$\begin{aligned}&\int _0^t e^{-\alpha (t-s)}\beta _s \mathrm{d}s = {K}^{-1}\int _{0<u<s<t}^{} e^{-\alpha (t-s)}\eta _udsdu \end{aligned}$$

(82)

$$\begin{aligned}&=K^{-1}\int _{0}^{t}\frac{1-e^{-\alpha (t-u)}}{\alpha }\eta _udu\nonumber \\&\quad \le \frac{K^{\prime }}{K\alpha }\left[ t-\frac{1-e^{\alpha t}}{\alpha }\right] \end{aligned}$$

(83)

$$\begin{aligned}&=\frac{K^{\prime }t}{K \alpha }=\frac{K^{\prime }t}{K_0} \end{aligned}$$

(84)

This implies that $\mathbb {E} \Vert \varvec{e}_t\Vert ^2$ $\approx \frac{K^{\prime }}{K_0}$ for t $\rightarrow$ $\infty$.

That is, the mean square error remains bounded as t $\rightarrow$ $\infty$.

So the bound is decided by the parameters $K_0$ and K. $K^{\prime }$ is a measure of the state noise plus measurement noise energy, while $K_0$ is a lower bound for the Lyapunov matrix. The upper bound for the limiting mean square error estimation error is $\propto$ $\frac{K}{K_0}$.

Higher $K^{\prime }$ $\implies$ higher noise power $\implies$ larger mean square error. Higher $K_0$ $\implies$ larger Lyapunov matrix V $\implies$ lower mean square error energy.

6 Robustness of DEKF to uncertainty

We further elaborate on the same theme but with an unknown parameter vector $\varvec{\theta }_0$ like parameter uncertainty entering into the state equation and designing the DEKF based on a guess parameter vector $\varvec{\theta }$. The true state vector is $X_t( \widehat{\varvec{\theta }}_0)$. We derive using the Ito’s calculus an upper bound for $\mathbb {E} \Vert X_t(\varvec{\theta }_0)-\widehat{ X_t}(\varvec{\theta })\Vert ^2$ in terms of $\Vert \varvec{\theta }-\varvec{\theta }_0\Vert ^2$ assuming that $\delta \varvec{\theta }=\varvec{\theta }-\varvec{\theta }_0$ and the uncertainty is small and thereby establish conditions for robustness of the DEKF.

Actual model

$$\begin{aligned} d\varvec{X}_t&= \varvec{f}(t, \varvec{X}_t, \varvec{\theta }_0)+\varvec{g}(t, \varvec{X}_t, \varvec{\theta }_0)d\varvec{B}_t \end{aligned}$$

(85)

$$\begin{aligned} d\varvec{Y}_t&= \varvec{h}(t,\varvec{X}_t)dt + \sigma d \varvec{V}_t \end{aligned}$$

(86)

Assumed model

$$\begin{aligned} d\widetilde{X}_t&= \varvec{f}(t,\widetilde{\varvec{X}}_t, \varvec{\theta })+\varvec{g}(t,\widetilde{\varvec{X}}_t, \varvec{\theta })d\varvec{B}_t \end{aligned}$$

(87)

$$\begin{aligned} d\widetilde{Y}_t&= \varvec{h}(t,\widetilde{\varvec{X}}_t)dt + \sigma d \varvec{V}_t \end{aligned}$$

(88)

EKF is based on assumed state model and original output mass moments.

$$\begin{aligned}&d \widehat{\varvec{X}}_t=\varvec{f}(t, \widehat{\varvec{X}}_t,\varvec{\theta })dt\nonumber \\&\quad + P_t H^T (t, \widehat{\varvec{X}}_t)(d Y_t - \varvec{h}(t, \widehat{\varvec{X}}_t)dt) \end{aligned}$$

(89)

$$\begin{aligned}&\dfrac{d\varvec{P}_t}{dt}=\varvec{F}(t, \widehat{\varvec{X}}_t,\varvec{\theta })\varvec{P}_t + \varvec{P}_t \varvec{F}^T (t, \widehat{\varvec{X}}_t, \varvec{\theta }) \nonumber \\&\quad +\varvec{a} (t, \widehat{\varvec{X}}_t, \varvec{\theta })-\varvec{P}_t \varvec{H}^T (t, \widehat{\varvec{X}_t})\varvec{H}(t, \widehat{\varvec{X}}_t)P_t \end{aligned}$$

(90)

$$\begin{aligned}&e_t= X_t-\widehat{X}_t\equiv X_t(\theta _0)-\widehat{X}_t(\theta ) \end{aligned}$$

(91)

$$\begin{aligned}&d\varvec{e}_t=(\varvec{f}(t,\varvec{X}_t,\varvec{\theta }_0)-\varvec{f}(t, \widehat{\varvec{X}}_t,\varvec{\theta }))dt \nonumber \\&\quad +\varvec{g}(t, \varvec{X}_t, \varvec{\theta }_0)d B_t-P_t H^T (t, \widehat{\varvec{X}}_t) \nonumber \\&\quad ((\varvec{h}(t, X_t)-h(t,\widehat{X}_t))dt +\sigma d V_t) \end{aligned}$$

(92)

Let $L_t = P_t H^T (t, \widehat{\varvec{X}}_t)$. Then

$$\begin{aligned} d\varvec{e}_t&\approx F(t, \widehat{X}_t, \theta _0)(X_t-\widehat{X}_t)dt -\dfrac{\partial f}{\partial \theta }(t,\widehat{X}_t)\delta \varvec{\theta } dt \nonumber \\&\ \quad +\varvec{g}(t, \widehat{X}_t, \varvec{\theta }_0)d\varvec{B}_t- \varvec{L_t H(t, \widehat{X}_t)(X_t-\widehat{X}_t)dt}\nonumber \\&\ \quad -\sigma L_t d\varvec{V}_t \end{aligned}$$

(93)

or

$$\begin{aligned} d \varvec{e}_t&\approx (\varvec{F}_t)\varvec{e}_t dt+\varvec{G}_t d\varvec{B}_t-L_t H_t \varvec{e}_t dt\nonumber \\&-\sigma L_t d\varvec{V}_t -\varvec{F}_{\theta t} \delta \varvec{\theta } dt =(F_t - L_t H_t)\varvec{e}_t dt\nonumber \\&+ \varvec{G}_t d\varvec{B}_t -\sigma L_t d\varvec{V}_t-\varvec{F}_{\theta t}\delta \varvec{\theta } dt \end{aligned}$$

(94)

where $H(t,\hat{X_t})=H_t=h^{\prime }(t,\hat{X(t)})$. Let

$$\begin{aligned}&\dfrac{\partial \varPhi (t,\tau )}{\partial t}= (F_t- L_t H_t)\varPhi (t,\tau ),\quad t\ge \tau \end{aligned}$$

(95)

$$\begin{aligned}&\varPhi (\tau ,\tau )=I \end{aligned}$$

(96)

$$\begin{aligned} Then,\quad \varvec{e}_t&\approx \int _0^t \varPhi (t,\tau )(\varvec{G}_\tau d\varvec{B}_\tau -\sigma L_\tau d\varvec{V}_\tau ) \nonumber \\&\quad - \int _0^t \varPhi (t,\tau )F_{\theta \tau }\delta \theta d\tau \end{aligned}$$

(97)

$$\begin{aligned}&\mathbb {E}[\Vert \varvec{e}_t\Vert ^2] =\mathbb {E} [\Vert X_t (\varvec{\theta }_0)-\widehat{X}_t (\varvec{\theta })\Vert ^2]\end{aligned}$$

(98)

$$\begin{aligned}&\approx \mathbb {E} \int _0^t Tr \{\varvec{\varPhi } (t,\tau )(\varvec{G}\tau \varvec{G}^T \tau +\sigma ^2 \varvec{L}\tau \varvec{L}^t\tau )\varvec{\phi }^{T} (t,\tau )\}d\tau \nonumber \\&\quad + \delta \varvec{\theta }^T \mathbb {E}\left\{ \left( \int _0^t \varvec{\varPhi } (t,\tau )\varvec{F}_{\theta \tau }d\tau \right) \left( \int _0^t \varvec{\varPhi }(t,\tau )\varvec{F}_{\theta \tau } d\tau \right) ^T \right\} \delta \varvec{\theta } \end{aligned}$$

(99)

Let

$$\begin{aligned}&\mathbb {E} [\Vert e_t\Vert ^2]_{\delta \varvec{\theta }=0}=\xi _0 (t), \end{aligned}$$

(100)

$$\begin{aligned}&\mathbb {E} [\Vert e_t\Vert ^2]=\xi _0 (t)+\delta \xi (t) \end{aligned}$$

(101)

Then

$$\begin{aligned} \delta \xi (t)= \delta \varvec{\theta }^T \mathbb {E}\left\{ \left( \int _0^t\varvec{\varPhi }(t,\tau )\varvec{F}_{\theta \tau }d\tau \right) \left( \int _0^t\varvec{\varPhi }(t,\tau )\varvec{F}_{\theta \tau }d\tau \right) ^T \right\} \delta \varvec{\theta } \end{aligned}$$

(102)

where

$$\begin{aligned} \varvec{F}_{\theta \tau }=\dfrac{\partial f}{\partial \varvec{\theta }}(t,\widehat{X}_t, \theta _0). \end{aligned}$$

$$\begin{aligned} |\partial \xi (t)|\le K_t \Vert \delta \varvec{\theta }\Vert ^2 \end{aligned}$$

(103)

where

$$\begin{aligned} K_t=\left\| \mathbb {E}\left\{ \left( \int _0^t\varvec{\varPhi }(t,\tau )\varvec{F}_{\theta \tau }d\tau \right) \left( \int _0^t\varvec{\varPhi }(t,\tau )\varvec{F}_{\theta \tau }d\tau \right) ^T \right\} \right\| _S \end{aligned}$$

(104)

$\Vert \cdot \Vert _S$ denoting spectral norm, such that largest eigenvalue.

This discussion is summarized in the form of Theorem 2.

Theorem 2

If the actual system model is given by (85), (86) and the assumed model by (87),(88), then with $\widehat{X}_t$ obtained from the EKF applied to the assumed model, and the estimated state error $e_t=X_t(\theta _0)-\widehat{X_t}(\theta _0)$, we have $|\mathbb {E}[||e_t||^2] -\mathbb {E}||e_t||^2|_{\delta \theta =0}| \le \delta {\theta }^TK_t\delta \theta$ where $K_t$ is given by (104).

Typically, the eigenvalue of the “forcing function with estimation error feedback $(F_t-L_tH_t)$” for the state estimation error with parametric uncertainty will have negative real part which means that $\varPhi (t,\tau )$ will asymptotically behave as sum of terms of the form $e^{-\lambda (t-\tau )}$, where $Real(\lambda )>0$. Thus, if sensitivity of forcing drift function $F_{\theta \tau }$ with respect to parameter is bounded with time, the error response $\int _{0}^{t}\varPhi (t,\tau )F_{\theta \tau } d\tau$ to the sensitivity of the drift function will converge as $t \rightarrow \infty$ and $K_t$ will be bounded as $t \rightarrow \infty$.

7 Application of proposed DEKF to a Phantom Omni Robot™

In this section, the performance of the proposed algorithm is illustrated by applying it to a Phantom Omni Robot™available in the laboratory and the performance of DEKF is also compared against the method proposed in [6] (Table 1).

7.1 Dynamics of Phantom Omni Robot™

The dynamic model of the robot defined as in (2) and physical parameters as per [6] is given as below: The inertia matrix of the Phantom robot, assuming $q_2=0$, is

$$\begin{aligned} \varvec{M(q)}=\left[ {\begin{array}{ll} {\alpha _{1} + \alpha _{2} C_{{2,3}} + \alpha _{3} S_{{2,3}} + \alpha _{4} C_{3} + \alpha _{5} S_{3} } &{} 0 \\ 0 &{} {\alpha _{6} } \\ \end{array} } \right] \end{aligned}$$

(105)

and

$$\begin{aligned} \varvec{N(q,\dot{q})}=[V_1,V_3]^T \end{aligned}$$

(106)

where

$$\begin{aligned} V_1=&-2\alpha _2 \dot{q}_1\dot{q}_3 \sin (2q_3)+2\alpha _3\dot{q}_1\dot{q}_3\cos (2q_3) \nonumber \\&+\alpha _4 \dot{q}_1\dot{q}_3\cos (q_3)-\alpha _5 \dot{q}_1\dot{q}_3 \sin (q_3), \end{aligned}$$

(107)

$$\begin{aligned} V_3=&2\alpha _2 \dot{q}_1^2 \cos (q_3)\sin (q_3)-\alpha _3 \dot{q}_1^2 \cos (2q_3) \nonumber \\&-\dfrac{1}{2}\alpha _4 \dot{q}_1^2 \cos (q_3)+\dfrac{1}{2}\alpha _5 \dot{q}_1^2 \sin (q_3)\nonumber \\&+\alpha _7 \sin (q_3)+\alpha _8 \cos (q_3) \end{aligned}$$

(108)

Note that

$$\begin{aligned}&C_i=\cos (q_i), S_i=\sin (q_i), C_{2,i}\nonumber \\&\quad =\cos (2q_i), S_{2,i}=\sin (2q_i) \end{aligned}$$

(109)

Table 1 [6]

As per [6], $\varvec{c}=0.02\varvec{I}$.

Jacobian of the robot when $q_2=0$ is as below: :

$$\begin{aligned} \varvec{J}=\left\{ {\begin{array}{ll} {l_{2} + l_{3} S(q)_{3} } &{} 0 \\ 0 &{} {l_{2} S(q)_{3} } \\ \end{array} } \right\} ; \end{aligned}$$

(110)

Here $l_2$ and $l_3$ are the lengths of 2nd and 3rd link, respectively.

As there is no force sensor attached with the Phantom robot available in the laboratory, a reference disturbance signal $\varvec{d}_i(t)$ is generated. The equivalent joint disturbance torque on joint 1 and joint 3 if the supposed external task force $F = 1$ N on end effector is as below:

$$\begin{aligned} d_{i1}(t)&=J^T \times [F \ 0] =l_2+l_3 \times sin (q_2) \nonumber \\&=0.135+0.135 \times sin (q_2) \end{aligned}$$

(111)

$$\begin{aligned} d_{i3}(t)&= J^T \times [0 \ F] =l_2 \times sin (q_3)\nonumber \\&=0.135 \times sin (q_3) \end{aligned}$$

(112)

Here $d_{i3}$ may be considered as the disturbance due to the external payload ((1 / g) kg) or uncertainty in the mass ($\theta = (1/g)$ kg).

Here the system state vector X is as below:

$$\begin{aligned} \varvec{X}=[q_1,q_3,\omega _1,\omega _3,\eta _1,\eta _3]^T \end{aligned}$$

(113)

Thus, the system model in state space form can be written as:

$$\begin{aligned} \varvec{\dot{X}}&=[\omega _1,\omega _3,\dot{\omega }_1,\dot{\omega }_3, \dot{\eta }_1,\dot{\eta }_3]^T\end{aligned}$$

(114)

$$\begin{aligned}&=\varvec{f(t,\varvec{X})}+\varvec{g}(\varvec{q})\varvec{w} \end{aligned}$$

(115)

$$\begin{aligned}&=\left\{ {\begin{array}{llllll} {\omega _{1} } \\ {\omega _{3} } \\ {[M(q)]^{{ - 1}} \left( { - N\left[ {\begin{array}{ll} {\omega _{1} } \\ {\omega _{3} } \\ \end{array} } \right] + \left[ {\begin{array}{ll} {\tau _{1} } \\ {\tau _{3} } \\ \end{array} } \right] + \left[ {\begin{array}{ll} {d_{{i_{1} }} } \\ {d_{{i_{3} }} } \\ \end{array} } \right] } \right) } \\ 0 \\ 0 \\ \end{array} } \right\} \nonumber \\&\quad \ + \left[ {\begin{array}{llllll} 0 \\ 0 \\ {\left[ {M\left( {q_{1} } \right) ^{{ - 1}} } \right] } \\ \begin{aligned} &{}\left[ {M\left( {q_{3} } \right) ^{{ - 1}} } \right] \\ &{}L\left( {q_{1} } \right) \\ &{}L\left( {q_{3} } \right) \\ \end{aligned} \\ \end{array} } \right] w \end{aligned}$$

(116)

7.2 DEKF

According to Sect. 4, by defining

$$\begin{aligned} \varvec{\widehat{X}}=[\widehat{q}_1,\widehat{q}_3,\widehat{\omega }_1,\widehat{\omega }_3,\widehat{\eta }_1,\widehat{\eta }_3]^T \end{aligned}$$

(117)

the extended active observe is given by (41) and (42) as below:

$$\begin{aligned} \varvec{\dot{\widehat{X}}}&=\varvec{f}(\varvec{t},\varvec{\widehat{X}})+\varvec{PH}^T \varvec{\sigma }_v^{-1} (\varvec{\dot{z}}-\varvec{\widehat{q}}) \end{aligned}$$

(118)

$$\begin{aligned} \varvec{\dot{P}}&= \varvec{\widehat{f}}^{\prime } \varvec{P}+\varvec{P}\varvec{\widehat{f}}^{\prime T}+\varvec{\sigma }_w\varvec{\widehat{g}}\varvec{\widehat{g}} ^T - \varvec{P} \varvec{H}^{T}\varvec{\sigma }_v^{-1} \varvec{H P} \end{aligned}$$

(119)

$\varvec{\sigma }_v$, $\varvec{\sigma }_w$, $\varvec{P}$ and $\varvec{\widehat{g}}$ are defined as (46), (47), (48) and (49), respectively, and for the present measurement linear system

$$\begin{aligned}&\varvec{\dot{z}}=\varvec{ HX} + \varvec{\eta }_X=[q_1, q_3]^T+[\eta _1, \eta _3]^T \end{aligned}$$

(120)

Here

Fig. 2

Omni bundle robot

$$\begin{aligned}&\varvec{H}= \left[ {\begin{array}{llllll} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} } \right] \end{aligned}$$

(121)

$$\begin{aligned}&\varvec{\widehat{f}}^{\prime }=\dfrac{\partial \varvec{f}}{\partial \varvec{\widehat{X}}} = \left[ {\begin{array}{llllll} {\frac{{\partial f_{1} }}{{\partial \hat{q}_{1} }}} &{} \quad {\frac{{\partial f_{1} }}{{\partial \hat{q}_{3} }}} &{} {\frac{{\partial f_{1} }}{{\partial \hat{\omega }_{1} }}} &{} {\frac{{\partial f_{1} }}{{\partial \hat{\omega }_{3} }}} &{} {\frac{{\partial f_{1} }}{{\partial \hat{\eta }_{1} }}} &{} {\frac{{\partial f_{1} }}{{\partial \hat{\eta }_{3} }}} \\ {\frac{{\partial f_{2} }}{{\partial \hat{q}_{1} }}} &{} {\frac{{\partial f_{2} }}{{\partial \hat{q}_{3} }}} &{} {\frac{{\partial f_{2} }}{{\partial \hat{\omega }_{1} }}} &{} {\frac{{\partial f_{2} }}{{\partial \hat{\omega }_{3} }}} &{} {\frac{{\partial f_{2} }}{{\partial \hat{\eta }_{1} }}} &{} {\frac{{\partial f_{2} }}{{\partial \hat{\eta }_{3} }}} \\ {\frac{{\partial f_{3} }}{{\partial \hat{q}_{1} }}} &{} {\frac{{\partial f_{3} }}{{\partial \hat{q}_{3} }}} &{} {\frac{{\partial f_{3} }}{{\partial \hat{\omega }_{1} }}} &{} {\frac{{\partial f_{3} }}{{\partial \hat{\omega }_{3} }}} &{} {\frac{{\partial f_{3} }}{{\partial \hat{\eta }_{1} }}} &{} {\frac{{\partial f_{3} }}{{\partial \hat{\eta }_{3} }}} \\ {\frac{{\partial f_{4} }}{{\partial \hat{q}_{1} }}} &{} {\frac{{\partial f_{4} }}{{\partial \hat{q}_{3} }}} &{} {\frac{{\partial f_{4} }}{{\partial \hat{\omega }_{1} }}} &{} {\frac{{\partial f_{4} }}{{\partial \hat{\omega }_{3} }}} &{} {\frac{{\partial f_{4} }}{{\partial \hat{\eta }_{1} }}} &{} {\frac{{\partial f_{4} }}{{\partial \hat{\eta }_{3} }}} \\ {\frac{{\partial f_{5} }}{{\partial \hat{q}_{1} }}} &{} {\frac{{\partial f_{5} }}{{\partial \hat{q}_{3} }}} &{} {\frac{{\partial f_{5} }}{{\partial \hat{\omega }_{1} }}} &{} {\frac{{\partial f_{5} }}{{\partial \hat{\omega }_{3} }}} &{} {\frac{{\partial f_{5} }}{{\partial \hat{\eta }_{1} }}} &{} {\frac{{\partial f_{5} }}{{\partial \hat{\eta }_{3} }}} \\ {\frac{{\partial f_{6} }}{{\partial \hat{q}_{1} }}} &{} {\frac{{\partial f_{6} }}{{\partial \hat{q}_{3} }}} &{} {\frac{{\partial f_{6} }}{{\partial \hat{\omega }_{1} }}} &{} {\frac{{\partial f_{6} }}{{\partial \hat{\omega }_{3} }}} &{} {\frac{{\partial f_{6} }}{{\partial \hat{\eta }_{1} }}} &{} {\frac{{\partial f_{6} }}{{\partial \hat{\eta }_{3} }}} \\ \end{array} } \right] \end{aligned}$$

(122)

$$\begin{aligned}&= \left[ {\begin{array}{lll} {0^{{2 \times 2}} } &{} {I^{{2 \times 2}} } &{} \quad {0^{{2 \times 2}} } \\ {\frac{{\partial \hat{F}}}{{\partial \hat{q}}} + \frac{{\partial \hat{G}(q)}}{{\partial \hat{q}}}\left( {I^{{2 \times 2}} \otimes \hat{\eta }} \right) } &{} {\frac{{\partial \hat{F}}}{{\partial \hat{\omega }}}} &{} {\hat{G}(q)} \\ {0^{{2 \times 2}} } &{} {0^{{2 \times 2}} } &{} {0^{{2 \times 2}} } \\ \end{array} } \right] \end{aligned}$$

(123)

7.3 Controller

An acceleration controller as shown in Fig. 1 is designed by computed torque method where the disturbances are not taken into account. It means that controller is designed for nominal model of manipulator without considering payload and friction (Fig. 2). The controller is designed as

$$\begin{aligned} \varvec{\widehat{f}_c}&=\varvec{M(\widehat{q})(\ddot{q}_d}+\varvec{K_d(\dot{q}_d}-\varvec{\dot{\widehat{q}})}+\varvec{K_p(q_d}-\varvec{\widehat{q}))} \nonumber \\&+\varvec{N(\widehat{q}}, \varvec{\dot{\widehat{q}})} \end{aligned}$$

(124)

Here $\varvec{K}_p$ and $\varvec{K}_d$ are positive definite gain matrices.

7.3.1 Initial conditions

The measurement of forces requires additional sensors as the Phantom Omni$^{\mathrm{TM}}$ is not equipped with the ability to measure applied loads. Instead of affixing a sensor to measure the input on the robot, an artificial input force was generated. All the initial positions and velocities of the joints are set to zero. The sample period $T_s$ is set equal to 0.01. The controller gain $\varvec{K}_p$ and $\varvec{K}_d$ for both approaches are chosen as $\varvec{K}_p=100I$ or $\varvec{K}_d=20I$. The specific observe gain and initial conditions for DEKF are chosen as follows:

$$\begin{aligned}&cov.(w)=cov.(\tilde{w})=10^{-7} \end{aligned}$$

(125)

$$\begin{aligned}&\varvec{P}_0=diag\left[ 10^{-5},10^{-5},10^{-5},10^{-5},10^{-1},10^{-1}\right] \end{aligned}$$

(126)

$$\begin{aligned}&\varvec{\sigma }_v= \left[ {\begin{array}{ll} {10^{{ - 7}} } &{} 0 \\ 0 &{} {10^{{ - 7}} } \\ \end{array} } \right] \end{aligned}$$

(127)

7.3.2 Experimental results

The following tests have been performed to investigate the performance of the proposed method.

• Test signal I: Signal with white Gaussian measurement noise of standard deviation $10^-7$.

• Test signal II: Signal with white Gaussian measurement noise of standard deviation $10^-5$.

The results of desired, estimated and actual trajectory tracking and disturbance tracking for proposed DEKF under different noise conditions are shown in Figs. 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12.

Figures 3 and 4 show the experimental results for desired trajectory ($\varvec{q}_d$), actual trajectory with noise ($\varvec{q} + noise$) and estimated trajectory ($\widehat{\varvec{q}}$) for joint 1 and joint 3, respectively, and demonstrate the good performance of the proposed technique.

Figure 5 shows that the actual tracking errors ($\varvec{q}-(\varvec{q}_a+noise)$) and estimated tracking errors ($\varvec{q}-\widehat{\varvec{q}}$) are converging after 1 s in the presence of noises.

Table 2 demonstrates that the performance of the proposed DEKF is better as compared to [6] and [20] in the presence of measurement noises (covariance $10^{-7}$).

Figures 6 and 7 show the experimental results for reference disturbance trajectory ($\varvec{d}_i(t)$) and estimated disturbance trajectory ($\widehat{\varvec{d_i}}(t)$) for both joints and demonstrate the good performance of the proposed technique in the presence of measurement noises (covariance $10^{-7}$).

Figure 8 shows that the disturbance tracking errors are converging. Corresponding Table 3 demonstrates that the performance of the proposed DEKF is better compared to [6] and [20] in the presence of measurement noises (covariance $10^{-7}$).

Fig. 3

Tool tracking with cov. of measurement noise $10^{-7}$

Fig. 4

Tool tracking with cov. of measurement noise $10^{-7}$

Fig. 5

Tracking error with cov. of measurement noise $10^{-7}$

Fig. 6

Disturbance tracking with cov. of measurement noise $10^{-7}$

Fig. 7

Disturbance tracking with cov. of measurement noise $10^{-7}$

Fig. 8

Disturbance tracking error with cov. of measurement noise $10^{-7}$

Fig. 9

Tracking error with cov. of measurement noise $10^{-5}$

Fig. 10

Disturbance tracking with cov. of measurement noise $10^{-5}$

Fig. 11

Disturbance tracking with cov. of measurement noise $10^{-5}$

Fig. 12

Disturbance tracking error with cov. of measurement noise $10^{-5}$

Experiments were repeated with increased measurement noise (covariance $10^{-5}$), and the results are shown in Figs. 9, 10, 11 and 12.

Results are mentioned in the last column of Tables 2 and 3. It is demonstrated that now error is more due to an increase in noise, but even then it is better compared to [6] and [20]. The reason is that the conventional disturbance does not filter out all the noise. Moreover, it does not give an accurate estimate of the disturbance unless $\varvec{\dot{d}_i}(t) \ \rightarrow \ \varvec{0}.$

This is because the equation $\varvec{\dot{\widehat{d}}_i}(t)=\varvec{L(q)}\times (\varvec{d}_i(t)-\varvec{\widehat{d}}_i(t) ) \ \implies (\varvec{d}_i(t)-\varvec{{\widehat{d}}_i}(t))\rightarrow \varvec{0}$, if and only if $\varvec{\dot{\widehat{d}}_i}(t) \rightarrow \varvec{0}$, assuming L(q) is bounded and with positive real part for all its eigenvalues and

$$\begin{aligned} \varvec{\dot{d}}_i(t)-\varvec{\dot{\widehat{d}}_i}(t)\rightarrow \varvec{0}, \varvec{\dot{\widehat{d}}_i}(t)\rightarrow \varvec{0}\implies \varvec{\dot{\widehat{d}}_i}(t)\rightarrow \varvec{0}. \end{aligned}$$

It is also noted that if the eigenvalues of L(q) all have (positive) real part, then boundedness of $(\varvec{d}_i(t)-\varvec{{\widehat{d}}_i}(t))$ implies boundedness of $\varvec{{\widehat{d}}_i}(t)$ and hence boundedness of $\varvec{{{d}}_i}(t)$.

For $\varvec{\dot{d}_i}(t)\rightarrow \varvec{0},$ we require zero noise in $\varvec{d}_i(t)$, i.e., $\varvec{d}_i(t)$ be asymptotically differentiable with zero derivative. However, Brownian motion is not differentiable. Hence, its distributional derivative which is white noise is not differentiable. So in order to get rid of extra noise in the disturbance estimate, we once again pass $\varvec{\widehat{d}}_i(t)$ through the EKF, thereby removing the extra noise in it.

Table 2 Experimental study: position tracking RMS error $(\times 10^{-3})$

Table 3 Experimental study: disturbance tracking RMS error $(\times 10^{-3}$)

Remark 4

Comparison with [7]

In [7], Eq. (9a) shows that the rate of change of the external force/disturbance $\varvec{f}_e$ equals zero plus a small noisy term $G.\xi _{fe}$ having known covariance. The EKF has then been applied to estimate this external force whose rate of change is white Gaussian noise. On the other hand, in the present work, we have not assumed such a specific model for the disturbance. In the present work , it is assumed that the disturbance consists of a nonrandom component plus a purely random component and applied the disturbance observer plus an EKF to obtain estimates of the nonrandom component. If we try to apply the method of [7] to our disturbance model, then we would require to know exactly what the nonrandom component is. The DO gets rid of this need. Further, the graph (1c) of [7] shows that whenever there is a sudden change even though slow change in the actual disturbance, the EKF is not instantly able to track this change. It takes a certain settling time for the disturbance estimate to converge to the actual disturbance. On the other hand, the presented work in graph Fig. 6 shows that good disturbance tracking is achieved even for quiet rapidly varying disturbances. The settling time appears in our graph to be smaller. We should, however, acknowledge that the complexity of our algorithm is much more than that of [7] since both EKF and disturbance observer are used.

8 Conclusion

The conventional disturbance observer dynamics has been included in the dynamical state model of the robot by introducing an additional white noise term as the difference between the true disturbance and its first estimate provided by the disturbance observer. Thus, the entire set of state variables is passed through an EKF, resulting in real-time state-cum-disturbance estimate based on noisy measurements. Results are superior as shown in our experimental studies. Using Ito’s formula for Brownian motion, and Gronwall inequality, we have derived an upper bound for the mean square state estimation error. This upper bound depends on the strength of the Lyapunov matrix as well as on the state and measurement noise mean square strength. The proposed technique is applicable to any type of nonlinear dynamical system and for different types of disturbance rejection algorithms.